1 Introduction

Clear evidence of global warming has been found in many areas of the planet. Concerning temperature, there is no question that Earth’s average temperature is increasing (Sánchez-Lugo et al. 2019), and there is a general consensus to conclude the existence of an increasing trend in its mean evolution. Most of the works on climate change focus on the analysis of mean values; however, other relevant aspects are changes in variability and the tails of the distributions. Many works show the interest of analysing whether the occurrence of extremes is affected by climate change (Benestad 2004; Xu and Wu 2019; Saddique et al. 2020). Moreover, consequences of global warming on human health, agriculture, and other fields are often related to the occurrence of increasingly intense extremes (Coumou and Rahmstorf 2012).

Although of great interest, the analysis of non-stationary behaviour in extremes is acknowledged to be difficult due to the scarcity of data. It is also difficult to link it to the mean evolution of temperature since, given the small magnitude of this trend in terms of the variability of the daily temperatures, its effect on the extremes is not evident. Even assuming that global warming affects the occurrence of extremes, there may be considerable climate variability in different areas of the planet, and more research on this topic is needed. Conducting this type of study would be eased by the existence of simple statistical tools, in the same way that studies about the mean temperature have been favoured by the availability of simple non-parametric tests, such as the Mann–Kendall (MK) test (Kendall and Gibbons 1990).

Climate models that do not adequately represent non-stationary behaviours in the extremes can yield important biases in the results, especially in extreme value statistics such as return values or return periods. For example, ensembles of climate-model simulations are often useless since the frequency of extremes is too low to be well sampled by the ensemble (Durran 2020). Statistical models that represent the whole distribution of temperature also tend to badly fit the tails of the distributions. The validation of climate models must include analysing their capability to properly reproduce the most extreme values, but specific statistical tests to this end are not available.

In this context, it is of great interest to develop statistical tools to analyse non-stationary behaviours in the extremes. The annual maxima or the excesses over the threshold are the traditional approaches to study extremes in environmental sciences, and they are still commonly used (Prosdocimi and Kjeldsen 2021). However, a different approach based on the analysis of records is proposed in this work. This approach has some important advantages due to the probabilistic properties of records. In particular, the fact that the distribution of the occurrence of records in an independent identically distributed (i.i.d.) series \((X_t)\) does not depend on the distribution of \(X_t\). This property makes it easier to develop distribution-free statistics, use Monte Carlo methods to implement inference tools, and join the information of the records of different series. Another advantage of using records is that they do not require the information of the whole series. This is common, for example, in sports or in old climate series. Coumou et al. (2013) underlines the interest of this type of analysis and the importance of quantifying how the number of temperature records is changing worldwide and establishing its relationship with global warming.

Different approaches have been used to study the occurrence of temperature records. Redner and Petersen (2007) compared the observed values of records with the expected values under a stationary climate in a descriptive way and using simulations with given distributions. Benestad (2004) compared the observed and expected numbers of records under stationarity in a more formal way using a \(\chi ^2\) test and graphical tools. Another common approach is to assume a Gaussian distribution of the temperature. For example, Newman et al. (2010) used simulations to determine the influence of trends and long-term correlations on record-breaking statistics. Franke et al. (2010) investigated the asymptotic behaviour of the probability of record at a given time, and characterised it under several distributions. Coumou et al. (2013) used the probabilities of records by Franke et al. (2010) assuming a Gaussian distribution to make descriptive comparisons with the observed records in monthly temperatures. Wergen and Krug (2010) and Wergen et al. (2014) also used those probabilities: they found that they were useful only at a monthly scale but found difficulties quantifying the effect of slow changes in daily temperature. Although all these approaches are useful, there is a lack of formal tests to evaluate the effect of climate change on very extreme temperatures.

The aim of this work is to propose a new approach based on the occurrence of records to detect non-stationary behaviours in the extremes of temperature series, as a tool to assess the existence of global warming. To that end, statistical tests to detect those non-stationary behaviours are required, and they have to consider the specific characteristics of climate series, such as serial correlation and seasonal behaviour. The underlying idea is to use the distribution of the occurrence of records in an i.i.d. series \((X_t)\) to study whether the observed records are compatible with that behaviour. First, we consider the type of tests by Foster and Stuart (1954) based on the number of records, but we also propose some statistics based on the likelihood and the score function of the record indicator binary variables. In particular, we obtain the expression of a score-sum statistic based on those variables, and we prove that it is a particular case of the general family of weighted statistics based on the number of records proposed by Diersen and Trenkler (1996). The advantage of this score-sum statistic is that the weights do not have to be empirically selected since they are analytically obtained.

To improve the power of the statistics based on the upper records, Foster and Stuart (1954) considered the four types of records that can be obtained from a series: upper and lower records from the forward and the backward series. To join all the information in one test, they defined statistics based on the number of each type of record. In addition to this type of statistic, we suggest another approach to join the information, to combine the p-values of the tests for each type of record. To that end, and given the dependence between the four types of records, we calculate the covariance between the four statistics, and we apply the Brown method. Graphical tools based on the previous statistics that allow us to detect where the deviation of the null hypothesis appears are also proposed. Finally, an analysis of the size and the power of the tests under different situations is carried out, including common distributions used in the analysis of climate extremes, such as Pareto and Extreme value distributions. All the tools described in this work are implemented in the R-package RecordTest (Castillo-Mateo 2021), publicly available from CRAN.

The outline of the paper is as follows. Section 2 describes the motivating problem and the data. Section 3 presents two families of tests: the first uses the upper records only, and the second joins the information of four types of records. A simulation study to compare the size and power of the proposed tests is shown in Sect. 4. Section 5 describes some graphical tools, and Sect. 6 analyses the effect of global warming on the extremes of daily temperature in Madrid (Spain). Finally, Sect. 7 summarises the main conclusions.

2 Description of the problem

The motivating problem of this work is the analysis of the effect of global warming on the extremes of a daily maximum temperature series, and the series in Madrid (Spain) is used as an example. Our aim is not only to objectively establish the existence of non-stationary behaviour at extreme temperatures but also to identify the time, the periods of the year, and the features where it occurs.

2.1 Data

The series of daily maximum temperatures in Madrid, \(T_x\), recorded in \(^\circ\)C from 01/01/1940 to 31/12/2019 is obtained from the European Climate Assessment & Dataset (Klein Tank et al. 2002); the observations of the 29th of February have been removed. Madrid is located in the centre of the Iberian Peninsula (40.4\(^\circ\) N 3.7\(^\circ\) W) at 667 m a.s.l. and has an inland Mediterranean climate (Köppen Csa). Winters are cold and summers are hot, with average temperatures in January and July of 10 and 31 \(^\circ\)C, respectively.

The temperature series shows seasonal behaviour, and a strong serial correlation is clearly significant. Figure 1 shows the mean evolution of \(T_x\), which has a slight trend, much lower than the variability of the series. Thus, it is not clear if this trend affects the extremes, particularly the occurrence of records. In addition, the trend in the mean temperature differs across the days of the year. This can be observed in Fig. 2 (left), which shows \({\hat{\theta }}_i\), the slope of a linear trend estimated by least-squares in the subseries of each day of the year, standardised in mean and standard deviation. The mean of the slopes is 0.0075, but they move from -0.0025 to 0.025.

Fig. 1
figure 1

Daily maximum temperature and lower (blue) and upper (red) records, Madrid

Full size image

Figure 2 (right) represents the evolution of the annual mean of \(T_x\) and its records. This plot shows that the increase in temperature and the occurrence of records at an annual scale are clearer than those at daily temperatures. This suggests that global warming manifests itself not only by global record-breaking temperatures but also by a higher number of days with extreme temperatures.

In summary, the temperature series present the following characteristics: strong seasonal behaviour, serial correlation, and different trend evolution within the year. It is noteworthy that the strong seasonal behaviour yields not only different distributions of the variables but also a high variability of the entire series. Moreover, to study the effect of global warming on a daily scale, which is essential in climate applications, the increase in the number of warmer days must be considered. In the next section, we suggest an approach to arrange the data that deals with all these problems.

Fig. 2
figure 2

(Left) Slopes of the linear trend in \(T_x\) on each day of the year; red stars mark the days whose series can be considered independent. (Right) Annual mean of \(T_x\) and upper (red) and lower (blue) records, Madrid

Full size image

2.2 Data preparation

A common approach to remove the seasonal behaviour of a daily series with annual seasonality \((X_{1,1},X_{1,2},\ldots ,X_{1,365},X_{2,1},X_{2,2},\ldots ,X_{T,365})\) is to split it into 365 subseries, one for each day of the year (Hirsch et al. 1982),

$$\begin{aligned} \left( \begin{array}{cccc} X_{1,1} &{} X_{1,2} &{} \cdots &{} X_{1,365} \\ X_{2,1} &{} X_{2,2} &{} \cdots &{} X_{2,365} \\ \vdots &{} \vdots &{} &{} \vdots \\ X_{T,1} &{} X_{T,2} &{} \cdots &{} X_{T,365} \end{array} \right) _{T \times 365}. \end{aligned}$$

In this way, each column in the matrix is a series formed by serially uncorrelated observations with no seasonal behaviour. Serial uncorrelatedness is checked by applying Pearson correlation tests to study whether the correlation between the series and the lagged series is null. The resulting 365 series do not have the same distribution, but given that the distribution of the occurrence of records does not depend on the distribution of i.i.d. series, the results can be aggregated.

The series of consecutive days are clearly correlated between them. To obtain a set of uncorrelated series that facilitates the development of inference tools, only a subset of the 365 series available is considered. To that end, the following approach is applied: given that the series at day k is in the subset, the correlation between series k and \(k+1\) is tested; if the correlation is not significant, series \(k+1\) is included in the subset; otherwise, the correlation between series k and \(k+2\) is tested. This step is repeated until a series \(k+i\), which is not significantly correlated with series k, is found. Applying this approach to the temperature series in Madrid, and starting at 1\(^{st}\) January, we obtain \(M=58\) series of length \(T= 80\). The selected days are marked with red stars in Fig. 2 (left). One flaw of this method is that we are not using all the information in the 365 series available but, an interpretation is that it provides the effective sample size of the 365 correlated series. We also note that the set of selected subseries may depend on the method applied to assess the correlation.

In summary, the data preparation approach suggested here provides a set of M uncorrelated series with no seasonal behaviour. The transformation of one series into M subseries will be useful to obtain more evidence from the available data, as we will see in Sect. 3.

2.3 Challenges to analyse the tails of temperature series

To develop tests that are useful to detect non-stationarity in the temperature extremes, we have to consider all the characteristics of daily temperature and how data have to be arranged for analysis. Thus, we need tests with a high power to detect weak deviations of the null hypothesis, such as linear or other types of trends that may be small compared to the variability of the entire series. Second, non-parametric tests with few assumptions would be preferable so that they can be applied in a wide range of situations. Finally, due to the arrangement of the data resulting from splitting the series, the tests must be able to join information from several series, possibly with different distributions.

3 Statistical tests to study i.i.d. series

In this section, we review and propose a set of tests to study non-stationary behaviours in the occurrence of records that satisfy all the requirements described in the previous section. First, we recall some properties of the occurrence of records and the Monte Carlo method used in the development of the tests, and we state the null hypothesis to be analysed. Then, two families of tests are proposed, one based on the upper records and the other that joins the information of four types of records.

3.1 Background

3.1.1 Basic definitions and the classical record model

Given a series of variables \((X_t)\), an observation of \(X_i\) is called an upper record (or a record) if its value exceeds all the previous observations, that is, \(X_i > \max _{ t<i} (X_t)\). Analogously, \(X_i\) is a lower record if \(X_i< \min _{t<i}(X_t)\). Given that \(\min _{t<i} (X_t)=-\max _{t<i} (-X_t)\), lower records can be defined in terms of the upper records of the negative series, and all the properties for the upper records can also be applied to the lower records.

The basic variables that characterise the occurrence of records in a series are the binary variables \(I_t\), with \(t \ge 1\), defined as

$$\begin{aligned} I_t = {\left\{ \begin{array}{ll} 1 &\quad {\text{if }\,X_t\,\text{is a record}} \\ 0& \quad {\text{if }\,X_t \,\text{ is not a record} }. \end{array}\right. } \end{aligned}$$

Variable \(I_1\) is always 1. \(N_t\) is defined as the number of records up to time t, \(N_t = \sum _{i=1}^t I_i\).

The classical record model corresponds to the situation where we have the records of a series of i.i.d. continuous variables \((X_t)_{t \ge 1}\), with F being the common cumulative distribution function. An important result for the classical record model states that the distribution of record times does not depend on F (Arnold et al. 1998). The following properties, which are a consequence of the previous result, characterise in more detail the behaviour of variables \(I_t\) and \(N_t\). They are useful for developing non-parametric tests with asymptotic distributions and easing the implementation of Monte Carlo approaches.

Property 1

Given a sequence of i.i.d. continuous variables \((X_t)\), the sequence of variables \((I_t)\) are mutually independent and each \(I_t\) is \(Bernoulli(p_t)\) distributed with,

$$\begin{aligned} p_t=P(I_t=1)=1/t, \ \ \ t= 1,2, \ldots. \end{aligned}$$

Property 2

Given a series of i.i.d. continuous variables \((X_t)\), the series of the corresponding variables \((N_t)\) converges in distribution to a normal distribution,

$$\begin{aligned} \frac{N_t- \mu _t}{\sigma _t} \overset{D}{\longrightarrow } N(0,1) \end{aligned}$$

where \(\mu _t=E(N_t)=\sum _{i=1}^t \frac{1}{i}\) and \(\sigma ^2_t=V(N_t)=\sum _{i=2}^t \frac{1}{i}\left( 1-\frac{1}{i}\right)\). Consequently, if t is large enough, \(N_t\) can be approximated by a \(N\left( \mu _t, \sigma _t \right)\) distribution.

3.1.2 Monte Carlo method under the classical record model

Property 1 states that, under the hypothesis of i.i.d. series, the sequence of variables \((I_t)\) are mutually independent and \(I_t\) is Bernoulli(1/t) distributed, regardless of the continuous distribution F of \((X_t)\). This makes easy the calculation of pivotal statistics based on \((I_t)\). In addition, the Monte Carlo method is also easy to apply: for any F, a Bernoulli(1/t) distribution can be used to generate samples of the variables \(I_t\) in i.i.d. series. Then, the implementation of the Monte Carlo method is standard: a series of T independent Bernoulli(1/t) variables is generated, and the pivotal statistic \({\mathcal {R}}\) is obtained. Repeating this step B times, a sample of observations of \({\mathcal {R}}\) under the null hypothesis, \({\mathcal {R}}_1, \ldots , {\mathcal {R}}_B\), is obtained, and the p-value is estimated as \({\widehat{pv}}=\sum _{b=1}^B I^{{\mathcal {R}}}_b /B\) where \(I^{{\mathcal {R}}}_b\) is the binary variable linked to \({\mathcal {R}}_b\ge {\mathcal {R}}_o\), and \({\mathcal {R}}_o\) is the observed statistic.

The Monte Carlo method can also be used with statistics that are functions of dependent binary variables, as we will see in Sect. 3.3.2. The only difference from the previous approach is that a series of T independent N(0, 1) variables (or any other continuous distribution) must be simulated first. Then, the corresponding series of the dependent record indicator variables \(I_t\) are obtained and used to calculate the pivotal statistic \({\mathcal {R}}\).

3.1.3 Notation and null hypothesis

In all the tests, we assume that there are M (\(\ge 1\)) mutually independent series of length T available, \((X_{t1}), (X_{t2}), \ldots , (X_{tM})\). These series can result from splitting the original series, or series measured at different spatial points for example. To keep the notation simple, it is assumed that all the series have the same length T, but this restriction is not necessary.

Given \((X_{t1}), (X_{t2}), \ldots , (X_{tM})\), we define the series of binary variables indicating the occurrence of records, \((I_{t1}), (I_{t2}), \ldots , (I_{tM})\), and the series of the number of records \((N_{t1}), (N_{t2}), \ldots , (N_{tM})\). We also define the number of records at time t in the M series, \(S_t= I_{t1}+ I_{t2}+ \ldots + I_{tM}.\)

The null hypothesis of all the proposed tests is

$$\begin{aligned} H_0: p_{tm}= 1/t, \ \ \ \ \ t=1,\ldots , T , \quad m=1, \ldots , M \end{aligned}$$
(1)

with \(p_{tm}=P(I_{tm}=1)\). In the context of global warming, the most general alternative hypothesis is

$$\begin{aligned} H_1: p_{tm}> 1/t, \ \ \ \ \ \text{for at least one } t=1,\ldots , T, \quad m=1, \ldots , M. \end{aligned}$$
(2)

Hypothesis (2) includes the existence of a monotonous positive trend in the mean, a usual assumption of global warming, but it is more general. It also includes other types of non-stationarity, for example, nonmonotonous trends or series with increasing variability.

3.2 Tests based on the upper records

This section presents several approaches to building tests, assuming that only the upper records are available. First, we review and propose some modifications to a family of statistics based on the number of records \(N_t\). Second, a new family of tests based on the likelihood function of the \(I_t\) variables is proposed.

3.2.1 Tests based on \(N_T\)

Property 2 states the normal asymptotic distribution of \(N_T\), the number of records in a series. This property was used by Foster and Stuart (1954) to define the d-statistic based on the difference between the upper and the lower records. Diersen and Trenkler (1996) found that the efficiency of the d-statistic and other similar statistics is improved by splitting a series of lengths T into k series of lengths T/k. Taking these results into account, the number of records statistic is defined as

$$\begin{aligned} {\mathcal {N}}= \sum _{m=1} ^M N_{Tm} = \sum _{t=1}^T \sum _{m=1} ^M I_{tm}= \sum _{t=1}^T S_t. \end{aligned}$$
(3)

\({\mathcal {N}}\) is asymptotically normal under the null hypothesis since \(N_{Tm}\) are independent variables and are asymptotically normal when \(T \rightarrow \infty\) (Property 2). On the other hand, by the central limit theorem, each variable \(S_t\) is also asymptotically normal under the null hypothesis, when \(M\rightarrow \infty\). This means that the normal approximation of \({\mathcal {N}}\) is obtained when any or both M and T increase and that even with moderate values, a good approximation can be expected. The mean and the variance under the null are

$$\begin{aligned} e_{{\mathcal {N}}}=E({\mathcal {N}})=M \sum _{t=1}^T \frac{1}{t} \ \ \ \text{ and } \ \ \ v_{{\mathcal {N}}}=V({\mathcal {N}})=M\sum _{t=2}^T \frac{1}{t} \left( 1-\frac{1}{t}\right) . \end{aligned}$$
(4)

Using the previous distribution under the null, a test based on \({\mathcal {N}}\) is built. The p-value is \(P(Z> ({\mathcal {N}}_0-0.5-e_{{\mathcal {N}}})/\sqrt{v_{{\mathcal {N}}}})\), where \({\mathcal {N}}_0\) is the observed value of \({\mathcal {N}}\) and \(Z\sim N(0,1)\); note that since \({\mathcal {N}}\) takes integer values, a continuity correction has been applied.

It is noteworthy that using Property 1 and the independence of the M series, \(S_t \sim Binomial(M,1/t)\) under the null hypothesis. This means that the exact distribution of \({\mathcal {N}}\) is Poisson-Binomial, that is, the distribution of the sum of T independent Binomial(M, 1/t) variables with \(t=1, \ldots T\). It does not have an explicit expression but it can be computed with numerical methods. However, it is not worth using since we have checked that the exact and asymptotic normal distributions are equivalent even with \(M=1\) and low values of T.

Weighted statistic. Diersen and Trenkler (1996) considered that more powerful statistics could be obtained by weighting the records according to their position in the series. The motivation is that the probability that an observation exceeds the actual record is inversely proportional to the number of previous observations. After an empirical study with different weights, the authors recommended the use of linear weights \(w_t= t-1\). They found that the asymptotic relative efficiency of the weighted tests improved with respect to the unweighted.

In our case, the weighted number of records statistic is

$$\begin{aligned} {\mathcal {N}}^w= \sum _{t=1}^T \sum _{m=1} ^M w_tI_{tm}= \sum _{t=1}^T w_tS_t. \end{aligned}$$
(5)

Under the null hypothesis, \({\mathcal {N}}^w\) is asymptotically normal when \(M \rightarrow \infty\) since under those conditions \(S_t\) are asymptotically normal. However, we do not have normality when \(T \rightarrow \infty\), since \(\sum _{t=1}^T w_t I_{tm}\) is no longer asymptotically normal (Diersen and Trenkler 2001). The mean and the variance are \(E({\mathcal {N}}^w)=M \sum _{t=1}^T w_t\frac{1}{t}\) and \(V({\mathcal {N}}^w)=M\sum _{t=2}^T w_t^2\frac{1}{t} \left( 1-\frac{1}{t}\right)\), and a test analogous to that based on \({\mathcal {N}}\) can be built.

Statistics with estimated variance The previous tests are based on the asymptotic normal distribution of the statistics with the expectation and variance obtained under the null. A disadvantage of these tests is that the expectation increases when the null hypothesis is not true but the variance also changes. This issue could diminish the power of the tests, since the statistic tends to take higher values but possibly with higher variability. We propose an alternative by standardising the statistic

$$\begin{aligned} \tilde{{\mathcal {N}}}^w_S=\frac{{\mathcal {N}}^w-E({\mathcal {N}}^w)}{\sqrt{{\widehat{V}}({\mathcal {N}}^w)}}. \end{aligned}$$

Assuming that \(V(I_{tm})\) is the same in the M series and denoting \(N_T^w=\sum _{t=1}^T w_t I_t\), we have \(V({\mathcal {N}}^w)= M \ V(N_T^w)\). \(V(N_T^w)\) can be estimated by the sample variance of the M values \(N_T^w\) obtained from \((X_{tm})\). Under the null hypothesis, \(\tilde{{\mathcal {N}}}^w_S\) has a Student’s t distribution with \(M-1\) degrees of freedom, and with \(p_t>1/t\), the statistic will tend to be far from 0. This statistic is also more robust to the existence of serial correlation. It is noteworthy that in correlated i.d. series, the probability of record is not 1/t, but the deviations are negligible even with medium correlations.

3.2.2 Tests based on the likelihood function of \(I_t\)

Given M independent series of independent variables \((I_{tm})\), the likelihood is

$$\begin{aligned} {\mathcal {L}}(\mathbf {p_{TM}} \mid \mathbf {I_{TM}})= \prod _{m=1}^M \prod _{t=2}^T p_{tm}^{I_{tm}}(1-p_{tm})^{1-I_{tm}} \end{aligned}$$
(6)

where \(\mathbf {p_{TM}}=(\mathsf {p_{T1}}, \ldots , \mathsf {p_{TM}})\) with \(\mathsf {p_{Tm}}=(p_{1m},\ldots , p_{Tm})\), and analogously \(\mathbf {I_{TM}}=(\mathsf {I_{T1}}, \ldots , \mathsf {I_{TM}})\) with \(\mathsf {I_{Tm}}=(I_{2m},\ldots , I_{Tm})\). Note that for \(t=1\), the corresponding factor is \(1^1(1-1)^{1-1}=1\).

Our aim is to propose tests based on the likelihood for studying the null hypothesis in (1). Standard likelihood tests assume that parameter values in the null hypothesis are interior points of the maintained hypothesis. However, in the one-sided alternative in (2), the parameters lie on the boundary of the parameter space so that standard regularity conditions fail to hold, and usual asymptotic distributions are no longer valid Gourieroux et al. (1982). We propose tests under two different assumptions: first, the probabilities of record at time t of the M series are allowed to be different, and second, it is assumed that they are equal (but possibly different from 1/t). The most common example of the second situation is when the M series have the same distribution.


General test for M independent series

If the M series are not assumed to have the same probabilities of record at time t, there are \(M(T-1)\) different probabilities \(p_{tm}\), without any restriction between them. Then, the number of unknown parameters \(p_{tm}\) is equal to the number of observations, and they cannot be estimated. An approach based on the score function, which only requires the estimation of the parameters under the null, is suggested.


Score-sum statistics. King and Wu (1997) proposed a general method of constructing a locally most mean powerful unbiased score test for one-sided alternatives. It has a small-sample optimal power property when no nuisance parameters are present, as in this case.

The statistic is based on the sum of the score vector, evaluated under \(H_0\). In this case, using the likelihood in (6) and the null hypothesis in (1), the score vector is the \(M(T-1)\) vector, \(\mathbf {q}_0=(q'_{1,0}, \ldots , q'_{M,0})\) where \(q_{m,0}\) is a subvector of length \(T-1\)

$$\begin{aligned} q_{m,0}=\left[ \frac{t}{t-1} (t I_{tm}-1)\right] _{t=2, \ldots , T}. \end{aligned}$$

The information matrix under the null, \({\mathcal {I}}_0\), is a diagonal \(M(T-1) \times M(T-1)\) matrix with diagonal vector \({\mathcal {I}}'_d=({\mathcal {I}}'_{d1}, \ldots , {\mathcal {I}}'_{dM})\), where each subvector is

$$\begin{aligned} {\mathcal {I}}_{dm}=\left[ \frac{t^2}{t-1} \right] _{t=2, \ldots , T}. \end{aligned}$$

Then, we consider the statistic

$$\begin{aligned} {\mathcal {S}}=\frac{\sum _{m=1} ^M q_{m,0}\mathbf {1}_{T-1}}{\sqrt{\mathbf {1}_{M(T-1)}' {\mathcal {I}}_0 \mathbf {1}_{M(T-1)}}}=\frac{\sum _{t=2}^T t(t S_{t}-M)/(t-1) }{\sqrt{M \sum _{t=2}^T t^2/(t-1)}}, \end{aligned}$$
(7)

where \(\mathbf {1}_K\) is the unity vector of length K. Assuming standard regularity conditions but without a requirement that the true parameter is an interior point of the parameter space and using the asymptotic normal distribution of the score vector, the distribution of \({\mathcal {S}}\) under the null is asymptotically N(0, 1) when \(M \rightarrow \infty\). Using this distribution, we can build a test, and the p-value for the alternative in (2) is \(P(Z > {\mathcal {S}}_0)\), where \({\mathcal {S}}_0\) is the observed value of \({\mathcal {S}}\).

It is noteworthy that \({\mathcal {S}}\) is a linear function of variables \(S_t\) and \(t =2, \ldots , T\), with weights proportional to \(t^2/(t-1)\). This means that it is a particular case of the weighted statistic \({\mathcal {N}}^w\), with the advantage that the considered weights are analytically justified.


Tests for M independent series with the same distribution

The tests proposed in this section assume that the probabilities of records in the M series are equal, but they can be different from 1/t. One advantage of this assumption is that the number of unknown parameters, \(T-1\), is lower, and they can be estimated. In addition, it could be expected that in cases where the assumption is true, these tests would be more powerful than \({\mathcal {S}}\). However, the power study in Sect. 4 shows that this is not true. Since the use of these tests is not recommended, they are only briefly described here.

Shapiro (1988) showed that given a vector \(\mathbf {y} \sim N(0,\mathbf {V})\) of dimension n and a convex cone C, the statistic

$$\begin{aligned} {\bar{\chi }}^2=\mathbf {y}^T\mathbf {V}^{-1}\mathbf {y}-\min _{\mathbf {b} \in C} (\mathbf {y}-\mathbf {b})^T \mathbf {V}^{-1}(\mathbf {y}-\mathbf {b}) \end{aligned}$$

is distributed as \({\bar{\chi }}^2(V)\), a mixture of \(\chi ^2\) distributions. If \(\mathbf {V}\) is the identity matrix and \(C=\{\mathbf {b}: \mathbf {b} \ge 0\}\), the weights of the mixture are \(w_i={n \atopwithdelims ()i} 2^{-n} \ \ \text{ for } i=1, \ldots , n\). We apply this approach to \(\mathbf {y}={\mathcal {I}}_0^{-1/2}\mathbf {q}_0\), which under the null has an asymptotic distribution N(0, 1). The resulting statistic is

$$\begin{aligned} {\mathcal {T}}={\sum _{t=2}^T} \frac{(tS_t-M)^2}{M(t-1)} I_{S_t>M/t} \end{aligned}$$
(8)

and using the asymptotic distribution, a test can be built as previously described.

We also derive a statistic based on the likelihood ratio function using the approach by Gourieroux et al. (1982) to deal with one-sided alternatives

$$\begin{aligned} {\mathcal {R}}= -2\sum _{t=2}^T \left( -S_t \log \left( \frac{tS_t}{M}\right) +(M-S_t)\left[ \log \left( \frac{t-1}{t}\right) - I_{S_t<M}\log \left( \frac{M-S_t}{M} \right) \right] \right) I_{S_t >M/t}. \end{aligned}$$

Under the null hypothesis, it has a \({\bar{\chi }}^2({\mathcal {I}}^{-1}_0)\) asymptotic distribution. Since the numerical calculation of this distribution is computationally expensive, a Monte Carlo method is used, but the power performance is worse than \({\mathcal {T}}\).

3.3 Tests joining information from different types of records

When the entire series is available, the power of a test based on records can be improved by joining the information from the binary variables of the occurrence of lower records, denoted \((I_t^{L})\), and the occurrence of records in the backward series. This idea was suggested by Foster and Stuart (1954) and Diersen and Trenkler (1996). The backward series are the series obtained when the order of the terms in the series are reversed so that we start by observing the last term,

$$\begin{aligned} I_{t}^B=\left\{ \begin{array}{ll} 1 &{} \text{ if } X_{T-t+1}> \max _{i>T-t+1} (X_i) \text{ (record) } \\ 0 &{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

Note that t is the index of the position in the backward series, so that \(I_{t}\) and \(I_{t}^{B}\) do not correspond to the same year. As variables \(I_t\), under the null, \(I_{t}^{B} \sim Bernoulli(1/t)\). Analogously, we define the binary variables for the occurrence of its lower records \(I_t^{BL}\).

Two approaches are suggested to join the information from the four types of records. The first step is to obtain the type of statistic described in the previous section for each of the four types of records. Then, we can build a joint statistic, or we can join the resulting p-values using Fisher’s type method. In both cases, it is necessary to characterise the dependence between the individual statistics and the expression of the correlation between them has to be obtained. The approaches presented here can be applied to any of the statistics in Sect. 3.2, but the results are presented for \({\mathcal {S}}\) since, as will be seen in Sect. 4, it is the most powerful statistic.

3.3.1 Correlation between statistics under the null

The statistic \({\mathcal {S}}\) in (7) can be expressed as \({\mathcal {S}}=\sum _{t=2}^T w_t S_t +K\), where K is a constant and

$$\begin{aligned} w_t=\frac{ t^2}{(t-1)\sqrt{M \sum _{t=2}^T t^2/(t-1)}}. \end{aligned}$$

All the calculations are expressed in terms of the weights \(w_t\); in this way, the notation is simpler and the results are easily generalized to other \({\mathcal {N}}^w\) statistics. \({\mathcal {S}}^L\), \({\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\) denote the statistics based on the corresponding lower records or backward series. Note that using these weights, \(V({\mathcal {S}})=V({\mathcal {S}}^L)=V({\mathcal {S}}^{B})=V({\mathcal {S}}^{BL})=1\).

Correlation between \({\mathcal {S}}\) and \({\mathcal {S}}^L\) (\({\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\)). It can be proved that for \(t, t' >1\),

$$\begin{aligned} Cov(I_{tm}, I_{t'm}^{L})=\left\{ \begin{array}{ll} -\frac{1}{t^2} &{} \text{ if } t = t' \\ 0 &{} \text{ if } t \ne t' \end{array} \right. \end{aligned}$$

and \(Cov(S_t, S_{t'}^L)=MCov(I_{tm}, I_{t'm}^{L})\). Using this and \(V({\mathcal {S}})=V({\mathcal {S}}^L)=1\),

$$\begin{aligned} Cor({\mathcal {S}}, {\mathcal {S}}^L) = Cov({\mathcal {S}}, {\mathcal {S}}^L) =- M \sum _{t=2}^T \frac{w_t^2}{t^2}. \end{aligned}$$

Note that the resulting correlation does not depend on M since \(w_t^2\) is multiplied by a factor 1/M. These statistics are asymptotically independent, and even for quite low T, the correlation is negligible, for example, \(-0.044\) for \(T=50\).

Correlation between \({\mathcal {S}}\) and \({\mathcal {S}}^{B}\) (\({\mathcal {S}}^{L}\) and \({\mathcal {S}}^{BL}\)). Using that \(E(I_tI_{t'}^{B})=P(I_t=1, I_{t'}^{B}=1)\), it is proved that for \(t, t' >1\),

$$\begin{aligned} Cov(I_{tm}, I_{t'm}^{B})=\left\{ \begin{array}{ll} 0 &{} \text{ if } t' < T-t+1 \\ \frac{1}{T}-\frac{1}{t}\frac{1}{T-t+1} &{} \text{ if } t' = T-t+1 \\ -\frac{1}{t t'} &{} \text{ if } t' > T-t+1 \end{array} \right. \end{aligned}$$

and the correlation is

$$\begin{aligned} Cor({\mathcal {S}},{\mathcal {S}}^{BL}) =M\sum _{t=2}^{T-1} w_t w_{T-t+1} \left( \frac{1}{T}-\frac{1}{t}\frac{1}{T-t+1} \right) -M\sum _{t=2}^{T} \sum _{t'=T-t+2} ^{T} \frac{w_t w_{t'}}{tt'}. \end{aligned}$$

These statistics show an increasing negative dependence, non-negligible; it is \(-0.667\) for \(T=50\), and it approaches \(-2/3\) with increasing T.

Correlation between \({\mathcal {S}}\) and \({\mathcal {S}}^{BL}\) (\({\mathcal {S}}^{L}\) and \({\mathcal {S}}^{B}\)). It is proved that for \(t,t' >1\),

$$\begin{aligned} Cov(I_{tm}, I_{t'm}^{B})=\left\{ \begin{array}{ll} 0 &{} \text{ if } t' < T-t+1 \\ \frac{1}{t}\left( {T \atopwithdelims ()t}^{-1}-\frac{1}{T-t+1} \right) &{} \text{ if } t' = T-t+1 \\ {T \atopwithdelims ()t}^{-1} \left(\sum _{q=t}^T {q \atopwithdelims ()t} \frac{1}{q(q-T+t'-1)}\right)-\frac{1}{tt'} &{} \text{ if } t' > T-t+1. \end{array} \right. \end{aligned}$$

Then,

$$\begin{aligned} Cor({\mathcal {S}},{\mathcal {S}}^{BL})= & {} M\sum _{t=2}^{T-1} w_t w_{T-t+1} \frac{1}{t}\left( { T \atopwithdelims ()t}^{-1}-\frac{1}{T-t+1} \right) + \\&+M \sum _{t=2}^{T} \sum _{t'=T-t+2} ^{T} w_t w_{t'} \left[ {T \atopwithdelims ()t}^{-1}\sum _{q=t}^T {q \atopwithdelims ()t} \frac{1}{q(q-T+t'-1)}-\frac{1}{tt'} \right] . \nonumber \end{aligned}$$
(9)

A simulation study shows that these statistics are asymptotically independent, and even for low T, the correlation is negligible, smaller than 0.03 for \(T=50\).

3.3.2 Generating a joint statistic

The idea of this approach is to join the information of \({\mathcal {S}}\), \({\mathcal {S}}^{L}\), \({\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\) into one statistic (Foster and Stuart 1954). To that end, it must be taken into consideration that, under the alternative of an increasing trend, \({\mathcal {S}}\) and \({\mathcal {S}}^{BL}\) tend to have high positive values (since \(p_t>1/t\)), while \({\mathcal {S}}^{L}\) and \({\mathcal {S}}^{B}\) have negative values (since in the corresponding series, \(p_t<1/t\)). To unify the behaviour of the four statistics, we will consider linear combinations of \({\mathcal {S}}\); see (7), \(-{\mathcal {S}}^{L}\), \(-{\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\). The simplest option is to join the statistics that are asymptotically independent. For example,

$$\begin{aligned} {\mathcal {S}}2={\mathcal {S}}+{\mathcal {S}}^{BL}, \end{aligned}$$
(10)

whose asymptotic distribution under the null is \(N(0,\sqrt{2})\). We also consider

$$\begin{aligned} {\mathcal {S}}4={\mathcal {S}}- {\mathcal {S}}^{L}-{\mathcal {S}}^{B}+{\mathcal {S}}^{BL}, \end{aligned}$$
(11)

that joins the four statistics available. Its expectation under the null is 0, and its variance is calculated using the covariances in Sect. 3.3.1. \({\mathcal {S}}4\) has an asymptotic normal distribution when \(M\rightarrow \infty\) since it is the sum of M independent variables with the same distribution under the null. The p-value is also calculated using the Monte Carlo method in Sect. 3.1.2. The aim of this double calculation is to check the validity of the asymptotic normal distribution and state the values of M and T where the approximation can be used. The Monte Carlo method can be applied since \({\mathcal {S}}4\) is a pivotal statistic.

One advantage of this approach is its flexibility to define statistics, especially when the Monte Carlo method is used. Depending on the aim of the test, other statistics can be of interest, for example \({\mathcal {S}}-{\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}-{\mathcal {S}}^L\) are a better option to study only the behaviour of the upper and the lower tail of the distribution, respectively. Other definitions have been tried, such as \({\mathcal {S}}-{\mathcal {S}}^{L}\), but the simulation analysis showed that \({\mathcal {S}}4\) is more powerful.

3.3.3 Generating a joint p-value

The idea of this approach is to join the information of P p-values, \(P_i\), from the tests based on \({\mathcal {S}}\), \(-{\mathcal {S}}^{L}\), \(-{\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\) using Fisher’s type method. Standard Fisher’s approach states that the distribution of \({\mathcal {X}}=-2 \sum _{i=1}^P \log P_i\) under the null is \(\chi ^2_{2P}\), but it requires independent statistics. Using this approach, we propose the test \({\mathcal {F}}2\) that joins the p-values from \({\mathcal {S}}\) and \({\mathcal {S}}^{BL}\),

$$\begin{aligned} {\mathcal {F}}2=-2(\log P_{{\mathcal {S}}}+\log P_{{\mathcal {S}}^{BL}}). \end{aligned}$$
(12)

We also propose the test \({\mathcal {B}}4\) that joins the p-values of the four statistics using the modification by Kost and McDermott (2002) of the Brown approach to join dependent p-values. If the statistics are normally distributed, as the score statistics, the distribution of \({\mathcal {X}}\) under the null can be approximated by \(c\chi ^2_f\), where \(c=V({\mathcal {X}})/(2E({\mathcal {X}}))\) and \(f=2E({\mathcal {X}})^2/V({\mathcal {X}})\). The expected value is \(E({\mathcal {X}}) = 2P\) and, using an approximation for the covariance \(Cov(-2\log P_i, -2\log P_j)\),

$$\begin{aligned} V({\mathcal {X}})\approx & {} 4P+ 2\sum _{i=1}^P \sum _{i<j}^P (3.263\rho _{ij}+0.710 \rho _{ij}^2+0.027\rho _{ij}^3) \end{aligned}$$
(13)

where \(\rho _{ij}\) is the correlation between the statistics i and j. Another restriction to join the p-values is that the statistics must have the same behaviour (increase or decrease) under the alternative. To achieve this, the p-values of the statistics \({\mathcal {S}}\), \(-{\mathcal {S}}^{L}\), \(-{\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}\) must be joined,

$$\begin{aligned} {\mathcal {B}}4=-2(\log P_{{\mathcal {S}}}+\log P_{-{\mathcal {S}}^{L}}+\log P_{-{\mathcal {S}}^{B}}+\log P_{{\mathcal {S}}^{BL}}). \end{aligned}$$
(14)

Then, c and f are

$$\begin{aligned} c\approx & {} 1+\frac{1}{4} \sum _{l=1}^3 \left( 3.263\rho _l+0.710\rho _{l}^2+0.027\rho _{l}^3 \right) \\ f= & {} 8/c \end{aligned}$$

where \(\rho _1=\rho _{S,-S^{L}}\), \(\rho _2=\rho _{S,-S^{B}}\) and \(\rho _3=\rho _{S,S^{BL}}\), defined in Sect. 3.3.1.

4 Size and power analysis of the tests

This section summarises the main results from a simulation analysis of the size and power of the tests previously described. First, the tests based on the upper records, and second, the tests that require the entire series are analysed. The estimations are based on 10,000 replications and a significance level \(\alpha =0.05\).

In the size analysis, i.i.d. series with a N(0, 1) distribution are generated without loss of generality since, under the null, the distribution of the statistics does not depend on the distribution of \((X_t)\). The size of the tests is estimated for \(M=1, 4\) and 12 and \(T=25, 50\) and 100. The values of M correspond to common situations: non-split data, quarterly and monthly split data.

The power study focuses on comparing the tests under ‘difficult conditions’ since when M and T are high, or the series has a strong trend, all the statistics have a similar high power that approaches 1. Thus, only small sample sizes, \(M=1, 4, 12\) and \(T=25\) and 50, and small trends are shown in the study. The power is estimated using series with a monotonous positive trend \(\theta\) since they satisfy the alternative hypothesis \(H_1: p_{tm}>1/t\). Although other situations can lead to this alternative, a positive monotonous trend is the most common way of modelling global warming. Then, the series is generated as a trend plus a noise term

$$\begin{aligned} X_{tm}=\theta _t+Y_{tm}. \end{aligned}$$
(15)

Noise terms \(Y_{tm}\) with different distributions are used to generate the series. We consider N(0, 1) and other distributions commonly used in climate and environmental sciences. Series in these fields often require asymmetric and semibounded distributions (defined in \((0, \infty )\)), such as the exponential or gamma distribution for rainfall, generalised Pareto (GP) for peaks over threshold applied to temperature or hydrological series, or generalised extreme value (GEV) for annual maximum temperatures or other maxima. Three kinds of monotonous trends were initially considered: linear, concave and convex trends, \(\theta _t=\theta t\), \(\theta _t=\theta \sqrt{tT}\), and \(\theta _t=\theta t^2/T\), so that all of them increase to \(\theta T\) when \(t \rightarrow T\). Given that very similar results are obtained in the three cases, only the results of the linear trend are shown. Concerning the magnitude, values \(\theta =0.005, 0.01,0.025\) and 0.05 are considered. Note that in the case of N(0, 1) noise, the trend \(\theta\) corresponds to the \(100 \times \theta\) percentage of the standard deviation.

In climate analysis, it is likely that the series used to implement the test do not exhibit the same trend, for example, in different seasons. Consequently, an alternative \(H_{1,\theta _m}\) corresponding to this situation is included in the analysis: it uses M series generated with different trends \(\theta _{tm}=\theta _m t\) in (15); the trend values \(\theta _m\) are randomly generated from a N(0.0075, 0.005) distribution. Values 0.0075 and 0.005 are the mean and standard deviation estimated from the sample of trends obtained in the temperature subseries in Madrid.

4.1 Comparison of the tests using only upper records

A thorough study of all the statistics described in Sect. 3.2 was performed. Only the results for \({\mathcal {N}}\), \({\mathcal {S}}\) and \({\mathcal {T}}\), see (3), (7) and (8) respectively, are summarised here since the statistics that are linear weighted functions of \(S_t\) (\({\mathcal {N}}^w\) and \({\mathcal {S}}\)) yield similar results; the standardised version \(\tilde{{\mathcal {N}}}^w_S\) neither improves the power with uncorrelated series. The performance of \({\mathcal {T}}\) and \({\mathcal {R}}\), the statistics for M series with the same probabilities of record, are also very similar between them.

Size analysis Table 1 summarises the size of the three statistics. It is adequate in all cases, even for \({\mathcal {N}}\) and \({\mathcal {S}}\), which have an asymptotic distribution. The size of \({\mathcal {S}}\), which is asymptotic when \(M \rightarrow \infty\), for \(M=1\) is slightly higher than the nominal value.

Table 1 Estimated size with \(\alpha =0.05\) of the tests based on the upper records
Full size table

Power analysis Figure 3 summarises the power of the tests with series with a N(0, 1) noise term and a trend. The following conclusions are obtained,

  • The comparison of \({\mathcal {N}}\) and \({\mathcal {S}}\) shows that there is a clear increase in the power when weights are used. However, the value of the weights is not so relevant, and we found that the linear weights, obtained empirically, are equivalent, in terms of the power, to the theoretically derived weights from \({\mathcal {S}}\).

  • Unexpectedly, the tests \({\mathcal {T}}\) and \({\mathcal {R}}\), which assume that the M series have the same probabilities of record, have a power lower than \({\mathcal {S}}\) even when that assumption is true.

  • The power of the three tests increases with both T and M with a similar pattern.

  • All the tests have a similar and high power with medium sample size and not very weak trends. However, \({\mathcal {S}}\) provides the best power under difficult conditions: it is over 0.9 for \(\theta =0.05\) with \(M=4\) and \(T=50\) or with \(M=12\) and \(T=25\) and for \(\theta =0.025\), with \(M=12\) and \(T=50\). For \(\theta \le 0.01\) and small sample sizes (\(T\le 50\) and \(M\le 12\)), the tests are not useful since the power is low.

Fig. 3
figure 3

Power analysis of tests based on upper records using series with N(0, 1) noise terms and the same trend

Full size image

Alternative with series with different trends. The pattern of the power with series under the alternative \(H_{1,\theta _m}\) is very similar to that obtained with series with a constant trend, and \({\mathcal {S}}\) provides the best results in all the settings (see Figure S.1 in Supplementary Material). The values are also equivalent; for example, the power of \({\mathcal {S}}\) under \(H_{1,\theta _m}\) with random trends with mean 0.0075 and \(T=50\) and \(M=12\) is 0.3, while its counterpart with series with \(\theta =0.0075\) is 0.29.

Alternative with negative trends. The analysis of negative trends is not of great interest in climate. However, given that the occurrence of upper records in a series with a negative trend is symmetric to the occurrence of lower records with a positive trend, a brief analysis is carried out. The results are shown in Figure S.2 in the Supplementary Material, and the conclusions are analogous, although the power is slightly lower.

Some analyses using distributions other than the normal distribution are carried out, and as in the previous cases, \({\mathcal {S}}\) is the most powerful test. More results with other distributions are presented in the next section. In summary, \({\mathcal {S}}\) is the most powerful test in all the considered situations. Consequently, it is used to build the tests that join the information of different types of records.

4.2 Comparison of the approaches to join different types of records

This section summarises the performance of the approaches proposed to join the information from different types of records. We have a twofold objective: to analyse the improvement of the power when more than one type of record is used and to study whether it is more effective to build a joint statistic or a joint-p-value. Thus, the tests based on \({\mathcal {S}}2\), \({\mathcal {S}}4\), \({\mathcal {F}}2\) and \({\mathcal {B}}4\), see (10), (11), (12), and (14), respectively, are compared in the study.

Size analysis Table 2 summarises the size estimated for the four tests. It is adequate, although the tests based on only two statistics, especially \({\mathcal {F}}2\), tend to yield sizes slightly higher than the nominal value when M is low.

Table 2 Estimated size with \(\alpha =0.05\) of the tests joining different types of records
Full size table

Power analysis  Figure 4 summarises the power of the tests with series with N(0, 1) noise terms and a trend; the statistic \({\mathcal {S}}\), based only on the upper records, is also included for comparison purposes. The following conclusions are obtained.

  • The pattern of the power is quite similar in all settings: the joint tests are clearly more powerful than \({\mathcal {S}}\), but the differences between them are small.

  • Although the improvement resulting from joining information from different types of records is clear, the increase in the power with four types of records over two types is much lower. The power of \({\mathcal {S}}2\) and \({\mathcal {F}}2\) is slightly higher than \({\mathcal {S}}4\) and \({\mathcal {B}}4\) when \(M=1\); however, the power of \({\mathcal {S}}4\) increases faster with M. In any case, the differences are negligible, and given that the sizes of \({\mathcal {S}}4\) and \({\mathcal {B}}4\) are better with low sample sizes and that the computation time is similar, tests joining four types of records should be preferable.

  • Concerning the approach to join the information, both joint statistics and joint p-values have a similar power in these settings. The power of \({\mathcal {B}}4\) is slightly lower with \(M=1\), but the differences are negligible.

  • As expected, the power of the joint tests increases with both M and T, and it is over 0.8 for quite low sample sizes: for \(\theta =0.05\) with \(M=4\) and \(T=25\) or with \(M=1\) and \(T=50\) and for \(\theta =0.025\) with \(M=4\) and \(T=50\). To obtain a power higher than 0.8 for \(\theta =0.01\), a value \(M=20\) is required with \(T=50\), and with \(M=12\), a value \(T=62\). Analogously, for \(\theta =0.005\), a value \(M=80\) is required with \(T=50\), and with \(M=12\), a value \(T=115\).

Fig. 4
figure 4

Power analysis of tests based on four types of records using series with N(0, 1) noise terms and the same trend

Full size image

Alternative with series with different trends. The conclusions about the power with series under the alternative \(H_{1,\theta _m}\) are analogous. Figure 5 shows that the power of the four joint tests is higher than \({\mathcal {S}}\) and similar among them. The value of the power is very similar to that obtained with the M series with the same trend: it is 0.45 with \(T=50\) and \(M=12\), while the counterpart with the M series with trend \(\theta =0.0075\) is 0.43. A power higher than 0.8 is obtained with \(T=50\) and \(M=36\).

Fig. 5
figure 5

Power analysis of tests based on four types of records using series with N(0, 1) noise terms and different trends

Full size image

Alternative with series with non-normal distributions. The power of the tests is now estimated using distributions commonly used in climate and with different types of tails (one-side bounded, heavier and lighter tails than the normal, etc.). Figure 6 summarises the power of tests \({\mathcal {S}}4\) and \({\mathcal {B}}4\) when they are applied to a series with a trend plus the one-side bounded distribution GP with shape parameter \(\xi =-0.1\) (values \(-0.5< \xi <0.5\) are common in climate) and \(\sigma =1\). In this case, the power is higher than that with normal noise terms in all settings. Even for \(\theta =0.005\) the power of \({\mathcal {B}}4\) is higher than 0.9 with \(T=50\) and \(M=4\), and for \(\theta =0.01\) it is also higher with \(T=25\) and \(M=12\). The power with noise terms \(GP(\sigma =1,\xi =0)\), that is exponential distribution, \(GP(\sigma =1,\xi =-0.5)\), and \(GP(\sigma =1,\xi =-1)\), that is uniform distribution (two-side bounded), also have a higher power than the normal, see Figs. S.3, S.4 and S.5 in the Supplementary Material. The effect of the type of tails on the power is confirmed using the GEV distribution; Figs. S.6, S.7 and S.8 summarise the power for shape parameters \(\xi =-0.05, 0,0.5\) and \(\sigma =1\). The results lead to the conclusion that in one or two-side bounded distributions or in distributions with one or two tails lighter than the normal distribution, the power of the record tests is higher. With the GP distribution, the record tests are even more powerful than the MK test to detect trends in the mean. In effect, Fig. 6 shows that the power of MK is lower, specially with weak trends. This means that, in this type of distribution, the detection of trends is most powerful if we focus on the behaviour of the bounded or light tail instead of focusing on the mean evolution. In that case, the power of \({\mathcal {B}}4\) is higher than \({\mathcal {S}}4\).

Fig. 6
figure 6

Power analysis of tests based on four types of records using series with \(GP(\sigma =1, \xi =-0.1)\) noise terms

Full size image

In summary, we conclude that the union of different types of records clearly improves the power of the test. We propose the use of tests based on \({\mathcal {B}}4\) or \({\mathcal {S}}4\), although, with bounded or light tail distributions, \({\mathcal {B}}4\) is slightly more powerful.

5 Graphical tools to detect non-stationary behaviour in records

The use of statistical tests is essential to obtain objective conclusions about the existence of non-stationary behaviours in the extremes. However, the use of graphical tools is also important to explore and characterise the existence of non-stationarity. Basic exploratory plots based on the times of occurrence of the records were used in Sect. 2, but here, we suggest some more elaborated plots together with confidence intervals (CIs). Two types of plots, based on variables \(N_t\) and estimated probabilities \(p_t\), are proposed.

5.1 Plots based on \({\bar{N}}_t\)

Using Property 2 and the approach in Sect. 3.2, it is obtained that the mean number of records up to time t in the M series, \({\bar{N}}_t=\sum _{m=1} ^M N_{tm}/M\), is asymptotically normal (both in M and T) under the null. Using this result, approximate CI for \(\mu _t=E(N_t)\), that is \(\sum _{i=1}^t \frac{1}{i}\) under the null, are

$$\begin{aligned} {\bar{N}}_t \pm z_{1-\alpha /2}\sigma _t/\sqrt{M}, \end{aligned}$$

where \(z_{1-\alpha /2}\) is the \(1-\alpha /2\) percentile of a N(0, 1) distribution. These intervals together with the point estimator \({\bar{N}}_t\), and its expected value under the null can be plotted versus time. The resulting band is not a real confidence band of the values \(\mu _t\) due to the dependence between the different \({\bar{N}}_t\). However, it is useful to observe deviations from stationarity in the evolution of the number of records and to identify the time point from which this deviation is significant. Another advantage is that the four types of records can be displayed in the same plot since their expected behaviour under the null hypothesis is the same.

The same approach can be used to make plots joining the number of lower and upper records in forward and backward series, which are also asymptotically normal when \(M \rightarrow \infty\). It is noteworthy that at each time t, it is necessary to calculate the forward and backward records in the series observed only up to time t, not the number of backward records up to t for the series observed up to time T. If we define \({\bar{D}}_t=\sum _{m=1} ^M D_{tm}/M\) with \(D_{tm}=N_{tm}-N_{tm}^L-N_{tm}^{B,t}+N_{tm}^{BL,t}\), where \(N_{tm}^{B,t}\) denotes the number of records in the backward series \((X_{tm})\) of the first t observations, the expected value of \({\bar{D}}_t\) under the null is 0.

5.2 Plots based on \({\hat{p}}_t\)

The maximum likelihood estimators \({\hat{p}}_t=S_t/M\) satisfy \(E({\hat{p}}_t)= 1/t\) under the null, or equivalently, \(E(t{\hat{p}}_t)= 1\). When \((X_t)\) is not an i.i.d. sequence, there does not exist a general expression for \(p_t\) and \(E(t{\hat{p}}_t)\). Assuming a series with a linear trend \(\theta\), Ballerini and Resnick (1985) proved that \(p_t\) has an asymptotically constant limit \(\lim _{t \rightarrow \infty } p_t= \beta _0\) if the distribution has a finite first moment. The assumption of \(p_t=\beta _0+\beta _1/t\) is compatible with the previous result. Then, it is reasonable to consider as a general alternative, the regression model \(E(t{\hat{p}}_t)=\beta _1 +\beta _0 t\), for \(t>1\), whose expected behaviour under the null is \(\beta _0=0, \beta _1=1\). Consequently, the plot of \(t {\hat{p}}_t\) versus time under the null hypothesis should be a random cloud of points centred around 1, and the fitted regression line should be \(Y=1\).

This model is heteroscedastic under the null, since \(V(t{\hat{p}}_t)=(t-1)/M\). This implies that weighted least square estimators \({\hat{\beta }}_0^W\) and \({\hat{\beta }}_1^W\) with weights equal to the reciprocal of the variance must be used. CI for \(E(t{\hat{p}}_t)\) can be obtained using that \(t{\hat{p}}_t=tS_t/M\) and \(S_t \sim Binomial(M,1/t)\) under the null hypothesis.

6 Analysing the effect of global warming in records of daily temperature

The tests and graphical tools described in the previous sections are used to analyse the effect of global warming in the records of the series presented in Sect. 2, the daily temperature series in Madrid.

Joint analysis of the tails. Given that the complete series is available, and that our first aim is to study the existence of non-stationary behaviour in the tails of daily temperature, we start by applying tests based on different types of records. Taking into account the power study, the tests \({\mathcal {S}}4\) and \({\mathcal {B}}4\) are the most appropriate to assess \(H_0: p_{tm}=1/t\). The resulting p-values, 2.4e–07 and 7.0e–08, lead to conclude at any usual significance level that the probability of record is higher than expected in an i.i.d. series. This means that there is evidence of non-stationarity in the occurrence of records due to an increasing trend.

Figure 7 shows the mean number of records \({\bar{D}}_t\) versus time, and it allows us to identify when the previous non-stationary behaviour appears and to characterise it over time. It is significant from 1980, and the value of the statistic shows an increasing trend from 2000.

Fig. 7
figure 7

Mean number of records \({\bar{D}}_t\) versus time and 90% CI under i.i.d. series, Madrid

Full size image

Separate analysis of the upper and lower tails. We are also interested in studying whether this non-stationary behaviour appears in both tails of the distribution or only in one of them, and whether it is equally strong in both cases. To separately analyse the behaviour of the upper and lower records, we use the statistics \({\mathcal {S}}-{\mathcal {S}}^{B}\) and \({\mathcal {S}}^{BL}-{\mathcal {S}}^L\) respectively. The resulting p-values are 1.5e–06 and 0.006 so that although there is evidence of non-stationary behaviour in both tails, it is clearer in the upper records.

To study in more detail where non-stationary behaviour appears, Fig. 8 (left) shows the time plot of the number of upper and lower records in the forward and backward series, \({\bar{N}}_t\), \({\bar{N}}_t^{L}\), \({\bar{N}}_t^{B}\) and \({\bar{N}}_t^{BL}\), respectively. The forward series show weaker deviations of the i.i.d. hypothesis, and non-stationarity only appears in the upper records from 1990, becoming slightly significant from 2015. On the other hand, the backward series shows clearer deviations. This behaviour reveals that the effects of global warming are stronger in the upper tail and in the last years of the observed period. After five years of observations, the cumulative number of upper records in the backward series is significantly lower than expected in an i.i.d. series, and the consequences affect the rest of the period. However, from 1940 to 1980, the evolution of the number of records is quite parallel to the behaviour expected in a stationary series. The number of lower records is significant mainly due to the observed values between 1970 and 80, higher than expected in an i.i.d. series.

Figure 8 (right) shows the estimated probabilities of upper record \(t{\hat{p}}_t\) for each year t together with the regression line and the confidence band. In an i.i.d. series, the slope of the regression line should be zero, while a positive slope is observed. In addition, many of the estimated probabilities are outside the CI from approximately 1980. This plot allows us to identify the specific years where the probability of record is much higher than expected. Similar plots can be made for the other types of records, and they confirm the previous conclusions.

Fig. 8
figure 8

Cumulative number of upper and lower records in the forward and backward series, \({\bar{N}}_t\), \({\bar{N}}_t^{L}\), \({\bar{N}}_t^{B}\) and \({\bar{N}}_t^{BL}\), and 90% CI under i.i.d. series (left). Regression line of \(t{\hat{p}}_t\) versus time and 90% CI under i.i.d. series (right), Madrid

Full size image

Analysis of the tails by season. To study whether non-stationary behaviour differs across the seasons of the year and to identify the periods where it is stronger, the previous tests are applied separately to the four seasons of the year: winter (DJF), spring (MAM), summer (JJA) and autumn (SON).

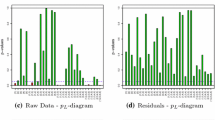
The resulting p-values are summarised in Table 3. If both tails are analysed jointly, using \({\mathcal {S}}4\) and \({\mathcal {B}}4\), the non-stationary behaviour is significant in all seasons except spring. However, if we study only the upper records, \({\mathcal {S}}-{\mathcal {S}}^B\), the evidence of trend is strong in summer and autumn but weak in winter. Concerning the lower records, \({\mathcal {S}}^{BL}-{\mathcal {S}}^L\), there is evidence of a decrease only in winter. No changes in lower records may be caused by an increase in variability. Figure 9 shows the cumulative number of each type of record by season. The plot in spring suggests that although the joint tests are non-significant, the number of upper backward records is significantly lower than expected, but it is compensated by the higher than expected lower forward number of records. Analysing two separate periods, it is concluded that it is due to a decreasing trend before 1970 and an increasing trend afterwards.

Table 3 p-values of the record tests by season
Full size table
Fig. 9
figure 9

Cumulative number of upper and lower records in the forward and backward series, \({\bar{N}}_t\), \({\bar{N}}_t^{L}\), \({\bar{N}}_t^{B}\) and \({\bar{N}}_t^{BL}\), and 90% CI under i.i.d series, by season, Madrid

Full size image

7 Conclusions

In the context of global warming, it is clear the interest of analysing the existence of non-stationary behaviour in the tails of a series, particularly in its records. This work reviews and proposes several statistical tests and complementary tools to detect this type of behaviour in climate series, using the properties of the occurrence of records in series i.i.d. More precisely, the tests assess the null hypothesis \(H_0: p_{tm}=1/t\) versus the alternative \(H_1: p_{tm}>1/t\). From a methodological point of view, the following conclusions are obtained.

  • The approach proposed to arrange the data, based on splitting the series, solves two usual problems of climate series: seasonal behaviour and serial correlation. There is another advantage of having M subseries of records available. Joining their information into one statistic, we are taking into account the increase of both, the magnitude of the highest temperatures and the number of warm days, maintaining a daily scale.

  • A family of six tests based on the upper records is introduced. \({\mathcal {N}}\) is based on the number of records, and \({\mathcal {N}}^w\) and \(\tilde{{\mathcal {N}}}^w_S\) are weighted versions of the previous one, the latter using an estimation of the variance. \({\mathcal {S}}\) is based on the likelihood function. Assuming that the M series have the same distribution, two statistics based on the score and the likelihood ratio, \({\mathcal {T}}\) and \({\mathcal {R}}\), are considered. Asymptotic distributions are obtained for most of the previous statistics. In addition, the Monte Carlo method can be used to estimate the p-value in all cases, since they are pivotal statistics. This method is used to check the validity of the asymptotic distributions, revealing that they are valid even for \(M=1\) and low values of T. We conclude that statistics that are linear weighted combinations of variables \(S_t\), \({\mathcal {N}}^w\) and \({\mathcal {S}}\) are the most powerful. Statistic \({\mathcal {S}}\), whose weights are analytically justified, is proposed as the best test based on the upper records.

  • The second family of tests aims to join the information of different types of records: the upper and the lower records of the forward and the backward series. Four statistics, \({\mathcal {S}}2\), \({\mathcal {S}}4\) (based on joint statistics) and \({\mathcal {F}} 2\) and \({\mathcal {B}}4\) (based on joint p-values), that include two or four types of records are considered. A power study shows that the union of two or more types of records clearly improves the power of \({\mathcal {S}}\) based only on the upper records. The union of the statistics or the p-values yields tests with similar power. The power of the joint tests with series with N(0, 1) noise terms is high even with small sample sizes and weak trends. The power is higher for series with noise terms with one or two-side bounded distributions or distributions with one or two light tails, such as GP and GEV, which are often used in climate analysis. For GP distributions, even for a weak trend \(\theta =0.005\), the power of \({\mathcal {B}}4\) is higher than 0.9 with \(T=50\) and \(M=4\). The approaches suggested to join the information of different types of records are very flexible. They allow us to define other statistics to study specific features, such as non-stationary behaviour only in the upper or lower tail, or give more weight to a particular type of record.

  • From the considered record tests, \({\mathcal {B}}4\) and \({\mathcal {S}}4\) are the most powerful. These tests have important advantages that make them specifically useful in the analysis of global warming. First, they have a high power to detect weak trends. They are non-parametric and require few assumptions, so that they can be applied in a wide range of situations. Moreover, they are able to join the information of M independent series, a property that is useful to deal with seasonal behaviour. This property can also be useful in the spatial analysis since it allows us to join series from different locations and to obtain global conclusions over the area of interest. The tests are complemented with graphical tools that aim to characterise where and when non-stationary behaviour occurs. Finally, all the tests and tools are easy to apply and are implemented in the R-package RecordTest.

The proposed inference tools are used to analyse the effect of global warming on the extremes of the daily temperature in Madrid. It is concluded that there is strong evidence of non-stationary behaviour in the tails of the distribution that affects the occurrence of records. This non-stationary behaviour is statistically significant from approximately 1980, and it increases from 2000. The behaviour is stronger in the upper tail, especially in the last years of the observed period. Moreover, the behaviour among seasons is not homogenous: it is significant in all seasons except spring. If we focus on the behaviour in the lower tail, it is only significant in winter.

The tests and graphical tools in this work are useful to analyse the extremes of observed series. In addition, they can also be used as tools for validating the capability to reproduce the most extreme values of climate models representing the entire distribution of a variable. This feature is important since a misrepresentation of the tails can yield important biases in their conclusions. The only condition to apply the tools for validating the tails of a climate model is that the model can generate trajectories of the variable under study. Examples include Earth system models (Wehner et al. 2020) and statistical models fitted by Bayesian or other parametric methods. The general idea is to apply the tools to the trajectories generated by the climate model and to the observed series and to compare the results. The tests can also be used in other fields where the study of records is important including hydrology, finance, etc.