Abstract
Understanding the structure of precipitation and its separation into stratiform and convective components is still today one of the important and interesting challenges for the scientific community. Despite this interest and the advances made in this field, the classification of rainfall into convective and stratiform components is still today not trivial. This study applies a novel criterion based on a clustering approach to analyze a high temporal resolution precipitation dataset collected for the period 2002–2018 over the Sicily (Italy). Starting from the rainfall events obtained from this dataset, the developed methodology makes it possible to classify the rainfall events into four different classes, which can be related to the convective and stratiform components of the events on the basis of their hyetograph shapes and average intensities. The results show that the occurrence of stratiform events is always much higher than the convective ones, especially in the winter and spring seasons, while from the summer to the mid-autumn the rainfall depth due to convective events results to be higher than that due to the stratiform events. Moreover, the comparison with a more widely accepted separation methodology demonstrates the physical consistency of the proposed methodology.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Natural hazards, such as floods and landslides, have direct impacts on planning and management of earth resources and human health risks. Such events have gone up to unprecedented levels in several parts of the globe during the last decades (Andersson-Sköld and Nyberg 2016; Gariano and Guzzetti 2016; Hoeppe 2016; Messeri et al. 2015). This increase has been often attributed to urbanization, forest management practices, and especially to the increasing occurrence of climatic extremes (e.g., heavy rainfall) (Arnone et al. 2018; Shukla et al. 2019; Pumo et al. 2017).
Since most of the floods and landslides depend on precipitation characteristics, such as intensity and duration, which depend, in turn, on the mechanisms that generate precipitation, understanding the genesis of the precipitation could be helpful to predict the occurrence of such natural disasters. In this context, one of the most interesting research topics focuses on understanding the genesis of precipitation and its separation into stratiform and convective components.
Convective and stratiform components are mainly related to the physical mechanisms responsible for the generation of the precipitation. Convective precipitation, which is usually characterized by rapid processes starting at the base of the cloud, is characterized by high intensities and short durations. On the contrary, the mechanisms that generate a stratiform rainfall are usually slower and start at the top of the cloud, where precipitation particles that fall to the ground as raindrops have their early history as ice particles (Houze 1997). This type of precipitation is related to horizontal growth conditions with greater areas of influences, higher durations and lower rainfall intensities as compared to the convective precipitation (Houze 2014).
Despite advances made in recent years, the distinction between convective and stratiform precipitation is not trivial and still today a challenge (Cipolla et al. 2020). The first attempts to deal with such a separation began during the 80’s and were mostly concerned with the spatial aspect of the problem, i.e., to distinguish between convective and stratiform regions. Based on a previous work by Houze (1973), starting from the data registered on 10 December 1978 over the South China Sea from the Winter Monsoon Experiment (WMONEX), Churchill and Houze (1984) identified convective regions on the assumption of a couple of rules. The first rule classified as the core of a convective structure all those cells that had a peak rainfall rate at least twice of the rainfall rate of the surrounding 400 km\(^2\) area. For each core so identified, the surrounded 150 km\(^2\) of area was considered convective. In addition, regardless of the previous criterion, a second rule classified as convective any area with a rainfall intensity higher than or equal to 20 mm/h. Garand (1986), before, and Adler and Negri (1988), later, proposed the first methods based on the use of infrared and/or visible data for distinguishing between convective and stratiform precipitation. They developed a technique capable to locate all local minima in an array of infrared data, which are assumed to be the cores of a convective structure. Chong and Hauser (1989) made a distinction based on a comparison between water budget in both convective and stratiform regions of a squall line. Starting from the method developed by Churchill and Houze (1984), during 90’s many other authors tried to develop a methodology to distinguish between convective and stratiform regions (Caniaux et al. 1995; Steiner et al. 1995; Tao et al. 1993, 2000; Xu 1995). Moving forwards to the 2000s, some authors used weather radar imagery (Rigo and Llasat 2004), or remote sensing techniques, which use the brightness temperature (Anagnostou and Kummerow 1997; Hong et al. 1999), to address the spatial issue of convective regions identification.
One of the most debated issues of all the previous approaches is related to the appropriateness to separate rainfall regions into only two classes (Houze 1997; Kyselỳ et al. 2016). With this regard, as early as 90’s Mapes and Houze (1993) classified one-third of the radar echoes observed in their study as “intermediary” because their structure appeared to be neither obviously convective nor obviously stratiform. Looking at the radar observations in the Tropics, Houze (1997) noticed many radar echoes composed of convective rain alongside stratiform precipitation. These observations, which seemed to be paradoxical, were generated in the older convection regions, where the humid air moved slower upwards than in the younger convective regions.
At the start of the 2000s, as well as with the spatial issue, many authors began to develop methods aimed to distinguish between convective and stratiform rainfall events based on the ground observations. Starting from the rainfall collected in between 1927 and 1981 close to the city of Barcelona, Spain, Llasat (2001) proposed a classification into convective and stratiform events on the base of an event-based parameter \(\beta\). The author proposed to classify as convective all of those rainfall events in which \(\beta\) was greater than zero according to the following criteria: \(\beta =0\) non-convective, \(0<\beta \le 0.3\) slightly convective, \(0.3<\beta \le 0.8\) moderately convective, \(0.8<\beta \le 1.0\) strongly convective. Tremblay (2005), using a year of precipitation collected over the entire world from the World Meteorological Organization (WMO), revealed that the relationship between cumulative precipitation and rain intensity over different periods (e.g., 6 h, 1 day, 1 week, and 1 year) can be well described by a negative exponential law. The same author identified a threshold equal to 20 mm/6 h for partitioning precipitation into convective and stratiform components. In general, after the work of Tremblay (2005), the practice of a critical intensity threshold to discriminate between the two components has been widely adopted (Cipolla et al. 2020; Feloni et al. 2019; Ruiz-Leo et al. 2013), since its simplicity and since it requires only time series of precipitation.
Also in this case, the number of classes to correctly separate rainfall events is one of the most important issues to deal with. With this respect, Rulfová and Kyselỳ (2013) introduced a class of mixed/unresolved events to take into account all those events that, according to their algorithm, could be classified as both convective and stratiform events or do not have a sufficiently clear distinction between those two classes. In order to overcome the potential drawbacks due to the application of a fixed critical intensity threshold, based on the use of a couple of reanalysis indexes, Cipolla et al. (2020) developed a fuzzy framework to distinguish between annual maxima precipitation mainly related to convective and stratiform components. This framework involved the use of a third class (mixed/unresolved) to include all those annual maxima precipitation not belonging to the convective or stratiform classes.
This study tries to address questions regarding the clustering of precipitation on the base of its mechanism of generation. Since one of the weaknesses of the above-mentioned studies is the use of an arbitrary intensity threshold to classify the precipitation, which makes their results affected by a certain degree of subjectivity, one of the most important question to be addressed is whether it is possible to find a more objective method capable to classify precipitation based on its characteristics (e.g., intensity, duration, total rainfall events, etc.).
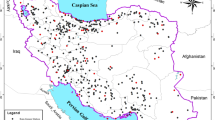
In order to answer this question, a novel criterion based on a PCA-based clustering approach (denoted FPCAC), which is a variant of a k-means algorithm based on the principal component rotation of data, has been here used. The study area is the Sicily (Italy), which is the largest island of Mediterranean Sea. With this regard, the precipitation dataset of the regional agency SIAS (Servizio Informativo Agrometeorologico Siciliano—Agro-meteorological Information Service of Sicily) has been used because of its high temporal resolution, quality, and availability of up-to-date data. Specifically, data from forty rain gauge stations spread over the entire island have been collected for the period 2002–2018 and with a temporal resolution of 10 minutes.
The paper is organized as follows: Sect. 2 introduces the case study (i.e., Sicily) together with the SIAS database, while Sect. 3 describes the FPCAC algorithm. Section 4 shows the application of FPCAC algorithm to the case study and its results. Finally, in Sect. 5, a conclusive discussion about the methodology developed and future developments is provided.
2 Case study and dataset
Sicily (Italy) is the largest island of the Mediterranean Sea and covers an area of about 25,000 km\(^2\) (Fig. 1). The elevation varies a lot across the island, ranging from 0 m a.s.l. (above sea level) along the coast to more than 3,000 m a.s.l. at the volcano Etna. Sicily has always experimented a high spatial and temporal variability of precipitation. With regard to the spatial variability, Di Piazza et al. (2011) obtained a spatial distribution of the mean annual precipitation (MAP) over Sicily with higher MAP recorded in the northeast of the region, where it reaches about 1,900 mm, and lower MAP in the southeastern part of the island (about 360 mm). The overall mean of the MAP over the island is about 700 mm. With reference to the temporal variability, instead, rainfall is mostly concentrated in winter, whilst the summer season (i.e., June, July, and August) is usually almost rainless. In regard to air temperature, Sicily is a region with a temperate-mesothermal (Mediterranean) climate with an average temperature in the hottest months greater than 22 \(^\circ\)C. The highest values of mean annual temperature (MAT) are around 18.5\(\div\)19.5 \(^\circ\)C along the coast, while the lowest values (10.5\(\div\)13.5 \(^\circ\)C) characterize higher elevations, with a minimum above the Etna volcano. The warmest areas are the flat lands in the North West nearby the city of Trapani and in the South East close to the city of Catania, both with a relevant agricultural tradition.
In the last years, many areas of the island have been experiencing some very intense rainfall events, usually concentrated between the end of summer and the autumn, that cause urban floods and flash floods with consequent economic damages and, sometimes, human lives losses. This is demonstrated by some extreme events that occurred in Sicily in the last few years, some of which are reported here. On 1 October 2015, the city of Catania was flooded because of a heavy rainfall with an intensity peak of about 65 mm/h. In November 2016, 160 mm of rainfall fell in three hours flooded the city of Licata, causing several damages to people and some economic activities. On 8 August 2018, in only twenty minutes, a precipitation of about 75 mm/h intensity endangered the city of Palermo, flooding most of the old city and several other districts of the city. Between 1 and 3 November 2018, a series of some heavy rainfalls in the east and south parts of the island caused thirteen fatalities and more than two hundred and thirty displaced people. The total rainfall reached in three days about one third of the mean annual precipitation of some of the affected areas. On 15 July 2020, the city of Palermo was affected by the heavier rainfall event ever recorded in Palermo during the last ninety years. The precipitation, with a maximum hourly intensity of 87.8 mm/h and a cumulative rainfall of 134 mm fell in about two hours, caused the flooding of the ring road of Palermo and its underpasses with several damage to cars and inconveniences to people. In one of the underpasses the water level reached a depth of about 5 m. Moreover, the precipitation caused some flash floods from some small hilly and mountain catchments around the city that carried out mud and debris from the slopes of hills and mountains to the city.
Dataset from the regional agency SIAS (Servizio Informativo Agrometeorologico Siciliano—Agro-meteorological Information Service of Sicily) has been here used because of its high temporal resolution, quality, and availability of up-to-date data. The entire database includes about one hundred rain gauge stations distributed over the entire island that collect the data with a temporal resolution of 10 min. Specifically, because of the internal policy of SIAS and the long time required for acquiring the entire dataset, only data from forty rain gauge stations homogeneously distributed over the entire island have been collected for the period 2002–2018 (Fig. 1). The 10-min rainfall data of these stations have been used to identify the rainfall events to be analyzed with the proposed method. The partition of the rainfall dataset into events has been accomplished by fixing the duration of the minimum inter-event time, which is the time that follows (or precedes) a rainfall event, equal to 1 h and discarding all those events with a total rainfall depth lower than 1 mm (Dunkerley 2008). The number of events extracted from the database is equal to 65,829 with a duration ranging from a minimum of 10 minutes to a maximum of about 45 hours and a mean intensity ranging between 0.25 and 85.2 mm/h. Empirical cumulative distribution functions (ECDFs) of duration and mean rainfall intensity, obtained as the ratio between the event total rainfall depth and the event duration, are reported in Fig. 2a, b, respectively. As it is possible to observe, the 90% of the total events last less than about 5 minutes (Fig. 2a) and have a mean intensity of about 6 mm/h (Fig. 2b) with a median value of 1.67 h for the duration (Fig. 2a) and 2 mm/h for the intensity (Fig. 2b).
3 Methodology: the functional PCA-based clustering approach
When data are observed as functions of time we refer to as functional data, referring to n pairs \((t_i, y_i)\) where \(y_i\) is the value of an observable variable x at time \(t_i\), and focusing on a set of functions defined on [0, T], such that:
Therefore, assuming that a functional for replication i can be represented by a set of discrete measured values \(y_{i1},y_{i2}, \cdots , y_{in}\) the first task is to convert these values to a function \(x_i\) with values \(x_i(t)\) computable for any t, called functional objects. In the functional context the counterparts of variable values are functional values \(x_l(t), l=1,\cdots , p\) and the discrete index j in the multivariate context is now replaced by the continuous index s, such that:
with \(\beta (s)\) weight functions and \(\varOmega _s\) a subset of \({\mathbb {R}}\). In the literature, the term harmonic is used to refer to principal component of variation in curves analysis (see Ramsay (2004) for more details). The clustering approach based on a functional principal component analysis (FPCA), hereafter denoted as FPCAC algorithm, was proposed by Adelfio et al. (2011). The FPCAC looks for clusters of functions according to the direction of largest variance, outlined by the FPCA scores, assigning events to the best cluster based on a proper distance measure. It introduces a variation of the trimmed k-means robust curve clustering (RCC) algorithm (Garca-Escudero and Gordaliza 2005), which is a kind of robust version of k-means methodology through a trimming procedure. In few words, given a q-dimensional data sample \({\varvec{X}}_1, {\varvec{X}}_2, \ldots , {\varvec{X}}_n\) with \({\varvec{X}}_i= X_{i1}, \ldots , X_{iq}\), and fixed the number of clusters k, the trimmed k-means clustering algorithm looks for the k centers \(C_1, ..., C_k\) that are solution of the minimization problem:
where \(\alpha\) is the trimming size, Y is the set of subsets of \({\varvec{X}}_1, \cdots , {\varvec{X}}_n\) containing \([n(1-\alpha )]\) data points, and [x] is the integer part of x. This method allocates each non-trimmed observation to the cluster identified by its closest center, \(C_j\), dealing with possible outliers by the given proportion of observations to be discarded, \(\alpha\). This curve clustering procedure is based on a least-squares fit to cubic B-spline q-dimensional functions bases, applying the trimmed k-means clustering as Eq. (3) on the resulting coefficients, taking the advantages of very fast computation and great flexibility of the B-splines. The starting point of the FPCAC is to find a linear approximation of each curve (named harmonic) obtained through a finite p-dimensional vector of coefficients (i.e., the FPCA scores, denoted in Sect. 4.1 by the vector \({\varvec{H}}\)). Once fixed the number of clusters k, a modified version of the trimmed k-means algorithm, which considers the matrix of the FPCA scores instead of the coefficients of a linear fitting to B-spline bases, is used. As shown in Adelfio et al. (2011), the proposed approach has the advantage of an immediate use of PCA for functional data avoiding some objective choices related to spline fitting as in RCC. Simulations and applications suggested also the well behavior of the FPCAC algorithm, both in terms of stable and easily interpretable results. The selection of the best number of clusters k was performed with the silhouette method Rousseeuw (1987), since it is a measure widely used and accepted (by the scientific community) to establish the goodness of a cluster choice. The method returns a value ranging between \(-\,1\) and \(+\,1\) that is a measure of how similar an object is to its own cluster compared to other clusters; the higher the silhouette value, the better the match to the own cluster. For each observation, i, in the cluster, \(C_i\), the silhouette method defines a width, s(i), as:
where a(i) is the average dissimilarity between i and all the other points of the cluster to which i belongs, b(i) is the dissimilarity between i and its “neighbor” cluster, and \(|C_i|\) is the cluster dimension. Finally, since the mean s(i) over all the data of the entire dataset is a measure of how appropriately the data have been clustered, averaging the mean silhouette width of each cluster, the optimal number of clusters was selected by choosing the k with the maximum value of the mean s(i) (Kaufman and Rousseeuw 1990). Recently, in Sottile and Adelfio (2019), the authors applied the proposed methodology in different applied context, e.g., they applied and compared the FPCAC method to cluster several characteristics of earthquake events recorded in Italy by the INGV (National Institute of Geophysics and Volcanology) seismic network and to group the estimated quantile regression coefficients of some determinants of a measure of lung function in order to highlight similiraties of effects.
4 Results
4.1 Clustering of rainfall data by FPCAC
This section presents an application of the FPCAC algorithm to the rainfall data of the SIAS dataset. The main aim of the analysis is to separate the observed rainfall into stratiform and convective components, trying to characterize the rainfall events using the hyetograph shape and its mean intensity. The analysis has been carried out for each station and is based on the rainfall event profile, which is defined as the cumulative rainfall depth derived at the event scale and normalized by the event duration. The rainfall event profiles have been transformed into continuous series using a third-degree B-spline interpolation. The continuous rainfall profile extraction process is represented in Fig. 3 with reference to the event \(\#\)1398 extracted from the rainfall dataset collected at the Palermo rain gauge. Fig. 3a shows a subset of the Palermo rain gauge (i.e., from 12:00 of 30 November 2013 to 12:00 of 1 December 2013) including the event \(\#\)1398 (red bars in Fig. 3a, b) and some events that precede and follow it. The event extends from the 18:00 of 30 November 2013 to the 17:10 of 1 December 2013 (Fig. 3b) and is characterized by a duration of 11 hours and 10 minutes, a total rainfall depth of 107.4 mm (cyan curve in Fig. 3b), and a mean rainfall intensity of 9.48 mm/h. Figure 3c shows the rainfall event profile and its third-degree B-spline interpolation (i.e., the continuous rainfall profile). The FPCAC algorithm was applied to the continuous rainfall profile to classify the rainfall events for each station. The number of classes k that provides the best grouping of events, as already discussed in Sect. 3, was obtained with the silhouette method; an initial interval of possible values of k was fixed in the range 2–8. For almost all the stations, the most suitable value of k provided by the silhouette method resulted always equal to 4. Just 7 out of 40 stations showed similar silhouette values for \(k=3\) and \(k=4\) making the choice irrelevant. Therefore, in order to better compare results among the stations, the number of optimal clusters was fixed at \(k=4\). As an example, Fig. 4 shows the results of the silhouette method when applied to the rain gauges of Palermo and Catania, since they are the two largest cities of the island and representative of the climate in the western and eastern regions of the island, respectively. Figure 5 summarizes the results of the FPCAC algorithm when applied to the rain gauges of Palermo (upper panels) and Catania (lower panels); panels a) and c) show the scatterplot of the first two harmonic scores (i.e., \(H_1\) and \(H_2\)) for individual curves, while panels b) and d) represent the average continuous rain profiles for each cluster and the shaded areas are the confidence bands based on 10\(^\text {th}\) and 90\(^\text {th}\) percentiles of all profiles within each cluster. As it is possible to notice in Fig. 5, in both cases, the four clusters are well distinguished both in terms of scores and average continuous rain profiles. More in details, looking at the scatterplots of scores, it is possible to observe that the cluster C4 (blue diamonds) is characterized by negative values of the first component \(H_1\) (which explain about 90% of the variance of all eigenfunctions), while \(H_1\) score for the clusters C2 (red dots) and C3 (green triangles) range between 0 and 10; cluster C1 (black squares), finally, has higher scores (greater than 10) of \(H_1\). Under the same duration, in panels b) and d) of Fig. 5 it is possible to observe as the rainfall profile for the cluster C1 (black curve), on average, is always higher than that for the cluster C2 (red curve), which is always higher than that for the cluster C3 (green curve), which is always higher than that for the cluster C4 (blue curve). Moreover, as the duration increases, the rainfall depth grows faster moving from C4 to C1. This mainly depends on the different intensities that characterize the four clusters and can be explained looking at the Fig. 6, which shows the boxplots for the four clusters when the results for all the forty rain gauges are considered; more in details, Fig. 6a, b, and c show the overall mean rainfall intensity, rainfall depth, and event duration, respectively. As it is possible to observe in Fig. 6a, the intensities for the C1 (black boxplot) can be much higher than those of the other clusters and especially the C4 (blue boxplot). As expected, observing the Fig. 6, it is possible to notice that the four clusters are well distinguished both in terms of rainfall intensity (Fig. 6a) and rainfall depth (Fig. 6b) while, with regard to the event duration (Fig. 6c), clusters C1 and C2 show similar median values but different interquartile ranges (higher in C2). More in details, moving from C1 to C4 both the rainfall intensity and depth noticeable decrease, while the rainfall duration slightly increases. Moreover, keeping in mind that a rainfall event can be due to a mixture of both convective and stratiform mechanisms (Houze 1997), as already discussed in the Introduction, it was possible to relate each one of the four clusters to one of the precipitation generation mechanisms (i.e., convective and stratiform) following an approach similar to that of Llasat (2001) that has been discussed in the Introduction. More in details, the cluster C4 (blue boxplots in Fig. 6), which is characterized by the lowest average intensity, is related to the stratiform precipitation, since they are usually characterized by lower intensities (Feloni et al. 2019; Llasat 2001; Ruiz-Leo et al. 2013; Tremblay 2005). Conversely, the cluster C1 (black boxplots in Fig. 6 is related to the definitely convective precipitation, since it is characterized by higher average intensities, which are usually associated to a convective precipitation. Finally, the intermediate clusters (i.e., C2 and C3—red and green boxplots in Fig. 6, respectively) are associated to precipitations whose convective mechanism becomes less and less important (Houze 1997); C2 and C3 are renamed as possibly convective and slightly convective, respectively.
Methodology to go from the 10 min rainfall SIAS database to the rain event profile; a subset of rainfall collected at the Palermo rain gauge; b event \(\#\)1398 extracted from the dataset of the Palermo rain gauge; c rainfall event profile and third-degree B-spline interpolation (continuous rainfall profile)
Results of FPCAC algorithm, applied to the rain gauges of Palermo (upper panels) and Catania (lower panels). Panels a and c show the scatterplot of the first two harmonic scores (\(H_1\) vs \(H_2\)) for individual curves, while panels b and d represent the average rain profiles for each cluster; the shaded areas are the confidence bands based on 10th and 90th percentiles of all profiles within each cluster
In the light of these results, looking back at the continuous event rainfall profiles shown in the right panels of Fig. 5, it is possible to notice that, as the duration increases, the rainfall depth grows faster for the convective precipitations than for the stratiform one; this is more and more evident as greater is the convective character of the cluster (i.e., definitely convective cluster).
Table 1 reports, for each station and for the four clusters, the summary statistics (i.e., mean value, standard deviation, minimum and maximum values) for the mean rainfall intensity, total rainfall depth, and event duration. From the observation of Table 1 and Fig. 6, it is possible to find out that the convective events (i.e., slightly, possibly, and definitely convective) are characterized by higher intensities (Fig. 6a) and rainfall depths (Fig. 6b) than the stratiform ones; also their variability (i.e., interquartile ranges in Fig. 6a, b, respectively) is higher than that of the stratiform events.
With the aim to highlight any differences of the mechanisms that generate precipitation in different periods of the year, a seasonal analysis has been carried out as well. Figure 7 shows the monthly occurrences of the four different clusters (i.e., the percentages of events for a given class and a given month over the total number of events in that month) and the monthly percentage of total rainfall depth belonging to the four clusters (stratiform in blue, slightly convective in green, possibly convective in red, and definitely convective in black) for the investigated period. As it is possible to observe in Fig. 7a, the occurrence of stratiform events is always much higher than the remaining ones, especially in the winter and spring seasons (i.e., from December to May), where a percentage between about the 70% (i.e., May) and about the 80% (December to April) of events is due to the stratiform component. If one looks at the aggregation of slightly, possibly, and definitely convective clusters into a unique class, it is possible to notice that during the summer the number of convective events is higher than that of stratiform events, especially from July to September, where the convective component is between about the 55% and the 60% of the total events.
Distributions of a the monthly percentages of the number of events for a given class and a given month over the total number of events in that month and b the total rainfall depth regarding all the clusters for the investigated period, obtained joining the results of the FPCAC algorithm applied to all the forty rain gauges
Looking at the percentages relative to the rainfall depth in Fig. 7b, instead, the stratiform rainfalls are still the main contributing factors during the winter period (i.e., from December to May) with a percentage ranging between about the 55% (i.e., May and December) and about the 65% (i.e., January to March) of the total rainfall depth. On the contrary, from June to November, the rainfall depth due to convective events is much higher than that due to stratiform events, with a percentage ranging between about the 60% in November and about the 85% in August of the total rainfall depth. In this period, differently than the case of rainfall events shown in Fig 7a, the contribute of stratiform events is lower than that of each convective class (e.g., July and August) or of some of them (e.g., September and October). Such a result matches reality, since during the summer and the early autumn the air masses moving over the hot water of the Mediterranean Sea become warmer and humid thus generating local convection processes that are the cause of very heavy rainfalls (Dayan et al. 2015), usually referred to as convective precipitations, over the island.
4.2 Comparison of results with the Llasat (2001) methodology
The physical consistency of the proposed methodology is evaluated by comparing its results with those obtained with the methodology proposed by Llasat (2001). It is important to underline that such a methodology, which is here used as a benchmark, although is widely accepted in the literature, is itself a model; consequently, the results of this comparison should be interpreted in a context of model versus model analysis.
The Llasat (2001) methodology introduces an event-based parameter \(\beta\) that takes into account the ratio between the rainfall exceeding a fixed mean intensity threshold, T, and the total rainfall depth of the event. This parameter can be assessed as:
where N is the total number of integration time steps (here equal to ten minutes) into which the rainfall event is subdivided, \(I_i\) is the rainfall intensity in the i-th time step expressed in mm/h and \(\theta (I_i-T)\) is the Heaviside function equal to 1 when \(I_i > T\) and 0 when \(I_i\le T\). As already made explicit in the Introduction, the author proposed to use the parameter \(\beta\) to characterize the rainfall events into four classes according to their greater or lesser convective character.
With regard to the choice of the threshold, T, here a value of 20 mm/h has been set by extrapolating the values used by Llasat (2001). Starting from this value, for each station of the SIAS dataset, the percentage of events falling within the four classes above-mentioned was evaluated. Since the definition of the two intermediate classes provided by Llasat (2001) is rather subjective, it has been decided to merge the three classes referred to the convective events (i.e., slightly, possibly, and definitely convective) into a single convective class and compare the two methodologies considering only two classes, i.e., the convective and the stratiform.
In order to assess the goodness of agreement between the two methodologies, firstly the observed agreement index (OA) between them, i.e., the number of all correct predictions divided by the total number of the dataset, is used. Figure 8a shows the ECDF of the OA between the proposed and the Llasat (2001) methodologies. As it is possible to notice in Fig. 8a, for all the stations, the OA between the two methodologies in classifying events as stratiform and convective is higher than 0.75, with about the 60% of the stations characterized by an OA greater than 0.8 and a peak of about 0.91 for the station of Enna.
ECDFs of a OA and b Cohen’s kappa coefficient between the proposed methodology and the Llasat (2001) methodology. In panel b shaded area highlights moderate agreement between the two methodologies
Secondly, in order to take into account the possibility of an eventual agreement occurring by chance, a further comparison between the results was made by means of the Cohen’s kappa coefficient (Cohen 1960), which is a statistic usually used to measure inter- and intra-rater reliability for categorical variables. Since Cohen’s kappa considers the possibility of the agreement occurring by chance, it results more robust than the simple percent agreement. The coefficient measures the agreement between two raters as:
where \(p_o\) is the relative observed agreement among raters (i.e., accuracy), and \(p_e\) is the hypothetical probability of chance agreement.
Figure 8b shows the ECDF for the Cohen’s kappa coefficient for the two-class classification. As it is possible to notice from the Fig. 8b, all the values of Cohen’s kappa are between 0.3 and 0.7, thus indicating an agreement between the two methodologies. More than 60% of stations have a Cohen’s kappa-index greater than 0.4, thus indicating a moderate-substantial agreement between the two methodologies, while about the 35% of stations fall in the fair agreement class (0.21 \(<\textit{kappa}<\) 0.40) according to Landis and Koch (1977) classification.
In order to verify that the agreement between the two methods was not accidental, the p-value with a level of significance, \(\alpha =0.05\), is calculated. For all the rain gauge stations, the p-value is always smaller than \(\alpha\) and, therefore, the null hypothesis that “observed agreement is accidental” is always rejected.
It is worth pointing out here that, while the Llasat (2001) methodology requires the definition of some a-priori classes, the methodology here proposed, being based on a cluster analysis that exploits the shape of the hyetographs (i.e., cumulative rainfall depth, mean intensity), does not require any a-priori classes definition.
5 Conclusions
This study presents a new method to classify rainfall events identifying the generation mechanisms and separating the stratiform from the convective component. The method, which is a statistical approach based on a PCA-based clustering approach, was applied to a precipitation dataset collected for the Sicily in between 2002 and 2018 by the SIAS.
Despite advances made in recent years, the distinction between convective and stratiform precipitation based on ground observations is not trivial and still today a challenge (Cipolla et al. 2020). Although many authors in the last years have faced this issue, they always developed methodologies based on the use of an arbitrary threshold to separate the two components (Feloni et al. 2019; Llasat 2001; Ruiz-Leo et al. 2013; Tremblay 2005).
As compared to these methodologies, one of the main novelties of this study is that the criterion presented does not use a threshold to distinguish between convective and stratiform components, since it uses a cluster analysis based on the similarity of the shape of rainfall events and their characteristics (e.g., total rainfall depth and mean intensity), which makes it an approach more objective than the previous ones.
Despite the different approach, the comparison with a more conventional and widely accepted approach (Llasat 2001) showed the physical consistency of the proposed approach. Starting from the same threshold proposed by Llasat (2001) to classify precipitation into stratiform and convective components, the results showed a good agreement with those obtained with the Llasat (2001) approach.
As already said, the methodology here proposed has been applied to only forty of the about one hundred rain gauge stations distributed over the entire island. A further investigation, then, will concern the application of the methodology to the entire and updated SIAS database, in order to find eventual regional patterns that show the presence of a more marked convective component as compared to the stratiform one or vice versa. Starting from this result, a new further application will concern the investigation of the effects due to some aspects, such as morphology (e.g., interaction of steep orography on the coasts with winds carrying humid air masses from the Mediterranean Sea, especially in between the end of the summer and the autumn, may be the cause convective events), that could affect the characteristics of precipitation.
Moreover, since the methodology of Llasat (2001) here used as benchmark is still a model, as already highlighted, in order to have a more physical-based comparison of results, a future development will concern the use of reanalysis data, which consider some meteorological variables that can be good descriptors of the occurrence of stratiform/convective precipitations.
Availability of data and material
Data are available on request due to privacy or other restrictions.
References
Adelfio G, Chiodi M, D’Alessandro A, Luzio D (2011) Fpca algorithm for waveform clustering. J Commun Comput 8(6):494–502
Adler R, Negri A (1988) A satellite infrared technique to estimate tropical convective and stratiform rainfall. J Appl Meteorol 27(1):30–51
Anagnostou E, Kummerow C (1997) Stratiform and convective classification of rainfall using ssm/i 85-ghz brightness temperature observations. J Atmos Oceanic Technol 14(3):570–575
Andersson-Sköld Y, Nyberg L (2016) Effective and sustainable flood and landslide risk reduction measures: an investigation of two assessment frameworks. Int J Disaster Risk Sci 7(4):374–392
Arnone E, Pumo D, Francipane A, La Loggia G, Noto L (2018) The role of urban growth, climate change, and their interplay in altering runoff extremes. Hydrol Process 32(12):1755–1770
Caniaux G, Lafore J, Redelsperger J (1995) A numerical study of the stratiform region of a fast-moving squall line. Part II: relationship between mass, pressure, and momentum fields. J Atmos Sci 52(3):331–352
Chong M, Hauser D (1989) A tropical squall line observed during the COPT 81 experiment in west Africa Part II: water budget. Mon Weather Rev 117(4):728–744
Churchill D, Houze R (1984) Development and structure of winter monsoon cloud clusters on 10 December 1978. J Atmos Sci 41(6):933–960
Cipolla G, Francipane A, Noto L (2020) Classification of extreme rainfall for a Mediterranean region by means of atmospheric circulation patterns and reanalysis data. Water Resour Manag 34(10):3219–3235
Cohen J (1960) A coefficient of agreement for nominal scales. Educ Psychol Meas 20(1):37–46
Dayan U, Nissen K, Ulbrich U (2015) Atmospheric conditions inducing extreme precipitation over the eastern and Western Mediterranean. Nat Hazards Earth Syst Sci 3(11):
Di Piazza A, Conti F, Noto L, Viola F, La Loggia G (2011) Comparative analysis of different techniques for spatial interpolation of rainfall data to create a serially complete monthly time series of precipitation for Sicily. Italy. Int J Appl Earth Obs 13(3):396–408
Feloni E, Baltas E, Nastos P, Matsangouras I (2019) Implementation and evaluation of a convective/stratiform precipitation scheme in Attica region, Greece. Atmos Res 220:109–119
Garand L (1986) Automated recognition of oceanic cloud patterns and its application to remote sensing of meteorological parameters. PhDT
Garca-Escudero L, Gordaliza A (2005) A proposal for robust curves clustering. J Classif 22:185–201
Gariano S, Guzzetti F (2016) Landslides in a changing climate. Earth-Sci Rev 162:227–252
Hoeppe P (2016) Trends in weather related disasters-consequences for insurers and society. Weather Clim Extremes 11:70–79
Hong Y, Kummerow C, Olson W (1999) Separation of convective and stratiform precipitation using microwave brightness temperature. J Appl Meteorol 38(8):1195–1213
Houze R (1973) A climatological study of vertical transports by cumulus-scale convection. J Atmos Sci 30(6):1112–1123
Houze R (1997) Stratiform precipitation in regions of convection: A meteorological paradox? Bull Am Meteorol Soc 78(10):2179–2196
Houze R (2014) Cloud Dynamics. Academic Press, Cambridge
Kaufman L, Rousseeuw P (1990) Partitioning around medoids (program PAM). Wiley, Hoboken, pp 68–125
Kyselỳ J, Rulfová Z, Farda A, Hanel M (2016) Convective and Stratiform precipitation characteristics in an ensemble of regional climate model simulations. Clim Dyn 46(1–2):227–243
Landis J, Koch G (1977) The measurement of observer agreement for categorical data. Biometrics 33(1):159–174
Llasat M (2001) An objective classification of rainfall events on the basis of their convective features: application to rainfall intensity in the northeast of spain. Int J Climatol 21(11):1385–1400
Mapes B, Houze R (1993) Cloud clusters and superclusters over the oceanic warm pool. Mon Weather Rev 121(5):1398–1416
Messeri A, Morabito M, Messeri G, Brandani G, Petralli M, Natali F, Grifoni D, Crisci A, Gensini G, Orlandini S (2015) Weather-related flood and landslide damage: a risk index for Italian Regions. PLoS ONE 10(12):e0144468
Pumo D, Arnone E, Francipane A, Caracciolo D, Noto L (2017) Potential implications of climate change and urbanization on watershed hydrology. J Hydrol 554:80–99
Ramsay J (2004) Functional data analysis. Encyclopedia of Statistical Sciences 4
Rigo T, Llasat M (2004) A methodology for the classification of convective structures using meteorological radar: application to heavy rainfall events on the mediterranean coast of the iberian peninsula. Nat Hazards Earth Syst Sci 4:59–68
Rousseeuw P (1987) Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20:53–65
Ruiz-Leo A, Hernández E, Queralt S, Maqueda G (2013) Convective and stratiform precipitation trends in the spanish mediterranean coast. Atmos Res 119:46–55
Rulfová Z, Kyselỳ J (2013) Disaggregating convective and stratiform precipitation from station weather data. Atmos Res 134:100–115
Shukla P, Skea J, Calvo Buendia E, Masson-Delmotte V, Pörtner H, Roberts D, Zhai P, Slade R, Connors S, Van Diemen R (2019) IPCC, 2019: Climate Change and Land: an IPCC special report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems. Intergovernmental Panel on Climate Change (IPCC)
Sottile G, Adelfio G (2019) Clusters of effects curves in quantile regression models. Comput Stat 34(2):551–569
Steiner M, Houze R, Yuter S (1995) Climatological characterization of three-dimensional storm structure from operational radar and rain gauge data. J Appl Meteorol 34(9):1978–2007
Tao W, Simpson J, Sui C, Ferrier B, Lang S, Scala J, Chou M, Pickering K (1993) Heating, moisture, and water budgets of tropical and midlatitude squall lines: comparisons and sensitivity to longwave radiation. J Atmos Sci 50(5):673–690
Tao W, Lang S, Simpson J, Olson W, Johnson D, Ferrier B, Kummerow C, Adler R (2000) Vertical profiles of latent heat release and their retrieval for Toga Coare convective systems using a cloud resolving model, ssm/i, and ship-borne radar data. J Meteorol Soc Jpn 78(4):333–355
Tremblay A (2005) The stratiform and convective components of surface precipitation. J Atmos Sci 62(5):1513–1528
Xu K (1995) Partitioning mass, heat, and moisture budgets of explicitly simulated cumulus ensembles into convective and stratiform components. J Atmos Sci 52(5):551–573
Funding
Open access funding provided by Università degli Studi di Palermo within the CRUI-CARE Agreement. The authors received no specific funding for this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Code availability
The FPCAC clustering algorithm is publicly available from “The Comprehensive R Archive Network” and included in the R package clustEff at the webpage https://CRAN.R-project.org/package=clustEff.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sottile, G., Francipane, A., Adelfio, G. et al. A PCA-based clustering algorithm for the identification of stratiform and convective precipitation at the event scale: an application to the sub-hourly precipitation of Sicily, Italy. Stoch Environ Res Risk Assess 36, 2303–2317 (2022). https://doi.org/10.1007/s00477-021-02028-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-021-02028-7