Analysis of spherical monofractal and multifractal random fields

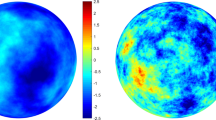
Abstract

The Rényi function plays an important role in the analysis of multifractal random fields. For random fields on the sphere, there are three models in the literature where the Rényi function is known explicitly. The theoretical part of the article presents multifractal random fields on the sphere and develops specific models where the Rényi function can be computed explicitly. For all considered models explicit expressions of their multifractal spectrum are obtained. Properties of the models and dependencies of their characteristics on parameters are investigated. Then these results are applied to the Cosmic Microwave Background Radiation data collected from the Planck mission. The main statistical model used to describe these data in the literature is isotropic Gaussian fields. We present numerical multifractality studies and methodology based on simulating random fields, computing the Rényi function and the multifractal spectrum for different scenarios and actual CMB data. The obtained results can also find numerous potential applications for other geoscience, environmental and directional data.

Appendix A Proofs

Proof

(Theorem 5.1) By Remark 4.1, from the weak convergence of the measures $\mu _k$ to $\mu$ and the assumption of exponential boundedness of the covariance function of the mother field, it follows that

$$\begin{aligned} E \mu ^q_k(B^3) \rightarrow E\mu ^q(B^3), \quad k \rightarrow \infty . \end{aligned}$$

By the Lyapunov’s inequality, see (Loéve 1977, p.162),

$$\begin{aligned} E \mu ^q_k(B^3) \le (E\mu ^2_k(B^3))^{q/2}, \, \text {for} \, q \in [1,2]. \end{aligned}$$

Therefore, to guarantee $E\mu ^q(B^3)< +\infty , \, q \in [1,2],$ it is sufficient to provide such b and $\sigma ^2_{\varLambda }$ that

$$\begin{aligned} \sup _{k\in {\mathbb {N}}} E\mu ^2_k(B^3) < +\infty . \end{aligned}$$

By (4), the non-negativity of $\varLambda _{k}(y)$ and independence of $\varLambda ^{(i)}$ it holds

$$\begin{aligned} E\mu ^2_k(B^3)= & {} E \int _{B^3} \int _{B^3} \varLambda _k(y)\varLambda _k(\tilde{y})d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} E[\varLambda _k(y)\varLambda _k(\tilde{y})]d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} E \prod ^k_{i=0} \varLambda ^{(i)}(yb^i) \varLambda ^{(i)}(\tilde{y}b^i) d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} \prod ^k_{i=0} E\varLambda ^{(i)}(yb^i) \varLambda ^{(i)}(\tilde{y}b^i) d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} \prod ^k_{i=0} \biggl (E(\varLambda ^{(i)}(yb^{i})-1)(\varLambda ^{(i)}(\tilde{y}b^i)-1)\\&+E \varLambda ^{(i)}(yb^i) + E \varLambda ^{(i)}(\tilde{y}b^i) -1 \biggl ) d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} \prod ^k_{i=0}(Cov(\varLambda (yb^i), \varLambda (\tilde{y}b^i))+1)d\tilde{y}dy\\= & {} \int _{B^3} \int _{B^3} \prod ^k_{i=0}\left( 1+ \sigma ^2_{\varLambda }\rho _{\varLambda }(\Vert y- \tilde{y}\Vert b^i)\right) d\tilde{y}dy\\\le & {} \int _{B^3} \int _{B^3} \prod ^k_{i=0}(1+ \sigma ^2_{\varLambda }C e^{-\gamma \Vert y- \tilde{y}\Vert b^i})d\tilde{y}dy\\\le & {} \int _{B^3} \int _{B^3} \prod ^{\infty }_{i=0}(1+ \sigma ^2_{\varLambda }C e^{-\gamma \Vert y- \tilde{y}\Vert b^i})d\tilde{y}dy. \end{aligned}$$

From the inequality $1+a \le e^a$, it follows that

$$\begin{aligned} E\mu ^2_k(B^3) \le \int _{B^3} \int _{B^3} \prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-\gamma \Vert y- \tilde{y}\Vert b^i}}d\tilde{y}dy. \end{aligned}$$

Introducing the new variables $z=y$, $\tilde{z} = y-\tilde{y},$ one obtains

$$\begin{aligned} E\mu ^2_k(B^3) \le \int _{B^3} dz\int _{B^3-B^3} \prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-\gamma \Vert \tilde{z}\Vert b^i}}d\tilde{z}, \end{aligned}$$

where $B^3-B^3 = \{\tilde{z}: \tilde{z}=y-\tilde{y}, \, y, \, \tilde{y} \in B^3 \}.$

Hence, by using the spherical change of variables,

$$\begin{aligned}&E\mu ^2_k(B^3) \le |B^3|\int ^{diam(B^3)}_{0} {r}^{2}\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-\gamma {r} b^i}}dr\\&\quad = \frac{|B^3|}{\gamma ^{3}}\int ^{\gamma diam(B^3)}_{0} {r}^{2}\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-r b^i}}d\tau . \end{aligned}$$

As the exponent $e^{\sigma ^2_{\varLambda }C e^{-r b^i}}$ is a decreasing function of r, selecting $n(r) = \max (0, -[\log _b(r)]),$ $r>0,$ we obtain

$$\begin{aligned}&\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-r b^i}} \le \prod ^{n(r)-1}_{i=0} e^{\sigma ^2_{\varLambda }C e^{-r b^i}}\prod ^{\infty }_{i=n(r)} e^{\sigma ^2_{\varLambda }C e^{-r b^i}}\\&\quad \le e^{\sigma ^2_{\varLambda }C n(r)}\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-r b^{i+n(r)}}} \le e^{\sigma ^2_{\varLambda }C n(r)}\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-b^i}}. \end{aligned}$$

Notice that

$$\begin{aligned}&\prod ^{\infty }_{i=0} e^{\sigma ^2_{\varLambda }C e^{-b^i}} = e^{\sigma ^2_{\varLambda }C \sum ^{\infty }_{i=0} e^{-b^i}} \le e^{\sigma ^2_{\varLambda }C \sum ^{\infty }_{i=0} e^{-(1+(b-1)^i)}}\\&\quad = e^{\frac{\sigma ^2_{\varLambda }C}{e}\sum ^{\infty }_{i=0} {e^{-(b-1)}}^i} = e^{{\frac{\sigma ^2_{\varLambda }C}{e}} {\frac{1}{1-e^{-(b-1)}}}} < +\infty . \end{aligned}$$

Therefore,

$$\begin{aligned} E\mu ^2_k(B^3)&\le {\frac{|B^3|}{\gamma ^{3}}}{e^{\frac{\sigma ^2_{\varLambda }C}{e(1-e^{-(b-1)})}}} \int ^{\gamma diam(B^3)}_{0} z^{2} e^{\sigma ^2_{\varLambda }C n(z)}dz \\&= {\frac{|B^3|}{\gamma ^{3}}}{e^{\frac{\sigma ^2_{\varLambda }C}{e(1-e^{-(b-1)})}}} \int ^{\gamma diam(B^3)}_{0} z^{2}\max \left( 1, \, z^{-\frac{\sigma ^2_{\varLambda }}{\ln {(b)}}}\right) dz. \end{aligned}$$

The integral is finite if $2-\frac{\sigma ^2_{\varLambda }C}{\ln {(b)}} > -1,$   i.e. $b> e^{\frac{\sigma ^2_{\varLambda }C}{3}}$. $\square$

Proof

(Theorem 7.1) By the definition of Model 4 it follows that

$$\begin{aligned}&E \varLambda (x) = E(Y^2(x)) = \rho _Y(0) =1, \\&\sigma ^2_{\varLambda } = Var \varLambda (x) = E(Y^4(x))-1 =2,\\&Cov(\varLambda (x), \varLambda (y)) = E(Y^2(x)-1)(Y^2(y)-1) \\&\quad = 2\rho _{Y}^2(\Vert x-y \Vert ). \end{aligned}$$

To compute the covariance, we used the property

$$\begin{aligned} E(H_k(Y(x))H_l(Y(y))) = \delta _k^l k! \rho _{Y}^k(\Vert x-y \Vert ), \quad x,y \in {{\mathbb {R}}}^{3}, \end{aligned}$$

(24)

where $H_k(u), \, k \ge 0, \, u \in {\mathbb {R}},$ are the Hermite polynomials, see Peccati and Taqqu (2011). For $k=2$, the Hermite polynomial of order 2 is $H_2(u) = u^2 -1.$

Thus, Model 4 satisfies Conditions 1 and 2.

Note that the condition $|\rho _{\varLambda }(r)| \le Ce^{-\gamma r}, \, r>0, \, \gamma >0,$ is equivalent to

$$\begin{aligned} |\rho _{Y}(r)| \le C^{'}e^{-\gamma ^{'}r}, \, r>0, \, \gamma ^{'}>0. \end{aligned}$$

(25)

So, if (25) is satisfied, then one can apply Theorems 4.1 and 4.2 and the Rényi function of the limit measure equals to

$$\begin{aligned} T(q) = q-1-\frac{1}{2}\log _b E Y^{2q}(x). \end{aligned}$$

Finally, noting that for $p > -1$ and $Z \sim N(\mu , \sigma ^2)$

$$\begin{aligned} E |Z-\mu |^{p} = \sigma ^p \frac{2^{p/2}\varGamma (\frac{p+1}{2})}{\sqrt{\pi }} \end{aligned}$$

(26)

finalises the proof. $\square$

Proof

(Example 7.1) By Remark 5.1, it is enough to check that

$$\begin{aligned} \sup _{k \in N}E \mu _k^4(B^3)= & {} \sup _{k \in N}\int _{B^3}\int _{B^3}\int _{B^3}\int _{B^3} \prod _{i=0}^{k}E\left( \prod _{j=1}^4 Y^2 (y_j b^i)\right) \\&\times \prod _{j=1}^4 dy_j < +\infty . \end{aligned}$$

Notice, that by Wick’s theorem

$$\begin{aligned} E\left( \prod _{j=1}^4 Y^2(y_j b^i)\right) = \sum _{p \in P_4^2} \prod _{(j, \tilde{j}) \in p} Cov(Y(y_j b^i), Y(y_{\tilde{j}}b^i)), \end{aligned}$$

(27)

where the sum is over all parings p of $\{1,1,2,2,3,3,4,4\},$ which are distinct ways of partitioning $\{1,1,2,2,3,3,4,4\}$ into pairs (i, j). The product in (27) is over all pairs contained in p, see Janson (1997).

Notice that for the pairing $p^{*}=\{(1,1),(2,2),(3,3),(4,4)\}.$

$$\begin{aligned} \prod _{(j, \tilde{j}) \in p^{*}}Cov(Y(y_j b^i), Y(y_{\tilde{j}}b^i)) = \prod _{j=1}^4 E Y^2(y_j b^i) = 1. \end{aligned}$$

In all other cases of pairing there is at least one pair $(j, \tilde{j})$ such that $j \ne \tilde{j}$. Therefore, the expectation $E(\prod _{j=1}^4 Y^2(y_j b^i))$ equals

$$\begin{aligned} 1+ \sum _{{\begin{array}{c} p \in P_4^2 \\ p \ne p^{*} \end{array}}}\prod _{(j, \tilde{j}) \in p}Cov(Y(y_j b^i), Y(y_{\tilde{j}}b^i)). \end{aligned}$$

As, $1+a < e^a$, it can be estimated by

$$\begin{aligned} \exp \left( {\sum _{{\begin{array}{c} p \in P_4^2 \\ p \ne p^{*} \end{array}}}\prod _{(j, \tilde{j})\in p} Cov(Y(y_j b^i), Y(y_{\tilde{j}}b^i))}\right) . \end{aligned}$$

As at least for one pairing $(j, \tilde{j}) \in p \ne p^{*}$ it holds that $j \ne \tilde{j},$ then one can use the upper bound

$$\begin{aligned} |Cov(Y(y_j b^i), Y(y_{\tilde{j}}b^i))| \le \sigma _Y^2 C e^{-\gamma \Vert y_j - y_{\tilde{j}}\Vert b^i}, \end{aligned}$$

and the approach from the proof of Theorem 5.1.

Namely,

$$\begin{aligned}&E\left( \prod _{j=1}^4 Y^2(y_j b^i)\right) \le e^{\sum _{p \in p_4^2}\prod _{(j, \tilde{j})\in p}\sigma _Y^2 C e^{-\gamma \Vert y_j - y_{\tilde{j}}\Vert b^i}}\\&\quad \le e^{{(\max (\sigma _{\varLambda }^2 C, 1))^4}{\sum _{1 \le j \le \tilde{j} \le 4} e^{-\gamma \Vert y_j - y_{\tilde{j}}\Vert b^i}}}. \end{aligned}$$

Hence,

$$\begin{aligned}&\sup _{k \in N}\int _{B^3}\int _{B^3}\int _{B^3}\int _{B^3} \prod _{i=0}^{k}E\left( \prod _{j=1}^4 Y^2 (y_j b^i)\right) \prod _{j=1}^4 dy_j \\&\quad \le \int _{B^3}\int _{B^3}\int _{B^3}\int _{B^3} \prod _{i=0}^{\infty }e^{{(\max (\sigma _{\varLambda }^2 C, 1))^4}{\sum _{1 \le j \le \tilde{j} \le 4} e^{-\gamma \Vert y_j - y_{\tilde{j}}\Vert b^i}}} \\&\quad \le \left( \int _{B^3}\int _{B^3}\int _{B^3}\int _{B^3} \prod _{i=0}^{\infty }e^{6{(\max (\sigma _{\varLambda }^2 C, 1))^4}{\sum _{1 \le j \le \tilde{j} \le 4} e^{-\gamma \Vert y_j - y_{\tilde{j}}\Vert b^i}}}\prod _{j=1}^4 dy_j\right) , \end{aligned}$$

where the last inequality follows from the generalized Hölder’s inequality

$$\begin{aligned} {\left\| \prod _{k=1}^{K}f_k\right\| }_{1} \le \prod _{k=1}^{K} {\Vert f_k \Vert }_{p_k}, \end{aligned}$$

with $\sum _{k=1}^{K}{p_k}^{-1}=1$. In our case $K=6$ is the number of different j and $\tilde{j}$ satisfying $1 \le j \le \tilde{j} \le 4.$

Finally, similar to the proof of Theorem 5.1, from equation (18) we obtain the condition $b > e^{{\frac{6 {(\max (\sigma _{\varLambda }C, 1))}^4}{3}}}.$ $\square$

Proof

(Theorem 7.2) It follows from (26) that

$$\begin{aligned} E \varLambda (x)= & {} E Y^{2k}(x) = \sigma ^{2k}{\frac{2^k \varGamma (k+\frac{1}{2})}{\sqrt{\pi }}} =1,\\ \sigma ^2_{\varLambda }= & {} Var \varLambda (x) = E(Y^{4k}) -1\\= & {} {\left( \frac{\sqrt{\pi }}{2^k \varGamma (k+\frac{1}{2})}\right) }^2 {\frac{2^{2k}\varGamma (2k+\frac{1}{2})}{\pi }}-1\\= & {} \frac{\sqrt{\pi }\varGamma (2k+ \frac{1}{2})}{{\varGamma }^2(k+\frac{1}{2})} - 1 < +\infty . \end{aligned}$$

To compute the covariance function we use (24) and the following Hermite expansion (Abramowitz and Stegun 1948, page 775)

$$\begin{aligned} z^{2k} = (2k)! \sum _{i=0}^{k} \frac{H_{2k-2i}(z)}{2^i i!(2k-2i)!}. \end{aligned}$$

Therefore,

$$\begin{aligned}&Cov(\varLambda (x), \varLambda (y)) = E(Y^{2k}(x)-1)(Y^{2k}(y)-1) \nonumber \\&\quad = \frac{\pi E(\tilde{Y}^{2k}(x)\tilde{Y}^{2k}(y))}{2^{2k}{\varGamma }^2(k+\frac{1}{2})}-1\nonumber \\&\quad = ((2k)!)^2\frac{\pi }{2^{2k}{\varGamma }^2(k+\frac{1}{2})}\sum _{i=0}^k \frac{E[H_{2k-2i}(\tilde{Y}(x))H_{2k-2i}(\tilde{Y}(y))]}{2^{2i}(i!)^2((2k-2i)!)^2}-1\nonumber \\&\quad = ((2k)!)^2\frac{\pi }{2^{2k}{\varGamma }^2(k+\frac{1}{2})}\sum _{i=0}^k \frac{{\tilde{\rho }}^{2k-2i}(\Vert x-y \Vert )}{2^{2i}(i!)^2(2k-2i)!}-1, \end{aligned}$$

(28)

where $\tilde{Y}(x) = Y(x)/\left( \frac{\sqrt{\pi }}{2^k \varGamma (k+\frac{1}{2})}\right) ^{1/{2k}}$ is a zero-mean unit variance Gaussian HIRF with the covariance function

$$\begin{aligned} {\tilde{\rho }}(\Vert x-y \Vert ) = \left( \frac{2^k \varGamma (k+\frac{1}{2})}{\sqrt{\pi }}\right) ^{1/k}\rho _Y(\Vert x-y \Vert ). \end{aligned}$$

Notice, that for $i=k$ in (28) by the Legendre duplication formula

$$\begin{aligned} \frac{((2k)!)^2 \pi }{2^{2k} {\varGamma }^2(k+\frac{1}{2})2^{2k}(k!)^2}&= \frac{{\varGamma }^2(2k+1)\pi }{2^{4k}{\varGamma }^2(k+\frac{1}{2})k^2{\varGamma }^2(k)}\\&= \frac{(2k)^2{\varGamma }^2(2k)\pi }{2^{4k}k^2 2^{2-4k}\pi {\varGamma }^2(2k)} = 1. \end{aligned}$$

Hence,

$$\begin{aligned} Cov(\varLambda (x), \varLambda (y))= \frac{((2k)!)^2\pi }{2^{2k}{\varGamma }^2(k+\frac{1}{2})}\sum _{i=0}^{k-1}\frac{(2^k \varGamma (k+\frac{1}{2}))^{2+\frac{2i}{k}}}{2^{2i}(i!)^2(2k-2i)!\pi ^{1/2k}}{\tilde{\rho }}^{2k-2i}(\Vert x-y \Vert ). \end{aligned}$$

Therefore, if $|{\tilde{\rho }}(r)| \le C^{'}e^{-\gamma ^{'}r}, \, r>0,\, \gamma ^{'}>0,$ then the covariance function of Model 5 satisfies the condition $|\rho _{\varLambda }(r)| \le Ce^{-\gamma r}, r>0, \, \gamma >0,$ and the Rényi function equals

$$\begin{aligned} T(q) = q-1-\frac{1}{2}\log _{b} E Y^{2kq}(x) = q-1-\frac{1}{2}\log _{b}\left( \frac{2^{kq}\varGamma (kq+\frac{1}{2})}{\sqrt{\pi }}\right) . \end{aligned}$$

$\square$

Proof

(Theorem 7.3) By properties of the chi-square distribution, it follows that

$$\begin{aligned} E \varLambda (x)= & {} \frac{2}{k}E Y(x) =1, \quad Var \varLambda (x) = \frac{4}{k^2}Var Y(x) = \frac{2}{k} < +\infty ,\\ Cov(\varLambda (x), \varLambda (y))= & {} \frac{4}{k^2}\rho _Y(\Vert x-y \Vert ). \end{aligned}$$

Notice that if $Y(x) = \frac{1}{2}(Z_1^2(x)+\ldots +Z_k^2(x)), \, x \in {{\mathbb {R}}}^3,$ where $Z_i(x),$ $i=1,\ldots ,k,$ are independent zero-mean unit variance components of k-dimensional vector Gaussian HIRF with a covariance function $\rho _Z(r), \, r \ge 0$ of each component, then

$$\begin{aligned} Cov(\varLambda (x), \varLambda (y)) = \frac{4}{k^2}\cdot \frac{k}{2}\rho _Z^2(\Vert x-y \Vert ) = \frac{2}{k}\rho _Z^2(\Vert x-y \Vert ). \end{aligned}$$

Therefore, Model 6 satisfies Conditions 1 and 2 and $|\rho _\varLambda (r)| \le Ce^{-\gamma r}, \, r>0$, $\gamma >0$, if $|\rho _{Y}(r)| \le C'e^{-\gamma ^{'}r}$ or $|\rho _{Z}(r)| \le C'e^{-\gamma ^{'}r}, \, r \ge 0, \gamma ^{'}>0.$

Then, the corresponding Rényi function is given by (20). $\square$