Nonparametric location–scale model for the joint forecasting of $\hbox {SO}_{{2}}$ and $\hbox {NO}_{{x}}$ pollution episodes

Abstract

We present a method to forecast pollution episodes with a bivariate response. The method simultaneously estimates the concentrations of two pollutants, using historical data. It is based on a location–scale model where the means and the standard deviations are approximated by kernel smoothers in additive models, while the variance–covariance matrix is obtained from the residuals of the previous models. The method provides not only an estimation of the concentration of both pollutants over time but also uncertainty regions covering a specific percentage of the data. The suitability of the model was tested with both simulated and real data (specifically $\hbox {SO}_2$ and $\hbox {NO}_x$ concentrations from a coal-fired power station). The results have proved highly satisfactory in both cases. The percentage of data covered by the uncertainty region, its area and a new loss function, a variant of the pinball loss function, were used as metrics to evaluate the performance of the model.

Appendix: flexible additive transformed model estimation

In order to obtain the estimated additive models in Eq. (3), we have used a backfitting algorithm based on local polynomial kernel smoothers. For mathematical notation simplicity, we consider in this section Y as our response variable and ${\mathbf {X}}=(X_1, \ldots , X_p)$ the vector of covariates. In this regression framework, we consider the transformed additive model:

$$\begin{aligned} E(Y|{\mathbf {X}})= H\left( { \eta _{{\mathbf {X}}} }\right) =H\left( { \alpha + \sum _{j=1}^p f_{j}(X_{j}) }\right) \end{aligned}$$

(18)

where H is a known link function and $\eta =\alpha + \sum _{j=1}^p f_{j}(X_{j})$ is the systematic component. Moreover, in order to guarantee the identification, we assume that $E[f_j(X_j)=0]$. To estimate the model given in (18) we proposed an interactive algorithm based on the New Raphson procedure (extends the ACE—Alternating Conditional Expectation algorithm Hastie and Tibshirani 1990) in combination with a backfitting approach (Yu and Lu 2004).

Let $\{\mathbf {X}_i, Y_{ir}\}_{i=1}^n$ be an independent random sample of $(\mathbf {X}, Y)$. For fitting (18) it is necessary to minimize

$$\begin{aligned} S(\eta )=\sum _{i=1}^n \left( { Y_i - H\left( { \eta _{{\mathbf {X}}_i} }\right) }\right) ^2 \end{aligned}$$

To solve this problem we need to use an iterative process. Here we have used a modified Newton–Raphson algorithm the steps of which are as follows:

Initialize. Compute ${\hat{\alpha }}=H^{-1} ({\bar{Y}})$ with ${\bar{Y}}=n^{-1}\sum _{i=1}^n Y_i$, for the initial estimates, ${\hat{f}}_{1}^0\ldots ={\hat{f}}_{p}^0=0$, ${\hat{\eta }}_i^0={\hat{\alpha }}$, for $i=1,\ldots ,n$.

Step 1. Construct the linearized response ${{\tilde{Y}}}$ and the weights W so that

$$\begin{aligned} {{\tilde{Y}}}_i={\hat{\eta }}_i^0 + \frac{Y_i-H({\hat{\eta }}_i^0)}{H'({\hat{\eta }}_i^0) } \quad \mathrm{and} \quad W_i=\frac{H'({\hat{\sigma }}_i^0)^2 }{{\hat{\sigma }}_i^2} \end{aligned}$$

with $H'({\hat{\partial }})=\delta H / \delta \partial$ and ${\hat{\sigma }}_i^2$ and estimation of $Var(Y_i| {\hat{\mu }}_i^0)$. The estimated ${\hat{\sigma }}_i^2$ can be obtained by fitting an additive model to $(Y_i-H\left( {{\hat{\eta }}_i^0}\right) )^2$.

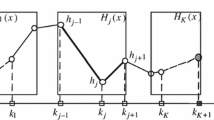
Step 2. Fit an additive model to ${{\tilde{Y}}}$ weighted by W and compute the updates ${\hat{f}}_j$, for $j=1,\ldots ,p$. At this step, we have used an inner backfitting algorithm based on local polynomial kernel smoothers:

• Step 2.1: Cycle $j=1,\ldots ,p$, calculating the partial residuals

  $$\begin{aligned} R_i^j={{\tilde{Y}}}_i - {\hat{\alpha }} - \sum _{k=1}^{j-1}{{\hat{f}}_{k}(X_{ik})} - \sum _{k=j+1}^p{{\hat{f}}_{k}^0(X_{ik})} \end{aligned}$$

  and compute for $i=1,\ldots ,n$ the updates ${\hat{f}}_j (X_{ij})$ for $i=1,\ldots ,n$, where the linear kernel estimate of $f_j^\tau$ at a localization x is given by ${\hat{f}}_j (x)={\hat{a}}$, with $({\hat{a}}, {\hat{b}})$ being the minimizers of

  $$\begin{aligned} \sum _{i=1}^n W_i \left( { R_i^j - a-b(X_{ij}-x)}\right) K\left( \frac{X_{ij} - x}{h_j}\right) ^2 \end{aligned}$$

  (19)

  where $K(\cdot )$ denotes a kernel function (a symmetric density) and $h_j>0$ is the smoothing parameter. At this step, the obtained estimates ${\hat{f}}_j$ must be refocused by considering ${\hat{f}}_j (X_{ij})={\hat{f}}_j (X_{ij})- n^{-1}\sum _{l=1}^n {\hat{f}}_j (X_{lj})$ .

  Here, we have used a Gaussian kernel and the bandwidth $h_j$ is recalculated in each iteration following t cross-validation procedure

  $$\begin{aligned} CV=\sum _{i=1}^n{ W_i \left( R_i^j - {\hat{f}}_j^{(-i)}(X_{ij})\right) ^2} \end{aligned}$$

  (20)

  where ${\hat{f}}_j^{(-i)}(X_{ij})$ is the leave-one-out estimator at $X_{ij}$ obtained from the sample without the i-th data vector.

• Step 2.2: Repeat Step 2.1 replacing ${\hat{f}}_{j}^0 (X_{ij})$ by ${\hat{f}}_{j} (X_{ij})$ for $j=1,\ldots ,p$ and $i=1,\ldots ,n$, until the convergence criterion

  $$\begin{aligned} \frac{ \sum _{i=1}^n \left( { {\hat{f}}_{j}(X_{ij})-{\hat{f}}_j^0(X_{ij})}\right) ^2}{ \sum _{i=1}^n \left( { {\hat{f}}_{j}^0(X_{ij})}\right) ^2+0.001} \le \varepsilon \quad \text {for all } \quad j=1,\ldots ,p \end{aligned}$$

  is reached.

Step 3. Repeat Steps 1–3 with ${\hat{\eta }}_i^0$ being replaced by ${\hat{\eta }}_i= {\hat{\alpha }} + \sum _{j=1}^p {{\hat{\alpha }}_j \cdot X_{ij}}+ \sum _{j=1}^p {\hat{f}}_j(X_{ij})$ for $i=1,\ldots ,n$ until

$$\begin{aligned} \frac{ |\textit{MSE} ({\hat{\eta }}_0, Y) -\textit{MSE} ({\hat{\eta }}, Y)|}{\textit{MSE}({\hat{\eta }}_0, Y)} \le \varepsilon \end{aligned}$$

where $\varepsilon$ is a small threshold and the mean squared error $\textit{MSE}({\hat{\eta }},Y)$ is defined as $\textit{MSE}({\hat{\eta }},Y)=n^{-1}\sum _{i=1}^n W_i(Y_i-H({\hat{\eta }}_i))^2$.