1 Introduction

Earthquakes are expressions of complex systems in which many components interact with each other. They are natural phenomena that affect multiple time–space scales, and of which we only have indirect measurements that are strongly affected by uncertainty, despite modern seismographic systems (such as site effects in the propagation of waves). These phenomena can be investigated on different, coherent time–space–magnitude scales, where they show different critical aspects and are related to different goals; e.g., focusing on a single event, the aim is to determine its parameters through the recordings provided by various stations. Moving up to the next level, i.e., expansion of the time–space scale, there is the problem of the modeling of the sequence of secondary events that follow a strong earthquake, and the estimation of its length and width. Climbing up to the next hierarchical level, we deal with the occurrence of destructive earthquakes that are generated by faults or systems of indistinguishable, interacting faults, embedded in the reciprocal sliding of plates. Ideally, through combination of the equations that govern the physical processes of the generation of a fault rupture with those of the fault interactions, we can model the whole phenomenon. Clearly we are far from this level of knowledge, and many of the studies performed at various levels do not benefit from the results obtained for the other levels.

Starting from the goal we want to pursue, we choose the resolution level at which to observe the phenomenon, the time–space–magnitude scales for its description, what are the relevant variables, and what ones are treatable as fluctuations. Moving to a level means to adopt those interaction models that capture the emerging system behavior, also using information or models from lower levels. In this study, our objective is to consider the time evolution of disastrous earthquakes, which means to move on medium-large scales, and to model their occurrence in the forecasting perspective by combining knowledge gained at different levels.

In the past, phenomenological analyses of seismicity led mainly to two patterns: time-independent point processes on regional and long-term scales; and self-exciting models to describe typically the increase in seismic activity over short space–time scales immediately after large earthquakes. Later, it was noted that even catalogs without secondary shocks show clusters. These observations, and the need to consider jointly the previous patterns to provide a better description of the phenomenon, have brought us to hybrid models that widely require measurements of geodetic and geological quantities. The global earthquake activity rate (GEAR) model (Kagan 2017) provides long-term forecasting with no explicit time dependence, that is based on the linear combination and log-linear mixing of two ‘parent’ forecasts: smoothed-seismicity forecasts and tectonic forecasts based on a strain-rate map that is converted first into a long-term seismic moment rate, and then into earthquake rates. The most recent version of the Uniform California Earthquake Rupture Forecast (UCERF3) (Field et al. 2017) is a hierarchical model that covers both long-term (decades to centuries) probabilities of fault rupture and short-term (hours to years) probabilities of clustered seismicity. The hierarchical structure is composed of three levels, each of which is conditional on the previous level: a time-independent model is at the first level, then there is a renewal model, and finally an epidemic-type aftershock sequence (ETAS) model (Ogata and Zhuang 2006; Ogata 2011), to represent spatiotemporal clustering. Also the hybrid time-dependent probabilistic seismic hazard model (Gerstenberger et al. 2016) developed in New Zealand after the Canterbury earthquake sequence (September 4, 2010, \(M_w \ 7.1\)) is a combination of three types of models: smoothed seismicity background models as long-term models; EEPAS (‘Every Earthquake a Precursor According to Scale’) models (Rhoades and Evison 2004), to take into account the precursory scale increase phenomenon on the medium-term scale, and two aftershock models in the short-term clustering class (Ogata 1998; Gerstenberger et al. 2004).

Models of the self-correcting class are the only ones, on large space–time scales, that attempt to incorporate physical conjecture into the probabilistic framework. They are inspired by the elastic rebound theory by Reid (1911), which was transposed into the framework of stochastic point processes by Vere-Jones (1978), through the first version of the stress-release model. Subsequent versions of this model express the presence of clusters of even large earthquakes, in terms of possible interactions among neighboring fault segments (Bebbington and Harte 2003).

Summarizing, most probability models used in earthquake forecasting belong to the two classes of self-exciting and self-correcting models, which are conflicting from the point of view of the hazard function: a piecewise decreasing function for self-exciting models, and a piecewise increasing function for self-correcting models. To conciliate this dissent, Schoenberg and Bolt (2000) proposed the Short-term Exciting Long-term Correcting (SELC) models by simply putting together the conditional intensity functions of two point processes, one from each class, and fitting the models to two datasets of micro and moderate earthquakes that occurred in California, over periods of 7 years and 30 years. With the same goal, Varini (2005, 2008) used a state-space model to estimate the different phases of a seismic cycle, in which the state process is a homogeneous pure jump Markov process with three possible states associated with the Poisson, ETAS, and stress-release models. In both of the proposals, the results were not completely satisfactory, because of the different scales at which the triggering and strain-release mechanisms appear to operate for SELC models, and of the difficulty in fitting the sudden changes of state in the case of the state-space model. Again, in the perspective that the physical system passes through different states during the earthquake generation process, Votsi et al. (2014) considered a discrete-time hidden semi-Markov model, the states of which are associated with different levels of the stress field.

In this study, we propose a new stochastic model for earthquake occurrences, hereinafter denoted as the compound model, which takes into account the following points: (a) the benefit of exploiting a stochastic model inspired by elastic rebound theory; (b) the need to consider jointly the opposite trends that characterize self-exciting and self-correcting models; and (c) the idea to superimpose behaviors characteristic of different time-scales in a single hierarchical model.

Let us consider all of the earthquakes that are associated with a seismogenic source, and select \(m_0\) as the magnitude threshold so that the time period in which the dataset can be considered as complete includes a sufficient number of strong earthquakes according to the seismicity of the region under examination; e.g., in Italy, an earthquake of \(M_w \ge 5.3\) can already be considered as strong. These damaging events are responsible for most of the release of seismic energy. We put them in the first level of our model, and assume that these leader events follow the stress-release model (Rotondi and Varini 2007). At the second level, there are the subordinate events; i.e., those that occur between two consecutive leaders and show the tendency to cluster in closeness to them. We consider the occurrence times of these events as ordered failure times in the time interval limited by the two leaders, and we model them through distributions belonging to the family of the generalized Weibull distributions with a bathtub-shaped hazard function, so as to match the clustering trend close to the extremes of the interval. We examine the model in the Bayesian perspective; hence, in addition to the elements of the model, we assign prior distributions of the model parameters, which include the available information on the phenomenon drawn from the literature in the case of previously studied components of the models. As for the new components, i.e., the generalized Weibull distributions, an objective Bayesian perspective is followed in assigning the prior distributions of their parameters, through combination of the empirical Bayes method and use of vague-proper prior distributions.

The proposed model is applied to the sequence of earthquakes associated with one of the most active composite seismogenic sources (CSS) of the Italian Database of Individual Seismogenic Sources (DISS, version 3.0.2). This is located in the central Apennines, and includes the L’Aquila earthquake, one of the most recent destructive earthquakes in Italy. Then we report the parameter estimates and the performance of the model in terms of the marginal likelihood. Moreover, we compare our model with the stress-release and ETAS models on the basis of two validation criteria: the Bayes factor and the information criterion by Ando and Tsay.

2 Superimposed point processes: failure process and self-correcting model

2.1 The two conflicting model classes

First of all we recall the basic version of the hazard function of the two classes of self-exciting and self-correcting models, which are conflicting from the point of view of the hazard function. The conditional intensity function of the former class is:

$$\begin{aligned} \lambda _{exc} (t \mid {\mathcal{H}}_t) = \mu + \sum _{i: t_i < t} g(t-t_i \mid {\mathcal{H}}_t) \end{aligned}$$

where \({\mathcal{H}}_t\) is the history of the process up to but not including t and \(\{t_i\}_{i \ge 1}\) the occurrence times. The triggering function \(g(\cdot )\) may have one of the following forms: \(g(t)= \phi \, e^{-\theta \, t}\), \(g(t)= \sum _{k=1}^K \phi _k \, t^{k-1} \, e^{-\theta \, t}\), \(g(t)= \displaystyle {\frac{k}{(t+\phi )^{\theta }}}\) (Vere-Jones and Ozaki 1982); it implies that any new event increases the chance of getting other events immediately after. The ETAS model is probably the most well-known example of this class; it is defined by:

$$\begin{aligned} \lambda _{ETAS}(t \mid {\mathcal{H}}_t) = \mu + K \, \sum _{i: t_i < t} \frac{\displaystyle { e^{a \, (m_i-m_0) }}}{\left( c + t-t_i \right) ^p}. \end{aligned}$$

On the contrary, in the self-correcting class, the chance of new events decreases immediately after an event occurs; this is due to conditional intensity functions of the form:

$$\begin{aligned} \lambda _{corr} (t \mid {\mathcal{H}}_t) = exp \left( X_0 + c t - \sum _{i=1}^{N[0,t)} Z_i \right) , \end{aligned}$$

being N[0, t) the number of events falling in the time interval [0, t) and \(\{Z_i\}_{i\ge 1}\) is a sequence of random variables.

2.2 A proposal of conciliation

Let us consider the earthquakes of magnitude at least \(m_0\) that hit a seismic region. Among these, we distinguish the ‘leader’ events as the main events of a magnitude that exceeds the magnitude threshold \(m_{th}\) (\(m_{th} > m_0\)) from the remaining events, which we consider as ‘subordinate’ events. The first subset of n leader events is denoted by:

$$\begin{aligned} \text{ leaders } = \left\{ (t_i, m_i): \, m_i \ge m_{th}, \ i=1,...,n \right\} \ ; \end{aligned}$$

for each pair \((t_i, t_{i+1}), \, i=1, ... ,n-1\), we have the possibly empty set of \(n_i\) subordinate events \(\left\{ (\tau _{ij}, \mu _{ij}): \, \mu _{ij} \ge m_0 , \ t_i< \tau _{ij} < t_{i+1}, \ j=1,...,n_i \right\}\) so that as a whole the second subset is denoted by:

$$\begin{aligned} \text{ subordinates } = \left\{ (\tau _{ij}, \mu _{ij}): \ \mu _{ij} \ge m_0, \ t_i<\tau _{ij}<t_{i+1}, \ j=1, ... , n_i, \ i=1, ... , n-1 \right\} \, \end{aligned}$$

where \(t_i\) and \(\tau _{ij}\) are the occurrence times of the earthquakes, and \(m_i\) and \(\mu _{ij}\) are their magnitudes.

The occurrence times are modeled through the superposition of two stochastic processes under the assumption of separability with respect to magnitude. In terms of conditional probability, the proposed model can be outlined as follows:

$$\begin{aligned} Pr \left\{ \mathrm{leaders},\, \mathrm{subordinates} \right\}= & {} Pr \left\{ \mathrm{subordinates} \mid \mathrm{leaders} \right\} \times { Pr} \left\{ \mathrm{leaders} \right\} \\= & {} Pr \left\{ \mathrm{subordinates}' \, \mathrm{times} \mid \mathrm{leaders} \right\} \\&\times \, Pr \left\{ \mathrm {subordinates}' \, \mathrm{magnitude} \mid \mathrm{leaders} \right\} \times \\&\times \, Pr \left\{ \mathrm {leaders}' \, \mathrm {times} \right\} \times { Pr} \left\{ \mathrm {leaders}' \, \mathrm {magnitude} \right\} . \end{aligned}$$

The leader events are assumed to be a realization of a marked point process, whereas the distribution of the subordinate events is conditional on the leader events, according to a reliability (or failure) model, as hereinafter described.

Stochastic modeling of magnitude Let G(m) denote the probability distribution function of the magnitude, and g(m) its density function on the domain \(m \ge m_0\). In particular, it turns out that the distribution of the leader magnitude is truncated on \([m_{th}, +\infty )\), whereas the distribution of the subordinate magnitude is truncated on \([m_0, +\infty )\).

According to the Gutenberg-Richter law, we assume that the magnitude is exponentially distributed with rate b; i.e., \(g(m)= b e^{-b \, m}\). Therefore, the magnitude distributions for the leader and subordinate events are respectively given by:

$$\begin{aligned} \begin{aligned} g_{\ell }(m \mid m \ge m_{th})&= \displaystyle \frac{g_{\ell }(m)}{1-G_{\ell }(m_{th})} = b_{\ell } e^{-b_{\ell } (m-m_{th})}\, , \\ g_s(m \mid m \ge m_0)&= \displaystyle \frac{g_s(m)}{1-G_s(m_0)} = b_s e^{-b_s (m-m_0)} \, . \end{aligned} \end{aligned}$$

Different magnitude distributions can also be considered; e.g., the Pareto (Schoenberg and Patel 2012) and the tapered Pareto (Kagan and Schoenberg 2001) models.

Stochastic modeling of leader events A seismic sequence of strong earthquakes is usually interpreted as realization of a marked point process \({\mathcal{N}}^{*}\), meant as a random counting measure defined on the space \({\mathbb{R}}^2\), where the second coordinate m is a mark (i.e., a measure of the size of the event) that is associated with the first temporal coordinate t (i.e., the occurrence time of the event) (Daley and Vere-Jones 2003). The marked point process \({\mathcal{N}}^{*}\) is uniquely determined by its conditional intensity function \(\lambda ^{*} (t,m \mid {\mathcal{H}}_t)\), for any \((t,m) \in {\mathbb{R}}^2\), which represents the probability of the occurrence at time t of an event with magnitude m conditional on the history \({\mathcal{H}}_t\) of the process prior to t. Under the assumption of separability with respect to magnitude, the conditional intensity function of \({\mathcal{N}}^{*}\) can be expressed as:

$$\begin{aligned} \lambda ^{*}(t, m \mid {\mathcal{H}}_t) = \lambda (t \mid {\mathcal{H}}_t)\ g(m \mid m \ge m_{th}) \ . \end{aligned}$$

The temporal component \(\lambda (t \mid {\mathcal{H}}_t)\) represents the conditional intensity function of the point process \({\mathcal{N}}\) that only describes the occurrence times. Therefore the expected number of events over [0, t), regardless of their magnitude, is given by:

$$\begin{aligned} E(N[0,t)) = \displaystyle \int _0^t \lambda (s \mid {\mathcal{H}}_s) ds \, . \end{aligned}$$

Among the point processes presented in the seismological literature, the stress-release model is particularly suitable to assign N for strong earthquakes. Its conditional intensity function is given by:

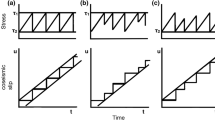
$$\begin{aligned} \lambda (t \mid {\mathcal{H}}_t) = exp \left\{ \alpha +\beta \left[ \rho t - \sum _{i: t_i<t} x_i \right] \right\} \ , \end{aligned}$$
(1)

where \(\alpha\), \(\beta\), and \(\rho\) are parameters, and \(x_i\) is a proxy measure of the size of the i-th earthquake, which is generically indicated as ‘stress’. The rationale behind the stress-release model is the Reid’s elastic rebound theory, according to which an earthquake is the result of the elastic rebound caused by the sudden release of the strain energy previously stored along the fault. In the stochastic version of this, which was first proposed by Vere-Jones (1978), the level of ‘stress’ in the seismic region is assumed to increase linearly over time at the rate \(\rho >0\), and to suddenly decrease by a quantity \(x_i\) as the i-th earthquake occurs, for all \(i=1,...,n\). Following this line of reasoning, the conditional intensity function might be any monotonic increasing function of the level of stress. As indicated in (1), this function is usually an exponential function of the level of stress, with parameters \(\alpha \in {\mathbb{R}}\) and \(\beta >0\). Hence, it turns out that a high (or low) level of stress, e.g., due to a period without (or with many) events, implies increasing (or decreasing) value of the occurrence probability. This means that the stress-release model belongs to the family of self-correcting point processes. In other words, it automatically compensates for deviations from its mean, to keep a balance between stress loading and stress release.

Different measures of the size of an earthquake can be adopted, like Benioff’s strain, seismic moment, seismic energy, or scaled energy. The application of the stress-release model to Italian seismogenic sources (Varini et al. 2016) has shown that among those abovementioned, the scaled energy is the quantity that provides the best performance of the model. The scaled energy is given by the ratio between the seismic energy \(E_s\) and the seismic moment \(M_0\) of the earthquake. By expressing \(E_s\) according to Senatorski (2007) and \(M_0\) according to Kanamori and Brodsky (2004), each \(x_i\) is given by:

$$\begin{aligned} x_i = \frac{E_s}{M_0} \propto \frac{M_0^{1.5}/\sqrt{A_i}}{M_0} = \sqrt{\frac{M_0}{A_i}} \, , \end{aligned}$$

where the rupture area \(A_i\) is approximated through the regression models of Wells and Coppersmith (1994) for different focal mechanisms.

Then, given the occurrence times \((t_1, t_2, \ldots , t_n)\) of the n leader events in the time interval \([t_1,t_n]\), the log-likelihood function of parameters \(\varvec{\theta }_{\ell } = (\alpha , \beta , \rho )\) has the following expression:

$$\begin{aligned} \log {\mathcal{L}}(\varvec{\theta }_{\ell }) = \sum _{i=1}^{n} \log \lambda (t_i \mid {\mathcal{H}}_{t_i}, \varvec{\theta }_{\ell }) - \int _{t_1}^{t_n} \lambda (s \mid {\mathcal{H}}_s, \varvec{\theta }_{\ell }) \ ds . \end{aligned}$$

An interesting property of the stress-release model is that the distribution of the waiting time W of the next event at any instant \(t>0\) follows the Gompertz distribution (Varini and Rotondi 2015):

$$\begin{aligned} F(w \mid {\mathcal{H}}_t) = 1 - \exp \{ - \phi _t \ ( e^{{\eta w }} -1) \} \, , \end{aligned}$$

where \(\phi _t=\displaystyle \frac{\lambda (t \mid {\mathcal{H}}_t)}{\beta \rho }\) is the shape parameter, and \(\eta =\beta \rho\) is the scale parameter. As the instantaneous occurrence probability \(\lambda (t \mid {\mathcal{H}}_t)\) and the shape parameter \(\phi _t\) are directly proportional, the parameter \(\phi _t\) expresses the propensity at time t to the occurrence of the next event; i.e., the larger \(\phi _t\) becomes as time t passes, the larger the failure probability \(F(\omega )\) is that the next event happens up to and including time \((t+\omega )\). This matches the self-correcting property of the stress-release model, and reveals its predictive behavior.

Stochastic modeling of subordinate events The subset of subordinate events consists of earthquakes of magnitude lower than the magnitude threshold \(m_{th}\) or of secondary events triggered by leader events, possibly also of magnitude higher than \(m_{th}\). The identification of seismicity patterns in a region might be a controversial issue, but there is generally wide agreement on some features, as, for example, on clustering after mainshocks and on the sometimes observed increase in activity before a strong shock. Accordingly, it should expected that the occurrence times of the subordinate events are gathered more in the neighborhood of the main events, in correspondence with those that are called aftershocks and foreshocks. This means that it is reasonable to expect a bathtub-shaped hazard function for the occurrence time of subordinate events between two consecutive leaders; i.e., a function that decreases just after a leader event has happened, then possibly remains constant, and finally increases with the approach of another leader event.

Generalized Weibull distributions (Lai 2014) form a large family of distributions, which include the standard Weibull distribution as a special case, the hazard function of which shows a large variety of shapes: monotone, unimodal, bathtub, modified bathtub (or upside-down) (Bebbington et al. 2007). Among these distributions, we have considered in particular the modified (MW) and additive (AW) Weibull models. Table 1 shows the expression of their density function \(f^*(x)\), the cumulative distribution function \(F^*(x)=\displaystyle \int _0^x f^*(u) du\), the survival function \(S^*(x)=1-F^*(x)\), and the hazard function \(h^*(x)=f^*(x)/S^*(x)\).

Table 1 Properties of the modified (MW) and additive (AW) Weibull distributions that were applied to subordinate events: \(f^*(x)\) is the density function, \(F^*(x)\) is the distribution function, \(S^*(x)\) is the survival function, and \(h^*(x)\) is the hazard function
Full size table

The hazard functions in Table 1 can take a variety of shapes according to the variation of the model parameters. For the MW model, \(h^*(x)\) is always increasing if its shape parameter is \(a_1 >1\), and it has a bathtub shape otherwise. In the latter case, the turning point of \(h^*(x)\) is given by \(x^* = (\sqrt{a_1}-a_1)/c_1\). The AW model is a two-fold competitive risks model where the hazard function is the sum of the hazard functions of two Weibull distributions. Therefore, \(h^*(x)\) is increasing if both shape parameters \(a_1\) and \(a_2\) are larger than 1, decreasing if \(a_1<1\) and \(a_2<1\), and bathtub shaped if \(a_1<1\) and \(a_2>1\), or vice versa; in the last case the turning point is given by \(x^* = \displaystyle {{\left[ - \frac{a_2 (a_2-1) \, b_1^{a_1}}{a_1(a_1-1) \, b_2^{a_2}}\right] }^{1/(a_1-a_2)}}\).

We note that the subordinate events fall in bounded intervals \((t_i, t_{i+1})\) with different lengths \(t_{i+1}-t_i\) (\(i=1,...,n-1\)), whereas the distributions in Table 1 have unbounded support \({\mathbb{R}}^+\). A possible solution to this problem is to normalize each time \(\tau _{ij}\) to a range of 0-1, as follows:

$$\begin{aligned} s_{ij}=\frac{\tau _{ij}-t_i}{t_{i+1}-t_i}\ , \end{aligned}$$

and then to assume that the normalized times \(s_{ij}\) are realizations of order statistics of a distribution F(s) on (0, 1). In other words, given the number \(n_i\) of subordinate events in \((t_i, t_{i+1})\), their normalized occurrence times \(s_{i1}\), \(s_{i2}\), \(\dots\), \(s_{i n_i}\) are items of an iid sample from F(s) arranged in increasing order.

The distribution F(s) can be derived from truncating any probability distribution \(F^*(s)\) to the support (0, 1), so that we have for any \(s\in (0,1)\):

  • cumulative distribution function \(F(s)=\displaystyle \frac{F^*(s)}{F^*(1)}\),

  • density function \(f(s)= \displaystyle \frac{f^*(s)}{F^*(1)}\),

  • survival function \(S(s)=\displaystyle \frac{F^*(1)-F^*(s)}{F^*(1)}\),

  • hazard function \(h(s)=\displaystyle \frac{f^*(s)}{F^*(1)-F^*(s)}\).

With regard to the number of subordinate events in the i-th interval between the two consecutive leader events that occur at time \(t_i\) and \(t_{i+1}\), this is assumed to be a Poisson random variable with parameter \(\gamma \, (t_{i+1}-t_i)\); therefore, it holds that:

$$\begin{aligned} Pr (n_i \mid t_i, t_{i+1}) = e^{\displaystyle - \gamma \, (t_{i+1}-t_i)} \, \frac{\gamma \, {(t_{i+1}-t_i)}^{n_i}}{n_i!} \qquad n_i=0,1,2,...\, . \end{aligned}$$

Let \(\varvec{\theta }_s\) denote the parameter vector of F(s). The expression of the likelihood function of \(\varvec{\theta }_s\) and \(\gamma\) given the data is the following:

$$\begin{aligned} \begin{aligned} {\mathcal{L}}(\varvec{\theta }_s, \gamma )&= \prod _{i=1}^{n-1} Pr (n_i \mid t_i, t_{i+1}) \cdot Pr (\tau _{i1}, \tau _{i2}, \dots , \tau _{in_i} \mid n_i, \varvec{\theta }_s) \\&= \displaystyle \prod _{i=1}^{n-1} e^{\displaystyle - \gamma \, (t_{i+1}-t_i)} \, \frac{\gamma \, {(t_{i+1}-t_i)}^{n_i}}{n_i!} \cdot \left[ n_i! \prod _{j=1}^{n_i} f(s_{ij} \mid \varvec{\theta }_s ) \right] \, , \end{aligned} \end{aligned}$$

which takes account of both the probability of the number \(n_i\) of subordinate events in \((t_i,t_{i+1})\), and given \(n_i\), the probability distribution of the normalized times in that interval, for all \(i=1,2,\dots ,n-1\). Note that the factor \(n_i!\) arises because there are \(n_i!\) equally likely iid unordered samples from F(s) that generate the ordered sequence of normalized times \(\tau _{i1}, \tau _{i2}, \dots , \tau _{in_i}\).

A further level of dependency of the subordinate events from the leaders can be introduced by assuming that shape parameters depend on the actual hazard level of the stress-release model. That means that the hazard function of subordinate events can take different shapes in the intervals between consecutive leaders; e.g., in the MW model, one of the parameters in the turning point can be made time-dependent as follows: \(a_1 (t) = a_1 / \lambda (t\mid {\mathcal{H}}_t)\); and in the AW model, it is possible to set \(a_1(t) = a_1\ \lambda (t\mid {\mathcal{H}}_t)\) and \(a_2(t) = a_2 / \lambda (t\mid {\mathcal{H}}_t)\). We plan to develop these indications in future investigations.

3 Bayesian inference and model comparisons

In this section, we deal with the problem of estimation of the model parameters following the Bayesian pardigm and applying Markov chain Monte Carlo (McMC) methods for sampling from the posterior probability distributions of the parameters. In this way, we obtain not only the parameter estimates, typically as their posterior means, but also a measure of their uncertainty, as expressed through the simulated posterior distribution of each parameter.

Let \(\varvec{\theta }=(b_{\ell }, b_{s}, \gamma , \varvec{\theta }_{\ell }, \varvec{\theta }_s)\) be the vector of all of the model parameters to be estimated. In Bayesian inference, \(\varvec{\theta }\) is considered as a random vector that follows a prior distribution \(\pi _0 (\varvec{\theta })\). This prior has to be assigned by accounting for the available information on the parameters regardless of the data D. Then, through Bayes’ theorem, the posterior distribution is obtained by updating the prior \(\pi _0 (\varvec{\theta })\) through information provided by the new observations:

$$\begin{aligned} \pi (\varvec{\theta } \mid D) = \frac{{\mathcal{L}}(D \mid \varvec{\theta }) \, \pi _0 (\varvec{\theta })}{\int _{\varvec{{\varTheta }}} {\mathcal{L}}(D \mid \varvec{\theta }) \, \pi _0 (\varvec{\theta }) \, d \varvec{\theta }} \end{aligned}$$

where the denominator \({\mathcal{L}}(D) = \displaystyle \int _{\varvec{{\varTheta }}} {\mathcal{L}} (D \mid \varvec{\theta }) \, \pi _0(\varvec{\theta }) \, d \varvec{\theta }\) is the marginal likelihood of the data, and \({\mathcal{L}} (D \mid \varvec{\theta })\) is the likelihood function given by:

$$\begin{aligned}&{\mathcal{L}}(D \mid \varvec{\theta }) \nonumber \\&\quad = \prod _{i=1}^n \lambda (t_i \mid {\mathcal{H}}_{t_i}, \varvec{\theta }_{\ell })\ exp \left\{ -\displaystyle \int _{t_1}^{t_n} \lambda (u \mid {\mathcal{H}}_u, \varvec{\theta }_{\ell }) \, du\right\} \, \cdot \displaystyle \prod _{i=1}^n \frac{g_{\ell }(m_i \mid b_{\ell })}{1-G_{\ell }(m_{th} \mid b_{\ell })} \cdot \end{aligned}$$
(2)
$$\begin{aligned}&\qquad \displaystyle \prod _{i=1}^{n-1} \left\{ e^{\displaystyle - \gamma \, (t_{i+1}-t_i)} \, \frac{\gamma \, {(t_{i+1}-t_i)}^{n_i}}{n_i!} \cdot \left[ n_i! \prod _{j =1}^{n_i} f(s_{ij} \mid \varvec{\theta }_s ) \, \frac{g_s(m_{ij} \mid b_s)}{1-G_s(m_0 \mid b_s)} \right] \right\} . \end{aligned}$$
(3)

The present formulation of the compound model is limitated to the case in which the data set begins and ends with leader events. If the time interval under examination was \([t_1,T)\) with \(t_n < T\) and \(n_n \ge 0\) subordinate events had occurred after the last leader, the likelihood function should be modified in the following way: (i) the products in (3) go up to n (set \(t_{n+1}=T\)) and (ii) it has to be multiplied by the marginalization, with respect to the variable \(u \in (T, +\infty )\), of the probability that the next leader event is at u (\(u > T\)) joined with the probability of all the possible configurations of subordinate events in (T, u). The analysis of this case is beyond the aim of the present work and will be object of future research.

If we assume, as is natural, that the components of the vector \(\varvec{\theta }\) are independent, so that we have \(\pi _0(b_{\ell }, b_s, \gamma , \varvec{\theta }_{\ell }, \varvec{\theta }_s) = \pi _0(b_{\ell }) \cdot \pi _0(b_s) \cdot \pi _0(\gamma ) \cdot \pi _0(\varvec{\theta }_{\ell }) \cdot \pi _0(\varvec{\theta }_s),\) the problem can be decomposed into the computation of the four posterior distributions:

  • \(\pi (b_{\ell } \mid m_i, i=1,..,n) \propto \displaystyle \prod _{i=1}^n \frac{g_{\ell }(m_i \mid b_{\ell })}{1-G_{\ell }(m_{th} \mid b_{\ell })} \; \pi _0 (b_{\ell })\)

  • \(\pi (b_s \mid (m_{ij}, j=1,.., n_i), i=1,..,n) \propto \displaystyle \prod _{i=1}^{n-1} \prod _{j =1}^{n_i} \frac{g_s(m_{ij} \mid b_s)}{1-G_s(m_0 \mid b_s)} \; \pi _0 (b_s)\)

  • \(\pi (\gamma \mid (n_{ij}, j=1,..,n_i), t_i, i=1,..,n ) \propto \displaystyle \prod _{i=1}^{n-1} e^{\displaystyle - \gamma \, (t_{i+1}-t_i)} \, \frac{\gamma \, {(t_{i+1}-t_i)}^{n_i}}{n_i!} \; \pi _0(\gamma )\)

  • \(\pi (\varvec{\theta }_s \mid {\mathcal{H}}_T) \propto \displaystyle \prod _{i=1}^n \lambda (t_i \mid {\mathcal{H}}_{t_i}, \varvec{\theta }_{\ell }) \ exp \left\{ -\displaystyle \int _{t_1}^{t_n} \lambda (u \mid {\mathcal{H}}_u, \varvec{\theta }_{\ell }) \, du\right\} \; \pi _0(\varvec{\theta }_{\ell })\)

  • \(\pi (\varvec{\theta }_s \mid (s_{ij}, j=1,..,n_i), n_i, t_i, i=1,..n) \propto \displaystyle \prod _{i=1}^{n-1} \, \left[ n_i! \prod _{j =1}^{n_i} f(s_{ij} \mid \varvec{\theta }_s ) \right] \; \pi _0(\varvec{\theta }_s)\) .

To avoid the computation of multi-dimensional integrals that is required in the evaluation of the normalizing constant, we resort to McMC methods based on the stochastic simulation of Markov chains that have the desired distributions as their equilibrium distribution. The states of the chain after a large number of steps can be used as samples from the desired distribution. The Metropolis–Hastings (MH) algorithm is a general McMC method for obtaining a sequence of random samples from a probability distribution, and the integrals with respect to this function can be approximated according to the ergodic theorem. All of the other methods can be considered as special cases of the MH algorithm. In the Bayesian context, the target distribution is the posterior distribution \(\pi (\theta \mid D)\) of the parameter \(\theta\). Applying the McMC method, we obtain not only the parameter estimate given by its posterior mean, but also a measure of the uncertainty around the estimate, as expressed by the simulated posterior distribution. The MH algorithm is summarized below.

Metropolis–Hastings algorithm

  step 1 : select \(\theta _0\) from \(\pi _0(\theta )\) and set \(i=1\),

  step 2 : draw a candidate \({{\tilde{\theta }}}\) from the proposal distribution \(q (\theta \mid \theta _{i-1})\),

  step 3 : compute the acceptance probability

         \(\alpha ({\tilde{\theta }} \mid \theta _{i-1})= min \left( 1, \ \displaystyle \frac{\pi _0({\tilde{\theta }}) \, {\mathcal{L}}(D \mid {\tilde{\theta }}) \, q (\theta _{i-1} \mid {\tilde{\theta }})}{\pi _0(\theta _{i-1}) \, {\mathcal{L}}(D \mid \theta _{i-1}) \, q ({\tilde{\theta }} \mid \theta _{i-1})}\right) \, ,\)

  step 4 : accept \({\tilde{\theta }}\) as \(\theta _i\) with probability \(\alpha ({\tilde{\theta }} \mid \theta _{i-1})\), set \(\theta _i = \theta _{i-1}\) otherwise,

  step 5 : repeat steps 2-4 a number R of times to get R draws from the posterior distribution, with optional burn-in and/or thinning.

The initial value \(\theta _0\) of the parameter is generated from the prior distribution \(\pi _0(\theta )\). Then, given \(\theta _{i-1}\), for each iteration \(i=1,2,\ldots\), a candidate \({\tilde{\theta }}\) is drawn from a proposal distribution \(q (\theta \mid \theta _{i-1})\), and accepted with probability \(\alpha ({\tilde{\theta }} \mid \theta _{i-1})\). Due to the Markovian nature of the simulation, the first values of the chain are highly dependent on the starting value and are usually removed from the sample as burn-in. The proposal distribution is chosen such that it is easy to sample from it, and it covers the support of the posterior distribution. In general some practical rules are proposed in the literature to adjust the proposal. One of these is to modify the variance \(\sigma ^2\) of the proposal so as to optimize the acceptance rate, i.e., the fraction of the proposed samples that is accepted in a window of the last N samples, with N sufficiently large. Indeed, if \(\sigma ^2\) is too small, the acceptance rate will be high, but the chain will mix and converge slowly. On the other hand, if \(\sigma ^2\) is too large, the acceptance rate will be very low and again the chain will converge slowly. It is generally accepted (Gamerman and Lopes 2006) that a reasonable acceptance rate is about 20% to 50%. Another critical point is the correlation between successive states of the chain, which reduces the amount of information contained in a given number of draws from the posterior distribution. A simple, yet efficient, method that deals with this issue is to only keep every d draws from the posterior, and to discard the rest. This is known as thinning the chain. Although the asymptotic convergence of the chain to the equilibrium distribution is theoretically proven, we make inferences based on a finite Markov chain, and hence the main problem is to establish how long we must run our chain until convergence. The R package BOA (Smith 2007) provides functions for summarizing and plotting the output from McMC simulations, as well as diagnostic tests of convergence. It must be stressed, however, that no method can truly prove convergence; diagnostics can only detect failure to converge.

Prior elicitation The possibility of expressing our information on the phenomenon through prior distributions of the model parameters is an advantage of the Bayesian approach, although it can also be a critical point when the parameters are not strictly related to easily measurable physical quantities, such as the parameters \(\varvec{\theta }_{\ell } = (\alpha , \beta , \rho )\) of the stress-release model. To overcome this issue, we then assign the prior distributions following an objective Bayesian perspective. This approach combines the empirical Bayes method and the use of vague-proper prior distributions (Berger 2006). First, we choose the families of the prior distributions according to the support of the parameters (e.g., \(\beta\) and \(\rho\) are positive parameters, and \(\alpha\) lies on the real line), and we set the prior parameters—hyperparameters—equal to the prior mean and variance of the corresponding model parameter. For instance, let us assume that a generic parameter \(\psi\) follows a priori the Gamma distribution Gamma(\(\xi , \nu\)) where \(\xi = E_0 (\psi )\) and \(\nu = var_0 (\psi )\). According to the empirical Bayes method, preliminary values of the hyperparameters \(\varvec{\eta } = (\xi , \nu )\) are obtained by maximizing the marginal likelihood:

$$\begin{aligned} \hat{\varvec{\eta }}_{EB} = \arg \max _{\varvec{\eta } \, \in H} \, \int _{\psi \in {\varPsi }} {\mathcal{L}} (D \mid \psi ) \, \pi _0 \, (\psi \mid \varvec{\eta }) \, d \, \psi \end{aligned}$$
(4)

and by setting the standard deviation to 90% of the corresponding mean (\(\sqrt{\nu } \approx 0.9 \, \xi\)), to avoid the estimate provided for the variance through the maximation (Eq. 4) being too close to zero. This procedure clearly implies a double use of the data: first in assigning the hyperparameters, and then in evaluating the posterior distributions. This philosophically undesirable double use can become a serious issue when the sample size is fairly small, as in our case. A solution is provided by calculation of the marginal likelihood on a grid of hyperparameter vectors that covers a large subset of the space surrounding the empirical Bayes estimates \(\hat{\varvec{\eta }}_{EB}\), and choice of priors that span the range of the likelihood function (Berger 2006); i.e., the hyperparameters are varied around their preliminary estimates \(\hat{\varvec{\eta }}_{EB}\) and those values that include most of the mass of the likelihood function are chosen, as long as they do not extend too far. Figure 1 shows the values obtained for the marginal \(\log\)-likelihood function \({\mathcal{L}} (D)\) as hyperparameters of the prior distribution of \(\varvec{\theta }_{\ell }\) vary (we note that the hyperparameters are linked to the expected means \(E_0(\alpha ), E_0(\beta )\), and \(E_0(\rho )\)). For a more detailed description of this procedure, we refer the reader to Varini and Rotondi (2015).

Fig. 1
figure 1

Values of the marginal \(\log\)-likelihood \({\mathcal{L}} (\varvec{\theta }_{\ell })\) obtained by varying the prior hyperparameters. The width of the darkest areas gives a hint of the dispersion of the corresponding prior distributions

Full size image

Model comparison We now compare the new proposed model with the representative ones of the two classes of self-exciting and self-correcting models. For the former, the ETAS model was chosen, and for the latter, the stress-release  model. Among the Bayesian oriented criteria for model selection, we adopt the classical Bayes factor and the Ando and Tsay criterion. The Bayes factor aims at model comparison by looking for the model that best fits the data, whereas the Ando and Tsay criterion chooses which model gives the best predictions of future observations generated by the same process as the original data.

Given the models \({\mathcal{M}}_1\) and \({\mathcal{M}}_2\), and the dataset D, the Bayes factor is the ratio of the posterior odds to prior odds:

$$\begin{aligned} BF_{12} = \frac{Pr(D \mid {\mathcal{M}}_1)}{Pr(D \mid {\mathcal{M}}_2)} = \frac{Pr({\mathcal{M}}_1 \mid D )}{Pr({\mathcal{M}}_2 \mid D )} \div \frac{Pr({\mathcal{M}}_1)}{Pr({\mathcal{M}}_2)} . \end{aligned}$$

Assuming that the prior probabilities of the two models are equal, the Bayes factor coincides with the posterior odds. The densities \(Pr( D \mid {\mathcal{M}}_k), \, k=1,2\) are the marginal likelihoods, also referred to as evidence for \({\mathcal{M}}_k\), obtained by integrating over the parameter space with respect to the prior distributions \(\pi (\theta _k \mid {\mathcal{M}}_k)\):

$$\begin{aligned} Pr(D \mid {\mathcal{M}}_k) = \int Pr(D \mid \theta _k, {\mathcal{M}}_k) \, \pi (\theta _k \mid {\mathcal{M}}_k) \, d \theta _k . \end{aligned}$$

According to the interpretation of Jeffreys’ scale given by Kass and Raftery (1995), values in the three ranges (0, 0.5), (0.5, 1), (1, 2) of the \(\log _{10} BF_{12}\) indicate barely worth mentioning, positive, and strong evidence in favor of the model \({\mathcal{M}}_1\), respectively.

Different information criteria are proposed in the literature to determine the predictive accuracy of a model. Among these, the Watanabe-Akaike information criterion (WAIC) (Watanabe 2010) is considered to be fully Bayesian, because the predictive distribution is averaged over the posterior distribution \(\pi (\theta \mid D)\). If, as in our case, the data are not independent given parameters, the Ando and Tsay criterion (Ando and Tsay 2010) should be used, where the joint density can be decomposed into the product of the conditional densities \(Pr(D \mid \theta ) = \prod _{i=1}^N Pr(y_i \mid y_{(1:i-1)}, \theta )\) being \(D = (y_1, \ldots , y_N)\). The definition of this criterion is the following:

$$\begin{aligned} PL({\mathcal{M}}_k) = \frac{1}{N} \left( \int \log \, Pr( D \mid \theta , {\mathcal{M}}_k) \, \pi (\theta \mid D) \, d \theta \, - \, \frac{p}{2} \right) \end{aligned}$$
(5)

where the bias correction p is the dimension of the parameter vector, and it is applied to adjust for the higher accuracy of the prediction of the observations than the accuracy of the prediction of the future data. The integral (5) can be evaluated by exploiting samples from the posterior \(\pi (\theta \mid D)\) obtained in the McMC estimation procedure. Moreover, to be on the same scale as other criteria, we multiply by \(-2 \, N\) so that we have:

$$\begin{aligned} PL({\mathcal{M}}_k) = p \, - \, \frac{2}{R} \sum _{j=1}^R \log Pr( D \mid \theta ^{(j)}, {\mathcal{M}}_k ) . \end{aligned}$$
(6)

4 Application

4.1 Dataset construction

In the present study, we used publicly available databases (at the time this study was carried out): the Database of Individual Seismogenic Sources (DISS, version 3.0.2; DISS Working Group 2007), and the Parametric Catalog of Italian Earthquakes version 2004 (CPTI04; Gruppo di lavoro CPTI 2004), and its most recent release v1.5 (CPTI15; Rovida et al. 2016). DISS is a large repository of geological, tectonic and active fault data for Italy and the surrounding areas. The database stores two main categories of parameterized crustal fault sources: individual seismogenic sources (ISS) and composite seismogenic sources (CSS), both of which are considered to be capable of releasing earthquakes of \(M_w\) 5.5 or greater. This threshold value characterizes potentially destructive earthquakes in Italy. To allow for potential underestimation of the earthquake magnitudes, we considered all of the main earthquakes with moment magnitude larger than 5.3 as strong. Whereas the ISS are assumed to show ‘characteristic’ behavior with respect to rupture length and expected mean and maximum magnitude, the CSS have more loosely defined length that can comprise two or more individual sources, and they can produce earthquakes of any size, up to an assigned maximum. In particular, we considered the Salto Lake-Ovindoli-Barrea CSS025 source that straddles the backbone of the central Apennines. This source has been hit by some of the most complex and destructive earthquakes in Italy, where the main ones were September 9, 1349 (\(M_w\) 6.5, Aquilano), January 13, 1915 (\(M_w\) 7.0, Avezzano), May 7, 1984 (\(M_w\) 5.9, Abruzzo Appennines), and finally April 6, 2009 (\(M_w\) 6.26 L’Aquila). According to Basili, as one of the compilers of DISS (Basili et al. 2008), 38 earthquakes drawn from CPTI04 and of magnitude greater than \(m_0 = 4.45\), can be associated with the CSS025 source (Basili R., personal communication); we adopted this value as minimum threshold in agreement with the choice made in elaborating the most recent Italian reference seismic hazard model (Meletti et al. 2017). In light of the most recent catalog, CPTI15, we updated the events of this set and added the secondary events. Indeed, contrary to CPTI04, CPTI15 is not declustered and contains all of the available and known foreshock and aftershocks data; we note that the aftershocks are marked by the compilers of the catalog. In this way, we obtained a set of \(N = 58\) earthquakes, as listed in Table 2, that occurred after 1873, to guarantee the completeness of the catalog for the considered level of magnitude, according to the change-point method (Rotondi and Garavaglia 2002). This set consists of 9 leader events with \(M_w \ge 5.3\), and 49 subordinate events. To simplify the implementation of the model, the set starts and ends with a leader event; the spatial and time distribution of the data is given in Fig. 2.

Table 2 List of the earthquakes associated with the Italian composite seismogenic source 25 (database DISS v. 3.0.2) with magnitude of at least 4.45
Full size table

4.2 Graphical method and statistical tests for identification of failure models

Before fitting the new model to the dataset, we checked whether informal testing of hypotheses supports our conjectures on the shape and aging properties of the hazard function of the subordinate events. As we noted in Sect. 2, for each interval \((t_i, t_{i+1})\) the normalized occurrence times \(s_{i1}\), \(s_{i2}\), \(\dots\), \(s_{i n_i}\) can be considered as an ordered sample of failures from the lifetime distribution F(s) on (0, 1). For \(i=1,\ldots ,n_i\), we collect these failure times in a single set \((X_1, X_2, \ldots , X_{n_s})\) of \(n_s =\sum _{i=1}^{n-1} n_i\) random variables, and let \(\varvec{X}_{n_s} = (X_{(1)}, X_{(2)}, \ldots , X_{(n_s)})\) denote the vector of the associated order statistics: \(X_{(1)} \le X_{(2)} \le \ldots \le X_{(n_s)}\). The total time spent on test by the \(n_s\) sample units until the failure of the longest living unit is defined as: \(T_{n_s} = \sum _{j=1}^{n_s} X_{(j)} = \sum _{j=1}^{n_s} (n_s -j +1) (X_{(j)} - X_{(j-1)})\), where \(D_j = (n_s -j +1) (X_{(j)} - X_{(j-1)})\) is called a normalized spacing. \(T_{n_s}\) is known as the total-time-on-test (TTT) statistic; other statistics can also be considered:

  • successive TTT-statistics \(T_k = \sum _{j=1}^k X_{(j)} + (n_s -k) X_{(k)}\)

  • scaled TTT-statistics \(T_k^* = \displaystyle \frac{T_k}{T_{n_s}}\)

for \(k=1,2,\ldots ,n_s\). As the only continuous distribution with constant hazard rate is the exponential distribution, we examine the trend of the hazard function by testing the null hypothesis \(\hbox {H}_0\): ‘\(F(\cdot )\) is exponential’, against the alternative hypothesis, \(\hbox {H}_a\): ‘\(F(\cdot )\) is not exponential’. Among the numerous existing goodness-of-fit tests, we choose the Barlow–Proschan test based on the scaled TTT statistics (Barlow and Campo 1975). Under \(\hbox {H}_0\), the random variable \(W = \sum _{k=1}^{n_s -1} T_k^*\) has mean \(\displaystyle \frac{n_s-1}{2}\) and variance \(\displaystyle \frac{n_s-1}{12}\), and it is asymptotically normally distributed. Hence the hypothesis is rejected with significance level \(\alpha\), if \(w \ge u_{\alpha } \sqrt{\displaystyle \frac{n_s-1}{12}} + \displaystyle \frac{n_s-1}{2}\) where \(u_{\alpha }\) denotes the upper 100 \(\alpha\)% percentile of the standard normal distribution. To test the hypothesis \(\hbox {H}_0\) against the alternative hypothesis \(\hbox {H}_a\), ‘\(F(\cdot )\) is bathtub shaped’, Bergman (1979) proposed to evaluate the following quantities:

$$\begin{aligned}{ll} V_{n_s}^*= & {} \left\{ \begin{array}{l} \min \left\{ i \ge 1: \; T_i^* \ge \displaystyle \frac{i}{n_s} \right\} \\ n_s \; \mathrm{if} \; T_i^* < \displaystyle \frac{i}{n_s} \; \mathrm{for} \; i= 1,2, \ldots , n_s -1; \\ \end{array} \right\} \\ K_{n_s}^*= & {} \left\{ \begin{array}{l} \max \left\{ i \le n_s - 1: \; T_i^* \le \displaystyle \frac{i}{n_s} \right\} \\ 0 \; \mathrm{if} \; T_i^* > \displaystyle \frac{i}{n_s} \; \mathrm{for} \; i= 1,2, \ldots , n_s -1; \\ \end{array} \right\} \\ G_{n_s}^*= & {} \begin{array}{l} V_{n_s}^* + n_s - K_{n_s}^* \\ \end{array} \end{aligned}$$

where \(G_{n_s}^* \in [2, n_s +1]\), and to reject \(\hbox {H}_0\) in favor of \(\hbox {H}_a\) when \(G_{n_s}^*\) is large. Then Aarset (1985) gave an asymptotic result for the \(Pr(G_{n_s}^* = n_s -k)\):

$$\begin{aligned} \lim _{n \rightarrow \infty } n \, Pr(G_{n_s}^* = n_s -k) = 2 \displaystyle \frac{k^{k+1}}{(k+1)!} \exp (-k) . \end{aligned}$$

The p-value for the Barlow–Proschan test applied to the \(n_s\)=49 normalized failure times is \(1.02 \times 10^{-5}\). As far as the Bergman test is concerned, with \(V^*_{49} = 36\) and \(K^*_{49} = 35\), we get \(G^*_{49} = 50\), which is the largest possible value for \(G^*_{49}\) that corresponds to the p-value 0.105. Hence we reject the hypothesis of constant hazard rate in favor of non-exponential and bathtub-shaped hazard, respectively.

Informal procedures just based on graphs can also be useful to discriminate the behavior of the hazard function. The TTT plot is obtained by plotting \(T_k^*\) on the ordinate against the empirical cumulative distribution function \(F_{n_s}(x_{(k)}) = k/n_s\) on the abscissa, and connecting the \(n_s\) points by straight lines. When F(s) is an exponential distribution (constant hazard rate), then the TTT plot is a \(45^{\circ }\) line that runs from (0,0) to (1,1). Instead, the TTT plot is concave (convex) for an increasing (decreasing) hazard function. For the nonmonotonic hazard rate, the TTT plot has a bathtub shape (decreasing-increasing course) or an inverted bathtub shape (increasing-decreasing course). In the former, the TTT plot is convex and lies below the \(45^{\circ }\) line in the leftmost part, and is concave and lies above the \(45^{\circ }\) line in the rightmost part of the plot; vice versa in the latter case. Figure 3 shows the TTT plot for the \(n_s=49\) normalized failure times associated with the subordinate events. Also in this case, there are clear indications in favor of the bathtub behavior of the failure rate of those events, in agreement with the generalized Weibull functions we adopted in Sect. 2.

Fig. 2
figure 2

Left: Epicenters of the analyzed events, which are associated with the composite seismogenic source 25 (polygon) of the Italian DISS database (release 3.0.2): Stars, leader events numbered in chronological order, diamonds, subordinate events of the same color as the leader event that precedes them. Right: Magnitude versus occurrence time. Red lines, leader events; blue lines, subordinate events

Full size image
Fig. 3
figure 3

TTT plot of the \(n_s = 49\) normalized failure times associated with the subordinate events

Full size image

4.3 Results

Before illustrating the results achieved by fitting the three models, as the stress-release, ETAS and compound models, separately for the selected data, we want to make a clarification regarding the dataset. The CPTI15 parametric catalog from which these data were extracted is the richest collection of both historical and instrumental information on Italian seismicity. However, just for this reason, it has characteristics that both advantage and disadvantage the classical models for hazard assessment. It cannot include all of the secondary events of past strong earthquakes, as required by the ETAS model, nor include just earthquakes that release most of the energy stored in a fault structure, as implied by the stress-release model. For this reason we do not expect the best performance from these two models, which also explains the need for a composite model.

Following the approach explained in Sect. 2 for prior elicitation, the parameters are assigned to the prior distributions of all of the model parameters, which are reported in Table 3. As we will see later, the compound model \({\mathcal{C}}_{MW}\) with MW distribution for the ordered failure times provides slightly better performance than the model \({\mathcal{C}}_{AW}\) with AW distribution. For this reason, and for the sake of space, we omit here some of the results concerning the AW case in Table 3 and in the following. We note that the parameters of every distribution, including Gamma distributions, correspond to mean and variance contrary to the common parametrization.

Table 3 Prior distributions of the parameters of the three models, as the compound, stress-release, and ETAS models. The parameters correspond to mean and variance. The modified Weibull distribution with parameters \(a_1, \, b_1, \, c_1\) models the failure times of the subordinate events in the compound model
Full size table

The marginal likelihood, on a \(\log _{10}\) scale, of the three models indicates: \(\log _{10} {\mathcal{L}}_{SR}(data) = -54.850\) for the stress-release model; \(\log _{10} {\mathcal{L}}_{ETAS}(data) = -8.551\) for the ETAS model; and \(\log _{10} {\mathcal{L}}_{{\mathcal{C}}_{MW}}(data) = -2.745\) and \(\log _{10} {\mathcal{L}}_{{\mathcal{C}}_{AW}}(data) = -2.847\) for the compound model with the MW and AW distributions, respectively. In light of these results, we evaluate the Bayes factor of the compound model \({\mathcal{C}}_{MW}\) (\({\mathcal{M}}_1\)) with respect to the stress-release model (\({\mathcal{M}}_2\)) and with respect to the ETAS model (\({\mathcal{M}}_2\)). Here, we have \(\log _{10} BF_{12} = 52.105\) and \(\log _{10} BF_{12} = 5.806\), respectively. By analogy, using the model \({\mathcal{C}}_{AW}\), we have \(\log _{10} BF_{12} = 52.003\) and \(\log _{10} BF_{12} = 5.704\), respectively. Comparing the Bayes factors with Jeffreys’ scale (Kass and Raftery 1995) it can be seen that the evidence in favor of the compound model is decisive; although, as observed at the beginnig of this subsection, such an evidence is not surprising given the type of catalog analyzed, the strength of this evidence is so large that we are confident about the possibility of obtaining good performances also in other applications. Details of the computational aspects relating to the evaluation of the Bayes factor can be found in Rotondi and Varini (2007).

Through the MH algorithm (Sect. 3) we have now generated sequences of \(R_{tot} = 5{,}500{,}000\) samples from the posterior distributions of the parameters, of which 500,000 are discarded as burn-in. To reduce autocorrelation, these chains are then thinned, with discarding of all but every 125-th value. Lognormal distributions are used as proposal distributions, with the mean equal to the current value of the Markov chain and the variance such that the value of the resulting acceptance rate is in the range (25%, 40%). Finally, some diagnostics are applied to check the convergence of each Markov chain to its target distribution, which are implemented in BOA R package. The posterior mean and standard deviation of each model parameter are reported in Table 4. As an example of the posterior distributions produced by the MH algorithm, Fig. 4 shows the prior and posterior densities of the parameters \(\gamma\), \(\rho\), and a of the compound, stress-release, and ETAS models, respectively.

As for the ETAS model, we note that the parameter estimates satisfy the conditions that make the process non-explosive, that is, \({\hat{p}}>1\), \({\hat{b}} > {\hat{a}}\), and \({\hat{K}} < ({\hat{b}}-{\hat{a}})/{\hat{b}}\). The estimated loading rate, \({\hat{\rho }}=0.016\), of the stress release component of the compound model is consistent with the value obtained in Varini et al. (2016) by taking into account the events exceeding the magnitude threshold \(M_w \, 5.3\), associated with the Italian composite seismogenic sources that share the same tectonic characteristics. The same parameter in the stress-release model has larger value, \({\hat{\rho }}=0.20\), because it must compensate for larger stress release due to the analysis of the entire data set.

An element that differentiates the bathtub-shaped hazard functions of the two considered generalized Weibull distributions is their turning point \(t^*\). Their explicit expression, given in Sect. 2.2, is not appropriate in our case because the respective hazard functions h(s) are truncated on (0, 1); hence we have calculated them numerically obtaining \(x^* = 0.186\) and \(x^* = 0.335\) for the modified and additive Weibull distributions respectively. This suggests that the modified Weibull distribution performs better than the additive one when the considered seismicity has shorter aftershock sequences, with respect to the average time between pairs of consecutive strong earthquakes.

Fig. 4
figure 4

Examples of the prior and posterior densities of the \(\gamma\), \(\rho\), and a parameters of the compound, stress-release and ETAS models, respectively

Full size image
Table 4 Posterior means and standard deviations (in brachets) of the parameters of the compound, stress-release, and ETAS models. The modified Weibull distribution with parameters \(a_1, \, b_1, \, c_1\) models the failure times of the subordinate events in the compound model
Full size table

On the basis of the Markov chains generated through the MH algorithm, we have estimated in two ways the conditional intensity functions \(\lambda _{SR}\) and \(\lambda _{ETAS}\) of the stress-release and ETAS models, and the hazard h(s) and density f(s) functions of the generalized Weibull distributions. The first is to replace the parameter estimates in the functions to obtain the so-called plug-in estimates; e.g., for every \(\tau \in (t_i, t_{i+1}), \, i=1, \ldots ,n-1\), the plug-in estimate of the density function of the modified Weibull distribution is given by \({\hat{f}} (s \mid \hat{\varvec{\theta }}_a) = {\hat{f}}^* \left( \displaystyle \frac{\tau -t_i}{t_{i+1}-t_i} \mid \hat{\varvec{\theta }}_a \right) /(t_{i+1}-t_i)\), where \(\hat{\varvec{\theta }}_a = \left( {\hat{a}}_1, {\hat{b}}_1, {\hat{c}}_1 \right)\) is the vector of the posterior estimates. The second way is to estimate the density function through the ergodic mean:

$$\begin{aligned} {\tilde{f}}^* \left( \displaystyle \frac{\tau -t_i}{t_{i+1}-t_i} \right) /(t_{i+1}-t_i) = \frac{1}{R} \sum _{j=1}^R f^* \left( \displaystyle \frac{\tau -t_i}{t_{i+1}-t_i} \mid \varvec{\theta }_a^{(j)} \right) /(t_{i+1}-t_i), \end{aligned}$$

where \(\varvec{\theta }_a^{(j)} = \left( a_1^{(j)}, b_1^{(j)}, c_1^{(j)} \right)\) is the jth element of the Markov chains generated for each parameter by the MH algorithm. Through the sequence \({\left\{ f^* \left( \displaystyle \frac{\tau -t_i}{t_{i+1}-t_i} \mid \varvec{\theta }_a^{(j)} \right) \right\} }_{j=1}^R\), we can also obtain the median and quartiles of the point-wise estimates \({\tilde{f}}^*(s)\). These estimates are shown in Fig. 5, for the ergodic mean, plug-in estimate, and median, with the 10% and 90% quantiles. Analogously, we evaluated the estimates of the hazard function \(h^*(\tau )\), as shown in Fig. 6, and of the conditional intensity function of the stress-release and ETAS models, as shown in Fig. 7, for the ergodic mean, plug-in, and median, with the 10% and 90% quantiles.

Through the Markov chains generated in the estimation procedure, we evaluated the Ando and Tsay information criterion (6) with the natural logarithm. This provided \(PL_{SR} = 254.878\) for the stress-release model, \(PL_{ETAS} = 38.518\) for the ETAS model, and \(PL_{{\mathcal{C}}_{MW}} = 16.464\) (\(PL_{{\mathcal{C}}_{AW}} = 16.328\)) for the compound model. Both of the model selection criteria show strong evidence in favor of the compound model with respect to the other candidates.

Fig. 5
figure 5

Top: Estimates of the density function of the modified Weibull distribution, as ergodic mean (blue line), plug-in estimate (dotted line), and median (black line), with 10% and 90% quantiles (gray line). Bottom: Magnitude versus occurrence time of the data

Full size image
Fig. 6
figure 6

Compound model: estimates of the hazard function of the modified Weibull distribution, as ergodic mean (red line), plug-in (dotted line) estimate, and median (black line). These are practically indistinguishable from each other. Also shown: 10% and 90% quantiles (gray line)

Full size image
Fig. 7
figure 7

Estimates of the conditional intensity function of the stress-release (left) and ETAS (right) models, as ergodic mean (red line), plug-in estimate (dotted line), and median (black line). These are practically indistinguishable from each other. Also shown: 10% and 90% quantiles (gray line)

Full size image

5 Final remarks

In this study we propose a new compound model for earthquake occurrences that captures contrasting features of seismic activity related to the clustering and elastic rebound processes. Other models in the literature share this aim, but they originated in contexts that differ both for the availability of geological and geodetic data and the wealth of historical information. Indeed, some seismically active regions are charactized by mainly linear faults, such as the Sant Andreas fault that extends for roughly 1300 km through California. When an earthquake takes place along that fault, it means that some section of that system has ruptured, which reduces the probability of that subsection participating in a future earthquake. On the contrary, in Italy we have complex, fragmented fault systems that extend 40–50 km in southern Italy and just 10–20 km in central Italy, the components of which are small faults that are related to each other in a dynamic way.

A weak point of the proposed model is a consequence of its multi-level structure; in fact, because of its hierarchical structure, uncertainty in forecasting a single variable increases; e.g., for the law of the total variance, the error (var(N)) in the number of subordinate events N is the sum of the expected variance of N as we average over all values of the length \({\varDelta }t\) of the interval between two consecutive leader events (\(E[var(N| \, {\varDelta }t)]\)), and the variability of \(E(N| \, {\varDelta }t)\) itself (\(var[E(N| \, {\varDelta }t)]\)).

As indicated in the text, more general versions of the model can be investigated which allow time-dependent parametrization of the generalized Weibull distribution (see Sect. 2.2) and can be applied to more general data sets (see Sect. 3). Moreover we plan to examine in the future which zones are most suitable for the application of the new model: seismogenic sources, when the events associated with their fault structures are known; or larger areal sources characterized by their tectonic properties.