Abstract
Intensity–duration–frequency (IDF) curves of extreme rainfall are used extensively in infrastructure design and water resources management. In this study, a novel regional framework based on quantile regression (QR) is used to estimate rainfall IDF curves at ungauged locations. Unlike standard regional approaches, such as index-storm and at-site ordinary least-squares regression, which are dependent on parametric distributional assumptions, the non-parametric QR approach directly estimates rainfall quantiles as a function of physiographic characteristics. Linear and nonlinear methods are evaluated for both the regional delineation and IDF curve estimation steps. Specifically, delineation by canonical correlation analysis (CCA) and nonlinear CCA (NLCCA) is combined, in turn, with linear QR and nonlinear QR estimation in a regional modelling framework. An exhaustive comparative study is conducted between standard regional methods and the proposed QR framework at sites across Canada. Overall, the fully nonlinear QR framework, which uses NLCCA for delineation and nonlinear QR for estimation of IDF curves at ungauged sites, leads to the best results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Heavy rainfall events are responsible for damaging floods across the world. Hence, an appropriate characterization of rainfall extremes is important in the fields of water management, civil engineering, building design, and public safety, among many others. Producing reliable estimates of the frequency and magnitude of extreme rainfall events has long been a pressing and widely studied problem in science and engineering (e.g., El Adlouni et al. 2007; Chu et al. 2009; Matonse and Frei 2013; Langousis et al. 2016).
In this respect, Intensity–Duration–Frequency (IDF) curves, which summarize the magnitude of extreme rainfall events for specified return periods (e.g., 2- to 100-year) and storm durations (e.g., 5-min to 24-h), are widely used in hydrological infrastructure design, as well as other engineering applications (e.g., Willems 2000; Langousis and Veneziano 2007; Cheng and AghaKouchak 2013). When sufficiently long historical data series exist, curves can generally be estimated with reasonable accuracy based on standard extreme value analysis methods. In Canada, for example, IDF curves are estimated by fitting the Gumbel distribution to annual maximum rainfall series (Hogg et al. 1989).
In many parts of the world, however, dense networks of short-duration rainfall observing sites with long records do not exist. This raises the following question: how then does one obtain IDF curves at partially gauged or ungauged sites? In this case, estimates are typically made using some form of regional frequency analysis (RFA). Initially developed for hydrological flood frequency analysis purposes (Darlymple 1960), RFA pools information on extremes from gauged sites in a region and then transfers that information to ungauged sites (e.g., Stedinger 1983; Cunnane 1988; Hosking and Wallis 2005; Wallis et al. 2007; Renard and Lall 2014). A fundamental assumption of RFA is that the region of interest is sufficiently homogenous, i.e., gauged sites should be selected so that the similarity with the ungauged target site is maximized. Hence, the so-called the delineation of homogeneous regions (DHR) of the study area forms the first step in RFA.
A large body of RFA literature has dealt with delineation approaches for identifying geographically contiguous regions, geographically non-contiguous regions, or hydro-climatological neighborhoods regions (e.g., Nathan and McMahon 1990; Chokmani and Ouarda 2004; Wazneh et al. 2015; Rodriguez et al. 2016). Among the various delineation methods, neighborhood approaches, mainly the region of influence (ROI) and canonical correlation analysis (CCA) methods, are the most prominent. A review of each method is provided in Burn (1990) and Cavadias (1990), respectively. Within the CCA framework, a recent work by Ouali et al. (2016a) on nonlinear CCA (NLCCA) has demonstrated the added value of considering nonlinear relationships when identifying homogeneous regions.
Once a homogenous region has been identified, information on rainfall extremes is then transferred to the ungauged site. Two main quantile estimation methodologies are in common use, namely the parametric index flood approach (Darlymple 1960), which is known as the ‘index-storm’ approach when dealing with rainfall extremes (e.g., Schaefer 1990; Brath et al. 2003; Di Baldassarre et al. 2006; Cannon 2015; Pizarro et al. 2015), and the at-site regression approach (e.g., Pandey and Nguyen 1999). To avoid any potential confusion, it is worth noting that the at-site regression terminology used in the rest of this paper refers to the regional regression model using at-site quantiles estimates as the response variable.
The index-storm approach fits a common parametric probability distribution to scaled annual rainfall maxima for a given storm duration in the region; the scaling factor, the so-called “index-storm”, varies in space and is often taken to be the at-site sample mean. Given the parameters of the regional distribution and an estimate of the index-storm at an ungauged location (e.g., by a regression equation with physiographic and climate variables as predictors), one can then estimate IDF curves at the ungauged location. A common issue with the index-storm approach is the assumption of a constant coefficient of variation within a specified homogeneous region, which has been questioned in a number of studies in different regions of the world (Schaefer 1990; Asquith 1998; Alila 1999).
This limitation has, in part, motivated the development of the at-site regression approach to RFA. An ordinary least-square (OLS) regression model, with physiographic and climate variables as predictors, is used to estimate at-site quantiles within the delineated region. This approach has demonstrated good performance in previous RFA studies dealing with flood events (e.g., Pandey and Nguyen 1999; Shu and Burn 2004; Ouarda et al. 2006; Haddad and Rahman 2012; Ouali et al. 2017). One major issue with the at-site regression approach is that it only provides an estimate of the conditional mean of the response variable, rather than the quantiles that make up the IDF curves. Hence, fitting the OLS regression model naturally requires that the at-site quantiles be estimated first; these at-site values are then used as the response variable in the regression model. Because short-duration precipitation series at many sites are of insufficient length to accurately estimate the at-site quantiles, the use of OLS regression may not adequately represent the true regional predictor-response relationship of interest. Overall, at-site regression in RFA makes inefficient use of the available data.
To address this deficiency, Ouali et al. (2016b) proposed the quantile regression (QR) model for RFA of extreme hydrological events and estimation of extremes at ungauged sites. Unlike OLS regression, which involves at-site estimation of quantiles as a pre-processing step, QR directly links the physiographic and climate predictors to the annual maxima at all sites within the delineated region, i.e., it estimates the conditional quantiles directly, thus avoiding the at-site frequency analysis step and its inherent uncertainties. The focus of Ouali et al. (2016b) was on the efficiency of the QR approach relative to OLS regression. They did not address the delineation step of RFA. Moreover, while the nonlinear aspect of hydro-metrological processes has long been recognized, they only considered a linear version of the QR model. Advantages of nonlinear QR models for modelling precipitation data have been demonstrated by Cannon (2011), albeit in a climate downscaling context.
In the current study, the focus lies on: (1) the use of regional QR methods, which can make more efficient use of available information than classical approaches, for estimating rainfall IDF curves; (2) an exploration of methods for delineating homogeneous regions for each site of interest; and (3) the investigation of the potential added value of nonlinear methods for both delineation and estimation steps. The ultimate goal is the development of a QR framework for RFA that provides more accurate estimates of design storms at ungauged sites. Drawing on work by Cannon (2011) and Ouali et al. (2016a, b), linear and nonlinear methods are evaluated for both the regional delineation and IDF curve estimation models. Specifically, delineation by canonical correlation analysis (CCA) and nonlinear CCA is combined, in turn, with IDF curve estimates by QR and nonlinear QR in a regional modelling framework. An exhaustive comparative study is conducted between standard regional methods and the proposed QR framework at sites across Canada.
The outline of this paper is as follows. Section 2 briefly describes the observational data. Section 3 gives background on the statistical methods. Section 4 details the implementation of the proposed approaches. Section 5 summarizes results of this study and includes a discussion of main findings. Finally, Sect. 6 draws a few concluding remarks and avenues for future research.
2 Data
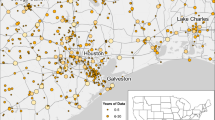
Rainfall data used in the current study consist of annual rainfall maxima series obtained from Environment and Climate Change Canada for 564 tipping bucket rain gauge (TBRG) stations across Canada. The available extreme rainfall observations are recorded over the period between 1905 and 2013 for 5, 10, 15, 30-min and 1, 2, 6, 12, 24-h durations. This spans time scales from short duration convective events (e.g., 5-min to 2-h) to longer duration cyclonic weather systems (e.g., 6- to 24-h). Table 1 summarizes characteristics of the rainfall data for each duration. Figure 1 shows the geographical locations of the recording stations, as well as the associated record lengths for the 24-h duration. There are 14,740 station-years for the 24-h duration, which has the longest average record length. Hence, most of results presented here will mainly deal with the 24-h storm-duration. Figure 2 shows frequency distributions of record length for each of the storm durations.
As a practical matter, it is worth pointing out that quality control and basic checks are applied prior to publication of the TBRG data set. This may reduce inhomogeneity in the data series. More details regarding the TBRG network, instrumentation, and quality control procedures can be found in Shephard et al. (2014). In order to be deemed reliable, the data underwent further checking of statistical assumptions, mainly independence and stationarity of the series. To validate the serial independence assumption, the annual maxima data are tested for serial correlation using the Ljung-Box-Q test (Ljung and Box 1978) under the null hypothesis of zero correlation. For the 24-h duration, the null hypothesis was rejected at just 9% of sites at a 5% significance level (5% of sites at a 1% significance level). Similar rejection rates were found for the remaining storm durations. To check for the stationarity assumption at each site, the non-parametric Mann–Kendall test for monotonic trend was conducted at a 5% significant level for all storm durations. Except for three cases (Charlottetown A, ID 8300300 for long durations; BEAUSOLEIL, ID 6110617 and CYPRUS LAKE CS, ID 6121940 for short durations), no significant trend was detected.
Apart from the rainfall data set, a second set of physiographic variables is also required for DHR and for use as predictors in the regional regression equations. A simple set of variables is used here, namely longitude (LON), latitude (LAT), elevation above sea level (ELv), surface roughness (RGH), slope (SLP), and aspect (ASP). A summary of basic statistics of this data set is tabulated in Table 2.
3 Statistical methods
The following section provides a brief description of the statistical methods that make up the RFA approaches under consideration, as well as information on the statistical criteria used to evaluate model performance. Each RFA approach consists of a method for DHR in combination with a method for quantile estimation. Details on the implementation of each RFA approach will be provided in Sect. 4.
3.1 Delineation of homogeneous regions
Delineation of homogeneous regions (DHR) identifies sites with similar hydro-meteorological characteristics based on some measure of distance, usually measured in hydro-meteorological, geographic/physiographic, or some combined spaces. DHR is often the most critical step of RFA. Overall accuracy depends strongly on how homogeneous regions have been identified. For this reason, and given the large geographical extent of the study area, close attention is paid to DHR in this study.
In the following, a short overview of three DHR methods used in this work is provided. This includes Canonical Correlation Analysis (CCA), nonlinear CCA (NLCCA), and region of influence (ROI) methods.
3.1.1 Canonical correlation analysis
Canonical Correlation Analysis (CCA) is a multivariate statistical technique that is commonly used to identify co-varying modes of large-scale climate variability, often for use in seasonal climate prediction tasks (e.g., Barnston and Ropelewski 1992; Shabbar and Barnston 1996; Giannini et al. 2000; Werner et al. 2013). In the hydrological RFA context, CCA is instead used to define the multivariate space for identifying hydrological neighborhoods. Indeed, CCA is considered as one of the most powerful DHR methods (Ouarda et al. 2001). Despite its high performance in hydrological applications, to best of the authors’ knowledge, CCA has not been adopted in RFA of precipitation extremes.
In order to represent the relationship between two sets of variables, CCA creates new canonical variables resulting from linear combinations of the original sets of variables (e.g., physiographic and hydrological/climatological variables). Hence, a new canonical space is built under constraints of unit variance and maximum correlation between pairs of canonical variables. Once subsets of canonical variables have been identified, an examination of similarities between grouped sites is carried out to verify the significance of the canonical correlation coefficients. The location of the target site in the hydrological canonical space is identified and neighbouring gauged sites are found using the Mahalanobis distance (or other distance metric). The homogeneous region is formed by selecting the sites closest to the target site in the canonical space. For more detailed descriptions of CCA for DHR, the reader is referred to Cavadias (1990) and Ouarda et al. (2001).
3.1.2 Nonlinear canonical correlation analysis
Driven by the need to account for nonlinear relationships between two sets of variables, a nonlinear version of linear CCA based on artificial neural networks (ANN), NLCCA, was developed by Hsieh (2000) and extended by Cannon and Hsieh (2008). Subsequently, NLCCA has been recommended for use in DHR for flood frequency analysis by Ouali et al. (2016a) and Ouali et al. (2017).
Similar to CCA, NLCCA produces new canonical variables as nonlinear (rather than linear) combinations of the two original sets of variables (e.g., physiographic and hydrological/climatological variables). Again, the new canonical space is built under constraints of unit variance and maximum correlation between pairs of nonlinear canonical variables. Initially, the first NLCCA mode is extracted from the set of physiographic variables and the set of hydro-climatological variables. After retrieving the first NLCCA mode from the data, the method is applied for a second time to the residual (i.e., the original data minus the first NLCCA mode) to extract the second mode. Once the canonical variables that explain a given percentage of explained variance are identified, the neighborhood of each target site is identified following the same scheme as in the linear case. Figure 3 illustrates the concept of DHR using the NLCCA.
3.1.3 Region of influence (ROI)
Given its simplicity and popularity in RFA of precipitation extremes, the region of influence (ROI) approach is also adopted in the current study. The ROI for a given site is formed according to the following procedure; initially, a metric distance (often the Euclidian distance and, less frequently, the Mahalanobis distance) is used to determine the proximity of each site to the target site in the physiographic space. In ascending order of distance, sites closest to the target site are added successively into the ROI for the target site. This continues until a given homogeneity condition is no longer satisfied. For further details about this method, interested readers are referred to Burn (1990).
3.2 Regional quantile estimation
In this section, the statistical foundations of the QR and QRNN methods used for quantile estimation are presented. Henceforth, in a regression terminology, predictors are physiographic attributes of each site belonging to the homogeneous region of the ungauged site, and response denotes the regional quantile at this site associated with a fixed return period.
Recall that the commonly used index storm approach is also involved here for comparison purposes.
3.2.1 Quantile regression
As outlined in the introduction, the main issue with the OLS estimator for RFA is its estimation of the conditional mean of the response distribution. The model minimizes a sum of squared residuals cost function whose solution is given by the conditional mean. In the RFA context, the objective function is thus taken to be the difference, measured in terms of the sums of squared residuals, between the OLS regression predictions and the previously estimated at-site quantiles.
Analogous to the OLS regression, a more robust regression model is provided through minimizing the sum of absolute residuals. The solution of this optimization problem is given by the conditional median, and the regressive model is known as the median regression or the least-absolute deviations (LAD) regression (Chen et al. 2008). In the same direction, and in order to provide estimates of any other quantile order, Koenker and Bassett (1978) introduced the QR model, a technique that directly provides the conditional quantile of the response variable Y, given a set of predictors X.
This model is based on the minimization of the absolute deviation between observations and regression estimates asymmetrically weighted by the quantile p, denoted by the QR loss function:
where b is the vector of regression coefficients and \(\rho_{p} (.)\) is the check function (also known as the tilted absolute value, tick, or pinball loss function) defined as:
Unlike classical OLS regression models, QR estimates conditional values of each individual quantile p, thus providing a complete picture of the stochastic relationships between random variables.
In the RFA framework, the motivation behind using this technique lies in its ability to directly model the quantiles of the raw data rather than the at-site estimated quantiles (Ouali et al. 2016b). This means that the QR, when combined with an appropriate delineation method, avoids the need to estimate the at-site quantiles prior to regression modeling, which implies that misspecifications of the at-site distributions can be avoided. Moreover, using this model, the whole available data set, even sites with extremely short record lengths, is involved in the calibration procedure, thus enabling one to account for much more information than traditional RFA approaches.
3.2.2 Quantile regression neural network
QR and OLS regression models assume linear predictor-response relationships. Given the complexity of precipitation processes (e.g., Hewitson and Crane 1996), it might be worthwhile exploring nonlinear tools to provide a more accurate estimation of rainfall IDF curves at ungauged sites. In this respect, a nonlinear variant of QR based on the ANN model, the QR neural network (QRNN), is exploited in the current study following Taylor (2000) and Cannon (2011). An attractive characteristic of the ANN, which motivates the use of the QRNN for RFA, is its ability to deal with complex relationships that may be revealed within large amounts of data.
From a conceptual viewpoint, estimates of the conditional quantiles using the QRNN are given by:
where \(w_{j}^{(0)}\) and \(b^{(0)}\) are the output-layer weights and bias respectively, f is the output-layer transfer function and gj is the jth hidden-layer transfer function often taken to be the hyperbolic tangent function. The number of hidden nodes, J, controls the nonlinearity of the resulting model. The QRNN is trained by means of the cost function given in Eq. (1). The resulting output is the conditional regional quantile associated for a fixed return period.
Given the flexibility of the ANN architecture, the QRNN is able to represent complex predictor–response relationships. However, as the skill of an ANN-based model is sensitive to its chosen configuration, e.g., the number of hidden-layer nodes J, one must choose the QRNN model parameters with care. Details about the optimization procedure as well as other theoretical details can be found in Taylor (2000) and Cannon (2011).
3.3 Assessment of model performance
The regional models under consideration draw upon several statistical methods. Hence, their application to estimate IDF curves at ungauged sites should be carefully assessed. A leave-one-out cross-validation procedure is adopted for assessing the performance of each model. Records from each gauged site are temporarily removed from the data set used to fit the models, i.e., the site is assumed to be “ungauged”. RFA is then conducted based on data from the remaining sites. Finally, estimated values are compared to the original at-site estimates at the withheld site. This procedure is repeated, with each location acting in turn as an “ungauged” site.
Performance is typically measured by means of statistical evaluation criteria such as the root-mean-square-error (RMSE). For almost all classical regional approaches that make use the at-site estimated quantile, the model assessment is performed assuming that the at-site estimation is the reference value; residual errors are calculated between the at-site estimated quantiles and the RFA estimates. However, given the uncertainty associated to the at-site estimated quantiles, this may be misleading. In reality, these at-site estimates are subject to errors resulting from insufficient data series record length, the choice of the probability distribution, and associated parameter estimation uncertainty.
This issue was raised by Ouali et al. (2016b), who suggested that RFA models instead be assessed using the raw observed values rather than the at-site estimated quantiles. The proposed criterion, the mean of the piecewise loss function (MPLF), is a summation of QR loss function values computed at each site standardized by the number of stations-years:
where \(n = \sum\nolimits_{i = 1}^{N} {n_{i}}\) denotes the number of stations-years. While the main concept of the MPLF criterion is based on the QR objective function, it may be applicable not only to the evaluation of QR models but to any quantile estimation approach. In the forecast verification literature, the MPLF is referred to as the quantile score; it is a proper scoring rule for probabilistic forecasts (Bentzien and Friederichs 2014).
It is straightforward to define a MPLF ratio (\(R_{MPLF}\)) for each \(p \in (0,1)\), expressed as follows:
where \(MPLF_{0}\) is the MPLF of the typical empirical model, and \(MPLF_{M}\) is the leave-one-out cross-validated MPLF of the model of interest. Values of this ratio will typically lie between 0 and 1; for cross-validated regional estimates that match the in-sample performance of the reference, the ratio is equal to 1. Indeed, for approaches using the at-site estimated quantiles as reference, the best model would be the one that provides results as close to the at-site estimated values, taken here to be the empirical estimates. Thus, values close to 1 mean that the estimator has good performance skill, while values close to 0 indicate that the estimator performance is poorer than the reference empirical model.
4 Model design
In the current section, the implementation of each statistical method used in this work is described. For reference, Table 3 lists the various combinations of DHR and estimation methods considered in the remainder of the paper. Steps of the RFA procedure are summarised in Fig. 4.
4.1 Delineation of homogeneous regions
To calculate rainfall intensities for a specific return period and duration at ungauged site, homogeneous regions must first be identified. The three DHR techniques considered in this study (CCA, NLCCA and ROI) are neighborhood approaches; each ungauged site is assigned to its own set of neighboring sites within its homogeneous region.
Using the ROI approach, each neighbor site has been identified based on standardized Euclidian distance between characteristics of the potential sites and the site of interest. Site characteristics consist of geographical locations and physiographic attributes (Table 2).
In the case of CCA and NLCCA, apart from geographic and physiographic attributes, rainfall information is also considered when constructing the canonical spaces. Figure 5 shows scatter plots of all storm durations. Relationships between long storm durations (≥ 6 h) and between short durations (< 6 h) appear to be different; no strong association exist between long duration cyclonic systems and short duration convective systems. Hence, the DHR using CCA and NLCCA is performed according to storm type; long and short storm duration records are separated into different sets when forming the linear and nonlinear canonical spaces (Fig. 4). This makes sets of 6 physiographical attributes and 3 climatological attributes for the long storm durations (6, 12, and 24 h) and 6 climatological attributes for the short storm durations (5, 10, 15, 30, 60 and 120 min).
It is worth noting that for any considered DHR method, the delineated region must be statistically homogeneous. It has been recognized in the literature (Castellarin et al. 2001; Ouarda et al. 2001) that this condition is strongly related to region size as homogeneity typically decreases as region size increases. Homogeneous regions have thus been identified such that they are neither excessively large (to ensure a minimum degree of homogeneity) nor too small (to obtain sufficiently accurate T-year quantile estimates). Given this trade-off and to ensure that comparisons between methods are fair, a fixed region size of 80 sites, satisfying the 5T guideline of the FEH (1999), is used for all DHR methods, durations, and return periods.
4.2 Regional quantile estimation
The aim of this step is to provide estimates of the rainfall intensities at the site of interest for the given return period and duration. As detailed above, new RFA methods, based on linear and nonlinear QR, are proposed in this study and compared to classical index-storm approaches.
4.2.1 Index storm
In this study, the index storm approach is based on the Gumbel distribution estimated using the method of maximum likelihood to estimate at-site rainfall intensities for different durations and return periods. In a RFA context, the index-storm value is typically the mean of observed data values (rainfall intensities or flood). Here, the index-storm value is instead taken to be the median of the rainfall intensity values at each site, since this measure is more robust (Grover et al. 2002).
In the remainder of this paper, the index-storm approach is combined with ROI, CCA and NLCCA DHR approaches, which results in three different RFA models.
4.2.2 QR-based models
As mentioned earlier, the QR approach to RFA (under both linear and nonlinear forms) allows one to make use of rainfall information from all sites within the region, irrespective of record length. QR models are nonparametric and directly use raw rainfall data as the response variable. They do not require prior specification of a probabilistic form and do not require estimation of at-site quantiles prior to RFA, e.g., as is the case with the OLS regression approach. All available rainfall data can be used to fit the QR model, including sites with extremely short data records.
Six variables, LON, LAT, ELv, RGH, SLP and ASP are used as predictors to estimate rainfall intensities using linear and nonlinear QR models. Separate models are fit for each combination of duration (5, 10, 15, 30, 60 min and 2, 6, 12 and 24 h) and return period (2, 5, 10, 20, 50 and 100 years). In contrast to the linear QR model, the nonlinear QRNN requires one to select the appropriate level of model complexity via the number of hidden nodes J [Eq. (3)]. For sake of parsimony, we consider only the simplest possible QRNN model (J = 1). Again, the linear and nonlinear QR models are combined with CCA and NLCCA methods of DHR.
5 Results and discussion
Homogeneous regions were created using the three considered DHR methods (ROI, CCA and NLCCA). Results for a selected site (CALGARY INT’L A) are shown in Fig. 6. Due to differences in storm development processes associated with long and short storm durations, homogeneous regions for the selected site based on the same method (either CCA or NLCCA) differ for short and long storm durations. Similarly, the region for ROI differs from either CCA or NLCCA as the latter methods take into account rainfall information in the construction of the canonical spaces, whereas ROI is based exclusively on standardized Euclidean distance in the space of the physiographic variables.
Each of the RFA models is used to estimate rainfall intensities for specific durations and return periods across Canada. The entire data set, excluding the held-out cross-validation site, is used for calibration purposes. However, for reliable and robust cross-validation, only sites having record lengths exceeding 40 years are used to estimate cross-validated model performance statistics.
For illustration purposes, Fig. 7 shows scatter plots of the regional and at-site estimated rainfall intensities, over 66 sites with more than 40 years of record, associated with the 24 h duration and 50 years return period. Due to the use of long records, at-site estimates are assumed to be accurate and hence regional estimates should be consistent with the at-site values. As noted in Sect. 3.3, this assumption is questionable; verification results based on the MPLF, which do not rely on the at-site quantile estimates, are presented below. The index storm models, especially ROI-Gumbel, show large biases, generally underestimating relative to the at-site rainfall estimates. On the other hand, both CCA-QRNN and NLCCA-QRNN provide better estimates for small rainfall intensities than the remaining QR approaches, which generally tend towards overestimation. The largest at-site value (8.36 mm/h) was underestimated by all models except NLCCA-QRNN.
Further analysis of model performance can be achieved via standard statistics such as correlation coefficient, RMSE, and standard deviation. Accordingly, we make use of the Taylor diagram, which offers a concise graphical representation of these three statistics, to summarize how well each model performs with respect to the at-site Gumbel model. Hence, a perfect RFA model would lie at 1 on the abscissa. Two Taylor diagrams are shown in Fig. 8 for 10 min and 24 h storm duration and for return periods of: (a) 5 years and (b) 50 years. In these figures, each dot represents results of a particular RFA model. For both return periods, the two QRNN models (CCA-QRNN and NLCCA-QRNN) have strong correlations with the reference at-site model whereas the other models have much lower correlations, especially ROI-Gumbel (< 0.2). In terms of RMSE, the pattern of model performance is similar; the two QRNN-based models are the closest to the reference model.
Recall that one of the main objectives of the present study is to assess the performance of the proposed RFA methods with respect to their ability to provide accurate regional estimates of rainfall intensities for several storm durations and return periods. To this end, cross-validated estimates of \(R_{MPLF}\)[Eq. (5)] are shown in Fig. 9 for all storm durations and return periods. It is worthwhile to emphasize that higher credibility is imparted to the MPLF criterion (or the \(R_{MPLF}\)) as it is a raw data based statistic that does not rely on prior estimation of the at-site quantiles. Overall, the index storm approaches (ROI-Gumbel, CCA-Gumbel and NLCCA-Gumbel) perform worst, especially for long return periods. For long storm durations and small return periods (< 10 year), the good estimation ability of the regional probabilistic distribution combined with a good DHR method (especially NLCCA) provide reasonable performance levels, comparable to that of the linear and nonlinear QR models. Although differences between the QR-based RFA approaches are modest, the overall performance of NLCCA-QRNN is generally the best, followed by CCA-QRNN for small durations, and QR-based approaches (CCA-QR and NLCCA-QR) for long durations.
For illustration, Fig. 10 provides regional IDF curves based on NLCCA-QR for the CALGARY INT’L A site (ID 3031093). Since the main goal of creating regional IDF curves is to characterise the behaviour of extreme rainfall at ungauged locations, an estimate of the associated uncertainty is crucial. However, given the spatial dimension of the RFA procedure, an assessment of the regional uncertainty is significantly more complex than for at-site estimation. Indeed, the most straightforward way to proceed is by resampling sites from the homogeneous region and then estimating regional quantiles based on the resampled datasets. Nevertheless, doing so in a naïve fashion will destroy the spatial correlation structure of the original data set and lead to inaccurate estimates of predictive uncertainty. In the current study, estimation of uncertainty in the regional quantiles is performed following the vector bootstrap approach used in Burn (2003) and GREHYS (1996). In the vector bootstrap, years are resampled such that all sites with a data value in a given year are added to the resampled data set. This permits the estimation of uncertainty bounds for regional IDF curves while preserving the spatial correlation structure of the original data set. To illustrate, 95% confidence intervals are estimated and plotted in Fig. 10. As expected, uncertainty increases with return period and decreases with storm duration.
6 Conclusions
This study investigated the performance of several rainfall RFA approaches based on QR. Goals were to: (1) assess ability of QR-based methods to adequately estimate rainfall intensities at ungauged sites, (2) consider the added value of nonlinear methods for modelling RFA relationships, and finally (3) to estimate IDF curves at ungauged sites. Regional models were constructed for rainfall annual maxima data at different durations across Canada using linear and nonlinear statistical techniques for identifying homogeneous regions (CCA and NLCCA) and then estimating the desired return value for each storm duration (QR and QRNN).
Model performance was assessed using a comprehensive cross-validation procedure. Consistent with the findings of Ouali et al. (2016b) for streamflow, results suggest that QR models can be used to accurately estimate extreme rainfall quantiles at ungauged sites. All of the QR-based models under consideration, both linear and nonlinear, outperformed the standard ROI-Gumbel approach and, more generally, the index-storm approaches (CCA-Gumbel and NLCCA-Gumbel). Results also showed that NLCCA outperformed CCA for DHR, QRNN outperformed QR for quantile estimation, and, overall, that the combination of NLCCA-QRNN outperformed all remaining RFA approaches. Nonlinearity needs to be considered in both the regionalisation and quantile estimation steps of RFA.
Despite the promise of the QR-based methods, there are some obvious avenues for improvement. With respect to QRNN model design, additional flexibility and nonlinearity could be incorporated in the model structure in conjunction with methods for controlling overfitting (e.g., ensemble ANN methods). Indeed, the efficiency of ensemble ANN models, irrespective of the QR model, has been recognized in a number of regional flood frequency studies (e.g., Shu and Burn 2004, Shu and Ouarda 2007). In the same regard, additional nonlinear variants of the QR model can be likewise investigated to achieve more general findings, specifically the QR additive model (Koenker 2011).
From a practical perspective, all RFA models considered in this work are stationary. There is an increasing recognition that characteristics of sub-daily rainfall extremes may change with global warming. As pointed out by Zhang et al. (2017), there is a need to combine information from the latest generation of regional climate models with statistical methods that leverage spatial information, which could include the QR-based RFA models investigated here, to reliably project future changes in IDF curves.
Change history
25 August 2018
The article Estimation of rainfall intensity–duration–frequency curves at ungauged locations using quantile regression methods, written by D. Ouali, A. J. Cannon, was originally published electronically on the publisher’s internet portal (currently SpringerLink) on 28 May, 2018 without open access.
References
Alila Y (1999) A hierarchical approach for the regionalization of precipitation annual maxima in Canada. J Geophys Res Atmos 104(D24):31645–31655
Asquith WH (1998) Depth-duration frequency of precipitation for Texas, US Department of the Interior, US Geological Survey
Barnston AG, Ropelewski CF (1992) Prediction of ENSO episodes using canonical correlation analysis. J Clim 5(11):1316–1345
Bentzien S, Friederichs P (2014) Decomposition and graphical portrayal of the quantile score. Q J R Meteorol Soc 140(683):1924–1934
Brath A, Castellarin A, Montanari A (2003) Assessing the reliability of regional depth-duration-frequency equations for gaged and ungaged sites. Water Resour Res 39(12):1367
Burn DH (1990) Evaluation of regional flood frequency analysis with a region of influence approach. Water Resour Res 26(10):2257–2265
Burn DH (2003) The use of resampling for estimating confidence intervals for single site and pooled frequency analysis/Utilisation d’un rééchantillonnage pour l’estimation des intervalles de confiance lors d’analyses fréquentielles mono et multi-site. Hydrol Sci J 48(1):25–38
Cannon AJ (2011) Quantile regression neural networks: implementation in R and application to precipitation downscaling. Comput Geosci 37(9):1277–1284
Cannon AJ (2015) An intercomparison of regional and at-site rainfall extreme value analyses in southern British Columbia, Canada. Can J Civ Eng 42(2):107–119
Cannon A, Hsieh W (2008) Robust nonlinear canonical correlation analysis: application to seasonal climate forecasting. Nonlinear Process Geophys 15(1):221–232
Castellarin A, Burn D, Brath A (2001) Assessing the effectiveness of hydrological similarity measures for flood frequency analysis. J Hydrol 241(3):270–285
Cavadias G (1990) The canonical correlation approach to regional flood estimation. Reg Hydrol 191:171–178
Chen K, Ying Z, Zhang H, Zhao L (2008) Analysis of least absolute deviation. Biometrika 95(1):107–122
Cheng L, AghaKouchak A (2013) Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci Rep 4:7093
Chokmani K, Ouarda T (2004) Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour Res 40(12):W12514
Chu P-S, Zhao X, Ruan Y, Grubbs M (2009) Extreme rainfall events in the Hawaiian Islands. J Appl Meteorol Climatol 48(3):502–516
Cunnane C (1988) Methods and merits of regional flood frequency analysis. J Hydrol 100(1–3):269–290
Darlymple T (1960) Flood frequency methods. US Geol Surv Water Suppl Pap 1543A:11–51
Di Baldassarre G, Castellarin A, Brath A (2006) Relationships between statistics of rainfall extremes and mean annual precipitation: an application for design-storm estimation in northern central Italy. Hydrol Earth Syst Sci Dis 10(4):589–601
El Adlouni S, Ouarda T, Zhang X, Roy R, Bobée B (2007) Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour Res 43(3):1–13
FEH (1999) Handbook, flood estimation. Institute of Hydrology, Wallingford
Giannini A, Kushnir Y, Cane MA (2000) Interannual variability of Caribbean rainfall, ENSO, and the Atlantic Ocean. J Clim 13(2):297–311
GREHYS (1996) Inter-comparison of regional flood frequency procedures for Canadian rivers. J Hydrol 186(1–4):85–103
Grover PL, Burn DH, Cunderlik JM (2002) A comparison of index flood estimation procedures for ungauged catchments. Can J Civ Eng 29(5):734–741
Haddad K, Rahman A (2012) Regional flood frequency analysis in eastern Australia: bayesian GLS regression-based methods within fixed region and ROI framework–quantile regression versus parameter regression technique. J Hydrol 430–431:142–161
Hewitson B, Crane R (1996) Climate downscaling: techniques and application. Clim Res 7(2):85–95
Hogg WD, Carr DA, Routledge B (1989) Rainfall Intensity–Duration–Frequency Values for Canadian Locations. Environment Canada, Atmospheric Environment Service, Ottawa
Hosking JRM, Wallis JR (2005) Regional frequency analysis: an approach based on L-moments. Cambridge University Press, Cambridge
Hsieh WW (2000) Nonlinear canonical correlation analysis by neural networks. Neural Netw 13(10):1095–1105
Koenker R (2011) Additive models for quantile regression: model selection and confidence bandaids. Braz J Prob Stat 25(3):239–262
Koenker R, Bassett G Jr (1978) Regression quantiles. Econom J Econom Soc 46:33–50
Langousis A, Veneziano D (2007) Intensity-duration-frequency curves from scaling representations of rainfall. Water Resour Res. https://doi.org/10.1029/2006WR005245(2)
Langousis A, Mamalakis A, Puliga M, Deidda R (2016) Threshold detection for the generalized Pareto distribution: review of representative methods and application to the NOAA NCDC daily rainfall database. Water Resour Res 52(4):2659–2681
Ljung GM, Box GE (1978) On a measure of lack of fit in time series models. Biometrika 65(2):297–303
Matonse AH, Frei A (2013) A seasonal shift in the frequency of extreme hydrological events in southern New York State. J Clim 26(23):9577–9593
Nathan R, McMahon T (1990) Identification of homogeneous regions for the purposes of regionalisation. J Hydrol 121(1–4):217–238
Ouali D, Chebana F, Ouarda T (2016a) Non-linear canonical correlation analysis in regional frequency analysis. Stoch Env Res Risk Assess 30(2):449–462
Ouali D, Chebana F, Ouarda T (2016b) Quantile regression in regional frequency analysis: a better exploitation of the available information. J Hydrometeorol 17(6):1869–1883
Ouali D, Chebana F, Ouarda TB (2017) Fully nonlinear statistical and machine-learning approaches for hydrological frequency estimation at ungauged sites. J Adv Model Earth Syst 9(2):1292–1306
Ouarda TB, Girard C, Cavadias GS, Bobée B (2001) Regional flood frequency estimation with canonical correlation analysis. J Hydrol 254(1):157–173
Ouarda T, Cunderlik J, St-Hilaire A, Barbet M, Bruneau P, Bobée B (2006) Data-based comparison of seasonality-based regional flood frequency methods. J Hydrol 330(1):329–339
Pandey G, Nguyen V-T-V (1999) A comparative study of regression based methods in regional flood frequency analysis. J Hydrol 225(1):92–101
Pizarro R, Valdés R, Abarza A, Garcia-Chevesich P (2015) A simplified storm index method to extrapolate intensity–duration–frequency (IDF) curves for ungauged stations in central Chile. Hydrol Process 29(5):641–652
Renard B, Lall U (2014) Regional frequency analysis conditioned on large-scale atmospheric or oceanic fields. Water Resour Res 50(12):9536–9554
Rodriguez RD, Singh VP, Pruski FF, Calegario AT (2016) Using entropy theory to improve the definition of homogeneous regions in the semi-arid region of Brazil. Hydrol Sci J 61(11):2096–2109
Schaefer M (1990) Regional analyses of precipitation annual maxima in Washington State. Water Resour Res 26(1):119–131
Shabbar A, Barnston AG (1996) Skill of seasonal climate forecasts in Canada using canonical correlation analysis. Mon Weather Rev 124(10):2370–2385
Shephard MW, Mekis E, Morris RJ, Feng Y, Zhang X, Kilcup K, Fleetwood R (2014) Trends in Canadian Short-duration extreme rainfall: including an intensity–duration–frequency perspective. Atmos Ocean 52(5):398–417
Shu C, Burn DH (2004) Artificial neural network ensembles and their application in pooled flood frequency analysis. Water Resour Res. https://doi.org/10.1029/2003WR002816(9)
Shu C, Ouarda T (2007) Flood frequency analysis at ungauged sites using artificial neural networks in canonical correlation analysis physiographic space. Water Resour Res. https://doi.org/10.1029/2006WR005142(7)
Stedinger JR (1983) Estimating a regional flood frequency distribution. Water Resour Res 19(2):503–510
Taylor JW (2000) A quantile regression neural network approach to estimating the conditional density of multiperiod returns. J Forecast 19(4):299–311
Wallis J, Schaefer M, Barker B, Taylor G (2007) Regional precipitation-frequency analysis and spatial mapping for 24- and 2-h durations for Washington State. Hydrol Earth Syst Sci Dis 11(1):415–442
Wazneh H, Chebana F, Ouarda T (2015) Delineation of homogeneous regions for regional frequency analysis using statistical depth function. J Hydrol 521:232–244
Werner JP, Luterbacher J, Smerdon JE (2013) A pseudoproxy evaluation of Bayesian hierarchical modeling and canonical correlation analysis for climate field reconstructions over Europe. J Clim 26(3):851–867
Willems P (2000) Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J Hydrol 233(1):189–205
Zhang X, Zwiers FW, Li G, Wan H, Cannon AJ (2017) Complexity in estimating past and future extreme short-duration rainfall. Nat Geosci 10(4):255–259
Acknowledgements
The authors would like to thank the anonymous reviewers for their valuable comments. This research was performed while the first author was with the Climate Data and Analysis Section, Climate Research Division, Science and Technology Branch, Environment and Climate Change Canada.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ouali, D., Cannon, A.J. Estimation of rainfall intensity–duration–frequency curves at ungauged locations using quantile regression methods. Stoch Environ Res Risk Assess 32, 2821–2836 (2018). https://doi.org/10.1007/s00477-018-1564-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-018-1564-7