Abstract
The aim of this study is to estimate likely changes in flood indices under a future climate and to assess the uncertainty in these estimates for selected catchments in Poland. Precipitation and temperature time series from climate simulations from the EURO-CORDEX initiative for the periods 1971–2000, 2021–2050 and 2071–2100 following the RCP4.5 and RCP8.5 emission scenarios have been used to produce hydrological simulations based on the HBV hydrological model. As the climate model outputs for Poland are highly biased, post processing in the form of bias correction was first performed so that the climate time series could be applied in hydrological simulations at a catchment-scale. The results indicate that bias correction significantly improves flow simulations and estimated flood indices based on comparisons with simulations from observed climate data for the control period. The estimated changes in the mean annual flood and in flood quantiles under a future climate indicate a large spread in the estimates both within and between the catchments. An ANOVA analysis was used to assess the relative contributions of the 2 emission scenarios, the 7 climate models and the 4 bias correction methods to the total spread in the projected changes in extreme river flow indices for each catchment. The analysis indicates that the differences between climate models generally make the largest contribution to the spread in the ensemble of the three factors considered. The results for bias corrected data show small differences between the four bias correction methods considered, and, in contrast with the results for uncorrected simulations, project increases in flood indices for most catchments under a future climate.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Future flood hazard projections are essential for flood risk management and adaptation to climate change. Among the many issues related to estimating the occurrence and intensity of floods under a future climate, accounting for the various sources of uncertainty sources in the modelling chain required to produce such estimates remains a major problem (Tian et al. 2016). The climate projections used for such analyses are obtained from Global Climate Model (GCM) simulations, which are dynamically downscaled to a regional level using regional climate models (RCMs). Despite considerable recent progress in global climate modelling, the variability and uncertainty of climate model outputs have not improved substantially (Knutti and Sedláček 2013). In applying such projections to assess, for example, future changes in flooding, the question arises as to how other sources of uncertainty within the modelling chain add to the intrinsic uncertainty in the climate projections. In particular, how are simulations of catchment-scale hydrological processes affected by global- and regional- scale uncertainties when deriving estimates for changes in flood indices?
Analysis of the potential impact of climate change on floods in Poland has been addressed in a number of previous studies at both global and European scales (Lehner et al. 2006; Hirabayashi et al. 2008; Dankers and Feyen 2008; Rojas et al. 2012; Madsen et al. 2014; Alfieri et al. 2015). Changes in flood indices (e.g. 100-year flood) have been estimated using gridded hydrological model simulations for a large area (e.g. Europe) forced with climate model projections. The studies differ in the number and selection of climate models (from one to 12 GCMs), emission scenarios (IS92a, SRES A1B, SRES A2, SRES B2, and RCP8.5), bias corrections (uncorrected or corrected by quantile mapping methods), hydrological model (Lisflood, WaterGAP and MIROC), in the choice of extreme event indices (POT or annual maxima) and in the distribution used for their description (Gumbel and log Pearson type III). Not surprisingly, the outcomes of the analyses also differ substantially. The results presented by Lehner et al. (2006) for two climate models with emission scenario SRES A1B without bias correction indicate increases in the magnitude of the 100-year flood in East and Central Poland by the end of the 21st century. On the other hand, Dankers and Feyen (2008) presented an assessment of changes in the 100-year return level using uncorrected time series from two RCMs driven by one GCM for two emission scenarios (SRES A2 and B2). The outcomes of that analysis for Poland strongly depend on the climate model and the emission scenario. The results of the hydrological simulations presented in EEA (2008), which are based on LISFLOOD driven by uncorrected HIRHAM-HadAM3H/HadCM3 climate simulations under the IPCC SRES A2 scenario, project decreases in Q100 for northern Poland, the River Bug and some tributaries of the rivers Vistula and San. The largest positive changes (increases in Q100) are projected for rivers located in western and southern Poland. The study of Rojas et al. (2012) is based on the output from 12 climate models available from the ENSEMBLES project (van der Linden and Mitchell 2009) for scenario SRES A1B. In that work the climate data are bias corrected before being used in the hydrological model. Whilst the results indicate differences in the projected changes in Q100 for different climate models, the majority of simulations show decreases in Q100 over Poland.
Alfieri et al. (2015) investigated changes in the frequency of river floods in Europe using the newest uncorrected set of climate simulations available within the EURO-CORDEX initiative following the RCP8.5 emission scenario. Their analysis included changes in the mean annual maximum flow and the 100-year flow between three periods, 2006–2035, 2036–2065 and 2066–2095, relative to the reference period 1976–2005. The estimated changes in the indices had similar patterns for the three periods considered. Regional differences in projected changes were found across Poland. Positive changes (increases) were generally found in the western and southern parts of Poland whilst negative changes were found in NE Poland (i.e. similar to Dankers and Feyen 2008). There were, however, a large spread in the results for the different climate models.
At a catchment scale, analyses of the impact of climate change on floods in Poland have previously been performed for two catchments in NW Poland (Orla and Wełna) within the framework of the project “Development and implementation of a strategic adaptation plan for the sectors and areas vulnerable to climate change” with the acronym KLIMADA (klimada.mos.gov.pl). Changes in flood quantiles and the mean annual flood were analysed for the periods 2021–2050 and 2071–2100 relative to a 1971–2000 reference period for bias corrected simulations from eight climate models available from the ENSEMBLES project for the SRES A1B scenario. A comparison of the median from the ensemble of climate models in these three periods indicates an increase in flood quantiles up to the 10-year return period and a decrease in flood quantiles with return periods higher than 20 years for the two catchments. The results of the assessment indicate significant differences between projections derived from different climate models.
In summary, the available studies assessing the influence of climate change on floods in Poland are limited in number and provide different estimates of changes. Virtually all of them report results for large-scale, rather than catchment-scale, hydrological model applications. In addition, almost all of the studies report very large uncertainties due to differences in the results for different climate models. Other sources of uncertainty, such as differences between emission scenarios or bias correction methods, also appear to influence the sign of the projected changes as well as their magnitude (Osuch et al. 2016). A number of recent studies have presented a quantification of the factors contributing to the spread between the projections derived for various models and methods using ANOVA theory (Yip et al. 2011; Finger et al. 2012; Moreira et al. 2013; Bosshard et al. 2013; Ott et al. 2013; Vetter et al. 2015), and different sets of uncertainty sources have been considered in these studies. For example, Yip et al. (2011) quantified the contribution of emission scenarios, climate models and internal variability to the spread in projections for the global mean and decadal mean of surface air temperature. Bosshard et al. (2013) analysed uncertainty due to different climate models, bias correction methods and hydrological models in projected changes in seasonal mean flow and flow quantiles. The results indicate that climate model variability is the main source of variability in the estimated indices. The other sources are, however, also important and are, therefore, not negligible. Some of the uncertainties are, however, not explained by the direct influence of a single source, but by the interactions between multiple sources, e.g. climate models and emission scenarios. The application of ANOVA theory allows this effect to also be evaluated.
The primary aim of this paper is to estimate changes in flood indices in the 21st century in nine catchments in Poland. The indices are estimated following a simulation approach including catchment-scale hydrological modelling based on future climate projections. These projections are obtained from the EURO-CORDEX initiative and represent simulations under the RCP4.5 and RCP8.5 emission scenarios. Time series of precipitation and air temperature from different RCM/GCM combinations for the periods, 1971–2000, 2021–2050 and 2071–2100, are used in the hydrological modelling. As the resulting estimates span a large range, the second aim of this work is to quantify and assess the relative contribution of the emission scenarios, climate models and bias correction methods to the total spread in the projected changes in extreme river flow indices. Such a study has not previously been undertaken for Poland and provides much needed results for use in developing climate change adaptation policies related to the occurrence of floods.
The paper is structured as follows. Section 2 describes the location and characteristics of the nine study catchments. A description of the models and methods used in the simulation chain, including climate models, bias correction methods, hydrological modelling, extreme flow indices and the analysis of the uncertainty, is presented in Sect. 3. The results are presented in Sect. 4 and the discussion and conclusions are presented in Sect. 5.
2 Study catchments
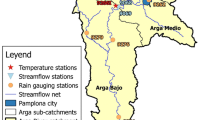
The study area consists of nine catchments in Poland (Fig. 1) having different hydro-climatic conditions. Four catchments, Nysa Kłodzka, Wisła, Dunajec, and Biała Tarnowska, are located in southern Poland. These catchments all have a relatively high mean elevation (i.e. >500 m.a.s.l.), while the remaining catchments (Oleśnica, Myśla, Flinta, Guber, and Narewka) are located in more lowland areas. The catchment area ranges from 297 to 1555 km2, and the catchments are characterized by semi-natural conditions without significant changes in land use in recent years or significant river regulation. According to the CORINE land cover database (CORINE 2006), the catchments are covered mostly by forest, excepting the Wisła and Biała Tarnowska catchments where agriculture is the dominant land use. In the Narewka and Flinta catchments, the percentage of forested area is higher than in the other catchments, approximately 79 and 91 %, respectively. The percentage of the catchment area affected by urban land use varies from almost zero at Narewka to approximately 10 % for the Oleśnica catchment. These nine catchments were selected to sample a range of hydroclimatological conditions across Poland. In order to ensure hydrological simulations of good quality, the requirement of minimal land use change and river regulation was imposed, such that reliable hydrological model calibration could be undertaken for daily discharge. This requirement, in most cases, precludes the use of larger catchments, and is also one of the factors that distinguishes the work presented here from the larger-scale applications of hydrological models reported in previous studies.
The climatic conditions in these catchments, presented as mean annual air temperature and mean annual total precipitation over the 1971–2000 period, are shown in Table 1. There are significant differences among the catchments. The mean air temperature varies from 5.4 °C for Dunajec to 8.4 °C for Myśla, while Myśla has the lowest annual precipitation (540 mm/year) and Dunajec has the highest (1098 mm/year) amongst the nine catchments. The flood regimes also differ between the catchments, and peak flows are driven predominantly by rainfall (Biała Tarnowska), snow-melt (Oleśnica, Flinta, Myśla, Guber, and Narewka) or a combination of rainfall and snowmelt (Nysa Kłodzka, Wisła and Biała Tarnowska). A description of the methods used for this classification of flood regimes is presented in Romanowicz et al. (2016).
3 Methods
3.1 Climate simulation
The analyses were carried out using the climate projections recently available from EURO-CORDEX, the European branch of the international CORDEX initiative sponsored by the World Climate Research Program (WCRP). The main aim of the CORDEX program has been to organize an internationally coordinated framework to produce improved regional climate change projections for all land regions world-wide (Giorgi et al. 2009; Jacob et al. 2014; Kotlarski et al. 2014).
The EURO-CORDEX database consists of a large set of climate model simulations for historical periods and future periods under several emission scenarios. Historical simulations are available for the period 1950–2005, whilst projections are available for the period 2006–2100 at daily, monthly and seasonal temporal resolutions. The EURO-CORDEX simulations for the 2006–2100 period were run under several emission scenarios defined in the Fifth Assessment Report of the IPCC (IPCC AR5 2013) and explained in detail in Moss et al. (2010). These scenarios (so-called Representative Concentration Pathways, RCPs) for the emission of greenhouse gases and atmospheric pollutants emission scenarios do not specify socioeconomic scenarios, but assume different pathways leading to different trajectories of radiative forcing during the twenty-first century. In this paper, results representing two emission scenarios were analysed: RCP4.5 and RCP8.5, corresponding to increases in radiative forcing of 4.5 or 8.5 W/m2 respectively by the end of the century relative to pre-industrial conditions.
Several research centres have participated in the CORDEX initiative. As of mid-2015, results are so far only available for some of the proposed climate models. Given this constraint and due to the need for simulations representing both historical and future periods, results from 7 EURO-CORDEX climate models were used for the work presented here (Table 2). These seven models are based on four RCMs (CCLM4-8-17, HIRHAM5, RACMO22E and RCA4) driven by three different GCMs (CNRM-CM5, EC-EARTH and MPI-ESM-LR). All seven models have the same spatial resolution, i.e. 0.11° on a rotated latitude-longitude grid in rotated coordinates giving a quasi-uniform resolution of approximately 12.5 km. For the EUR11 domain, the simulations are available for 424 × 412 grid cells with defined coordinates that enables selection of the grid cells closest to the area of the interest. All results were imported into MATLAB, and the grid cells located closest to the geometrical centre of each of the study catchments were then extracted.
Table 2 Precipitation and temperature time series for three time periods were used for further analyses: a reference period, 1971–2000, and two future periods, 2021–2050 (near future) and 2071–2100 (far future).
3.2 Bias correction
The time series of daily air temperature and daily precipitation totals extracted from the climate models have been compared with observations from synoptic stations (point measurements) for the reference period (1971–2000). The outcomes indicate significant biases, especially for daily precipitation, which require correction before a local study can be performed.
In this work we used four quantile mapping methods (empirical quantile mapping, and three distribution based mappings: double gamma, single gamma and Birnbaum-Sanders) for bias correction of the precipitation time series and one method for the correction of air temperature (empirical quantile mapping). The corrections were carried out for daily data for each individual climate model, catchment and month of the year, so that discrepancies in seasonal patterns, particularly of rainfall, could be corrected. The methods have been selected due to the feasibility of applying them to a range of climate projections (in contrast, for example, with more complex weather pattern-based corrections) as well as their suitability for evaluating extremes (Sunyer et al. 2012; Sorteberg et al. 2014; Ajaaj et al. 2015).
The quantile mapping QM method has been developed based on the quantile–quantile relationship between an observed and a simulated time series. The approach is widely applied for correction of climate simulations of precipitation (Gudmundsson et al. 2012) and has also been previously used for temperature. The QM method is based on the assumption that a transformation (h) exists such that the distribution of quantiles describing the simulated time series of precipitation (PRCM) can be mapped onto the quantile distribution of the observations (PObs), i.e.:
The transformation of quantiles from simulated to observed time series can be estimated using parametric or non-parametric approaches.
In the parametric approach, the probability distributions of the observed and simulated time series are modelled using an appropriate theoretical distribution, and the parameters of the distribution are estimated from the observed or simulated data. For precipitation, the gamma distribution is often used for this purpose (e.g. Piani et al. 2010), i.e.
where α and β are parameters of a distribution f(x), and Γ (·) is the gamma function, and only wet days (P > 0.0 mm/day) are used in the fitting of this function. The inverse of the derived gamma distribution for observed time series is then used to correct the quantiles of simulations, following the transformation:
where F Obs denotes the cumulative distribution function (cdf) of the observations and F RCM is the cdf of simulated values.
In the second step the distribution parameters are estimated and the inverse of the derived gamma distribution for observed time series is used to correct the quantiles of the simulations. The quantile–quantile relationship is approximated using linear or nonlinear functions (Piani et al. 2010; Gudmundsson et al. 2012). In this work the power function with three parameters was applied to parametrize the quantile transformation.
where coefficients b and c are calibrated for the best fit, x 0 is an estimated threshold value of precipitation below which modelled precipitation is set to zero. In addition to the correction of precipitation values, the number of wet days is also corrected based on the empirical probability of non-zero values in the observations. This is a necessary part of the bias correction, as RCMs tend to simulate too many wet days with low values of precipitation. All values for precipitation below this threshold (x 0 ) are set to zero for the simulated data. The transformation h and the wet day correction derived for the control period are further applied in the correction of precipitation data for future periods. In this paper, the results of bias correction using the method described above are referred to as the ‘single gamma method’ and are denoted as SGM.
Analyses of the use of the various probability distributions, such as the gamma function, for describing precipitation time series have indicated that due to differences in the frequency of low, normal and high precipitation intensities, fits to extreme precipitation intensities can be inadequate. As a solution to this problem, the application of two possibly overlapping distributions that represent normal and extreme precipitation has been proposed (Yang et al. 2010; Willems et al. 2012). In this work, two gamma distributions were applied to each precipitation time series, and the parameters for each of these were estimated independently for two subsets of the time series, separated by the 95th percentile, i.e.
where the suffix 95 denotes the subset of the extreme precipitation values. The derived parameters are then applied to correct data for the future periods. As this method entails the application of two gamma functions, we call this the ‘Double Gamma’ method, and it is hereafter referred to as ‘DGM’.
The choice of other probability distributions suitable for describing daily precipitation time series has been the subject of many previous studies (e.g. Wilks 1999; Sharma and Singh 2010; Li et al. 2013, 2014). The potentially suitable set of distributions includes the exponential, Weibull, lognormal, Pareto, and Pearson III distributions. The analyses of a wide range of possible distributions for describing observed daily precipitation time series evaluated using suitable statistical tests (i.e. Anderson–Darling, Chi square and Lilliefors) shows that in the case of the Nysa Kłodzka catchment the Birnbaum-Sanders distribution (Birnbaum and Saunders 1969) provides a suitable fit. That distribution was developed for a lifetime model for materials that are affected by cyclic patterns of stress and is applied frequently in reliability applications of model failures times. It is a continuous, unimodal and positively skewed distribution. The density of the Birnbaum-Sanders distribution is described as follows:
where β and γ are the distribution parameters.
The Birnbaum-Sanders distribution has not previously been used for bias correction, so its inclusion here is largely exploratory. According to Leiva (2016), however, several recent studies have used the Birnbaum–Saunders distribution for other types of environmental data including rainfall characteristics, contamination risk resulting from nutrient accumulation in surface waters, wind energy flux and air quality. This distribution was, therefore, also considered as a bias correction method in this study, and is hereafter denoted as the ‘BSM’ method.
An alternative to distribution-based quantile mapping is the non-parametric empirical quantile mapping method (Gudmundsson et al. 2012; Sunyer et al. 2015), and this method has been widely applied in climate change impact studies in hydrology in recent years. This method is also used here and will hereafter be referred to as ‘QUANT’. The method follows a similar procedure to the distribution matching described above, but without the selection and parameterisation of a theoretical distribution. In applying this method, the empirical cumulative distributions are estimated for the observed and simulated time series at fixed intervals, and in this work an interval of 0.01 was applied. The relative differences between the observed and simulated cdfs are estimated for each interval and are then smoothed using monotonic cubic spline interpolation. In the case of precipitation correction, and similar to the distribution-based methods presented here, the number of wet days is corrected based on a Bernoulli function for estimating the probability of wet days in the observed data, relative to the modelled data. This procedure can sometimes lead to problems during very dry summer months simulated by some of the RCMs, as a sufficient number of wet days is not available to develop a robust correction. The transformations derived in the reference time period are also applied to correct RCM data for the future periods, thus assuming that the corrections are invariant with respect to climate change.
For air temperature, only bias correction by empirical quantile mapping (QUANT) has been applied. To maintain the climate change signal in the air temperature, the residuals were corrected after removing the difference in the air temperature between the reference and the future periods (Hempel et al. 2013).
3.3 Hydrological modelling
Flow simulations were carried using the HBV model (Bergström 1995; Lindström 1997; Lindström et al. 1997; Booij 2005; Booij and Krol 2010). This hydrological model has often been used to study the influence of climate change on hydrological processes (e.g. Bergström et al. 2001; Graham et al. 2007; Akhtar et al. 2008; Cloke et al. 2013; Demirel et al. 2013; Tian et al. 2014). A detailed description of the version of the HBV model applied in this work is presented in Romanowicz et al. (2013) and Osuch et al. (2015). The model was run using a daily time step, and daily precipitation, daily mean air temperature, and potential evapotranspiration (PET) were used as input data. In this study PET was estimated using the Hamon method based on daily mean air temperature (Hamon 1961). The catchment average precipitation and air temperature were calculated by the Thiessen polygon method using data available from meteorological stations. The model was calibrated using flow observations from the reference period 1971–2000 and validated using observations for the period 2001–2010. The Nash–Sutcliffe (NS) efficiency criterion (Nash and Sutcliffe 1970) was used as the calibration objective function. The results of model calibration and validation are presented in Table 3. The Nash–Sutcliffe criterion is greater than 0.6 for all catchments for the model calibration, and the best model fit (NS = 0.7866) was achieved for the Biała Tarnowska catchment. The results of validation are very good for the four mountainous catchments and for the lowland catchment Guber, all having NS values higher than 0.7. In the case of the other lowland catchments, comparison of the simulated with the observed values gives somewhat poorer results, with NS values varying from 0.5145 for Oleśnica to 0.6117 for the Flinta catchment.
In addition to the NS values, the results of calibration and validation were quantified using the volumetric bias (VB) defined as the ratio of the sum of the simulated daily values to the sum of the observed daily flows. For the calibration period, the VB values are less than 1 in all cases and range from 0.7655 for Oleśnica to 0.9638 for Myśla catchment. The results for validation indicate an underestimation of simulated flow volumes for Dunajec, Wisła, Biała Tarnowska, Nysa Kłodzka, Oleśnica and Guber with the largest differences for Oleśnica (0.7117). An opposite tendency (i.e. an overestimation of flow volumes during the validation period) was found for Narewka, Flinta and Myśla.
Hydrological model performance as interpreted from the Nash–Sutcliffe values and volumetric biases confirm the overall suitability of the HBV model for simulations of hydrological conditions in the nine catchments considered, although there are differences in the model performance between catchments.
3.4 Extreme flow indices
The analyses of extreme flows were carried out for two types of indices, the mean annual maximum flow (MAMF) and flood quantiles with a return period of 10, 20, 50 and 100 years (Q10, Q20, Q50 and Q100), and were estimated for three 30-year periods (1971–2000, 2021–2050 and 2071–2100). The MAMF was calculated directly from the annual maxima time series extracted from the simulated daily discharge for each period. The flood quantiles were estimated using the annual maxima time series and a suitable probability distribution for representing the extreme quantiles. For this purpose, the observed and simulated time series were fitted to the Inverse Gaussian probability distribution following previous studies (Markiewicz et al. 2006; Strupczewski et al. 2006, 2011; Markiewicz et al. 2015). The suitability of that distribution for the observed discharge series (in the reference period) as well as for simulated series in all three periods was tested using the Chi square goodness of fit test, the Anderson–Darling test and the One-sample Kolmogorov–Smirnov test. The applicability of other distributions, e.g. a lognormal distribution, for the description of simulated annual maxima was tested with negative results. Flood quantiles were then estimated for each catchment, climate model, and bias correction method for the three time periods using the Inverse Gaussian probability distribution.
3.5 Quantification of uncertainty due to climate models and bias correction
An analysis of changes in floods indices due to climate change have been carried out for seven climate models, four bias correction methods and two emission scenarios. Results can be generally compared using the median value from the ensemble of 7 climate models. In addition, the spread in the projected changes resulting from climate models, bias correction methods and emission scenarios is also of interest. That evaluation was carried out using two approaches. Firstly, the spread of the estimated changes in flood indices due to the differing climate models, is illustrated using box plots. The relative contribution of the ensemble components to the spread in the estimated changes can also be analysed using a variance decomposition technique following an ANOVA analysis (Von Storch and Zwiers 2001), and this is our second approach.
To implement this second approach, we consider the following ANOVA model:
where \(IN_{ijk}\) is a value of an extreme flow indicator (e.g. relative change in Q10) for the ith climate model, jth bias correction method and kth emission scenario. The first element on the right hand side of Eq. (7) denotes the overall mean. The next three elements represent the principal contributions to the variance corresponding to the climate model (CM), the bias correction method (BC) and the emission scenario (EC). The following three elements describe interactions that quantify effects that do not combine additively (Yip et al. 2011). The last element represents errors (i.e. the unexplained variance). Following ANOVA theory, the model allows the total variance in changes of the analysed extreme flow indices to be decomposed into variance explained by different elements of the impact modelling chain (emission scenarios (EC), climate models (CM), bias correction methods (BC)) and the interactions between them (CM*BC, CM*EC, BC*EC). The analyses were carried out using the Type III sums of squares ANOVA in Matlab. Together with estimates of the variance contribution of the different elements to the variance, their significance level can also be calculated. In this work, elements with p-values larger than 0.05 were removed as individual terms in Eq. 7, and their effects were added to the error term.
In addition, the N-way ANOVA analysis was applied to test the equality of the mean response for groups. Rejection of the null hypothesis (the equality of group means) leads to the conclusion that not all group means are the same, but does not provide further information on which group means are different. The N-way ANOVA analyses was, therefore, supplemented by Tukey’s honestly significant difference criterion procedure (Tukey 1949) that is available within “multcompare” function in Matlab. The results of such comparison between groups are shown as a graph of the estimates and the comparison intervals. For each group the population marginal mean is shown by a symbol (square in our case) and the interval represented by a continuous line extending from the symbol. Two group means are significantly different if their intervals are disjoint, and they are not significantly different if their intervals overlap.
4 Results
4.1 A comparison of climate simulations in the reference period
Validation of the model simulations against observations is an important step in a climate change impact study. The variables considered in such a validation study will influence the assessment of the relative performance of the different climate simulations. This step should, therefore, include the analysis of the climatic variables used as input data for the hydrological modelling as well as their performance in estimating extreme flow indices. In the case of climatic variables, various characteristics that may influence hydrological indices could be selected for validation, and climatic variables which are relevant for flood indices include mean annual and monthly air temperature, annual and monthly sum of precipitation, maximum daily precipitation and 3-day accumulated annual maximum precipitation. In the assessment of the performance of bias correction presented here, the monthly air temperature and monthly mean precipitation are considered as target climatic variables.
4.1.1 Air temperature
An analysis of differences in the biases in raw and corrected mean monthly air temperature due to differences between catchments, climate models and months using N-way ANOVA is shown in Fig. 2. The results show differences between the observed and uncorrected data, and, in general, point towards an underestimation of mean monthly air temperature for most months, catchments and climate models, relative to the observed values. In the summer months (June, July, August), one or more climate models overestimate the observed air temperatures. For the case of uncorrected simulations, there are differences in biases between months, catchments and climate models. Taking into account differences between months, the smallest biases were estimated for July (−0.7 °C) and September (−0.8 °C), while the largest for March (−2.3 °C). Marginal means in these months can be distinguished at the 0.05 significance level. The differences in the marginal means due to climate models are also significant. The smallest biases were estimated for MPI-ESM-LR-RCA4 model (−0.3 °C) while the largest for EC-EARTH-RACMO22E (−2.4 °C). A comparison of the biases in uncorrected air temperature simulations between catchments also shows significant differences. The outcomes for Narewka, Flinta, Oleśnica and Myśla are in range of −1.0 °C to −0.5 °C. Larger marginal means of the biases were estimated for Guber (−1.1 °C), Biała Tarnowska (−1.5 °C), Dunajec (−1.6 °C), Nysa Kłodzka (−2.4 °C), and the largest is for the Wisła catchment (−2.9 °C). This comparison indicates larger errors in monthly air temperature in mountainous catchments than in lowland catchments. Application of bias correction significantly reduces the biases in mean monthly air temperature, such that the biases in the corrected data are very small (less than 0.05 °C).
4.1.2 Precipitation
Results of test of differences between relative biases in raw mean monthly sums of precipitation due to differences between catchments, climate models and months using N-way ANOVA are shown on the left in Fig. 3. The upper panel presents differences in the marginal mean as a result of differences between catchments. The largest biases (68.0 %) are associated with the Nysa Kłodzka catchment located in SW Poland while the biases are less than 40 % for the other catchments. The Narewka catchment has the smallest bias amongst the catchments (i.e. 13.7 %). Differences in the marginal means estimated for the seven climate models are presented in the middle panel of Fig. 3. For three climate models (CNRM-CM5-CCLM4-8-17, EC-EARTH-CCLM4-8-17 and EC-EARTH-RACMO22E), the marginal means are less than 20 %, indicating a good correspondence between the climate model data and local observations. The results for the other climate models indicate a poorer correspondence, with relative biases of up to 55.9 % for the MPI-ESM-LR-RCA4 model. With respect to differences between months, the smallest biases were associated with June (−0.4 %) and July (−4.0 %). These two months have negative biases whilst all other months have positive biases. The largest relative differences between simulations and observations are found for the winter months January (83.1 %) and February (71.5 %).
The precipitation time series were corrected using four methods: QUANT, SGM, DGM and BSM. The comparison of relative biases between the observed and the corrected simulated monthly sums of precipitation over the period 1971–2000 is presented in the right column of Fig. 3. The results indicate a significant improvement in the precipitation simulations with small differences in performance between catchments, climate models, months and methods.
The relative biases estimated for corrected and observed mean monthly precipitation in the reference period are characterized by negative values (up to −2.1 %) for almost all catchments except Nysa Kłodzka (3.4 %), where the bias correction was more difficult due to the shape of the empirical cumulative distribution function of the observations. The differences between climate models are small and vary from −2.9 % for CNRM-CM5-CCLM4-8-17 to 0.5 % for MPI-ESM-LR-RCA4. The marginal means estimated for differences between months are similar and are in the range of −3.3 to 2.0 %. With respect to the relative performance of the different bias correction methods, the smallest average difference (−0.1 %) was obtained for the SGM method, where the average difference is the average of the biases for all months, catchments and climate models for a given method. The DGM and QUANT methods showed a similar performance, (1.2 and 2.1 %, respectively), while the BSM (−7.5 %) had the poorest performance amongst the four methods. The results show, however, that bias correction significantly reduces the differences between the precipitation data simulated by the RCMs and local observations in the reference period for all catchments, climate models, months and methods. The evaluation of the performance of bias correction methods presented here is based on the analysis of mean monthly precipitation, following bias correction of daily data for each month. Analyses of alternative measures could lead to a different ranking of the methods and to different conclusions; therefore, all four methods were used to correct the simulated precipitation time series prior to their use in the hydrological simulations.
4.2 Validation of flows in the reference period
Following the methods presented in Sect. 2, daily flow was simulated using the HBV model driven by projected meteorological variables, and extreme flow indices were derived from the resulting time series for daily discharge. A comparison of the simulated extreme flow indices for the 1971–2000 period for uncorrected and corrected time series is presented in the form of boxplots in Figure S1 of the Supplementary Materials. The simulations were validated against indices estimated from discharge series simulated by the HBV model using observed air temperature and precipitation time series.
Using an ANOVA analysis, the marginal means of the relative biases for different climate models, bias correction methods, catchments and flow indices were estimated and are presented in Fig. 4. A comparison of the marginal means calculated for the seven climate models is shown in the upper left panel. The differences in the relative biases are not large, especially in comparison with other factors. The largest biases were estimated for the CNRM-CM5-CCLM4-8-17 model (20.3 %), whilst the smallest for the EC-EARTH-RACMO22E model (7.8 %).
Although there are differences in the performance of the 4 bias correction methods (upper right panel), there are, in general, statistically significant differences between the raw and corrected simulations. The marginal mean of the relative bias of the flood indices estimated for the uncorrected simulations is 58.9 % whilst for the corrected simulations it is −11.5 % for DGM, 0.6 % for BSM, 6.6 % for QUANT and 14.8 % for SGM. The smallest relative biases were achieved with the BSM method, whilst the outcomes of the precipitation analysis (Sect. 4.1.2) indicated that this method gave the poorest results of the four bias correction methods. A negative value of the population marginal mean was only found for the DGM method.
The estimates of the biases for the nine catchments are presented in the lower left panel of Fig. 5. There are statistically significant differences in the marginal means. The largest biases were found for the Guber catchment (56.8 %). Two other lowland catchments (Narewka and Myśla) are also characterized by large biases in the estimated flow indices. The results for other catchments range from −11.7 % for Flinta to 11.0 % for Biała Tarnowska. The Narewka catchment is characterized by a large relative bias in the extreme flow indices, although it was found to have the smallest bias in precipitation.
A comparison of the biases between the different extreme flow indices (MAMF and flood quantiles Q10, Q20, Q50 and Q100) for the nine catchments is presented in lower right panel in Fig. 5. The results for four flood quantiles are very similar and decreases in the biases are visible for the higher return periods. The marginal mean of the relative bias of MAMF (18.4 %) is statistically different than estimates for Q20, Q50 and Q100.
The largest spreads in the marginal means were found for differences between catchments and also between uncorrected and corrected climate simulations. Other sources (climate models and choice of flood indices) resulted in smaller differences between estimated population marginal means.
4.3 Hydrological projections
Following the methods presented in the second section, hydrological projections for uncorrected and corrected climatic variables were derived for two future periods 2021–2050 and 2071–2100 for the nine study catchments. Two types of indices (mean annual maximum flow and flood quantiles) were calculated using the simulated flow series.
4.3.1 Change in mean annual maximum flow
The results of median relative changes in MAMF between the near future and the reference period are presented in Tables 4 and 5 for both emission scenarios, RCP4.5 and RCP8.5, and both future periods. The median changes from the ensemble of climate models for uncorrected climate simulations are negative for Dunajec, Nysa Kłodzka, Oleśnica, Narewka, Flinta and Guber. The largest projected decrease (−18.8 %) was estimated for the Guber catchment. The results for two other catchments (Biała Tarnowska and Wisła) indicate increases of MAMF of 15.5 and 7.8 % respectively. In the case of Myśla the estimated change based on uncorrected RCM data is less than 1 %.
A comparison of the outcomes for uncorrected and bias corrected data indicates different results for the bias corrected simulations. For six out of nine catchments, the application of bias correction reverses the direction of the projected changes from negative for the uncorrected data to positive for the simulations based on bias corrected data. These changes in direction are seen for all bias correction methods considered and for all catchments excepting the DGM method for the Narewka catchment. The magnitude of changes for corrected time series depends on the catchment and on the bias correction method. Relatively small increases are estimated for Narewka (6.6 %), Dunajec (7.6 %) and Flinta (8.1 %). Increases larger than 20 % are obtained for the Biała Tarnowska, Wisła, Nysa Kłodzka and Myśla catchments. Taking into account differences between bias correction methods, a similarity in the results is visible with small differences between methods. The largest increases are estimated for simulations based on data corrected with the QUANT and BSM methods, but there are differences between catchments.
Figure 5 shows, in the form of boxplots, changes in MAMF between the near future and the reference period for both emission scenarios RCP4.5 and RCP8.5 and both future periods estimated for seven climate models. A significant variability between the results from different climate models is apparent. The largest spread in the outcomes for climate models is seen for the Nysa Kłodzka and Guber catchments, where the maximum change from an ensemble of climate models is larger than 100 % for Nysa Kłodzka (SGM method) and for Guber for the QUANT and BSM methods. The smallest differences between climate models were obtained for the Flinta catchment.
A comparison of the estimated changes in mean annual maximum flow between the two emission scenarios (RCP4.5 and RCP8.5) for the same period (near future) indicate the same tendency on changes and very similar magnitudes.
4.3.2 Changes in flood quantiles
The estimated relative changes in flood quantiles Q10 and Q100 for the emission scenario RCP4.5 are presented in Tables 6 and 7 respectively. The values represent median changes from an ensemble of seven climate models. The results for uncorrected climate simulations for the near future indicate decreases in Q10 for the Dunajec, Oleśnica, Narewka, Myśla and Guber catchments. The outcomes for the 100-year return period show decreases in the Oleśnica, Narewka, Myśla, and Guber catchments. The most intense decreases are simulated for Guber (−28.1 %), Narewka (−21.4 %) and Oleśnica (−12.6 %). Increases in the flood quantile Q100 greater than 10 % are projected for three mountainous catchments (Biała Tarnowska, Wisła and Nysa Kłodzka).
A comparison of the estimated changes in flood quantiles between the far future and the reference periods also indicates differences between catchments. Decreases in the Q100 of more than 10 % are projected for Guber catchment located in NE Poland. Increases of Q100 higher than 10 % are simulated for four mountainous catchments (Dunajec, Biała Tarnowska, Wisła and Nysa Kłodzka) and also for Myśla.
An application of bias correction influences the projected changes in flood quantiles. The results for bias corrected data are consistent between methods for mountainous catchments in the near future and for all catchments in far future. The outcomes show increases in Q10 and Q100 for most of the catchments, periods and emission scenarios with some exceptions (e.g. changes in Q100 in Flinta for clim2 RCP4.5). The magnitude of these changes depends on catchments.
The results for the emission scenario RCP8.5 are shown in the Supplementary Materials (Tables S1 and S2). The direction of changes in flood quantiles is similar to these for RCP4.5 with small differences in the magnitude of the projected changes.
4.3.3 Comparison of estimated changes
The analysis of changes in extreme flow indices were carried out for seven climate models, four bias correction methods, nine catchments, two emission scenarios and five flow indices. To assess the differences in the population marginal means, the N-way ANOVA was applied. The analyses were conducted separately for both future periods, 2021–2050 and 2071–2100. The results are presented in Fig. 6. Four panels on the left show results for relative changes in the extreme flow indices estimated between the near future (2021–2050) and the reference period, while on the right the relative changes between the far future (2071–2100) and the reference period are shown. The difference in population marginal means estimated for seven climate models is available in the upper panels. Statistically significant differences between these results were found. For the near future period, larger relative changes were estimated for the two simulations driven by the MPI-ESM-LR global climate model. The estimated changes for other simulations are smaller than 35 %. The changes in the far future are larger than those projected for the near future and vary from 55.2 to 97.0 %. In that case there are no statistically significant differences due to different global climate models, except for one simulation. The population marginal mean for CNRM-CM5-CCLM4-8-17 is statistically different (higher) than for other climate models.
A comparison of differences in estimated changes due to bias correction is shown in the second row from the top. In the near future the DGM method (21.1 %) gives statistically different results relative to the QUANT, SGM and BSM methods (29.7, 31.0 and 33.9 %). In the far future the largest changes are estimated for simulations based on bias correction with the QUANT method (84.2 %). The other methods simulate very similar changes (DGM—71.0 %, SGM—64.6 % and BSM—68.5 %). An additional test of the differences in the results due to application of uncorrected and corrected data confirmed the significance of these differences.
The differences in the results between the nine catchments are presented in the third row from the top. In the near future the relative changes can be grouped according to flood regime. The largest changes were found in catchments having a mixed flood regime in the current climate (Wisła, Biała Tarnowska and Nysa Kłodzka). Significantly smaller changes were estimated for catchments with snowmelt flood regimes, i.e. Flinta, Narewka, Guber, Myśla and Oleśnica. The outcomes for Oleśnica, Guber and Myśla are significantly greater than for other lowland catchments. In the far future, this same pattern of results as a function of the flood regime under the current climate is no longer apparent. In that case, the smallest changes were estimated for Flinta catchment (8.6 %) while the largest for Nysa Kłodzka (126.2 %).
A comparison of the relative changes estimated for the two emission scenarios indicates that for both future periods the differences are statistically significant. Larger changes are associated with the emission scenario RCP8.5 as compared with RCP4.5.
The variability in the estimates of changes in extreme flows due to choice of index is presented in the bottom row of panels in Fig. 6. The outcomes for the near future show that estimates of Q100 (34.6 %) are higher than for other tested indices i.e. MAMF (22.5 %). In the far future, there are no statistically significant differences between these five indices. The population marginal means are 68.5 % for MAMF, 69.9 % for Q10, 71.5 % for Q20, 74.4 % for Q50, and 76.2 % for Q100.
4.4 Quantification of variability due to climate models and bias correction
The previous section has illustrated the significant variability in the results for different climate models, as well as differences due to the choice of the bias correction method and the emission scenario. Quantification of the variability in MAMF and flood quantiles due to climate models and bias correction was carried out using an ANOVA procedure for each catchment following the methods presented in Sect. 3.5.
The variability in estimated changes in the MAMF in the near future due to the differences between the seven climate models (CM), four bias correction methods (BC) and two emission scenarios (ES) is presented in Fig. 7. The results indicate that differences between climate models is the most important factor contributing to the overall spread in the results in all catchments, except Flinta. This factor explains from 34 to 75 % of the variability in the projected changes in the MAMF. The contribution of the differing bias correction methods to the overall variance in the ensemble of results is also apparent in seven of the nine catchments (excepting Dunajec and Wisła). This contribution varies from 3 to 24 % of the total variance. Differences introduced by the two emission scenarios considered is apparent in the results for four catchments (Biała Tarnowska, Wisła, Nysa Kłodzka, and Myśla). In all catchments, the interaction terms CM*BC and CM*ES also contribute to the variance, while the term BC*ES does not. The latter can be explained by the relatively small contribution of ES and BC in comparison with CM. These outcomes may, however, also reflect the different number of cases (and, thus, the range of possibilities) represented for each factor (7 climate models, 4 bias correction methods and two emission scenarios).
Relative contributions to the total variance in estimates for the percentage change in the mean annual flood (MAMF) in 2021–2050 (clim1) relative to the 1971–2000 reference period. See Eq. 7 for an explanation of the components. Changes of MAMF between clim1 and reference periods
A similar analysis was performed for the changes in flood quantiles (Q10, Q20, Q50 and Q100). The outcomes for different quantiles are similar; therefore, only results for changes in Q100 for the near and far future periods are presented in Fig. 8. In the near future, the climate models are the main source of variability in changes of Q100 for Biała Tarnowska (69.61 %), Nysa Kłodzka (66.93 %), Narewka (63.28 %), Wisła (59.25 %), Flinta (57.86 %), and Dunajec (54.99 %) catchments. Bias correction methods were found to make a statistically significant contribution to the variance in seven of the nine catchments (Oleśnica, Guber, Myśla, Narewka, Nysa Kłodzka, Biała Tarnowska and Wisła). The influence of emission scenarios (ES) is significantly smaller than other factors, with the largest contribution being 4.52 % for the Wisła catchment. Interaction effects (CM*BC, CM*ES and BC*ES) explain from 21.68 % (Biała Tarnowska) to 65.73 % (Oleśnica) of the variability in the projected relative changes in Q100. The impact of bias correction methods on changes in Q100 in the near future, calculated as a sum of BC, CM*BC and BC*ES, depends on the catchment and varies from 7.93 % (Guber) to 38.64 % (Myśla).
Relative contributions to the total variance in estimates for the percentage change in Q100 for the two future periods, 2021–2050 (clim1) and 2071–2100 (clim2) relative to the 1971–2000 reference period. See Eq. 7 for an explanation of the components. Changes of MAMF between clim1 and reference periods
For the far future period, not all the factors were found to be statistically significant and the unexplained variance is significantly higher (up to 62.95 % for Myśla). The effect of differences between climate models is smaller in comparison with the results for the near future. Similar to the results for the near future, the influence of BC was significant for almost all catchments (except Wisła). In addition, interactions of the bias correction methods with the climate models have made a larger contribution to the variance in the projected changes in Q100 (up to 51.40 % for Biała Tarnowska). The contribution of the two emission scenarios to the variance is small in comparison with other factors and is statistically significant for Nysa Kłodzka, Oleśnica, Narewka and Guber.
5 Discussion and conclusions
The aim of this study is the estimation of changes in flood indices in the 21st century in nine catchments in Poland. The HBV rainfall-runoff conceptual model has been used to obtain daily flows in catchments under changing climatic conditions, following the RCP4.5 and RCP8.5 emission scenarios. Climate projections were obtained from the EURO-CORDEX initiative, and time series of precipitation and air temperature from different RCM/GCMs for three periods, 1971–2000, 2021–2050 and 2071–2100, were used. Changes in the mean annual flood (MAMF) and in flood quantiles with a return period of 10, 20, 50 and 100 years have been analysed, and the effects of bias correction on the estimated changes have been evaluated. The simulations using uncorrected climate simulations indicate decreases in the flood indices in the lowland catchments and increases in the mountainous catchments. For six out of the nine catchments, the direction of change goes from being negative (i.e. indicating a decrease) for simulations based on uncorrected climate data to positive for simulations based on bias corrected projections. The decomposition of the variability in the relative changes of flood indices due to the differences between seven climate models, four bias correction methods, nine catchments, and two emission scenarios was performed using ANOVA together with Tukey’s Honestly Significant Difference Procedure. The analyses were carried out separately for the two future periods (2021–2050 and 2071–2100). In both future periods, climate model variability (CM) is the most important factor contributing to this variability, although its dominance as the most important source of variability is less in the far future period, 2071–2100, as compared with the period 2021–2050.
We have compared our results with those published by Dankers and Feyen (2008), Rojas et al. (2012) and Alfieri et al. (2015), as these authors all consider the impact of climate change on floods in Europe using hydrological simulations based on climate projections. However, it should be noted that there are significant differences in many aspects of those studies that will affect such an assessment, including the hydrological models used in the studies and the spatial scale. The above-mentioned papers have used large-scale hydrological models and have applied these to the whole of Europe, basing calibration on data from large rivers without taking into account changes in land use or water management. In our approach, the analyses are carried out for nine medium-sized catchments (having areas of up to 2000 km2), and these catchments have been specifically selected to avoid problems associated with land use or water management changes and river regulation during the calibration period. In addition, in our case, the hydrological model is catchment-based and it has been calibrated and validated for each individual catchment in order to ensure a good performance in the simulation of flows. Despite differences in the choice of climate models and emission scenarios, the results of Dankers and Feyen (2008) also indicate decreases in Q100 in the northern part of Poland, and they also found a strong dependence of the results on the choice of climate model, but also on the emission scenario. A comparison of our results based on the uncorrected climate simulations with those of Alfieri et al. (2015) is more straight forward, as they have also used EURO-CORDEX simulations run under RCP8.5 and there is some overlap between the climate models considered. Their results project a decrease in flood hazard in NE Poland and increases in the western and southern parts of Poland, and these projections agree with our results. An analysis of the influence of climate change on future floods in Europe using bias corrected data was also carried out by Rojas et al. (2012). In that work 12 climate models from the ENSEMBLES project for the SRES A1B scenario were applied. The results indicate differences in the changes of Q100 between catchments, but the majority of simulations show decreases in Q100 over Poland, and this is at odds with the findings of our study.
A number of previous researchers (Ehret et al., 2012; Themeßl et al. 2012; Huang et al. 2014) have stated that bias correction by quantile mapping method does not improve the representation of extremes. Our results contradict those findings. In this work we have used four versions of the quantile mapping method (empirical quantile mapping, and three distribution based mappings: double gamma, single gamma and Birnbaum-Sanders) for correction of the precipitation time series and one method for air temperature correction (empirical quantile method). The bias correction significantly improves the simulations of air temperature and precipitation time series. In particular, the seasonality of precipitation, which is important for simulating the correct flood regime, is improved by bias correction. We have shown that the application of bias correction significantly reduces biases in estimated flood indices for the reference period, as compared with those estimated using uncorrected climate simulation data. The quantification of performance of four bias correction methods using N-way ANOVA and Tukey’s Honestly Significant Difference Procedure indicates that the smallest biases in extreme flow indices were obtained for simulations based on precipitation corrected using the BSM method. However, the direct assessment of the performance of this method for correction of precipitation leads to the opposite conclusion, i.e. it produced the smallest degree of improvement in the precipitation series amongst the four bias correction methods. This result illustrates that the criteria used for evaluating the results of a bias correction for precipitation are not necessarily consistent with requirements for the appropriate simulation of extreme flow events. There are many factors that influence flood generating processes. In catchments where the flood regime is driven by long-term heavy rainfall, the use of the 3-day or longer accumulated precipitation could, for example, be considered as a validation criterion. For catchments with snowmelt dominated flood regimes, the seasonality of precipitation is of paramount importance, and in this case the mean monthly precipitation totals could be chosen as the most informative single criterion.
Our results show that in some catchments the direction of change in flood indices for uncorrected and corrected projections have opposite signs. This may raise a question regarding the validity of the application of corrected climatic variables in the impact studies. The results for the reference period presented here show, however, that uncorrected simulated precipitation patterns have a distorted seasonality and that this results in highly biased flood indices. We have shown that bias correction significantly improves estimates of high flows for the reference period, and therefore should be considered as an important component for catchment-based hydrological impact studies. On the other hand, bias correction does change relationships between climate variables and can violate conservation principles (Ehret et al. 2012). In addition, consistency between the spatio-temporal fields of climate variables (Finger et al. 2012) and consistency of climate change signals (Hagemann et al. 2011; Cloke et al. 2013; Gutjahr and Heinemann 2013; Teng et al. 2015) may be altered. Other problems which potentially undermine a reliable interpretation of the results of projections include neglected feedback mechanisms and an assumed stationarity in the parameters derived for a period with available observations, i.e. the reference period, but later used for changed conditions during future periods. Proposed solutions to this problem include presenting results for both bias corrected and non-corrected inputs and the analysis of the worst case scenario (Osuch et al. 2016). The best, but also the most challenging, solution could be achieved by the improvement of climate models (Ehret et al. 2012) such that the bias correction is not required. Unfortunately the available climate simulations for Poland are highly biased, particularly for precipitation, such that some type of adjustment is required if the goal of an application is the simulation of hydrological processes at a catchment scale. Bias correction methods could be improved by taking into account, for example, the correlation between air temperature and precipitation, considering weather pattern-based approaches, or by introducing multivariate matching criteria such as recently considered by Mehrotra and Sharma 2016. In addition to improvements in climate modelling, the performance and versatility of hydrological models should also be enhanced such that, for example, the effects of changes in vegetation during a warm climate on hydrological flood regimes can also be assessed.
References
Ajaaj A, Mishra AK, Khan AA (2015) Comparison of BIAS correction techniques for GPCC rainfall data in semi-arid climate. Stoch Environ Res Risk Assess. doi:10.1007/s00477-015-1155-9
Akhtar M, Ahmad N, Booij MJ (2008) The impact of climate change on the water resources of Hindukush-Karakorum- Himalaya region under different glacier coverage scenarios. J Hydrol 355:148–163. doi:10.1016/j.jhydrol.2008.03.015
Alfieri L, Burek P, Feyen L, Forzieri G (2015) Global warming increases the frequency of river floods in Europe. Hydrol Earth Syst Sci 19:2247–2260. doi:10.5194/hess-19-2247-2015
Bergström S (1995) The HBV model. In: Singh VP (ed) Computer models of watershed hydrology. Water Resources Publications, Highlands Ranch, CO, pp 443–476
Bergström S, Carlsson B, Gardelin M, Lindström G, Pettesson A, Rummukainen M (2001) Climate change impacts on runoff in Sweden—assessments by global climate models, dynamical downscaling and hydrological modelling. Climate Res 16(2):101–112. doi:10.3354/cr016101
Birnbaum ZW, Saunders SC (1969) A new family of life distributions. J Appl Probab 6(2):319–327. doi:10.2307/3212003
Booij MJ (2005) Impact of climate change on river flooding assessed with different spatial model resolutions. J Hydrol 303:176–198. doi:10.1016/j.jhydrol.2004.07.013
Booij MJ, Krol MS (2010) Balance between calibration objectives in a conceptual hydrological model. Hydrol Sci J 55:1017–1032. doi:10.1080/02626667.2010.505892
Bosshard T, Carambia M, Goergen K, Kotlarski S, Krahe P, Zappa M, Schar C (2013) Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour Res 49:1523–1536. doi:10.1029/2011WR011533
Cloke HL, Wetterhall F, He Y, Freer JE, Pappenberger F (2013) Modelling climate impact on floods with ensemble climate projections. Q J Roy Meteor Soc 139:282–297. doi:10.1002/qj.1998
CORINE (2006) EEA, CORINE land cover. European Environment Agency. Land cover and land use database. http://reports.eea.europa.eu/CORO-landcover/en. Accessed on May, 2014
Dankers R, Feyen L (2008) Climate change impact on flood hazard in Europe: an assessment based on high-resolution climate simulations. J Geophys Res 113:D19105. doi:10.1029/2007JD009719
Demirel MC, Booij MJ, Hoekstra AY (2013) Impacts of climate change on the seasonality of low flows in 134 catchments in the River Rhine basin using an ensemble of bias-corrected regional climate simulations. Hydrol Earth Syst Sci 17:4241–4257. doi:10.5194/hess-17-4241-2013
EEA (2008) Impact of Europe’s changing climate—2008 indicator-based assessment. European Environment Agency Report no 4/2008—JRC Reference Report no. JRC47756
Ehret U, Zehe E, Wulfmeyer V, Warrach-Sagi K, Liebert J (2012) Should we apply bias correction to global and regional climate model data? Hydrol Earth Syst Sci 16:3391–3404. doi:10.5194/hess-16-3391-2012
Finger D, Heinrich G, Gobiet A, Bauder A (2012) Projections of future water resources and their uncertainty in a glacierized catchment in the Swiss Alps and the subsequent effects on hydropower production during the 21st century. Water Resour Res 48:W02521. doi:10.1029/2011WR010733
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: the CORDEX framework. WMO Bulletin 58(3):175
Graham LP, Andréasson J, Carlsson B (2007) Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods—a case study on the Lule River basin. Clim Change 81(S1):293–307. doi:10.1007/s10584-006-9215-2
Gudmundsson L, Bremnes JB, Haugen JE, Engen-Skaugen T (2012) Technical note: downscaling RCM precipitation to the station scale using statistical transformations—a comparison of methods. Hydrol Earth Syst Sci 16(9):3383–3390. doi:10.5194/hess-16-3383-2012
Gutjahr O, Heinemann G (2013) Comparing precipitation bias correction methods for high-resolution regional climate simulations using COSMO-CLM. Theor Appl Climatol 114:511–529. doi:10.1007/s00704-013-0834-z
Hagemann S, Chen C, Haerter JO, Heinke J, Gerten D, Piani C (2011) Impact of a statistical bias correction on the projected hydrological changes obtained from three GCMs and two hydrology models. J. Hydrometeorol. 12:556–578. doi:10.1175/2011jhm1336.1
Hamon WR (1961) Estimation potential evapotranspiration. Proc ASCE J Hydraul Div 87 (HY3), 107–120
Hempel S, Frieler K, Warszawski L, Schewe J, Piontek F (2013) A trend-preserving bias correction—the ISI-MIP approach. Earth Syst Dyn 4:219–236. doi:10.5194/esd-4-219-2013
Hirabayashi Y, Kanae S, Emori S, Oki T, Kimoto M (2008) Global projections of changing risks of floods and droughts in a changing climate. Hydrol Sci J 53(4):754–773
Huang S, Krysanova V, Hattermann FF (2014) Does bias correction increase reliability of flood projections under climate change? A case study of large rivers in Germany. Int J Climatol 34:3780–3800. doi:10.1002/joc.3945
IPCC AR5 (2013) In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds), Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge and New York, NY
Jacob D, Petersen J, Eggert B, Alias A, Christensen OB, Bouwer LM, Braun A, Colette A, Deque M, Georgievski G, Georgopoulou E, Gobiet A, Menut L, Nikulin G, Haensler A, Hempelmann N, Jones C, Keuler K, Kovats S, Kroner N, Kotlarski S, Kriegsmann A, Martin E, van Meijgaard E, Moseley C, Pfeifer S, Preuschmann S, Radermacher C, Radtke K, Rechid D, Rounsevell M, Samuelsson P, Somot S, Soussana JF, Teichmann C, Valentini R, Vautard R, Weber B, Yiou P (2014) EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg Environ Change 14(2):563–578
Knutti R, Sedláček J (2013) Robustness and uncertainties in the new CMIP5 climate model projections. Nat Climat Change 3:369–373. doi:10.1038/nclimate1716
Kotlarski S, Keuler K, Christensen OB, Colette A, Deque M, Gobiet A, Goergen K, Jacob D, Luthi D, van Meijgaard E, Nikulin G, Schar C, Teichmann C, Vautard R, Warrach-Sagi K, Wulfmeyer V (2014) Regional climate modelling on European scales: a joint standard evaluation of the Euro-CORDEX RCM ensemble. Geosci Model Dev 7(4):1297–1333
Lehner B, Döll P, Alcamo J, Henrichs H, Kaspar F (2006) Estimating the impact of global change on flood and drought risks in Europe: a continental, integrated assessment. Climat Change 75:273–299
Leiva V (2016) The Birnbaum-Saunders distribution. Elsevier, Amsterdam
Li Z, Brissette F, Chen J (2013) Finding the most appropriate precipitation probability distribution for stochastic weather generation and hydrological modelling in Nordic watersheds. Hydrol Process 27:3718–3729. doi:10.1002/hyp.9499
Li Z, Li C, XU Z, Zhou X (2014) Frequency analysis of precipitation extremes in Heihe River basin based on generalized Pareto distribution. Stoch Environ Res Risk Assess 28:1709. doi:10.1007/s00477-013-0828-5
Lindström G (1997) A simple automatic calibration routine for the HBV model. Nord Hydrol 28(3):153–168
Lindström G, Johansson B, Persson M, Gardelin M, Bergström S (1997) Development and test of the distributed HBV-96 hydrological model. J Hydrol 201(1–4):272–288. doi:10.1016/S0022-1694(97)00041-3
Madsen H, Lawrence D, Lang M, Martinkova M, Kjeldsen TR (2014) Review of trend analysis and climate change projections of extreme precipitation and floods in Europe. J Hydrol 519:3634–3650
Markiewicz I, Strupczewski WG, Kochanek K, Singh VP (2006) Relationships between three dispersion measures used in flood frequency analysis. Stoch Environ Res Ris Assess 20:391. doi:10.1007/s00477-006-0033-x
Markiewicz I, Strupczewski WG, Bogdanowicz E, Kochanek K (2015) Generalized exponential distribution in flood frequency analysis for polish rivers. PLoS One 10(12):e0143965. doi:10.1371/journal.pone.0143965
Mehrotra R, Sharma A (2016) A multivariate quantile-matching bias correction approach with auto- and cross-dependence across multiple time scales: implication for downscaling. J Climat 29(10):3519–3539
Moreira E, Mexia JT, Pereira LS (2013) Assessing homogeneous regions relative to drought class transitions using an ANOVA-like inference. Application to Alentejo, Portugal. Stoch Environ Res Risk Assess 27:183. doi:10.1007/s00477-012-0575-z
Moss RH, Edmonds JA, Hibbard KA, Manning MR, Rose SK, van Vuuren DP, Carter TR, Emori S, Kainume M, Kram T, Meehl GA, Mitchell JFB, Nakicenovic N, Riahi K, Smith SJ, Stouffer RJ, Thomson AM, Weyant JP, Wilbanks TJ (2010) The next generation of scenarios for climate change research and assessment. Nature 463:747–756. doi:10.1038/nature08823
Nash JE, Sutcliffe JV (1970) River flow forecasting through conceptual models. Part I: a discussion of principles. J Hydrol 10:282–290
Osuch M, Romanowicz RJ, Booij MJ (2015) The influence of parametric uncertainty on the relationships between HBV model parameters and climatic characteristics. Hydrol Sci J 60(7–8):1299–1316. doi:10.1080/02626667.2014.967694
Osuch M, Romanowicz RJ, Lawrence D, Wong WK (2016) Trends in projections of standardized precipitation indices in a future climate in Poland. Hydrol Earth Syst Sci 20:1947–1969. doi:10.5194/hess-20-1947-2016
Ott I, Duethmann D, Liebert J, Berg P, Feldmann H, Ihringer J, Kunstmann H, Merz B, Schaedler G, Wagner S (2013) High-resolution climate change impact analysis on medium sized river catchments in Germany: an ensemble assessment. J Hydrometeorol 14:1175–1193. doi:10.1175/JHM-D-12-091.1
Piani C, Haerter JO, Coppola E (2010) Statistical bias correction for daily precipitation in regional climate models over Europe. Theor Appl Climatol 99:187–192
Rojas R, Feyen L, Bianchi A, Dosio A (2012) Assessment of future flood hazard in Europe using a large ensemble of bias-corrected regional climate simulations. J Geophys Res-Atmos 117:D17109. doi:10.1029/2012JD017461
Romanowicz RJ, Osuch M, Grabowiecka M (2013) On the choice of calibration periods and objective functions: a practical guide to model parameter identification. Acta Geophys 61(6):1477–1503. doi:10.2478/s11600-013-0157-6
Romanowicz RJ, Bogdanowicz E, Debele SE, Doroszkiewicz J, Hisdal H, Lawrence D, Meresa HK, Napiórkowski JJ, Osuch M, Strupczewski WG, Wilson D, Wong WK (2016) Climate change impact on hydrological extremes: preliminary results from the Polish-Norwegian Project. Acta Geophys 64(2):477–509. doi:10.1515/acgeo-2016-0009
Sharma MA, Singh JB (2010) Use of probability distribution in rainfall analysis. NY Sci J 3(9):40–49
Sorteberg A, Haddeland I, Haugen JE, Sobolowski S, Wong WK (2014) Evaluation of distribution mapping based bias correction methods. Norwegian Centre for Climate Services report no 1/2014
Strupczewski W, Mitosek HT, Kochanek K, Singh VP, Weglarczyk S (2006) Probability of correct selection from lognormal and convective diffusion models based on the likelihood ratio. Stoch Environ Res Ris Assess 20:152. doi:10.1007/s00477-005-0030-5
Strupczewski WG, Kochanek K, Markiewicz I, Bogdanowicz E, Węglarczyk S, Singh VP (2011) On the tails of distributions of annual peak flow. Hydrol Res 42(2–3):171–192. doi:10.2166/nh.2011.062
Sunyer MA, Madsen H, Ang PH (2012) A comparison of different regional climate models and statistical downscaling methods for extreme rainfall estimation under climate change. Atmos Res 103:119–128. doi:10.1016/j.atmosres.2011.06.011
Sunyer MA, Hundecha Y, Lawrence D, Madsen H, Willems P, Martinkova M, Vormoor K, Bürger G, Hanel M, Kriaučiuniene J, Loukas A, Osuch M, Yücel I (2015) Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe. Hydrol Earth Syst Sci 19:1827–1847. doi:10.5194/hess-19-1827-2015
Teng J, Potter NJ, Chiew FHS, Zhang L, Wang B, Vaze J, Evans JP (2015) How does bias correction of regional climate model precipitation affect modelled runoff? Hydrol Earth Syst Sci 19:711–728. doi:10.5194/hess-19-711-2015
Themeßl MJ, Gobiet A, Heinrich G (2012) Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim Change 112:449–468. doi:10.1007/s10584-011-0224-4
Tian Y, Booij MJ, Xu Y-P (2014) Uncertainty in high and low flows due to model structure and parameter errors. Stoch Environ Res Risk Assess 28:319. doi:10.1007/s00477-013-0751-9
Tian Y, Xu Y-P, Booij MJ, Cao L (2016) Impact assessment of multiple uncertainty sources on high flows under climate change. Hydrol Res 47(1):61–74. doi:10.2166/nh.2015.008
Tukey J (1949) Comparing individual means in the analysis of variance. Biometrics 5(2):99–114
van der Linden P, Mitchell JFB (eds) (2009) ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project. Met Office Hadley Centre, FitzRoy Road, Exeter EX1 3 PB
Vetter T, Huang S, Aich V, Yang T, Wang X, Krysanova V, Hattermann F (2015) Multi-model climate impact assessment and intercomparison for three large-scale river basins on three continents. Earth Syst Dyn 6:17–43. doi:10.5194/esd-6-17-2015
Von Storch H, Zwiers F (2001) Statistical analysis in climate research. Cambridge University Press, Cambridge
Wilks DS (1999) Interannual variability and extreme-value characteristics of several stochastic daily precipitation models. Agr Forest Meteorol 93:153–169
Willems P, Olsson J, Arnbjerg-Nielsen K, Beecham S, Pathirana A, Bulow Gregersen I, Madsen H, Nguyen VTV (2012) Impacts of climate change on rainfall extremes and urban drainage systems. International Water Association, London, New York
Yang W, Andreasson J, Graham LP, Olsson J, Rosberg J, Wetterhall F (2010) Distribution-based scaling to improve the usability of regional climate model projections for climate change impact studies. Hydrol Res 41:211–229
Yip S, Ferro C, Stephenson DB (2011) A simple, coherent framework for partitioning uncertainty in climate predictions. J Clim 24:4634–4643. doi:10.1175/2011JCLI4085.1
Acknowledgments
The work was undertaken within the project “Climate Change Impacts on Hydrological Extremes (CHIHE)” Pol-Nor/196243/80/2013, which is supported by the Norway-Poland Grants Program administered by the Norwegian Research Council. This work was partially supported within statutory activities no. 3841/E-41/S/2016 of the Ministry of Science and Higher Education of Poland. The hydro-meteorological data were provided by the Institute of Meteorology and Water Management (IMGW), Poland.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Osuch, M., Lawrence, D., Meresa, H.K. et al. Projected changes in flood indices in selected catchments in Poland in the 21st century. Stoch Environ Res Risk Assess 31, 2435–2457 (2017). https://doi.org/10.1007/s00477-016-1296-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-016-1296-5