Minimum relative entropy theory for streamflow forecasting with frequency as a random variable

Abstract

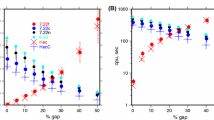
This paper develops a minimum relative entropy theory with frequency as a random variable, called MREF henceforth, for streamflow forecasting. The MREF theory consists of three main components: (1) determination of spectral density (2) determination of parameters by cepstrum analysis, and (3) extension of autocorrelation function. MREF is robust at determining the main periodicity, and provides higher resolution spectral density. The theory is evaluated using monthly streamflow observed at 20 stations in the Mississippi River basin, where forecasted monthly streamflows show the coefficient of determination (r ²) of 0.876, which is slightly higher in the Upper Mississippi (r ² = 0.932) than in the Lower Mississippi (r ² = 0.806). Comparison of different priors shows that the prior with the background spectral density with a peak at 1/12 frequency provides satisfactory accuracy, and can be used to forecast monthly streamflow with limited information. Four different entropy theories are compared, and it is found that the minimum relative entropy theory has an advantage over maximum entropy (ME) for both spectral estimation and streamflow forecasting, if additional information as a prior is given. Besides, MREF is found to be more convenient to estimate parameters with cepstrum analysis than minimum relative entropy with spectral power as random variable (MRES), and less information is needed to assume the prior. In general, the reliability of monthly streamflow forecasting from the highest to the lowest is for MREF, MRES, configuration entropy (CE), Burg entropy (BE), and then autoregressive method (AR), respectively.

Appendices

Appendix 1: Cepstrum analysis

Cepstrum is defined as the inverse Fourier transform of the log-magnitude of Fourier spectrum. For a given streamflow time series y(t), the cepstrum can be computed using the following steps.

First, taking the Fourier transform of the original series y(t), one obtains

$$ Y(f) = \sum\limits_{n = - \infty }^{\infty } {y(t)e^{ - 2\pi nif} } $$

(26)

where Y(f) is the Fourier transform of y(t). Taking the inverse Fourier transform of the log-magnitude of Eq. (26) one obtains the cepstrum of the Fourier transform as

$$ C(n) = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {\log \left| {Y(f)} \right|e^{2\pi nif} df} $$

(27)

It is known that the Fourier transform of autocorrelation leads to the spectral density, which is

$$ q(f) = \sum\limits_{n = - \infty }^{\infty } {\rho (n)e^{ - 2\pi nif} } $$

(28)

Thus, similar to Eq. (26), the cepstrum of autocorrelation can be defined by the inverse Fourier transform of the log-magnitude of P(f), which yields

$$ e(n) = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {\log \left| {q(f)} \right|e^{2\pi nif} df} $$

(29)

However, it is known that the spectral density by definition can also be written as

$$ q(f) = \{ FT[y(t)]\}^{2} $$

(30)

Thus, the following relationship between the cepstrum and the cepstrum of the autocorrelation can be obtained:

$$ e(n) = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {\log \left| {FT[y(t)]} \right|^{2} e^{2\pi nif} df} = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {2\log \left| {Y(f)} \right|e^{2\pi nif} df} = 2C(n) $$

(31)

Appendix 2: Cepstrum of data of finite length

Consider only the positive part of the autocorrelation function $\rho (n)$, for n > 0 and let e(n) be the cepstrum estimated from $\rho (n)$, n > 0, which is

$$ e(n) = \frac{1}{2\pi }\int\limits_{ - \pi }^{\pi } {\log \left| {p*(f)} \right|e^{2\pi nif} df} $$

(32)

where the spectral density p * (f) is obtained by Fourier transform from the positive half of $\rho (n)$, for n > 0. It is noted that p * (f) is analytical. Using only the positive part of ρ(n) ensures that ρ(n) is the minimum-phase function and for a minimum phase system the input and output are uniquely determined. This means e(n) can be uniquely determined from ρ(n). Let us define a two-sided output in the way that

$$ \hat{\rho }(n) = \left\{ {\begin{array}{*{20}c} {2e(n),} \\ {e(0),} \\ {2e( - n),} \\ \end{array} \begin{array}{*{20}c} \\ {} \\ {} \\ \end{array} } \right.\begin{array}{*{20}c} {n \,>\, 0} \\ {n\, = \,0} \\ {n\, < \,0} \\ \end{array} $$

(33)

In such a way, $\hat{\rho }(n)$ can also be uniquely determined by $\rho (n)$ and vice versa.

Since p ^*(f) is analytical, $\log p*(f)$ can also be considered as analytical. In such a case, following Oppenheim and Schafer (1975), there is the following relationship between the derivatives of z transformed $\hat{\rho }(n)$ and ρ(n):

$$ \hat{\rho }^{\prime}(z) = \frac{{\rho^{\prime}(z)}}{\rho (z)} $$

(34)

which is equivalent to

$$ z\hat{\rho }^{\prime}(z) = \sum\limits_{{}}^{{}} {[ - n\hat{\rho }(n)]z^{ - n + 1} } = \frac{{z\rho^{\prime}(z)}}{\rho (z)} $$

(35)

The following difference equation can be obtained from Eq. (35):

$$ z\rho^{\prime}(z) = z\hat{\rho }'(z)\rho (z) $$

(36)

Taking the inverse z transform of Eq. (36), one obtains

$$ n\rho (n) = \sum\limits_{k = \infty }^{\infty } {k\hat{\rho }(n)\rho (n - k)} $$

(37)

Dividing Eq. (37) by n, the relationship between input and output becomes

$$ \rho (n) = \sum\limits_{k = - \infty }^{\infty } {(\frac{k}{n})\hat{\rho }(n)\rho (n - k)} $$

(38)

Transforming Eq. (38) with the use of Eq. (33), the autocorrelation function can be obtained from the following recursive formula (Oppenheim and Schafer 1975):

$$ \rho (n) = \left\{ {\begin{array}{*{20}c} {\frac{\rho (0)}{2}e(n) + \sum\limits_{k = 1}^{n - 1} {\frac{k}{n}e(k)} \rho (n - k)],} \\ {\exp e(n),} \\ {\rho ( - n),} \\ \end{array} \begin{array}{*{20}c} \\ {} \\ {} \\ \end{array} } \right.\begin{array}{*{20}c} {n\, >\, 0} \\ {n\, =\, 0} \\ {n\, <\, 0} \\ \end{array} $$

(39)

On the other hand, the cepstrum e(n) can be obtained from the reverse relation of Eq. (39) as:

$$ e(n) = \left\{ {\begin{array}{*{20}c} {\frac{2}{\rho (0)}[\rho (n) - \sum\limits_{k = 1}^{n - 1} {\frac{k}{n}e(k)} \rho (n - k)],} \\ {\log \rho (n),} \\ {0,} \\ \end{array} \begin{array}{*{20}c} \\ {} \\ {} \\ \end{array} } \right.\begin{array}{*{20}c} {n\, >\, 0} \\ {n\, =\, 0} \\ {n\, <\, 0} \\ \end{array} $$

(40)