Abstract
As flood inundation risk maps have become a central piece of information for both urban and risk management planning, also a need to assess the accuracies and uncertainties of these maps has emerged. Most maps show the inundation boundaries as crisp lines on visually appealing maps, whereby many planners and decision makers, among others, automatically believe the boundaries are both accurate and reliable. However, as this study shows, probably all such maps, even those that are based on high-resolution digital elevation models (DEMs), have immanent uncertainties which can be directly related to both DEM resolution and the steepness of terrain slopes perpendicular to the river flow direction. Based on a number of degenerated DEMs, covering areas along the Eskilstuna River, Sweden, these uncertainties have been quantified into an empirically-derived disparity distance equation, yielding values of distance between true and modeled inundation boundary location. Using the inundation polygon, the DEM, a value representing the DEM resolution, and the desired level of confidence as inputs in a new-developed algorithm that utilizes the disparity distance equation, the slope and DEM dependent uncertainties can be directly visualized on a map. The implications of this strategy should benefit planning and help reduce high costs of floods where infrastructure, etc., have been placed in flood-prone areas without enough consideration of map uncertainties.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
Hydraulic modeling of river floods has received a significant boost during the last 10 years; not only thanks to improved computers and hydraulic modeling software, but also to the capabilities and user-friendliness of geographical information systems (GIS). During the same period, new legislation, such as EU’s flood directive, demands that flood risks are incorporated into risk and management plans, and together, this has led to production of numerous flood risk maps. Although these maps may have been produced by professionals who are aware of the different inaccuracies and uncertainties underlying the maps, they are often used by people who have little or no experience of neither hydraulic nor digital elevation modeling. Furthermore, as these maps tend to form the basis for many decisions in spatial and physical planning of the built environment, there is a need for tools that can communicate the intrinsic uncertainties always present in the maps.
There are different types of uncertainties involved in flood risk mapping (see e.g. Pappenberger et al. 2008 and Merwade et al. 2008, for general treatise on this subject). The most immediate is which model to be used (e.g. Wagener and Gupta 2005), but in practice, the most commonly treated uncertainty is which magnitude of flow to use for a certain flood return period. This can be handled by running the model with different water discharges and thereby get a range of flood inundation areas. Other ways of treating uncertainty is through Monte Carlo simulations, i.e., feeding the model with slightly varied input of all input parameters, and where the large number of output maps in turn can be related to flood prediction uncertainty on how accurate the modeled results are (e.g. Apel et al. 2008). Obviously, specific objects and parameters in the hydraulic model can also influence the accuracy of the produced results. For example Koivumäki et al. (2010) studied the effects of buildings in the model, Pappenberger et al. (2006) looked at the effects of boundary conditions and bridges, and Cook and Merwade (2009) and Castellarin et al. (2009) treated the effects of cross-section location and spacing. As the hydraulic modeling usually involves calibration against a previous flood event, the importance of roughness is also widely known. By varying river bed and floodplain roughness values in a range that theoretically can be expected, minimum and maximum extents of the flooded area can be modeled. Although modelers have acknowledged the implications of roughness for a long time, it is not until recent years that any efforts have been made to see how much this type of uncertainty affects the results (see e.g. Pappenberger et al. 2005; Werner et al. 2005; Casas et al. 2006; Schumann et al. 2007; Wilson and Atkinson 2007; Brandt 2009; Warmink et al. 2013; Wu in press). This is probably due to the type of uncertainty which earlier has been considered the main constraint for successful modeling, viz. the quality of the digital elevation model (DEM).
1.2 Previous research on delineation uncertainties related to DEMs
Before the advent of LiDAR, the results from hydraulic models, which could be based on detailed surveyed cross sections, were overlain on DEMs of poor resolution. In Sweden, e.g., up to only a couple of years ago, the only elevation database of national coverage has been Lantmäteriet’s (the Swedish mapping, cadastral and land registration authority) with 50 m cell resolution (other countries have had similar resolutions). Very rarely, there have been DEMs of higher quality available. Due to the poor quality of the elevation models, in Sweden all such maps were given a notification that they should not be used for detailed planning. Hence, there have been some studies with the specific objective to study how the quality of DEMs affects the accuracy of inundation boundary delineation from 1D hydraulic models, which end products are water levels at each modeled cross section. By comparing these modeled levels with measured levels, several studies have shown that the accuracy of predicting correct levels is surprisingly high, irrespectively of the quality of DEM (e.g. Casas et al. 2006; Yacoub and Sanner 2006; Brandt 2009). Only with poor DEMs (i.e., cell sizes bigger than 10–25 m) together with steep river slopes, or abrupt slope change, the water levels may deviate significantly between modeled and real conditions (Brandt 2009). However, when it comes to the spatial extent, which is important when the inundation extents are transferred to maps, high-resolution DEMs of high quality may also produce inaccurate results.
An early attempt to look at spatial deviations was done by Zhang and Montgomery (1994) on two areas in the USA. They gridded spot elevation data to DEMs of 2, 4, 10, 30, and 90 m resolution. They noticed that better resolution than 10 m lead to improved modeling results. However, the best two DEMs did not produce any significant improvements; most probably due to the catchments being characterized by moderately to steep terrain gradients. Later, Werner (2001) used laser altimetry data for a reach of the river Saar in Germany. The original cell resolution was 2.5 m, which then was aggregated by averaging neighboring cell values to cell sizes of 5, 10, and 25 m. He concluded that a cell resolution of 10 m indicated the break when flood extents started to deviate significantly.
When the modeled areas are big, high-resolution DEMs usually contain enormous amounts of data. Therefore, it is of interest to see how much the original laser data can be filtered, without losing predictability performance. For an area around Leith Creek, North Carolina, Omer et al. (2003) looked at the angle α between two surveyed data points (Fig. 1). If a pre-determined angle is exceeded, the point will be preserved, but if it is not exceeded it will be removed from the dataset. In this way the number of points will be reduced, leading to less computer storage, faster analysis times, but also a DEM of poorer quality. The original dataset had ca 0.0288 points/m2, equivalent to 5.89 m cell size. By testing different threshold values of α, their recommendation is that α should be less than 4°, which in their case represented about 38 % of the original number of points, i.e., ca 0.0111 points/m2, equivalent to 9.50 m cell sizes.
Angle used to determine if point should be filtered away or kept in the DEM (cf. Omer et al. 2003)
Another study was undertaken by Casas et al. (2006). They looked at an area next to the Ter River, Spain, and tested different DEMs ranging from 1 to 4 m in cell size. The DEMs were derived from laser altimetry data, GPS surveyed data, 5 m contour data (scale 1:5000), as well as combinations between them, together with or without bathymetric data. They concluded that for a 500 m3/s discharge, the 4 m resolution DEM yielded inundated area differences up to 7.3 %. However, if higher discharges were used (3000 m3/s), the differences were reduced to 2.6 %. Therefore they argued that coarser resolution will have less consequence in floodplain areas.
Raber et al. (2007) looked at Reedy Fork Creek, North Carolina, and started with laser altimetry data with a mean point distance of 1.35 m, which later were filtered in several steps down to 9.64 m. By comparing statistics over the modeled inundated areas, they concluded that it is enough with 4 m mean point spacing. For better DEMs they did not see any significant differences between the model results.
Cook and Merwade (2009) studied the Brazos River, Texas, and Strouds Creek, North Carolina, for different resolutions (laser altimetry data of 3 m for Brazos River and 6 m for Strouds River, as well as 10 and 30 m USGS data for both rivers) combined with different qualities of cross-section resolutions. Although their research focus was on inundated area differences, they did notice that for the smaller Strouds River (with a width of 9.5 m during normal conditions) the average width of a modeled flood where 25 % wider when poor DEMs were used. Similarly, the larger Brazos River’s (with a width of 175 m during normal conditions) average width was 5 % wider. This effect was doubled when laser altimetry data were integrated in the cross-section profiles.
1.3 Aim and objectives
Nowadays flood risk maps are usually based on DEMs with quite high quality. In Sweden, a new national elevation dataset of 2 m resolution is under production, and thanks to the detailed appearance of the maps, many users as well as hydraulic modelers tend to put high confidence in them and consider the results to be very accurate, i.e., with a flood-boundary position accuracy of just one or two raster cells. However, there are a few studies available that have shown that these maps may also suffer severely from DEM-derived uncertainties, but despite the recognition of the problem, it seems that practically no attempts have been made to actually visualize the uncertainties of these maps (cf. Lim et al. 2016). Considering the fact that there still are accuracy and uncertainty issues due to the quality of the DEMs, together with the absence of effective visualization techniques to represent these issues, the general aim of this paper is to provide insights into the importance of DEMs influence on 1D hydraulic modeling. The specific objectives are to produce: (1) a general equation capable of describing the uncertainties related to the DEM resolution and the floodplain characteristics, here represented by the slope perpendicular to the flow direction, and (2) an algorithm capable of illustrating the uncertainties of flood boundary mapping, related to the quality of the DEMs.
2 Prior studies of Eskilstuna and Testebo rivers
All previously mentioned studies focus on the DEMs global resolution, despite the relatively obvious influence of the local terrain; especially the slope characteristics perpendicular to the flow direction. Where cross sections have steep slopes, the inundation delineation is more certain than for cross sections with gentle slopes. Hence, river side areas with gentle perpendicular slopes call for elevation data of higher resolution to reduce the uncertainty of inundation extent delineation (Brandt 2005). This is also supported by Colby and Dobson (2010) who in their study on rivers in North Carolina concluded that the “extent and internal pattern of flooding in the low-relief coastal plains was found to be especially sensitive to the representation of terrain”. Therefore, a first attempt to look into this problem in detail was carried out for two areas of Eskilstuna River, Sweden (reported in Brandt 2009): one with relatively steep side slopes and one with relatively flat side slopes. These areas were modeled with the 1D hydraulic software HEC-RAS (Hydrologic Engineering Center 2008) for a steady state flow of 198 m3/s and tested for inundation boundary delineation with several DEMs of varying cell resolution (besides this, that study also looked at the effect of systematic vertical errors of the surrounding terrain as well as the relative importance of errors between roughness and DEM resolution).
The northern investigated area in Eskilstuna River is 2241 m long, consists of two parts with a water power station in between, and has relatively steep side slopes. The original point cloud has a point spacing of 1.36 points/m2. The southern area, on the other hand, is 1731 m long, has relatively gentle side slopes, and has a point spacing of 1.64 points/m2. This is equivalent to raster DEMs of 0.86 and 0.78 m cell sizes, respectively. These datasets were then degraded step-by-step through both removal of points and by introducing random errors in order to fully simulate higher flight heights in accordance with the scanner equipment specifications (cf. Klang and Klang 2009, for full details).
When comparing the modeled river widths (based on degraded DEMs) with the width considered to be the truth (based on original point cloud with no introduced errors), the mean disparity for all cross sections was around 0 m (less than ±2 m irrespectively of point density or cell size), except for the poorest DEM of 50 m cell size, where the mean disparity was ca 16 m. The seemingly good results were due to cancelling-out effects of the existence of both negative and positive width differences. Therefore, the mean of the absolute disparity values were also calculated. Then it was clear that the cell resolution negatively affects the results; not only will poorer resolution give poorer spatial accuracy (expressed as width disparities), it is also clear that areas with gentler side slopes have higher width disparities than do areas with steeper side slopes (Fig. 2). However, even if there was a general correlation between slope and width disparity, the width disparity at each cross section varied quite randomly. Some cross sections showed no difference between the different DEMs, while other cross sections for the poorest resolutions differed more than 130 m.
River width disparities between modeled floods using reference DEM and degraded DEMs when the mean of absolute width differences have been used (based on Brandt 2009). Inset shows the effect of systematic errors in the DEM of surrounding terrain on water level and inundation width
Figure 3a shows the differences between the reference model and two of the degraded models of 3.83 and 50 m cell size, as well as the inundated area when the already existing 50 m DEM (Lantmäteriet’s) is used. Therefore, in a later study, to get a more robust analysis, about 400 transects were laid out across the river and checked for disparities between the reference model and the degraded models (cf. Brandt and Lim 2012). The disparity distances were then plotted against the river side slope (Fig. 3b). From this diagram it can be seen that modeled inundation boundaries can be significantly different from the “true” ones, especially at gentle river side slopes.
a Disparities between modeled floods using reference DEM and degraded DEMs with 3.83 and 50 m cell size on two areas along the Eskilstuna River, Sweden. The red line represents the inundated area based on Lantmäteriet’s (denoted National Land Survey) old 50 m DEM (from Brandt 2009). b Disparity distances between results based on the reference model and the degenerated DEMs and Lantmäteriet’s old 50 m DEM. Also included are visually estimated envelope curves for each DEM resolution range (from Brandt and Lim 2012), as well as an inlay on how disparity distances and the river side slopes were calculated
A follow up on the Eskilstuna study was done on the Testebo River, Sweden (Brandt and Lim 2012; also cf. Lim 2009, 2011). Instead of a reference model of high-resolution laser altimetry data and degenerated DEMs, this area used reference records of inundation extents from the 1977-year flood, together with laser altimetry data and the old 50 m DEM from Lantmäteriet as test models. Furthermore, two separate and independent modeling attempts using the same laser altimetry data were done, one by Brandt and one by Lim, to also see how much the modeler will impact the analysis. As can be seen in Fig. 4a there are places with relatively big disparities between modeled and actual flood extent boundaries. These are mainly located in flat terrain. Also apparent is that the disparities between the modelers are smaller than the disparities between any of the modelers and the reference flood map (Fig. 4b).
a Modeled floods using laser altimetry data (one by Brandt and one by Lim) and using the 50 m DEM from Lantmäteriet (denoted National Land Survey). The flood in 1977 serves as the reference inundation area. b Disparity distances between the different models. From Brandt and Lim (2012)
3 Representing DEM-derived uncertainties of flood maps
This work has focused on two aspects of accuracies and uncertainties related to the elevation models that are used for inundation mapping. One is related to the cell resolution of the DEM and the other is related to the river channel and floodplain slope perpendicular to the flow direction.
3.1 DEMs used for creating an uncertainty equation
To be able to test the influence on resolution, the already existing DEMs from the previous projects were used. In that process, the strategy was to simulate the behavior of the Leica ALS50 LiDAR instrument at different flight heights (cf. Klang and Klang 2009 for full details of this process), and hence these DEMs have the advantage of being more similar to real recordings at different flight heights, than if simple aggregation of cells or re-interpolation of original LiDAR points were to be performed. The original DEMs, with an initial point spacing of 1.64 and 1.36 points/m2, corresponding to cell sizes of 0.78 and 0.86 m, respectively, had been degraded and downsampled to a number of different DEMs (Table 1) of gradually increased point spacing or cell size. The DEMs were the same as for the two areas shown in Fig. 3a (Brandt 2009).
3.2 Estimating the uncertainties due to DEM resolution and floodplain slopes
The previous studies show that it should be possible to create an equation for disparity distances (Dd) according to:
where S is terrain slope perpendicular to the flow direction, δ is the cell size of the DEM and P is the percentile of interest (confidence) for estimating the uncertainties.
The first step to create a general equation that describes disparity distances involved plotting the disparities against the perpendicular slopes. Using the same transects described in Brandt and Lim (2012), disparity was measured as the absolute value of the distance between the modeled and the “true” flood boundary (based on the reference DEM). The slope was then calculated from the same coordinate pairs of the reference DEM (also cf. Fig. 3b). Next, for each resolution the slopes were divided into seven classes where different percentiles were calculated for each slope class (Table 2), and a regression model was developed linking the percentiles to terrain slope and DEM resolution, i.e., a quantile regression was performed (cf. e.g. Koenker and Hallock 2001). As there were very few observations in the two smallest slope classes, these were excluded from the regression analyses. The total number of observations for each DEM differs; partly because there were a few observations with slopes steeper than 1.78 m/m, i.e., steeper than the slope classes used for the regression analysis (in analogy with the smallest slope classes), and partly because of removal of observations where the slope was exactly 0 m/m (the reasons being: it is not possible to define the logarithm of 0, and these observations would belong to a slope class even smaller than those that were not included in the regression analysis). Then, when the logarithm of the percentile disparities for each slope class were plotted against the logarithm of the slope classes it is clear that they plot as straight lines with high coefficients of determination (R2) (Fig. 5).
Disparity distances between modeled and true flood boundaries plotted against the perpendicular slopes for 1.4, 3.83, and 50 m DEMs, respectively (Note The peculiar linear pattern arises due to the limiting factor of using elevation values with cm precision for slope calculation). Also plotted are percentile values for each slope class and their corresponding regression lines (for classes 0.0056–0.5623 m/m)
The general equation describing the regression lines, seen in Fig. 5, can be expressed as:
However, from Fig. 5 it can also be seen that the regression lines vary in both position and degree of slope, i.e., the lines’ c coefficients and z exponents vary depending on the resolution and the desired confidence. If the c coefficients are plotted against the resolution it can be seen that c is increasing when resolution gets poorer and confidence percentile gets higher (Fig. 6a).
a Variation of the c coefficient depending on resolution (or DEM cell size) and confidence (percentile, P). Regression lines are included for 10, 50, and 90 percentiles, respectively. b Variations of a coefficient and b exponent depending on confidence. c Variation of the b exponent depending on resolution and confidence. d Variation of the x and y coefficients depending on desired confidence
Although in the figure it can be seen that the matching between the data points and regression line is weaker for the coarse resolution DEMs, relatively strong correlation coefficients are achieved. The lines in Fig. 6a can be represented with the following equation:
When plotting the a coefficients and b exponents against the confidence percentiles, it appears that a increases exponentially with increasing confidence percentile while b has a relatively weak correlation, where the mean value is 0.970 with a standard deviation of 0.049 (Fig. 6b). Hence the b exponent may be represented by a constant. The c coefficient can therefore be described with the following equation:
Also the z exponent increases when resolution gets poorer (Fig. 6c), although the correlation coefficients are not as high as for the c coefficient, according to the following general equation:
However, when plotting the x and y coefficients against the confidence percentiles, it appears that x is constant with a mean value of 0.1124 and a standard deviation of 0.0062, and that y increases with increasing confidence percentile (Fig. 6d). The z exponent can therefore be described with the following equation:
The final equation then becomes:
As a check the Dd equation has been plotted against the empirical data (Fig. 7). Also included is a disparity distance example from Tärnsjö (Fig. 7c) (location taken from the study by Vähäkari 2006), which serves as the most extreme disparity known to the author.
4 Constructing the algorithm
4.1 Algorithm for visualizing flood boundary delineation uncertainties
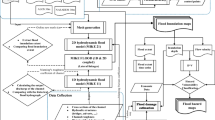
Based on the results from Table 2 and Figs. 5, 6, it is possible to construct an algorithm for direct visualization of the uncertainties related to the quality of the DEM and the perpendicular side slopes. This example will use the modeled inundation polygon, the already existing cross sections in the hydraulic model, and a DEM as input. In short the following procedure is followed (Fig. 8): (1) First the cross sections are prepared for the analysis and different input variables are determined. (2) Then each cross section is checked where (and whether) it is intersected by the modeled flood boundary. From the intersection, an iterative process, going one cross section node at a time, will look both toward the center of the river (determining the inner uncertainty boundary) and in the opposite direction away from the river (determining the outer uncertainty boundary) until the disparity distance from the Dd equation is exceeded. As the areal extent of inundation is derived using a regular grid of raster cells, with individual elevation values, there is a need to translate the disparity distance locations of the cross sections to elevation values. At the coordinates of disparity distance exceedance, elevation values are sampled or calculated based on the Dd equation, one lower elevation defining the inner boundary of uncertainty and one higher elevation defining the outer boundary of uncertainty (by using the Dd equation, the algorithm can consider abrupt ends due to e.g. buildings giving a so called “wall effect”). (3) Next the nodes in all cross sections are populated with the uncertainty elevation values and two TINs are created; one with values representing the inner uncertainty boundary and the other the outer uncertainty boundary. These TINs are then rasterized (this point-to-TIN-to-raster conversion will ensure that water levels will always fall in the downstream direction whereas direct raster interpolation from points may produce elevation artifacts). (4) Finally the DEM can be compared with the uncertainty rasters yielding three distinctive areas: not flooded areas (at least according to the percentile used), areas uncertain to be flooded, and flooded areas (at least according to the percentile used).
4.2 Resulting pseudo code
The following variables are used:
Boolean: flag
Integers: m max (number of cross sections); m (cross section number), n (cell or point number in a cross section)
Float: DI flag , DO flag , (previous valid distances of inner and outer uncertain flood area, respectively); ws (water surface elevation); c, z (coefficient and exponent values taken from the D d equation); δ (cell resolution)
Float arrays: x, y, h (coordinates and elevations of cross section nodes/cells); DI, DO, SI, SO (inner and outer uncertainty distances and slopes, respectively); RXSI, RXSO, LXSI, LXSO (inner and outer uncertainty elevations for right and left cross sections, respectively
-
1.
Count the number of cross sections (m max ). Determine the cell resolution (δ) of the DEM and use the disparity equation (D d ) for the desired probability.
-
2.
Split all cross sections at river channel center. Define cross sections as LEFT or RIGHT.
-
3.
Let m = 1.
-
4.
Repeat until number of cross sections has been exceeded, i.e., m > m max .
-
4.1.
If RIGHT cross section (cross section should be seen looking in the downstream direction, where cells are ordered from left (negative cell positions in the river channel) to right (positive cell positions on the ground).
-
4.1.1.
Determine the coordinates, i.e., x(0) and y(0), and elevation, h(0), of the DEM cell, where the modeled flood boundary intersects the cross section, i.e., the raster cell (or point) Cell (0). If no intersection exists, exclude that cross section from the analysis.
-
4.1.2.
Let n = 0, flag = false, DI(0) = 0.
-
4.1.3.
Repeat until the distance of the inner flood area, DI, for Cell (n − 1), is longer than the D d for the same slope of that between the Cell (n − 1) and Cell (0), or that all cells in the cross section has been treated:
-
4.1.3.1.
Get the coordinates and elevation of Cell (n)’s neighboring cell, i.e. x(n − 1), y(n − 1), and h(n − 1) at Cell (n − 1), and calculate the distance, DI(n − 1), and slope, SI(n − 1), from Cell (0) to Cell (n − 1).
-
4.1.3.2.
If SI(n − 1) > 0 (i.e. the terrain is higher at Cell (n − 1), creating an island) then n = n − 1, else flag = true, DI flag = DI(n), and compare DI(n − 1) with the D d for desired probability for the absolute value of slope of SI(n − 1). If D d is exceeded then stop, else n = n − 1.
-
4.1.3.1.
-
4.1.4.
If flag = false then DI flag = δ/2 (This accounts for cross sections where no cells in the inner part of the cross section have negative slopes, i.e. no certain flooding seems to occur).
-
4.1.5.
If ws(m) – exp[(ln DI flag – ln c)/z]*DI flag > h(n − 1) then inner uncertainty boundary elevation RXSI(m) = ws(m) – exp[(ln DI flag – ln c)/z]*DI flag else RXSI(m) = h(n − 1) (This accounts for the wall effect; see Sect. 4.3).
-
4.1.6.
Let n = 0, flag = false, DO(0) = 0.
-
4.1.7.
Repeat until the distance of the outer flood area, DO(n + 1), for Cell (n + 1), is longer than the D d for the same slope of that between the Cell (n + 1) and Cell (0), or that all cells in the cross section has been treated:
-
4.1.7.1.
Get the coordinates and elevation of Cell (n)’s neighboring cell, i.e. x(n + 1), y(n + 1), and h(n + 1) at Cell (n + 1), and calculate the distance, DO(n + 1), and slope, SO(n + 1), from Cell (0) to Cell (n + 1).
-
4.1.7.2.
If SO(n + 1) < 0 (i.e. the terrain is lower at Cell (n − 1), creating a water pond) then n = n + 1, else flag = true, DO flag = DO(n), and compare DO(n + 1) with the D d for desired probability for the absolute value of slope of SO(n + 1). If D d is exceeded then stop, else n = n + 1.
-
4.1.7.1.
-
4.1.8.
If flag = false then DO flag = δ/2 (This accounts for cross sections where no cells in the outer part of the cross section have positive slopes, i.e. no certain dry ground seems to occur).
-
4.1.9.
If ws(m) + exp[(ln DO flag – ln c)/z]* DO flag < h(n + 1) then outer uncertainty boundary elevation RXSO(m) = ws(m) + exp[(ln DO flag – ln c)/z]* DO flag else RXSO(m) = h(n + 1) (This accounts for the wall effect).
-
4.1.1.
-
4.2.
Else LEFT cross section (follow 4.1, but beware of sign changes, </> changes, and change of RXSI/RXSO to LXSI/LXSO.
-
4.3.
Let m = m + 1.
-
4.1.
-
5.
Assign cross sections, i.e. both LEFT and RIGHT, with elevation values from XSI and XSO elevation values.
-
6.
Create two point themes where the point locations are taken from the nodes in the cross section lines. One theme with associated inner elevation values and one with outer elevation values.
-
7.
Create two TINs from the point themes. One based on inner elevation values and one based on outer elevation values. Rasterize the TINs to the same extent as the DEM to create uncertainty rasters.
-
8.
Compare the uncertainty rasters with the DEM. If cell elevations in uncertainty raster for outer elevations < DEM then cell is not flooded. If cell elevations in uncertainty raster for inner elevations > DEM then cell is flooded. Other alternatives results in uncertain with respect to flooded/not flooded.
4.3 Calculation of wall effect
Figure 9 illustrates how the water elevations for the cross sections can be calculated (for outer uncertainty boundary elevation in the RIGHT cross section). When the distance to cell C(n + 1) is greater than the Dd for the same slope (i.e., between location of the modeled flood boundary location and the cell C(0)), the uncertainty elevation (from the Dd equation) of cell C(n) is compared with the ground elevation of cell C(n + 1). The elevation can be calculated by adding the water surface elevation to the product of the distance and slope from Eq. 2:
If the computed uncertainty elevation for cell C(n) is lower than the ground elevation of cell C(n + 1) the former elevation is used; if not, the ground elevation of cell C(n + 1) is used. By doing that, extremely high uncertainty elevations will not occur, due to for example vertical walls in the cross section. Also, when there is no wall, the resulting uncertainty elevation will be slightly higher (i.e. more conservative, or on the “safe side”) compared with using an elevation from a cell farther away.
4.4 Applying the algorithm
To test the Dd equation and the algorithm, two DEMs were chosen, 3.83 m and 50 m, respectively, with a 95 percentile confidence. The results can be seen in Fig. 10, where red areas represent the areal range that is uncertain to be flooded. It is 95 % certain that the flood boundary will be within this area. The remaining 5 % are divided into blue areas that are almost certain to be flooded and areas outside of the red areas that are almost certain not to be flooded.
Resulting uncertainty areas for 95 percentile confidence. Upper figure shows the 0.78 m DEM with “true” inundation extents, middle shows the 3.83 m DEM, and the lower figure the 50 m resolution case. The lines in the lower two figures represent the “true” inundation extents. Blue areas are almost certain to be flooded, red areas are uncertain to be flooded (containing 95 % of the possible inundation delineations), and remaining areas are almost certain not to be flooded
5 Discussion and conclusion
Previous research has produced relatively consistent recommendations from 4 to 10 m DEM resolution. Better resolution than that has not produced any significant improvements in inundation boundary prediction. Yet there are numerous real case examples on disparities where the models clearly have failed and where the water boundary may be several hundreds of meters wrong, even when LiDAR data has been used as input (also cf. e.g. Croke et al. 2014 who stressed the importance of geomorphological understanding during flood risk management). Casas et al. (2006) argued that coarser resolution will have less consequence when discharge increases, i.e., floodplain areas will be more accurately mapped than near river areas. This may be true with respect to difference in total surface area of the true and modeled inundation. But, even if the flow rates are bigger, the flood boundary perimeter should be of roughly the same length, provided the river flows through a pronounced river or floodplain valley, and therefore the uncertainty problem will still persist at the modeled inundation boundaries. To overcome unpleasant surprises, extra caution should therefore be taken when either the DEMs are of poor resolution or that the terrain adjacent to the modeled inundation boundary is flat.
It is generally possible to construct an equation for the uncertainty of floodplain boundaries depending on DEM resolution and terrain slope. Except for the relation between z exponent and resolution, high correlation coefficients were yielded for all coefficients and exponents. This is probably due to the topographical character of the areas the modeling is based on; or in other words, the geographical areas of this study are not enough flat for sufficiently long distances. Hence, the main weakness in the data lies in the number of observations for the poorest DEM resolution together with the characteristics of the geographical area. Although there are very flat areas, these are not very big, making it impossible to get big disparities. This will also impact the equation. Most probable, the z exponent is too big, i.e., the slopes of the lines in Fig. 7 should be sloping steeper in the negative direction. Therefore, to have a more conservative and “safe” estimate on risks, the z exponent could be set to the value for the highest resolution (~–0.72), irrespectively of DEM resolution. Furthermore, as the same transects, with approximately 10 m spacing, are used for all DEM resolutions, the same DEM cells are used several times for calculation of the transect slopes of the coarse resolution DEMs. This is not the case for fine-resolution DEMs. Another problem may be the usage of retransforming logged values in the regression analysis (cf. Granger and Newbold 1976 or, for a hydrological example, Jansson 1985). No correction has been applied in this work and therefore some of the coefficients and exponents are probably underestimated.
As the disparity distance equation has been developed from elevation and slope values taken from the reference DEM, this may give erroneous estimates when applying the algorithm on DEMs of lower qualities. Therefore, in future research an equation based on the slopes derived from the lower quality DEMs will be created to see if that may affect the results. Also important is not to use the equation for higher confidences than 95 %. For example it is possible to get computed disparity distances that are shorter than those that were actually observed, even when 100 % is used as input. As can be seen in Fig. 7, there are not exactly 10 % of observations above and below the 90 percentile lines for the three DEMs shown. This arises mainly due to the combination of the 14 DEMs. The magnitudes of these errors (which can be seen as the uncertainty of the disparities for a given probability) have not been calculated in this study, as the primary focus have been on modeling and visualizing the uncertainties of the flood boundary lines, not the uncertainties of the uncertainties. However, when more robust data have been gathered for a wider range of geographical settings, it will be of interest to also study this (cf. Roscoe et al. 2012 for such a procedure).
High confidence percentages have to be treated using extreme value statistics. If more data, especially coarse resolution data, had been available, another option would be to use envelope curves. In this study envelope curves were created through increasing the 95 % confidence level by one magnitude. When comparing these envelope curves with the visually determined curves in Brandt and Lim (2012), there are strong indications that the z exponent is too big (cf. Fig. 4b), again calling for a z value closer to −0.72, also for poorer resolutions. Furthermore, the importance of regularly, and not too sparsely, placed cross sections can be seen in Fig. 10. For the 50 m DEM case, the inundated areas do not follow the trunk river in the western (left) part. This can be attributed to cross sections not expanding long enough, making them disqualified in the algorithm which in the end therefore produced too low water levels for this area.
To test the applicability of the equation and resulting algorithm, future research will look at another river where river side slopes are much gentler, as already now it can be seen that the disparities are higher for the Testebo River than the Eskilstuna Rivers, for the same slope. However, the disparities at Testebo River are compared against an actual flood event that may not have been mapped good enough, whereas Eskilstuna River’s are compared against a reference DEM. This means that the Dd equation developed for Eskilstuna River provides a measure of uncertainties only related to the DEM, whereas the disparities for Testebo also contain other types of uncertainties. Also, higher precision than cm on elevations has to be used to avoid the linear patterns seen in Fig. 5. This will also reduce the risk of getting 0 m/m slopes that make the use of logarithm functions problematic. More studies on other rivers, following both the Eskilstuna case of totally focusing on the DEM, as well as other cases that are compared with actual flood events, should both verify the approach as well as making adjustment of the equation possible. Finally, as this kind of uncertainty only represents one type of uncertainty, i.e., random errors in the DEM, other types including friction parameter errors, systematic errors of DEMs, rain and reach input of water flow, model structure, operator errors, etc. should also be considered. Therefore, being humble describing the uncertainties of the presented flood risk maps is to be recommended.
References
Apel H, Merz B, Thieken AH (2008) Quantification of uncertainties in flood risk assessments. Int J River Basin Manag 6(2):149–162. doi:10.1080/15715124.2008.9635344
Brandt SA (2005) Resolution issues of elevation data during inundation modeling of river floods. In: Jun B-H, Lee S-I, Seo I-W, Choi G-W (eds) Water engineering for the future: choices and challenges. Proceedings of XXXI International Association of Hydraulic Engineering and Research congress, Seoul, September 11–16 2005. Korean Water Association, Seoul, pp 3573–3581
Brandt SA (2009) Betydelse av höjdmodellers kvalitet vid endimensionell översvämningsmodellering. FoU-rapport Nr 35, Högskolan i Gävle
Brandt SA, Lim NJ (2012) Importance of river bank and floodplain slopes on the accuracy of flood inundation mapping. In: Murillo Muñoz RE (ed) River flow 2012: vol 2. Proceedings of the international conference on fluvial hydraulics, San José, 5–7 Sept 2012. CRC Press/Balkema (Taylor & Francis), Leiden, The Netherlands, pp 1015–1020
Casas A, Benito G, Thorndycraft VR, Rico M (2006) The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf Process Landforms 31(4):444–456. doi:10.1002/esp.1278
Castellarin A, Di Baldassarre G, Bates PD, Brath A (2009) Optimal cross-sectional spacing in Preissmann scheme 1D hydrodynamic models. J Hydraul Eng 135(2):96–105. doi:10.1061/(ASCE)0733-9429(2009)135:2(96)
Colby JD, Dobson JG (2010) Flood modeling in the coastal plains and mountains: analysis of terrain resolution. Nat Hazards Rev 11(1):19–28. doi:10.1061/(ASCE)1527-6988(2010)11:1(19)
Cook A, Merwade V (2009) Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J Hydrol 377(1–2):131–142. doi:10.1016/j.jhydrol.2009.08.015
Croke J, Reinfelds I, Thompson C, Roper E (2014) Macrochannels and their significance for flood-risk minimisation: examples from southeast Queensland and New South Wales, Australia. Stoch Environ Res Risk Assess 28(1):99–112. doi:10.1007/s00477-013-0722-1
Granger CWJ, Newbold P (1976) Forecasting transformed series. J R Stat Soc Ser B (Methodological) 38(2):189–203
Hydrologic Engineering Center (2008) HEC-RAS: river analysis system. User’s manual, version 4.0. US Army Corps of Engineers, Hydrologic Engineering Center, Davis
Jansson M (1985) A comparison of detransformed logarithmic regressions and power function regressions. Geogr Ann 67A(1/2):61–70. doi:10.2307/520466
Klang D, Klang K (2009) Analys av höjdmodeller för översvämningsmodellering. http://www.geoxd.se/GeoXD_Analys%20av%20hojdmodeller.pdf. Accessed 02 April 2015
Koenker R, Hallock K (2001) Quantile regression. J Econ Perspect 15(4):143–156. doi:10.1257/jep.15.4.143
Koivumäki L, Alho P, Lotsari E, Käyhkö J, Saari A, Hyyppä H (2010) Uncertainties in flood risk mapping: a case study on estimating building damages for a river flood in Finland. J Flood Risk Manag 3(2):166–183. doi:10.1111/j.1753-318X.2010.01064.x
Lim NJ (2009) Topographic data and roughness parameterisation effects on 1D flood inundation models. B.Sc thesis, University of Gävle
Lim NJ (2011) Performance and uncertainty estimation of 1- and 2-dimensional flood models. M.Sc thesis, University of Gävle
Lim NJ, Brandt SA, Seipel S (2016) Visualisation and evaluation of flood uncertainties based on ensemble modelling. Int J Geogr Inf Sci 30(2):240–262. doi:10.1080/13658816.2015.1085539
Merwade V, Olivera F, Arabi M, Edleman S (2008) Uncertainty in flood inundation mapping: current issues and future direction. J Hydrol Eng 13(7):608–620. doi:10.1061/(ASCE)1084-0699(2008)13:7(608)
Omer CR, Nelson EJ, Zundel AK (2003) Impact of varied data resolution on hydraulic modeling and floodplain delineation. J Am Water Resour Assoc 39(2):467–475. doi:10.1111/j.1752-1688.2003.tb04399.x
Pappenberger F, Beven K, Horritt M, Blazkova S (2005) Uncertainty in the calibration of effective roughness parameters in HEC-RAS using inundation and downstream level observations. J Hydrol 302(1–4):46–69. doi:10.1016/j.jhydrol.2004.06.036
Pappenberger F, Matgen P, Beven KJ, Henry J-B, Pfister L, de Fraipont P (2006) Influence of uncertain boundary conditions and model structure on flood inundation predictions. Adv Water Resour 29(10):1430–1449. doi:10.1016/j.advwatres.2005.11.012
Pappenberger F, Beven KJ, Ratto M, Matgen P (2008) Multi-method global sensitivity analysis of flood inundation models. Adv Water Resour 31(1):1–14. doi:10.1016/j.advwatres.2007.04.009
Raber GT, Jensen JR, Hodgson ME, Tullis JA, Davis BA, Berglund J (2007) Impact of Lidar nominal postspacing on DEM accuracy and flood zone delineation. Photogramm Eng Remote Sens 73(7):793–804
Roscoe KL, Weerts AH, Schroevers M (2012) Estimation of the uncertainty in water level forecasts at ungauged river locations using quantile regression. Int J River Basin Manag 10(4):383–394. doi:10.1080/15715124.2012.740483
Schumann G, Matgen P, Hoffmann L, Hostache R, Pappenberger F, Pfister L (2007) Deriving distributed roughness values from satellite radar data for flood inundation modelling. J Hydrol 344(1–2):96–111. doi:10.1016/j.jhydrol.2007.06.024
Vähäkari A (2006) Simulering av översvämningar i Nedre Dalälven. M.Sc thesis, Uppsala Universitet
Wagener T, Gupta HV (2005) Model identification for hydrological forecasting under uncertainty. Stoch Environ Res Risk Assess 19(6):378–387. doi:10.1007/s00477-005-0006-5
Warmink JJ, Straatsma MW, Huthoff F, Booij MJ, Hulscher SJMH (2013) Uncertainty of design water levels due to combined bed form and vegetation roughness in the Dutch River Waal. J Flood Risk Manag 6(4):302–318. doi:10.1111/jfr3.12014
Werner MGF (2001) Impact of grid size in GIS based flood extent mapping using a 1D flow model. Phys Chem Earth (B) 26(7–8):517–522. doi:10.1016/S1464-1909(01)00043-0
Werner MGF, Hunter NM, Bates PD (2005) Identifiability of distributed floodplain roughness values in flood extent estimation. J Hydrol 314(1–4):139–157. doi:10.1016/j.jhydrol.2005.03.012
Wilson MD, Atkinson PM (2007) The use of remotely sensed land cover to derive floodplain friction coefficients for flood inundation modeling. Hydrol Proc 21(26):3576–3586. doi:10.1002/hyp.6584
Wu XZ (in press) Probabilistic solution of floodplain inundation equation. Stoch Environ Res Risk Assess. doi: 10.1007/s00477-015-1025-5
Yacoub T, Sanner H (2006) Vattenståndsprognoser baserade på översiktlig kartering. En fallstudie. SMHI. Hydrologi nr 100
Zhang W, Montgomery DR (1994) Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour Res 30(4):1019–1028. doi:10.1029/93WR03553
Acknowledgments
Thanks are due to Nancy Joy Lim, both for commenting on the manuscript as well as discussing the entire project, and the anonymous reviewers for their constructive criticism. The study has been financially supported by the EU through Tillväxtverket (Project GLOBES 2, number 170430) and Lantmäteriet (Project: “Kvalitetsbeskrivning av geografisk information vid översvämningskartering”).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author declares that he has no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Brandt, S.A. Modeling and visualizing uncertainties of flood boundary delineation: algorithm for slope and DEM resolution dependencies of 1D hydraulic models. Stoch Environ Res Risk Assess 30, 1677–1690 (2016). https://doi.org/10.1007/s00477-016-1212-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-016-1212-z