A neural network based general reservoir operation scheme

Abstract

Construction of dams and the resulting water impoundments are one of the most common engineering procedures implemented on river systems globally; yet simulating reservoir operation at the regional and global scales remains a challenge in human–earth system interactions studies. Developing a general reservoir operating scheme suitable for use in large-scale hydrological models can improve our understanding of the broad impacts of dams operation. Here we present a novel use of artificial neural networks to map the general input/output relationships in actual operating rules of real world dams. We developed a new general reservoir operation scheme (GROS) which may be added to daily hydrologic routing models for simulating the releases from dams, in regional and global-scale studies. We show the advantage of our model in distinguishing between dams with various storage capacities by demonstrating how it modifies the reservoir operation in respond to changes in capacity of dams. Embedding GROS in a water balance model, we analyze the hydrological impact of dam size as well as their distribution pattern within a drainage basin and conclude that for large-scale studies it is generally acceptable to aggregate the capacity of smaller dams and instead model a hypothetical larger dam with the same total storage capacity; however we suggest limiting the aggregation area to HUC 8 sub-basins (approximately equal to the area of a 60 km or a 30 arc minute grid cell) to avoid exaggerated results.

1 Introduction

Construction of dams and the resulting water impoundments are one of the most common engineering procedures implemented on river systems. Half of the major global river systems are affected by dams (Dynesius and Nilsson 1994). There are over 45,000 operational large dams globally with an estimated aggregate storage capacity of over 6000 km³ (Vörösmarty et al. 1997; WCD 2000; ICOLD 2011; Lehner et al. 2011) trapping over 17 % of global annual runoff (Nilsson et al. 2005; Piao et al. 2007). Dams increase the storage of water in river systems by 700 % and triple the mean residence time of water in the rivers (Vörösmarty et al. 1997). Dams impact ecosystems by flow regulation, upstream flooding, change in sedimentation patterns, draining floodplain wetlands and altering water temperature patterns (Vörösmarty and Sahagian 2000; Kingsford 2000; Syvitski et al. 2005). Overlooking those impacts may significantly affect modelling results and influence decisions addressing water management issues.

In the context of this paper, reservoir or dam operation refers to alteration of the outgoing flow regime via accumulation of the incoming flow and delayed release of water over time. One major problem in dams’ impact studies is the lack of reliable methods for simulating reservoir operation. In reality, dams are regulated in different ways and virtually each dam has a unique operating rule (Simonovic 1992; Wurbs 1993). Actual reservoir operating rules are not available to the public, thus their direct use in models is infeasible, especially for macro-scale applications where hundreds or thousands of dams exist in the study domain.

To address this problem, metrics have been proposed to assess the aggregate hydrologic behavior of dam regulated rivers. For example, Graf (1999) used the total reservoir storage in a watershed as a measure of changes in flow regimes and associated downstream effects. Nilsson et al. (2005) used the percentage of the annual discharge of a river system that can be contained by the reservoirs within that system as a measure to quantify flow regulation by dams (Dynesius and Nilsson 1994). Vörösmarty et al. (1997) used the ratio of aggregated reservoir storage along river networks and the mean annual river discharge to calculate the mean local aging of water and showed how large dams might change the residency time in rivers. They used a similar approach to study the impact of reservoir construction on sediment transport to the ocean (Vörösmarty et al. 2003).

Conceptual or empirical relationships have also been used to model reservoir operation. Meigh et al. (1999) and Döll et al. (2003) used an empirical relationship to simulate the monthly release from dams based on reservoir water storage ($Q_{out} \sim S^{b}$). Coe (2000) modelled dam operation by assuming that a reservoir is full in the month of average maximum inflow and is at its minimum storage for the month of average minimum inflow. He calculated the storage for other months assuming a linear relation between those upper and lower limits. Wisser et al. (2010a) used a relationship between daily inflow and average long-term inflow to calculate the daily release from a reservoir. Haddeland et al. (2006) calculated reservoir storage and release to meet monthly irrigation and hydropower demand. Hanasaki et al. (2006) predicted monthly release based on reservoir characteristics, river discharge and water use information. Their model tries to meet the industrial, domestic and irrigation water demand (Yoshikawa et al. 2013). Recent studies have applied remote sensing applications to model dam characteristics like storage, surface area and water level (Coe and Birkett 2004; Peng et al. 2006; Gao et al. 2012).

1.1 Artificial neural networks in hydrology

Artificial neural networks (ANN) have been successfully used in various water resources studies (Hsu et al. 1995; Maier and Dandy 2000; Govindaraju 2000a, b) notably in river flow forecasting (Karunanithi et al. 1994; Zealand et al. 1999; Coulibaly et al. 2000; Coulibaly and Baldwin 2008) and also to solve reservoir operation optimization problems through dynamic programming (Raman and Chandramouli 1996; Fontane et al. 1997; Jain et al. 1999; Rani and Moreira 2010). It has been demonstrated that performances of ANN-based models are similar or superior over conventional statistical and stochastic models for prediction of river flows (Abrahart and See 2000; Cigizoglu 2003; Rani and Moreira 2010).

Here for the first time we use ANN to map the general input/output relationships in actual operating rules of real world reservoirs. Our goal is to parameterize actual dam operation data by using ANN and develop a general reservoir operation scheme (GROS) that is suitable for use in large-scale hydrological models and is sufficiently accurate in simulating the operation of existing reservoirs. GROS enables us to collectively investigate the impact of dams and reservoirs operation on hydrological systems. We seek to limit the input requirements to essential and conveniently calculable data. For regional and global studies, accurate water demand data with applicable resolution is rarely available; therefore, we do not use water demand as an input to GROS. We compare the performance of GROS with a monthly reservoir model developed by Hanasaki et al. (2006) and a daily reservoir model developed by Wisser et al. (2010a).

1.2 Assessment of hydrologic alteration caused by dams

Dams alter the frequency, duration and timing of annual flooding and drought events. While this has beneficiary effects on human water security, aquatic biota is distressed by these changes as they rely on the natural hydrologic cycle for food and reproduction (Pringle et al. 2000; Kingsford 2000). Earlier works have analyzed the impact of dams on natural hydrology by comparing pre and post-dam flow regime from gage station data (Thoms and Sheldon 2000; Magilligan and Nislow 2005). This approach is only valid if no substantial change exists in other factors affecting the hydrologic regime between two periods. Impacts of climate variability and other anthropogenic disturbances such as water use, land cover change, and water transfer projects between the two periods should be accounted for (Yang et al. 2008; Chen et al. 2010). Moreover when comparing data from two periods, it is impossible to see how a different damming strategy could have affected the hydrology of that region.

2 Development of GROS

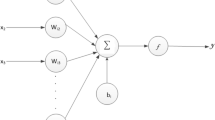
We are using ANN to develop our GROS for use in large-scale hydrological models to simulate the operation of existing reservoirs. The architecture of the ANN used in this study (Fig. 1) is determined by trial and error (Basheer and Hajmeer 2000; Rafiq et al. 2001). Each input set consists of three vectors; if t represents the daily time step, the three input vectors are: Inflow = [I _t , I _t−1, I _t−2], Release = [R _t−1, R _t−2] and Storage = [S _t−1], which are used to calculate the daily release (output) from reservoir [R _t ]. Based on our analysis of significance of inputs (discussed in Sect. 2.1), using inflow and release data from previous time steps (i.e. t−3, t−4, etc.) does not have a significant impact on performance of the ANN and since storage levels do not fluctuate substantially every day, we limited the inputs to daily reservoir storage volume, three consecutive days of inflow, and release in past 2 days. Redundant inputs increase the likelihood of overfitting and decrease ANN prediction ability (Tetko et al. 1996; Maier et al. 2010).

Fig. 1

Architecture of the artificial neural network used in developing GROS. t stands for daily time step, I for inflow, R for release and S for Storage. W and b represent weights and biases. Rectangles in green are input layers, rectangles in gray are hidden layers, and rectangle in orange is the output layer. Numbers shown for each hidden layer show the number of nodes in that layer

Inflow, release and storage data are each handled by a separate input layer. The three elements of the inflow vector [I _t , I _t−1, I _t−2] are connected to a hidden layer with six nodes. The two elements of the release vector [R _t−1, R _t−2] are connected to a hidden layer with four nodes, and the storage [S _t−1] is connected to a hidden layer with two nodes. Outputs from these layers are connected to the fourth layer with six nodes which are connected to the fifth layer with one node. The sigmoid hyperbolic tangent was selected as the transfer function for all the hidden layers since it provides better accuracy and faster learning speed compared to other sigmoid transfer functions (Adeloye and De Munari 2006; Taormina et al. 2012). The Log-sigmoid transfer function was used in the output layer to ensure that the output is always between 0 and 1. Testing with multiple learning algorithms, the Levenberg–Marquardt algorithm had the best performance (Maier and Dandy 2000; Kişi 2007).

Daily inflow, release and storage data of 12 dams (Table 1) are used in calibration and validation of the ANN. On average each dam has 23 years of daily data. These dams represent a wide range of storage sizes (1.5–32.3 km³), inflows (38.5–2993.5 m³/s), residence time (45–1089 days) and purpose. Two of the 12 dams (Sirikit and Bhumibol) are in Thailand where the climate is different compared to the other sites, which are all in the USA. Data from these two dams were excluded from the ANN training process to be used exclusively as independent validation datasets to ensure that the final ANN has not overfitted to the specific training sites. The input/output pairs from the other 10 dams were randomly divided into three subsets of training (60 %), cross training (20 %) and validation (20 %) (Table 1). In ANN specific terminology, the training set is used for determining the ANN weights and biases to minimize the error function and maximize accuracy in each iteration. The cross training set is used to oversee the training process and improve ANN generalization by minimizing overfitting. An overfitted ANN yields high accuracy on training data but fails to generalize from the training data, thus has poor performance on new, independent input data. The validation dataset provides an unbiased estimate of the generalization error (Govindaraju 2000a).

Table 1 List of the dams used in this study

Data used in this study comes from 12 dams with different operating rules, spanning several orders of magnitude. If the actual data is used directly, the training process will fail as no significant pattern will be detectable between inputs and outputs. To avoid this problem, the data were rescaled to be dimensionless, ranging from 0 to 1. For each dam, flow (m³/s) was converted to daily volume (m³) to be comparable to storage (m³); then all the data for each dam were divided by the maximum capacity of that dam. To use outputs of ANN in a hydrological model, the scaling procedure should be reversed (Appendix 1) by multiplying it by the maximum capacity of the dam to get the daily volume of released water (m³) and then converting it to flow rate (m³/s).

This trained ANN is the core of our GROS. Appendix 1 contains a simplified algorithm that explains how GROS simulates the daily reservoir release. Using GROS in a water balance model (WBM_plus) (Wisser et al. 2010b), we isolated reservoir effects from other disturbances (i.e. water withdrawal, flow diversions and climate variability) and studied the impact of dams with various storage sizes and distribution patterns on river system dynamics. We calculated Colwell’s parameters (Colwell 1974) and used the Indicators of hydrological alteration (Richter 1996) and Range of Variability Approach (Richter et al. 1997) to show how dams impact rivers hydrology under different scenarios (Mathews and Richter 2007).

2.1 Significance of ANN inputs

We used an Improved Stepwise method (Gevrey et al. 2003) to identify the importance of inputs used in developing GROS. The change in the sum of square errors (SSE) is calculated when that input and its corresponding weights are removed from the Neural Network. The most important variables are those which cause the largest change in SSE.

Table 2 lists the SSE and coefficient of determination (R²) for 10 experiments that show how eliminating inputs from ANN training affects its performance. From the six single inputs used in this study (I _t , I _t−1, I _t−2, R _t−1, R _t−2, S _t−1), daily storage (S _t−1) is the most significant input. S _t−1 represents the fraction of dam filled with water in each day. Inputs from older times have a smaller impact on ANN performance. Among the inputs, inflow at time t−2 (I _t−2) had the smallest impact on SSE.

Table 2 Significance of ANN inputs using the improved stepwise method

2.2 Model performance

We evaluated the performance of GROS against observed time series and compared the outcomes against existing daily and monthly reservoir models (Hanasaki et al. 2006; Wisser et al. 2010a). Wisser et al. (2010a) use a simple relationship linking daily reservoir inflow I _t (m³/s) and long-term mean inflow I _m (m³/s) to calculate daily reservoir release R _t (m³/s) as:

$$ R_{t} = \left\{\begin{array}{ll} kI_{t} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;~I_{t} \ge I_{m} ~ \hfill \\ \lambda I_{t} + \left( {I_{m} - I_{t} } \right)I_{t}\;\;\;\;I_{t} < I_{m} \hfill \\ \end{array} \right. $$

(1)

where k and λ are empirical constants set to 0.16 and 0.6, respectively.

Hanasaki et al. (2006) categorized reservoirs as irrigation and non-irrigation and developed a set of rules for monthly release from reservoirs based on their intended purpose and water demand. For a non-irrigation reservoir, monthly release was parameterized as:

$$ r_{m, y}^{\prime} = i_{mean} $$

(2)

where  $r_{m, y}^{\prime}$  is the provisional monthly release (m³/s), and i _mean is the mean annual inflow (m³/s).

For an irrigation reservoir, monthly release was parameterized as:

$$ \begin{aligned} r_{{m,y}}^{\prime } & = \;\;\;\;\;\left\{ \begin{array}{ll} \frac{{i_{{mean}} }}{2} \times \left( {1 + \frac{{\sum\nolimits_{{area}} {\left\{ {k_{{alc}} \times (d_{{irg,m,y}} + d_{{ind}} + d_{{dom}} } \right\}} }}{{d_{{mean}} }}} \right),\quad\;\,\;\;\quad\quad(d_{{mean}} \ge 0.5 \times i_{{mean}} ) \hfill \\ i_{{mean}} + \sum\limits_{{area}} {\left\{ {k_{{alc}} \times (d_{{irg,m,y}} + d_{{ind}} + d_{{dom}} } \right\}} - d_{{mean}} ,\;(d_{{mean}} \ge 0.5 \times i_{{mean}} ) \hfill \\ \end{array} \right. \hfill \\ d_{{mean}} &= \;\;\sum\limits_{{area}} {\left\{ {k_{{alc}} \times (d_{{irg,m,y}} + d_{{ind}} + d_{{dom}} } \right\}} \hfill \\ \end{aligned} $$

(3)

where k_alc is an allocation coefficient for grids with more than one reservoir upstream. d_irg,m,y is the monthly irrigation water withdrawal (m³/s); d_dom is the domestic water withdrawal (m³/s); d_ind is the industrial water withdrawal (m³/s); and d_mean is the mean annual total water demand of the reservoir (m³/s). The subscripts m, y and mean, indicate month, year and annual mean, respectively. The term ∑_area indicates integration over the basin downstream reservoir.

The monthly release r_m,y (m³/s) was calculated as

$$ r_{m, y} = \left\{\begin{array}{ll} k_{rls, y} \times r_{m, y}^{\prime}, & \quad \left(c \ge 0.5 \right) \\ \left(\frac{c}{0.5} \right)^{2} k_{rls,y} \times r_{m,y}^{\prime} + \left\{1 - \left( \frac{c}{0.5} \right)^{2} \right\} i_{m,y} , & \left( 0 \le c \le 0.5\right) \\ \end{array} \right. $$

(4)

where c is the storage capacity to mean total annual inflow ratio (c = C/I _mean ); and k_rls,y is the release coefficient, which reflects water storage at the beginning of the operational year; $r_{m, y}^{\prime}$ is the provisional monthly release.

We used the observed inflow time series as inputs to GROS and calculated the daily release from the reservoirs (Appendix 1). Based on analysis of observed data, the minimum storage level for reservoirs is set to 10 % of capacity. Nash–Sutcliffe efficiency coefficient (E) (B1), coefficient of determination (R²) (B2) and normalized root mean square error (NRMSE) (B3) are calculated for simulated dam releases (Fig. 2).

Fig. 2

RMSE, E and R² of Daily simulated release using GROS and Wisser et al. (2010a). NRMSE of monthly release simulation using GROS, Hanasaki et al. (2006) and Wisser et al. (2010a). All dams average shows the arithmetic mean for all the 12 dams

Simulation results from GROS are significantly more accurate than the outputs from the other two models. On average, GROS reduces the NRMSE (and RMSE) for simulated daily release by 72 % compared to Wisser et al. (2010a) method. For monthly simulated release, the average NRMSE (and RMSE) for Wisser et al. (2010a) and Hanasaki et al. (2006) models are comparable to each other at around 0.65 but the average NRMSE (and RMSE) for GROS is 0.11, nearly 80 % smaller. The average daily Nash efficiency coefficient is 0.86, and R-squared is 0.85 using GROS.

Accuracy of GROS outputs for simulated release from Bhumibol and Sirikit dams which were excluded from the development of ANN to be used as independent validation datasets, confirms that the ANN used in GROS is not overfitted to its training datasets.

3 Methods for assessing alteration of flow regimes by dams

We used Colwell’s parameters (Colwell 1974), a suite of indicators of hydrological alteration (Richter 1996) and range of variability approach (Richter et al. 1997) to demonstrate how changes in storage size and distribution pattern of dams in a drainage basin alter their hydrological impacts.

Colwell (1974) proposed three parameters of predictability, constancy and contingency to describe patterns of temporal fluctuation in physical and biological phenomena. Predictability is a measure of temporal uncertainty across successive time domains spanning a periodic phenomenon. Maximum predictability occurs when the state of a phenomenon is known with absolute certainty in time. Maximum constancy happens when the state of a phenomenon is always constant. Contingency shows to what degree state of the phenomena depends on time. Values of these parameters range from 0 to 1 (Colwell 1974; Poff and Ward 1989).

Richter (1996) proposed the indicators of hydrologic alteration (IHA) for assessing the degree of hydrologic alteration attributable to human influence within an ecosystem. IHA consists of 32 indices (Table 3) selected to quantitatively describe hydrological alterations caused by anthropogenic disturbances between pre-impact and post-impact time periods (Richter 1996; TNC 2009). The range of variability approach (RVA) defines a range of variation (i.e. mean ± 1SD) for IHA parameters from pre-impact period data (i.e. before dam construction). The degree to which the RVA target range is not attained at the post-impact period (i.e. after dam construction) is a measure of Hydrologic Alteration (Richter et al. 1997).

Table 3 Summery of IHA hydrological parameters

We implemented GROS in WBM_plus and used various scenarios to understand how variation in size and location of dams in a drainage basin changes their hydrological impact. Size and location of dams in each scenario is allocated based on analysis of national inventory of dams (NID) database (USACE 2013) to be representative of real-world conditions (Appendix 4).

Discharges were simulated for a length of 25 years (1986–2010) for each scenario using MERRA precipitation and temperature data (Rienecker et al. 2011) and a gridded 3-min (longitude × latitude) simulated topological network (Vörösmarty et al. 2000) of a large arbitrary drainage basin with 36,450 km² area (Fig. 3). The average discharge at the mouth of this drainage basin is 690 m³/s and low pulse and high pulse thresholds (mean ± 1SD for IHA and RVA analysis) are at 86.3 and 1293 m³/s.

Fig. 3

HUC 8 sub-basins contained in the study domain

3.1 The significance of water storage capacity of a single dam

Analysis of the NID database (USACE 2013) reveals that real world dams, with different purposes and significantly different storage capacities, may be built on rivers with statistically similar flow conditions (Appendix 4). Therefore, storage capacity is a critical input to reservoir models and models that do not use storage values for simulation of release cannot reliably capture the impact of dam operation. For example Wisser et al. (2010a) reservoir operation model (Eq. 1) does not use water storage in its calculations thus simulated release will be identical for dams with significantly different storage capacities. Hanasaki et al. (2006) use ratio of storage capacity to mean total annual inflow (Eq. 4); but the way it is formulated does not enable the model to respond to change in storage capacity properly.

We assumed five scenarios to show the advantage of GROS compared to other models and to quantify how variation in the size of a dam changes its hydrological impact. In the first scenario, flow was simulated without any dams. For the other scenarios, operation of a dam with 5, 10, 15 and 20 km³ storage volume was simulated at the mouth of the drainage basin (Fig. 6, S4).

Figure 4 shows how variation in storage capacity of a dam affects its impact on extreme flow conditions. The IHA and RVA analysis results are presented in Table 7 and Fig. 5. As expected, the impact of dams on natural hydrology increases as storage capacity increases.

Fig. 4

Impact of change in storage size of a dam on natural flow

Fig. 5

RVA analysis for the 32 IHA parameters using GROS for dams with different storage capacities

Dams decrease the range of fluctuations in the magnitude of monthly flows (IHA parameter 1–12). Magnitude, frequency and duration of extreme water conditions were considerably affected by dams operation (IHA parameter 13–23). Dams shifted the date of the occurrence of the minimum and maximum flows by up to 2 months (IHA parameter 24–25). There were no low pulses and the number of high pulses was reduced (IHA parameter 26–29). Because of the flow regulation by dams, the frequency and rate of daily flow change were also significantly reduced (IHA parameter 30–32).

The Colwell’s parameters also consistently change with the increase in dam capacity (Table 4). Dams reduce the range of flow compared to natural conditions by reducing the magnitude of high flows and increasing the magnitude of low flows (Table 7; Fig. 5). As the storage capacity of dams increases, the standard deviation and coefficient of variation (CV = σ/μ) of flows decrease. Limiting the range of flow variation also results in an increase in the value of Constancy, which respectively increases Predictability (Table 4).

Table 4 Colwell’s parameters for dams with different storage sizes

3.2 The significance of distribution patterns of water storage capacity of multiple dams in a basin

Working with incomplete reservoir databases that do not list relatively small reservoirs is a concern in reservoirs impacts studies (ICOLD 2011; Lehner et al. 2011). This is especially important as most of the world’s dams are relatively small structures (Rosenberg et al. 2000). Hydrological impacts of individual small dams may be relatively small, but the aggregate effects of numerous small dams may be substantial.

In regional and global studies it is challenging to match reservoirs with the correct rivers in the model due to inaccurate or missing geo-referencing information in many databases. To address these issues, it is customary to aggregate the storage capacity of multiple reservoirs in a watershed (Graf 1999; Nilsson et al. 2005) or a grid cell (Vörösmarty et al. 1997; Hanasaki et al. 2010) and assume only one larger reservoir exists on the main river of that watershed or grid cell.

By studying the hydrological impact of different distribution patterns of dams in a drainage basin, we show how the hydrological impact of numerous, dispersed, small dams compares to the impact of a few larger ones. We also investigate if this is a valid approach to aggregate the capacity of smaller dams and instead model a hypothetical larger dam with the same total storage capacity.

We used GROS in WBM_plus to model river flow and operation of reservoirs under four scenarios (Table 5; Fig. 6). Based on our analysis (Appendix 4) the total storage volume of dams in the basin was set to 20 km³. In scenario S1, 475 relatively small dams are on lower order streams of tributary branches. For scenario S2, there is a single dam in each HUC 12 sub-watersheds with the storage volume equal to aggregated storage volume of smaller dams from scenario S1 in that HUC 12 sub-watershed. Scenario S3 is similar to scenario S2 except that storage volumes are aggregated to HUC 8 sub-basins. In scenario S4 storage volume of all the dams in the basin is aggregated into one 20 km³ dam.

Table 5 Five scenarios to study the impact of dams’ distribution patterns

Fig. 6

Location of dams in each scenario

Figure 7 illustrates parts of the drainage basin disturbed by reservoirs operation and the accumulated upstream storage volume at each grid cell. Figure 8 shows how variation in the distribution pattern of water storage capacity in a basin impacts some of the extreme flow conditions. Analysis results for IHA and RVA methods are summarized in Table 8 and Fig. 9, and results for the Colwell’s parameters are presented in Table 6. In general, the hydrological impact on the water flow leaving the basin increases from scenario S1 to scenario S4; larger dams have a larger hydrological impact and they are generally located on larger streams, and thus regulate larger amounts of water.

Fig. 7

Parts of the basin disturbed by the dams and the accumulated upstream storage volume (km³)

Fig. 8

Impact of change in storage distribution pattern of dams on natural flow

Fig. 9

RVA analysis for the 32 IHA parameters using GROS for different water storage distribution patterns

Table 6 Colwell’s parameters for different dam distribution patterns

Magnitudes of monthly flows (IHA parameter 1–12) are very similar for scenarios S1–S3. From scenario S1–S4, as the number of dams decreases and their capacity increases, they have a larger impact on magnitude, frequency and duration of extreme water conditions (IHA parameter 13–23). Date of the minimum and maximum flows (IHA parameter 24–25) is approximately the same for scenarios S1–S4 and is not sensitive to the distribution pattern of dams. The same is true for low and high pulses (IHA parameter 26–29). The frequency and rate of flow changes (IHA parameter 30–32) do not show a significant difference between different scenarios.

Colwell’s parameters for scenarios S1 and S2 are similar. Generally as the number of dams decreases and their size increases and they move from small streams to larger ones, their impact on Colwell’s parameters increases.

4 Summary of results and discussion

By using ANN, we developed a new general reservoir operation scheme (GROS) which may be added to daily hydrologic routing models for simulating the releases from dams, in regional and global-scale studies. GROS is specifically designed to provide a broad perspective of the general behavior of dams and improve our understanding of the large-scale hydrological impact of dams operation in a relatively easy and efficient way. Comparisons with two other models using a variety of performance metrics verify that using GROS to model the operation of reservoirs can significantly improve the accuracy of the simulation of daily and monthly reservoir release time series.

Analysis of the NID database shows that dams with significantly different storage capacities may be located on rivers with similar flow characteristics. General reservoir models should be tested for their response to changes in storage capacity of dams before being implemented into hydrological models. One advantage of GROS over other models is that it properly responds to changes in storage capacity of dams and therefore can be reasonably used for simulating reservoir releases in regional and global domains where hundreds and thousands of dams with various storage capacities exist.

Using GROS in WBM_plus we investigated the practice of aggregating the storage capacity of multiple reservoirs in a watershed and simulating the operation of a hypothetical larger reservoir with the same total storage capacity. For this purpose we aggregated the storage capacity of dams in three scales, HUC 12 sub-watersheds (scenario S2), HUC 8 sub-basins (scenario S3) and basin level (scenario S4) and compared their hydrological impact on the water flow that leaves the basin. Based on our analysis results, hydrological impact of the original condition (scenario S1) is almost identical to scenario S2 (HUC 12 level aggregation) and very similar to scenario S3 (HUC 8 level aggregation). We conclude that for large-scale studies it is generally acceptable to aggregate the capacity of smaller dams and model a hypothetical larger dam with the same total storage capacity; however we suggest limiting the aggregation area to HUC 8 sub-basins (average of 3861 km² in this experiment) or a grid cell of approximately 60 km or 30 arc minute resolution to avoid exaggerated results.

Based on analysis of significance of capacity and distribution pattern of dams in the way they alter water flow out of a basin, hydrological parameters are mostly affected by the total storage capacity in the basin rather than the pattern in which storage is distributed in the basin. However, it should be noted that a few large dams have a greater impact on hydrological parameters compared to numerous smaller dams with the same total storage capacity. In our experiment, hydrologic alteration of the flow leaving the basin caused by a single large dam was greater than the combined impact of 475 relatively smaller dams with the same cumulative storage. This means that a single large reservoir is a more effective structure to regulate water compared to numerous smaller reservoirs with the same cumulative water storage capacity. Having only one large dam on the main stream of a basin decreases the level of river fragmentation as tributary branches are not affected by the dam operation. These points should be considered for both cases of building new dams and restoration of rivers by dam removal.

Appendices

Appendix 1: GROS algorithm

This is the simplified algorithm of GROS.

Subscript t represents the daily time step. I _o , R _o and S _o stand for inflow (m³/s), release (m³/s) and storage (m³) of dam in their original form. MaxS stands for maximum storage capacity (m³) of dam. I, R and S, without the subscript o, stand for the values scaled between 0 and 1. The number 86,400 is the number of seconds in a day.

Appendix 2: Equations

Equations of Nash–Sutcliffe efficiency coefficient (B1), coefficient of determination (B2) and normalized root mean square error are (B3) demonstrated here. O stands for observation data, P stands for predicted (simulated) values and N is total number of simulations.

$$ E = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - P_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - \bar{O}} \right)^{2} }} $$

(5)

$$ R^{2} = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - \bar{O}} \right)\left( {P_{i} - \bar{P}} \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - \bar{O}} \right)^{2} } \sqrt {\mathop \sum \nolimits_{i = 1}^{N} \left( {P_{i} - \bar{P}} \right)^{2} } }}} \right)^{2} $$

(6)

$$ NRMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {O_{i} - P_{i} } \right)^{2} }}{{N \bar{O}^{2} }}} $$

(7)

The Hydrologic Alteration in RVA method is defined as:

$$ \frac{Observed\;frequency - Expected \;frequency}{Expected\;frequency} $$

(8)

where “Observed” is the count of years in which observed value of the hydrologic parameter fell within the RVA targeted range and”Expected” is the count of years for which the value is expected to fall within the RVA targeted range.

Appendix 3: Hydrological alteration analysis results

See Tables 7 and 8.

Table 7 IHA analysis using GROS for dams with different storage capacities

Table 8 IHA analysis using GROS for different storage distribution pattern of dams

Appendix 4: Analyzing NID for the purpose of scenario development

Size and location of the hypothetical dams in this study are selected based on criteria obtained by analyzing NID dataset (USACE 2013) with reference to a gridded 3-min (longitude × latitude) Simulated Topological Network (Vörösmarty et al. 2000) which we use in WBM_plus. Three categories of dams and reservoirs were analyzed; (1) small dams with storage capacity between 5 × 10⁶ and 5 × 10⁷ m³; (2) medium dams with storage capacity between 5 × 10⁷ and 5 × 10⁸ m³; (3) large dams with storage capacity larger than 0.5 km³. To find the appropriate location for each size category we used the middle 50th percentile of average flow, upstream catchment area and residency time (ratio of capacity to average flow) of NID dams. The middle 50th percentile was used to avoid miss match between actual location of dams and their location on simulated network and also to remove outliers.

We defined small dams to be located on rivers with mean flow between 1 and 52 m³/s; upstream catchment area between 58 and 3499 km²; and residency times between 3 and 184 days. Medium dams are located on rivers with mean flow between 3 and 60 m³/s; upstream catchment area between 373 and 4929 km²; and residency time between 61 and 498 days. Large dams are located on rivers with mean flow larger than 9 m³/s; upstream catchment area larger than 2080 km²; and residency time between 140 and 1978 days. Residency time range gives a minimum and maximum limit for storage capacity at each location.