Empirical fragility analysis of building damage caused by the 2011 Great East Japan tsunami in Ishinomaki city using ordinal regression, and influence of key geographical features

Abstract

Tsunamis are disastrous events typically causing loss of life, and extreme damage to the built environment, as shown by the recent disaster that struck the East coast of Japan in 2011. In order to quantitatively estimate damage in tsunami prone areas, some studies used a probabilistic approach and derived fragility functions. However, the models chosen do not provide a statistically sound representation of the data. This study applies advanced statistical methods in order to address these limitations. The area of study is the city of Ishinomaki in Japan, the worst affected area during the 2011 event and for which an extensive amount of detailed building damage data has been collected. Ishinomaki city displays a variety of geographical environments that would have significantly affected tsunami flow characteristics, namely a plain, a narrow coast backed up by high topography (terrain), and a river. The fragility analysis assesses the relative structural vulnerability between these areas, and reveals that the buildings surrounding the river were less likely to be damaged. The damage probabilities for the terrain area (with relatively higher flow depths and velocities) were lower or similar to the plain, which confirms the beneficial role of coastal protection. The model diagnostics show tsunami flow depth alone is a poor predictor of tsunami damage for reinforced concrete and steel structures, and for all structures other variables are influential and need to be taken into account in order to improve fragility estimations. In particular, evidence shows debris impact contributed to at least a significant amount of non-structural damage.

Introduction

The density of coastal populations is increasing, accompanied by increased human activities, developments, and changes in land-use (Levy and Hall 2005), thus having an effect on the impact of extreme events such as tsunamis. After a tsunami attack, the resulting damage to structures is a useful indicator of the vulnerability of exposed coastlines. Buildings that can sustain tsunami forces can save lives, and will contribute to the reduction of the financial losses caused by the disaster. Two recent large scale events, namely the 2004 Indian Ocean tsunami and the 2011 Great East Japan tsunami, yielded improvements in data collection and availability, thus have stimulated research into tsunami-induced damage estimations. The methods involved the determination of threshold depths associated with an observed damage level (Shuto 1993), qualitative vulnerability assessments such as the PTVA method (Papathoma and Dominey-Howes 2003; Dominey-Howes and Papathoma 2007), damage ratios (Leone et al. 2011; Valencia et al. 2011), and fragility functions (a more exhaustive review is available in Suppasri et al. 2013a, b). Fragility functions are empirical stochastic functions, which relate the probability for a building to reach or exceed a given damage state, to a measure of tsunami intensity. In comparison with other methods, fragility functions provide quantitative and detailed information on the probability of damage, therefore, they are one of the most advanced and informative tool for tsunami damage estimation. Previous studies deriving and utilizing fragility functions have found many factors to be influential on the extent of building damage, both in terms of hazard (e.g. flow depth) and structural vulnerability (e.g. structural material), which can be defined here as the capacity of a building to resist the impact of a given hazard (i.e. Koshimura et al. 2009; Suppasri et al. 2011, 2012).

From a vulnerability standpoint, and in addition to the construction type, a building’s likelihood to suffer high levels of tsunami damage may be greatly affected by environmental features. The recent findings by Suppasri et al. (2013a, b) show that on a large scale, the dominant type of coastline of a particular geographical area will visibly affect the probability of buildings to suffer extensive damage. In particular, it was found that due to the amplification of the 2011 tsunami waves along the ria-type Sanriku coast in Japan, the probability of building damage was visibly increased, in comparison with the plain coast. It is thought that geographical features at the city scale will similarly influence building damage probability, by altering the flow characteristics.

Therefore, existing fragility functions have given to date a very useful indication of relative building fragility, according to various parameters. However, from a statistical standpoint these have fallen short of giving truly reliable estimations of tsunami damage probability. The first issue with existing curves lies in the assumptions that are made regarding the statistical distribution of the response (i.e. damage). Following the methodology used for the derivation of seismic fragility functions (Porter et al. 2007), this distribution is often assumed to be normal or lognormal, leading to a linear least squares fitting of the curve. However, this assumption is by nature erroneous, as damage state is a discrete, ordinal response and the aforementioned distribution is only applicable to continuous variables (Rossetto et al. 2013). In addition, many of the assumptions associated with the linear least squares fitting (such as homoscedasticity and independence of the errors) typically do not hold when applied to the available tsunami damage data (Charvet et al. 2013). The second issue is the level of data aggregation, which leads to the dismissal of a significant amount of points when linear least squares regression is used. Indeed, this procedure does not recognise that some bins have a higher number of buildings than others, and cannot deal with the bins which do not contain any damaged buildings, or only contain damaged buildings (due to the fact the inverse normal distribution function does not converge for probabilities of 0 or 1). In addition, depending on the level of data aggregation significant information may not be captured by the model (Charvet et al. 2014). The building damage analysis conducted by Reese et al. (2011) was the first study in the tsunami engineering field which implemented more realistic stochastic models to represent damage probability. The authors used generalized linear models (GLM), as described in Mc Cullagh and Nelder (1989), more specifically logistic regression, to derive fragility functions based on building damage in Samoa (after the 2009 tsunami). GLM relax many assumptions associated with the simple linear model, and allow the response variable to follow a number of distributions, thus addressing the shortcomings of linear regression analysis. Logistic regression allows the response to be modelled as a discrete, binary outcome (i.e. a given damage state is either reached or exceeded or not), however it does not take into account the ordered nature of damage state. This may lead to inconsistent results in some cases, such as fragility functions that cross – thus implying the damage states DS _i+1 may be reached before DS _i as the intensity measure increases, which is impossible. A logical improvement from this method would be to assume the response follows a multinomial distribution, a generalization of the binomial distribution which allows the outcome to belong to one of n ordered categories (1, 2,…, n). Multinomial distributions can represent either ordered or unordered outcomes, in the case of an ordered outcome (i.e. damage state) ordinal regression may be used (Gelman and Hill 2007).

The aims of this study are therefore:

• To assess potential differences in the probability of building damage according to geographical location at the city scale. The case study will be Ishinomaki city, as it suffered the most extensive damage after the 2011 Japan tsunami and three representative types of geographical features are present: a “plain” area, a “terrain” area (were buildings are concentrated on a narrow band between the ocean and high topography), and a “river” area (buildings located close to the river banks and beyond);

• To use more realistic estimations methods of building damage probability by applying GLM, more specifically ordinal regression, to the extensive disaggregated dataset of building damage following the 2011 Great East Japan tsunami, available for Ishinomaki city.

Data and methods

Presentation of the data

The extensive database of building damage in Ishinomaki city (56,950 buildings) following the 2011 tsunami was used for the present analysis. The information available for most individual buildings includes geographical localization, measured tsunami flow depth, level of damage observed (as described in Table 1), and construction material. Considering the modified scale and damage description in Table 1, DS2 and DS3 essentially represent levels of non-structural damage (i.e. damage to walls), DS4 and DS5 represent levels of structural damage (i.e. damage to columns).

Table 1 Classification and description of building damage for Ishinomaki city

In some cases, information regarding the building’s structural material is missing. When this is the case, the corresponding data points are dismissed for the analysis. Indeed, as mentioned previously construction material has been consistently found to be an important parameter in determining the severity of tsunami damage, therefore should be taken into account. In addition, the removal of points with missing information does not negatively affect the power of the statistical analysis as the total number of data points remaining is large enough. According to Green (1991), when performing regression analysis with one predictor variable (in our case, tsunami flow depth) and expecting a strong relationship between the predictor and the response variable (i.e. between flow depth and damage state), the effect size can be considered large, leading to a minimum sample size of 24 points. Finally, for a number of buildings in the database, the damage observed is obviously not due to tsunami forces, i.e. (DS ≠ DS0|h = 0), h being the tsunami flow depth measured from ground level. In such cases, the points have also been dismissed.

With regards to the damage scale, it can be seen that the original DS5 and DS6 do not represent mutually exclusive damage states, nor do they necessarily represent an increase in tsunami intensity. Rather, they represent different failure modes of the structure. In order to apply GLM analysis to the data, such requirements must be met (Mc Cullagh and Nelder 1989), therefore in this study these two levels will be aggregated transforming the given seven-state (DS0–DS6) into a six-state damage scale (DS0–DS5).

Geographical data split

During a tsunami attack, the damage to buildings is strongly determined by the tsunami loads/forces acting on the structure. Reviews such as FEMA (2008), Chock et al. (2011) highlight the different force components that typically act on a structure as the tsunami flows inland, these different types of forces can be classified as follows:

• Hydrostatic forces (largely determined by the flow depth),

• Hydrodynamic forces (largely determined by flow depth and velocity),

• Debris impact forces (debris velocity, mass and stiffness),

• Scour (mainly determined by soil characteristics, flow approach angle and cyclic inflow/outflow).

In order to produce a meaningful regression analysis, it is intended to group buildings which have been subjected to similar tsunami actions. Unfortunately, forces and velocities cannot be retrieved in the field survey, and the only parameter that can be directly measured is the flow depth, which drives mainly the hydrostatic load. Therefore, we choose to subdivide the densely urbanized part of Ishinomaki city into different geographical areas, based on environmental characteristics, inundation frames produced from numerical simulations (courtesy of Dr Bricker, Tohoku University) and field surveys (Haraguchi and Iwamatsu 2011). It is thought that each of these areas will display different characteristics which will affect the principal mechanisms of inundation therefore the relative forces and probability of damage. Three main inundations types can be distinguished:

• (1) Flooding of the plain/flat land (P), with no major obstacle to the flow—typically the inundation distance is large, but the flow depth is moderate (i.e. less than 5 m).

• (2) Flooding of coastal areas against higher terrain (T), typically the inundation distance is smaller due to the higher topography blocking flow ingress, but runup and flow depths are greater. In contrast with the plain, this area benefited from coastal protection (seawalls, control forest, breakwater).

• (3) Flooding along the river (R)—the tsunami waves travel at higher speed along the river channel and are thus capable of reaching further inland through this process. They can also be amplified due to a bottleneck effect when high topography is present on either sides of the river. However, the characteristics of flooding on either side of the river banks will be mainly determined by the water height above the dyke, and head difference.

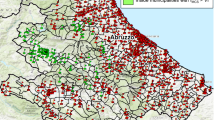
Throughout the whole area surveyed, scour (Fig. 1) and debris impact (Fig. 2) appear to be sporadically present, however the amount of data available (location of visible scour and/or debris impact) is very limited and does not allow for deciding whether such effects were significant at the city scale in comparison to other types of forces, nor do they provide enough information to define specific geographical areas of action for scour and debris impact. The locations of these effects are shown in Fig. 3, we expect that if such mechanisms of damage are significant a pattern will be present in the model errors. Moreover, in most cases (see Fig. 2a, b) the evidence suggests that the impact of debris triggered damage to walls and non-structural components, thus if this effect is significant the error graphs corresponding to intermediate damage states (i.e. DS2 and DS3, see definitions in Table 1) would display some obvious trends.

Fig. 1

Examples of visible scour in Ishinomaki city—locations shown in Fig. 3

Fig. 2

Examples of visible debris impact in Ishinomaki city—locations shown in Fig. 3

Fig. 3

Map of the city of Ishinomaki with locations of the buildings surveyed and outline of the three areas under investigation (in green, to the West: the P area, in blue, to the North: the R area, in red, to the East: the T area). Scour and debris impact points are also shown

Ordinal regression method

Model

Stochastic models all comprise a systematic component (i.e. the fitted function), and a random component, which describes the distribution of the response around its mean. Simple linear regression assumes the response variable follows a normal (or log-normal) distribution, and that it is linearly related to an explanatory variable through a set of regression parameters (that is, the mean and standard deviation of the normal (log-normal) distribution function). GLM are a generalization of this concept, this time the response can follow one of a number of distributions—in this study, a multinomial distribution (which corresponds to the random component of the model):

$$ Y_{i,k} \sim \prod\limits_{i = 0}^{I} {\frac{{N_{k} !}}{{Y_{i,k} !}}} P\left( {DS = ds_{i} |x_{k} } \right)^{{Y_{i,k} }} . $$

(1)

And the fragility function, or systematic component, is expressed through a “link” function g which is itself a function of a linear predictor η, expressed as follows:

$$ g(\mu_{i} ) = \eta_{i} = \theta_{0,i} + \sum\limits_{j = 1}^{p} {\theta_{i,j} X_{j} } . $$

(2)

In Eq. (1) (Forbes et al. 2011), Y _i,k corresponds to the counts of buildings being at damage level ds _i ($i \in {\mathbb{N}};\quad 0\; \le \;i\; \le \;5$) for each value of the tsunami intensity measure x _k ; and N _k is the total number of buildings. In Eq. (2) (Mc Cullagh and Nelder 1989, p. 27), X _j are the p explanatory variables that can be used for the regression analysis, and {θ _0,i ,…, θ _i,j } are parameters of the model to be estimated. In the case of Ishinomaki city, the only hazard parameter that has been measured is the tsunami flow depth, therefore X ₁ = h and the linear predictor is a simple linear function of flow depth. Generally, for regression based on binary or multinomial outcomes, the appropriate link functions g are the logit, probit or complementary loglog functions (Fig. 4) as described in Rossetto et al. (2013).

Fig. 4

Link Functions to be used with the multinomial distribution

For binomial and multinomial models, the variance function associated with the distribution is a function of the mean μ:

$$ var [Y ]= \phi \mu (1 - \mu ). $$

(3)

In Eq. (3), ϕ is the theoretical dispersion parameter which is assumed to have a value of 1 when the data closely follows the chosen distribution (here, multinomial).

In ordinal regression analysis, the ordering of the categorical outcome is taken into account by taking a special case of multinomial outcome and assuming the fragility curves corresponding to different damage states have the same slope θ _j but different intercepts θ _0,i . Therefore, the observed probabilities of reaching or exceeding a given damage state can be substituted in Eq. (2) and expressed as a function of the linear predictor η, thus expressing the required fragility function μ _i , as follows:

$$ g\left({\mu_{i} |h_{k} } \right) = \theta_{0,i} + \theta_{1} h_{k} . $$

(4)

The method used to find the parameter values in Eq. (4) for the cumulative distribution function to be fitted to the data is the maximum likelihood estimation (MLE). MLE is the standard way of performing GLM regression analysis and is an iterative procedure that will find the optimum combination of parameter values—in other words, through the link function the likelihood L(θ|Y)of obtaining the actual observations by fitting the mean curve μ _i is maximized. A detailed description of MLE is outside the scope of this paper, but the interested reader can refer to Mc Cullagh and Nelder (1989), or Myung (2003) for a description of the practical implementation of this method.

Diagnostics

Following the recommendations of Rossetto et al. (2013), diagnostics need to be performed to assess the relative and absolute goodness-of-fit of the fragility curves. Because a number of different link functions can be chosen, the next step will be to assess relative goodness-of-fit by using the Akaike information criterion (AIC) (Akaike 1974):

$$ {\text{AIC}} = 2q - 2\ln (L), $$

(5)

Where q is the number of parameters in the model, and L is the maximized likelihood function of the mean curve. This measure essentially sums the deviance (−2ln(L)), which is a measure of the overall error, simultaneously taking into account the number of parameters in each model. The best fit corresponds to the model which has the smallest AIC.

Finally, the absolute goodness-of-fit can be assessed by comparing the observed and expected (model) probabilities for each damage state. A model that fits the data perfectly will result in equal expected and observed probabilities, thus a linear trend along the 45° line. A decent model should result in most points being close to such line, without any obvious non-linear trend.

Results and discussion

Because we dispose of only one explanatory variable h, it is possible to run the analysis directly with the counts of buildings for each value of h where measurements are available. As such, the sample size n indicated in Table 2 corresponds to the total number of points used for the regression, the total number of buildings in each class being given by N.

Table 2 AIC (5) obtained for the buildings in the P area, with values corresponding to the best fitted model are in bold

Plain

20,682 buildings were surveyed in the P area of Ishinomaki City, after the considerations highlighted in Sect. 2.1 and removal of incomplete or erroneous data (e.g. missing information on building material, damage unexplained by flow depth), 15,736 buildings were analyzed.

Table 2 shows the different AIC values, by link function chosen and construction material. The fragility curves corresponding to the models with the smallest AIC are plotted in Fig. 5, along with the corresponding data. An initial examination of the curves shows that the vulnerability of wooden and masonry structures is higher than the vulnerability of RC and steel buildings. However, we can also see that the behavior of the data is erratic for RC buildings, extremely scattered for steel buildings, whereas the trend is much more obvious for wood and masonry structures. For the latter types of buildings, there is very little or no data points classified as DS4, resulting in equal estimations of the probability of damage for both DS4 and DS5. It is very likely that many buildings which had actually reached level DS4 were classified as DS5 in the field, due to the slightly subjective description of damage provided for these levels. For example, “Heavy damage to several walls and some columns” (DS4) can easily be classified as being “Destructive damage to walls (more than half of wall density) and several columns (bend or destroyed)” (DS5). To an extent, the definitions of DS4 and DS3 can trigger a similar issue (“damage to some walls”—DS3, “damage to several walls”—DS4).

Fig. 5

Damage probability data and fragility functions derived for the P area (Plain), for the four structural types (RC—logit, Steel—comp. loglog, Wood—logit, Masonry—comp. loglog)

The diagnostics plots in Fig. 6 reveal that indeed the model’s fit to the data is poor for RC and steel buildings, which is expected given the amount of scatter in the data and indicates that flow depth is not a good predictor of tsunami damage for these types of structures. The differences between the observed and expected probabilities become more pronounced as the damage level increases, the worse estimations corresponding to damage states that are representative of structural damage (DS4 and DS5). For wooden buildings, the observed and predicted probabilities are consistent however a trend is present, particularly obvious in the high probability regions (μ > 0.6) with the model systematically overestimating damage probability for non-structural damage (DS2 and DS3), and systematically underestimating damage probability for structural damage (DS4 and DS5). The opposite is true in the low probability region (μ < 0.6). This is likely due to the action of one or several missing variables, which if known should be included in the model (2). This hypothesis is supported by the observations from Yu et al. (2013), who noted in the context of flood damage analysis that sediment flow velocity, flood duration and sediment load have are likely to influence damage estimations. The underestimations may be due to the action of debris, as mentioned in Sect. 2.2 they were likely to have a significant influence on at least non-structural elements (photographic evidence), possibly also for structural damage and collapse, although visual evidence for this is harder to detect on post-tsunami survey images. The potential misclassifications highlighted previously are also likely to influence such trend, for example we can observe that some of the non structural high damage probability data in Fig. 5 is shifted to the right (leading to overestimation of DS2 and DS3), while it is shifted to the left for DS5. Finally, the diagnostic plots in Fig. 6 show a very good fit for DS1 for all structures, with a probability of 1. This is because the probability of a building to experience at least minor flooding (see Table 1) is intrinsically linked to the inundation depth and will reach its maximum as soon as the flow interacts with any building.

Fig. 6

Diagnostic plots corresponding to the fragility curves shown in Fig. 5 (P area)

Terrain

22,810 buildings were surveyed in the T area of Ishinomaki City, after the considerations highlighted in Sect. 2.1 and removal of incomplete data, 18,289 buildings were analyzed.

Table 3 indicates the AIC values for different building construction types in the T area, and different link functions. The fragility curves corresponding to the models with the smallest AIC are plotted in Fig. 7, along with the corresponding data.

Table 3 AIC (5) obtained for the buildings in the T area, with values corresponding to the best fitted model are in bold

Fig. 7

Damage probability data and fragility functions derived for the T area (Terrain), for the four structural types (RC—probit, Steel—probit, Wood—probit, Masonry—logit)

Again the probability of damage given by the model is higher for wooden and masonry structures (in comparison with the other structural types), whereas scatter in the data for RC and steel buildings is important. Similarly to the fragility curves derived for the P area, there is little or no difference between the damage probabilities corresponding to DS4 and DS5. The exact same remarks made for the diagnostics of the P area (Sect. 3.1) can be made for the diagnostics of the T area (Fig. 8).

Fig. 8

Diagnostic plots corresponding to the fragility curves shown in Fig. 7 (T area)

River

13,458 buildings were surveyed in T area of Ishinomaki City, after the considerations highlighted in Sect. 2.1 and removal of incomplete data, 11,150 buildings were analyzed.

Table 4 indicates the AIC values for different building construction types in the R area, and different link functions. The fragility curves corresponding to the models with the smallest AIC are plotted in Fig. 9, along with the corresponding data.

Table 4 AIC (5) obtained for the buildings in the R area, with values corresponding to the best fitted model are in bold

Fig. 9

Damage probability data and fragility functions derived for the R area (River), for the four structural types (RC—probit, Steel—probit, Wood—probit, Masonry—logit)

In this area, scatter in the data for RC and steel buildings is still important, and the model cannot provide a satisfactory fit to the data, as shown also by the large departure from the perfect estimations line in Fig. 10. However, from this figure we can also see that there are less model misclassifications for all damage states in comparison with the results obtained for the plain and terrain areas (RC and steel buildings in Figs. 6 and 8, respectively), yielding a slightly improved damage probability estimation. In addition, the trend that was visible for the wooden buildings of the aforementioned areas is no longer present, despite some underestimation of damage probability for higher damage states (Fig. 10). This indicates that flow depth, while still not a satisfactory predictor of tsunami damage, performs visibly better in the R area. A likely reason for this might be the dominant mechanism of inundation along the river banks, namely dyke overtopping (as mentioned in Sect. 2.2). Indeed, while the tsunami height and velocities may increase in the river channel, the velocities of the water inundating the shores and beyond will be mainly determined by the head difference between the overtopping water surface and the ground, following a process similar to river flooding. As such, the flow velocity would be related to flow depth, which would allow the model to capture this effect through h and explain the slightly enhanced goodness-of-fit. Similarly to the fragility curves derived for the P and T areas, there is little or no difference between the damage probabilities corresponding to DS4 and DS5; and the estimations for DS1 are again very satisfactory.

Fig. 10

Diagnostic plots corresponding to the fragility curves shown in Fig. 9 (R area)

Fragility comparisons between the three geographical areas in Ishinomaki city

The results of this study show that for all three areas, the correlation between flow depth and damage probability observations for steel and RC buildings is low, yielding a poor fit of the fragility curves, particularly in the case of structural damage. The scatter is less pronounced for masonry buildings, and best for wooden buildings, despite a trend being present around the perfect predictions line in the diagnostics plot.

Therefore, in order to assess if the different geographical characteristics of Ishinomaki City (i.e. plain, terrain and river) significantly altered building damage probability, we choose to compare the fragility curves corresponding to the structural material for which the most reliable estimations have been obtained, namely wooden buildings. Representative damage levels for comparison are DS3 and DS5, because they express probabilities for extensive non-structural and structural damage, respectively.

A first examination of the fragility functions in Fig. 11 shows that the most vulnerable area to tsunami damage, both structural and non-structural, appears to be the plain; whereas the probability of damage for the buildings bordering the river is visibly lower than both in the plain and terrain areas. A common assumption usually made for binomial and multinomial distributions is that the theoretical dispersion parameter ϕ associated with the variance function takes the value of 1 (Eq. (3), Sect. 2.3.1), so the resulting variance is independent of any deviations from the fit and could be underestimated. Because of the systematic deviations observed for wooden buildings in Figs. 6, 8, and 10, and to prevent misleadingly narrow confidence intervals, we have chosen to use instead an estimated dispersion parameter $\hat{\phi }$ (Fahrmeir and Tutz 2001), expressed as:

Fig. 11

Comparison between fragility functions representative of structural and non-structural damage states, for wooden buildings across the three areas of study. The 95 % confidence intervals for the buildings of the Plain are displayed with long dashes (dark green), of the Terrain with small dashes (dark red), and of the River with a dotted line (dark blue)

$$ \hat{\phi } = \frac{1}{N - p}\sum\limits_{m = 1}^{N} {\sum\limits_{k = 1}^{n} {\hat{r}_{mk}^{2} } } . $$

(6)

In Eq. (6), $\hat{r}$ represents the Pearson residuals (see Mc Cullagh and Nelder 1989; Fahrmeir and Tutz 2001), which similarly to deviance, are a measure of the model’s error. In the case of DS5, the confidence intervals for the plain and terrain areas overlap, indicating that the probability of a wooden building to suffer heavy structural damage (collapse) is similar in both areas. In the case of DS3, the buildings of the plain area appear significantly more vulnerable to tsunami-induced non-structural damage for flow depths higher than 0.5 m, whereas for flow depths higher than 1 m the confidence intervals corresponding to the fragility curves of the buildings from the terrain and river areas start to overlap. This may indicate that buildings from the terrain and river areas are possibly equally likely to suffer non structural damage for higher tsunami flow depths.

This result may at first appear to be in slight contradiction with the results obtained by Suppasri et al. (2013a, b), who highlighted a higher damage probability for the buildings of the “ria” coast, (in comparison with the “plain” coast), due to the propensity of this type of coastline (saw-toothed) to amplify tsunami waves. The present analysis focuses on the main city of Ishinomaki, not the ria coast to the North. The T area in this study displays a similar inland topography (i.e. mountainous), however, only a small proportion of the buildings in the city of Ishinomaki analyzed in this study are bordering a ria coastline (to the southeast in Fig. 3). The rest of the city is facing Ishinomaki Bay and is characterized by a relatively smooth coastline.

In addition, despite the relatively higher flow depths measured in the T in comparison with the P area, the former benefited from coastal protection along most of the seafront (breakwater, seawell and control forest). These visibly contributed to reduce flow depths and velocities inland, which could have contributed to reduce the severity of tsunami damage.

Other areas

The fragility analysis was also conducted separately for small areas which were thought to be particularly susceptible to tsunami damage (and for which enough points were available), namely:

• The river island approximately 1 km from the river mouth, in the direct path of the fast tsunami flow travelling along the river and the river banks which were not protected by a dyke,

• Terrain A for it is unprotected, backed up by high topography blocking the advancement of the tsunami and close to the river mouth,

• Terrain B for it is located on the border of a canal and backed up by high topography.

These areas are represented in Fig. 12, only wooden buildings were used due to the low number of data points available for other types of structures. The results (Fig. 13) show that the curves are driven by a majority of data points corresponding to a 100 % damage probability exceedance for all damage levels. In other words, in these areas the probability of reaching or exceeding structural damage levels (wood) is very high. For example, there is certainty of collapse for the buildings located in Terrain A for water depths as low as 2 m. Non-structural damage is almost certain (approx. 90 %) for wooden buildings located in the other aforementioned areas, for water depths as low as 0.5 m, as well as collapse from about 3 m.

Fig. 12

Other areas particularly likely to experience high levels of tsunami damage in Ishinomaki city

Fig. 13

Fragility curves for specific local areas which were likely to experience higher levels of damage, for all three areas the logit link function was chosen for it provided a relatively better fit through AIC comparison

Conclusions

The present study focused on the analysis of the disaggregated, extensive database of damage caused by the 2011 Great East Japan tsunami for the city of Ishinomaki in order to derive fragility functions and assess the differences in building fragility according to their geographical location. More precisely, three main areas were identified in the city of interest: the plain, terrain and river areas, each of them being representative of different characteristics of the tsunami flow. The only explanatory variable available was the tsunami flow depth, measured during field surveys after the event. Advanced statistical methods were used in order to address the shortcomings of previous stochastic models in giving reliable estimations of probability of damage exceedance due to tsunami. More specifically, ordinal regression presents many advantages over simple linear regression, notably the relaxation of assumptions associated with the latter, the use of individual points without unnecessary dismissal (i.e. inverse normal distribution function not converging), and the distribution of the response which is allowed to be discrete and ordered (thus consistent with the damage scale). While a comparable measure of goodness-of-fit for the previously published models and current (ordinal) model cannot be used due to differences in parameter estimation procedure and modeled response type, such considerations are important for the following reasons:

• The violation of statistical assumptions leads to the impossibility of making further inference about the data (e.g. confidence intervals), and/or creates bias in the parameters,

• The use of all the dataset increases the power of the analysis,

• The use of individual data points (instead of data aggregated into bins) does not hide any information, i.e. it does not make any assumption on appropriate bin width, and distribution within each bin—which will affect the shape of the curve,

• The response, if it is not related to a latent continuous normally distributed variable, cannot be appropriately modelled by a continuous (normal) distribution.

The fitted curves indicated that in all three areas, damage probabilities for wooden and masonry structures were visibly higher than for RC and steel structures. These results are consistent with previous studies examining the influence of construction material on building damage probability. Comparisons between the three areas for wooden buildings show that the plain appears to be the most vulnerable area to tsunami damage (non-structural), followed by the terrain and finally the river area. For structural damage, the probabilities of building collapse in the plain and terrain areas are not significantly different from each other but significantly higher than for the river area. Initially the damage probabilities in the terrain area were expected to be higher than in the plain, due to the potentially higher flow depths and velocities. These results are testimony of the effectiveness of coastal protection (breakwater and forest present along a portion of the T area), as the terrain area could have been expected to suffer more severe damage due to relatively higher flow depths and velocities. While coastal protection cannot prevent tsunami-induced damage, it can reduce its magnitude. The presence of the old Kitakami river allowed the tsunami to travel further inland with greater speed, therefore increasing the extent of the affected area and the amount of damaged buildings. However, the tsunami-induced river flood did not increase the magnitude of tsunami damage (i.e. more buildings were damaged but they were not comparatively more damaged), in fact this area displayed the lowest damage probabilities for all building types and all damage states.

It is important to note that the present geographical split is based on the 2011 tsunami, which is extremely rare [corresponding to a level 2 tsunami—one in a hundred years event or less frequent (Shibayama et al. 2013)]. It is expected that smaller, more frequent tsunamis (i.e. level 1 events) would not match the inundation extent of the 2011 event; thus the “plain”, “terrain” and “river” areas would have to be redefined to match the corresponding zones of action for the specific hydrodynamics. For example, areas which may be characterized by river flooding for relatively small tsunamis are better characterized as “plain” or “terrain” for large, infrequent tsunamis such as the one under investigation in this study. In order to obtain fragility estimations by geographical area for such scenarios, numerical inundations modeling, combined with Monte Carlo simulations (e.g. Dias et al. 2009; Yu et al. 2013) can be carried out in order to reassess geographical boundaries for a range of realistic incoming wave height distributions (Kim et al. 2013).

The diagnostics reveal that in all cases, flow depth is a poor predictor of tsunami damage for RC and steel structures, the goodness-of-fit of the model decreasing as the damage level increases, and the most scatter being observed for structural damage (i.e. DS4 and DS5). The diagnostics also show that the model, based on flow depth only, captures more of the variation for wooden and masonry buildings, yielding a better fit. However, some effect which is not captured by the model triggers slight systematic under and overestimations of damage probability. This uncertainty cannot be explained by a lack of data points, or any aggregation of the database which typically hides a lot of information, so these results strongly indicate variables other than flow depth are key in the determination of tsunami-induced damage, notably the variables that drive other determinant tsunami forces: flow velocity (hydrodynamic load), scour, and debris (size, stiffness). This hypothesis is supported by visual evidence (non-structural damage triggered by debris impact in Fig. 2, scour-induced structural damage in Fig. 1); and by the fact that the uncertainty visibly decreases for the damage probability estimations in the river area, where overtopping was the main mechanism of inundation thus velocity is largely explained by flow depth. Thus, adding these variables is crucial to improving fragility estimations. In addition, there is possibility that the uncertainty in flow depths measurements increases for higher damage states; for example, when a building is washed away there is no possibility to measure flow depth directly at the (previous) location of the structure, and the value is usually assumed to be the same as the closest possible site where it could be retrieved. Further improvements should also include a representation of uncertainty in the parameters used, as described for instance by Yu et al. (2013).

While the use of GLM and ordinal regression for the determination of tsunami damage probability has the potential to bring considerable improvements to damage and loss estimations from a stochastic modeling point of view, the model estimations will only ever be as good as the data and further effort should now concentrate on the collection, estimation and inclusion of such influential variables in order to improve fragility estimations to be used for risk assessment in the future.