Stochastic model for hepatitis B virus infection through maternal (vertical) and environmental (horizontal) transmission with applications to basic reproductive number estimation and economic appraisal of preventive strategies

Abstract

Elucidating the temporal natural history of Hepatitis B virus (HBV) infection provides not only useful information for assessing the spread of HBV infection but also a bedrock for economic appraisal of population-based preventive strategies (such as universal vaccination). HBV transmissions are transmitted through the maternal (vertical) route and environmental (horizontal) route. As the infection process from susceptible to active virus replication and finally to recovery state or to carrier state through both routes is not directly observable, mathematical models were therefore proposed to quantitatively elucidate the dynamic process of HBV infection with time. We began with a simple two-state model (from susceptible to infection) and further developed a five-state (including susceptible, latent phase, active viral replication, carrier, and recovery states) stochastic process to quantify the dynamics of HBV infection, making allowances for a mixed proportion of vertical and horizontal transmissions. The data used in the estimation, which were collected before implementation of a policy for universal HBV vaccination, were derived from several previous serum prevalence studies, including both low (northern) and high (southern) HBV prevalence areas, in Taiwan. The parameters obtained from stochastic models were converted to compute the basic reproductive number (R₀) in each study to indicate the extent of the spread of HBV infection. By linking the temporal natural history of HBV infection with the previously established Markov process for the sequelae of HBV infection (chronic hepatitis infection, liver cirrhosis, and hepatocelluar carcinoma), we developed a Markov cycle decision tree to evaluate the two population-based preventive strategies related to vaccination and maternal lamivudine use with a cost-effectiveness analysis. In the five-state model, horizontal transmission was found to contribute more to HBV infection than vertical transmission in the northern area (59 vs. 41 %), whereas vertical transmission was more likely than horizontal transmission in the southern area (80 vs. 20 %). After considering the parameters of the two transmission routes, annual infection rate (person-years) for susceptible subjects was higher in the northern area (0.35) than the southern area (0.011). A similar finding was noted for annual rate of the transition from the latent period to active viral replications (1.12 in the northern area and 0.072 in the southern area). Annual rate of the conversion from active viral replication to the carrier state was higher in the southern area (0.184) than the northern area (0.119). Annual recovery rates were 0.014 in the northern area and 0.024 in the southern area for the carrier and 0.048 and 0.088 for transient viremia. The R₀ at age 30 using the parameters obtained from the five-state stochastic model was estimated as 4.88 in the northern and 7.03 in the southern area. Regarding the findings of economic appraisal, both preventive strategies were cost-saving, yielding the negative value of incremental cost-effectiveness ratio, compared with the baseline group (no intervention), regardless of areas. The preventive strategies in the southern area were more cost-saving than those in the northern area. The consolidation of elucidating the temporal natural history of HBV infection, estimating basic reproductive number, and conducting an economic appraisal of population-based preventive strategy can aid health policy-makers in designing effective preventive strategies in other countries worldwide where HBV is still prevalent. However, the empirical findings on transmission routes and the temporal evolution of HBV infection varying with areas should be considered with great caution as only two studies were modeled.

1 Introduction

The temporal natural history of hepatitis B virus (HBV) infection and its sequale (such as chronic hepatitis, liver cirrhosis, and hepatocellular carcinoma) are long and heterogeneous (Chu 2000; Liaw and Chu 2009). The panorama of the evolutionary process is often defined as a kind of chronic infectious disease. To assess the spread of HBV infection and to conduct an economic appraisal of population-based preventive strategies of reducing its sequale, it is indispensable to understand the temporal natural history of HBV infection and the subsequent progressions to various chronic liver diseases and even death from HCC.

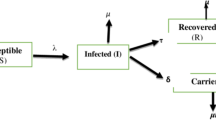
Regarding the dynamic HBV infection process, it is well documented that hepatitis B virus infection is contracted by either vertical transmission through maternal route or horizontal transmission through environmental routes (including the sharing of personal hygiene facilities, occupational exposure during medical procedures, the sharing of syringes, the process of getting tattoos, and sexual intercourse) (Kao and Chen 2002). After entering into the susceptible host, the virus starts to propagate. The time interval required for the propagation is defined as latent period after exposure to HBV. As acute infection may occur due to active virus replication, the infected subject becomes highly contagious (an infective case). In the wake of acute infection, one can either recover or become a chronic carrier detected by the presence of HBsAg (the surface antigen of HBV) for more than 6 months. This dynamic process of HBV infection for an individual from being susceptible until recovery or becoming a carrier is diagrammed in the upper panel of Fig. 1. Elucidating the natural history of HBV infection provides insight into the design and planning of preventive strategies of HBV infection by considering both mother-acquired and environment-driven transmissions. In addition to the individual temporal natural history of HBV infection, the dynamic process of such HBV infection can also be characterized from the population viewpoint by contact rate, transmission probability, and recovery rate, which are three measures that give the estimated basic reproductive number (R₀), an indicator of the number of secondary cases produced by a primary case in traditional infectious disease models, including the widely used susceptible-infectious-recovered (SIR) model (Anderson et al. 1992). Numerous studies have been devoted to estimating this indicator for various infectious diseases (Pybus et al. 2001; Yang et al. 2009). Two studies have already focused on modeling the effect of vaccination or antivirus treatment on the transmission, the prevalence, and the incidence of HBV infection (O’Leary et al. 2010; Pang et al. 2010). The effect of unsafe injection on HBV infection and also HIV cross-infection has been also elucidated with a mathematical model (Aylward et al. 1995). However, the application of the SIR or related models to a chronic infectious disease such as hepatitis B virus (HBV) infection and HCC and its related diseases is often subject to whether the temporal natural history of the infection process is well understood and whether the data are directly observed during the infectious process.

Fig. 1

Temporal natural history model for hepatitis B virus infection and the Markov process of its sequelae. f Fraction of vertical transmission, $\lambda$ infection rate after birth, $\alpha$ rate of transition to active viral replication, $\nu$ recovery rate for carrier, $\omega$ recovery rate for active viral replication, $\varepsilon$ carrier rate. The upper panel is to delineate the states in hollow circles representing the temporal natural history for hepatitis B virus infection in which the relevant parameters were estimated in different studies listed in Table 1. The lower panel is to delineate the states in shadowed circles representing for the sequales following asymptomatic carrier. The two processes were articulated as a unified Markov process model for the cost-effectiveness analysis of the two preventive strategies for hepatitis B virus infection

There are several obstacles to applying conventional infectious disease models to the temporal natural history of HBV infection in order to estimate R₀. It is not possible to distinguish between vertical and horizontal transmission for HBV on the basis of serological surveys of antibodies to the HBV core protein (anti-HBc), which are indicative of past infections only (Stevens et al. 1975, 1985; Ni et al. 2007; Tseng et al. 2011). This complicates the understanding of the HBV transmission process through environmental and maternal routes. The risk of chronic infection is highest among those who acquired infection early in life (Stevens et al. 1975, 1985; Ni et al. 2007; Tseng et al. 2011). In addition to vertical transmission, viral latency before progressing to active viremia cannot be distinguished from recovery after resolution. More importantly, it is often difficult to know the exact time of intermediate states when a specific state is observed using survey results. For example, a carrier identified by the presence of both HBV surface and internal antigens (HBsAg and HBeAg, respectively) at time t had entered the latent state at time s and evolved into active viremia at time u, where s < u < t. To tackle the mixture of both the transmission and censored problems relating to time to different disease states as shown in Fig. 1, a five-state stochastic process was therefore proposed to estimate the parameters based on the empirical data prior to the introduction of HBV vaccine and to translate these parameters into the estimated R₀.

More importantly, as HBV infection is a chronic infection disease, it may progress throughout the carrier’s lifetime to severe liver-related diseases, including chronic acute hepatitis, compensated and decompensated liver cirrhosis, HCC, and death, as shown in the bottom panel of Fig. 1. The process of its sequale has been previously modeled by another Markov model (Crowley et al. 2000). However, the link between the dynamic HBV infectious process with emphases on both horizontal and vertical transmissions and the Markov model for sequale has been barely addressed. To relate the estimated parameters governing the natural history of HBV infection to its sequale, particularly the destination of death from HCC, is a sine qua non for a cost-effectiveness analysis of various population-based preventive strategies of reducing long-term outcomes such as HCC and death.

The aims of this study were therefore several-fold and achieved with a step-by-step procedure. These included the application of a simple two-state model (susceptible and infection) and the development of a five-state stochastic process for modeling the temporal natural history of HBV infection from susceptible state to carrier or recovery state by considering a mixture of both vertical and environmental transmissions. We then applied this process model to two empirical Taiwanese datasets, one for southern and one for northern areas, that contained sufficient information to define different states of the temporal natural history of HBV infection so as to estimate the parameters. The R₀ was therefore computed by simulating the proportion of susceptible population based on the estimated parameters. The corresponding basic reproductive numbers were also computed on the basis of a simple two-state model (only considering the transition process between susceptible and infection) based on the seven empirical datasets (five empirical datasets together with the two Taiwanese datasets used in the five-state stochastic model). The comparisons of R₀ were then made between the five-state stochastic model and the two-state model. Finally, by linking the temporal natural history of HBV infection underpinning the five-state stochastic model with the sequale of HBV infection captured by the previously developed Markov model, a cost-effectiveness analysis was conducted to evaluate the two population-based preventive strategies (universal vaccination plus and hepatitis B immunoglobulin (HBIG) injection (strategy 1) and the lamivudine-treated group with routine vaccination (strategy 2)) compared with the baseline group (no intervention).

2 Materials and method

2.1 Data

To model the natural transmission dynamics of HBV illustrated in the upper panel of Fig. 1, empirical data were needed before any population-based preventive strategy (such as universal vaccination plus and hepatitis B immunoglobulin (HBIG) injection and the lamivudine-treated group with routine vaccination) was implemented. To the best of our knowledge, few empirical studies that were conducted before universal vaccination could be used to estimate the dynamic process of HBV infection. We searched relevant articles through the computerized databases Medline, and the Cochrane electronic library by combining several keywords “Hepatitis B” with the either of other three words “serology”, “prevalence”, and “epidemiology”. Furthermore, the reference lists of published articles were also used to search for other relevant studies.

The inclusion criteria for selecting studies consisted of the following: (1) the studies conducted between 1902 and 1990 (the time near the implementation of universal HBV vaccination); (2) the studies published in an English-language peer-reviewed journal; (3) the studies having available data on serological markers for the two-state model and the five-state model. The details of the respective study designs have been described in full elsewhere and are summarized in Table 1 (Sung et al. 1984; Hsu et al. 1986; Chung et al. 1988; Wu et al. 1980; Yodfat et al. 1982; Kashiwagi et al. 1983; Chen et al. 1987). All seven studies included the measurement of anti-HBc, which was necessary for the two-state model (susceptible versus infection). For the five-state model (see below), given that the measurements of HBsAg, anti-HBc, and HBeAg were necessary, data from only two studies in northern (Study 1) and southern (Study 2) areas of Taiwan were retrieved. One study in the capital of Taiwan (Study 3) also contained this information, but since it only followed individuals up to 15 years of age, this dataset could not be used for the five-state model.

Table 1 Brief summary of previous studies

With the available seroprevalence data, states were defined as follows. The latent and recovery states were defined by the presence of anti-HBc, whereas the susceptible state was denoted by a negative result. The presence of HBeAg and HBsAg represented active viral replication and carrier, respectively. The rest of this section is organized into three parts. Section 2.2 specifies how we constructed the two-state and five-state models of the temporal natural history of HBV infection. Section 2.3 delineates how we estimated R₀ by the application of those transmission parameters. Section 2.4 demonstrates how we evaluated the efficacy of various population-based preventive strategies (universal vaccination plus and hepatitis B immunoglobulin (HBIG) injection and the lamivudine-treated group with routine vaccination) based on the results of the other two sections.

2.2 Model specification for temporal natural history of HBV infection

Following Anderson et al. (1992), the temporal natural history model of infectious disease was proposed by including susceptible, infective, and immune or recovery states. To develop a model with a step-by-step procedure, we began with a two-state model delineating the simplest form of HBV infection, from susceptible to infection, according to the presence of anti-HBc (Table 1). This two-state model was essentially the accelerated failure time model used for the parametric survival analysis (Collett 2003). In this parametric analysis, we applied three different distributions for time of transition from susceptible to infection, including the exponential, Weibull, and log-logistic functions, to test the assumption whether the transition hazard rate was constant over time (with exponential distribution) or varied with time (with Weibull and log-logistic distribution).

As a subject with HBV infection may be still an infectious carrier even after the relief of symptoms in the case, the basic two-step model was extended to a five-state model that is composed of susceptible, latent period, active viral replication, carrier, and immune status. Transmission modes, including vertical and horizontal transmissions, were also quantified (Fig. 1).

In the light of Fig. 1 which is an extension of the Anderson and May model (1991), let X(t) represent a stochastic process defined by a state space, Ω = {S, L, T, C, R}, where S, L, T, C, R stand for susceptible, latent period, active viral replication, the carrier state, and recovery, respectively. For ease of presentation, the realization of these five states was assigned from 1 to 5, corresponding to the order of states defined in the above-mentioned state space, Ω. Individuals started at the susceptible state (S), presenting as negative for HBsAg, then were infected at a rate of λ after birth and entered the latent period (L), with the presence of anti-HBc. The proportions of vertical and horizontal transmissions are denoted as f and 1 − f, respectively. HBV replication after transmission and active viral replication (T), as evidenced by HBeAg in the serum, developed at a rate of α. After infection, if the host cleared the virus and developed immunity with anti-HBc at a rate of ω, they were classified as being in the recovery (R) state. Those who failed to do the same remained in the carrier state (C), with the presence of HBsAg in the serum at a rate of ε. Few carriers are considered to recover and gain immunity at a rate of ν. Note that the transmission rates jumping from one state to another state were constant with time, i.e., they were homogeneous Markov processes, though differing from the two-state model such that the process from susceptible to infection was mixed with multistates wherein the transition rates varied with time.

2.2.1 Intensity matrix

Following Fig. 1, two intensity matrixes were developed: one for the pathway following vertical transmission, denoted by Q₁,

$$ Q_{1} = \begin{array}{*{20}c} S \\ L \\ T \\ \begin{gathered} C \hfill \\ R \hfill \\ \end{gathered} \\ \end{array} \left( {\begin{array}{*{20}c} S & L & T & C & R \\ { - \epsilon } & \epsilon & {} & {} & {} \\ {} & { - \alpha } & \alpha & {} & {} \\ {} & {} & { - (\omega + \varepsilon )} & {\omega} & \varepsilon \\ {} & {} & {} & {- \nu} & {\nu} \\ \end{array} } \right) $$

and the other for horizontal transmission, denoted by Q₂,

$$ Q_{1} = \begin{array}{*{20}c} S \\ L \\ T \\ \begin{gathered} C \hfill \\ R \hfill \\ \end{gathered} \\ \end{array} \left( {\begin{array}{*{20}c} S & L & T & C & R \\ { - \lambda } & \lambda & {} & {} & {} \\ {} & { - \alpha } & \alpha & {} & {} \\ {} & {} & { - (\omega + \varepsilon )} & {\varepsilon} & \omega \\ {} & {} & {} & {- \nu} & {\nu} \\ \end{array} } \right) $$

where S–R is defined as above. The notations were defined as follows, λ: infection rate after birth; ξ: infection rate before birth; α: rate of transition to transient viremia; ω: recovery rate for transient viremia; ε: carrier rate; ν: recovery rate for carrier. It should be noted that the parameter of ξ (infection rate before birth) was not directly estimated since the infection time was not exactly known. Instead of estimating ξ, we modeled the proportion of vertical transmission (f) and other parameters (such as α, ω, ε, and ν) contained in Q₁. We assumed there was no latent state for vertical transmission. The proportion of horizontal transmission was therefore denoted by 1 − f.

2.2.2 Transition probabilities

In this subsection, we developed a series of transition probabilities during time t denoted by P _ij (t) (where i and j were equal from 1 to 5) corresponding to the intensity matrix. If the time at birth was set as 0, the transition time (t) defined above would then be equal to the age at survey, denoted by a. Each transition probability from state i to state j at age a was denoted by P _ij (a). It should be noted that although the transition probabilities could be derived from the current state (i) to the next state (j) in any state transition between 1 and 5, the state transition began with the state greater than two was not directly observable and there was a lacking of empirical data for estimation. We therefore only focused on the derivation of transition probabilities starting from state 1 (S: susceptible) with available empirical data listed in Table 1. According to the definition mentioned above, conditional probability equations were developed and can be seen in the Appendix 1.

For estimation of the above model, we first needed to specify the likelihood function. The notations u _a , v _a , w _a , y _a , and z _a indicated the number in each state: susceptible, latent period, acute infection, carrier, and recovery at a given age, a. The state space of age was A. Thus,

$$ {\text{Log likelihood }} = \sum\limits_{a \in A} {\left[ {u_{a} \times \log P_{11} \left( a \right) +\,v_{a} \times \log P_{12} \left( a \right) + w_{a} \times \log P_{13} \left( a \right) +\,y_{a} \times \log P_{14} \left( a \right) + z_{a} \times \log P_{15} \left( a \right)} \right]} $$

Using Study 2 (Table 1) as an example for illustrating the likelihood function:

$$ \begin{aligned} {\text{Log likelihood }} = &\,34 \times \log P_{11} \left( 7 \right) + 88 \times \log \left[ {P_{12} \left( 7 \right) +\,P_{15} \left( 7 \right)} \right] + 18 \times \log P_{13} \left( 7 \right) + 10 \times \log P_{14} \left( 7 \right) \\ & + 23 \times \log P_{11} \left( {12} \right) + 92 \times \log \left[ {P_{12} \left( {12} \right) + P_{15} \left( {12} \right)} \right] + 19 \times \log P_{13} \left( {12} \right) + 16 \times \log P_{14} \left( {12} \right) \\ & + \cdots + 14 \times \log P_{14} \left( {64.5} \right) \\ \end{aligned} $$

We estimated the six parameters in this model by maximizing the log likelihood function by using the Newton–Raphson method.

2.3 R₀ estimation

Following the SIR model, R₀ was inversely proportional to the ratio of the susceptible population.

$$ R_{0} = \frac{1}{x*}, $$

x*: the proportion of the susceptible population.

$$ \chi^{ * } = \int\limits_{0}^{\infty } {e^{{ - \int_{0}^{a} {\delta (u)} du}} } da, $$

where δ(.) represents the hazard function of infection.

To cope with the intractability of integration, we used the intensity matrix (Q) mentioned above to simulate the proportion of the susceptible population. Let the probability of being in each state at time t, P(t), be a square, 5 × 5 matrix. If age = t, then P can be written as P = ADA⁻¹, where A is the eigenvector of matrix Q, and D is the diagonal matrix whose diagonal elements are the exponential function of the corresponding eigenvalues of matrix Q (i.e., $D_{ii} = e^{{\varphi_{i} t}}$, where $\varphi_{i}$ is ith eigenvalue of Q). For the details on the derivation of eigenvectors and eigenvalues of Q, refer to Cox and Miller (1965).

A beta distribution was assigned to the proportion of the susceptible population (x*), with a range between 0 and 1. With the estimated x* and total population number (n) provided by the data, we can calculate the standard error of the proportion of the susceptible population, S, by the following formula:

$$ S^{2} = \frac{\chi * (1 - \chi * )}{n + 1}, $$

which provided the basis for the estimation of 95 % confidence interval (CI) of R₀.

2.4 Cost-effectiveness analysis of population-based preventive strategies

Two intervention strategies were compared, including the routine vaccination plus HBIG and the lamivudine-treated group with routine vaccination included for pregnant women at the last month before delivery. We used a birth cohort, consisting of approximately 200,000 newborns in the year 2008 in Taiwan, as our simulated cohort.

To conduct a cost-effectiveness analysis between the two intervention strategies, we built a Markov cycle decision tree by conjoining the temporal natural history of HBV infection (the upper panel of Fig. 1) developed in Sect. 2.2 with the previously established Markov process modeling the sequale of HBV infection (the bottom panel of Fig. 1) from asymptomatic carrier, through intermediate states (including chronic active hepatitis, compensated or decompensated liver cirrhosis, hepatocelluar carcinoma) and finally to death from HCC. The detailed decision tree consisting of both processes is given in Appendix 2. A Markov cycle tree with one cycle in a year was adopted to simulate such a complex disease process for each newborn from birth to 80 years of age. In addition to the estimated parameters on temporal natural history of HBV infection, which are shown in Sect. 2.2 and also Fig. 1, the parameters regarding the sequale of HBV infection were adopted from a previous study (Hung and Chen 2009). A cost-effectiveness analysis of two preventive strategies compared with no vaccination was performed by using an incremental cost-effectiveness ratio (ICER) indicator (defined as an additional cost per quality-adjusted life years (QALYs) over a life time) for assessing whether the preventive strategy was cost-saving (less cost and more benefit) or cost-effective. The detailed procedures of doing cost-effectiveness analysis with Markov cycle tree and their relevant assumptions are delineated in Appendix 2.

3 Results

3.1 Two-state model

Table 2 shows the estimated results of the two-state model (susceptible to infection) after fitting data from available studies by the three survival distributions of exponential, Weibull, and log-logistics functions. It was found from the comparison between the observed and fitted values that the exponential distribution had a larger discrepancy than the two other distributions. The shape parameters obtained from the Weibull and log-logistic distributions suggest that the force of infection was not constant, but increased with time at a decreasing rate (Fig. 2). Compared with the results using data from the northern areas of Taiwan (Studies 1 and 3 in Table 1), the scale parameter estimated from southern area (Study 2) was larger. The cumulative risk of infection using the above equation showed a sharp increase in infection starting at birth. This suggests that a higher infection rate at birth (i.e., vertical transmission) among subjects in southern areas.

Table 2 Parameter estimation in the two-state model

Fig. 2

Comparison of the cumulative risk of infection for the two-state models with exponential and Weibull distributions

3.2 Five-state stochastic model

Table 3 shows the proportion of vertical transmission was two times higher in the southern area (Study 2) (80.2 %) than the northern area (Study 1) (41.4 %). The estimated transition parameters for the five-state model are also listed in Table 3. All these transition rates were expressed in the unit of person-years. After making allowance for the parameters of transmission mode, the annual infection rate for susceptible subjects was three times higher in Study 1 (northern area) (0.035) than in Study 2 (southern area) (0.011). The transition rate (in person-years) from the latent period to transient viremia was slightly higher in Study 1 (northern area) (1.112) compared with Study 2 (southern area) (0.072). On the other hand, the annual transition rate from active viral replication to carrier was higher in Study 2 (southern area) (0.088) than in Study 1 (northern area) (0.048). Similar findings were observed for the higher transition rates from active viral replication to recovery and from carrier to recovery in Study 2 (southern area) compared with those in Study 1 (northern area).

Table 3 Parameter estimation in the five-state stochastic model

3.3 Model fitting

The cumulative risks by state are shown in Fig. 3, which shows there was a lacking of discrepancy between the expected and observed numbers for southern areas (χ²[25] = 23.875, p = 0.53). In northern areas, the proportion of vertical transmission decreased to 40 %, with relatively high infection rates after birth (0.035 persons/year). However, the results of model fitting were not satisfactory (χ²[31] = 75.44, p < 0.001) because of the sparse data on children aged less than 3 years, which accounted for the discrepancy between the observed and expected values, particularly in the states of latency and recovery in early childhood in northern areas (Fig. 3B-d).

Fig. 3

Cumulative risk by state in five-state model

3.4 R₀ estimation

The application of annual infection rates derived from the two-state model using a Weibull distribution yielded the estimated results of R₀, as shown in Table 4. By integrating the age-dependent infection rates in Table 4, R₀ was estimated as 1.24–17.11 by the age of 30. This suggests that one HBV-infected carrier will spawn 1–17 offspring of infectious subjects. The estimated R₀ was higher in Taiwan compared to other countries, with the highest estimation of 11.02 in Kaohsiung, a southern city in Taiwan, compared to the lowest value of 1.24 in Japan for the age of 30. The R₀ and the 95 % confidence interval (CI) estimated from the five-state model are also illustrated in Table 5. By using the five-state model, the R₀ at age 30 was estimated as 4.88 and 7.03 in northern and southern areas, respectively. The discrepancy in the two estimations of R₀ by the two- and five-state models was larger in Study 2 (southern area of Taiwan). In Taiwan, the R₀ was higher in southern areas compared to the northern areas in both the two- and five-state models.

Table 4 The age of a case and its corresponding reproductive number estimation in the two-state model

Table 5 The age of a case and its corresponding reproductive number estimation in the five-state model

3.5 Results of economic appraisal on preventive strategies

By using the estimated results of the five-state model for the Studies 1 and 2 together with other parameters and cost from a previous study (Hung and Chen 2011) as detailed in Appendix 2, Table 6 shows the results of cost, QALYs and the incremental cost-effectiveness ratio. As far as the ICER indicators are concerned, two preventive strategies dominated over no intervention group regardless of study selected because the ICER values were negative, indicating more gain in QALY but less cost (cost-saving) for the two intervention groups as compared with no intervention. Furthermore, the supplemental lamivudine to routine vaccination was also superior to then routine vaccination only strategy. It is also noted in Table 6 that the preventive strategies in the southern area were more cost-saving than those in the northern area as the values of the ICERs were smaller in the southern area than the northern area.

Table 6 Results of cost-effectiveness analysis in northern and southern areas in Taiwan

4 Discussion

Three major findings were demonstrated by consolidating three related parts from dynamic infection process to economic appraisal of intervention strategies with the application. The first part is to build a five-state stochastic process for modeling the temporal natural history of HBV infection characterized by the unobserved infectious process between intermediate state transitions and long-term disease progression of the sequale of HBV infection taking both vertical and horizontal transmission into account in the two areas in Taiwan. Fitting empirical data with the proposed five state model, we found vertical transmission and other transmission parameters were different between the two areas. The chance of vertical transmission was higher in the south (Study 2, a high endemic area of HBV infection) than the north (Study 1, a low endemic area of HBV infection). The second part is the application of parameters obtained from the five-state model to give area-dependent estimates of R₀, supporting a higher R₀ in the high endemic area compared to the low endemic area. Finally, conducting an economic appraisal with the development of a Markov decision tree with the incorporation of the parameters relating to the five-state stochastic process and also those pertaining to the Markov process of the sequale of HBV infection together with the corresponding costs demonstrated the two population-based preventive strategies (the routine vaccination plus HBIG and the lamivudine-treated group with routine vaccination) were more cost-effective or cost-saving (more gain of QALY and less cost) compared with no intervention. Both preventive strategies dominated over no intervention (cost-saving) and even more so in the high endemic area.

There were several novel ideas in methodological development as well as applications to quantify the temporal natural history of HBV infection and the process of its sequale. We started from a simple two-state process to model the transition between susceptible and infection by using Weibull, log-logistic, and exponential distribution models. The Weibull and log-logistic distribution can be adapted to data with non-constant infection rates. The two-state model was used to quantify the instantaneous rate of infection with HBV when other information other than anti-HBc was incomplete from the empirical data, such as the five other types of data listed in Table 1. In our two-state model, the Weibull distribution accurately described the process from susceptible to infection states, except in infants and elderly individuals. The discrepancy for those of a young age may be due to immature immunity and the appearance of serum biomarkers. The incident age of chronic outcomes for HBV infection was within five decades, and competitive death causes may account for the discrepancy in the elderly population. Such discrepancy may also suggest that the HBV infectious process was heterogeneous with age. This prompted us to consider the application of stochastic processes to model the temporal nature of HBV infection as multistate outcomes.

From a methodological viewpoint, in spite of several previous attempts by using stochastic processes to model the dynamics of infectious diseases (Mikler et al. 2007; Reiczigel et al. 2010), this is the first study, to the best of our knowledge, to develop a five-state stochastic model to estimate the parameters governing the temporal natural history of HBV by taking both vertical and horizontal transmissions based on the two different areas of empirical data prior to the introduction of HBV vaccine in Taiwan. Compared with the two-state survival model, the advantages of using the five-state stochastic model are that it appears to be more flexible to deal with the heterogeneity of HBV infection as it not only elucidated the instantaneous rate of each transition from susceptible through latent period, active viremia, and until the carrier state or the recovery state but also estimated the proportion of vertical and horizontal transmission. In addition, the use of five-state stochastic process can deal with the censored problems, that is, when the time to each outcome may not be exactly known.

The application of stochastic processes also led to a more precise estimation of R₀, particularly in a high endemic area, as the two-state model did not consider a mixture of horizontal and vertical transmissions, resulting in the underestimation of the R₀ values for those of young age and overestimation of the R₀ values for adults in areas where HBV transmission occurred mainly via vertical routes. The estimated results on R₀ from the five-state model would be more valid than those from the two-state model.

Translating the temporal natural history of HBV infection into an R₀ gave an indication of the spread of HBV infection with different transmission routes in different areas. The reproductive number for HBV infection was estimated at 0.69–1.11 in the low endemic areas of the Netherlands and UK (Kretzschmar et al. 2002). In these areas, the HBV transmission route was environmental with horizontal transmission, and the spread of HBV infection was therefore lower in their countries than our study because vertical transmission was rampant in Taiwan, particularly in southern area. This was also supported by the finding that R₀ was higher in the south than in the north because most susceptible individuals became infected via vertical transmission in southern areas. Mother-to-infant transmission was usually the major route in high endemic areas. In Taiwan, at least 40 % of carriers were infected by their mothers (Beasley et al. 1983b). Furthermore, the carrier rate rose to 74–90 % if their mothers were HBsAg- and HBeAg-positive (Beasley et al. 1983a, b). The most important evidence for the proportion of vertical transmission came from a serological study that took place within 6 months after birth, which was compatible with the timing of perinatal infection. Several studies conducted in Far East Asia before universal vaccination (between 1975 and 1985) showed a 30–70 % transmission rate from an asymptomatic carrier mother to her infant (Stevens et al. 1975; Xu et al. 1985). These reported proportions of vertical transmission were similar to that in our study.

It would be of great interest to throw light on the temporal natural history of HBV infection and elucidate the transmission route and the estimation of not only the instantaneous rates of virus replication but also the chance of becoming a carrier or recovery after acute infection. Such modeling also forms an essential underlying framework for conducting a cost-effectiveness analysis that compares different population-based preventive strategies by unifying the temporal natural history of HBV infection with the Markov process on the progression of its sequale to form a Markov decision tree given the assignment of relevant costs corresponding to each health state during the evolution of the disease process. This would provide the foundation for the economic appraisal of population-based preventive strategies like universal vaccination and HBV immunoglobulin. The universal vaccination of infants was feasible and effective for reducing the number of HBV carriers by preventing vertical transmission after birth and horizontal transmission by long-term immunity. Treatment with HBV immunoglobulin was effective for reducing vertical transmission when combined with vaccination. As the effectiveness of both intervention strategies in reducing vertical transmission or horizontal transmission was highly dependent on the transmission route and also the rate of being carrier or the recovery that may differ according to location, it is of paramount importance to elucidate the temporal natural history of HBV infection before assessing the effectiveness of these strategies in reducing the sequale of chronic liver diseases and death from HCC. On the cost side, as these population-based intervention strategies often require enormous costs the balance between cost and effectiveness in terms of incremental cost-effectiveness ratio (ICER), a useful indicator used in cost-effectiveness analyses, would be of great value to health-policy makers because the results of ICERs may vary from area to area depending on the underlying transmission routes and the rate of being a carrier or recovering.

Based on the parameters estimated from the high-endemic area of Taiwan, relative to other Western countries, the implementation of preventive strategies such as universal vaccination in infants and maternal lamivudine use was cost-saving compared with no intervention. Although the results were consistent regardless of northern or southern areas, it can be seen that costs were saved even more in the south than in the north. However, it should be noted that for areas with low endemic HBV infection and a low proportion of vertical transmission such as in Western countries, such preventive strategies may neither be cost-saving nor even cost-effective. It is hoped that our proposed five-state stochastic model can be extended to shed light on how vaccination and anti-virus treatment can stop the spread of HBV as they did in two prior studies (O’Leary et al. 2010; Pang et al. 2010) and can also assess how different transmission resources can lead to HBV infection or other cross-infection as seen in another previous study (Aylward et al. 1995).

The limitations of this study were three-fold. Firstly, our five-state stochastic model, based on the estimated parameters from Table 3, fitted well in the southern area (a high endemic area), but there was inconsistency in the northern area (a low endemic area), particularly in the category of children aged under 6 years. As the number of latent state and recovery within this age range was sparse, it was difficult to assess whether random fluctuation or inadequacy of the model led to a poor fit. Another reason for the inconsistency may stem from the underestimation of the transmission rate from the susceptible to latent period states. We compared the observed data from Study 4 with the estimated values using the parameters of Study 1 (the data from Studies 1 and 4 were from Taipei), and the estimated number of HBsAg-positive subjects fitted well, but the number of susceptible subjects was underestimated. Due to the discrepancy between the expected number and the observed one, the temporal natural history for the children below 6 years of age in low endemic areas should be validated and the interpretation should be made with caution.

A second limitation could be that the virus was divided into four major serotypes (adr, adw, ayr, ayw) based on antigenic epitopes present on its envelope proteins. The genotypes had a distinct geographical distribution and played an important role in the progression of HBV infection. However, there was no population study of viral subtype available before universal vaccination.

In addition, the clinical outcome of HBV infection was determined by the virological factors and host factors. There were several host genetic factors that modulated the immune response to HBV infection and the process of viral clearance. Different HLA phenotypes and tumor necrosis factor-α (TNF-α) gene polymorphisms associated with recovery from HBV infection in different areas have been observed in Taiwan.(Wu et al. 2004; Kao et al. 2010) The different HLA phenotypes in different areas may be the reason for the higher rate of transition from viremia to recovery and carrier to recovery for the southern versus northern populations. Further incorporation of information on viral subtypes or HLA phenotypes and TNF-α gene polymorphisms into our formula of hazard function as a covariate may be a possible solution.

Thirdly, the difference between southern and northern areas may be one of the reasons for the distinct pattern of HBV infection process in Taiwan. As the dynamics of an infectious disease must be dependent on the host as well as the infectious agent, the environment socioeconomic status may be an important determinant in the process of infection. Unfortunately, most studies conducted in Asia suffer from a lack of description about socioeconomic status. The comparison between the two areas in Taiwan provides some indications of this aspect insofar as Study 2 was situated in a southern area classified as a rural city whereas Study 1 was located in a northern urban city. The disparity between the two areas in Taiwan might be due to the level of urbanization. However, as we only studied two areas with the five-state stochastic model and the fact that the number of children included in Study 1 (urban) was small, we are simply unable to generalize our results based on two studies. The generalizability of our five-state model should be verified in future study.

In conclusion, we developed a five-state stochastic model to quantify the proportion of maternal (vertical) and environmental (horizontal) transmission and also the subsequent transition to active viremia, carrier, and resolution of HBV in the two areas with high and low prevalence of HBV infection. These parameters were further converted to estimate the basic reproductive number to reflect the spread of HBV infection. Economical evaluation was also conducted by using a Markov cycle tree unifying the temporal natural history of HBV infection with the process of the sequale of HBV infection to demonstrate cost-saving results of various population-based preventive strategies. All these findings seem area-dependent. Consolidating all information on the temporal natural history of HBV infection, the estimation of basic reproductive number, and economic appraisal of population-based preventive strategy can serve as valuable aids for health policy-makers in designing effective preventive strategies in other countries worldwide where HBV are still prevalent. However, the empirical findings on transmission routes and the temporal evolution of HBV infection varying with areas should be considered with caution as only two studies were modeled.

Appendices

Appendix 1

• 1. Transition probability from susceptible to carrier,

  $$ \begin{aligned} {\text{P}}_{ 1 4} \left( a \right) \;{= } & {\text{ P }}\left( {{\text{susceptible}} \to {\text{carrier at age}}\;a} \right) \\ = &\,{\text{P }}\left( {{\text{carrier through vertical transmission }}\left[ {{\text{Q}}_{ 1} } \right]{\text{ at age }}a} \right) \\ & + {\text{P }}\left( {{\text{carrier through horizontal transmission }}\left[ {{\text{Q}}_{ 2} } \right]{\text{ at age}}\;a} \right) \\ = &\,f \times \left[ {\int\limits_{0}^{a} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - u} {\varepsilon e^{ - (\varepsilon + \omega )\gamma } } e^{ - \nu (a - u - \gamma )} d\gamma du} \right] + \left( { 1- f} \right) \times \left[ {\int\limits_{0}^{a} {\lambda e^{ - \lambda s} } \int\limits_{0}^{a - s} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - s - u} {\varepsilon e^{ - (\varepsilon + \omega )\gamma } } e^{ - \nu (a - s - u - \gamma )} d\gamma duds} \right] \\ \end{aligned} $$

  Recall that those who were vertical transmission would pass through active viral replication assuming no latent state.

• 2. Transition probability from susceptible to recovery,

  $$ \begin{aligned} {\text{P}}_{ 1 5} \left( a \right)\,=&\,{\text{ P }}\left( {{\text{susceptible}} \to {\text{recovery at age}}\;a} \right) \\ =\,&{\text{P }}\left( {{\text{recovery through vertical transmission }}\left[ {{\text{Q}}_{ 1} } \right]{\text{ at age}}\;a} \right) \\ & + {\text{P }}\left( {{\text{recovery through horizontal transmission }}\left[ {{\text{Q}}_{ 2} } \right]{\text{ at age}}\;a} \right) \\ =\,& {\text{P }}\left( {{\text{susceptible}} \to {\text{transient viremia}} \to {\text{recovery through vertical transmission }}\left[ {{\text{Q}}_{ 1} } \right]{\text{ at age}}\;a} \right) \\ & + {\text{P }}\left( {{\text{susceptible}} \to {\text{transient viremia}} \to {\text{recovery through horizontal transmission }}\left[ {{\text{Q}}_{ 2} } \right]{\text{ at age}}\;a} \right) \\ & + {\text{P }}\left( {{\text{susceptible}} \to {\text{carrier}} \to {\text{recovery through vertical transmission }}\left[ {{\text{Q}}_{ 1} } \right]{\text{ at age}}\;a} \right) \\ & + {\text{P }}\left( {{\text{susceptible}} \to {\text{carrier}} \to {\text{recovery through horizontal transmission }}\left[ {{\text{Q}}_{ 2} } \right]{\text{ at age}}\;a} \right) \\ = &\,\left( {1 - f} \right) \times \left[ {\int\limits_{0}^{a} {\lambda e^{ - \lambda s} } \int\limits_{0}^{a - s} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - s - u} {\omega e^{ - (\varepsilon + \omega )\gamma } } d\gamma duds} \right] \\ & + f \times \left[ {\int\limits_{0}^{a} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - u} {\omega e^{ - (\varepsilon + \omega )\gamma } } d\gamma du} \right] \\ & + \, \left( { 1- f} \right) \times \int\limits_{0}^{a} {\lambda e^{ - \lambda s} } \int\limits_{0}^{a - s} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - s - u} {\varepsilon e^{ - (\varepsilon + \omega )\gamma } } \int\limits_{0}^{a - s - u - r} {\upsilon e^{ - \upsilon \beta } } d\beta d\gamma duds \\ & + \left[ {f \times \int\limits_{0}^{a} {\alpha e^{ - \alpha u} } \int\limits_{0}^{a - u} {\varepsilon e^{ - (\varepsilon + \omega )\gamma } \int\limits_{0}^{a - s - u - r} {\upsilon e^{ - \upsilon \beta } } d\beta } d\gamma du} \right] \\ \end{aligned} $$

• 3. Transition probability from susceptible to transient viremia,

  $$ \begin{aligned} {\text{P}}_{ 1 3} \left( a \right){ = }\,& {\text{P }}\left( {{\text{susceptible}} \to {\text{transient viremia at age}}\;a} \right) \\ =\,& {\text{P }}\left( {{\text{transient viremia through vertical transmission }}\left[ {{\text{Q}}_{ 1} } \right]{\text{ at age}}\;a} \right) \\ =\,& \left( { 1- f} \right) \times \left[ {\int\limits_{0}^{a} {\lambda e^{ - \lambda s} } \int\limits_{0}^{a - s} {\alpha e^{ - \alpha u} } e^{ - (\varepsilon + \omega )(a - s - u)} duds} \right] + f \times \left[ {\int\limits_{0}^{a} {\alpha e^{ - \alpha u} } e^{ - (\varepsilon + \omega )(a - u)} du} \right] \\ \end{aligned} $$

• 4. Transition probability from susceptible to latent period,

  $$ {\text{P}}_{ 1 2} \left( a \right) = \, \left( { 1- f} \right) \times \left[ {\int\limits_{0}^{a} {\lambda e^{ - \lambda s} } e^{ - \alpha (a - s)} ds} \right] + {\text{f}} \times e^{ - \lambda a} $$

• 5. Transition probability staying in susceptible,

  $$ {\text{P}}_{ 1 1} \left( a \right) = \, \left( { 1- f} \right) \times e^{ - \lambda a} $$

Appendix 2

2.1 Two intervention strategies

The two intervention strategies, as opposed to no intervention, that were compared in a cost-effectiveness analysis were routine vaccination and hepatitis B immunoglobulin (HBIG) injection (present strategy for nationwide immunization program) and the lamivudine-treated group with routine vaccination. Note that lamivudine was prescribed in addition to routine vaccination for pregnant women at the last month before delivery (Supplementary Fig. 1).

2.2 Markov decision tree and assignment of parameters

As mentioned in the text, we built up a Markov cycle tree by conjoining the five-state stochastic process pertaining to the temporal natural history of HBV infection (the upper panel of Fig. 1 and the upper panel of Supplementary Fig. 1b) with a previously-designed Markov process for the sequale of HBV infection (the lower panel of Fig. 1 and Supplementary Fig. 1b). The decision tree starts from the three decision nodes of no intervention, routine vaccination and hepatitis B immunoglobulin (HBIG) injection, and the lamivudine-treated group with routine vaccination. The basic idea for constructing the Markov decision tree is to construct the tree structure for the baseline group (no intervention) as it represents the subjects following the temporal natural history of HBV infection and also the Markov process for the sequale of HBV infection. As depicted in Supplementary Fig. 1, the detailed tree structure for the temporal natural history of HBV takes other causes of death into account. Each node represents the chance of moving from the current state to the possible outcomes in the next cycle following the Markov assumption. For example, the susceptible state at the current time may be in latent state or still in the susceptible state in the next cycle if the patient did not die from other causes of death. Based on the Markov assumption, annual transition probabilities for each chance node were computed by the application of instantaneous rates listed in Table 3. For example, the annual transition probability from susceptible to latent state (h₁) was estimated by the transition parameter λ in Table 3.

$$ {\text{h}}_{ 1} = 1- { \exp }( - \lambda ) $$

The estimations of h₂–h₅ were also derived from α, ε, ω, ν in Table 3 in a similar manner. The annual transition probabilities for each transition are listed in Supplementary Table 1.

The lower panel of Supplementary Fig. 1b gives a delineation of the Markov cycle tree for the evolution of the sequale of HBV infection starting from asymptomatic carrier until death from HCC. Note that the terminal status (denoted by the triangle) of each tree represents the state at the end of each cycle and would return the corresponding state to the beginning of the Markov node (denoted by the circle (M)), following the Markov assumption except death defined as an absorbing state that no longer moves. The entire cohort was simulated by using the Markov cycle tree in this way to give a series of outcomes during HBV infection and also various sequale after asymptomatic carrier state for the baseline group (no intervention). The parameters related to the Markov cycle tree on the progression to the sequale of HBV infection and also the utility for each state (for more detail, see the previous study (Hung and Chen 2009)) are shown in the decision tree.

The tree structures for the two intervention groups were similar to the baseline group. The only difference between the intervention group and the baseline group was the assignment of the parameters by changing the transmission parameters governing the temporal natural history of HBV infection according to the efficacy of intervention. For example, the efficacy of vaccine plus HBIG and lamivudine in reducing vertical transmission vertical transmission through the efficacy of both interventions were adjusted between the susceptible, the latent state, and immunity in the tree structure. Listed in Supplementary Table 1, these base-case estimates were assigned to the decision tree structure. For the parameters relating to the temporal natural history of HBV infection, we did not specify their distribution because they were estimated from the empirical data. The parameters related to the sequale of HBV infection were assigned with gamma or beta distribution by using Bayesian conjugated method to update the parameters from different studies.

2.3 Assignment of cost parameters

In addition to the cost involved in each specific test, since the Markov cycle tree can keep track of each disease state in each cycle, it is very straightforward to assign the corresponding cost parameter to each disease. Detailed in Supplementary Table 2 are the base-case estimates of cost, which were further converted to $US with year 2008 values. The indirect costs were approximated by production loss due to early death, which was estimated by using Taiwan’s per capita income multiplied by the offset between the age of death and age of retirement based on the capital approach (Supplementary Table 2). All analyses were carried out from a societal perspective. All costs were discounted at 3 % annually.

2.4 Outcome measures

The outcome related to effectiveness is quality-adjusted-life-year (QALY) gained in each preventive strategy. Note that the utility values are those quoted from a previous cost-effectiveness study on the prevention of hepatitis B in Asian and Pacific Islander adults, as described in Supplementary Table 1.

2.5 Probability analyses

A series of incremental cost-effectiveness ratios (ICERs) were simulated with probabilistic sensitivity analysis, employing Monte Carlo simulation based on the specific assigned distributions of parameters mentioned above.