1 Introduction

Accurate hydrological prediction is not only an important non-engineering measure to ensure flood control safety and increase water resources use efficiency, but also can provide guidance for reservoir planning and management. Runoff is a complicated hydrologic process and has many influencing factors, such as geomorphology, climate, human activity, etc. This makes inflow series become a nonlinear and highly complex non-stationary series. Consequently, it is challenging to calculate accurate and reliable predictions. A number of models for dealing with hydrologic time series prediction have been developed, such as classic regressive analysis techniques (Matalas 1967; Salas et al. 1982), and more sophisticated methods based on the use of fuzzy logic (Chang and Chen 2001; Nayak et al. 2005), artificial neural network (Hsu et al. 1995; Aksoy and Dahamsheh 2009), chaos theory (Sivakumar 2009), support vector machine (SVM) (Liong and Sivapragasm 2002), genetic programming (GP) (Whigam and Crapper 2001) and so on.

Support vector machine, introduced by Vapnik (1995), is a robust algorithm for regression analysis in many disciplines (Wang et al. 2009a) and can effectively handle nonlinear problems. SVM is based on structural risk minimization (SRM), which avoids the curse of dimensionality and over-learning problems effectively. At the same time SRM can cause the solution to be captured in a local minimum and minimize the empirical error and model complexity simultaneously. As it has good generalization ability with a finite data sample, and performs better than the traditional models such as neural network model (Yoon et al. 2011), much research has been devoted to the formulation and development of SVM for improving the quality of hydrologic prediction (Bray and Han 2004; Yu et al. 2006; Lin et al. 2009; Noori et al. 2011).

Genetic programming (Koza 1992) is also a popular prediction model. GP uses evolutionary theory and natural selection to identify and screen the importance of each input variable to achieve the best results (Makkeasorn et al. 2008). Moreover, it can produce an explicit model expression, namely the function equation between input variables and targets. In addition, GP is an alternative way to reduce the over-fitting problems and improve generalization of resulting models (Kisi et al. 2012). GP has become popular in hydrologic forecasting and has been successfully applied (Sheta and Mahmoud 2001; Liong et al. 2002; Aytek and Alp 2008; Kisi and Shiri 2011).

However, a runoff time series can be viewed as a combination of quasi-periodic signals contaminated by noise (Wu and Chau 2011). It is necessary to filter the runoff time series with preprocessing techniques to reduce noise and improve the prediction ability of hydrologic systems. Singular spectrum analysis (SSA) (Vautard et al. 1992) is an effective technique for analyzing time series. The main purpose of SSA is to decompose the original series into a sum of series, so that each component in this sum can be identified as either a trend, periodic, quasi-periodic or noise component (Golyandina et al. 2001). As a consequence, SSA can be used to perform a spectrum analysis on input data, distinguishing noises and inverting the remaining components to yield a “filtered” time series (Sivapragasam et al. 2001).

In the last decade, SSA has been increasingly applied to hydrological forecasting. For instance, Sivapragasam et al. (2001) proposed a hybrid model based on SSA coupled with SVM, predicting runoff and rainfall in the Tryggevælde and Singapore, respectively. The results were compared with the non-linear prediction (NLP) method, showing that the proposed model yields a significantly higher accuracy in the prediction than that of NLP. Marques et al. (2006) concluded that SSA can extract important components of a hydrologic time series with characteristic irregular behavior, such as precipitation, runoff series and water temperature, and can provide good forecasts. Chau and Wu (2010) adopted SSA to decompose the raw data to develop a hybrid model integrating artificial neural networks and support vector regression for daily rainfall prediction. Results showed that SSA exhibited considerable accuracy in rainfall forecasting and the hybrid model performed very well. Wu and Chau (2011) found that SSA can considerably improve the performance of the rainfall–runoff model and eliminate the lag effect. Zhang et al. (2011) combined SSA and auto regressive integrated moving average (ARIMA) for annual runoff forecasting, with good results.

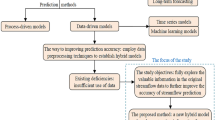
Wu and Chau (2011) pointed out that the present study does not require accurately resolving the raw rainfall and runoff signals into trends, oscillations, and noises. Generally, a rough resolution is used for the separation of signals and noises. Because of this, noise may be not a pure random series and contain hydrological information. Current applications of SSA in hydrology only selected the filtered series as model inputs without considering noise series (Sivapragasam et al. 2001; Marques et al. 2006; Wu et al. 2009). If noises series is not considered, model performance might be affected. So the object of this study is to develop a robust forecasting frame of hydrological prediction that can make a quick and accurate prediction for monthly inflow with the aid of SSA, to prove that noise contain hydrological information and to analyze the influence of noises on prediction accuracy. A new method that considering both filtered and noise series as model inputs will be proposed. The paper is organized as follows. Firstly, the SSA was applied to pre-process the original inflow series. Secondly, SAR (1), SVM and GP models were constructed and trained when model inputs were the original series, filtered series and noise, respectively. Thirdly, performances of these models under different model inputs were compared and discussed. Finally, conclusions were given.

2 Methodology

2.1 Singular spectrum analysis

Singular spectrum analysis is a suitable analysis method for researching period oscillatory behavior. It is also a statistical technique starting from a dynamic reconstruction of the time series and is associated with the empirical orthogonal function (EOF). Generally, SSA can be considered as a special application of EOF decomposition. The main purpose of SSA is to convert a one-dimensional time series into a multi-dimensional matrix with a given window length, which is treated with orthogonal decomposition. If the pairs of eigenvalues are produced obviously and the corresponding EOF is almost periodic or orthogonal, this corresponding EOF can be considered as the oscillatory behavior of the time series.

Application of SSA is summarized as follows. Assume that the series is a nonzero series F = {f 0, f 1,…,f N−1} (f i  ≠ 0) and the length of the series is N (>2). Given a window length L, the one-dimensional time series can be transferred into a sequence of L-dimensional vectors X i  = {f i−1,…, f i+L−2}T, (i = 1,…, K = N − L + 1). The K vectors X i will form the columns of the (L × K) trajectory matrix

$$ X = \left[ {\begin{array}{*{20}c} {f_{0} } & {f_{1} } & {f_{2} } & \ldots & {f_{K - 1} } \\ {f_{1} } & {f_{2} } & {f_{3} } & \ldots & {f_{K} } \\ {f_{2} } & {f_{3} } & {f_{4} } & \ldots & {f_{K + 1} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {f_{L - 1} } & {f_{L} } & {f_{L + 1} } & \ldots & {f_{N - 1} } \\ \end{array} } \right] $$
(1)

The singular value decomposition (SVD) of the trajectory matrix X is then performed. Let S = XX T. The eigenvalues and eigenvectors of S are calculated and sorted by decreasing magnitude. According to the conventional EOF computation, an expansion of the matrix X is represented as

$$ x_{i + j} = \sum\limits_{k = 1}^{L} {a_{i}^{k} {\mathbf{E}}_{j}^{k} } $$
(2)

where i = 1,…,N − L + 1, j = 1,…, L, k = 1,…, L, a k i are the time principal components (T-PC), and E k j is the corresponding eigenvector, which can be denoted by T-EOF. The key step of SSA is to reconstruct a new one dimensional series of length N using each component of the T-PC and T-EOF. The process is expressed as follows

$$ x_{i}^{k} = \left\{ {\begin{array}{*{20}c} {\frac{1}{i}\sum\limits_{{j = 1}}^{L} {a_{{ij}}^{k} {\mathbf{E}}_{j}^{k} } \quad 1 \le i \le L - 1} \hfill \\ {\frac{1}{L}\sum\limits_{{j = 1}}^{L} {a_{{ij}}^{k} {\mathbf{E}}_{j}^{k} } \quad L \le i \le N - L + 1} \hfill \\ {\frac{1}{{N - i + 1}}\sum\limits_{{j = i - N + L}}^{L} {a_{{ij}}^{k} {\mathbf{E}}_{{ij}}^{k} } \quad N - L + 2 \le i \le N} \hfill \\ \end{array} } \right. $$
(3)

Equation (3) produces an N-length time series F k , such that the initial series F is decomposed into the sum of L series

$$ F = \sum\limits_{k = 1}^{L} {F_{k} } $$
(4)

If the number of contributing components is p, then the filtered series is the sum of p series

$$ F = \sum\limits_{k = 1}^{p} {F_{k} } $$
(5)

The sum of the remaining series is noise. As mentioned above, these reconstructed components can be associated with the trend, oscillations or noise of the original time series with proper choices of L and p.

2.2 Support vector machine

Support vector machine (Vapnik 1995) is known as a classification and regression procedure. Given by a set of N samples of \( \{ {\mathbf{x}}_{k} ,y_{k} \}_{k - 1}^{N} \cdot {\mathbf{x}} \in R^{m} ,y \in R, \) where x is an input vector of m components and y is a corresponding output value, an SVM estimator (f) on regression can be expressed as

$$ f({\mathbf{x}}) = {\mathbf{w}} \cdot \phi ({\mathbf{x}}) + b $$
(6)

where w is a weight vector, and b is a bias. The optimal w, b can be found by the SVR. φ denotes a nonlinear transfer function that maps the input vectors into a high-dimensional feature space in which, theoretically, a simple linear regression can cope with the complex nonlinear regression of the input space. Normally, a kernel function \( K(x_{i} ,x_{j} ) = (\phi (x_{i} ) \cdot \phi (x_{j} )) \) can be used to yield inner products in the feature space, after which the computation in the input space can be performed. In the present study, a Gaussian radial basis function (RBF) is adopted in the form of \( K(x_{i} ,x_{j} ) = \exp ( - \parallel x_{i} - x_{j} \parallel /2\sigma^{2} ) \). Once parameters \( \alpha_{i} ,\alpha_{i}^{\ast} \) and b 0 are obtained, the final approximation function f (x i ) becomes

$$ f(x_{i} ) = \sum\limits_{i = 1}^{n} {(\alpha_{k} - \alpha_{k}^{\ast} )} K(x_{k} ,x_{i} ) + b_{0} ,\quad k = 1, \ldots ,s $$
(7)

where x k is the support vector, α k and \( \alpha_{k}^{\ast} \) are parameters associated with support vector x k , and n and s represent the number of training samples and support vectors, respectively. Three parameters (C, ε, σ) need to be optimized in order to identify the optimal f (x i ).

2.3 Genetic programming

Genetic programming derives from the Darwinian principle of natural selection. It allows the solution of problems using evolutionary processes including crossover, mutation, duplication and deletion (Koza 1992). GP starts by initializing a population that compounds the random members known as individuals. The fitness of each individual is evaluated with respect to the training data and the ‘parents’ are selected out of the fitter individuals. The parents mate and reproduce massive amounts of offspring. Similarly, the fitness of each offspring is tested against the training data. Some high fitness offspring may be kept and be allowed to reproduce, while some low fitness offspring may be rejected. The creation of offspring continues iteratively until the offspring that fits the training data best is produced. The representation of GP can be viewed as a parse tree-based structure composed of the function set and terminal set (Wang et al. 2009b). An example of such a parse tree can be seen in Fig. 1. The structure of GP can be used to describe the relationship between the input and output very well. A more detailed explanation of GP can be found in Koza (1992).

Fig. 1
figure 1

GP parse tree representing function \( y = a - \sqrt {b + x} \)

Full size image

2.4 Seasonal autoregressive model

Assuming that a seasonal hydrological time series is represented by X t,τ , in which t defines the year and τ defines the season, such that τ = 1,…,m and m is the number of seasons in the year. In this paper, τ represents a month. A time series defined as

$$ X_{t,\tau } = \mu_{\tau } + \varphi_{1,\tau } (X_{t,\tau - 1} - \mu_{\tau - 1} ) + \cdots + \varphi_{p,\tau } (X_{t,\tau - q} - \mu_{\tau - q} ) + \varepsilon_{t,\tau } $$
(8)

is called a seasonal autoregressive model of order q, in which ε t,τ is an uncorrelated normal variable with mean zero and variance \( \sigma_{\tau }^{2} (\varepsilon ) \). The model is often denoted as the SAR (q) model. The SAR (1) model is developed by making q = 1 in Eq. (8) as

$$ X_{t,\tau } = \varphi_{0,\tau } + \varphi_{1,\tau } X_{t,\tau - 1} + \varepsilon_{t,\tau } $$
(9)

in which the parameters φ 0,τ and φ 1,τ can be estimated by

$$ \varphi_{0,\tau } = \mu_{\tau } - \varphi_{1,\tau } \mu_{\tau - 1} $$
(10)
$$ \varphi_{1,\tau } = r_{1,\tau } \sigma_{\tau - 1} /\sigma_{\tau } $$
(11)
$$ r_{1,\tau } = \frac{{\sum\nolimits_{t = 1}^{n} {(X_{t,\tau } - \mu_{\tau } )(X_{t,\tau - 1} - \mu_{\tau - 1} )} }}{{(n - 1)\sigma_{\tau } \sigma_{\tau - 1} }} $$
(12)

where μ τ , σ τ are the τth month mean and stand deviation, respectively, and r 1,τ is the first order autoregressive coefficient of the τth month.

3 Proposed method

To analyze the influence of noise on the inflow prediction process, a new prediction method is proposed and developed. As illustrated by Fig. 2, the original inflow series is decomposed into filtered series and noise by SSA. The current method only uses filtered series as the model input to predict inflow series (solid line in Fig. 2). While the proposed method considers both filtered and noise series as inputs, the sum of both model prediction results is the final predicted inflow series.

Fig. 2
figure 2

Flowchart of the proposed method

Full size image

The proposed method can be summarized as follows.

3.1 Data normalization

Data normalization is an essential step because it can not only avoid attributes in greater numeric ranges dominating those in smaller numeric ranges, but also avoid numerical difficulties during calculation (Wang et al. 2009a). In the present study, the monthly runoff series are normalized using

$$ x_{norm} = \frac{{x - \overline{x} }}{\sigma } $$
(13)

where x norm is the result of normalization, x is the observed flow, \( \overline{x} \) is the average of the observed flow, and σ is the standard deviation of observed flow.

3.2 SSA parameters selection

There are two parameters in SSA: the window length L and number of contributing components p. An appropriate L should be able to clearly resolve different oscillations hidden in the original signal. If L is too small, closely spaced frequencies are unlikely to be resolved and certain trend components would be mixed with other components of the series. If L is too large, the statistical significance of the estimated periodicities is compromised (Zhang et al. 2011). Generally, the range of window length L should be determined firstly. Under each possible window length, the precision of models are obtained. The root mean square error (RMSE) is selected as the evaluation criterion, i.e.

$$ RMSE = \sqrt {\frac{1}{n}\sum\limits_{t = 1}^{n} {(\widehat{{Q_{t} }} - Q_{t} )^{2} } } $$
(14)

where n is the number of observed inflow data, \( \widehat{{Q_{t} }} \) and Q t are the predicted and observed inflow at time t, respectively. The window length corresponding to the minimum RMSE is the appropriate L.

Given a window length L, the original series is decomposed into L components. The subsequent task is to determine the number of contributing components p (≤L) and to distinguish the signal and noise. Based on the perspective of linear correlation, the positive or negative cross-correlation function (CCF) values indicate that the corresponding components as inputs of model make the positive or negative contribution to outputs of model. Therefore, first the CCF values between components and the original series are calculated. The number of positive CCF values is the optimal value of p and the components which have positive CCF values are contributing components. Then, the sum of contributing components is the filtered series and the sum of the remaining components is noise.

3.3 Screen the predictive factors

The objective of predicting a time series is to build a relationship between antecedent values and future values, namely predicting outputs from inputs based on past records. The relationship is shown as follows:

$$ Y = f({\mathbf{x}}^{m} ) $$
(15)

where x m is a m-dimensional input vector consisting of variables x 1,…,x i ,…,x m , Y is the output variable, f is a nonlinear function. Similarly,the process of monthly inflow prediction is to find the relationship between the inflow at time x i+m and the inflow x i+1, x i+2,…,x i+m−1:

$$ x_{i + m} = f(x_{i + 1} ,x_{i + 2} , \ldots ,x_{i + m - 1} ) $$
(16)

where m corresponds to the number of antecedent inflow values. Clearly, the selection of appropriate model inputs plays an important role in runoff prediction since it provides the basic information about the hydrologic system being modeled (Wang et al. 2009a). In this study, the autocorrelation function (ACF) is employed to select m.

3.4 Prediction models

Building the SVM model, there are three parameters: the penalty coefficient (C), error tolerance (ε) and gamma (σ) in the RBF kernel function. C indicates a positive constant that determines the degree of penalized loss when a training error occurs. But, Wang et al. (2003) indicated that prediction error is scarcely influenced by C. ε is a trade-off between the sparseness of the representation and closeness to the data. Generally, the larger ε, the fewer number of support vectors and thus the representation of solutions are sparser. But a larger ε also can depreciate the approximation accuracy placed on the training points (Cao and Tay 2003). There are many methods to select these parameters, such as genetic algorithms (Chen et al. 2004), the stepwise search (Dong et al. 2005), SCE-UA algorithm (Lin et al. 2006). However, compared with these advanced methods, Hsu et al. (2003) indicated that the grid search is simple and doesn’t require too much computational time. Furthermore, the grid-search can be easily parallelized because each parameter is independent. So this paper adopted the grid search method to obtain the values of C and ε.

The procedure to develop GP model is as follows. The first step is to create an initial population of individuals of a certain size by randomly. The second is fitness function. The fitness value of each individual in a population is determined by RMSE. The third is to choose the terminal sets and the function sets to create the chromosomes. The terminal sets consist of the predictive factors and constants. In this study, four basic arithmetic operators (+, −, ×, ÷) and the basic mathematical function (√) constitute the function sets. Only five mathematical functions were selected because GP can do what it can to apply the existing functions to solve problems, even if the required functions are missed. Finally, the last step is to choose the set of genetic operators and their rates.

Once the structures of prediction models are determined, the simulated and predicted results of the original series, filtered and noise series can be calculated, respectively. For convenience, the prediction models are named as SSA-SVM and SSA-GP models when SVM and GP models simulate and predict the filtered runoff series with the help of SSA. When the noise series is considered, the prediction models are named as modified SSA-SVM and SSA-GP models.

3.5 Evaluate model performances

Four criteria are selected to evaluate the prediction model performance based on Chinese Hydrological Forecasting (or prediction) guidelines.

  1. (1)

    Nash–Sutcliffe efficiency (NS)

    $$ NS = \left( {1 - \frac{{\sum\nolimits_{t = 1}^{n} {(Q_{ot} - Q_{pt} )^{2} } }}{{\sum\nolimits_{t = 1}^{n} {(Q_{ot} - \overline{{Q_{ot} }} )^{2} } }}} \right) $$
    (17)
  2. (2)

    Water Balance efficiency (WB)

    $$ WB = \frac{{\sum\nolimits_{t = 1}^{n} {Q_{pt} } }}{{\sum\nolimits_{t = 1}^{n} {Q_{ot} } }} $$
    (18)
  3. (3)

    Relative error of annual average maximum monthly flow (REmax)

    $$ RE_{\hbox{max} } = \frac{1}{l}\sum\limits_{j = 1}^{l} {\left| {1 - \frac{{Q_{pj,\hbox{max} } }}{{Q_{oj,\hbox{max} } }}} \right|} \times 100\% $$
    (19)
  4. (4)

    Relative error of annual average minimum monthly flow (RE min)

    $$ RE_{\hbox{min} } = \frac{1}{l}\sum\limits_{j = 1}^{l} {\left| {1 - \frac{{Q_{pj,\hbox{min} } }}{{Q_{oj,\hbox{min} } }}} \right|} \times 100\% $$
    (20)

    where n is the number of observed flow data, Q pt and Q ot are the predicted and observed flow at time t, respectively, \( \overline{{Q_{ot} }} \) is the average value of observed flow during calibration period, Q pj,max and Q oj,max are the annual maximum predicted and observed monthly flow, Q pj,min and Q oj,max are the annual minimum predicted and observed monthly flow in the jth year, respectively, and l is the number of year. Values of NS and WB closer to 1 indicate better prediction results. Values of REmax and REmin closer to zero indicate that the model has a good ability to predict the maximum and minimum monthly flow, respectively.

4 Case study

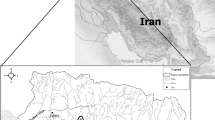
The Three Gorges Reservoir (TGR), located on the Yangtze River (Fig. 3), was selected as a case study. The Yangtze River, the longest river in the Asia, and the third longest in the world, is about 6,300 km (3,915 miles) long, flowing from its source in Qinghai province, eastward into the East China Sea at Shanghai city. The upper of Yangtze River is intercepted by the TGR with a length of main course about 4.5 × 103 km and drainage area of 1 × 106 km2.

Fig. 3
figure 3

Location of the TGR in the Yangtze River basin in China

Full size image

The monthly inflow series of TGR with an observation period from January 1882 to December 2010 (129 years and 1,548 months) was selected in this study. These inflow data were recorded at the Yichang hydrological station and were reverted to the inflow series before building the TGR. Xiong and Guo (2004) carried out a trend test and change-point analysis on annual discharge series of the Yangtze River at the Yichang during the period 1882–2001. At the 5 % significance level, the annual mean discharge series exhibited a slightly deceasing trend. Although many changes to land and water use have occurred, no statistically significant trends were detected in the inflow time series (Xu et al. 2007). Based on the above analysis, it indicates that the data is reliable and can be used for prediction.

The monthly runoff series was separated as training and testing periods, and the data series from January 1882 to December 2000 was used for training (or calibration) while the remaining 10-year was used for testing (or validation). Table 1 lists related statistical information of the whole data and two datasets, including mean (μ), standard deviation (S x ), coefficient of variation (C v ), skewness coefficient (C s ), minimum (X min), and maximum (X max). It can be observed from Table 1 that the minimum and maximum monthly flows are within training data series.

Table 1 Statistical information of monthly inflow in the TGR
Full size table

5 Results analysis and discussion

5.1 SSA decomposition of monthly inflow series

Since the monthly inflow time series has obvious periodicity, namely 12 months, and the window length must be greater than 1. A interval of [2, 12] is examined to choose L in this study. Given a window length L, the original series can be decomposed into the filtered series and noise. Two filtering methods, CCF method and enumeration method, were recommended by Chau and Wu (2010) to identify a contributing or noncontributing component in SSA decomposition. The enumeration method is to examine all input combinations. If the widow length is L, there are 2L combinations for LRCs. This method may be computationally intensive if L is taken a large number. The CCF method was adopted in this study since its principle is simple and convenient in practice. Table 2 shows the values of CCF between each component and the original series under various window lengths L. Taking L = 3 as an example, the last two components have positive CCF values, which means that they are contributing components and the optimal p is equal to 2. The sum of contributing components is the filtered series, and the first component is noise. Similarly, the values of p under other window lengths can be gotten, which are listed in Table 2.

Table 2 Cross-correlation function values and number of contributing components under various window lengths L
Full size table

After the filtered and noise series have been distinguished, correlation coefficients between original series, filtered series and noise are calculated and listed in Table 3. It is shown that correlation coefficients between the original series and filtered series are over 0.98, which illustrates that the filtered series can obtain main trend and periodic signals from the original series. When L is 2, the correlation coefficient between the original series and noise is 0.57. This means that the closely spaced frequencies have not been resolved completely and certain trend components are mixed in the noise. The similar conclusion is observed by the correlation coefficient (0.39) between the filtered series and noise. When L is over 2, all correlation coefficients between the original series and noise fluctuate around 0.25. It indicates that no matter which the window length is, the slight positive relativity between the original series and noise always exists. This explains why the noise may contain some useful information and should be considered. Meanwhile, the result also indicates that the value of L (L > 2) has little impact on the degree of correlation. When L is over 2, all correlation coefficients between the filtered series and noise are almost equal to 0. They are mutually independent and should be simulated by models separately.

Table 3 Correlation coefficients between original series, filtered series and noise
Full size table

Under each possible window length, the accuracies of models are calculated using RMSE. The minimum RMSE represents the best model performance. As shown in the Fig. 4 and Table 4, the minimum RMSE value of the SSA-SAR, SSA-SVM and SSA-GP models is achieved when L equals 2, 12 and 7, respectively. This means that the appropriate window length L of the SSA-SAR, SSA-SVM and SSA-GP models are 2, 12 and 7, respectively.

Fig. 4
figure 4

RMSE values for SSA-SAR, SSA-SVM and SSA-GP models under various window lengths L

Full size image
Table 4 RMSE values of the SSA-SAR, SSA-SVM and SSA-GP models under various window lengths L
Full size table

5.2 Input selection

SAR (1), as a traditional forecasting model, has been widely used in monthly inflow prediction. It was used as the benchmark for comparison of model performance in this study. The predictive factor of SAR (1) model is the previous inflow. The ACF was employed to select the predictive factors for the SVM and GP models. Figure 5 shows ACF values of the original monthly runoff series and the filtered series under various window lengths for lags 1–24. When the lag is 12 months, ACF values of all series reach their peaks. This result illustrates that the intensity of correlation is the strongest between the antecedent twelve inflows and the next period inflow, and they contain the most information to predict the next inflow. Therefore, the predictive factors were the antecedent twelve inflows when the prediction models simulate and predict the original series and filtered series, respectively.

Fig. 5
figure 5

Autocorrelation function of the original and filtered series under various window lengths L

Full size image

The first 100 noise data points are plotted in Fig. 6, which shows that the noise has some regularity and is not exactly white noise. The ACF values of noise are shown in Fig. 7. When the lag equals 1 or 3, the values of ACF are relatively large. This result indicated that some information is still contained in the noise and that it is therefore necessary to model it. To obtain a more robust forecasting model, it is recommended that the more predictive factors in models should be taken. Thus the predictive factors of noise selected the antecedent three inflows.

Fig. 6
figure 6

The first 100 noise data points of three models

Full size image
Fig. 7
figure 7

Autocorrelation function of the noise for the SVM and GP models

Full size image

5.3 Inflow prediction by SAR (1) model

The NS, WB, REmax, REmin are used to evaluate SAR (1) model performances, with results during training and testing periods listed in Table 5. During the training period, SAR (1) models perform well with higher values of NS. All WB values are equal to 1. During the testing period, the model efficiency index NS values are near 0.75 and the values of WB are over 1. The performances of SAR (1) models are unsatisfactory, which shows that SAR (1) model has a weak extrapolating ability. With the help of SSA, model performances in terms of NS get better during the testing period, increasing from 0.73 to 0.76. But all values of WB exhibit no change. The maximum and minimum inflows even get the poorer predictions. This indicates that the SSA has no obvious positive effect on SAR (1) model performance no matter whether the noise is considered. Figure 8 plots the observed and predicted inflows hydrographs by the SAR, SSA-SAR and modified SSA-SAR models, respectively. It can be seen that the prediction curves are relatively gentle. All predicted inflows can fit the dynamic changing regularity of monthly inflows in a year. But from the inter-annual scale to analyze the forecast results of each month, the predicted inflows are close to average values. The main reason is that the error term in SAR (1) model is thought to obey normal distribution.

Table 5 Performance results of the SAR, SVM and GP models for TGR
Full size table
Fig. 8
figure 8

Observed and predicted inflow hydrographs by the SAR, SSA-SAR and modified SSA-SAR models during testing period

Full size image

5.4 Inflow prediction by SVM model

This paper adopted the grid search method to obtain the values of C and ε and the search space of parameters is C ∈ (2−1, 28), ε ∈ (2−5, 2−1), respectively. The σ value is important in RBF and can lead to under fitting and over fitting in prediction (Noori et al. 2011). It has a default value in Statistica software equal to 1/k, where k is the number of input variables. So the search space of σ is (0, 2) and a lager σ is chosen initially and successively reduced to obtain better SVM model outputs. The best fitting σ value can be obtained by trial and error. The optimal parameters of SVM models are calculated and summarized in Table 6.

Table 6 Parameter values of the SVM model
Full size table

Table 5 lists the performances of SVM models. When the model input is original series, the accuracy of SVM model during the testing period is unsatisfactory. The NS and WB indexes are 0.77 and 0.96, respectively. The values of REmax and REmin are more than 20 %. When the filtered series is used as model input, a significant improvement of SSA-SVM model performance is obtained. While the best performance is the modified SSA-SVM model which considers the influence of noise series. The NS index increases from 0.89 to 0.96, while the WB index rises from 0.9 to 0.96, which is closer to 1. The relative prediction errors of maximum and minimum inflows decline significantly. The values of REmax and REmin are only 13 and 12 % during the test period. Meanwhile, Fig. 9 plots the observed and simulated inflow hydrographs by the SVM, SSA-SVM and modified SSA-SVM models, respectively. It also demonstrates that the inflows hydrograph predicted by the modified SSA-SVM model fits the observed inflows best, and the predicted peak inflows are much closer to the observed values than other models.

Fig. 9
figure 9

Observed and predicted inflow hydrographs by the SVM, SSA-SVM and modified SSA-SVM models during testing period

Full size image

5.5 Inflow prediction by GP model

Before using GP model to predict the inflow, genetic operators and their rates have to be set. Wang et al. (2012) suggested that the population size (Psize) is set to be a value between 150 and 300, a high crossover probability (Pc) is chosen between 0.5 and 0.8, and a low mutation probability (Pm) is often chosen between 0.001 and 0.1. As long as the parameters values are in these ranges, parameters sensitivities on the results are weak. In this study, the parameters are selected as follows: population size  =  250, the number of offspring in a generation = 500, reproduction rate = 0.05, crossover rate = 0.5 and mutation rate = 0.05. The stopping criterion is 5 min of processing time on an Intel Core 2.33 GHz computer.

Once the GP model was built, the antecedent twelve inflows were used as inputs to train the model in the evolutionary process firstly. Nevertheless, not all of the input variables survived during final selection. The simplified function form of the GP model for the original inflow series is expressed by

$$ x_{13} = \left( {x_{1} + x_{1}^{1/2} x_{3}^{ - 3/8} x_{5}^{1/16} x_{7}^{ - 5/8} x_{12} + x_{12}^{1/4} } \right)x_{5}^{ - 1/4} x_{7}^{ - 1/2} + x_{1}^{1/4} x_{3}^{1/4} x_{12}^{1/2} , $$
(21)

where x1,…,x12 are the antecedent twelve inflow values and x13 is the next period inflow value.

The simplified function form of the SSA-GP model for the filtered inflow series is expressed by

$$ x_{{13,f}} = \left( {2^{{ - \frac{1}{{16}}}} x_{{2,f}}^{{\frac{7}{{16}}}} x_{{11,f}}^{{ - \frac{1}{{32}}}} + \left( {x_{{2,f}} + x_{{4,f}} + x_{{12,f}} + x_{{12,f}} \left( {x_{{10,f}}^{{\frac{1}{8}}} x_{{11,f}}^{{\frac{1}{4}}} x_{{12,f}}^{{\frac{1}{4}}} + x_{{12,f}}^{{\frac{1}{2}}} } \right)^{{^{{\frac{1}{2}}} }} } \right)/x_{{11,f}} } \right)x_{{12,f}}^{{\frac{1}{2}}} $$
(22)

where x1, f ,…, x12, f are the antecedent twelve filtered inflow values and x13, f is the next period filtered inflow value.

When the noise series is considered, the simplified function form for the noise modeled by GP model is

$$ x_{4, n} = - \frac{13}{9}x_{3, n} - \frac{4}{3}x_{2, n} - \frac{2}{3}x_{1, n} $$
(23)

where x1,n ,…,x3,n are the antecedent three noise values and x4,n is the next period noise value.

The filtered and noise series are predicted by the above equations. The performances of GP models during training and testing periods were listed in Table 5. Meanwhile, Fig. 10 plots the observed and predicted inflows hydrographs by the GP, SSA-GP and modified SSA-GP models.

Fig. 10
figure 10

Observed and predicted inflow hydrographs by the GP, SSA-GP and modified SSA-GP models during testing period

Full size image

As shown in Table 5, the GP model performs poorly, with a small NS value (0.71) during the testing period and REmin values (55 and 46 %) during training and testing periods, respectively. The SSA-GP model performs well, with NS, WB, REmax and REmin values of 0.9, 1.01, 15 and 14 %, respectively during testing period. But the modified SSA-GP model performs best with high model efficiency and small relative errors. Compare with SSA-GP model, the values of NS increase from 0.92, 0.90 to 0.97, and 0.96 during the training and testing periods, respectively. The values of REmax decrease from 15 to 8 % during testing period. Figure 8 shows that the peak inflows predicted by the modified SSA-GP model are much closer to the observed inflows, and the change tendency is also identical with that of observed values.

5.6 Comparative analysis

There are some similarities in these three models. As observed from Table 5, the models perform well during training period. The main reason is that the training data has a large size (119 years) which allows models to be trained very well. The performances of these models during non-flood season are superior to that during flood season. This is because the runoff is mainly produced by rainfall during flood season, while the factors influencing runoff during non-flood season are stable. Since heavy rainfall is a random variable, so flood event also is a random variable which is hard to be simulated and predicted.

With the help of SSA, SSA-SVM and SSA-GP models which have excellent generalization ability perform much better than SSA-SAR (1) model. The filtered series exhibits more obvious trend or periodic signals and has better regularity. Using the filtered series as model inputs, the training data and testing data can have more similar patterns. So the results from the extrapolation are more reliable and accuracy can be significantly improved. When the noise is considered, it brings about a significant improvement of SVM and GP models performance, particularly in simulation of peak discharges and low flows. The explanation of this phenomenon is that the peak discharges and low flows are less frequently occurred in the observed inflow series. Thus they do not represent the main trend and periodic signals, and can be regarded as noise when the original series is decomposed into filtered and noise series.

Compare the modified SSA-SVM model with the modified SSA-GP model, their NS values are same, but the former performs better than the latter at low flows with small REmin values. The modified SSA-GP model is superior slightly to the modified SSA-SVM model at peak discharges with small REmax values. In addition, there is an obvious strength in GP model that it can reveal the relationship between the input and output by explicit mathematical formulations, while SVM is a black-box model where the inputs and outputs are known.

Flood forecasting has an important impact on reservoir flood control and utilization operation. Table 7 lists the predicted inflows by three modified models during flood season in testing period. The qualified rate α suggested by the Ministry of Water Resources of China (MWR 2000) is used to measure the forecasting errors of flood discharges. It is defined as the percentage rate that the forecasting relative errors of flood discharges is within a permitted error ε p (e.g. ±20 % in Chinese practice). Three grade levels (Grades A–C) for flood forecasting are classified according to the value of α as illustrated in Table 8. It is observed from Table 7 that the qualified rates of modified SSA-SVM model and modified SSA-GP model are 95 and 90 %, respectively. That means that the forecast levels have reached the Grade A, and the predicted inflows can be used in reservoir operation and management. But the qualified rate of modified SSA-SAR (1) model is only 58 %, which indicates that the model cannot be used in practice.

Table 7 The predicted inflows by three modified models in flood season during testing period
Full size table
Table 8 Forecast accuracy grade levels specified by MWR
Full size table

6 Conclusion

Singular spectrum analysis is a data-preprocessing method, decomposing the original series into the filtered and noise series. Current application of SSA only selects filtered series as model input without considering noises. The main contribution of this study was to propose a new method that considerers both filtered and noises series and prove that noise contains hydrological information and cannot be ignored. Owing to spatial confined, the boundary bias issue in SSA was not considered in this paper. All the oscillations detected are modulated by SSA at the end of the time series due to a lack of data beyond the time series. This will result in many estimates having much worse bias near the boundary than in the interior and affecting model performance. Some techniques can deal with the boundary bias problem, such as the reflection, replication, and transformation techniques. These will be the focuses in our future research.

In this paper, the TGR was adopted as case study, SAR (1), SVM and GP models were chosen as forecasting models, and four criteria were selected to evaluate the performance of various models. Main findings are as follows.

  1. (1)

    The window length in SSA has a crucial influence on the improvement of model performances. In previous studies, the related selection methods are based on empirical criteria. To determine the appropriate window length, this paper developed a quantitative method that assumes the range of window lengths and selects the possible values one by one. The model accuracy under each window length can be calculated successively and the optimal window length can be identified through the performance of models in terms of RMSE. The result produced by this method is more reliable.

  2. (2)

    The performance of the SAR (1), SVM and GP models show that the forecasting accuracy in terms of four evaluation measures during the testing period are inferior to the accuracy during the training period. With the help of SSA, the performance of SVM and GP models significantly increase, while there is no obvious positive change in performances of SAR (1) models.

  3. (3)

    No matter which the window length is, the slight positive relativity between the original series and noise always exists, which indicates that the noise still contains some information. In order to improve model performance, the noise should be considered. It is proved by the result that the modified SSA-SVM and SSA-GP models perform better than SSA-SVM and SSA-GP during training and testing periods, particularly for maximum monthly inflows.

In summary, the current application of SSA in hydrology which only selects the filtered series as model input should be improved. The modified SSA-SVM and SSA-GP models are both promising in modeling monthly inflow data series and can be used as tools for middle and long-term hydrological prediction. The proposed methodology in this study may prove valuable for researchers who are interested in using SSA to predict time series.