Spatio-temporal analysis and derivation of copula-based intensity–area–frequency curves for droughts in western Rajasthan (India)

Abstract

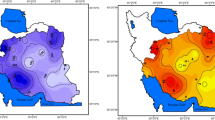
This study presents spatio-temporal analysis of droughts in one of the most drought prone region in India–western Rajasthan and develops drought intensity-area-frequency curves for the region. The meteorological drought conditions are analyzed using 6-month standardized precipitation index (SPI-6) estimated at spatial resolution of 0.5° × 0.5°. Spatio-temporal analysis of SPI-6 indicates increase in frequency of droughts at the central part of the region. The non-parametric Mann–Kendall test for seasonal trend analysis showed increase in number of grids under drought during the study period. Further, bivariate frequency analysis of drought characteristics—intensity and areal extent is carried out using copula methods. For modeling joint dependence between drought variables, three copula families namely Gumbel-Hougaard, Frank and Plackett copulas are evaluated. Based on goodness-of-fit as well as upper tail dependence tests, it is found that the Gumbel-Hougaard copula best represents the drought properties. The copula-based joint distribution is used to compute conditional return periods and drought intensity–area–frequency (I–A–F) curves. The I–A–F curves could be helpful in risk evaluation of droughts in the region.

Appendix

1.1 Mann–Kendall test

The most popular non-parametric test to detect trends in hydroclimatic variables is the Mann–Kendall (MK) test (Mann 1945; Kendall 1975), which evaluates randomness of the data against trend. The null hypothesis$H_{0}$ for this test assumes that no temporal trend exists, and the alternate hypothesis H ₁ assumes that a significant temporal trend (upward or downward) exists.

The test statistic Z _MK is computed as,

$$ Z_{MK} = \left\{ \begin{gathered} \;\frac{S - 1}{{\sqrt {Var\left( S \right)} }}\quad if\;S > 0; \hfill \\ \;0,\quad if\;S = 0; \hfill \\ \;\frac{S + 1}{{\sqrt {Var\left( S \right)} }}\quad if\;S < 0 \hfill \\ \end{gathered} \right. $$

(17)

where S is defined by,

$$ S = \sum\limits_{k = 1}^{n - 1} {\sum\limits_{j = k + 1}^{n} {\text{sgn} \left( {x_{j} - x_{k} } \right)} } ,\quad \text{sgn} \left( {x_{j} - x_{k} } \right) = \left\{ \begin{gathered} 1,\quad if\;(x_{j} - x_{k} ) > 0 \hfill \\ 0,\quad if\;(x_{j} - x_{k} ) = 0 \hfill \\ - 1,\quad if\;(x_{j} - x_{k} ) < 0 \hfill \\ \end{gathered} \right. $$

(18)

where x _j and x _k are the data points in time periods j and k ($j > k$) respectively, and n is number of observed data points. According to Kendall (1975) for n ≥ 10, the test statistic S is approximately normally distributed with the mean of E(S) = 0, and the variance of,

$$ Var\left( S \right) = \frac{1}{18}\left[ {n\left( {n - 1} \right)\left( {2n + 5} \right) - \sum\limits_{i = 1}^{g} {t_{i} \cdot (i) \cdot \left( {i - 1} \right) \cdot \left( {2i + 5} \right)} } \right] $$

(18)

where g is the number of tied groups and t _i is the number of data points in the i-th group. Later, it was also noted that a correction factor ($\eta$) should be incorporated in Var(S) to correct the influence of serial correlation on the test (Hamed and Rao 1998). The modified variance Var ^*(S) is given by,

$$ Var^{*} \left( S \right) = Var\left( S \right) \cdot \eta ,\;\eta \; = \;1 + \frac{2}{{n\left( {n - 1} \right)\left( {n - 2} \right)}} \times \sum\limits_{i = 1}^{n - 1} {1\left\{ {\left| {\rho_{S} (i)} \right| \ge \rho_{\alpha }^{*} } \right\}} \times \left[ {\left( {n - i} \right)\left( {n - i - 1} \right)\left( {n - i - 2} \right)\rho_{S} \left( i \right)} \right] $$

(19)

where $\rho_{S} \left( i \right)$ is the autocorrelation corresponding to ith lag of ranks of the observations (i = 1, 2,…up to $\left\lfloor {{n \mathord{\left/ {\vphantom {n 4}} \right. \kern-0pt} 4}} \right\rfloor$ lags); $\rho_{\alpha }^{*}$ is confidence interval of auto-correlation at significance level of α which is approximately $\pm \frac{2}{\sqrt n }$ at α = 0.05; $1\left\{ \Uptheta \right\}$ is a logical indicator function of set $\Uptheta$ and taking the value of either 0 (if $\Uptheta$ is false) or 1 (if $\Uptheta$ is true). Hence, the modified MK test statistics is given as

$$ Z_{MK}^{*} = \frac{{Z_{MK} }}{\sqrt \eta } $$

(20)

For seasonal Mann–Kendall test, the statistics S _i for each time period are summed to form the overall test statistic S _seasonal and $Var^{*} \left( {S_{i} } \right)$ is computed across m season by summing individual seasonal variance (Hirsch et al. 1982)

$$ S_{seasonal} = \sum\limits_{i = 1}^{m} {S_{i} } $$

(21)

$$ Var^{*} \left( {S_{seasonal} } \right) = \sum\limits_{i = 1}^{m} {Var^{*} \left( {S_{i} } \right)} $$

(22)

Corresponding test statistic Z_MK is computed using Eq. 17.

In a two-tailed test for trend at significance level of α, $H_{0}$ should be rejected, if $\left| {Z_{MK}^{*} } \right| > Z_{critical}$ (i.e., accept alternate hypothesis that significant trend exists in the time series), where $Z_{critical} \; = \;Z_{{{{1 - \alpha } \mathord{\left/ {\vphantom {{1 - \alpha } 2}} \right. \kern-0pt} 2}}}$ at significance level α. At α = 0.05 and 0.10, the values of standard normal variate $Z_{{{{1 - \alpha } \mathord{\left/ {\vphantom {{1 - \alpha } 2}} \right. \kern-0pt} 2}}}$ are 1.96 and 1.64 respectively. Hence in the time series (at significance level of α), an upward trend exits if $Z_{MK}^{*}$ > $Z_{critical}$, and decreasing trend exists if $Z_{MK}^{*}$ < $- Z_{critical}$.

1.2 Sen’s slope estimator

If a trend exists in a time series then the slope (change per unit time) can be estimated by a simple nonparametric procedure developed by Sen (1968). The method to estimate Sen’s slope estimator is described below.

• The slope estimates (say b _i ) of N pairs of data are first computed by,

$$ b_{i} = \frac{{\left( {x_{j} - x_{k} } \right)}}{j - k},\quad i \, = 1,{ 2}, \, \ldots ,N,{\text{ and }}j > k $$

(23)

where x _j and x _k are the data points in time periods j and k ($j > k$) respectively. Here, if there are n values of data in the time series, it results in as many as N = ⁿC₂ number of slope estimates (i.e., b _i values).

• Then, the Sen’s slope estimator (b _np ) is the median of those N number of b _i values:

$$ b_{np} = \left\{ \begin{gathered} b_{{{{(N + 1)} \mathord{\left/ {\vphantom {{(N + 1)} 2}} \right. \kern-0pt} 2}}} ,\quad {\text{if}}\,N\;{\text{is}}\;{\text{odd}} \hfill \\ \,\frac{1}{2}\left( {b_{{{N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}}} + b_{{{{(N + 1)} \mathord{\left/ {\vphantom {{(N + 1)} 2}} \right. \kern-0pt} 2}}} } \right),\quad {\text{if}}\,N\;{\text{is}}\;{\text{even}} \hfill \\ \end{gathered} \right. $$

(24)