Combining climate model output via model correlations

Abstract

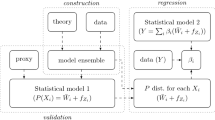
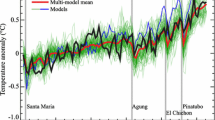
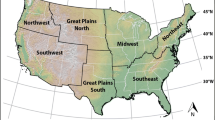
In climate science, collections of climate model output, usually referred to as ensembles, are commonly used devices to study uncertainty in climate model experiments. The ensemble members may reflect variation in initial conditions, different physics implementations, or even entirely different climate models. However, there is a need to deliver a unified product based on the ensemble members that reflects the information contained in whole of the ensemble. We propose a technique for creating linear combinations of ensemble members where the weights are constructed from estimates of variation and correlation both within and between ensemble members. At the heart of this approach is a Bayesian hierarchical model that allows for estimation of the correlation between ensemble members as well as the study of the impact of uncertainty in the parameter estimates of the hierarchical model on the weights. The approach is demonstrated on an ensemble of regional climate model (RCM) output.

Appendix

The form for S _ϕ  = V ⁻¹(ϕ) in (4) was assumed to be induced by a type of Markov random field, a spatial statistical model ideal for gridded or lattice type spatial observations (Rue and Held 2005). The essential idea behind such models is the characterization of the spatial dependence through the specification of conditional distributions that link the observation at each spatial location on the lattice to its neighbors. The collection of conditional distributions effectively leads to the specification of the joint precision matrix (inverse covariance matrix) for all of the locations on the grid or lattice.

Assuming Gaussian conditional distributions, these conditional autoregressive (CAR) models are specified through the conditional mean and variance. A very simple specification of the mean and variance are given by

$$ \hbox{E}[y_i|{{\mathbf{Y}}}_{-i}] = \mu_i + \phi \sum_{j\in N_i} (y_j-\mu_j) \qquad \hbox{Var}[y_i|{{\mathbf{Y}}}_{-i}] = \sigma^2, \quad i=1,\ldots, n, $$

(8)

where Y = [y ₁,…,y _n ], Y _−i indicates all of the elements of Y except the ith one, N _i denotes a collections of indices representing the neighbors of the ith location on the lattice, and ϕ is a partial or conditional correlation between two neighbors. This collection of conditional distributions can be shown to lead to joint Gaussian distribution with mean ${\varvec{\mu}}=[\mu_1,\ldots,\mu_n]$ and with covariance matrix ${\varvec{\Upsigma}} = \sigma^2({{\mathbf{I}}}_n - \phi{\mathbf {C}})^{-1}$ with I _n the n × n identity matrix and C the n × n incidence matrix determined by the neighborhood structures {N _i }.

The choice of neighborhoods often plays a crucial role in the behavior of CAR models. For example, in the simple specification in (8), one might simply choose neighbors as grid boxes that share an edge. The version of a Markov random field model used in this work follows a Kronecker form between the precision matrices for two one-dimensional processes, both indexed by the dependence parameter ϕ with one process for the rows and the other for the columns of the output grid for the climate models (see Sain et al. 2008b). Specifically, the conditional means and variances for interior grid boxes are given by

$$ \begin{aligned} \hbox{E}[y_{i}|{{\mathbf{Y}}}_{-i}] &= \mu_{i} + \frac{\phi}{1+\phi^2} \sum_{j \in N_{1i}} (y_{j} - \mu_{j}) - \left(\frac{\phi}{1+\phi^2}\right)^2 \sum_{j \in N_{2i}} (y_{j} - \mu_{j})\\ \hbox{Var}[y_{i}|{{\mathbf{Y}}}_{-i}] &= \sigma^2 \frac{1}{(1+\phi^2)^2},\\ \end{aligned} $$

where N _1i and N _2i represents indices for neighboring grid boxes that share an edge or vertices, respectively. (Note that the specification for boundary and corner grid boxes are slightly different; see Sain et al. 2008b, for details.) While this formulation is more complex, the (unconditional) spatial covariance structure is stationary (which the formulation in (8) lacks) and the additional neighbors gives more smoothness to the spatial fields.

Finally, it is important to note that the specification of these models defines the inverse of the covariance matrix, typically referred to as the precision matrix. Furthermore, the precision matrix is generally a sparse matrix. Hence, one can dramatically improve computational performance of the statistical model for large spatial grids, both in terms of the storage of the precision matrix and the linear algebra computations associated with computing the likelihood (see also Furrer and Sain 2009).