Steady flows driven by sources of random strength in heterogeneous aquifers with application to partially penetrating wells

Abstract

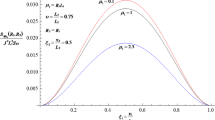
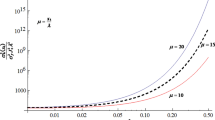
Average steady source flow in heterogeneous porous formations is modelled by regarding the hydraulic conductivity K(x) as a stationary random space function (RSF). As a consequence, the flow variables become RSFs as well, and we are interested into calculating their moments. This problem has been intensively studied in the case of a Neumann type boundary condition at the source. However, there are many applications (such as well-type flows) for which the required boundary condition is that of Dirichlet. In order to fulfill such a requirement the strength of the source must be proportional to K(x), and therefore the source itself results a RSF. To solve flows driven by sources whose strength is spatially variable, we have used a perturbation procedure similar to that developed by Indelman and Abramovich (Water Resour Res 30:3385–3393, 1994) to analyze flows generated by sources of deterministic strength. Due to the linearity of the mathematical problem, we have focused on the explicit derivation of the mean head distribution G _d (x) generated by a unit pulse. Such a distribution represents the fundamental solution to the average flow equations, and it is termed as mean Green function. The function G _d (x) is derived here at the second order of approximation in the variance σ² of the fluctuation $\varepsilon \left({{\mathbf{x}}}\right) = 1- \frac{K{\left({{\mathbf{x}}}\right)}}{K_{A}}$ (where K _A is the mean value of K(x)), for arbitrary correlation function ρ(x), and any dimensionality d of the flow domain. We represent G _d (x) as product between the homogeneous Green function G ⁽⁰⁾ _d (x) valid in a domain with constant K _A , and a distortion term Ψ _d (x) = 1 + σ²ψ _d (x) which modifies G ⁽⁰⁾ _d (x) to account for the medium heterogeneity. In the case of isotropic formations ψ _d (x) is expressed via one quadrature. This quadrature can be analytically calculated after adopting specific (e.g.. exponential and Gaussian) shape for ρ(x). These general results are subsequently used to investigate flow toward a partially-penetrating well in a semi-infinite domain. Indeed, we construct a σ²-order approximation to the mean as well as variance of the head by replacing the well with a singular segment. It is shown how the well-length combined with the medium heterogeneity affects the head distribution. We have introduced the concept of equivalent conductivity K ^eq(r,z). The main result is the relationship $\frac{K^{\rm eq}\left(r,z\right)} {K_{A}} = 1-\sigma^{2}\psi^{\left(w\right)}\left(r,z\right)$ where the characteristic function ψ^(w)(r,z) adjusts the homogeneous conductivity K _A to account for the impact of the heterogeneity. In this way, a procedure can be developed to identify the aquifer hydraulic properties by means of field-scale head measurements. Finally, in the case of a fully penetrating well we have expressed the equivalent conductivity in analytical form, and we have shown that $K^{({\rm efu})}\leq K^{\rm eq}\left(r\right) \leq K_{A}$ (being $K^{({\rm efu})}$ the effective conductivity for mean uniform flow), in agreement with the numerical simulations of Firmani et al. (Water Resour Res 42:W03422, 2006).

Appendices

Appendix A: Derivation of the mean Green function

The mean Green function results from the first of Eq. (11a) as G _d (x) = G ⁽⁰⁾ _d (x) + σ² G ⁽²⁾ _d (x), being G ⁽⁰⁾ _d (x) = FT⁻¹[k ⁻²]. The second order correction G ⁽²⁾ _d (x) is expressed as difference (see the first of (12)) between G ⁽²⁾ _d,q (x), which accounts for a flux-type condition, and G ⁽²⁾ _d,h (x) that adjusts the previous one to satisfy the condition of given head. The terms G ⁽²⁾ _d,q (x) and G ⁽²⁾ _d,h (x) are calculated as follows:

$$ G_{d,q}^{\left(2\right)}\left({{\mathbf{x}}}\right) =\hbox{FT}^{-1} \left[{\widetilde{g}}\left({{\mathbf{k}}}\right) {\widetilde{G}}_{d}^{\left(0\right)}\left(k\right) \right] \qquad G_{d,h}^{\left(2\right)}\left({{\mathbf{x}}}\right) = \hbox{FT}^{-1}\left[{\widetilde{s}}\left({{\mathbf{k}}}\right) {\widetilde{G}}_{d}^{\left(0\right)}\left(k\right) \right]. $$

(68)

The problem is therefore reduced to compute the inverse (68) with ${\widetilde{g}}\left({{\mathbf{k}}}\right)$ and ${\widetilde{s}}\left({{\mathbf{k}}}\right)$ given by (11b). The correction G ⁽²⁾ _d,q (x) was derived by Indelman (2001), and we recall it for the sake of completeness

$$ G_{d,q}^{\left(2\right)}\left({{\mathbf{x}}}\right) = \frac{G_{d}^{\left( 0\right)}\left(x\right)}{d}+ \frac{d} {2} \int\limits_{\Upomega_{\left(d\right)}}d {{\mathbf{x}}}^{\prime}\rho \left({{\mathbf{x}}}^{\prime}\right) \left\vert {{\mathbf{x}}}- {{\mathbf{x}}}^{\prime}\right\vert^{2}\left[\left(\frac{x^{\prime 2}-\cdot {{\mathbf{x}}}^{\prime}}{x^{\prime}\left\vert {{\mathbf{x}}}- {{\mathbf{x}}}^{\prime}\right\vert}\right)^{2}-\frac{1} {d}\right] {\overline{\overline{G}}}_{d}^{\left(0\right)}\left(x^{\prime}\right) {\overline{\overline{G}}}_{d}^{\left(0\right)}\left(\left\vert {{\mathbf{x}}}-{{\mathbf{x}}}^{\prime}\right\vert \right) $$

(69)

where ${\overline{\overline{G}}}_{d}^{\left(0\right)}\left(x^{\prime}\right)$ is defined by (19). Instead, the explicit expression of the term G ⁽²⁾ _d,h (x) is presented here for the first time.

In order to calculate G ⁽²⁾ _d,h (x) we make use of the second of (13), i.e.,

$$ G_{d,h}^{\left(2\right)}\left({{\mathbf{x}}}\right) =\int\limits_{\Upomega_{\left(d\right)}}d{{\mathbf{x}}}^{\prime}s\left({{\mathbf{x}}} ^{\prime}\right) G_{d}^{\left(0\right)}\left(\left\vert {{\mathbf{x}}}-{{\mathbf{x}}}^{\prime}\right\vert \right). $$

(70)

Then, substituting (15) into (70) leads (after integrating by parts) to

$$ G_{d,h}^{\left(2\right)}\left({{\mathbf{x}}}\right) =-\int\limits_{\Upomega_{\left(d\right)}}d{{\mathbf{x}}}^{\prime}\rho \left({{\mathbf{x}}}^{\prime}\right) \frac{\partial}{\partial x_{m}^{\prime}}G_{d}^{\left(0\right)}\left(x^{\prime}\right) \left[\frac{\partial}{\partial y_{m}}G_{d}^{\left(0\right)}\left(y\right) \right]_{y=\left\vert {{\mathbf{x}}}-{{\mathbf{x}}}^{\prime}\right\vert}. $$

(71)

By noting that $\frac{\partial}{\partial x_{m}} = \frac{x_{m}} {x} \frac{d}{dx},$ one has

$$ G_{d,h}^{\left(2\right)}\left({{\mathbf{x}}}\right) =\int\limits_{\Upomega_{\left(d\right)}}d{{\mathbf{x}}}^{\prime}\rho \left({{\mathbf{x}}}^{\prime}\right) \left(x^{\prime 2}-{{\mathbf{x}}}\cdot {{\mathbf{x}}}^{\prime}\right) \frac{\overline{\overline{G}}_{d}^{\left(0\right)}\left(x^{\prime}\right)} {x^{\prime}} \frac{{\overline{\overline{G}}}_{d}^{\left(0\right)}\left(\left\vert {{\mathbf{x}}}- {{\mathbf{x}}}^{\prime}\right\vert \right)}{\left\vert {{\mathbf{x}}}-{{\mathbf{x}}}^{\prime}\right\vert}. $$

(72)

Finally, dividing (69) and (72) by G ⁽⁰⁾ _d (x) leads to (18a), (18b).

Appendix B: Derivation of the second-order correction in the case of a fully penetrating well

By letting Δ → ∞ in (48) one has

$$ \left\langle h_{2}\left(r\right) \right\rangle = \frac{-b} {6\pi} \left[\alpha +\ln \frac{r}{2} + \frac{1} {2} \int\limits_{0}^{\infty}d\zeta \Upupsilon \left(\zeta^{2}+r^{2}\right) \right], $$

(73)

with ${\Upupsilon} \left(x\right)$ given by (43). It is convenient to represent the integral appearing into (73) as $\int\limits_{0}^{\infty}d\zeta {\Upupsilon} \left(\zeta^{2}+r^{2}\right) ={{\mathcal{I}}}_{1}\left(r\right) -{{\mathcal{I}}}_{2}\left(r\right),$ being

$$ {{\mathcal{I}}}_{1}\left(r\right) =\left\{\begin{array}{ll}\int\limits_{0}^{\infty}d\zeta \left(\frac{2} {\sqrt{\zeta^{2}+r^{2}}} + \sqrt{\zeta^{2}+r^{2}}-1\right) \exp \left(-\sqrt{\zeta^{2}+r^{2}}\right) & \hbox{exponential} \\ \\ \int\limits_{0}^{\infty}d\zeta \left(\frac{2}{\sqrt{\zeta^{2}+r^{2}}}-\pi \sqrt{\zeta^{2}+r^{2}}\right) \exp \left[-\frac{\pi} {4}\left(\zeta^{2}+r^{2}\right) \right] & \hbox{Gaussian} \end{array}\right. $$

(74)

and

$$ {{\mathcal{I}}}_{2}\left(r\right) =\left\{\begin{array}{ll} \int\limits_{0}^{\infty}d\zeta \left(\zeta^{2}+r^{2}\right) \hbox{Ei} \left(-\sqrt{\zeta^{2}+r^{2}}\right) & \hbox{exponential}\\\\ \frac{\pi^{2}}{2} \int\limits_{0}^{\infty}d\zeta \left(\zeta^{2}+r^{2}\right) \hbox{erfc}\left[\frac{1}{2}\sqrt{\pi \left(\zeta^{2}+r^{2}\right)} \right] & \hbox {Gaussian}. \end{array}\right. $$

(75)

In order to evaluate ${{\mathcal{I}}}_{1}\left(r\right)$ we introduce the new variable $u=\sinh^{-1}\left(\frac{\zeta}{r}\right)$ so that it yields ${{\mathcal{I}}}_{1}\left(r\right) =\exp \left(-\frac{\pi} {8} r^{2}\right) \left[\left(1-\frac{\pi}{4}r^{2}\right) {\hbox{K}}_{0}\left(\frac{\pi}{8}r^{2}\right) - \frac{\pi}{4}r^{2} {\hbox{K}}_{1}\left(\frac{\pi}{8}r^{2}\right) \right]$ (e.g., Gradshteyn and Ryzhik 1965) for Gaussian, and ${{\mathcal{I}}}_{1}\left(r\right) =\left(2+r^{2}\right) {\hbox{K}}_{0}\left(r\right)$ (e.g., Gradshteyn and Ryzhik 1965) for exponential autocorrelation.

To calculate ${{\mathcal{I}}}_{2}\left(r\right)$ we first integrate (75) by parts

$$ {{\mathcal{I}}}_{2}\left(r\right) =\left\{\begin{array}{ll}-\frac{1} {3} \int\limits_{0}^{\infty}d\zeta \frac{3 r^{2}+\zeta^{2}} {\zeta^{2}+r^{2}} \zeta^{2}\exp \left(-\sqrt{\zeta^{2}+r^{2}}\right) & \hbox{exponential} \\ \\ \frac{\pi^{2}} {6} \int\limits_{0}^{\infty}d\zeta \frac{3 r^{2}+\zeta^{2}} {\sqrt{\zeta^{2}+r^{2}}} \zeta^{2}\exp \left[-\frac{\pi} {4} \left(\zeta^{2}+r^{2}\right) \right] & \hbox{Gaussian}. \end{array}\right. $$

(76)

Hence, by carrying out the quadratures in (76), and after some algebraic derivations (which we omit for brevity), one obtains (56)–(57).

Appendix C: Derivation of the head variance for a fully penetrating well

Starting from the general expression (58) of the head fluctuation, and by applying the method of images, the head variance for a fully-penetrating can be written as

$$ \begin{aligned} \sigma_{h}^{2}\left(r\right) &= \pi^{-1}\int \int \int\limits_{-\infty}^{+\infty} \int\limits_{-\infty}^{+\infty}d{{\mathbf{r}}}^{\prime}d{{\mathbf{r}}}^{\prime \prime} dz^{\prime}dz^{\prime \prime}{{\mathcal{G}}}\left({{\mathbf{x}}}^{\prime}; {{\mathbf{r}}}\right) {{\mathcal{G}}}\left({{\mathbf{x}}}^{\prime \prime};{{\mathbf{r}}} \right) \frac{\partial}{\partial x_{m}^{\prime}}h^{\left(0\right)}\left(r^{\prime}\right) \frac{\partial}{\partial x_{n}^{\prime \prime}} h^{\left(0\right)}\left(r^{\prime \prime}\right)\\ &\quad \times \frac{\partial^{2}}{\partial x_{m}^{\prime}\partial x_{n}^{\prime \prime}} \int\limits_{-\infty}^{+\infty}\int\limits_{-\infty}^{+\infty}dk^{\prime}dk^{\prime \prime}\exp \left[-j\left(k^{\prime}z^{\prime}+k^{\prime \prime} z^{\prime \prime}\right) \right] \left\langle {\widetilde{\varepsilon}} \left({{\mathbf{r}}}^{\prime}, k^{\prime}\right) {\widetilde{\varepsilon}} \left({{\mathbf{r}}}^{\prime \prime},k^{\prime \prime}\right) \right\rangle, \quad \left(m,n=1,2\right)\end{aligned} $$

(77)

being

$$ {{\mathcal{G}}}\left({{\mathbf{x}}};{\varvec{\alpha}}\right) = \frac{1} {4\pi} \left(\frac{1}{\sqrt{\left\vert {{\mathbf{x}}}_{h}- {\varvec{\alpha}}\right\vert^{2}+z^{2}}}- \frac{1} {\sqrt{x_{h}^{2}+z^{2}}}\right) \qquad {{\mathbf{x}}}\equiv \left({{\mathbf{x}}}_{h},z\right). $$

(78)

In Eq. (77) we have represented the fluctuation ɛ by means of its FT along the stationarity axis, i.e., $\varepsilon \left({{\mathbf{r}}}, z\right) =\int\limits_{-\infty}^{+\infty}\frac{dk}{\sqrt{2\pi }}\exp \left(-jkz\right) {\widetilde{\varepsilon}}\left({{\mathbf{r}}}, k\right).$ By using the stationarity property $\left\langle {\widetilde{\varepsilon}}\left({{\mathbf{r}}}^{\prime}, k^{\prime}\right) {\widetilde{\varepsilon}}\left({{\mathbf{r}}}^{\prime \prime},k^{\prime \prime}\right) \right\rangle =\sqrt{2\pi} \sigma^{2} \delta \left(k^{\prime}+k^{\prime \prime}\right) \widetilde{\rho}\left(\left\vert {{\mathbf{r}}}^{\prime}-{{\mathbf{r}}}^{\prime \prime}\right\vert, k^{\prime \prime}\right),$ and carrying out the quadratures over z′ and z″, one obtains

$$ \frac{\sigma_{h}^{2}\left(r\right)}{\sigma^{2}} =\int \int \int\limits_{0}^{\infty}\frac{d{{\mathbf{r}}}^{\prime}d{{\mathbf{r}}}^{\prime \prime}dk}{\left(2\pi \right)^{5/2}}{{\mathcal{K}}}_{k}^{r}\left ({{\mathbf{r}}}^{\prime}\right) {{\mathcal{K}}}_{k}^{r}\left({{\mathbf{r}}}^{\prime \prime}\right) \frac{\partial}{\partial x_{m}^{\prime}}h^{\left(0\right)}\left(r^{\prime}\right) \frac{\partial}{\partial x_{n}^{\prime \prime}}h^{\left(0\right)}\left(r^{\prime \prime}\right) \frac{\partial^{2}\widetilde{\rho}\left(\left\vert {\bf r}^{\prime}-{\bf r}^{\prime \prime}\right\vert ,k\right)}{\partial x_{m}^{\prime}\partial x_{n}^{\prime \prime}} $$

(79)

where ${{\mathcal{K}}}_{k}^{r}\left({\varvec{\alpha}}\right) = \hbox{K}_{0}\left(k\left\vert {\varvec{\alpha}}-{{\mathbf{r}}}\right\vert \right) -\hbox{K}_{0}\left(k\alpha \right).$ Noting that

$$ \frac{\partial^{2}{\widetilde{\rho}}\left(\left\vert {{\mathbf{r}}}^{\prime}- {\bf r}^{\prime \prime}\right\vert ,k\right)}{\partial x_{m}^{\prime}\partial x_{n}^{\prime \prime}} = \left. -\frac{\alpha_{m}\alpha_{n}}{\alpha^{2}} \frac{\partial^{2}} {\partial \alpha^{2}} {\widetilde{\rho}} \left(\alpha ,k\right) + \alpha^{-1}\left(\frac{\alpha_{m}\alpha_{n}} {\alpha^{2}} -\delta_{m,n}\right) \frac{\partial}{\partial \alpha} {\widetilde{\rho}} \left(\alpha ,k\right) \right\vert_{{\varvec{\alpha}} = {{\mathbf{r}}}^{\prime} - {{\mathbf{r}}}^{\prime \prime}}, $$

(80)

and accounting for $\frac{\partial}{\partial x_{m}}h^{\left(0\right)}\left(r\right) = \frac{x_{m}}{r}\frac{d} {dr} h^{\left(0\right)}\left(r\right),$ leads to

$$ \sigma_{h}^{2}\left(r\right) = \frac{\sigma^{2}}{\left(2\pi \right)^{5/2}} \int \int \int\limits_{0}^{\infty} \frac{d{{\mathbf{r}}}^{\prime} d{{\mathbf{r}}}^{\prime \prime}dk}{r^{\prime}r^{\prime \prime}}\frac{d} {dr^{\prime}} h^{\left(0\right)}\left(r^{\prime}\right) \frac{d} {dr^{\prime \prime}} h^{\left(0\right)}\left(r^{\prime \prime}\right) {{\mathcal{K}}}_{k}^{r}\left({{\mathbf{r}}}^{\prime}\right) {{\mathcal{K}}}_{k}^{r}\left({{\mathbf{r}}}^{\prime \prime}\right) {{\vartheta}}_{k}\left({{\mathbf{r}}}^{\prime}, {{\mathbf{r}}}^{\prime \prime}\right), $$

(81)

being the function ${{\vartheta}}_{k}\left({{\mathbf{r}}}^{\prime}, {{\mathbf{r}}}^{\prime \prime}\right)$ dependent on the shape of ρ, i.e.,:

$$ {{{\vartheta}}}_{k}\left({{\mathbf{r}}}^{\prime}, {{\mathbf{r}}}^{\prime \prime}\right) = \left. \frac{\overline{\chi}}{\alpha^{2}} \frac{\partial ^{2}}{\partial \alpha^{2}} {\widetilde{\rho}}\left(\alpha ,k\right) -\alpha ^{-1}\left({{\mathbf{r}}}^{\prime}\cdot {{\mathbf{r}}}^{\prime \prime}+ \frac{\overline{\chi}}{\alpha^{2}}\right) \frac{\partial}{\partial \alpha} {\widetilde{\rho}}\left(\alpha, k\right) \right\vert_{\alpha =\left\vert {{\mathbf{r}}}^{\prime}-{{\mathbf{r}}}^{\prime \prime}\right\vert} $$

(82)

$$ {\overline{\chi}} = \left(r^{\prime 2}-{{\mathbf{r}}}^{\prime}\cdot {{\mathbf{r}}} ^{\prime \prime}\right) \left(r^{\prime \prime 2}-{{\mathbf{r}}}^{\prime}\cdot {{\mathbf{r}}}^{\prime \prime}\right). $$

(83)

Finally, switching to polar coordinates ${{\mathbf{r}}}^{\prime}\equiv r^{\prime}\left(\cos \theta^{\prime},\sin \theta^{\prime}\right),$ and ${{\mathbf{r}}}^{\prime \prime}\equiv r^{\prime \prime}\left(\cos \theta^{\prime \prime},\sin \theta^{\prime \prime}\right)$ into (81) leads to (62).