Introduction

Relationships between tree rings and climate underpin environmental reconstructions (e.g., Cook et al. 2007) and eco-physical understanding of species’ stressors (e.g., Gazol et al. 2020), which are increasingly important in a warming climate (Pierce et al. 2018). Such foundational linkages are commonly based on samples from lower positions on trunks, most often at breast height (BH, 1.4 m), where long series from living trees are easily accessible from the ground. A growing body of evidence based both on stem analysis of dead trees (e.g., Zhang et al. 2020) and rope-based sampling of living trees (e.g., Ishii et al. 2017) points to the limitations of lower trunk samples for quantifying growth of whole trees. Biomass increments estimated by diameter changes at BH compared to measurements across the height gradient are generally biased for tall species (Sillett et al. 2015a, b, 2019a, 2020), suggesting that whole-trunk sampling may be necessary to characterize climate–growth relationships.

Tree-ring formation occurs as carbon is invested in various components (e.g., trunks, branches, roots) via xylogenesis, a dynamic process that involves both internal (e.g., hormones) and external (e.g., climate) controls during various phases of cell formation in the vascular cambium (De Micco et al. 2019). Climate influences growth via availability of resources (e.g., water) and rates and timing of physiological processes (e.g., temperature-influenced cambial reactivation, hormone concentrations; Fritts 1976; Vaganov et al. 2011; Begum et al. 2013; St. George 2014; Rathgeber et al. 2016). Climatic constraints on wood formation may differ along the main trunk due to factors such as phloem transport of sugars and hormones across long distances and increasing water stress with height above ground (Speer 2010; Kerhoulas and Kane 2012; Buttò et al. 2020). As trees grow taller, water entering via roots must be transported farther upward through the xylem to sustain photosynthesis and transpiration as gravity and friction resist its movement, diminishing stem turgor (Koch et al. 2004; Woodruff et al. 2004). In response to excessive water stress, trees close leaf stomata to stop transpiration (which curtails photosynthesis) and sustain stem turgor (McDowell et al. 2008; Peters et al. 2023). Radial growth is controlled by source limitations (i.e., availability of photosynthate) and by a tree’s inability to convert photosynthate to biomass when stem turgor is too low for cell division and enlargement in the vascular cambium (sink limitations; Körner 2015; Rathgeber et al. 2016). Both source and sink limitations are influenced by climate (Zweifel et al. 2021; Cabon et al. 2022).

Dendroclimatic sensitivity varies by trunk axial position, and, while the direction of relationships is generally consistent among heights, the nature of this variation is not uniform among species. For Pinus ponderosa, the relative strength of models explaining climatic parameters (temperature, drought, water year precipitation) based on radial increments declines with height from treetops (22 m) followed by base of live crown (10 m) then BH (Kerhoulas and Kane 2012). Stem analysis of 389 Pinus contorta shows that upper trunk radial increment is related to conditions during the year of growth (e.g., early summer temperature, late winter to early spring moisture), while lower trunk radial increment is related to conditions in prior seasons (Chhin et al. 2010). For Picea schrenkiana, relationships between radial increment and temperature are weaker at BH than upper positions to 20 m (Zhang et al. 2020). Assessment of Abies alba and Picea abies at three positions up to 16.7 m reveals that BH series are not comparably sensitive to climate, with species- and altitude-specific differences (van der Maaten-Theunissen and Bouriaud 2012). In addition to varying axial relationships for conifers, the angiosperm Fagus sylvatica shows climate-related differences in growth partitioning between the trunk and crown (Latte et al. 2016) and growth prioritization in the upper stem during drought conditions (Peters et al. 2020). Drought response of nine deciduous and coniferous species show inconsistencies along the main stem (up to 29 m) with less pronounced responses with increasing stem height for most species (Hoffmann et al. 2018).

Sequoiadendron giganteum (giant sequoia) is well-suited for investigation of dendroclimatic variation along the trunk given its extreme height (up to 96.5 m, Sillett et al. 2021), strong crossdating, and extensive dendrochronological history. Sequoiadendron is a foundational species of modern dendrochronology (Douglas 1919) known for generally complacent annual rings punctuated by strong, narrow marker years that support multi-millennial ring-width chronologies with regional coherence of signal (Brown et al. 1992). While radial increments show positive but not robust inter-annual correlations with growing season drought metrics (Carroll et al. 2014), prominent low-growth years correspond with extremely arid conditions and have been used to assess regional drought frequency over millennia (Hughes and Brown 1992). Inter-annual sensitivities also reveal consistent negative relationships between ring indices and maximum and minimum temperature in June (Carroll et al. 2014). These relationships make sense in the context of a species growing in wet geomorphic locations amid an overarching climate of cool, wet winters followed by warm, dry summers in California’s Sierra Nevada (Ray 2016). Sequoiadendron tree rings have been used to reconstruct snow water equivalent (SWE) as melting snow provides water during dry summer months (Touchan et al. 2021); while precipitation as snow, which may not fully reflect snowpack, lacked significant relationships (Wang et al. 2012; Carroll et al. 2014) and only 2–4% of precipitation falls after snowmelt (Sillett et al. 2019b).

As Sequoiadendron grows in drought-prone environments, it has several adaptations to alleviate water stress exacerbated by great height. Phenotypic plasticity of Sequoiadendron foliage exhibits environmental responsiveness whereby denser upper crown foliage is better able to withstand water stress via succulence, low surface area-to-volume ratios, and specialized leaf anatomy (Chin and Sillett 2016). A suite of leaf- and crown-level physiological mechanisms, including strong stomatal regulation, seasonal redistribution of leaf water, leaf toughening, and leaf shedding help Sequoiadendron maintain favorable water status during drought (Ambrose et al. 2015, 2018). These strategies likely contributed to the relatively low mortality rate of Sequoiadendron (albeit with unprecedented levels of foliage dieback; Stephenson et al. 2018) compared to other mixed conifers of the Sierra Nevada during the 2012–2016 hotter drought (Nydick et al. 2018). Although morphological, anatomical, and physiological adjustments allow Sequoiadendron to regulate water status (Ambrose et al. 2016), hydraulic limitations associated with great height may control carbon allocation and radial increments along the trunk.

The preponderance of dendrochronological study of Sequoiadendron has utilized ground-based sampling of increment cores from live trees or sections from dead trees. Targeting positions close to ground level increased the likelihood of accessing preserved fire scars and facilitated creation of a 3000-yr fire history (Swetnam et al. 2009). Fire-affected sections often show growth irregularities, and these were generally avoided for the SWE reconstruction (Touchan et al. 2021). Nevertheless, samples acquired near bases of large trees, even away from fire scars, can influence the expression of growth rings by virtue of irregular morphology. For example, Sequoia sempervirens (Carroll and Sillett 2023) and four eucalypt species (Brookhouse and Brack 2008) show reduced inter-series correlation at basal compared to upper trunk positions. As the largest tree species on Earth, lower trunks of Sequoiadendron can have highly irregular shapes with pronounced buttressing and fire caves (Sillett et al. 2019b) that may hinder expression of climate-induced ring-width variation.

Recent work on Sequoiadendron utilizing rope-based techniques for whole-trunk sampling permits spatially explicit assessment of this species. Initial sampling at six locations supported baseline ring-width chronologies, climatic sensitivity analysis, as well as quantification of tree age, biomass, and development (Carroll et al. 2014; Sillett et al. 2015b). Additional cores from the same trees (for biomass increment; Sillett et al. 2019b) as well as new trees (Sillett et al. 2021; Williams et al. 2021) increase replication and promote extension of millennial-length Sequoiadendron chronologies. Such chronologies fit within a rich chronicle for this species and can be assessed for their signal strength and regional coherence. Selection of trees with suitable within-trunk replication allows for appraisal of dendroclimatic relationships across the axial (trunk height) gradient. Given Sequoiadendron’s propensity for intermittent but prominent low-growth years, axial variation in the expression of such years is relevant to consider. Here we update and expand Sequoiadendron chronologies and investigate how dendroclimatic sensitivity and relative increments during low-growth years vary by height above the ground.

Methods

Tree selection and sampling

A total of 61 living Sequoiadendron from nine forest locations were studied from 2005–2020 for various research objectives (Carroll et al. 2014; Sillett et al. 2015b, 2019b, 2021; Williams et al. 2021; Tables 1 and S1). Locations spanned the 150 km2 geographic distribution of Sequoiadendron groves (Table 1), including the South Grove of Calaveras Big Trees State Park (CBT), Mariposa Grove in Yosemite National Park (MAR), Redwood Mountain Grove in Kings Canyon National Park (RMG), the adjacent Whitaker Forest managed by the University of California (WF), Giant Forest in Sequoia National Park (GF), Mountain Home Grove in Mountain Home Demonstration State Forest (MH), and Freeman Creek, Red Hill, and Alder Creek Groves in Giant Sequoia National Monument (FC, RH, AC). Sequoiadendron generally occupies wet topographic positions, including adjacent to perennial streams and meadows pooling water from granitic plateaus, though some trees were growing upland farther from surface water. All study locations (except AC) are further described elsewhere (see Sillett et al. 2015b, 2019b).

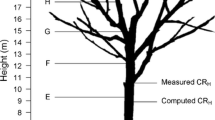
Table 1 Description of nine Sequoiadendron study locations sequenced from north to south
Full size table

Trees ranged from 26.1–96.5 tall (mean = 74.2 m), 39–814 cm fDBH (functional diameter at breast height, or diameter of a circle with equivalent area, mean = 409 cm), and 100–3298 yr old (mean 1077 yr, see Sillett et al. 2019b for description of age calculations beyond innermost crossdated rings), and most trees occupied dominant or co-dominant crown positions (Table S1). Increment cores were collected at regular intervals along main trunks, and positions above breast height (BH, 1.4 m) were accessed via free-hanging ropes. Generally, each height had 2 cores or 3–4 cores when trunk diameters exceeded 2 or 3 m, respectively. Irregularities (e.g., branch collars, fire occlusions) were avoided as much as possible, and cores were generally evenly spaced around the circumference. Trees at AC and RH had shallow cores at BH and top of buttress (TB), and deeper cores aiming for pith at 10-m increments from 10 m to treetop. Trees at MAR followed the same regimen but had no cores below 10 m. Five locations (CBT, RMG, GF, MH, FC) with 1-ha plots trees were regularly sampled from BH to treetop with some variation in collection height, and 21 of these trees were re-sampled at ~ 5-yr intervals near the original coring positions (Sillett et al. 2019b), providing series to update previously published chronologies (Carroll et al. 2014). Within-tree sampling at WF was most variable due to disparate research goals. Core sampling followed the dominant reiterated (i.e., resprouted) trunk toward treetop when applicable.

Crossdating and chronologies

Cores were dried, glued to wooden mounts, sanded with progressively finer grit (> 600), and inspected under a stereo microscope to discern ring boundaries. Ring widths were measured to 0.001 mm using WinDendro software (v.2009b, Régent Instruments Inc., Québec, Canada) with images at 1200 dpi from an EPSON Expression 10000XL scanner. Crossdating occurred by listing visual marker years with statistical validation via staggered correlation analysis using Cofecha software (Holmes 1983) and proceeded, first, among cores within a tree, then, between trees per location. Crossdating was categorized for all years following previously defined protocol (Carroll et al. 2014; Carroll and Sillett 2023) and differentiated between series with high and moderate confidence to identify sections with some ambiguity (e.g., Lorimer et al. 1999).

Due to intensive within-tree sampling, chronologies were generated for each of 61 trees and then combined accordingly for nine locations and one regional chronology. Tree chronologies included series with high confidence in crossdating and ≥ 30 yr length. Series were standardized to ring-width indices via ARSTAN (Cook 1985) using a cubic smoothing spline with a 50% frequency cutoff at 32 yr (32-yr spline) to remove geometric growth trends and low-frequency variation. Standard (STD) tree chronologies were combined into nine respective location chronologies and one composite chronology with no further detrending and used a biweight robust mean to reduce the influence of outliers (Cook and Kairiukstis 1990). Chronology statistics of rbar (mean between-tree or between-series correlation, as applicable) and expressed population signal (EPS) were calculated with dplR library in R (Bunn 2008; R Core Team 2023). EPS expresses signal strength, depends on sample depth and rbar, and has a commonly used threshold of 0.85 (Wigley et al. 1984). We used Sierra Nevada regional ring-width data spanning 23 locations from the International Tree-Ring Data Bank (CA726; Touchan et al. 2021) as a comparison for inter-annual variation to confirm crossdating. The 260 raw series from CA726 were detrended in the same manner described above to generate an analogous chronology. Staggered Pearson correlation analysis on overlapping 50-yr segments via Cofecha produced comparative statistics among chronologies.

Dendroclimatic relationships

Key climatic variables were selected based on previous study (Hughes and Brown 1992; Carroll et al. 2014; Touchan et al. 2021) and included June minimum temperature (Tmin), June maximum temperature (Tmax), a drought index, and snow water equivalent (SWE, amount of water in snowpack). We confirmed inter-annual relationships between location chronologies (STD) and climate using bootstrapped Pearson’s correlation analysis with the treeclim package in R (Zang and Biondi 2015).

For location-specific June Tmin and Tmax, we used 4-km monthly PRISM data (1900–present; PRISM Climate Group 2023, www.prism.oregonstate.edu, accessed 1 May 2023). All temperature records were detrended with a 32-yr spline to focus on inter-annual variation. For the location-specific drought index, we utilized standardized precipitation evapotranspiration index (SPEI) using a 12-month window ending in September. SPEI z-values (1902–2018) were acquired from the CSIC database via KNMI Climate Explorer (http://climexp.knmi.nl, accessed 3 May 2023) for each location with 0.5-degree spatial resolution. SPEI is a multi-scalar index that considers precipitation and potential evaporation, incorporating a temperature component (Vicente-Serrano et al. 2010). Values for April-1 SWE volume for the southern Sierra Nevada (1940–2018) were based on multiple data streams of snow reanalysis and in situ snow courses via Huning and AghaKouchak (2020). Regional temperature and SPEI data were generated using KNMI Climate Explorer for CSIC and PRISM data, respectively.

Height-related climatic sensitivity and expression of low-growth years

We conducted a tree-level analysis of climatic sensitivity and expression of low-growth rings with a complete block design using radial increments at regular height intervals along the main trunk. Two complementary datasets were utilized: trees with representative rings at (1) BH, 10 m, and 10-m intervals to 60 m above ground and (2) 10–60 m above ground at 10-m intervals. Inclusion of shallow BH cores limited the number of trees with a complete dataset to analyze but incorporated this important position. Trees were considered for analysis if they had cores at each height or interpolated rings based on cores ≤ 10 m both above and below sampling height. For the 33 trees used in axial analyses, mean distance from target height was 0.2 m, and 13 trees had interpolated rings for 1, 2, or 3 heights. All positions were on main trunks except one 60-m position on a reiterated trunk with a cambial age of 982 yr. These 33 trees represented nine locations, ranged from 65.5–96.5 m tall (mean = 78.7 m), 229–814 cm fDBH (mean = 470 cm), and 305–2531 yr old (mean = 1353 yr; Table S1).

To generate radial increments, ring widths from replicate cores per height were averaged and extended as far back in time as possible using local relationships between multi-core averages when only single cores remained. Wood radius at measurement height was computed by subtracting adjusted bark radius from total radius, where bark radius was first predicted from diameter and height using equations for Sequoiadendron (Sillett et al. 2015b) and then adjusted by scaling relationships between observed and predicted radii. Measured rings were scaled to fresh widths using the ratio of freshly extracted and mounted core lengths (± 1 mm) per location. The sum of measured ring widths from cambium to pith (if reached) was forced to equal wood radius. Wood radii were decremented by annual rings across the trunk height gradient with rings at intervening heights of measurement (no crossdated core samples) computed by interpolation. Rings with high and moderate confidence in crossdating were utilized almost exclusively. In the few instances when crossdating was not achieved, increments were interpolated from the nearest dated series.

We calculated Pearson’s correlation coefficients between location-specific climatic variables and ring indices at each axial position for trees with suitable data. To control for long-term growth trends and varying cambial ages along the trunk, we detrended and standardized radial increments per height with a 32-yr spline via dplR (Bunn 2008). Years considered vary depending on climate records and last year of ring indices with maximum windows of 1940–2018 for SWE and 1900–2019 for Tmax, Tmin, and SPEI. To determine if correlations differed among heights, we used nonparametric Friedman’s rank sum tests in an unreplicated, complete block design (tree as blocking variable, height as group, correlation coefficient as dependent variable). Differences between categories were evaluated with exact post hoc tests for all pairwise comparisons of Friedman rank sums (Eisinga et al. 2017) with P value adjustment for multiple comparisons to control for false discovery rate (Benjamini and Hochberg 1995). Tests were run using stats and PMCMRplus packages in R (Pohlert 2022; R Core Team 2023).

We determined if expression of low-growth years differed among heights using proportional radial increment (PRI) as the dependent variable in the Friedman’s rank sum test, run with the same method described in the preceding paragraph. For each low-growth year per height, PRI was calculated as the radial increment of the low-growth year divided by the mean radial increment for the 10 years before and after to provide a relativized metric. Low-growth years were defined as those with the smallest radial increments per tree selected from the common period shared by all axial positions under investigation (BH to 60 m; 10–60 m). Up to 3 low-growth years were analyzed per tree if the ring index exceeded two standard deviations below the mean for the common period based on the STD tree chronology. For years near the end of series (e.g., 2014), as many years as remained were used. If multiple low-growth years were identified in the 10-year window (e.g., 2014 and 2015), then only the narrowest was considered per tree. To eliminate pseudo-replication, PRI was averaged at each height per tree (N = 33).

In addition to the tree-specific analysis, we compared composite chronologies per height interval with regional climatic variables. The robust biweight mean was used to combine detrended radial increments into the STD version of height-specific chronologies via dplR (Bunn 2008). Height-specific chronologies were generated using the same trees as the BH to 60 m (N = 18) and 10–60 m (N = 31) analyses. We used bootstrapped Pearson correlation analysis via treeclim in R to assess relationships between height chronologies and regional climatic variables (1940–2011 for SWE; 1902–2011 for Tmax, Tmin, and SPEI).

Climatic sensitivity of upper vs. lower trunk

To increase tree replication, we relaxed delineation of axial positions from 10-m intervals to two categories (upper vs. lower trunk) and used 44 trees with representative cores at both positions spanning 1900–2011 (Table S1). Upper trunk was the highest position on the trunk below any reiterations (mean = 63 m, range 40–87 m). Lower trunk was the lowest position at or above the top of buttress (mean = 13 m, range 8–31 m). Only measured ring widths crossdated with high confidence were used (no interpolations). A target of two cores were selected per position, but five trees had only one core per position. If more than two cores were eligible, we chose those with strong crossdating correlations (via Cofecha outputs) and similar radial position (e.g., azimuth) between upper and lower trunk cores. We combined series into STD versions of upper and lower trunk regional chronologies, detrended with a 32-yr spline to focus on inter-annual variation as previously described, and, again, used bootstrapped correlation analysis in treeclim to generate Pearson coefficients with regional climatic variables.

Results

Ring-width chronologies

Standardized ring indices for 61 Sequoiadendron (mean = 19 series) supported three new (MAR, AC, RH) and six updated (CBT, WF, RMG, GF, MH, FC; Carroll et al. 2014) location chronologies ranging 928–1973 yr in length (Table 2, S1, S2). Tree-level crossdating was near complete (98.6 ± 0.3 and 0.5 ± 0.2% rings dated with high and moderate confidence, respectively; mean ± 1 SE) with 0.15 ± 0.04% missing rings. Chronology lengths exceeded 1000 yr for 17 trees and 500 yr for 36 trees (Table S1). Location chronologies were composed of 4–18 trees (mean = 134 series) and had robust signal strength (rbar = 0.521 ± 0.02, EPS = 0.86 ± 0.01; Table 2). The oldest chronology (AC) reached the year 47 CE, but two-tree replication extended to 622 CE. The nine location chronologies expressed shared inter-annual variation with each other and with a pre-established composite chronology (CA276; Touchan et al. 2021): mean correlation for overlapping 50-yr segments (N = 79) exceeded 0.45 (P ≤ 0.001) for 71 segments, and the lowest correlation (r = 0.26) was for the earliest century where AC had only one-tree replication (Fig. 1). Among chronologies, the innermost section of CBT was weakest with a mean correlation of 0.20 for overlapping segments from 719–825 CE. Strong crossdating and inter-location synchrony supported the development of a 61-tree regional chronology (47–2019 CE) with declining replication back in time but strong signal strength (EPS ≥ 0.85) from 744 CE to present (Fig. 2). Sixty-five percent of years in the lowest decile of this robust portion were shared with the extreme drought years defined by Hughes and Brown’s (1992) analysis of three locations. Raw measurements of ring widths for all series dated with high confidence (regardless of inter-series correlations) are provided in Table S3.

Table 2 Sampling intensities, crossdating summaries, and chronology statistics for nine Sequoiadendron study locations sequenced from north to south
Full size table
Fig. 1
figure 1

Overlapping correlations among standardized ring-width indices for Sequoiadendron at nine locations and a composite chronology. Location IDs correspond to Table 1. The composite chronology was accessed via the International Tree-Ring Data Bank and is composed of 23 locations (CA726; Touchan et al. 2021). Pearson’s correlation coefficients (r) are for 50-yr segments lagged by 25 yr. Each cell represents a 50-yr segment, bottom number is first year of associated segment. Strength of colors corresponds to correlations, where white is r = 0.328, the cutoff for one-tailed significance at P = 0.01

Full size image
Fig. 2
figure 2

Sequoiadendron chronology composed of 61 trees at nine locations across the species range with signal strength and sample depth. Tree-level chronologies are detrended with a 32-yr spline to focus on inter-annual variation, and standard versions are combined by robust biweight mean with no further detrending. Sample depth conveys number of trees with ring indices and is truncated when < 2 trees. Expressed population signal (EPS), a metric of chronology representativeness, is shown in blue relative to a 0.85 threshold. Lighter gray ring indices correspond to EPS values < 0.85

Full size image

Confirmation of baseline climatic relationships

Inter-annual ring indices for Sequoiadendron at nine locations correlated with the four climate variables selected for investigation based on prior research (Fig. 3). Clear trends in direction of relationships were evident across locations: negative correlations with June Tmax and Tmin and positive correlations with SWE and SPEI. Correlation strength varied by location with most showing inter-annual relationships significant at P < 0.05 and some at P < 0.001. All locations expressed stronger relationships with June Tmax than Tmin, while SWE and SPEI were similar.

Fig. 3
figure 3

Bootstrapped Pearson’s correlation coefficients (r) between key climatic variables and inter-annual ring-width chronologies at nine locations for Sequoiadendron. Location IDs match Table 1. Climate variables are June maximum and minimum temperature (Tmax and Tmin, respectively), April 1 snow water equivalent (SWE), and standardized precipitation evapotranspiration index (SPEI) for the 12-month window ending in September. Window of analysis varies depending on climate record and last year of chronology (maximum window = 1900–2019 for SPEI, Tmax, and Tmin; 1940–2018 for SWE). Levels of significance indicated by italics for P < 0.05, bold for P < 0.01, * for P < 0.001

Full size image

Height-related climatic sensitivity and expression of low-growth years

Tree-level analysis showed that height above ground affected both climatic sensitivity and expression of low-growth years for Sequoiadendron. Specifically, differences were identified for correlations of radial increments with June Tmax, June Tmin, and SWE (but not SPEI), as well as for PRI of low-growth years compared to surrounding decades (Table 3), and pairwise comparisons indicated which categories differed using complementary analyses of 1.4–60 m and 10–60 m. June Tmax exhibited the clearest trend of increasing sensitivity with height above ground (N = 31; Fig. 4). Explained variance increased from BH (2.1%) to 60 m (7.5%, N = 18). June Tmin exhibited similar but weaker trends: the 60-m position ranked higher than some lower positions (10, 20, 40 m; N = 31) and BH (N = 18). For correlations with SWE, BH ranked lower than 10 or 20 m positions (N = 18). PRI for low-growth years was higher at BH (0.750) compared to all higher positions (0.647 ± 0.003; mean ± 1 SE) for the 18-tree analysis, while no differences were apparent among 10–60 m positions (N = 31).

Table 3 Summary of Friedman’s nonparametric rank sum tests for differences in climate sensitivities and expression of low-growth years by incremented axial positions in Sequoiadendron
Full size table
Fig. 4
figure 4

Sensitivity of radial growth to June temperatures varies by axial position (height above ground) for Sequoiadendron based on comparisons of Friedman rank sums. Values are squared Pearson’s correlation coefficients (r, between ring increment and climate), expressing % variance. Window of analysis is 1900–2019 for June Tmax (maximum temperature) and Tmin (minimum temperature). Complementary analyses are presented for height categories from 10–60 m (left) and 1.4–60 (right). Tree replication in Table 3. Bars show mean ± 1 SE. Differences between heights determined by exact post hoc tests for all pairwise comparisons of Friedman rank sums. Categories not connected by same letter are significantly different (P ≤ 0.05)

Full size image

Radial increments from the same trees (N = 18 and 31) were combined into height-specific chronologies for comparison with regional climatic variables, supplementing relationships expressed by tree-level analyses. June Tmax and June Tmin showed generally increasingly negative correlations with height above ground with the strongest (r = -0.44, P < 0.0001) between June Tmax and the 60-m chronology composed of 31 trees (Table 4). Correlations were not significant (P < 0.01) for Tmax at BH or for Tmin at BH or 10 m for the 18-tree analysis. SWE correlated with lower trunk positions but not BH or heights ≥ 40 m (P < 0.01). The strongest relationship for SWE was with the 10-m chronology composed of 31 trees (r = 0.45, P < 0.0001). All positions showed positive relationships with SPEI (P < 0.01) with strongest correlations at 10 m for both analyses. Overall, we observed increasing variance explained by height for temperature variables and decreasing variance explained by height for hydroclimate variables, except for weak correlations at BH (Fig. 5). The maximum variance explained was at 60 m for June Tmax and Tmin and at 10 m for SWE and SPEI, but none exceeded exceed 20%.

Table 4 Bootstrapped Pearson's correlation coefficients (r) between Sequoiadendron tree-ring chronologies and regional climatic variables
Full size table
Fig. 5
figure 5

Percent variance explained between Sequoiadendron tree-ring chronologies and regional climate variables by axial position (height above ground). Complementary analyses are for heights from 10–60 m (left, 31 trees) and 1.4–60 (right, 18 trees). Tmax (maximum temperature) and Tmin (minimum temperature) are for June, SWE (snow water equivalent) is for April 1, and SPEI (standardized precipitation evapotranspiration index) is for the 12-month window ending in September. Window of analysis for SWE = 1940–2011 and 1902–2011 for Tmax, Tmin, and SPEI

Full size image

Climatic sensitivity of upper vs. lower trunk

Upper and lower trunk chronologies representing 44 Sequoiadendron across the geographic distribution substantiated differing inter-annual sensitivities to climate depending on height above ground (Fig. 6). Relationships had similar directions, but the strength varied by trunk position. Upper trunk chronologies were negatively correlated with June Tmax and Tmin at P < 0.001, while lower trunk chronologies exhibited weaker correlations. Lower trunk chronologies (but above top of buttress) showed positive correlations with SWE at P < 0.001 while the upper trunk relationship was weaker (P = 0.03). Both upper and lower trunk chronologies correlated with SPEI at P < 0.001, but lower trunk correlations were higher (r = 0.42 vs. 0.32).

Fig. 6
figure 6

Bootstrapped Pearson's correlation coefficients (r) for upper vs. lower trunk Sequoiadendron chronologies and regional climate variables. Upper and lower trunk chronologies are composed of 44 trees, most with 2 series per position. Tmax (maximum temperature) and Tmin (minimum temperature) are for June, SWE (snow water equivalent) is for April 1, and SPEI (standardized precipitation evapotranspiration index) is for the 12-month window ending in September. Correlations span the common window of 1940–2011 for SWE and 1902–2011 for the others. Red conveys strength for negative correlations and blue for positive correlations. Levels of significance indicated by italics for P < 0.05, bold for P < 0.01, * for P < 0.001

Full size image

Discussion

Updated and expanded Sequoiadendron ring-width chronologies

With trees of only 30 species documented > 1000 yr old (Liu et al. 2022), the addition or amendment of 9 location chronologies spanning 928–1973 yr enhances the tree-ring catalog (St. George 2014). Constituent tree-level chronologies (17 > 1000 yr) derived from 61 Sequoiadendron show strong crossdating and a generally robust shared signal (Table S1, Fig. 1) that support a composite chronology (Fig. 2) similar to other assessments of this species (Brown et al. 1992; Hughes et al. 1996; Touchan et al. 2021). Of note is the addition of a nearly 2000-yr chronology at AC (Table 2), a grove not yet represented in dendrochronological study as it was recently acquired by the Save the Redwoods League for eventual transfer to Giant Sequoia National Monument (Fimrite 2019). While ground-based Sequoiadendron dendrochronology is the norm, we include a component of within-trunk sampling of living trees at a level only achieved for a handful of tall conifer species (Sillett et al. 2021). The effort to attain and analyze samples spanned years, and these data are paired with intensive tree-level measurements and calculations (Sillett et al. 2015b, 2019b) providing an important compendium (Table S3). The within-tree sample design opens an array of research possibilities, and here we examine how climatic sensitivity varies with height above ground.

Axial variation of climate sensitivity and expression of low-growth years

Sequoiadendron augments the number of species with growth–climate relationships that vary with axial position on the main trunk (see Latte et al. 2016 Table1 for partial list). Multiple approaches corroborate the general trends of increasing sensitivity to June Tmax and Tmin with height above ground and decreasing sensitivity to hydroclimate variables of SWE and SPEI with height above ground (except BH). Optimizing the relationship between tree ring and environmental metrics is a fundamental step in developing proxies that extend beyond historical records. Such analyses are often employed at the landscape level, targeting trees near range margins where climate is more limiting (Fritts 1976; Camarero et al. 2021). The same strategy can be used at the tree level, focusing on more sensitive positions along the trunk. Relatively weak dendroclimatic relationships at BH as well as PRI of low-growth years both indicate that irregular basal trunk morphology dampens climate-induced tree-ring signals. The buttressed region of large trunks in tall species such as Eucalyptus regnans, Picea sitchensis, Pseudotsuga menziesii, Sequoia sempervirens, and Sequoiadendron giganteum is so complex that 3D footprint analysis is necessary to extract functional diameters (e.g., fDBH) for allometric estimation of biomass and accurate carbon accounting (Dean et al. 2018; Kramer et al. 2018; Sillett et al. 2021). While basal sampling has clearly not hindered crossdating of Sequoiadendron (Douglass 1919), and such ring series have long supported successful climatic assessments (Hughes and Brown 1992; Touchan et al. 2021), dendroclimatic signals can be maximized by sampling above the buttress on large individuals such as used in this study (Table S1). Tree-climbing is a technical and time-intensive endeavor not available for all research, but these findings are applicable to fallen trunks that are well-preserved given Sequoiadendron’s extremely decay-resistant heartwood (Sillett et al. 2021). Remnant stumps are also present in some groves, and some may reach heights that reduce the influence of basal buttressing.

Contrasting axial relationships between Sequoiadendron radial growth and temperature versus hydroclimate variables may be influenced by temporal and spatial components of biophysical processes. June is a period of maximum light availability for photosynthesis combined with abundant soil water from snowmelt. Among 70 Sequoiadendron groves, snow cover persistence decreases from March to June followed by a ~ 3-month recession of soil moisture (Ray 2016). During the early growing season, ring formation on Sequoiadendron is generally more apparent in upper than lower trunks (personal observations from variable coring dates) as assimilates are allocated from sources (foliage) to sinks (e.g., roots; Gower et al. 1995; Lacointe 2000). Hot temperatures in June greatly increase evaporative demand, and if air vapor pressure deficit drops too low, leaf stomata must close to maintain turgor and avoid embolism, thus limiting carbon assimilation during upper trunk ring formation (Zweifel et al. 2007; McDowell et al. 2008). Sequoiadendron exhibits strong stomatal regulation, especially in upper crown foliage, due to height-related increases in both light availability and water stress (Ambrose 2015, 2016, 2018; Williams et al. 2017, 2021). Patterns hold for both June Tmax and Tmin, possibly reflecting the spatial variation of source and sink limitations on ring formation during this time of year; high daytime temperature and evaporative demand limit carbon assimilation, and drier air at night limits the ability of trees to convert fixed carbon into biomass (Zweifel et al. 2021). Axial variation in sink limitations may explain the trend of increasing heartwood fungicide content (instead of ring formation) with height in closely related S. sempervirens (Sillett et al. 2022) and may also apply to Sequoiadendron.

As snowmelt dissipates, conifers of the Sierra Nevada become increasingly water stressed later in the growing season (Royce and Barbour 2001; Blankinship et al. 2014) when cell enlargement may be more active (and sensitive to environmental constraints) in the lower trunk, but more research on cambial phenology along the height gradient is needed to align phases of xylogenesis with seasonal timing (Monson et al. 2018). Decreasing water availability necessitates stronger stomatal control so trees can rehydrate growing tissues (Peters et al. 2023). Axial trends are generally stronger for SWE than SPEI which makes sense given that SPEI integrates temperature but does not adequately consider snowpack (Vicente-Serrano et al. 2010; Staudinger et al. 2014; Tian et al. 2021). In addition, drought-induced reductions in photosynthesis and water availability may cause a decrease in phloem conductivity that slows transport to the lower trunk (Salmon et al. 2019; Peters et al. 2020), causing increased sensitivity at lower heights as observed in several species (Bouriaud et al. 2005; Hoffmann et al. 2018). Moreover, structural complexity of old individual Sequoiadendron, which develop reiterated trunks, limbs up to 2 m diameter, crown spreads > 25 m, and crown depths > 70 m (Sillett et al. 2015b, 2019b), creates a dynamic environment for water availability, carbon assimilation, and environmental sensitivity (Niinemets 2007) that must influence axial relationships.

We document axial variation in dendroclimatic relationships for Sequoiadendron and propose several mechanisms, but some important considerations remain. Stored mobile carbon can act as a buffer for growth particularly during stressful periods (Sala et al. 2012), and species-specific differences in non-structural carbohydrates mediated tree growth responses to a hot drought (2011–2012) in the southwestern US (Peltier et al. 2021). Lagged growth–climate dynamics may explain differential axial relationships for P. contorta, where hot and dry early summer limit upper trunk growth while prior year’s conditions drive lower trunk sensitivity (Chhin et al. 2010). We use regionally coherent inter-annual variation (Fig. 1) and climatic sensitivities (Fig. 3) as the basis for grouped analysis, but differences in landscape position may also influence axial relationships (van der Maaten-Theunissen and Bouriaud 2012). In the Sierra Nevada, snow cover persistence varies with topography, elevation, and aspect (Ray 2016), time to reach soil dryness ranges by up to 4 weeks due to heterogeneity (Bales et al. 2011), and Sequoiadendron canopy water content during drought varies with geological substrate and topography (Paz-Kagan et al. 2018). Further analysis would benefit from consideration of interactions of co-occurring stresses as well as finer-resolution climatic metrics. Our approach prioritizes a maximum climate window (e.g., 1900–present), which limits inclusion of some of the highest samples; so, although we far exceed the upper heights of comparable analyses, concentrating future sampling on near-treetop positions, including reiterated trunks, could further elucidate relationships and inform proposed mechanisms.

Conclusion

Within-trunk sampling of Sequoiadendron provides spatially explicit data permitting ring-width chronologies (at tree-, location-, and regional-levels) and documentation of axial variation in dendroclimatic sensitivities that can be leveraged to maximize environmental reconstructions for this long-lived species (> 3000 yr; RMTRR 2023). Basal positions of large trees have been targeted for fire histories and are easily accessible from ground, but their irregular morphology can mute climatic signals and expression of low-growth years compared to higher above the ground. While Sequoiadendron employs multiple strategies to maintain favorable water status during drought (Chin and Sillett 2016; Ambrose et al. 2016, 2018; Williams et al. 2021), hot June temperatures and low soil moisture curtail radial growth with axial trends likely attributable to seasonal timing of intra-trunk ring formation, stomatal regulation, and maintenance of stem turgor (Peters et al. 2023). Such relationships are relevant for understanding carbon dynamics and biophysical responses to changing conditions as the Sierra Nevada experiences hotter droughts (Griffin and Anchukaitis 2014; Diffenbaugh et al. 2015) and reduced snowpack (Ashfaq et al. 2013; Berg and Hall 2017). Axial variation in dendroclimatic relationships should be explored for other tall conifers of western North America that have been similarly sampled (P. sitchensis, P. menziesii, S. sempervirens) and have divergent ecologies (Ambrose et al. 2009; Kramer et al. 2018; Chin and Sillett 2019; Sillett et al. 2021).