Introduction

Tree rings have been used for a long time in areas outside the tropics as a powerful tool for the retrospective analysis of tree growth and its response to environmental factors. Stable carbon and oxygen isotope composition of the wood or wood constituents in these rings are increasingly included in the analyses for inferring environmental conditions and tree physiological responses (McCarroll and Loader 2004; Sternberg 2009). However, the absence of distinct annual rings in many tropical trees has so far prohibited the general use of these tools in the tropics. Although the existence of annual rings in some species of tropical trees has been known for a long time (Jacoby 1989), the more general use of ring chronologies in the tropics is of more recent date. An increasing number of reports show that annual boundaries can indeed be formed in the wood of tropical trees when a dormancy period is induced by a dry season (Worbes 2002; Heinrich et al. 2008). Seasonally deciduous species are most likely to form distinct rings, but evergreens may also do so (Brienen and Zuidema 2005). Environmental stresses other than drought have also been shown to induce an annual pattern in wood structure, such as flooding and a seasonally high salinity (Schöngart et al. 2002; Verheyden et al. 2004a). The recognition of annual rings has opened opportunities for a classical dendrological approach as used for temperate trees (e.g. Brienen and Zuidema 2006). The identification of distinct rings has furthermore opened the possibility to use stable isotopes for deriving past environmental responses in these trees (Poussart et al. 2004; Verheyden et al. 2004b; Hietz et al. 2005; Cullen et al. 2008; Brienen et al. 2010). However, a large number of evergreen tropical trees do not form distinct annual tree rings, particularly so in the humid tropics that lack a pronounced dry season (Jacoby 1989). This is a serious shortcoming since it precludes a dendrological approach and the use of stable isotopes for retrospectively analyzing the effect of environmental factors on tree growth and for palaeoclimatology.

The use of stable carbon isotopes in plant material in general and tree rings in particular has become wide spread when a good model became available predicting environmental effects on isotopic ratios (δ13C) (Farquhar et al. 1982, 1989). Discrimination against 13C during photosynthetic CO2 assimilation in C3 plants decreases with decreasing ratio of intercellular to atmospheric CO2 concentration (C i/C a). This denotes increasing stomatal limitation of photosynthesis caused by either a decrease in stomatal conductance (g s) and/or an increase in photosynthetic rate (A). The resulting increased intrinsic water use efficiency (A/g s) is thus associated with isotopically enriched plant carbon (increased δ13C). Drought typically increases stomatal limitation of photosynthesis, whereas shading reduces it, thus showing corresponding excursions in δ13C (Francey and Farquhar 1982). In tree rings, the straightforward interpretation of these model predictions is complicated by post assimilation fractionation processes. In particular, wood growth from stored reserves rather than from current assimilates complicates matters. This results in carry-over effects from the previous growth season to early wood formation in the next in addition to fractionation associated with starch metabolism (Helle and Schleser 2004; Kagawa et al. 2006; Gessler et al. 2009).

The mechanistic understanding of variation in δ18O in plant material became available more recently (Roden et al. 2000; Barbour 2007; Sternberg 2009). The oxygen in water exchanges with that in CO2 before its assimilation and in carbonyl groups of assimilates. Assimilates, thus carry the isotopic signal of leaf water, albeit at about 27‰ enrichment. The δ18O of leaf water is the result of the δ18O of water taken up by the tree (source water) and subsequent enrichment during transpiration and exchange with atmospheric water vapor in the leaf. Further downstream with synthesis of wood constituents in the stem, another exchange step occurs. The isotopic composition of source water is thus dominant in stem wood, since source water forms the basis of leaf water and is partially exchanged during the synthesis of wood constituents from sucrose.

Seasonal variation in precipitation also exists in humid tropical climates. Dry seasons could thus be reflected in an increased δ13C of wood then synthesized from current assimilates. Wet seasons in the tropics are characterized by 18O depleted precipitation water (Araguas-Araguas et al. 2000), thus leading to a reduced δ18O of source water. A parallel seasonality is thus expected for δ13C and δ18O. When sampled at a sufficiently high radial resolution relative to the level of growth assumed for a certain site, the stable isotope composition of the wood is thus potentially suitable for the identification of annual tree rings when not anatomically distinct. Another prerequisite for a successful application of this approach is that seasonal variation in environmental conditions is sufficiently large such that the annual pattern in isotopic composition of the wood is sufficiently pronounced. This would open opportunities for retrospectively analyzing tree growth. Inter-annual variation in precipitation and other environmental conditions is likely to result in between-ring variation in isotopic composition. Past environmental conditions and tree responses could thus be inferred. Variation in δ13C in the radial direction in tropical wood samples without rings analyzed by Leavitt and Long (1991) suggested an annual pattern. More recent reports do show the potential of this approach for trees with a non-distinct ring structure from Costa Rica (Evans and Schrag 2004; Anchukaitis et al. 2008) and Thailand (Poussart and Schrag 2005). The tropical climates of these areas are characterized by a single annual wet and a pronounced dry season. In our study area, Central Guyana, two wet and two dry seasons can be distinguished that are not very pronounced (Ter Steege and Persaud 1991) (Fig. 1). The different precipitation pattern compared to the previous studies may induce a different isotopic signal. The majority of the trees in the area do not exhibit a distinct ring pattern (Miller and Détiene 2001).

Fig. 1
figure 1

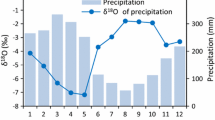
Precipitation in the Mabura Hill area where the study was carried out. Precipitation was recorded at the sample site and in the vicinity (see text). No data are available for the period 1993–1996. The annual mean was 2,680 mm. a Monthly averages for these data. b Deviations from the seasonal mean during the observation period. The four seasons were distinguished as shown in (a) with legend in (b)

Full size image

The principal objective of this study was to further investigate the potential of the use of stable isotopes for the identification of annual rings in trees from the humid tropics that have no anatomically distinct rings. After identification of annual rings, the data are used to investigate the potential for analyzing relationships with environmental variability and tree responses. The study was carried out in the rainforest of Central Guyana with the two species Goupia glabra and Carapa guianesis. Cores were taken from trees of which the diameter increment had been measured. This provided a reference for dating the wood. Measurement of isotopic ratios was done at a sufficiently high resolution to detect intra-annual variation in δ13C and δ18O.

Materials and methods

Study site, trees and sampling

The study was carried out in the rainforest in Central Guyana about 40 km south of the township Mabura Hill in the West Pibiri compartment of a timber harvesting concession (5°02′N; 58°37′W). Cores were taken from trees in permanent sample plots where diameter increment rates have been measured since September 1993 (van der Hout 1999). The species Carapa guianensis Aublet and Goupia glabra Aublet were selected because the wood is rather homogeneous and their growth rates were relatively high. The species will further be referred to by their genus names. The average radial increment rate measured on all trees >20 cm diameter on three ha was 0.9 mm per year, whereas the rates for Carapa and Goupia were 1.9 ± 1.5 and 1.4 ± 1.1, respectively. Hence, the increment rates of the sample trees were generally above average (Table 1). Goupia is a common species of secondary forests and Carapa is most common in marsh forests and along rivers and creeks. Both species are also regularly found in the mixed primary forests on the well-drained brown loamy sands (Ferralsols) of the research site. They are evergreen in the area, although seasonal periodicity in leaf fall and leaf growth may exist.

Table 1 List of the four trees that were sampled for the isotopic measurements with stem diameter and growth rate
Full size table

Cores were sampled from opposite sides (north and south) of the stems of two trees of each species growing in an undisturbed experimental plot at May 2, 2002. The cores were taken at breast height with a power driven 10 mm core drill until a depth of about 4 cm, which covered at least the radial increment over the measurement period. The cores were air dried and rectangular pieces were trimmed to approximately 5 × 5 mm. The upper transverse surface was planed and photographed. One core of each species was tangentially cut in slices of 200 μm thickness using a device with a cutting knife and a screw for advancing the sample. One core per species was cut at a thickness of 60 μm using a sledge microtome (Polycut E, Leica microsystems, Bentheim, Germany). The Carapa wood had occasional axial parenchyma bands that were used to align the samples. The rays were used to further align the samples of both species.

Stable isotope analysis

From the 200 μm slices, three samples of ca. 0.2 mg were taken for isotopic analysis on whole wood; one for δ13C and two for δ18O analysis. The samples were cut from one side of the slice. The 60 μm slices were subdivided into three parts, also one for the δ13C and two for δ18O measurements. All slices were analyzed except for the 60 μm slices of the Goupia core for which every other slice was measured. The samples were weighed and packed into tin capsules (δ13C) and silver capsules (δ18O). Prior to measurement of δ18O, the samples were vacuum dried at 60°C for 2 days. The samples were combusted (δ13C) or pyrolized (δ18O) at 1,080°C in an elemental analyzer (Carlo Erba, Milan, Italy) coupled to an isotope ratio mass spectrometer (OPTIMA, Micromass Ltd, Manchester, UK). In the case of δ18O measurements, the autosampler was covered with a hood and flushed with Argon gas in order to avoid any contamination from air. The δ13C and δ18O values are expressed relative to the VPDB and VSMOW standards, respectively. The reproducibility for replicate measurements of tree-ring samples is better than 0.1‰ for δ13C and <±0.3‰ for δ18O.

The amount of material of the 60 μm slices was insufficient for cellulose extraction. A comparison between whole-wood and cellulose was made as follows. Separate series of 200 μm slices were cut from parts of the cores beyond the depth where diameter increment rates were known at around 35 mm. These were used for comparison of δ13C and δ18O in whole-wood and cellulose. The middle part of the slice was used for the measurement on whole-wood. The remainder of the slice was extracted for α-cellulose according to common procedures described by Green (1963) and modified after Loader et al. (1997).

Precipitation

At a nearby station of the Guyana hydrometeorological service (Great Falls; approximately 40 km north of the sample site), precipitation is measured. However, a continuous record is not available for most of the experimental period. In the framework of a larger research program carried out in the area (Tropenbos–Guyana program), meteorological measurements were done between 1991 and 1993 at a site about 25 km north of the sample site (Jetten 1994) and between 1996 and 2000 at the sample site (van Dam 2001). The available precipitation records are shown in Fig. 1. The monthly averages presented in Fig. 1 are similar to the averages for the period 1965–1973 measured at the nearby Great Falls meteorological station (Jetten 1994) and provide a good picture of the local precipitation pattern. Precipitation water δ18O values were taken from the Water Isotope System for Data Analysis, Visualization, and Electronic Retrieval (WISER) database (http://nds121.iaea.org/wiser/). The nearest station with a similar climate is Cayenne (WMO Station Code 8140501) in French Guyana at about 475 km to the east for which the data are reproduced in (Fig. 2).

Fig. 2
figure 2

Monthly averages for δ18O in precipitation water for the period 1969–1975, Cayenne, French Guiana [Water Isotope System for Data Analysis, Visualization, and Electronic Retrieval (WISER) database, http://nds121.iaea.org/wiser/]

Full size image

Results and discussion

Whole-wood with cellulose comparison

The thin 60 μm slices were too small for cellulose extraction. The isotopic composition of whole-wood was compared with that of cellulose in larger samples to establish the relationship between the two. They typically show similar patterns in δ13C with somewhat higher values in cellulose (Helle and Schleser 2004; Loader et al. 2003, Verheyden et al. 2005; Harlow et al. 2006; Eglin et al. 2008). This was confirmed for the series of Carapa and Goupia that were used for this comparison (Fig. 3a, b). The small radial variation of δ13C in whole-wood was reflected in the cellulose at 1.1‰ and 0.9‰ enrichment, respectively, which resulted in high correlation coefficients (0.92 and 0.89 for Carapa and Goupia, respectively).

Fig. 3
figure 3

Comparison of isotope composition of whole-wood and α-cellulose. In the panels are shown δ13C (a, b), δ18O (c, d), Carapa guianensis (a, c), Goupia glabra (b, d). A sequence of 200 μm thick slices was taken from a part of cores at around 35 mm depth where no diameter increment was measured

Full size image

The δ18O values were on average 5.5‰ (Carapa) and 4.0‰ (Goupia) higher for cellulose compared to whole-wood (Fig. 3c, d). The correlation between δ18O in wood and in cellulose was also highly significant, but not as tight as for δ13C (correlation coefficients of 0.55 and 0.77 for Carapa and Goupia, respectively). Good agreement of δ18O in whole-wood and cellulose and correlation of δ18O in whole-wood with climate data is often found (Borella et al. 1999; Barbour et al. 2001; Jäggi et al. 2003; but see Ferrio and Voltas 2005; Battipaglia et al. 2008). These comparisons with cellulose gave confidence in the use of whole-wood during the following analytical procedure for interpreting radial variation in isotopic ratios based on existing models that are based on cellulose. Nevertheless, the relatively large unexplained variance for δ18O means that radial variation in whole-wood values can be partly the result of variation in chemical composition and/or isotopic variation in other compounds than cellulose.

Radial variation in isotopic composition

The three cores of Carapa had a mean δ18O of 25.3‰ and a mean δ13C of -27.3‰ (Fig. 4). Minima and maxima in δ18O could be distinguished with amplitude of 1–4‰ at distances of a few millimeters. These were particularly clear in the Carapa tree 47 (Fig. 4). This scale of a few millimeters is similar to the annual radial increment rate (Table 1). A cyclic increase and decrease in δ18O could thus be distinguished at a near annual scale in many cases. The variation in δ13C at this near annual scale was much less (0.5–1.5‰). Minima in δ13C often coincided with the minima in δ18O in the case of Carapa tree 47 as also evident from a positive correlation between δ13C and δ18O (Fig. 4; Table 2). This was less evident in tree 61 that showed a negative correlation (Table 2).

Fig. 4
figure 4

Radial variation in δ18O (filled circle) and δ13C (open circle) in the three cores of Carapa guianensis plotted against the distance from the cambium inward. The diamond symbols on the X-axis represent the times of diameter measurements: September 1993, February 1995, January 1996, March 1997, October 2000 and May 2002. Annual boundaries at the middle of the main rainy season (May–June) were distinguished primarily on the basis of δ18O when they are expected to be lowest. These are shown as vertical dashed lines with the corresponding years in italic. Cores 61-S and 47-N were sampled at a frequency of 200 μm and 47-S at 60 μm. Cores 47-S and 47-N were sampled from the south and north side of the same tree. Corresponding annual boundaries are connected with dashed lines

Full size image
Table 2 Correlation between δ13C and δ18O within individual cores
Full size table

Trends in isotopic composition of the wood could also be distinguished on a longer time scale. In the Carapa tree 61 (Fig. 4), δ18O decreased abruptly about 2‰ at 11 mm and δ13C increased about 1‰ at 15 mm. Such longer term trends were absent for δ18O in the two cores from the Carapa tree 47. Average values were also similar for both cores. However, δ13C reached values of about -28.5‰ in the first few mm and again at around 15 mm in the 47-S core. This was not found in the 47-N core where values remained at an average of -26.5‰ throughout. Such variation in δ13C around the circumference of a tree stem is frequently found (e.g. Leavitt and Long 1991; Schleser 1999).

The δ18O values in the Goupia cores were slightly lower (mean 24.7‰) compared to the Carapa cores and the δ13C values were somewhat higher and were different between the two trees, -25.2‰ and -26.6‰ for the trees 42 and 17, respectively (Fig. 5). Clear minima and maxima in δ18O at a near annual scale could also be distinguished for Goupia, although the amplitude of the cyclic variation was somewhat less compared to Carapa. The average δ18O amplitude was around 2‰, with an occasionally more pronounced cyclic variation in δ18O such as between 4 and 10 mm in the Goupia tree 42, around 8 mm in the Goupia 17-N core and between 9 and 18 mm in the 17-S core (Fig. 5). As in Carapa, the amplitude of variation of δ13C in the Goupia cores was also around 1‰. No obvious longer-term trend in mean isotopic ratio could be distinguished in the Goupia cores.

Fig. 5
figure 5

Radial variation in δ18O (filled circle) and δ13C (open circle) in the three cores of Goupia glabra plotted against the distance from the cambium inward. The diamond symbols on the X-axis represent the times of diameter measurements (for dates see Fig. 4). Annual boundaries at the middle of the main rainy season (May–June) are shown as vertical dashed lines with the corresponding years in italic. Cores 42-S and 17-N were sampled at a frequency of 200 μm and 17-S at 120 μm. Cores 17-S and 17-N were sampled from the south and north side of the same tree. Corresponding annual boundaries are connected with dashed lines

Full size image

The two isotopic ratios were correlated in the three Carapa cores (Table 2) and the δ13C minima often coincided with the δ18O minima in this species, particularly for tree #47 where 13 of the 15 annual boundaries were characterized by a low δ18O and δ13C (see below). This was expected when both isotopic ratios were forced by seasonal changes. However, only one Goupia core showed a significant but not very tight correlation between the two isotopes (Table 2) and the minima for δ18O and δ13C coincided in only 55% of the cases.

Intra-annual variation and annual boundaries

The cyclic variation in δ18O over distances in the order of magnitude of the annual radial increment rate (Figs. 4, 5; Table 1) suggests a forcing by seasonally varying environmental conditions. For the most nearby station where precipitation water was measured for δ18O, Cayenne in French Guiana, a 3‰ lower δ18O was reported for the middle of the rainy season compared to the dry season (Fig. 2). Similar or even larger seasonal differences are reported for several stations in the humid tropics of west and central Amazonia (WISER database, http://nds121.iaea.org/wiser/). Source water determines largely the isotopic composition of wood (Roden and Ehleringer 1999). The low δ18O in precipitation water is thus likely to be a principal driving force for a low in δ18O in wood, since evaporative enrichment is relatively less important in the rainy season. In the dry season, isotopic enrichment in the leaf (Farquhar and Gan 2003) and in the upper soil layers (Jackson et al. 1995; Bonal et al. 2000a) on top of the higher δ18O in precipitation water is likely to have further increased δ18O in the wood and may thus have enlarged the amplitude of seasonal variation. A complicating factor is that the depth of water uptake of the trees is unknown, and the isotopic composition of soil water may vary with depth as found for a comparable forest in French Guiana (Bonal et al. 2000a). Nevertheless, a valid assumption is that a low δ18O in the cores would represent wood formed in the rainy season and high values represent wood formed in the drier seasons. The cores were sampled at the beginning of the rainy season (2 May 2002) and the low δ18O of the precipitation water was apparently already reflected in the most recently formed wood directly under the cambium of some cores (Figs. 4 , cores 61-S and 47-S, 5, core 42-S), but in other cores not yet (Figs. 4, core 47-N, 5, core 17-S and 17-N). The number of data points at the minimum d18O is small in most cases. This is remarkable when it is assumed that this indicates the wood that is formed in the rainy season, because it suggests that a small fraction of the wood is formed in this season that is at least 4 months. A possible reason could be that the minimum of δ18O in precipitation is of shorter duration that the rainy season as a whole.

The variation in δ13C of about 1‰ within the annual radial growth of 2 mm in both species (Figs. 4, 5) was small compared to the intra-annual variation reported from temperate (Leavitt and Long 1991; Helle and Schleser 2004; Roden et al. 2009) and other tropical areas (Poussart et al. 2004; Verheyden et al. 2004b). Part of the intra-annual variation in δ13C in deciduous temperate trees is caused by utilization of stored reserves for wood formation in spring (Gessler et al. 2009). That is not likely to play an important role in two species that may only lose part of their foliage in the dry season. Increased stomatal limitation of photosynthesis in the dry season because of decreased water availability as measured in comparable forest (Huc et al. 1994; Bonal et al. 2000b; Dünisch and Morais 2002) and/or increased irradiance are other possible candidates for explaining intra-annual variation in δ13C. An effect of water availability on δ13C in wood has been shown in the area where trees were sampled along a slope from a sandy ridge to a moist valley (Pons et al. 2005). However, dry season droughts as occurred during the measurement period induced only small increases in δ13C in both species. These dry periods are apparently not stressful for the trees where they were sampled.

Based on the above reasoning, annual boundaries were drawn that supposedly represent the middle of the rainy season (May–June). A minimum in δ18O was used as the principal criterion, preferably supported by more than one data point. A low δ13C was used as a secondary argument. Using those criteria, the core Carapa 61-S showed a reasonably good match with the radial increment rate (Fig. 4). The isotopic patterns in the two cores from opposite sides of the tree Carapa 47 did not seem to match (Fig. 4). However, when different growth rates in different years were assumed for the two sides of the stem, then the patterns showed a better match. The isotopic pattern shows evidence for faster growth of the south compared to the north side of the stem up to 12 mm depth, but slower growth between 12 and 20 mm. The cores from both sides showed also a reasonable match with the measured radial growth. The parenchyma bands visible in the cores of Carapa were fewer then the annual boundaries based on isotopes and also based on the radial increment over the measured period. Hence, anatomical increment zones are not likely to be annual in Carapa as also concluded by Dünisch et al. (2002). Some uncertainty remains with the identification of annual boundaries where the minimum in δ18O is not so clear and does not coincide with a minimum in δ13C. This can be seen in the cores 61-S (at 3.1, 15 and 20.3 mm) and 47-N (at 9.5 mm) that were both sampled at a lower resolution compared to 47-S. We conclude that annual rings can be distinguished in the wood of Carapa guianensis with reasonable certainty on the basis of radial variation in isotopic ratios, particularly when sampled at high resolution.

The core Goupia 42-S showed a clear cyclic isotopic pattern to a depth of 11 mm depth, but less so beyond that point (Fig. 5). Nevertheless, when applying the criteria, the annual boundaries matched radial growth reasonably well. The two cores from the Goupia 17 tree were also difficult to match. A satisfactory match was only possible when a faster growth rate of the north side than the mean radial increment rate to a depth of 25 mm was assumed and a slower growth of the south side up to 14 mm (Fig. 5). Beyond 14 mm depth in the S core, there is evidence of accelerated growth, although the isotopic pattern became less clear towards the end. The cross section of the Goupia samples showed some variation in frequency of vessels and axial parenchyma, but this was not associated with the radial growth and/or annual boundaries distinguished based on stable isotopes. In addition, in samples of Goupia glabra some uncertainty remained regarding the demarcation of annual boundaries. Nevertheless, we can also conclude for this species that, although variation in δ18O was less, annual rings can be distinguished with reasonable certainty from radial variation in isotopic ratios. In both species, δ18O was much more useful for distinguishing annual boundaries compared to δ13C.

Other studies have also identified annual rings in tropical rainforest trees where they are anatomically non-distinct. Those done with trees from drier tropics and/or tropical climates with a single pronounced dry season often yielded a clear annual pattern in δ18O and in some cases also δ13C with larger intra-annual variation (Poussart et al. 2004; Poussart and Schrag 2005; Anchukaitis et al. 2008). The tree sampled in the humid La Selva forest in Eastern Costa Rica by Evans and Schrag (2004) showed similar intra-annual variation in δ18O as in the present study and annual cycles could also be recognized. Hence, annual rings can be identified by means of radial variations in δ18O not only in tropical climates with a pronounced dry season, but also in the more humid tropics. However, independent verification of age, e.g. with radio carbon, would be necessary when applying the technique to longer sequences (Poussart et al. 2004; Poussart and Schrag 2005).

Relationships with climate variability

A negative relationship of amount of precipitation with δ18O in wood is expected since correlation with amount also exists with δ18O in precipitation water (Bonal et al. 2000a). Likewise, a negative relationship is also supposed to be present for δ13C because of the decreasing stomatal limitation with increasing precipitation. These relationships would result in a positive correlation between δ13C and δ18O. This was indeed found for the three Carapa cores, but only for one of the three Goupia cores (Table 2). Poussart and Schrag (2005) and Roden (2008) found similarities of annual δ18O cycles between trees growing in the same area when the seasonal variation in the wood was forced by δ18O of precipitation water and isotopic enrichment in the dry season. Variations in minima and maxima in δ18O was evident in our samples (Figs. 4, 5), but a clear matching between the cores from different trees was not possible.

The correlation of various precipitation parameters with isotopic parameters was analyzed. Precipitation parameters were, annual totals (May–April), the main rainy season (restricted to the generally wettest part, May–July), the part of the year outside the main rainy season (September–March) and the main dry season (September–November). Data were derived from the local observations (Fig. 1), which unfortunately have missing data for the 1994–1996 period, and from the climate research unit dataset CRU TS 2.1 (Mitchell and Jones 2005) that contains interpolated precipitation data for the whole measurement period. The CRU data are on average 21% higher than the measured data, which is similar for the 1965–1973 period of continuous records at the Great Falls meteorological station near the samples site (Jetten 1994). The CRU data are apparently representing an overestimate of the precipitation at the sample site. Isotopic data were averaged per identified year, and the minimum and maximum values in each year, the putative rainy and dry seasons, respectively, were calculated as the average for three data points. The number of data points was increased to cover the same radial interval (0.6 mm) for the 60 μm high-resolution cores (Carapa 47-S and Goupia 17-S).

No significant correlations were found of precipitation parameters with δ13C, also no non-significant trends were evident (data not shown). Relationships of δ18O with precipitation were also not unequivocal. Nevertheless, in some cores, the expected negative trend of annual and rainy season precipitation with δ18O was present (Table 3), but that was significant in only one case (Carapa 47-S with annual CRU data). Although the minima in δ18O were not related to the amount of rainy season precipitation, the amplitude of intra-annual variation in δ18O was positively related to the locally measured rainy season precipitation in one case (Carapa 47-N with recorded data) (Table 3). The ENSO event of 1997/1998 with reduced precipitation in the main rainy season of 1997 and in the following seasons (Fig. 1) was also not reflected by a higher δ18O and/or δ13C. Some other studies of isotopic variation in tropical trees lacking visually distinct annual rings report better relationships with precipitation, such as Poussart and Schrag (2005) for Northern Thailand, Anchukaitis et al. (2008) for montane forest and Evans (2007) for a lowland forest in Costa Rica. The climate in these locations is characterized by a single dry season, which, in the case of Thailand and the montane forest in Costa Rica, was accompanied by larger annual amplitude of variation in δ18O compared to our study. A reason for the lack of clear relationships between precipitation and δ18O could be the presence of a second dry and wet season in our area, which may complicate the pattern of the intra-annual isotopic variation. Further reasons could be a small effect of climatic variation on δ18O of precipitation water, uptake of water from greater depths where the isotopic signal is different from precipitation water, the short chronologies resulting in few data points and uncertainties with the demarcation of annual boundaries.

Table 3 Correlation of precipitation with δ18O in the three cores of the two species each
Full size table

Conclusions

The small radial variation in δ13C makes this parameter unsuitable for the identification of annual rings in the homogeneous wood of the two species that were investigated, and also as proxy for temporal variability in water availability. However, annual rings could be identified with reasonable certainty mainly based on radial variation in δ18O, but suitability of δ18O as precipitation proxy needs further investigation. Longer tree chronologies including stronger climatic anomalies may result in a more distinct climate signal. The rings identified with stable isotopes, when supported by alternative dating methods, can be used to retrospectively analyze growth. The large numbers of samples required for a dendrological approach may still be prohibitive, but the method may become more practically useful when prototypes of high precision automatic analysis methods like UV-Laser Ablation-combustion-Isotope Ratio Mass-Spectrometry (LA-IRMS, Schulze et al. 2004) or Laser-Micro-Dissection Pyrolysis Mass-Spectrometry (LMD-P-IRMS) are developed into marketable commodity.