Graph-enhanced deep material network: multiscale materials modeling with microstructural informatics

Abstract

This study addresses the fundamental challenge of extending the deep material network (DMN) to accommodate multiple microstructures. DMN has gained significant attention due to its ability to be used for fast and accurate nonlinear multiscale modeling while being only trained on linear elastic data. Due to its limitation to a single microstructure, various works sought to generalize it based on the macroscopic description of microstructures. In this work, we utilize a mechanistic machine learning approach grounded instead in microstructural informatics, which can potentially be used for any family of microstructures. This is achieved by learning from the graph representation of microstructures through graph neural networks. Such an approach is a first in works related to DMN. We propose a mixed graph neural network (GNN)-DMN model that can single-handedly treat multiple microstructures and derive their DMN representations. Two examples are designed to demonstrate the validity and reliability of the approach, even when it comes to the prediction of nonlinear responses for microstructures unseen during training. Furthermore, the model trained on microstructures with complex topology accurately makes inferences on microstructures created under different and simpler assumptions. Our work opens the door for the possibility of unifying the multiscale modeling of many families of microstructures under a single model, as well as new possibilities in material design.

1 Introduction

During the past decades, the desire to design complex materials and the necessity to understand their behavior have given rise to extensive research in multiscale modeling [1]. Traditionally, multiscale modeling has been performed using the finite element method (FEM) or the fast Fourier transform (FFT). Well-established software applications in the industry that allow to run multiscale simulations, such as LS-DYNA [2], are based on these methods. However, FEM and FFT-based multiscale modeling can be daunting due to their high computational cost. To overcome this challenge, researchers explored several possibilities. Data-driven techniques [3,4,5] were proposed to bypass material modeling at the microscopic scale. Another novel and notable effort was to use neural networks to create FE-like shape functions, which results in a lot more accuracy than FEM with the same number of degrees of freedom [6,7,8]. Interest also grew in accelerating modeling at the microscale through machine learning (ML), thus making ML-based multiscale modeling [9] notably gain in popularity. Various types of ML models were used over the years for this purpose, from which we may mention: feedforward neural networks [10, 11], recurrent neural networks [12,13,14], convolutional neural networks [15,16,17], graph neural networks [18,19,20]. Besides these conventional neural network models, a deep material network (DMN) was recently introduced by Liu et al. [21] to model 2D homogenization problems and was later extended to 3D [22]. DMN sets itself apart from other neural network models in several aspects. First, it is designed at its core for multiscale modeling; this contrasts with conventional neural networks designed to be as general and applicable to different fields as possible. In DMN, the analytical solution to the problem of determining the homogenized properties of a two-phase laminate is used as its building block. This custom design allows DMN to capture the behavior of materials with only a few parameters that hold physical meanings. Second, because of its physics-based design, it can be used to predict material nonlinearity (e.g., elastoplasticity, damage, hyperelasticity), although solely trained on linear elastic data. This is because the homogenization behavior considered in DMN is independent of material nonlinearity. Due to its unique characteristics and capacity for fast and reliable predictions, DMN even found its way into legacy software in the industry [23, 24].

A non-negligible amount of research has been carried out on DMN. Liu et al. [21] showed its capacity to implicitly learn the volume fractions of various 2D representative volume elements (RVE) types, including matrix-inclusion, amorphous, and anisotropic. Liu and Wu [22] explored the applicability of DMN to 3D problems for RVEs, such as a particle-reinforced microstructure and a carbon fiber reinforced polymer (CFRP) composite. Gajek et al. [25] set to establish the basic mechanical principles of DMN. These works and others [1, 26, 27] all support the ability of the network to learn the physics of microstructures. However, this particularity of DMN entails that it can only be confidently used to represent the specific microstructure it is fitted for. Representing new microstructures implies training new DMNs.

Fig. 1

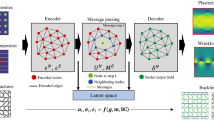
Illustration of the framework used in this work. Initially, microstructures are transformed into equivalent graph representations. During training, the graph data is used to obtain a GNN-DMN model through feature extraction and microstructure-informed transformation. After training, the GNN-DMN model generates inference-ready DMNs from the graph representation of any microstructure given to it as input. These DMNs are stand-alone and can be used independently to predict the material responses of the corresponding microstructures

Many took notice of this limitation and sought to generalize DMN by taking advantage of the macroscopic description of microstructures. Liu et al. [28] proposed a transfer learning approach based on fiber volume fraction. At an initial stage, a DMN was trained for a particle-reinforced 2D RVE with a low fiber volume fraction. After fitting, they used a simplistic function to extrapolate the parameters of the learned DMN for another RVE with higher fiber content. The obtained parameters were then used as initialization for training the latter RVE. Huang et al. [29] built on the concept presented by Liu et al. [28] and proposed the so-called microstructure-guided DMN (MgDMN), based on a parameter space defined by orientation state and volume fraction. The previous two methods are a posteriori interpolation strategies in the sense that new DMNs are obtained through post-processing. In contrast, Gajek et al. [30] proposed an a priori interpolation strategy. They modified the formulation of DMN such that orientation angles in the network are themselves functions of the fiber orientation tensor [31] of short-fiber reinforced composites. They trained this modified DMN for selected cases in the fiber orientation space and then used it to interpolate properties for other microstructures within that space. These approaches [28,29,30] have contributed significantly to facilitating the application of DMN to multiple microstructures.

Apart from DMN, other research works have established the feasibility of directly learning from microstructure data. We may list works utilizing convolutional neural networks (CNNs) [15,16,17, 32]. Yang et al. [15] combined CNN and principal component analysis (PCA) to predict the nonlinear behavior of composite microstructures from their image representation. Eidel [17] used a 3D CNN architecture to predict the homogenized elastic properties of two-phase microstructures under different types of boundary conditions. Besides convolutional neural networks, graph neural networks (GNNs) [18,19,20] have recently gained in popularity in the sphere of material modeling. For instance, Vlassis et al. [18] used GNNs to predict the hyperelastic energy functionals of polycrystals. To do so, they designed a hybrid network architecture. GNNs [33] performed unsupervised classification, transforming the graph representation of polycrystals into feature vectors. A multi-layer perceptron performed the regression task of predicting energy, making predictions about energy functionals based on the feature vector and the polycrystals’ second-order right Cauchy-Green deformation tensor. Vlassis and Sun [19] used a graph auto-encoder neural network architecture to compress so-called plasticity graphs into vectors of internal variables. Nonetheless, these models lack the key benefit of DMN. They cannot be used to simulate material nonlinearity if trained on linear elastic data.

Despite this wealth of progress, research leveraging ML to learn from microstructure data in order to generalize DMN is currently non-existent in the literature. Hence, we pioneer in this work the use of ML-based microstructure informatics [34] to fill this gap in the research on DMN. In this regard, we can either start from the image representation of microstructures (hence using CNNs) or their graph representation (hence using GNNs). Given the straightforwardness of converting meshes from our mesh-based RVE tool into graphs, we select the latter. Learning from the graph data of microstructures frees us from the constraint of being restrained to a specific material system. This is because graphs can store features representing microstructural properties within their nodes, such as material phase at a given location. Switching from one material system (e.g., composites) to another (e.g., polycrystals) suffices to alter the features stored in graph nodes. We term our model a hybrid graph neural network-deep material network (GNN-DMN) model. It learns to derive DMNs based on the graph representation of microstructures. Each derived DMN is a stand-alone model. In other words, during inference, the GNN-based part of the hybrid model is used only once to set parameters for the derived DMNs. Afterward, each derived DMN can be used independently for linear or nonlinear predictions, such that their prediction speed remains the same as for conventional DMNs.

We subsequently introduce our framework and the rationale behind it in Sect. 2. Section 3.1 introduces our approach to viewing microstructures as graphs. In Sect. 3.2, we present the architecture of our hybrid GNN-DMN model through which we first transform graphs into geometric feature vectors. Then, we explain the process of deriving new DMNs given these geometric feature vectors. Section 3.3 details the data flow in the model during offline training and online prediction, while Sect. 4 describes the generation of the data necessary for training. With the necessary knowledge laid out, we present practical examples of using the model in Sect. 5. We show its successful use for microstructures with circular inclusions in Sect. 5.1 and others with ellipse-shaped inclusions in Sect. 5.2. Finally, we conclude with discussions and conclusions in Sects. 6 and 7, and provide some possible directions for future research endeavors.

2 Framework

The framework used in this work is depicted in Fig. 1. Microstructures are modeled as graphs, encoding relevant microscopic details. As such, these graphs serve as approximate representations of the microstructures. Subsequently, we use machine learning, mainly GNNs, to learn to extract relevant features from these graphs. These extracted features are transformed into parameters characterizing equivalent DMNs for the microstructures under consideration. The GNN-DMN model derived from this process is fine-tuned based on the microstructures encountered during the training phase. Once the GNN-DMN model has been calibrated, it can effortlessly generate new DMN parameters for any input microstructure (graph) provided to it. Such DMNs are inference-ready and can be used independently for linear or nonlinear predictions. The rationale underlying this approach is subsequently detailed in the rest of this section.

Table 1 Features assigned to each graph node

Based on the original formulation by Liu et al. [21], a DMN tree of N layers is defined by two sets of parameters: rotation angles $\theta ^{k}_{h=0,1,...,N}$ at every node, and weights $w^{k}_{N}$ (derived from so-called activations $z^{k}_{N}$) at nodes in the bottom layer N. Here, the subscripts denote the layer of the tree, while the superscripts refer to the position of a node at a specific layer. For simplicity, we utilize a flattened representation $\varvec{p}=\texttt {concat(} z^{k}_{N}, \theta ^{k}_{h}\varvec{)}$ by concatenating the activations and rotation angles of DMN. DMN aims to predict the homogenized compliance matrix $\bar{\varvec{D}}$ of a RVE. This process can be expressed by the following function $\mathcal {\varvec{F}}$ such that

$$\begin{aligned} \bar{\varvec{D}} = \mathcal {\varvec{F}}(\varvec{D}^{1}, \varvec{D}^{2} | \, \varvec{p}) \end{aligned}$$

(1)

where ${\varvec{D}}^{1}$ and ${\varvec{D}}^{2}$ respectively refer to the compliance matrices of phase 1 and phase 2 in a two-phase RVE. $\mathcal {\varvec{F}}$, which is a function of the input ${\varvec{D}}^{1}$ and ${\varvec{D}}^{2}$, is parameterized by $\varvec{p}$. Liu et al. [21] demonstrated that the weights in a trained DMN network reflect the material volume fractions of its corresponding RVE. Subsequent studies [22, 25, 27, 29] corroborated this fact. Huang et al. [29] later showed the ability of DMN to predict, via its learned orientation angles, the orientation tensors of short-fiber reinforced polymer (SFRP) composites. Several papers [21, 22, 25, 28, 30] have substantiated the link between the parameters learned by DMN and the geometry of microstructures. For these reasons, we postulate that the parameters $\varvec{p}$ in any trained DMN model can be expressed as functions of the physical domain $\varvec{\Omega }$ of the microstructure it represents. Based on this postulate, we may write

$$\begin{aligned} \varvec{p} = \varvec{p}(\varvec{\Omega }) \end{aligned}$$

(2)

such that $\varvec{p}$ is dependent on the physical domain $\varvec{\Omega }$. Hence, the homogenization function $\mathcal {\varvec{F}}$ in Eq. (1) can be re-written to obtain a more general function $\mathcal {\varvec{M}}$ as

$$\begin{aligned} \bar{\varvec{D}} = \mathcal {\varvec{M}}(\varvec{D}^{1}, \varvec{D}^{2}| \, \varvec{p}(\varvec{\Omega })) \end{aligned}$$

(3)

where $\mathcal {\varvec{M}}$ is parameterized by $\varvec{p}(\varvec{\Omega })$. While Eq. (1) was restrictive, such that the trainable parameters could only be optimized for a single microstructure, Eq. (3) is more comprehensive. It allows the parameters to be explicit functions of the physical domains $\varvec{\Omega }$ they aim at capturing. This provides increased flexibility whereby multiple microstructures can be simultaneously trained. The function $\mathcal {\varvec{M}}$ takes into account all the key elements affecting the computation of average properties in a homogenization process, namely the physical domain $\varvec{\Omega }$ of the microstructure and the properties of its constituent materials (i.e., $\varvec{D}^{1}, \varvec{D}^{2}$). Naturally, the form of Eq. (3) begs the question of how to derive parameters $\varvec{p}$ from arbitrary domains $\varvec{\Omega }$. We will demonstrate the feasibility of this idea by viewing discretized meshes of microstructures as graphs.

3 Hybrid graph neural network-deep material network model

3.1 Microstructure informatics

3.1.1 From meshes to graphs

Our end goal is to compute the average properties of RVEs. The solution to this micro-scale problem traditionally involves approximating the continuous domain of the RVE with a finite set of discrete mesh elements through the process known as discretization. The discretization of a domain $\varvec{\Omega }$ can be mathematically represented as follows

$$\begin{aligned} \varvec{\Omega } \approx \varvec{M} = (\mathbb {N}^{M}, \mathbb {F}^{M}, \mathbb {E}^{M}) \end{aligned}$$

(4)

Fig. 2

Meshes are transformed into equivalent graphs as follows. Each element in a mesh is regarded as a node in a graph, with the connectivity of the graph nodes reflecting the connectivity of the mesh elements. Moreover, node features are assigned to the nodes to encode important details about the geometry of the underlying microstructures

where $\varvec{\Omega }$ is the continuous domain of a RVE. $\varvec{M}$ is the discretized mesh approximating this domain; it is a triple constituted by a set $\mathbb {N}^{M}$ of mesh nodes, a set $\mathbb {F}^{M}$ of mesh elements and a set $\mathbb {E}^{M}$ of element edges. In 2D, each element edge in $\mathbb {E}^{M}$ links two nodes in $\mathbb {N}^{M}$, such that $\mathbb {E}^{M} \subseteq \mathbb {N}^{M} \times \mathbb {N}^{M}$ is a set of ordered pairs from $\mathbb {N}^{M}$. As to the mesh elements in $\mathbb {F}^{M}$, each is uniquely defined by an ordered list of nodes in $\mathbb {N}^{M}$. For instance, if the mesh is linear triangular, then $\mathbb {F}^{M} \subseteq \mathbb {N}^{M} \times \mathbb {N}^{M} \times \mathbb {N}^{M}$. If quadrilateral elements are used, then $\mathbb {F}^{M} \subseteq \mathbb {N}^{M} \times \mathbb {N}^{M} \times \mathbb {N}^{M} \times \mathbb {N}^{M}$.

Inspired by previous works [18,19,20], we view the meshes $\varvec{M}$ as graphs. In the context of graph theory, a graph $\varvec{G} = (\mathbb {V}^{G},\mathbb {E}^{G})$ is a two-element tuple of a set $\mathbb {V}^{G} = \{ v^{G}_{i} \}_{i=1}^{n}$ of n graph nodes (or vertices) and a set $\mathbb {E}^{G}$ of edges (or links) that capture the relationships among the graph nodes. $\mathbb {E}^{G}$ is a set of ordered pairs from $\mathbb {V}^{G}$ such that $\mathbb {E}^{G} \subseteq \mathbb {V}^{G} \times \mathbb {V}^{G}$. Using the following correspondence, we transform meshes $\varvec{M}$ into graphs $\varvec{G}$. Given the discretized mesh $\varvec{M}$, each mesh element $f^{M}_{i}$ within it is regarded as a graph vertex $v^{G}_{i}$ in a graph $\varvec{G}$. In other words, we resort to the mapping $\varvec{\phi }$,

$$\begin{aligned} \varvec{\phi }: \mathbb {F}^{M} \rightarrow \mathbb {V}^{G} \end{aligned}$$

(5)

where $\varvec{\phi }$ is a bijection as there is a one-to-one correspondence between $\mathbb {F}^{M}$ and $\mathbb {V}^{G}$. Each vertex in the graph is paired with exactly one element in the mesh. Conversely, each element in the mesh corresponds to a graph vertex. If any two mesh elements respectively $f^{M}_{i}$ and $f^{M}_{j}$ share at least a mesh node (i.e., $f^{M}_{i} \cap f^{M}_{j} \ne \varnothing$), an edge is deemed to exist between their corresponding vertices in the graph. This correspondence yields a mapping $\varvec{\psi }$

$$\begin{aligned} \varvec{\psi }: \mathbb {N}^{M} \rightarrow \mathbb {E}^{G} \, | \, \forall e^{G}_{i} \in \mathbb {E}^{G}, \, \exists n^{M}_{j} \in \mathbb {N}^{M}, \, \varvec{\psi }(n^{M}_{j})=e^{G}_{i} \end{aligned}$$

(6)

where unlike $\varvec{\phi }$, $\varvec{\psi }$ is a surjection. For each edge $e^{G}_{i}$ in the graph $\varvec{G}$, there exists at least a mesh node $n^{M}_{j}$ in the mesh $\varvec{M}$ corresponding to it. This is because two mesh elements may have more than one node in common. Transforming meshes into graphs via the introduced mappings $\varvec{\phi }$ and $\varvec{\psi }$ yield a data structure encoding information about the relationships among mesh elements. However, an additional link remains for the graphs to fully represent microstructures, namely geometric features at the microscopic level.

3.1.2 Encoding microstructural details in graphs

We consider the physics of microstructures through node features (Fig. 2). Each node $v^{G}_{i}$ in the graph $\varvec{G}$ is associated with a node feature vector $\varvec{h}_{i}$. Important information characterizing the microstructures may be stored in these feature vectors. The nature of such information may vary depending on the problem at hand (e.g., polycrystalline, composite materials). In this work, we are first tackling the modeling of composite microstructures. Hence, we consider four features relevant to this task and list them in Table 1.

The vector $\varvec{h}_{i}$ represents the feature vector for a given graph node. We then refer to the set of all node feature vectors as $\mathbb {H} = \{ \varvec{h}_{i} \}_{i=1}^{|\mathbb {V}^{G}|}$, and update the definition of the graph $\varvec{G}$ such that

$$\begin{aligned} \varvec{G} = (\mathbb {V}^{G},\mathbb {E}^{G}, \mathbb {H}) \end{aligned}$$

(7)

where it is constituted by a set $\mathbb {V}^{G}$ of graph nodes, a set $\mathbb {E}^{G}$ of node edges, and a set $\mathbb {H}$ of node feature vectors. We must notice that the graph $\varvec{G}$ holds virtually all information about the domain $\varvec{\Omega }$ of microstructures. Hence, we may regard $\varvec{G}$ as a reliable estimation of $\varvec{\Omega }$. Recalling the expression for estimating the parameters of DMN in Eq. (2), we may then write an approximation of this function as

$$\begin{aligned} \varvec{p} = \varvec{p}(\varvec{\Omega }) \approx \varvec{p}(\varvec{G}) \end{aligned}$$

(8)

which conveys that the parameters $\varvec{p}$ are approximately functions of graphs $\varvec{G}$. Estimating $\varvec{p}$ can then be narrowed down to processing graph data through appropriate functions. For this purpose, we turn to graph neural networks and fully-connected neural networks.

3.2 Model architecture

We propose a hybrid graph neural network-deep material network (GNN-DMN) model (Fig. 3) that seeks to predict the homogenized tangents $\bar{\varvec{D}}$ of microstructures from their graph representation $\varvec{G}$ and material properties: $\varvec{D}^{1}$ and $\varvec{D}^{2}$. The model consists of two segments. The first segment, termed as graph-based feature extraction, aims to compress the input graphs $\varvec{G}$ into fixed-size vectors. The purpose here is to extract relevant features from the complex graph data. Such vectors would theoretically contain a reduced form of the geometry encoded in the initial graphs. Hence, we hereafter refer to these vectors as geometric feature vectors. The second segment, referred to as microstructure-informed transformation, utilizes the geometric feature vectors to generate DMNs tailored for each input graph. We subsequently elaborate on the internal mechanisms of these two segments.

Fig. 3

Overall architecture of the proposed GNN-DMN model. The model first encodes the graph representations $\varvec{G}$ of various microstructures into corresponding geometric feature vectors $\varvec{X}_{feats}$. It then derives separate DMNs from these feature vectors; the parameters of a universal DMN, relied on during this step, are optimized during training. The thus derived DMNs can be used to predict the homogenized properties of the various input microstructures

3.2.1 Graph-based feature extraction

As mentioned previously, the objective in this segment is to compress large graph data into fixed-size vectors. The initial features encoded at the graph nodes are a choice dependent on the task in the target. For our purpose of the graphs representing the microstructures as faithfully as possible, we encoded four features at the graph nodes (Table 1). With each graph node corresponding to a mesh element, we considered the area of each mesh element, the xy coordinates of its centroid, whether that element is in the matrix or inclusion phase, and finally, whether the element is on the boundary of the microstructure. The total dimension of the starting graph node features amounts hence to 7 (Table 1).

We start by performing message passing (MP) on the initial graphs. Message passing is the terminology used to describe the procedure by which a node in a graph neural network aggregates information from its neighborhood and updates its own state. Many message-passing formulations have been proposed in various graph neural network variants. We may mention GCN [33], GraphSAGE [35], GAT [36], GATv2 [37], etc. We carry out message passing through GATv2, which we selected for its expressive dynamic attention and superior performance [37] over other popular counterparts. These characteristics of GATv2 would facilitate the model to pay attention to the details distinguishing different microstructures. Optimally, the features should be projected into higher dimensions to facilitate the acquisition of complex and useful insights. For that, we selected a dimension of $d=64$, with which our model has yielded good results. Nevertheless, a different size could also be chosen. Message passing, however, restricts information sharing to the vicinity of the graph nodes. Given that our goal is to extract global features, we juxtapose the MP layers with fully connected layers. Simply put, these fully-connected layers change the graph node data without taking into account their connectivity. This trick facilitates the transmission of information farther than the immediate neighborhood of the nodes. This entire process, which is depicted by the left part of the box in Fig. 4, is also listed in Table 2. The superscripts $(\bullet )$ in Table 2 are used to differentiate between input and output data, as well as between the different network layers or parameters. The message passing process MP for GATv2 has been described in Appendix A. Weights $\varvec{W}^{(l)}$ and biases $\varvec{b}^{(l)}$ have also been defined for fully-connected layers in Appendix A.

Fig. 4

The first segment of the model through which the graph representations of microstructures are compressed into feature vectors, retaining meaningful information about them

Table 2 Transformation of graph node features through message passing and fully connected layers

At the current stage, each microstructure is still represented by a graph, with the main change being that the content and dimension of the node features have been modified. In the context of graph neural networks, the number of nodes among graph samples does not need to be the same. However, we want to collapse each graph into a single vector. In other words, we wish to infer global graph features from local node features. For that purpose, one can resort to an array of choices for graph pooling [38] operations such as average pooling, TopKPooling, DiffPool, etc. We selected average pooling, which bears similarities with the task of homogenization, as follows

$$\begin{aligned} \varvec{y}^{(0)} = \frac{1}{ |\mathbb {H}^{(4)}| }\sum _{\varvec{h}_{i} \in \mathbb {H}^{(4)}} \varvec{h}_{i} \end{aligned}$$

(9)

Here, $\varvec{y}^{(0)}$ denotes the graph-level feature vector obtained by averaging over the node feature vectors in $\mathbb {H}^{(4)}$ (Table 2).

Following the obtention of graph-level features through pooling, two fully connected layers map the pooled $\varvec{y}^{(0)}$ to the final output $\varvec{X}_{feats}$ containing learned relevant information about the input graph. This stage is illustrated in the right part of the box in Fig. 4 and also listed in Table 3. We used a softmax function in the last layer to express the output in terms of probabilities. Nevertheless, other activation functions could also be experimented with. At this final layer, we reduced the dimension of the vector to $d=32$. For a discussion on the influence of the size of d, please see the comments in Sect. 6.

Table 3 Transformation of the pooled global graph features into $\varvec{X}_{feats}$

In summary, the sequence of operations in this segment may be succinctly expressed through the following function $\mathcal {\varvec{H}}$

$$\begin{aligned} \varvec{X}_{feats} = \mathcal {\varvec{H}}(\varvec{G} \, | \, \Theta _{\mathcal {\varvec{H}}}) \end{aligned}$$

(10)

in which $\varvec{X}_{feats}$ denotes the learned geometric feature vector. $\mathcal {\varvec{H}}$ represents the chain of operations described above. It takes graphs $\varvec{G}$ as input and is parameterized by $\Theta _{\mathcal {\varvec{H}}}$ which refers to the fitting parameters of the neural networks in use.

3.2.2 Microstructure-informed transformation

In the second segment (Fig. 5), we exploit the global feature vector $\varvec{X}_{feats}$ given by Eq. (10). Since it is already embedded with essential information about the input graphs, we could use it alone to infer the parameters $\hat{\varvec{p}}$ of the target DMNs. However, we employ an alternative strategy that appears more easily trainable. Alongside $\varvec{X}_{feats}$, we utilize the parameters $\bar{\varvec{p}}$ of a universal DMN to infer the targets $\hat{\varvec{p}}$. This DMN is universal in the sense that it is used to infer $\hat{\varvec{p}}$ for all the input microstructures. Moreover, its parameters $\bar{\varvec{p}}$ are learnable, entailing that they are optimized based on the sample microstructures encountered during training. The depth of DMN trees is to be chosen in proportion to the complexity of the problem at hand. Previous works [21, 28] have shown that a DMN of $N=5$ layers should be appropriate for the category of 2D matrix-inclusion composites, which we will be considering. Hence, we set the depth of the universal DMN to $N=5$. Likewise, we consider the target trees to have the same number of layers. This setup leads the total number of parameters in $\bar{\varvec{p}}$ and $\hat{\varvec{p}}$ to be equal to $d=3\times 2^{N}-1=95$.

Fig. 5

The second segment of the model where the information from learned feature vectors is leveraged to derive new DMNs

We utilize three layers of fully connected networks (Table 4) to obtain $\hat{\varvec{p}}$ from a series of nonlinear transformations applied to the compressed feature vector $\varvec{X}_{feats}$ and the flattened representation of the parameters $\bar{\varvec{p}}$ of the universal DMN model. The input to the first layer is simply the concatenation $\texttt {concat}(\varvec{X}_{feats}, \bar{\varvec{p}})$, having a dimension $d=32+95=127$. We used Softplus as the activation function in the final layer to guarantee the positiveness of the output values. This is necessary as no weights can be negative in the DMN parameters [21]. The transformation sequence listed in Table 4 may be expressed as the function $\mathcal {\varvec{T}}$ such that

$$\begin{aligned} \hat{\varvec{p}} = \mathcal {\varvec{T}}(\varvec{X}_{feats}, \bar{\varvec{p}} \, | \, \Theta _{\mathcal {\varvec{T}}}) \end{aligned}$$

(11)

where $\mathcal {\varvec{T}}$ is parameterized by $\Theta _{\mathcal {\varvec{T}}}$, which represents the fitting parameters of the fully-connected networks.

Table 4 Sequence of transformations used to obtain the derived DMN parameters $\hat{\varvec{p}}$

Unlike the original formulation of DMN in which the parameters for a given microstructure are found by optimizing Eq. (1), they are here obtained through a combination of the functions $\mathcal {\varvec{H}}$ and $\mathcal {\varvec{T}}$, respectively given in Eqs. (10) and (11). We may merge these two equations as

$$\begin{aligned} \hat{\varvec{p}}= \mathcal {\varvec{T}}(\mathcal {\varvec{H}}(\varvec{G} \, | \, \Theta _{\mathcal {\varvec{H}}}), \bar{\varvec{p}} \, | \, \Theta _{\mathcal {\varvec{T}}}) \end{aligned}$$

(12)

By further simplifying Eq. (12), we may write

$$\begin{aligned} \hat{\varvec{p}} = \hat{\varvec{p}}(\varvec{G} \, | \, \Theta _{\mathcal {\varvec{H}}}, \Theta _{\mathcal {\varvec{T}}}, \bar{\varvec{p}}) \end{aligned}$$

(13)

which simply means that the derived parameters $\hat{\varvec{p}}$ are a function of the input graphs $\varvec{G}$. This function is parameterized by the parameters $\Theta _{\mathcal {\varvec{H}}}$ and $\Theta _{\mathcal {\varvec{T}}}$ of the neural networks in the graph-based feature extraction and microstructure-informed transformation steps, as well $\bar{\varvec{p}}$ of the universal DMN.

3.3 Data flow in model

3.3.1 Offline training

Before revealing the performance of the model, we pause to explain the data flow in it during offline training and online prediction (Fig. 6). First, we start with offline training. A DMN defined by the parameters $\hat{\varvec{p}}$ obtained via Eq. (13) can take any $(\varvec{D}^{1}, \varvec{D}^{2})$ pair and predict the homogenized tangent $\bar{\varvec{D}}$ for the microstructure represented by the corresponding graph $\varvec{G}$. By reference to Eq. (3), we may write the predictions of this DMN as

$$\begin{aligned} \bar{\varvec{D}} = \mathcal {\varvec{M}}(\varvec{D}^{1}, \varvec{D}^{2} \, | \, \hat{\varvec{p}}) \end{aligned}$$

(14)

We may substitute Eq. (13) into Eq. (14) such that

$$\begin{aligned} \bar{\varvec{D}} = \mathcal {\varvec{M}}(\varvec{D}^{1}, \varvec{D}^{2} \, | \, \hat{\varvec{p}}(\varvec{G} \, | \, \Theta _{\mathcal {\varvec{H}}}, \Theta _{\mathcal {\varvec{T}}}, \bar{\varvec{p}})) \end{aligned}$$

(15)

By separating the input data from the free parameters in Eq. (15), we may write the function $\mathcal {\varvec{M}}$ for the entire model as

$$\begin{aligned} \bar{\varvec{D}} = \mathcal {\varvec{M}}(\varvec{G}, \varvec{D}^{1}, \varvec{D}^{2} \, | \, \Theta _{\mathcal {\varvec{H}}}, \Theta _{\mathcal {\varvec{T}}}, \bar{\varvec{p}}) \end{aligned}$$

(16)

The inputs to the model are the graph representation $\varvec{G}$ of microstructures and the tangents $\varvec{D}^{1}, \varvec{D}^{2}$ of their constituent materials. Its fitting parameters are $\Theta _{\mathcal {\varvec{H}}}$, $\Theta _{\mathcal {\varvec{T}}}$, and $\bar{\varvec{p}}$, which have already been defined. The final outputs of the model $\mathcal {\varvec{M}}$ are homogenized tangents $\bar{\varvec{D}}$. For details regarding the prediction of homogenized tangents through DMN, we refer interested readers to consult previous works [1, 21].

Fig. 6

Illustration of the data flow in the model. During training, the graph-based model learns to derive DMNs to predict homogenized tangents $\bar{\varvec{D}}$. The model can produce new DMNs based on newly given microstructures during its online use. These given DMNs can, in turn, be used to model the nonlinear response of such microstructures

By comparing Eq. (16) with Eq. (1), we notice why this new formulation enables us to handle multiple microstructures. For Eq. (1), a single microstructure and its material properties are selected. From there, the network is fitted for this microstructure alone. In contrast, Eq. (16) additionally considers the graph representation $\varvec{G}$ of a given microstructure. As such, the homogenized $\bar{\varvec{D}}$ is dependent, not only on $\varvec{D}^{1}$ and $\varvec{D}^{2}$, but also on $\varvec{G}$. As a result, it suffices to change the input graph to the network to simulate the response of other microstructures. Using the same input material properties but different graphs would result in different homogenized $\bar{\varvec{D}}$. During fitting, multiple microstructures are simultaneously trained. The parameters of the model to be optimized are $\Theta _{\mathcal {\varvec{H}}}$, $\Theta _{\mathcal {\varvec{T}}}$, and $\bar{\varvec{p}}$. To penalize the departures of predictions from target values, the following cost function [21] is defined:

$$\begin{aligned} J_{0}( \mathcal {M}) = \frac{1}{2N_s} \sum _{i}^{N_s} \frac{ \Vert \bar{\varvec{D}}_{i} - \bar{\varvec{D}}_{i}^{DNS} \Vert _{F}^{2}}{\Vert \bar{\varvec{D}}_{i}^{DNS}\Vert _{F}^{2}} \end{aligned}$$

(17)

$\bar{\varvec{D}}_{i}$ and $\bar{\varvec{D}}_{i}^{DNS}$ respectively denote values predicted by the model and obtained via direct numerical simulation. $N_s$ is the number of samples being considered. $\Vert \cdot \Vert _{F}$ denotes the Frobenius norm. The Frobenius norm $\Vert \varvec{A} \Vert _{F}$ of a matrix $\varvec{A}$ is defined as

$$\begin{aligned} \Vert \varvec{A} \Vert _{F} = \sqrt{ \sum _{i=1}^{m} \sum _{j=1}^{n} |a_{ij}|^2 } \end{aligned}$$

(18)

Besides the initial cost in Eq. (17), we additionally subject the weights at the bottom layer of the universal DMN to the arbitrary constraint:

$$\begin{aligned} \sum _{i}^{2^N} \bar{w}_{N}^{i} = \alpha \end{aligned}$$

(19)

$\alpha$ is a scalar that controls the magnitudes of its fitted weights. We choose to set it equal to $2^{N-2}$ as in these works [21, 22, 28]. The final cost function applied to the outputs of the model $\mathcal {M}$ is

$$\begin{aligned} J(\mathcal {M}) = J_{0}(\mathcal {M}) + \lambda L(\bar{w}) \end{aligned}$$

(20)

with the scalar $\lambda$ being a hyperparameter to be selected, and $L(\bar{w}_{N}^{k})$ being equal to

$$\begin{aligned} L(\bar{w}_{N}^{k}) = \left( \sum _{k}^{2^N} \bar{w}_{N}^{k} - \alpha \right) ^2 \end{aligned}$$

(21)

such that

$$\begin{aligned} J(\mathcal {M}) = \frac{1}{2N_s} \sum _{i}^{N_s} \frac{ \Vert \varvec{\bar{D}}_{i} - \varvec{\bar{D}}_{i}^{DNS} \Vert _{F}^{2}}{\Vert \varvec{\bar{D}}_{i}^{DNS}\Vert _{F}^{2}} + \lambda \left( \sum _{k}^{2^N} \bar{w}_{N}^{k} - \alpha \right) ^2 \end{aligned}$$

(22)

Equation (22) is the final cost function used throughout the training process. We implemented all the aspects of our model using the Pytorch [39] machine learning framework, taking advantage of its automatic differentiation system [40] to implement DMN. We used its built-in modules to define the fully connected networks and utilized the implementation by PyTorch Geometric [41] of GATv2. During training, learning rates of $10^{-2}$ and $10^{-4}$ were used to respectively tune the parameters of the universal DMN in the two examples that will be introduced in Sect. 5. As to the remaining parameters of the model, a learning rate of $10^{-4}$ was used in both cases.

3.3.2 Online prediction

After training, the optimal parameters $\Theta _{\mathcal {\varvec{H}}}$, $\Theta _{\mathcal {\varvec{T}}}$, and $\bar{\varvec{p}}$ of the model are fully determined. From Eq. (13), we notice that a given derived DMN $\hat{\varvec{p}}$ is completely defined by these learned parameters. Thus, during inference, we use Eq. (13) as an initialization step to obtain $\hat{\varvec{p}}$ for any given microstructure. The thus-obtained parameters define a stand-alone DMN model (Fig. 6). This particularity allows us to take full advantage of all the benefits traditionally accompanying DMNs. We can use this derived DMN to predict linear elastic properties and employ a Newton–Raphson scheme to carry out nonlinear predictions, as shown in previous works [21, 22]. Results demonstrating this capability of the GNN-DMN model to yield stand-alone DMNs able to model nonlinearity will be presented in Sect. 5.

4 Data generation

4.1 Generation of microstructures

We generate RVEs for training the model based on the random sequential adsorption (RSA) method [42]. Before starting the process, we select the microstructural descriptors of the RVEs. For instance, we might wish to generate microstructures with circular, fixed-size inclusions embedded in the matrix material. In this case, the determinant microstructural descriptor would be the inclusion volume fractions. Then, based on the target descriptors, we determine the required quantity of inclusions to be dispersed in the matrix.

At the initialization of the process, we start with an empty surface of the matrix. Then, we select a particle and randomly place it within that surface. Since this is the first particle placement, overlapping is not an issue. We then turn to the next particle and try to place it in a new location. Because of a pre-existing inclusion in the matrix, there exists a probability of overlap with it. If such is the case, a location is resampled until it satisfies our criterion of non-collision. This procedure is repeated until all inclusions have been placed onto the RVE matrix. Besides, we use special treatments for particles positioned on the RVE boundary to ensure its periodicity. The corresponding algorithm is provided in Appendix B.

4.2 Generation of material properties

To enable the network to develop the ability to produce proper DMNs for the RVEs generated as described above, we rely on their material properties. For training, conventional DMNs predict homogenized tangents $\bar{\varvec{D}}$ from the constituent tangents $\varvec{D}^{1}$, $\varvec{D}^{2}$ of their corresponding RVEs. Thus, we prepare such material data for each microstructure. For the input properties $\varvec{D}^{1}$ and $\varvec{D}^{2}$, we sample them for each phase in the RVEs. Concerning the homogenized tangents $\bar{\varvec{D}}$, we compute them by carrying out different tests on the RVEs. The dimensionality of the RVE problem determines the number of tests required. Since our problem is a 2D one, we carry out three tests. Two of these tests are in the orthogonal directions 1 and 2, while the third is an in-plane shear test. These sets of tests, which we carried out using the RVE package [43] available in LS-DYNA, are as follows.

For the first test, we constrain the RVE with $\tilde{\epsilon }_{11} = \delta$, where $\delta$ is a non-zero small number (e.g., $\delta =10^{-12}$). The other strain components are left unconstrained. After the completion of the finite-element simulation, we obtain the stress and strain response of the RVE as:

$$\begin{aligned} \varvec{\epsilon } =[\tilde{\epsilon }_{11}, \tilde{\epsilon }_{22}, \tilde{\epsilon }_{12}]^{T}, \varvec{\sigma } = [\tilde{\sigma }_{11}, 0, 0]^{T} \end{aligned}$$

Given these, we compute three components of the fourth-rank compliance tensor $\mathbb {D}_{ijkl}$:

$$\begin{aligned} \mathbb {D}_{1111}&= \tilde{\epsilon }_{11} / \tilde{\sigma }_{11} \nonumber \\ \mathbb {D}_{2211}&= \tilde{\epsilon }_{22} / \tilde{\sigma }_{11} \nonumber \\ \mathbb {D}_{1211}&= \tilde{\epsilon }_{12} / \tilde{\sigma }_{11} \end{aligned}$$

(23)

For the second uniaxial test, we apply a macroscopic uniaxial loading $\tilde{\epsilon }_{22} = \delta$, which allows us to obtain:

$$\begin{aligned} \varvec{\epsilon } =[\tilde{\epsilon }_{11}, \tilde{\epsilon }_{22}, \tilde{\epsilon }_{12}]^{T}, \varvec{\sigma } = [0, \tilde{\sigma }_{22}, 0]^{T} \end{aligned}$$

from which we compute

$$\begin{aligned} \mathbb {D}_{1122}&= \tilde{\epsilon }_{11} / \tilde{\sigma }_{22} \nonumber \\ \mathbb {D}_{2222}&= \tilde{\epsilon }_{22} / \tilde{\sigma }_{22} \nonumber \\ \mathbb {D}_{1222}&= \tilde{\epsilon }_{12} / \tilde{\sigma }_{22} \end{aligned}$$

(24)

Finally, we apply a macroscopic shear loading $\tilde{\epsilon }_{12} = \delta$, which allows us to obtain:

$$\begin{aligned} \varvec{\epsilon } =[\tilde{\epsilon }_{11}, \tilde{\epsilon }_{22}, \tilde{\epsilon }_{12}]^{T}, \varvec{\sigma } = [0, 0, \tilde{\sigma }_{12}]^{T} \end{aligned}$$

from which we compute

$$\begin{aligned} \mathbb {D}_{1112}&= \tilde{\epsilon }_{11} / \tilde{\sigma }_{12} \nonumber \\ \mathbb {D}_{2212}&= \tilde{\epsilon }_{22} / \tilde{\sigma }_{12} \nonumber \\ \mathbb {D}_{1212}&= \tilde{\epsilon }_{12} / \tilde{\sigma }_{12} \end{aligned}$$

(25)

The homogenized compliance matrix $\bar{\varvec{D}}$ in Mandel notation is then computed using these nine values in the compliance tensor $\mathbb {D}_{ijkl}$.

5 Examples

In this section, we investigate the performance of our model. We consider two families of microstructures for that. The first example explores the application of the model to microstructures with fixed-size circular inclusions in their matrix. Such microstructures are usually described by the total volume fraction of the inclusions. However, this description is not deterministic, as there can be multiple realizations of microstructures having the same inclusion volume fraction. We include these multiple realizations in our training data. Nevertheless, we recognize the simplicity of this class of microstructures. With this in mind, we design a second example with more complex microstructures whose inclusions vary in shape, size, and orientation. Hence, the collection of these microstructures constitutes a superset of those in Example 1. The results showed the ability of the GNN-DMN model to perform well on this more difficult task. Furthermore, the model fitted on microstructures in the second example was able to yield accurate predictions for microstructures in the first example, for which it has not been trained. This capability hints at the possibility of developing a generalized model for composites with our approach. It is worth mentioning that the basis of this work is that, given an RVE, the GNN-DMN model can learn to derive a DMN for it. Hence, we did not study the influence of RVE size on the homogenized properties. However, various other publications [44, 45] have studied this aspect, which we refer the readers to consult.

5.1 Example 1: microstructures with circular inclusions

5.1.1 Dataset

In this first example, we consider microstructures with circular inclusions. Each microstructure can be globally defined by the total volume fraction $v_{f}$ of its inclusions. Nevertheless, this descriptor, namely the inclusion volume fraction $v_{f}$, is not fully representative. Generally speaking, there always exists a randomness in realizing an RVE based on global descriptors. This randomness is inherently due to the shape (i.e., size, inclination) of the inclusions and their locations. We are considering circles with a rotational symmetry of order $\infty$. Therefore, the placement of a circular inclusion is uniquely determined for a given location within the matrix. For instance, this would not be true if the inclusion were elliptical, as its orientation would have to be considered. Considering the aforementioned point, randomness can then possibly be induced by the size of the inclusions and their positions. However, we choose to set the radii of all inclusions constant. Eventually, we remain with a single source of randomness: the distributions of the circular inclusions in the RVE.

To generate the microstructures needed for training, we uniformly sample $v_{f}$, such that $v_{f} \in U[0.10, 0.40]$. We build three sets of microstructures from the volume fractions: the training (200 RVEs), validation (50 RVEs), and test (50 RVEs) set. These samplings within the prescribed volume fraction range give rise to many RVEs sharing the same global descriptors (e.g., $v_{f}$). This can readily be observed in Fig. 7, where two microstructures have the same number of inclusions. Each microstructure is then discretized into a mesh. A mixed triangular-quadrilateral elements discretization scheme has been used in all cases. The resolution of the meshes is rather fine, the number of elements varying from $\sim 7000$ to $\sim 10{,}000$. All of those meshes are transformed into graphs $\varvec{G}$ following the procedure detailed in Sect. 3.1, with the features encoded at the graph nodes being those listed in Table 2. Plots of the graph representations of sample microstructures can be seen in Fig. 7. The number of nodes in the graphs directly corresponds to the number of elements in the meshes; hence, the order of the graphs likewise ranges from $\sim 7000$ to $\sim 10{,}000$.

Fig. 7

The first row shows examples of microstructures in the training set. The second row shows their corresponding graphs, constructed from meshes. The colors are used to distinguish between graph nodes belonging to the matrix and the reinforcement

Fig. 8

Sampling of elastic properties for the constituent phases of the RVEs. Young’s modulus is constant in phase 1, while it varies in phase 2

Fig. 9

Evolution of the error on the predicted tangents and volume fractions during training of the model for 200 epochs

Besides the graphs, elastic tangents are also required as inputs within our proposed framework. Consequently, we generate 300 triples $({\varvec{D}}^{1}, {\varvec{D}}^{2}, \bar{{\varvec{D}}})$ for each microstructure via direct numerical simulations (DNS). Figure 8 shows the sampling space of the material properties used for obtaining $\varvec{D}^{1}$ and $\varvec{D}^{2}$. The constituent phases of the RVEs are assumed to be linear isotropic. The elastic moduli E and Poisson’s ratios v were sampled as follows. The Young’s modulus $E^{1}$ of phase 1 was held equal to unity, i.e. $log_{e}(E^{1})=0$. In contrast, $E^{2}$ was allowed to vary for phase 2 such that $-5 \le log_{e}(E^{2}) \le 5$. In other words, its magnitude could be $\sim 150$ times as high (or as low) as $E^{1}$. The Poisson’s ratio v for both phases was allowed to vary between 0 and 0.5. We assumed a state of plane strain such that the input compliance matrices in Mandel notation are given by

$$\begin{aligned} \varvec{D}^p = \frac{1 + v^{p}}{E^{p}} \begin{bmatrix} 1 - v^{p} &{}\quad -v^{p} &{}\quad 0 \\ -v^{p} &{}\quad 1 - v^{p} &{}\quad 0 \\ 0 &{} \quad 0 &{}\quad 1 \end{bmatrix},\quad p=1,2 \end{aligned}$$

(26)

where $E^{p}, v^{p}$ denote the Young’s modulus and Poisson’s ratio for each phase. The homogenized tangents $\bar{{\varvec{D}}}$ were obtained according to the procedure described in Sect. 4.2.

5.1.2 Offline training

The cost function detailed in Sect. 3.3.1 is used to optimize the parameters of the model. To quantify the accuracy of predicted tangents during the training process, an error function is separately defined as

$$\begin{aligned} \text {average error} = \frac{1}{N_s} \sum _{i}^{N_s} \frac{ \Vert \bar{\varvec{D}}_{i} - \bar{\varvec{D}}_{i}^{DNS} \Vert _{F}}{\Vert \bar{\varvec{D}}_{i}^{DNS}\Vert _{F}} \end{aligned}$$

(27)

Not only do we evaluate the tangents predicted by the different generated DMNs, but we also perform a sanity check on the physics of those DMNs. For that, we monitor the learned inclusion volume fractions [21] throughout the fitting process. As such, we define a volume fraction error

$$\begin{aligned} \text {volume fraction error} = \frac{1}{N_m} \sum _{i}^{N_m} \frac{ | {V_f}_{i}^{model} - {V_f}_{i}^{truth} |}{| {V_f}_{i}^{truth}|}\nonumber \\ \end{aligned}$$

(28)

in which $N_m$ represents the total number of microstructures. ${V_f}_{i}^{model}$ represents the volume fraction obtained from the parameters of created DMNs, and ${V_f}_{i}^{truth}$ represents the volume fraction which can be computed from information in the RVE mesh.

Next, we proceed to train our GNN-DMN model. We do so for 200 epochs (Fig. 9). The computed errors for the training set decreased to $2.24\%$ at the end of the fitting process. The model showed a comparable performance on the validation set, for which the error was evaluated at $2.32\%$. Not only did the model demonstrate its ability to predict the homogenized tangents accurately, but it also displayed its capacity to capture the topological information of the meshes taken as inputs. We notice errors of respectively $0.32\%$ and $0.45 \%$ on the predicted volume fractions for microstructures in the training and validation sets.

Fig. 10

Visualization of the DMN parameters (shown in (b)) generated by the model for three different microstructures (shown in (a)). The microstructures, respectively, have inclusion volume fractions of 15.95%, 33.13%, and 38.04%. In comparison, the generated DMNs predict 16.15%, 32.81%, and 37.41%

For illustration purposes, we show a visualization (Fig. 10) of the treemaps of DMNs generated for three different microstructures in the test set. A treemap is a space-filling method of visualizing tree structures [46]. Using this method, one can represent each leaf node in a DMN as rectangles occupying areas proportional to the fraction of their weight to the sum of the weights of all leaf nodes. The DMN tree structure dictates the exact location of each of these rectangles. Moreover, given that each leaf node belongs either to the matrix or inclusion, a binary color code is assigned accordingly. These RVEs, respectively, have inclusion volume fractions of 15.95%, 33.13%, and 38.04% (Fig. 10a). The corresponding DMNs (Fig. 10b) exhibit volume fractions of 16.15%, 32.81%, and 37.41%, which are close to the targets. Thus, the model effectively learned to assign different parameters depending on the input microstructure.

5.1.3 Online prediction: elastic properties

The end goal of generating different DMNs is to use them as substitutes for traditional simulation tools in the evaluation of material properties. In light of this consideration, we select a set of material properties listed in Table 5. This set corresponds to a matrix (phase 1) being elasto-plastic and the inclusions (phase) being purely elastic. We carry out DNS based on this set of values for the 50 microstructures in the test set. In a similar fashion, we use the trained DMNs to accomplish the same task as DNS.

At first, we restrict ourselves to the elastic response of the RVEs and evaluate their homogenized elastic properties. The homogenized properties which we consider are the longitudinal Young’s modulus $\bar{E}_{11}$ (Fig. 11a), the transverse Young’s modulus $\bar{E}_{22}$ (Fig. 11b) and Poisson’s ratio $\bar{v}_{12}$ (Fig. 11c). We recall that, for each volume fraction, several RVE realizations may exist. Thus, in Fig. 11, we notice multiple predictions for some volume fractions. By comparing the predictions of the model for the elastic moduli $\bar{E}_{11}$ and $\bar{E}_{22}$, we notice that the results are comparable with those of DNS. As for the homogenized Poisson’s ratio $\bar{v}_{12}$, we notice a more significant variability of the reference values for a given volume fraction. The GNN-DMN model seems to underestimate this variability. Nonetheless, the influence of this underestimation would be minor as the differences mostly occur from the third decimal place of the target values. Hence, the model is dependable in its ability to estimate elastic properties.

Table 5 Selected material properties. Phase 1 is assumed to be elastoplastic, while phase 2 is modeled to have a linear elastic behavior

Fig. 11

Predicted homogenized, a longitudinal Young’s modulus $\bar{E}_{11}$, b transverse Young’s modulus $\bar{E}_{22}$, and c Poisson’s ratio $\bar{v}_{12}$ for microstructures in the test set in comparison with numerical simulations

5.1.4 Online prediction: nonlinear responses

Next, we turn to the performance of the model when it comes to the nonlinear response of the RVEs. We consider two microstructures from the test set. For each of them, we perform three loading-unloading-reloading tests using all the properties listed in Table 5. Two are uniaxial tests in the two orthogonal directions (i.e., 1 and 2), while the last is an in-plane shear test. The results for both of them are reported in Fig. 12a and b. From inspection, we notice a close agreement between the responses predicted by the model and those determined via DNS. To be able to quantify the accuracy of the stress responses, we define the errors on the predicted stresses as [29]:

$$\begin{aligned}&\text {mean-relative error} \nonumber \\&\quad = \frac{ \frac{1}{n} \sum _{i=1}^{n} |\sigma _{i}^{DNS} - \sigma _{i}^{model}|}{\max _{i=1,...,n} |\sigma _{i}^{DNS}|} \end{aligned}$$

(29)

$$\begin{aligned}&\text {max-relative error} \nonumber \\&\quad = \frac{\max _{i=1,\ldots ,n} |\sigma _{i}^{DNS} - \sigma _{i}^{model}|}{\max _{i=1,\ldots ,n} |\sigma _{i}^{DNS}|} \end{aligned}$$

(30)

Fig. 12

a, b Nonlinear prediction with derived DMNs for selected microstructures in the test set. The properties used are those listed in Table 5. c Distribution of the errors yielded by the created DMNs for the nonlinear prediction performed based on the same properties for all microstructures in the test set

Based on the definitions given in Eqs. (29) and (30), the mean-relative errors for the three tests in Fig. 12a are $2.23\%, 3.23\%, 1.93\%$, while their max-relative errors are $5.86\%, 7.93\%, 5.39\%$. By comparison, the mean-relative errors for Fig. 12b are $2.06\%, 1.26\%, 0.33\%$, while the max-relative errors are $4.54\%, 2.78\%, 2.05\%$. These scalar values give us an indication of what curves for particular error magnitudes might resemble.

Given that we have a visual representation of what the computed stress errors look like, we repeat the same tests for all the microstructures in the test set. Figure 12c displays histograms of the computed errors for the nonlinear response of those 50 microstructures. Considering the mean-relative error, the mean of the distributions for the three tests are respectively $1.89\%$, $1.84\%$ and $1.29\%$. As to the max-relative error, the mean of the distributions are $6.65\%$, $5.54\%$ and $4.48\%$. Comparing with the statistics of Fig. 12a-b, these are reliable results. The overall training results, as well as the linear and nonlinear predictions, thus prove the capability of our model to generalize on this family of RVE well.

Fig. 13

a Sampling space of descriptors (i.e., volume fraction, number of particles, semi-axis ratio) for the RVEs. The training, validation, and test set, respectively, comprise 200, 50, and 80 RVEs. b Examples of RVEs in the training set. We notice the variety in the shape and size of inclusions in the microstructures

5.2 Example 2: microstructures with elliptic inclusions

The previous example proved the capacity of our model to learn the micromechanics of the family of RVEs with circular inclusions. Here, we attack a more challenging case of microstructures with more complex topologies.

5.2.1 Dataset

We consider RVEs with inclusions of varying quantities, shapes, and sizes. Thus, we define a three-dimensional descriptor space specified by the number of particles $N_{p}$ in each RVE, the semi-axis aspect ratio $A_{r}$ of these ellipse-shaped particles, as well as the volume fraction $v_{f}$ occupied by the particles. The actual sizes of the particles in the RVEs are deduced from $N_{p}$ and $v_{f}$. As to the orientations of the particles during their placement in the RVEs, they are assigned randomly. Based on these descriptors, we generate 200 microstructures for the training set and 50 for the validation set. We also separately generate a test set with 80 microstructures. The corresponding space of descriptors sampled through Latin hypercube sampling [47] is shown in Fig. 13a, while Fig. 13b shows examples of RVEs obtained in the training set. We readily notice the diversity among them. The microstructures vary in the sizes, shapes, and distribution of their inclusions. As in the first example, we generate 300 $({\varvec{D}}^{1}, {\varvec{D}}^{2}, \bar{{\varvec{D}}})$ for each microstructure. The material properties in this case are identical to those shown in Fig. 8.

5.2.2 Offline training

We then train the GNN-DMN model for 100 epochs (Fig. 14). At the end of the training, the model yielded an average error of $3.66\%$ for RVEs in the training set and $3.93\%$ for those in the validation set. As to the physics learned by the generated DMNs, they are also accurate. We observe volume fraction errors of $1.66\%$ and $1.84\%$ for the training and validation sets.

Fig. 14

Evolution of the errors on the predicted tangents and volume fractions during training. The model was trained for a total of 100 epochs

Fig. 15

Three different microstructures from the test set are shown in (a). Corresponding treemaps from DMNs generated by the model are shown in (b)

Fig. 16

Predicted longitudinal Young’s modulus $\bar{E}_{11}$, transverse Young’s modulus $\bar{E}_{22}$ and Poisson’s ratio $\bar{v}_{12}$ for microstructures in the test set, a via direct numerical simulation and b by our GNN-DMN model

For illustration purposes, we select three dissimilar RVEs from the test set (Fig. 15a). The first one, with a low volume fraction (20.44%), has inclusions with a high aspect ratio. The second one also has inclusions with a high aspect ratio but has a a lower volume fraction (17.70%). The last one has a volume fraction of 39.11% and inclusions with a low aspect ratio. Figure 15b shows treemaps drawn from the weights in the corresponding DMNs. The volume fractions predicted are respectively 21.57%, 18.61%, and 37.92%. Although the predictions look less accurate compared with those of Example 1, it is nonetheless surprising to notice the ability of the model to generate adequate DMNs when considering the diversity of microstructures in the dataset.

5.2.3 Online prediction: elastic properties

We then proceed to scrutinize the performance of this newly fitted model in predicting the homogenized properties of RVEs in the test set using the elastic constants listed in Table 5. We utilize 3D plots (Fig. 16) whose axes correspond to the space of RVE descriptors. The color of each point indicates the result for the RVE it represents. Figure 16a shows the predicted longitudinal $\bar{E}_{11}$, transverse $\bar{E}_{22}$ Young’s moduli, and Poisson’s ratio $\bar{v}_{12}$ obtained via DNS. Figure 16b shows the same results as predicted by each DMN. A visual inspection indicates a good similarity between the two groups. But, to be more rigorous, we quantify the corresponding errors. The mean of the relative errors for $\bar{E}_{11}$, $\bar{E}_{22}$, and $\bar{v}_{12}$ are respectively $1.55\%$, $1.39\%$ and $0.96\%$.

5.2.4 Online prediction: nonlinear responses

Last but not least, we evaluate the use of the model for nonlinear predictions. We choose to consider a complex loading case in which all the in-plane strain components (i.e., $\epsilon _{11}, \epsilon _{22}$ and $\epsilon _{12}$) are constrained. We generate the load curves shown in Fig. 17 through a Gaussian process with a radial basis function (RBF) kernel. The loading considered is applied in a total of 250 steps. We then subject each RVE in the test to such a loading via DNS to obtain their stress responses. GNN-DMN is also used for the same purpose. For illustration, we show, in Fig. 18a and Fig. 18b, results for two very different microstructures. We notice comparable stress values between the results of DNS and those of GNN-DMN. To be more explicit, the mean-relative errors (Eq. (29)) are respectively $1.34\%$ and $1.01\%$, while the max-relative errors (Eq. (30)) are respectively $4.62\%$ and $3.78\%$. We further assess these errors for all the microstructures in the test set. The resulting histogram is displayed in Fig. 18c. Considering the mean-relative error, the average of the distribution is $1.24\%$, while its maximum is $1.81\%$. As to the max-relative error, the histogram values average $4.08\%$ and do not exceed $6.16\%$. Such statistics are comparable with results reported by Huang et al. [29]. Beyond the simple case in Example 1, our proposed model shows its capacity to learn the topology of more complex microstructures and derive appropriate DMNs that can be confidently used for complex nonlinear predictions.

Fig. 17

Strain loading obtained through a Gaussian process with a radial basis function kernel. The load is applied in 250 steps

Fig. 18

a, b Nonlinear prediction with interpolated DMN models for selected microstructures in the test set. The properties used are listed in the Table 5. c Distribution of the nonlinear prediction errors (for all the microstructures in the test set) yielded by the generated DMNs

6 Discussions

Table 6 Performance of the GNN-DMN model from Example 2 in predicting the nonlinear response of microstructures in the test set of Example 1

6.1 Generalization across datasets

In designing Example 2, we increased the complexity of the space used to generate the microstructures. We transitioned from a single variable, namely volume fraction, to a trio of variables, including volume fraction, aspect ratio, and the count of particles. Hence, from a set theory standpoint, we can view the collection of microstructures in Example 2 as a superset encompassing the set of microstructures in Example 1. The microstructures in Example 2 exhibited significant dissimilarities compared to those in Example 1, with none of the latter datasets appearing in the former. Nevertheless, it would be intriguing if the model fitted in Example 2 could still yield accurate results for the microstructures in the first example. Practically, this bears important implications, suggesting that there might not be a necessity to train distinct models for simple classes of microstructures. Instead, a highly general model could be trained and applied to specific applications, directly or via minor fine-tuning. We explore this possibility next.

We picked the 50 microstructures in the test set of Example 1, and then used the GNN-DMN model fitted in Example 2 to predict their nonlinear responses. The properties used for the constituent materials are identical to those use previously and outlined in Table 5. We report in Table 6 the statistics of the errors for these predictions and additionally provide in Fig. 19 instances of such predictions. Contrasting the values with those obtained in Sect. 5.1.4, we realize that the results are comparable. This observation is very promising. It points to the idea that a graph-enhanced DMN model opens the possibility of incorporating diverse training data featured with multiple microstructural descriptors to derive a universal material network for families of microstructures.

Fig. 19

Illustration of the generalization capability of the GNN-DMN model across datasets. The model obtained through training based on the microstructures in the dataset of Example 2 can be directly used to make predictions during inference for the microstructures in Example 1

6.2 Observation on the geometric feature vectors

In previous works [28,29,30], macroscopic descriptions of microstructures (e.g., volume fraction) were explicitly used to derive DMNs. In using the graph representation of microstructures, the GNN-DMN model is, from the outset, blind to the relevance of such statistical descriptors discovered through experience. With the initial graph data compressed into geometric feature vectors $\varvec{X}_{feats}$, we set out to investigate whether they can reflect the importance of certain macroscopic descriptors to the microstructures’ behavior.

For that purpose, we carry out a principal component analysis (PCA) [48] on the learned geometric feature vectors $\varvec{X}_{feats}$ for microstructures in the test set of Example 2. PCA is a dimensionality reduction technique commonly used to visualize high-dimensional data. In PCA, the data undergoes a transformation resulting in a new set of orthogonal variables known as principal components, allowing for easy identification of the largest variations in the data. Figure 20 shows scatter plots resulting from PCA, in which each dot corresponds to a geometric feature vector. For simplicity, only the first two principal components are visualized. Each dot is color-coded based on the volume fraction of the underlying microstructure on the left and the aspect ratio of the reinforcement particles on the right. We readily notice that a clear trend is captured for the volume fractions, with the magnitude increasing along the first principal axis. A similar argument, although to a lesser extent, can be made for the aspect ratio along the second principal component. Hence, one could theoretically study and infer the importance of specific macroscopic descriptors from the feature vectors. These trends revealed through PCA also provide a subtle indication of why the model trained in Example 2 could perform well on the microstructures in Example 1. The analysis here constitutes a preliminary look at this particularity. However, this is an aspect that deserves its own study.

Fig. 20

The results of PCA on the geometric feature vectors $\varvec{X}_{feats}$ produced by GNN-DMN for the microstructures in the test set of Example 2. Each dot corresponds to the embedding of a feature vector. On the left, the embeddings are color-coded based on the volume fraction of the microstructures. On the right, they are color-coded based on the aspect ratio of the inclusions in the microstructures

6.3 Hyper-parameter tuning

The previous two examples established the validity of GNN-DMN. Here, we add a few additional comments. The first regards the performance of the model if we were to train it for longer and also change the dimension of the learned geometric feature vector $\varvec{X}_{feats}$ (Eq. (10)). Figure 21 shows results for various sizes of $\varvec{X}_{feats}$ including $d=8, 16, 32$ and 64. The model was additionally trained for close to a thousand epochs. Increasing the dimension of $\varvec{X}_{feats}$ enables errors to decrease faster. As seen in the left and right plots of Fig. 21, the curves from $d=32$ and $d=64$ escape the initial “plateau” faster than when lower dimensions are used. Interestingly, the highest dimension $d=64$ did not lead to the most accurate model. Whether we consider the average tangent or volume fraction errors, the model with $d=32$ yielded the lowest values. As for the model’s reliability in predicting homogenized tangents when trained for many more epochs, additional improvements remain to be made. The validation set yields comparable errors independently of the dimension of the geometric feature vector. In contrast, the training set is more sensitive to those changes. At lower dimensions $d=8$ and $d=16$, we notice a slight overfitting of the model. The overfitting tendency becomes more accentuated when $d=32$ or $d=64$, in which cases the gap between the training and validation errors widens faster. We have not tackled overfitting in this work, but we anticipate that it is an aspect worth investigating in the future.

Fig. 21

Study of the effects of the size of the geometric feature vector on the accuracy of the trained model

6.4 Computational cost

The second aspect concerns the computational cost of GNN-DMN. The models reported in this study were trained on a Tesla V100 GPU with a memory of 32GB from NVIDIA. During the training of the examples, a batch size of 50 was utilized, which amounts to a total of $200 \times 300 \div 50 = 1200$ iterations per epoch. For instance, the model of Example 2, which was trained for 100 epochs, necessitated 23 h and 10 min to attain its reported performance. This time is equivalent to less than a day, which is very acceptable given the accuracy of the model in the results that have been reported.

We moreover compare the computational cost of the derived deep material network during online prediction against that of the RVE package in LS-DYNA. We draw the reader’s attention to the fact that we follow other works [21, 27, 49] using a CPU instead of a GPU during inference. In our experience, using DMN on GPU is more time-consuming. This is arguably due to the structure and small size of DMN. Gregg et al. [50] showed that the use of GPU is not always beneficial as, depending on the nature of the task and size of the data, the transfer of data to/from the GPU can take longer than the operation performed by the GPU. During training, the large size of GNN dominates, such that it is more efficient to train the GNN-DMN model on GPU. During inference, however, after initialization of the derived DMN parameters using the trained GNN, only the derived DMNs are utilized for nonlinear prediction through Newton–Raphson iterations, hence the choice of CPU. The efficient use of DMN on GPU is a topic that has not yet been investigated in the literature. Future research drawing inspiration from this work [8], for instance, which attained up to four orders of magnitude improvement in computational efficiency with GPU, might pave the way for that. With these details being stated, the workstation used was equipped with a 13th generation Intel Core^™ i9-13900K processor. The RVE package spent approximately 130 s on the uniaxial tests shown in Example 1 and 90 s on the loading test shown in Example 2. In comparison, derived deep material networks spent around 25 and 22 s in both cases. This corresponds to speedups 5 and 4 times, respectively. However, it is worth mentioning that the DMN implementation used in this case is not optimized, hence resulting in the difference with speedup factors previously mentioned in the literature [21, 24, 27, 49]. For instance, Liu et al. [21] reported a 150X speedup on a small strain problem. A more recently proposed and more efficient DMN (micromechanics-based material network) [27] even reported up to 4 orders of gains in speedup. Given the gap being stated, a more efficient implementation of DMN has been underway, resulting in two to three orders of gains in speedup. However, its integration into GNN-DMN is being studied and will be reported in the near future. To sum up, this increase in time efficiency with GNN-DMN is especially appealing for applications to multiscale problems in which microstructure topology at the smaller scale varies by location. Multiple deep material networks can be instantly derived using GNN-DMN and readily incorporated into a multiscale framework for faster simulations.

6.5 Microstructure representation

Lastly, we focused on using the graph representation of microstructures. We selected this approach because of the straightforward correspondence between meshes used by LS-DYNA, which we used as an RVE tool, and graphs. However, we are aware that an alternative approach would be to start from the image representation of microstructures and employ convolutional neural networks to learn from them. This research route is equally feasible, and we might explore it in the future.

7 Conclusions

In this work, we have explored the implementation of a graph-based model aimed at unifying the multiscale modeling of microstructures under a single umbrella. Whereas the original formulation of DMN focused on reducing the representation of a single RVE, our model further takes the graph representations of RVEs as input, thus making it readily applicable to different microstructures. Besides, the model generates, as part of its pipeline, parameters $\hat{\varvec{p}}$ for DMNs representing the input microstructures, thus making it a tool for compressing RVEs into equivalent DMNs. Different examples showed the capability of the model to discriminate among dissimilar microstructures. In Example 1, the model was successfully applied to various microstructures with fixed-size circular inclusions. These RVEs had a single microstructural descriptor, i.e., the inclusion volume fraction. The model learned to create corresponding DMNs with parameters reflecting this descriptor. The use of these DMNs to predict linear properties and nonlinear behavior was illustrated through several results. These capabilities were also demonstrated in Example 2, which considered microstructures with multidimensional descriptors whose inclusions varied in shape, size, and orientation. The key features of our GNN-DMN model can be summarized as follows:

• 1. We directly incorporated microstructural-level graph representations and homogenized linear elastic data to train a GNN-DMN model as the unified representation of microstructures.

• 2. The DMNs obtained through our approach are stand-alone models that can be used separately for online inference of the nonlinear behaviors of new microstructures, thus leveraging the advantages of using a model with few degrees of freedom.

• 3. The GNN-DMN model obtained from complex microstructures can be used to infer the mechanical behaviors of more simple ones, indicating that our model can potentially handle families of microstructures.

Next, we envision 3D GNN-DMNs trained on various heterogeneous material systems. These would include particle-based, fiber-reinforced composites, polycrystalline materials, etc. Such an endeavor would help accelerate our understanding of materials. Moreover, this model is a perfect candidate for developing new materials through inverse material design. Given its graph input, the model enables the possibility of designing materials at their microstructural level for specific properties. However, for this goal to be attained, extensive research must be undertaken to enhance the expressivity of the model in extracting graph features. In the distant future, our approach will open the door to the possibility of developing a large-scale model (in analogy with large language models) whose purpose would be to generate twin DMNs for a diversity of microstructures.

Appendices

Appendix A: Neural network formulations

Two types of ML models are involved in the treatment of the graph data: fully-connected neural networks and graph neural networks (specifically GATv2).

1.1 A.0.1 Fully-connected neural network

In a fully-connected neural network, an input layer, one (or many) hidden layer(s), and an output layer are sequentially stacked together with so-called activation functions to create a nonlinear mapping between inputs and outputs. Let $\varvec{h}_{i-1} \in \mathbb {R}^{F_{i-1} \times S}$ be the input to the layer i in a fully-connected network. $F_{i-1}$ is the number of features for each sample at the previous layer $i-1$, and S is the number of samples. The output $\varvec{h}_{i}$ of this layer is given by

$$\begin{aligned} \varvec{h}_{i} = \text {act} \left( \varvec{W}_i^{T} \cdot \varvec{h}_{i-1} + \varvec{b}_{i} \right) \end{aligned}$$

(A1)

with the weight matrix $\varvec{W}_{i} \in \mathbb {R}^{F_{i-1} \times F_{i}}$ and bias $\varvec{b}_{i} \in \mathbb {R}^{F_{i}}$. The symbol $\bullet ^{T}$ represents transposition. During matrix manipulation, the bias term is broadcasted along the dimension of the S samples. $\text {act}(\bullet )$ is an activation function such as the Rectified Linear Unit (ReLU) or Softplus. In the case of the ReLU, we have $\text {ReLU}(\bullet ) = \max (0, \bullet )$. If Softplus is used, then $\text {Softplus}(\bullet ) = \log (1+\exp (\bullet ))$.

1.2 A.0.2 Message passing in GATv2

Graph neural networks are tailored to learn from graph-structured data. They do so by updating the features of each node based on the features of its neighboring nodes and edges. This process is otherwise known as message passing between the nodes. Several GNN models have been proposed over the years, and they mostly differ in the way the message passing is carried out. In this work, we made use of GATv2 [37] and detail below its message passing process.

Let us consider a graph $\varvec{G} = (\mathbb {V}^{G},\mathbb {E}^{G})$. Each vertex $v^{G}_{i}$ in the set $\mathbb {V}^{G}$ is associated with a feature vector $\varvec{h}_{i} \in \mathbb {R}^{F}$. $\mathbb {R}$ here denotes the set of all real numbers, while the subscript F refers to the dimension of the vector $\varvec{h}_{i}$. The objective through message passing is to aggregate information from nodes in the neighborhood $\mathcal {N}_{i}$ of $v^{G}_{i}$ to obtain a new feature vector $\varvec{h}_{i}' \in \mathbb {R}^{F'}$ for it. Here, the neighborhood $\mathcal {N}_{i}$ refers to nodes in $\varvec{G}$ with which $v^{G}_{i}$ is connected. Some graph neural networks such as GCN [33] consider the importance of information from nodes in the neighborhood based on preset coefficients. GATv2 instead learns attention coefficients $\alpha _{ij}$ to determine the relative importance of different nodes. The scalar $\alpha _{ij}$ denotes the attention coefficient between node $v^{G}_{i}$ and another node $v^{G}_{j} \in \mathcal {N}_{i}$. To obtain $\alpha _{ij}$, a scoring mechanism $e:\mathbb {R}^{F'} \times \mathbb {R}^{F'} \rightarrow \mathbb {R}$ is first calculated as

$$\begin{aligned} e(\varvec{h}_{i}, \varvec{h}_{j}) = \varvec{a}^{T}\text {LeakyReLU} \left( \varvec{W} \cdot \texttt {concat}(\varvec{h}_{i}, \varvec{h}_{j}) \right) \end{aligned}$$

(A2)

where $\texttt {concat}(\varvec{h}_{i}, \varvec{h}_{j})$ simply means that we concatenate the two vectors. $\varvec{W} \in \mathbb {R}^{2F' \times 2F}$ is a learnable weight matrix. $\varvec{a} \in \mathbb {R}^{2F'}$ is a weight vector whose optimal values have to be trained as well. The LeakyReLU activation function is given by

$$\begin{aligned} \text {LeakyReLU}(x) = {\left\{ \begin{array}{ll} x &{} \quad \text {if } x \ge 0 \\ \beta \times x &{}\quad \text {if } x < 0 \\ \end{array}\right. } \end{aligned}$$

(A3)

in which $\beta$ is a scalar multiplier; $\beta$ is usually set by default to 0.01. The values obtained through the scoring mechanism e are then normalized through the softmax function to obtain the actual attention coefficients $\alpha _{ij}$ as

$$\begin{aligned} \alpha _{ij}&= \text {softmax}_{j} \left( e(\varvec{h}_{i}, \varvec{h}_{j}) \right) = \frac{\exp \left( e(\varvec{h}_{i}, \varvec{h}_{j}) \right) }{\sum _{v^{G}_{k} \in \mathcal {N}_{i}} \exp \left( e(\varvec{h}_{i}, \varvec{h}_{k})\right) } \end{aligned}$$

(A4)

With the relative importance $\alpha _{ij}$ computed for all nodes in the neighborhood, the updated feature vector $\varvec{h}_{i}'$ for node $v^{G}_{i}$ is found as

$$\begin{aligned} \varvec{h}_{i}' = \text {act} \left( \sum _{v^{G}_{j} \in \mathcal {N}_{i}} \alpha _{ij} \cdot \varvec{W} \varvec{h}_{j} \right) \end{aligned}$$

(A5)

in which $\text {act}(\bullet )$ is an activation function. We have used ReLU as activation function in the message passing layers. Hence, in our model

$$\begin{aligned} \varvec{h}_{i}'&= \text {MP}(\varvec{h}_{i}) = \text {ReLU} \left( \sum _{v^{G}_{j} \in \mathcal {N}_{i}} \alpha _{ij} \cdot \varvec{W} \varvec{h}_{j} \right) \end{aligned}$$

(A6)

in which MP stands for the message passing process through which the feature vector for a node $v^{G}_{i}$ is transformed. We refer to the set of all the node features in $\varvec{G}$ as $\mathbb {H} = \{ \varvec{h}_{i} \}_{i=1}^{|\mathbb {V}^{G}|}$. Referring to Eq. (A6) and abusing notation, we may write their transformation as

$$\begin{aligned} \mathbb {H}' = \text {MP}(\mathbb {H}) \end{aligned}$$

(A7)

where $\mathbb {H}'$ represents all updated node features. GATv2 further allows the flexibility of using multi-head attention [51]. However, we have not made use of it in the present work.

Appendix B: Microstructure generation

Algorithm 1

Micro-structure creation