A Hu-Washizu variational approach to self-stabilized quadrilateral Virtual Elements: 2D linear elastodynamics

Abstract

A recent mixed formulation of the Virtual Element Method in 2D elastostatics, based on the Hu-Washizu variational principle, is here extended to 2D elastodynamics. The independent modeling of the strain field, allowed by the mixed formulation, is exploited to derive first order quadrilateral Virtual Elements (VEs) not requiring a stabilization (namely, self-stabilized VEs), in contrast to the standard VEs, where an artificial stabilization is always required for first order quads. Lumped mass matrices are derived using a novel approach, based on an integration scheme that makes use of nodal values only, preserving the correct mass in the case of rigid-body modes. In the case of implicit time integration, it is shown how the combination of a self-stabilized stiffness matrix with a self-stabilized lumped mass matrix can produce excellent performances both in the compressible and quasi-incompressible regimes with almost negligible sensitivity to element distortion. Finally, in the case of explicit dynamics, the performances of the different types of derived VEs are analyzed in terms of their critical time-step size.

1 Introduction

Modern advanced applications of the Finite Element Method in the fields of fluid and solid mechanics are often jeopardized by mesh related problems, such as mesh generation, mesh distortion, mesh adaptation and problems due to incompressibility. The Virtual Element Method (VEM) is a polygonal/polyhedral Finite Element Method [1, 2] that has the potential of overcoming most of this type of problems. However, its engineering application in fields like non-linear elasticity, elastoplasticity, viscoplasticity and other strongly non-linear problems, such as contact and impact problems is still limited. While the VEM has the advantage to be almost insensitive to element distortion, allowing for non-convex polygonal or polyhedral elements with arbitrary number of edges, in most cases, it requires a non-consistent stabilization term to obtain a well-posed discrete problem. The number of singular modes to be stabilized increases with the number of edges/faces and the element formulation becomes more cumbersome as the polynomial order of the solution over the edges/faces increases. In practical engineering applications, however, the interest is focused mainly on low order elements of simple shapes, such as triangles/tetrahedra or quadrilaterals/hexahedra. This is mainly due to the existence of very effective meshing tools, highly diffused in the engineering community, that can efficiently mesh highly complicated geometries with this type of elements. The possibility to relax some of the mesh regularity constraints in the meshing process would represent a huge step forward, significantly reducing the meshing costs. Furthermore, in highly nonlinear problems, such as those mentioned above, the standard practice is to use low order elements, especially in dynamic problems, where it is of outmost importance to limit the spurious highest eigenfrequencies.

In light of the above considerations, in this paper, we extend to 2D elastodynamics the Hu-Washizu based mixed VEM formulation for quadrilaterals previously developed for 2D elastostatics [3]. For the case $k=1$, k being the displacement polynomial degree over the element edges, in [3], we proposed a VEM formulation based on the Hu-Washizu mixed variational principle. Restricting the attention to quadrilateral and pentagonal elements, we showed how it is possible to obtain self-stabilized VEs, i.e., not exhibiting any singular modes other than rigid body modes, by a suitable choice of the strain model. For the case of 4-node quadrilaterals, we were able to provide a rigorous proof of stability in [4]. The main ingredient of the formulation turned out to be the discretized compatibility operator and we presented two different approaches for its computation, one requiring additional moment Degrees of Freedom (DOFs), and the other, based on a projection of the displacement field, making use of nodal DOFs only. In both cases, the resulting VEs were self-stabilized, while preserving the distortion insensitivity feature of standard VEs. Furthermore, the self-stabilized elements with additional moment DOFs also exhibited superior performances in the incompressible limit, even though a theoretical proof of their locking-free property is still missing. The self-stabilized VEs of the first type, those requiring additional moment DOFs, are substantially identical to those proposed in [5] following an approach different from the one considered here, which is based on a Hu-Washizu variational statement. The self-stabilized elements of the second type make use of the technique proposed in [6, 7] for the computation of the integral over the element domain.

While the number of papers considering VEM formulation has grown considerably in recent times (see [8,9,10,11,12,13,14,15,16,17] as a non-exhaustive sample of papers concerning elastostatic problems), the application to elastodynamics has received so far relatively little attention. In [18], Vacca considered the numerical approximation of the wave equation with conforming virtual elements, adopting an elliptic projection operator for the stiffness matrix definition. The performance of high-order VEM for the numerical modeling of wave propagation in 2D elastic media has been investigated both theoretically and numerically in [19], proving stability and convergence of the semidiscrete approximation in the energy norm and deriving error estimates. In [20, 21], Park et al. proposed a VEM for small strains linear elastodynamics problems combined with an explicit time integration scheme. In [21], it has been shown how a B-bar VEM version can be conveniently formulated to treat incompressible and nearly incompressible problems. The low-order VEM has been extended to 2D and 3D finite strains elastodynamics by Cihan et al. in [22], where the mass matrix has been obtained as the second derivative of a potential function with respect to the nodal accelerations. Using an implicit Newmark time-integration scheme, it has also been shown that a singular (i.e., not stabilized) mass matrix can be conveniently used in most structural applications without appreciable accuracy loss.

To obtain a fully self-stabilized quadrilateral VE to be used for elastodynamics applications, in this paper we combine the self-stabilized stiffness matrices proposed in [3] with a self-stabilized mass matrix, obtained by means of a novel integration scheme, exact for linear polynomials, that makes use of nodal values only, and directly produces a lumped mass matrix. The obtained lumped mass matrix has positive diagonal entries, preserves the correct mass in the case of rigid-body modes and, being diagonal, is immediately ready for use with explicit time-integration schemes. For a recent discussion on mass-lumping schemes, see, e.g. [23, 24]. In the case that a consistent mass matrix is preferred, e.g. when implicit time integration schemes are used, we also show how this can be obtained following a standard approach [19,20,21], consisting of a projection of the unknown acceleration field onto a first order polynomial space and of a subsequent stabilization.

Two types of self-stabilized elements were proposed in [3]: elements with and without internal moment DOFs. In the first case, the presence of two additional moment DOFs requires in dynamics the imposition of non-physical initial conditions associated to these DOFs and leads to higher maximum eigenfrequencies with respect to those of an 8-DOFs 4-node element. Moreover, the physical interpretation of the lumped masses associated to these DOFs is missing, making the use of VEs with moment DOFs questionable in explicit dynamics, where a lumped mass matrix is needed and the critical time step is inversely proportional to the maximum eigenfrequency of the mesh. For these reasons, the moment DOFs are statically condensed in the stiffness matrix at the element level, allowing for their direct use with a mass matrix based on nodal accelerations only.

The convergence properties of the different VEs and their accuracy is tested on several problems, including a quasi-incompressible problem, making use of an implicit time-integration scheme. For possible usage with an explicit time-integration scheme, the eigenvalue analysis of the different elements is also comparatively discussed.

In the first part of this work, the mixed variational formulation of the 2D linear elastodynamic continuum problem is presented. Then, the virtual element discretization is introduced and the construction of the VEM mass matrix is explained in detail, for both the self-stabilized lumped version and the stabilized consistent one. Subsequently, the construction of two 4-node fully self-stabilized (in terms of both stiffness and mass matrices) VEs are presented. Finally, numerical applications are discussed to validate the proposed elements.

Voigt notation is adopted throughout this work, hence the stress tensor components are collected in the stress vector $\varvec{\sigma }$ and strain components in the strain vector $\varvec{\varepsilon }$. Moreover, the material elastic tensor is replaced by the matrix of material elastic moduli $\textbf{D}$.

2 Hu-Washizu formulation of the virtual element method for 2D linear elastodynamics

2.1 Hu-Washizu formulation of the continuum problem

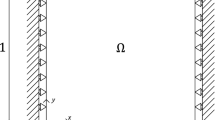
Let us consider a two-dimensional (2D) solid occupying a domain $\mathrm {\Omega } \subset \mathbb {R}^2$, whose boundary $\partial \mathrm {\Omega }$ consists of a constrained part $\partial _u\mathrm {\Omega }$ and a free part $\partial _p\mathrm {\Omega }$, with $\partial _u\mathrm {\Omega } \cap \partial _p\mathrm {\Omega } = \emptyset$ and $\partial _u\mathrm {\Omega } \cup \partial _p\mathrm {\Omega } = \partial \mathrm {\Omega }$. On the former, displacements $\bar{\textbf{u}}$ are imposed; on the latter, surface tractions $\textbf{p}$ are applied. The solid is also subjected to body forces $\textbf{b}$ and $\rho$ is the mass density. The two in-plane displacement components are gathered into the vector $\textbf{u}$ and the accelerations into the vector $\ddot{\textbf{u}}=\partial ^2\textbf{u}/\partial t^2$. The data and the unknowns of the problem depend both on the position vector $\textbf{x}$ with respect to a Cartesian reference system and on the time t. The solid body is assumed to move in the time interval $[0, t_f]$, where $t=0$ is the initial time instant and $t=t_f$ is the final one.

As starting point, we consider the definition of the three-field Hu-Washizu functional for plane elastostatics:

(1)

with $\textbf{u}=\bar{\textbf{u}}$ on $\partial _u\Omega$. In (1), is the compatibility differential operator:

(2)

where $\partial _{(\cdot )}$ represents the partial derivative with respect to $(\cdot )$. Its transpose is the equilibrium differential operator. According to the Hu-Washizu approach, no relation is assumed a priori between the three fields.

As it is well known, the first variation of the functional in (1) with respect to the three fields $\textbf{u}$, $\varvec{\varepsilon }$ and $\varvec{\sigma }$, returns the weak form of the governing equations, equilibrium, compatibility and linear elasticity, for the small strains, linear elastostatics problem. The weak form of the linear elastodynamic problem at a given time $t\in [0, t_f]$ can be obtained by simply adding the virtual work done by the inertia forces indicated as $\delta \Pi ^{in}$:

(3)

Integrating by parts the integral containing , the weak form of the governing equations is obtained:

(4)

$$\begin{aligned}&\int _\mathrm {\Omega } \delta \varvec{\varepsilon }^T(\varvec{\sigma }-\textbf{D}\varvec{\varepsilon })d\mathrm {\Omega }=0\quad \forall \delta \varvec{\varepsilon }\quad \text {constitutive law} \end{aligned}$$

(5)

(6)

where $\mathbb {N}$ is the matrix containing the components $n_x$ and $n_y$ of the outward normal $\textbf{n}$ to the boundary:

$$\begin{aligned} \mathbb {N} = \begin{bmatrix} n_x &{} \quad 0 &{} \quad n_y\\ 0 &{} \quad n_y &{} \quad n_x\\ \end{bmatrix} \end{aligned}$$

(7)

2.2 Virtual elements based on Hu-Washizu principle

The starting point of a Virtual Element scheme is the tessellation of the body $\Omega$ by means of general polygons (the elements). In this paper we only consider quadrilaterals, which, however, can be highly distorted or even non-convex. Let $\varvec{\xi }$ be the vector containing the scaled local coordinates in 2D:

$$\begin{aligned} \xi = \frac{x-x_C}{h_e}, \quad \eta = \frac{y-y_C}{h_e} \end{aligned}$$

(8)

where $x_C$ and $y_C$ are the cartesian coordinates of the element centroid and $h_e$ is the element diameter (hereafter referred to as element size).

Following the Hu-Washizu approach, an independent modeling of the three unknown fields is considered. Furthermore, accelerations are modeled by means of the same shape functions $\textbf{N}_u$ used for the displacement field:

$$\begin{aligned}&\textbf{u}(\varvec{\xi }, t)\approx \textbf{u}^h(\varvec{\xi }, t)=\textbf{N}_u(\varvec{\xi })\hat{\textbf{u}}(t), \nonumber \\&\varvec{\varepsilon }(\varvec{\xi }, t)\approx \varvec{\varepsilon }^h(\varvec{\xi }, t)= \textbf{N}_\varepsilon (\varvec{\xi })\hat{\varvec{\varepsilon }}(t) \end{aligned}$$

(9)

$$\begin{aligned}&\varvec{\sigma }(\varvec{\xi }, t) \approx \varvec{\sigma }^h(\varvec{\xi }, t)= \textbf{N}_\sigma (\varvec{\xi })\hat{\varvec{\sigma }}(t), \nonumber \\&\ddot{\textbf{u}}(\varvec{\xi }, t)\approx \ddot{\textbf{u}}^h(\varvec{\xi }, t)=\textbf{N}_u(\varvec{\xi })\ddot{\hat{\textbf{u}}}(t) \end{aligned}$$

(10)

where $\textbf{N}_u$, $\textbf{N}_\varepsilon$, $\textbf{N}_\sigma$ are the matrices of shape functions, of dimensions $2\times n_u$, $3\times n_\varepsilon$, $3\times n_\sigma$, $n_u$, $n_\varepsilon$ and $n_\sigma$ denoting the number of parameters used for the modeling of the corresponding discretized fields. It is worth noting that the shape functions in (9)–(10) depend directly on the intrinsic coordinates defined in (8), without any nonlinear geometry mapping as in isoparametric elements. The displacement shape functions in $\textbf{N}_u$ are required to be continuous across adjacent elements, whereas the interpolation functions contained in $\textbf{N}_\varepsilon$ and $\textbf{N}_\sigma$ are continuous inside each element, but may not be so across element boundaries.

From now onwards, the attention will be focused on a single quadrilateral VE, denoted by $\Omega _e$. For notation convenience, subscript e will be omitted unless strictly necessary.

As discussed in [3], strain and stress parameters in (9)–(10) are required to be generalized variables in the sense of Prager [25], that is to say that their product has to properly represent the element energy, i.e.:

$$\begin{aligned}&\hat{\varvec{\sigma }}^T\hat{\varvec{\varepsilon }} = \int _{\mathrm {\Omega }_e}\varvec{\sigma }^T\varvec{\varepsilon }d\mathrm {\Omega } = \hat{\varvec{\sigma }}^T\left( \int _{\mathrm {\Omega }_e} \textbf{N}_\sigma ^T\textbf{N}_\varepsilon d\mathrm {\Omega }\right) \hat{\varvec{\varepsilon }}, \nonumber \\&\int _{\mathrm {\Omega }_e} \textbf{N}_\sigma ^T\textbf{N}_\varepsilon d\mathrm {\Omega } = \textbf{I} \end{aligned}$$

(11)

where $\textbf{I}$ is the $n_\varepsilon \times n_\varepsilon$ identity matrix. To this end, a possible choice for the stress interpolation functions $\textbf{N}_\sigma$ is:

$$\begin{aligned}&\underset{3\times n_\varepsilon }{\textbf{N}_\sigma } = \textbf{N}_\varepsilon \left( \int _{\mathrm {\Omega }_e} \textbf{N}_\varepsilon ^T\textbf{N}_\varepsilon d\mathrm {\Omega }\right) ^{-1} = \underset{3\times n_\varepsilon }{\textbf{N}_\varepsilon }\ \underset{n_\varepsilon \times \ n_\varepsilon }{\textbf{G}^{-1}}, \nonumber \\&\textbf{G} = \int _{\mathrm {\Omega }_e} \textbf{N}_\varepsilon ^T\textbf{N}_\varepsilon d\mathrm {\Omega } \end{aligned}$$

(12)

Replacing the local element models (9) and (10) into the weak form (4) of equilibrium, one obtains the element contribution to the discretized system of dynamic equilibrium equations:

$$\begin{aligned} \textbf{M} \ddot{\hat{\textbf{u}}}+\textbf{C}^T\hat{\varvec{\sigma }}=\textbf{F} \end{aligned}$$

(13)

where $\textbf{C}$, $\textbf{M}$ and $\textbf{F}$ are defined as:

• Element compatibility matrix

  

  (14)

  with

  

  (15)

• Element consistent mass matrix

  $$\begin{aligned} \underset{n_u\times n_u}{\textbf{M}}=\int _{\mathrm {\Omega }_e}\rho \textbf{N}_u^T\textbf{N}_u d\mathrm {\Omega } \end{aligned}$$

  (16)

• Element equivalent nodal external forces vector

  $$\begin{aligned} \underset{n_u\times 1}{\textbf{F}} = \underbrace{\int _{\mathrm {\Omega }_e} \textbf{N}_u^T\textbf{b} d\mathrm {\Omega }}_{\textbf{F}^b}+\underbrace{\int _{\partial _{p} \mathrm {\Omega }_e}\textbf{N}_u^T\textbf{p}ds}_{\textbf{F}^p}= \textbf{F}^b+\textbf{F}^p \end{aligned}$$

  (17)

Replacing now (9) and (10) into the local weak forms (5)–(6) of constitutive law and compatibility, one finally obtains their corresponding discretized forms:

$$\begin{aligned} \hat{\varvec{\sigma }} = \textbf{E}\hat{\varvec{\varepsilon }} ,\quad \hat{\varvec{\varepsilon }} = \textbf{C}\hat{\textbf{u}} \end{aligned}$$

(18)

where:

$$\begin{aligned} \textbf{E} = \int _{\mathrm {\Omega }_e}\textbf{N}_\varepsilon ^T\textbf{D}\textbf{N}_\varepsilon d\mathrm {\Omega } \end{aligned}$$

(19)

is the discretized elasticity matrix of element $\Omega _e$. Replacing (18) in (13), one obtains the system of equations of motion:

$$\begin{aligned} \textbf{M}\ddot{\hat{\textbf{u}}}(t)+\textbf{K}\hat{\textbf{u}}(t) = \textbf{F}(t) \end{aligned}$$

(20)

where:

$$\begin{aligned} \underset{n_u\times n_u}{\textbf{K}} = \underset{n_u\times n_\varepsilon }{\textbf{C}^T}\ \underset{n_\varepsilon \times n_\varepsilon }{\textbf{E}}\ \underset{n_\varepsilon \times n_u}{\textbf{C}} \end{aligned}$$

(21)

is the local consistent (with the displacement and strain models) stiffness matrix, symmetric and positive semi-definite. If $n_u-n_{\varepsilon } \le 3$ and the columns of $\textbf{C}$ are linearly independent, $\textbf{K}$ has a degree of singularity equal to the number of rigid body modes in 2D (equal to three) and no stabilization is needed. Otherwise, zero-energy (hourglass) modes can arise. In this paper, we consider quadrilateral low order VE schemes for which $\textbf{K}$ does not exhibit unphysical rank deficiency. We remark that, even though in the VEM the displacement shape functions are not known, the integral in (14) can be computed. Indeed, to compute the matrix $\textbf{A}$ in (15), we integrate by parts:

(22)

The term $\textbf{A}_1$ is easily computable since the functions in $\textbf{N}_u$ are explicitly known on the element boundary. The second term $\textbf{A}_2$, when different from zero, is usually computed thanks to the introduction of internal DOFs, additional to the usual nodal DOFs on the boundary. A technique for its computation without introducing additional DOFs will be concisely illustrated in Sect. 3.4.

3 Description of the 4-node self-stabilized Virtual Elements

We now introduce the low-order quadrilateral VEM schemes on which we will focus in this paper. In order to obtain a matrix $\textbf{K}$, see (21), with the correct rank, we follow the approach detailed in [3], where two different methods have been proposed for the elastostatic problem. Both procedures are based on an enlarged strain field, containing linear terms, with respect to the standard lowest order VEM, which is characterized by constant strains inside the element. The main difference between the two procedures lies in the number of adopted displacement degrees of freedom. The first technique makes use of two additional internal moment DOFs, whereas the second one involves only nodal displacement DOFs. For the first procedure, a local condensation of the two internal moment DOFs is introduced. Moreover, this condensation, which does not affect the excellent behavior in the nearly-incompressible regime, permits to use the mass matrix of the 4-node element without moment DOFs, allowing for a more physical construction of the lumped version to be used in explicit dynamics.¹

In what follows, we first present the way to form the mass matrix. For the construction of the self-stabilized stiffness matrix with and without moments and of the equivalent nodal forces vector for the two procedures, the reader is referred to [3].

3.1 Construction of the VEM self-stabilized consistent mass matrix

We begin by remarking that, when dealing with the VEM, the element consistent mass matrix $\textbf{M}$ defined in (16) is not directly computable since the functions contained in $\textbf{N}_u$ are virtual. However, a lumped mass matrix for a quadrilateral VE can be directly obtained following the simple procedure illustrated below, without the need of any stabilization.

To compute the integral in (16), we need to find a quadrature formula for a generic quadrilateral (convex or non-convex, see Fig. 15), such that:

• The formula makes use of nodal values only, i.e. of points where the integrand function is known

• It is exact for linear polynomials

• Weights are strictly positive.

The first two requirements can be satisfied for any quadrilateral (convex or non-convex) in the following way: let $\textbf{x}_C=(x_C,y_C)$ be the centroid of our quadrilateral $\Omega _e$ and let $T_i^{\textbf{x}_C}$ be the signed area of the triangle $\smash {\overset{\triangle }{T}}_i^{\textbf{x}_C}$ having vertices ${\textbf{x}_C}=(x_C,y_C)$, ${\textbf{x}}_i=(x_i,y_i)$ and ${\textbf{x}}_{i+1}=(x_{i+1},y_{i+1})$, i.e.:

$$\begin{aligned} T_i^{\textbf{x}_C} := \dfrac{1}{2}\,\det \begin{bmatrix} 1 &{} \quad 1 &{} \quad 1 \\ x_C &{} \quad x_i &{} \quad x_{i+1} \\ y_C &{} \quad y_i &{} \quad y_{i+1} \end{bmatrix} \end{aligned}$$

(23)

where we agree that ${\textbf{x}}_{5}={\textbf{x}}_1$ and $T_0^{\textbf{x}_C}=T_4^{\textbf{x}_C}$. If we define the weights $\omega _i$ as:

$$\begin{aligned} \omega _i := \dfrac{T_{i-1}^{\textbf{x}_C}+T_i^{\textbf{x}_C}}{2}, \end{aligned}$$

(24)

the resulting quadrature formula:

$$\begin{aligned} \int _{\Omega _e} f({\textbf{x}})d\mathrm {\Omega } \approx \sum _{i=1}^{4} \omega _i \, f({\textbf{x}}_i) \end{aligned}$$

(25)

has degree of precision 1, i.e., it is exact for linear polynomials. A detailed derivation of the formula in (25) is reported in Appendix 1. Since the integrand function is evaluated at the vertices $\textbf{x}_i$, the rectangular terms in (16) vanish and the matrix resulting from the application of (25) to (16) leads to a diagonal mass matrix.

If the polygon is non-convex, the above construction does not ensure that all weights are positive. In particular, if the centroid coincides with a vertex, the corresponding weight will be zero. To overcome this difficulty we define another quadrature formula for a quadrilateral in the following way.

Fix a diagonal and split the quadrilateral into two triangles along the chosen diagonal, and then consider the quadrature formula given by integrating linear polynomials exactly on each triangle separately. By repeating the procedure with the other diagonal, we end up with two quadrature formulas; if the quadrilateral is non-convex, only one of them will have positive weights. In any case, we select the formula whose minimum weight is larger.

Finally, we compare the weights so obtained with the ones given by (24) and we take the formula whose minimum weight is larger. In this way it is guaranteed that the final formula will satisfy all requirements above.

In what follows, the lumped mass matrix obtained with this procedure will be referred to as self-stabilized mass matrix.

3.2 Construction of the VEM stabilized consistent mass matrix

3.2.1 Non-diagonal VEM stabilized consistent mass matrix

The technique illustrated in the previous Section provides a self-stabilized lumped mass matrix. When implicit time-integration schemes are used, a consistent, non-diagonal mass matrix is often used. As remarked in the previous Section, the consistent mass matrix cannot be directly computed in the VEM and it has to be evaluated only in an approximate way: we then split the displacement field in a part projected onto the space $\textrm{P}_1$ of polynomials of degree up to 1 and in the remaining one. The former is evaluated exactly, while the latter is approximated. For the construction of the two parts, we make use of the definition of deformation, rigid-body and hourglass modes introduced in [3].

Let us start with the virtual work done by the inertia forces at element level:

$$\begin{aligned} \delta \Pi _e^{in} = \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T\rho \ddot{\textbf{u}}d\mathrm {\Omega } \end{aligned}$$

(26)

The approximate displacement field can be decomposed into the deformation/rigid and hourglass parts as:

$$\begin{aligned} \textbf{u}(\varvec{\xi },t)= & {} \textbf{u}_{\scriptscriptstyle {\mathrm {D+R}}} (\varvec{\xi },t)+\textbf{u}_{\scriptscriptstyle {\textrm{H}}}(\varvec{\xi },t)\nonumber \\= & {} \textbf{N}_u(\varvec{\xi })\hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}(t) +\textbf{N}_u(\varvec{\xi })\hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}(t) \end{aligned}$$

(27)

where $\hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}$ and $\hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}$ are combinations of displacement parameters producing deformation/rigid body modes and hourglass modes, respectively, such that:

$$\begin{aligned} \hat{\textbf{u}}=\hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}} +\hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} \end{aligned}$$

(28)

An analogous decomposition holds for the approximate acceleration field:

$$\begin{aligned} \ddot{\textbf{u}}(\varvec{\xi },t) = \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi },t)+ \ddot{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}(\varvec{\xi },t)= \textbf{N}_u(\varvec{\xi })\ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\mathrm {D+R}}}(t)+ \textbf{N}_u(\varvec{\xi })\ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\textrm{H}}}(t) \end{aligned}$$

(29)

The sets of parameters $\hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}$ and $\hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}$ can be expressed in terms of the so-called natural parameters [26] through the following linear transformation:

$$\begin{aligned} \hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}} = \textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u\hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u, \quad \hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} = \textbf{T}^{\scriptscriptstyle {\textrm{H}}}_u\hat{\textbf{p}}^{\scriptscriptstyle {\textrm{H}}}_u \end{aligned}$$

(30)

where each column of $\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u$ ($\textbf{T}^{\scriptscriptstyle {\textrm{H}}}_u$) defines an independent deformation/rigid body mode (hourglass mode) and the terms in $\hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u$ ($\hat{\textbf{p}}^{\scriptscriptstyle {\textrm{H}}}_u$) define the amplitude of the corresponding mode. Similar expressions can be assumed also for the accelerations:

$$\begin{aligned} \ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\mathrm {D+R}}} = \textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u\ddot{\hat{\textbf{p}}}^{\scriptscriptstyle {\mathrm {D+R}}}_u, \quad \ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\textrm{H}}} = \textbf{T}^{\scriptscriptstyle {\textrm{H}}}_u\ddot{\hat{\textbf{p}}}^{\scriptscriptstyle {\textrm{H}}}_u \end{aligned}$$

(31)

In our low order case, the part of the displacement model responsible for $\textbf{u}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })$ is the one containing the polynomials of degree at most 1, i.e. linear displacements. The remaining non-polynomial functions in $\textbf{N}_u(\varvec{\xi })$ are the two hourglass modes $\textbf{u}_{\scriptscriptstyle {\textrm{H}}}(\varvec{\xi })$ (one per each component). Since 3 parameters are required for the definition of a complete linear polynomial, 6 parameters $\hat{\textbf{p}}_u^{\scriptscriptstyle {\mathrm {D+R}}}$ are required for $\textbf{u}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })$. In other words, one can write:

$$\begin{aligned} \textbf{u}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })= \textbf{N}_1(\varvec{\xi })\hat{\textbf{p}}_u^{\scriptscriptstyle {\mathrm {D+R}}}= \textbf{N}_u(\varvec{\xi })\hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}= \textbf{N}_u(\varvec{\xi })\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \hat{\textbf{p}}_u^{\scriptscriptstyle {\mathrm {D+R}}} \end{aligned}$$

(32)

with $\textbf{N}_1$ defined as:

$$\begin{aligned} \textbf{N}_1(\varvec{\xi }) = \begin{bmatrix} 1 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad \eta &{} \quad 0 \\ 0 &{} \quad 1 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad \eta \\ \end{bmatrix} \end{aligned}$$

(33)

Replacing (27) and (29) in (26) and noticing that deformation/rigid body modes and hourglass modes are orthogonal, one obtains:

$$\begin{aligned} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T \rho \ddot{\textbf{u}}d\mathrm {\Omega }= \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\mathrm {D+R}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}d\mathrm {\Omega }+\int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\textrm{H}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}d\mathrm {\Omega } \end{aligned}$$

(34)

For the construction of the VEM mass matrix, the two terms at the r.h.s. of (34) will be analyzed separately.

Let us focus on the first term. Considering (27) and (29), this term can be written as:

$$\begin{aligned}{} & {} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })\rho \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })d \mathrm {\Omega }\nonumber \\{} & {} \quad =\delta \hat{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}^T \int _{\mathrm {\Omega }_e}\rho \textbf{N}_u^T(\varvec{\xi })\textbf{N}_u(\varvec{\xi }) d\mathrm {\Omega }\ \ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\mathrm {D+R}}} \end{aligned}$$

(35)

Substituiting (30) and (31) in (35), one gets:

$$\begin{aligned}&\int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })\rho \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}(\varvec{\xi })d\mathrm {\Omega } \nonumber \\ {}&\quad = (\delta \hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u)^T\int _{\mathrm {\Omega }_e} \rho \left( \textbf{N}_u(\varvec{\xi })\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u\right) ^T \textbf{N}_u(\varvec{\xi })\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_ud\mathrm {\Omega }\ \ddot{\hat{\textbf{p}}}^{\scriptscriptstyle {\mathrm {D+R}}}_u \end{aligned}$$

(36)

Noticing from (32) that $\textbf{N}_u(\varvec{\xi })\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u =\textbf{N}_1(\varvec{\xi })$, one can express the projection term as:

$$\begin{aligned} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\mathrm {D+R}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}d\mathrm {\Omega }= (\delta \hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u)^T \int _{\mathrm {\Omega }_e}\rho \textbf{N}_1^T\textbf{N}_1 d\mathrm {\Omega }\ \ddot{\hat{\textbf{p}}}^{\scriptscriptstyle {\mathrm {D+R}}}_u \end{aligned}$$

(37)

Replacing (30) in (28), pre-multiplying both members by $(\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u)^T$, exploiting the orthogonality between $\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u$ and $\textbf{T}^{\scriptscriptstyle {\textrm{H}}}_u$ and solving for $\hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u$, one obtains the expressions:

$$\begin{aligned}&\hat{\textbf{p}}^{\scriptscriptstyle {\mathrm {D+R}}}_u = \underbrace{[(\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u)^T \textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u]^{-1} (\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u)^T}_{\varvec{\Pi }^0_1} \hat{\textbf{u}} =\varvec{\Pi }^0_1\hat{\textbf{u}} \end{aligned}$$

(38)

$$\begin{aligned}&\ddot{\hat{\textbf{p}}}^{\scriptscriptstyle {\mathrm {D+R}}}_u = \varvec{\Pi }^0_1\ddot{\hat{\textbf{u}}} \end{aligned}$$

(39)

where the $6\times n_u$ operator:

$$\begin{aligned} \varvec{\Pi }^0_1=\big [\big (\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big )^T \textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big ]^{-1} \big (\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big )^T \end{aligned}$$

(40)

defines the projection of the approximate displacement field onto the linear functions. The operator $\varvec{\Pi }^0_1$ is easily computable following the procedure illustrated in [3].

Replacing (38) and (39) in (37), one finally has:

$$\begin{aligned} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\mathrm {D+R}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\mathrm {D+R}}}d\mathrm {\Omega }&=\delta \hat{\textbf{u}}^T\underbrace{\left( \varvec{\Pi }^0_1\right) ^T\int _{\mathrm {\Omega }_e}\rho \textbf{N}_1^T\textbf{N}_ 1 d\mathrm {\Omega }\ \varvec{\Pi }^0_1}_{\textbf{M}^c}\ddot{\hat{\textbf{u}}} \nonumber \\&=\delta \hat{\textbf{u}}^T\textbf{M}^c\ddot{\hat{\textbf{u}}} \end{aligned}$$

(41)

where $\textbf{M}^c$ denotes the part of the consistent mass matrix $\textbf{M}$ associated with the projection of the displacement field onto $\textrm{P}_1$, defined as:

$$\begin{aligned} \textbf{M}^c=\left( \varvec{\Pi }^0_1\right) ^T\int _{\mathrm {\Omega }_e}\rho \textbf{N}_1^T\textbf{N}_ 1 d\mathrm {\Omega }\ \varvec{\Pi }^0_1 \end{aligned}$$

(42)

As it is, this matrix is symmetric and positive semi-definite.² To obtain a positive definite mass matrix, it is necessary to add the term associated with the remainder of the projection, indicated as $\textbf{M}^s$, as discussed below. It is worth recalling that zero-mass eigenmodes, as in the case of a singular mass matrix, are pathological, since they are associated to an infinite eigenfrequency.

Following the same path of reasoning as for the projection term, let us write:

$$\begin{aligned} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\textrm{H}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} d\mathrm {\Omega }=\delta \hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}}^T \int _{\mathrm {\Omega }_e}\rho \textbf{N}_u^T\textbf{N}_ud\mathrm {\Omega }\ \ddot{\hat{\textbf{u}}}_{\scriptscriptstyle {\textrm{H}}} \end{aligned}$$

(43)

As detailed in [3], the hourglass parameters can be computed as $\hat{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} = \textbf{H}\hat{\textbf{u}}$, where

$$\begin{aligned} \textbf{H} = \textbf{I}-\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big [\big (\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big )^T\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big ]^{-1} \big (\textbf{T}^{\scriptscriptstyle {\mathrm {D+R}}}_u \big )^T \end{aligned}$$

(44)

Hence, one obtains:

$$\begin{aligned} \int _{\mathrm {\Omega }_e} \delta \textbf{u}^T_{\scriptscriptstyle {\textrm{H}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} d\mathrm {\Omega }=\delta \hat{\textbf{u}}^T\textbf{H}^T\int _{\mathrm {\Omega }_e} \rho \textbf{N}_u^T\textbf{N}_ud\mathrm {\Omega }\ \textbf{H}\ddot{\hat{\textbf{u}}} \end{aligned}$$

(45)

Since $\textbf{N}_u$ is unknown, the integral on the r.h.s. is approximated as $\rho |\mathrm {\Omega }_e|\textbf{I}$, where $|\mathrm {\Omega }_e|$ is the element area and $\textbf{I}$ is the $n_u\times n_u$ identity matrix. In this way, taking into account that $\textbf{H}^T\textbf{H}=\textbf{H}$, one eventually has:

$$\begin{aligned} \int _{\mathrm {\Omega }_e}\delta \textbf{u}^T_{\scriptscriptstyle {\textrm{H}}} \rho \ddot{\textbf{u}}_{\scriptscriptstyle {\textrm{H}}} d\mathrm {\Omega }\approx \delta \hat{\textbf{u}}^T\underbrace{\rho |\mathrm {\Omega }_e|\textbf{H}}_{\textbf{M}^s} \ddot{\hat{\textbf{u}}}=\delta \hat{\textbf{u}}^T\textbf{M}^s\ddot{\hat{\textbf{u}}} \end{aligned}$$

(46)

thus the $n_u\times n_u$ approximation of the element stabilizing mass matrix is:

$$\begin{aligned} \textbf{M}^s=\rho |\mathrm {\Omega }_e|\textbf{H} \end{aligned}$$

(47)

The consistent mass matrix $\textbf{M}$ is then evaluated as:

$$\begin{aligned} \textbf{M} = \textbf{M}^c+\textbf{M}^s \end{aligned}$$

(48)

This matrix turns out to be symmetric and positive definite.

Remark 1

Though its presentation is different, the construction of the mass matrix illustrated above is identical to the one presented in several other papers (see, e.g., [19,20,21]). $\square$

Remark 2

It is worth noting that the mass matrix stabilization (47) already contains the density multiplied by the element area that plays the role of a stabilization parameter. Numerical tests confirm that this parameter is good enough to stabilize the mass matrix and that it ensures good accuracy. However, it should be noted that in a large strain framework, Cihan et al. in [22] showed that a singular consistent mass matrix, without stabilization, can be safely used together with an implicit time-integration scheme, obtaining good accuracy.

3.2.2 Lumping of the stabilized consistent mass matrix

If needed, the non-diagonal stabilized consistent mass matrix can be lumped by using one of the lumping techniques existing in the literature. One of the most general and popular mass lumping techniques is the so-called diagonal scaling lumping or HRZ lumping (from the initials of the authors Hinton, Rock and Zinckiewicz) [27]. Unlike other methods, this technique always leads to non-negative diagonal masses.

According to the HRZ scaling, the diagonal entries of the element lumped mass matrix are given by:

$$\begin{aligned} {[}\textbf{M}^l_e]_{ii}=C\ [\textbf{M}_e]_{ii} \end{aligned}$$

(49)

where $[\textbf{M}_e]_{ii}$ is the ii-component of the local consistent mass matrix $\textbf{M}_e$. The scaling coefficient C is determined in such a way that the total element mass is preserved,³ namely from the condition:

$$\begin{aligned} \underbrace{\frac{\textrm{tr}(\textbf{M}_e^l)}{2}}_{\mathrm {mass\ in\ one\ direction}} = \underbrace{\rho |\Omega _e|}_{\mathrm {total\ element\ mass}} \end{aligned}$$

(50)

where the trace of $\textbf{M}_e^l$ is divided by 2 since 2D problems are considered. From (50) and (49), the expression of the coefficient C can be derived:

$$\begin{aligned} C = \frac{2\rho |\Omega _e|}{\textrm{tr}({\textbf{M}_e})} \end{aligned}$$

(51)

This technique has been applied for the lumping of the stabilized consistent mass matrix of the previous section, both in the case of the standard VEM and of the VEM with self-stabilized stiffness, to be used for the element eigenfrequency analysis that will be carried out in Sect. 5.2. A comparison between the HRZ and the row-sum lumping techniques for the VEM can be found in [21].

3.3 Elements with locally condensed internal degrees of freedom

Let us first focus on the scheme with additional moment DOFs. The acronym VEM4SS is used to denote 4-node Self-stabilized virtual elements with linear displacements along the edges. A necessary condition to have a self-stabilized element is that $n_u-n_\varepsilon \le 3$. As discussed in [3], different strain fields can be used to construct self-stabilized virtual elements according to this procedure. A first possibility is to adopt the following 7 parameters strain model:

$$\begin{aligned} \textbf{N}_\varepsilon = \begin{bmatrix} 1 &{} \quad 0 &{} \quad 0 &{} \quad \eta &{} \quad 0 &{} \quad \xi \ {} &{} \quad 0\\ 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad \eta \\ 0 &{} \quad 0 &{} \quad 1 &{} \quad \xi &{} \quad \eta &{} \quad 0 &{} \quad 0\\ \end{bmatrix} \end{aligned}$$

(52)

where the first three columns define a constant strain state (as for the standard lowest order VEM), the fourth and the fifth columns correspond to the two hourglass modes and the last two are necessary to define a complete first order polynomial for each strain component and to make the consistent stiffness matrix $\textbf{K}$ self-stabilized. Therefore, in this case $n_\varepsilon =7$.

Alternatively, also the following 9 parameters (i.e., $n_\varepsilon =9$) strain model can be used:

$$\begin{aligned} \textbf{N}_\varepsilon = \begin{bmatrix} 1 &{} \quad 0 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad 0 &{} \quad \eta &{} \quad 0 &{} \quad 0\\ 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad 0 &{} \quad \eta &{} \quad 0\\ 0 &{} \quad 0 &{} \quad 1 &{} \quad 0 &{} \quad 0 &{} \quad \xi &{} \quad 0 &{} \quad 0 &{} \quad \eta \\ \end{bmatrix} \end{aligned}$$

(53)

Since both strain models contain linear terms, the first moments of the displacement shape functions are required to compute the matrix $\textbf{A}_2$ in (22), hence two internal moment DOFs are introduced. Therefore, the final number of displacement DOFs is $n_u=2\times 4+2 = 10$. Hence, $\textbf{N}_u$ is a $2\times 10$ matrix. For both the proposed elements, $n_u-n_\varepsilon \le 3$ and, if the rows of the compatibility matrix $\textbf{C}$ are independent, the element consistent stiffness matrix $\textbf{K}$ has rank deficiency 3, i.e., the element is self-stabilized.

The presence of the two additional internal DOFs is however problematic in dynamics, requiring the imposition of unphysical initial conditions associated to these DOFs and leading to higher maximum eigenfrequencies with respect to those of an 8-DOFs 4-node element. Moreover, the applicability of the usual mass lumping techniques is questionable in the presence of the two moment DOFs. All these observations are particularly relevant in explicit dynamics, where a lumped mass matrix is usually adopted and the critical time step is inversely proportional to the maximum eigenfrequency of the mesh.

To remedy this situation, a Guyan-type static condensation [28] of the local VEM stiffness matrix is introduced, considering as master (denoted by subscript m) DOFs the 8 nodal displacement DOFs and as slave (subscript s) DOFs the 2 moment DOFs at each time instant $t^{n+1}$ in the time integration scheme. According to this procedure, the local static system is partitioned as:

$$\begin{aligned} \begin{bmatrix} \underset{8\times 8}{\textbf{K}_{mm}} &{} \quad \underset{8\times 2}{\textbf{K}_{ms}} \\ \underset{2\times 8}{\textbf{K}_{sm}} &{} \quad \underset{2\times 2}{\textbf{K}_{ss}} \end{bmatrix} \begin{Bmatrix} \underset{8\times 1}{\hat{\textbf{u}}_m^{n+1}}\\ \underset{2\times 1}{\hat{\textbf{u}}_s^{n+1}} \end{Bmatrix} = \begin{Bmatrix} \underset{8\times 1}{\textbf{F}_m^{n+1}}\\ \underset{2\times 1}{\textbf{0}} \end{Bmatrix} \end{aligned}$$

(54)

where it is assumed $\textbf{F}_s^{n+1}=\textbf{0}$ and the vector $\textbf{F}_m^{n+1}$ is computed in the same way as for the standard lowest order VEM (i.e., without moment DOFs).

The expression of the reduced element stiffness matrix $\tilde{\textbf{K}}$ is then obtained as:

$$\begin{aligned} \underbrace{(\textbf{K}_{mm}-\textbf{K}_{ms}\textbf{K}_{ss}^{-1} \textbf{K}_{sm})}_{\tilde{\textbf{K}}}\hat{\textbf{u}}_m^{n+1} = \textbf{F}_m^{n+1} \end{aligned}$$

(55)

Summarizing, the first approach with self-stabilized 4-node elements in dynamics is based on the use of an $8\times 8$ self-stabilized element stiffness matrix $\tilde{\textbf{K}}=\textbf{K}_{mm}-\textbf{K}_{ms} \textbf{K}_{ss}^{-1}\textbf{K}_{sm}$ and an $8\times 8$ stabilized mass matrix whose construction has been explained in Sect. 3.2. The local equivalent nodal forces vector at each time instant $t^{n+1}$ is given by $\textbf{F}_m^{n+1}$.

The approach described above has been implemented for the 4-node element with both 7 and 9 strain parameters, according to (52) and (53). These two elements, when used in conjunction with the self-stabilized lumped mass matrix of Sect. 3.1 are indicated by the acronyms VEM4SS7-10DOFs-LC and VEM4SS9-10DOFs-LC, respectively, where LC stands for Locally Condensed, i.e., condensed at element level. The acronyms VEM4SM7-10DOFs-LC and VEM4SM9-10DOFs-LC will be used instead in conjunction with the consistent Stabilized Mass matrix of Sect. 3.2. The acronym SM stands for Stabilized Mass.

3.4 Elements without additional internal degrees of freedom

The elements described here and those described in Sect. 3.3 differ for the computation of matrix $\textbf{A}_2$ in (22), necessary to compute the compatibility matrix $\textbf{C}$ and, hence, the VEM element stiffness matrix. The matrix $\textbf{A}_2$ in (22) contains the integral of the unknown displacement virtual shape functions $\textbf{N}_u$, hence its computation is not immediate. Rather than considering the moments of the displacement shape functions not pertinent to boundary nodes as additional DOFs, as in the case of the elements introduced in the previous Section, according to the proposed strategy the integral in $\textbf{A}_2$ is computed by replacing $\textbf{N}_u$ with its approximation obtained by projecting the gradient of $\textbf{N}_u$ onto the gradient of known polynomial functions $\textbf{N}_1$ of degree 1, following the procedure illustrated in [3]. In this way, only the 8 nodal DOFs are used and there is no need for the static condensation of moment DOFs.

Having the same displacement DOFs as the standard lowest order VEM element, the local equivalent nodal forces vector at time $t^{n+1}$, i.e. $\textbf{F}^{n+1}$, can be computed as in the standard VEM. For applications in dynamics, also this element is used in conjunction with the $8\times 8$ self-stabilized mass matrix described in Sect. 3.2.

The approach described above for the computation of the compatibility matrix $\textbf{C}$ has been implemented for the 4-node element with both 7 and 9 strain parameters, according to (52) and (53). Consistently with the nomenclature used in 3.3, these two elements are respectively indicated by the acronyms VEM4SS7-8DOFs and VEM4SS9-8DOFs when they are used in conjunction with the self-stabilized mass matrix of Sect. 3.1. The acronyms VEM4SM7-8DOFs and VEM4SM9-8DOFs will be used instead in conjunction with the consistent Stabilized Mass (SM) matrix of Sect. 3.2.

4 Implicit time integration: numerical applications

The virtual elements with self-stabilized stiffness and lumped-mass matrices described in the previous Sections have been implemented into a MATLAB code. The consistent stabilized mass matrix has also been implemented for comparison purposes and for usage with the standard quadrilateral VE. In the case of the standard quadrilateral VEM, requiring a stabilization, the usual diagonal matrix-based stabilization technique of the stiffness matrix has been considered, together with the consistent mass matrix, lumped through the HRZ method.

The implicit average acceleration time integration scheme (implicit Newmark’s method with parameters $\beta =1/4$ and $\gamma =1/2$) has been used for the cases tested in this Section, together with the lumped self-stabilized mass matrix of Sect. 3.1 and with a time step $\Delta t=10^{-2} s$.

Note that the results obtained with self-stabilized VEs together with the lumped version of the consistent stabilized mass matrix (VEs with the acronym SM) are almost identical to those obtained with the self-stabilized mass matrix of Sect. 3.1 (VEs with the acronym SS). For this reason, only results relative to the lumped self-stabilized mass matrix are reported hereafter.

Units of measure are not specified, but they have been chosen to be consistent (e.g. $\textrm{mm}$ for lengths; $\mathrm {N/mm^2}$ for surface tractions, stresses, Young modulus and Lamé constants; $\mathrm {Mg/mm^3}$ for mass density).

4.1 Convergence test with known analytical solution

The first application of the VEM is related to a classical 2D plane strain convergence test with known analytical solution. Specifically, the problem domain, depicted in Fig. 1, is a unit square $\Omega =[0,1]^2$ with constrained displacements all over its boundary $\partial _u \Omega \equiv \partial \Omega$, i.e., $\partial _p \Omega =\emptyset$.

Fig. 1

Convergence test with analytical solution: problem domain

The problem data are:

• Lamé constants $\lambda = 1$ and $\mu = 1$ (corresponding to $E = 2.5$ and $\nu = 0.25$)

• Mass density $\rho =1$

• Time interval $[0, t_f]$, with $t_f=2\ s$

• Loading period $\textrm{T}=1\ s$

• Body forces in $\Omega \times [0, t_f]$

  $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} b_x &{}= \sin \left( \frac{2\pi t}{\textrm{T}}\right) \{-\pi ^2\big [-(\lambda +3\mu ) \sin (\pi x)\sin (\pi y) \\ &{}\quad +(\lambda +\mu )\cos (\pi x)\cos (\pi y)\big ]+-4\pi ^2\rho \sin (\pi x)\sin (\pi y)\}\\ b_y &{}= \sin \left( \frac{2\pi t}{\textrm{T}}\right) \{-\pi ^2\big [-(\lambda +3\mu ) \sin (\pi x)\sin (\pi y) \\ &{}\quad +(\lambda +\mu )\cos (\pi x)\cos (\pi y)\big ]+ -4\pi ^2\rho \sin (\pi x)\sin (\pi y)\} \end{aligned} \end{array}\right. } \end{aligned}$$

  (56)

• Kinematic boundary conditions on $\partial _u \Omega \times [0,t_f]$

  $$\begin{aligned} {\left\{ \begin{array}{ll} \bar{u}_x = 0\\ \bar{u}_y = 0 \end{array}\right. } \end{aligned}$$

  (57)

• Initial conditions in $\Omega$ at $t=0$

  $$\begin{aligned} {\left\{ \begin{array}{ll} u_{x0} = 0\\ u_{y0} = 0\\ \dot{u}_{x0} = \frac{2\pi }{\textrm{T}}\sin (\pi x)\sin (\pi y)\\ \dot{u}_{y0} = \frac{2\pi }{\textrm{T}}\sin (\pi x)\sin (\pi y)\\ \end{array}\right. } \end{aligned}$$

  (58)

The analytical solution of the problem in terms of displacements in $\Omega \times [0, t_f]$ is given by:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_x = \sin \left( \frac{2\pi t}{\textrm{T}}\right) \sin (\pi x)\sin (\pi y)\\ u_y = \sin \left( \frac{2\pi t}{\textrm{T}}\right) \sin (\pi x)\sin (\pi y) \end{array}\right. } \end{aligned}$$

(59)

Three different quadrilateral meshes with an increasing number of elements have been tested for the assessment of the VEM convergence: a square mesh, a mesh with convex distorted quadrilateral elements and a mesh with convex and non-convex quadrilateral elements (Fig. 2). Convergence upon mesh refinement has been assessed in terms of the mean $L^2$-norm of the strain error in a time period $\textrm{T}$, defined as:

$$\begin{aligned} \Vert e_{\epsilon }\Vert _{L^2,\ \textrm{T}} = \frac{1}{n_t}\sum _{i=1}^{n_t}\sqrt{\sum _{e=1}^{n_e} \int _{\Omega _e} \Vert \varvec{\varepsilon }_{t_i}-\varvec{\varepsilon }^h_{t_i}\Vert ^2 d\Omega } \end{aligned}$$

(60)

where $n_t$ is the number of time instants in a discretized time period $\textrm{T}$ (in this specific example $n_t=101$ since $\textrm{T}=1\ s$ and $\Delta t = 10^{-2}\ s$), being $t_1$ the initial time instant of the period and $t_{n_t}$ the end of the period. $\varvec{\varepsilon }_{t_i}$ and $\varvec{\varepsilon }^h_{t_i}$ denote respectively the exact and the approximate strain field over the generic element of the virtual element mesh at time instant $t_i$. The integrals in (60) are computed numerically by means of the usual subtriangulation technique, evaluating the exact and the approximate strains at the quadrature points. According to the subtriangulation integration procedure, a convex quadrilateral element is divided into 4 subtriangles connecting its centroid to the four vertices (2 subtriangles if the element is non-convex, connecting the vertex in the concave angle to the other vertices). A standard Gaussian procedure for triangles is then considered for each subtriangle.

Five types of VEs are considered and their performances are compared: standard VEs, with stiffness stabilization and lumped version (with HRZ method) of the stabilized consistent mass matrix, denoted as VEM4; self-stabilized VEs with 8 nodal DOFs, 2 internal moments and static condensation of the two moments in the element stiffness matrix, denoted as VEM4SS7-10DOFs-LC (7 strain parameters, 10 DOFs, Local static Condensation); self-stabilized VEs with 8 nodal DOFs, 2 internal moments and static condensation of the two moments in the element stiffness matrix, denoted as VEM4SS9-10DOFs-LC (9 strain parameters, 10 DOFs, Local static Condensation); self-stabilized VEs with 8 nodal DOFs and no moments DOFs, denoted as VEM4SS7-8DOFs (7 strain parameters, 8 DOFs); self-stabilized VEs with 8 nodal DOFs and no moment DOFs, denoted as VEM4SS9-8DOFs (9 strain parameters, 8 DOFs).

Fig. 2

Convergence test with analytical solution: quadrilateral meshes for comparison with the self-stabilized VEM

The results of VEM convergence analyses show that in all cases the slope of the error $\Vert e_{\epsilon }\Vert _{L^2,\ \textrm{T}}$ agrees with the first order convergence behavior of the method as the mean element size h decreases, when plotted in a log-log scale as a function of h. Figure 3 shows the convergence curves for the different considered meshes, obtained using the standard lowest order quadrilateral VEs, denoted as VEM4, and the self-stabilized VEs presented in Sect. 3. As can be seen, all the self-stabilized elements exhibit the right order of convergence of the standard VEM.

The response in the time interval $[0, t_f]$ of the DOF along x at the point $x=y=0.5$ is studied.⁴ This displacement component will be indicated as reference DOF. Due to the absence of damping, the response is characterized by an undamped oscillatory motion. The approximate solutions are compared to the exact one, the latter obtained by introducing the coordinates $x=y=0.5$ in (59), obtaining $u_x(0.5,0.5,t)=\sin (\frac{2\pi t}{\textrm{T}})$.

The responses in time are reported in Fig. 4 for the different meshes together with the exact analytical solution. For meshes finer than those used in the plots, the exact and the approximate solutions are indistinguishable. The plots in Fig. 4 have been obtained by subdividing the oscillation period in 100 time steps. The same problem has also been analyzed with the mesh of convex distorted quadrilaterals of Fig. 2b, considering VEM4SS7-10DOFs-LC and VEM4SS7-8DOFs VEs and using 20, 30 and 50 time steps. The results are shown in Fig. 5. For both VEs types, the exact and the approximate solutions are almost perfectly superposed, for all time-step sizes.

Fig. 3

Convergence test with analytical solution: comparison of standard VEM and self-stabilized VEM for different quadrilateral meshes

Fig. 4

Convergence test with analytical solution: response in time in terms of reference DOF, comparison with standard VEM and analytical solution for different meshes

Fig. 5

Convergence test with analytical solution: response in time in terms of reference DOF for different number of time increments per period, convex distorted quad mesh with 384 elements

4.2 Cook’s beam problem

The geometry of the problem is shown in Fig. 6. A linear elastic, tapered cantilever beam, with the left end restrained in both directions, is loaded at the right edge by a uniform shear force acting along the y direction, defined as: $p_x(t)=0$, $p_y(t) = \bar{p}\sin (\frac{2\pi t}{\textrm{T}})$ with $\bar{p}=6.25\times 10^{-3}$ and $\textrm{T}=1\ s$. Plane strain conditions and small displacements are assumed. The results are expressed in terms of the time history of the vertical displacement $u_y^{\scriptscriptstyle {A}}$ of point A in Fig. 6. Both the compressible and the nearly incompressible cases are considered with the following properties: Young’s modulus $E=70$, Poisson’s ratio $\nu =0.33$ (compressible case), $\nu =0.49995$ (nearly incompressible case) and mass density $\rho =0.1$. Since an analytical solution is not available, a reference solution for both the compressible and almost incompressible cases has been generated using the finite element software Abaqus with a mesh of 9545 4-node quadrilateral CPE4IH (hybrid, linear pressure, incompatible modes) bilinear plane strain elements.

The analyses, conducted with the five different VE types used in the previous section, are carried out using the two meshes, a structured and an unstructured quad mesh, shown in Fig. 7, with increasing number of elements: 200, 400, 1600 and 6400 elements for the structured mesh; 210, 498, 1917, 5435 elements for the unstructured mesh. The time histories for the compressible case are shown in Figs. 8 and 9, for the structured and unstructured mesh, respectively, together with the reference solution. Good convergence upon mesh refinement is achieved in all cases. An accuracy comparable to the one of the reference solution is already recovered when meshes of 1600 (structured) and 1917 (unstructured) elements are used.

The results for the nearly incompressible case are shown in Figs. 10 and 11, for the structured and unstructured mesh, respectively. For the structured mesh, the standard VEM and the 7 and 9 strain parameters, self-stabilized elements without internal moments, VEM4SS7-8DOFs and VEM4SS9-8DOFs, exhibit a severe locking for all mesh densities, with oscillation amplitudes significantly smaller than expected. In contrast, the VEM4SS7-10DOFs and VEM4SS9-10DOFs with internal moment DOFs and element static condensation, provide locking-free responses for all mesh densities, with increasing accuracy upon mesh refinement. A rather poor result in terms of accuracy is obtained only with the VEM4SS7-10DOFs element in the coarsest mesh case. These results confirm what had already been observed in [3] for the static case, where the VEM4SS7-10DOFs and VEM4SS9-10DOFs elements have shown to provide almost completely locking-free results in a number of applications.

Remark 3

The dynamic analysis of the incompressible Cook’s membrane with stabilized B-Bar VEM has been considered also in [21]. However, note that in the present case, accurate results for the same problem have been obtained with self-stabilized VEs, without any special provision to mitigate a possible locking response.

5 Explicit time integration: critical time step size

Fig. 6

Cook’s beam: problem domain

Fig. 7

Cook’s beam: quadrilateral meshes for comparison with self-stabilized VEM

The explicit central difference time integration scheme is usually employed in the case of highly non-linear, high strain rate dynamics simulations, with relatively short duration. The central difference scheme is only conditionally stable and the used time step size has to be smaller than a critical value. Furthermore, in explicit dynamics, the use of a lumped diagonal matrix is necessary for the explicit inversion of the mass matrix. The proposed new node-based integration scheme for VEs has the advantage that it directly produces a lumped mass matrix. These two aspects, time step size and lumped mass matrix are fundamental for the computational efficiency of explicit dynamics simulations and are discussed below in connection with the proposed self-stabilized VEs.

5.1 Critical time step size

In the undamped case, the central difference scheme is stable for:

$$\begin{aligned} \Delta t \le \Delta t_{cr}=\frac{2}{\omega _{max}} \end{aligned}$$

(61)

where $\Delta t$ is the adopted time step and $\Delta t_{cr}$ is the critical time step, strictly related to the maximum eigenfrequency $\omega _{max}$ of the mesh.

The estimation of the critical time step is basically reduced to the computation of $\omega _{max}$ by solving the global eigenvalue problem:

$$\begin{aligned} \textrm{det}(\textbf{K}-\omega ^2\textbf{M})=0 \end{aligned}$$

(62)

where $\textbf{K}$ and $\textbf{M}$ are the assembled stiffness and mass matrices, while $\omega ^2$ denotes the generic eigenvalue (square of the eigenfrequency) of the system.

For a mesh with a large number of elements, the computation of $\omega _{max}$ can be very expensive. An effective iterative algorithm for the global estimation of $\omega _{max}$ can be found in [29]. A less expensive, though less accurate but conservative, estimate of $\Delta t_{cr}$ can be alternatively obtained making use of the element upper bound theorem, see [30], for the maximum global eigenfrequency, stating that:

Fig. 8

Cook’s beam: time history of vertical displacement at point A under mesh refinement, structured quad mesh, compressible case ($\nu =0.33$)

Fig. 9

Cook’s beam: time history of vertical displacement at point A under mesh refinement, unstructured quad mesh, compressible case ($\nu =0.33$)

Fig. 10

Cook’s beam: time history of the vertical displacement of point A under mesh refinement, structured quad mesh, nearly incompressible case ($\nu =0.49995$)

Fig. 11

Cook’s beam: time history of vertical displacement at point A under mesh refinement, unstructured quad mesh, nearly incompressible case ($\nu =0.49995$)

$$\begin{aligned} \omega _{max}\le \underset{e}{\textrm{max}}\{ \omega _{max}^e \} \end{aligned}$$

(63)

where $\omega _{max}^e$ denotes the maximum eigenfrequency of the generic element composing the mesh. $\omega _{max}^e$ is computed for each element solving the local eigenvalue problem:

$$\begin{aligned} \textrm{det}(\textbf{K}_e-\omega _e^2\textbf{M}_e)=0 \end{aligned}$$

(64)

and the maximum $\omega _{max}^e$ among all the elements is used to evaluate a lower bound for the critical time step size:

$$\begin{aligned} \Delta \bar{t}_{cr}=\frac{2}{\underset{e}{\textrm{max}}\{ \omega _{max}^e \}}\le \Delta t_{cr}=\frac{2}{\omega _{max}} \end{aligned}$$

(65)

Another, alternative element-based estimate of the critical time step size can be achieved by imposing that a dilatational stress wave cannot traverse an entire virtual element in a single time step. This leads to the following estimate:

$$\begin{aligned} \Delta \bar{t}_{cr}=\frac{l_e}{c_d}\le \Delta t_{cr} \end{aligned}$$

(66)

where $c_d$ is the speed of a dilatational stress wave in the considered medium and $l_e$ is a characteristic element size, usually taken as the maximum between the minimum element edge and the minimum distance between the element centroid and its nodes. A discussion on the selection of the characteristic length for VEs can be found in [21]. In the analysis of the following Section, the maximum element eigenvalue will be used for the critical time step estimate.

5.2 Eigenfrequency analysis of single 4-node elements

As discussed in the previous Section, the maximum stable time step size strongly depends on the element size and shape. Since VEs can take almost any shape, without any restriction on convexity, it is expected that the element shape could greatly affect the critical time step size. The maximum eigenfrequencies of the three element shapes shown in Fig. 12, with comparable edge lengths, but of extremely different shapes, have been computed to assess the influence of shape on the critical time step size. The following material properties have been considered: Lamé constants $\lambda =\mu = 1$, (equivalent to $E=2.5$ and $\nu =0.25$) and mass density $\rho =0.1$. Plane strain conditions have been assumed. Since the lumped version of the stabilized consistent mass matrix and the lumped self-stabilized one lead to the same maximum eigenfrequency, only the latter element will be considered in the study.

For each shape, the five different types of VEs have been considered: VEM4 (i.e. standard VEM), VEM4SS7-10DOFs-LC, VEM4SS9-10DOFs-LC, VEM4SS7-8DOFs, VEM4SS9-8DOFs. In addition, for the convex elements, also a standard 4-node FEM with full integration has been considered. The results are shown in Figs. 13 and 14. In all cases, the first three zero eigenfrequencies are associated to rigid-body modes.

From Fig. 13a, b, one can see that the same maximum eigenfrequency, and hence the same critical time step size, is obtained by all element types for all convex shapes. When the element is non-convex (see Fig. 13c), the self-stabilized elements without moment DOFs (VEM4SS7-8DOFs and VEM4SS9-8DOFs) exhibit instead a maximum eigenfrequency that is about 20% larger than the other elements. For all element types, distortion leads to an increase of the maximum eigenfrequency, achieving a peak in the non-convex case. As far as the elements VEM4SS7-10DOFs-LC and VEM4SS9-10DOFs-LC are concerned, i.e. the VEs with two moment DOFs that are statically condensed in the stiffness matrix, one can conclude that the static condensation does not affect the critical time step size.

Figure 14 shows the effect of the element shape on the eigenfrequencies for the different element types. As already noted, in all cases a distortion leads to a progressive increase of the maximum eigenfrequency, which is particularly evident in Figs. 14e and f, i.e., for elements VEM4SS7-8DOFs and VEM4SS9-8DOFs.

From these analyses, one can conclude that the self-stabilized elements VEM4SS7-10DOFs-LC, VEM4SS9-10DOFs-LC, with static condensation in the stiffness matrix of the moments DOFs, exhibit the correct convergence rate, optimal accuracy for distorted meshes, the best performances in the quasi-incompressible limit, without compromising the critical time step size for explicit dynamic analyses.

Fig. 12

Eigenfrequency analysis: tested 4-node elements

Fig. 13

Eigenfrequency analysis: comparison of the eigenfrequencies resulting from different approaches, lumped mass matrix

Fig. 14

Eigenfrequency analysis: effect of element distortion on eigenfrequencies, lumped mass matrix

6 Conclusions

A recent mixed formulation of the Virtual Element Method (VEM) in 2D elastostatics [3], based on the Hu-Washizu variational principle, has been extended to 2D elastodynamics. The main feature of the mixed VEM formulation is that self-stabilized VEs can be obtained, avoiding the complication and, to a certain extent, arbitrariness of a stabilization. For first order quadrilateral elements in elastodynamics, we have shown how a fully self-stabilized VEM formulation, where by fully self-stabilized we mean that both the stiffness and the mass matrix do not require a stabilization, can be obtained using the Hu-Washizu mixed approach proposed in [3] for the stiffness matrix and a new, node-based integration scheme for the mass matrix. The new method provides directly a stabilized lumped mass matrix, which is ideally suited for applications with explicit time-integration schemes. In the case that a consistent mass matrix is needed, it has been shown how the stabilized mass matrix of the standard VEM for first order quads can be conveniently combined with the stiffness matrix of the self-stabilized first order quads derived in [3]. It has also been observed that the lumped version obtained by using the HRZ [27] diagonal scaling method is identical to the one directly obtained with the new integration rule.

As for the stiffness matrix, we have considered the two types of self-stabilized elements proposed in [3]: elements with and without moment DOFs. In the first case, the moment DOFs have been statically condensed at the element level, allowing for their direct use with a mass matrix based on nodal accelerations only.

By means of numerical tests, we have shown that the combination of a self-stabilized stiffness matrix with a self-stabilized lumped mass matrix can produce excellent results both in the compressible and quasi-incompressible regimes in the case of implicit time integration. In particular, the self-stabilized elements with statically condensed moment DOFs, VEM4SS7-10DOFs-LC and VEM4SS9-10DOFs-LC, have exhibited the best accuracy in both the compressible and quasi-incompressible case, also with respect to the standard VEM.

Fig. 15

The polygon $\Omega _e$

In the case of explicit dynamics, the different types of derived VEs have been analyzed in terms of their critical time step size. It has been observed that in the case of non-convex shapes, the maximum eigenfrequency of the self-stabilized elements without moment DOFs is significantly higher than for the other element types, making their usage in explicit dynamics problematic. In contrast, the maximum eigenfrequency of the self-stabilized elements with moment DOFs has resulted to be no more sensitive to element distortion than the standard FEs (for convex elements) and VEs, making these elements very promising for application in explicit dynamics problems.

Appendix A Quadrature formula for generic quadrilaterals

In order to deal with general quadrilaterals (convex and non-convex), we derive a quadrature formula which integrates exactly first-degree polynomials having the vertices as integration points. We will actually construct the quadrature formula for a general polygon; hence, in this subsection only, $\Omega _e$ will denote a general polygon (convex or non-convex) with $N_V$ vertices whose coordinates are $\textbf{x}_i=(x_i,y_i)$, $i=1,\dots ,N_V$.

Let $\textbf{x}$ be a generic point (inside or outside the polygon) and $T_i^\textbf{x}$ the signed area of the triangle $\smash {\overset{\triangle }{T}}_i^\textbf{x}$ having vertices $\textbf{x}=(x,y)$, $\textbf{x}_i=(x_i,y_i)$ and $\textbf{x}_{i+1}=(x_{i+1},y_{i+1})$, i.e.:

$$\begin{aligned} T_i^\textbf{x}:= \dfrac{1}{2}\,\det \begin{bmatrix} 1 &{} \quad 1 &{} \quad 1 \\ x &{} \quad x_i &{} \quad x_{i+1} \\ y &{} \quad y_i &{} \quad y_{i+1} \end{bmatrix} \end{aligned}$$

(67)

where we agree that $\textbf{x}_{N_V+1}=\textbf{x}_1$ (see Fig. 15, left). The centroid $\textbf{x}_C$ of the polygon can be computed by taking the weighted sum of the centroids of the triangles $\smash {\overset{\triangle }{T}}_i^\textbf{x}$:

$$\begin{aligned} \textbf{x}_C&= \sum _{i=1}^{N_V} \dfrac{T_i^\textbf{x}}{|\Omega _e|}\,\dfrac{(\textbf{x}_i+\textbf{x}_{i+1}+\textbf{x})}{3} \nonumber \\&= \dfrac{1}{|\Omega _e|}\sum _{i=1}^{N_V} {T_i^\textbf{x}}\,\dfrac{(\textbf{x}_i+\textbf{x}_{i+1})}{3}+\dfrac{\textbf{x}}{3} \nonumber \\&= \dfrac{1}{|\Omega _e|}\sum _{i=1}^{N_V} \dfrac{\textbf{x}_i}{3}\, \big (T_{i-1}^\textbf{x}+T_i^\textbf{x}\big )+\dfrac{\textbf{x}}{3} \end{aligned}$$

(68)

where we define again for simplicity $T_0^\textbf{x}:=T_{N_V}^\textbf{x}$. If we take as $\textbf{x}$ the centroid itself $\textbf{x}_C$, we obtain the identity:

$$\begin{aligned} \textbf{x}_C = \dfrac{1}{|\Omega _e|}\sum _{i=1}^{N_V} \dfrac{\textbf{x}_i}{3}\, \big (T_{i-1}^{\textbf{x}_C}+T_i^{\textbf{x}_C}\big )+\dfrac{\textbf{x}_C}{3} \end{aligned}$$

(69)

i.e.:

$$\begin{aligned} \textbf{x}_C = \dfrac{1}{|\Omega _e|}\sum _{i=1}^{N_V} \dfrac{\big (T_{i-1}^{\textbf{x}_C}+T_i^{\textbf{x}_C}\big )}{2}\,\textbf{x}_i. \end{aligned}$$

(70)

Hence, if we define the weights $\omega _i$ as (see Fig. 15, right):

$$\begin{aligned} \omega _i := \dfrac{T_{i-1}^{\textbf{x}_C}+T_i^{\textbf{x}_C}}{2}, \end{aligned}$$

(71)

we have the following representation of the centroid as linear combination of the vertices:

$$\begin{aligned} \textbf{x}_C=\dfrac{1}{|\Omega _e|}\sum _{i=1}^{N_V} \omega _i \,\textbf{x}_i. \end{aligned}$$

(72)

Note that some of the weights $\omega _i$ might be negative if the centroid lies outside the polygon. Finally, observing that if $p_1$ is a polynomial of degree one we have:

$$\begin{aligned} \int _{\Omega _e} p_1(\textbf{x})d\mathrm {\Omega } = |\Omega _e| \, p_1(\textbf{x}_C), \end{aligned}$$

(73)

we can easily deduce by (72) the equality:

$$\begin{aligned} \int _{\Omega _e} p_1(\textbf{x})d\mathrm {\Omega } = \sum _{i=1}^{N_V} \omega _i \, p_1(\textbf{x}_i). \end{aligned}$$

(74)

The corresponding quadrature formula with nodes $\textbf{x}_i$ and weights $\omega _i$ is exact for linears and it works for general polygons (convex or non-convex). If the polygon is non-convex, the weights $\omega _i$ might be negative.