1 Introduction

Topology optimization is an advanced structural design method that aims to achieve the optimal structural configuration by distributing materials in a rational manner to meet specified load conditions, properties, and constraints. Compared to size and shape optimization, topology optimization is not dependent on the initial configuration and offers a broader design space. Due to its advantages, topology optimization has become a widely used technique in engineering structural design.

Several topology optimization approaches have been developed over the past few decades, including but not limited to the density approach [1,2,3], the level set approach [4,5,6], the evolutionary structural optimization approach [7,8,9], the phase field method [10,11,12], and the moving morphable components [13,14,15]. For a comprehensive review of these approaches, interested readers are referred to [16]. Among these approaches, the density-based topology optimization method is particularly popular. In this approach, discrete optimization problems of 0–1 are transformed into continuous optimization problems to relax the binary design form. Initially, material layouts were controlled by density variables using the homogenisation method, which is mathematically complex and challenging to implement [17]. Subsequently, an alternative method called Solid Isotropic Materials with Penalty (SIMP) was proposed. SIMP enforces exponential penalties on elemental elastic modulus [18]. Due to its simplicity and high computational stability, SIMP quickly became the most widely adopted topology optimization method.

Traditional density-based approaches primarily focus on compliance design, which involves minimizing the elastic strain energy of a structure under given external loads, a volume constraint, and linear elastic material behavior. While these approaches are efficient, they often lead to high stress concentrations in the designed layout, necessitating troublesome sequential changes [19], especially when stress states exceed the material strength. To address this issue, researchers are dedicated their efforts to stress-constrained topology optimization [20]. The stress-constrained topology optimization can be approached in two ways: either as a conventional stiffness-based topology optimization with additional stress constraints [19, 21] or as a volume minimization problem subject to equilibrium equations and stress constraints [22, 23]. It is important to note that, in the conventional stress-constrained topology optimization, linear elastic structural analysis is employed despite the inclusion of additional stress constraints. This means that only elastic behavior of materials is considered, leading to more conservative designs.

Recently, Kammoun et al. [24] introduced a density-based topology optimization formulation that incorporates limit plasticity. Building upon the lower bound finite element limit analysis, this method ensures the optimization process maintains a statically admissible stress field. As such, it can determine the ultimate plastic limit of a structure during topology optimization. Subsequently, an alternative plasticity-based formulation was presented in [25], enabling both upper and lower bound finite element limit analysis through the use of different elements. However, the formulation in [25] only yields a grey design. To address this limitation, an extension of the work in [25] was proposed in [26], allowing for black-and-white designs. Notably, this extension demonstrates that the method does not require a stress-relaxation technique. Another formulation for topology optimization incorporating plastic limit analysis was put forth in [27]. Unlike the approaches in [24,25,26], the formulation in [27] seeks to maximize the load-bearing capacity of the structure, while considering material strength properties and a material volume constraint.

Despite the progress made in developing topology optimization methods based on plastic limit analysis, the majority of contributions have been limited to two-dimensional (2D) cases [24,25,26,27]. Building upon the work presented in [26], this paper introduces a novel plasticity-based method specifically tailored for three-dimensional (3D) topology optimization. The proposed method integrates a mixed rigid-plastic analysis formulation into the density-based topology optimization approach to account for plasticity effects. By applying an exponential penalty to the objective function, a black-and-white solution is achieved. To enhance computational efficiency in 3D modelling, linear tetrahedral elements, known for their favorable mesh refinement properties, are employed. The issue of volumetric locking associated with these constant stress elements is addressed by utilizing the smoothed finite element technique. In 3D formulations with von Mises yield criterion, an additional constraint, not required in plane-stress cases, must be included to prevent the occurrence of spherical stress states in void regions. The developed plasticity-based method exhibits excellent convergence rates and computational efficiency for 3D topology optimization. To illustrate its features and advantages, a series of numerical examples are presented with results compared to these from the traditional stress-constrained method.

2 Mixed smoothed finite element limit analysis

2.1 Mixed limit analysis

Limit analysis determines the maximum load that a mechanical system can withstand. There are three categories of limit analysis: the upper bound (kinematical) formulation, the lower bound (static) formulation, and the mixed formulation. The kinematical formulation considers the displacement as the only variable and provides an upper limit for the maximum load. On the other hand, stress is the sole variable in the static formulation, resulting in a lower limit for the maximum load. The mixed formulation makes use of both displacement and stress as variables. According to [28, 29], a mixed limit analysis formulation can be expressed as a min–max optimization problem

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{\mathbf{u}} \mathop {~~\max }\limits_{{\left( {\boldsymbol{\sigma },\alpha } \right)}} ~~~~~\alpha + \mathop \smallint \limits_{\Omega }^{{}} \boldsymbol{\sigma }^{T} \nabla ^{T} \left( \mathbf{u} \right)d\Omega - \alpha \mathop \smallint \limits_{{\Gamma _{t} }}^{{}} \bar{\mathbf{t}}^{T} \mathbf{u}d\Gamma - \mathop \smallint \limits_{\Omega }^{{}} \mathbf{b}^{T} \mathbf{u}d\Omega } \hfill \\ {{\text{subject}}\;{\text{~to}}~~~~~~f\left( \boldsymbol{\sigma } \right) \le 0} \hfill \\ \end{array} $$
(1)

where

\({\varvec{\sigma}} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\sigma_{xx} } & {\sigma_{yy} } & {\sigma_{zz} } \\ \end{array} } & {\begin{array}{*{20}c} {\sigma_{yz} } & {\sigma_{zx} } & {\sigma_{xy} } \\ \end{array} } \\ \end{array} } \right)^{T} \user2{ }\) is the Cauchy stress;

\({\mathbf{u}}\) is the displacement;

\({\mathbf{b}}\) is the body force;

\(\overline{\user2{t}}\) is the prescribed traction;

\(f\left( {\varvec{\sigma}} \right)\) is the yield function;

\(\alpha\) is the collapse load factor meaning \(\alpha \overline{\user2{t}}\) the ultimate force the structure can sustain; and \(\nabla\) is the differential operator matrix taking the form of

$$ \nabla = \left[ {\begin{array}{*{20}l} {\frac{\partial }{\partial x}} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\frac{\partial }{\partial z}} \hfill & {\frac{\partial }{\partial y}} \hfill \\ 0 \hfill & {\frac{\partial }{\partial y}} \hfill & 0 \hfill & {\frac{\partial }{\partial z}} \hfill & 0 \hfill & {\frac{\partial }{\partial x}} \hfill \\ 0 \hfill & 0 \hfill & {\frac{\partial }{\partial z}} \hfill & {\frac{\partial }{\partial y}} \hfill & {\frac{\partial }{\partial x}} \hfill & 0 \hfill \\ \end{array} } \right] $$
(2)

As illustrated in (1), both the stress and displacement fields are considered as independent variables in the mixed limit analysis. Remarkably, the mixed formulation is versatile since it can also provide a rigorous upper bound solution, as demonstrated in [28, 30, 31].

2.2 Nodal integration based mixed FELA formulation

In this section, we derive the formulation for 3D smoothed Finite Element Limit Analysis (FELA) based on the limit analysis problem (1). This formulation allows the use of linear tetrahedral elements without encountering volumetric locking issues. The computational domain is discretized using four-node tetrahedral elements whereas the integration is carried out over cells rather than finite elements. In the following, we will provide a comprehensive explanation of domain discretization, cell construction, and numerical interpolation and integration, which together yield the final formulation for 3D mixed smoothed FELA.

2.2.1 Domain discretization and cell construction

For clarity, we will initially consider a 2D case to explain the process of domain discretization and cell construction. However, it should be noted that extending this approach to 3D cases is forthright.

Figure 1a shows a 2D domain that has been discretized using three-node triangles. To facilitate the construction of cells, each triangle is divided into three quadrilaterals of equal area by connecting the centroid of the triangle to its three mid-edge points as depicted in Fig. 1b. These quadrilaterals have an area equivalent to one-third of the triangle’s area. In this context, the cell associated with each node consists of one-third of the triangles that are adjacent to that node. Figure 1b highlights two representative cells, specifically the cells associated with the \(k{\text {th}}\) and \(l{\text {th}}\) nodes for the purpose of illustration.

Fig. 1
figure 1

Cell construction in 2D: a a domain discretized using linear triangular element, and b cells constructed for the domain

Full size image

Cell construction in 3D can be achieved using a similar procedure. Initially, the domain is discretized using four-node tetrahedrons. Each tetrahedron is then divided into four hexahedrons, as illustrated in Fig. 2a. This division is accomplished by connecting the centroid of each surface triangle (green nodes) to the three mid-point nodes of that surface triangle (yellow nodes) and to the centroid of the tetrahedron (red node). In the 3D case, the four resulting hexahedrons have equal volume, each corresponding to one-fourth of the volume of the tetrahedron. The cell associated with each node in the 3D domain consists of all hexahedrons that are adjacent to that particular node. To illustrate this, Fig. 2b provides an example of the cells constructed for a cube.

Fig. 2
figure 2

Cell construction in 3D: a division of a tetrahedron into four hexahedrons, and b cells constructed based on tetrahedrons for a cube

Full size image

2.2.2 Numerical interpolation and integration

The optimization problem (1) involves two master fields, namely the displacement and the stress. We start by approximating the displacement field, \({\varvec{u}}\), using the four-node tetrahedron as shown in Fig. 3. The approximation is given by:

$$ {\varvec{u}}\left( {\varvec{x}} \right) \approx \user2{N\hat{u}} $$
(3)
Fig. 3
figure 3

Mapping the four-node tetrahedron from the physical Cartesian coordinate to the natural coordinates

Full size image

In the above equation, the symbol \(\left( {\hat{ \cdot }} \right)\) denotes the variable at mesh nodes, and \({\varvec{N}}\) is the shape function defined as:

$$ {\varvec{N}} = \left[ {\begin{array}{*{20}c} {N_{{}}^{1} } & 0 & 0 & {N_{{}}^{2} } & 0 & 0 & {N_{{}}^{3} } & 0 & 0 & {N_{{}}^{4} } & 0 & 0 \\ 0 & {N_{{}}^{1} } & 0 & 0 & {N_{{}}^{2} } & 0 & 0 & {N_{{}}^{3} } & 0 & 0 & {N_{{}}^{4} } & 0 \\ 0 & 0 & {N_{{}}^{1} } & 0 & 0 & {N_{{}}^{2} } & 0 & 0 & {N_{{}}^{3} } & 0 & 0 & {N_{{}}^{4} } \\ \end{array} } \right] $$
(4)

with

$$ \left\{ {\begin{array}{*{20}l} {N_{{}}^{1} = 1 - \xi - \eta - \zeta } \\ {N_{{}}^{2} = \xi } \\ {N_{{}}^{3} = \eta } \\ {N_{{}}^{4} = \zeta } \\ \end{array} } \right. $$
(5)

where \(\xi\), \(\eta\), and \(\zeta\) are the natural coordinates as depicted in Fig. 3.

The strain, \(\nabla^{T} {\varvec{u}}\), in (1) is uniform within each tetrahedron given by:

$$ \nabla^{T} {\varvec{u}} \approx \nabla^{T} \left( {\user2{N\hat{u}}} \right) = \user2{B\hat{u}} $$
(6)

in which \({\varvec{B}}\) is the strain–displacement matrix expressed as below

$${\varvec{B}}={\nabla }^{T}{\varvec{N}}=\left[\begin{array}{cccccccccccc}{b}_{1}& 0& 0& {b}_{2}& 0& 0& {b}_{3}& 0& 0& {b}_{4}& 0& 0\\ 0& {c}_{1}& 0& 0& {c}_{2}& 0& 0& {c}_{3}& 0& 0& {c}_{4}& 0\\ 0& 0& {d}_{1}& 0& 0& {d}_{2}& 0& 0& {d}_{3}& 0& 0& {d}_{4}\\ {c}_{1}& {b}_{1}& 0& {c}_{2}& {b}_{2}& 0& {c}_{3}& {b}_{3}& 0& {c}_{4}& {b}_{4}& 0\\ 0& {d}_{1}& {c}_{1}& 0& {d}_{2}& {b}_{2}& 0& {d}_{3}& {c}_{3}& 0& {d}_{4}& {c}_{4}\\ {d}_{1}& 0& {c}_{1}& {d}_{2}& 0& {c}_{2}& {d}_{3}& 0& {b}_{3}& {d}_{4}& 0& {b}_{4}\end{array}\right]$$
(7)

In Eq. (7), the coefficients are partial derivatives of the shape functions with respect to the physical Cartesian coordinates. Specifically, they are calculated by

$$ \left\{ {\begin{array}{*{20}c} {b_{1} = \frac{{\partial N_{{}}^{1} }}{\partial x};b_{2} = \frac{{\partial N_{{}}^{2} }}{\partial x};b_{3} = \frac{{\partial N_{{}}^{3} }}{\partial x};b_{4} = \frac{{\partial N_{{}}^{4} }}{\partial x}} \\ {c_{1} = \frac{{\partial N_{{}}^{1} }}{\partial y};c_{2} = \frac{{\partial N_{{}}^{2} }}{\partial y};c_{3} = \frac{{\partial N_{{}}^{3} }}{\partial y};c_{4} = \frac{{\partial N_{{}}^{4} }}{\partial y}} \\ {d_{1} = \frac{{\partial N_{{}}^{1} }}{\partial z};d_{2} = \frac{{\partial N_{{}}^{2} }}{\partial z};d_{3} = \frac{{\partial N_{{}}^{3} }}{\partial z};d_{4} = \frac{{\partial N_{{}}^{4} }}{\partial z}} \\ \end{array} } \right. $$
(8)

where \(x\), \(y\), and \(z\) are physical Cartesian coordinates. The derivative of shape functions with respect to physical coordinates can be determined using the chain rule

$$ \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{{}}^{i} }}{\partial x}} \\ {\frac{{\partial N_{{}}^{i} }}{\partial y}} \\ {\frac{{\partial N_{{}}^{i} }}{\partial z}} \\ \end{array} } \right] = {\varvec{J}}_{{}}^{ - 1} \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{{}}^{i} }}{\partial \xi }} \\ {\frac{{\partial N_{{}}^{i} }}{\partial \eta }} \\ {\frac{{\partial N_{{}}^{i} }}{\partial \zeta }} \\ \end{array} } \right] $$
(9)

with Jacobian matrix being

$$ {\varvec{J}} = \left[ {\begin{array}{*{20}c} {\frac{\partial x}{{\partial \xi }}} & {\frac{\partial y}{{\partial \xi }}} & {\frac{\partial z}{{\partial \xi }}} \\ {\frac{\partial x}{{\partial \eta }}} & {\frac{\partial y}{{\partial \eta }}} & {\frac{\partial z}{{\partial \eta }}} \\ {\frac{\partial x}{{\partial \zeta }}} & {\frac{\partial y}{{\partial \zeta }}} & {\frac{\partial z}{{\partial \zeta }}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{u}^{1} }}{\partial \xi }} & {\frac{{\partial N_{u}^{2} }}{\partial \xi }} & {\frac{{\partial N_{u}^{3} }}{\partial \xi }} & {\frac{{\partial N_{u}^{4} }}{\partial \xi }} \\ {\frac{{\partial N_{u}^{1} }}{\partial \eta }} & {\frac{{\partial N_{u}^{2} }}{\partial \eta }} & {\frac{{\partial N_{u}^{3} }}{\partial \eta }} & {\frac{{\partial N_{u}^{4} }}{\partial \eta }} \\ {\frac{{\partial N_{u}^{1} }}{\partial \zeta }} & {\frac{{\partial N_{u}^{2} }}{\partial \zeta }} & {\frac{{\partial N_{u}^{3} }}{\partial \zeta }} & {\frac{{\partial N_{u}^{4} }}{\partial \zeta }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } & {z_{1} } \\ {x_{2} } & {y_{2} } & {z_{2} } \\ {x_{3} } & {y_{3} } & {z_{3} } \\ {x_{4} } & {y_{4} } & {z_{4} } \\ \end{array} } \right] $$
(10)

Substituting Eqs. (3) and (6) into min–max problem (1), we have

$$ \begin{array}{*{20}l} {\mathop {\min }\limits_{{\hat{\user2{u}}}} \mathop {\text{ max}}\limits_{{\left( {{\varvec{\sigma}},\alpha } \right)}}\quad \;\; \alpha + \mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{\sigma}}^{T} {\varvec{B}}d{\Omega }\hat{\user2{u}} - \alpha \mathop \smallint \limits_{{{\Gamma }_{t} }}^{{}} \overline{\user2{t}}^{T} {\varvec{N}}d{\Gamma }\hat{\user2{u}} - \mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{b}}^{T} {\varvec{N}}d{\Omega }\hat{\user2{u}}} \hfill \\ {{\text{subject to }}\quad f\left( {\varvec{\sigma}} \right) \le 0} \hfill \\ \end{array} $$
(11)

The minimization part of (11) can be resolved analytically, leading to the following maximization problem:

$$ \begin{array}{*{20}l} {\mathop {\text{ max }}\limits_{{\left( {{\varvec{\sigma}},\alpha } \right)}}\quad \quad \;\alpha } \hfill \\ {{\text{subject to}} \;\mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{\sigma}}^{T} {\varvec{B}}d{\Omega } = \alpha \mathop \smallint \limits_{{{\Gamma }_{t} }}^{{}} \overline{\user2{t}}^{T} {\varvec{N}}d{\Gamma } + \mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{b}}^{T} {\varvec{N}}d{\Omega }} \hfill \\ \qquad \qquad \quad{{ }f\left( {\varvec{\sigma}} \right) \le 0} \hfill \\ \end{array} $$
(12)

The nodal integration of maximization problem (12) over cells result in

$$ \begin{array}{*{20}l} {\mathop { {\text{max}} }\limits_{{\left( {{\varvec{\sigma}},\alpha } \right)}} \qquad\;\;\;{ }\alpha } \hfill \\ {{\text{subject to }}\left\{ {\begin{array}{*{20}l} {\overline{\user2{B}}^{{\text{T}}} \hat{\user2{\sigma }} = \overline{\user2{F}}_{{{\text{ext}}}} } \hfill \\ {f^{i} \left( {\hat{\user2{\sigma }}} \right) \le 0\;\; { }i = 1, 2, \cdots , NN} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} $$
(13)

in which the notation \(\left( \cdot \right)^{i}\) represents the value of \(\left( \cdot \right)\) at the \(i {\text{th}}\) node, unless otherwise specified, and \(NN\) is the total number of nodes, which is also equal to the total number of cells (\(NC\)), indicating that the yield criterion is applied to all nodes. In (13), the stress is denoted by the symbol \(\hat{\user2{\sigma }}\), which is a vector comprising stress components at all mesh nodes. Notably, the stress at each node can be considered as a weighted average of the stress at the tetrahedrons adjacent to that node. For instance, this includes the tetrahedrons that make up the cell associated with that specific node.

The global matrix \(\overline{\user2{B}}^{{\text{T}}}\) is calculated based on nodal integration as

$$ \overline{\user2{B}}^{{\text{T}}} = \mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{B}}_{{}}^{{\text{T}}} d{\Omega } = \mathop \sum \limits_{i = 1}^{NN} \left( {\frac{1}{{V^{i} }}\mathop \sum \limits_{j = 1}^{ne} \left( {\frac{1}{4}{\varvec{B}}_{ij}^{{\text{T}}} V^{j} } \right)} \right) $$
(14)

in which \(\sum \left( \cdot \right)\) represents the standard finite element assembly operator; \(V^{i}\) is the volume of the \(i{\text{th}}\) cell; \(V^{j}\) is the volume of the \(j{\text{th}}\) tetrahedron; \(ne\) is the total number of tetrahedron elements adjacent to the \(i{\text{th}}\) node; and \({\varvec{B}}_{ij}^{{}}\) is the strain–displacement operator at the \(i{\text{th}}\) node, which is estimated based on the \(j{\text{th}}\) adjacent tetrahedron. Therefore, \(\frac{1}{{V^{i} }}\mathop \sum \nolimits_{j = 1}^{ne} \left( {\frac{1}{4}{\varvec{B}}_{ij}^{{\text{T}}} V^{j} } \right)\) represents the weighted average of \({\varvec{B}}_{{}}^{{\text{T}}}\) at the \(i{\text{th}}\) node.

Similarly, \(\overline{\user2{F}}_{{{\text{ext}}}}\) is estimated based on nodal integration

$$ \overline{\user2{F}}_{{{\text{ext}}}} { } = \alpha \mathop \smallint \limits_{{{\Gamma }_{t} }}^{{}} \overline{\user2{t}}^{T} {\varvec{N}}d{\Gamma } + \mathop \smallint \limits_{{\Omega }}^{{}} {\varvec{b}}^{T} {\varvec{N}}d{\Omega } = \alpha \mathop \sum \limits_{i = 1}^{NN} \beta_{{\Gamma }}^{i} \left( {\tilde{\user2{t}}_{{\text{n}}}^{i} {\Gamma }^{i} } \right) + \mathop \sum \limits_{i = 1}^{NN} \left( {\tilde{\user2{b}}_{{\text{n}}}^{i} V^{i} } \right) $$
(15)

in which \({\Gamma }^{i}\) is the nodal contour area; and \(\beta_{{\Gamma }}^{i}\) is a factor that equals to one if the node belongs to a Neumann boundary and is null otherwise.

Hence, the formulation for mixed smoothed FELA can be summarized as:

$$\begin{array}{l}\underset{\left({\varvec{\sigma}},\alpha \right)}{\mathrm{max }} \qquad \quad \;\; \alpha \\ \text{subject to }\;\left\{\begin{array}{l}{\overline{{\varvec{B}}} }^{\mathrm{T}}\widehat{{\varvec{\sigma}}}={\overline{{\varvec{F}}} }_{\mathrm{ext}}\\ {f}^{i}\left(\widehat{{\varvec{\sigma}}}\right)\le 0\; i=1, 2, \cdots , NN\end{array}\right.\\ \text{where } \qquad \left\{\begin{array}{l}\boldsymbol{ }\\ {\overline{{\varvec{B}}} }^{\mathrm{T}}=\sum_{i=1}^{NN}\left(\frac{1}{{V}^{i}}\sum_{j=1}^{ne}\left(\frac{1}{4}{{\varvec{B}}}_{j}^{\mathrm{T}}{V}^{j}\right)\right)\\ {\overline{{\varvec{F}}} }_{\mathrm{ext}} =\alpha \sum_{i=1}^{NN}{\beta }_{\Gamma }^{i}\left({\widetilde{{\varvec{t}}}}_{\mathrm{n}}^{i}{\Gamma }^{i}\right)+\sum_{i=1}^{NN}\left({\widetilde{{\varvec{b}}}}_{\mathrm{n}}^{i}{V}^{i}\right)\end{array}\right.\end{array}$$
(16)

Although the above maximization problem lacks the upper/lower bound feature, the solution obtained from this formulation is often much closer to the exact solution for the bearing capacity of a structure [32].

3 Topology optimization formulation

3.1 Black-and-white topology optimization in limit analysis

Based on reference [25], density-based topology optimization in limit analysis can be formulated as a volume minimization problem by introducing a new design variable, ‘density’ \(\rho \in \left[ {0,1} \right]\), in (16). The modified optimization problem, considering the density variable, can be expressed as:

$$ \begin{array}{*{20}l} {\mathop {\text{ min }}\limits_{{\left( {\hat{\user2{\sigma }},\hat{\user2{\rho }}} \right)}} { }\qquad \quad{\varvec{L}}^{{\text{T}}} \hat{\user2{\rho }}} \hfill \\ {{\text{subject to }}\;\left\{ {\begin{array}{*{20}l} {\overline{\user2{B}}^{{\text{T}}} \hat{\user2{\sigma }} = \overline{\user2{F}}_{{{\text{ext}}}} } \hfill \\ {f^{i} \left( {\hat{\user2{\sigma }},\hat{\user2{\rho }}} \right) \le 0{ }\;i = 1, 2, \cdots , NN} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} $$
(17)

where \(\hat{\user2{\rho }} = \left[ {\rho_{1} , \rho_{2} , \cdots ,\rho_{NN} } \right]^{{\text{T}}}\) is a vector consisting of density at all nodes, and \({\varvec{L}} = \left[ {V_{1} , V_{2} , \cdots ,V_{NC} } \right]^{{\text{T}}}\) is a vector consisting of the volumes of all cells. \(NN\) refers to the total number of nodes, which is equal to the total number of cells \(NC\). In this study, we have employed the von Mises yield criterion to enable consistent comparisons between the developed method and the traditional stress-constrained topology optimization approach (i.e., PolyStress [33]). This is because a stress constraint for the traditional stress constrained topology optimization is usually expressed as the von Mises equivalent stress as indicated in [34]. However, it is crucial to highlight that the developed framework is flexible and can accommodate other plasticity models. For instance, the Mohr–Coulomb model and the Rankine model can also be incorporated within the proposed methodology following [27, 35]. The yield criterion for the ith node/cell (i.e., \(f^{i}\) in (16)) is defined as:

$$ f^{i} = \sqrt {3J_{2} } - \rho_{i} f_{y} \le 0 $$
(18)

where \(J_{2} = \frac{1}{6}\left( {\sigma_{x} - \sigma_{y} } \right)^{2} + \frac{1}{6}\left( {\sigma_{y} - \sigma_{z} } \right)^{2} + \frac{1}{6}\left( {\sigma_{z} - \sigma_{x} } \right)^{2} + \sigma_{xy}^{2} + \sigma_{yz}^{2} + \sigma_{zx}^{2}\) is the second invariant of the deviatoric stress, \(f_{y}\) is the yield stress, and \(\rho_{i}\) denotes the density at the ith node.

Remark 1

The modified criterion (18) indicates that when \(\rho_{i} = 0\), shear stresses are zero (i.e., \(\sigma_{xy}^{{}} = \sigma_{yz}^{{}} = \sigma_{zx}^{{}} = 0\)) but a spherical stress state (i.e., \(\sigma_{x} = \sigma_{y} = \sigma_{z}\)) is allowed. To address this issue, an additional inequality condition \(f_{sp}^{i} = \left| {\sigma_{x} + \sigma_{y} + \sigma_{z} } \right| - kf_{y} \rho_{i} \le 0\) should be enforced for each node as suggested in [24], where \(k\) is a constant with a sufficiently large value. Obviously, this additional condition ensures that stress states are unaffected when \(\rho_{i} = 1\), while all stress components are zero when \(\rho_{i} = 0\) recalling (18).

Remark 2

Formulation (17) tends to produce grayscale solutions. To obtain a black-and-white layout, penalties should be applied to the objective function. Following [26, 36], the vector \({\varvec{L}}\) is replaced with \(\tilde{\user2{L}} = \left[ {c_{1} V_{1} , c_{2} V_{2} , \cdots ,c_{NC} V_{NC} } \right]^{{\text{T}}}\), where the penalty factor for the ith node is determined by.

$$ c_{i} = e^{{p\left( {1 - \rho_{i}^{*} } \right)}} $$
(19)

The above exponential penalty function is based on \(\rho_{i}^{*}\), the density at the ith node obtained in the previous iteration, and a constant, \(p\). The performance of this exponential penalty function has been investigated in [26, 36].

Thus, the black-and-white topology optimization formulation in the context of mixed smoothed FELA can be summarized as:

$$\begin{array}{ll}\underset{\left(\widehat{{\varvec{\sigma}}},\widehat{{\varvec{\rho}}}\right)}{\mathrm{min }}& \;{\widetilde{{\varvec{L}}}}^{\mathrm{T}}\widehat{{\varvec{\rho}}}\\ \text{subject to }& \left\{\begin{array}{l}\begin{array}{l}{\overline{{\varvec{B}}} }^{\mathrm{T}}\widehat{{\varvec{\sigma}}}={\overline{{\varvec{F}}} }_{\mathrm{ext}}\\ {f}^{i}\left(\widehat{{\varvec{\sigma}}},\widehat{{\varvec{\rho}}}\right)\le 0\\ {f}_{sp}^{i}\left(\widehat{{\varvec{\sigma}}},\widehat{{\varvec{\rho}}}\right)\le 0 \;\; i=1, 2, \cdots , NN\end{array}\\ 0\le {\widehat{\rho }}^{i}\le 1\qquad \; i=1, 2, \cdots , NN\end{array}\right.\\ \mathrm{where}& \left\{\begin{array}{c}\begin{array}{l}{\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\widetilde{{\varvec{L}}}}^{\mathrm{T}}=[{c}_{1}{V}_{1}, {{c}_{2}V}_{2},\cdots ,{c}_{NC}{V}_{NC}]\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! {\overline{{\varvec{B}}} }^{\mathrm{T}}=\sum_{i=1}^{NN}\left(\frac{1}{{V}^{i}}\sum_{j=1}^{ne}\left(\frac{1}{4}{{\varvec{B}}}_{j}^{\mathrm{T}}{V}^{j}\right)\right)\end{array}\\ {\overline{{\varvec{F}}} }_{\mathrm{ext}} =\alpha \sum_{i=1}^{NN}{\beta }_{\Gamma }^{i}\left({\widetilde{{\varvec{t}}}}_{\mathrm{n}}^{i}{\Gamma }^{i}\right)+\sum_{i=1}^{NN}\left({\widetilde{{\varvec{b}}}}_{\mathrm{n}}^{i}{V}^{i}\right)\end{array}\right.\end{array}$$
(20)

The above optimization problem can be reformulated as a standard second-order cone programming (SOCP) problem, as described in [26, 37]. It can then be resolved straightforwardly using the advanced primal–dual interior point method available in MOSEK [38].

3.2 Density filtering and mesh refinement

Checkerboard issues are a common problem in density-based topology optimization. To address this issue, the proposed method employs density filtering, as outlined in [39]. The filtered density at the ith point is calculated using the following equation:

$$ \tilde{\rho }_{i}^{{}} = \frac{{\mathop \sum \nolimits_{{j \in N_{n} }} w\left( {x_{j} } \right)v_{j} \rho_{j}^{{}} }}{{\mathop \sum \nolimits_{{j \in N_{n} }} w\left( {x_{j} } \right)v_{j} }} $$
(21)

where \(v_{j}\) is the volume of the jth cell; \(\rho_{j}^{{}}\) is the density at the jth node; and \(N_{n} \) denotes the total number of nodes located within the filtering region of the ith node. The filtering region is defined as a circle with a radius of \(R\). The weighting function, denoted as \(w\left( {x_{j} } \right)\), is a Gaussian (bell shape) distribution function, as suggested in [39]:

$$ w\left( {x_{j} } \right) = e^{{ - \frac{1}{2}\left( {\frac{||{x_{j} - x_{i} ||}}{{\sigma_{d} }}} \right)^{2} }} $$
(22)

in which \(x_{i}\) represents the coordinates of the ith node whose density is filtered, and \(x_{j}\) represents the coordinates of the jth nodes within the filtering region. It has been shown in [26] that the above weighting function performs well for plasticity-based topology optimization in 2D cases. Therefore, it is adopted for 3D studies in this paper. The parameter \({ }\sigma_{d}\) in Eq. (22) is set as \(R/2\), where \(R\) is 1.5 times the mesh size, as suggested in [26].

3.3 Algorithm steps

To summarize, the basic steps of the topology optimization procedure are as follows:

  1. (i)

    Assume an initial density \(\rho = 1\) for all nodes in the domain;

  2. (ii)

    Calculate the exponential penalty factor \(c_{i}\) using (19) for each node;

  3. (iii)

    Solve the optimization problem (20) using MOSEK to obtain the density field;

  4. (iv)

    Perform density filtering for each node using (21) and use the filtered value as the density at each node;

  5. (v)

    Check the convergence criterion: cease the iteration if the criterion is satisfied (i.e., the change in the objective function, \(Obj = \tilde{\user2{L}}^{{\text{T}}} \hat{\user2{\rho }}\),between two iterations fulfils \(\bigg {|} \frac{{Obj_{{{\text{n}} + 1}} - Obj_{{\text{n}}} }}{{Obj_{{{\text{n}} + 1}} }}\bigg {|} \le {\text{tolerance value}}\)); otherwise, go back to step (ii) and repeat the process.

It is acknowledged that 3D topology optimization often requires significant computational resources. Therefore, enhancing the computational efficiency of the proposed method is of paramount importance. While developing a parallelized computing scheme for resolving SOCP problems is a common approach, we would also like to emphasize the potential of employing warm start strategies to improve computational efficiency. This is particularly relevant in our solution scheme, which involves an iterative procedure where the SOCP problem is repeatedly solved in step (iii) to obtain a converged density field. Research has shown that warm start strategies can substantially enhance the efficiency of the interior point method when solving SOCP problems. For more detailed information on this topic, interested readers are encouraged to refer to [40, 41].

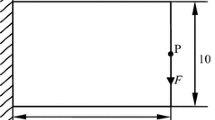
Remarkably, in conventional stress-constrained topology optimization, elastic finite element analysis is conducted with stress constrains. This means that all materials are assumed to behave elastically, and the structure is considered to fail when any local yielding occurs. The maximum load that the structure can sustain is denoted as \({P}_{e}\), as shown in Fig. 4. In contrast, the plasticity-based topology optimization method developed in this study treats the material as rigid plastic. By incorporating plastic limit theory into the optimization problem (20), the external force represents the load-bearing capacity of the layout, denoted as \({P}_{Y}\) in Fig. 4, as indicated in the work of plasticity-based topology optimization [24, 26, 27]. Consequently, the developed plasticity-based topology optimization method generally provides a more efficient solution compared to the conventional stress-constrained method. This will be demonstrated through numerical examples in the following section.

Fig. 4
figure 4

Illustration of the load–displacement curve for a structure made of elastic-perfectly plastic materials

Full size image

4 Numerical examples

In this section, several examples are presented to demonstrate the correctness and robustness of the proposed method. All simulations were conducted on a DELL PC with a 2.20 GHz CPU and 32.0 GB memory, running on Microsoft Windows server (Version 10.0). The final SOCP problem was solved using MOSEK [38], an advanced optimization tool designed for solving large-scale optimization problems. The implementation of the method was carried out in the MATLAB environment (R2021b).

4.1 A short plate

The first example involves a thin short plate subjected to a shear load, as depicted in Fig. 5. This classical problem has been widely employed for the verification of various topology optimization methods [42,43,44]. In this study, the plate has dimensions of 1 m × 1 m × 0.01 m. The left surface of the plate is clamped, and a shear force of \(F=90 \mathrm{kN}\) is applied at the lower right corner of the plate. The material used in the analysis has a yield stress of \({f}_{y}=220 \mathrm{MPa}\). The mesh size is set to 0.01 m, resulting in one layer element along the thickness direction. A total of 60,000 elements are employed in this simulation. Throughout all the simulations, the penalization factor is set to \(\mathrm{p}=5\), which is considered sufficiently large to achieve a black-and-white layout, as suggested in [26]. The constant \(k\) for the spherical stress state is set to \(1\times {10}^{3}\), unless otherwise specified.

Fig. 5
figure 5

A plate under shear load

Full size image

Remarkably, the adopted plastic model in this study is the rigid-perfectly plastic model with von Mises yield criterion, which assumes incompressible materials. Traditional constant stress elements, such as the three-node triangular element in 2D and the four-node tetrahedral element in 3D, are uncompetitive for such problems due to volumetric locking issues. This issue has been extensively discussed in the literature [37, 45, 46], and its adverse impact on topology optimization has also been explored in [42]. To overcome the volumetric locking issues associated with incompressibility, the mixed smoothed finite element formulation developed in [37] is employed in this study for constructing 3D limit analysis based topology optimization. The effectiveness of this formulation in tackling incompressibility issues has been demonstrated in [37] and is not repeated in this study. In the following, we will present a comparison between the simulation results obtained from the developed 3D plasticity-based method and the traditional stress-constrained topology optimization method (i.e. PolyStress) [33].

The final layouts obtained from both simulations are shown in Fig. 6a and b. Albeit they appear similar, the amount of material required differs. Figure 6c illustrates the convergence history of the two methods in terms of the volume ratio. It can be observed that the developed method achieves a converged volume ratio of 20%, which is lower than that obtained from PolyStress (i.e., 28.2%). This discrepancy arises from the adoption of the plasticity theory in the developed topology optimization formulation. Our approach allows for material yielding as long as the global structure remains stable which means it targets the loading capacity of the overall structure. In contrast, the traditional stress constrained method solves the elastic governing equation of the structure and restricts yielding in all material points, implying that the structure designed using PolyStress behaves elastically under the applied load. This point can be further verified by examining the distribution of von Mises stress across the layouts from the two methods. Figure 7a illustrates that a significant portion of the layout obtained from the developed method exhibits a von Mises stress equal to the yield stress (e.g. 220 MPa) indicating that the structure has reached its maximum sustainable state. In contrast, fewer parts of the layout obtained from PolyStress possess a von Mises stress equal to the yield stress. Additionally, it is worth noting that the proposed method demonstrates a faster convergence rate in terms of volume ratios compared to the conventional stress-constrained method, as shown in Fig. 6c. In fact, a converged solution is obtained with 5 iterations using the developed method.

Fig. 6
figure 6

Simulation results: a layout from this study; b layout from PolyStress [33]; and c convergence history in terms of volume ratio

Full size image
Fig. 7
figure 7

Distribution of von Mises Stress on the designed layout for a short plate from from (a) the plasticity-based method developed in this study and (b) PolyStress

Full size image

4.2 A clamped beam

As the second example, we consider a double-clamped beam as shown in Fig. 8. The length and height of the designed domain are 20 m and 5 m, respectively, and the thickness of the beam varies from t = 0.01 to 10 m. The yield stress of the material is set to 300 kPa. A uniform pressure of \(\mathrm{p}=15.3\) kPa is applied to the top central zone with a length of 2.5 m. Due to symmetry, only half of the domain is considered in the modelling process.

Fig. 8
figure 8

An illustration of a double clamped beam

Full size image

4.2.1 Thin beam & mesh refinement

We begin by focusing on a thin beam with a thickness of \(t=0.01\) m. The mesh size used on x–y plane is 0.15 m, and only one layer is assigned in the thickness direction (i.e. z axis) resulting in 20,604 nodes and 60,000 elements in the simulation. Figure 9 illustrates the evolutionary history of the structure in the optimal design using both PolyStress and the plasticity-based method. A grey design is obtained in both approaches if no iterations are conducted. A satisfactory black-and-white layout is achieved with 8 iterations using the developed method (Fig. 9), and the volume ratio from the developed method is 33% (Fig. 10). PolyStress also produces a black-and-white layout similar to that from our approach. Nevertheless, the layout of the structure varies slightly even after 8 iterations. This fluctuation is evident in the curve of volume ratio against iteration, as shown in Fig. 10. In contrast, the volume ratio exhibits little change for iteration greater than 6 in the modelling using our developed method. The volume ratio from our method is 33%, which is lower than the 45% obtained from the traditional stress-constrained approach. Notably, the curves of the volume ratio against iteration from this study and the 2D plasticity-based method using quadratic elements [26] are in good agreement, which further validates the proposed method.

Fig. 9
figure 9

The layout from PolyStress and the developed limit analysis-based topology optimization method at different iterations

Full size image
Fig. 10
figure 10

Volume ratio versus iteration in different approaches under different approaches

Full size image

To further compare the results from the method developed in this study and the conventional stress-constrained topology optimization method, the distribution of VM stress on the layouts from the two methods is shown in Fig. 11, and the percentage distribution is shown in Fig. 12. These results are obtained using uniform meshes, and the mesh sizes for the two simulations are the same (0.15 m). As expected, most areas of the layout from the developed plasticity-based method exhibit a VM stress equal to the yield stress, whereas many parts of the layout from PolyStress have a VM stress smaller than the yield stress. The quantitative comparison shown in Fig. 12 indicates that the percentages of VM stress located in the ranges of 0–30 kPa and 270–300 kPa from the developed method are larger than these from PolyStress. Very low percentages of VM stress in the range from 30–270 kPa also demonstrates the efficiency of the adopted exponential penalty function in Eq. (19).

Fig. 11
figure 11

Distribution of von Mises Stress on the designed layout for a thin beam from (a) the plasticity-based method developed in this study and (b) PolyStress

Full size image
Fig. 12
figure 12

Distribution of the percentage of von Mises Stress

Full size image

Noteworthily, 3D simulations are generally computationally demanding. To reduce the computational burden, we employ a simple and efficient mesh refinement scheme. The basic idea is to check the density of each node and the length of all edges associated with the node. If both the density and edge length exceed given threshold values, an additional point is added to the middle of the associated edge for mesh refinement.

To illustrate the efficiency of this approach, we re-analyze this example with mesh refinement. Initially, we discretize the domain with a larger mesh size of \({h}_{e}=0.2\) m, resulting in 4,556 nodes and 13,068 meshes. The mesh refinement is carried out using a density threshold of 0.9, and an edge threshold of 0.15 m, which is identical to the mesh size used in the simulation without mesh refinement. Figure 13 shows the evolution of the layout in the two simulations. Clearly, a satisfactory black-and-white structure is obtained with 5 iterations in the simulation with mesh refinement. In contrast, more than 7 iterations are required in the simulation without mesh refinement. The convergence history in terms of volume ratio against iteration for the two cases is illustrated in Fig. 14. As observed, the volume ratio exhibits little variation for iterations greater than 7 in the simulation with mesh refinement, whereas there is a slight fluctuation, with a magnitude of less than 2%, in the case without mesh refinement.

Fig. 13
figure 13

The layouts from the developed method with/without mesh refinement at different iteration steps

Full size image
Fig. 14
figure 14

Convergence history in terms of volume ratio against iteration

Full size image

The computational cost for the two cases is presented in Table 1. The simulation with mesh refinement requires only half of the elements and nodes compared to the simulation without mesh refinement to achieve a similar solution. The time required for the simulation with mesh refinement for 9 iterations is 150.34 s – approximately 36% of the time required in the case without mesh refinement. Remarkably, there is no need for 9 iterations in the simulation with mesh refinement, as a converged solution is obtained at 7 iterations (Fig. 14), suggesting that the computational cost of the case with mesh refinement should be even lower than 150.34 s.

Table 1 Computing cost for the simulation with/without mesh refinement
Full size table

4.2.2 A thick beam

With mesh refinement, we further investigate a beam with a significant thickness of \(t=5\) m. The parameters and the imposed pressure are the same as those in Sect. 4.2.1. The domain is initially discretized using a total of 41,106 nodes and 225,000 meshes.

Figure 15 illustrates the evolution of the layout at different iteration steps. As shown, a converged black-and-white layout is obtained at the 6th iteration step, which is in line with the curve of volume ratio against iteration shown in Fig. 16. The volume ratio in this case is 32.5%, slightly lower than the ratio for the thin beam case (33.1%). This is because the topology structure can be optimized in the thickness direction, resulting in an optimal spatial structure as depicted in Fig. 17a. Figure 17b displays the normalized VM stress. As seen, the normalized VM stress is less than 1 in most parts of the designed structure surface, given that the surface is in the thin blur area. This aligns with the distribution of the normalized VM stress on the three specific slices at \(z=\) 2.5 m, 4.3 m, and 5.0 m (Fig. 17c–e). When subjected to the given pressure, most inner parts of the structure have a \({\sigma }_{VM}\) equal to 1, while a thin layer exists on the surface of the optimal structure. Remarkably, the layouts on the three slices differ from each other, indicating that optimized structure adapts to different sections along the thickness direction. The number of node and element at the 6th iteration is 211,546 and 1,291,368, respectively, and the computational cost for iterations from step 1 to 6 is 10.9 h.

Fig. 15
figure 15

The layout evolution of a beam with \(\mathrm{t}=5\) m obtained from the developed method

Full size image
Fig. 16
figure 16

The layout evolution of a beam with \(\mathrm{t}=5\) m obtained from the developed method

Full size image
Fig. 17
figure 17

Topology optimization results of a thick beam: a optimal layout, and the normalized VM stress on b the structure and slices at c z = 2.5 m, d z = 4.3 m, and e z = 5.0 m

Full size image

It is worth noting that extracting a manufacturable structure from the 3D density fields obtained from topology optimization is nontrivial. Here, we conducted a more detailed investigation into the extraction of structure from different density ranges. The topologies extracted from four density ranges, namely \(\rho >0.1\), \(\rho >0.3\), \(\rho >0.5\), and \(\rho >0.7\), are illustrated in Fig. 18. Very little difference can be identified for the four layouts, which echoes the distribution of density shown in Fig. 19. A large portion of the design domain possesses density either close to 0 or 1. Consequently, in this study, all layouts are extracted for \(\rho >0.5\) unless otherwise specified.

Fig. 18
figure 18

Layout extracted under different density ranges

Full size image
Fig. 19
figure 19

Distribution of the percentage of density

Full size image

4.3 Bridge design

The final example in this study focuses on the design of a bridge. Figure 20 depicts the design domain with dimensions of \(18\mathrm{m}\times 6\mathrm{m}\times 4\mathrm{m}\). The bridge is clamped at the two bottom supports, indicated by the shaped zones, each measuring \(2\mathrm{m}\times 4\mathrm{m}\). A uniformly distributed traffic load F = 875 kPa is applied to the top blue plate in the design. The plate has a thickness of 0.1 m and is positioned 4.5 m from the top and 1.4 m from the bottom of the design domain. The yield stress of the material is 10 MPa, and the density of the blue plate is set to be one in the simulation. The initial discretization of the design domain employs a mesh size of \({h}_{e}=0.2\) m, resulting in 59,241 nodes and 324,000 elements. Mesh refinement is carried out using a density threshold of 0.9 and an edge threshold of 0.08 m. The tolerance value for this case is set to 0.5%.

Fig. 20
figure 20

The bridge design domain (unit: m)

Full size image

Table 2 presents the simulation history in terms of the volume ratio and error. A converged result is achieved with 5 iterations, and the error, defined as \(\bigg{|}\frac{ {Obj}_{\mathrm{n}+1}-{Obj}_{\mathrm{n}} }{{Obj}_{\mathrm{n}+1}}\bigg{|}\) from the 5th iteration, is 0.24%, which is lower than the tolerance value of 0.5%. The resulting converged layout has a volume ratio of 12.3%.

Table 2 Convergence history of the bridge design
Full size table

Figure 21 shows the design history of the bridge. As the number of iterations increases, the bridge structure gradually undergoes optimization, resulting in a trail bridge structure. The optimized structure features two walls with holes in the upper part of the domain, with the holes separated from each other by several cable-like structures. The lower part of the bridge consists of two hollow piers connecting to the areas with fixed boundaries. The computational cost for this design is 6.55 h, and the converged solution is achieved with a total of 154,615 nodes and 909,331 elements.

Fig. 21
figure 21

Evolution history of the bridge layout

Full size image

Additionally, the effect of the height of the deck surface on the bridge design is investigated. The deck surface is varied at the heights of 1 m, 2 m, 3 m, 4 m, 5 m, 6 m from the bottom of the design domain. Figure 22 shows that as the deck height increases, the volume ratio decreases. For lower deck heights, the optimal bridge design includes piers as well as upper part arch-like structure to support the traffic load as illustrated in Fig. 23. On the other hand, for higher deck heights, the structure features piers with a more complex topology and does not have an upper structure.

Fig. 22
figure 22

Volume ratio against the height of deck

Full size image
Fig. 23
figure 23

Optimal structures from the developed approach for a deck at different heights

Full size image

5 Conclusions

This paper presents a method for 3D black-and-white topology optimization of continuum structures considering plasticity. The method combines density-based topology optimization and mixed limit analysis, formulating a sequence of continuous convex topology optimisation problems. These problems are efficiently solved using the primal–dual interior point method in modern optimisation engine. To enhance computational efficiency, mesh refinement operations are introduced using linear tetrahedral elements. Volumetric locking issues commonly associated with linear tetrahedral elements are effectively addressed by incorporating the smoothed finite element technique.

In contrast to conventional stress-constrained topology optimisation approaches, the proposed plasticity-based method eliminates the need for a separate finite element structural analysis procedure. It offers a more cost-effective design solution by allowing material yielding as long as the global structure remains stable. This stands in contrast to the traditional stress-constrained method where structures are restricted to elastic behavior only. The correctness and robustness of the developed 3D plasticity-based approach are demonstrated through a series of classical numerical examples. Qualitative and quantitative comparisons with traditional stress-constrained approaches validate the effectiveness of the proposed method.