Computational instability analysis of inflated hyperelastic thin shells using subdivision surfaces

Abstract

The inflation of hyperelastic thin shells is a highly nonlinear problem that arises in multiple important engineering applications. It is characterised by severe kinematic and constitutive nonlinearities and is subject to various forms of instabilities. To accurately simulate this challenging problem, we present an isogeometric approach to compute the inflation and associated large deformation of hyperelastic thin shells following the Kirchhoff–Love hypothesis. Both the geometry and the deformation field are discretized using Catmull–Clark subdivision bases which provide the required $C^1$-continuous finite element approximation. To follow the complex nonlinear response exhibited by hyperelastic thin shells, inflation is simulated incrementally, and each incremental step is solved using the Newton–Raphson method enriched with arc-length control. An eigenvalue analysis of the linear system after each incremental step assesses the possibility of bifurcation to a lower energy mode upon loss of stability. The proposed method is first validated using benchmark problems and then applied to engineering applications, where the ability to simulate large deformation and associated complex instabilities is clearly demonstrated.

1 Introduction

Many important applications involve thin structures composed of natural rubber, synthetic elastomers or soft biological tissue undergoing nonlinear and large reversible deformations. The response of these systems is often characterised by severe kinematic and constitutive nonlinearities and is subject to various types of instabilities. An accurate, efficient and robust isogeometric approach is developed here to simulate the various instabilities that can occur. The proposed method can predict the mechanical behaviour of thin shells with arbitrary geometry, and provide guidance for the design and application of highly-deformable thin structures.

Modelling of slender structures, such as rods, membranes, plates, and shells, that exhibit both material and geometric nonlinearities is particularly challenging. In these structures, one or more characteristic dimensions are negligible with respect to the others. They can be modelled as lower-dimensional manifolds embedded in the three-dimensional space with appropriate kinematic simplifications. In this work, we consider the case of incompressible hyperelastic thin shells, which can be regarded as two-dimensional surfaces with a small thickness (membranes and plates are a particular subcase of shell structures). Thin shells can undergo large deformation, even when subjected to small external loads, and their analysis requires careful consideration of kinematic, constitutive, and geometric nonlinearities. The simplest kinematic approximation for shell models is the Kirchhoff hypothesis. This states that lines perpendicular to the mid-surface remain straight and perpendicular to the mid-surface after deformation, thereby neglecting out-of-plane shearing, and leading to the well-established Kirchhoff–Love thin shell theory, which is governed by a fourth-order partial differential equation. The resulting weak formulation of the governing equation seeks for solutions in spaces where the components of the Hessian have a bounded $L^2$ norm. This requires a discretization where approximations are at least globally $C^1$ continuous [77]. Traditional finite element methods, based on Lagrange polynomials, only provide $C^0$ continuity. The required continuity can be obtained using more exotic finite element approximations, such as Argyris finite element spaces on triangles [3] or their equivalent on quadrilaterals [38]. Ivannikov et al. [35] adopted a TUBA (T-Rex Unstructured Boundary-conforming Adaptive meshing) family of plate finite elements to provide a $C^1$ continuous discretization for the Kirchhoff–Love shell. Other alternatives include the weak imposition of the required continuity using discontinuous Galerkin methods [54] and meshless methods [34, 43].

An alternative approach that guarantees $C^1$ continuity comes from the isogeometric paradigm, where the basis functions of the finite element spaces are inspired by computer-aided design (CAD) principles. One of the earliest presentations of this approach was by Cirak et al. [18] who developed a finite element formulation based on Loop subdivision surfaces for Kirchhoff–Love thin shells. This was later extended to hyperelastic thin shells by Cirak and Ortiz [17]. Subdivision surfaces are a mature CAD tool widely used in the animation industry and for engineering design. One of their strengths is that they guarantee global $C^1$ continuity for arbitrary control point topologies (including extraordinary vertices, i.e., vertices on a surface shared by a number of cells different from four, and hanging node vertices), and allow for fast evaluation using standard cubic spline functions in all ordinary patches (i.e., all patches where vertices are shared exactly by four cells). Shell formulations based on subdivision surfaces have been extended to applications including fracture [19], shape optimisation [6, 14], fluid–structure interaction [20], structural-acoustic analysis [15, 16, 45] and piezoelectricity [48]. The use of more general non-uniform rational B-splines (NURBS) basis functions in the finite element context was proposed by Hughes et al. [32] in 2005. It was applied to linear elastic and, later, hyperelastic thin shells by Kiendl et al. [40, 41]. This formulation has been used to solve fluid–structure interaction problems by coupling shell formulation with an isogeometric BEM formulation [28]. Takizawa et al. [65] derived a hyperelastic thin shell formulation with isogeometric discretization, where the out-of-plane deformation mapping is taken into account. Tepole et al. [67] developed an isogeometric formulation of Kirchhoff–Love shells to analyse biological membranes. Roohbakhshan and Sauer [60] also used an isogeometric rotation-free shell formulation to model soft tissues. Huynh et al. [33] studied the elastoplastic large deformation behaviour of thin shell structures using the isogeometric approach. IGA has also been extensively applied to analyse hyperelastic solids [8, 10, 22, 27]. An attractive feature of subdivision surfaces is that they can be evaluated using spline functions while retaining a simple polygonal mesh data structure. They are also able to represent complex geometries and permit extraordinary vertices which enables local refinement and patch-conforming approximations, both challenges for NURBS.

Buckling of thin structures has also been studied using IGA shell formulations. Guo et al. [24] proposed an IGA framework for the buckling analysis of trimmed elastic shells. Verhelst et al. [69] presented a formulation of stretch-based material models for isogeometric Kirchhoff–Love shells which was used to simulate the tension wrinkling of a thin sheet.

The inflation of thin structures made from rubber-like materials has numerous important engineering applications, including tyres, airbags, air springs, buffers, pneumatic actuators [44], and soft grippers [25]. The large deformation of inflated hyperelastic circular plates has been studied extensively using semi-analytical approaches [1, 26, 62, 75]. The inflation of other axisymmetric thin structures, including cylindrical [23, 39, 56, 59], spherical [2, 70, 74] and toroidal [58, 66, 68] membranes, has also been investigated semi-analytically. Holzapfel et al. [30] presented a general formulation of thin incompressible membranes to investigate biological tissues using the finite element method. Bonet et al. [11] analysed hyperelastic membranes containing an enclosed fluid with a finite element approach. Rumpel et al. [61] also developed a finite element model for gas and fluid-supported membrane and shell structures.

The inflation of hyperelastic membranes and thin shells often involves different types of instabilities. Limit point instability is one of the most common and widely studied forms of instability in inflating thin structures. Upon inflation up to a critical pressure, thin hyperelastic structures lose stiffness and can undergo very large inflation with only a small pressure increment [9, 12, 39, 47, 51, 63, 66]. Another well-known instability of hyperelastic membranes and thin shells is global buckling which breaks geometrical symmetry. It manifests as a bifurcation from symmetric deformation to asymmetric deformation in an inflated structure at a critical loading point. Koiter [42] pioneered a method to evaluate the critical load to cause such instability by analysing the second and higher variations of the total potential energy. This method has been used to analyse the bifurcation of inflating circular [7, 62], cylindrical [59], and toroidal [58, 66, 68] membranes. In the nonlinear finite element method, onset of instability can be checked by an eigenvalue analysis of the stiffness (tangent) matrix after each load step. As the smallest eigenvalue approaches zero, the structure is at a critical point of instability. Moreover, the eigenvector corresponding to the near-zero eigenvalue provides information about the tangent direction of the new solution correspondng to potential loss of stability. By examining the eigenvector, it is possible to determine whether the instability is a bifurcation or a limit point. If the eigenvector breaks the symmetry of the geometry, then it is a bifurcation, which may result in a change in the configuration of the structure. The method of using the eigenvector to check for instability and to induce bifurcation was introduced by Wagner and Wriggers [71], De Borst [21] and Wriggers and Simo [73].

Most of the aforementioned instability analyses of hyperelastic thin structures are limited to simple geometries, and computations performed until the onset of bifurcation. Rapid developments in manufacturing, soft robotics, and biomedical engineering motivate the need to overcome such restrictions. To this end, an incompressible nonlinear hyperelastic thin shell formulation is implemented using an isogeometric approach based on Catmull–Clark subdivision surfaces. The proposed method is able to handle both kinematic and constitutive nonlinearities of hyperelastic thin shells with arbitrary geometry. We demonstrate that multiple types of instability associated with the large deformation of hyperelastic thin shells can be captured. Furthermore, we are able to compute the important post-bifurcation response. Specific attention is paid here to thin shells undergoing large inflation and the various resulting instabilities including limit point, and loss of symmetry bifurcations.

The manuscript is organised as follows. Section 2 introduces the notation and defines the various coordinate systems. Section 3 introduces the thin shell formulation, where Sects. 3.1 and 3.2 define the geometric definitions and kinematics of nonlinear Kirchhoff–Love thin shells, respectively. Section 3.3 presents the constitutive relations of incompressible Mooney–Rivlin material adapted to the specific shell formulation. Thereafter, Sect. 3.5 derives the governing equation of a nonlinear Kirchhoff–Love thin shell using the principle of virtual work. Section 4 introduces the Catmull–Clark subdivision surfaces and discusses the implementation details of the isogeometric nonlinear finite element method for hyperelastic thin shell. In Sect. 5, the algorithm to simulate the nonlinear deformation of hyperelastic thin shells is illustrated, and the difficulties in capturing the snap-through and bifurcation bucklings of inflated hyperelastic thin structures are emphasised. Finally, four numerical examples are presented: a circular plate problem validates the proposed method, and the snap-through buckling of a spherical shell is simulated with the results agreeing well with analytical solutions. The third numerical example investigates the bifurcation of a toroidal thin shell, while the last simulates the inflation of an airbag.

2 Notation

2.1 Brackets

Square brackets $[ \, ]$ are used to group algebraic expressions. Round brackets $( \,)$ are used to denote the dependencies of a function. If brackets are used to denote an interval, then $(\,)$ stands for an open interval and $[\,]$ is a closed interval. Curly brackets $\{\,\}$ are used to define sets.

2.2 Symbols

A variable typeset in a normal weight font represents a scalar. A bold weight font denotes a first- or second-order tensor. An overline indicates that the variable is defined with respect to the reference configuration. If absent, the variable is defined with respect to the deformed configuration. A scalar variable with superscript or subscript indices normally represents the components of a vector or second-order tensor. Upright font is used to denote matrices and vectors.

Indices $i,j,k,\dots$ vary from 1 to 3, while $\alpha , \beta , \gamma ,\dots$, used to indicate surface variable components, vary from 1 to 2. Einstein summation convention is used throughout.

The comma symbol in a subscript represents a partial derivative, for example, $A_{,\beta }$ is the partial derivative of A with respect to the $\beta \text {th}$ coordinate.

2.3 Coordinates

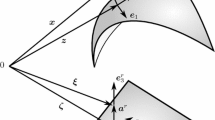
${\textbf{c}}_i$ represent the basis vectors of an orthonormal system in three-dimensional Euclidean space and x, y and z are its coordinates. $\varvec{\theta }^i$ denote the basis vectors in the local element space and $\theta ^1,\theta ^2$ and $\theta ^3$ are its coordinates. The three covariant basis vectors for a surface point are denoted as ${\textbf{a}}_i$, where ${\textbf{a}}_1, {\textbf{a}}_2$ are tangential vectors and ${\textbf{a}}_3$ is the normal vector.

3 Nonlinear Kirchhoff–Love shell formulation

The proposed formulation for hyperelastic thin shell combines the approaches of Cirak and Ortiz [17] and Kiendl et al. [41]. Any differences with the theory presented here are summarised at the end of each subsection.

3.1 Geometry

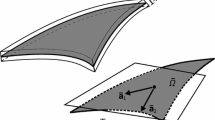
Consider a shell in its reference configuration occupying a physical domain ${\bar{\Omega }} \subset {\mathbb {R}}^3$, as shown in Fig. 1. Each point $\bar{{\textbf{r}}} \in {\bar{\Omega }}$ is mapped from the parametric domain defined by the coordinate system $\{ \theta ^1, \theta ^2, \theta ^3\}$. The Kirchhoff–Love hypothesis states that lines perpendicular to the mid-surface of the thin shell remain straight and perpendicular to the mid-surface after deformation. Hence, assuming the shell has a uniform thickness ${\bar{h}}$ in the reference configuration, the point $\bar{{\textbf{r}}}$ in the shell-space can be defined using a point on the mid-surface ${\bar{\Gamma }}$, denoted $\bar{{\textbf{x}}} \in {\bar{\Gamma }}$, and the associated unit normal vector $\bar{{\textbf{n}}}$ as

$$\begin{aligned} \bar{{\textbf{r}}} = \bar{{\textbf{x}}} + \theta ^3 \bar{{\textbf{n}}}, \end{aligned}$$

(1)

where $\theta ^3 \in [-{{\bar{h}}}/{2}, {{\bar{h}}}/{2}]$.

Fig. 1

A Kirchhoff–Love shell occupying a physical domain ${\bar{\Omega }}$. Each point $\bar{{\textbf{r}}} \in {\bar{\Omega }}$ can be defined using quantities on the mid-surface ${\bar{\Gamma }}$ on the shell as $\bar{{\textbf{r}}} = \bar{{\textbf{x}}} + \theta ^3 \bar{{\textbf{n}}}$

Figure 2 shows the reference and the deformed configuration of the mid-surface. Both configurations can be mapped from the parametric domain of the mid-surface. The points on the mid-surface in the reference and the deformed configurations are denoted by $\bar{{\textbf{x}}}$ and ${\textbf{x}}$, respectively. The mid-surface point in the deformed configuration ${{\textbf{x}}}$ can be related to the mid-surface point in the reference configuration $\bar{{\textbf{x}}}$ as

$$\begin{aligned} {\textbf{x}} = \bar{{\textbf{x}}} + {\textbf{u}}, \end{aligned}$$

(2)

where ${\textbf{u}}$ denotes the displacement. Moreover, the covariant basis vectors in the mid-surface of the reference and the deformed configuration are computed as

$$\begin{aligned} \bar{{\textbf{a}}}_\alpha = \frac{\partial \bar{{\textbf{x}}}}{\partial \theta ^\alpha }, \quad \text {and} \quad {{\textbf{a}}}_\alpha = \frac{\partial {{\textbf{x}}}}{ \partial \theta ^\alpha }. \end{aligned}$$

(3)

Thus, the unit normal vectors in the two configurations are defined by

$$\begin{aligned} \bar{{\textbf{n}}} = \bar{{\textbf{a}}}^3 = \frac{\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2}{\bar{J}} \equiv \bar{{\textbf{a}}}_3, \quad \text {and} \quad {{\textbf{n}}} = {{\textbf{a}}}^3 = \frac{{{\textbf{a}}}_1 \times {{\textbf{a}}}_2}{{J}} \equiv {{\textbf{a}}}_3, \nonumber \\ \end{aligned}$$

(4)

and ${\bar{J}}$ and J are the respective mid-surface Jacobians given by

$$\begin{aligned} \bar{J} = |\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2|,\quad \text {and} \quad J = | {{\textbf{a}}}_1 \times {{\textbf{a}}}_2|. \end{aligned}$$

(5)

Fig. 2

Position vectors in the reference configuration $(\bar{{\textbf{x}}} \in {\bar{\Gamma }})$ of the mid-surface and deformed configuration $({\textbf{x}} \in \Gamma )$ of the mid-surface are related by the displacement vector ${\textbf{u}}$. ${\bar{\Gamma }}$ is spanned by the covariant basis $\{ \bar{{\textbf{a}}}_1, \bar{{\textbf{a}}}_2 \}$ while $\Gamma$ is spanned by the covariant basis $\{ {\textbf{a}}_1, {\textbf{a}}_2\}$

The covariant components of the metric tensors for the mid-surface points $\bar{{\textbf{x}}}$ and ${\textbf{x}}$ are respectively given by

$$\begin{aligned} \bar{a}_{ij} = \bar{{\textbf{a}}}_i \cdot \bar{{\textbf{a}}}_j, \quad \text {and} \quad {a}_{ij} = {{\textbf{a}}}_i \cdot {{\textbf{a}}}_j. \end{aligned}$$

(6)

The corresponding contravariant metric tensors $\bar{a}^{ik}$ and $a^{ik}$ are defined by

$$\begin{aligned} \bar{a}^{ik}\bar{a}_{kj} = \delta ^{i}_{j}, \quad \text {and} \quad a^{ik}a_{kj} = \delta ^{i}_{j}, \end{aligned}$$

(7)

where $\delta ^{i}_{j}$ denotes the Kronecker delta.

The thickness stretch $\lambda _3$ for a finitely deformed shell is defined by

$$\begin{aligned} \lambda _3 = \frac{h}{{\bar{h}}}, \end{aligned}$$

(8)

where $h(\theta ^1,\theta ^2)$ is the shell thickness in the deformed configuration. We introduce a vector ${\textbf{d}}$ combining the thickness stretch and normal vector as

$$\begin{aligned} {\textbf{d}} = \lambda _3 {\textbf{a}}_3, \end{aligned}$$

(9)

to write the position vector ${\textbf{r}}$ of a point in the deformed configuration of the shell-space as

$$\begin{aligned} {{\textbf{r}}} = {{\textbf{x}}} + \theta ^3 {{\textbf{d}}}, \quad \text {with} \quad {\textbf{x}} = {\textbf{x}}(\theta ^1,\theta ^2),\, {\textbf{d}} = {\textbf{d}}(\theta ^1,\theta ^2). \end{aligned}$$

(10)

Thus, the three-dimensional covariant basis vectors in the shell-space of the reference and the deformed configurations, respectively, follow as

$$\begin{aligned} \bar{{\textbf{g}}}_\alpha = \frac{\partial \bar{{\textbf{r}}}}{\partial \theta ^\alpha } = \bar{{\textbf{a}}}_\alpha + \theta ^3 \bar{{\textbf{a}}}_{3,\alpha }, \quad \bar{{\textbf{g}}}_3 = \frac{\partial \bar{{\textbf{r}}}}{\partial \theta ^3} = \bar{{\textbf{a}}}_3, \end{aligned}$$

(11)

and

$$\begin{aligned} {{\textbf{g}}}_\alpha = \frac{\partial {{\textbf{r}}}}{\partial \theta ^\alpha } = {{\textbf{a}}}_\alpha + \theta ^3 {\textbf{d}}_{,\alpha }, \quad {{\textbf{g}}}_3 = \frac{\partial {{\textbf{r}}}}{\partial \theta ^3} = {{\textbf{d}}}. \end{aligned}$$

(12)

The components of the covariant metric tensors in the shell-space are given by

$$\begin{aligned} \bar{g}_{ij} = \bar{{\textbf{g}}}_i \cdot \bar{{\textbf{g}}}_j\quad \text {and} \quad g_{ij} = {\textbf{g}}_i \cdot {\textbf{g}}_j, \end{aligned}$$

(13)

and the contravariant components of the metric tensor at point ${\textbf{r}}$ follow as

$$\begin{aligned} \bar{g}^{ij} = \bar{{\textbf{g}}}^{i} \cdot \bar{{\textbf{g}}}^{j} \quad \text {and} \quad {g}^{ij} = {{\textbf{g}}}^{i} \cdot {{\textbf{g}}}^{j}, \end{aligned}$$

(14)

where $\bar{{\textbf{g}}}^i$ and ${{\textbf{g}}}^i$ denotes the contravariant basis vectors in reference and deformed configuration of the shell-space defined by

$$\begin{aligned} \bar{{\textbf{g}}}^i \cdot \bar{{\textbf{g}}}_j = \delta ^i_j \quad \text {and} \quad {{\textbf{g}}}^i \cdot {{\textbf{g}}}_j = \delta ^i_j. \end{aligned}$$

(15)

The geometric definitions provided compare to those in the literature as follows. Cirak and Ortiz [17] introduced a stretch $\lambda _3$ to capture the change of thickness, while Kiendl et al [41] defined the third coordinate $\theta ^3$ in terms of the deformed thickness only introducing the thickness when presenting the kinematics. The proposed method follows the approach of Cirak and Ortiz.

3.2 Kinematics

The three-dimensional deformation gradient in the shell-space is defined by

$$\begin{aligned} {\textbf{F}}={\textbf{g}}_{i} \otimes \bar{{\textbf{g}}}^{i}. \end{aligned}$$

(16)

The corresponding right Cauchy-Green deformation tensor follows as

$$\begin{aligned} {\textbf{C}} = {\textbf{F}}^{{\textrm{T}}} \cdot {\textbf{F}} = g_{ij}\bar{{\textbf{g}}}^{i} \otimes \bar{{\textbf{g}}}^{j}, \end{aligned}$$

(17)

and its inverse is defined as

$$\begin{aligned} {{\textbf{C}}}^{-1} = {\textbf{F}}^{-1} \cdot {\textbf{F}}^{-\textrm{T}} = {g}^{ij} \bar{{\textbf{g}}}_i \otimes \bar{{\textbf{g}}}_j. \end{aligned}$$

(18)

Thus, the components of ${{\textbf{C}}}^{-1}$ are the components of the contravariant metric tensor defined in Eq. (14). Upon substituting Eq. (12) into (17), the right Cauchy-Green deformation tensor can be expanded as

$$\begin{aligned} {\textbf{C}}= & {} g_{\alpha \beta } \, \bar{{\textbf{g}}}^{\alpha } \otimes \bar{{\textbf{g}}}^{\beta }+\lambda _3^{2} \bar{{\textbf{g}}}^{3} \otimes \bar{{\textbf{g}}}^{3} + [{\textbf{a}}_\alpha \cdot {\textbf{d}} + \theta ^3{\textbf{d}}_{,\alpha }\cdot {\textbf{d}} ] \bar{{\textbf{g}}}^{\alpha } \otimes \bar{{\textbf{g}}}^{3} \nonumber \\{} & {} + [{\textbf{a}}_\beta \cdot {\textbf{d}} + \theta ^3{\textbf{d}}_{,\beta }\cdot {\textbf{d}} ] \bar{{\textbf{g}}}^{3} \otimes \bar{{\textbf{g}}}^{\beta }. \end{aligned}$$

(19)

The third and fourth terms are the components corresponding to shear along the thickness direction. Since ${\textbf{a}}_\alpha$ and ${\textbf{n}}$ are always perpendicular to each other, ${\textbf{a}}_\alpha \cdot {\textbf{d}} = 0$. The term $\theta ^3{\textbf{d}}_{,\alpha } \cdot {\textbf{d}} = \theta ^3\lambda _3 \lambda _{3,\alpha }$ can also be neglected. The change of the thickness stretch with respect to the mid-surface coordinates $(\lambda _{3,\alpha })$ is generally small for hyperelastic shells under uniform inflation. This is commonly known as the long wave assumption [50]. Furthermore, this term is multiplied by the thickness coordinate $\theta _3$ which is also very small for thin shells. Based on these arguments, we neglect the out-of-plane shear terms to simplify the right Cauchy–Green deformation tensor to

$$\begin{aligned} {\textbf{C}}=g_{\alpha \beta } \, \bar{{\textbf{g}}}^{\alpha } \otimes \bar{{\textbf{g}}}^{\beta }+\lambda _3^{2} \bar{{\textbf{g}}}^{3} \otimes \bar{{\textbf{g}}}^{3}. \end{aligned}$$

(20)

We note that this simplification may not be applicable for shells with rapidly spatially varying thickness where large loads may introduce localised deformation and instabilities such as necking. However, we do not consider such problems in this work.

Ignoring higher-order terms, the components of the covariant metric tensors read

$$\begin{aligned} g_{\alpha \beta }=a_{\alpha \beta }-2 \theta ^{3} b_{\alpha \beta }, \end{aligned}$$

(21)

with the first and second fundamental forms of the mid-surface of the deformed configuration

$$\begin{aligned} a_{\alpha \beta } = {\textbf{a}}_\alpha \cdot {\textbf{a}}_\beta \quad \text {and} \quad b_{\alpha \beta } = {\textbf{a}}_{\alpha ,\beta } \cdot {\textbf{d}} =\lambda _3 {\textbf{a}}_{\alpha ,\beta } \cdot {\textbf{a}}_3. \end{aligned}$$

(22)

Finally, the Green-Lagrange strain tensor can be expressed as

$$\begin{aligned} {\textbf{E}} =\frac{1}{2}[{\textbf{C}} - {\textbf{I}}] = \frac{1}{2} [g_{\alpha \beta } - {\bar{g}}_{\alpha \beta }] \bar{{\textbf{g}}}^{\alpha } \otimes \bar{{\textbf{g}}}^{\beta }+ \frac{1}{2} [\lambda _3^{2}-1] \bar{{\textbf{g}}}^{3} \otimes \bar{{\textbf{g}}}^{3}. \end{aligned}$$

(23)

Similar to Eq. (21), the components of the covariant metric tensor in the reference configuration read

$$\begin{aligned} \bar{g}_{\alpha \beta }=\bar{a}_{\alpha \beta }-2 \theta ^{3} \bar{b}_{\alpha \beta }, \end{aligned}$$

(24)

with the first and second fundamental forms of the mid-surface of the reference configuration

$$\begin{aligned} \bar{a}_{\alpha \beta } = \bar{{\textbf{a}}}_\alpha \cdot \bar{{\textbf{a}}}_\beta \quad \text {and} \quad \bar{b}_{\alpha \beta } = \bar{{\textbf{a}}}_{\alpha ,\beta } \cdot \bar{{\textbf{a}}}_3. \end{aligned}$$

(25)

Therefore, the Green–Lagrange strain tensor is expressed as

$$\begin{aligned} {\textbf{E}} = \left[ \varepsilon _{\alpha \beta }+\kappa _{\alpha \beta } \theta ^{3} \right] \bar{{\textbf{g}}}^{\alpha } \otimes \bar{{\textbf{g}}}^{\beta } + \frac{1}{2} [\lambda _3^2 - 1] \bar{{\textbf{g}}}^{3} \otimes \bar{{\textbf{g}}}^{3}, \end{aligned}$$

(26)

with the mid-surface strain and curvature

$$\begin{aligned} \varepsilon _{\alpha \beta } = \frac{1}{2} [a_{\alpha \beta } - \bar{a}_{\alpha \beta }]\quad \text {and} \quad \kappa _{\alpha \beta } =[- b_{\alpha \beta } + \bar{b}_{\alpha \beta }], \end{aligned}$$

(27)

corresponding to the stretching and bending strains, respectively. The components of the right Cauchy-Green deformation and Green-Lagrange strain tensors are denoted as $C_{ij}$ and $E_{ij}$, respectively, in the following sections.

Cirak and Ortiz [17] preserved the partial derivative of $\lambda _3$, while the proposed method neglects this in accordance with the long-wave assumption, which is similar to the approach in [41].

3.3 Constitutive relations

The Piola–Kirchhoff stress tensor is a conjugate variable to the Green–Lagrange strain tensor. It is defined in terms of the covariant base vectors in the reference configuration as

$$\begin{aligned} {\textbf{S}} = S^{ij}\bar{{\textbf{g}}}_i \otimes \bar{{\textbf{g}}}_j. \end{aligned}$$

(28)

The components of the total differential of the Piola-Kirchhoff stress tensor, i.e., the elastic stiffness tensor, can be computed using the chain rule as

$$\begin{aligned} \textrm{d} S^{ij} = \frac{\partial S^{ij}}{\partial E_{kl}} \mathrm {~d} E_{kl}=2 \frac{\partial S^{ij}}{\partial C_{kl}} \mathrm {~d} E_{kl} = {\mathbb {C}}^{ijkl} \mathrm {~d} E_{kl}, \end{aligned}$$

(29)

where ${\mathbb {C}}^{ijkl}$ are the components of the fourth-order elastic stiffness tensor $\varvec{{\mathbb {C}}}$.

We are concerned with incompressible hyperelastic solids in this work. The incompressibility constraint is given by

$$\begin{aligned} \text {det} ({\textbf{F}}) = 1. \end{aligned}$$

(30)

The Piola-Kirchhoff stress tensor for incompressible hyperelastic solids [29] is expressed as

$$\begin{aligned} S^{ij} = 2\frac{\partial W }{\partial C_{ij}} - {\tilde{p}} {C}^{ij}, \end{aligned}$$

(31)

where $C_{ij}$ are the covariant components of the Cauchy-Green strain tensor ${\textbf{C}}$, while ${C}^{ij}$ are the contravariant components of ${{\textbf{C}}}^{-1}$. For the present shell formulation, $C_{ij} = g_{ij}$ and ${C}^{ij} = {g}^{ij}$ as defined in Eq. (17) and (18), respectively. The Lagrange multiplier ${\tilde{p}}$ enforcing incompressibility is identified as the hydrostatic pressure within the hyperelastic solid. The three-dimensional constitutive equations presented can be simplified to two dimensions by using the plane stress condition for thin shells $(S^{33} = 0)$ coupled with the incompressibility constraint (30). This allows one to analytically determine the Lagrange multiplier ${\tilde{p}}$. Thereafter, the general expression of the stress tensor and the fourth-order elastic tensor can be derived. The detailed derivations for applying the plane stress conditions can be found in Appendix A.1. The hyperelastic solid is modelled using the Mooney–Rivlin constitutive law and the explicit expression of the stress tensor and elastic tensor components are provided in Appendix A.2.

3.4 Stress resultants for thin shells

The thin shell formulation considers a three-dimensional solid as a two-dimensional surface with a thickness. Thus, the internal forces arise as the stress resultants integrated through the thickness. These are decomposed into the normal force $\hat{{\textbf{n}}}$ and the bending moment $\hat{{\textbf{m}}}$, with their components calculated from the Piola–Kirchhoff stress as

$$\begin{aligned} n^{\alpha \beta } =\int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} S^{\alpha \beta } J_c \mathrm {~d} \theta ^{3}, \quad \text {and} \quad m^{\alpha \beta } =\int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} S^{\alpha \beta } \theta ^{3} J_c \mathrm {~d} \theta ^{3},\nonumber \\ \end{aligned}$$

(32)

where

$$\begin{aligned} J_c = \frac{|[\bar{{\textbf{g}}}_1 \times \bar{{\textbf{g}}}_2] \cdot \bar{{\textbf{g}}}_3|}{|[\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2] \cdot \bar{{\textbf{a}}}_3|} \end{aligned}$$

(33)

denotes the change of the in-plane Jacobian along the thickness direction. Based on (26) and (27) for $E_{\alpha \beta }$, their total differentials are calculated as

$$\begin{aligned} \textrm{d} n^{\alpha \beta }&=\left[ \int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } J_c \mathrm {~d} \theta ^{3}\right] \mathrm {~d} \varepsilon _{\gamma \delta }+\left[ \int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \theta ^{3} J_c \mathrm {~d} \theta ^{3}\right] \mathrm {~d} \kappa _{\gamma \delta } ,\end{aligned}$$

(34a)

$$\begin{aligned} \textrm{d} m^{\alpha \beta }&=\left[ \int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \theta ^{3} J_c \mathrm {~d} \theta ^{3}\right] \mathrm {~d} \varepsilon _{\gamma \delta }\nonumber \\&\quad +\left[ \int _{-\frac{{\bar{h}}}{2}}^{\frac{{\bar{h}}}{2}} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta }\left[ \theta ^{3}\right] ^{2} J_c \mathrm {~d} \theta ^{3}\right] \mathrm {~d} \kappa _{\gamma \delta }, \end{aligned}$$

(34b)

where $\hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta }$ denotes the in-plane components of the fourth-order elastic tensor, the details of which are provided in "Appendix A.2".

3.5 Virtual work principle

The virtual work principle is applied to determine the governing equations for the nonlinear thin shell theory. This states that

$$\begin{aligned} \delta {\mathcal {W}}_\text {int} - \delta {\mathcal {W}}_\text {ext} = 0, \end{aligned}$$

(35)

where the internal virtual work is given by

$$\begin{aligned} \delta {\mathcal {W}}_\text {int} = \int _{{\bar{\Gamma }}} \left[ n^{\alpha \beta } \delta \varepsilon _{\alpha \beta } + m^{\alpha \beta } \delta \kappa _{\alpha \beta }\right] \mathrm {~d} {\bar{\Gamma }}, \end{aligned}$$

(36)

and the external virtual work by

$$\begin{aligned} \delta {\mathcal {W}}_\text {ext} ={\hat{h}}\int _\Gamma b_i \delta u_i \,{\textrm{d}} \Gamma + {\hat{h}} \int _{S_t} \tau _i \delta u_i \, {\textrm{d}} S_t, \end{aligned}$$

(37)

with

$$\begin{aligned} {\hat{h}} = \int _{-\frac{h}{2}}^{\frac{h}{2}} J_c \mathrm {~d} \theta ^3. \end{aligned}$$

(38)

Here, $b_i$ denotes the components of the body force. The components $\tau _i$ are prescribed tractions at the boundary $S_t\in \partial \Gamma$, where $\partial \Gamma = \emptyset$ for enclosed geometries. For convenience, the internal virtual work is integrated in the reference configuration, while the external virtual work is calculated in the deformed configuration.

4 Numerical implementation

4.1 Catmull–Clark subdivision surfaces

The fundamental idea of subdivision surfaces is to generate a smooth surface by repeatedly refining a coarse control grid using a subdivision scheme that generalises bi-cubic uniform B-spline knot insertion. For arbitrary initial meshes, this scheme generates limit surfaces that are $C^2$ continuous everywhere except at extraordinary vertices where they guarantee a $C^1$ limiting surface. For regular vertices, the limit surface generated by the Catmull–Clark subdivision scheme is identical to a bi-cubic B-spline surface. Figure 3a shows a patch of a subdivision surface with its control grid for regular vertices. The grid divides the parametric domain of the surface patch into nine elements, see Fig. 3b. The surface point $\bar{{\textbf{x}}}$ in the central element can be interpolated using a tensor product of two cubic B-splines with 16 control points as

$$\begin{aligned} \bar{{\textbf{x}}}(\theta ^1, \theta ^2) = \sum _{a=0}^{15} {\tilde{N}}_a(\theta ^1,\theta ^2){\textbf{P}}_{a}, \end{aligned}$$

(39)

where ${\textbf{P}}_{a}$ is the $a^{\text {th}}$ control point and ${\tilde{N}}_a$ denotes the corresponding local base function for the element which is defined by

$$\begin{aligned} {\tilde{N}}_a(\theta ^1,\theta ^2) = N_{a\%4}(\theta ^1)N_{\lfloor {a/4}\rfloor }(\theta ^2), \end{aligned}$$

here $\lfloor \bullet \rfloor$ is the modulus operator and $\%$ denotes the remainder operator which gives the remainder of the integer division.

Fig. 3

a An example patch of a Catmull-Clark subdivision surface. b The parametric domain of the patch and the corresponding bases functions

As a result of the tensor-product nature, each vertex in a subdivision surface control grid is connected with only four elements. One defines the number of elements connected as the ‘valence’ of the vertex. A regular vertex in a Catmull–Clark surface control grid has a valence of 4. However, contrary to NURBS surfaces, Catmull–Clark subdivision surfaces can handle irregular cases where the valence of a vertex is not equal to 4. Thus it allows one to handle complex geometry with arbitrary topology. These vertices are known as ‘extraordinary vertices’ and require a different algorithm for the evaluation of the limiting surface, introduced in [64]. In the numerical implementation, a reduction of convergence rates has been observed around extraordinary vertices [46], but the convergence rate can be improved by reparameterisation [37, 72, 76]. Catmull–Clark subdivision surfaces display $C^1$ continuity at extraordinary vertices [57], otherwise they possess $C^2$ continuity. Therefore, Catmull–Clark subdivision surfaces provide an adequate $C^1$ continuous discretisation to satisfy the requirement of the Galerkin formulation of Kirchhoff–Love shells, where the test and trial functions must be in the Hilbert space $H^2(\Omega )$ [18].

4.2 Discretisation and linearisation

The displacement of the mid-surface is discretised using Catmull-Clark subdivision bases as shape functions, that is

$$\begin{aligned} {\textbf{u}} = \sum _{A = 1} ^{n_b} N^{A} {\textbf{u}}^{A}, \end{aligned}$$

(40)

where $n_b$ is the total number of basis functions and is equal to the total number of the control points, $N^{A}$ is the basis function corresponding to the $A^{\text {th}}$ control point. We note here that A is the global index of the control point. ${\textbf{u}}^{A}$ denotes the $A^{\text {th}}$ nodal displacement vector with three components corresponding to three Cartesian coordinates denoted as $u^{A}_i$, leading to the total number of degrees of freedom to interpolate ${\textbf{u}}$ equal to $3n_b$. The derivative of ${\textbf{u}}$ with respect to the $r^\text {th}$ degree of freedom is denoted as

$$\begin{aligned} \delta _{r}{\textbf{u}} = \frac{\partial {\textbf{u}}}{\partial u_r} = N^{A} {\textbf{c}}_i, \end{aligned}$$

(41)

where the degree of freedom index $r \in [1, 3n_b]$, can be expressed as $r = 3[A-1] + i$. Thus, $u_r$ denotes the $i^\text {th}$ component of ${\textbf{u}}^A$ and ${\textbf{c}}_i$ are the orthonormal basis vectors. Thus the derivative of the strain components $\varepsilon _{\alpha \beta }$ and $\kappa _{\alpha \beta }$ with respect to the $r^\text {th}$ degree of freedom can be expressed as

$$\begin{aligned} \begin{aligned} \delta _{r}\varepsilon _{\alpha \beta }&= \frac{1}{2} [ \delta _{r}{{\textbf{a}}_{\alpha }} \cdot {\textbf{a}}_{\beta } + \delta _{r}{{\textbf{a}}_{\beta }} \cdot {\textbf{a}}_{\alpha }],\\ \delta _{r}\kappa _{\alpha \beta }&= - \lambda _3 [\delta _{r} \textbf{a}_{\alpha , \beta }\cdot {\textbf{a}}_3 + {\textbf{a}}_{\alpha ,\beta }\cdot \delta _{r}{\textbf{a}}_{3}] - \delta _r \lambda _3 [{\textbf{a}}_{\alpha ,\beta } \cdot {\textbf{a}}_3]. \end{aligned} \end{aligned}$$

(42)

The derivatives of ${\textbf{a}}_{\alpha }$ and ${\textbf{a}}_{\alpha ,\beta }$ are easily expressed using the first and second derivatives of the basis functions as

$$\begin{aligned} \delta _{r}{{\textbf{a}}_{\alpha }} = N^{A}_{,\alpha } {\textbf{c}}_i, \quad \delta _{r}{{\textbf{a}}_{\alpha ,\beta }} = N^A_{,\alpha \beta } {\textbf{c}}_i. \end{aligned}$$

(43)

The derivatives of the normal vector $\delta _{r} {\textbf{a}}_3$ and the thickness stretch $\delta _r \lambda _3$ can be found in Appendix A. The derivatives of the internal and external virtual work with respect to the $r^\text {th}$ degree of freedom are given by

$$\begin{aligned} \begin{aligned} \delta _r {\mathcal {W}}_{\text {int}}&= \int _{{\bar{\Gamma }}} \left[ n^{\alpha \beta } \delta _{r}\varepsilon _{\alpha \beta } + m^{\alpha \beta } \delta _{r}\kappa _{\alpha \beta } \right] \mathrm {~d} {\bar{\Gamma }},\\ \delta _r {\mathcal {W}}_{\text {ext}}&={\hat{h}}\int _\Gamma b_i \delta _r u_i \,{\textrm{d}} \Gamma , \end{aligned} \end{aligned}$$

(44)

where the boundary traction contribution has been ignored for simplicity. The global residual vector $\varvec{\textsf{R}}$ is defined by

$$\begin{aligned} \varvec{\textsf{R}} = \varvec{\textsf{F}}^{\text {int}} - \varvec{\textsf{F}}^{\text {ext}}, \end{aligned}$$

(45)

where $\varvec{\textsf{F}}^{\text {int}}$ and $\varvec{\textsf{F}}^{\text {ext}}$ are two global vectors with $3n_b$ components each, with $r^\text {th}$ components $\delta _r {\mathcal {W}}_{\text {int}}$ and $\delta _r {\mathcal {W}}_{\text {ext}}$, respectively. The system is in equilibrium when the residual vector $\varvec{\textsf{R}} = \varvec{\textsf{0}}$. The global tangential stiffness matrix $\varvec{\textsf{K}}$ of size $3n_b \times 3n_b$ has entries in $r^{\text {th}}$ row and $s^{\text {th}}$ column given by

$$\begin{aligned} K^{rs} = \delta _s\delta _r {\mathcal {W}}_{\text {int}} - \delta _s\delta _r {\mathcal {W}}_{\text {ext}}, \end{aligned}$$

(46)

where

$$\begin{aligned} \begin{aligned} \delta _s\delta _r {\mathcal {W}}_{\text {int}}&= \int _{{\bar{\Gamma }}} \left[ \delta _{s} n^{\alpha \beta } \, \delta _{r}\varepsilon _{\alpha \beta } + n^{\alpha \beta } \, \delta _{s}\delta _{r}\varepsilon _{\alpha \beta } + \delta _{s} m^{\alpha \beta } \, \delta _{r}\kappa _{\alpha \beta } \right. \\&\quad \left. + m^{\alpha \beta } \, \delta _{s}\delta _{r}\kappa _{\alpha \beta } \right] \mathrm {~d} {\bar{\Gamma }} \\ \delta _s\delta _r {\mathcal {W}}_{\text {ext}}&= {\hat{h}}\int _\Gamma \delta _s b_i \,\delta _r u_i \,{\textrm{d}} \Gamma , \end{aligned} \end{aligned}$$

(47)

and

$$\begin{aligned} \delta _s n^{\alpha \beta }= & {} \left[ \int _{-\bar{h} / 2}^{\bar{h} / 2} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } J_c \mathrm {~d} \theta ^{3}\right] \delta _s \varepsilon _{\gamma \delta }\nonumber \\{} & {} +\left[ \int _{-\bar{h} / 2}^{\bar{h} / 2} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \theta ^{3} J_c \mathrm {~d} \theta ^{3}\right] \delta _s \kappa _{\gamma \delta } \nonumber \\ \delta _s m^{\alpha \beta }= & {} \left[ \int _{-\bar{h} / 2}^{\bar{h} / 2} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } \theta ^{3} J_c \mathrm {~d} \theta ^{3}\right] \delta _s \varepsilon _{\gamma \delta }\nonumber \\{} & {} +\left[ \int _{-\bar{h} / 2}^{\bar{h} / 2} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta }\left[ \theta ^{3}\right] ^{2} J_c \mathrm {~d} \theta ^{3}\right] \delta _s \kappa _{\gamma \delta }, \end{aligned}$$

(48)

and

$$\begin{aligned} \begin{aligned} \delta _{s}\delta _{r}\varepsilon _{\alpha \beta }&= \frac{1}{2} [ \delta _{r}{{\textbf{a}}_{\alpha }} \cdot \delta _{s} {\textbf{a}}_{\beta } + \delta _{r}{{\textbf{a}}_{\beta }} \cdot \delta _{s} {\textbf{a}}_{\alpha }], \\ \delta _{s} \delta _{r}\kappa _{\alpha \beta }&= - \delta _{s}\lambda _3 [\delta _{r} \textbf{a}_{\alpha ,\beta }\cdot {\textbf{a}}_3 + {\textbf{a}}_{\alpha ,\beta }\cdot \delta _{r}{\textbf{a}}_{3}] \\&\quad - \lambda _3 [ \delta _{r} \textbf{a}_{\alpha , \beta }\cdot \delta _{s} {\textbf{a}}_3 + \delta _{s} {\textbf{a}}_{\alpha ,\beta }\cdot \delta _{r}{\textbf{a}}_{3} + {\textbf{a}}_{\alpha ,\beta }\cdot \delta _s\delta _{r}{\textbf{a}}_{3}] \\&\quad - \delta _s \delta _r \lambda _3 [{\textbf{a}}_{\alpha ,\beta } \cdot {\textbf{a}}_3] - \delta _r \lambda _3 [\delta _s{\textbf{a}}_{\alpha ,\beta } \cdot {\textbf{a}}_3 + {\textbf{a}}_{\alpha ,\beta } \cdot \delta _s{\textbf{a}}_3]. \end{aligned} \end{aligned}$$

(49)

The second derivative of the normal vector $\delta _{s}\delta _{r} {\textbf{a}}_3$ and $\delta _s \delta _r \lambda _3$ are computed and detailed in the Appendix A. It is important to note that for inflated thin shells, the external load $\varvec{\textsf{F}}_\text {ext}$ is a follower load and is thus a function of the displacements. Hence the load increment must consider the deformation of the geometry and the term $\delta _s\delta _r {\mathcal {W}}_{\text {ext}}$ is included in the tangential stiffness matrix. For example, if the external load is a uniform pressure inside an enclosed hyperelastic thin shell, the first variation of the external virtual work with respect to the degrees of freedom is given by

$$\begin{aligned} \delta _r {\mathcal {W}}_{\text {ext}} = \int _{\Gamma } p [{\textbf{a}}_3 \cdot \delta _r {\textbf{u}}] \mathrm {~d} \Gamma , \end{aligned}$$

(50)

where ${\textrm{d}} \Gamma = {\mathcal {J}} {\textrm{d}} \bar{\Gamma }$. Using expression (70) allows the second derivative of the external virtual work with respect to the degrees of freedom to be derived as

$$\begin{aligned} \delta _s\delta _r {\mathcal {W}}_{\text {ext}} = \int _{{\bar{\Gamma }}} p \left[ [\delta _{s}{\textbf{a}}_1 \times {\textbf{a}}_2 + {\textbf{a}}_1 \times \delta _{s}{\textbf{a}}_2] \cdot \delta _r {\textbf{u}}\right] \bar{J}^{-1} \mathrm {~d} {\bar{\Gamma }}.\nonumber \\ \end{aligned}$$

(51)

Here, the pressure p is considered as an external load, and the global vector $\varvec{\textsf{F}}_{\text {ext}}$ must be regenerated for each load step.

5 Large deformation and associated instabilities

5.1 Nonlinear solution algorithm

The inflated thin structures considered are incompressible hyperelastic shells under uniform inflating pressure. The inflation of such soft and thin structures causes large deformations and a highly nonlinear mechanical response. The hyperelastic shell formulation involves both kinematic and constitutive nonlinearities.

Fig. 4

Algorithm for solving the nonlinear hyperelastic thin shell formulation

Figure 4 provides a flowchart illustrating the algorithm adopted for such nonlinear problems. Since the mechanical response of the hyperelastic shell structures is nonlinear and can be quite complex, the problem is solved incrementally and an arc-length method is employed [36]. For each increment, the Newton–Raphson method is used to solve the nonlinear system of equations. It begins with an initial guess of the global nodal displacement vector $\varvec{\textsf{u}}_0$. The linearised system of equations are formulated to solve the global vector of the incremental nodal displacements $\Delta \varvec{\textsf{u}}$ and the incremental load factor $\Delta \kappa$ (see Fig. 4). For each Newton iteration, the displacement is updated until the $L_2$ norm of the residual vector is less than a tolerance which is set as $0.01\%$ of the initial norm of the residual vector.

5.2 Limit point instability

Fig. 5

Representative volume-pressure plots for hyperelastic thin shells illustrating two types of instabilities: a Snap-through and b Bifurcation

The inflation of a hyperelastic thin shell induces instability due to the highly nonlinear mechanical response. The most well-known instability phenomenon for inflated membranes/shells is snap-through. Figure 5a shows a plot of the enclosed volume against the internal pressure of an ideal hyperelastic shell. The structure has large initial stiffness when the internal pressure is relatively low and thus appears difficult to inflate. With the increase of internal pressure, the enclosed volume changes accordingly, and the structure gradually loses its stiffness. When the pressure approaches the limit point, the structure dramatically loses its stiffness, undergoes very large inflation and jumps to a new equilibrium state. For a thin shell with imperfections, snap-through may occur prior to reaching the limit point. In order to capture the non-uniqueness in the solution for structures exhibiting post-buckling behaviour, a path-following and branching method is used to compute the relationship between pressure and volume.

5.3 Bifurcation from the principal solution

For a closed hyperelastic shell with initial geometric symmetry, the inflated structure will remain symmetric until the internal volume exceeds a critical value, whereafter the structure may lose symmetry under a small perturbation. This is due to the non-uniqueness of the solution of the nonlinear problem and the total energy for the non-symmetrical state being lower than that of the symmetric state. The point where the solution curve differs is called the bifurcation point and is shown in Fig. 5b. The bifurcation phenomenon is widely observed in mechanical experiments due to manufacturing imperfections and perturbations. However, numerically simulating bifurcation instability is difficult because it is a sudden change in a highly nonlinear problem. Moreover, a slight change in the geometry or material property may significantly affect the critical point at which the bifurcation occurs. The proposed method to determine bifurcation assesses the stiffness matrix of the structure after solving each load increment. An accompanying eigenvalue analysis is performed by solving

$$\begin{aligned} {[}\tilde{\varvec{\textsf{K}}}-\lambda _e\varvec{\textsf{I}}]\varvec{\textsf{u}}_e = \varvec{\textsf{0}}, \end{aligned}$$

(52)

where $\tilde{\varvec{\textsf{K}}}$ is the reduced tangent matrix after applying the essential boundary conditions for eliminating the rigid body motion and rotation, $\lambda _e$ is an eigenvalue, $\varvec{\textsf{I}}$ denotes an identity matrix with the same size as $\tilde{\varvec{\textsf{K}}}$, and the corresponding eigenvector is denoted by $\varvec{\textsf{u}}_e$. Only the smallest few eigenvalues are critical as they dominate the instability reponse. If the smallest eigenvalue of the stiffness matrix is nearly zero, the solution of the next load increment may switch to another solution branch. In the present work, the corresponding eigenvector is used as the initial guess for the next load step in order to perturb the structure and induce the bifurcation. It is noteworthy that the eigenvector is a normalised vector, which needs to be scaled in order to serve as a displacement perturbation. The choice of the scaling factor is important: if the factor is too small, the solution will still follow the original path, and if the factor is too large, the system of equations will be difficult to solve. This method is embedded in the nonlinear algorithm and coloured in red in Fig. 4.

Fig. 6

a The initial control grid and the limit surface of the circular plate. b The deformed shape of the circular plate when dimensionless inflating pressure $p = 35$

6 Numerical examples

Four numerical examples are presented to illustrate the proposed method. The numerical formulation is implemented using the finite element library deal.II [4, 5]. We first solve the benchmark problem of the inflation of a Mooney–Rivlin circular plate to validate the method and demonstrate its accuracy. The inflation of a spherical shell is then simulated for both neo-Hookean and Mooney–Rivlin materials and validated against analytical solutions. This problem also demonstrates the ability of the arc-length method to follow a nonlinear path and capture the limit point instability. Next, the inflation of a Mooney–Rivlin toroidal shell is computed. Here, in addition to the limit point instability, we capture the bifurcation point and the post-bifurcation response of the toroidal shell. Finally, the ability of the proposed method to model the large and complex deformation of an arbitrary geometry is demonstrated by computing the inflation of an airbag modelled using a Saint Venant–Kirchhoff constitutive law. All computations are performed using dimensionless quantities.

6.1 Circular plate inflated with uniform pressure

The first example considered is a circular inflated hyperelastic plate. The plate is simply supported and the pressure is considered to be a uniform load which is always perpendicular to the deformed mid-surface of the plate. Thus the pressure is a follower load and it is a function of the deformation. This problem was first analysed in [55] and has become a benchmark problem for incompressible hyperelastic shells [17, 31, 53]. Figure 6a shows the initial control grid with 80 elements and the limit surface of the circular plate. The radius of the plate is 7.5 and the thickness is 0.5. The material parameters for the Mooney–Rivlin model are $c_1 = 80 \mu , c_2 = 20\mu$, where $\mu$ is the shear modulus. We define the dimensionless pressure $p = P/\mu$, where P is the real pressure. Figure 6b shows the deformed domain for $p=35$.

The converged numerical result is obtained after two uniform refinements (1440 elements) and is compared with the literature in Fig. 7. The result has a slight offset compared to Hughes and Carnoy [31] and Cirak and Ortiz [17], and agrees perfectly with the recent work by Nama et al. [53], whose shell theory is similar to [41] and was applied to problems in biomechanics. This numerical example demonstrates the ability of the proposed method to solve a problem combining both membrane and bending deformations.

Fig. 7

Variation of the inflating pressure p with the maximum displacement (max($|{\textbf{u}}|$)) for the inflation of a circular plate. Comparison of the solution based on the present formulation with those presented in the literature

6.2 Inflation of a spherical balloon

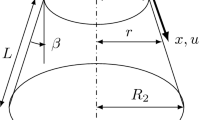
The second example considered is the inflation of a spherical balloon, which was analytically studied in Section 6.3 of [29]. It is a widely used benchmark problem for hyperelastic shell formulations [13, 17, 41]. Figure 8a shows the geometry for the spherical balloon. The balloon is inflated with uniform pressure applied from the inside. For an incompressible Mooney–Rivlin model, the analytical solution of the internal pressure of the balloon is

$$\begin{aligned} p = \frac{ 4 {\bar{h}}}{{\bar{R}}} \left[ c_1 [\lambda ^{-1} - \lambda ^{-7}] - c_2[\lambda ^{-5} - \lambda ]\right] , \end{aligned}$$

(53)

where ${\bar{R}}$ is the radius of the spherical shell in the reference configuration and ${\bar{h}}$ is the undeformed thickness. We take the values ${\bar{R}} = 10$ and ${\bar{h}} = 0.1$. For the spherical hyperelastic shell, the stretching of the mid-surface is the same in all directions, thus $\lambda _1 = \lambda _2 = \lambda$. Due to the incompressibility constraint, the thickness stretch can be computed as $\lambda _3 = 1/\sqrt{\lambda }$.

Fig. 8

a Geometrical setting of a spherical balloon in the reference and deformed configurations, showing only half of the cross-section. b The mesh of a quarter of the hemisphere (one-eighth of the full sphere) is used for the numerical test and the symmetry assumption is adopted by constraining the corresponding degree of freedom for the edges shown in the figure

Figure 8b shows the control mesh with 192 elements comprising one-quarter of the hemisphere used for the numerical simulation. As indicated, symmetry boundary conditions are applied to three edges by constraining the corresponding degrees of freedom. Two sets of material parameters are tested for this example. The parameters for the first case are $c_1 = 0.5 \mu$ and $c_2 = 0$, where $\mu = 4.225 \times 10^{5}$. When $c_2$ is set to zero, the constitutive model reduces to an incompressible neo-Hookean. The second case of parameters is $c_1 = 0.4375\mu$ and $c_2 = 0.0625\mu$, thus $c_1/c_2 = 7$. Figure 9 shows that the numerical results for both tests perfectly agree with the analytical solutions.

Fig. 9

Variation of the inflation pressure against the in-plane stretch values ($\lambda _1, \lambda _2$). The numerical and analytical stretch-pressure curves for the inflated balloons (Case 1: neo-Hookean model, $c_1 = 0.5 \mu$ and $c_2 = 0$; Case 2: Mooney–Rivlin model, $c_1 = 0.4375\mu$ and $c_2 = 0.0625\mu$, where $\mu = 4.225 \times 10^{5}$ ). Excellent agreement is observed between the analytical and numerical solutions for both material models. The inflated profiles of the two cases are shown to the right. A full undeformed balloon is shown uncoloured (grey) for both cases and the deformed profiles for increasing load steps are shown as hemispheres. The colour indicates the value of internal pressure. For the second case, the balloon may experience snap-through during inflation

For the first case, the internal pressure of the spherical balloon reaches the limit point when $\lambda = 1.38$. If the volume of the balloon keeps increasing, the internal pressure gradually decreases. However, in the second case, the internal pressure will first decrease after the limit point and then rise again, exceeding the pressure at the limit point. The complex nonlinear response of the structure is captured by the arc-length method. Figure 9 also shows the inflated profiles of the spherical balloon for both cases and the internal pressure values are indicated with the colouring. If the two balloons are inflated using pressure control, the neo-Hookean balloon will “explode” when it is pressurised beyond the limit point, because that is the maximum pressure it can withstand. The Mooney–Rivlin balloon may undergo a sudden and large deformation at the limit point due to the increased pressure and reach a new equilibrium state. This is the snap-through phenomenon which is normally considered as an instability of the structure. With the nonlinear algorithm and arc-length method, the proposed formulation can easily capture this phenomenon numerically even for complex structures.

6.3 Loss of symmetry during the inflation of a toroidal thin shell

This example considers the bifurcation of an inflated toroidal thin shell. A torus is the simplest example of a genus 1 orientable surface. Toroidal membranes and shells are widely applied in engineering applications such as tyres, air springs, soft grippers and inflated actuators. The bifurcation instability (loss of symmetry) of a toroidal membrane is examined semi-analytically in [68]. Here, a similar problem is analysed numerically for a thin shell.

Fig. 10

A smooth toroidal surface is modelled with a relatively coarse control grid. a The control grid with 256 elements. b The limit surface of the toroidal thin shell

Fig. 11

Numerical computation of the variation of the applied pressure against the enclosed volume for the inflated toroidal thin shell is plotted in (a). In this case, bifurcation occurs immediately after the solution reaches the limit point. The asymmetric eigenmode at the bifurcation point is also shown. b The total energy of the bifurcated non-symmetric branch has lower total energy than the principle branch

Fig. 12

Deformed shapes of the toroidal thin shell during inflation for both principal (a, b) and bifurcated c, d solutions are shown. The locations of the deformation states ${\textbf{A}}_1$, ${\textbf{A}}_2$, ${\textbf{B}}_1$, ${\textbf{B}}_2$ in the pressure-volume curves are indicated in Fig. 11a

Fig. 13

Results for the simulation of inflation of a square airbag modelled using a St.Venant–Kirchhoff constitutive model at an internal pressure of $p=5000$. Due to the lack of convexity of the energy functional for such a nonlinear problem, The solution of the inflated airbag is not unique. Two deformed shapes are shown here, where a, b are for the initial load pressure $p_0 = 200$, while c, d are for $p_0 = 500$. The two deformed airbags have a similar total energy of $1.13 \times 10^6$ and $1.16 \times 10^6$, respectively

The structure is modelled as an enclosed hyperelastic thin shell and the inflation is simulated. The internal pressure of the thin shell is applied incrementally as an external force and the displacements are solved by using the Newton–Raphson method for each load step. After the deformed equilibrium state is achieved for each load step, an eigenvalue analysis of the stiffness matrix, as introduced in Sect. 5.3, is performed to check stability. When the stiffness matrix has nearly zero eigenvalues, the structure is in an unstable state where sudden geometric changes may occur to achieve a lower energy state. The eigenvector corresponding to the nearly zero eigenvalue indicates the direction of the possible sudden change. If it breaks the original symmetry of the structure, the inflated toroidal thin shell will bifurcate to a new non-symmetric branch. A control grid with 256 elements shown in Fig. 10a renders a limit mid-surface of the toroidal thin shell shown in Fig. 10b. The minimum bounding box for the limit surface is $[-10.6522,10.6522]\times [-1.80474,1.80474]\times [-10.6522,10.6522]$. It is a relatively slender torus and its aspect ratio is approximately 4.9. The thickness of the shell is set to 0.01 and the same material parameters $c_1$ and $c_2$ as for the spherical balloon example in Sect. 6.2 are adopted here.

Figure 11a shows the evolution of the internal pressure against the enclosed volume for the toroidal thin shell modelled with Catmull-Clark subdivision surfaces. When the thin shell is inflated to the limit point, the stiffness matrix has a pair of nearly zero eigenvalues whose corresponding eigenmodes are orthogonal and they are both non-symmetric. One of the eigenmodes is shown in the figure. The limit point is the earliest point at which bifurcation is likely to occur. The eigenmode is used to perturb the structure in the following load steps and a bifurcated solution is branched off from the principal solution. Fig. 11b indicates that the toroidal shell bifurcates to a non-symmetric branch with lower total energy. The inflated shapes of the toroidal thin shell for both branches are selectively plotted in Fig. 12.

6.4 Inflation of an elastic airbag

In the final example, we consider the problem of inflation of an elastic airbag. Due to the non-convex energy functional, this is a highly nonlinear problem and is widely considered a classic example to study complex deformation of membranes and thin shells [13, 17, 49, 52]. Due to the closely distributed multiple local minima, the computational solution to this problem is challenging. The numerical result is very sensitive to the computation parameters such as the initial load step, step size, element sizes and initial guesses. We present this numerical example to showcase the ability of the proposed method to capture complex deformation along with inflation. A subdivision surface with $256\,(16\times 16)$ elements is generated using a control mesh for a square plate in order to model a half airbag. Symmetry boundary conditions are applied to the four edges by constraining their degrees of freedom corresponding to the displacements in $z\text{- }$direction and the in-plane rigid body motion is also eliminated. The constitutive relation selected for this problem is the Saint Venant-Kirchhoff model as the airbag textile is often considered as inextensible. This strain energy density function is expressed as

$$\begin{aligned} W({\textbf{E}})=\frac{ E \, \nu }{ 2[1+\nu ][1-2\nu ]}[{\text {tr}}( {\textbf{E}})]^2+\frac{ E }{ 2[1+\nu ]}{\textbf{E}}: {\textbf{E}}. \end{aligned}$$

(54)

The Young’s modulus and Poisson’s ratio are set as $E = 5\times 10^8 \text { and }\nu = 0.4$, respectively. The length of the side of the square airbag is 1 and its thickness is set to 0.001. The airbag is inflated by incrementally increasing the pressure until the inflating pressure reaches the value $p = 5000$. Due to the highly nonlinear nature of the problem, we observe a bifurcation in the solution very close to the reference configuration. As a result, the initial load step determines the solution branch. Figure 13a shows the final deformed shape of the airbag for the case when the internal pressure $p_0 = 200$ is selected as the first load step. If $p_0$ increases to 500, the final deformed shape of the airbag is different, as shown in Fig. 13c. The complex deformations seen in Fig. 13a, c are easily captured with our thin shell formulation.

7 Summary and conclusions

An isogeometric approach for the analysis of inflated hyperelastic thin shell structures has been proposed. The Kirchhoff–Love hypothesis has been followed to develop the thin shell formulation. An incompressible Mooney–Rivlin model has been adopted to describe the constitutive behaviour of the material. Based on the principle of virtual work, the weak form of governing equations was formulated. The complex nonlinear response of the inflated hyperelastic thin shell has been numerically simulated with the aid of the arc-length method combined with a Newton–Raphson iterative approach to solve for displacements and internal pressure incrementally. Both the geometry and deformation field are discretised using the Catmull–Clark subdivision bases and a finite element framework with $C^1$ continuity is established. Two types of global instabilities of the inflated thin shell structures can be simulated, namely snap-through and bifurcation. The proposed method was first validated by considering the inflated circular plate benchmark problem. A numerical example of an inflated spherical shell further verified the formulation analytically. Moreover, the example demonstrated the ability of the proposed method to predict the snap-through phenomenon of hyperelastic shells with enclosed volumes. Thereafter, a toroidal hyperelastic thin shell was simulated to investigate the bifurcation of solution from a principal symmetric mode. After solving the displacements for each inflation increment, the eigenvalues of the stiffness matrix were checked, and the structure perturbed with the eigenvector if the corresponding eigenvalue approaches zero, thus inducing bifurcation. The numerical simulation shows that the toroidal thin shell analysed in the present work may lose its symmetry when the inflation reaches its limit point. Finally, a highly nonlinear problem of inflation of an airbag has been simulated to demonstrate the ability of the proposed method to capture complex states in finitely deformed thin shells.

The numerical examples demonstrate the challenges that are encountered in the simulation of the mechanical response of thin shells due to strong kinematic and constitutive nonlinearities. Even though the proposed formulation and numerical implementation are able to capture complex deformation states, care must be taken when selecting the initial loading values, arc-length parameters, and the scaling factor used in the eigenvalue analysis.

Appendix

1.1 Plane stress condition for thin-shells

Based on the Kirchhoff–Love assumption for thin shells, we neglect the shear strain components thereby writing the various components of Cauchy–Green deformation tensor and its inverse as

$$\begin{aligned} C_{\alpha \beta }&= g_{\alpha \beta }, \quad C_{\alpha 3} = C_{3 \alpha } = 0 \quad \text {and} \quad C_{33} = g_{33} = \lambda _3^{2}, \end{aligned}$$

(55a)

$$\begin{aligned} C^{\alpha \beta }&= g^{\alpha \beta }, \quad {C}^{\alpha 3} = {C}^{3 \alpha } = 0 \quad \text {and} \quad {C}^{33} = {g}^{33} = \lambda _3^{-2} . \end{aligned}$$

(55b)

Using equation (29), we write the in-plane stress components $S^{\alpha \beta }$ as

$$\begin{aligned} S^{\alpha \beta } = 2\frac{\partial W }{\partial C_{\alpha \beta }} - {\tilde{p}} {C}^{\alpha \beta }, \end{aligned}$$

(56)

For thin shells, the plane stress condition $S^{33} = 0$ results in

$$\begin{aligned} S^{33} = 2\frac{\partial W }{\partial C_{33}} - C^{33}{\tilde{p}} = 0, \quad \text {with} \quad C_{33} = \lambda _3^{2},\, C^{33} = \lambda _3^{-2}.\nonumber \\ \end{aligned}$$

(57)

Thus ${\tilde{p}}$ can be explicitly determined as

$$\begin{aligned} {\tilde{p}} = 2\frac{\partial W}{\partial C_{33}}{C}_{33} = 2\lambda _3^2\frac{\partial W}{\partial C_{33}}. \end{aligned}$$

(58)

Due to the plane-stress condition above, ${{\tilde{p}}} ={\tilde{p}}(C_{ij})$ thus can be considered as a function of the strain tensor ${\textbf{E}}$ or the right Cauchy–Green deformation tensor ${\textbf{C}}$. Thus the total derivative of the Piola–Kirchhoff stress tensor is now written as

$$\begin{aligned} \frac{{\textrm{d}} }{{\textrm{d}} {\textbf{E}}}\big ({\textbf{S}}\left( {\textbf{E}}, {\tilde{p}}({\textbf{E}})\right) \big ) = \frac{\partial {\textbf{S}}}{\partial {\textbf{E}}} + \frac{\partial {\textbf{S}}}{\partial {{\tilde{p}}}} \frac{\partial {{\tilde{p}}}}{\partial {\textbf{E}}} = 2\frac{\partial {\textbf{S}}}{\partial {\textbf{C}}} + 2\frac{\partial {\textbf{S}}}{\partial {{\tilde{p}}}} \frac{\partial {{\tilde{p}}}}{\partial {\textbf{C}}}.\nonumber \\ \end{aligned}$$

(59)

Upon comparison with Eqs. (29) and (56) and using (58), one can write the explicit expression for the in-plane components of the fourth-order tensor $\varvec{{\mathbb {C}}}$ as (see [41] for a detailed derivation)

$$\begin{aligned} {\mathbb {C}}^{\alpha \beta \gamma \delta }= & {} 4\frac{\partial ^2 W }{\partial C_{\alpha \beta } \partial C_{\gamma \delta }} - 2\frac{\partial {\tilde{p}}}{\partial C_{\gamma \delta }}{C}^{\alpha \beta } - 2\frac{\partial {\tilde{p}}}{\partial C_{\alpha \beta }}{C}^{\gamma \delta } \nonumber \\{} & {} - {\tilde{p}} [ {C}^{\alpha \beta } {C}^{\gamma \delta } - {C}^{\alpha \gamma } {C}^{\beta \delta } - {C}^{\alpha \delta } {C}^{\beta \gamma }], \end{aligned}$$

(60)

where, the partial derivative of the Lagrange multiplier can be calculated from Eq. (58) as

$$\begin{aligned} \frac{\partial {\tilde{p}}}{\partial C_{\alpha \beta }} = 2\frac{\partial ^2 W}{\partial C_{33} \partial C_{\alpha \beta }}\lambda _3^2. \end{aligned}$$

(61)

The derivatives of in-plane stress components are expressed as

$$\begin{aligned} \textrm{d} S^{\alpha \beta }= & {} 2 \frac{\partial S^{\alpha \beta }}{\partial C_{\gamma \delta }} \mathrm {~d} E_{\gamma \delta } + 2 \frac{\partial S^{\alpha \beta }}{\partial C_{33}}\nonumber \\ \mathrm {~d} E_{33}= & {} {\mathbb {C}}^{\alpha \beta \gamma \delta } \mathrm {~d} E_{\gamma \delta } + {\mathbb {C}}^{\alpha \beta 33} \mathrm {~d} E_{33}. \end{aligned}$$

(62)

Furthermore, the plane stress condition requires the incremental stress in the thickness direction to vanish, that is

$$\begin{aligned} {\textrm{d}} S^{33} = {\mathbb {C}}^{33\alpha \beta } {\textrm{d}} E_{\alpha \beta } + {\mathbb {C}}^{3333}{\textrm{d}} E_{33} = 0. \end{aligned}$$

(63)

This relation can be used to explicitly calculate the differential strain component ${\textrm{d}} E_{33} = -{\mathbb {C}}^{33\alpha \beta } {\textrm{d}} E_{\alpha \beta } / {\mathbb {C}}^{3333}$ and upon substituting it into Eq. (62), the in-plane tangent tensor $\hat{\varvec{{\mathbb {C}}}}$ is modified as

$$\begin{aligned} \hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta } = {\mathbb {C}}^{\alpha \beta \gamma \delta } - \frac{ {\mathbb {C}}^{\alpha \beta 33} {\mathbb {C}}^{33\gamma \delta }}{ {\mathbb {C}}^{3333}}, \end{aligned}$$

(64)

where

$$\begin{aligned} {\mathbb {C}}^{\alpha \beta 33}&= 4\frac{\partial ^2 W }{\partial C_{\alpha \beta } \partial C_{33}} - 2\frac{\partial {\tilde{p}}}{\partial C_{33}}{C}^{\alpha \beta }\nonumber \\ {}&\quad - 2\frac{\partial {\tilde{p}}}{\partial C_{\alpha \beta }}{C}^{33} - {\tilde{p}} [ {C}^{\alpha \beta } {C}^{33}]. \end{aligned}$$

(65)

The partial derivative of the Lagrange multiplier with respect to $C_{33}$ is given as

$$\begin{aligned} \frac{\partial {\tilde{p}}}{\partial C_{33}} = 2\frac{\partial ^2 W}{\partial C_{33}^2}\lambda _3^2 + 2 \frac{\partial W}{\partial C_{33}}. \end{aligned}$$

(66)

Thus Eq. (65) can be computed explicitly as

$$\begin{aligned} {\mathbb {C}}^{\alpha \beta 33} = -{C}^{\alpha \beta } \left[ 6 \frac{\partial W}{\partial C_{33}} +4 \frac{\partial ^{2} W}{\partial C_{33}^{2}} \lambda _3^2 \right] . \end{aligned}$$

(67)

Similarly, the other two terms in Eq. (64) are

$$\begin{aligned} {\mathbb {C}}^{33\gamma \delta }&= -{C}^{\gamma \delta } \left[ 6 \frac{\partial W}{\partial C_{33}} +4 \frac{\partial ^{2} W}{\partial C_{33}^{2}} \lambda _3^2 \right] , \nonumber \\ {\mathbb {C}}^{3333}&= -\lambda _3^{-2} \left[ 6 \frac{\partial W}{\partial C_{33}} +4 \frac{\partial ^{2} W}{\partial C_{33}^{2}} \lambda _3^2 \right] , \end{aligned}$$

(68)

and therefore a closed form expression for $\hat{{\mathbb {C}}}^{\alpha \beta \gamma \delta }$ is obtained by substituting (67) and (68) in Eq. (64).

1.2 Incompressible Mooney–Rivlin material

Due to incompressibility, the volume of the shell remains unchanged, that is

$$\begin{aligned} \int _{{\bar{\Gamma }}} \bar{h} \, {\textrm{d}} \bar{\Gamma } = \int _{\Gamma } \lambda _3 \bar{h} \, {\textrm{d}} {\Gamma }, \end{aligned}$$

(69)

where ${\textrm{d}} \Gamma = {\mathcal {J}} {\textrm{d}} \bar{\Gamma }$ and ${\mathcal {J}}$ is the in-plane Jacobian, which is expressed as

$$\begin{aligned} {\mathcal {J}} =\frac{|{\textbf{a}}_1 \times {\textbf{a}}_2|}{|\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2|} = \frac{J}{{\bar{J}}}. \end{aligned}$$

(70)

Thus the thickness stretch is the inverse of in-plane Jacobian, that is

$$\begin{aligned} \lambda _3 = {\mathcal {J}}^{-1} =\frac{|\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2|}{|{\textbf{a}}_1 \times {\textbf{a}}_2|}. \end{aligned}$$

(71)

This strain energy density per unit undeformed volume for a Mooney–Rivlin material model is expressed as

$$\begin{aligned} W({\textbf{C}}) = c_1[I_1 - 3] + c_2[I_2 - 3], \end{aligned}$$

(72)

where $I_1$ and $I_2$ are the first and second invariants of ${\textbf{C}}$, defined as

$$\begin{aligned}{} & {} I_1 = \text {tr}({\textbf{C}})= \lambda _1^2 + \lambda _2^2 + \lambda _3^2\quad \text {and} \nonumber \\{} & {} I_2 = \frac{1}{2}\left[ \text {tr}({\textbf{C}})^2 -\text {tr}({\textbf{C}}^2) \right] = \lambda _1^{-2} + \lambda _2^{-2} + \lambda _3^{-2}. \end{aligned}$$

(73)

If $c_2 = 0$, the model reduces to neo-Hookean. We explicitly provide the derivatives of the strain energy density for subsequent reference as

$$\begin{aligned}&\frac{\partial W}{\partial C_{\alpha \beta }} = c_1 \bar{g}^{\alpha \beta } + c_2[C_{\gamma \delta }\bar{g}^{\gamma \delta } \bar{g}^{\alpha \beta } - \bar{g}^{\alpha \gamma }C_{\gamma \delta }\bar{g}^{\delta \beta }], \nonumber \\&\frac{\partial W}{\partial C_{33}} = c_1 + c_2[C_{\gamma \delta }\bar{g}^{\gamma \delta } - \lambda _3^2], \nonumber \\&\frac{\partial ^2 W }{\partial C_{\alpha \beta } \partial C_{\gamma \delta }} = c_2\bar{g}^{\gamma \delta } \bar{g}^{\alpha \beta } - \frac{c_2}{2} [\bar{g}^{\alpha \gamma } \bar{g}^{\beta \delta } + \bar{g}^{\alpha \delta } \bar{g}^{\beta \gamma }], \nonumber \\&\frac{\partial ^2 W }{\partial C_{\alpha \beta } \partial C_{33}} = c_2 \bar{g}^{\alpha \beta }, \quad \frac{\partial ^{2} W}{\partial C_{33}^{2}} = 0. \end{aligned}$$

(74)

1.3 Variations of normal vector and thickness stretch

To simplify the expression, one denotes the normal vector as

$$\begin{aligned} {\textbf{a}}_3 = J^{-1} \tilde{{\textbf{a}}}_3. \end{aligned}$$

(75)

where

$$\begin{aligned} \tilde{{\textbf{a}}}_3 = {\textbf{a}}_{1}\times {\textbf{a}}_{2}. \end{aligned}$$

(76)

Then, the first and second derivatives of the normal vector are computed as

$$\begin{aligned} \delta _{r}{\textbf{a}}_{3}= & {} J^{-1}\delta _{r}\tilde{{\textbf{a}}}_{3}-J^{-2}[\delta _{r}J] \tilde{{\textbf{a}}}_{3},\nonumber \\ \delta _{s}\delta _{r}{\textbf{a}}_{3}= & {} J^{-1} [\delta _{s}\delta _{r}\tilde{{\textbf{a}}}_{3}]-J^{-2} [\delta _{s}\delta _{r}J] \tilde{{\textbf{a}}}_{3}-J^{-2} [\delta _{r}J][\delta _{s} \tilde{{\textbf{a}}}_{3}]\nonumber \\{} & {} -J^{-2} [\delta _{s}J][ \delta _{r}\tilde{{\textbf{a}}}_{3}] + 2 J^{-3} [\delta _{r}J][ \delta _{s} J] \tilde{{\textbf{a}}}_{3}, \end{aligned}$$

(77)

where

$$\begin{aligned} \begin{aligned} \delta _{r}\tilde{{\textbf{a}}}_{3}&= \delta _{r}{\textbf{a}}_1 \times {\textbf{a}}_2 + {\textbf{a}}_1 \times \delta _{r}{\textbf{a}}_2,\\ \delta _{r}J&={\textbf{a}}_{3} \cdot \delta _{r}\tilde{{\textbf{a}}}_{3},\\ \delta _{s}\delta _{r}\tilde{{\textbf{a}}}_{3}&= \delta _{r}{\textbf{a}}_1 \times \delta _{s}{\textbf{a}}_2 + \delta _{s}{\textbf{a}}_1 \times \delta _{r}{\textbf{a}}_2, \\ \delta _{s}\delta _{r}J&= J^{-1}\left[ \delta _{s}\delta _{r}\tilde{{\textbf{a}}}_{3} \cdot \tilde{{\textbf{a}}}_{3}+\delta _{r}\tilde{{\textbf{a}}}_{3} \cdot \delta _{s}\tilde{{\textbf{a}}}_{3}-[\delta _{r}\tilde{{\textbf{a}}}_{3} \cdot {\textbf{a}}_{3}][\delta _{s}\tilde{{\textbf{a}}}_{3} \cdot {\textbf{a}}_{3}]\right] . \end{aligned} \end{aligned}$$

(78)

Due to the incompressibility constraint of the material, the thickness stretch can be expressed as

$$\begin{aligned} \lambda _3 = \frac{|\bar{{\textbf{a}}}_1 \times \bar{{\textbf{a}}}_2|}{|{{\textbf{a}}}_1 \times {{\textbf{a}}}_2|} = \bar{J} J^{-1}, \end{aligned}$$

(79)

whose first and second derivatives are expressed as

$$\begin{aligned} \begin{aligned} \delta _r \lambda _3 =&-\bar{J} [ J]^{-2}\delta _r J,\\ \delta _s \delta _r \lambda _3 =&-\bar{J} \left[ -2[J]^{-3}\delta _sJ \, \delta _r J + [J]^{-2} \delta _s\delta _r J\right] .\\ \end{aligned} \end{aligned}$$

(80)