Abstract
This work describes the implementation of a novel dynamic Arbitrary Lagrangian Eulerian (ALE) formulation for the simulation of pavement structures loaded by rolling tires in a finite element framework. The proposed formulation enables the simulation of dynamic effects like acceleration, deceleration and variation of the wheel load on the pavement. The ALE scheme is described for a hyperelastic St. Venant-Kirchhoff material capable of finite deformations. With the adoption of this dynamic ALE formulation, a significant improvement in terms of speed and efficiency of the simulation is achieved in comparison to a classical transient Lagrangian formulation. This is primarily because only the relevant portion of the mesh around the applied load needs to be discretized and simulated. Another benefit is that a cumbersome moving load formulation does not need to be implemented. The results show satisfactory agreement with a conventional Lagrangian simulation with a moving load.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
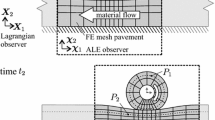
A pavement is typically a longish structure, with generally identical material properties along the length. In the design stage of such structures, it is often required to simulate a moving vehicle load. If conventional methods are used for such a simulation, the entire length of the pavement in the path of the load would need to be discretized. This leads to slow and inefficient simulations. To overcome this drawback, the work at hand details an alternative simulation strategy based on the Arbitrary Lagrangian Eulerian (ALE) approach. The ALE methodology is most commonly applied in situations where there are exceptionally large deformations. These large deformations can cause finite elements in a simulation to have severely distorted aspect ratios. This directly results in poor quality of the resulting solution fields. The ALE approach can help in overcoming this drawback, when it is used as a mesh adaptation technique [1,2,3,4,5]. The ALE approach is also commonly used in the field of fluid mechanics, particularly to simulate fluid - structure interactions [6, 7]. Nackenhorst proposed a framework to apply the ALE concept to rolling tires [8]. Based on this work, Wollny et al. then conceptualized the application of the ALE framework in the context of pavement structures [9, 10]. The main advantage of applying the ALE concept to pavement structures is that only a small region of interest around the wheel load needs to be discretized. This is contrary to a conventional Lagrangian simulation, where the entire pavement structure in the wheel path needs to be simulated. This conventional method therefore requires the discretization of a considerably larger region, and is costly in terms of computation time, see Fig. 1. This aspect is even more prominent when a fine mesh discretization is required at the loaded region. In the conventional Lagrangian approach, the entire load path needs to be discretized with a fine mesh, whereas from the moving ALE reference frame, the load appears to be stationary, and the region, where a fine mesh is required, is considerably reduced. Also, in the ALE reference frame, the material of the pavement appears to flow through the mesh.
In the steady state ALE framework, the wheel load is assumed to have a constant amplitude and velocity. It is known that the transient response of a body can be quite different from the static or steady state response. To investigate this, the work at hand aims to further develop the steady state ALE framework for pavements presented by Wollny et. al. [9]. The framework introduced in this contribution accounts for transient effects from wheel loads - acceleration, deceleration and changes in amplitude of the loading.
This paper is organized as follows. The next Sect. 2 gives a brief overview of the kinematics involved in the ALE formulation. Then, Sect. 3 describes the conversion of the strong form of the balance of linear momentum to the weak form in the ALE reference configuration. Following this, the linearization and consequent discretization of the weak form into a possible finite element framework is described in Sect. 4. An additional consideration required for the dynamic ALE formulation is the displacement (solution field) update, and this is described in Sect. 5. Then, several numerical studies are performed to highlight the performance of the dynamic ALE formulation, and the results obtained are presented in Sect. 6. Finally, the conclusions drawn are summarized in Sect. 7.
2 ALE kinematics
The central idea in the use of the ALE concept for pavements is a change in perspective, i.e. the ALE reference coordinates move in time with the applied load. This implies a formulation in an intermediate configuration [8, 9] as shown in Fig. 2. Consider any point defined by position vector \({\varvec{X}}\) in the initial configuration. It undergoes only rigid body movement \({\varvec{u}}_{ rig }\) to reach the ALE reference configuration. The position of the point with respect to the moving coordinate system \({\varvec{e}}_{\text {i}}^{\text {ALE}}\) in this reference configuration is given by \(\varvec{\chi }\). The position of the moving ALE reference coordinate system \({\varvec{e}}_{\text {i}}^{\text {ALE}}\) is defined with respect to the Lagrangian coordinate system \({\varvec{e}}_{\text {i}}^{\text {Lagrange}}\), which is fixed in space, with the help of vector \(\varvec{\chi }_{\text {0}}^{\text {ALE}}\). The initial position \({\varvec{X}}\) of a particle can be described by
where it is to be noted that with the ALE framework, it is possible to fix the vector \(\varvec{\chi }\) so that it does not depend on time. In this case, the vector \(\varvec{\chi }\) would point to different material points at different instances of time. Thus, from the perspective of the ALE reference configuration, the material of the pavement appears to flow through the finite element mesh. In case the ALE reference frame is moved with the same velocity as the moving wheel load, the load is always applied on the same mesh point, and all the fields that are related to the Lagrangian frame (displacements, velocity, and acceleration) need to be advected through the mesh with the apparent motion of the material points. In the case of pavement, the rate of apparent motion of the material points through the mesh in the ALE configuration is given by the so-called guiding velocity, \({\varvec{w}}\), which is expressed as
There is also the assumption that only rigid body translation or rotation occurs from initial configuration to ALE reference configuration, and thereafter, the full deformation to the current configuration takes place. The position of the point in the current configuration can be described with respect to the initial configuration as \({\varvec{x}}\), and with respect to the ALE reference configuration as \(\varvec{\varphi }\). Thus, the current position \({\varvec{x}}\) of a particle in the body can be expressed in the different configurations as
Thus, from Eqs. (2) and (3), the guiding velocity can be described as
since pavements are fixed in space, there is no rigid body motion, and \({\varvec{u}}_{\text {rig}} = {\varvec{0}}\). It is to be noted that this is not the case when considering the ALE framework for tires as in the work of Nackenhorst [8].
3 Balance of linear momentum
The balance of linear momentum is the basis for most mechanical finite element formulations [11, 12]. The strong form of the balance law in the ALE configuration [2, 8, 9] is given by
where \({\hat{\rho }}\) refers to the density in the ALE configuration, \(\varvec{\hat{\underline{P}}}\) is the first Piola-Kirchhoff stress in the ALE configuration, and \({\varvec{b}}\) refers to the applied body forces. Using an arbitrary test function \(\varvec{\eta }\) and integrating Eq. (5) over the volume of the body, the weak form of the balance of linear momentum is obtained in the ALE configuration as
where \(\varvec{\hat{T}}\) is the external surface traction. The work at hand is mostly concerned with the first term in Eq. (6). To accurately treat the velocity and acceleration terms in the ALE frame, the advection equations for these quantities are considered as given by
and
respectively [2, 8, 9]. Equations (7) and (8) transfer the velocity and acceleration fields through the mesh with the apparent motion of the material points during a given time step. Since the position vector in the current configuration can be expressed as \({\varvec{x}} = \varvec{\chi }_\text {0}^\text {ALE} + \varvec{\varphi }\), Eq. (7) can be written as
since \(\text {Grad}\varvec{\chi }_{\text {0}}^{\text {ALE}} = \varvec{\underline{0}}\). Moreover, Eq. (8) can be expanded out based on the above Eq. (9) as
When the acceleration from the above Eq. (10) is substituted into the first term of Eq. (6), the following expression can be obtained
In the above Eq. (11), it is noteworthy, that the last expression involves second order gradients. Nackenhorst proposed a formulation, which involved transformation of the term involving second order gradients into terms with surface integrals, and this is provided in the following Sect. 3.1. In this paper, a novel formulation is proposed specifically for pavements, which involves the direct evaluation of the term with second order gradients in Eq. (11). This new formulation for pavements is presented in Sect. 3.2. Later, through numerical examples in Sect. 6.1, these two formulations are compared in terms of accuracy and computation time.
3.1 Formulation with surface integrals
To work-around the implementation of the last expression of Eq. (11), which requires the computation of second derivatives of the shape functions with respect to global coordinates in a finite element formulation, Nackenhorst expressed the second order gradients in terms of surface integrals [8], and the resulting expression is given as
3.2 Formulation with second order gradients
On the other hand, even the second derivatives of the standard trilinear shape functions for a common 8-node brick type finite element are non-zero, and can be computed. Thus, it is possible to directly discretize the last term of Eq. (11) using second derivatives of the shape functions. The Eq. (11) can then be simplified for pavements, and written as
since for pavements, \(\text {Grad}{\varvec{w}} = \varvec{\underline{0}}\). Furthermore, it can be noted that in Eqs. (12) and (13), additional terms that depend on the rate of change of the guiding velocity, specifically the first and fourth terms, are considered. These terms are not considered in the work of Nackenhorst [8] because in steady state rolling, the time derivative of the guiding velocity vanishes. These terms that depend on the rate of change of guiding velocity take into account, the effects of acceleration or deceleration of the tire load on the pavement.
4 Linearization and discretization
For the implementation into any finite element formulation, it is necessary to linearize and discretize the above Eqs. (12) and (13).
4.1 Linearization and discretization of the formulation with surface integrals
The linearization and discretization of the formulation with surface integrals given in Sect. 3.1 is considered. This yields force type contributions (\({\varvec{f}}_{1}\) to \({\varvec{f}}_{8}\)), which are subtracted from the external applied forces \({\varvec{f}}_{ext}\), and tangent type contributions (\(\varvec{\underline{K}}_{1}\) to \(\varvec{\underline{K}}_{8}\)), which aid in the search for the increment of the state variable \(\varvec{\varphi }\) in a Newton-Raphson iterative solution scheme [12]. Since the transient case is considered, there are terms that depend on the velocity and acceleration in the ALE reference frame. Hence, the Newton-Raphson iterative solution scheme for values at iteration \(j+1\) based on known quantities at iteration j, can be expressed as
The above Eq. (14) can be expressed in terms of the individual tangent contributions (\(\varvec{\underline{K}}_{1}\) to \(\varvec{\underline{K}}_{8}\)), and internal force contributions (\({\varvec{f}}_{1}\) to \({\varvec{f}}_{8}\)) as
where it is to be noted, that since the first term of Eq. (12) does not contain any terms that depend on the state variable \(\varvec{\varphi }\). Hence, there is no associated tangent contribution (\(\varvec{\underline{K}}_{1} = \varvec{\underline{0}}\)). The linearization of each term in Eq. (12) is described separately for the sake of clarity. The first term can be expressed in terms of the rate of change of the guiding velocity \({\varvec{w}}\) as
The rate of change of guiding velocity can be calculated from the prescribed values of guiding velocity at each time step, and is known explicitly at each time step. Therefore, there is only a force type contribution from the first term. This can be described, after discretization for an arbitrary finite element e as
where the term \(\varvec{\underline{H}}\) is a matrix with orderly arrangement of the shape functions, and \(\varvec{\eta }\) is an arbitrary test function. The matrix \(\varvec{\underline{H}}\) can be written as
where \(N_{k}(\varvec{\xi })\) refers to the shape function associated with iso-parametric coordinates \(\varvec{\xi }\) and node k of a given finite element. Further, the matrix \(\varvec{\underline{H}}\) is used to project the nodal values of any quantity \({\widetilde{\square }}\) to the integration points in the finite element (e.g. \(\varvec{\eta }(\varvec{\xi }) = \varvec{\underline{H}}\cdot \widetilde{\varvec{\eta }}\)). Moreover, the rate of change of the guiding velocity is constant throughout the finite element mesh, and so, the above Eq. (17) can be written as
The second term depends on the acceleration in the ALE frame, and can be linearized with respect to the acceleration as
The discretization of the above Eq. (20) results in contributions to both the forces and the tangent given by
respectively. The third term in Eq. (12) depends on the velocity in the ALE frame, and can be linearized with respect to the velocity as
The discretization of the above Eq. (22) results in contributions to both the forces and the tangent given by
respectively. Here, the term \(\varvec{\underline{A}}\) refers to the following matrix
where \(N_{k,i}w_{i}\) is defined as the summation \(\sum _{i}N_{k,i}w_{i}\). \(N_{k,i}\) is the derivative of the shape function associated with node k along the i direction, and \(w_{i}\) is the component of the guiding velocity along the i direction. The fourth term in Eq. (12) depends on the current coordinates within the ALE frame, and can be linearized with respect to this as
The discretization of the above Eq. (25) results in contributions to both the forces and the tangent, expressed as
respectively. Here, the matrix \(\varvec{\underline{A'}}\) is defined as
where \({\dot{w}}_{i}\) refers to the component of \(\frac{\partial {\varvec{w}}}{\partial t}\big \vert _{\chi }\) along the i direction. It is important to note that the matrix \(\varvec{\underline{A'}}\) can be determined in a relatively straightforward fashion in the case of pavements, since all nodes in the mesh have the same guiding velocity at any given point of time. However, in the case of rolling wheels, since there is generally a non-zero angular guiding velocity, the determination of this matrix requires the storage of time history data of the guiding velocity itself. The fifth term in Eq. (12) can be linearized with respect to the velocity in the ALE reference frame as
The discretization of the above Eq. (28) results in terms that contribute to both forces and the tangent, and can be described by
respectively. The sixth term of Eq. (12) can be linearized with respect to the current coordinates in the ALE reference frame, and this results in
Equation (30) can be discretized and yields contributions to both forces and the tangent. These force and tangent contributions are described as
respectively. The seventh and eighth terms in Eq. (12) are surface integrals and need to be treated for each surface of every finite element. The seventh term in Eq. (12) depends on the velocity in the ALE reference frame, and can be linearized as
Equation (32) contributes to both force and tangent terms when discretized as demonstrated below
respectively. Finally, the eighth term in Eq. (12) can be linearized with respect to the current coordinates in the ALE reference frame, as
The above Eq. (34) can then be discretized and contributes to both forces and the tangent. These are given by
respectively. Thus, all the terms of Eq. (12) are discretized and can be implemented in a finite element framework. All the element tangent type contributions are assembled into the global material tangent, and all the element forces are assembled into the global internal forces array. The summary of the discretized terms from Eq. (12) are provided in Table 1, after discarding the arbitrary test function \(\varvec{\eta }\).
4.2 Linearization and discretization of the formulation with second order gradients
In a similar manner as in the previous Sect. 4.1, the linearization and discretization of the five terms in Eq. (13) of Sect. 3.2 result in force type contributions (\({\varvec{f}}_{1}\) to \({\varvec{f}}_{5}\)), and tangent type contributions (\(\varvec{\underline{K}}_{1}\) to \(\varvec{\underline{K}}_{5}\)). The iterative solution scheme for values at iteration \(j+1\) based on known quantities at iteration j can then be set up as
Further, in the linearization of Eq. (13), only the fifth term is new, and involves second order gradients. The linearization of the fifth term in Eq. (13) can be expressed as
The discretization of the above Eq. (37) results in contributions to both forces and the tangent, and can be written as
In the above equations, the term \(\varvec{\underline{A}}''\) refers to the following matrix
where \(N_{i,jk}\) refers to the second derivative of the shape function corresponding to node i with respect to the global coordinates \(\varvec{\chi }\). The summary of the discretized terms from Eq. (13) are provided in Table 2, after discarding the arbitrary test function \(\varvec{\eta }\).
It is worth mentioning that both formulations of the dynamic ALE framework presented in this contribution (see Sects. 3.1 and 3.2), produce non symmetric tangent matrices, when implemented into a finite element formulation.
4.3 Stress response
Furthermore, for the stress response, a simple St. Venant-Kirchhoff hyperelastic material formulation is implemented along with the dynamic ALE framework. The strain energy density function for this material in the ALE configuration is given by
where \({\hat{\lambda }}\) and \({\hat{\mu }}\) are Lame’s parameters, and \(\hat{\varvec{\underline{E}}}\) is the Green-Lagrange strain tensor. The second Piola-Kirchhoff stress tensor \(\hat{\varvec{\underline{S}}}\) is defined as
The fourth order material constitutive tensor \(\varvec{\underline{\underline{\mathbb {C}}}}\) can be obtained by further partially differentiating Eq. (41) with respect to \(\hat{\varvec{\underline{E}}}\) as
For the sake of brevity, the linearization and discretization of the above Eqs. (41) and (42) are not shown here, but can be found in the works of Holzapfel [11] or Wriggers [12], for example.
5 Additional consideration: update of displacement field
The formulation presented thus far is to perform the calculations for a single time step. However, in the dynamic case, it is required to carry out the simulation for multiple time steps with the help of a time integration algorithm. In the finite element framework [13], a Newmark time integration scheme is adopted [12]. This makes the solution of a given time step depend upon the solution at the previous time step. Since the ALE formulation calculates the solution for a different set of material points for every time step, it becomes necessary to update the displacement field. The updated displacement field ensures that the Newmark time integration scheme is initialized to the correct displacement values corresponding to the material points, which would flow into the mesh nodes at the start of the time step. The displacements of the mesh nodes must therefore be updated between time steps, see Fig. 3, so that the Newmark time integration scheme is initialized properly, and the material appears to flow through a stationary mesh from the ALE reference point. It is worth mentioning that this displacement update procedure is not required if a steady state case is considered, because the displacements of a given time step do not depend on the displacements of the previous time step. In order to update the displacement field at the end of one time step and before the next, the algorithm as described in Table 3 is adopted.
The results of the ALE simulation are found to match the results of the Lagrangian simulation to a satisfactory extent with the algorithm presented in Table 3 included in the implemented framework, and are discussed in detail in the next section.
6 Numerical examples
Several numerical studies are undertaken in order to test the capabilities of the proposed dynamic ALE framework for pavements. In this section, the studies performed are described, and the obtained results are presented. It is worth mentioning that in all the transient analyses carried out, the Newmark time integration scheme is used. All simulations are run on a desktop computer with an Intel Core i5 10400 processor and 32 GB RAM. The typical specimens used in the various simulations are depicted in Fig. 4. Further, the finite element meshes utilized in all the numerical simulations are structured meshes, with uniform element size.
6.1 Evaluation of the dynamic ALE framework under steady state loading
It stands to reason, that if a quasi-static load case is applied to the dynamic ALE framework, all the rate dependent terms in the formulation would vanish, and the solution should match that of a steady state simulation. To test this, a quasi-static solver is used with the dynamic ALE framework, and the response of a body as described in Fig. 4a is studied, when under loading as described in Fig. 5. That is, the pressure load is applied in the very first time step as an impact load at \(t = \) 0.1 s, and, thereafter, its magnitude is kept constant. The position of the load is then changed such that it accelerates to the prescribed guiding velocity between \(t = \) 0.9 s and \(t = \) 1.0 s, and, afterwards, the load is moved with this constant velocity. It is worth mentioning that the load is physically moved over the body in the case of Lagrangian simulations, whereas the material flows under the load in the ALE simulation. The response of the body obtained from the dynamic ALE framework is then compared to the response obtained from a standard Lagrangian simulation, where the load is moved over a larger body as depicted in Fig. 4(b). The material and geometric parameters used in both simulations are listed in Table 4. The obtained displacement along the Z-direction under the loaded node is plotted against time in Fig. 6.
From Fig. 6, it is clear that the results obtained are as expected, and the solution from the dynamic ALE framework does indeed converge to the steady state case. The solution is also in reasonable agreement with the large body Lagrangian simulation. One of the major advantages of using the ALE framework is the reduction in the size of the mesh required, and the consequent reduction in computation times. For the above example, the simulation with the ALE framework based on second order gradients (as per Sect. 3.2) required 16.29 minutes, and the simulation with the ALE framework based on surface terms (as per Sect. 3.1) required 16.44 minutes. These times are in contrast to the Lagrangian simulation, which required 59.94 minutes despite taking advantage of a symmetric tangent matrix. It can also be observed in Fig. 6 that both surface and second order gradient based formulations produce identical results. However, the framework based on surface terms (as described in Sect. 3.1) is slower than the framework based on second order gradients (as per Sect. 3.2). This is because the evaluation of surface terms require special surface sub-elements. The 8 node brick type finite elements used here require six surface sub-elements to evaluate the surface terms. The dynamic ALE framework based on second order gradients is computationally more efficient, as these surface sub-elements are not required. The evaluation of surface sub-elements in a parent finite element imposes a large computational cost, especially in cases where higher order finite elements are used. Therefore, the framework based on surface terms is not pursued further in this work.
6.2 Evaluation with dynamic loading
In this section, the capabilities of the dynamic ALE framework are highlighted. A transient solver is used to obtain the dynamic response of the body as depicted in Fig. 4a with the dynamic ALE framework under the same loading scenario as described in Fig. 5. A comparison is then made to a transient Lagrangian simulation, where the load is moved over the body as shown in Fig. 4b. The material and geometric parameters used are listed in Table 5. The resulting displacements along the Z-direction under the load are plotted in Fig. 7.
From the results shown in Fig. 7, it can be observed that the displacements obtained from the dynamic ALE framework match those from a Lagrangian simulation satisfactorily for all types of finite elements chosen (8, 20 and 27 node bricks). Also from Fig. 7, one can infer that the transient response of the body can be significantly different from the quasi-static response. This can be attributed to the choice of a relatively large material density in comparison to the Young’s modulus, and the resulting large inertia of the body. Another observation is the oscillatory nature of the response from the Lagrangian simulations. This can be explained by the fact that the load is moved in the Lagrangian simulations. When the load is not exactly at a node in the finite element mesh, the resulting displacement is interpolated to be smaller in magnitude, when compared to the resulting displacement where the load is exactly positioned at a mesh node. A smoothing procedure can be adopted wherein only the points, where the load is close to a mesh node, are considered. This results in an even better agreement between the results obtained from the ALE simulation and the Lagrangian simulation, as depicted in Fig. 7.
6.3 Influence of material density
In the previous Sect. 6.2, it is observed that the transient response of the body strongly depends on the choice of material density. To investigate this further, in this section, several simulations are run, each with a different value of material density, and the results from the dynamic ALE framework are compared to those from a Lagrangian simulation. The loading scenario is as described in Fig. 5. The geometry of the specimen used for simulations with the dynamic ALE framework is depicted in Fig. 4a, while that chosen for the Lagrangian simulation is described in Fig. 4b. The material parameters chosen are given in Table 6. The obtained results are shown in Fig. 8.
From the results depicted in Fig. 8, it is clear that the obtained displacements from the ALE and the Lagrangian simulations match reasonably well for all values of material density considered. Any discrepancies can be attributed to the occurrence of boundary reflections, and the interpolation error due to the movement of the load in the Lagrangian simulations. The interpolation error can be minimized by choosing to interpolate the values of displacement at those times when the load is close to a node on the finite element mesh. The boundary reflections however are not a physical phenomenon. In reality, the material of the pavement subsoil stretches out infinitely in all directions, and, thus, boundary reflections do not occur. Boundary reflections are typically more prominent in materials with relatively low values of density, as the propagation speed of elastic waves in such materials is relatively high [14].
6.4 Effects of acceleration and deceleration
In this section, the acceleration and deceleration of the wheel load are considered by applying a loading scenario as described in Fig. 9. That is, the pressure load is applied as a ramp over the period of \(t = \) 1 s and is kept constant in amplitude afterwards. The position of the load is moved such that between \(t = \) 2 s and \(t = \) 4 s, it accelerates to reach the guiding velocity specified, then it maintains this velocity between \(t = \) 4 s and \(t = \) 10 s, and finally decelerates to zero velocity between \(t = \) 10 s and \(t = \) 11.2 s, reaching the final position.
The specimen, load and boundary conditions used in the ALE simulation are described in Fig. 4a, and those for the Lagrangian simulation are depicted in Fig. 4b. The material and geometric parameters used in the simulations are listed in Table 7. The displacement along the Z-direction under the load obtained from both the ALE and Lagrangian simulations are plotted in Fig. 10. Also, contour plots of the distribution of the Cauchy stress components \(\varvec{\underline{\sigma }}_{yy}\) and \(\varvec{\underline{\sigma }}_{zz}\) are shown in Figs. 11 and 12 at various stages of the simulation, respectively.
Figures 10, 11 and 12 show that the dynamic ALE framework presented in this work is capable of accurately representing the behaviour of the body under both accelerating and decelerating loads. The obtained results agree to a reasonable extent with the full body Lagrangian simulation. It is also worth mentioning that in the example considered above, the mesh discretization used for the ALE simulation is considerably smaller (864 elements) than that chosen for the Lagrangian simulation (4480 elements). This directly results in a much faster simulation with the dynamic ALE framework. The ALE simulation takes 31.3 minutes to complete, whereas the Lagrangian simulation takes 2.5 hours to complete, despite the latter taking advantage of a symmetric tangent matrix.
6.5 Realistic material parameters and loading
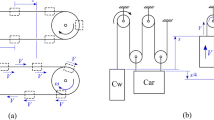
The dynamic ALE framework presented in this work has been demonstrated to be able to accurately produce results that are reasonably close to conventional methods. In this section, the capabilities of the dynamic ALE framework are highlighted by choosing a small mesh size with a high guiding velocity. The corresponding conventional Lagrangian simulation would not be feasible with the available computational resources. The material parameters are changed to more closely resemble those of a typical pavement. The specimen, load and boundary conditions used in the ALE simulation are described in Fig. 4a. The loading scenario is identical to the one described in Fig. 9. The material parameters used are provided in Table 8. Two cases of loading are considered. In the first case, the pressure load is assumed to be from a tire loaded with 5 tonne acting on a square patch of side 0.2 m. The guiding velocity is set to -25 m/s in this case to simulate a moving truck. In the next case, the pressure load is assumed to be from a tire loaded with 0.5 tonne acting on a square patch of side 0.2 m. The guiding velocity is set to \(-50\) m/s in this case to simulate a moving car. The resulting displacements along the Z-direction under the load are plotted in Figs. 13 and 14 for the two load cases respectively.
From Figs. 13 and 14, it can be observed that the presented dynamic ALE framework is capable of producing the response of the pavement structure in a scenario where the conventional method would take an unreasonable amount of time to compute (with the available computational resources). However, it should be noted that given sufficient computational capabilities, the problem can be solved through conventional methods. A traditional Lagrangian simulation would also require a complicated finite element mesh discretization, or the simulation of an accelerating or decelerating load through contact mechanics, both of which can be avoided with the use of the dynamic ALE framework. Also, another interesting observation is the increase in displacements when the load is beginning to accelerate or decelerate. The dynamic ALE framework is able to capture this effect satisfactorily.
6.6 Layered pavement structure with oscillating load
In this final example, all aspects of the dynamic ALE framework are tested. A two layer pavement structure is simulated with a load that accelerates, oscillates in amplitude and also decelerates. The specimen, load and boundary conditions used in the ALE simulation are described in Fig. 15. The material parameters used are listed in Table 9. The loading applied is depicted in Fig. 16. The load is very similar to the one used in the previous example (see Fig. 9), but between 6 s and 8 s, the amplitude of the load oscillates sinusoidally up to \(\pm 20\%\) at a frequency of 10 Hz. The obtained displacements along the Z-direction under the loaded node are plotted in Fig. 16. Also, contour plots of the distribution of the Cauchy stress components \(\varvec{\underline{\sigma }}_{yy}\) and \(\varvec{\underline{\sigma }}_{zz}\) are shown in Figs. 17 and 18 at various stages of the simulation, respectively.
Thus, from the results presented in Figs. 16, 17 and 18, it is clear that the described dynamic ALE framework can successfully capture effects of acceleration, deceleration and variation of amplitude of the loading and provide meaningful results in a reasonable time-frame.
Distribution of Cauchy stress component \(\varvec{\underline{\sigma }}_{yy}\) [N/cm\(^2\)] at different time steps of the simulation, (a) Time = 3 s (acceleration), (b) Time = 5 s (constant velocity), (c) Time = 6.025 s (minimum load amplitude), (d) Time = 6.075 s (maximum load amplitude), (e) Time = 10.6 s (deceleration), (f) Time \(= 12.2\) s (last time step)
Distribution of Cauchy stress component \(\varvec{\underline{\sigma }}_{zz}\) [N/cm\(^2\)] in the central X-Z plane at different time steps of the simulation, (a) Time = 3 s (acceleration), (b) Time = 5 s (constant velocity), (c) Time = 6.025 s (minimum load amplitude), (d) Time = 6.075 s (maximum load amplitude), (e) Time = 10.6 s (deceleration), (f) Time = 12.2 s (last time step)
7 Conclusions and outlook
In this work, the steady state ALE framework for pavements is successfully extended to the dynamic domain. The presented dynamic ALE framework can accurately capture the dynamic effects such as acceleration, deceleration and change in amplitude of the wheel load. The capabilities of this novel dynamic ALE framework serve to increase the efficiency of simulations, by greatly reducing the domain that needs to be discretized. The proposed framework is capable of accurately describing the response of a hyperelastic material at large deformations. Several numerical studies are performed to validate the framework against conventional Lagrangian simulations. Further, the influence of the material density on the transient response of the body has been studied. It is also demonstrated in this work, that using the presented dynamic ALE framework results in significant gains in terms of speed of computation, when compared to conventional methods, despite requiring an additional displacement update procedure and the generation of a nonsymmetric tangent matrix. Furthermore, in a future contribution, this framework is to be extended to account for the inelastic behaviour of materials like asphalt, concrete or the subsoil itself. Another aspect worth exploring is the prevention of the non-physical boundary reflections. This could greatly improve the quality of the obtained results. Further contributions could be made by expanding the dynamic ALE framework to tire structures as well. This would enable a fully coupled dynamic tire and pavement interaction simulation with a significant increase in efficiency.
References
Benson D (1989) An efficient, accurate, simple ale method for nonlinear finite element programs. Comput Methods Appl Mech Eng 72:305–350
Donea J, Huerta A, Ponthot J, Rodríguez-Ferran A (2004) Arbitrary Lagrangian–Eulerian methods. Wiley Online Library, Encyclopedia of Computational Mechanics. Chap. 14
Bayoumi H, Gadala MS (2004) A complete finite element treatment for the fully coupled implicit ALE formulation. Comput Mech 33:435–452
Nazem M, Carter J, Airey D (2009) Arbitrary Lagrangian–Eulerian method for dynamic analysis of geotechnical problems. Comput Geotech 36:549–557
Zreid I, Behnke R, Kaliske M (2021) ALE formulation for thermomechanical inelastic material models applied to tire forming and curing simulations. Comput Mech 67:1543-1557
Benson D (1992) Computational methods in Lagrangian and Eulerian hydrocodes. Comput Methods Appl Mech Eng 99:235–394
Codina R, Houzeaux G, Coppola-Owen H, Baiges J (2009) The fixed-mesh ALE approach for the numerical approximation of flows in moving domains. J Comput Phys 228:1591–1611
Nackenhorst U (2004) The ALE-formulation of bodies in rolling contact: theoretical foundations and finite element approach. Comput Methods Appl Mech Eng 193:4299–4322
Wollny I, Kaliske M (2013) Numerical simulation of pavement structures with inelastic material behaviour under rolling tyres based on an arbitrary lagrangian eulerian (ALE) formulation. Road Mater Pavement Des 14:71–89
Wollny I, Hartung F, Kaliske M (2016) Numerical modeling of inelastic structures at loading of steady state rolling. Comput Mech 57:867–886
Holzapfel G (2000) Nonlinear solid mechanics: a continuum approach for engineering. Wiley, Chichester
Wriggers P (2008) Nonlinear finite element methods. Springer, Berlin
Taylor R (2020) FEAP—finite element analysis program. University of California, Berkeley. http://projects.ce.berkeley.edu/feap
Achenbach J (2012) Wave propagation in elastic solids. Elsevier Science Publishers B.V, Amsterdam
Acknowledgements
The present work has been developed under the research Project No. 453596084–SFB/TRR 339, which has been granted by the German Research Foundation (Deutsche Forschungsgemeinschaft). This financial support is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Anantheswar, A., Wollny, I. & Kaliske, M. A dynamic ALE formulation for structures under moving loads. Comput Mech 73, 139–157 (2024). https://doi.org/10.1007/s00466-023-02360-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02360-5