Comparison of arterial wall models in fluid–structure interaction simulations

Abstract

Monolithic fluid–structure interaction (FSI) of blood flow with arterial walls is considered, making use of sophisticated nonlinear wall models. These incorporate the effects of almost incompressibility as well as of the anisotropy caused by embedded collagen fibers. In the literature, relatively simple structural models such as Neo-Hooke are often considered for FSI with arterial walls. Such models lack, both, anisotropy and incompressibility. In this paper, numerical simulations of idealized heart beats in a curved benchmark geometry, using simple and sophisticated arterial wall models, are compared: we consider three different almost incompressible, anisotropic arterial wall models as a reference and, for comparison, a simple, isotropic Neo-Hooke model using four different parameter sets. The simulations show significant quantitative and qualitative differences in the stresses and displacements as well as the lumen cross sections. For the Neo-Hooke models, a significantly larger amplitude in the in- and outflow areas during the heart beat is observed, presumably due to the lack of fiber stiffening. For completeness, we also consider a linear elastic wall using 16 different parameter sets. However, using our benchmark setup, we were not successful in achieving good agreement with our nonlinear reference calculation.

1 Introduction

We are interested in fluid–structure interaction (FSI) problems in biomechanics, notably the interaction of blood flow with arterial walls. In hemodynamics the densities of the fluid and the structure are similar, that is, $\rho _f\approx \rho _s$, and the structure is soft, compared to other FSI applications, for instance, in aeroelasticity. In this regime, strong FSI coupling schemes are most suitable, and monolithic FSI coupling schemes have been demonstrated to be most competitive; see, e.g., [7, 12, 13, 15, 17, 20, 31,32,33, 36, 44].

Table 1 A comparison of different Steklov–Poincaré fluid–structure interaction algorithms, that is, Dirichlet–Neumann, Neumann–Dirichlet, Neumann–Neumann (using different scaling factors), and the monolithic Dirichlet–Neumann preconditioner (composed GCE [13])

In [16], we have compared, in the context of hemodynamics, different segregated strong coupling schemes based on Steklov–Poincaré formulation of the FSI problem [14]. We have considered Dirichlet–Neumann, Neumann–Dirichlet, Neumann–Neumann (using different scalings) and a monolithic approach, that is, the composed Dirichlet–Neumann preconditioner [13]. The monolithic approach [13] was significantly faster, by a factor of two to four, than the fastest segregated approach (segregated Dirichlet–Neumann) and showed a better parallel scalability [16, Table 1]; see also Table 1.

Here, the Dirichlet–Neumann algorithms refer to using $S_s'^{-1}$, the inverse of the structure tangent, as a preconditioner for $S'_f + S'_s$, the sum of the tangents of the fluid and structure Steklov–Poincaré operators. The segregated Dirichlet–Neumann method [14], the scaled Neumann–Neumann method [16], and the monolithic Dirichlet–Neumann method [13] are closely related, and the performance will be very similar if exact solvers are used for the tangent problems. Therefore, the performance benefit of the monolithic method comes from the use of inexact solvers for the blocks.

Our focus is on the application of sophisticated structural models for the arterial wall since we are interested in quantities inside the arterial wall, such as the transmural stresses, which are associated with atherogenesis, that is, the narrowing of arteries due to plaque formation. Note that by sophisticated structural models we refer to geometrically and physically nonlinear, hyperelastic, and anisotropic models since the main interest here is the analysis of the blood–wall interaction under physiological conditions. If supra-physiological loadings are to be analyzed, for example, resulting from balloon-angioplasty, then even more complex models describing the stress-softening response associated with microscopic damage need to be applied; see, e.g. [5, 9]).

The state of the art in the hyperelastic modeling of the passive response of arterial wall tissue considers (almost) incompressibility and also anisotropy from stiffening collagen fibers. The resulting problems are already difficult to solve iteratively without FSI, that is, as a structural mechanics problem alone [11, 23]. It was then shown in [6, 7] that FSI simulations with such challenging structural models are feasible. It is known from experiments that arterial walls show some visco-elastic behavior; we therefore have also considered visco-elastic effects in our FSI simulations [6, 7]. However, it was already concluded in [6] that the influence of viscoelasticity on our quantities of interest, for example, the wall shear stresses, is rather small. Therefore, we usually focus on almost incompressible, anisotropic hyperelastic models without viscoelasticity.

However, since much simpler models for the structure are often used in hemodynamics, it is of interest to investigate the structural model’s influence on the simulation results. Our FSI simulations in [26] have already indicated that sophisticated structural models, such as the model denoted $\Psi _A$ in [4, 7, 10] (originally introduced in [8]), result in a qualitatively different deformation of the wall compared to Neo-Hooke oder linear elasticity [26, Section 6.3 and Fig. 18]. We also showed in numerical tests that, even for the relatively small time steps necessary in our context, adding a coarse level to an overlapping Schwarz preconditioner [26, Fig. 19] will accelerate the convergence. In this paper, we now investigate in more detail how the response of simpler structural models, such as Neo-Hooke, is different from the results obtained with more sophisticated models, which incorporate the almost incompressibility of biological soft tissue as well as the anisotropy from stiffening collagen fibers in the arterial wall.

2 Arterial wall models

Let $\textbf{F}:=\nabla \varphi$ be the deformation gradient mapping infinitesimal vectorial elements in the reference configuration onto the current configuration. The mapping of infinitesimal volume elements is then described by $J:=\det \textbf{F}$. In order to automatically fulfill the principle of objectivity, we consider models formulated in the right Cauchy-Green deformation tensor ${\textbf{C}}:={\textbf{F}}^T{\textbf{F}}$. For hyperelastic materials, a strain energy density function $\Psi$ as a function of the deformation tensor is defined. In order to guarantee a physically reasonable material response avoiding a loss of material stability [40], here, polyconvex energy functions in the sense of [3] will be considered. By evaluation of the second law of thermodynamics, the 2nd Piola-Kirchhoff stress tensor and the Cauchy stress tensor can be computed by

$$\begin{aligned} \textbf{S} = 2\frac{\partial \Psi }{\partial \textbf{C}} \quad \text{ and }\quad \varvec{\sigma } = J^{-1}\textbf{F}\textbf{S}\textbf{F}^T, \end{aligned}$$

respectively. Based on the Cauchy stress tensor, the von Mises stresses can be computed. For a convenient construction of suitable strain energy density functions, often the invariants of the functional arguments in the energy function are considered. For isotropic materials, the principle invariants of ${\textbf{C}}$, that is,

$$\begin{aligned} I_1=\textrm{tr}\,{\textbf{C}}, \quad I_2=\textrm{tr}[\textrm{Cof}({\textbf{C}})], \quad I_3=\det {\textbf{C}}, \end{aligned}$$

with $\textrm{Cof}(\textbf{C})=\det (\textbf{C})\textbf{C}^{-T}$, are taken into account and thus, $\Psi :=\Psi (I_1,I_2,I_3)$. Note that in the context of soft biological tissues, often the dependence on the second invariant is omitted. Thereby, the material response is mainly governed by normal stretches described through $I_1$ and volume changes described by $I_3=(\det \textbf{F})^2$. As a result of embedded collagen fibers, arterial wall tissues behave anisotropically. The fibers are mainly wound crosswise helically around the artery and in healthy arteries symmetrically disposed with respect to the axial direction. Around these main fiber family directions, fibers are stochastically dispersed; cf., e.g., [22]. Assuming a weak interaction between the fiber families, the resulting anisotropy can be modelled by superimposing two transversely isotropic models. For the individual fiber family and thus, the description of transverse isotropy, the structural tensor ${\textbf{M}}=\textbf{a} \otimes \textbf{a}, \Vert \textbf{M}\Vert =1$ [43] is considered as additional argument in the strain energy density function. Herein, the preferred direction vector $\textbf{a}$ describes the fiber orientation. Thus, for a coordinate-invariant formulation, the mixed invariants

$$\begin{aligned} J_4=\textrm{tr}[{\textbf{C}\textbf{M}}], \quad J_5=\textrm{tr}[{\textbf{C}^2\textbf{M}}], \end{aligned}$$

are taken into account. Whereas $J_4$ describes the square of the stretch in fiber direction $\textbf{a}$, the physical meaning of $J_5$ is unclear.

Table 2 Material parameter sets for the Neo-Hooke model

Fig. 1

Cauchy stress $\sigma$ vs. strain $\Delta l/l_0$ in uniaxial test conditions for the experimental data and the different material models. A good fit cannot be achieved using the Neo-Hooke material model, however, NH$_1$ yields a sufficient fit for the $\Delta l/l_0<0.2$. See Tables 2 and 3 for the corresponding fitted material parameters of the NH$_1$–NH$_4$ as well as the $\Psi _{\textrm{A}}$, $\Psi _{\textrm{B}}$, and $\Psi _{\textrm{E}}$ models, respectively

2.1 Simple, isotropic material model: Neo-Hooke

As a simple, isotropic nonlinear material model, we consider a standard compressible Neo-Hookean energy. It is often written in the form

$$\begin{aligned} \Psi _{\textrm{NH}} = \Psi _{\textrm{vol}} + \Psi _{\textrm{isoch}}, \end{aligned}$$

where the volumetric and isochoric parts are given by

$$\begin{aligned} \Psi _{\textrm{vol}} = \frac{\kappa }{2} ( \ln (I_3^{1/2}) )^2 \quad \text{ and }\quad \Psi _{\textrm{isoch}} = \frac{\mu }{2} ( I_3^{-1/3}I_1 - 3). \end{aligned}$$

The material parameters are $\kappa$ and $\mu$ and modulate an increase of energy related to a volume change and a change of isochoric deformations, respectively. Due to the fact that soft biological tissues are mostly assumed to be almost incompressible, here, the volumetric energy will be used as a penalty function to adjust for the quasi-incompressibility constraint. Since the stresses are obtained as derivatives of the energy functions with respect to the deformation tensor, an increase of $\mu$ thus corresponds to an increase in stiffness and for incompressibility mainly modulates the slope in stress–strain diagrams of uniaxial tension tests. Since the Neo-Hookean model is not able to catch the stiffening of the tissue caused by the collagen fibers, the parameters were fitted by hand to the experiments in [28]; see also [8]. There, uniaxial tension tests were performed in circumferential and axial direction of human artery segments. Whereas the parameter set NH$_1$ was fitted to approximate the slope of the experimental curves (media) in the range $0<\Delta l/l_o<0.2$, the set NH$_2$ approximately corresponds to the average slope of the experimental curve in the range $0<\Delta l/l_o<0.235$ and thus, results in a slightly stiffer behavior. NH$_3$ and NH$_4$ were chosen significantly stiffer in order to obtain a similar lumen area as the anisotropic models before the start of the heart beat; see also Sect. 4.1. The parameter sets are summarized in Table 2.

The resulting stress-stretch curves are compared with the experiments in Fig. 1. Note that the experimental data shows a slight hysteresis resulting from a negligible visco-elastic response. We will see in the FSI simulations in Sect. 4 that, for NH$_1$ and NH$_2$, the resulting material behavior is significantly softer compared to the sophisticated, anisotropic models; see Fig. 4.

For the sets NH$_3$ and NH$_4$ the in- and outflow lumen in the simulations presented later is, at the end of the ramp, similar to the lumen areas of the sophisticated models. These parameter sets correspond well for a specific loading scenario in a structural problem, but due to their artificially stiff response, the associated stress–strain curves will not match well the experimental curves on average. For all parameter sets, the compression modulus $\kappa$ was chosen such that the volume change of the model response was kept below 1% in the uniaxial tension tests.

Note that, in the benchmark computations presented in [7, Figure 21], based on the material model $\Psi _A$, the increase of the arterial circumference during the heartbeat was below $20\,\%$.

2.2 Anisotropic material models

Following the analysis in [10], we consider different anisotropic and quasi-incompressible material models for arterial walls. They are of the form

$$\begin{aligned} \Psi _{\textrm{X}} = \Psi _{\textrm{X, iso}} (I_1,I_3) + \sum _{a=1}^2 \Psi _{\textrm{X}, (a)}^{\textrm{ti}} (I_1,I_3,J_4^{(a)},J_5^{(a)}) \end{aligned}$$

where $X\in \{A,B,E\}$. Herein, the mixed invariants are considered separately for the two fiber family directions $\textbf{a}^{(a)},a = 1,2$, i.e., $J_4^{(a)} = \text{ tr }(\textbf{C}\textbf{M}^{(a)})$ and $J_5^{(a)} = \text{ tr }(\textbf{C}^2\textbf{M}^{(a)})$ with $\textbf{M}^{(a)} = \textbf{a}^{(a)}\otimes \textbf{a}^{(a)}$. In detail, the individual functions are

Table 3 Material parameter sets for nonlinear, anisotropic models

Model $\Psi _A$ [8]

$$\begin{aligned}&\Psi _{\textrm{A, iso}} (I_1,I_3) = \epsilon _1 (I_3^{\epsilon _2} + I_3^{-\epsilon _2} -2) + c_1 (I_1 I_3^{-1/3}-3), \\&\Psi _{\textrm{A}, (a)}^{\textrm{ti}}(I_1,J_4^{(a)},J_5^{(a)}) = \alpha _1 \left\langle I_1 J_4^{(a)} - J_5^{(a)} -2 \right\rangle ^{\alpha _2}, \end{aligned}$$

Model $\Psi _B$ ( isochoric and anisotropic part from [29])

$$\begin{aligned}&\Psi _{\textrm{B, iso}} (I_1,I_3) = \epsilon _1 (I_3^{\epsilon _2} + I_3^{-\epsilon _2} -2) + c_1 (I_1 I_3^{-1/3}-3), \\&\Psi _{\textrm{B}, (a)}^{\textrm{ti}} (I_3,J_4^{(a)}) = \frac{k_1}{2k_2} \left( \exp \left( k_2 \left\langle J_4^{(a)} I_3^{-1/3} - 1 \right\rangle ^{2} \right) - 1 \right) , \end{aligned}$$

Model $\Psi _E$ (anisotropic part from [30])

$$\begin{aligned}&\Psi _{\textrm{E, iso}} (I_1,I_3) = \epsilon _1 (I_3^{\epsilon _2} + I_3^{-\epsilon _2} -2) + c_1 (I_1 - 3 - \ln (I_3)) ,\\&\Psi _{\textrm{E}, (a)}^{\textrm{ti}} (J_4^{(a)}) = \frac{k_1}{2k_2} \left( \exp \left( k_2 \left\langle J_4^{(a)} -1 \right\rangle ^2 \right) - 1 \right) . \end{aligned}$$

Herein, the Macauley brackets $\langle (\bullet )\rangle := ((\bullet ) - |(\bullet )|)/2$ filter out negative values. Note that $\Psi _{\textrm{A, iso}} = \Psi _{\textrm{B, iso}}$. The models $\Psi _B$ and $\Psi _E$ are based on the well-known Holzapfel, Gasser, and Ogden model, where the transversely isotropic parts do not include $I_1$ and $J_5$. They are formulated such that a specifically stiff response is purely generated in the fiber directions. In contrast to this, the model $\Psi _A$ includes $J_5$ and even a coupling of $I_1$ with $J_4$. Although $J_5$ may not directly have a physical meaning, the term $I_1 J_4 - J_5$ as part of $\Psi _A$ was found in [39] to describe the change of infinitesimal area elements with normal vectors perpendicular to the fiber direction. Due to the coupling term $I_1 J_4$ in this model, a somewhat dispersed stiffness around the fiber direction is also included. Note that more sophisticated models for the description of fiber dispersion are available (cf., e.g., [22]), which allow for a more independent and less phenomenological quantification of dispersion intensity. Only the model $\Psi _B$ is formulated in a volumetric-isochoric split. Whereas this may enable a more direct quantitative interpretation of the material parameters, it also renders the model response questionable under purely volumetric loading since the stress response will then be purely isotropic. In addition to that, the uncontrolled volume change in the isochoric energy may be problematic in finite element formulations where, for example, the volume change is only considered as volume average of each finite element, or associated terms are used for reduced integration. Summarizing, all models are quasi-incompressible, provided that sufficiently large parameters in the volumetric penalty functions are considered, they are highly nonlinear, anisotropic, polyconvex, and widely used, but each of them has certain advantages and disadvantages. We use the parameters for the media fitted in [10, Figure 2] to the experiments performed in [28] which are given in Table 3. Note that the parameters used here for $\Psi _A$ correspond to $\Psi _A$ Set 2 in [10] and are identical to the parameters used for $\Psi _A$ in [7]. Although the models $\Psi _A$ and $\Psi _B$ have the same isotropic part $\Psi _{\mathrm{*, iso}}$, the parameters for $\Psi _{\mathrm{*, iso}}$ are not the same.

Note that all parameters for the simple isotropic and the sophisticated anisotropic models were obtained from adjusting to uniaxial tension tests which correspond to extreme values of stress ratios of circumferential to axial stresses ranging from 0 to infinity, which are often found difficult, already for engineering materials [34]. In real arteries, however, a uniaxial stress scenario cannot be expected and rather biaxial stress scenarios appear with stress ratios of moderate intensity in between the extreme values. Therefore, in principle, it would be advantageous to also include biaxial test data, but these are in turn technically difficult to obtain for soft biological tissues and their accuracy should be considered critically, especially for experiments performed on individual layers like the media and adventitia of small arteries. Uniaxial tests may therefore be considered more reliable, but the level of information regarding the mechanical response is rather restricted compared to biaxial tests; cf., e.g., [21]. Therefore, in general, it is recommended to calibrate a model to the average of many test results including uniaxial and biaxial tests with varying load ratios and not to overaccelerate the use of isolated test results. However, here we are rather interested in a qualitatively realistic, characteristic response and thus, a perfect match of the models with the experimental data should not be overrated. Therefore, the somewhat better agreement of model $\Psi _A$ with the nonlinear experimental stress–strain response (cf. Fig. 1) should not be given too much importance.

3 The curved tube fluid–structure benchmark problem

Although the final goal is the simulation of patient-specific arteries [4], the systematic, comparable analysis of numerical schemes is enhanced by concentrating on standardized boundary value problems. Therefore, we make use of the benchmark problem introduced in [7], a curved tube with an elastic wall; the inner radius of the tube is 0.15 cm, the outer radius is 0.21 cm, the radius of the curvature is 1 cm and the length of the straight part towards the outflow is also 1 cm; see [7, Figure 1] and also our figures in Sect. 4. As a result, the in- and outflow areas are approximately 0.0707 cm$^2$ at the start of our simulations.

3.1 Mesh

We use a tetrahedral mesh with matching fluid and solid nodes at the interface. The mesh has 66,648 degrees of freedom for the fluid velocity $\textbf{u}$, 3515 d.o.f. for the fluid pressure p, 425,700 d.o.f. for the solid displacement $\textbf{d}_s$, 28,044 d.o.f. for the Lagrange multipliers $\lambda$ enforcing the balance of normal stresses across the interface, and 66,648 d.o.f. for the fluid mesh displacement $\textbf{d}_f$. In particular, we use Mesh #3 in [7, Table 6], where mesh convergence has been observed [7, Figure 21 and Figure 44] for ${\bar{F}}$ finite elements.

3.2 Boundary conditions

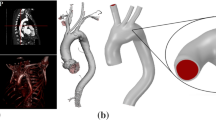
The displacement of the structure is fixed in axial direction at the faces at both ends of the tube as well as at the red nodes in Fig. 2. Combining these boundary conditions, we obtain a statically determined structure (Fig. 3).

Fig. 2

Boundary conditions for the structure: At the red nodes the displacement is fixed in y-direction, that is, $d_y = 0$. Moreover, the nodes at the inlet and outlet are fixed in axial direction. Image taken from [7] (copyright Wiley)

Fig. 3

Distribution of the von Mises stresses in the arterial wall for the anisotropic material model $\Psi _A$ at the peak inflow flow rate, that is, at time $t=0.536$ s

As the inflow boundary condition for the blood flow, we prescribe a parabolic velocity profile over the cross-section of the inlet. The flow rate then varies over time as shown in Fig. 4 (top, left). In particular, we first increase the inflow velocity until a flow rate of 3.0 cm/s is reached using a smooth cosine-shaped profile during the first 0.1 s, and then keep the flow rate fixed for another 0.1 s; we also denote this first phase of the simulation as the ramp phase. Afterwards, we employ the flow rate profile for a heartbeat in a coronary artery created in [7]. In particular, the flow rate profile has been computed based on a simplified simulation using inflow pressure data from [2] for a coronary artery; as a result of this procedure, the temporal profile is lacking the backflow to be expected in the diastolic phase of the heartbeat.

As in [7], we use an absorbing boundary condition [35] as the outflow boundary condition, with the aim of reducing wave reflections arising at the outlet of the artery. Note that these absorbing boundary conditions are based on a one-dimensional model for the fluid and a simple linear model for the structure, that is, it uses a simple relation between the outflow area A and the pressure P,

$$\begin{aligned} P=\frac{\beta }{\pi }\left( \sqrt{A}-\sqrt{A_0}\right) , \end{aligned}$$

where $A_0$ is the area at $t=0$, and $\beta$ is a parameter. In our nonlinear setting, this absorbing boundary condition will not remove reflections completely. Note that we have chosen $\beta$ as in [7], such that it corresponds to a Young modulus of 120 kPa and a Poisson ratio of 0.49. We have used these values for all numerical experiments, that is, for all material models and all parameter sets. It is clear that, for parameter sets corresponding to a significantly different stiffness of the structure, the of $\beta$ will not be suitable to remove wave reflections, and some difficulties in our simulations may be due to this effect; see Sect. 4.

4 Numerical results

In our numerical experiments, we consider the fluid–structure interaction of fluid flow in the curved tube benchmark geometry defined in [7]. For a detailed description of the FSI problem, we refer to [7] or Sect. 1. The benchmark in [7] was computed using $\Psi _A$ with the same parameters as here; see Sect. 2.2 for all material parameters. Since we deal with a rather large artery, it is sufficient to model the blood flow as a Newtonian fluid, neglecting shear-thinning effects. In particular, we employ the Navier–Stokes equations, using a constant viscosity of $3 \times 10^{-3}$ Pa s.

Fig. 4

Temporal evolution of the flow rate (left), area (middle), and pressure (right) at the inflow (top) and the outflow (bottom) for Neo-Hooke using different parameter sets, that is, for the models NH$_1$–NH$_4$. For NH$_1$ and NH$_2$, the simulation fail before the beginning of the heartbeat phase

The geometry consists of a curved and a straight section and can be seen as an idealized coronary artery; in particular, it corresponds only to the media, neglecting the intima and adventitia of the arterial wall. The tube is composed of a single material, that is, we use the nonlinear hyperelastic material models described in Sect. 2 and the corresponding parameters. The fiber angle is set to $\beta _f = 43$ degrees. As the spatial discretization, we use $P_2$–$P_1$ (Taylor–Hood) finite elements for the fluid and $P_2$ elements for the geometry problem. For the structure, we use either $P_2$ elements for the linear elastic or Neo-Hooke wall models or ${\bar{F}}$ finite elements [41, Section 45] (corresponding to a $P_2$–$P_0$–$P_0$ discretization in the linear case) for the anisotropic wall models. We solve the monolithic system containing the fluid, the solid, and the geometry, using matching nodes at the fluid–structure interface. As in [7], a convective explicit (CE) approach is used, resulting in stronger limits for the size of the time steps than a fully implicit method. We have also implemented a fully implicit scheme. Here, we are, however, interested in the influence of the material response rather than the numerics and the performance.

As the software framework, we use the LifeV software library [1], based on Trilinos [27], coupled to the Finite Element Analysis Program (FEAP 8.2); cf. [19, 25] for a description for the lightweight interface coupling both software packages. All computations discussed in this section have been carried out on the supercomputer magnitUDE at Universität of Duisburg-Essen.

Following [7, section 4.2] and as described in Sect. 3.2, we use a smooth ramp to apply an interior blood pressure of 80 mmHg to initiate the necessary prestretch of the arterial wall before the start of the heart beat. Using a smooth ramp can reduce unwanted oscillations by an order of magnitude; see, e.g., [6, section 4.2.2]. As a result from the prescribed flow rate, which reaches a maximum flow rate of approximately 8 cm/s at 5.36 s, we arrive at a Reynolds number of up to approximately 1130.

4.1 Flow rate, lumen area, and pressure at the in- and outflow

4.1.1 Neo-Hooke models NH$_1$ and NH$_2$

Our simulations show several difficulties with the Neo-Hooke parameter sets NH$_1$ and NH$_2$; see Fig. 4.

Fig. 5

Temporal evolution of the flow rate (left), area (middle), and pressure (right) at the inflow (top) and the outflow (bottom) for the different material models $\Psi _A$ (parameter set 2) [8] to $\Psi _E$ [30] and, additionally, for two Neo–Hooke (NH$_3$ and NH$_4$) parameter sets. The time interval $t=0$ s to $t=0.1$ s is the smooth ramp which introduces the prestretch, the heartbeat starts at $t=0.2$ s. We see significant differences between the $\Psi _{\mathrm{*}}$ models and the Neo–Hooke model with respect to the outflow area: for NH$_3$ and NH$_4$ the outflow area has a significantly larger amplitude during the heart beat, presumably, since the model lacks fiber stiffening. Interestingly, $\Psi _A$ (with parameter set 2) yields a significantly larger outflow area than the other $\Psi _{\mathrm{*}}$ models

First, we observe that the sets NH$_1$ and NH$_2$ result in a material behavior, which is significantly softer than the other models: for NH$_1$ and NH$_2$, already briefly after the ramp phase (which ends at $t=0.1$ s), the outflow areas are significantly larger than the maximum outflow area during the heart beat in the benchmark [7]; see Fig. 4. Second, for both data sets, the computations fail near the end of the ramp shortly after strong oscillations are visible in the outflow pressure and flow rate. It can be assumed that this is due to the wave reflections at the outflow: for NH$_1$ and NH$_2$ the absorbing boundary condition, using the parameters described in Sect. 3.2, does not work well enough. Another potential reason may be that a structural instability problem appears in those simulations. Such bifurcation phenomena in extended membrane-like but thick-walled materials have already been shown in, e.g., [24]. The analytical analysis of such problems is, however, restricted to simplifications and thus, with limited validity for the benchmark problem considered here.

However, it is already clear from the ramp phase that NH$_1$ and NH$_2$ will result in in- and outflow areas which are larger than the ones for the sophisticated models; see Fig. 4. We will therefore consider the parameter sets NH$_3$ and NH$_4$ in Sect. 4.1 for the comparison in the heart beat phase.

4.1.2 Sophisticated arterial wall models

Results for the sophisticated wall models are compared in Fig. 5. It is interesting that the in- and outflow areas are significantly larger for $\Psi _A$ than for $\Psi _B$ and $\Psi _E$. The results for $\Psi _A$, however, match those computed earlier in the benchmark [7]. Consulting the data fits in Fig. 1 (or [10, Figure 2]), we observe that the curves for $\Psi _B$ and $\Psi _E$ seem to be quite similar, whereas the curves for $\Psi _A$ have a slightly different shape: the curve for $\Psi _A$, for the circumferential direction, is steeper for large stretches than for the other models. This is especially visible for $\Delta l/l_0>0.25$. On the other hand, it is below the curves of $\Psi _B$ and $\Psi _E$ for $\Delta l/l_0 \approx 0.225$.

Considering the numerical values of the parameters (see Table 3), let us note that for $\Psi _A$ the exponent $\varepsilon _2$ is smaller than for the other two models while the multiplicative constants $c_1$ and $\varepsilon _2$ are larger.

Note that one may be tempted to compute an (average) circumferential stretch, for instance, at the outflow from the increase in area. For $\Psi _A$, the increase in area from 0.070 cm$^{2}$ to almost 0.093 cm$^{2}$, visible in Fig. 5, corresponds to an (average) circumferential stretch of only about 1.15 or an increase of 15 percent. For an adequate analysis of the stress–strain response, this value is, however, misleading since the stress (and the stretch) is far from homogeneous along the circumferential and radial direction; see Figs. 3, 9 and 11. This is to be expected since due to the nonlinear material response, a moderate change of stretch results in a strong change of stress across the thickness. The stresses in the wall are also concentrated at the interior of the wall, that is, at the interface to the fluid; see Figs. 9 and 11.

This result may also seem surprising, since the earlier quasistatic computations in [10] indicate a smaller lumen for $\Psi _A$ than for the other models. However, in [10] a higher internal blood pressure of 24 kPa ($\approx 180$ mmHg) was simulated, and a plaque was present in the lumen. Indeed, the larger lumen observed in [10] seems to be due to localized stretch near the plaque; see [10, Figures 7 to 11]; also note that the thickness of the model was only 2 mm in [10, Figures 7 to 11].

We also observe that the results in Fig. 4 are quite similar for $\Psi _B$ and $\Psi _E$ in terms of flow rate, pressure, and lumen area. However, for $\Psi _B$ small oscillations are visible during the ramp phase; see Fig. 5 for $0<t<0.2$ s and the zoom into the same data in Fig. 6. The oscillations then vanish during the heart beat. However, since the ramp phase is only used to introduce the prestretch, we still consider this a valid simulation, despite the visible oscillations.

4.1.3 Heart beat phase using the sophisticated wall models and the Neo-Hooke models NH$_3$ and NH$_4$

We have also created two parameter sets for Neo-Hooke, NH$_3$ and NH$_4$ which show a similar in- and outflow area as the $\Psi _{\mathrm{*}}$ models; see Fig. 4. The sets NH$_3$ and NH$_4$ were chosen such that they have, at the end of the ramp, a similar in- and outflow lumen area as the models $\Psi _B$ and $\Psi _E$; see Fig. 5. The set NH$_3$ is slightly softer, the set NH$_4$ is slightly stiffer. For both Neo-Hooke sets the lumen area is slightly smaller than for $\Psi _A$; see Fig. 4.

It is clear from our simulations that the amplitude of the lumen area is much larger in NH$_3$ and NH$_4$ than in all other $\Psi _{\mathrm{*}}$ models; see Fig. 5. This is, presumably, due to lack of fiber stiffening, which is present in the $\Psi _{\mathrm{*}}$ models. This is also a clear indication that high stresses are present, locally, in the simulations with the $\Psi _{\mathrm{*}}$ models.

Only relatively small differences between the models are visible in the flow rate and pressure.

Fig. 6

Zoom into the time interval [0 s, 0.1 s] for the temporal evolution of the outflow area in Fig. 5 (bottom, middle): Numerical instabilities are visible for $\Psi _B$ during the ramp phase; cf. Fig. 5 for the full plot

Fig. 7

Norm of the displacement of the arterial wall for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$ at $t=0.2$ s, that is, at the beginning of the heartbeat phase. The initial geometry of the artery without deformation is shown in red

4.2 Comparison of displacements

In Figs. 7 and 8, the displacement of the structure is depicted at $t=0.2$ s and $t=0.536$ s, respectively. Significant differences are visible in the displacement.

While differences between the two Neo-Hooke models NH$_3$ and the stiffer NH$_4$ are visible, these differences are small compared to the sophisticated models $\Psi _A$, $\Psi _B$, and $\Psi _E$. First, the displacements for the Neo-Hooke models are significantly smaller for $t=0.2$ s as well as for $t=0.536$ s. Second, the tube bends outwards for the Neo-Hooke models, whereas it bends inwards for the $\Psi _{\mathrm{*}}$ models. We see from these results that, when the Neo-Hooke material model is used with parameters which result in a similar lumen area, then the structure is significantly stiffer than in the other models. Lacking the terms for the stiffening fibers, the Neo-Hooke model shows a completely different qualitative behavior than the other models. This impact of anisotropic models compared to isotropic ones is in line with observations already made without considering FSI in simulations of straight arteries (idealized tubes or atherosclerotic arteries) under internal pressure; cf., e.g., [38].

When comparing the models $\Psi _A$, $\Psi _B$, and $\Psi _E$, it is striking that the displacement is smaller in $\Psi _A$ than in the other $\Psi _{\mathrm{*}}$ models and that the displacement is higher in the $\Psi _E$ model than in the other models. Note that in Sect. 4.1, $\Psi _A$ showed a larger lumen area than the other $\Psi _{\mathrm{*}}$ models.

Fig. 8

Norm of the displacement of the arterial wall for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$ at the peak inflow flow rate, that is, at time $t=0.536$ s. The initial geometry of the artery without deformation is shown in red

4.3 Comparison of the stresses

When comparing the stresses of the different material models and parameter sets, all $\Psi _{\mathrm{*}}$ models show a very similar stress distribution; see Fig. 9 for $t=0.2$ s and Fig. 11 for $t=0.536$ s. All models show a very strong concentration of the stresses at the lumen interface and very low stresses at the outside of the tube.

The stress distributions of the Neo-Hooke models is, however, significantly different. The stresses are less localized at the lumen interface, instead significant stresses are visible in the complete cross section of the tube. Both observations are valid at $t=0.2$ s as well as at $t=0.536$ s (Fig. 10).

Fig. 9

Visualization of the von Mises stresses for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$ at $t=0.2$ s, that is, at the beginning of the heartbeat phase

Fig. 10

Visualization of the von Mises stresses for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$at $t=0.2$ s. Here, the color scale of $\Psi _E$ is used for all plots; see Fig. 9 for the respective results with individual color scales

Fig. 11

Visualization of the von Mises stresses for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$ at the peak inflow flow rate, that is, at time $t=0.536$ s

Fig. 12

Visualization of the von Mises stresses for for $\Phi _A$, $\Phi _B$, $\Phi _E$, NH$_3$, and NH$_4$at time $t=0.536$ s. Here, the color scale of $\Psi _E$ is used for all plots; see Fig. 11 for the respective results with individual color scales

4.4 Linear elastic wall models

We have also performed simulations using a linear elastic wall model. It is clear that a good fit of a linear elastic model to the experimental data cannot be achieved since the strongly nonlinear response of the wall cannot be reproduced; cf. Fig. 1. Furthermore, if the geometrically linearized setting is considered, the solution of mechanical equilibrium equations in the undeformed configuration may not match well with the large deformations appearing in the artery. However, the aim of this analysis is to highlight the unphysical (pathological) behavior when using linear models. To avoid an analysis, where a potentially good-natured problem is considered accidentally, we have performed a large number of simulations using 15 different linear elastic parameter sets; see Fig. 13, where we also have provided $\Psi _A$ as a reference. The set LE$_n$ refers to $E = n \times 1{,}000{,}000$ dyn/cm$^2$ and $\nu =0.49$, which corresponds to a slightly compressible material (Fig. 12).

We observe in Fig. 13 that the softest parameter set (LE$_1$) is quite close to the reference model $\Psi _A$ in the time interval $0\,\text {s}<t<0.05$ s with respect to the inflow and outflow areas as well as for the inflow and outflow pressures. Of course, in this time interval less than half of the stretch in the inflow and outflow areas has occurred. However, briefly after 0.05 s, oscillations are visible and the simulation fails. Using stiffer parameter sets (LE$_2$, $\ldots$ , LE$_{14}$), the oscillations occur later, however, the inflow and outflow area as well as the pressure move further away from the reference $\Psi _A$. Only for LE$_{15}$ unphysical oscillations in the simulation are avoided.

It can be assumed that the onset of the oscillations and the subsequent failure of the simulations for LE$_1$ to LE$_{14}$ are at least partially due to our boundary conditions; see Sect. 3.2. In particular, the absorbing boundary condition may not be effective enough to remove wave reflections at the outflow for these parameter sets and the scarce boundary conditions for the structure may be prone to amplify oscillations, especially for soft wall models. Alternatively, again, a structural instability may be responsible here. In general, geometrically and physically linear problems do not show bifurcation problems. However, the FSI calculations based on the geometrically linear structural model and the normal forces acting on the actual solid–fluid interface lead to a system with non-conservative loading conditions. These forces can then be interpreted as follower loads acting on the actual solid surface. This renders the originally geometrically linear problem nonlinear and indeed, structural instability may appear. But how to address the associated analysis for this case is still an open research question.

The stiffest parameter set LE$_{15}$ avoids any visible oscillations for $0\,\text {s}<t<0.1$ s, however, the behavior in the simulation of the ramp phase is clearly too stiff if compared to the reference model $\Psi _A$: the inflow and outflow areas are significantly too small at $t=0.1$ s. However, the inflow and outflow pressures are quite close to the reference for $t=0.1$ s.

Despite the oscillations in the ramp phase, we have also computed the heart beat phase with the linear elastic models which did not fail. Here, we observe very large displacements which clearly seem unphysical; see Fig. 14 for LE$_5$ at $t=0.13$ s. From the large displacements we conclude that, during the heart beat, LE$_5$ seems to be significantly too soft, if compared to the reference. On the other hand, it is clearly visible that, during the ramp phase, it is too stiff, compared to the reference.

Fig. 13

Temporal evolution of the flow rate (left), area (middle), and pressure (right) at the inflow (top) and the outflow (bottom) for linear elasticity using different parameter sets, where LE$_1$ is exhibits the softest and LE$_1$5 the stiffest behavior

Fig. 14

Norm of the displacement of the arterial wall for LE$_5$ at 0.13 s. Large deformations due to soft material behavior. In the left plot, the initial geometry of the artery without deformation is shown in red

We can conclude that using linear elastic wall models, using our setup, we were not successful in achieving a good agreement with the nonlinear reference.

4.5 Numerical properties of the nonlinear wall models

The numerical properties of the wall models are not identical. It is interesting that, although the results in Fig. 5 are quite similar for $\Psi _B$ and $\Psi _E$, numerically, their performance is quite different.

In Fig. 15, we present the time steps used in the simulation, and in Fig. 16, we compare the Newton steps needed for each second of simulation time. In Fig. 17, we compare the number of GMRES iterations needed for each second of simulation time.

For the time stepping, we chose an initial time step of $10^{-4}\,\,\textrm{s}$ which was increased to $10^{-3}\,\,\textrm{s}$ at $0.2\,\,\textrm{s}$. However, we have observed, that for $\Psi _B$, initially, for $0<t<0.1$ s, five times smaller time steps were needed to achieve convergence; note that the time steps size has been adjusted manually until convergence could be achieved. As a consequence, also the number of Newton iterations and the number of GMRES iterations for each second of simulation time is larger for $0<t<0.1$s; see Figs. 16 and 17. However, we see that also for $t>0.1$s the computational cost remains higher for $\Psi _B$ than for all other models: in Fig. 17, $\Psi _B$ needs, on average, the largest number of GMRES iterations, which indicates worse numerical properties of the linearized systems.

We also see that the computational cost in terms of iteration numbers is significantly smaller for the Neo-Hooke models compared to $\Psi _A$, $\Psi _B$, and $\Psi _E$: for example, for $t>0.2$ s the number of GMRES iterations for each second of simulation time is smaller by almost a factor of two or more for the Neo-Hooke models.

Among the $\Psi _{\mathrm{*}}$ models, the model $\Psi _A$ needs the lowest number of GMRES iterations for each second of simulation time although the difference to $\Psi _E$ is small.

Fig. 15

Time step sizes used in the simulations. For $\Psi _B$, initially, smaller time steps are needed due to the instabilities shown in Fig. 6

Fig. 16

Newton iteration counts for each second of simulation time for the different models. Initially, for $0\,\text {s}<t<0.1$ s, significantly more Newton iterations are needed for $\Psi _B$ for each second of simulation time; this is due to smaller time step sizes as shown in Fig. 15

Fig. 17

Krylov iteration counts for each second of simulation time. Initially, for $0\,\text {s}<t<0.1$ s, significantly more GMRES iterations are needed for $\Psi _B$; this is due to smaller time step sizes as shown in Fig. 15

5 Conclusion

We have performed and analyzed monolithic fluid–structure interaction simulations in a curved tube benchmark geometry using three different sophisticated hyperelastic material models developed for arterial walls which have been successfully fitted to experimental data. These models account for the almost incompressibility of biological soft tissue as well as for the anisotropy from collagen fiber stiffening in arterial walls. We have also performed simulations using a simple Neo-Hooke model for the wall using four different parameter sets. We have found that the three sophisticated hyperelastic models showed a qualitatively similar behavior. Using the Neo-Hooke hyperelastic energy the results turned out to be different, even qualitatively. Additional simulations using the geometrically linearized setting and a linear elastic material model have shown significant numerical issues and a non-realistic qualitative and quantitative response in the considered benchmark problem. With view to the numerical performance, two of the anisotropic models from [8, 30] have shown good properties, whereas the model based on the well-known anisotropic function [29] required a significantly larger number of Newton and GMRES iterations. Apparently, a purely isochoric, anisotropic strain energy density poses a challenge with respect to the numerical computation. Summarizing, several material models which show a quite comparable stress–strain response under uniaxial tension in circumferential- and axial direction, will not automatically lead to comparable results in simulations of arterial walls. Thereby, the results show that the decision for a particular material model should be made carefully and appears not to be a black box task.

Appendices

Appendix

A monolithic algorithm for fluid–structure interaction

The benchmark problem used in this paper was introduced in [7] and is more suitable for the setting of cardiovascular FSI simulations than other established FSI benchmarks. The following subsections briefly describe the computational setting used in this paper based on [7].

1.1 A.1 Fluid–structure interaction in ALE formulation

We consider the coupling of an incompressible Newtonian fluid occupying $\Omega ^f$ and a purely elastic solid body $\Omega ^s$.

The structural problem is described by the conservation of momentum of the solid body in Lagrangian coordinates over the time interval (0, T] is

$$\begin{aligned} \rho _s \displaystyle \frac{\partial ^2 \textbf{d}_s}{\partial t^2} - \nabla \cdot \mathbf {(FS)} = 0 \quad \text{ in } \Omega ^s\,\times \,(0,T], \end{aligned}$$

(A.1)

where $\rho _s$ is the structural density, $\textbf{d}_s$ the structural displacement, and $\textbf{FS}$ are the first Piola-Kirchhoff stresses.

For an unsteady problem, the solid body $\Omega ^s$ deforms over time, resulting in a temporal parametrization $\Omega ^s_t$ with $\Omega ^s_0 = \Omega ^s$. To account for the deformation of the fluid domain, we consider the fluid problem in an Arbitrary Lagrangian Eulerian (ALE) formulation. The incompressible Navier-Stokes equations then read

$$\begin{aligned} \begin{array}{ll} \rho _f \left( \displaystyle \frac{\partial \textbf{u}}{\partial t}\biggr |_{\textbf{X}} + ((\textbf{u}-\textbf{w}) \cdot \nabla ) \textbf{u} \right) - \nabla \cdot \varvec{\sigma }_f(\textbf{u}, p) \\ \quad = 0 \text{ in } \Omega ^f_t\,\times \,(0,T], \\ \quad \nabla \cdot \textbf{u} = 0 \text{ in } \Omega ^f_t\,\times \,(0,T], \\ \end{array} \end{aligned}$$

(A.2)

where $\rho _f$ is the fluid density, $\textbf{u}$ the fluid velocity, p the pressure, and $\frac{\partial }{\partial t}\bigr |_{\textbf{X}} = \frac{\partial }{\partial t} + \textbf{w}\cdot \nabla$ the ALE derivative. Furthermore, $\varvec{\sigma }_f(\textbf{u}, p) = 2 \mu _f \varvec{\epsilon } (\textbf{u}) - p \textbf{I}$ is the Cauchy stress tensor, $\varvec{\epsilon } (\textbf{u}) = \frac{1}{2}\left( \nabla \textbf{u} + (\nabla \textbf{u})^T\right)$ is the strain rate tensor, and $\mu _f$ the dynamic viscosity. The temporal parametrization of the fluid domain $\Omega ^f_t$ is given by the ALE map

$$\begin{aligned} \begin{array}{rll} \mathcal {A}_t: &{} \Omega ^f &{} \rightarrow \Omega ^f_t \\ &{} \textbf{X} &{} \mapsto \mathcal {A}_t(\textbf{X}) = \textbf{X} + \textbf{d}_f(\textbf{X}), \end{array} \end{aligned}$$

which describes a deformation of the fluid domain. Here, $\textbf{d}_f$ is the displacement and $\textbf{w} = \frac{\partial \textbf{d}_f}{\partial t} \biggr |_{\textbf{X}}$ velocity of the fluid domain.

Then, the coupling of the fluid and solid problems Eqs. (A.1) and (A.2), respectively, is driven by suitable interface conditions. In particular, the geometric adherence of the fluid and solid domains is given by

$$\begin{aligned} \textbf{d}_f = \textbf{d}_s \quad \text{ on } \Gamma \,\times \,(0,T], \end{aligned}$$

and the coupling conditions for the velocities and the stresses are

$$\begin{aligned}&\frac{\partial \textbf{d}_s}{\partial t} = \textbf{u} \circ \mathcal {A}_t \quad \text { and} \\&(\text{ det }[\textbf{F}])^{-1}\textbf{F}^{-T} \, \varvec{\sigma }_f \, \textbf{n}_f \circ \mathcal {A}_t + (\textbf{FS})\, \textbf{n}_s = 0. \end{aligned}$$

We compute the ALE map by solving the geometry problem

$$\begin{aligned} \begin{array}{rll} -\Delta \textbf{d}_f = &{} \textbf{0} &{} \text{ in } \Omega ^f, \\ \textbf{d}_f = &{} \textbf{d}_s &{} \text{ on } \Gamma , \\ \textbf{d}_f \cdot \textbf{n}_f = &{} 0 &{} \text{ on } \partial {\Omega ^f}\backslash \Gamma . \end{array} \end{aligned}$$

1.2 A.2 Monolithic algorithm for fluid–structure interaction

After discretization in space and time, the fully coupled nonlinear FSI system reads

$$\begin{aligned}{} & {} \left( \begin{array}{lllllll} F(\textbf{u}_f^{n+1},p^{n+1},\textbf{d}_f^{n+1} ) &{} + &{} 0 &{} + &{} C_1^T \,\varvec{\lambda }^{n+1} &{} + &{} 0 \\ 0 &{} + &{} S \, (\textbf{d}_s^{n+1}) &{} + &{} C_3^T \, \varvec{\lambda }^{n+1} &{} + &{} 0 \\ C_1 \, \textbf{u}_f^{n+1} &{} + &{} \displaystyle C_2 \, \textbf{d}_s^{n+1} &{} + &{} 0 &{} + &{} 0 \\ 0 &{} + &{} C_4 \textbf{d}_s^{n+1} &{} + &{} 0 &{} + &{} H\,\textbf{d}_f^{n+1} \end{array} \right) \nonumber \\{} & {} \quad = \left( \begin{array}{l}\textbf{b}_f\\ \textbf{b}_s \\ C_2\,\textbf{d}_s^{n}\\ 0 \end{array} \right) . \end{aligned}$$

(A.3)

Here, $\varvec{\lambda }$ is the vector of Lagrange multipliers which are used to enforce the balance of normal stresses across $\Gamma$. Let us note that the fluid subproblem F and the solid subproblem S are nonlinear (unless a linear elastic wall model is used), whereas the geometry subproblem H is linear. The matrices $C_1$ and $C_2$ are used to enforce the continuity of the velocity on $\Gamma$, the transposed matrices $C_1^T$ and $C_3^T$ account for the balance of normal stresses, while $C_4$ accounts for the geometric adherence. In the case of conforming meshes and conforming discretizations at the fluid–structure interface, we have $C_1|_{\Gamma } = I|_{\Gamma }, C_3|_{\Gamma } = -I|_{\Gamma }, C_2|_{\Gamma } = 1/\Delta t \, C_3, C_4|_{\Gamma } = I|_{\Gamma }$, where $I|_{\Gamma }$ is the identity matrix defined on the interface $\Gamma$.

1.3 A.3 Linearization and parallel preconditioner

We solve the nonlinear problem Eq. (A.3) using Newton’s method. At each time step, we need to solve

$$\begin{aligned} J_{\text {CE}} (\textbf{x}_k^{n+1}) \varvec{\delta }_{k+1} = - \textbf{r} (\textbf{x}_k^{n+1}), \end{aligned}$$

(A.4)

where we k is the index for the Newton iterations, $J_{\text {CE}} (\textbf{x}_k^{n+1})$ is the Jacobi matrix, $\textbf{r} (\textbf{x}_k^{n+1})$ the residual, $\varvec{\delta }_{k+1}$ the Newton correction, and $\textbf{x}_k^{n+1}=(\textbf{u},p,\textbf{d}_s,\varvec{\lambda },\textbf{d}_f)$ is the solution vector.

The Jacobi matrix associated to the FSI problem reads

$$\begin{aligned} J_{\textrm{CE}}= \begin{pmatrix} F &{} 0 &{} C_1^T &{} D_{\textbf{d}_f}F\\ 0 &{} D_{\textbf{d}_s}S &{} C_3^T &{} 0\\ C_1 &{} C_2 &{} 0 &{} 0\\ 0 &{} C_4 &{} 0 &{} H \end{pmatrix}, \end{aligned}$$

where $D_{\textbf{d}_f}F$ denotes the shape derivatives (see, e.g., [18]) and $D_{\textbf{d}_s}S$ the linearization of the solid part.

For each k, we solve (A.4) using the Generalized Minimal Residual (GMRES) method [37], preconditioned by an approximated monolithic Dirichlet–Neumann preconditioner $P_{\textrm{DM}}$; cf. [13]. The preconditioner $P_{\textrm{DM}}$ is constructed from $J_{\textrm{CE}}$ by neglecting the coupling block $C_3^T$ and then applying a block factorization to $J_{\textrm{CE}}$,

$$\begin{aligned} P_{\textrm{DM}}= \begin{pmatrix} I &{} 0 &{} 0 &{} 0\\ 0 &{} D_{\textbf{d}_s}S &{} 0 &{} 0\\ 0 &{} 0 &{} I &{} 0\\ 0 &{} 0 &{} 0 &{} I \end{pmatrix} \begin{pmatrix} I &{} 0 &{} 0 &{} 0\\ 0 &{} I &{} 0 &{} 0\\ 0 &{} 0 &{} I &{} 0\\ 0 &{} C_4 &{} 0 &{} H \end{pmatrix} \begin{pmatrix} F &{} 0 &{} C_1^T &{} D_{\textbf{d}_f}F\\ 0 &{} I &{} 0 &{} 0\\ C_1 &{} C_2 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} I \end{pmatrix}. \end{aligned}$$

The inverse of each factor of $P_{\textrm{DM}}$ is approximated by one-level algebraic additive Schwarz preconditioners; cf. [42].