Abstract
In recent years, a lot of progress has been made in the field of material modeling with artificial neural networks (ANNs). However, the following drawbacks persist to this day: ANNs need a large amount of data for the training process. This is not realistic, if real world experiments are intended to be used as data basis. Additionally, the application of ANN material models in finite element (FE) calculations is challenging because local material instabilities can lead to divergence within the solution algorithm. In this paper, we extend the approach of constrained neural network training from [28] to elasto-plastic material behavior, modeled by an incrementally defined feedforward neural network. Purely stress and strain dependent equality and inequality constraints are introduced, including material stability, stationarity, normalization, symmetry and the prevention of energy production. In the Appendices, we provide a comprehensive framework on how to implement these constraints in a gradient based optimization algorithm. We show, that ANN material models with training enhanced by physical constraints leads to a broader capture of the material behavior that underlies the given training data. This is especially the case, if a limited amount of data is available, which is important for a practical application. Furthermore, we show that these ANN models are superior to classically trained ANNs in FE computations when it comes to convergence behavior, stability, and physical interpretation of the results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The correct description of material behavior is an important part in structural analysis. For isothermal deformable solids, phenomenological material models bridge the gap between strains describing relative motion and the corresponding stresses. Usually, a mathematical function is defined in order to relate stresses or stress rates to the current strains, their rates or other loading history dependent strain and stress quantities. These functions contain material parameters, which can be fitted to experimental data. The approach of substituting these analytical material models with artificial neural networks (ANN) is part of the research areas of solid and computational mechanics for more than three decades. This means, the analytical function is replaced with an ANN and the training process fits its internal parameters, called weights, to the given data. Since feedforward ANNs are universal function approximators [4], it is theoretically possible to use them for any material behavior, as long as a corresponding functional mapping can be defined. In 1991, the cyclic behavior of concrete was modeled with an incremental approach in [7]. Thereupon, a lot of progress has been made in the 1990 s and early 2000 s, for example, the implementation of an ANN material model into an FE code in [17], the introduction of an analytical tangent in [11] and the application of additional history variables for hysteretic behavior in [34].
From the point of view of elasto-plastic material behavior, these and other early works are mostly limited to the simulation of loading paths similar to the ones that have been trained, to monotonic loading without unloading or to two-dimensional applications. This may be due to a lack of computational resources, which could explain the gap of publications in the years that followed. However, in the very recent years, material modeling with ANNs experienced a renaissance. The following subjective overview does not aim to be exhaustive: A specific input vector definition containing plastic dissipation is applied in [35]. Proper orthogonal decomposition is used to transform the given data efficiently in [12]. Not a stress quantity, but the material tangent decomposition are approximated with ANNs in [33] and compared to other approaches. In [18], deep material networks where developed as an efficient surrogate model for numerical homogenization, including plasticity. For path dependent material behavior, recurrent neural networks are also gaining interest. A comparison to feedforward ANNs can be found in [27] and [9]. An approximation of the yield surface is done in [20].
Despite these successes, common ANN disadvantages still remain a challenge until today. In order to achieve a more or less generalized ANN material model for a huge range of possible loading paths, the training process needs an enormous amount of data. From our experience, this is especially the case for recurrent neural networks. Furthermore, the ANN learns physical properties, e.g., objectivity or material stability, only indirectly from the given data. This and the high nonlinearity of the ANN mapping function lead to inevitable numerical instabilities when it comes to the application in FE simulations. This is especially the case when a limited amount of data is available. The consideration of physical properties in ANN material models is therefore very important and has been done in several ways. In [1], so called hints are introduced, to incorporate a priori known information in the training process in order to learn an unknown function reliably. Lagrange multipliers are investigated in [21]. The authors in [6] enforced a symmetric material tangent by creating special network structures with dependent parameters and setting specific weights to zero. Furthermore, the incorporation of physics in ANN material modeling has received a lot of attention in the last years. For example, in [14], input convex neural networks are used, leading to ANN material models fulfilling the polyconvexity condition exactly. In [19], thermodynamics-based ANNs are introduced by defining the energy- and dissipation potentials as additional outputs and calculating new stresses and history variable states as their gradient. Also in [2] convex neural networks are used to fulfill the stability condition, additionally to physically motivated constraints for normalization, which are added to the data loss function. The latter has also been done a bit earlier in [28], where constraint optimization techniques were used to introduce arbitrary physical information into the training process in order to model hyperelastic materials with ANN. Based on only 121 strain–stress data points extracted from experiments, it was possible to train ANNs stable enough to be applied in challenging three-dimensional FE simulations.
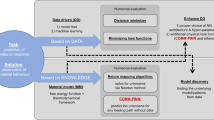
In this paper, the concept of constrained neural network training from [28] is extended and applied to small-strain plasticity. Equality and inequality constraints are introduced, considering material stability, stationarity, normalization, the prevention of energy production and symmetry. The disadvantages mentioned above, e.g., instabilities, are weakened down to a point, where the ANN material concept is feasible to use. This is shown for the approximation of yield surfaces, considering isotropic hardening behavior, and within FE simulations in plain stress and three-dimensional conditions. The highlights can be summarized as follows:
-
Enforcement of equality and inequality constraints during ANN training,
-
Introduction of a practical sampling strategy for the corresponding constraint samples,
-
Definition of purely strain and stress based constraints for small-strain plasticity,
-
Studies with respect to the physical interpretation of the ANN material model,
-
Application to two- and three-dimensional FE simulations,
-
Overview on how to implement the constraints into gradient based ANN training.
The paper is organized as follows. In Sect. 2 the incremental plasticity model with feedforward neural networks is recapped. Sect. 3 deals with the treatment of equality and inequality constraints during ANN training and the definition of specific physical constraints for small-strain plasticity. The implementation of the ANN material model into an FE framework, including the treatment of history variables, is shown in Sect. 4. The method is applied to three numerical examples in Sect. 5. The Appendices A-F provide the equations for an efficient implementation of the introduced constraints within a gradient based training strategy.
2 ANN model for rate-independent plasticity
A feedforward neural network (ANN) is a function
with the \(n_i\)- dimensional input vector \(\mathbf{{x}}\) and the \(n_o\)- dimensional output vector \(\mathbf{{z}}\). The free parameters, called weights, are collected in the \(n_w\)- dimensional vector \(\mathbf{{w}}\).
2.1 Overview of ANN mapping and training
All calculations in this paper are done with a fully connected feedforward ANN or multilayer perceptron (MLP). Its mapping algorithm (1) is described in Appendix A. Due to its differentiability, the Jacobian matrix
can be calculated analytically, which is shown in Appendix B. The weights are tuned during the training process, based on a set of P samples
with input vectors \(\mathbf{{x}}\) and target vectors \(\mathbf{{t}}(\mathbf{{x}})\). The goal of the training process is to determine a suitable set of weights \(\hat{\mathbf{{w}}}\), such that the ANN provides a good approximation
of their input and output behavior and also a good generalization when interpolating. By defining the error
considering deviation from the training data in a mean square sense, the determination of the weights \(\hat{\mathbf{{w}}}\) can be defined as the nonlinear optimization problem
There are lots of first and second order methods known for solving (6) in the literature, see [8] for an overview. In our studies, a Quasi Newton method with a Wolfe condition line search strategy [30, 31] is used. At the beginning of the training process, the weights are initialized as uniform random numbers between -1 and 1. In each epoch, considering all training samples, the weights are updated with the help of the gradient of the error function
which can be calculated via backpropagation [23, 29]. This is shown in Appendix C. The training process is terminated after a fixed number of epochs or with an early stopping strategy [8]. In practical applications, one is often satisfied with a solution \(E(\hat{\mathbf{{w}}})>E(\mathbf{{w}}_{\text {min}})\), which leads to a sufficient approximation. This depends on defined tolerances.
2.2 ANN material formulation for plasticity
We limit the following sections to rate-independent small-strain plasticity. The work-consistent Voigt notations of the infinitesimal strain tensor \({\varvec{\varepsilon }}\) and the Cauchy stress tensor \({\varvec{\sigma }}\) are chosen as strain and stress measures. They are
in the three-dimensional case, with \(n_s=6\) strain and stress variables, respectively. They reduce to \(n_s=3\) in a plain stress condition and in one dimension \(n_s\) is 1. To approximate material behavior with feedforward ANNs, the input and output vectors must be defined such that \(\mathbf{{z}}(\mathbf{{x}})\) is a function. For example: Cauchy elastic materials can be formulated with the strains as the only input variables and the stresses as output variables. However, in the case of plasticity, this is not possible, because the stress–strain behavior is path-dependent. This issue is illustrated in Fig. 1 on the rights side. Within this paper, the ANN input and output vectors are in the general case defined as
This is also illustrated in Fig. 1 for the one-dimensional case with linear hardening. The starting point for each incremental step is an equilibrium state defined by the \(n_s\) strains \({\varvec{\varepsilon }}\), the \(n_s\) stresses \({\varvec{\sigma }}\) and \(n_h\) additional, strain and stress dependent history variables \(\mathbf{{h}}\). They are required for hardening behavior and can be interpreted as additional internal variables. They have to be chosen by the user and have a significant impact on the ANNs ability to learn specific material behavior, e.g., several hardening phenomena. For unknown material behavior, this can be achieved by trial-and-error or more sophisticated pruning algorithms, which select important input variables, while deleting unnecessary ones. In the context of this paper, we use only one additional scalar history variable, if it is required for isotropic hardening. For example, in the following sections we use the total work done up to the current equilibrium state as additional history variable. However, depending on the desired material behavior, multiple variables can also be defined. It should be noted, that there is no single perfect choice for the history variables, which is discussed in the footnote of Sect. 2.4. Furthermore, additional parameters \(\mathbf{{p}}\), which are not directly related to strain or stress quantities, can be considered as part of the input vector. These could be, for example in the case of concrete, the water-cement value, the time between production and testing of the specimen or the porosity of the material. In the following, they are considered independent of the stresses and strains. They should not be confused with classical material parameters of analytical material models, like Young’s modulus. To summarize, the input vector contains \(n_i = 3n_s+n_h+n_p\) variables. Depending on the specific application, several components of the input vector can be omitted. For example: linear elastic ideal plastic solids need only the strain increments and the stresses as input variables.
The number of output variables is the number of stress variables \(n_o=n_s\). Given a strain increment \(\varDelta {\varvec{\varepsilon }}\), the ANN material model calculates the corresponding stress increment \(\varDelta {\varvec{\sigma }}\). Different strain increments lead to different new equilibrium states. With the new strains and stresses \({\varvec{\varepsilon }}+ \varDelta {\varvec{\varepsilon }}\) and \({\varvec{\sigma }}+ \varDelta {\varvec{\sigma }}\), the history variables can be updated afterwards. There are also other options to define the input and output vectors, see for example [12, 34].
The material tangent
can be calculated with the forward pass of Appendix B by extracting the corresponding partial derivatives of the whole ANN Jacobian.
2.3 Incremental data sampling
The available data must be prepared and transformed, depending on the ANN input and output vector definitions. Within this paper, the data basis is always made of ordered paths
consisting of N strain–stress pairs each. The starting point \(({\varvec{\varepsilon }}_0,{\varvec{\sigma }}_0)\) is typically \((\mathbf{{0}},\mathbf{{0}})\), but this is not obligatory. These paths could be gathered by experiments, numerical homogenization or, as in this paper, by analytical benchmark material models. It is important to mention, that all further calculations are based on pure strain and stress information, which can be obtained by real experiments. Other formulations, for example based on plastic strains or plastic potential functions, ease the treatment of plasticity with ANNs, but the application to real data is at least questionable, because it is often not possible to split the stress and strain data in elastic and plastic parts.
2.3.1 Transformation to incremental vectors
In order to transform the given paths (11) to data samples for the ANN training, the input and output vector definitions (9) must be used. First, if history variables \(\mathbf{{h}}\) are considered, they must be calculated for each path and therein for each strain–stress pair incrementally, depending on the specific definition. For each path, starting typically with \(\mathbf{{h}}_0 = \mathbf{{0}}\), the updating formula can be of the following form
leading to the extended paths
which now include the history variables. The additional parameters \(\mathbf{{p}}\) are assumed to be constant within each path. The increments \(\varDelta {\varvec{\varepsilon }}\) and \(\varDelta {\varvec{\sigma }}\) can be obtained by subtracting strain–stress pairs from each other, keeping in mind the right order. Eventually, this leads to ANN data samples with the input and output vectors
The index delay \(\varDelta n\) must be greater or equal to 0, in order to maintain the temporal order. Often, \(\varDelta n=1\) is used and increments are defined only with two consecutive data pairs \(({\varvec{\varepsilon }}_n,{\varvec{\sigma }}_n, \mathbf{{h}}_n)\) and \(({\varvec{\varepsilon }}_{n-1},{\varvec{\sigma }}_{n-1}, \mathbf{{h}}_{n-1})\). However, numerical experience shows, that a set of delays, for example \(\varDelta n\in \{0,1,2,3\}\), leads to better training results. If a delay \(\varDelta n > 1\) is used, one must take care of changes in loading direction. This is shown in Fig. 2. Incremental samples can only be defined safely within single loading directions. Giving a loading direction with M strain–stress pairs, for a set of \(n_n\) index delays \(\varDelta n\), the corresponding number of ANN input samples is
For the exemplary path in Fig. 2 with two loading directions and \(\varDelta n\in \{0,1,2,3\}\), the total number of possible ANN training samples is 48. Double samples can be deleted afterwards. One advantage of broadly distributed \(\varDelta n\) is the higher \(\varDelta {\varvec{\varepsilon }}\)-range covered, which is useful during training and in applications of the ANN model within FE calculations.
2.4 Example: 1D plasticity with a poor data basis
The given ANN notation, sampling strategy and application to inelastic material behavior is demonstrated based on a one-dimensional linear elastic–plastic material with linear isotropic hardening.
2.4.1 ANN material definition and topology
In order to represent elasto-plastic behavior with isotropic hardening, a reduced ANN mapping is defined as
For this example, the strain state can be neglected as input variable, it would be useful for kinematic hardening. Further non-strain input variables \(\mathbf{{p}}\) are not considered. To capture the effect of isotropic hardening, the additional history variable is defined as the total work up to the current stateFootnote 1
The ANN from Appendix A is used with topology [3-10-10-1] resulting in 161 weights. In an a priori calculation, considering multiple loading paths and a huge amount of data, this topology was determined to be suitable for representing plasticity with linear isotropic hardening for one dimension. This is important to isolate the effect of a small amount of data from a possible effect of not enough weights.
2.4.2 Training data: one cyclic strain–stress path
The training data is gathered from an analytical material model. The material parameters are the Young’s modulus \(C = 100\), the initial yield stress \(Y_0 = 0.3\) and the hardening modulus \(C_p = 10\). Units are omitted. Starting from an equilibrium state with current strain \(\varepsilon _n\), stress \(\sigma _n\), plastic strain \(\varepsilon ^p_n\) and hardening variable \(\alpha _n\) and a given new strain state \(\varepsilon _{n+1}\), the new stress state \(\sigma _{n+1}\) and the internal variables \(\varepsilon ^p_{n+1}\) and \(\alpha _{n+1}\) can be calculated with a simple radial return algorithm, see Algorithm 1. More background information can be found in [24].

A purely strain controlled calculation does not need the material tangent \(C_T\); stress controlled unloading does. One single training path is generated, including four loading directions: Starting from \((\varepsilon _0,\sigma _0)=(0,0)\), one hysteresis is performed by a strain controlled loading in 20 steps to \(\epsilon =0.01\), then to \(\epsilon =-0.01\) and back to \(\epsilon =0.01\) again, before a final stress controlled unloading to \(\sigma = 0\) is applied. This can also be seen in Fig. 3 on the left. The resulting path contains \(N=81\) strain–stress pairs \((\varepsilon _n,\sigma _n)\). In order to rewrite the given strain–stress paths into ANN training samples, the history variable must be calculated incrementally, see Sect. 2.3.1. Starting from \(h^E_0=0\), the discrete history value update is
when utilizing the trapezoidal rule. The extended cyclic path \(\{(\varepsilon _n,\sigma _n,h_n^E)\}_{n=0}^N\) consists of four loading directions to calculate incremental samples from. Each loading direction contains \(M=20+1\) samples. With an index delay set of \(\varDelta n\in \{0,1,2\}\), this leads with Eq. (15) to \(P = 240\) data samples in total. Please note, that no information about the used material model is required to evaluate the internal variable given by Eq. (18), which also allows one to use it in case of pure data-driven approaches, i.e., when stress and strain data series from experiments are used.
2.4.3 Training process and test scenario
ANN performance after pure data training of example of Sect. 2.4: from 15 training runs, all ANNs [3-10-10-1] are able to reproduce the training path (left) but are not able to predict reliably the correct stress response to an unknown loading scenario (right)
All 240 data samples are used for the training process, which is stopped after 10 000 epochs. We define another loading process with consecutive loading and unloading steps in the tension domain as a test scenario, which is depicted in Fig. 3 on the right. We decided to consider only the tension range \(\varepsilon > 0\) for the test scenario, because no initial loading data for the compression range is available in the training process. ANN results of a pure compression test would therefore not be reliable – with or without constraints. The weights leading to the minimum root mean squared error (RMSE) between the ANN and the reference solution of the testing scenario are saved, which is equivalent to an early stopping strategy. Due to the random weights initialization, the training process is inherently stochastic. Therefore, 15 training runs, with the same data and topology, but different weight initializations, are done in order to get an understanding about the reliability of the ANN approximation.
2.4.4 Results and discussion
All of the 15 trained ANNs are able to predict the given training path reliably. Considering the test path scenario, the best (\(RMSE=0.057\)) and the worst (\(RMSE=0.276\)) ANN realizations of all 15 training runs are given in Fig. 3. The average RMSE is 0.131. Although some realizations achieve a very good approximation, there is a strong scatter between the individual results.
The information from only one hysteresis is obviously not enough to represent the material behavior under arbitrary loading conditions successfully and reliably, meaning for every training run. This problem occurs especially when training ANNs with real experimental data. In general it is not possible to gather these data under arbitrary strain and stress combinations and in any quantity. As can be seen in Fig. 3 on the right, the ANN material model can lack physical properties and be unstable, even as a one-dimensional material model. The following section introduces constraints for regularizing the training process, leading to better approximations in regions not sampled appropriately.
3 Enforcing constraints for rate-independent plasticity
Every material model should meet specific physical principles, which depend on the desired material behavior. In theory, for an infinite amount of data and weights, an ANN should learn these characteristics implicitly from the given data, without defining them explicitly. In practice, especially experimental data can be scarce, limited in the strain and stress information and noisy. Depending on the seriousness of these issues, the ANN learns the physical properties only approximately, not at all or fails entirely to learn a reasonable material behavior. Enforcing constraints during the training process can solve this issue and can lead consequently to more stable numerical calculations. In [28], the concept of constrained neural network training is described for arbitrary equality constraints and is applied to hyperelastic material modeling. The current section extends this approach to inequality constraints and defines physical restrictions for rate-independent plasticity. The introduced constraints are physically motivated, only based on strain and stress information and do not require the adherence to classical material models.
3.1 Enforcing constraints via error term extension
In general, the optimization problem (6) can be extended by \(n_{eq}\) equality and \(n_{ie}\) inequality constraints, leading to the following constrained optimization problem
where ’s.t.’ means ’subjected to’. These constraints restrict the solution space for the input variables \(\mathbf{{w}}\). An introductory example can be found in [28]. In the case of differentiable error and constraint functions, a suitable strategy to solve problem (19) is an appropriate extension to the objective function, i.e., the data error function
This leads to the unconstrained optimization problem
which has the same solution and is therefore equivalent to the initially constrained optimization problem (19). For more information, see [13]. This unconstrained minimization problem can be solved by the same optimization algorithms as the classical ANN training. Accordingly, the calculation of the corresponding gradient
is needed. These gradients depend on the method defining \({\bar{E}}\) and the specific constraints, which are described in detail in the following sections.
3.1.1 The classical penalty method
In this paper, the error term extension \({\bar{E}}\) is always formulated with the classical penalty method [22]. For the equality constraints \(h_i(\mathbf{{w}})\) from problem (19), the penalty function is defined as
The penalty factor \(\upepsilon >0\) controls the relative importance compared to the data error E. It has to be chosen by the user. Mathematically, the constraints are only fulfilled exactly for \(\upepsilon \rightarrow \infty \). For example, the exact or L1-penalty method [22] reaches exactness mathematically for a finite penalty factor. However, this is not necessarily an advantage in the case of ANN training. A comparison between these two methods and a discussion about exactness is given in [28] and the references therein. The corresponding penalty error gradient needed for the training process is
with the constraint gradient terms \(\nabla h_i(\mathbf{{w}})\), which depend on the specific constraints defined. In the case of inequality constraints of problem (19), the penalty function can be formulated as
If the constraint is active with \(g_j < 0\), i.e., needs to be penalized, the summand simplifies to \(g_j^2\) as in the equality case of Eq. (23). If it is inactive, the summand is zero. This motivates an active set strategy, see for example [13], which is shown in the following.
3.1.2 Penalty term approximation with constraint samples
In general, especially physically motivated constraint functions \(h_i\) and \(g_j\) cannot be defined directly with respect to the weights \(\mathbf{{w}}\). They may depend for example on ANN inputs \(\mathbf{{x}}\), outputs \(\mathbf{{z}}\) or its partial derivatives. For example, in [28] the material tangent symmetry is formulated with the equivalence of partial derivative pairs. These kind of constraints cannot be transformed into a term solely depending on the weights and need therefore further treatment.
Considering only a single equality constraint \(h(\mathbf{{w}})\), the corresponding penalty error term (23) is approximated by means of a set of constraint samples
which leads to
The quality of this approximation improves with the number of constraint samples \(P^C\) and approaches a limit. This convergence behavior is demonstrated and investigated in [28].Footnote 2 In contrast to the data samples in definition (3), no data target values are required, but only some synthetic samples of the ANN inputs. Thus, in case of data-driven ANN material modeling, no extra experimental data beyond the original data set is required and in case of ANN-based surrogate modeling no extra computational (e.g. finite element) simulations are needed to consider the physical constraints.
Now, considering a single inequality constraint \(g(\mathbf{{w}})\), its approximation can be written as
By defining an active set
with all indices of samples that violate the constraint, the error term approximation can be rewritten to
Thus, considering inequality constraints compared to equality constraints only requires a prior calculation of all data points and thus a creation of the active set before the error value and its gradient can be calculated in the same way as for equality constraints. It should be noted, that the denominator in the prefactor contains the number of all constraint samples \(P^C\) and not only the active ones.
At this point it should be explicitly noted again that the constraint samples \(\mathbf{{x}}^C\) and the data samples \(\mathbf{{x}}\) are totally independent from each other. The constraint samples have to be defined in order to incorporate arbitrary constraints, containing ANN input, output and derivative information, into the gradient-based training process. However, they can, but do not have to be connected to the existing data samples.
3.2 Sampling strategy for constraint samples
In order to enforce constraints with the extended error function strategy, the constraint samples \(\mathbf{{x}}^C\) must be defined to approximate the penalty terms in Eqs. (27) and (30). It is advantageous to generate arbitrary constraint samples, which are not part of the training set, i.e., the data samples. This is possible, because the constraint error terms depend only on the sample input vectors \(\mathbf{{x}}\) and not on some data target values \(\mathbf{{t}}\). In fact, if only the data samples are used, the huge potential of the proposed method is not exploited. A reasonable sampling strategy for rate-independent plasticity is given in the following section.
3.2.1 Convex hull as training space
The incremental training samples are calculated from given strain–stress paths, as shown in Sect. 2.3. The resulting space that these incremental data points occupy is not rectangular, nor are the data points evenly distributed in it. This strongly depends on the paths used for sampling and the ANN input and output vector definition. Usually, the resulting input data \(\mathbf{{x}}\) is sparsely and not evenly distributed in a typically non-convex and high-dimensional subspace of \({\mathbb {R}}^{n_i}\). Theoretically, the constraint samples could be generated in the whole vector space \({\mathbb {R}}^{n_i}\). However, from a numerical point of view, it is reasonable to restrict this space close to the given data samples. The ANN should not be used outside the training space anyway. In the examples of this paper, it is always ensured that the ANN is not used outside of the training data. Therefore, the definition of the corresponding training space \(\varOmega \subset {\mathbb {R}}^{n_i}\) determines the sampling space for the constraint samples \(\mathbf{{x}}^C\). A simple and naive approach would be to define the training space as the smallest hyperrectangle containing all training samples. However, in higher dimensions, this leads to most of the space lying outside of the physically reasonable domain. Therefore, as a more practical approach, we define the training space \(\varOmega \) as the convex hull of all given training samples. The convex hull is the smallest possible convex set, which includes the given training samples. This is illustrated in Fig. 4 for two input variables.
3.2.2 Random sampling inside the convex hull
We aim for a strategy to randomly generate \(P^C\) samples inside the training space \(\varOmega \), i.e., the convex hull of all data sample input vectors \(\mathbf{{x}}\). A straightforward method would be to generate random points inside a bounding hyperrectangle of \(\varOmega \) and delete all points, which do not lie inside of \(\varOmega \) afterwards. It turns out, that testing whether a point lies inside a convex set or not gets very time-consuming in higher dimensions. Therefore, we propose a different strategy. We utilize a property of convex sets: if two points lie inside the convex set, then every new point on a straight line between them automatically lies inside of \(\varOmega \) as well. This is illustrated in Fig. 4. By randomly choosing two input vectors \(\mathbf{{x}}_{(1)}\) and \(\mathbf{{x}}_{(2)}\) from the training sample set (3) and a uniformly distributed random number \(\theta \) between 0 and 1, a constraint sample
can be generated, which lies inside \(\varOmega \) per definition. All constraint samples for the symmetry constraint, the stability constraint and the energy dissipation constraint are generated with this method. These constraints are introduced in Sect. 3.3.
Scatter plot of two-dimensional training samples and corresponding training space \(\varOmega \) as their convex hull, with boundary \(\partial \varOmega \). A constraint sample \(\mathbf{{x}}^C\) can be sampled on a straight line between two samples \(\mathbf{{x}}_{(1)}\) and \(\mathbf{{x}}_{(2)}\)
3.2.3 Random sampling of zero-increment samples
Some constraints do not need to be fulfilled inside the whole training space \(\varOmega \), but on a subset defined by zero-valued strain increments, leading to
Thus, the calculation of new samples with Eq. (31) needs a slight modification. After the generation of the constraint sample, just set \(\varDelta {\varvec{\varepsilon }}\) to \(\mathbf{{0}}\). This additional step is needed for the normalization constraint and the stationarity constraint.
3.3 Constraints for rate-independent plasticity
Five different constraints for rate-independent plasticity are introduced in this section. They are physically motivated, depend only on strains and stresses and do not need elements of classical material formulations, like distinct loading and unloading cases or plastic strains. The following constraints are given in physical space and the corresponding penalty term is defined. Please note, that not all constraints must be considered simultaneously and it is also possible to weight different constraints according to their importance within the ANN material modeling process. In the Appendices C - F, the transformation to the training space, normalizationFootnote 3 for better training performance and the calculation of the corresponding gradient is shown for a fully connected feedforward ANN.
3.3.1 Incremental normalization
As normalization condition, we define that zero-valued strain increments must lead to zero-valued stress increments
This excludes for example relaxation, which would be expected for viscous material behavior. This constraint must only be enforced inside the subset \(\mathbf{{x}}^0\in \varOmega ^0\), with \(\varDelta {\varvec{\varepsilon }}=\mathbf{{0}}\), see definition (32). From an implementation point of view, this constraint can be interpreted as additional artificial data samples with target values \(\mathbf{{t}}_{(k)}^0\equiv \mathbf{{0}}\). Therefore, the penalty error term
can be defined analogously to the data error term. In Appendix C its transformation and the calculation of the corresponding gradient \(d{\bar{E}}^{0}/d\mathbf{{w}}\) is shown. It should be noted, that the constraint target values \(t_{j(k)}^0=0\) do transform to non-zero values, considering the transformation given in Eq. (69). Additional normalization is not needed in this case. The generation of an arbitrary number of constraint samples \(\mathbf{{x}}^0\) is described in Sect. 3.2.3.
3.3.2 Stationarity of the normalization condition
The normalization condition of Sect. 3.3.1 must not change with a variation of the initial equilibrium state (\({\varvec{\varepsilon }},{\varvec{\sigma }},\mathbf{{h}}\)) or material parameters \(\mathbf{{p}}\). This means, while changing the other input variables, the stress increment value must remain zero. Therefore, the partial derivatives of the ANN output with respect to these inputs vanish
This constraint is also defined on the subset \(\mathbf{{x}}^0\in \varOmega ^0\), with \(\varDelta {\varvec{\varepsilon }}=\mathbf{{0}}\), see definition (32). If the strain increments are the first \(n_s\) input variables, the physical penalty error, including all possible partial derivatives of (35), writes
All together, there are \((n_i-n_s)\cdot n_s\) constraint terms for each constraint sample \(\mathbf{{x}}_{(k)}^0\). For example, in a plain stress state with \(n_s=3\) and without additional history variables \(n_h=0\) and additional parameters \(n_p=0\), this leads already to 18 additional terms per sample. The generation of an arbitrary number of constraint samples \(\mathbf{{x}}^0\) is described in Sect. 3.2.3. Transformation to the training space, normalization for better training convergence and calculation of the corresponding gradient \(d{\bar{E}}^{0S}/d\mathbf{{w}}\) is given in Appendix D.
3.3.3 Tangent symmetry: maximum plastic dissipation
In classical elasto-plasticity, see for example [24], a distinction is made between non-associated and associated flow rules. The latter are calculated by gradients of the convex yield surface, which acts as a plastic potential. This can also be derived from the principle of maximum plastic dissipation, meaning that the physically correct stress state is the one, which maximizes the plastic dissipation on the given plastic strain rate. Within this framework, due to the potential character, this is equivalent to the material tangent having major symmetries and eventually to its Voigt notation being symmetric. In the 3D-case, this is
This motivates the enforcement of the material tangent symmetry, although no plastic strains are defined directly. Without the definition of plastic strains, a direct mathematical connection to the principle of maximum plastic dissipation or another physical principle remains to be done. If the strain- and stress increments are the first \(n_s\) input and output variables, the physical penalty error function is
In a plain stress condition, the penalty function contains three derivative pairs per constraint sample \(\mathbf{{x}}^C\), while 15 pairs are needed for 3D materials. Transformation to the training space, normalization for better training convergence and calculation of the corresponding gradient \(d{\bar{E}}^{D}/d\mathbf{{w}}\) is given in Appendix D.
3.3.4 Material stability
A material is considered stable, if \(d{\varvec{\sigma }}\cdot d{\varvec{\varepsilon }}\ge 0\) holds for all strain and stress states and infinitesimal strain and stress differentials. Materials which exhibit a damage behavior do not fulfill this condition. Transferring this condition to the finite steps of the ANN material model, the inequality constraint reads
This must be valid for all equilibrium states, material parameters and strain increments. Therefore it is enforced inside the whole training space \(\varOmega \). The corresponding physical penalty error term reads
if the strain and stress increments are the first \(n_s\) input and output variables, respectively. As a reminder: the error is only defined on the active set \({\mathbb {I}}_a\) of all samples \(\mathbf{{x}}^C\), which do not fulfill the inequality (39). Therefore, in order to evaluate this error term and the corresponding gradient, the active set has to be calculated a priori. Transformation to the training space, normalization for better training convergence and calculation of the corresponding gradient \(d{\bar{E}}^{St}/d\mathbf{{w}}\) is given in Appendix E.
3.3.5 No energy production in a direct reversal
When taking two consecutive strain steps with an equal amount but different signs, energy production is not allowed. This is illustrated in Fig. 5 for a one-dimensional example. Starting from an equilibrium point \([\varepsilon ,\sigma ,h]\) going one step \(+\varDelta \varepsilon \) forward to \([\varepsilon ^I,\sigma ^I,h^I]\) and directly back to \([\varepsilon ,\sigma ^{II},h^{II}]\), the energy loss
must be greater or equal to zero. In the equality case, the material would be elastic.Footnote 4 The generalization to \(n_s\) strain- or stress variables is the inequality constraint
where the \({\varvec{\sigma }}^I\)-state cancels out. This constraint can be enforced inside the whole training space. An active set \({\mathbb {I}}_a\) must be calculated in advance to determine the constraint samples, which are part of the error function. The uniqueness of this constraint is, that two consecutive ANN evaluations are part of the error term. The stress of the second step
depends on the ANN stress increment of the first step
and the second step
which again depends on the previous step \(\varDelta {\varvec{\sigma }}^{I}\) via its input vector. Therefore, two ANN forward passes with matching input vectors have to be calculated in order to build the penalty error term
Furthermore, the calculation of the gradient needs to take into account the dependencies of the second stress increment from the first, by applying the chain rule. This includes the stresses and also the history variables. Due to the uniqueness of this constraint, Appendix F derives the corresponding gradient \(d{\bar{E}}^{E}/d\mathbf{{w}}\) exclusively for this case and for the input vector definition used within this paper.
3.4 Changes due to different input and output definitions
In this paper, the input and output vector definitions (9) are used. Of course, these are not the only ones possible. For example, in [34], the input vector does not contain the strain increment and the previous strain state, but the current and previous strain states \({\varvec{\varepsilon }}_{n+1}\) and \({\varvec{\varepsilon }}_n\) directly. The output vector is the current stress \({\varvec{\sigma }}_{n+1}\) instead of the corresponding increment. The overall information passed to the ANN is equivalent, only provided in a different way. The constraints of Sec. 3.3 must be transformed accordingly to match the desired input and output vector definitions. For example: with the input and output vector definitions from [34], the normalization constraint (33) of Sect. 3.3.1 would transform to
with \(\varDelta {\varvec{\varepsilon }}={\varvec{\varepsilon }}_{n+1}-{\varvec{\varepsilon }}_n\) in this context. Furthermore, the terms for the stationarity constraint of Sect. 3.3.2 would transform to
with \(\mathbf{{I}}\) being the identity matrix. In conclusion: the physical constraints are valid for different input and output definitions, but they must be redefined properly. The backpropagation algorithms of Appendices C, D and E provide all necessary information, also for different input and output vector definitions.
3.5 Comparison to other approaches considering physics for ANN material modeling
As written in Sect. 1, there has been made a lot of effort in the last years in order to incorporate physical information into the subject of ANN material modeling. Most of these approaches, like the TANNs of [19], or the input convex neural networks from, e.g., [2] and [14] utilize specialized ANN architectures. For example, the latter define the stresses not as output, but as partial derivatives of the neuron in the last layer with respect to the inputs, i.e., the strains. With additional restrictions to the weights and the activation functions, it is assured that the output of this last neuron serves as a convex potential, leading to the material model being stable and energy conserving, in the case of hyperelastic material modeling. In all of these approaches, the physical restrictions are fulfilled exactly, not only in the training domain, but for every input vector.
This is in contrast to our approach, where we weakly enforce the constraints with a penalty function. Additionally, the penalty parameter has to be chosen. In [28], we tested an alternative, exact penalty approach, but the results were similar. In our opinion, the classical penalty function is a good compromise between efficient implementation and exactness through the choice of the penalty factor. Furthermore, the constraint samples have to be generated in order to define these penalty terms. By defining the corresponding sample space as for example the convex hull of the training data, we limit the domain in which the constraints are enforced. However, from our perspective, this is not much of a drawback, because the ANN material model should not be used outside of the training domain in the first place.
Nevertheless, it is because of these drawbacks, that, if possible, architecture-based physical enhancement should always be considered. However, the advantage of our method is the flexibility to define arbitrary physical constraints and the easy implementation in combination with the classical ANN architecture. Of course, both methods can be combined as well, leading to some constraints being enforced exactly through the specific architecture and others only enforced weakly.
3.6 Introductory example: 1D plasticity with constraints
In order to show the influence and benefits of the constraints, the introductory example with the poor data basis of Sect. 2.4 is utilized, while the training data and ANN definitions remain the same. Additionally to the data error containing the \(P=240\) samples, the penalty error terms from the introduced physical constraints are minimized as well.
3.6.1 Constraints and constraint samples
The symmetry constraint of Sect. 3.3.3 cannot be applied for a one-dimensional material model. The normalization, stability and energy constraints are used with a penalty factor \(\upepsilon = 10^4\). For the stationarity constraint \(\upepsilon = 10^2\) holds. This constraint is very restrictive and needs usually a careful choice of the penalty factor. As investigated in [28], scarce data needs a higher penalty factor. The limit from which the choice of the penalty factor affects the training process negatively is rather high. Penalty factors, which are too low, have no negative impact, but also no positive. The number of constraint samples for the normalization and stationarity constraint is \(P^C=100\). It is lower than the \(P^C=1\,000\) samples for the stability and energy dissipation constraints. This is reasonable because the space for the latter ones is the whole convex hull \(\varOmega \), whereas the other ones are only sampled on the subset with \(\varDelta \varepsilon = 0\). The 1 000 samples are shown in Fig. 6, as well as the convex hull defined by the training data, in which these constraint samples are generated. As can be seen: the convex hull is not perfectly filled, there are concentrations to the center and several edges have no data at all. This is not really a problem and could be compensated by a more sophisticated post processing of the data, which is not done here. The convex hull sampling has proven to be reliable and useful in the context of constraints for rate-independent plasticity. For the energy dissipation constraint, the derivative of the history variable with respect to the stresses is needed:
3.6.2 Results and discussion
ANN performance after training with constraints of the example presented in Sect. 3.6: from 15 training runs, all ANNs [3-10-10-1] trained on hysteresis data (left) are able to predict the stress response of an unknown test loading path (right) reasonably and more reliably
In Fig. 7, the best (0.057) and worst (0.134) ANN realizations with respect to the RMSE of the testing scenario are shown. The average RMSE of the 15 ANNs is 0.090 in this case. Contrary to the results of Sect. 2.4, where the average RMSE is 0.131, all 15 ANNs trained with physical constraints are able to predict the unknown loading path more reasonably and more reliably. Even if the curve of the worst realization does not lie exactly on the reference solution, it is still physical, does not diverge and covers the correct stress space, including hardening behavior. It should be noted, that the approximation of the training path is still as good as in Fig. 3 for the ANN without constraints. This is important, because the constraints affect the mapping of the data only to a small extent, which is also shown and investigated in [28]. The crucial point here is, that even with a limited data basis, i.e., with only one loading path in this case, in all started training processes, the unknown loading paths are all physically reasonable approximated. This indicates, that the constraints stabilize the ANN training in a way, that it is less sensitive to a change in the initial training conditions. This makes the ANN as a material model more reliable.
4 Implementation into a finite element model
A brief description on how to implement the ANN material model into an FE framework is given in this section. For details, the reader is referred to, e.g., [32]. We limit this section to the description of geometrically linear and materially nonlinear three-dimensional solids. Plain stress formulations used in the numerical examples of Sect. 5 could be derived similarly.
4.1 FE discretization
The principle of virtual work for a three-dimensional solid with volume V is
with the Cauchy stress tensor \({\varvec{\sigma }}\) and the virtual linear strain tensor \(\delta {\varvec{\varepsilon }}\) in their Voigt notations. The virtual work of external loads is assumed to be independent of the displacement field \(\mathbf{{u}}\). Due to the nonlinear material model the linearization of the virtual work
is required to solve the nonlinear Eq. (50) within a Newton iteration scheme. The linearization
of the material model is calculated with the material tangent \(\mathbf{{C}}_T\). In the context of the finite element method, the residual \(\delta \pi \) and its linearization \(\varDelta \delta \pi \) are calculated on a subset \(V_e\subset V\), the volume of the finite element e. From the isoparametric local ansatz for the element displacement field \(\mathbf{{u}} = \mathbf{{N}}\mathbf{{v}}_e\) follow the virtual strains \(\delta {\varvec{\varepsilon }}=\mathbf{{B}}\delta \mathbf{{v}}_e\) and the strain increments \(\varDelta {\varvec{\varepsilon }}=\mathbf{{B}}\varDelta \mathbf{{v}}_e\). The vectors \(\mathbf{{v}}_e\), \(\delta \mathbf{{v}}_e\) and \(\varDelta \mathbf{{v}}_e\) contain the physical, virtual and linearized element nodal displacements, respectively. The matrix \(\mathbf{{B}}\) contains derivatives of the ansatz functions, which are given in the matrix \(\mathbf{{N}}\). Both matrices depend on the specific finite element formulation used and are not described here in more detail. The stresses \({\varvec{\sigma }}\) are part of the vector of internal forces
and the material tangent \(\mathbf{{C}}_T\) is part of the tangential stiffness matrix
Usually, these integrals are calculated with numerical integration. Together with the element load vector \(\mathbf{{P}}_e\), the discretized residual and its linearization are obtained as
with the element residual vector \(\mathbf{{G}}_e\). After assembling the element quantities \(\mathbf{{G}}_e\) and \(\mathbf{{K}}_{Te}\) to the whole structure \(V\approx \bigcup _e V_e\), and assuming arbitrary virtual nodal displacements \(\delta \mathbf{{v}}\), the system of linear equations
can be solved for the nodal displacement increments \(\varDelta \mathbf{{v}}\) within a Newton iteration scheme.
4.2 ANN plasticity algorithm
The ANN constitutive model provides the current stresses \({\varvec{\sigma }}^{\text {ANN}}\) and the material tangent \(\mathbf{{C}}_T^{\text {ANN}}\) at each integration point. Their calculation is described in Sect. 2.2. They are part of the vector of internal forces (53) and the tangential stiffnes matrix (54). An overview on how to implement the described ANN material model in an incremental iterative FE algorithm is illustrated in Fig. 8. In contrast to classical elasto-plastic implementations, no radial return mapping algorithms, see for example [32], are needed. This simplifies the calculation of the material tangent, which do not depend on consistent linearization of the chosen implicit integration scheme but only on the derivative of the explicit ANN mapping. Stresses, strains and possibly other history variables must be stored for each integration point. They have to be updated at the end of the corresponding load step. The strain increment in the input vector is defined with respect to the last converged strain state of the corresponding integration point. Another simplification in terms of numerical implementation is the independence of the ANN algorithm of the material behavior, see Appendices A and B. In the context of this paper, the ANN material model is implemented in an extended version of the general purpose finite element program FEAP [25].
From a computational point of view, the ANN material model, even without the need of a local iteration algorithm, is in most cases slower than analytical material models. Of course, this highly depends on the ANN topology, i.e., the number of layers and neurons. This is not a major drawback in our view, as the objective is not to substitute for analytical material models, but to train ANN material models directly with data from laboratory experiments or from numerical homogenization, i.e., without an analytical material model.
5 Numerical examples
In this section, the performance of the constrained ANN training is investigated in three numerical examples. The first one is concerned with the approximation of yield surfaces, considering isotropic hardening. The other two examples will deal with the FE simulation of structures, including a plain stress and a three-dimensional shell problem. It has been observed, that the global convergence behavior is better with a symmetrized material tangent
and thus a symmetric global tangent matrix \(\mathbf{{K}}_T\), see [28]. Therefore the ANN material tangent is symmetrized for all following FE simulations.
5.1 Approximation of a yield surface using a limited data basis
In classical elasto-plasticity, the yield surface \(F({\varvec{\sigma }},a, \mathbf{{b}})\) defines the boundary of the purely elastic stress space. It serves as a condition, whether the current stress \({\varvec{\sigma }}\) corresponds to an elastic state (\(F<0\)) or not (\(F=0\)). With hardening, the yield surface may change while yielding. There are two well known concepts describing basic hardening phenomena. Isotropic hardening is a self-similar growing of the yield surface, depending on the scalar hardening variable a. Kinematic hardening describes the rigid motion of the yield surface in stress space, usually described by back stresses \(\mathbf{{b}}\). Data-based ANN material models do not need the definition of yield surfaces, hardening variables or back stresses in order to approximate these phenomena. Nevertheless, in order to get a better understanding of the underlying material behavior, the calculation of equivalent ANN yield surfaces can be advantageous, which has been done for example in [20]. In the following, we will investigate the capability of ANN material models to approximate the underlying yield surface and its evolution in terms of isotropic hardening for a plain stress state, considering only a limited data basis, meaning in this case only two loading paths.
5.1.1 ANN material definition and topology
The reduced ANN material mapping from Sect. 2.4.1 is extended to two dimensions
with \(n_i=7\) input variables and \(n_o=3\) output variables. The incremental update of the additional scalar history variable \(h_E\) is therefore
The ANN from Appendix A is used with topology [7-20-20-20-20-3] resulting in 1483 weights. This is suitable for representing plasticity with linear isotropic hardening in a plain stress state, which has been checked a priori.
5.1.2 Data and constraint samples
The artificial experimental data is gathered from an analytical material model. The material parameters for the von Mises plasticity model with linear isotropic hardening are given in Table 1. The four strain–stress paths used to generate the training data are illustrated in Fig. 9 and consist of a tension and a compression test to \(\varepsilon _{11}=\pm 0.003\) and an equibiaxial tension and an equibiaxial compression test to \(\varepsilon _{11}=\varepsilon _{22}=\pm 0.003\). For the calculation of these paths, see for example [24]. Each path consists of a loading and an unloading direction with \(M=21\) samples each, leading to 168 strain–stress pairs in total. For each of these samples, the history state for \(h^E\) must be calculated, as described in Sect. 2.3.1, with \(h^E_0=0\).
Generally, these four paths are not sufficient to represent the underlying material behavior. Assuming isotropy, we can transform the frame of reference of the given paths. Giving a rotation matrix
with a rotation angle \(\theta \), the matrix forms of the strain and stress tensors can be transformed to a rotated coordinate system
After rearranging the components again to the corresponding vector forms, a new strain–stress path can be used
The history variable \(h^E\) is frame invariant, hence \(h^{E*}_n=h^E_n\). By defining 20 uniformly distributed random rotation angles \(\theta \in \) between 0 and \(2\pi \), the four loading paths are extended to 84, with \(3\,528\) material equilibrium states in total. Now, these states can be transformed to proper training data for the ANN, by using the definitions (59) and the procedure of Sect. 2.3.1. This leads, with the definition of the index delays \(\varDelta n \in \{0,1,2,3,4\}\) in this example, eventually to \(15\,960\) samples, see Eq. (15). Finally, as a post processing, we delete double samples and truncate the total number of samples randomly to \(P=10\,000\) data samples \((\mathbf{{x}},\mathbf{{z}})\) to train the ANN.
Strain–stress paths for the approximation of the yield surfaces in Sect. 5.1: uniaxial and equibiaxial tension and compression tests
All five constraints from Sect. 3.3 are used to stabilize the training process. The penalty factor is chosen to be \(\upepsilon =1\) for all of them. The constraint samples are gathered with the convex hull strategy proposed in Sect. 3.2. For the normalization and stationarity constraints, which are only enforced on a subspace with \(\varDelta {\varvec{\varepsilon }}= \mathbf{{0}}\), \(P^C = 200\) samples \(\mathbf{{x}}^{0}\) are generated, respectively. For the other three constraints, \(P^C = 5\,000\) samples \(\mathbf{{x}}^{C}\) are sampled for each of them. For a brief discussion on the training time with the additional backpropagation algorithms needed for the constraints can be found in [28]. The ANN is trained with or without constraints for 10 000 epochs. Early stopping or L2-regularization are not considered here.
5.1.3 Calculation of an ANN yield surface
Random straight strain paths in the rectangular space formed by the three strain components \(\varepsilon _{11},\varepsilon _{22}\) and \(2\varepsilon _{12}\). All paths start from \({\varvec{\varepsilon }}= \mathbf{{0}}\) and end at the cuboid boundaries of \(\pm 0.003\). The initial history value \(h_0^E\) can be greater than 0 to simulate a previous loading hisory
For the von Mises plasticity model, the analytical yield surfaces can be illustrated by ellipses in the space of the principal stresses \(\sigma _1\) and \(\sigma _2\),
with the current yield stress \(Y\ge Y_0\). In order to approximate these ellipses with our trained ANN material model, we define 50 random straight loading paths in strain space, going from the origin to the boundaries of the rectangular bounding space, as illustrated in Fig. 10. These boundaries are given by the training data and are for all strain vector components \(\pm 0.003\). Along each path, we want to find the stress state, which is by our definition the beginning of yielding. For ANN material models, purely based on strain and stress information, a strain or stress based yield threshold must be defined, in order to define yielding mathematically. Within this example, we use the following yield criterion. It is illustrated in Fig. 11 for the one-dimensional case. As described in Sect. 3.3.5, one can calculate the dissipated energy \(\varDelta D\) for every loading step \(\varDelta {\varvec{\varepsilon }}\) followed by a direct unloading step with \(-\varDelta {\varvec{\varepsilon }}\). By defining an energy threshold \(D_0\), one can define a yield criterion as follows: if this energy threshold is exceeded in three consecutive loading- and unloading steps, as depicted in Fig. 11, the yield stress state is defined as the first stress state of this series. For the energy threshold \(D_0\), we choose 20% of the work done in the first loading step of the current loading path. If needed, the number of random paths, the energy threshold and the number of required consecutive exceedings can be chosen otherwise. Due to the definition \(\sigma _1>\sigma _2\), the 50 stress states can be mirrored at the \(\sigma _1=\sigma _2\)-axis in order to fill the full space. Furthermore, if the initial value of the history variable \(h^E_0\) is chosen to be greater than zero at the beginning of a loading path, it is possible to calculate subsequent yield surfaces and observe the influence of the given ANN history variable on the yielding behavior. This is shown in the next section. It should be noted, that the history variable \(h^E\) grows also in the elastic range, but vanishes completely in a purely elastic loading cycle. Changing the initial value, simulates previous loading cycles outside the elastic domain.
5.1.4 Results and discussion
We compare two different training configurations: one with and one without the introduced constraints. As an error measure, we define the mean distance between the initial ANN yield surface (\(h_0^E=0\)) stresses and the analytical points of the initial yield surface over the 50 strain paths,
Due to the random initialization of the weights, the data augmentation and the constraint sampling, the ANN training is a random process. Therefore, we run 15 training processes for each of these configurations. The averaged errors \(\sigma ^{\text {err}}\), their standard deviations and the minimum and maximum values are given in Table 2. The realizations leading to the minimum, i.e., best \(\sigma ^{\text {err}}\) of the yield surfaces with and without constraints are given in Fig. 12.Footnote 5 Additionally, the yield surfaces for different non-zero starting values \(h_0^E \in [0.05,0.1]\,kN/cm^2\) are shown.
Approximation of the initial \(\big (h_0^E=0\,kN/cm^2\big )\) and subsequent \(\big (h_0^E>0\,kN/cm^2\big )\) yield surfaces after isotropic hardening, with the ANN material models. The best realization of the ANN trained without constraints is on the left, the best realization of the ANN trained with constraints is on the right. \(\sigma ^{\text {err}}\,[kN/cm^2]\) corresponds to the initial yield surface error
Despite using data augmentation, the classically trained ANN is not able to approximate the underlying yield surface reliably. It should be noted, that this issue does not change with classical L2-regularization, more data through augmentation or with another yield surface criterion. The given loading paths of Fig. 9 simply provide not enough information to train an ANN to represent this behavior. Furthermore, the data training error for both ANN configurations behave similar and do not indicate the quality of a yield surface approximation. As can be seen in the statistics of Table 2, the constraints lead to an overall lower yield surface error. Not only the mean value, but also the range of errors decreases. This implicates, that the introduced constraints lead to better and more reliable ANN material models, when it comes to strain or stress states, which have not been seen during the training process. In addition, the ANN correctly shows the isotropic hardening behavior. This indicates the correct choice of the ANN history variable \(h^E\) as well as a good interpolation within the whole training space.
5.2 Aluminum sheet with a hole under cyclic loading
In this example, the elastoplastic behavior of a square aluminum sheet of side length \(100\,cm\), thickness \(2\,cm\) and a central hole with radius \(10\,cm\) is investigated. The geometry of the system, the loading function with varying magnitude and the FE model are shown in Fig. 13. The latter is build on a quarter of the system by taking advantage of the double symmetry. The FE model consists of 200 four-node isoparametric plain stress elements with linear shape functions for the displacements \(u_1\) and \(u_2\). The FE discretization is refined closer to the hole. The 80 load steps are equidistantly distributed within the pseudo time t between 0 and 8.
5.2.1 ANN definition, constraints, data and training
In order to capture the effect of kinematic hardening, the strain state of the previous equilibrium state must be incorporated into the input vector. This leads to the mapping
with \(n_i=9\) input variables and \(n_o=3\) output variables. The information about the current strain state \({\varvec{\varepsilon }}\) is sufficient to describe kinematic hardening, even if no additional history variables \(\mathbf{{h}}\) are considered.Footnote 6 The topology is chosen as [9-25-20-15-10-3], which is sufficient to approximate the desired material behavior. This has been checked a priori.
The training data is gathered from a von Mises plasticity model with parameters from Table 3. Altogether, 22 strain–stress paths are used to generate the incremental ANN training data. They all are one-loop hysteresis with stress controlled unloading afterwards and are bounded by the strain input space \(\varepsilon _{11},\varepsilon _{22},2\varepsilon _{12}\in [-0.02,0.02]\). They consist only of one or two non-zero stress components. No path with all three stress components being simultaneously non-zero is used. An overview of all paths is given in Table 4, two of them are illustrated in Fig. 14. By assuming the same material behavior in the tension and compression domain, one could gather these paths by only six real world experiments. Each path and therefore each hysteresis consists of four loading directions to calculate the incremental samples. Here, each loading direction containts \(M=40+1\) samples, equidistantly defined in the strain space. Within this example, all possible index delays are used: \(\varDelta n\in [0,1,...,40]\), leading to 861 incremental samples for each direction and eventually to 75 768 incremental samples \(\{[\varDelta {\varvec{\varepsilon }},{\varvec{\varepsilon }},{\varvec{\sigma }}],\varDelta {\varvec{\sigma }}\}\) in total. They are randomly truncated to 20 000. It should be noted, that taking more than 20 000 samples does not change the results of this example significantly. From the 20 000 data samples, 80% are used as training set and the remaining 4 000 data samples are used as test set for an early stopping strategy. The training process is terminated after 10 000 epochs. The weights resulting in the minimum test set error are saved and used to calculate the following results.
We investigate two different ANN material models, one trained with the introduced constraints and one without them. They are compared to an FE solution with the reference von Mises material model. The state-of-the-art (SOTA) ANN material model \(\text {ANN}_{\text {SOTA}}\) is trained without the introduced constraints. In addition to an early stopping-strategy, an L2-regularization is applied with a penalty factor of \(\upepsilon =10^{-5}\). The latter has been found to be the best choice by trial and error. This regularization penalizes high weight values. It is necessary to stabilize the training process but does not introduce additional physical information. The ANN material model \(\text {ANN}_{\text {CONS}}\) is trained with fourFootnote 7 of the introduced constraints but without additional regularization. The penalty factor is chosen to be \(\upepsilon =1\) for all of them. The constraint samples are gathered with the convex hull strategy proposed in Sect. 3.2. For the normalization constraint 2 000 samples \(\mathbf{{x}}^0\) are generated. For the stability, symmetry and energy production constraints, 20 000 samples \(\mathbf{{x}}^C\) are sampled, respectively.
5.2.2 Results and discussion
Sheet with a hole under triangular cyclic loading: observation of the strains \(\varepsilon _{22}\) and stresses \(\sigma _{22}\) at integration point 1 of element 140 (left) and the displacement \(u_2\) at node 211 (right). Comparison of the ANN material model with (CONS) and without (SOTA) constraints to the reference von Mises solution
Sheet with a hole under triangular cyclic loading: plot of the ratio of von Mises equivalent stress \(\sigma _e\) of Eq. (67) to the initial yield stress \(Y_0\) for the ANN material models at \(t=7\) trained with constraints (\(\text {ANN}_{\text {CONS}}\)) and trained without constraints (\(\text {ANN}_{\text {SOTA}}\)) They are compared to the reference solution with the von Mises material model
The displacement \(u_2\) of node 211 over pseudo time t and the strain–stress curve \((\varepsilon _{22},\sigma _{22})\) of integration point 1 of element 140 are depicted in Fig. 15. At this integration point, the maximum magnitudes of these strain and stress components are reached, while the highest Mises equivalent stress
is at the edge of the hole. In Fig. 16, the ratio of the von Mises equivalent stress \(\sigma _e\) to the initial yield stress \(Y_0\) is illustrated at \(t=7\). It should be noted, that the amount of training data, constraint data, L2-regularization and loading history has been chosen in a way, that both approaches, meaning also the state-of-the-art one, can calculate a full loading path. This allows the investigation of the direct impact of physical regularization compared to the other, purely mathematical one. It is assured, that within the whole loading path, no integration point suffers from a strain–stress state which lies outside of the training space.
If physical constraints are applied, the overall structural behavior of the sheet can be excellently represented with the ANN material model, even if the response at the integration points differ a little bit. However, even at the material point a perfect agreement with the reference solution can not be expected because the available data is limited to the numerical experiments given in Table 4. The structural response is composed on the interaction of all integration points, loading and boundary conditions and the structural geometry. Therefore, local differences can, if the overall physical behavior is sufficient, balance each other out on average. Additionally, within this example, the influence of plasticity on the structural level is small, which can be seen in Fig. 16. However, a robust plasticity model is required near to the hole to represent the yielding behavior. Here, the results of the ANN material model with constraints are much closer to the reference solution. However, exactly the same result cannot be expected at this point, because the ANN did not have information about stress states with three non-zero components. But, with the introduced constraints, it is able to generalize this behavior reasonably, leading to a stable numerical calculation. On the other side, the ANN trained only with L2-regularization is also able to perform a complete calculation, but fails at representing the full structural behavior reliably. Due to the incorrect distribution of the yielding areas, see Fig. 16, the structural response differes significantly, even in the first loading direction, as can be seen in Fig. 15 (right). On the material level, the strain–stress curves differ more from the reference solution. This is due to the L2-regularization not being physically motivated, which leads to unreasonable elastic and plastic responses within areas of the sample space, which are not represented sufficiently by the given data.
5.3 Channel-section beam
In this example, a steel channel-section cantilever with a vertical tip force at the free end is investigated using an ANN as a three-dimensional material model. Elasto-plastic solutions for shell formulations are presented for example in [5] and [15]. However, in this paper, we use other dimensions and material definitions. The von Mises plasticity model parameters, considering isotropic hardening, are given in Table 5. The beam has a length of \(2\,m\), the web and the flanges are \(4\,mm\) thick. The height of \(30\,cm\) and the width of \(10\,cm\) are measured with respect to the corresponding middle surfaces. The geometry of the system, the position of the load and the FE model are shown in Fig. 17. The latter consists of 64 shell elements along the length direction, 12 along the web and 4 shell elements along the flanges, i.e., 1280 shell elements in total. The isoparametric quadrilateral shell element is based on a Reissner-Mindlin theory and a three-field variational formulation. It was originally published in [26]. In [15], it was extended by independent thickness strains in order to allow arbitrary 3D constitutive equations. The present version [10] is additionally capable of calculating the stress state in layered structures with different materials. Here, three numerical layers are used with 6 gaussian integration points in thickness direction in order to consider the elasto-plastic behavior. For the present calculation, four EAS parameters for the membrane strains, four for the bending strains and two for the shear strains are used, respectively. The analysis is done with an arc length method with a prescribed displacement increment \(\varDelta w = 0.2\,cm\) at the load application point. The maximum tip displacement of \(w_{max}=6\,cm\) is reached after 30 loading steps, before the structure is unloaded again.
5.3.1 ANN definition, constraints, data and training
The ANN definition of Eq. (59) is used, but with \(n_i=13\) input variables and \(n_o=6\) output variables in the three-dimensional case. The same history variable as in Sect. 5.1 is used to capture the effect of isotropic hardening. The ANN topology is chosen to be [13-30-25-20-15-6], resulting in 2 126 weights. This is sufficient to approximate the desired material behavior and has been checked a priori.
The training data is gathered from the analytical three-dimensional von Mises plasticity model with the parameters from Table 5. Altogether, 14 strain–stress paths are defined as experimental basis. All paths are one-loop hysteresis with stress controlled unloading afterwards. Only one or two stress components are non-zero during each test. No path with more than two non-zero stress components is used. The strain vector components are bounded by \(\pm 0.01\). Each path and therefore each hysteresis consists of four loading directions to calculate incremental samples from. Here, each loading direction contains \(M=40+1\) samples, equidistantly defined in the strain space. An overview of all paths is given in Table 6. Similar to the previous numerical example, by assuming the same material behavior in the tension and compression domain, one could gather these paths by only six real world experiments.
In order to train an ANN sufficiently, as in the yield surface example of Sect. 5.1, the data must be enriched by rotating the frame of reference. This is described in detail in Sect. 5.1.2. Therefore, by defining 20 random rotations,Footnote 8 the initial 14 paths are extended to 294. Now, these new paths can be used to calculate incremental samples from. By using all possible index delays \(\varDelta n\in [0,1,...,40]\), 3444 incremental samples per loading path and 1 012 536 incremental samples in total can be calculated. They are truncated randomly to 20 000. From the 20 000 data samples, 80% are used as training data and the remaining 4 000 samples are used as test set for an early stopping strategy. The training process is terminated after 10 000 epochs. The weights resulting in the minimum test set error are saved and used to calculate the following results.
We compare the \(\text {ANN}_{\text {SOTA}}\) material model with L2 regularization (\(\upepsilon =10^{-5}\)) with the \(\text {ANN}_{\text {CONS}}\) material model. The latter is trained with four of the introduced constraints, without the stationarity restriction. For the normalization constraint 1000 samples \(\mathbf{{x}}^0\) are generated. For the symmetry and energy constraints, 10000 samples \(\mathbf{{x}}^C\) are sampled, respectively. For these constraints the penalty factor \(\upepsilon \) is 1. It turns out, that for this examples the material stability is very important. Therefore, we use 50 000 samples \(\mathbf{{x}}^C\) for the stability constraint with a penalty factor \(\upepsilon =100\) for this constraint.
5.3.2 Results and discussion
Channel-section beam: load-deflection curve of the load application point (left) and the deformed configuration at maximum displacement (right). A convergence study is done from step 7 to step 8, see Table 7
The load-deflection curve of the displacement w at the load application point can be seen in Fig. 18. The external load is not located in the center of shear. Therefore, the beam twists immediately, leading to large displacements and rotations. As a side effect, the resulting compression stresses at the top flange lead to local buckling, which can also be seen in Fig. 18. From the seventh to the eighth loading step, a Newton convergence study with respect to the residual norms is given in Table 7.
While the non-enhanced ANN material model leads to early divergence, the ANN trained with constraints is able to calculate the whole loading and unloading process. The structural behavior at the loading path can be approximated very well, including the local buckling phenomenon. On the other hand, the unloading curve differs considerably. As already stated in the previous example, an exact representation inside the whole three-dimensional stress space cannot be expected, as the available information was very limited. The reason for the rather poor approximation of the unloading behavior can be the fact, that the size of the elastic regime compared to the plastic one is very small and was not sampled sufficiently in this example. Of course, considering a lot more data would improve this behavior. At this point, it should be noted, that this structure, with complex three dimensional stress states inside the shell layers can be calculated, even if only reduced two-dimensional material information was available in the first place. Furthermore, looking at the convergence study in Table 7, the superior performance in terms of Newton convergence rates is evident, which has already been discussed and shown in [28] for another example.
6 Conclusion
In this paper, the concept of constrained ANN training is extended to the application of modeling elasto-plastic material behavior. After introducing the treatment of equality and inequality constraints and a suitable sampling strategy for constraint samples, specific constraints are given for elasto-plastic material behavior. Subsequently, the concept is applied to three numerical examples.
We have shown, that the consideration of constraints during the ANN training leads to stable numerical material models, which can be used in challenging FE calculations. Even the channel-section beam example, with complicated three-dimensional stress states inside the shell layers can be calculated with data only containing two non-zero stress components. The given concept is applicable on every ANN architecture based on optimization strategies and it is not limited to a specific material formulation. Due to the purely strain and stress based nature of the introduced method, it can easily be applied to real world experimental data in the future. Furthermore, the application as a surrogate material model for numerical homogenization is possible. Whenever the amount of available data is limited, this approach seems to be an excellent way to add information to the training process. We are convinced that physically enhancing ANN training with constraint optimization techniques has a great potential in ANN material modeling, alone, or as a supplement to other strategies enhancing ANNs with physical information.
In the context of this paper and for the sake of simplicity, we applied the constrained ANN training to data from well known and relatively simple von Mises plasticity models with linear hardening behavior. The future objective is to apply this concept to experimental data or data from numerical homogenization, where no macroscopic material model is known a priori. For example, in [28], an ANN is trained from limited experimental data of vulcanized rubber, with excellent results. Furthermore, additional parameters as discussed in Sect. 6 can be considered. This leads to a larger input space and therefore to more data required in order to learn the corresponding underlying dependencies. In this case, the constraint optimization strategy could lead to a significant reduction of the necessary data. Other future work may deal with treatment of large strain plasticity, viscous material behavior or damage. Therefore, new constraints have to be formulated, which can easily be implemented with the algorithms presented in detail in the Appendices of this paper.
Notes
In general, the definition of additional history variables is arbitrary. A more obvious choice in this case could be, for example, the maximum absolute stress value reached up to the current state. However, its monotonicity has several downsides when it comes to ANN material approximation. From our numerical experience, monotonically growing history variables show a tendency to be overestimated by the ANN during loading paths, which can eventually lead to excessive stress increases, far beyond the training range. This is especially a problem with scarce data. However, this work-based history variable does not show this kind of drawback and is therefore well suited for isotropic hardening behavior.
The training success with respect to the data is not affected significantly, if the number of constraint samples is very high. Therefore, as a rule of thumb, the number of constraints samples can be chosen as high as possible, and is only limited by the computational effort one is willing to invest.
The error terms of the transformed data and the constraints can differ in magnitudes, due to the derivatives. This can result in a poor training performance. Therefore, the constraint error terms can be normalized to improve the convergence behavior in the optimization process, as introduced in [28].
This constraint could also be used as equality constraint for Cauchy-elastic material, but not for general elasticity.
Please note, that it is not possible to compare other than the initial yield surfaces quantitatively, because no connection can be made between the ANN history variable \(h^E\) and the history variable of the analytical material model, which is the accumulated equivalent plastic strain.
This can easily be shown for a one-dimensional example with linear kinematic hardening, by transforming the back-stresses with \(b=C_T(\varepsilon -C^{-1})\).
The stationarity constraint is omitted here. This constraint can be very restrictive and the penalty factor must be chosen more carefully, see example of Sect. 3.6.
In 3D space, the definition of random rotations can be done in several ways. Here, we defined it with a random rotation angle and a random rotation direction and used Rodrigues’ formula to define the corresponding rotation matrix, similar to [28]. This is a relatively simple approach, but sufficient in this case.
The denominator of the strain increment fraction can be zero. This can be handled numerically by assigning a small fraction to all zero valued strain increments. On the other hand, the denominator strain increment in \(\varLambda _j\) cancels with the same increment in \(\bar{\beta _j}\), which can motivate another implementation.
References
Abu-Mostafa YS (1990) Learning from hints in neural networks. J Complex 6(2):192–198. https://doi.org/10.1016/0885-064x(90)90006-y
As’ad F, Avery P, Farhat C (2022) A mechanics-informed artificial neural network approach in data-driven constitutive modeling. Int J Numer Meth Eng 123(12):2738–2759. https://doi.org/10.1002/nme.6957
Bishop C (1993) Curvature-driven smoothing: a learning algorithm for feedforward networks. IEEE Trans Neural Netw 4(5):882–884
Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2(4):303–314
Eberlein R, Wriggers P (1999) Finite element concepts for finite elastoplastic strains and isotropic stress response in shells: theoretical and computational analysis. Comput Methods Appl Mech Eng 171(3–4):243–279. https://doi.org/10.1016/s0045-7825(98)00212-6
Freitag S, Muhanna RL, Graf W (2012) A particle swarm optimization approach for training artificial neural networks with uncertain data. In: Proceedings of the 5th international conference on reliable engineering computing (REC 2012), Brno, Czech Republic, Litera, pp 151–170. https://rec2012.fce.vutbr.cz/documents/papers/freitag.pdf
Ghaboussi J, Garrett JH, Wu X (1991) Knowledge-based modeling of material behavior with neural networks. J Eng Mech 117(1):132–153. https://doi.org/10.1061/(asce)0733-9399(1991)117:1(132)
Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT Press
Gorji MB, Mozaffar M, Heidenreich JN, Cao J, Mohr D (2020) On the potential of recurrent neural networks for modeling path dependent plasticity. J Mech Phys Solids 143:103972. https://doi.org/10.1016/j.jmps.2020.103972
Gruttmann F, Wagner W (2020) An advanced shell model for the analysis of geometrical and material nonlinear shells. Comput Mech 66(6):1353–1376
Hashash YMA, Jung S, Ghaboussi J (2004) Numerical implementation of a neural network based material model in finite element analysis. Int J Numer Meth Eng 59(7):989–1005. https://doi.org/10.1002/nme.905
Huang D, Fuhg JN, Weißenfels C, Wriggers P (2020) A machine learning based plasticity model using proper orthogonal decomposition. Comput Methods Appl Mech Eng 365:113008. https://doi.org/10.1016/j.cma.2020.113008
Jorge Nocedal SW (2006) Numerical optimization. Springer-Verlag GmbH
Klein DK, Fernández M, Martin RJ, Neff P, Weeger O (2022) Polyconvex anisotropic hyperelasticity with neural networks. J Mech Phys Solids 159:104703. https://doi.org/10.1016/j.jmps.2021.104703
Klinkel S, Gruttmann F, Wagner W (2008) A mixed shell formulation accounting for thickness strains and finite strain 3d material models. Int J Numer Meth Eng 74(6):945–970
LeCun YA, Bottou L, Orr GB, Müller KR (2012) Efficient BackProp. Springer, Berlin, Heidelberg, pp 9–48
Lefik M, Schrefler B (2003) Artificial neural network as an incremental non-linear constitutive model for a finite element code. Comput Methods Appl Mech Eng 192(28–30):3265–3283. https://doi.org/10.1016/s0045-7825(03)00350-5
Liu Z, Wu C, Koishi M (2019) A deep material network for multiscale topology learning and accelerated nonlinear modeling of heterogeneous materials. Comput Methods Appl Mech Eng 345:1138–1168. https://doi.org/10.1016/j.cma.2018.09.020
Masi F, Stefanou I, Vannucci P, Maffi-Berthier V (2021) Thermodynamics-based artificial neural networks for constitutive modeling. J Mech Phys Solids 147:104277. https://doi.org/10.1016/j.jmps.2020.104277
Mozaffar M, Bostanabad R, Chen W, Ehmann K, Cao J, Bessa MA (2019) Deep learning predicts path-dependent plasticity. Proc Natl Acad Sci 116(52):26414–26420. https://doi.org/10.1073/pnas.1911815116
Márquez-Neila P, Salzmann M, Fua P (2017) Imposing hard constraints on deep networks: Promises and limitations. https://doi.org/10.48550/ARXIV.1706.02025
Murray W, Wright MH, Gill PE (1982) Practical optimization. Academic Press Inc., London
Rumelhart DE, Hinton GE, Williams RJ (1986) Learning internal representations by error propagation. Bradford Books, Cambridge
Simo JC, Hughes TJR (1998) Computational inelasticity. Springer, New York. https://doi.org/10.1007/b98904
Taylor RL (2022) FEAP - finite element analysis program. http://projects.ce.berkeley.edu/feap/
Wagner W, Gruttmann F (2005) A robust non-linear mixed hybrid quadrilateral shell element. Int J Numer Meth Eng 64(5):635–666
Wang K, Sun W (2018) A multiscale multi-permeability poroplasticity model linked by recursive homogenizations and deep learning. Comput Methods Appl Mech Eng 334:337–380. https://doi.org/10.1016/j.cma.2018.01.036
Weber P, Geiger J, Wagner W (2021) Constrained neural network training and its application to hyperelastic material modeling. Comput Mech 68(5):1179–1204. https://doi.org/10.1007/s00466-021-02064-8
Werbos PJ (1982) Applications of advances in nonlinear sensitivity analysis. In: system Modeling and Optimization. Springer-Verlag, London, pp 762–770
Wolfe P (1969) Convergence conditions for ascent methods. SIAM Rev 11(2):226–235
Wolfe P (1971) Convergence conditions for ascent methods. II: some corrections. SIAM Review, USA, pp 185–188
Wriggers P (2010) Nonlinear finite element methods. Springer, Berlin, Heidelberg
Xu K, Huang DZ, Darve E (2020) Learning constitutive relations using symmetric positive definite neural networks. J Comput Phys. https://doi.org/10.48550/ARXIV.2004.00265
Yun GJ, Ghaboussi J, Elnashai AS (2008) A new neural network-based model for hysteretic behavior of materials. Int J Numer Meth Eng 73(4):447–469. https://doi.org/10.1002/nme.2082
Zhang A, Mohr D (2020) Using neural networks to represent von mises plasticity with isotropic hardening. Int J Plast 132:102732. https://doi.org/10.1016/j.ijplas.2020.102732
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
MLP definitions and data forward pass
The ANN used in this paper is a fully connected multilayer perceptron (MLP). In Fig. 19, its topology and the used terminologies are shown for neurons, weights and layers. A specific MLP topology is labeled with its neuron quantities summarized in square brackets: [\(n_{i}\) - \(n_1\) -... - \(n_{n_h}\) - \(n_o\)]. The aim of the following appendices is to provide all forward and backward passes in a compact vector matrix notation, which can be used for an efficient implementation of the introduced constraints. All vectors are defined as column vectors. The input and output variables are arranged in the vectors \(\mathbf{{x}} = [x_1,...,x_{n_i}]^T\) and \(\mathbf{{z}} = [z_1,...,z_{n_o}]^T\). They are linearly and independently transformed into the ’training space’,
This accelerates training convegence, see e.g. [16]. In this papers studies, \(m_{xi}\) and \(m_{zj}\) are the mean values of the corresponding input and output variables of all given samples. The \(s_{xi}\) and \(s_{zj}\) are the standard deviations, respectively. The transformed in- and output variables are summarized in the vectors \(\hat{\mathbf{{x}}}\) and \(\hat{\mathbf{{z}}}\). The following forward passes of the Appendices A and B are defined for one single sample \(\mathbf{{x}}\). The output y of neuron m in layer L
is calculated with the weighted sum from the previous layer
and the activation function g(s). For the hidden layers, a hyperbolic tangent function is used, for the output layer, the identity function \(g_{\text {out}}(s)=s\) is applied. The bias-neuron output \(y_0^{[L]}\equiv -1\) is constant for every layer. Therefore, the corresponding weights \(w_{m0}^{[L]}\) perform a shift in the activation function. The neuron outputs and weighted sums are arranged in the vectors
of every layer L. If the bias-value is not included, a bar is added to the symbol: \(\bar{\mathbf{{y}}}^{[L]}\in {\mathbb {R}}^{n_L}\). With this notation in mind, the input and output layer can be written as \(\mathbf{{y}}^{[0]}=[-1,\hat{\mathbf{{x}}}^T]^T\) and \(\bar{\mathbf{{y}}}^{[n_h+1]}=\hat{\mathbf{{z}}}\). For each layer, the weights are stored in a matrix as
The weights are defined with the ’receiving’ neuron index as first subscript, in front of the index of the ’giving’ neuron. The first column contains the bias-weights. If omitted, then a bar is added to the symbol: \(\bar{\mathbf{{W}}}^{[L]}\in {\mathbb {R}}^{n_L\times n_{L-1}}\). The weighted sum vector
and the neuron output vector, without bias value,
can be written for each layer in vector–matrix notation. With these definitions in mind, a complete forward calculation of the MLP mapping \(\mathbf{{x}} \mapsto \mathbf{{z}}\) can be done with Algorithm 2.

MLP tangent forward pass
For the material tangent \(d{\varvec{\sigma }}/d{\varvec{\varepsilon }}\), several, but not all MLP derivatives are needed. This Appendix provides a forward pass to calculate the partial derivative of the MLP outputs with resprect to a single input \(\partial \mathbf{{z}}/\partial x_i\) for one single sample \(\mathbf{{x}}\). It is part of the whole Jacobian of Eq. (2). This is convenient for the used plasticity model and for the backward pass of Appendix D. First, considering the transformations of Eqs. (68) and (69), the partial derivatives transform as
Considering the derivative of an arbitrary neuron output, applying the chain rule and the weighted sum formula of Eq. (71), one obtains the forward update rule
The partial derivatives of the neuron outputs and the weighted sums are ordered for layer L and input variable \(\hat{x}_i\) in the following vectors,
while \(\mathbf{{y}}_{,i}^{[L]}=[0,\bar{\mathbf{{y}}}^{[L]T}_{,i}]^T\in {\mathbb {R}}^{n_L+1}\). The vector of activation function derivatives
can be calculated and saved within the forward pass of Algorithm 2. With the weight matrices, excluding the bias-weight-column, the derivatives can be written as
with \(\circ \) being the element-wise product. For the first hidden layer, \(\mathbf{{s}}^{[1]}_{,i}\) is the \(i^{\text {th}}\)-column of the \(\bar{\mathbf{{W}}}^{[1]}\)-matrix. In the last layer \(\mathbf{{g}}'_{\text {out}}\) must be used for \(\mathbf{{y}}^{[n_h+1]}_{,i}=\hat{\mathbf{{z}}}_{,i}\). With these definitions in mind, a complete forward calculation for the MLP Jacobian part \(\partial \mathbf{{z}}/\partial x_i\) can be done with Algorithm 3.

This procedure is practical in combination with the backpropagation algorithms for derivatives, see Appendix D, or if only specific partial derivatives are needed. However, if the whole Jacobian is wanted, the formula
can be applied, with \(\mathbf{{1}}^{[L]} = [1,1,\ldots ,1]^T \in {\mathbb {R}}^{n_L}\) and \(n_0=n_i\).
MLP backward pass for data
In this section, the classical backpropagation algorithm is described in the introduced notation, which matches the other backpropagation algorithms in the Appendices D, E and F. However, the basic algorithm is known for decades [23, 29]. It can be used for the training data error and the normalization constraint error. The neuronal neighborhood in Fig. 20 illustrates local neuronal dependencies. For easy formula reading: the layer indices are defined as l(eft), m(id), r(ight). Given a set of P training or constraint samples \(\{\mathbf{{x}}_{(k)}, \mathbf{{t}}_{(k)}\}, k=1,...,P\), the error function is usually defined in the training space,
see transformations in Eqs. (68) and (69). The penalty factor \(\upepsilon \) is usually 1 for training samples, but could vary for the normalization constraint. If the transformed differences between MLP and target outputs are stored in the matrix
the error can be written with help of the frobenius norm \(||\cdot ||\),
The error gradient with respect to the weights \(\nabla E = dE/d\mathbf{{w}}\) is part of the training algorithm. The gradient components
are sorted for each layer L in a matrix,
matching the weight matrix definition (74). Traditionally, the \(\delta \)-values are defined as
Here, they are sorted for all samples and neurons layer-wise in a matrix as follows,
The neuron output vectors from definition (72) of layer L are sorted for all samples in the matrix
With these definitions, the gradient matrix of Eq. (88), regarding all P samples, can be calculated with one matrix multiplication
The \(\mathbf{{Y}}^{[L]}\)-matrices can be obtained by the forward pass of Appendix A. Simultaneously, the matrices of activation function derivatives
can be calculated for every layer, with \(\mathbf{{G}}'^{[n_h+1]}=\mathbf{{G}}'_{\text {out}}\). The \({\varvec{\delta }}^{[L]}\)-matrices are calculated with a backpropagation algorithm. Starting at the output layer, the \(\delta \)-values can be calculated by using Eq. (89):
Beginning at Eq. (89) and taking advantage of the chain rule, considering dependencies from the next layer \(L+1\), together with Eq. (71), the \(\delta \)-updating rule becomes
which can be written in matrix notation:
With these definitions in mind, the layer-wise defined gradients can be calculated with Algorithm 4.

In the case of most higher order training algorithms, the gradient \(\nabla E\) is needed in vector form. After calculating the matrices \(\nabla E^{[L]}\) for every layer they can easily be rearranged to a vector form, as long as the order matches the one from the corresponding weights vector \(\mathbf{{w}}\in \mathbb {R}^{n_w}\). The ordering of the \(n_w\) weights in the weight vector \(\mathbf{{w}}\) is in our implementation as follows: first the layers, then the ’receiving’ neurons and finally the ’giving’ neurons:
MLP backward pass for derivative combinations
The constraints for tangent symmetry and stationarity add ANN derivatives in different ways to the error function. The following Appendix aims for an efficient implementation of the corresponding gradient. In [28], a single gradient component of an ANN derivative is shown, based on [3]. In general \(n_d\) linear combinations of two ANN derivatives
can be penalized, with the two constants \(c_{d_1}\) and \(c_{d_2}\) and the derivative indices \(j_1,i_1,j_2,i_2\) per pair d specifying the constraint type. The calculation of derivative components is shown in Appendix B. For example: in the case of the plain stress symmetry constraint, the constants are \(c_{d_1}\equiv 1\) and \(c_{d_2}\equiv -1\). The index relationships are shown in Table 8.
The error terms are defined in the non-transformed or physical space. Considering the tangent transformation from Eq. (77), they each transfer to
They are for example part of the penalty error function
which is defined on arbitrary samples \(\mathbf{{x}}_{(k)},k=1,\ldots ,P\). The normalization numbers \(\alpha \) were introduced in [28] and stabilize the training process with constraints. Here, they depend on the data normalization and are defined as
The gradient value
can be rewritten as the sum of derivative values by redefining the indices:
The factors \(f_{ij(k)}\) depend on the error term \(E_{d(k)}\) the derivative \(z_{j,i(k)}\) was part of, the corresponding normalization number \(\alpha _d\) and data transformation values \(s_{zj}\) and \(s_{xi}\). For example: in the case of the plain stress symmetry constraint, the set of input indices is therefore \({\mathbb {I}}=\{1,2,3\}\). The sets of output indices \({\mathbb {J}}(i)\) contain all indices of output variables, which are differentiated with respect to \(\hat{x}_i\). In this case \({\mathbb {J}}(1)=\{2,3\}\), \({\mathbb {J}}(2)=\{1,3\}\) and \({\mathbb {J}}(3)=\{1,2\}\), see Table 8. Also for the symmetry constraints, the derivative factors are
For the stationarity constrain of Sec 3.3.2, the following parameters and index sets must be used: \(c_{d1}\equiv 1\), \(c_{d2}\equiv 0\), \(\alpha _d = \alpha _{ji} = s_{zj}/s_{xi}\), \({\mathbb {I}}=\{n_s+1,...,n_i\}\) and \({\mathbb {J}}(i)\equiv {\mathbb {J}}=\{1,...,n_s\}\). The advantage of this rearrangement becomes clear in the following backpropagation algorithm, which allows to collect the output index sum into a single variable. Starting from Eq. (103), using the independence of \(\mathbf{{w}}\) and \(\mathbf{{x}}\) to change the order of the derivatives and the chain rule combined with the definition of the weighted sum of Eq. (71), the gradient value can be transformed to
By defining the new variables
and making use of the product rule, the gradient value eventually becomes
The neuron output derivatives \(y_{l,i(k)}^{[L]}\) of Layer L can be sorted for all samples k in the matrix
as in Eq. (91), with the vectors of Eq. (79) and the leading zeros. Due to the bias values, its first row contains only zeros. By packing the \(\delta \)-values for every index i in a matrix \({\varvec{\delta }}^{[L]}_i\) as in Eq. (96) and the \(\gamma \)-values in the same manner in the matrix \({\varvec{\gamma }}^{[L]}_i\), together with the matrix of neuron outputs \(\mathbf{{Y}}^{[L]}\) from Eq. (91), the gradient per layer L can be calculated with
The neuron output matrices \(\mathbf{{Y}}^{[L]}\) and its derivatives \(\mathbf{{Y}}^{[L]}_{,i}\) can be obtained in the forward passes of Algorithms 2 and 3, as well as the matrices of activation function derivatives \(\mathbf{{G}}'^{[L]}\) and analogous \(\mathbf{{G}}''^{[L]}\). The \({\varvec{\delta }}^{[L]}_i\)- and \({\varvec{\gamma }}^{[L]}_i\)-matrices are calculated via backpropagation. Starting with the \(\delta _i\)-values at the output layer: by using Eq. (106), they can be calculated with
with the matrix of derivative factors per input index i
Beginning at Eq. (106) and taking advantage of the chain rule, considering dependencies from the next layer \(L+1\), together with Eq. (71), the \(\delta _i\)-updating rule can be obtained in matrix notation as
similar to Eq. (96). The initial conditions at the output layer for the \(\gamma _i\)-values can be derived from definition (107) as
The matrices of weighted sum derivatives
can also be calculated within the forward pass of Algorithm 3. The updating rule for \(\gamma _i\)-values can be obtained in a similar way as the one for \(\delta _i\). Starting at Eq. (107), considering dependencies from the next Layer \(L+1\), together with Eq. (71) and the product rule, we obtain
By changing the order of summation and identifying the \(\delta _i\) and \(\gamma _i\)-values of the next layer, we obtain the updating rule
In matrix form it is
With these definitions in mind, the layer- and input index-wise defined gradient matrices can be calculated with Algorithm 5.

MLP backward pass for scalar product
The stability constraint of Sect. 3.3.4 and the isotropy constraint defined in [28] penalize a scalar product of vectors containing network input and output variables. Exemplary, for the stability constraint defined in this paper, the error function
with the scalar product
is suitable, when the first \(n_o\) input variables are defined as the strain increments. In the case of an inequality constraint, the sum only contains the active set members. The normalization number for this error term can be defined as
By defining the variables
the gradient values
can be calculated layer wise
with the neuron output matrix from Eq. (91) and by sorting the \(\delta \)-values as in Eq. (90). The \(\mathbf{{Y}}^{[L]}\)-matrices can be obtained by the forward pass of Appendix A. The \({\varvec{\delta }}^{[L]}\)-matrices are calculated with a backpropagation algorithm. Starting at the output layer, the \(\delta \)-values can be calculated by using Eq. (122),
Beginning at Eq. (122) and taking advantage of the chain rule, considering dependencies from the next layer \(L+1\), together with Eq. (71), the \(\delta \)-updating rule can be obtained in matrix notation as
as in the other backpropagation algorithms. With these definitions in mind, the layer-wise defined gradient matrices can be calculated with Algorithm 6.

MLP backward pass for Energy loss constraint
The constraint of Sect. 3.3.5 contains two consecutive ANN evaluations, which leads to a more complex and specific calculation of the gradient. This Appendix exclusively deals with the calculation of this gradient. Starting from the error term of Eq. (46), the central objective is the partial derivative \(\partial \sigma ^{II}_{j}(\mathbf{{x}}^{CI},\mathbf{{w}})/\partial w\). For the moment, the weight indices are neglected and only one constraint sample \(\mathbf{{x}}^C\) is considered. The input vector
depends on the intermediate ANN output \(\varDelta {\varvec{\sigma }}^{I}(\mathbf{{x}}^C,\mathbf{{w}})\). The weights are the same for both evaluations. By applying the chain rule, considering the dependencies of the intermediate stress and history variables from the first ANN evaluation, the partial derivative is
It contains the direct derivatives of both stress increments with respect to the weight and the indirect derivative considering dependencies of the stresses and additional history variables. The derivatives of the stress increments with respect to the stresses and the history variables can be obtained from the Jacobian from Appendix B, keeping in mind the correct input vector \(\mathbf{{x}}^{CI}\). The derivatives of the history variables with respect to the stresses depends on the definition of the history variables. An example is given in Sect. 3.6. Inserting this partial derivative into the partial derivative of the error function of Eq. (46), considering only one sample at the moment and a unit penalty factor, we obtain:
It is possible to rearrange the sum over the stress increments from the error function of Eq. (129) and the partial derivative of Eq. (128) in such a way that the partial derivatives of the ANN outputs with respect to the weights can be bracket out,
with the parts from the chain ruleFootnote 9
In summary, by defining \(\beta _j^{II}:={\bar{\beta }}_j s_{zj}\) and \(\beta _j^I:={\bar{\beta }}_j s_{zj}\varLambda _j\), the error term gradient for this constraint in the transformed space is
considering all active samples. From now on, the derivation of the backpropagation algorithm is straightforward. By defining the two matrices
the corresponding delta-values at the output layer can be calculated with
The matrices of weighted sum derivatives are defined analogously to Eq. (93) and depend on the input vectors used. The delta-values can be backpropagated like the ones of the previous sections,
and can be used to calculate the gradient matrices per layer
The neuron outputs \(\mathbf{{Y}}^{I[L-1]T}\) are from the forward pass with \(\mathbf{{x}}^C\) and the neuron outputs \(\mathbf{{Y}}^{II[L-1]T}\) are from the forward pass with \(\mathbf{{x}}^{IC}\). With these definitions in mind, the layer-wise defined gradient matrices can be calculated with Algorithm 7.

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weber, P., Wagner, W. & Freitag, S. Physically enhanced training for modeling rate-independent plasticity with feedforward neural networks. Comput Mech 72, 827–857 (2023). https://doi.org/10.1007/s00466-023-02316-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02316-9