Abstract
Soft materials are of major interest for biomechanics applications due to their high deformability and susceptibility to experience damage events under different loading scenarios. The present study is concerned with modelling damage evolution processes in these nonlinear materials whose structural responses are prone to locking when low-order kinematic interpolation is employed in the context of nonlinear Finite Element schemes. For this reason, a pair of gradient-enhanced continuum damage schemes are proposed with the aim of tackling mechanical failure problems in applications that exhibit shear and volumetric locking. In particular, we present the consistent formulation and the assessment of the corresponding performance of (i) a mixed displacement-enhanced assumed strain Q1Q1E24 employing a total Lagrangian formulation, and (ii) a three-field mixed displacement-pressure-Jacobian Q1Q1P0 formulation. The novel Q1Q1E24 and Q1Q1P0 formulations are consistently derived and numerically implemented, providing a satisfactory agreement with respect to ABAQUS built-in elements handling the treatment of shear and volumetric locking, respectively, in conjunction to the modelling damage phenomena via the use of a penalty-based gradient-enhanced formulation. This performance is examined via several numerical applications. Furthermore, the final example justifies the need for a formulation combining both mixed FE approaches to simulate problems encompassing both locking issues (shear and volumetric locking), which can be performed using a combination of the Q1Q1E24 and Q1Q1P0 herein proposed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Soft materials, characterized by a highly nonlinear behavior at large deformations, encompass a wide range of both industrial and biomechanical applications like adhesives [1,2,3], soft tissues [4,5,6,7,8] and composite structures [9,10,11,12]. Several academic efforts using numerical approaches have been pursued in order to test their mechanical performance, followed by their subsequent failure. In fact, these developed models, which require a profound knowledge of fracture mechanics, are comprised of the advent of solid experimental methods based upon them, which encompasses a still relevant challenge in Computational Mechanics. Within this frame, several numerical techniques have been employed so far in order to address nonlinear fracture modelling of soft materials, which include the eXtended Finite Element Method (XFEM) [13,14,15], cohesive zone models (CZM) [16,17,18], phase-field fracture methods (PF) [19,20,21,22,23,24], the combination of these last two techniques [25,26,27,28,29], and gradient-enhanced Continuum Damage approaches (CDM), which will be the technique under investigation in this article.
Non-local approaches such as PF or gradient-enhanced CDM have emerged as continuum formulations that ensure the well-posedness of equations, avoiding strong mesh sensitivity and thus leading to vanishing localized failure regions. This is fulfilled through internal length scales accompanying an Euler–Lagrange equation [30, 31]. These kinds of contributions have been discussed in detail; see [32,33,34]. In particular, gradient-enhanced CDM has been successfully exploited for a countless variety of both geometrically linear [35,36,37] and nonlinear models [38,39,40,41,42], including the extension to gradient-enhanced damage plasticity [43,44,45,46].
Among the yet-to-fully-tackle damage applications for gradient-enhanced CDM, deformable nearly incompressible hyperelastic materials constitute a recurrent topic due to their increasing range of applications, from rubber-like polymers to biomedical materials [47, 48]. Being amply reported in the related literature, numerical modelling of nearly incompressible hyperelastic materials using displacement-based (single field) FE schemes suffer from the well-known volumetric locking, which overestimates the stiffness of materials when the Poisson ratio is high (\(\nu \sim 0.5\)) [49]. In engineering practice, the problem can be solved by the use of meshless techniques [50,51,52,53], smothered FE approaches (sFEM) [54,55,56], discontinuous Galerkin methods [57,58,59,60] or by lower integration algorithms of the divergence terms, among other alternatives. In particular, a mixed three-field displacement-pressure-Jacobian mixed FE formulation which uses a lower-order approximation for the Lagrange multipliers associated with the volumetric pressure [61,62,63,64,65] has been employed, being named Q1P0 or Simo-Taylor-Pister elements.
This formulation, pioneered by the aforementioned authors [66] and enhanced by Simo and Taylor [67], and Miehe [68], is based on a local multiplicative split of the deformation gradient into deviatoric and volumetric parts, considering both the pressure and the Jacobian, which appear in the volumetric contribution, as primary unknowns, besides the displacement field. A disadvantage of the Q1P0 formulation is that it might provide unphysical solutions for compressible problems [69]. Being recently applied to model ductile damage [70] and fracture by means of a PF approach [71,72,73], we aim for the development of a Q1Q1P0 formulation with its combination with the gradient-enhanced CDM technique with the target of modelling damage in nearly incompressible hyperelastic materials avoiding volumetric locking issues. It should be mentioned that the proposed formulation for Q1Q1P0 element differs from the one utilized by ABAQUS hybrid elements, as the latter only employs a two-field displacement-pressure formulation, being it employed to model CDM by Ostwald et al. [74].
Importantly, shear locking can also alter the compliance of the specimen with bending effects in large deformation analysis [75]. In order to overcome this shear locking pathology, several techniques have been proposed in the last decades: use of higher order Finite Element (FE) formulations [76,77,78], isogeometric analysis [79,80,81,82], reduced integration [83, 84] and the application of mixed methods and formulations, such as the approach for incompatible modes [85] or the enhanced assumed strain technique [86,87,88], among others. The latter will be the one implemented within this approach.
The enhanced assumed strain (EAS), also named Q1E[\(\bullet \)], being \(\bullet \) the number of incompatible modes considered, is a method developed by Simo and Armero [87] for nonlinear continuum elements which, relying on the Hu-Washizu variational principle, enrich the deformation modes stemming from the single field displacement solution by means of several incompatible deformation modes at the element level. This method relies crucially on an additive decomposition of the deformation gradient into a conforming and an enhanced part which accounts for these incompatible modes. The resulting formulation corrects the over-stiffening of the structure by avoiding the phenomenon of shear locking. This technique has been widely applied to solid shells in order to suppress shear locking associated with bending modes [89,90,91,92,93,94]. This technique’s major drawback lies in the instability associated with rank deficiency in the stiffness matrix which appears under compressive states [95], which remains an open question in the Computational Mechanics field. Having also been applied to non-local damage approaches such as PF frameworks [96,97,98] and very recently to CDM with reduced integration schemes [99], in this research, we aim at developing a full integration formulation combining the EAS method considering 24 incompatible deformation modes, \(\texttt {Q1E24}\), with a gradient-enhanced CDM approach to analyze damage in samples under bending loads which are prone to display shear locking phenomena, i.e., \(\texttt {Q1Q1E24}\).
In light of the previous discussion and after addressing potential locking events in CDM using non-local formulations, we present two non-local gradient-enhanced CDM approaches to solve locking issues. They are tailored within the geometrically nonlinear setting based on the work of Dimitrijević and Hackl [40], but by introducing an internal damage variable based on the model of Liebe et al. [100], in the line of the work by Waffenschmidt et al. [42]. Within the cited approach, the concept of enhancing the energy function via a gradient term of the independent damage variable is combined with a penalty parameter that simulates the equivalence between the local and non-local damage parameter, being this approach in line with the micromorphic gradient-type dissipative framework proposed by Forest [101]. This coupled two-equation (linear momentum and non-local damage balance) framework for large deformations is formulated in a weak form. The hyperelastic constitutive response is affected by the non-local damage scalar, which is approximated via an exponential law that triggers the deterioration of the structure when it overpasses a threshold.
Two displacement-continuum damage approaches will be built over this primary framework capturing damage in hyperelastic materials prone to shear and volumetric locking. For the former application, the EAS technique is included to encompass 24 incompatible deformation modes, implementing a formulation Q1Q1E24 that is suitable to model compressible samples subjected to bending. Then, separately, the mixed three-field Q1Q1P0 approach is formulated to tackle volumetric locking in nearly incompressible samples. The resulting coupled, highly nonlinear system of equations is solved via two Newton–Raphson type solution schemes: one local and one global employing a user-element subroutine UEL in the FE commercial software ABAQUS. In summary, we are presenting in this manuscript the first full-integration enhanced assumed strain (Q1Q1E24) and a novel mixed displacement-pressure-Jacobian (Q1Q1P0) schemes for gradient-enhanced CDM modelling and we have tested their performance by comparing them with the already-formulated standard CDM damage approach, i.e., Q1Q1.
This paper is structured as follows. The basic theory, which includes the constitutive behavior, the non-local gradient-enhanced damage formulation, and the thermodynamical postulates for the standard Q1Q1 element, is developed in Sect. 2. Section 3 displays the variational theorems for this Q1Q1 formulation and the two proposed ones, i.e., Q1Q1E24 and Q1Q1P0, providing a further insight on the numerical implementation in Sect. 4. To validate and test the potential of the proposed frameworks, a wide variety of numerical examples which consists of compressible and nearly incompressible large deformation problems prone to exhibit volumetric and shear locking have been addressed in Sect. 5. Some final remarks and conclusions are provided in Sect. 6.
2 Theoretical formulation
This section outlines the fundamental concepts and definitions of the current numerical framework addressing the use of gradient-enhanced for a standard CDM scheme, being specialized later for EAS and mixed u-p-J formulations. The proposed numerical methodology is specialized for hyperelastic material models.
2.1 Basic definitions and constitutive formulation at local level
Complying with standard nonlinear Continuum Mechanics, let an arbitrary spatial point defined in the current configuration be defined as \(\textbf{x} := \varvec{\varphi }(\textbf{X},t)\), being \(\varvec{\varphi }(\textbf{X},t)\) the nonlinear deformation map which projects the material points \(\textbf{X}\) from the initial configuration \(\Omega _0\subset \mathbb {R}^n\) to the current one \(\Omega \subset \mathbb {R}^n\). The transformation of the differential line elements throughout the deformation process is characterized by the deformation gradient \(\textbf{F}\) whose definition renders
being \({\textbf{1}}\) the second-order identity tensor and \(\textbf{H}(\textbf{X},t)\), the material displacement gradient tensor. The Jacobian, i.e., the ratio of the deformed to the undeformed volume, being the determinant of \(\textbf{F}\), shall fulfill the condition of \(J = \text {det}[\textbf{F}] > 0\). In order to track the motion of the body from the material to the spatial configuration at time t, the displacement vector is defined as:
Accordingly, the right and left Cauchy–Green tensors are obtained as, respectively:
We postulate the existence of local free energy function \(\Psi \). Without loss of generality, we consider a nonlinear compressible neo-Hookean constitutive law. This expression is plotted in Eq. (4)
where \(\mu \) and \(\lambda \) are the shear constant and \(\lambda = K - \frac{2}{3}\mu \), respectively, with K as the volumetric constant; and \(I_1\) is the first invariant of the right Cauchy–Green tensor that is defined as \(I_1: =\text {tr}[\textbf{C}]\). The particular form given in Eq. (4) also holds for the spatial configuration taking the left Cauchy–Green strain tensor as the main argument, i.e, \(\Psi ^{\text {loc}}(\textbf{b})\) and therefore, \(I_1=\text {tr}[\textbf{b}]\).
From Eq. (4), the second Piola–Kirchhoff tensor \(\textbf{S}\) can be computed as follows
For the spatial configuration, a push-forward operation is performed to obtain the Cauchy stress tensor \(\varvec{\sigma }\)
In order to compute an ABAQUS UEL subroutine, the local tangent operators, which are required in order to compute the Jacobians, can be computed directly from the derivation from the material description:
where \(\textbf{I}_{C}^{\text {sym}}\) is a fourth-order tensor that has the following expression: \(\textbf{I}_{C}^{\text {sym}} := {-}\partial \textbf{C}^{-1}/{\partial \textbf{C}} = [\textbf{C}^{-1}\overline{\otimes }\textbf{C}^{-1} + \textbf{C}^{-1}\underline{\otimes }\textbf{C}^{-1}]/2 = [C^{-1}_{ik}C^{-1}_{jl}+C^{-1}_{il}C^{-1}_{jk}]/2\), which employs the non-standard dyadic products. To obtain the spatial counterpart \(\mathfrak {e}\), we perform the push-forward operation on Eq. (7)
where \(\textbf{I}^{\text {sym}} = [{\textbf{1}}\overline{\otimes }{\textbf{1}} + {\textbf{1}}\underline{\otimes }{\textbf{1}}]/2\) denotes the fourth-order symmetric identity tensor.
Based on Liebe et al. [100], we define a scalar damage function \(f_d (\kappa )\), which recalling [42], \(f_d (\kappa )\) should be at least twice differentiable, and tracks the material degradation relying on the evolution of a local variable \(\kappa \in [0,\infty ]\), and whose evolution is ruled by the achievement of a threshold value \(\kappa >\kappa _0\) in order to cause a loss in the stiffness of the structure. Therefore, we can state:
These conditions guarantee two clearly differentiated states: \(f_d = 1\) identifies an intact stiffness at the spatial point level, whereas \(f_d = 0\) denotes a fully deteriorated stiffness state. This belongs to the formulation of the local damage model, whose linking procedure with the non-local damage framework will be envisaged in the subsequent sections.
2.2 Gradient-enhanced non-local formulation
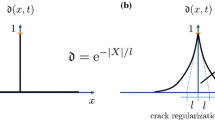
In line with the approach proposed by Dimitrijević and Hackl [40], a regularized damage material response is achieved by the definition of a gradient-enhanced non-local function term \(\Psi ^{\text {nloc}}{(\phi , \nabla _{\textbf{X}}\phi ,\kappa )}\) in the reference configuration:
This non-local contribution can be split into two separate terms: \(\Psi ^{\text {nloc}}_{\text {grd}}{(\nabla _{\textbf{X}}\phi )}\) containing the material gradient of the non-local damage field variable \(\phi \), which stands for the first term of a Taylor series expansion of \(\phi \) at the material point; and \(\Psi ^{\text {nloc}}_{\text {plty}}(\phi , \kappa )\) is a penalty term which correlates the local damage variable \(\kappa \) with the non-local damage variable \(\phi \). The energy terms are specified as follows:
where \(c_d\) consists in a parameter that characterises the non-local character of the formulation; \(\beta _d\), a penalty parameter that enforces the local damage \(\kappa \) and non-local damage \(\phi \) variables to be equivalent; and \(\gamma _d\), a switch parameter that is introduced to range between a local and non-local gradient-enhanced model, respectively and the corresponding value is ranged like \(\gamma _d\in \{0,1\}\).
Consequently, the expression for the internal free energy function considering the previous non-local terms is given by
With these expressions at hand, we define the material expressions for the damage-like vector field \(\textbf{Y}\) and the scalar damage-like variable Y:
whose spatial values \(\textbf{y}\) and y are obtained via push-forwarding Eqs. (14)–(15)
2.3 Thermodynamic consistency
The thermodynamic consistency of the constitutive framework outlined above is examined through the exploitation of the Clausius-Plank inequality (local internal dissipation (\(\mathcal {D}_{int}\)) inequality) [40], which under isothermal conditions is given by
Following [42], we focus our attention on the corresponding damage-related terms leading to the definition of a reduced local dissipation \(\mathcal {D}_{\text {red}}\):
where we have introduced the thermodynamic force g as the derivative with respect to the local damage variable \(\kappa \):
We now define a thermodynamic force \(q\ge 0\), which is conjugated to the classical scalar damage variable d, as follows:
Accordingly, the Clausius-Plank inequality holds when the reduced dissipation condition satisfies \(\mathcal {D}_{\text {red}}\ge 0\), if \({\partial }_d\kappa >0\). In fact, q takes the interpretation of the energy release rate, consisting of the addition of a local and a non-local contribution that reads as
Complying with these equations, we can now define the damage condition:
where \(\Phi _d<0\) stands for the purely elastic behavior and \(\Phi _d=0\) notes a damaged state. According to Simo and Hughes [102], an optimization problem regarding a Lagrange multiplier \(\lambda \) can be proposed to represent the evolution of the damage variable
where \(\kappa _d\) concerns the initial damage threshold. This last equation gives rise to the Karush-Kuhn-Tucker (KKT) conditions to model both the initiation and termination of damage.
which, can be expressed in a more detailed way as
The continuous formulation for damage is completed with the definition of the damage function itself \(f_d(\kappa )\), which follows an exponential-type law.
with \(\eta _d>0\) standing for the exponential saturation parameter. It is worth mentioning that we have introduced a damage threshold parameter \(\kappa _d\) that differs from the proposed approach by Dimitrijević and Hackl [40] and that was introduced in Waffenschmidt et al. [42], in order to avoid over-compensation of the damage curve due to the logarithmic expression in \(\Psi ^{\text {loc}}\) [Eq. (4)] that may lead to enhance the stress-strain curve, rather than weakening it.
3 Variational formulation
3.1 Variational formulation of standard gradient-enhanced damage models: material and spatial formulations
The total potential energy of a system, \(\Pi \), is obtained from the combination of an internal contribution \(\Pi _{\text {int}}\), which considers the action of internal forces, and an external contribution \(\Pi _{\text {ext}}\) due to the addition of volume and surface forces, i.e., \(\Pi = \Pi _{\text {int}} - \Pi _{\text {ext}}\).
Restricting the analysis of conservative loading cases, we can express the total potential of the system in the reference position of the arbitrary body under consideration as follows
Since the problem is governed by the principle of minimum potential energy, the expression for the equation concerning the mechanical problem in the material configuration is obtained as
that, can be particularized for each independent field as:
Let \(\mathfrak {V}^{u} = \left\{ \delta \textbf{u} \in [H^{1}( \Omega _{0})]: \delta \textbf{u} = \textbf{0} \text{ on } \partial \Omega _{0,u} \right\} \) be the space of admissible displacement variations, and \(\mathfrak {V}^{\phi } = \left\{ \delta \phi \in [H^{1}( \Omega _{0})]: \nabla _{\textbf{X}} \delta \phi \cdot \textbf{N} = 0 \text{ on } \partial \Omega _{0} \right\} \), the space of admissible test functions for non-local damage function. Furthermore, in the previous expression, the second Piola–Kirchhoff stress tensor renders \(\textbf{S} : = 2f_d(\kappa ) \partial _{\textbf{C}} \Psi ^{\text {loc}}\), and \(\textbf{F}^{V}\) and \(\mathbf {\overline{T}}\) denote the body force and the traction vectors in the reference volume \(\Omega _{0}\) and surface \(\partial \Omega _{0}\), respectively.
The previous system of equations can be expressed in the spatial configuration by applying a standard push-forward operation:
expressed in the current volume \(\Omega \) and surface \(\partial \Omega \) and with \(\varvec{\sigma }\) identifying the Cauchy stress tensor that is accordingly affected by the degradation function \({f_d(\kappa )}\).
Upon the use of the product rule and the divergence theory on Eqs. (30)–(31), the governing equations for the balance of linear momentum [Eqs. (34)–(35)] and evolution of the non-local damage field \(\phi \) [Eqs. (36)–(37)] are expressed in the reference configuration \(\Omega _0\)
Replicating the previous procedure for Eqs. (32)–(33) in the case of the current configuration, the Euler–Lagrange equations in the spatial form are given by
being \(\textbf{N}\) and \(\textbf{n}\) both the normal vectors in the material and spatial configuration, respectively.
3.2 Variational formulation of gradient-enhanced damage models for enhanced assumed strain formulations
This section tailors the already established standard CDM model by combining it with the EAS method. Regarding this novel application, it is performed to alleviate shear locking pathologies in damage using low-order displacement interpolation in the subsequent finite element discretization scheme.
We focus our development on the additive decomposition of the Green-Lagrange strain tensor into a displacement derived (\(\textbf{E}^{u}\)) and an enhancing counterpart \(\tilde{\textbf{E}}\) as follows [103]: \(\textbf{E} = \textbf{E}^{u} +\tilde{\textbf{E}}\). This differs from the alternative EAS scheme proposed by Simo and Armero [87] that accounts for the additive decomposition of the deformation gradient \(\textbf{F} = \textbf{F}^{u} +\tilde{\textbf{F}}\). Moreover, note that in the following derivation, the free-energy function is expressed in terms of the Green-Lagrange strain tensor. However, there exists a direct relation concerning the right Cauchy–Green tensor.
The point of departure of the formulation is based on the construction of the multi-field Hu-Washizu functional, where the displacement, the enhancing strain, the stress, and the non-local damage variable are the independent fields. This functional is given by
where \(\Pi _{\text {ext}} (\textbf{u})\) identifies the external contribution due to the prescribed domain and boundary actions.
Let \(\mathfrak {V}^{u} = \left\{ \delta \textbf{u} \in [H^{1}( \Omega _{0})]: \delta \textbf{u} = \textbf{0} \text{ on } \partial \Omega _{0,u} \right\} \) be the space of admissible displacement variations; \(\mathfrak {V}^{\tilde{E}} =[ L_{2} ( \Omega _{0})]\), the space of the admissible enhancing strain; and \(\mathfrak {V}^{\phi } = \left\{ \delta \phi \in [H^{1}( \Omega _{0})]: \nabla _{\textbf{X}} \delta \phi \cdot \textbf{N} = 0 \text{ on } \partial \Omega _{0} \right\} \), the space of admissible test functions for non-local damage function. The first variation of the total potential energy with respect to independent fields gives the following general expression:
The previous expression can be particularized as follows from Eq. (42):
Exploiting the orthogonality condition between the stress field \(\textbf{S}\) and the enhancing strain field \(\tilde{\textbf{E}}\) [87], the weak form of the coupled IBVP (Initial Boundary Value Problem) can be reduced to three independent fields, namely the displacement, the enhancing strain, and the non-local damage fields.
The weak form given in Eq. (44) (recalling \(\textbf{S} : = 2f_d(\kappa ) \partial _{\textbf{C}} \Psi ^{\text {loc}} = f_d(\kappa ) \partial _{\textbf{E}} \Psi ^{\text {loc}}\)) is given by
In Eqs. (45)–(47), \(\delta \Pi ^{*}_{\text {int}}\) and \(\delta \Pi ^{*}_{\text {ext}}\) stand for the internal and external contributions of the generic field (\(*\)). In what follows, we turn our interest to the internal contribution of each independent field.
3.3 Variational formulation of gradient-enhanced damage models for penalty-based mixed formulations for nearly incompressible materials
The second presented methodology concerned in this investigation is the mixed Jacobian-pressure formulation originally proposed by Simo et al. [66]. In line with this work, we first perform a modification in the local strain energy density \(\Psi _{\text {loc}}\) to a nearly incompressible neo-Hookean approach:
where \(\bar{I_1}\) is the first invariant of the isochoric left Cauchy–Green tensor \(\bar{\textbf{b}}\) and reads as \(\bar{I_1} = J^{-2/3}I_1 = J^{-2/3}\text {tr}[\textbf{b}]\).
For the current three-field variational problem, we consider three fields as primary unknowns of the system \(\{\textbf{u},\tilde{p},\tilde{J}\}\), where:
-
\(\tilde{p}\) is the Lagrange multiplier that accounts for the pressure response \(p = \frac{\partial {\Psi ^{\text {loc}}_\text {vol}}}{\partial J}\).
-
\(\tilde{J}\) is the dilatation, a constraint variable for the Jacobian of the material \(J(\textbf{u})\).
For convenience, we express the total potential of the system in the current configuration:
Again we denote: (i) \(\mathfrak {V}^{u} = \left\{ \delta \textbf{u} \in [H^{1}( \Omega )]: \delta \textbf{u} = \textbf{0} \text{ on } \right. \left. \partial \Omega _{0,u} \right\} \) is the space of admissible displacement variations, (ii) \(\delta \tilde{p} \in L^2(\Omega )\) stands for the space of virtual pressure, (iii) \(\delta \tilde{J} \in L^2(\Omega )\) regards the space of virtual dilatation and (iv) \(\mathfrak {V}^{\phi } = \left\{ \delta \phi \in [H^{1}( \Omega )]: \nabla _{\textbf{x}} \delta \phi \cdot \textbf{n} = 0 \text{ on } \partial \Omega \right\} \) the space of admissible test functions for non-local damage function.
The first variation of the functional with respect to independent fields renders
The previous expression can be expanded as follows.
The weak form of the coupled IBVP (Initial Boundary Value Problem) can be reduced to four independent fields, namely the displacement, the pressure, the dilatation and the non-local damage fields. It is given by
with the isochoric contribution of the Cauchy stress \(\varvec{\sigma }_{\text {iso}}\) being easily obtained from the derivation of the local strain energy density as
In addition to this, it is worth highlighting the expressions for the Jacobians obtained by the volumetric and isochoric contributions:
It is observed how the damage function term \(f_d\) only multiplies the isochoric term. Therefore, for the forthcoming expressions in Sect. 4.1, when we refer to damaged stress and stiffness, they refer to the isochoric terms. The volumetric contribution is left unchanged.
4 Algorithmic treatment and finite element implementation details
This section outlines the description of the algorithmic description for the general gradient-enhanced damage formulation (Sect. 4.1), and subsequently, in Sect. 4.2, we describe the finite element implementation details describing the resulting operators and the interpolation schemes for each of the formulations given in Sects. 3.1–3.3.
4.1 Gradient-enhanced damage framework—algorithmic setting
This section details the algorithmic scheme within the context of an iterative and sequential solution scheme using nonlinear FE. In the sequel, we provide condensed information concerning the material and spatial formulations given in Sect. 3.1 in line with the salient results of Waffenschmidt et al. [42].
Recalling Eq. (24), this expression represents a nonlinear differential equation that should be numerically integrated within the time step interval \(\Delta t = t_{n+1} - t_{n}\ge 0\) where \(t_{n+1}\) is the current time step and \(t_{n}\) is the previous equilibrium solution of the system relying on a Newton-Rahpson-based solution of the corresponding nonlinear FE formulation. The backward Euler integration scheme of the damage variable \(\kappa \) at the current time step \(n+1\) renders
where \(\gamma _{n+1} = \Delta t\lambda _{n+1}\) is the Lagrange multiplier at time \(t_{n+1}\). Therefore, the incremental Karush-Kuhn-Tucker conditions take the form:
The flux and source equations can be updated for a material description:
where the superscript \([\bullet ]^{\text {und}}\) refers to undamaged variables.
The spatial approach is obtained by just push-forwarding the magnitudes:
where \(\kappa _{n+1} = \kappa _{n}\) for an elastic incremental step. Complying with Eq. (23), for our incremental scheme, the incremental Lagrange multiplier \(\gamma _{n+1}\) is obtained by fulfilling the consistency equation:
This nonlinear equation is solved by means of a Newton–Raphson (N-R) iterative scheme at the material point level: expanding Eq. (67) in a first-order Taylor series at \(\gamma _{n+1}^{k}\) for a k-th N-R iteration, we obtain
where \(\text {r}_{n+1}^{k}=\Phi _{d, n+1}(\kappa _{n+1}^k)\) is the residual in the k-th iteration step and \(\text {d}_{\gamma }\text {r}_{n+1}^{k}\) is the Jacobian of this residual, which reads
Now that we can calculate \(\gamma _{n+1}\), the N-R scheme checks if the residual is below a pre-defined tolerance, and accordingly, the internal damage variable (Eq. (59)) and the flux and source terms for stresses and non-local damage magnitudes (Eqs. (61)–(66)) are updated. We now have all the ingredients for the global algorithm setting that is thoroughly summarised in Algorithm 1. For this, we compute the derivatives for all the source values required to complete the Jacobian formulation. For the sake of brevity, we consider \(f_d(\kappa _{n+1})=f_d\) in this series of equations. Complying with a material configuration approach:
and applying a push-forward for the spatial approach:
with

4.2 Finite element formulation and implementation details
This section addresses the FE derivation and the main implementation details of the proposed coupled system of nonlinear equations for each of the variational formulations proposed in Sect. 3.
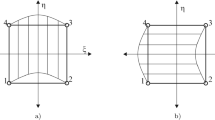
The baseline kinematic description for the displacement approximation complies with standard first-order 3-D 8-node hexahedral elements. The parametric space is defined as: \(\mathcal {A} : = \{ \varvec{\xi }= (\xi ,\eta ,\zeta ) \in \mathbb {R}^{3} | -1 \le \xi ,\eta ,\zeta \le +1; i =1,2,3 \} \). The related literature has deeply reported the poor performance of this fundamental displacement formulation for bending-dominated applications and nearly incompressible elasticity, motivating the development of several mixed FE formulations.
For the sake of clarity, we specify the main differences between the three approaches herewith proposed:
-
A nonlinear CDM approach for the spatial configuration using the formulation of Sect. 3.1.
-
A novel nonlinear CDM approach for the material configuration considering the enhanced assumed strain (EAS) technique (Sect. 3.2).
-
A novel nonlinear CDM approach for the spatial configuration considering a mixed Finite Element formulation that accounts for the influence of the hydrostatic pressure p and the Jacobian J (Sect. 3.3).
In Sect. 4.2.1, we outline the interpolation of the displacements and the non-local damage variable that holds for the standard gradient-enhanced damage model and for the mixed formulations herein proposed. Subsequently, Sects. 4.2.2–4.2.4 detail for the discrete representations encompassing the residuals and the Jacobian matrices given for each one of the three different proposed approaches.
4.2.1 Discretisation scheme for the displacement and the non-local damage variable
Complying with standard isoparametric FEM, the reference and the current geometries can be interpolated using standard trilinear shape functions \(N^{I}\) (\(\textbf{N}(\varvec{\xi })\) in matrix notation) as
where \({\textbf {X}}_{I}\) and \({\textbf {x}}_{I}\) stands the nodal positions in the reference and the current configurations, respectively, and setting \(n_{n} = 8\) is the number of nodes. These nodal locations can be expressed in the corresponding vectors: \(\overline{{\textbf {X}}}\) and \(\overline{{\textbf {x}}}\).
The interpolation of the displacements \(\textbf{u}\) and the non-local damage variable \(\phi \) renders
where \(\textbf{d}\) represents the nodal displacement vector, and \(\varvec{\overline{\phi }}\) represents the nodal values of the non-local damage variable; both defined at the element level.
The material and spatial gradients of the shape functions \(\textbf{N}\) can be read as
with \(\varvec{\xi }\) referring to the parametric coordinate system with coordinates \(\varvec{\xi } = \{\xi ,\eta ,\zeta \}\); and \(\mathbf {J_e}\) and \(\mathbf {j_e}\) as the material and spatial Jacobians of the isoparametric transformation, which allow the computation of the deformation gradient \(\textbf{F}\) as follows:
With the previous definitions at hand, the corresponding material gradient quantities can be discretized as, for a material description,
whereas the spatial gradients render
4.2.2 FE formulation of the gradient-enhanced damage model for spatial configuration—Q1Q1
The point of departure for the finite element formulation of the displacement-based gradient-enhanced damage model recalls the variational formalism defined in Eqs. (32)–(33), defining a coupled problem.
The insertion of the interpolation scheme for \(\textbf{u}\) and \(\phi \) leads to a discrete version of the residual forms denoted by \(\textbf{R}^{\textbf{d}}\) and \(\textbf{R}^{\overline{\phi }}\) that are defined as:
For the application of Newton-type solution algorithms for the iterative solution of the boundary value problem, the linearization of the weak form is computed as follows:
where \(\Delta _{*} [\bullet ]\) denotes the directional derivative operator with respect to the field \(*\).
Computing the derivatives of the residuals, we reach the Jacobian expressions that are required to solve the global N-R scheme:
which leads to the following linearised system of equations that is solved by the global iterative N-R monolithic scheme
4.2.3 FE formulation of the gradient-enhanced damage model EAS-based elements—Q1Q1E24
For its numerical implementation and in line with the previous investigations for Enhanced Assumed Strain (EAS) mixed FE formulations, we herewith recall a material formulation defined in the reference configuration of the body. This formulation has been exploited for its usage in the modelling for solid shells [87, 93, 94, 96,97,98, 104,105,106], as it is proven to block the appearance of shear locking in structures under bending configurations.
Recalling from Sect. 3.2, the Cauchy–Green right tensor is computed as follows:
The current definition of the enhancing part of the Green-Lagrange tensor relies on the formulation proposed by Andelfinger and Ramm [89] and Bischoff and Ramm [103], whose specific details are omitted for brevity reasons.
The enhanced strain field is defined at the element level via the matrix operator \(\textbf{M}(\varvec{\xi })\)
where
where \(\textbf{T}_{\textbf{0}}^{\text {-T}}\) is the transpose of the inverse of a matrix that accounts for the terms of the Jacobian from the initial configuration \(\mathbf {J_e}\) that reads:
Without any loss of generality, we recall the incompatible strain modes defined in [89] encompassing 24 incompatible modes leading to the following particular form of the matrix \(\textbf{M}_{\mathbf {\xi }}\):
Therefore, the incompatible strains \({\varvec{\varsigma }}\) are added into the FE implementation as an extra degree of freedom. The consistent linearization of this system is obtained through the Gateaux directional derivative concept, resulting in
The linearised system of equations solved for the global N-R monolithic scheme reads
where the term for the residual of the incompatible strains \(\textbf{R}^{\varsigma }\) is given by
and the tangent terms that form part of the Jacobian matrix read as
where \(\nabla _{\textbf{X}}\textbf{N}\) accounts for the nonlinear term that is added to the expression defined in Eq. (86), specific for material configuration schemes [75]. This is expressed for every node by:
where \(N_{i,j}\) is the derivative of the nodal shape function \(N_i\) with respect to the j-coordinate and \(F_{ij}\) accounts for the terms of the deformation gradient \(\textbf{F}\). This expression is also included in his respective terms for the internal residuals and their associated Jacobians for the reference configuration.
Following the approach proposed by [93], since inter-element continuity is not required for the enhanced strains, they can be removed as a DOF through a standard static condensation process, thus reaching the system of equations proposed in Eq. (98), having the element stiffness contributions like
and the newly defined residuals as
4.2.4 FE formulation of the gradient-enhanced damage model for spatial configuration employing a mixed FE formulation—Q1Q1P0
For the second novel approach that we have developed, the present formulation relies on the fundamental derivations by Simo and Hughes [66] and subsequently exploited by Miehe [68], whose effectiveness for modelling quasi-incompressible materials (\(\nu \rightarrow 0.5\)) has been profusely assessed in the last two decades. In this concern, we recall a particular model where the primary unknowns are: (i) the displacement field \(\textbf{u}\), (ii) the Lagrange multiplier for pressure \(\tilde{p}\), and (iii) the independent kinematic variable \(\tilde{J}\).
In line with the two previous approaches, we start by getting the residuals for these three primary unknowns by discretising from Eq. (51):
The consistent linearization of this system is obtained through the Gateaux directional derivative concept, resulting in
By deriving the residuals, we reach the expression for the Jacobian matrices:
What is observed in this formulation is that in addition to the normal formulation, we have to introduce shape functions for the interpolations for the mixed variables related to the pressure \(N^{\tilde{p}}\) and the dilatation \(N^{\tilde{J}}\). However, since they do not have to satisfy the continuity between the elements, we can suppose that their values, \(N^{\tilde{p}}\) and \(N^{\tilde{J}}\), have a constant scalar value of 1.
As outlined above, this mixed finite element is herewith reformulated in order to accommodate gradient-enhanced damage models, taking Eq. (51) as the basis for its derivation. Therefore, we obtain that the baseline three-field mixed formulation is coupled with the non-local gradient-enhanced damage model, leading to a system of four residual equations.
As inter-element continuity is not required for both the pressure and the dilatation DOFs, they can be removed from the system of equations by employing a standard static condensation process, reaching the system proposed in Eq. (98), obtaining both the residual and stiffness contributions like
where \(\overline{K} = {(}K^{\tilde{p}\tilde{J}}{)^{-1}}K^{\tilde{J}\tilde{J}}{(}K^{\tilde{J}\tilde{p}}{)^{-1}}\).
5 Numerical examples
The forthcoming section is dedicated to the resolution of several numerical simulations involving compressible and incompressible hyperelastic materials in order to test the capabilities in damage modelling of the Q1Q1 (Sect. 4.2.2), Q1Q1E24 (Sect. 4.2.3) and Q1Q1P0 (Sect. 4.2.4) schemes.
The first of the experiments consists of a validation example employing a nearly-incompressible block under a compressive state, adopted from the work in Sect. 4.2 of Reese et al. [107]. Furthermore, this instance does not consider the gradient-enhanced CDM approach, and we aim to validate the mixed u-p-J formulation.
The next numerical experiment consists of a series of parametric studies carried out on a plate with a hole to study the influence of the regularisation properties of the model. We adopt the example in Sect. 5.2 of the work by Waffenschmidt et al. [42], replicating the dependence on the mechanical behavior for the compressible samples and analyzing the performance for nearly incompressible materials.
The last experiment aims to simulate a challenging example for a large deformation problem vulnerable to both shear and volumetric pathologies. For this, based on the proposed example in Sect. 4.1 in the work by Reese et al. [107], we propose a notched cylindrical shell subjected to an extreme bending load.
5.1 Benchmark example—nearly incompressible block under compression
Taken from Reese et al. [107], it is modelled the quarter of a cubic brick (symmetry conditions are considered on the planes X and Y) with 1,000 brick elements under a compressive status, i.e., a displacement of \(u_z = -0.5\) mm is applied on the area in bold of Fig. 1, where it is observed the bottommost surface as fixed in the cubical structure. Mimicking the properties of the reference example, we consider a Shear Modulus \(\mu = 80.194\) MPa and a Poisson ratio \(\nu = 0.49999\), thus considering a nearly incompressible material. Since this model aims to analyze the potentiality of the three proposed approaches in modelling this highly deformed state, avoiding locking pathologies, no damage interaction is proposed within this example. This means that we model Q1, Q1E24 and Q1P0 FE formulations.
In order to quantify the differences in performance among the three proposed frameworks, it is plotted the deformed configuration (Fig. 2) and the reaction force–displacement curves (Fig. 3) for every algorithm. Emphasizing the main advantages and disadvantages of them, it is itemized for every technique, in particular, the results obtained, also comparing with one sample run with ABAQUS C3D8H hybrid elements:
-
Q1 formulation: It can be envisaged that the performance here is not satisfying overall. Starting from the left image in Fig. 2, it is observed a high deformation on the outer surfaces of the block due to the over-stiffening of the structure caused by the large deformation process. Confirming this aspect with the force–displacement curve in Fig. 3, it is deduced that the main reason for this behavior is the volumetric locking that exhibits the solid by employing this algorithm, whose force–displacement curve highly overestimates the mechanical answer of the material, compared with the result obtained for the ABAQUS hybrid element.
-
Q1E24 Formulation: There were not found any results for this scheme due to convergence issues since the correction that the EAS method does on the global N-R scheme is considerably high in order to find an approximate solution for the software under incompressibility. To tackle this issue, it was tried to run the simulation with different element sizes, but without any improvement in the convergence of the scheme, displaying the unsuitability of this formulation to model incompressible specimens.
-
Q1P0 Formulation: Without any doubt, the mixed u-p-J FE formulation proves to comply as the most robust performance in order to avoid the volumetric locking pathology. Its deformed configuration (right image, Fig. 2) captures the performance of a material under a compressive load in the center of the upper surface. Furthermore, it shows a strong correlation in the mechanical behavior (see Fig. 3), yet considerably better performance in terms of convergence, with the hybrid two-field ABAQUS elements, as this latter shows, through mid-testing, premature failure (Fig. 4). These results exhibit that the mixed u-p-J formulation has a worth-mentioning potentiality in quantifying the response of the incompressible sample and, at the same time, avoiding locking pathologies, unlike Q1 discretization and the ABAQUS C3D8H element, thus providing its solid capability in modelling nearly incompressible hyperelastic materials under large deformation states.
5.2 Plate with a hole—compressible hyperelastic material
5.2.1 Test details
As for the second numerical example, the deformation of a plate with a hole under a traction load is considered. The geometry and boundary conditions for the full model are exhibited in Fig. 5. In line with the previous example, considering symmetry conditions on both X, Y, and Z planes, specifically, only one eighth part of the sample is modelled for the sake of reducing the computational cost. The bottommost surface is considered to be clamped, whereas the topmost one is subjected to a vertical displacement \(u_z\) up until the post-peak behavior of the sample. The material properties employed for this approach are plotted in Table 1 for a Poisson ratio of \(\nu = 0.25\). Among the parameters for the non-local damage:
-
The \(\beta _d\) parameter has been calibrated in order to ensure a solid convergence for the local N-R monolithic scheme.
-
\(\gamma _d\) has the value of the unity to guarantee a non-local damage framework if \(c_d>0\).
These compressible specimens will be run with algorithms encompassing both Q1Q1 and Q1Q1E24 formulations, not considering Q1Q1P0 as they are not suitable to model problems with \(\nu < 0.45\). The parameters related to the damage law i.e., both the damage threshold \(\kappa _d\) and the saturation \(\eta _d\) magnitudes along with the non-local regularisation parameter \(c_d\) will be modified throughout these series of tests where the first aim will be the validation of the proposed CDM models with the constitutive behavior of the elements from ABAQUS, on one side, and the failure pattern, on the other (Sect. 5.2.2). Once they are verified, a quick study to test the mesh objectivity is carried out. We study the mechanical performance of the sample with different discretizations (Sect. 5.2.3). Subsequently, with the most suitable algorithm and in line with [42], we will run several numerical examples changing \(c_d\) in order to test the influence of this magnitude in the compressible specimens (Sect. 5.2.4).
5.2.2 Quantitative and qualitative validation
First, in order to validate the CDM approaches, it is required to verify the mechanical performance of the proposed algorithms with the theoretical ABAQUS elements. To establish a quantitative standpoint with them, the damage parameters of both \(\kappa _d\) and \(\eta _d\) have to be adjusted properly. According to [42], higher values of \(\eta _d\) do accelerate the onset of the damage process, being deviated from the purely neo-Hookean response plotted by the ABAQUS elements at lower stages of the corresponding loading process. On the contrary, really small saturation parameters approximate the curve to the theory but do delay the damage onset considerably after the deformation range considered. In addition to this, by considering a damage threshold of \(\kappa _d \ = 0 \ \text {MPa}\), i.e., the damage onset happens upon loading, not augmenting the stiffness of the mechanical curve. Thus, we have fixed a value of \(\eta _d= 0.1 \ \text {MPa}^{-1}\) and \(\kappa _d \ = 0 \ \text {MPa}\) for these validation tests with a discretization of 9,525 hexahedral elements and a regularisation parameter of \(c_d = 1000 \ \text {MPa}^{-1}\,\text {mm}^{2}\). Having conducted all of them successfully, we display the reaction force–displacement curves for the samples with standard CDM (Q1Q1) and CDM + EAS (Q1Q1E24) formulations in comparison with the purely neo-Hookean response run with ABAQUS C3D8 elements and it is envisaged the same performance for each scheme, see Fig. 6. Both formulations display a solid equivalence with the ABAQUS elements’ curve on the first stages of testing and, upon damage propagation, they both manage to capture the post-peak softening of the curve. Even though we get the same quantitative results, the most advantageous model for these configurations without shear locking is the Q1Q1 formulation, as the CDM + EAS model (Q1Q1E24) considers incompatible strains, which add up computational cost to the problem.
Reaction force–displacement curves for the compressible plate with a hole for the validation probes conducted with a standard CDM (Q1Q1) and CDM + EAS (Q1Q1E24), respectively, compared with ABAQUS C3D8 elements. Employed non-local damage parameters encompass: \(\eta _d= 0.1 \,\text {MPa}^{-1}\), \(\kappa _d \ = 0 \, \text {MPa}\) and \(c_d = 1000 \, \text {MPa}^{-1}\,\text {mm}^{2}\)
Having tested the verification quantitatively with ABAQUS samples, for a qualitative address, we plot the evolution of crack propagation for three different displacements, see Figs. 7a–c. In order to get a clear damage pattern, we have calibrated the non-local damage parameters for a final failure around \(u_z \ = 20 \ \text {mm}\), employing for this: \(\eta _d= 1 \ \text {MPa}^{-1}\), \(\kappa _d \ = 1 \ \text {MPa}\) and \(c_d = 500 \ \text {MPa}^{-1}\,\text {mm}^{2}\). Following an expected behavior, the first isocontour at Fig. 7a reveals its nucleation near the notched region (a stress concentrator) only to be continued by a mode I propagation, see Fig. 7b. In the end, it is observed that upon reaching the end of the width of the plate, the crack grows in the direction of the height of the specimen, see Fig. 7c. Therefore, with these micrographs of a foreseeable failure pattern, we can also verify the proposed CDM approach qualitatively, obtaining similar results for Q1Q1 and Q1Q1E24 formulations. It is important to highlight that a tolerance in the function \(f_d<0.05\) has been established to avoid ill-conditioning in the equations; the reader is referred to [42] for further information on this aspect.
5.2.3 Mesh objectivity
Isocontour plots for the damage function \(f_d\) of a plate with a hole plotting the crack pattern for several displacements: (a) \(u_z = 7.32 \, \text {mm}\), (b) \(u_z = 8.42 \, \text {mm}\) and (c) \(u_z = 19.10 \, \text {mm}\). Employed non-local damage parameters encompass: \(\eta _d= 1 \, \text {MPa}^{-1}\), \(\kappa _d \ = 1 \, \text {MPa}\) and \(c_d = 500\, \text {MPa}^{-1}\,\text {mm}^{2}\)
Another required calibration for CDM approaches concerns the verification for mesh independence, as the condition for mesh-objectivity is associated with the damage evolution being independent of the discretisation for high enough regularisation parameters \(c_d\). Therefore, we run a test for three different hexahedral meshes employing the non-local damage properties exhibited in Table 2: one coarse (810 elements), one medium-sized (9,595 elements) and one considerably refined (75,360 elements) mesh. The three simulations are compared by plotting the damage function isocontour \(f_d\) for a displacement of \(u_z = {8} \ \text {mm}\) in Fig. 8, and they turn out to be practically identical for both formulations Q1Q1 and Q1Q1E24, thus providing that the dissipation energy is independent of the size of the element.
5.2.4 Parametric study on the regularisation parameter \(c_d\)
Having proven that the results reasonably adjust to the theoretical nonlinear elastic behavior and that the proposed frameworks are mesh-objective, with the medium-sized discretisation (9,525 hexahedral elements), we have carried out a parametric analysis by leaving the degree of regularisation parameter \(c_d\) as a free variable. As in [42], in order to quantify the dependence of the mechanical behavior to this parameter, a parametric analysis is made with a range of \(c_d = \{10, 100, 500, 1000\} \ \text {MPa}^{-1}\,\text {mm}^{2}\) for the three different proposed formulations with the mechanical properties in Table 1. The employed parameters for the degradation law are \(\eta _d= 1 \ \text {MPa}^{-1}\) and \(\kappa _d \ = 1 \ \text {MPa}\).
Looking to prove the validity of both standard CDM and CDM + EAS approach to model this specimen, we exhibit the reaction-force displacement curves for values of \(c_d \ = 1000 \ \text {MPa}^{-1}\,\text {mm}^{2}\), \(c_d \ = 500 \ \text {MPa}^{-1}\,\text {mm}^{2}\) and \(c_d \ = 100 \ \text {MPa}^{-1}\,\text {mm}^{2}\) plotted in Figs. 9a–c, respectively. In fact, we can establish that both the standard CDM approach referred to as the current configuration, and the combined CDM + EAS approach, referred to as the reference configuration, do manage to capture the full mechanical behavior of the specimen until the failure of the sample, even though this last one requires more computational cost due to the calculation of the incompatible strains.
Staying with the most computationally efficient formulation i.e., Q1Q1, we realize a further comparison for the results with different \(c_d\) in Figs. 10 and 11. For the first series of images (Fig. 10), we have plotted several contour plots of the damage function \(f_d\) for different \(c_d\) and, nucleating from the notched region, the major difference is observed in the range of the affected region, being the gradient wider for lower values of \(c_d\), and the minimum value of \(f_d\), decreasing as the \(c_d\) parameter is augmented. Furthermore, by plotting the reaction force–displacement (Fig. 11a) and the minimum \(f_d\) value (Fig. 11b), we basically obtain that the failure of the specimen gets delayed by just increasing this regularisation parameter, increasing the maximum force and softening the collapse of the graph, being this result in line with what is exhibited in [42]. In addition to this, it is worth noting that the result for \(c_d = 10 \ \text {MPa}^{-1}\,\text {mm}^{2}\) falls short of reaching the peak behavior of the curve as it displays convergence issues, being this due that the mesh is not discretised enough for this low value of \(c_d\), meaning that for this mesh, the limit value of \(c_d\) for total convergence falls between this value and \(c_d = 100 \ \text {MPa}^{-1}\,\text {mm}^{2}\).
Isocontour plots for the damage function \(f_d\) for plates with a hole with different regularisation parameter \(c_d\) at \(u_z = 6.5 \, \text {mm}\). In here: (a) \(c_d = 100 \, \text {MPa}^{-1}\,\text {mm}^{2}\), (b) \(c_d = 500 \, \text {MPa}^{-1}\,\text {mm}^{2}\) and (c) \(c_d = 1000 \, \text {MPa}^{-1}\,\text {mm}^{2}\)
5.3 Plate with a hole—quasi-incompressible hyperelastic material
5.3.1 Test details
The next numerical example that we have considered is an incompressible version of the previous example, i.e., we increase the value of the bulk modulus K up to a value \(\sim 10^{7}\) MPa, associated with a Poisson ratio of \(\nu = 0.49999\). With only that subtle change, the same experiments that were carried out for the Sect. 5.2 are repeated, keeping the same geometry as Fig. 5 and the same material properties plotted in Table 1, except the aforementioned K.
For these series of tests, the schemes employed consist in both Q1Q1 and Q1Q1P0 formulations, as the EAS technique has been checked not to be appropriate to model nearly incompressible specimens (see Sect. 5.1). In line with the previous section for compressible samples (Sect. 5.2), we start with the verification of the CDM models by comparing them with the hybrid elements from ABAQUS (Sect. 5.3.2). Upon verification, we repeat the parametric analysis of the previous sections where we study the dependence of \(c_d\) on the mechanical behavior of the now nearly incompressible specimens (Sect. 5.3.3), where we end up elucidating which is the better formulation to conduct these numerical experiments.
5.3.2 Quantitative and qualitative validation
For the comparison between the standard (Q1Q1) and the three-field mixed CDM formulations (Q1Q1P0) with the referential two-field ABAQUS C3D8H element, required for computations with \(\nu > 0.475\), we plot the force–displacement curves in Fig. 12 for the conducted experiments run with damage properties: \(\eta _d= 0.5 \ \text {MPa}^{-1}\), \(\kappa _d \ = 0 \ \text {MPa}\) and \(c_d = 1000 \text {MPa}^{-1}\,\text {mm}^{2}\). It is observed that although the graphs manage to capture the post-peak behavior, it is the Q1Q1P0 formulation the better performer for this problem, as at the early stages of the curve, it solidly matches the ABAQUS referential graph, unlike the Q1Q1 which slightly overestimates the trajectory due to volumetric locking pathologies caused by \(\nu \sim 0.5\). The failure pattern for both formulations resembles the one plotted in Fig. 7, which are not shown here for the sake of brevity but do provide the qualitative check for the testing of nearly incompressible specimens.
Reaction force–displacement curves for the nearly incompressible plate with a hole for the validation probes conducted with a standard (Q1Q1) and the mixed u-p-J CDM formulations (Q1Q1P0), respectively, compared with ABAQUS C3D8H elements. Employed non-local damage parameters encompass: \(\eta _d= 0.5 \, \text {MPa}^{-1}\), \(\kappa _d \ = 0 \, \text {MPa}\) and \(c_d = 1000 \, \text {MPa}^{-1}\,\text {mm}^{2}\)
5.3.3 Parametric analysis on the regularisation parameter \(c_d\)
Considering the parameters for the degradation law to be \(\eta _d= 1 \ \text {MPa}^{-1}\) and \(\kappa _d \ = 1 \ \text {MPa}\), we perform the tests of extensive pulling for the nearly incompressible plates, conducting a parametric analysis in a range of \(c_d = \{10, 100, 500, 1000\} \ \text {MPa}^{-1}\,\text {mm}^{2}\). The results for both Q1Q1 and Q1Q1P0 formulations at (a) \(c_d \ = 1000 \ \text {MPa}^{-1}\,\text {mm}^{2}\), (b) \(c_d \ = 500 \ \text {MPa}^{-1}\,\text {mm}^{2}\) and (c) \(c_d \ = 100 \ \text {MPa}^{-1}\,\text {mm}^{2}\) are represented in Fig. 13. According to what was aforementioned in Sect. 5.3.2, standard CDM formulation provides an over-stiffened curve due to the incompressibility of the model that leads to the phenomenon of volumetric locking that does not address this scheme. For that reason, the most robust scheme to model this problem is deduced to be the Jacobian-pressure mixed framework. Even though that Q1Q1 theory provides a more prolonged softening of the curve during crack propagation, it is deduced from these results that the Q1Q1P0 element covers the volumetric locking pathology by considering both pressure and dilatation terms, see Eqs. (130)–(131), and that is proven by the reduction in the stiffness of the constitutive response of the sample shown in all the examples in Fig. 13.
Subsequently, it is exhibited the (a) reaction force–displacement curves and (b) the evolution of the minimum value of the damage function \(f_d\) associated with every displacement in Fig. 14, where is envisaged an overall analogous pattern than the one plotted for the compressible cases conducted with the standard CDM formulation, see Fig. 11, i.e., both peak force and displacement are augmented monotonically with the increase of the regularisation parameter. In addition to this, the slope for the decrease of the minimum value of \(f_d\) for changing displacements is also increased. Although not so robust on convergence as the Q1Q1 formulation for compressible specimens, with the quantitative and qualitative results provided in this section, Q1Q1P0 has provided to be a more solid formulation to model these incompressible experiments.
5.4 Cylindrical shell under a bending load—compressible materials
5.4.1 Test details
With the objective of addressing the further potential of the present frameworks (so far, the Q1Q1 and the Q1Q1E24 formulations have been proven to model large deformation problems for compressible specimens, while the Q1Q1P0 scheme have performed very robustly with volumetric locking pathologies in an incompressible problem), we aim to model the challenging problem of a cylindrical shell under a bending load. For this, a notched cylindrical specimen with the geometry and BCs exhibited in Fig. 15 is analyzed under extreme bending conditions to capture the capabilities of both EAS and three-field mixed FE formulations in modelling this large deformation problem prone to show locking pathologies. In line with the previous example, we have modelled both series of compressible and nearly incompressible material specimens. The notch has been considered to induce the onset of damage happening in the center.
Starting with the former cases, we have carried out several experiments with the material and damage properties plotted at Table 3 for specimens with a discretisation of 12,328 hexahedral elements. In order to avoid boundary effects, for the extremities of the cylindrical shell (where the fixed and the displacement conditions are applied), the damage saturation parameter \(\eta _d\) has been increased, so the damage pattern is not affected by these phenomena. The final deformed configuration with the mesh for the bending experiments is displayed in Fig. 16, exhibiting the amount of deformation in the sample experiments.
In line with the plate tests, we have started this subsection by simulating this experiment to establish a comparison between the formulations suitable for compressible specimens modelling, i.e., Q1Q1 and Q1Q1E24, with the referential ABAQUS elements in Sect. 5.4.2, additionally presenting the failure isocontour for this problem.
Subsequently, a parametric analysis on addressing the damage saturation parameter \(\eta _d\) is carried out in Sect. 5.4.3, where the main pursued aim is the comparison of both algorithms in displaying their potentiality to model this large deformation complex problem.
5.4.2 Quantitative and qualitative validation
To compare with a referential standpoint, we have conducted several tests with a damage saturation parameter \(\eta _d = 0.1 \ \text {MPa}^{-1}\) with Q1Q1 and Q1Q1E24 formulations, along with the theoretical ABAQUS elements with (C3D8I) and without (C3D8) incompatible deformation modes.
The displayed force–displacement curves, exhibited in Fig. 17, do reveal that the standard CDM approach (Q1Q1) follows the trajectory described by the ABAQUS C3D8 element in the early stages. However, both elements are affected by parasitic shear locking, showing an over-stiffening of the curve caused by this pathology. Concerning the CDM + EAS formulation (Q1Q1E24), it is observed a solid correlation between the mechanical performance of this element with the curve of the ABAQUS C3D8I element, which is the one required to model this kind of problems prone to locking i.e., under bending loads. It is worth highlighting that the match of these two curves is not perfect due to the EAS contribution being regularised via \(f_d\), affecting the terms in Eqs. (108)–(111), as these are multiplied by the function damage, meaning that the correction gets reduced as soon as the material gets damaged, being the EAS contribution eliminated upon total damage. This regularisation is done in order to avoid the convergence issues that arise by using this formulation, as the correction in the stiffness curve grows considerably throughout the experiment. However, this aspect does not undermine the potentiality of the CDM + EAS approach to model compressible materials under shear locking, as the correlation is very robust with the referential curve.
The damage evolution of the specimen during the test is displayed in Fig. 18. The crack onset occurs in the center of the width of the sample (Fig. 18a), being propagated afterwards in Mode I in the Z-direction, first to the extremities of the specimen (Fig. 18b) and then, in the direction towards the notch (Fig. 18c). These isocontours have been obtained from a test conducted by employing the for the Q1Q1E24 formulation with a damage saturation parameter of \(\eta _d = 0.5 \ \text {MPa}^{-1}\), demonstrating to be consistent with analysis until failure of a specimen under extreme bending conditions.
5.4.3 Parametric analysis on the saturation parameter \(\eta _d\)
This section is focused on analyzing the role of the saturation parameter in the mechanical performance of the specimen. Varying this \(\eta _d\) parameter in a range of \(\eta _d = \ \{0.5, 1, 2\} \ \text {MPa}^{-1}\) for both the Q1Q1 and the Q1Q1E24 formulations. The differences among them for \(\eta _d \ = \ 0.5 \ \text {MPa}^{-1}\) (Fig. 19a), \(\eta _d \ = \ 1 \ \text {MPa}^{-1}\) (Fig. 19b) and \(\eta _d \ = \ 2 \ \text {MPa}^{-1}\) (Fig. 19c) are exhibited by means of the force–displacement curves, where it can be deduced that the CDM + EAS formulation (Q1Q1E24) is verified to be a very effective tool to conduct the problem of extreme bending for compressible notched cylindrical shells, as is the better performer to tackle the shear locking phenomenon that causes an over-stiffening in the curves.
Intending to plot the \(\eta _d\) dependence on one single image, we put together the reaction force–displacement curves for the Q1Q1E24 formulation, along with the evolution of the minimum value of \(f_d\) in Fig. 20. It is deduced that the role of this parameter is similar to the one of \(c_d\), progressively delaying the failure of the sample along with augmenting the peak force when this saturation magnitude is increased.
5.5 Cylindrical shell under a bending load—incompressible materials
5.5.1 Test details
The last series of experiments consists of the modelling of the previous examples in Sect. 5.4, now for nearly incompressible specimens, carried out in order to test the validity of the mixed u-p-J CDM formulation (Q1Q1P0) to model this tricky problem. Employing the same configuration as in Fig. 15 and the same properties as in Table 3, but this time, changing the bulk modulus K up to a value of \(\sim 10^{7}\) MPa, associated with an established Poisson ratio of \(\nu = 0.49999\) and in line with what has been realized in the previous sections, we start by comparing the results of Q1Q1 and Q1Q1P0 schemes with the same tests conducted with ABAQUS elements in Sect. 5.5.2. Once this demonstration has been fulfilled, a last parametric analysis addressing the dependence on the saturation parameter \(\eta _d\) is conducted in Sect. 5.5.3.
Load–displacement curves for the incompressible cylindrical shell test conducted for Q1Q1 and Q1Q1P0 formulations compared with the ABAQUS hybrid theoretical curves with (C3D8IH) and without considering incompatible modes (C3D8H). The employed saturation parameter has been \(\eta _d = 0.1 \, \text {MPa}^{-1}\)
5.5.2 Quantitative and qualitative validation
Displaying the same failure pattern as the one exhibited for compressible specimens (see Fig. 18, which is not included here for the sake of brevity), we focus now on a quantitative viewpoint with the two proposed formulations along with the referential ABAQUS elements, see Fig. 21. First, we can definitely conclude that Q1Q1 formulation is not suitable to model this problem as both the volumetric and shear locking cause a very abrupt rise of the load of the sample, justifying the invalidation of this formulation.
Concerning the mixed u-p-J CDM (Q1Q1P0) formulation, it can be observed that it covers the volumetric locking solidly, as the curve is below the one related to the behavior of the hybrid element ABAQUS C3D8H. However, it falls short of covering the shear locking, as this graph is considerably less compliant than the hybrid ABAQUS element that considers incompatible deformation modes (C3D8IH), i.e., the one required to run this simulation. Observing how robustly did perform the Q1Q1E24 formulation in the compressible cases analyzed in Sect. 5.4, the extension of the present formulation of \(\texttt {Q1Q1P0}\) to \(\texttt {Q1Q1P0E24}\) is proposed to model these specimens and will be addressed in future work.
5.5.3 Parametric analysis on the saturation parameter
Considering the same range for the damage saturation parameter \(\eta _d = \{0.5, 1, 2\} \ \text {MPa}^{-1}\), at last, we plot in a single curve all the load-displacement curves for different \(\eta _d\) conducted by Q1Q1P0 (see Fig. 22a), along with the minimum value of the degradation law \(f_d\) for every displacement (see Fig. 22b). What is envisaged in this last representation is an analogy of what was exhibited before for the compressible specimens: with the reduction in \(\eta _d\), the softening in the quantitative response associated with the mechanical performance is delayed. Therefore, even though there is no solid correlation with the theory, the \(\texttt {Q1Q1P0}\) formulation has proven to be the one among the three conducted schemes to proportionate conclusive results for the large deformation bending tests applied on cylindrical shells.
6 Conclusions
Within this article, a duo of gradient-enhanced continuum damage formulations has been developed to model failure in compressible and incompressible isotropic hyperelastic specimens, with the main focus of addressing the volumetric and shear locking pathologies. Among these experiments, the samples have been tested to a wide range of different types of loading, including traction, compression, and bending, comparing the two novel schemes, Q1Q1E24 and Q1Q1P0, with the Q1Q1 referential CDM formulation.
Making a one-by-one analysis of the performance of the aforementioned schemes, first, the spatial standard CDM framework (Q1Q1), based on the one proposed by [42], has been validated in this work to be a remarkable instrument in modelling damage in compressible structures subject to extensive pulling. However, it has exhibited both volumetric and shear locking in incompressible specimens under compression and bending status, respectively.
Therefore, in order to overcome these locking pathologies, the 24-incompatible modes EAS technique Q1Q1E24 and the mixed displacement-Jacobian-pressure FE formulation Q1Q1P0 have been proposed for their use. Q1Q1E24 scheme is proven to solve the shear locking phenomenon in compressible samples, while the employment of Q1Q1P0 formulation, by considering both the pressure and the dilatation as separate DOFs, has been demonstrated to be a more than a remarkable instrument in modelling complex incompressible cases, correcting the volumetric locking pathology.
We also have demonstrated that Q1Q1E24 element performs poorly in predicting damage in incompressible materials, while Q1Q1P0 overestimates the curve in structures subject to bending loads, i.e., displaying shear locking. Therefore, to tackle this, further approaches combining EAS with the mixed Jacobian-pressure formulations will be proposed in the future. In addition to this, an extension to model anisotropic hyperelastic almost incompressible materials is proposed here for future work, being envisaged as a compelling but challenging extension of the proposed frameworks, considering the distortion that such kind of materials exhibit during pure pressure loading [108].
References
Hoang-Ngoc C-T, Paroissien E (2010) Simulation of single-lap bonded and hybrid (bolted/bonded) joints with flexible adhesive. Int J Adhes Adhes 30(3):117–129. https://doi.org/10.1016/j.ijadhadh.2009.12.002
Long R, Shull KR, Hui C-Y (2010) Large deformation adhesive contact mechanics of circular membranes with a flat rigid substrate. J Mech Phys Solids 58(9):1225–1242. https://doi.org/10.1016/j.jmps.2010.06.007
Dispersyn J, Hertelé S, Waele WD, Belis J (2017) Assessment of hyperelastic material models for the application of adhesive point-fixings between glass and metal. Int J Adhes Adhes 77:102–117. https://doi.org/10.1016/j.ijadhadh.2017.03.017
Guccione JM, McCulloch AD, Waldman LK (1991) Passive material properties of intact ventricular myocardium determined from a cylindrical model. J Biomech Eng 113(1):42–55. https://doi.org/10.1115/1.2894084
Pamplona DC, Gonçalves PB, Lopes SRX (2006) Finite deformations of cylindrical membrane under internal pressure. Int J Mech Sci 48(6):683–696. https://doi.org/10.1016/j.ijmecsci.2005.12.007
Grytz R, Meschke G (2009) Constitutive modeling of crimped collagen fibrils in soft tissues. J Mech Behav Biomed Mater 2(5):522–533. https://doi.org/10.1016/j.jmbbm.2008.12.009
Rodríguez J, Merodio J (2011) A new derivation of the bifurcation conditions of inflated cylindrical membranes of elastic material under axial loading. Application to aneurysm formation. Mech Res Commun 38(3):203–210. https://doi.org/10.1016/j.mechrescom.2011.02.004
Alhayani AA, Rodríguez J, Merodio J (2014) Competition between radial expansion and axial propagation in bulging of inflated cylinders with application to aneurysms propagation in arterial wall tissue. Int J Eng Sci 85:74–89. https://doi.org/10.1016/j.ijengsci.2014.08.008
Holzapfel GA, Gasser TC (2001) A viscoelastic model for fiber-reinforced composites at finite strains: Continuum basis, computational aspects and applications. Comput Methods Appl Mech Eng 190(34):4379–4403. https://doi.org/10.1016/S0045-7825(00)00323-6
Miehe C (2002) Strain-driven homogenization of inelastic microstructures and composites based on an incremental variational formulation. Int J Numer Methods Eng 55(11):1285–1322. https://doi.org/10.1002/nme.515
deBotton G, Hariton I, Socolsky EA (2006) Neo-Hookean fiber-reinforced composites in finite elasticity. J Mech Phys Solids 54(3):533–559. https://doi.org/10.1016/j.jmps.2005.10.001
Charmetant A, Vidal-Sallé E, Boisse P (2011) Hyperelastic modelling for mesoscopic analyses of composite reinforcements. Compos Sci Technol 71(14):1623–1631. https://doi.org/10.1016/j.compscitech.2011.07.004
Areias PMA, Belytschko T (2005) Non-linear analysis of shells with arbitrary evolving cracks using XFEM. Int J Numer Methods Eng 62(3):384–415. https://doi.org/10.1002/nme.1192
Belytschko T, Gracie R, Ventura G (2009) A review of extended/generalized finite element methods for material modeling. Model Simul Mater Sci Eng. https://doi.org/10.1088/0965-0393/17/4/043001
Roth S-N, Léger P, Soulaïmani A (2015) A combined XFEM-damage mechanics approach for concrete crack propagation. Comput Methods Appl Mech Eng 283:923–955. https://doi.org/10.1016/j.cma.2014.10.043
Tvergaard V (2003) Cohesive zone representations of failure between elastic or rigid solids and ductile solids. Eng Fract Mech 70(14):1859–1868. https://doi.org/10.1016/S0013-7944(03)00128-0. (Cohesive Models)
Yang QD, Cox BN, Nalla RK, Ritchie RO (2006) Fracture length scales in human cortical bone: the necessity of nonlinear fracture models. Biomaterials 27(9):2095–2113. https://doi.org/10.1016/j.biomaterials.2005.09.040
García-Guzmán L, Távara L, Reinoso J, Justo J, París F (2019) Analysis of 3d printed trapezoidal interfaces by means of a novel cohesive-based analytical approach. J Multiscale Model 10(03):1842001. https://doi.org/10.1142/S1756973718420015
Miehe C, Schänzel L-M (2014) Phase field modeling of fracture in rubbery polymers. Part I: finite elasticity coupled with brittle failure. J Mech Phys Solids 65:93–113. https://doi.org/10.1016/j.jmps.2013.06.007
Raina A, Miehe C (2016) A phase-field model for fracture in biological tissues. Biomech Model Mechanobiol 15(3):479–496. https://doi.org/10.1007/s10237-015-0702-0
Kumar A, Francfort GA, Lopez-Pamies O (2018) Fracture and healing of elastomers: a phase-transition theory and numerical implementation. J Mech Phys Solids 112:523–551. https://doi.org/10.1016/j.jmps.2018.01.003
Talamini B, Mao Y, Anand L (2018) Progressive damage and rupture in polymers. J Mech Phys Solids 111:434–457. https://doi.org/10.1016/j.jmps.2017.11.013
Tang S, Zhang G, Guo TF, Guo X, Liu WK (2019) Phase field modeling of fracture in nonlinearly elastic solids via energy decomposition. Comput Methods Appl Mech Eng 347:477–494. https://doi.org/10.1016/j.cma.2018.12.035
Mandal TK, Nguyen VP, Wu J-Y (2020) A length scale insensitive anisotropic phase field fracture model for hyperelastic composites. Int J Mech Sci 188:105941. https://doi.org/10.1016/j.ijmecsci.2020.105941
Paggi M, Reinoso J (2017) Revisiting the problem of a crack impinging on an interface: a modeling framework for the interaction between the phase field approach for brittle fracture and the interface cohesive zone model. Comput Methods Appl Mech Eng 321:145–172. https://doi.org/10.1016/j.cma.2017.04.004
Paggi M, Corrado M, Reinoso J (2018) Fracture of solar-grade anisotropic polycrystalline silicon: a combined phase field-cohesive zone model approach. Comput Methods Appl Mech Eng 330:123–148. https://doi.org/10.1016/j.cma.2017.10.021
Quintanas-Corominas A, Turon A, Reinoso J, Casoni E, Paggi M, Mayugo JA (2020) A phase field approach enhanced with a cohesive zone model for modeling delamination induced by matrix cracking. Comput Methods Appl Mech Eng 358:112618. https://doi.org/10.1016/j.cma.2019.112618
Kumar Asur Vijaya, P.K., Dean, A., Reinoso, J., Paggi, M. (2021) A multi phase-field-cohesive zone model for laminated composites: application to delamination migration. Compos Struct 276:114471. https://doi.org/10.1016/j.compstruct.2021.114471
Marulli MR, Valverde-González A, Quintanas-Corominas A, Paggi M, Reinoso J (2022) A combined phase-field and cohesive zone model approach for crack propagation in layered structures made of nonlinear rubber-like materials. Comput Methods Appl Mech Eng 395:115007. https://doi.org/10.1016/j.cma.2022.115007
Lasry D, Belytschko T (1988) Localization limiters in transient problems. Int J Solids Struct 24(6):581–597. https://doi.org/10.1016/0020-7683(88)90059-5
Polizzotto C, Borino G, Fuschi P (1998) A thermodynamically consistent formulation of nonlocal and gradient plasticity. Mech Res Commun 25(1):75–82. https://doi.org/10.1016/S0093-6413(98)00009-3
de Vree JHP, Brekelmans WAM, van Gils MAJ (1995) Comparison of nonlocal approaches in continuum damage mechanics. Comput Struct 55(4):581–588. https://doi.org/10.1016/0045-7949(94)00501-S
de Borst R, Pamin J (1996) Some novel developments in finite element procedures for gradient-dependent plasticity. Int J Numer Methods Eng 39(14):2477–2505. https://doi.org/10.1002/(SICI)1097-0207(19960730)39:14<2477::AID-NME962>3.0.CO;2-E
Pamin J (2005) Gradient plasticity and damage models: a short comparison. Comput Mater Sci 32(3):472–479. https://doi.org/10.1016/j.commatsci.2004.09.018. (IWCMM)
Peerlings RHJ, de Borst R, Brekelmans WAM, de Vree JHP (1996) Gradient enhanced damage for quasi-brittle materials. Int J Numer Methods Eng 39(19):3391–3403. https://doi.org/10.1002/(SICI)1097-0207(19961015)39:19<3391::AID-NME7>3.0.CO;2-D
Kuhl E, Ramm E (1999) Simulation of strain localization with gradient enhanced damage models. Comput Mater Sci 16(1):176–185. https://doi.org/10.1016/S0927-0256(99)00060-9
Kuhl E, Ramm E, Borst R (2000) An anisotropic gradient damage model for quasi-brittle materials. Comput Methods Appl Mech Eng 183:87–103. https://doi.org/10.1016/S0045-7825(99)00213-3
Steinmann P (1999) Formulation and computation of geometrically non-linear gradient damage. Int J Numer Meth Eng 46(5):757–779. https://doi.org/10.1002/(SICI)1097-0207(19991020)46:5<757::AID-NME731>3.0.CO;2-N
Liebe T, Menzel A, Steinmann P (2003) Theory and numerics of geometrically non-linear gradient plasticity. Int J Eng Sci 41(13):1603–1629. https://doi.org/10.1016/S0020-7225(03)00030-2. (Damage and failure analysis of materials)
Dimitrijevic B, Hackl K (2008) A method for gradient enhancement of continuum damage models. Tech Mech 1:43–52
Wcisło B, Pamin J, Kowalczyk-Gajewska K (2013) Gradient-enhanced damage model for large deformations of elastic-plastic materials. Arch Mech 65:407–428
Waffenschmidt T, Polindara C, Menzel A, Blanco S (2014) A gradient-enhanced large-deformation continuum damage model for fibre-reinforced materials. Comput Methods Appl Mech Eng 268:801–842. https://doi.org/10.1016/j.cma.2013.10.013
Al-Rub RKA, Voyiadjis GZ (2006) A finite strain plastic-damage model for high velocity impact using combined viscosity and gradient localization limiters: Part I—theoretical formulation. Int J Damage Mech 15(4):293–334. https://doi.org/10.1177/1056789506058046
Brepols T, Wulfinghoff S, Reese S (2017) Gradient-extended two-surface damage-plasticity: micromorphic formulation and numerical aspects. Int J Plast 97:64–106. https://doi.org/10.1016/j.ijplas.2017.05.010
Alipour A, Reese S, Wulfinghoff S (2019) A grain boundary model for gradient-extended geometrically nonlinear crystal plasticity: theory and numerics. Int J Plast 118:17–35. https://doi.org/10.1016/j.ijplas.2019.01.009
Brepols T, Wulfinghoff S, Reese S (2020) A gradient-extended two-surface damage-plasticity model for large deformations. Int J Plast 129:102635. https://doi.org/10.1016/j.ijplas.2019.11.014
Rivlin RS, Saunders DW, Andrade ENDC (1951) Large elastic deformations of isotropic materials VII. Experiments on the deformation of rubber. Philos Trans R Soc Lond Ser A Math Phys Sci 243(865):251–288. https://doi.org/10.1098/rsta.1951.0004
Rodriguez EK, Hoger A, McCulloch AD (1994) Stress-dependent finite growth in soft elastic tissues. J Biomech 27(4):455–467. https://doi.org/10.1016/0021-9290(94)90021-3
Hughes T (2000) The finite element method: linear static and dynamic finite element analysis. vol 78 (2000)
Belytschko T, Lu YY, Gu L (1994) Element-free Galerkin methods. Int J Numer Methods Eng 37(2):229–256. https://doi.org/10.1002/nme.1620370205
Atluri SN, Zhu T-L (2000) The meshless local Petrov-Galerkin (MLPG) approach for solving problems in elasto-statics. Comput Mech 25(2):169–179. https://doi.org/10.1007/s004660050467
Ortiz A, Puso MA, Sukumar N (2010) Maximum-entropy meshfree method for compressible and near-incompressible elasticity. Comput Methods Appl Mech Eng 199(25):1859–1871. https://doi.org/10.1016/j.cma.2010.02.013
Zhang GY, Wittek A, Joldes GR, Jin X, Miller K (2014) A three-dimensional nonlinear meshfree algorithm for simulating mechanical responses of soft tissue. Eng Anal Bound Elem 42:60–66. https://doi.org/10.1016/j.enganabound.2013.08.014
Dai KY, Liu GR, Nguyen TT (2007) An n-sided polygonal smoothed finite element method (nSFEM) for solid mechanics. Finite Elem Anal Des 43(11):847–860. https://doi.org/10.1016/j.finel.2007.05.009
Liu GR, Nguyen-Thoi T, Lam KY (2009) An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J Sound Vib 320(4):1100–1130. https://doi.org/10.1016/j.jsv.2008.08.027
Nguyen-Thoi T, Liu GR, Lam KY, Zhang GY (2009) A face-based smoothed finite element method (FS-FEM) for 3D linear and geometrically non-linear solid mechanics problems using 4-node tetrahedral elements. Int J Numer Methods Eng 78(3):324–353. https://doi.org/10.1002/nme.2491
Hansbo P, Larson MG (2002) Discontinuous Galerkin methods for incompressible and nearly incompressible elasticity by Nitsche’s method. Comput Methods Appl Mech Eng 191(17):1895–1908. https://doi.org/10.1016/S0045-7825(01)00358-9
Kaufmann P, Martin S, Botsch M, Gross M (2009) Flexible simulation of deformable models using discontinuous Galerkin fem. Graph Models 71(4):153–167. https://doi.org/10.1016/j.gmod.2009.02.002. (Special Issue of ACM SIGGRAPH/Eurographics Symposium on Computer Animation 2008)
Nguyen NC, Peraire J (2012) Hybridizable discontinuous Galerkin methods for partial differential equations in continuum mechanics. J Comput Phys 231(18):5955–5988. https://doi.org/10.1016/j.jcp.2012.02.033
Wulfinghoff S, Bayat H, Alipour A, Reese S (2017) A low-order locking-free hybrid discontinuous Galerkin element formulation for large deformations. Comput Methods Appl Mech Eng 323:353–372. https://doi.org/10.1016/j.cma.2017.05.018
Malkus DS, Hughes TJR (1978) Mixed finite element methods—reduced and selective integration techniques: a unification of concepts. Comput Methods Appl Mech Eng 15(1):63–81. https://doi.org/10.1016/0045-7825(78)90005-1
Pastor M, Quecedo M, Zienkiewicz OC (1997) A mixed displacement-pressure formulation for numerical analysis of plastic failure. Comput Struct 62(1):13–23. https://doi.org/10.1016/S0045-7949(96)00208-8
Li KP, Cescotto S (1997) An 8-node brick element with mixed formulation for large deformation analyses. Comput Methods Appl Mech Eng 141(1):157–204. https://doi.org/10.1016/S0045-7825(96)01071-7
Bonet J, Burton AJ (1998) A simple average nodal pressure tetrahedral element for incompressible and nearly incompressible dynamic explicit applications. Commun Numer Methods Eng 14(5):437–449. https://doi.org/10.1002/(SICI)1099-0887(199805)14:5<437::AID-CNM162>3.0.CO;2-W
Chiumenti M, Cervera M, Codina R (2015) A mixed three-field FE formulation for stress accurate analysis including the incompressible limit. Comput Methods Appl Mech Eng 283:1095–1116. https://doi.org/10.1016/j.cma.2014.08.004
Simo JC, Taylor RL, Pister KS (1985) Variational and projection methods for the volume constraint in finite deformation elasto-plasticity. Comput Methods Appl Mech Eng 51(1):177–208. https://doi.org/10.1016/0045-7825(85)90033-7
Simo JC, Taylor RL (1991) Quasi-incompressible finite elasticity in principal stretches. Continuum basis and numerical algorithms. Comput Methods Appl Mech Eng 85(3):273–310. https://doi.org/10.1016/0045-7825(91)90100-K
Miehe C (1994) Aspects of the formulation and finite element implementation of large strain isotropic elasticity. Int J Numer Methods Eng 37(12):1981–2004. https://doi.org/10.1002/nme.1620371202
Loehnert S, Munk L (2020) A mixed extended finite element for the simulation of cracks and heterogeneities in nearly incompressible materials and metal plasticity. Eng Fract Mech 237:107217. https://doi.org/10.1016/j.engfracmech.2020.107217
Bargellini R, Besson J, Lorentz E, Michel-Ponnelle S (2009) A non-local finite element based on volumetric strain gradient: application to ductile fracture. Comput Mater Sci 45(3):762–767. https://doi.org/10.1016/j.commatsci.2008.09.020. (Proceedings of the 17th international workshop on computational mechanics of materials)
Alessi R, Freddi F, Mingazzi L (2020) Phase-field numerical strategies for deviatoric driven fractures. Comput Methods Appl Mech Eng 359:112651. https://doi.org/10.1016/j.cma.2019.112651
Mang K, Wick T, Wollner W (2020) A phase-field model for fractures in nearly incompressible solids. Comput Mech 65(1):61–78. https://doi.org/10.1007/s00466-019-01752-w
Tian F, Zeng J, Zhang M, Li L (2022) Mixed displacement-pressure-phase field framework for finite strain fracture of nearly incompressible hyperelastic materials. Comput Methods Appl Mech Eng 394:114933. https://doi.org/10.1016/j.cma.2022.114933
Ostwald R, Kuhl E, Menzel A (2019) On the implementation of finite deformation gradient-enhanced damage models. Comput Mech 64(3):847–877. https://doi.org/10.1007/s00466-019-01684-5
Wriggers P (2008) Nonlinear finite element methods. vol 4. https://doi.org/10.1007/978-3-642-56865-7
Babuska I, Szabo BA, Katz IN (1981) The p-version of the finite element method. SIAM J Numer Anal 18(3):515–545. https://doi.org/10.1137/0718033
Düster A, Niggl A, Nübel V, Rank E (2002) A numerical investigation of high-order finite elements for problems of elastoplasticity. J Sci Comput 17(1):397–404. https://doi.org/10.1023/A:1015189706770
Düster A, Hartmann S, Rank E (2003) p-fem applied to finite isotropic hyperelastic bodies. Comput Methods Appl Mech Eng 192(47):5147–5166. https://doi.org/10.1016/j.cma.2003.07.003
Hughes TJR, Cottrell JA, Bazilevs Y (2005) Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput Methods Appl Mech Eng 194(39):4135–4195. https://doi.org/10.1016/j.cma.2004.10.008
Beirão da Veiga L, Lovadina C, Reali A (2012) Avoiding shear locking for the Timoshenko beam problem via isogeometric collocation methods. Comput Methods Appl Mech Eng 241–244:38–51. https://doi.org/10.1016/j.cma.2012.05.020
Thai CH, Kulasegaram S, Tran LV, Nguyen-Xuan H (2014) Generalized shear deformation theory for functionally graded isotropic and sandwich plates based on isogeometric approach. Comput Struct 141:94–112. https://doi.org/10.1016/j.compstruc.2014.04.003
Yin S, Hale JS, Yu T, Bui TQ, Bordas SPA (2014) Isogeometric locking-free plate element: a simple first order shear deformation theory for functionally graded plates. Compos Struct 118:121–138. https://doi.org/10.1016/j.compstruct.2014.07.028
Belytschko T, Liu W, Moran B (2000) Nonlinear finite elements for continua and structures. Wiley. https://doi.org/10.1055/s-2006-943830
Bayat HR, Wulfinghoff S, Kastian S, Reese S (2018) On the use of reduced integration in combination with discontinuous Galerkin discretization: application to volumetric and shear locking problems. Adv Model Simul Eng Sci 5(1):10. https://doi.org/10.1186/s40323-018-0103-x
Wilson EL, Taylor RL, Doherty WP, Ghaboussi J (1973) Incompatible displacement models. In: Fenves SJ, Perrone N, Robinson AR, Schnobrich WC (eds) Numerical and computer methods in structural mechanics. Academic Press, pp 43–57. https://doi.org/10.1016/B978-0-12-253250-4.50008-7
Simo JC, Rifai MS (1990) A class of mixed assumed strain methods and the method of incompatible modes. Int J Numer Methods Eng 29(8):1595–1638. https://doi.org/10.1002/nme.1620290802
Simo JC, Armero F (1992) Geometrically non-linear enhanced strain mixed methods and the method of incompatible modes. Int J Numer Methods Eng 33(7):1413–1449. https://doi.org/10.1002/nme.1620330705
Mueller-Hoeppe DS, Loehnert S, Wriggers P (2009) A finite deformation brick element with inhomogeneous mode enhancement. Int J Numer Methods Eng 78(10):1164–1187. https://doi.org/10.1002/nme.2523
Andelfinger U, Ramm E (1993) EAS-elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements. Int J Numer Methods Eng 36(8):1311–1337. https://doi.org/10.1002/nme.1620360805
Betsch P, Stein E (1995) An assumed strain approach avoiding artificial thickness straining for a non-linear 4-node shell element. Commun Numer Methods Eng 11(11):899–909. https://doi.org/10.1002/cnm.1640111104
Klinkel S, Gruttmann F, Wagner W (1999) A continuum based three-dimensional shell element for laminated structures. Comput Struct 71(1):43–62. https://doi.org/10.1016/S0045-7949(98)00222-3
Eberlein R, Wriggers P (1999) Finite element concepts for finite elastoplastic strains and isotropic stress response in shells: theoretical and computational analysis. Comput Methods Appl Mech Eng 171(3):243–279. https://doi.org/10.1016/S0045-7825(98)00212-6
Reinoso J, Blázquez A (2016) Application and finite element implementation of 7-parameter shell element for geometrically nonlinear analysis of layered CFRP composites. Compos Struct 139:263–276. https://doi.org/10.1016/j.compstruct.2015.12.009
Reinoso J, Paggi M, Areias P, Blázquez A (2019) Surface-based and solid shell formulations of the 7-parameter shell model for layered CFRP and functionally graded power-based composite structures. Mech Adv Mater Struct 26(15):1271–1289. https://doi.org/10.1080/15376494.2018.1432802
Wriggers P, Reese S (1996) A note on enhanced strain methods for large deformations. Comput Methods Appl Mech Eng 135(3):201–209. https://doi.org/10.1016/0045-7825(96)01037-7
Reinoso J, Paggi M, Linder C (2017) Phase field modeling of brittle fracture for enhanced assumed strain shells at large deformations: formulation and finite element implementation. Comput Mech 59(6):981–1001. https://doi.org/10.1007/s00466-017-1386-3
Kumar PKAV, Dean A, Sahraee S, Reinoso J, Paggi M (2022) Non-linear thermoelastic analysis of thin-walled structures with cohesive-like interfaces relying on the solid shell concept. Finite Elem Anal Des 202:103696. https://doi.org/10.1016/j.finel.2021.103696
Kumar Asur Vijaya, P.K., Dean, A., Reinoso, J., Paggi, M. (2022) Nonlinear thermo-elastic phase-field fracture of thin-walled structures relying on solid shell concepts. Comput Methods Appl Mech Eng 396:115096. https://doi.org/10.1016/j.cma.2022.115096
Barfusz O, van der Velden T, Brepols T, Reese S (2022) Gradient-extended damage analysis with reduced integration-based solid-shells at large deformations. Comput Methods Appl Mech Eng 389:114317. https://doi.org/10.1016/j.cma.2021.114317
Liebe T, Steinmann P, Benallal A (2001) Theoretical and computational aspects of a thermodynamically consistent framework for geometrically linear gradient damage. Comput Methods Appl Mech Eng 190(49):6555–6576. https://doi.org/10.1016/S0045-7825(01)00250-X
Forest S (2009) Micromorphic approach for gradient elasticity, viscoplasticity, and damage. J Eng Mech 135(3):117–131. https://doi.org/10.1061/(ASCE)0733-9399(2009)135:3(117)
Simo JC, Hughes TJR (1998) Computational inelasticity, vol 7, 1st edn. Interdisciplinary applied mathematics. Springer, New York. https://doi.org/10.1007/b98904
Bischoff M, Ramm E (1997) Shear deformable shell elements for large strains and rotations. Int J Numer Methods Eng 40(23):4427–4449. https://doi.org/10.1002/(SICI)1097-0207(19971215)40:23<4427::AID-NME268>3.0.CO;2-9
Miehe C (1998) A theoretical and computational model for isotropic elastoplastic stress analysis in shells at large strains. Comput Methods Appl Mech Eng 155(3):193–233. https://doi.org/10.1016/S0045-7825(97)00149-7
Budarapu PR, Reinoso J, Paggi M (2017) Concurrently coupled solid shell-based adaptive multiscale method for fracture. Comput Methods Appl Mech Eng 319:338–365. https://doi.org/10.1016/j.cma.2017.02.023
Guillén-Hernández T, Reinoso J, Paggi M (2022) Phase field model for fracture analysis of functionally graded power-based shell structures. Mech Adv Mater Struct 29(1):78–88. https://doi.org/10.1080/15376494.2020.1751354
Reese S, Wriggers P, Reddy BD (2000) A new locking-free brick element technique for large deformation problems in elasticity. Comput Struct 75(3):291–304. https://doi.org/10.1016/S0045-7949(99)00137-6
Pence TJ (2014) Distortion of anisotropic hyperelastic solids under pure pressure loading: compressibility, incompressibility and near-incompressibility. J Elast 114(2):251–273. https://doi.org/10.1007/s10659-013-9438-1
Acknowledgements
AVG acknowledges the financial support from Erasmus+ funding (Project 2020-1-IT02-KA103-078114) for his visiting time in University of Seville during the period 15/03-15/06 2022. JR appreciates the financial support of the Junta de Andalucía Consejería de Economía y Conocimiento, Junta de Andalucía, and European Regional Development Fund (Project P20-00595) and Ministerio de Ciencia e Innovación (TED2021-131649B-I00). BD acknowledges funding from the National Science Foundation (NSF) through the DMREF program under grant number CMMI 2119716. MP would like to thank the Italian Ministry of University and Research for supporting the project of national interest PRIN “XFAST-SIMS: Extra fast and accurate simulation of complex structural systems” (MUR code 20173C478N).
Funding
Open access funding provided by Scuola IMT Alti Studi Lucca within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Valverde-González, A., Reinoso, J., Dortdivanlioglu, B. et al. Locking treatment of penalty-based gradient-enhanced damage formulation for failure of compressible and nearly incompressible hyperelastic materials. Comput Mech 72, 635–662 (2023). https://doi.org/10.1007/s00466-023-02314-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02314-x