1 Introduction

Shear assisted process extrusion (ShAPE) and friction stir welding (FSW) are related solid phase processes that apply mechanical forces to heat up and remold source materials by plunging a rotating tool into the material. Typically all necessary heat for processing is supplied by the interaction of the tool and material, giving solid phase processes the potential to be less expensive and more efficient than conventional approaches. The micro-structures and properties of final products from these processes are often tightly linked to the processing temperature [1,2,3,4,5]. Thus it is crucial to predict the effect of material processing parameters on the temperature field. A complete model of the interactions between temperature, mechanical inputs, and heat generation requires fully coupled thermo-mechanical models that can be both time and computationally intensive.

Extensive modeling has been undertaken for FSW processes, many employing fluid dynamics models but solid-based models have also been used [6,7,8,9,10,11]. More recently as friction stir extrusion (FSE) processes have become better developed more modeling of FSE has also been done [12,13,14,15]. The severe deformation of materials and thermo-mechanical interaction make modeling FSE and FSW processes difficult. Different approaches have been developed to model deformation, temperature and mass flow. For example, smoothed particle hydrodynamics approaches [12, 16], have been successful on these difficult problems. However, the simulation time can be on the order of days even when using high performance computing resources [12]. Models also require many parameters that are challenging to measure and/or have large uncertainty, which limits the predictive capability of the models. Schmidt et al. [17] proposed lower fidelity models of FSW for applications that do not require the detail provided by full physics models and suggested the use of experimental or phenomenological based constraints to bridge the gap between simplified thermodynamics and the physics of the process. In related thermo-mechanical modeling work neural networks have been trained to replace classical constitutive equations and are then used to simplify model solutions [18,19,20]. With sufficient data neural networks have the potential to be more accurate than approximation theories for constitutive relationships and can be efficient tools for bridging multiple scales. Recent efforts on methods for integrating physics knowledge into machine learning architectures are surveyed in [21]. A prominent approach called physics informed neural networks (PINNs) bypass traditional solvers by learning solutions that satisfy physical relations (e.g., partial differential equations PDE) and have shown promise for thermo-mechanical modeling [22, 23]. In this work, we take a machine learning approach to model temperature during an FSE process by coupling a simplified thermodynamics model with a learned neural network model of heat generation due to mechanical inputs.

Specifically, we model temperature dynamics under Shear Assisted Processing and Extrusion (ShAPE), a recently developed FSE process [24, 25]. ShAPE extrudes plasticized source materials including powder, flake, chips, and solid billets through a rotating die into consolidated tubes, rods, or wires. Temperature dynamics due to heat transport during processing such as conduction and convection can be captured with conventional models. However, it is challenging to model heat generation under ShAPE which includes contributions from multiple sources including friction between the tool and the billet as well as plastic deformation [26]. Generally, most of the heat generation during ShAPE and FSW is attributed to plastic deformation mechanisms [12, 27]. It is well known that aside from the elastic–plastic properties of materials, a number of factors such as grain size, grain texture, and loading condition also affect the plastic deformation, hence, the heat generation and temperature. Crystal plasticity theory takes into account these important factors [28]. In this work, crystal plasticity theory is used to simulate the effect of grain structures and loading conditions on heat generation during ShAPE. Due to the scale of ShAPE using crystal plasticity simulations to directly model temperature at the macro scale is computationally intractable. Moreover, accurately predicting macro temperature dynamics requires precise knowledge of material properties and micro-structural evolution during processing which is difficult or impossible to measure.

In this work we present a novel approach for learning the complicated feedback between process inputs and heat generation is solid state processing which is critical to process design and control. We demonstrate how combining a simplified model of heat dynamics with a learned neural network can accurately fit experimental measurements. Further, we construct an interpretable approach and show that the learned relationships between process inputs and heat generation from our model qualitatively match what we found using crystal plasticity simulations.

This paper is laid out as follows, in Sect. 2 we describe the ShAPE process. Section 3 details the modeling of the heat generation due to plastic deformation under typical stress states during ShAPE. Section 4 describes the dynamic model of temperature evolution using machine learning, and Sect. 5 reports the results against experimental data. Finally, conclusions and remarks are given in Sect. 6.

2 Shear assisted processing and extrusion

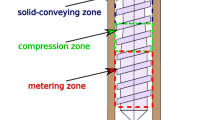
Shear Assisted Processing and Extrusion (ShAPE) includes a shear tool that applies a rotational shear force and an axial extrusion force to plasticize billet material. The plasticized material is then extruded through a die along the inner bore of the rotating shear tool, which can produce hollow or solid extrusion structures. Figure 1a schematically shows the structure of the ShAPE equipment. The red lines denote the interface region between the billet materials and tool face where friction heat is generated by axial extrusion force and high shear stress, as well as where plastic deformation and dynamic crystallization (DRX) take place. Figure 1b illustrates the micro-structure evolution in the high shear region during processing that was found in [29], from coarse grained unhomogenized billet material to highly refined grains in the processed zone. The microstructures in the high shear region can strongly affect the final microstructure and mechanical properties of extruded structures. Full detailed descriptions of ShAPE can be found in [24, 25, 29].

Fig. 1
figure 1

Schematic of ShAPE (a) and the high shear region at the tool interface (b)

Full size image

During ShAPE, the billet material in the high shear region undergoes compressive and shear stresses. The ShAPE process parameters including: axial extrusion force, rotation speed, extrusion rate, and the geometry of the die, determine the local stress fields and temperature, and therefore the microstructural evolution and DRX kinetics. The deformation and microstructure evolution mechanisms are different in the different zones shown in Fig. 1b. In the processed zone the initial coarse grains have been refined and the dominant plastic deformation mechanism is grain boundary sliding. While in the transition zones I and II plastic deformation associated with both dislocation generation and sliding occurs [29]. Here we capture heat generation during processing using crystal plasticity modeling, therefore for the crystal plasticity simulations we consider a representative volume in the transistion zones, which have polycrystalline structures under compressive and shear deformation (see Fig. 2).

3 Heat generation associated with plasticity deformation

On the surface layer, both surface friction and plastic deformation generate heat. The total heat generation rate can be described by

$$\begin{aligned} {\dot{Q}}(\omega ,f) = {{\dot{Q}}}_{f}(\omega ,f) + {{\dot{Q}}}_{p}(\omega ,f,\ldots ), \end{aligned}$$
(1)

where \({{\dot{Q}}}_{f}(\omega ,f)\) and \({{\dot{Q}}}_{p}(\omega ,f,\ldots )\) in units of \([J/(\text {s}\ \text {m}^{3})]\) are the heat generation rate from surface friction and plastic deformation, respectively. The heat generation rate associated with the surface friction mainly depends on the geometry of tool surface, extrusion force (f) and the rate (rpm) of tool rotation \((\omega )\). The heat generation rate associated with plastic deformation not only depends on local stress and strain fields, but also local microstructures such as grain size, grain orientation and plastic deformation mechanisms (dislocation sliding, twinning, as well as any permanent crystal structure transitions).

Crystal plasticity theory takes crystallographic anisotropy and different plastic deformation mechanisms into account in modelling the mechanical behavior of polycrystalline materials. The Düsseldorf Advanced Material Simulation Kit (DAMASK) is an open source code-base for crystal plasticity modeling [30]. It can simulate the plastic deformation through different mechanisms including dislocation slip, twinning and phase transformations. In this work, we use DAMASK to simulate the plastic deformation in polycrystalline Aluminum (Al). We use the model simulations to explore the relationships between ShAPE process inputs and heat generation to both inform the construction of and compare against a machine learning approach to learn the heat generation rate \({{\dot{Q}}}_{p}(\omega ,f,\ \ldots )\) in a dynamic temperature model.

Only part of plastic work converts to heat. The Taylor-Quinnery coefficient \(\beta \), defined as as

$$\begin{aligned} \beta = \frac{{{\dot{Q}}}_{p}}{{{\dot{W}}}_{p}} \, \end{aligned}$$
(2)

quantifies the relationship between the power of plastic work \({{\dot{W}}}_{p}\) and generated heat rate \({\dot{Q}}_{p}\) [31, 32]. The coefficient \(\beta \) is a material constant that depends on temperature and strain rate. For a given material structure and applied mechanical load \({{\dot{W}}}_{p}\) can be calculated using crystal plasticity and then \({{\dot{Q}}}_{p}\) can be calculated as well supposing that \(\beta \) is known.

In order to calculate \({\dot{W}}_{p}\) using crystal plasticity simulations, we consider a representative volume element (RVE) in the high shear region, which has polycrystalline structures under compressive and shear deformation as illustrated in Fig. 2. In the RVE we assume the grains are randomly oriented and the average grain size is 200 (\(\mu m\)) based on the observed micro-structure characteristics reported in the ShAPE study [29].

Fig. 2
figure 2

Representative volume element (RVE) of polycrystalline structure and boundary conditions used in the simulations, where P is the applied compressive stress, \({\dot{\gamma }}\) is the applied shear strain rate, ’num’ is the grain number in the RVE, and \(X_{1}X_{2}X_{3}\) are Cartesian coordinates

Full size image

Shear deformation does not change the volume of the RVE. With a low applied compressive pressure in the ShAPE process, the volume change should be small. Therefore, periodic boundary conditions, which enable the use of fast Fourier transforms (FFT) in DAMASK for accurately and efficiently solving the deformation equations are applied in the \(X_{1}\)-, \(X_{2}\)-, and \(X_{3}\)- directions. Uniform compressive stress P and shear strain rate \(({\dot{\gamma }})\) were considered. The boundary conditions are expressed as volume-averaged values due to the periodic boundary conditions used in the spectral solver of DAMASK. We use the power form of the plastic constitutive law for the plastic deformation simulations [33]:

$$\begin{aligned} {{\dot{\gamma }}}^{\alpha } = {{\dot{\gamma }}}_{0} \left|\frac{\tau ^{\alpha }}{\xi ^{\alpha }} \right|^{n} \text {sgn}\left( \tau ^{\alpha } \right) \end{aligned}$$
(3)

where \({\dot{\gamma }}_0\) is the reference strain rate. \({\dot{\gamma }}^\alpha \) and \(\tau ^\alpha \) are the shear strain rate and resolved shear stress of the \(\alpha \) slip system. n is the stress exponent; \(\xi ^\alpha \) is the slip resistance and evolves following

$$\begin{aligned} {{\dot{\xi }}}^{\alpha } = h_{0}\Sigma _{\alpha ' = 1}^{N_{s}}\left|{{\dot{\gamma }}}^{\alpha '} \right|\left( 1 - \frac{\xi ^{\alpha '}}{\xi _{\infty }^{\alpha '}} \right) ^{a} h^{\alpha \alpha '} \end{aligned}$$
(4)

Here, \(N_{s}\) is the total number of slip systems, and for the face-centered cubic (FCC) material of aluminum, \(N_{s} = 12\). \(h_{0},a,\xi _{\infty }^{\alpha '}, \text {and} h^{\alpha \alpha '}\) are material parameters. \(h_{0}\) and \(a\) are model-specific fitting parameters. \(\xi _{\infty }^{\alpha '}\) bounds the resistance evolution. \(h^{\alpha \alpha '}\) is the component of the slip-slip interaction matrix between slip systems \(\alpha \) and \(\alpha '\) that describes crystal hardening, i.e., self-hardening for \(\alpha = \alpha '\) and latent hardening for \(\alpha \ne \alpha '\)

The elastic–plastic properties of single crystal aluminum used in the constitutive laws at different temperature are summarized in Table 1, where \(C_{11}\), \(C_{12}\), and \(C_{44}\) are the nonzero Voigt components of the elastic stiffness constants [33,34,35,36]. The properties at 27 \(^{\circ }\text {C}\) were taken from [33, 34]. The elastic stiffness constants were calculated using the empirical formula given in [35]. The other parameters were estimated using the method given in [36].

Table 1 Mechanical properties of single crystal aluminum at different temperatures [33,34,35,36]
Full size table

Consider the RVE and boundary conditions shown in Fig. 2. The physical dimension of the RVE is \(256l_{0} \times l_{0} \times {256\,l}_{0}\), where \(l_{0}\) is the characteristic length which can be determined by correlating the simulation cell and the simulated grain size. For example, consider that the RVE in Fig. 2 consists of 36 grains. Assume the average grain size (i.e., diameter) is \(d = 200\) \(\upmu \)m, then \(l_{0} = \sqrt{36\big (\frac{1}{4}\pi d^{2}\big )/256^{2}} = 4.15\,\upmu \text {m}\)

3.1 Effect of strain rate on heat generation rate

One of the principal operator inputs during ShAPE processing is the rpm of the tool and torque applied to rotate the tool against the billet material. To understand the effects of tool rotation we simulate the effect of applied shear strain rate on the power of plastic work and consequently through the relation (2) the heat generation rate.

A set of randomly chosen Euler angles (\(\phi _{1}\), \(\Phi \), \(\phi _{2}\)) is used for representing the grain orientations. For given compressive stress (P), and shear strain rate (\({\dot{\gamma }}\)), the predicted stress–strain curves are plotted in Fig. 3. It is seen from Fig. 3 that the shear stress increases with increasing applied shear strain rate.

Fig. 3
figure 3

Stress–strain curves versus applied shear strain rate \({\dot{\gamma }}\) \((\text {s}^{-1})\) with applied compressive stress \(P = 20\) MPa and shear stress in the same direction as the applied shear strain

Full size image
Fig. 4
figure 4

Plot of the power of plastic work versus applied shear strain rate \({\dot{\gamma }}\) \((\text {s}^{-1})\) and shear strain at room temperature when \(P = 20\) MPa

Full size image
Fig. 5
figure 5

a Stress–strain curves and b Power of plastic work, respectively, versus temperature and applied shear strain when \(P=20~\text {MPa}\) and \({\dot{\gamma }}=100/s\)

Full size image

Using the crystal plasticity simulations, the power of plastic work can be calculated by

(5)

where \(V_0\) is the RVE volume. \({\dot{\gamma }}^\alpha \) and \(\tau ^\alpha \) are the same as those in (3), respectively, the shear strain rate and resolved shear stress of slip system \(\alpha \). The power of plastic work, \({\dot{W}}_p\), is a volume average of plastic work rate. Figure 4 displays the power of plastic work versus applied shear strain rate and shear strain at room temperature when \(P=20\,\text {MPa}\), a typical compressive stress used for ShAPE with aluminum alloys [37].

We also simulate the effect of temperature on the stress–strain curves and the power of plastic work. The results can be seen from Fig. 5.

The effect of temperature on stress–strain curves and the power of plastic work are very similar, Lower temperature is associated with higher stress and higher power of plastic work. We also found as shown in Figs. 4 and 5b that the power of plastic work \(({{\dot{W}}}_p)\) does not change much when the shear strain is larger than 20%.

We plot \({\dot{W}}_p\) versus the applied shear strain rate in Fig. 6 at room temperature \((27\,^{\circ }\text {C})\) and a shear strain of 20% which is indicated in Fig. 4 by the dashed vertical line. A nearly linear relationship between \({{\dot{W}}}_p\) and \({\dot{\gamma }}\) can be identified from Fig. 6. Similarly, nearly linear relationship between \({{\dot{W}}}_p\) and \({\dot{\gamma }}\) hold for higher temperatures: \(120\,^{\circ }\text {C}\) and \(270\,^{\circ }\text {C}\), as shown in Fig. 6. Due to the relation (2) between the power of plastic work and the heat generation rate, the simulations indicate also that the heat generation rate will depend linearly on the the shear strain rate, with a decreasing slope as the temperature of the material increases.

Fig. 6
figure 6

Power of plastic work \(({\dot{W}}_{p})\) versus applied shear strain rate at shear strain = 20% across different temperatures, suggests a linear relationship between shear strain rate and \({\dot{W}}_{p}\), hence also heat generation rate, with a decreasing slope as temperature increases

Full size image

3.2 Effect of extrusion force on heat generation rate

Aside from tool rotation, the other main operator input in ShAPE processing is the speed and thus force at which billet material is extruded through the rotating die. We capture the extrusion force during ShAPE processing as the compressive stress on the material in the crystal plasticity simulations. We evaluate the effect of compressive stress on the heat generation rate by predicting the power of plastic work versus applied shear strain at varying compressive stress (P) conditions, the results are plotted in Fig. 7.

It can be seen that the stress–strain is almost independent of the applied pressure used in the simulations. We found at the earlier stage of deformation the shear stress slightly decreases with the increase of applied compressive stress for a given applied strain rate. However, at the later stage of deformation both the stress–strain curves and the power of plastic work are independent of the applied compressive stress.

Fig. 7
figure 7

Power of plastic work \(({\dot{W}}_{p})\) versus applied compressive stress (P) and shear strain at room temperature when \({\dot{\gamma }}=100/s\), suggests that \({\dot{W}}\), hence also the heat generation rate, is relatively invariant to applied compressive stress

Full size image

The crystal plasticity simulations demonstrate that \({\dot{W}}\) linearly depends on shear strain rate while it has very weak dependence on the applied compressive stress. We expect that the shear strain rate should be approximately proportional to the power input to rotating the tool, where power is computed as the product of the torque applied to rotate the tool and the tool rpm. Because the torque is associated with the shear stress applied by tool rotation the power input is proportional to the shear stress and rpm. Under given extrusion force, torque and tool rotation, the applied strain rate should be proportional to rpm (or the power input). On the other hand the applied compressive stress should be directly related to the extrusion force. Therefore, these results suggest heat generation will be relatively invariant to extrusion force, while roughly proportional to the tool power input. Indeed, as detailed in Sects. 5.3 and 5.4 we found tool power input to be sufficient to describe the experimental data, whereas inclusion of extrusion force as an input to the neural network model of heat generation resulted in worse fits to the data.

4 Modeling temperature dynamics

We construct a simplified model of the temperature dynamics of ShAPE targeting faster evaluation for development of processing conditions and controls for use of ShAPE in new material applications.

To significantly reduce computational cost we reduce the domain to one dimension along the extrusion axis. That is we assume at any distance from the tool interface the billet material is homogeneous from the center axis to the wall of the billet container. Note that this assumption also ignores that a mandrel runs along the center axis as shown in 1a. While these assumptions may limit the accuracy that can be achieved, they also greatly reduce the computational requirements and can make effective models for fitting experimental data.

We model temperature of the billet on the domain \((x,t) \in (0,L) \times (0,\infty )\) with \(x=0\) the interface between the billet and tool, and \(x=L\) the plane L millimeters from the tool interface into the billet. Let \(V_{A}\) the cross sectional area of the billet, and \(dS_{A}\) the length of the interface between the billet and container around each cross section. Given the specific heat \(c_{\rho }\), density \(\rho \), and thermal conductivity k of the billet material we consider the temperature dynamics given by the conduction convection equation

$$\begin{aligned} c_{\rho }\rho \frac{\partial T}{\partial t} = k\frac{\partial ^{2}T}{\partial x^{2}} - c_{\rho }\rho v\frac{\partial T}{\partial x} + {\dot{Q}}(\phi )\frac{\lambda }{V_{A}} e^{- \lambda x} - h\frac{dS_{A}}{V_{A}}\left( T - T_{w} \right) \nonumber \\ \end{aligned}$$
(6)

subject to the initial and boundary conditions

$$\begin{aligned}&\frac{\partial T}{\partial x}(L,t) = 0,\ \ \forall \ t \ge 0 \end{aligned}$$
(7a)
$$\begin{aligned}&\frac{\partial T}{\partial x^{2}}(0,t) = 0,\ \ \forall \ t \ge 0 \end{aligned}$$
(7b)
$$\begin{aligned}&T(x,0) = T_{0}(x), \ \ \forall \ x \in (0,L) \, . \end{aligned}$$
(7c)

For quick reference Table 2 gives a summary of the model variables. The term \( h\frac{dS_{A}}{V_{A}}\left( T - T_{w} \right) \) captures the cooling of the billet material, as the container holding the billet is subject to active water cooling in the ShAPE process which we simplify as direct cooling of the billet with a fluid temperature \(T_{w}\) taken to be the ambient temperature.

We model the volume heat flux into the billet material with the term

$$\begin{aligned} {\dot{Q}}(\phi )\frac{\lambda }{V_{A}} e^{- \lambda x} \end{aligned}$$
(8)

where \({\dot{Q}}\) is the total heat input given the state of the system and control inputs \(\phi \), and we assume that the heat flux is exponentially distributed moving away from the tool interface according to \(\lambda e^{- \lambda x}\). Heat input is commonly modeled as a surface flux in FSW, which can be a convenient steady state assumption and avoids the need to account for how heat is generated through the volume [17], however we achieved better numerical results using a volumetric flux according to a fixed distribution. This approach for modeling heat input is suggested by Chen et al. for FSW based on their work using a computational fluid dynamics (CFD) model of steady state conditions under the assumption that heat input is a volumetric flux generated from plastic deformation [27]. They found the distribution of the heat flux to remain nearly constant over a range of weld parameters and propose modeling the volumetric flux as total heat input multiplied by a fixed distribution [27]. While here we suppose the distribution of heat flux is exponential, further work can be done to verify accurate distribution assumptions for instance with CFD modeling, but is outside of the scope of this paper.

Table 2 Model variables
Full size table

As discussed in Sect. 3 the total heat input term, \({\dot{Q}}\), contains contributions from multiple sources. Here we use a neural network as a universal function approximator to estimate the relationship between process inputs and heat generation from experimental data with a function \({\dot{Q}}\left( \phi ;\Theta \right) \), where \(\phi \in {\mathbb {R}}^{n}\) are the process inputs and \(\Theta \) are trainable weights. Specifically, we use a fully connected feed forward neural network where for hidden dimension \(h_{n} = 4\) and number of layers \(k = 5\) we construct the mapping

$$\begin{aligned}&\psi _{0} = \sigma (W_{0} \phi + b_{0}) ~ \end{aligned}$$
(9a)
$$\begin{aligned}&\psi _{i+1} = \sigma (W_{i+1} \psi _{i} + b_{i+1}) ~ \, \forall ~ i \in \{1,\dots k-1\} \, \end{aligned}$$
(9b)
$$\begin{aligned}&\psi _{k} = W_{k} \psi _{k-1} + b_{k-1} \end{aligned}$$
(9c)
$$\begin{aligned}&{\dot{Q}}(\phi ; \Theta ) = Q_{\min } + \sigma _{s}(\psi _{k})( Q_{\max } - Q_{\min } ) \end{aligned}$$
(9d)

where \(\sigma \) is the rectified linear unit function(ReLU) and \(\sigma _{s}\) is the sigmoid activation function - exact parameters given in Sect. 5.2. The neural network layers are given by the matrix bias pairs \((W_{0} \in {\mathbb {R}}^{n \times h_{n} }, b_{0} \in {\mathbb {R}}^{h_{n}} )\), (\(W_{i} \in {\mathbb {R}}^{h_{n} \times h_{n}}, b_{i}\in {\mathbb {R}}^{h_{n}})~ \forall ~i \in \{1, \dots k-1\}\), (\(W_{k} \in {\mathbb {R}}^{h_{n} \times 1}\), \(b_{k} \in {\mathbb {R}}\)), and are fit such that when used in the model (10) available experimental data is closely approximated. The last layer of the network (9) bounds the possible heat inputs to be in the interval \((Q_{\min }, Q_{\max })\) such that they are physically reasonable based on available information for the process and material.

Fig. 8
figure 8

Measurement data from a ShAPE extrusion. Plot (a) shows the extrusion velocity and tool rotation rate controls input by the operator during the extrusion. Plot (b) shows the measured power input and temperature trajectory

Full size image

5 Fit of temperature dynamics model to experimental data

We assess the model using experimental data from ShAPE extrusions of Aluminum 7075 tubes collected by Whalen et. al in experiments to demonstrate the high rate of extrusion possible with this process [1]. During the extrusions a temperature measurement was taken with a single thermocouple embedded in the face of the ShAPE tool halfway between the center axis and the outer diameter. The thermocouple was inset into the tool face such that it was not destroyed during processing but was still close to the interface of the tool and billet material so that it was close in temperature to the billet material as it was being extruded. Measurements were also taken of the extrusion force, extrusion rate, tool rotation rate, torque, and power input to tool rotations. All measurements were taken at a frequency of 100 Hz.

5.1 Dataset description

Extrusions proceed first by ’feathering’ the rate of tool rotation while ramping up the extrusion rate to heat up the billet material to a target temperature. Once at the target temperature an extrusion speed and tool rotation is set that seeks to maintain the target temperature through the remainder of the extrusion. Measurements from a representative experiment are shown in Fig. 8. In this work we focus on modeling the initial process control to ramp the temperature to a desired target therefore we consider only the first 55 s of measurement data from each experiment to capture this interval. Additionally, the first 2 s of measurement data are removed due to the noise they contain. We further applied a moving average filter to both the temperature and power measurements with a window size of 100 and 200 respectively to smooth out the high frequency noise present. Of the experiments conducted by Whalen et al. thirty experiments used the same homogenized AA7075 billet material and the same tool geometry across a range of target extrusion speeds from 120 to 360 millimeters per second, and target extrusion temperatures from 360 to 460 degrees Celsius. Of those trials, in eight the operator reported suspected issues with the thermocouple measurements so we excluded those trials, and used the remaining 22 trials for fitting the temperature model. Additional details for the experiments can be found in [1].

5.2 Numerical methods

The strong correlation between the shear strain rate and generation of heat found with the plasicity modeling in Sect. 3.1 suggests that the most impactful measured machine input with respect to ShAPE extrusion temperature is the power input to the tool rotations as that will be strongly correlated to the shear strain rate on the material in the high shear region at the tool interface where most of the heat is being generated. Therefore we take the state input to the neural network \(\phi \) to be the power input and current temperature. We use a five layer network of the form (9) with hidden dimension \(h_{n}\) of size four. The outputs for heat generation were bounded to within \(Q_{\min } = 0\) and \(Q_{\max } = 0.015\). The lower bound is set to ensure the value remains physically meaningful, while the upper bound is set under the assumption that the thermal energy produced must remain below the maximum observed tool power input measurement over the data-set.

For model fitting we use a scaled and simplified dynamics model given by

$$\begin{aligned} \frac{\partial {\widehat{T}}}{\partial t} = {\widehat{k}}\frac{\partial ^{2} {\widehat{T}}}{\partial x^{2}} - v\frac{\partial {\widehat{T}}}{\partial x} + {\dot{Q}}\left( \phi ;\Theta \right) \lambda e^{- \lambda x} - {\widehat{h}}\left( {\widehat{T}} - T_{w} \right) \nonumber \\ \end{aligned}$$
(10)

where \({\widehat{T}} = T / {\bar{T}}\) is the temperature scaled by \({\bar{T}}\), and \({\widehat{k}}\) and \({\widehat{h}}\) give the effective thermal conductivity and cooling coefficient respectively. We also bound the allowable values for \({\widehat{k}}\) and \({\widehat{h}}\) with the formulation

$$\begin{aligned}&{\widehat{h}} = h_{\min } + \sigma _{s}(\alpha _{h})( h_{\max } - h_{\min }), \end{aligned}$$
(11)
$$\begin{aligned}&{\widehat{k}} = k_{\min } + \sigma _{s}(\alpha _{k})( k_{\max } - k_{\min }), \end{aligned}$$
(12)

for learned parameters \(\alpha _{h}\) and \(\alpha _{k}\). We took the bounds to be (0, .1) and (30, 90) for \({\widehat{h}}\) and \({\widehat{k}}\) respectively, and scaled the temperature by \({\bar{T}} = 720 (\text {K})\). Bounds for \({\widehat{k}}\) were selected based on reported values for the thermal properties of Aluminium in the literature [38]. Note that here we assume the thermal capacity, conductivity and density will be invariant with respect to the material temperature, whereas as found in [38] a dependence on temperature is expected. While outside of the scope of this work, inclusion of a dependence on temperature could be learned, or used directly from available data as part of model fitting.

We solve the model (10) using an implicit upwind finite difference method, on a spatiotemporal discretization \((0,1, \dots ,J)\times (0,1, \dots , N)\) for J spatial points and N time points. Let \(T_{j}^{n}\) denote the temperature solution at time n and location j. The model (10) is approximated according to

$$\begin{aligned}{} & {} \frac{T_{j}^{n+1} - T_{j}^{n}}{\Delta t} \nonumber \\{} & {} \quad = \frac{1}{2}{\widehat{k}} \left( \frac{ T_{j+1}^{n+1} - 2T_{j}^{n+1} + T_{j-1}^{n+1} }{ \Delta x^{2}} + \frac{ T_{j+1}^{n} - 2T_{j}^{n} + T_{j-1}^{n} }{ \Delta x^{2}} \right) \nonumber \\{} & {} \qquad - \frac{1}{2} v \left( \frac{T_{j}^{n+1} - T_{j+1}^{n+1}}{\Delta x} + \frac{T_{j}^{n} - T_{j+1}^{n}}{\Delta x} \right) - \frac{1}{2} {\widehat{h}} \left( T_{j}^{n+1} + T_{j}^{n} - 2T_{w} \right) \nonumber \\{} & {} \qquad + {\dot{Q}}\left( \phi _{n} ;\Theta \right) \lambda e^{- \lambda x_{j}} \end{aligned}$$
(13)

and solved iteratively starting from a constant initial condition at room temperature. We discretize the time domain with a .01 (s) step-size and discretize the spatial domain from 0 to 10 (mm) with a 0.1 (mm) step size.

Given a set of experiments \({\mathcal {I}}\) with scaled temperature measurements \(\{ {\tilde{T}}^{n,i} \}_{n \in \{0,1, \dots N\} }\) at position \(x=0\), for each \(i \in {\mathcal {I}}\) we fit the model parameters to the scaled measurement data by minimizing the mean square error loss given by

$$\begin{aligned} {\mathcal {L}}= & {} \frac{1}{ \vert {\mathcal {I}} \vert } \sum _{i \in {\mathcal {I}}} \sum _{n = 0}^{N} (T_{0}^{n,i} - {\tilde{T}}^{n,i} )^{2}\nonumber \\{} & {} + \,\alpha \sum _{n = 0}^{N - 1}\big ( ( T_{0}^{n+1,i} - T_{0}^{n,i}) - ({\tilde{T}}^{n+1,i} - {\tilde{T}}^{n,i} ) \big )^{2} \end{aligned}$$
(14)

where \(\big \{T_{0}^{n,i}\big \}_{n \in \{ 0, \dots , N\} }\) is the model solution at position 0, for experiment inputs i. The loss terms

$$\begin{aligned} \alpha \sum _{n = 0}^{N - 1}( ( T_{0}^{n+1,i} - T_{0}^{n,i}) - ({\tilde{T}}^{n+1,i} - {\tilde{T}}^{n,i} ) )^{2} \end{aligned}$$

seek to penalize differences in the slope between the measured values and model outputs weighted by the parameter \(\alpha >0\). Inclusion of these terms was found to improve training performance and model fits to the data.

We fit model parameters to the data by minimizing the loss (14) with \(\alpha = 0.1\) using gradient descent. Model solutions were constructed in Neuromancer, an extensible library built on pytorch for differentiable parametric programming [39]. To compute the linear solutions necessary for the implicit method we used the torch.linalg.solve function as part of the pytorch package a differentiable routine that allows for the back-propagation of gradients for optimization [40]. The model was trained using the Adam optimizer, with a learning rate of 0.001 until the error rate converged, approximately 1000 epochs. Total training time took approximately 6 h running on an Intel core i9 processor.

To test model performance we randomly divided the data into four test extrusions, four validation extrusions, and the rest as a training set. The model parameters that performed best on the validation set over the training run were saved and performance was evaluated on the test set. Because of the low amount of data available, we performed ten such random divisions for cross validation. To make comparisons of the learned model parameters to the crystal plasticity modeling results, we trained to all of the available data to incorporate all available information.

5.3 Modeling results

We found the model to be able to closely capture the experimental data. Across the ten data splits the average point-wise absolute error on the test set was 18 degrees Celsius. An example of one such fit is shown in Fig. 9. When trained to all available data the model achieved an average point-wise absolute error of 15 degrees Celsius. Further analysis and comparisons to the crystal plasticity simulations are done with the model trained to the whole dataset.

Fig. 9
figure 9

Plot of a model temperature trajectory against the corresponding temperature measurements from an experimental trial, shows the close agreement at the measured position at the tool interface (\(x=0\)), and shows the model prediction for the temperature throughout the billet material

Full size image

The model also produces a prediction of the temperature profile throughout the domain as plotted in Fig. 9. The predicted temperature profile in the billet agrees with operator intuition, that the billet heats up close to a uniform temperature, and is then extruded while temperature is held close to a steady state. A prediction of the temperature profile in the billet as provided by this model can help to better inform control to maintain a more stable steady state. These predictions can also be compared to more detailed modeling and additional temperature measurements in the billet for validation.

Figure 10 shows that the learned relationship by the neural network model between the power input, temperature and heat input satisfies our expectation. More heat is generated as the power input to the tool is increased, with the most heat generated under high power at cooler billet temperatures. The model heat generation decreases as billet temperature increases in line with the material becoming more plastic and more energy being stored in deformations.

Fig. 10
figure 10

Plot of the neural network prediction of heat generation in response to input power and billet temperature shows a smooth response surface with the greatest heat generation at high power and low temperature in-line with the expected behavior

Full size image
Fig. 11
figure 11

Plots of neural network predicted heat generation as a function of the power input to the tool at varying billet temperatures show qualitative agreement with the crystal plasticity simulations at low temperature and high power

Full size image

5.4 Comparison with crystal plasticity simulations

The neural network prediction of heat generation is qualitatively similar to the crystal plasticity modeling results in some regimes. As shown in Fig. 11, at temperature conditions \(15^{\circ }\text {C}\) and \(120^{\circ }\text {C}\) the trained neural network model predicts a relationship close to linear between the power input and the generated heat for power input greater than 4kW, with a slight decrease in slope at \(120^{\circ }\text {C}\). Under our assumption that power input will be directly proportional to the shear strain rate these neural network predictions qualitatively match the crystal plasticity simulation results shown in Fig. 6.

At higher temperatures and low power the neural network predictions deviate from the crystal plasticity results. At low power the neural network predictions become nonlinear, which could represent a transition in the mechanism of heat generation, though it is important to note that there is limited data in the low power regime as power quickly ramps to values above 2kW across the experiments. A transition is also seen from linear to nonlinear in the neural network predictions as temperature of the material increases. A transition that is not predicted by the crystal plasticity modeling, and could represent phenomenon not currently accounted for in our crystal plasticity simulations. At higher temperatures and further into processing the material properties and microstructure become highly uncertain making reliable crystal plasticity modeling and simulation in this regime extremely difficult.

We also tested a temperature dynamics model using the measured extrusion force as an additional input to the neural network model of heat generation. We found the addition of extrusion force did not improve and in fact produced a slightly worse fit of the model to the experimental data, which is in agreement with the conclusion from the crystal plasticity simulations that suggest generation of heat from plastic deformation is relatively invariant to the extrusion force being applied. Of course some extrusion force is required to maintain contact with the tool face and for extrusion to proceed, but this work suggests that beyond the threshold required for extrusion the more relevant force measurement in consideration of process temperature is the torque applied to tool rotation. This result also suggests that friction may play a negligible role in the generation of heat during processing as we would expect heat generation due to friction between the billet and tool face to strongly depend on the extrusion force.

6 Discussion

Coupling a neural network model to fit the complicated physics of heat generation within a simplified conduction convection model of heat transport under ShAPE extrusions allowed for leveraging experimental data to construct a computationally simpler model than conventional approaches. Moreover, direct interpretability of the neural network inputs and outputs enabled comparison with crystal plasticity simulations to both guide construction of the model and evaluate the learned relationships between process inputs and heat generation after training. Qualitative agreement between the NN model and crystal plasticity simulations suggests a strong potential for generalizability of the model. Future work will explore the data requirements necessary to achieve good predictive capability as well as transferability of learned relationships to other material systems. Fast generalizability combined with fast evaluation times would make this modeling approach an excellent candidate to aid in process development for new material systems.