Physics-informed deep learning for three-dimensional transient heat transfer analysis of functionally graded materials

Abstract

We present a physics-informed deep learning model for the transient heat transfer analysis of three-dimensional functionally graded materials (FGMs) employing a Runge–Kutta discrete time scheme. Firstly, the governing equation, associated boundary conditions and the initial condition for transient heat transfer analysis of FGMs with exponential material variations are presented. Then, the deep collocation method with the Runge–Kutta integration scheme for transient analysis is introduced. The prior physics that helps to generalize the physics-informed deep learning model is introduced by constraining the temperature variable with discrete time schemes and initial/boundary conditions. Further the fitted activation functions suitable for dynamic analysis are presented. Finally, we validate our approach through several numerical examples on FGMs with irregular shapes and a variety of boundary conditions. From numerical experiments, the predicted results with PIDL demonstrate well agreement with analytical solutions and other numerical methods in predicting of both temperature and flux distributions and can be adaptive to transient analysis of FGMs with different shapes, which can be the promising surrogate model in transient dynamic analysis.

1 Introduction

Factionally graded materials (FGMs) are innovative materials with a spatial variation in composition and/or microstructure for the purpose of controlling variations in physical properties. Due to their excellent thermal properties, functionally graded materials (FGMs) have been widely used in the high temperature environments such as aerospace engineering (e.g. as thermal barrier coatings for aerospace structures [1]), microelectronics, power generation [2].

Various numerical models have been developed for solving transient heat conduction problems, such as such as finite-difference method (FDM) [3,4,5], finite-element method (FEM) [6, 7], meshless method [8,9,10], boundary element method (BEM) [11,12,13], localized Trefftz-based collocation method [14], to mention but a few. Recently, Fu et al. [15] summarized localized collocation methods (LCMs) and introduced the application of LCMs to solve heat conduction problems in those nonhomogeneous materials.

Apart from those traditional numerical methods, machine learning offers another novel opportunity to solve complex partial differential equations (PDEs). Such approaches can be traced back to the seminal work of Lagaris et al. [16] in 1997. However, such approaches gained in popularity only recently, probably due to advancements in machine learning techniques and associated open-sources tools such as TensorFlow or Pytorch. Some recent and innovative applications with artificial neural networks are summarized as follows: Khatir et al. [17] proposed two-stage approaches to study damage detection, localization and quantification in Functionally Graded Material (FGM) plate structures, with IsoGeometric Analysis (IGA) for modelling while using an improved damage indicator based on Frequency Response Function (FRF) for damage elements identification in first stage and improved Artificial Neural Network using Arithmetic Optimization Algorithm (IANN-AOA) for damage quantification problem in the second stage. Wang et al. [18] proposed a novel and intelligent algorithm based on deep learning to realize the recognition of different types of rail profiles and achieve rapid tracking of the railhead laser stripe. Ho et al. [19] combined feedforward neural networks and marine predator algorithm for structural health monitoring in different scenarios including a simply supported beam, a two-span continuous beam, and a laboratory free-free beam. Based on a coupled model between an artificial neural network (ANN) and antlion optimizer (ALO), Ho et al. managed to localize damages in fixed-free plate structures based on mode shape derivative based damage identification index [20].

Raissi et al. studied physics-informed machine learning by encoding physics with kernel matrix in Gaussian Processes [21, 22]. The physics-informed Gaussian Processes were applied in solving linear and nonlinear differential equations. They [23, 24] later introduced a physical informed neural networks for supervised learning of nonlinear partial differential equations such as the Burger’s equations or Navier–Stokes equations, see also their recent contributions in [25]. Two distinct models were tailored for spatio-temporal datasets: continuous time and discrete time models. Their physical informed neural networks were successfully applied in solving coupled high-dimensional forward-backward stochastic differential equations. The convergence behaviour of physics informed neural networks was studied by Shin et al. [26]. Fu et al. [27] proposed an extrinsic approach based on physics-informed neural networks (PINNs) for solving the partial differential equations on surfaces embedded in high dimensional space which manifested good accuracy and higher efficiency compared with the embedding approach. Karniadakis et al. [25] gave a comprehensive review on physic-informed machine learning framework and summarized the general approaches of introducing physics in machine learning framework and introduced some of the latest applications of physics-informed machine learning.

However, for the transient analysis with physics-informed neural networks, the current works mostly solve the PDEs with a continuous time model and applications are often limited in simple one-dimensional cases [28,29,30]. Yu et al. [30] applied PINN and extend physical-informed Neural Networks (XPINN) in solving steady and transient heat conduction problems in FGMs based on a continuous time scheme, for the transient analysis of 2D FGMs, however, only the radial coordinate and temporal coordinate are considered. Raissi et al. [21] pointed out that the continuous time model needs a large amount of collocation points in the entire spatio-temporal domain which makes the training prohibitively expensive, and typically fails to handle long-time prediction tasks [31].

In this study, we suggest the physics informed deep learning based collocation method with a discrete time scheme that avoids extra training data from simulations for three dimensional transient heat conduction analysis of FGMs. We also propose fitted activation functions suitable for transient heat transfer analysis. The proposed model will then be validated through several numerical examples. The remainder of this paper is organized as follows. In Sect. 2, we describe the physical model we present our deep collocation method in Sect. 3. Section 4 contains several numerical examples to demonstrate the performance of our approach before the manuscript concludes in Sect. 5.

2 Transient heat transfer analysis in 3D FGMs

The general transient diffusion equation for functional graded materials can be written as:

$$\begin{aligned} \nabla (k(\varvec{x},t)\nabla T(\varvec{x},t))=c(\varvec{x},t) \frac{\partial T(\varvec{x},t))}{\partial t}, \varvec{x} \in \Omega , 0 \leqslant t<\infty \end{aligned}$$

(1)

where $T(\varvec{x},t)$ is the temperature function, c is the specific heat, k the thermal conductivity and $\Omega$ denotes the domain and $\Gamma$ denotes its boundary. We assume that the thermal conductivity and specific heat vary exponentially in the $z-$direction:

$$\begin{aligned} \begin{aligned} k(\varvec{x},t)=k_0\exp (2\beta z) \\ c(\varvec{x},t)=c_0\exp (2\beta z) \end{aligned} \end{aligned}$$

(2)

where $\beta$ is the so-called non-homogeneous parameter. After substituting Equation (2) into Equation (1), we obtain

$$\begin{aligned} \nabla ^2 T(\varvec{x},t)+2\beta T_z=\frac{1}{\alpha }\frac{\partial T(\varvec{x},t))}{\partial t} \end{aligned}$$

(3)

with $\alpha =k_0/c_o$ and $T_z=\frac{\partial T}{\partial t}$. The Dirichlet boundary $\Gamma _D$ and von Neumann boundary $\Gamma _N$ conditions are given as:

$$\begin{aligned} \begin{aligned} T(\varvec{x},t)=\bar{ T}, \varvec{x} \in \Gamma _D,\\ q(\varvec{x},t)=-k(\cdot )\frac{\partial T(\varvec{x},t)}{\partial n}=\bar{q(\varvec{x},t)}, \varvec{x} \in \Gamma _N \end{aligned} \end{aligned}$$

(4)

where n is the unit outward normal to $\Gamma _N$. In this paper, we assume that the initial temperature to be zero.

3 Physics-informed neural network using collocation method

In this section, the deep learning based collocation method that using physics-informed deep neural networks with Runge–Kutta (RK) integration schemes is introduced. First, a series of collocation points will be generated in the physical domain and at the boundaries denoted by ${{\varvec{x}}}\,_\Omega =(x_1,...,x_{N_\Omega })^T$ and ${{\varvec{x}}}\,_\Gamma =(x_1,...,x_{N_\Gamma })^T$, respectively, which formulates the dataset of training. Then the time-dependent heat conduction equation will be discretized using the classical Runge–Kutta method – with q stages.

3.1 Collocation points generation

To generate randomly distributed collocation points, various sampling strategies have been developed. The Halton and Hammersley sequences generate random points by constructing the radical inverse [32]. They are both low discrepancy sequences. Another approach is based on the Korobov Lattice [33]. Sobol Sequence is a quasi-random low-discrepancy sequence to generate sampling points [34]. Latin hypercube sampling (LHS) is a statistical method, where a near-random sample of parameter values is generated from a multidimensional distribution [35]. Monte Carlo methods create sampling points by repeated random sampling [36]. We have compared different sampling strategies for the steady state heat conduction equations in nonhonogeneous media in a previous study and found that Latin hypercube sampling (LHS) could yield favourable results with increasing layers [37]. Therefore, Latin hypercube sampling (LHS) is selected to generate collocation points in the transient heat transfer analysis.

3.2 PINNs with discrete time models

3.2.1 Runge–Kutta methods with q stages

For a general time-dependent partial differential equation – as $u^{\prime }(t)=\mathcal {N}(t, u)$, by applying the general form of Runge-Kutta methods with q stages [21], an update iterative form can be obtained

$$\begin{aligned} \begin{array}{ll} u^{n} = u^n_i, \ \ i=1,\ldots ,q,\\ u^n = u^n_{q+1}, \end{array} \end{aligned}$$

(5)

where

$$\begin{aligned} \begin{array}{ll} u^n_i := u^{n+c_i} - \Delta t \sum _{j=1}^q a_{ij} \mathcal {N}[u^{n+c_j}], \ \ i=1,\ldots ,q,\\ u^n_{q+1} := u^{n+1} - \Delta t \sum _{j=1}^q b_j \mathcal {N}[u^{n+c_j}]. \end{array} \end{aligned}$$

(6)

with $u^{n+c_j}(x) = u(t^n + c_j \Delta t, x)$ for $j=1, \ldots , q$. Depending on the choice of the triple parameters $\{a_{ij},b_j,c_j\}$, an implicit or explicit time-stepping scheme can be obtained. Generally, the matrix $\varvec{A}=[a_{ij}]$ defines the Runge-Kutta matrix and $\varvec{b}=b_i$ and $\varvec{c}=c_i$ indicate the weights and nodes, which can be arranged in Butcher tableau as follows:

$$\begin{aligned} \begin{array}{c|c} \varvec{c} &{}\varvec{A} \\ \hline &{}\varvec{b}^T\\ \end{array}=\begin{array}{c|c} \begin{aligned} c_{1} \\ c_{2} \\ \vdots \\ c_{q} \end{aligned} &{}\begin{array}{cccc} a_{11} &{} a_{12} &{} \ldots &{} a_{1 q} \\ a_{21} &{} a_{22} &{} \ldots &{} a_{2 q} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ a_{q 1} &{} a_{q 2} &{} \ldots &{} a_{q q} \end{array} \\ \hline &{}\begin{array}{llll} b_{1} &{} b_{2} &{} \ldots &{} b_{q} \end{array}\\ \end{array} \end{aligned}$$

(7)

The theoretical error estimates for Runge–Kutta methods with q stages predict a temporal error accumulation of $\mathcal {O}\left( \Delta t^{2 q}\right)$ assuming that $\Delta t<1$. Otherwise the solution may not converge.

3.2.2 Discrete time approach

In a continuous time scheme, the neural network is used to approximate the mapping $(t, x) \mapsto u(t, x)$. The training data needs to be generated in the spatial-temporal domain, which can be too costly for analysis in high-dimensions, especially in the long time integration. On the other hand, we perform transient analysis in a discrete time scheme by placing a multi-output neural network prior on

$$\begin{aligned} \begin{bmatrix} u^{n+c_1}(x), \ldots , u^{n+c_q}(x), u^{n+1}(x) \end{bmatrix}. \end{aligned}$$

(8)

The neural network is used to approximate the mapping $(x) \mapsto (u^{n+c_1}(x), \ldots , u^{n+c_q}(x), u^{n+1}(x))$. This prior assumption along with equation (6) results in a physics informed neural network that takes x as an input and output:

$$\begin{aligned} \begin{bmatrix} u^n_1(x), \ldots , u^n_q(x), u^n_{q+1}(x) \end{bmatrix}, \end{aligned}$$

(9)

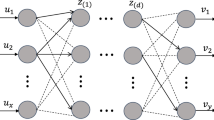
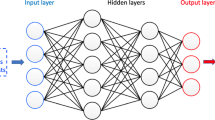
with $u\left( t^{n}, x\right) \approx u^n_{q+1}(x)$. The architecture of the neural network in this application can be found in Fig. 1. The colored round circle is the basic computational unit and the purple one on the output layer is the solution at time-step n.

Fig. 1

Basic structure of the deep feed-forward neural network

Fig. 2

Two suggested activation functions for this dynamic neural network

3.3 Activation functions

To introduce the non-linearity regarding material variations into the neural network of Fig. 1 and enable the back-propagation, the activation function $\sigma$ on hidden layers is defined. There are many activation functions $\sigma$ available such as sigmoids function and hyperbolic tangent function $\left( Tanh \right)$, to name a few [38]. Selecting the activation function in many cases still remains an open issue and commonly a trade-off between expressivity and trainability of the neural network [39]. For vibration analysis, Raissi et al. [40] report that the sinusoidal activation function is more stable than the hyperbolic tangent function $\left( Tanh \right)$. For transient analysis with PINNs using discrete time scheme, we also found that the hyperbolic tangent function $\left( Tanh \right)$ cannot converge but the sinusoidal activation function is also not stable for many cases. To our experience, the bipolar sigmoid function $f(x)=\frac{{e}^{x}-1}{{e}^{x}+1}$ [41] and sigmoid-weighted linear unit (SiLU) function $f(x)=x\times sigmoid(x)$ [42] yield better results in transient dynamic analysis. The two activation functions that fitted for transient analysis are shown in

The Bipolar sigmoid function is a continuous activation function with a gradual output value in the range $[-1,1]$, which looks similar to hyperbolic tangent function. However, the hyperbolic tangent function has a steeper slope. The sigmoid-weighted linear unit (SiLU) function resembles the classical ReLU activation but is nevertheless a smooth activation unbounded above but bounded below. Small negative values can capture underlying patterns from data, while large negative values may be filtered out to keep sparsity.

Fig. 3

Schematic of a physics-informed deep learning with discrete time scheme

3.4 Physics-informed deep learning formulation

Taking advantage of the Runge Kutta method – substituting Equation (6) to Equation (3), we have

$$\begin{aligned} \begin{array}{ll} T^n_i := T^{n+c_i} - \Delta t \sum _{j=1}^q a_{ij} (\alpha \nabla ^2 T^{n+c_j}(\varvec{x})+2\alpha \beta T_z^{n+c_j}(\varvec{x}) ), \ \ i=1,\ldots ,q,\\ T^n_{q+1} := T^{n+1} - \Delta t \sum _{j=1}^q b_j( \alpha \nabla ^2 T^{n+c_j}(\varvec{x})+2\alpha \beta T_z^{n+c_j}(\varvec{x} )). \end{array} \end{aligned}$$

(10)

Placing a multi-output neural network prior with coordinates as inputs $\varvec{x}$ on temperatures $(T^{n+c_1}(\varvec{x}), \ldots , T^{n+c_q}(\varvec{x}), T^{n+1}(\varvec{x}))$ yields

$$\begin{aligned} (T^{n+c_1}(\varvec{x}), \ldots , T^{n+c_q}(\varvec{x}), T^{n+1}(\varvec{x})) \approx \varvec{f}(\varvec{x};\theta ), \end{aligned}$$

(11)

Combined with Equation (10), we can devise the physics-informed neural network that outputs $(T^n_1(\varvec{x}),\ldots , T^n_q(\varvec{x}), T^n_{q+1}(\varvec{x}))$ which are approximated by

$$\begin{aligned}{} & {} (T^n_1(\varvec{x};\theta ), \ldots , T^n_q(\varvec{x};\theta ), T^n_{q+1}(\varvec{x};\theta )) \nonumber \\{} & {} \quad =\varvec{f}(\varvec{x};\theta ) -\Delta t [\varvec{A};\varvec{b}^T]\mathcal {N}(\varvec{f}(\varvec{x};\theta )). \end{aligned}$$

(12)

where $\mathcal {N}=\alpha \nabla ^2+2\alpha \beta$ is the differential operator. The loss function thus constructed from the mean square error is given by

$$\begin{aligned} Loss = MSE_n + MSE_{b}, \end{aligned}$$

(13)

with

$$\begin{aligned} MSE_n =\frac{1}{N} \sum _{j=1}^{q+1} \sum _{i=1}^{N_n} \Vert T^n_j(\varvec{x}^{n,i};\theta ) - T^{n,i}\Vert ^2, \end{aligned}$$

(14)

and

$$\begin{aligned} MSE_b =MSE_{T_{\Gamma _D}}+MSE_{q_{\Gamma _N}}. \end{aligned}$$

(15)

where $MSE_{T_{\Gamma _D}}$ and $MSE_{q_{\Gamma _N}}$ are defined as:

$$\begin{aligned} MSE_{T_{\Gamma _D}} =\frac{1}{N}_{\Gamma _D} \sum _{i=1}^q \sum _{i=1}^{N_{n_{\Gamma _D}}}\Vert T^{n+c_i}(\varvec{x}_{\Gamma _D}^{n,i};\theta )-\bar{ T}\Vert ^2 . \end{aligned}$$

(16)

and

$$\begin{aligned} MSE_{q_{\Gamma _N}} = \frac{1}{N}_{\Gamma _N} \sum _{i=1}^q \sum _{i=1}^{N_{n_{\Gamma _N}}}\Vert q^{n+c_i}(\varvec{x}_{\Gamma _N}^{n,i};\theta )-\bar{q}\Vert ^2. \end{aligned}$$

(17)

The transient analysis with discrete time PINNs model is reduced to an optimization problem:

$$\begin{aligned} \hat{\theta } = \mathop {\textrm{argmin}}\limits _{\theta \in R^K} Loss\left( \theta \right) \end{aligned}$$

(18)

Fig. 4

Random sampling inside the cubic domian

Fig. 5

a Predicted temperature and b analytical temperature distributions for the functionally graded unit cube at time $t=0.1s$

Fig. 6

Temperature profiles in z direction at different time levels for the FGM cube

Fig. 7

a Predicted flux and b analytical flux distributions for the functionally graded unit cube at time $t=0.005s$

Fig. 8

Temperature profile in z direction at time t=1 for the FGM cube problem with time-dependent boundary condition

Fig. 9

a Predicted temperature and b predicted flux distributions for the functionally graded unit cube at time $t=1s$

One of the most widely used optimization method to train the physics-informed neural network is the combined Adam-L-BFGS-B optimization algorithm. This strategy consists of training the network first using the Adam algorithm and after a defined number of iterations, we perform the L-BFGS-B optimization of the loss with a small number of executions.

The basic scheme of the ‘discrete physics-informed deep learning’ is shown in Fig. 3. A fully-connected neural network with space coordinates as inputs is first applied to approximate the temperature at Runge–Kutta nodes and at time step $(n+1)\Delta t$. Then, the derivatives of the temperature outputs are calculated using automatic differentiation (AD), which is then used to formulate the loss. The hyperparameters $\theta$ are learnt by minimizing the loss function.

4 Numerical examples

We demonstrate the presented approach through four benchmark problems; 100 stages are employed for the discrete time scheme. We fix the first six hidden layers with 20 neurons per layer and the rest layers are set to be $q+1$ (101) neurons per layer.

4.1 Case 1: FGMs with exponential material gradation

Let us consider a unit cube shown in Fig. 4 where the material properties vary smoothly and continuously in the z-direction. The initial and boundary conditions are given as follows:

$$\begin{aligned} T(x,y,z;0)=0, \end{aligned}$$

(19)

and

$$\begin{aligned} \left\{ \begin{matrix} q(1,y,z;t)=0; q(0,y,z;t)=0\\ q(x,1,z;t)=0; q(x,0,z;t)=0\\ T(x,y,1;t)=100; T(x,y,0;t)=0 \end{matrix}\right. \end{aligned}$$

(20)

The thermal conductivity parameter in Eq. (2) is $k_0 = 5$ and specific heat parameter is $c_0=1$ and non-homogeneous $\beta = 1$. The analytical solution for this problem is given as:

$$\begin{aligned} T(x,y,z;t){} & {} =T\frac{1-e^{-2\beta z}}{1-e^{-2\beta L}}+\sum _{n=1}^{\infty }B_nsin\left( \frac{n\pi z}{L}\right) \nonumber \\{} & {} \quad e^{-\beta z}e^{-(n^2\pi ^2/L^2+\beta ^2)\alpha t}, \end{aligned}$$

(21)

with

$$\begin{aligned} B_n{} & {} =-\frac{2Te^{\beta L}}{\beta ^2L^2+n^2\pi ^2}\Bigg [\beta Lsin(n\pi )\frac{1+e^{-2\beta L}}{1-e^{-2\beta L}}\nonumber \\{} & {} \quad -n\pi cos(n\pi )\Bigg ] \end{aligned}$$

(22)

$L=1$ being the length of the cube and $T=100$. A random sampling of collocation points as illustrated in Fig. 4 is generated inside the cubic, with 400 collocation points in the domain and 80 collocation points on the boundaries. The learning rate is set to 0.001.

Fig. 10

Geometry of the FGMs with irregular domain

Fig. 11

Random sampling inside the irregular domain

Fig. 12

Temperature profile in z direction at time $t= 0.00001\,s$ for the FGM with irregular domain

The predicted and analytical temperature at time $t=0.1 s$ are illustrated in Fig. 5. The temperature profiles in z direction at different time levels ranging from 0.002 to 0.1 s for the FGM cube are shown in Fig. 6 and compared with the analytical solution. At each time level the predicted temperature coincides with the analytical solution. The flux distribution at time $t=0.005 s$ is shown in Fig. 7 and agrees well with the analytical solution. The relative error between the predicted temperature and the analytical solution at time $t=0.1s$ inside the whole functionally graded cube is 3.661e$-$04.

4.2 Case 2: FGMs with time-dependent boundary condition

For this unit cube, the top surface is prescribed with a time-dependent boundary condition $T(x,y,1;t)=10t$ and all other surfaces are insulated. The initial and boundary conditions are given as

$$\begin{aligned} T(x,y,z;0)=0, \end{aligned}$$

(23)

and

$$\begin{aligned} \left\{ \begin{matrix} q(1,y,z;t)=0; q(0,y,z;t)=0\\ q(x,1,z;t)=0; q(x,0,z;t)=0\\ T(x,y,1;t)=10t; T(x,y,0;t)=0 \end{matrix}\right. \end{aligned}$$

(24)

The thermal conductivity and specific heat parameters in Equation (2) are $k_0 = 5$ and $c_0=1$. Non-homogeneous parameter $\beta = 1.5$. The temperature profile varies again only in z direction; see Fig. 8 at time $t=1s$ compared with a BEM solution using 1200 elements and FEM solution with 1000 linear brick elements [43]. The temperature and flux contours at time $t=1s$ can be found in Fig. 9. Compared with BEM and FEM, deep collocation method is more easy in implementation without the necessity of building elaborate grids and once the deep learning model is trained, it can be deployed to predict the temperature and flux distribution in seconds while maintain the same level of accuracy, which can be a suitable surrogate model for tradition numerical methods.

Table 1 Temperature distributions for irregular FGMs at different time levels

Fig. 13

Geometry of the functionally graded rotor

Fig. 14

Random sampling inside the rotor domian

Fig. 15

Temperature profile along the right top edge at time $t= 0.0066s$ for the FGM rotor problem

4.3 Case 3: FGMs with Irregular domain

Let us consider now a problem with an irregular domain as shown in Fig. 10. The inner and outer radii ($r_1$ and $r_2$) of this annular cylinder are 0.03 and 0.05. The height of this annular cylinder is 0.01. The central angle is $\frac{\pi }{3}$. The material parameters are set as: thermal conductivity parameter $k_0 = 5$, the specific heat parameter $c_0= 1$ and $\beta = 1.5$. The initial and boundary conditions are

$$\begin{aligned} T(r,\theta ,z;0)=0, \end{aligned}$$

(25)

and

$$\begin{aligned} \left\{ \begin{matrix} q(r_2,\theta ,z;t)=0; q(r_1,\theta ,z;t)=0\\ q(r,\frac{\pi }{3},z;t)=0; q(r,0,z;t)=0\\ T(r,\theta ,0.01;t)=1; T(r,\theta ,0;t)=0 \end{matrix}\right. \end{aligned}$$

(26)

where $r_{1} \le r \le r_{2}$ and $0 \le \theta \le \frac{\pi }{3}$.

First, we generate random collocation points inside the irregular physical domain as shown in Fig. 11, with 400 collocation points inside the domain and 200 collocation points on the boundaries.

Figure 12 depicts the temperature profile along the z direction at $t=0.00001s$ and compared with the reference solutions from MFS and FEM [43].

Table 1 shows the profile of the overall temperature distribution. The results agree well with the ones from [43]. The gradation of the temperature along z-axis matches the material gradation property of the FGM.

4.4 Case 4: Functionally graded rotor problem

Finally, we study a functionally graded rotor with eight holes presented in Fig. 13. Due to the symmetry, only one-eighth of the rotor is analyzed. The geometric parameters of this rotor are marked in Fig. 13. All lines with arrows imply the length, namely the inner radius is $R_{inner} =0.5$, outer radius is $R_{outer} =0.3$ and the height is 0.1; the diameter of the mounting hole is $Dia_{hole}=0.075$. The thermal conductivity and specific heat parameters in Equation (2) are $k_0 = 5$ and $c_0=1$. Non-homogeneous parameter $\beta = 1.5$. The initial conditions are

$$\begin{aligned} T(r,\theta ,z;0)=0 \end{aligned}$$

(27)

and temperature boundary conditions are imposed on the inner side/surface (0K) and outer side/surface (100K) while other surfaces are adiabatic in which the heat flux is set to 0. Figure 14 shows the collocation points for training. Our results are compared to results of ABAQUS simulations.

The temperature profile along the right top edge at time $t= 0.0066\,s$ is shown in Fig. 15 and the temperature distributions at different time levels is listed in Table 2. It can be observed that predicted temperature at specific locations and time matches well with ABAQUS results. The same can be observed for the evolution of temperature distribution with both numerical methods.

5 Conclusion

We presented a deep learning based collocation method for transient heat transfer analysis of three-dimensional functionally graded materials (FGMs). This deep collocation method combines the classical collocation method and the deep learning method in one framework which is easy in implementation and no necessity to build elaborate grids. For the deep learning model, a physics-informed neural network is combined with a q-stage Runge–Kutta discrete time scheme for transient heat transfer analysis. Nonlinear activation functions are adopted to introduce a nonlinearity into the neural network and fitted for dynamic analysis. We found the bipolar sigmoid function and sigmoid-weighted linear unit (SiLU) function most suitable for the physics-informed neural network for the transient analysis. Based on our previous study, Latin Hypercube sampling is selected for random sampling of collocation points making the proposed truly “meshfree” deep collocation method, such that it can deal with irregular shaped domains easily.

Table 2 Temperature contour at different time levels

Various numerical examples were studied to validate the performance of proposed method including FGMs with an irregular shape and heat conduction with a variety of boundary conditions. From numerical results, it can be concluded that both temperature and flux inside FGMs predicted by deep collocation method with discrete time scheme and fitted activation function agree well with analytical solutions and other classical numerical methods. The physics-informed deep collocation method can be promising as surrogate models for FEM in dynamic analysis.