Abstract
Mixed eight-node (hexahedron) solid-shell elements based on the standard or partial version of the three-field Hu–Washizu (HW) functionals are developed for Green strain. Three reduced representations of the assumed stress/strain fields are selected. They improve effectiveness, yet retaining good accuracy and convergence properties. At the outset, the standard HW functional and the assumed stress/strain representations of the 3D solid element B8-15P (Weissman in Int J Numer Methods Eng 39:2337–2361, 1996) are used to derive a solid-shell element with 51 parameters. To eliminate locking, the ANS method is applied to the thickness strain (Betsch and Stein in Commun Numer Methods Eng 11:899–909, 1995) and to the transverse shear strain (Dvorkin and Bathe in Eng Comput 1:77–88, 1984). It is a correct element which, however, yields too large displacements for coarse meshes and trapezoidal through-thickness shapes. To improve the above formulation, the \(\zeta \)-independent reduced representations of the assumed stress/ strain fields are selected and the transformations to Cartesian components are modified. The thickness strain is enhanced by the EAS method. The element with 35 parameters is derived from the standard/enhanced HW functional, but, to further reduce the assumed fields, partial/enhanced HW functionals are constructed from the 3D potential energy by applying the Lagrange multiplier method only to selected strain components. In the element with 27 parameters, this is applied to the constant in-plane strain and to the transverse shear strain while in the element with 19 parameters, to the constant in-plane strain only.Two other modifications are implemented to enhance the behavior of these elements: (A) the skew coordinates are used in the reduced representations of the in-plane stress/strain (Wisniewski and Turska in Int J Numer Methods Eng 90:506–536, 2012), and (B) the Residual Bending Flexibility correction of the transverse shear stiffness (MacNeal in Comput Struct 8(2):175–183, 1978) is adapted. Finally, the performance of the proposed solid-shell HW elements is demonstrated on several linear and non-linear examples for the linear elastic material and the hyper-elastic material. The proposed elements are compared to each other and to the best existing elements of this class.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The 8-node hexahedron solid-shell elements have already achieved a considerable level of maturity and have been successfully applied to model shell structures using various 3D constitutive laws, such as the finite strain \( J_2 \)-plasticity [44], the Functionally Graded material [45], and others. Nodal degrees of freedom at the bounding surfaces of the solid-shell elements allow for a convenient aggregation of layers and stress analysis of multi-layer composites [43, 36]. Besides the 8-node also 18-node solid-shell elements, based on bi-quadratic in-plane interpolations, have been developed, e.g. [14].
1.1 3D elements
The currently used 8-node solid-shell elements stem from the earlier developed 3D solid elements, such as e.g. the stress hybrid element of Pian and Tong [33], which is based on the Hellinger–Reissner functional and 18 stress parameters. Equivalent to it is the EAS element with 30 strain parameters of Andelfinger et al. [2] and the Hu–Washizu element of Weissman [46]. The latter element uses the above 18-parameter assumed stress, and the assumed strain with 33 parameters, where the first 18 have the same form as that used for the assumed stress, while the remaining 15 are associated with the incompressibility condition.
These three elements are of very good accuracy and pass the 3D constant strain patch test but involve a large number of parameters. The subsequent research aimed to reduce this number and to make these elements suitable for finite strain problems; a comprehensive overview can be found in Wriggers [57]. The most commonly used is the Enhanced Assumed Strain (EAS) method of Simo and Rifai [39], which is flexible and can employ the strain-driven constitutive algorithms. Wriggers and Reese [59] identified the problems related to the hourglass instabilities appearing for compression of the enhanced 2D plane strain 4-node elements of a compressible neo-Hookean material. Several methods of controlling the spurious modes were tested afterwards, see the overview in Korelc et al. [23]. A number of very good elements of this class were developed, see e.g. Simo et al. [37], Korelc and Wriggers [24], Glasier and Armero [13], Puso [35] and Korelc et al. [23].
We note that the 8-node 3D solid elements typically pass the 3D and membrane patch tests but fail the bending patch test, which puts in question their use in shell applications with one layer of elements through thickness.
1.2 Solid shell elements
The 8-node solid-shell elements, which are the subject of the current paper, use the same interpolation functions and constitutive modules as the 3D solid elements but also additional specialized methods to improve their behavior in thin shell applications involving bending/twisting-dominated problems.
-
1.
The 0th order thickness strain is improperly approximated for curved or trapozoidal through-thickness shape of elements (deformed or undeformed), which causes the so-called curvature thickness locking. The Assumed Natural Strain (ANS) method in the form proposed in Betsch and Stein [6] is used to circumvent it.
-
2.
The out-of-plane bending is impaired by the zero value of the 1st order thickness strain, which is called the volumetric (or dilatational or Poisson’s ratio or Poisson’s thickness) locking. To remedy this problem, the thickness strain is enhanced either using the EAS method or a specific representation of the assumed thickness strain; this question is discussed in more detail in the sequel.
-
3.
To reduce the transverse shear locking, the Assumed Natural Strain (ANS) method in the form proposed by Dvorkin and Bathe [12] is applied to the 0th order transverse shear strains.
These modifications significantly improve the 8-node solid-shell elements’ behavior and for this reason are indispensable in this class of elements.
Considering the standard shell models (Kirchhoff–Love or Reissner–Mindlin), the normal strain \( E_{33} \) is equal to zero due to inextensibility of the shell’s director. The classical remedy is to recover this strain from the zero-normal-stress condition, \( S_{33}=0 \), which for the strains \( E_{11} \) and \( E_{22} \) being linear in the thickness coordinate \( \zeta \in [-1,1] \), yields the \( E_{33} \), which is also linear in \( \zeta \). Then, however, the 3D constitutive equations must be modified (reduced), which is cumbersome for non-linear materials.
This problem can also be alleviated differently, by enhancing the shell kinematics with parameters describing the extension of a director. In Makowski and Stumpf [30, 40], the position vector in the deformed configuration is a quadratic polynomial of the thickness coordinate
where \( \textbf{d}\) is the current director, \( \lambda _0 \) and \( \lambda _1 \) are the thickness stretches and \( \textbf{a}_3 \) is the forward-rotated normal vector. In Simo et al. [38], the extensible-director kinematics with one thickness stretch \( \lambda \) is used, where
Ill-conditioning in the thin limit exhibited by this formulation is eliminated by applying the logarithmic thickness stretch \( \mu = \ln \lambda \). Equation (2) is used also in the formulation based on the Green strain in Betsch et al. [5], so the thickness strain \( E_{33} =\frac{1}{2}(\lambda ^2-1) \). The initial director is defined as \( \textbf{D}= \widetilde{\textbf{D}}/\Vert \widetilde{\textbf{D}} \Vert \), where \( \widetilde{\textbf{D}} \) is obtained by a linear interpolation of the nodal directors \( \textbf{D}_I \). Note that Eq. (2) does not contain the term \( \zeta ^2 \lambda _1 \) of Eq. (1), the purpose of which is to improve the bending behavior.
For solid-shells, we consider that the thickness strain \( E_{33} \) is not necessarily normal to the reference surface as is the normal strain. A constant part of the thickness strain \( E_{33}^0 \) is computed from displacements of the top and bottom bounding surfaces, so only the \(\zeta \)-dependent strain enhancement needs to be added. For 8-node 3D solid elements, a 4-parameter EAS enhancement was used in Andelfinger and Ramm [1] Eq. (34),
where \( \xi , \eta \in [-1,1] \) are the in-plane natural coordinates. Moreover, the first 3 terms of Eq. (3) were found to be sufficient to avoid the volumetric locking. The above enhancement was subsequently applied to solid-shells in Büchter et al. [7] Eq. (35) to relieve the Poisson’s thickness locking. Later on, Vu-Quoc and Tan [43] established that the first 3 parameters of Eq. (3) suffice to pass the out-of-plane bending patch test for solid-shells. The reference values for this test were worked out in this paper and since then this test became a standard for solid-shell elements.
The enhancement of Eq. (3) can also be accounted for in the assumed thickness strain representation of the HW elements, as e.g. in the 3D 8-node solid of Weissman [46] and the solid-shell of Klinkel et al. [20], where the first 3 terms of it are used.
Note that the thickness strain enhancement can also be formulated using the incompatible displacement \( (1-\zeta ^2) \, w_3 \, \textbf{d}\), where \( w_3 \) is an additional parameter, see Parisch [31]. This form of the enhancement, however, renders a problem with conditioning of the stiffness matrix in the thin limit.
Finally, we mention the papers on the solid-shell elements discussing the modifications necessary for hyperelastic and elastoplastic material laws. In Hauptmann et al. [16], they include the right Cauchy-Green deformation tensor, and the deformation gradient for elastoplasticity to make them consistent with the modified Green strain. In Hauptmann et al. [15], various methods to avoiding the volumetric locking for a nearly-incompressible material are compared.
1.3 Objectives of the current paper
The objective of the current paper is to develop several new eight-node (hexahedron) solid-shell elements based on either the standard or partial version of the three-field Hu–Washizu (HW) functionals. The partial HW functionals are constructed from the 3D potential energy by applying the Lagrange multiplier method to the difference between compatible and assumed strain for selected components only. The purpose is to obtain an effective element of high accuracy and good convergence properties using a minimal number of the assumed stress/strain parameters.
1. We start with developing the solid-shell HW element based on the standard HW functional with 51 parameters (HW51). The assumed stress/strain representations are as in the 3D solid element B8-15P of Weissman [46], but are treated here as contravariant, hence, a different transformation to the Cartesian components is used. This transformation is also different compared to this of Klinkel et al. [20]. Additionally, to eliminate locking for shell-type structures, we apply the ANS method in two forms, one proposed by Betsch and Stein [6] for the thickness strain \( E_{33}^0 \) and the other by Dvorkin and Bathe [12] for the transverse shear strain \( E_{\alpha 3}^0 \). This element is stable, passes the membrane/bending patch tests, and yields quite accurate results in the benchmark tests. Nonetheless, it uses a large number of parameters and is slightly too flexible, i.e. the mesh convergence is from above, so the displacements for coarse meshes are excessive in some tests.
Next we aim at obtaining elements of better effectiveness and accuracy than HW51, the standard or the partial version of the HW functional is used. Both the earlier mentioned ANS methods are also applied to the below-described three elements, which we refer to in this paper as the reduced representation elements.
For the standard HW functional, the formulation used in HW51 is modified in two ways: (a) the assumed stress/strain representations are reduced by omitting the \(\zeta \)-dependent terms, and (b) the thickness strain \( E_{33} \) is enhanced by the EAS method using the \(\zeta \)-dependent representation while the assumed thickness stress/strain representations are omitted. The above changes yield the element with 35 parameters (HW35).
Subsequently, the assumed representations are further reduced and two elements based on the partial HW functionals are developed. The Lagrange multiplier method is applied to the in-plane strain \( E_{\alpha \beta }^0 \) and the transverse shear strain \( E_{\alpha 3}^0 \) in the element with 27 parameters (HW27B), and only to the in-plane strain \( E_{\alpha \beta }^0 \) in the element with 19 parameters (HW19).
Two other modifications are implemented in the tested solid-shell elements to enhance their behavior: (A) the skew coordinates are used in the representations of the assumed in-plane stress/strain in the reduced representation elements, and (B) the Residual Bending Flexibility (RBF) correction of the transverse shear stiffness of MacNeal [26] is adapted to solid-shell elements. This correction is implemented also in the reference solid-shell elements.
3. The above four solid-shell elements are tested together with the two reference solid-shell elements, which are currently considered as the best in this class. This is the HSEE element of Klinkel et al. [20] and the EAS10 element, which is characterized in Sect. 5. Several other 2D and shell elements are also used in comparisons.
Very good performance of the developed solid-shell HW elements is demonstrated on several linear and non-linear examples for the linear elastic (SVK) material, and such aspects are considered as: accuracy, effects of skew coordinates and the RBF correction, and convergence properties of the Newton method and the arc-length method. Two examples are concerned with nearly-incompressible materials; the dilatation for the SVK material and \( \nu \approx 0.5 \) is tested and the hourglassing in the large strain compression for the modified neo-Hookean hyper-elastic material is checked.
1.4 Outline of the paper
The outline of the paper is as follows: the general characteristics of the solid-shell elements are provided in Sect. 2. The three-field Hu–Washizu functionals and the assumed stress/strain representations of the developed mixed/enhanced HW solid-shell finite elements are described in detail in Sect. 3. Specialized treatment of thickness and transverse shear strains is described in Sect. 4. Numerical tests in Sect. 5 demonstrate the performance of the developed reduced representation solid-shell elements. The paper is closed by final remarks in Sect. 6.
Notation: “parameter” is abbreviated to “p”. In the elements’ designations, the total number of elemental parameters is included, e.g. HW35 has 35p. Besides, regarding the components, “COV” stands for “covariant”, “CTV” for “contravariant” and “CART” for “Cartesian”. The elemental parameters are denoted as \( q_i \), \(i=1, \ldots , N_q \).
2 General characteristics of solid-shell elements
In this section, first the general characteristics of the solid-shell 8-node elements is given and, next, their kinematics is described.
2.1 Basic definitions for solid-shell element
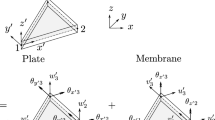
Consider a 8-node isoparametric solid-shell element with the nodes numbered as shown in Fig. 1. The element can be either flat or warped, similarly as the standard 4-node shell element, see e.g. [48]. The nodal “directors” are defined as the vectors linking the corresponding nodes at the bottom and top surfaces, i.e. 1–5, 2–6, 3–7 and 4–8. If these vectors are mutually skew (non-parallel), the element has a trapezoidal through-thickness shape.
Numbering of nodes and the reference elemental basis of 8-node solid-shell element. The element can be flat or warped. \(\zeta \) is the through-thickness coordinate
Consider the following vectors associated with the solid-shell element: the initial position \( \textbf{X}\), the current position \( \textbf{x}\), and the displacement \( \textbf{u}\). The above vectors are interpolated as follows:
where the standard tri-linear shape functions are,
\( \xi , \eta , \zeta \in [-1,+1] \) are the natural coordinates and \( \{ \xi _I, \eta _I, \zeta _I \} \) are the natural coordinates of nodes \( I=1,\ldots ,8 \). We assume that the \( \zeta \)-coordinate is associated with the thickness direction; the reference surface is at \(\zeta =0 \) while the bounding top/bottom surfaces at \(\zeta = \pm 1 \). The thickness direction \( (\xi =\mathrm{const.}, \eta =\mathrm{const.}, \zeta ) \) is in general not normal to the reference surface.
For a solid-shell element, the reference Cartesian basis \( \{ \textbf{i}_k \} \) (\(k=1,2,3\)) is constructed as follows. First, the vectors of the natural basis on the reference surface \( \zeta = 0 \) are defined as
where in the denominator k is a selector of the coordinate w.r.t. which we differentiate. In general, \( \textbf{g}_{k} \) are neither unit nor orthogonal to each other. The co-vectors \( \textbf{g}^{k} \) are defined in the standard way by \( \textbf{g}^{k} \cdot \textbf{g}_{l} = \delta ^{k}_{l} \) (\( k,l=1,2,3 \)).
Let us assume that \( \textbf{g}_1, \ \textbf{g}_2 \) are the tangent vectors and define in the tangent plane, mutually orthogonal vectors \( \textbf{i}_1, \ \textbf{i}_2 \) equally distant from \( \textbf{g}_1, \ \textbf{g}_2 \), see Fig. 2 in [52],
where the auxiliary vectors are
The normal unit vector \( \textbf{i}_3 \) is perpendicular to the tangent vectors \( \textbf{g}_1 \) and \( \textbf{g}_2 \), i.e.
As it is also perpendicular to \( \textbf{i}_1 \) and \( \textbf{i}_2 \), the vectors \( \textbf{i}_k \) form a Cartesian basis \( \{ \textbf{i}_k \} \).
We construct the elemental reference basis at the element’s center \( \{ \textbf{i}_k^0 \} \), where \( \textbf{i}_k^0 \doteq \left. \textbf{i}_k \right| _{\xi ,\eta ,\zeta =0} \), and transform \( \textbf{X}\) and \( \textbf{u}\) to this basis. Then, in the element, the local position vector is \( \textbf{X}= X \textbf{i}^0_1 + Y \textbf{i}^0_2 + Z \textbf{i}^0_3 \), and the Jacobian matrix \( \textbf{J}\doteq {\partial \textbf{X}}/{\partial \, \{ \xi ,\eta , \zeta \} } \) becomes
where \( \textbf{i}^0_1 = [1,0,0]^T \), \( \textbf{i}^0_2 = [0,1,0]^T \) and \( \textbf{i}^0_3 = [0,0,1]^T \); for more details on Jacobians see [48] Sect. 10.3. The Jacobian matrix at the element’s center is \( \textbf{J}_0 \doteq \left. \textbf{J}\, \right| _{\xi ,\eta ,\zeta =0} \).
Remark
For solid-shells, the “thickness” is defined as \( h = 2 \, \Vert \textbf{g}_3 \Vert \) and it is different from the standard thickness used for shells. The latter can be defined for solid-shells as a projection of the natural vector \( \textbf{g}_3 \) on the normal vector \( \textbf{i}_3 \), i.e. \( h = 2 \, ( \textbf{g}_3 \cdot \textbf{i}_3) \), where \( \textbf{g}_3 \) is obtained from Eq. (6) for \( k=3\).
2.2 Kinematics of solid-shells
The configuration space of the Cauchy continuum is defined as: \({\mathcal {C}} \doteq \{\varvec{\chi }: \ B \rightarrow R^3 \} \), where \( \varvec{\chi }\) is the deformation function defined on the reference configuration of the body B. The deformation function \(\varvec{\chi }: \ \textbf{x}= \varvec{\chi }(\textbf{X}) \) maps the reference (non-deformed) configuration onto the current (deformed) one. The deformation gradient is defined as
where \( \textbf{X}\) is the position vector in the initial (non-deformed) configuration and \( \textbf{x}\) in the current (deformed) one. The right Cauchy-Green deformation tensor and the Green strain are defined as
where \( \textbf{C}_0 \doteq \left. \textbf{C}\right| _{{\textbf {x}}={\textbf {X}}} \). We can linearize the strain \( \textbf{E}\) in the thickness coordinate \( \zeta \) at the reference surface \(\zeta =0 \) as follows:
where the 0th and 1st order strains are
We use the convective coordinates \( \varvec{\xi }\), and parameterize the position vectors as \( \textbf{X}(\varvec{\xi }) \) and \( \textbf{x}(\varvec{\xi }) \). The convective coordinates are associated with the natural coordinates \( \xi , \eta , \zeta \in [-1,+1]\), which are used in Eq. (4) to parameterize the domain of a finite element, and then \( \varvec{\xi }\doteq \{\xi , \eta , \zeta \} \). For the components in the Cartesian reference basis \( \{ \textbf{i}_k \} \), we obtain
where \( \textbf{x}_{,{\varvec{{\xi }}}} \doteq {\partial \textbf{x}}/{\partial \varvec{\xi }} \) and \( \textbf{J}\doteq {\partial \textbf{X}}/{\partial \varvec{\xi }} \) is the Jacobian matrix. Besides, \( \textbf{x}= \textbf{X}+ \textbf{u}\) where \( \textbf{u}\) is the displacement vector. From Eqs. (12) and (15), we see that the \( \mathrm CART \rightarrow COV \) and \( \mathrm COV \rightarrow CART \) transformations of components of the Green strain \( \textbf{E}\) are
where the covariant (COV) components of strain can be obtained as either
where \( \bar{\textbf{g}}_1 \doteq \partial \textbf{x}/\partial \xi \), \( \bar{\textbf{g}}_2 \doteq \partial \textbf{x}/\partial \eta \) and \( \bar{\textbf{g}}_3 \doteq \partial \textbf{x}/\partial \zeta \) are vectors of the natural basis \( \{ \bar{\textbf{g}}_i \} \) in the deformed (current) configuration.
Finally, we note that if the components \( \textbf{E}^\textrm{COV} \) are known then the 0th and 1st order strains of Eq. (14) are expressed in terms of the CART components as,
The last simplified form of \( \textbf{E}_1 \) is obtained using two assumptions: \( \left. \left( \textbf{J}^{-1}_{,\zeta } \right) \right| _{\zeta =0} \approx {\textbf{0}} \) and \( \left. \textbf{J}^{-1} \right| _{\zeta =0} \approx \, \textbf{J}_0^{-1} \).
3 Mixed/enhanced HW solid-shell finite elements
In this section, first the standard and partial Hu–Washizu functionals are described, and next the assumed stress/strain representations of the developed solid-shell HW elements are characterized.
Let us distinguish the tangent (in-plane) components \( \alpha ,\beta =1,2\), the through-thickness component 33 and the transverse shear components \(\alpha 3 \). The 0th order and the 1st order parts of stress/strain are designated by the superscripts “0” and “1”, respectively, i.e
where \( \zeta \in [-1,1]\) is the through-thickness coordinate and \( i,j=1,2,3 \).
3.1 Standard/partial HW functionals for solid-shells
Standard 3D HW functional Let us consider the 3D formulation based on the 2nd Piola–Kirchhoff stress \( \textbf{S}\) and the Green strain \( \textbf{E}\). The standard Hu–Washizu (HW) functional is mixed by definition and in addition to the compatible displacements \( \textbf{u}\), it involves also two independent fields of stresses and strains, designated as \( \textbf{S}^* \) and \( \textbf{E}^*\), respectively. In some elements, the enhanced strain \( \textbf{E}(\textbf{u}) + \textbf{E}^\textrm{enh} \) is used, where \( \textbf{E}^{\textrm{enh}} \) is the EAS enhancement of Sect. 4.1.
The standard form of the three-field HW functional is as follows:
where the strain energy density \( \mathcal {W}(\textbf{E}^*) \) is expressed by the independent strain \( \textbf{E}^* \). The independent stress \( \textbf{S}^* \) plays the role of the Lagrange multiplier of the constraint linking the independent strain \( \textbf{E}^* \) and the compatible strain \( \textbf{E}(\textbf{u}) \). Also, \( F_{ext} \) is the potential of the external loads, the body force, and the displacement boundary conditions and V is the volume of the 3D body in the initial configuration. In the current paper we use the strain energy density \( \mathcal {W} \) for the St.Venant-Kirchhoff (SVK) material and for the modified neo-Hookean hyper-elastic material (Sect. 5.3.6).
We develop the following two solid-shell elements based on the standard HW functional:
-
1.
For the solid-shell element HW51, the standard HW functional is
$$\begin{aligned}{} & {} {F}_{\textrm{HW51}} \doteq \int _V \left\{ \mathcal {W}(E_{ij}^*) \ + \ S_{ij}^* \cdot \left[ E_{ij} - E_{ij}^* \right] \right\} \ dV- \ F_{ext},\nonumber \\ \end{aligned}$$(21)where 51 elemental parameters are used. In this element, the assumed stress/strain representations depend also on the thickness coordinate \( \zeta \), see Sect. 3.4.1.
-
2.
For the solid-shell element HW35, the standard/enhanced HW functional is
$$\begin{aligned}{} & {} {F}_\textrm{HW35} \doteq \int _V \left\{ \mathcal {W}(E_{ij}^*) + \ \right. \nonumber \\{} & {} \quad S_{ij}^* \cdot \left[ E_{ij} + \zeta E_{ij}^{1 \, {\textrm{enh}}} \right. \left. \left. - E_{ij}^* \right] \right\} \ dV - \ F_{ext}, \end{aligned}$$(22)where 35 elemental parameters are used, and \( E_{ij}^{1 \, {\textrm{enh}}} \) results from the enhancement of the 1st order thickness strain, see Eq. (60). In this element, all the assumed stress/strain representations are \( \zeta \)-independent, and are defined in Sect. 3.4.2.
In both the above elements, the ANS method is used for the covariant 0th order thickness strain and the transverse shear strain, see Sects. 4.1 and 4.2
Partial HW functional for solid-shell elements To obtain an efficient finite element, a minimal number of elemental parameters, which guarantee the element’s stability and an acceptable accuracy, should be used. Typically, the standard HW functional is reduced to either the Hellinger–Reissner (HR) functional or the Enhanced Assumed Strain (EAS) functional. Another possibility exists for shells and solid-shells. We can introduce the partial HW functionals, which are obtained by the application of the Lagrange multiplier method to selected components of strain only.
We develop two solid-shell elements based on the partial shell HW functional, with the Lagrange multiplier method applied to the 0th order strain \( E_{ij}^0 \) as specified below:
-
1.
For the solid-shell element HW27B, the partial/enhanced HW functional is
$$\begin{aligned}{} & {} \widetilde{F}_{\textrm{HW27B}} \doteq \int _V \left\{ \mathcal {W}(\underline{E_{\alpha \beta }^{0*} + \zeta E_{\alpha \beta }^1} + \zeta E_{\alpha \beta }^{1 \, {\textrm{enh}}}, \right. \nonumber \\{} & {} \quad \left. E_{33}^0 +\, \zeta E_{33}^{1 \, \mathrm enh},E_{\alpha 3}^{0*} + \zeta E_{\alpha 3}^{1 \, {\textrm{enh}}}) \ + \ S_{\alpha \beta }^{0*} \cdot \left[ E_{\alpha \beta }^0 - E_{\alpha \beta }^{0*} \right] \right. \nonumber \\{} & {} \quad \left. \ +\, \ S_{\alpha 3}^{0*} \cdot \left[ E_{\alpha 3}^0- E_{\alpha 3}^{0*} \right] \right\} \ dV - \ F_{ext}, \end{aligned}$$(23)where the Lagrange multiplier method is applied to \( E_{\alpha \beta }^0 \) and \( E_{\alpha 3}^0 \) while \( E_{33}^0 \) and \( E_{\alpha \beta }^1 \) appear in the strain energy in the standard way. The underlined term in \( \mathcal {W} \) is the sum of the assumed 0th order strain \( E_{\alpha \beta }^{0*} \) and the compatible 1st order strain \( E_{\alpha \beta }^1 \) multiplied by \( \zeta \), and, \( S_{\alpha \beta }^{0*} \) and \( S_{\alpha 3}^{0*}\) are the Lagrange multipliers. In this element, all the assumed stress/strain representations are \( \zeta \)-independent, and are defined in Sect. 3.4.3.
-
2.
For the solid-shell element HW19, the partial/enhanced HW functional is
$$\begin{aligned} \widetilde{F}_{\textrm{HW19}}\doteq & {} \int _V \left\{ \mathcal {W}(\underline{E_{\alpha \beta }^{0*} + \zeta E_{\alpha \beta }^1} + \zeta E_{\alpha \beta }^{1 \, {\textrm{enh}}}, \right. \nonumber \\{} & {} \left. E_{33}^0+ \zeta E_{33}^{1 \, {\textrm{enh}}},E_{\alpha 3}^{0} + \zeta E_{\alpha 3}^{1 \, {\textrm{enh}}}) \ \right. \nonumber \\{} & {} \left. + \ S_{\alpha \beta }^{0*} \cdot \left[ E_{\alpha \beta }^0 - E_{\alpha \beta }^{0*} \right] \right\} \ dV- \ F_{ext}, \end{aligned}$$(24)where the Lagrange multiplier method is applied only to \( E_{\alpha \beta }^0 \) while \( E_{33}^0 \), \( E_{\alpha 3}^0 \) and \( E_{\alpha \beta }^1 \) appear in the strain energy in the standard way. \( S_{\alpha \beta }^{0*} \) is the Lagrange multiplier. Note that the same underlined term appears in Eqs. (23) and (24). In this element, all the assumed stress/strain representations are \( \zeta \)-independent, and are defined in Sect. 3.4.4.
In both the above functionals, \( E_{\alpha \beta }^{1 \, {\textrm{enh}}} \), \( E_{33}^{1 \, {\textrm{enh}}} \) and \( E_{\alpha 3}^{1 \, {\textrm{enh}}} \) result from the enhancement of the 1st order thickness strain, see Eq. (60).
We note that, compared to the element HW51, the elements HW35, HW27B and HW19 use the reduced assumed stress/strain representations, and in the sequel they are referred to as the reduced representation elements.
Finally, taking a variation of each of the governing functionals of Eqs. (21)–(24) and performing a consistent linearization of it, we obtain the tangent stiffness matrix \(\textbf{K}\) for a particular element. This procedure is standard and, therefore, not discussed here.
3.2 Skew coordinates
Consider two bases associated with the element’s center: the reference Cartesian basis \( \{ \textbf{i}_k \} \) and the natural basis \( \{ \textbf{g}_k^0 \} \) (\( k=1,2,3 \)). The position vector relative to the element center \( \textbf{X}_0 \) is given by \( \textbf{X}-\textbf{X}_0 \), and it can be expressed in these two bases as follows:
where the skew coordinates \( \xi _S, \eta _S, \zeta _S \) are associated with the natural basis \( \{ \textbf{g}_k^0 \} \), and x, y, z are the Cartesian coordinates. By taking a scalar product of this equation with the vectors \( \textbf{i}_k \), we obtain three equations, which can be solved for the skew coordinates,
where \( \textbf{J}_0 \) is the Jacobian of Eq. (10) at the element’s center. As x, y, z depend on the natural coordinates \( \xi , \eta , \zeta \), hence, for a 3D 8-node (tri-linear) element, Eq. (26) becomes
where \( A_{kl} \) (\( l=1, \ldots ,4\)) are the scalar coefficients. For a 2D 4-node (bi-linear) element, Eq. (27) is reduced to
where \( A_{11} = {(J_{,\eta })_0}/{J_0} \), \( A_{21} = {(J_{,\xi })_0}/{J_0} \) and \( J = \det \textbf{J}\). For parallelogram shapes, \( A_{ij} =0 \), so the difference between the natural and skew coordinates vanishes.
Note that the skew coordinates are introduced above quite generally, without resort to any particular approximation problem. In Yuan et al. [60], these coordinates appear as a by-product, when the equilibrium equations for 2D 4-node element are enforced for the 12-parameter representation of the assumed stress in terms of \( \xi , \eta \).
Remark
An important property of the skew coordinates is that the homogeneous equilibrium equations and the conditions of compatibility of strains are satisfied point-wise regardless of the element’s shape. For the natural coordinates, they are satisfied point-wise only for parallelogram shape elements, as verified for 2D in [50, 51]. In effect, the HR and HW elements with the assumed stress/strain representations expressed by the skew coordinates have an improved accuracy for irregular element’s shapes. This is also true for 4-node HW shell elements with 6 dofs/node, see [52].
For the 8-node solid-shell elements, we have to choose which of the two above defined forms of skew coordinates to use. In this paper, we selected the 2D version of Eq. (28) because it is simpler and its properties are well established and tested. Besides, the effects of skewness of \( \textbf{g}_3^0 \) and \( \textbf{g}_{\alpha }^0 \) are well circumvented by the ANS method for the thickness strain of Betsch and Stein [6], see Sect. 4.1.
We stress that the skew coordinates are used only in the reduced representation elements, to define the in-plane components (11, 22 and 12) of the assumed stress/strain representations, while the natural coordinates are applied in the other components.
3.3 Transformation operators for strain/stress vectors
Because of the symmetry of strain and stress tensors, instead of matrices we can use the vectors of their components
and define the transformation matrices to obtain these components with respect to another basis. Let us define the transformation matrix
where \( J_{ik} = \textbf{g}_i \cdot \textbf{i}^0_k \) (\(i,k=1,2,3\)) are the components of the Jacobian \( \textbf{J}\) and a, b are scalars. To perform the transformations between the contravariant (\( {\textrm{CTV }}\)) components and the Cartesian (\( {\textrm{CART }}\)) components of vectors (29), we define two operators
The use of these operators is equivalent to the matrix operations, as specified below.
-
1.
The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of components of strain can be written either as
$$\begin{aligned} \textbf{E}^{\textrm{CART}} = \textbf{J}\, \textbf{E}^{\textrm{CTV}} \textbf{J}^T \qquad \text{ or } \qquad \textbf{E}^{\textrm{CART}}_{\textrm{v}} = \textbf{T}_{\textrm{E}} \, \textbf{E}^{\textrm{CTV}}_{\textrm{v}}. \end{aligned}$$(32)We can check their equivalence, i.e. \( \left( \textbf{E}^{\textrm{CART}} \right) _{\textrm{v}} = \textbf{E}^{\textrm{CART}}_{\textrm{v}} \), where \( \left( \cdot \right) _{\textrm{v}} \) designates the operation of taking out the components of a matrix to obtain the strain vector of Eq. (29). Analogous equivalent relations can be written for components of stress,
$$\begin{aligned} \textbf{S}^{\textrm{CART}} = \textbf{J}\, \textbf{S}^{\textrm{CTV}} \textbf{J}^T \qquad \text{ or } \qquad \textbf{S}^{\textrm{CART}}_{{\textrm{v}}} = \textbf{T}_{\textrm{S}} \, \textbf{S}^{\textrm{CTV}}_{{\textrm{v}}}. \end{aligned}$$(33)The modified versions of the above transformations are used in Klinkel et al. [20]; we use them also in our HW solid-shell elements but they are modified in a different way than in the cited paper.
-
2.
The \( {\textrm{COV}} \rightarrow \textrm{CART} \) transformation of components of strain can be written either as
$$\begin{aligned} \textbf{E}^{\textrm{CART}} = \textbf{J}^{-T} \, \textbf{E}^{\textrm{COV}} \textbf{J}^{-1} \quad \text{ or } \quad \textbf{E}^{\textrm{CART}}_{{\textrm{v}}} = \textbf{T}_{\textrm{S}}^{-T} \textbf{E}^{\textrm{COV}}_{{\textrm{v}}}, \end{aligned}$$(34)where the inverse of \( \textbf{T}_{\textrm{S}} \) is used to transform the strain vectors \(\textbf{E}_{{\textrm{v}}}\). This transformation is used e.g. in Weissman [46] for the assumed strain together with that of Eq. (33) for the assumed stress. We use it only for comparison in some examples.
In the sequel, we additionally indicate where the operators \(\textbf{T}_\textrm{E}\) and \(\textbf{T}_{\textrm{S}}\) are computed. Then the superscript ”0” stands for the element’s center (\( \xi =\eta =\zeta =0 \)), while “\(\zeta =0\)” for the reference surface.
3.4 Assumed representations of strain/stress
The independent strains and stresses \( \textbf{E}^* \) and \( \textbf{S}^*\) are treated as the assumed fields, i.e. \( \textbf{E}^* \rightarrow \textbf{E}^a \) and \( \textbf{S}^* \rightarrow \textbf{S}^a \), which is indicated by the superscript “a”. These fields are selected separately for each solid-shell element described below.
3.4.1 Element HW51
This element is obtained from the standard three-field \( F_{HW} \) functional of Eq. (21). It is based on the assumed representations which were selected earlier for 8-node 3D elements: the 18p representation for stress of Pian and Tong [33] and the 33p for strain used in the 3D element B8-15P of Weissman [46]. Totally, the HW51 element has \( N_q = 18 + 33 = 51 \) additional parameters \( q_i \).
Assumed stress The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of components of stress of Eq. (33) is applied in the following form:
where \( \textbf{T}_\textrm{S}^{0} \) is computed at the element’s center. The assumed \( {\textrm{CTV}} \) representations are
where
Note that only 3 components, i.e. 11, 22 and 12, are \( \zeta \)-dependent. Totally, 18 parameters \( q_i \) are used for the assumed stress.
This 18p representation was proposed in Pian and Tong [33] for the assumed stress of 3D 8-node hybrid element. Subsequently it was also used in other 3D elements, e.g. in Andelfinger and Ramm [1] Eq. (34) and Weissman [46] Eqs. (41–42). Klinkel et al. [20] used it in the solid-shell element HSEE, where the transformation operators for particular terms of this representation are computed at different locations within an element.
Assumed strain The \( {{{\textrm{CTV}}}} \rightarrow \textrm{CART} \) transformation of components of strain of Eq. (32) is applied as follows:
where \( \textbf{T}_{\textrm{E}}^{0} \) is the operator at the element’s center. The assumed \( {{{\textrm{CTV}}}} \) representation consists of 2 parts, where the first one (underlined) has the same form as specified for stress in Eqs. (36–37) and involves 18p. The second part contains 15p and is as follows:
where
Totally, 33 parameters \( q_i \) are used for the assumed strain. Note that \( C_{33}^{1} \) involves the 3p which are used in Eq. (59), therefore, the EAS enhancement of \( E_{33} \) is not required.
Remark
Note the difference between the transformation rule for the assumed strains used in Weissman [46] Eq. (46) and ours of Eq. (38). In that paper, the \( \mathrm COV \rightarrow \textrm{CART} \) rule is used (it is identical to Eq. (34) in the current paper) while we use the \( {\textrm{CTV}} \rightarrow \textrm{CART} \) rule of Eq. (32). These rules are tested and compared for 4-node 2D HW elements in Wisniewski et al. [56]. The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) rule is found to be in general more accurate, see e.g. the two-element distortion test of Sect. 3.3 therein. It allows for the reduction of the number of parameters used for the assumed strain.
3.4.2 Element HW35
This element is obtained from the standard/enhanced functional \( {F}_\textrm{HW35} \) of Eq. (22). Totally, it has \( N_q = 13 +19 +3 = 35 \) additional parameters \( q_i \), where 13p are used for the assumed stress, 19p for the assumed strain and 3p to enhance the thickness strain.
Assumed stress The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of components of stress of Eq. (33) is applied as follows:
where \( \textbf{T}_\textrm{S}^{0} \) is computed at the element’s center and \( \textbf{T}_\textrm{S}^{\zeta =0} \) at the reference surface (\(\zeta =0\)). The assumed \( {\textrm{CTV}} \) representations are defined by \( \textbf{A}_{\textrm{v}} \) and \( \textbf{C}_{\textrm{v}} \) of Eq. (36), where
The above 13p representation is obtained from the 18p representation of Eq. (37) by omitting the \(\zeta \)-dependent terms and replacing the natural coordinates \( \xi ,\eta \) by the skew ones \( \xi _S,\eta _S \) in \( C_{11} \) and \( C_{22} \). Besides, the operator \( \textbf{T}_\textrm{S} \) in the second term of Eq. (35) is at the element’s center while here in Eq. (41) at the reference surface \( \zeta =0 \). Note that \( C_{12} = 0 \) but, because of the presence of \( q_4 \) in \( \textbf{A}_{\textrm{v}} \), the matrix which is inverted during the condensation out of additional parameters is non-singular.
Assumed strain The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of components of strain of Eq. (32) is applied as follows:
where \( \textbf{T}_\textrm{E}^{0} \) is computed at the element’s center and \( \textbf{T}_\textrm{E}^{\zeta =0} \) at the reference surface (\(\zeta =0\)). The assumed \( {\textrm{CTV}} \) representations are defined by \( \textbf{A}_{\textrm{v}} \) and \( \textbf{C}_{\textrm{v}} \) of Eq. (36), where
Totally, 19 parameters \( q_i \) are used for the assumed strain. The 0th order assumed thickness strain \( E_{33}^{a} \) involves 4 parameters; \( q_3 \) in \( \textbf{A}_{\textrm{v}} \) and 3p in \( C_{33} \). Also, 3p are used by the EAS method of Eq. (59) to enhance the 1st order thickness strain.
Comparison of HW35 and HSEE. The main differences between our HW35 and the reference HSSE (43p) of Kinkel et al. [20] are as follows:
-
1.
HSEE uses 43 parameters; 18 for the assumed stress, 18 for the assumed strain, and 7 for the enhancement of the 11, 22 and 33 strain components. HW35 uses 35 parameters; 13 for the assumed stress, 19 for the assumed strain and 3 to enhance the 33 strain component. HW35 uses skew coordinates in the in-plane assumed representations.
-
2.
The enhancing strain components of HSEE are
$$\begin{aligned} \widetilde{E}_{11}^\textrm{COV}= & {} q_1 \, \xi + q_2 \, \xi \eta ,\quad \widetilde{E}_{22}^\textrm{COV} = q_3 \, \eta + q_4 \, \xi \eta ,\nonumber \\ \widetilde{E}_{33}^\textrm{COV}= & {} (q_5 + q_6 \xi + q_7 \eta ) \, \zeta , \end{aligned}$$(45)where \( \widetilde{E}_{11}^\textrm{COV} \) and \( \widetilde{E}_{22}^\textrm{COV} \) are the enhancements of the 0th order strain, while \( \widetilde{E}_{33}^\textrm{COV} \) of the 1st order strain. In HW35, only the last one is used.
-
3.
Different transformations and representation are used for the assumed strain. In HSSE, the assumed strain is obtained via the \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of Eq. (32) applied as follows:
$$\begin{aligned} \widehat{\textbf{E}}{}^a_{\textrm{v}} = \textbf{T}^0_E \, \textbf{A}_{\textrm{v}} \ + \ \textbf{T}^0_E \, \widehat{\textbf{C}}_{\textrm{v}} \ + \ \textbf{T}_E \, \widehat{\widehat{\textbf{C}}}_{\textrm{v}}, \end{aligned}$$(46)where \( \textbf{T}_\textrm{E}^{0} \) is computed at the element’s center and \( \textbf{T}_\textrm{E} (\xi , \eta ,\zeta ) \) at Gauss integration points. Comparing to Eq. (43) for HW35, we see that the second term \( \textbf{T}^0_E \, \widehat{\textbf{C}}_{\textrm{v}} \) of Eq. (46) is not used, and \( \textbf{T}_E \) in the third term is replaced by \( \textbf{T}_E^{\zeta =0} \) computed at the reference surface. In the assumed representations, the components 11, 22 and 12 are different, and this difference does not vanish if the natural coordinates are replaced by the skew ones.
-
4.
In HSEE, the \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of components of stress of Eq. (33) is applied in the form analogous to that used for strain,
$$\begin{aligned} \widehat{\textbf{S}}{}^a_{\textrm{v}} = \textbf{T}^0_S \, \textbf{A}_{\textrm{v}} \ + \ \textbf{T}^0_S \, \widehat{\textbf{C}}_{\textrm{v}} \ + \ \textbf{T}_S \, \widehat{\widehat{\textbf{C}}}_{\textrm{v}}, \end{aligned}$$(47)where \( \textbf{T}_\textrm{S}^{0} \) is computed at the element’s center and \( \textbf{T}_\textrm{S} (\xi , \eta ,\zeta ) \) at Gauss integration points. Hence, the differences between the transformations used in these two elements are analogous to these for the assumed strain.
3.4.3 Element HW27B
This element is obtained from the partial/enhanced functional \( \widetilde{F}_\textrm{HW27B} \) of Eq. (23), in which only the membrane and transverse shear strain components are treated by the Lagrange multiplier method. Totally, it has \( N_q = 9 +15 +3 = 27 \) additional parameters \( q_i \), where 9p are used for the assumed stress, 15p for the assumed strain and 3p to enhance the thickness strain.
Assumed stress The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of Eq. (41) is applied, and the assumed \( {\textrm{CTV}} \) representation is defined as follows:
the components of \( \textbf{C}_{\textrm{v}} \) of Eq. (36) are
The skew coordinates \( \xi _S, \eta _S \) are used in \( C_{11} \) and \( C_{22} \). Totally, 9 parameters \( q_i \) are used for the assumed stress. Five of them correspond to the Pian and Sumihara membrane stress of [32], but expressed in skew coordinates, and 4 are added for the transverse shear stress.
Assumed strain The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of Eq. (41) is applied, and the assumed \( {\textrm{CTV}} \) representations are defined by \( \textbf{A}_{\textrm{v}} \) of Eq. (48) and \( \textbf{C}_{\textrm{v}} \) of Eq. (36), where
Totally, 15 parameters \( q_i \) are used for the assumed strain. Additionally the 3p EAS enhancement of Eq. (59) is used for the thickness strain.
3.4.4 Element HW19
This element is obtained from the partial functional \( \widetilde{F}_\textrm{HW19} \) of Eq. (24), in which only the in-plane components are treated by the Lagrange multiplier method. Totally, it has \( N_q = 5 + 11 + 3 = 19 \) additional parameters \( q_i \), where 5p are used for the assumed stress, 11p for the assumed strain and 3p to enhance the thickness strain.
Assumed stress The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of Eq. (41) is applied, and the assumed \( {\textrm{CTV}} \) representations are defined as follows:
and the components of \( \textbf{C}_{\textrm{v}} \) of Eq. (36) are
where the skew coordinates \( \xi _S, \eta _S \) are used in \( C_{11} \) and \( C_{22} \). Totally, 5 parameters \( q_i \) are used for the assumed stress, which corresponds to the Pian and Sumihara stress of [32], but expressed in skew coordinates.
Assumed strain The \( {\textrm{CTV}} \rightarrow \textrm{CART} \) transformation of Eq. (43) is applied, and the assumed \( {\textrm{CTV}} \) representations are defined as follows:
and the components of \( \textbf{C}_{\textrm{v}} \) of Eq. (36)
Totally, 11 parameters \( q_i \) are used for the assumed strain. Additionally the 3p EAS enhancement of Eq. (59) is used for the thickness strain.
Remark
If the bi-linear (underlined) terms in the assumed strain is omitted then we obtain the 9p representation, which is identical to that selected for the 2D element HW14-S [51]. The inverse constitutive equation and the Pian-Sumihara’s 5p stress representation was instrumental in selecting this representation. In effect, it is accurate and insensitive to transformations, see [56]. In the 8-node solid-shell element, however, it yields 2 large eigenvalues for the nearly-incompressible material, see Sect. 5.1. The underlined terms render that only one large eigenvalue is obtained for the HW19 element and the volumetric locking is avoided.
4 Treatment of thickness and transverse shear strains
In this section we discuss the specialized methods used to improve the thickness strain and the transverse shear strain. The covariant strain components are modified.
4.1 ANS method and EAS enhancement for the thickness strain
Two problems related to the thickness strain \( E_{33} \) of solid-shell elements can be identified.
A. For trapezoidal through-thickness shape of solid-shell elements, the initial natural vector \( {\textbf{g}}_3 \doteq \partial \textbf{X}/\partial \zeta \) is not normal to the reference surface \( \zeta =0 \). Also the current natural vector \( \bar{\textbf{g}}_3 \doteq \partial \textbf{x}/\partial \zeta \) becomes not normal to the reference surface \( \zeta =0 \) for certain types of deformation, e.g. the out-of-plane bending. In effect, the covariant 0th order thickness strain \( E_{33}^\textrm{COV} \) is improperly approximated, which causes the so-called curvature thickness locking. We denote the covariant thickness strain at the reference surface as \( \varepsilon _{33} \doteq E_{33}^\textrm{COV}|_{\zeta =0} \).
Example
Consider for simplicity a 2D solid-beam parameterized by \( \xi ,\zeta \in [-1,1]\). Define the current unit “director” and “thicknesses” at the reference line \( \zeta =0 \) as: \( \bar{\textbf{d}} \doteq \bar{\textbf{g}}_3^{\zeta =0} / \Vert \bar{\textbf{g}}_3^{\zeta =0} \Vert \) and \( \bar{h} \doteq 2 \Vert \bar{\textbf{g}}_3^{\zeta =0} \Vert \). \( \textbf{d}\) and h are used for the initial configuration,. Then the thickness strain at the reference line, obtained from Eq. (17) for \( i,j=3 \), is
For the parameterization of \( \textbf{x}\) of Eq. (4), we obtain \( \bar{\textbf{d}}(\xi ) = \frac{1}{2} (1-\xi ) \ \bar{\textbf{d}}_A + \frac{1}{2} (1+\xi ) \ \bar{\textbf{d}}_B, \) where A and B are the end-points (\(\xi =\pm 1\)) on the reference line. When \( \bar{\textbf{d}}_A \ \) and \( \bar{\textbf{d}}_B \) are non-parallel, such an interpolation of \( \bar{\textbf{d}}(\xi ) \) does not preserve its length, i.e.
The second term causes the thickness straining in bending, and to circumvent it Betsch and Stein [6] propose the ANS method. Within the ANS method, the product is interpolated using appropriate products at the end-points,
It is always equal to 1 because \( \bar{\textbf{d}}_A \) and \( \bar{\textbf{d}}_B \) are unit vectors. For the initial “director” \( \textbf{d}\) and the product \( \textbf{d}\cdot \textbf{d}\) of Eq. (54), we proceed in a similar way. Effectively, we can interpolate \( \varepsilon _{33} \) using the values at the end-points A and B,
where \( \left( \varepsilon _{33}\right) _A \) and \( \left( \varepsilon _{33}\right) _B \) are directly computed using not Eq. (54) but Eq. (17).
For the solid-shells we proceed similarly. First, the values of \( \varepsilon _{33} \) are computed at 4 corner points \( (\xi =\pm 1, \ \eta =\pm 1 ) \) at the reference surface \( \zeta =0 \); they are denoted as \( ( \varepsilon _{33})_I \), \( I=1,2,3,4 \). Next, this strain is interpolated within an element with the bi-linear shape functions \( N_I(\xi ,\eta ) \),
Finally, the Cartesian components of this strain are obtained using the \( \mathrm COV \rightarrow \textrm{CART} \) transformation of Eq. (34).
B. In the solid-shell kinematics, the 1st order thickness strain \( E_{33}^1 \) is equal to zero, which impairs element’s accuracy in the out-of-plane bending. An overview of the methods which have been used to enhance this strain in shells, 3D elements and solid-shell elements, is given in Sect. 1.
In the current paper, we use the 3-parameter EAS enhancement of the covariant 1st order thickness strain
and the standard transformation to Cartesian components,
where \( \textbf{T}_\textrm{S}^{0} \) is computed at the element’s center and \( J \doteq \det \textbf{J}\). This enhancement is used in all our solid-shells elements except HW51, in which the terms of Eq. (59) are included in the assumed strain representation, see Eq. (40).
4.2 ANS method for transverse shear strains
Let us denote the covariant components of the transverse shear strains at the reference surface \( \zeta =0 \) as
To reduce the transverse shear locking, the Assumed Natural Strain (ANS) method in the form proposed by Dvorkin and Bathe [12] is applied to \( \gamma _{13} \) and \( \gamma _{23} \) as follows:
-
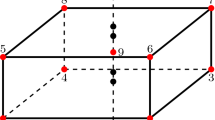
1.
First, the \( \gamma _{\alpha 3} \) (\(\alpha =1,2\)) are computed (sampled) at the middle points of element sides, at two points for each component, see Fig. 2. These values are denoted as \( \gamma _{13}^5, \gamma _{13}^7 \) and \( \gamma _{23}^6, \gamma _{23}^8 \).
-
2.
Next, the components \( \gamma _{\alpha 3} \) are interpolated over the element domain using the sampled values,
$$\begin{aligned} \widetilde{\gamma }_{13}(\xi , \eta )= & {} \frac{1}{2}\left[ (1-\eta ) \, \gamma _{13}^5 + (1+\eta ) \, \gamma _{13}^7 \right] ,\nonumber \\ \widetilde{\gamma }_{23}(\xi ,\eta )= & {} \frac{1}{2}\left[ (1-\xi ) \, \gamma _{23}^6 + (1+\xi ) \, \gamma _{23}^8 \right] . \end{aligned}$$(62)The interpolated components (designated by a tilde) are constant in the direction in which the derivative is calculated and linear in the other direction, which means that the ANS method is orientation-dependent.
-
3.
Finally, at the Gauss integration points, the Cartesian transverse shear strains are obtained by the \( \mathrm COV \rightarrow \textrm{CART} \) transformation of Eq. (34).
Location of sampling points for \( \gamma _{13} \) and \( \gamma _{23} \) at the \( \zeta =0 \) surface
Finally, the ANS modified strains of Eqs. (58) and (62) are transformed to the Cartesian components simultaneously with the compatible strain components,
and the enhancement vector \( \textbf{E}^\textrm{enh}_{\textrm{v}} \) of Eq. (60) is added to this vector.
4.3 RBF correction of transverse shear stiffness
Low-order finite elements, such as the two-node Timoshenko beam, the four-node Reissner-Mindlin shell and the eight-node solid-shell, lock for the sinusoidal bending because such a form of deformation is not properly represented by linear shape functions. To resolve this problem, the Residual Bending Flexibility (RBF) correction was proposed for beams and shells, see [26, 28]. This correction is beneficial also for very thin elements. Below the RBF correction is adapted to the 8-node solid-shell elements.
For a 2D beam element with a rectangular cross-section, we define the ratio of the shear energy \( \mathcal{W}_\gamma \) to the total energy as follows:
where \( \mathcal{W}_\kappa \) is the bending energy. For the Discrete Kirchhoff (DK) beam element based on cubic displacements (see e.g. [48] Sect. 13.1), the deflection for the sinusoidal bending is \( w(\xi ) = \frac{l}{4} \, \xi (\xi ^2 - 1) \, \theta \), so
where \( \theta \) is the nodal rotation and l is the element’s length. Let us define the RBF correction coefficient \( c_\textrm{RBF} \doteq c \) and the corrected shear modulus
where the underlined term is called the Residual Bending Flexibility. Note that G is multiplied by the shear correction factork to account for a parabolic distribution of the transverse shear stress through thickness. Its use is not indicated in [26] but is obvious. Note that the \( c_\textrm{RBF} \) and \( G^* \) depend on the material and geometrical properties of the element but not on the rotation \( \theta \).
Although the \( c_{\textrm{RBF}} \) and \( G^* \) are derived for the DK beam element, they can also be applied to the Timoshenko beam element based on linear interpolations. Similarly, a generalization of \( G^* \) can be applied to bi-linear 4-node plate and shell elements.
For the 8-node solid-shell element, we need to account for the transverse shear strains at the reference surface \( \zeta =0 \), hence we proceed similarly as for a 4-node shell element. The corrected \( G^* \) of Eq. (66) is applied separately for each direction, i.e.
where \( l_1 \) and \( l_2 \) are the lengths of vectors connecting opposite mid-side points at the reference surface. (The shear correction factor \( k = 5/6 \) is used in numerical examples of Sect. 5 unless defined differently.) Let us assume that h, \( G^*_1 \) and \( G^*_2 \) are constant over the reference surface and express the transverse shear strain energy for a single element as follows:
To pass the bending patch test, the ANS method of Sect. 4.2 should be applied to the transverse shear strain. Then the element performs well for bending but yields excessive results for twist. For instance, in the linear test of a slender straight cantilever modeled by one row of 4-node shell elements and twisted by a pair of forces, the rotation \( r_x \) of the tip is too large by about 38%, see [48] Sect. 15.3.1.
To avoid the excessive twist, the full RBF correction is applied to the average values of the transverse shear strains (“av”) and a fraction of it to the difference of them (designated by “d”), see [27]. To separate these parts, we re-write Eqs. (62) of the ANS method as follows:
Taking for instance only the two last rows of Eq. (63), we have
where each component is a linear function of \( \xi \) and \( \eta \), e.g. \( \gamma _{13}^{\textrm{CART}} =\bar{\gamma }{}_{13}^\textrm{av} \ + \ \bar{\gamma }{}_{13}^\textrm{d1} \, \xi \ + \ \bar{\gamma }{}_{13}^{\textrm{d2}} \, \eta \). To separate these terms in the strain energy \( \mathcal{W}_{\gamma } \) of Eq. (68), we assume that \( J(\xi ,\eta ) \approx J_0 \), where \( J_0 \) is the Jacobian determinant at the element’s center. Then
Finally, the integrand of the strain energy (68) is modified and the full RBF correction is applied only to the “av” strains and a fraction of it to the “d” strains,
with the corrected shear modulus of Eq. (67) additionally modified as follows:
where \( \epsilon \) is a corrective coefficient; \( \epsilon = 0.04 \) is selected in [26]. Ṅote that too small values of \( \epsilon \) cause problems with the conditioning of the tangent stiffness matrix. We proceed similarly with \( G^*_2 \, {\gamma }{}_{23}^2 \) of Eq. (68). The effects of the RBF correction are verified on several numerical examples in Sect. 5 and summarized in Sect. 5.4.
Comparison The shear correction factor for a Timoshenko beam element is defined in Tessler and Hughes [42] Eq. (4.14) as follows:
where \( k^2_* = \pi ^2/12 \) is the analytic shear correction factor, which corresponds to our \( k=5/6 \). Besides, \( r \doteq \sqrt{I/A} \), and for a rectangular cross-section, when \( A= b h \) and \( I=b h^3/12 \), it yields \( r^2 = h^2/12 \). Hence, the inverse of Eq. (74) divided by G is
We see that \( k^2_{\textrm{TH}} \) in the above formula is identical to \( c_{\textrm{RBF}} \) of Eq. (66) when the analytic shear correction factors (\(k^2_*\) and k) are defined in the same way.
5 Numerical tests
In this section, we describe the numerical tests of four 8-node Hu–Washizu (HW) solid-shell elements developed in the current paper, see Table 1. These elements are based on the Green strain and developed from either the standard HW functional of Eqs. (21) and (22), or the partial HW functionals of Eqs. (23) and (24).
The assumed representations of stresses/strains are described in Sects. 3.4.1, 3.4.2, 3.4.3 and 3.4.4. Of particular interest are the reduced representation HW elements (HW35, HW27B and HW19). In these elements, the in-plane components of the assumed strain/stress are expressed by the skew coordinates of Sect. 3.2. The number of parameters used for particular components of stress/strain is given in Table 2. The 0th and 1st order parts of stress/strain are designated by the superscripts 0 and 1, respectively. In the sequel, “parameter” is abbreviated to “p”.
Several methods of improving the behavior of solid-shells are applied and they are described as follows: the ANS methods for the thickness strain and the transverse shear strains in Sects. 4.1 and 4.2, the EAS method for the thickness strain in Sect 4.1, and the Residual Bending Flexibility (RBF) correction in Sect. 4.3.
The multipliers \( q_i \) of additional modes are eliminated on the element’s level and updated by the scheme U2, see [48]. All solid-shell elements are integrated using the \( 2 \times 2 \times 2 \) Gauss integration rule.
Two reference solid-shell elements are used:
-
1.
HSEE with 43p of Klinkel et al. [20], which is an HW element; it is described in detail and compared to our HW35 element in Sect. 3.4.2.
-
2.
EAS10, in which the 7p enhancement of Wilson et al. [47] is applied to the in-plane strain,
$$\begin{aligned} E_{11}= & {} q_1 \xi + q_2\xi \eta ,\qquad E_{22} = q_3 \eta + q_4 \xi \eta ,\nonumber \\ E_{12}= & {} q_5 \xi + q_6 \eta + q_7 \xi \eta , \end{aligned}$$(76)and the 3p enhancement of Eq. (59) to the thickness strain \( E_{33} \). The first version of this element is designated Q1A3E5 in [19]. In [20], two terms are added to the thickness strain enhancement to pass the bending patch test, as proposed in [43], and it is designated Q1A3E7.
These elements are derived using the automatic differentiation program AceGen described in [22, 25], and are tested within the finite element program FEAP developed by R.L. Taylor [41, 61]. The use of these programs is gratefully acknowledged. Our parallel multithreaded (OMP) version of FEAP is described in [18].
We tacitly assume that any consistent set of units is used for the data defined in numerical examples.
5.1 Eigenvalues of single element
The eigenvalues of the tangent matrix are computed for a single unsupported element, and for the material data: the Young’s modulus \( E =1 \) and the Poisson’s ratio \( \nu = 0.3 \).
First, a single element of size \( 1 \times 1 \times h \) and the thickness \( h=0.1 \) is checked. Then, several other element shapes are examined, such as a truncated pyramid, a rhomboid with parallel corner “directors” and a warped element with elevated nodes 3 and 7 in Fig 1. For all the shapes tested, our solid-shell elements have a correct number of zero eigenvalues (6).
For the triangular prism, e.g when nodes 3 and 4, and nodes 7 and 8, have the same coordinates, the number of zero eigenvalues remains correct. In the so-called thin limit, an additional zero eigenvalue appears for all tested solid-shell elements.
For the nearly-incompressible material, i.e. \(\nu =0.499999999 \), one large eigenvalue \( 8.5 \times 10^8 \) and 6 zero eigenvalues is obtained for all tested solid-shell elements. For the distorted shapes and the triangular prism, the number of large and zero eigenvalues remains the same. The absence of volumetric locking was additionally confirmed by the “Pure bending of a cantilever in plane strain” test of MacNeal [28].
5.2 Linear tests
5.2.1 Patch tests
The solid-shell elements fail the 3D patch test with non-parallel top and bottom bounding sides. Hence, the shell-type patch tests are adapted and performed.
The five-element patch of elements described in MacNeal and Harder [29] is used, with the material data: the Young’s modulus \( E=10^{6} \) and the Poisson’s ratio \( \nu = 0.25 \). The displacements are prescribed at the external nodes of the patch and computed at the internal nodes.
The reference results for the membrane patch test are the same as for the 4-node shell elements but additionally the values of \(u_3 \) and the thickness strain/stress \( (E_{33},S_{33}) \) must be checked. For the out-of-plane bending/twisting patch test, the reference results are given in VuQuoc and Tan [43] Table 2.
All our solid-shell elements yield correct displacements at the internal nodes and correct compatible strains and stresses at the Gauss Points.
5.2.2 Dilatation for out-of-plane bending
This test is used to detect the dilatational locking for the nearly-incompressible linear elastic material., The dilatation is the volume change for small strains only. Pure out-of-plane bending for plane strain is defined by the following displacements:
for which the small strains are
For the Poisson’s ratio \( \nu = 0.5 \), i.e. for the incompressible material, we obtain \( \epsilon _{33}= -z \) so the dilatation \( e = \epsilon _{11} + \epsilon _{22} + \epsilon _{33} = 0 \). This test is an adaptation of the pure in-plane bending test of [28], p. 216.
To obtain the nearly-incompressible material, we use the Poisson’s ratio \( \nu = 0.499999999 \), for which the dilatation should be \( e \approx 0 \). Besides, the Young’s modulus \( E=1 \), the thickness \( h=0.2 \), the half-length \( L=5 \) and the width \( w=1 \). The RBF correction of Sect. 4.3 is not used.
Dilatation for out-of-plane bending. Mesh and boundary conditions. Thickness h is shown not to scale
The \( 10 \times 1 \times 1 \)-element mesh is used, with 1 layer of elements in the through-thickness 0Z direction, see Fig. 3. The values of \( u_x \) and \( u_z \) of Eq. (77) are applied to 8 corner nodes and at \( x=z=0 \) to nodes 6, 17, 28 and 39. To render the plane strain state, the boundary condition \( u_y =0 \) is set for all nodes at \( y = \pm w/2 \).
The obtained results are presented in Table 3. Strains and the dilatation are computed in element no. 5 at point “C”, i.e. at \( (\xi ,\eta ,\zeta ) = (0,0,-0.5) \). The analytical solution at point “C” is \(\epsilon _{11}= 0.05 \). For all elements, \(\epsilon _{22} \approx 0 \) and \(\epsilon _{33} \approx -\epsilon _{11} \) are obtained as required, hence these components are not reported. The values of \( \epsilon _{11} \) only negligibly differ from the reference analytical value.
The transverse shear strain \( \epsilon _{13} \) and the dilatation e are close to zero, which indicates that all the tested and reference solid-shell elements are free from the transverse shear locking and the dilatational locking.
5.2.3 Cook’s membrane
In Cook’s test [8], the in-plane shear deformation dominates and the elements are skew and tapered. The membrane is clamped at one end, while at the other end, the uniformly distributed tangent load \(P=1\) is applied, see Fig. 4. The nodes shown in this figure are doubled to obtain the mesh for 8-node solid-shell elements. The data is as follows: \( E=1 \), \( \nu =1/3 \), and the thickness \( h=1\). Two meshes are used in computations; a coarse \(2\times 2\)-element mesh and a fine \(32\times 32\)-element mesh. For the reference 9-node 2D element the same number of nodes is used, and the \( 1 \times 1 \) and \( 16 \times 16 \)-element meshes.
The vertical displacements \( u_y \) at point A obtained in the linear analysis are presented in Table 4. The relative errors [in %] are also provided. All the tested solid-shell elements perform identically for the fine \(32\times 32\)-element mesh. Regarding the coarse \(2\times 2\)-element mesh, our elements based on the reduced representations and the skew coordinates (HW35, HW27 and HW19) are the most accurate ones but the difference between them and the other elements is small.
Cook’s membrane. Initial geometry and load
5.2.4 Two-element distortion test
This test is used to verify either the in-plane part or the through-thickness part of solid-shell elements. Bending always takes place in the X0Y plane, but the nodal “directors” are either aligned with the 0Z-axis (in-plane bending) or parallel to the X0Y-plane (out-of-plane bending).
The cantilever is modeled by two solid-shell elements, and a tilt of their common side is defined by the parameter d, see Fig. 5. The data is as follows: \(E=1500 \), \( \nu =0 \), \( h=1\), and \( P=10 \). The nodes shown in Fig. 5 are doubled to obtain the mesh for 8-node solid-shell elements, and the pair of forces \( \pm P \) is replaced by four forces \( \pm P/2 \). Boundary conditions are applied as described in [20].
Two-element distortion test. Initial geometry and load
In-plane bending In Fig. 6, the \( u_y \) displacement at the tip is shown for a varying distortion d. Up to \( d=1 \), for which the tilt of the common nodal “directors” is \( 45^{\circ } \), all the curves almost coincide. For \( d > 1 \), the curves for our HW51 and the reference EAS10 are identical, and the curves for all our reduced representations elements (HW35, HW27B and HW19) coincide.
Note that for larger distortions less accurate solutions are expected, see, e.g., [1] Fig. 8 and [56] Fig. 5. Besides, the curve for a very accurate 2D 4-node element HW14-S [51] has a plateau for \( d > 1 \). QE2 of [34] and HR5-S of [50] perform as HW14-S. As the curve for our reduced representations elements is the closest to this 2D solution, it seems to be better than the other curves.
In Fig. 6, we also show the results for two sets of transformation for stress-strain: (a) CTV-CTV of Eqs. (33) and (32) and (b) CTV-COV of Eqs. (33) and (34). For HW51, the curves for both transformations coincide, but for the reduced representations elements there is a significant difference between them. The CTV-CTV transformations yields more accurate solutions, hence, they are used in our solid-shell elements.
Out-of-plane bending In Fig. 7, the \( u_y \) displacement at the tip is shown for a varying distortion d. The results obtained without the RBF correction are presented. Our reduced representations elements (HW35, HW27B and HW19) and the reference EAS10, yield the analytical solution \( u_y=1 \) in the whole range of d.
Comparing our HW51 and the reference HSEE, the curves for them coincide and the error of them grows fast for increasing d. For \( d = 1 \), i.e. for the \( 45^{\circ } \) tilt of the common nodal “directors”, the relative error is 8.2%. Since the thickness strain is treated in these elements by the ANS method of Sect. 4.1, the cause of the error is not this strain. Note that this error is eliminated in HW35, where the \(\zeta \)-dependent terms are omitted in the assumed representations and the thickness strain is enhanced by the EAS method.
Finally, all our elements are tested using the two sets of transformations for the assumed stress-strain, CTV-CTV and CTV-COV, and the curves obtained are identical.
Two-element distortion test. In-plane bending
Two-element distortion test. Out-of-plane bending
5.2.5 Straight cantilever of trapezoidal elements
This classical test of MacNeal and Harder [29] is applied to the transverse deformation of solid-shell elements, as e.g. in Harnau et al. [14]. The accuracy of displacements for a trapezoidal through-thickness shape of solid-shell elements and the effects of the RBF correction of Sect. 4.3 are assessed.
The trapezoidal through-thickness shape of solid-shell elements, see Fig. 8, is obtained by tilting the common nodal “directors” by \( \pm \, 45^\circ \). The vertical force \( P=1 \) is applied at the right end, equally to the top and bottom nodes, causing out-of-plane bending and transverse shearing. The mesh consists of 6 elements, and the aspect ratio for the rectangular elements is 5. The nodes shown in Fig. 8 are doubled in the 0Y direction to obtain the mesh for 8-node solid-shell elements. The boundary conditions imposed at the left end of the cantilever eliminate the rigid body motion but enable the deformation in the 0Y and 0Z directions.
The data is as follows: \(E=10^{7} \), \( \nu =0.3 \), the length \( L = 6 \), the thickness \( h=0.2 \) and the width in the 0Y direction \( w =0.1 \).
The vertical displacement \( u_z \) at node A is presented in Table 5. All the tested solid-shell elements perform well for the rectangular mesh, for which the relative errors are in the range [− 0.76, − 0.78]% for computations without the RBF correction and in the range [0.06–0.08]% with the RBF correction. The RBF correction is beneficial for all tested and reference elements.
For the trapezoidal mesh, the range of relative errors is wider; [− 0.81, 4.67]% and [− 0.12, 5.49]% for computations without and with the RBF correction, respectively. The effects of the RBF correction are generally positive, except for our HW51 and the reference HSEE, for which the accuracy worsens. Nonetheless, for these elements the displacements are larger than the reference solution, excluding locking.
Note that all the reference 2D plane stress elements show locking for the trapezoidal shape but to different degrees. For the 9-node elements it is over 3 times smaller than for the 4-node ones, for which the error exceeds − 77%. For both, the errors are much bigger than for the solid-shell elements.
In Table 5, we also evaluate the effects of the ANS method for the thickness strain of Betsch and Stein [6]. Comparing the results obtained with and without this method for the trapezoidal mesh (the latter are designated “EAS10 w/o ANS [6]”), we conclude that it reduces the relative error from − 71.5 to − 0.84% for computations without the RBF, and from − 59.68 to − 0.15% for computations with the RBF correction; a significant reduction indeed.
Straight cantilever by trapezoidal elements. Geometry and meshes
Remark
The mesh of parallelogram (through-thickness) shape elements is obtained by tilting the common nodal “directors” by \( 45^\circ \), see Fig. 8. For this mesh and computations with the RBF correction, the maximum relative error of \( u_z \) is 0.78% for HSEE and 0.5% for HW51. For the other elements, it is much smaller. Generally, the error of parallelogram shape solid-shell elements is much smaller than for the trapezoidal shapes.
5.2.6 Curved 3D cantilever
The element’s distorted shape (Case 1, Fig. 9) and the skew (non-parallel) nodal “directors” (Case 2, Fig. 11) affect the accuracy of a solution, especially when the thickness h diminishes. By the nodal “directors” we designate the through-thickness vectors linking the corresponding bottom and top nodes; for a single element they are shown in Fig. 1.
The curved 3D cantilever is fixed at one end and loaded by a moment \( M_z \) at the other, see Fig. 9. The nodes shown in this figure are doubled in the radial direction to obtain the mesh for 8-node solid-shell elements. The external moment is assumed as \( M_z= \left( {R}/{h}\right) ^{-3} \), so a solution of a linear problem should remain constant. This moment is applied to solid-shell elements as two pairs of opposite tangent forces \( P = M_z/h/2 \).
The data is as follows: \(E=2 \times 10^5 \), \(\nu =0\), width \(b= 0.025\) and radius of curvature \(R=0.1\). The reference analytical solution for a curved beam is
where I is the moment of inertia. The FE mesh consists of 6 solid-shell elements.
Curved 3D cantilever. Case 1: a regular mesh and b distorted mesh
Case 1: Regular and distorted shapes The regular and distorted element’s shapes are shown in Fig. 9; the distortion is defined as in Koschnick et al. [21] p. 2454. For the distorted mesh, the 8-node solid-shell elements are warped (non-planar), which makes this case very demanding and for which the RBF correction can be beneficial.
The cantilever thickness is varied in the range \( h \in [ 10^{-2}, 10 ^{-4}] \), so the slenderness is \( R/h \in [ 10, 10^4 ] \) and \( L/h \in 2.6 \cdot [ 1, 10^4] \), where L is a circumferential length of a single rectangular element.
The scaled displacement \( u_y/ u_y^{\textrm{ana}} \) at point A obtained in the linear analysis are shown in Fig. 10, where two sets of results are presented, without and with the RBF correction.
-
(a)
Without the RBF correction, the best accuracy provides the reference EAS10, next are all the remaining elements, which perform nearly identically.
-
(b)
With the RBF correction, the best accuracy provides the reference EAS10 and ours HW51. Next are the remaining tested and reference elements, which nearly coincide. The curves for our HW35, HW27B and HW19 almost coincide.
For the slenderness \( \log _{10}(R/h) = 3 \), the RBF correction significantly improves the accuracy of displacements; reducing the error from 10 to 2% for EAS10, from 30 to 5% for our HW51 and from 30 to 10% for the remaining elements. For \( \log _{10}(R/h) = 4 \), the accuracy is unacceptable for all elements, without/with the RBF correction.
Curved 3D cantilever. Case 1. Distorted mesh. Scaled displacement \( u_y \) at point A a without RBF, b with RBF. (HW51* for regular mesh, without RBF)
Case 2: Radial and skew nodal “directors” For the curved cantilever, the nodal “directors” can be either radial or skew (non-parallel) as shown in Fig. 11 for the thickness \( h = 10^{-2} \) (\( R/h =10 \)). For the skew ones, the angle \( \varphi \approx 35^{\circ } \); it would decrease if h were decreased further. In the circumferential direction, the regular mesh of Fig. 9a is used.
The displacements \( u_y \) at point A (node 1) obtained in the linear analysis are shown in Table 6. The relative errors [in %] also are presented. The most accurate is the reference EAS10, then our reduced representation HW elements (HW19, HW27B and HW35). The latter elements perform similarly and the RBF correction has a small negative effect for them. For EAS10, this effect is more pronounced. The elements with a large number of parameters, such as our HW51 and the reference HSEE, perform worse than the other elements and effect of the RBF correction is negligible.
Curved cantilever. Case 2: a Radial and b skew nodal “directors”
5.2.7 Pinched cylinder with diaphragms
The purpose of this example is to show mesh convergence for the tested and reference HW solid-shell elements. This is one of the most severe tests for both inextensional bending and complex membrane states, see Belytschko et al. [4] p. 239.
A cylindrical shell is closed at both ends by rigid diaphragms and is pinched by two opposite forces P applied at the middle section, see Fig. 12a. The material and geometry data of [4] are as follows: \(E=3 \times 10^{6} \), \( \nu =0.3 \), \( R=300 \), \( L=300 \), \( h=3 \) and \( P=1 \). Because of symmetries, only one-eighth of the cylinder is analyzed, see Fig. 12b. The mesh of \( N \times N \times 1 \) solid-shell elements is used, where 1 element is used through-thickness. The number of elements per side \( N = 4,8,16,32,64 \).
Pinched cylinder with diaphragms. a Initial geometry and loads. b Mesh for 1/8 of the cylinder
The vertical displacement \( {\textrm{w}}_{FEM} \) under load at node A on the external surface is monitored, and its value obtained for the element HW35 and \( N=128\) is used as \( {\textrm{w}}_{REF} = 1.8757 \times 10^{-5} \) to obtain the scaled displacements. The results for various N are presented in Fig. 13; the reference curves (Ref. shell) are obtained using the 4-node shell element HW47 with 6 dofs/node of [52] (thick broken lines).
We see that the solutions for the tested and reference solid-shell elements almost coincide and are very close to the reference shell solutions. The positive effects of the RBF correction for coarse meshes are clear; the curves obtained without the RBF correction can be compared to Fig. 13 of [17]. For the densest mesh, the difference between the solutions without and with the RBF correction becomes very small, as expected.
The solutions obtained without the RBF correction converge monotonically from below and can be used to find the convergence rate for varying the number of elements per side N. Because the differences between the curves for our solid-shell HW elements are very small in Fig. 13; we further use only HW35. The relative error is defined as \( e_{w} = | (\mathrm{w_{HW35} - w_{REF}}) | / \mathrm{w_{REF}} \) and the \(\log _{10} e_{w}\) is plotted against \(\log _{10}(L/N) \) in Fig. 14, where L/N is the element’s size. Next the line is fitted to these 5 points, and \( y(x)= -3.04157 + 1.51914~x \) is obtained. Therefore the rate of convergence is 1.51914, which compares favorably with the rate for shell elements.
Pinched cylinder with diaphragms. Scaled displacement at A for varying N
Pinched cylinder with diaphragms. Log–log diagram and convergence rate
5.3 Non-linear tests
5.3.1 Roll-up of a clamped beam
This is a standard test to verify finite rotation procedures for beams and shells, but here it is used to asses the quality of solid-shell elements in pure bending.
The planar straight beam is clamped at one end and loaded by a bending moment M at the other end, see Fig. 15a. The nodes shown in this figure are doubled to obtain the mesh of 25 8-node solid-shell elements. The moment M is replaced by two pairs of opposite forces \( \pm P \), which are tangent to the free edge in the current configuration. The data is as follows: \(E=12 \times 10^6 \), \( \nu =0 \), the thickness \( h=0.1\), the width \( w=1\), the length \(L=10\). The RBF correction is irrelevant to this test.
A full circle is obtained for the bending moment \( M^* = 2 \pi EI/L = 628.319 \). The beam’s tip displacements up to \( M^* \) are shown in Fig. 15b, where the displacements \( u_x \) are marked by the dashed lines, \( -u_z \) by the continuous lines, and the 2D Timoshenko beam solution by the crosses. We see that the curves for all the solid-shell elements coincide in the scale of this figure.
More precise are the values of the tip’s displacements at \( M^* \) given in Table 7, where also the relative error of \( u_x \) [in %] is presented. All the solid-shell elements slightly lock, but the range of relative error is narrow [1.14–1.28]%. Least locks the reference EAS10 without the ANS for the thickness strain of [6], as then the error is 0.41%.
Roll-up of a beam. a Initial (straight) and final (circular) geometry. b Displacements of beam’s tip for rolling up into a circle
5.3.2 Pinched hemispherical shell with hole
The hemispherical shell with an \( 18^{\circ }\) hole is loaded by two pairs of equal but opposite external forces, see Fig. 16. The shell undergoes an almost in-extensional deformation, so a membrane locking of a solid-shell element can be detected by this test.
Due to the double symmetry, a quarter of the shell is modeled. One element is used through-thickness and three meshes with \(8\times 8 \), \(16\times 16\) and \(64\times 64\) elements over the surface. The nodes shown in Fig. 16 are doubled in the thickness direction to obtain the mesh for 8-node solid-shell elements, which have the shape of truncated pyramids. For reference, the 4-node and 9-node shell elements are used; for the latter the \(4\times 4\), \(8 \times 8\) and \(32 \times 32 \)-element meshes are used.
The data is as follows: \(E=6.825\times 10^{7} \), \( \nu =0.3 \), thickness \( h=0.04 \) of [29]. Non-linear solutions are also provided for a smaller thickness \( h=0.01 \), for which the elements are more prone to locking.
The results of linear analyses for the thickness \( h=0.04 \) are given in Table 8, where the inward displacement \( u_y \) under the force \( P=1 \) at the inner node is reported.
In general, the RBF correction renders that the displacements are larger than without using it. The relative error is reported for the \( 64 \times 64 \)-element mesh and the RBF correction reduces its range from [− 0.47, − 0.48]% to [− 0.27, − 0.28]%, so this correction is beneficial. Besides, it causes that all the solid-shell elements converge from above for the increasing mesh density.
Pinched hemispherical shell with hole. a Geometry and boundary conditions. b Deformed shape
The non-linear analyses are performed using the Newton method and the solution curves for the \(16 \times 16\)-element mesh are shown in Fig. 17. The curves computed without the RBF correction are indicated by thin continuous lines, and these computed with this correction by thin dashed lines. The reference curve is obtained using the 4-node shell element HW47 with 6 dofs/node of [52] (thick continuous line).
The solution curves coincide for all solid-shell elements in the whole range of load. They exactly follow the reference curve up to a certain level from which they start departing from it. Then the displacements become slightly either excessive or locked. It depends on whether the RBF correction is used or not.
We also include non-linear solution curves for the smaller thickness \( h=0.01 \), see Fig. 17. Comparing Figs. 17 and 18, we see that the RBF correction is certainly more beneficial for the smaller thickness \( h=0.01 \).
Pinched hemispherical shell with hole. \( h=0.04 \). Non-linear solutions obtained with and without the RBF correction
Pinched hemispherical shell with hole. \( h=0.01 \). Non-linear solutions obtained with and without the RBF correction
One-step non-linear test An overall effectiveness of a finite element in non-linear analyses depends not only on the time of a single Newton iteration but also on the radius of convergence and the rate of convergence, which can be characterized by the maximum \( \Delta P \) for which the Newton method converges and the number of iterations required.
This test is performed for the pinched hemisphere of \( h=0.01 \) and the \(16 \times 16 \)-element mesh. The maximum load for which the Newton method converges is found for each solid-shell element separately, increasing \( \Delta P \) by 0.1. The results obtained without and with the RBF correction are presented in Table 9.
We see that the HW elements with a large number of parameters, such as the reference HSEE (43 p) and ours HW51 and HW35, converge for bigger \( \max \Delta P \) and require less iterations. Those with less parameters, such as our HW27B and HW19, converge for a smaller \( \max \Delta P \). For them the RBF correction is particularly beneficial. The reference EAS10 requires the smallest \( \max \Delta P \) and the RBF correction does not improve this.
Comparing the performance of our reduced representation HW elements, we draw the following conclusions:
-
1.
Our HW51 and HW35 perform similarly, but HW35 uses less parameters. HW27B and HW19 perform likewise, hence the assumed transverse shear stress and strain (\( S^{0a}_{\alpha 3} \) and \( E^{0a}_{\alpha 3} \)), which are used in HW27B but not in HW19, are not required.
-
2.
Another formulation with 27 parameters has been tested, in which the assumed thickness stress and strain (\( S^{0a}_{33} \) and \( E^{0a}_{33} \)) are retained and the assumed transverse shear stress and strain (\( S^{0a}_{\alpha 3} \) and \( E^{0a}_{\alpha 3} \)) are omitted. Such an element performed worse than HW19, especially without the RBF correction.
5.3.3 Twisted beam
This test belongs is from MacNeal and Harder [29]. The initial geometry of the beam is twisted so all the elements are warped (non-flat), but the initial strain is equal to zero. The beam is clamped at one end and loaded by a force \( P_y \) at the other, see Fig. 19. The data is as follows: \(E=2.9\times 10^{7} \), \( \nu =0.22 \), the length \( L=12 \), the width \( w=1.1 \) and the twist angle is \(90^{\circ }\).
In our computations, the \(4\times 24\)-element mesh of the 8-node solid-shell elements and a small thickness \( h=0.0032\) are used. One element is used through thickness. For the reference shell elements, the \(4\times 24\)-element mesh is used for the 4-node HW47 and the \(2\times 12\)-element mesh for the 9-node MITC9i. This example is also computed without/with the RBF correction.
Twisted beam. a Initial mesh and load. b Deformed mesh at \( P_y=0.1 \)
The results of the linear analysis for \( P_y = 1 \times 10^{-6} \) are shown in Table 10, where the \( u_y \times 10^3 \) displacement at point A and its relative error are given. Without the RBF correction, our HW35 and HW27B are the most accurate, next are the reference elements EAS10 and HSEE, and finally HW51. The relative errors are in the range [0.07, − 0.46]%. With the RBF correction, the most accurate is the reference EAS10, next ours HW27B and HW19, then our HW51 and HW35 and the reference HSEE. The relative errors are in the range [0.10, − 0.67]%.
The non-linear load-deflection curves obtained for \( \Delta P_y = 1 \times 10^{-4} \) by the arc-length method are shown in Fig. 20, and the displacement \( u_y \) at point A is monitored. Without the RBF correction, the curves for all tested and reference elements coincide. With the RBF correction, all the curves except this for EAS10 coincide, and are slightly ‘softer’ than those obtained without the RBF correction. The softest is the reference EAS10, for which the solution curve coincides with that for the reference 4-node HW47.
Summarizing, the beam is extremely thin but the results are not corrupted by the membrane locking and are close to the reference ones.
5.3.4 Short C-beam
This example includes the right angle intersections of elements and is typically used to test shell elements with 3 rotational dofs/node, see [9]. It is useful also for solid-shell elements because of the through-thickness element’s shapes, for which the nodal “directors” are skew (non-parallel), see Fig. 21b.
The beam is fully clamped at one end and loaded by two vertical forces P/2 at the other end, see Fig. 21a, b. The data is as follows: \(E=10^{7} \), \(\nu =0.333\), the length \( L=36 \), the thickness \(h=0.05\). The web is modeled by \( 36 \times 6 \) elements and each flange by \( 36 \times 2 \) elements, so the total number of elements is 360. The vertical displacement \( u_z \) is monitored at point A, between the nodes to which the forces P/2 are applied.
Twisted beam. Out-of-plane load. Comparison of non-linear solutions
The linear reference solution \( u_z =1.1544 \times 10^3 \) is computed using the 16-node shell element in [10]. This value is confirmed by our results of Table 11, where the error is: (a) 0.1% or less for 4-node and 9-node shell elements, and (b) 0.24% for the 3D 8-node element and a dense mesh of 23040 elements, i.e. for the mesh density multiplier equal to 4, also through-thickness.
Short C-beam. a Initial geometry and load. b Shape of elements in cross-section Y0Z (thickness not to scale). c Deformed configuration at force \( P=112 \)
The linear solutions for \( P=1 \) and the mesh of 360 elements are given in Table 11, where the displacement \(-u_z \times 10^3 \) and its relative error are shown. Without the RBF correction, the range of relative errors is [2.08, 3.35]% while with this correction [3.19, 3.46]%. Our HW19 is the most accurate of the solid-shell elements, but the reference shell elements with 6 dofs/node are more accurate.
The non-linear solutions for the 360-element mesh are computed using the arc-length method with the initial \( \Delta P=5 \), see Fig. 22. The reference curve is obtained using the 4-node shell element HW47 of [52] (thick continuous line). The solution curves for the solid-shell elements with the RBF correction almost coincide and are slightly more stiff than the reference curve. The solution curve for the 3D 8-node solid element specified in Table 11 and the 360-element mesh (dotted line) is stiff.
It was also verified that the curves for HW51 and the two sets of transformation for the assumed stress/strain: (a) CTV-CTV of Eqs. (33) and (32) and (b) CTV-COV of Eqs. (33) and (34), coincide.
Short C-beam. Non-linear solutions obtained with the RBF correction for the 360-element mesh
L-shaped plate. a Initial geometry. b Deformed geometry. Note: P is applied as two forces P/2
5.3.5 L-shaped plate
The purpose of this non-linear test is to characterize the convergence of the solid-shell elements by comparing the last solution points reached in 10 steps.
The L-shaped plate is clamped at one end and the in-plane force P is applied at the other end. The data is as follows: \(E=71240 \), \( \nu =0.31 \), \( w=30 \), \( L=240\), and the thickness \( h=0.6 \), see [3]. A mesh of 64 square elements of size \( 15 \times 15 \) is used and two forces P/2 are applied to the top and bottom nodes to replace the force P, see Fig. 23. The RBF correction of Sect. 4.3 is used.
L-shaped plate. Non-linear solution. 10 steps with \(I_{req}=25 \)
The deformation associated with the primary solution path takes place in the X0Y plane and has a bifurcation point at which an out-of-plane deformation occurs. We add a small out-of-plane load \( P_z \) at point B to initiate this deformation. (More details related to a precise estimation of the bifurcation load are given in [48] p. 440.) The equilibrium problem is solved using the arc-length method for the prescribed initial load increment \( \Delta P \) and the requested number of iterations per step \( I_{req} \). The arc-length is modified at the beginning of each load step using the scaling parameter
where \( I_{prev} \) is the number of iterations in the previous (convergent) load step.
First, the non-linear solutions for all the tested and reference solid-shell elements are computed and they coincide with the reference curve (Ref.), obtained for the 4-node shell element HW47. Next, 10 steps are performed using the arc-length method for \( \Delta P = 0.5 \), \( P_3 = P/1000 \), and \( I_{req} = 25 \). In Fig. 24, the final solution points for particular elements are indicated. Two elements, our HW51 and the reference HSEE, cover the longest distance in 9 steps but diverge in the 10th step. In 10 steps, the longest distance covers our HW35, then our HW27B and HW19, and finally the reference EAS10.
5.3.6 Compression of a nearly-incompressible block
For the enhanced low-order solid elements and nearly incompressible materials, the hourglassing (zero-energy) modes can occur for large compressive (uniform) strains, see, e.g., [11, 13, 23, 24, 58, 59]. It is important to check this aspect for 2D 4-node plane strain elements and 3D 8-node solid elements as it indicates an instability of their formulation.
For the solid-shell elements, hourglassing does not seem to be recognized as a problem and, e.g. in [15], which deals with nearly-incompressible materials, this issue is not addressed. This can be explained by the fact that the solid-shell elements are mainly applied to shell structures, in which large compressive strains are prevented by design to avoid the loss of structural stability.
The purpose of this test is to establish whether hourglassing appears or not in our solid-shell HW elements and for this purpose we find the first zero eigenvalue and the associated eigenvector of their tangent matrix. Two orientations of the solid-shell elements are checked so they are compressed in either their in-plane or normal (through thickness) direction.
The block of size \( 1 \times 1 \times 1 \) is modeled by a mesh of \( 10 \times 10 \times 1 \) elements, see Fig. 25, where one element is used in the thickness direction (normal to the plane of figure). The block is supported in the vertical direction at the bottom and vertically compressed by a sequence of increments of displacement \( \Delta \text{ v } = 0.001 \) applied at the top. The Newton method is used to solve the equilibrium equations for each increment and 10 lowest eigenvalues of the tangent stiffness matrix are computed at the converged configurations using ARPACK. For the lowest eigenvalue equal to zero, the corresponding scaled eigenvector is plotted, so it can be seen directly whether hourglassing appears.
Compression of nearly-incompressible block. Problem definition
The modified neo-Hookean hyper-elastic material model is used, with the strain energy function \( \mathcal{W}\) defined in terms of the volumetric/deviatoric split of the deformation gradient \( \textbf{F}\),
where \( \textbf{C}=\textbf{F}^T \textbf{F}\) is the right Cauchy–Green deformation tensor and \( J = \det \textbf{F}\). The material constants are as follows: the shear modulus \( \mu = 20 \), the bulk modulus \( K = 4 \times 10^5 \) and the dimensionless parameter \( \beta =-2 \). The RBF correction of Sect. 4.3 is not used and the shear correction factor \( k =1 \).
The obtained critical strains for all the tested and reference solid-shell elements are given in Table 12. The reduced representation elements and the reference elements behave similarly and display hourglassing at the first (lowest) zero eigenvalue. The HW51 behaves differently; the zero eigenvalues appear at lower strains (two of them are reported) but there is no hourglassing for the in-plane compression. Nonetheless hourglassing appears for the normal compression of HW51.
For reference, this example is also computed using two 3D 8-node solid elements; our mGu-EADG12B and TSCG12 of [23], both integrated using the \( 2 \times 2 \times 2 \) Gauss rule. Our element uses the mean gradient of displacements (mGu), the \( \gamma \)-vectors and the Enhanced Assumed Displacement Gradient (EADG12B) with 12 parameters. It is slightly faster than TSCG12 but less accurate. Both these elements, are suitable for the material of Eq. (81).
The two lowest eigenvalues of the solid-shell element HW35 and the reference 3D solid elements are shown in Fig. 26. Interesting is the difference between the curves for the normal and in-plane compression of HW35 (thick lines), which is a result of using the techniques of Sect. 4 and characteristic for solid-shell elements. Note that the curves for HW35 and 3D mGu-EADG12B coincide while the curves for 3D TSCG12 are different.
Compression of a nearly-incompressible block. First eigenvalues for the solid-shell element HW35 and two 3D solid elements mGu-EADG12B and TSCG12
Compression of a nearly-incompressible block. Eigenvectors superimposed on the configuration corresponding to the lowest zero eigenvalue: a Solid-shell HW35 (in-plane compression) and 3D mGu-EADG12B. b 3D TSCG12
To detect hourglassing at the first zero eigenvalues, scaled eigenvectors are superimposed on the deformed configuration, see Fig. 27 for the in-plane compression. The HW35 and our 3D mGu-EADG12B display similar hourglassing while no hourglassing appears for the 3D TSCG12.
Finally, the reduced representation solid-shell HW elements show hourglassing at the first zero eigenvalue but it appears at the large strain equal to 0.37 for the in-plane compression. This is the level of strain for which the shell structures are unlikely to be designed.
5.4 Summary of results related to the RBF correction
The RBF correction was implemented to enhance the elements’ behavior in sinusoidal bending and for significant elements’ thinness. It was tested on several linear and nonlinear examples, the results of which are summarized below.
-
1.
Straight cantilever of trapezoidal elements of Sect. 5.2.5. For the rectangular mesh, all elements show a small improvement when the RBF correction is used. For the trapezoidal mesh, the errors of the reduced representation HW elements are diminished. The errors of HW51 and the reference HSSE are the largest; for the RBF correction they slightly increase to exceed 5%.
-
2.
Curved 3D cantilever of Sect. 5.2.6. Case 1 with warped elements. For the slenderness \( \log _{10}(R/h) = 3 \), the RBF correction significantly improves the accuracy, reducing the error from 10 to 2% for EAS10, from 30 to 5% for HW51 and from 30 to 10% for the reduced representation HW elements and the reference HSEE, see Fig. 10. Case 2 with skew nodal “directors”. All the reduced representation HW elements perform similarly, and the RBF correction has a small negative effect on them. HW51 and the reference HSSE yield excessive displacements of an over 12% error, which remains practically unchanged by the RBF correction.
-
3.
Pinched hemisphere with hole of Sect. 5.3.2. In the linear test, the RBF correction reduces the relative errors and they are smaller than 0.48% for the dense mesh, see Table 8. In the nonlinear test, all the elements perform almost identically. The solution curves follow the reference curve up to a certain load, and then gradually depart from it. The displacements obtained with the RBF correction are slightly excessive for the thickness \( h=0.04 \) and more exact for \( h=0.01 \), see Figs. 17 and 18. In the one-step non-linear test, the RBF correction is particularly beneficial for the reduced representation HW elements, and they all have a much bigger radius of convergence than the reference EAS10, see Table 9.
-
4.
Twisted beam of Sect. 5.3.3. In the linear test, the errors are smaller than 0.67%, and the effects of the RBF correction are ambiguous (positive or negative), see Table 10. In the non-linear test without/with the RBF correction, the curves for all HW elements coincide, and these obtained with the RBF correction are slightly ‘softer’. The softest is the reference EAS10, which exactly matches the reference 4-node HW47, see Fig. 20.
-
5.
Short C-beam of Sect. 5.3.4. In the linear test without the RBF correction, the errors are below 3.35%, which slightly increases to 3.46% when this correction is applied. All HW elements perform well, and HW19 is the most accurate, see Table 11. In the non-linear test, the solution curves obtained with the RBF nearly coincide for all elements, and are slightly more stiff than the reference curve.
-
6.
L-shaped plate of Sect. 5.3.5. In this non-linear test, the solution curves are obtained with the RBF correction and they coincide for all elements. Among the reduced representation HW elements, the biggest radius of convergence has HW35, then HW27B and HW19, see Fig. 24;
In conclusion, we see that the performance of the reduced representation HW elements is in the majority of tests improved by the RBF correction. The radius of convergence is definitely improved, and is larger than the one of the reference element EAS10.
6 Final remarks
The paper concerns the development of eight-node Hu–Washizu (HW) solid-shell elements, with particular emphasis on the reduction of the number of internal parameters. Four HW elements are developed and tested. They have correct rank, pass the membrane and bending patch tests and are free from the curvature thickness, transverse shear and volumetric locking.
-
1.
At the outset, an element based on a 51-parameter representation of the assumed stress/strain (HW51) is developed, next also three others (HW35, HW27B and HW19) using the reduced representations with 35, 27 and 19 parameters, respectively, including 3 parameters of the EAS enhancements of the thickness strain. (43 parameters are used in the reference HSEE element [20].) The latter two elements are based on the so-called partial HW functionals, which differs from the approach used in other papers, where the HW functional is needed for all strain components.
-
2.
All the reduced representations of the assumed stress/strain are \(\zeta \)-independent, where \( \zeta \) is the thickness coordinate, with the skew coordinates in the in-plane (11, 22 and 12) components. The assumed stress/strain representations involve respectively 13/19, 9/15 and 5/11 parameters, which is a reduction from 18/33 parameters of HW51.
-
3.
For the elements based on the reduced representations, the transformations used for the assumed stress/strain have a significant effect for distorted shapes, see Fig. 6. The contravariant (CTV-CTV) transformations yield more accurate solutions for such elements and, therefore, are applied to all of them. The transformation operators \( \textbf{T}_\textrm{S} \) and \( \textbf{T}_\textrm{E} \) are computed at the element center and at the reference surface (\(\zeta =0\)), which is slightly different than in the HSEE element, see Sect. 3.4.2.
-
4.
An interesting outcome of the paper is that the elements with a larger number of parameters, such as HW51 and the reference HSEE (43 p), are less accurate than the elements with the reduced representations for trapezoidal through-thickness shapes of elements, see Fig. 7, and Tables 5 and 6. This feature provides a strong argument for using the reduced representation elements.
-
5.
The convergence properties of the reduced representation elements indicate that HW35 has a larger radius of convergence than HW27B and HW19, see Sect. 5.3.2 (Table 9) and Sect. 5.3.5 (Fig. 24). The elements with a large number of parameters HW51 and the reference HSEE (43p) converge only slightly better. All HW elements converge much better than the enhanced strain element EAS10.
-
6.
By comparing the reduced representation HW elements with each other, we obtain that they are nearly equally accurate in the linear tests of Sects. 5.2.3, 5.2.4, 5.2.5 and 5.2.6. In non-linear tests, they perform similarly in Sects. 5.3.1, 5.3.2, 5.3.3, 5.3.4 and 5.3.5, while small differences are visible in Sects. 5.3.3 and 5.3.4. Hence, considering accuracy, some parameters of the richer assumed representations can be considered as redundant.
In summary, the developed HW elements with the reduced representations of the assumed stress/strain perform very well, especially for trapezoidal through-thickness shapes of elements (skew nodal “directors”). When a large radius of convergence is required then HW35 is advised. Otherwise, considering efficiency, we recommend the element with the smallest number of parameters HW19.
References
Andelfinger U, Ramm E (1993) EAS-elements for 2D- and 3D-, plate and shell structures and their equivalence to HR-elements. Int J Numer Methods Eng 36:1311–1337
Andelfinger U, Ramm E, Roehl D (1992) 2D- and 3D-enhanced assumed strain elements and their application in plasticity. In: Proc. COMPLAST 111, 1997–2007, Barcelona, Spain, 1992
Argyris J, Balmer H, Doltsinis JST, Dunne PC, Haase M, Kleiber M, Malejannakis GA, Mlejenek JP, Muller M, Scharp DW (1979) Finite element method—the natural approach. Comput Methods Appl Mech Eng 17(18):1–106
Belytschko T, Stolarski H, Liu WK, Carpenter N, Ong JSJ (1985) Stress projection for membrane and shear locking in shell finite elements. Comput Methods Appl Mech Eng 51:221–258
Betsch P, Gruttmann F, Stein E (1996) A 4-node finite shell element for the implementation of general hyperelastic 3D-elasticity at finite strains. Comput Methods Appl Mech Eng 130:57–79
Betsch P, Stein E (1995) An assumed strain approach avoiding artificial thickness straining for a non-linear 4-node shell element. Commun Numer Methods Eng 11:899–909
Büchter N, Ramm E, Roehl D (1994) Three-dimensional extension of nonlinear shell formulation based on the enhanced assumed strain concept. Int J Numer Methods Eng 37:2551–2568
Cook RD (1987) A plane hybrid element with rotational d.o.f. and adjustable stiffness. Int J Numer Methods Eng 24:1499–1508
Chróścielewski J, Makowski J, Stumpf H (1992) Genuinely resultant shell finite elements accounting for geometric and material nonlinearity. Int J Numer Methods Eng 35:63–94
Chróścielewski J, Makowski J, Pietraszkiewicz W (2004) Statics and dynamics of multi-segmented shells. Nonlinear theory and finite element method. IFTR PAS Publisher, Warsaw ((in Polish))
Crisfield MA, Moita GF, Jelenic G, Lyons LPR (1995) Enhanced lower-order element formulation for large strains. Comput Mech 17:62–73
Dvorkin EN, Bathe K-J (1984) A continuum mechanics based four-node shell element for general nonlinear analysis. Eng Comput 1:77–88
Glasier S, Armero F (1997) On the formulation of enhanced strain finite elements in finite deformations. Eng Comput 14(7):759–791
Harnau M, Schweitzerhof K, Hauptmann R (2000) On solid-shell elements with linear and quadratic shape functions for small and large displacements. In: ECCOMAS Congress, Barcelona 11-14 September 2000, pp 1–27
Hauptmann R, Doll S, Harnau M, Schweizerhof K (2001) “Solid-shell’’ elements with linear and quadratic shape functions at large deformations with nearly incompressible materials. Comput Struct 79:1671–85
Hauptmann R, Schweizerhof K, Doll S (2000) Extension of the solid-shell concept for large elastic and large elastoplastic deformations. Int J Numer Methods Eng 49:1121–41
Hauptmann R, Schweizerhof K (1998) A systematic development of ‘solid-shell’ element formulations for linear and non-linear analyses employing only displacement degrees of freedom. Int J Numer Methods Eng 42:49–69
Jarzebski P, Wisniewski K, Taylor RL (2015) On parallelization of the loop over elements in FEAP. Comput Mech 56(1):77–86
Klinkel S, Gruttmann F, Wagner W (1999) A continuum based three-dimensional shell element for laminated structures. Comput Struct 71(1):43–62
Klinkel S, Gruttmann F, Wagner W (2006) A robust non-linear solid shell element based on a mixed variational formulation. Comput Methods Appl Mech Eng 195:179–201
Koschnick F, Bischoff GA, Camprubi N, Bletzinger KU (2005) The discrete strain gap method and membrane locking. Comput Methods Appl Mech Eng 194:2444–2463
Korelc J (2002) Multi-language and multi-environment generation of nonlinear finite element codes. Eng Comput 18:312–327
Korelc J, Solinc U, Wriggers P (2010) An improved EAS brick element for finite deformation. Comput Mech 46:641–659
Korelc J, Wriggers P (1996) An efficient 3D enhanced strain element with Taylor expansion of the shape functions. Comput Mech 19:30–40
Korelc J, Wriggers P (2016) Automation of finite element methods. Springer, Berlin
MacNeal RH (1978) A simple quadrilateral shell element. Comput Struct 8(2):175–183
MacNeal RH (1986) The evolution of lower order plate and shell elements in MSC/NASTRAN. Element technology. In: Hughes TJR, Hinton E (eds) Finite element methods for plate and shell structures, vol 1. Pineridge Press, Swansea
MacNeal RH (1994) Finite elements: their design and performance. Mechanical engineering, vol 89. Marcel Dekker Inc., New York
MacNeal RH, Harder RL (1985) A proposed standard set of problems to test finite element accuracy. Finite Elem Anal Des 1:3–20
Makowski J, Stumpf H (1986) Finite strains and rotations in shells. In: Pietraszkiewicz W (ed) “Finite rotations in structural mechanics’’, 175–194. Springer, Berlin
Parisch H (1995) A continuum-based shell theory for non-linear applications. Int J Numer Methods Eng 38:1855–1883
Pian THH, Sumihara K (1984) Rational approach for assumed stress finite elements. Int J Numer Methods Eng 20:1685–1695
Pian THH, Tong P (1986) Relations between incompatible displacements and hybrid stress model. Int J Numer Methods Eng 22:2331–2343
Piltner R, Taylor RL (1995) A quadrilateral mixed finite element with two enhanced strain modes. Int J Numer Methods Eng 38:1783–1808
Puso MA (2000) A highly efficient enhanced assumed strain physically stabilized hexahedral element. Int J Numer Methods Eng 49:1029–1064
Rah K, Van Paepegem W, Habraken AM, Degrieck J, Alves de Sousa RJ, Valente RAF (2013) Optimal low-order fully integrated solid-shell elements. Comput Mech 51:309–326
Simo JC, Armero F, Taylor RL (1993) Improved version of assumed enhanced strain tri-linear element for 3D finite deformation problems. Comput Methods Appl Mech Eng 73:53–92
Simo JC, Rifai MS, Fox DD (1990) On stress resultant geometrically exact shell model. Part IV. Variable thickness shells with through-the-thickness stretching. Comput Methods Appl Mech Eng 81:91–126
Simo JC, Rifai MS (1990) A class of mixed assumed strain methods and the method of incompatible modes. Int J Numer Methods Eng 29:1595–1638
Stumpf H, Makowski J (1986) On large strain deformations of shells. Acta Mech 65:153–168
Taylor RL (2010) Program FEAP, Ver. 8.3. University of California, Berkeley
Tessler A, Hughes TJR (1983) An improved treatment of transverse shear in the Mindlin-type four-node quadrilateral element. Comput Methods Appl Mech Eng 39:311–335
Vu-Quoc L, Tan XG (2003) Optimal solid shells for non-linear analyses of multilayer composites. I. Stat Comput Methods Appl Mech Eng 192:975–1016
Wagner W, Gruttmann F (2005) A robust nonlinear mixed hybrid quadrilateral shell element. Int J Numer Methods Eng 64:635–666
Wagner W, Gruttmann F (2019) On a simple shell model for thin structures with functionally graded materials. In: Altenbach H et al (eds) Recent developments in the theory of shells, advanced structured materials, vol 110. Springer, Berlin, pp 687–710
Weissman SL (1996) High-accuracy low-order three-dimensional brick elements. Int J Numer Methods Eng 39:2337–2361
Wilson EL, Taylor RL, Doherty WP, Ghaboussi J (1973) Incompatible displacement models. In: Fenves SJ, Perrone N, Robinson AR, Schnobrich WC (eds) Numerical and computer methods in finite element analysis. Academic Press, New York, pp 43–57
Wisniewski K (2010) Finite rotation shells. Basic equations and finite elements for reissner kinematics. CIMNE-Springer
Wisniewski K, Panasz P (2013) Two improvements in formulation of nine-node element MITC9. Int J Numer Methods Eng 93:612–634
Wisniewski K, Turska E (2008) Improved four-node Hellinger–Reissner elements based on skew coordinates. Int J Numer Methods Eng 76:798–836
Wisniewski K, Turska E (2009) Improved four-node Hu–Washizu elements based on skew coordinates. Comput Struct 87:407–424
Wisniewski K, Turska E (2012) Four-node mixed Hu–Washizu shell element with drilling rotation. Int J Numer Methods Eng 90:506–536
Wisniewski K, Turska E (2018) Improved nine-node shell element MITC9i with reduced distortion sensitivity. Comput Mech 62:499–523
Wisniewski K, Turska E (2019) On performance of nine-node quadrilateral shell elements 9-EAS11 and MITC9i. In: Altenbach H et al. (eds) Recent developments in the theory of shells, series “advanced structured materials”, vol 110. Springer, pp 711–725
Wisniewski K, Turska E (2020) On transverse shear strains treatment in nine-node shell element MITC9i. In: Altenbach H, Chinchaladze N, Kienzler R, Müller W (eds) Analysis of shells, plates, and beams. Series: “advanced structured materials”, vol 134. Springer, pp 421–440
Wisniewski K, Wagner W, Turska E, Gruttmann F (2010) Four-node Hu–Washizu elements based on skew coordinates and contravariant assumed strain. Comput Struct 88:1278–1284
Wriggers P (2008) Nonlinear finite element methods. Springer, Berlin
Wriggers P, Korelc J (1996) On enhanced strain methods for small and finite deformations of solids. Comput Mech 18(6):413–428
Wriggers P, Reese S (1996) A note on enhanced strain methods for large deformations. Comput Methods Appl Mech Eng 135(3–4):201–209
Yuan K-Y, Huang Y-S, Pian THH (1993) New strategy for assumed stress for 4-node hybrid stress membrane element. Int J Numer Methods Eng 36:1747–1763
Zienkiewicz OC, Taylor RL (1989) The finite element method, vol 1, 4th edn. McGraw-Hill, Basic Formulation and Linear Problems
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wisniewski, K., Turska, E. Reduced representations of assumed fields for Hu–Washizu solid-shell element. Comput Mech 71, 957–990 (2023). https://doi.org/10.1007/s00466-023-02275-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-023-02275-1