1 Introduction

1.1 State of the art

In a seminal contribution, Griffith [1] postulated an energetic criterion for crack propagation in an elastic body. He noted that a preexisting crack propagates when, due to some loading, the energy release rate reaches a certain threshold. The dedicated material parameter is called the critical energy release rate or crack resistance. From a different perspective, Irwin [2] laid the foundation of what is now known as classical linear elastic fracture mechanics [3] by focusing on the stress field of a pre-cracked homogeneous, linear elastic body subjected to a load. He investigated three different loading conditions, the so-called fracture modes. In this setting, the stress state is singular with an \(r^{-1/2}\) singularity in the crack tip, r denoting the distance to the latter. The local stress state primarily depends on the prefactor of \(r^{-1/2}\) called the stress intensity factor by Irwin. Based on these stress intensity factors, Irwin postulated a criterion for crack propagation, which is triggered whenever the stress intensity factor surpasses a material dependent fracture toughness. In the setting of a linear elastic, isotropic and homogeneous material, the criteria proposed by Griffith and by Irwin, based on the critical energy release rate and on the fracture toughness, respectively, turned out to be equivalent.

Several extensions of classical fracture mechanics beyond linear isotropic elasticity have been proposed, such as for elastoplastic materials [4, 5] or anisotropic elastic solids [6,7,8,9]. In addition to these studies, which investigate when cracks propagate, Chambolle et al. [10] discuss how cracks propagate.

In the absence of analytical solutions, computational strategies prevail. Rice–Tracey [11] proposed a method to compute the local stress intensity factors numerically.

Classical finite element methods face challenges with resolving the stress singularity at an existing and propagating crack. Therefore, enriched and extended finite element methods, which account for a non-continuous solution field, were proposed [12, 13].

Nearly 25 years ago, Francfort and Marigo introduced a variational fracture model [14] based on Griffth’s original energy criterion. The model was formulated in terms of an energy functional to be minimized and added impetus to phase-field fracture mechanics [15, 16]. The latter is rather popular, as it permits to simulate both crack initiation and crack propagation in a common framework based on traditional finite element methods. The phase-field model may be interpreted as a regularization of the Francfort–Marigo model, inspired by the Ambrosio–Tortorelli approximation [17] of the Mumford–Shah functional [18]. Alternatively, the phase-field fracture model may be interpreted as a non-local damage model [19, 20].

Multiscale methods [21] are used to predict the macroscopic behavior of microstructured materials, explicitly accounting for the material behavior of the constituents and their arrangement on the microscale. Homogenization theories serve as the mathematical underpinning of modern multiscale methods. Seminal contributions focus on periodic homogenization [22,23,24], where the underlying microstructure is given by a periodic cell. Since microstructured materials are often random due to their manufacturing process [25], stochastic homogenization results [26, 27] have been established, where an infinitely large domain with a random microstructure is investigated. One method to evaluate effective properties based on stochastic homogenization results is by exploring representative volume elements (RVEs). For prescribed accuracy and fixed boundary condition type, a volume element is called representative provided it approximates the effective properties of the infinitely large domain up to this prescribed accuracy [28]. Since the size of the RVE is not known a priori and dependent on various factors, the RVE size is often found via computations on volume elements of increasing size [29, 30] until a desired degree of representativity is reached. For elliptic PDEs such as elasticity and conductivity, theoretical results show that for different boundary conditions applied to cells of finite size, i.e., periodic, Dirichlet or Neumann boundary conditions, the effective quantities evaluated on the cells share the same infinite-volume limit [31,32,33]. Yet, it is well known that the boundary conditions may have a strong influence on the necessary size of the RVE, see Kanit et al. [34].

In the field of fracture mechanics, multiscale approaches face additional difficulties compared to linear elastic or conductivity problems. One necessary ingredient for multiscale methods is a distinct scale separation, allowing the quantities of interest, displacements, stresses or strains, to be separable into a large-scale and small-scale component. In an elastic material without a crack, for instance, this separation leads to a cell formula on the microscale, from which effective quantities may be derived. This approach does not work within a cracked microstructure, since this crack and the stress singularity resulting from it would be present on both the micro- and the macroscale. On the other hand, investigations on volume elements of finite size may be conducted with phase-field fracture models [35, 36]. However, it is well known [37] that such a procedure will not, in general, lead to a macroscopic model for softening materials. Thus, special care is required. Hossain et al. [38] performed phase-field simulations on the microscale and defined the effective crack resistance as the maximum J-integral [39, 40] evaluated during the crack propagation.

For co-planar crack propagation in a perturbative framework, Lebihain et al. [41, 42] define the effective crack resistance by computing the energy release rate from the stress intensity factors. They consider three different ways to evaluate the effective crack resistance by taking either the maximum or two types of averages of the evaluated energy release rate along the crack propagation and demonstrate that these definitions lead to different results, in general. Upon a large-volume limit, the differences between these approaches vanish.

A different strategy is based on a periodic homogenization result of Braides et al. [43] for the Mumford–Shah [18] functional and energetic minimization. This result covers the Francfort–Marigo model of brittle fracture [14] in the case of anti-plane shear when considering a fixed quasi-static time discretization and neglecting crack irreversibility (for instance in the very first load step on an un-cracked specimen). Within their result, Braides et al. [43] show a decoupling of the volumetric part and the surface part of the Mumford–Shah functional. In the context of the Francfort–Marigo model this implies a decoupling of the effective stiffness and the effective crack energy in the anti-plane shear case. Furthermore, they provide specific formulas for both effective quantities. From their work the effective crack energy is defined as the area of the crack resistance-weighted minimal surface cutting through the microstructure. Numerical approaches to computing the effective crack energy have been proposed by the authors [44,45,46] using FFT-based algorithms and periodic boundary conditions. Recently, Michel–Suquet addressed the approach based on Braides et al.’s [43] homogenization result using an alternative solution strategy by pointing out similarities with limit load analysis [47]. Additionally, they provide a detailed discussion on the topic “effective crack resistance” vs. “effective crack energy” and possible advantages and limitations of the different approaches. In particular, at the heart of the question lies the presence of two small scales, i.e., a time step in the time discretization, and a length scale separating the microstructure from the macroscopic case. In the framework based on the approach of Braides et al. [43], the time step is fixed as the spatial scale tends to zero. As a consequence, a propagating crack would pass the microstructural cell within a single time step. In contrast, Hossain et al. [38] and Lebihain et al. [41, 42] fix the microstructure and simulate cracks propagating quasi-statically through the microstructure. These authors propose definitions of the effective crack resistance which are neither related to nor motivated by mathematical homogenization results. To avoid confusion we call the effective quantity based on the work of Braides et al. [43] the “effective crack energy”, since the term does not coincide with the definitions provided by Hossain et al. [38] and Lebihain et al. [41, 42].

Recently, the periodic homogenization result of Braides et al. has been extended by Cagnetti et al. [48] to the case of stochastic homogenization, i.e., the case of materials with random (stationary and ergodic) microstructure. Thus, the homogenization of the Mumford–Shah functional holds for a general random microstructure with distinct scale separation. Furthermore, they provide a formula for the effective crack energy on the infinite domain, which has the same form as the formula Braides et al. [43] established in the periodic setting. Yet, both results use a specific kind of boundary conditions. Moreover, their results are mostly quantitative, lacking qualitative character.

1.2 Contributions

The aim of this paper is to investigate the effective crack energy of solids with random microstructures and the influence of the imposed boundary conditions. We recapitulate the known periodic and stochastic homogenization results for the Francfort–Marigo model both in the anti-plane shear and the general case in Sect. 2.1. For both the periodic and the stochastic setting, the effective crack energy is expressed in terms of a multi-cell formula on specifically notched cubes, which we call Dirichlet boundary conditions. For periodic homogenization, this multi-cell strategy is overly arduous, and a single-cell formula is sufficient, provided periodic boundary conditions are used, as well. Therefore, it makes sense to investigate periodic boundary conditions for random materials, as well. Indeed, for periodic boundary conditions, powerful numerical tools for computing the effective quantities based on the fast Fourier transform (FFT) are available, which we summarize in Sect. 2.2. Dirichlet boundary conditions on the other hand are not easily integrated into this framework.

In a two-dimensional setting the problem of computing the effective crack energy reduces to finding weighted minimal paths. One prominent algorithm to compute such paths is the fast marching method introduced by Sethian [49, 50] where fast implementations are publicly available [51]. In the context of fracture mechanics, the fast marching method has already been used for fatigue fracture using stress intensity factors [52] and in combination with the extended finite element method [53,54,55]. We discuss a straightforward way to compute the effective crack energy with the help of the fast marching method in Sect. 3. One advantage of this method is that Dirichlet boundary conditions can easily be applied, since every point of a domain may be used as a starting or ending point.

Section 4 comprises the numerical results. We first validate the fast marching method in terms of accuracy of the discretization and compare the results for periodic boundary conditions with established tools. Finally, we investigate the influence of the boundary condition on the approximated effective crack energy for microstructure samples of increasing cell size. We compare Dirichlet and periodic boundary conditions and study their necessary size of the computational cell.

This article is based on the Master’s thesis of the second author [56] supervised at the institute of engineering mechanics (ITM), Karlsruhe Institute of Technology (KIT) in 2022.

2 The effective crack energy of heterogeneous random media

2.1 Homogenization results for the Francfort–Marigo model of brittle fracture

For a body \(\Omega \subset \mathbb {R}^d\), let \(\mathbb {C}:\Omega \rightarrow L(Sym(d))\) denote a field of positive definite stiffness tensors where we denote by L(Sym(d)) the space of linear operators on symmetric \(d\times d\) matrices. Furthermore, let \(\gamma :\Omega \rightarrow \mathbb {R}_{>0}\) be a field of local crack resistances bounded away from zero. For a fixed (pseudo-) time discretization, appropriate time-dependent boundary conditions, and a fixed time step, Francfort and Marigo [14] considered a crack evolution based on the functional

$$\begin{aligned} F(u,S) = \frac{1}{2}\int _{\Omega \backslash S} \nabla ^su : \mathbb {C}(x) : \nabla ^su \,dx + \int _{S}\gamma (x) \,dA. \end{aligned}$$
(2.1)

Here, S denotes the current crack surface and u stands for the accompanying the displacement field which may be discontinuous across S. The Francfort–Marigo model of brittle fracture considers an evolution governed by the minimization problem

$$\begin{aligned} (u^*,S^*) = \text {argmin}\,F(u,S) \end{aligned}$$
(2.2)

at each time step, subjected to the irreversibility condition \(S^*_{i+1}\supseteq S^*_{i}\). With the indices labeling the time steps, the irreversibility condition encodes the physically plausible fact that cracks may only grow upon loading.

Let us consider the case of an underlying periodic microstructure, i.e., the fields \(\mathbb {C}\) and \(\gamma \) are periodic with periodicity \(\eta \). For this periodic case and neglecting the irreversibility constraint, Braides et al. [43] proved a homogenization result for the Mumford–Shah functional [18], which corresponds to the Francfort–Marigo model in the case of anti-plane shear. The work of Braides et al. [43] includes a \(\Gamma \)-convergence result of the (anti-plane shear) Francfort–Marigo functional (2.1) to the spatially homogeneous functional

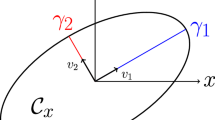
$$\begin{aligned} F_{\text {eff}}(u,S) = \frac{1}{2}\int _{\Omega \backslash S} \nabla ^su : \mathbb {C}_{\text {eff}} : \nabla ^su \,dx + \int _{S}\gamma _\text {eff}(n) \,dA\nonumber \\ \end{aligned}$$
(2.3)

as \(\eta \rightarrow 0\). This expression comprises a (possibly anisotropic) effective stiffness tensor \(\mathbb {C}_{\text {eff}}\) as well as an effective crack energy \(\gamma _\text {eff}:\,S^{d-1} \rightarrow \mathbb {R}_{>0}\), whose possible anisotropy is encoded via the dependence on the unit normal n. Braides et al. [43] provide explicit formulas for both the effective stiffness and the effective crack resistance. Remarkably, the elastic material properties do not affect the effective crack energy and vice versa. In particular, classical computational strategies for computing the effective linear elastic stiffness may be used [57]. The effective crack energy emerges by the following construction. Inside an infinite periodic continuation of our material with periodicity \(\eta \) we place a cube \(Q_L(n)\) of edge length L with its \(e_1\) axis rotated onto the prescribed normal n. On such a cube, we compute a \(\gamma \)-weighted minimal surface S cutting the cube under the constraint that the surface cuts the boundary of the cube at \( x_1 = L/2\) within the coordinate system of the cube, see Fig. 1 for a visual representation. The effective crack energy is given by the limit of these computed weighted minimal surfaces as the cube edge-length \(L\rightarrow \infty \). In mathematical terms, the effective crack energy is defined via

$$\begin{aligned} \gamma _{\text {eff}}(n) = \lim _{L\rightarrow \infty } \inf _S \frac{1}{L^{d-1}}\int _S \gamma \, dA. \end{aligned}$$
(2.4)

In a recent extension of the work of Braides et al. [43], Friedrich et al. [58] lift the restriction to the anti-plane shear case for their periodic homogenization result.

Fig. 1
figure 1

Visualization of the computation of the effective crack energy. The cube \(Q_L(n)\) is placed into the periodic structure. Depending on the material contrast \(\gamma _2/\gamma _1\) either the green or the red path is favored

Full size image

Let us take a closer look at the cell formula (2.4). From a computational point of view, the limit of \(L\rightarrow \infty \) is not practicable, as we can only deal with finite computational domains. To overcome this issue, we may restrict to a single cell \(Q_L\) and employ the boundary conditions used in the proof by Braides et al. [43], which we call Dirichlet boundary conditions. In this case, we fix the surface S on the boundary \(\partial Q_L\) of the cube at \(x_1 = L/2\) within the local coordinate system of the cube. Actually, any cut at \(x_1 \in [0,L]\) could be chosen. We choose \(x_1 = L/2\) for definiteness.

The approach by Braides et al. [59] involves a multi-cell formula (2.4) although the homogenization problem is periodic. As the integrand in the problem (2.4) is convex, it is reasonable to hope that a single-cell formula may prove sufficient for computing the effective crack resistance \(\gamma _{\text {eff}}\). This is indeed true, as shown by Braides et al. [59] and Chambolle and Thouroude [60]. More precisely, they showed that the effective crack energy \(\gamma _{\text {eff}}(n)\) in equation (2.4) may be computed on a single cell \(Y_\eta \) with period \(\eta \) and for fields with periodic boundary conditions

$$\begin{aligned} \gamma _{\text {eff}}(n) = {\inf _{p:Y_\eta \rightarrow \mathbb {R},~ \text {periodic}}}\frac{1}{|Y_\eta |} \int _{Y_\eta }\gamma \,\Vert n + \nabla p\Vert \,dx. \end{aligned}$$
(2.5)

Many materials of industrial relevance show a randomness in their microstructure composition, and periodic homogenization is not sufficient for describing those. Recently, Cagnetti et al. [48] proved an extension of the result of Braides et al. [43] to stochastic homogenization for the Francfort–Marigo model under anti-plane shear. Remarkably, the result provides a true extension of the periodic case. They show a \(\Gamma \)-convergence result to a functional of the form (2.3) and provide explicit expressions for both the effective stiffness and the effective crack energy, which—as for the periodic case—do decouple upon homogenization. These explicit expressions involve an infinite-volume limit.

The case of effective stiffnesses in stochastic homogenization is well-studied. To render computations on cells of finite size well posed, it is required to furnish the cells with appropriate boundary conditions. Upon an infinite-volume limit, the effects of the boundary conditions vanish [31,32,33]. However, for cells of finite size, the chosen type of boundary conditions does have an influence on the approximation quality of the “true” effective stiffness, see the works [31, 34] among numerous others. It can be shown—both theoretically and numerically—that optimal convergence rates are reached when using periodic boundary conditions and periodized ensembles of microstructures, see Schneider et al. [61] for a thorough discussion. For this reason, we restrict to periodic microstructures throughout this article.

In contrast to elastic and inelastic materials, very little is known about the influence of the boundary conditions when computing the effectiveFootnote 1 crack energy evaluated on cells of finite size. The aim of this work is to provide a first step in this direction. For the periodic boundary conditions and in three spatial dimensions, Schneider [44] proposed an algorithm for computing the effective crack energy on cells on finite size. The approach relies on Strang’s minimum cut/maximum flow duality [62].

Due to the tremendous computational effort involved, we restrict to two-dimensional microstructures. In this case, it is possible to compute shortest paths with fast marching, see Sect. 3, which is well-known among experts.

2.2 Computational approach for periodic boundary conditions—minimum cut/maximum flow

To compute the effective crack energy on a given cell Y with periodic boundary conditions we consider the minimization problem

$$\begin{aligned}&\frac{1}{|Y|} \int _{Y}\gamma \, \Vert \xi \Vert \,dx \rightarrow \min _{\xi \in {\mathcal {K}}_{\bar{\xi }}} \nonumber \\&\text {with} \quad {\mathcal {K}}_{\bar{\xi }} = \{\xi :Y\rightarrow \mathbb {R}^d\,|\, \xi = \bar{\xi } + \nabla p,~ \bar{\xi } \in \mathbb {R}^d,~p ~\text {periodic}\}, \end{aligned}$$
(2.6)

which seeks the periodic minimum cut through the cell Y with mean normal \(\bar{\xi }\). If the direction \(\bar{\xi }\) has length unity, the minimum value of this functional is the effective crack energy for unit normal \(n = \bar{\xi }\). Solving the problem (2.6) is numerically challenging since the functional to be minimized is not differentiable as a consequence of the 1-homogeneity of the integrand. To overcome this issue, Schneider [44] suggested to consider the formal dual problem, which is called the maximum flow problem. This duality was first described by Strang [62] who found that minimum cut is dual to maximum flow. The maximum flow problem seeks the periodic flow field \(v:Y\rightarrow \mathbb {R}^d\), solving

$$\begin{aligned} {\frac{1}{|Y|} \int _Y \bar{\xi }\cdot v \, dx \rightarrow \max _{\text {div}\, v = 0,~\Vert v\Vert \le \gamma }.} \end{aligned}$$
(2.7)

This problem may be interpreted as a linear program with linear and quadratic constraints. To solve this numerically, suitable discretizations and solvers are required. Schneider [44] used an FFT-based solution framework with a trigonometric collocation discretization [63, 64] and a finite element discretization with reduced integration [65]. He solved the governing equations with a primal dual hybrid gradient method [66, 67]. However, numerical difficulties arose in achieving high-accuracy solutions. This can be achieved using the combinatorial consistent maximum flow (CCMF) discretization [68], which, for small problems, may be embedded into classical second-order cone solvers [69, 70]. However, these may suffer from “memory limitations” [68]. As a remedy, Ernesti–Schneider [45] proposed an FFT-based solver for the CCMF discretization. Furthermore, improvements on the solver were introduced exploiting a damped version of the alternating direction method of multipliers (ADMM) [71, 72] with an adaptive penalty parameter choice. A similar approach has been proposed by Willot [73] who investigated the related problem of finding the effective conductivity of resistor networks. Michel–Suquet [74] proposed a different approach to computing the effective crack energy. For trigonometric collocation discretization [63, 64], they used classical numerical strategies to compute limit loads of structures [47].

Fig. 2
figure 2

Microstructure and minimum cut field (\(\xi \) in Eq. (2.6)) for an axis-aligned and a non-axis-aligned prescribed mean normal

Full size image

3 Finding the minimum cut with the fast marching method

3.1 From minimum cut to shortest path problems

To gain some intuition into minimum cut fields in two spatial dimensions, we consider a periodic microstructure of circular inclusions, shown in Fig. 2a. The structure contains 35 fillers, i.e., \(50\%\) area fraction. We consider tough inclusions, i.e., these have a (much) higher crack resistance than the matrix material. Figure 2b and c show the minimum cut for mean crack normals \(\bar{\xi } = e_1\) and \(\bar{\xi } = (3e_1 + e_2)/\sqrt{10}\). In both cases, the minimum cut field localizes and takes the shape of a crack path that cuts through the microstructure. However, a distinct difference is present between the two cases. For the axis-aligned case, the cut field traverses the microstructure once, cutting from left to right. For the non-axis aligned case, the cut field wraps around the microstructure several times in order to both preserve the mean normal of the cut and to retain periodicity.

Thus, at least for the axis-aligned case, it appears reasonable the minimum cut may be computed by an algorithm which returns a (weighted) shortest path [75,76,77]. Indeed, after fixing two corresponding points on opposing edges of the microstructure, a minimum weighted path joining the two points would have to be computed.

Fig. 3
figure 3

Periodic microstructures \(Q_L\) (with a periodic extension in y-direction), giving rise to possible problems for shortest path methods. (Color figure online)

Full size image

Some caution is advised with this kind of strategy, as the following two examples demonstrate. For a start, we consider the periodic microstructure shown in Fig. 3a with imposed crack normal \(\bar{\xi } = e_1\). If the crack resistance in the rectangles (shown in blue) is much higher than in the complement (shown in white), the minimum cut is forced to navigate through the white pathways. In this process, more than one unit cell needs to be crossed. In the example shown, the green curve crosses the horizontal “boundary” twice. Such a curve may be represented by a shortest path algorithm if periodicity in y-direction is accounted for. Otherwise the red curve would arise as the shortest path from left to right.

Unfortunately, taking periodicity in y-direction into account does not always offer the proper strategy, as the microstructure in Fig. 3b shows. A straight “obstacle” with high crack resistance is placed along the diagonal. For prescribed normal \(\bar{\xi } = e_1\), the minimum cut has to cross the obstacle. The shortest path strategy with periodic boundary conditions in y-direction, however, would give rise to the green path. Unfortunately, the shown path does not give rise to the correct path normal \(\bar{\xi } = e_1\), but to the normal n pointing in diagonal direction! If, instead, no periodicity in y-direction is permitted, the correct crack path (in red) is computed.

To summarize, the charming idea of working with shortest path algorithms to compute the effective crack energy for axis-aligned crack normals may be unsuited to some microstructures. Therefore, it is unavoidable to perform a validation against minimum cut methods. For the microstructure models considered in this article, such a comparison is contained in Sect. 4.3.

3.2 Finding shortest paths by the fast marching method

There is a deep connection between the eikonal equation and efficient path finding which led Sethian [49, 50] to devise computationally efficient algorithms for the latter. More precisely, consider a domain \(\Omega \subset \mathbb {R}^d\) and suppose a wave propagates through our domain, starting from some point \(x_0 \in \Omega \) at a given velocity \(v:\Omega \rightarrow \mathbb {R}_{>0}\). Then, the time \(T:\Omega \rightarrow \mathbb {R}_{\ge 0}\) this wave needs to arrive at point \(x\in \Omega \) solves the eikonal equation

$$\begin{aligned} \Vert \nabla T(x)\Vert = \frac{1}{v(x)},\quad x\in \Omega , \end{aligned}$$
(3.1)

with \(T(x_0) = 0\). If the velocity v is spatially homogeneous, the level sets of the travel time T describe concentric spheres around the starting point \(x_0\). For a heterogeneous velocity, the wavefront is refracted. Sethian [49, 50] introduced the fast marching method as a fast algorithm for solving the eikonal equation. The fast marching method is an integrated strategy where the spatial discretization and the strategy for solving the eikonal equation are well orchestrated. More precisely, the solution strategy uses a modification of Dijkstra’s algorithm [78] well-known in graph theory [79]. The fast marching method finds application in various fields ranging from shortest path finding [80,81,82] to simulating wildfire spreading [83] and within the extended finite element method [54, 55].

In d spatial dimensions and on a regular grid with \(N^d\) grid points, the fast marching method has the computational complexity \(O(N^d\log N)\). In contrast, iterative procedures for solving the eikonal equation (3.1) typically have a complexity of \(O(N^{d+1})\). This complexity reduction is partly caused by an underlying min-heap data structure [84].

Fig. 4
figure 4

Example for (non-unique) shortests path with Dirichlet (index “D”, red) and periodic (index “P”, green) boundary conditions

Full size image

The problem of computing the effective crack energy on a microstructure involves finding a weighted minimal surface, as we pointed out in Sect. 2, Eq. (2.4). For the special case of two-dimensional structures, this problem simplifies to finding shortest paths in a given two-dimensional microstructure, for which various methods are available [85, 86]. In particular, the fast marching method may be applied as follows.

Fig. 5
figure 5

Distance field and crack path for different boundary conditions for a single circular inclusion microstructure

Full size image
  1. 1.

    The crack resistance \(\gamma (x)\) serves as the weight in computing the weighted shortest path playing the role of a resistance for the crack to propagate. In contrast, for a propagating wave, the velocity v(x) enables the propagating wave to travel faster at a higher speed. Therefore we set the right hand side of the eikonal equation (3.1) to \(\gamma (x)\) instead of 1/v(x) for computing the effective crack energy with fast marching.Footnote 2

  2. 2.

    The solution field T(x) embodies the \(\gamma \)-weighted distance from point x to the origin \(x^0\). We therefore call it the distance field throughout this work.

  3. 3.

    To compute the effective crack energy of a given microstructure cell \(Y = [0,L]^2\) with crack normal \( n = e_2\) and Dirichlet boundary conditions, we choose a starting point \(x^0 =(0,L/2)^T\) and evaluate the distance field T in \(x^*=(L,L/2)^T\). The effective crack energy is given by \(T(x^*)/L\), see the red path in Fig. 4.

  4. 4.

    The solution for periodic boundary conditions with mean normal \(n=e_y\) is given by the \(\gamma \)-weighted shortest periodic path from the left hand side to the right hand side. To find this shortest path with the fast marching approach, we consider all paths with the starting point \(x^0 = (0,y)\) and end point \(x^* = (L,y)\) for some \(y\in [0,L]\), and select the starting point which returns the smallest crack energy, see the green path in Fig. 4. On a computational grid with \(N\times N\) pixels, this process includes N fast marching computations, which increases the computational complexity to \(O(N^3\,\log N)\).

  5. 5.

    The fast marching method enables computing the minimum crack energy in a straightforward way. However, the involved crack path is not directly accessible. Rather, different approaches are available to obtain the crack in postprocessing, see for instance Noyel et al. [77]. Using the fact that the shortest crack path is perpendicular to the level sets of the distance field T, we rely on a gradient descent method to compute the crack path from any point x to the origin \(x^0\). To do so, we compute a spline interpolation on the numerically evaluated gradient of the distance field T.

One advantage of the fast marching method over the maximum flow approach from Sect. 2.2 is that additional boundary conditions can easily be studied, as we can choose any point of \(\Omega \) as our starting or ending point. We consider three different cases, illustrated in Fig. 5, which shows the level sets of the distance field and the resulting crack path for a structure containing a single circular inclusion of diameter L/2 positioned at the center of a square with edge length L. The inclusion has a much higher crack resistance than the embedding matrix, forcing the crack path to avoid the inclusion altogether. The distance field and the crack path for Dirichlet boundary conditions is shown in Fig. 5a. The distance field describes concentric circles starting from the left hand side until the inclusion is reached and a refraction occurs. To draw the crack path, we start on the right hand side at \(y = L/2\) and follow the path perpendicular to the contour lines of the distance field. Notice that this path does not prescribe the shortest path from the right hand side of the structure to the origin on the left hand side. Indeed, Fig. 5b shows this shortest path originating in \(x^0\) to the right-hand side. To draw this path we select \(x^*\) as the point on the right hand side with the minimum effective crack energy and draw the path perpendicular to the contour lines of the distance field. Since the mean crack normal may differ from the prescribed mean normal we do not focus on this case in this paper. For periodic boundary conditions the crack path is not unique for this example, as both above and below the inclusion straight paths are possible, see Fig. 5c for one possible option.

Fig. 6
figure 6

Microstructure of a rotated square with anticipated crack path, distance field and crack path for Dirichlet boundary conditions

Full size image

4 Numerical investigations

4.1 Setup

The fast marching based algorithm for computing the effective crack energy was implemented in Python 3 based on the scikit-fmm module [51], which provides both first-order and second-order fast marching methods. These differ in the convergence order of the underlying approximation of first derivatives. The first-order fast marching method uses classical forward and backward differences, whereas for the second-order method a three point stencil approximation of forward and backward differences is used [87]. The crack paths were visualized by first computing the gradient of the resulting distance field by finite differences, interpolating this gradient field with bi-cubic splines and finally using gradient descent starting from the end point of the crack path.

For the computations based on the minimum cut/maximum flow approach, we relied on an in-house FFT-based code [44,45,46]. The continuous equations were discretized with the CCMF discretization [68] and solved by a damped version of the alternating direction method of multipliers (ADMM) [71, 72] with adaptive choice for the penalty parameter, see Ernesti–Schneider [45]. We chose a relative tolerance of \(10^{-4}\).

All fast marching computations were run on an ARM-based SoC Apple M1 with 8 GB of RAM using a single thread. The minimum cut/maximum flow computations were performed on a desktop computer with 32 GB of RAM and six 3.7 GHz cores.

4.2 A single rotated square inclusion

To investigate the accuracy of the fast-marching approach, we start with a structure containing a single square inclusion of edge length L/2, which is rotated at 45 degrees and positioned at the center of our computational domain of edge length L, see Fig. 6a. The crack resistance of the inclusion is given by \(\gamma _{\text {fib}}=10\,\gamma _{\text {mat}}\). We consider an initial double notch crack at \(y=0.5\,L\), i.e., Dirichlet boundary conditions. The analytical solution, which may be extracted from the structural measurements, see Fig. 6a, is \(\gamma _{\text {eff}}/\gamma _{\text {mat}} = \sqrt{3/2}\approx 1.22247\), see Fig. 6a.

Figure 6b shows a contour plot of the distance field. Starting from the initial notch on the left hand side, the distance field initially shows a circular expanding front. Upon hitting the inclusion, the field is refracted and a new circular front with the top/bottom edge of the inclusion as origin continues to the other side. Since the distance field is symmetric with respect to the x-axis, we slightly perturb the starting point for our gradient descent method in y-direction to break this symmetry and enforce a unique crack path. The evaluated crack path is shown in Fig. 6c. We observe that it matches the geometrically anticipated path.

Next, we investigate the quality of the solution with respect to the grid size. We compute the effective crack energy for different resolutions ranging from 100 to 6400 pixels per side length of our computational domain. Furthermore, we investigate the performance of both first-order and second-order fast marching methods. The results are shown in Fig. 7a, where the absolute values of the crack energy are depicted, as well as in Fig. 7b, which shows the relative error compared to the analytical solution. Both the first and the second-order methods converge to the analytical solution with a linear rate of convergence. However, the second-order approach leads to a higher accuracy than the first-order approach, even on a coarser grid. To reach the accuracy of the second-order fast marching using first-order requires almost four times more pixels per edge length. Hence, we rely on the second-order fast marching method for the remainder of this article.

Fig. 7
figure 7

Effective crack energy and relative error for the rotated square microstructure

Full size image
Fig. 8
figure 8

Microstructure containing 32 circular inclusions for different resolutions and distance field for periodic boundary conditions

Full size image

4.3 Comparison with minimum cut/maximum flow

In our next study, we investigate a periodic structure containing 32 uni-directional fibers and a filler fraction of \(50\%\), which are represented as circular inclusions, see Fig. 8. The structure was generated using a mechanical contraction algorithm [88]. The inclusion are considered tough, i.e., they have a higher crack resistance than the matrix and we set \(\gamma _\text {fib} = 10\,\gamma _\text {mat}\). We investigate various resolutions ranging from 128 to 4096 pixels per edge length.

In this section, we would like to investigate whether the results obtained with the fast-marching method and with the FFT-based technique give rise to similar results. Indeed, as discussed in Sect. 3.1, it is necessary to exclude certain pathological situations in order to gain confidence into the results obtained with the fast marching method. We wish to emphasize that due to the lack of uniqueness of the solutions to the minimization problem (2.6), we may only expect the obtained effective crack energies to be close. However, similarity of obtained minimum cracks is certainly sufficient for the latter to hold.

To enforce periodic boundary conditions in the fast-marching setting, we iterate over all pixels on the right hand side of the microstructure, evaluate the distance field at the same height on the other side and select the minimum. The distance field is shown in Fig. 8c. From the near center of the y-axis we observe a circular expanding front which is refracted at every inclusion.

For both, the fast marching and the minimum cut/maximum flow formulation and the two considered resolutions, the crack paths are shown in Fig. 9. Notice that the way these two methods extract the crack path is very different. Whereas the crack path of the fast marching method is computed via gradient descent along the distance field, the crack path of the minimum cut/maximum flow approach is given by the total minimum cut through the microstructure with mean normal \(e_y\), which is a field that localizes around the crack attaining large values whose magnitude has no physical meaning. This results from the fact that the minimum cut is given by the gradient of the periodic field p in equation(2.6) which has a jump discontinuity across the crack. Evaluating this quantity numerically results in large but finite values which tend to infinity as the pixel length goes to zero. Both methods find extremely similar crack paths. On a coarser grid of \(128^2\) pixels, the fast marching crack in Fig. 9b exhibits some small isolation distance to the inclusions, which is not the case for the minimum cut field. This isolation distance vanishes for higher resolutions, see Fig. 9d. These computational results resolve possible doubts about the expressivity of the fast marching results for the considered microstructures.

Fig. 9
figure 9

Periodic crack paths for minimum cut/maximum flow and fast marching method of a microstructure containing 32 circular inclusions for different grid sizes

Full size image
Fig. 10
figure 10

Effective crack energy and relative error comparing fast marching with minimum cut/maximum flow

Full size image

In Fig. 10, the effective crack energy for the two approaches under consideration is plotted against the resolution, together with the relative error, where we used the solution on the \(4096^2\) grid as the ground truth for each method. Both approaches show a linear rate of convergence with respect to the resolution per edge length. Furthermore, both approaches overestimate the effective crack energy on a coarser grid. However, in order to reach the accuracy of the minimum cut, the fast marching method requires between 1.5 and 2 times the resolution of the edge length. Notice the difference in the complexity of the two methods. The complexity of the minimum cut/maximum flow is mainly driven by the FFT, which has a complexity of \(O(N^2 \log N)\), as well as the number of required iterations, which ranged between 2000 and 7000 in order to reach the desired accuracy of \(10^{-4}\). The fast marching approach has a complexity of \(O(N^3 \log N)\) for periodic boundary conditions. As a result we noticed for resolutions below \(N = 2048\) that the fast marching method required less computational time than the minimum cut/maximum flow method, each running on a single thread. For \(N=4096\) the fast marching method required twice the computational time of minimum cut/maximum flow.

4.4 The influence of boundary conditions

In our next study we investigate the influence of the boundary conditions on the effective crack energy for computational cells of increasing size. We consider two types of boundary conditions, namely Dirichlet boundary conditions and periodic boundary conditions. For Dirichlet boundary conditions, we consider the crack propagating at \(y=0.5\,L\) to the other side of the domain at the same height. Fully periodic boundary conditions are attained by the minimum value when iterating over all pixels in y-direction using Dirichlet boundary conditions starting from each pixel. The material parameters are chosen as before, i.e., the inclusions are considered tough with a material contrast of 10.

A comparison of the crack paths for different boundary conditions is shown in Fig. 11, where we consider a microstructure with \(50\%\) circular inclusions, i.e., uni-directional continuous fibers. The crack path for the periodic boundary conditions interacts with less inclusions, resulting in a path with more straight segments compared to the Dirichlet boundary conditions.

Fig. 11
figure 11

Crack paths for different boundary conditions

Full size image

To further investigate the boundary conditions, we consider microstructures with \(30\%\) and \(50\%\) filler fraction and a varying number of inclusions ranging from \(5^2\) to \(80^2\). For each number of inclusions we consider 100 microstructure realizations which were generated using mechanical contraction [88]. For the Dirichlet boundary conditions we consider all realizations. To reduce the computational costs for periodic boundary conditions we only take half of the realizations into account for a fiber count of \(50^2\) and higher.

Fig. 12
figure 12

Comparison of the boundary conditions for \(30\%\) filler content

Full size image

The results for volume fractions \(30\%\) and \(50\%\) are shown in Figs. 12 and 13, respectively. Figures 12a and 13a show a histogram of the crack energy for \(25^2\) inclusions. On the y-axis, the number (in percent) of microstructures is shown whose effective crack energy corresponds to the x coordinate. We notice that the range of the periodic boundary condition is shifted to the lower values of the effective crack energy ranging, into the lower part of the Dirichlet boundary conditions. For the Dirichlet boundary conditions we notice some accumulation in the lower range up to \(\gamma _\text {eff} = 1.025\, \gamma _\text {mat}\) for \(30\%\) filler fraction and \(\gamma _\text {eff} = 1.06 \,\gamma _\text {mat}\) for \(50\%\) filler fraction. Above these thresholds both histograms show some dispersion. These dispersions result from the fact that for some microstructures, the initial crack in the Dirichlet boundary conditions starts in an inclusion. Hence, the crack has to exit the inclusion first which causes an increase of the effective crack energy.

Figures 12b and 13b show the scatter of the effective crack energy computed for all 100 microstructure realizations in the lower fiber count range. For both volume fractions, we observe that the Dirichlet boundary conditions result in a much wider range of possible values for the effective quantity \(\gamma _{\text {eff}}\) than the periodic boundary conditions. Furthermore, we observe a division of this wide range into wide scatter, about one third of the data for \(30\%\) filler fraction and on half of the data for a filler fraction of \(50\%\). Furthermore, we see an accumulation of the remaining data around lower effective values. Additionally, we notice that the range of the outliers decreases for increasing fiber count since these effects result from initial cracks inside of inclusions.

Fig. 13
figure 13

Comparison of the boundary conditions for \(50\%\) filler content

Full size image

To gain additional insight into the influence of the boundary conditions, we investigate the median as well as the upper and the lower percentile ranges in Figs. 12c and 13c. We observe that the range of effective crack energies for the two boundary conditions under consideration overlap for both volume fractions. Hence, for some microstructures, the Dirichlet boundary conditions result in the same effective crack energy as the periodic boundary condition for a possibly different microstructure realization. Furthermore, we notice that for both boundary conditions the total range and the mid percentile range become smaller for an increasing fiber count. The median lines are approaching each other as the fiber count increases, however, at a very low rate. In general, the range of possible values for the effective crack energy for Dirichlet boundary conditions is much wider compared to periodic boundary conditions. Furthermore, the median for periodic boundary conditions is roughly placed in the center of the data set. In contrast, for Dirichlet boundary conditions the median and the mid percentile range are placed in the lower quarter of the data sets, reflecting the aforementioned outliers.

Last but not least, we investigate the relative standard deviation of the two data sets over the fiber count, see Figs. 12d and 13d. We observe a decrease of the standard deviation as the fiber count increases. Furthermore, we notice that the standard deviation for periodic boundary conditions is more than one magnitude lower than for Dirichlet boundary conditions. Specifically, for a volume fraction of \(50\%\), we notice an increase of the standard deviation for the last microstructure sample with \(80^2\) fillers. A possible explanation for this effect may be found in Fig. 13c where we notice that the spread of the standard deviation is caused by some computations with lower effective crack energy compared to the median/mean value. These lower outliers are caused by sections of straight crack paths which are still possible and probable for very large microstructures.

To sum up, we strongly discourage from using the Dirichlet boundary conditions. Rather, periodic boundary conditions should be preferred.

5 Conclusion

In this work we studied the influence of the boundary conditions on the effective crack energy of heterogeneous materials. Based on homogenization result [43, 48, 58] for the Francfort–Marigo model of brittle fracture [14] in a quasi-static setting and without crack irreversibility, we investigated a method for computing the effective crack energy using the fast marching method [49]. We validated our approach and compared it to recent FFT-based methods using periodic boundary conditions [44, 45]. In addition to periodic boundary conditions, the fast marching method provides additional freedom in the boundary condition choice. With this freedom at hand we compared periodic and Dirichlet boundary conditions for a continuously reinforced composite with tough inclusions, containing filler fractions of \(30\%\) and \(50\%\). We noticed in a study with several realizations of volume elements of increasing size that the periodic boundary conditions result in a much lower spreading of the results compared to Dirichlet boundary conditions. This was reflected in the standard deviation, which was one magnitude lower for the periodic boundary conditions compared to Dirichlet boundary conditions. For an increasing size of the computational cell, we noticed that the medians approached each other. However, periodic boundary conditions should be preferred over Dirichlet boundary conditions due to the much lower standard deviation. This lower standard deviation indicates that the necessary computational cell for periodic boundary conditions is considerably smaller than for Dirichlet boundary conditions. Thus, we strongly recommend using periodic boundary conditions.

Applying periodic boundary conditions in the context of the fast marching method relied on an iterative process over one axis of the domain, i.e., increasing the complexity of the algorithm on an \(N\times N\) grid from \(O(N^2 \log N)\) for Dirichlet boundary conditions to \(O(N^3 \log N)\). For microstructures of moderate size, i.e., up to \(N = 2048\), the fast marching method is still competitive with an FFT-based solver for the minimum cut/maximum flow problem. However, for larger structures the higher complexity forms a strong argument against using fast marching for periodic boundary conditions.

Classical fast marching algorithms are only applicable to isotropic crack resistances in the plane. To cover anisotropies in the crack resistance [46], anisotropic fast marching methods [89] may be explored.

Last but not least, let us mention that it would be desirable to have mathematical results at hand which concern the influence of boundary conditions on the effective crack energy. Indeed, for elastic solids, results [31,32,33] are available which provide a list of suitable boundary conditions whose influence becomes negligible when going to the infinite-volume limit. Previous work by Bouchitte–Suquet [90, 91] for limit-load problem suggests that Dirichlet boundary conditions may be used, whereas Neumann boundary conditions give rise to different results. Further research may be necessary to clarify this issue for the problem at hand.