Abstract
Numerical models built as virtual-twins of a real structure (digital-twins) are considered the future of monitoring systems. Their setup requires the estimation of unknown parameters, which are not directly measurable. Stochastic model identification is then essential, which can be computationally costly and even unfeasible when it comes to real applications. Efficient surrogate models, such as reduced-order method, can be used to overcome this limitation and provide real time model identification. Since their numerical accuracy influences the identification process, the optimal surrogate not only has to be computationally efficient, but also accurate with respect to the identified parameters. This work aims at automatically controlling the Proper Generalized Decomposition (PGD) surrogate’s numerical accuracy for parameter identification. For this purpose, a sequence of Bayesian model identification problems, in which the surrogate’s accuracy is iteratively increased, is solved with a variational Bayesian inference procedure. The effect of the numerical accuracy on the resulting posteriors probability density functions is analyzed through two metrics, the Bayes Factor (BF) and a criterion based on the Kullback-Leibler (KL) divergence. The approach is demonstrated by a simple test example and by two structural problems. The latter aims to identify spatially distributed damage, modeled with a PGD surrogate extended for log-normal random fields, in two different structures: a truss with synthetic data and a small, reinforced bridge with real measurement data. For all examples, the evolution of the KL-based and BF criteria for increased accuracy is shown and their convergence indicates when model refinement no longer affects the identification results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Establishing a monitoring system for a transportation infra structure is essential in order to obtain information about its current state and, therefore, ensure its safety. Changes in material properties is one of the consequences of deterioration of a structure, affecting its response to static and dynamic loads, as well as its reliability. Although these changes might not be directly measurable, they can be inferred from monitoring data, given a model that represents the physics of the system. The latest trend in monitoring systems are the so called digital twins: virtual models of a real structure which reflect the structure’s current state based (directly or indirectly) on measurement data and can be used for predictive purposes. Setting up these systems usually requires a model identification process to calculate the unknown parameters of interest. The model identification problem is a computationally costly inverse optimization process, which can be unfeasible for real applications. In order to circumvent this problem, the underlying numerical model can be replaced by a surrogate model which can be evaluated more efficiently. There are many approaches constructing a suitable surrogate, from reduced-order models to machine learning methods. In each case, the surrogate’s accuracy has an influence on the identification results. The numerical error of the model is often assumed to be much smaller than the measurement error and, therefore, it is considered to have a minor influence.
In contrast, the focus of this paper is to explicitly investigate the influence of the surrogate’s accuracy on the model identification results. A new goal-oriented inference procedure is introduced, consisting of adaptively building models with increased accuracy, running Bayesian inference with them and checking the changes in the results (due to the difference in models) through two proposed metrics: the Bayes Factor (BF) and the Kullback-Leibler divergence (KL) between the predictive posteriors. Once these criteria reach convergence, a sufficiently accurate model is found. For this work, a computationally efficient surrogate model is used, obtained with the Proper Generalized Decomposition (PGD) [1, 2]. The inference method of choice is the variational Bayesian approach after [3], allowing a very efficient calculation of the two convergence criteria. Although the proposed procedure makes use of these two methods [4], it is certainly not limited to them. The problem of selecting a sufficiently accurate reduced-order model is presented in the context of identifying a spatially-varying Young’s modulus field which can account for variations in stiffness, e.g. caused by damage or manufacturing imperfections. For that purpose, the PGD approach is additionally extended to log-normal random field parameters.
The paper is structured as follows: Sect. 1.1 provides a general definition for model identification problems as well as different approaches to solve them, while Sect. 1.2 gives an introduction to the PGD method. Then in Sect. 2, the coupling of variational Bayesian inference with a PGD forward model is derived and in Sect. 3 possible convergence criteria regarding the model’s accuracy are discussed. Section 4 presents a simple demonstration example, to show how these criteria can be applied to define a sufficiently accurate model. Subsequently, the general PGD forward model for linear elasticity with a Young’s modulus modeled by a log-normal random field is derived (Sect. 5.1). Finally, the proposed convergence procedure with a PGD forward model is applied to identify spatially distributed stiffness fields in a truss example with synthetic data (Sect. 5.2) and a small, reinforced bridge with real measurement data (Sect. 5.3).
1.1 Model identification
Model identification problems are, in general terms, defined as inverse problems. They aim at inferring some unknown parameters \({\varvec{\theta }}\) of a certain model \({\mathcal {M}}\), given some measurements \({\varvec{y}}\) related to the model outputs \(g({\varvec{\theta }})\) depending on the model parameters. Under the assumption of an additive observation noise \({\varvec{e}}\), with noise parameters \({\varvec{\Phi }}\), this results in:
In the present paper, the additive noise is assumed to be Gaussianly distributed (\({\varvec{e}} \sim {\mathcal {N}}(0,{\varvec{\Phi }}^{-1}{\varvec{I}}) \)), with unknown noise precision matrix \({\varvec{\Phi }}\) to be inferred.
In deterministic methods for parameter identification, the solution is obtained by minimizing the difference between measurement data \({\varvec{y}}\) and the model output \({\varvec{g}}({\varvec{\theta }})\):
by e.g., least-squares, \(L_p\) norm or weighted least-squares ansatz [5]. These approaches use optimization methods to return the best estimate for the parameters of interest. Note, that the solutions are point-estimates of the parameters, i.e. the results carry no information about how reliable or probable they are. Probabilistic inference methods, on the other hand, provide a probabilistic description of information and beliefs, allowing for uncertainties. This is done through Bayes’ theorem considering all unknown parameters as \({\varvec{\Theta }}=[{\varvec{\theta }},{\varvec{\Phi }}]\)
where the prior probability density function (pdf) reflects the prior knowledge on the parameters \({\varvec{\Theta }}\), the likelihood defines the probability that the measurements \({\varvec{y}}\) are observed given parameters \({\varvec{\Theta }}\). The normalization term \(P ({\varvec{y}} \mid {\mathcal {M}})\) describes the evidence for the data \({\varvec{y}}\) considering the model \({\mathcal {M}}\). Note, the unknown parameters \({\varvec{\Theta }}\) include model \({\varvec{\theta }}\) as well as noise parameters \({\varvec{\Phi }}\). The posterior is a pdf that reflects the updated knowledge about the parameters after observation of the data [6]. Its computation however, is cumbersome when \(dim({\varvec{\Theta }})>>1\), which requires approximations.
There are two main categories of approximate Bayesian inference methods: sampling-based (e.g., Markov Chain Monte Carlo (MCMC)) and optimization-based (e.g., variational inference). In the former category, some of the most famous methods are the Metropolis-Hastings [7, 8], Gibbs [9] and Hamiltonian Monte Carlo [10] algorithms. MCMC methods are powerful tools for approximate Bayesian Inference, as they are asymptotically unbiased. Another advantage is their nonparametric nature [11], i.e., they do not require assumptions on the functional form of the posterior. However, there are also limitations associated with MCMC, namely the high cost of sample generation and the very larger number of samples needed. Variational inference, on the other hand, is often computationally more efficient, being more appropriate for high-dimensional problems with computationally involved forward models. It provides an approximation to probability density functions that are difficult to compute (intractable integrals) through optimization [12, 13], details are given in Sect. 2. In the works of [14] and [15], it was also used to infer material properties. Among the limitations of the method is the fact that, unlike MCMC, the inference results can be biased and their accuracy strongly depends on the family of approximating distributions employed. In this paper, the variational Bayesian inference algorithm proposed by [3] for nonlinear forward models is coupled with a PGD forward model. In this way, the efficient forward model directly increases the computational efficiency of the inference process even more and allows an efficient computation of the proposed convergence criteria.
1.2 Proper generalized decomposition (PGD)
PGD is a reduced-order modeling approach. The key idea of PGD is the a-priori computation of abacuses, like numerical tables, with which a parameter dependent solution of a system is given, for a defined parameter space. An overview of the PGD approach can be found e.g., in [1] as well as in [2], concerning their use for digital twins. The unknown solution field (e.g., a displacement field \({\varvec{u}}\)) depending on space \({\varvec{x}}\) and model parameters \({\varvec{\theta }}\) is approximated in a separable form
with n mode sets. Each set consists of lower dimensional PGD modes \(F_j^i\) depending only on a single PGD coordinate \(\theta _j\), the model parameters, and the space \({\varvec{x}}\). In some cases, even the space could be further separated in its components. The PGD modes are computed by solving the classical weak form of the given problem’s partial differential equation (PDE), e.g., the balance of linear momentum, now over the \(D=d_{{\varvec{x}}}+d_{{\varvec{\theta }}}\)-dimensional space. The multi-dimensional integral can also be separated into single lower dimensional integrals resulting from the chosen separated form of \({\varvec{u}}^n\) in Eq. (4). As a result, the exponential scaling of the computational effort in multidimensional problems is reduced to a linear scaling and the curse of dimensionality is bypassed. The approach resembles the canonical tensor decomposition, which is known as the most data sparse representation of a tensor. For more information about tensor approximations, the reader is referred to the works of [16] and [17] and their citations. In the last two decades, the PGD method has been developed for a variety of applications, among these, surgery simulations [18], design optimization [19, 20], data-driven applications [21], viscoelastic [20], elastoplastic [22], contact problems [23] as well as stochastic Galerkin methods [24, 25]. The PGD approach for stochastic problems was applied to linear structural dynamics in [26]. The application of PGD models to reduce the computational effort of sampling-based approaches, can be found in the context of reliability analysis in [27, 28] and for process calibration of additive manufacturing in [29]. Furthermore, Rubio et al. [30] used a PGD forward model for real-time identification and model updating based on Monte Carlo sampling as well as based on a transport map sampling [31]. Djatouti et al. [32] proposed a goal-oriented inverse method, coupling a PGD model and a variant of the modified constitutive relation error approach, which automatically identifies and updates only the model parameters with the highest influence. A PGD derivation for a Young’s modulus normal, random field was given in [33], which is here extended for a log-normal field.
2 Variational bayesian inference
For most problems, the analytical computation of the posterior distribution given in Eq. (3), for the specific (surrogate) model \({\mathcal {M}}^n\) (n refers to the numerical accuracy degree, e.g. number of modes in Eq. (4)) and the unknown parameters \({\varvec{\Theta }}\) is not feasible and approximations have to be made instead. In the variational Bayesian approach, this is done by choosing a simpler distribution \(q({\varvec{\Theta }}\mid {\mathcal {M}}^n)\) from a selected family of distributions to approximate the posterior [3, 13]. This approximation should be as close as possible to the true posterior, so a measure of “closeness” between the two distributions is used, namely the Kullback-Leibler (KL) divergence defined as
The optimal q is the one that minimizes the KL-divergence in Eq. (5). Notice that the reference to the model \({\mathcal {M}}^n\) was dropped in Eq. (5) for convenience, so, unless stated otherwise, it should be assumed that the pdfs are conditioned on the same model. The KL computation in Eq. (5) depends on the exact posterior, i.e., the term that should be approximated, so Eq. (5) must be rewritten in more tractable terms [3] (derivation can be found in appendix A) to obtain
where \(P({\varvec{y}},{\varvec{\Theta }}) = P({\varvec{y}}\mid {\varvec{\Theta }})P({\varvec{\Theta }})\) and the second term is called free energy. Since the log evidence is independent of the parameters \({\varvec{\Theta }}\), minimizing the KL is equivalent to maximizing the free energy F, which will then be the objective of the optimization. The free energy can be seen as a lower bound on the evidence of the measurements and, therefore, is also known as Evidence Lower BOund (ELBO).
Several algorithms fall into the variational inference family, e.g., Automatic Differentiation Variational Inference [34], Stochastic Variational Inference [35] and Coordinate-ascent Variational Inference [13]. The latter is the one applied in this paper, following the work of Chappell et al. [3]. In this approach, some assumptions are made to make the integrals in Eq. (6) tractable, namely: the linearization of the model, the mean field approximation and the conjugate-exponential restriction. When \({\varvec{g}}({\varvec{\theta }})\) is nonlinear, the formulation in [3] proposes a first-order Taylor series
where \({\varvec{J}}\) is the Jacobian matrix evaluated at the expansion point \({\varvec{m}}\).
The second assumption states that the joint posterior distribution can be factorized into independent partitions, as
where \(\Theta _i\) corresponds to a group of parameters, each group with its own separate posterior distribution. The last assumption imposes the use of priors that are conjugate to the likelihood (i.e., which have the same parametric form of the posterior) and that come from the exponential family. Then, by substituting Eq. (8) into Eq. (6) and applying calculus of variations, the approximate pdfs \(q(\Theta _i)\) that maximize the objective function Eq. (6) are given as
where \(\Theta _{-i}\) represents all parameters different from \(\Theta _i\).
Here, the set of latent (unknown) variables (referenced in Eq. (8) and Eq. (9)) consist of the two already mentioned groups: \({\varvec{\Theta }}=[{\varvec{\theta }},{\varvec{\Phi }}]\) considering model and noise parameters. In the following, it is assumed that only one noise term exists, with a single noise precision parameter \(\phi \).
In the context of this paper, the forward model \({\varvec{g}}({\varvec{\theta }})\) is given as a computationally efficient PGD model in separated form like Eq. (4) as an explicit function of the identification parameters \({\varvec{\theta }}\)
In the latter, it is assumed that displacement measurements at known sensor positions \({\varvec{x}}_s\) are used for the inference process. Otherwise, the required output (e.g., strains) has to be computed based on the PGD sensor displacement field \({\varvec{u}}_s^n\) in an additional step leading to a similar form with strain PGD modes. The PGD forward model in Eq. (10) is additionally approximated by the linearization (Eq. (7)). Since, the PGD mode functions \(F_j^i\) are standard polynomial shape functions for the interpolation and thus their evaluation as well as differentiation is computationally very efficient, the required Jacobian matrix in Eq. (7) can be computed very efficiently.
The prior for the model parameters is defined as a Multivariate Normal (\(P({\varvec{\theta }}) \sim \mathcal {MVN}({\varvec{\theta }};{\varvec{m_0}},\Lambda _0^{-1} )\)), with parameters \({\varvec{m_0}}\) as the mean vector and \(\Lambda _0\) as the precision matrix. For the noise parameter, a Gamma distribution (\(P(\phi ) \sim Ga(\phi ;s_0,c_0 )\)) is used for its prior, where \(s_0\) and \(c_0\) are the scale and shape parameters, respectively. For conjugacy, the corresponding posteriors are of the same type, i.e., \( q({\varvec{\theta }}) \sim \mathcal {MVN}({\varvec{\theta }};{\varvec{m}},\Lambda ^{-1} )\) and \(q(\phi ) \sim Ga(\phi ;s,c )\) (their definitions can be found in the appendix B).

The goal is then finding the optimal values of the parameters that define the posteriors. These are obtained through the following update equations given in [3]:
where \({\varvec{k}} = {\varvec{y}} - {\varvec{g(m)}}\), \({\varvec{m}}_{new} \text { and } {\varvec{m}}_{old}\) are the values of \({\varvec{m}}\) for the current and previous iteration of the update scheme. As summarized in algorithm 1, Eq. (11a)-Eq. (11d) are iteratively used to update the posterior parameters until the convergence of the free energy is reached, i.e. until the inference procedure has converged, as described in [3].
The free energy is expressed as
where N denotes the number of observations, \(\Gamma (c)\) is the gamma function and \(\Psi (c)\) the di-gamma function, as defined in [3]. It results from substituting the log likelihood \(log(P({\varvec{y,{\varvec{\Theta }}}}))\) and the posterior \(q({\varvec{\Theta }})\) expressions into the free energy definition in Eq. (6) and gives an estimate for the log evidence \(log(P({\varvec{y}}))\). Note, the expression in Eq. (12) slightly differs from the one that appeared in [3], but it is in line with the latest implementations from the same authors available at [36]. A detailed derivation and an implementation as a python package can also be found at [37].
3 Convergence criteria of PGD variational inference problem
Generally, the forward model in an inference problem should correspond to the simplest, yet sufficiently accurate, representation of the real experimental conditions. For prediction tasks, it is important to reduce the effect of model’s accuracy, especially due to numerical error sources, onto the identification results. Although it is possible to fit an inexact model to measurement data, predictions with such a model in new settings (e.g. new load case) would be erroneous.
The use of surrogate models lead to additional numerical error sources (number of modes/terms/degrees/training data/mesh resolution), resulting in a deviation of the surrogate model w.r.t. the reference (full order) model and making it extremely important to take into account the influence of these on the identification process. The focus of this paper is to explicitly measure the influence of the model’s numerical accuracy and derive a new iterative identification procedure which automatically identifies a sufficiently accurate model. The proposed method carries out inference successively on surrogate models of increasing numerical accuracy. In each step, the variations in the identification results are measured with nearly no extra cost by a Bayes factor Sect. 3.1 and the Kullback-Leibler divergence between the posterior predictive pdfs Sect. 3.2 is monitored. The proposed new adaptive inference procedure is described in Sect. 3.3.
3.1 Bayes Factor (BF) and free energy
A metric that is commonly used for model selection is the Bayes Factor (BF). In [38], the BF is also used to compare finite element models differing in terms of mesh resolution in the context of statistical FEM. The BF is based on a ratio of model evidences of two competing models, which naturally penalizes complexity as they integrate over the entire parameter space [39]. Considering the scenario where the two models \({\mathcal {M}}^{n}\) and \({\mathcal {M}}^{n-1}\) are available for selection (here differing in the numerical accuracy degree n), the BF is the “relative probability of the observed data under each of the two competing hypotheses” [40]. Assuming both models are equally likely, the BF can be written as
The higher the BF value, the more “evidence” there is in favor of the model in the numerator.
The major advantage of choosing the BF for model selection when performing the proposed variational Bayesian inference [3] is that the free energy Eq. (12) can be directly used as an approximation of the log-evidence. Under the assumption of a vanishing KL divergence (i.e. approximate posterior q and exact one P are identical), the free energy is equal to the log evidence (see Eq. (6)), allowing the BF to be approximated as
Since the variational Bayesian approach evaluates the free energy for every iteration, it is straightforward to compute the BF criterion. In case of sampling based inference approaches (e.g. Markov Chain Monte Carlo), the BF computation would require additional sampling. Another interesting aspect of the BF is that many authors have proposed qualitative ways to interpret the results. For instance, [41] interprets BF values between 1 and 3 as “not worth a bare mention”, while values \(>150\) indicate a “very strong” evidence against the model in the denominator.
In this paper, the BF is not used in the conventional model selection sense, but instead it is used as a convergence criterion when successively comparing two models with increased numerical accuracy \(n\in [1,N]\). For this reason, the focus is not finding the highest or lowest BF (i.e. having an indication of which model to favor), but on finding the point at which it converges to 1. The closest the BF is to one, the more similar the models being compared are, meaning that their differences in numerical accuracy are insignificant in terms of “evidence” in favor of one of the models. In this work, the convention adopted is to set the model in the numerator \({\mathcal {M}}^n\) as the one with the higher accuracy compared to \({\mathcal {M}}^{n-1}\).
3.2 KL-based metric
The second proposed metric to evaluate the effect of the model’s numerical accuracy is based on the Kullback-Leibler (KL) divergence between the posterior predictive pdfs \({\varvec{P}}_{{\varvec{y}}_{pred}}\) of two candidate models \({\mathcal {M}}^n\) (differing in the accuracy degree n):
By definition, the posterior predictive for a given model \({\mathcal {M}}^n\) is the distribution describing possibly unseen data \({\varvec{y}}_{pred}\), conditioned on the previous observations \({\varvec{y}}\) used to run inference. Given the posterior distribution \(P({\varvec{\Theta }}\mid {\varvec{y}})\), predicting new data can be obtained by integrating out the parameters \({\varvec{\Theta }}\) in
Although the typical application for the posterior predictive is to predict data for experimental setups not present in the training data, here it is used to reproduce the original observations \({\varvec{y}}\). This posterior predictive is then applied in the computation of the KL-based convergence criterion as a way to evaluate the difference in predictions when using models with increasing numerical accuracy \(n\in [1,N]\). The closer to zero the KL divergence in Eq. (15) is, the more likely it is that the models being compared produce almost identical results.
In the context of the variational inference introduced in Sect. 2, the unknown variable \({\varvec{\Theta }}\) consists of model and noise parameters (\({{\varvec{\theta }}}\) and \({\phi }\)) and the posterior \(P({\varvec{y}}\mid {\varvec{\Theta }})\) is approximated by the multiplication (see Eq. (8)) of a multivariate normal pdf for \({\varvec{\theta }}\) and a gamma pdf for \(\phi \)
Solving the inner integral for a fixed \(\phi \), the resulting posterior predictive pdf is again a multivariate normal (\(\mathcal {MVN}\)) distribution, according to the conjugate properties of the distributions in the exponential family and the linearisation of the model Eq. (7). The KL divergence between two \(\mathcal {MVN}\) distributions \(\mathcal {MVN}^n\) and \(\mathcal {MVN}^{n-1}\) for the two models \({\mathcal {M}}^n\) and \({\mathcal {M}}^{n-1}\), respectively, can be analytically expressed by [42]:
In the latter \(\{{\varvec{\mu }}_{n},{\varvec{\mu }}_{n-1}\}\) denotes the means, \(\{{\varvec{\Sigma _n}},{\varvec{\Sigma _{n-1}}}\}\) the covariance matrices of the two distributions with dimension \(N_d\). The means and covariance matrices of the posterior predictive with a fixed noise precision in Eq. (17) can be expressed as ([43, 44])
where \({\varvec{g}}_i\) indicates the current linearised model \({\mathcal {M}}^i\) with the Jacobian \({\varvec{J}}_i\). \({\varvec{m}}_i\), \({\varvec{\Lambda }}_i\) and \(\phi _i=s_i\,c_i\) are the posterior pdf parameters resulting from the inference with model \({\mathcal {M}}^i\) with \(i \in [n-1,n]\).
A different approach than the one used here (i.e. of setting a fixed \(\phi \)) would be to solve for the complete posterior predictive. For that, the outer integral could be approximated by a weighted sum regarding the posterior pdf \(q(\phi )\), resulting in a Gaussian mixture model (for each fixed \(\phi \) a corresponding normal distribution is obtained). However, in many cases, and in particular when the posterior of the noise precision \(\phi \) is rather narrow, an approximation using only its mean is already an accurate approximation. In this way, the KL computation from a variational Bayesian inference result is very efficient. Again, using a sampling based inference approach would lead to additional computations to sample the predictive posterior and compute the KL criteria.
3.3 Iterative inference algorithm

As main contribution, the iterative process summarized in algorithm 2 is proposed for the automatic identification of a sufficiently accurate surrogate. It consists of sequentially performing variational Bayesian (VB) inference, each time with a surrogate model of increased accuracy \({\mathcal {M}}^{n}\) (e.g. based on n PGD modes). After each VB run, the KL divergence as well as the Bayes Factor (BF) are computed with respect to the previous model \({\mathcal {M}}^{n-1}\) with lower accuracy (e.g. based on \(n-1\) PGD modes). If the KL-divergence in Eq. (15) approaches 0 (up to some tolerance \(tol_1\)) and/or the BF in Eq. (14) approaches 1 (up to some tolerance \(tol_2\)), the iterations are terminated. Sufficient tolerance values for \(tol_1\) and \(tol_2\) are discussed in the example sections in detail. For the applications presented here, one value for \(tol_1\) and one for \(tol_2\) were chosen to be used in all examples. Whether they are problem independent and can be used seamlessly in other contexts has yet to be investigated. Note, the focus is finding a sufficiently accurate model regarding numerical accuracy. Therefore, it is assumed that the model and its surrogate physically represents the problem. In order to improve the identification (e.g. avoiding the linearization at the MAP and prescribing a family of distributions for the posterior), a standard sampling approach (e.g. MCMC) can be run afterwards using the sufficiently accurate PGD forward model identified in algorithm 2.
The proposed inference process and the PGD forward models are implemented in Python, using FEniCS [45] as the finite element solver. The variational Bayesian implementation is available at [37].
4 Demonstration example
The hypothesis that the numerical model accuracy influences the inference results is demonstrated in a simple model identification problem. When the proposed procedure is applied with models of increased accuracy, the KL divergence and BF between the different runs converge to zero and one, respectively. The example also demonstrates how the influence of the model accuracy depends on the accuracy of the measurement data itself.
Demonstration example: (a) Convergence of the posterior pdf parameters \(\{m,\Lambda ,s,c\}\): difference of mean m to true value \(\theta _{true}=1\), standard deviation \(\sqrt{\Lambda ^{-1}}\) of the model parameters \(\theta \) and the difference of the identified noise standard deviation \(\sigma _e=\sqrt{(s\cdot c)^{-1}}\) to the true one \(\sigma _{e_{true}}=0.01\) with increasing number of terms n. (b) Convergence of the free energy \(F^n\) and BF to the model with \(n-1\) terms with increasing number of terms n
For the demonstration, the true model is described by the exponential function
for \(x \in [-0.5,0.5]\) with the model parameter \(\theta =1\). Synthetic measurement data at 10 x-values in the interval \([-0.5,0.5]\) are generated by adding a random measurement noise, described by \({\mathcal {N}}(0,0.01^2)\), to the true model output. In total, a dataset of 50 values is computed by considering 5 synthetic measurement series. For the inference problem, the model parameter’s prior pdf is given as \(P(\theta )={\mathcal {N}}(1.5,1^2)\). The noise prior’s shape \(c_0\) and scale \(s_0\) parameters are defined by prescribing the \(5\%\) and \(95\%\)-percentile noise precision values \(\phi \) to \(1/0.5^2\) (noise standard deviation 0.5) and \(1/0.0005^2\) (noise standard deviation 0.0005), respectively. The resulting noise prior reads \(P(\phi )=Ga(c_0=0.37,s_0=1379941.5)\).
The Taylor series expansion of the exponential function is used as surrogate model of the true function:
This model has similarities to a PGD model, according to Eq. (4), with \(n+1\) mode sets \(F_1^i(x)\) and \(F_2^i(\theta )\), which converges to the true model with \(n \rightarrow \infty \). The numerical accuracy of the model increases with the number of n, so that this number can be used to describe the current accuracy degree of the model.
In a first step, the inference is performed using the surrogate model \(f^n_{apr}\) with an increasing number of terms \(n \in [1,10]\), following algorithm 2. For all runs, the BF between two models with n and \(n-1\) approximation terms (Fig. 1(b)) and the Kullback-Leibler divergence \(KL({\varvec{P}}_{{\varvec{y}}_{pred}}^{({\mathcal {M}}^{n})}\Vert {\varvec{P}}_{{\varvec{y}}_{pred}}^{({\mathcal {M}}^{{\bar{n}}})})\) between models with different number of terms \(n \in [1,10]\) and \({\bar{n}} \in [n+1,10]\) are calculated (Fig. 2). Furthermore, the parameters of the approximated posterior pdfs – mean m and standard deviation \(\sqrt{\Lambda ^{-1}}\) of the model parameter \(\theta \), mean of the identified noise standard deviation \(\sigma _e=\sqrt{(c \cdot s)^{-1}}\) (given Fig. 1(a) compared to the known true values) – as well as the free energy F (Fig. 1(b)) are tracked over the increasing number of terms n. The predictive posterior for models with different numbers of terms n are given in Fig. 4.
The influence of the number of terms n on the identification results can be seen in Fig. 1. The inferred parameters \(\{m,\Lambda ,s,c\}\) vary depending on the number of terms in the model, but converge rapidly to the true values. The deviation decreases \(m - \theta _{true} \rightarrow 10^{-4}\) (Fig. 1). This is also observed in the convergence of the BF between two models with increasing accuracy (\({\mathcal {M}}^{n-1}\) and \({\mathcal {M}}^n\), where the former refers to the denominator and the latter to the numerator). In Fig. 1(b), the BF is plotted as a function of terms n with values in the range of [1/3 : 3] (note that the range [1 : 3] indicates an anecdotal evidence for \({\mathcal {M}}^n\) while [1/3 : 1] is considered anecdotal evidence for \({\mathcal {M}}^{n-1}\)). It converges to one with increasing terms n, which means that the free energy also converges to a fixed value. The BF criterion can exceed extremely high values in the first iterations steps (i.e. for models with a large difference in accuracy), indicating a high influence of adding these first terms on the model response correlating with high differences in the free energy. The KL divergence in Fig. 2 between different accurate models (n terms visa \({\bar{n}}\) terms with \(n\in [1,10]\) and \({\bar{n}}\in [n+1,10]\)) converges linearly in a semi log-scale with increasing number of modes. Whereby, all computed KL divergences varying the number of terms are here in one line, so that the diagonal \(KL({\varvec{P}}_{{\varvec{y}}_{pred}}^{({\mathcal {M}}^{n-1})}\Vert {\varvec{P}}_{{\varvec{y}}_{pred}}^{({\mathcal {M}}^n)})\) represents the convergence behavior as already proposed in algorithm 2.
In a second investigation, the measurement noise of the virtual measurement data is varied, simulating different degrees of sensor accuracy. The noise is modeled with normal distributions \([{\mathcal {N}}(0,\sigma _e^2)]\) with \(\sigma _e \in [10^{-1},10^{-2},10^{-3},10^{-4}]\). A sufficient number of data points is used, so that in all cases the assumed true noise value could be identified. The inference algorithm is run for each noise standard deviation \(\sigma _e\), with increasing accuracy of the surrogate model, and the KL divergence and BF are computed between two sequential models.
Figure 3 shows that both criteria again converge with increasing number of terms n, where differences can be seen regarding the given noise standard deviations of the measurements. The KL divergences curves are nearly parallel, indicating that a higher model accuracy is required for smaller measurement errors. The same issue can be seen with the BF, which converges to one with increasing number of terms, for decreasing measurement noise.
The implementation of this approach for practical examples requires to define thresholds for the tolerance values in algorithm 2. These values were chosen specifically for the examples presented and their applicability to any other problem has to be investigated. Choosing the KL tolerance to \(10^{-2}\) and a BF tolerance range [1/2, 2] for all setups results in models with 4, 5, 6, 7 terms for decreasing \(\sigma _e = [10^{-1},10^{-2},10^{-3},10^{-4}]\). This is inline with the expectation that a higher model accuracy (i.e. higher number of terms) is required for more accurate measurement data (here modeled by smaller deviations \(\sigma _e\)). For the case \(\sigma _e=0.01\), the influence of different model accuracy on the posterior distribution is plotted in Fig. 4. A model with 5 terms based on the proposed tolerance values leads to a very good agreement with the true model. Increasing the number of terms would not improve the identification results anymore. Furthermore, the number of 5 terms for \(\sigma _e=0.01\) is inline with the convergence of the posterior parameters after Fig. 1 confirming the proposed tolerance values.
5 Structural damage identification with random field material parameters
As mentioned in the introduction, the model parameter identification plays an important role in monitoring systems and digital twin applications. In this context, a common task is to identify structural changes and quantify the impact on key performance indicators. As application examples, the identification of damage phenomena for a 1D truss structure (with synthetic data) as well as a reinforced concrete bridge (with real measurement data) is addressed. The key idea is to include the stiffness variation in space due to undergone damage as a linear elastic material model with a Young’s modulus being modeled by a log-normal random field. The goal is to identify the posterior distribution of the random field based on measurement data with a sufficiently accurate PGD surrogate. Therefore, first a PGD model for the log-normal random field parameters is derived as an extension to the PGD approach for normal fields by [33].
5.1 PGD forward model for linear elasticity with a log-normal random field for the Young’s modulus
A linear elastic problem described by the general equations of mechanics (balance of momentum, kinematics for small displacements and isotropic linear elastic material law) is considered. The Young’s modulus E is assumed to depend on the spatial position \({\varvec{x}}\) and some new identification parameters \({\varvec{\theta }}\), reflecting damage. A log-normal distribution is assumed, following the suggestions of the European design standards [46] for material parameters. The log-normal distribution avoids negative Young’s moduli. Therefore, the Young’s modulus is given by a log-normal random field \(\varkappa _{LN}({\varvec{x}},{\varvec{\theta }})\) as
which is modeled as a transformation of an underlying normal random field [47] represented with a Karhunen-Loéve expansion (e.g., [48,49,50]). In Eq. (22), \( \mu ({\varvec{x}})\) is the mean value, \({V}_{j}\) are the eigenvectors, \(\lambda _{j}\) the eigenvalues of the covariance matrix (kernel) and \({\varvec{\theta }}\) the K variables (normally distributed with zero mean) of the underlying normal random field. Note that, due to this nonlinear transformation, the correlation of the log-normal field is not identical to the prescribed one in the normal field. The covariance matrix \({\varvec{C}}\) simulates the spatial dependency of the variables and is given by the covariance function \(c({\varvec{x}}_i, {\varvec{x}}_j)\), describing the correlation between two spatial points i and j. Among the many possible covariance functions [48], the squared exponential kernel function (i.e. belonging to the Matérn family) is used:
where r denotes the distance between two points \(\vert {\varvec{x}}_i-{\varvec{x}}_j \vert \), \(\sigma \) is the standard deviation and \(\varrho \) the correlation length of the random field. Based on a standard finite element discretization of the random field variables with a mesh size much smaller then the correlation length, the solution of the generalized eigenvalue problem for the correlation matrix \( {\varvec{M}}^T \, {\varvec{C}} \, {\varvec{M}} \, {\varvec{V}} = \lambda \, {\varvec{M}} \, {\varvec{V}} \) with the mass matrix \({\varvec{M}}\) leads to the eigenvalues and eigenvectors describing the underlying normal random field in Eq. (22). The number of random field variables K depends on the ratio between the correlation length and the structural dimension. For a study of the influence of the random field discretization on the identification process, the reader is referred to [47]. In this example, the number K is chosen based on the ratio of the eigenvalues
with a prescribed tolerance (given in the examples). The random field parameters (\(\mu \), \(\sigma \) and \(\varrho \)) are assumed to be known. The identification parameters are the K unknown field variables \({\varvec{\theta }}\) defined in Eq. (22).
The PGD approach is applied to generate a numerical abacus, giving the solution as a function of the spatial directions \({\varvec{x}}\) and the unknown model parameters \({\varvec{\theta }}\), here the random field variables. For this reason, the displacement field \({\varvec{u}}\) is approximated by a sum of n terms as
The PGD modes are numerically determined by solving the weak form of linear elasticity with the approximation \({\varvec{u}}^n\) from Eq. (25) over the multi-dimensional space \(\Omega ^D = \Omega ^{{\varvec{x}}}\bigotimes \limits _{j=1}^K \Omega ^{\theta _j}\), with its Neumann and Dirichlet boundaries \(\Gamma _N\) and \(\Gamma _D\),
In the latter, \(\delta \bullet \) denotes the variation of \(\bullet \). The strains \({\varvec{\varepsilon }}^n\) are given considering the kinematic law \({\varvec{\varepsilon }}^n = \mathrm{grad}({\varvec{u}}^n)\) in separated form affine to Eq. (25). \({\varvec{f}}^{n_f}\) is a given volume load, \({\varvec{t}}^{n_t}\) a specified surface load and \({\varvec{C}}^{n_c}_{el}\) refers to the linear elasticity tensor, all depending on the space \({\varvec{x}}\) and the random field parameters \({\varvec{\theta }}\). The Dirichlet condition \({\varvec{u}}^n = {\varvec{u}}^*\) completes the description of the problem above. For an efficient PGD computation, all \({\varvec{\theta }}\)-depending functions in Eq. (26) must be expressed as an affine separate representation to Eq. (25), allowing the separation of the multi-dimensional integral into D lower dimensional integrals [51]. This separated form is denoted by the subscripts (\(n_f\), \(n_t\), \(n_c\)) in Eq. (26) given the number of required terms for each function. In the investigated case, the loads are not depending on the parameters \({\varvec{\theta }}\) so that their separation is trivial. The linear elasticity tensor explicitly depends on the random field parameters \({\varvec{\theta }}\) and the space \({\varvec{x}}\) by the given Young’s modulus definition in Eq. (22)
with the averaged stiffness
for the averaged Young’s modulus \(E_0\) and the Poisson’s ratio \(\nu \). Since \(\varkappa _{LN}\) is a log-normal random field defined in Eq. (22), the separation of Eq. (27) is more complex than e.g. prescribing the Young’s modulus as a normal random field [33] and requires an approximation of the exponential function. Here, a Taylor series expansion of the field \(\varkappa _{LN}\) around the mean \({\varvec{\theta }}_0\) with a flexible number of terms is proposed to separate the dependency on \({\varvec{x}}\) and each \(\theta _i\). The Taylor series expansion can be reordered to obtain a separated representation (see appendix C)
affine to the assumed PGD model in Eq. (25). Inserting this separation into Eq. (27) leads to the required separated function of the linear elasticity tensor in Eq. (26)
There exist different ways to solve Eq. (26) in a discrete way computing the single PGD modes \(F_j^i\) [52]. Here, the progressive PGD strategy [53, 54] is used, where the problem is solved iteratively for each new set of basis functions. The computation is based on a fixed-point iteration involving the finite element computation of D small dimensional problems – one for each PGD coordinate. The detailed equations of each problem and the used convergence criteria are summarized in appendix D.
After a more elaborate computation – compared to a standard finite element model – of all PGD modes, the PGD reduced forward model \({\mathcal {M}}_{PGD}\) depending on the identification parameters \({\varvec{\theta }}\), required in the variational inference (Sect. 2), can be written as
where \({\varvec{x}}_s\) denotes the coordinates of the sensors with measurement data. Note, the mode functions \(F_j^i\) are only once computed and just need to be evaluated for each parameter set in the inference run. Furthermore, the spatial modes \({\varvec{F}}_1^i({\varvec{x}}_{s})\) can be precomputed and cached at these positions for an even more efficient computation during the inference process. Furthermore, the Jacobian with respect to the identification parameters, required for nonlinear forward models (Eq. (7)), can be computed by the derivative of the single one-dimensional modes also in a very efficient way, including only function evaluations
For the proposed iterative inference process in algorithm 2, it is important that the accuracy of the proposed PGD surrogate is mainly influenced by two aspects: the discretization error for each coordinate solving the discrete PGD modes and the truncation error (\(=\) number of mode sets n) [51]. Therefore, the accuracy of the PGD surrogate of each step n in algorithm 2 can be increased by either refining the mesh solving the PGD modes based on the discretized weak form Eq. (26) or increasing the number of modes. For that reason, using a PGD model in the proposed iterative inference algorithm 2 leads to two nested loops: one over the mesh refinement and one over the number of modes. Therefore, the PGD model accuracy degree will, from now on, be given by two superscripts \({\mathcal {M}}_{PGD}^{(k,n)}\), to differentiate between both aspects, where k refers to the mesh refinement degree and n to the number of modes of the current model. Furthermore, \(KL^{modes}\) and \(BF^{modes}\) denote the comparison of PGD models with the same mesh resolution k and different mode numbers, whereas \(KL^{mesh}\)/ \(BF^{mesh}\) refer to different mesh resolution by a fixed number of modes n.
5.2 1D truss example
In the academical truss example, a given stiffness variation over the length is identified using the variational inference, the introduced PGD model as forward model and synthetic displacements as measurement data. The influence of the number of modes and the refinement degree of the PGD forward model on the identified stiffness is demonstrated. The convergence of the introduced KL divergence criterion and the BF for increasing model accuracy is shown.
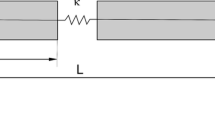
A 1D steel truss, with geometry and boundary conditions given in Fig. 5, is considered. A line load \(p=25\cdot 10^5\)kN/m is applied to the truss, and its position, given by \(X_p\), varies along the length \(L=3\)m. The stiffness of the truss is assumed to vary over the x-direction following Eq. (22) with \(E_0=210\cdot 10^6\)kN/\(\hbox {m}^2\) and fixed field parameters: \(\mu (x)=0\), \(\sigma =0.5\) and \(\varrho =2.5\)m. In general, these random field hyperparameters could be identified as well. Here, it is assumed that these parameters are known.
The first modes of the random field of the underlying normal field Eq. 22 are illustrated in Fig. 6. In this example, only four modes are used, related to a tolerance \(tol_{RF}=10^{-2}\) with Eq. (24). The random field’s covariance matrix is computed based on a mesh, defined by 50 linear elements allowing to precompute the random field modes for all PGD models by projecting the random field onto the x-mesh with a variable mesh size \(h_x\). By doing this, a new computation of the underlying eigenvalue problem for each mesh resolution is avoided. As discussed in Sect. 5.1 the log-normal random field is approximated by a Taylor series expansion \({\hat{\varkappa }}_{LN}\) with 8 terms.
In the identification process, synthetic measurement data are used. These are generated with a full order finite element model of the system in Fig. 5, with 600 linear elements (mesh size \(h_x=0.005\)m), and a Young’s modulus modeled with a bell-shaped function [55] as
where \(<\bullet >=0\) if \(\bullet <0\) and \(<\bullet >=\bullet \) if \(\bullet \ge 0\). The function \(\lambda _m(x)\) is plotted in Fig. 8. The synthetic data from the 50 sensors positioned over the length is shown in Fig. 7, for the load positions (\(X_p=0.75\)m, 1.65m and 2.55m), with adding a random measurement error described by \({\mathcal {N}}(0,0.001^2)\mathrm {[m]}\). As the true stiffness function is known here, the correlation length \(\varrho \) is chosen as the radius of the bell-shaped function, i.e., \(\varrho = 2.5\). For each load position, a separate PGD model is computed for \(\theta _i \in [-2.5:2.5]\). The priors for the random field variables are chosen as \(P({\varvec{\theta }})\sim \mathcal {MVN}({\varvec{\theta }};\mathbf {0},\mathbf {I})\) and for the noise precision as \(P(\phi ) \sim Ga(\phi ;c_0=0.46,s_0=2.2 \, 10^{6})\) [\(\hbox {m}^{-2}\)]. The prior’s shape and scale parameters are defined by prescribing the pdfs \(5\%\) and \(95\%\)-percentile precision values to \(1/(0.02\mathrm {m})^2\) and \(1/(0.0005\mathrm {m})^2\), respectively.
1D truss example: (a) Influence of number of modes n in PGD forward model on the posterior stiffness factor distribution \(\lambda (x)\) compared to the real one \(\lambda _m(x)\). The shaded region corresponds to the mean ± standard deviation. (b) Convergence of \(KL^{modes}\) between PGD models \({\mathcal {M}}_{PGD}^{4,{\bar{n}}}\) and \({\mathcal {M}}_{PGD}^{4,n}\) with different numbers \(n > {\bar{n}}\). Mesh refinement step 4 corresponds to a mesh size \(h=h_x=h_{\theta }=0.025\)
1D truss example: (a) Influence of mesh discretization in PGD forward model on the posterior stiffness factor distribution \(\lambda (x)\) compared to the real one \(\lambda _m(x)\) and the one identified using a FEM model with \(h=0.01\)m. The shaded region corresponds to the mean ± standard deviation. (b) Convergence \(KL^{mesh}\) between PGD model \({\mathcal {M}}_{PGD}^{k-1,8}\) and \({\mathcal {M}}_{PGD}^{k,8}\) with 8 modes. The mesh refinement steps are given by the mesh size \(h=h_{x}=h_{\theta }=[0.05,0.025,0.01,0.005]\). Beside that, the coarsest mesh is defined by \(h_{x}=0.3\)m and \(h_{\theta }=0.2\)
The inference algorithm 1 is run for the dataset illustrated in Fig. 7. A sensitivity analysis is performed - first by varying the mesh resolution with a fixed number of modes \(n=8\) and second by varying the number of modes with a fixed mesh size \(h=0.025\). The posterior stiffness factor distributions \(\lambda (x)\) and the corresponding KL divergences are given in Fig. 8, for varying the number of modes, and in Fig. 9, for different mesh resolutions. The posterior distribution \(\lambda (x)=\varkappa _{LN}(x,{\varvec{\theta }})\) is compared to the stiffness factor used to generate the synthetic measurement data \(\lambda _m(x)\). It is obtained by a propagation of the uncertainty with
using the covariance matrix \(\Lambda \) of the resulting posterior distribution \(q({\varvec{\theta }}\mid {\varvec{y}})\), the Jacobian of the field with respect to \({\varvec{\theta }}\) evaluated at the posterior mean \({\varvec{m}}\) of \(q({\varvec{\theta }}\mid {\varvec{y}})\). The shaded region is obtained by plotting the mean ± the standard deviation as the square root of the diagonal entries of \(\Lambda _\varkappa \). For comparison, the variational inference is run with a full finite element model and the identified stiffness factor is shown in Fig. 9. The resulting BF between two sequential PGD models as well as the free energy during both variations are given in Fig. 10.
It is possible to observe a very good agreement of the identified log-normal random field with the assumed stiffness variation (Fig. 8 and Fig. 9). There is also a clear influence of the model’s accuracy on the identified stiffness, but with an increased accuracy (higher number of modes (\(n>8\)) and/or smaller mesh sizes \((h < 0.05m)\) the solution converges. Fixing the number of modes to \(n=8\), the difference in the identification results using a PGD model with the mesh sizes 0.05m or 0.01m is vanishing in Fig. 9 and is in line with the reference run using a full order model. Here the KL criterion, the BF and the free energy also converge as model accuracy increases, although the KL has a less smooth convergence when compared to the demonstration example (Sect. 4). This is caused by the fact that the accuracy of the PGD itself does not converge monotonically with the number of modes [54]. This must be considered in the proposed adaptive way of selecting a sufficiently accurate model. Due to the non-smoothness, adding a new set of PGD modes will not necessarily improve the numerical accuracy of the model. For that reason, it is proposed to add always several new mode sets and compute the discussed convergence criteria.
Based on the results above, a PGD model with 8 modes and \(h=0.025\) could be selected as a sufficiently accurate model, where \(KL<2\cdot 10^{-2}\) and \(BF \in [0.5,2]\). This selection would be in line with the visual comparison of the identified stiffness function in Fig. 9 and Fig. 8. The tolerance values are in the same range as for the demonstration example. The resulting posterior distribution is shown in Fig. 11, where it is possible to identify a correlation between \(\theta _1\) and \(\theta _3\) and between \(\theta _2\) and \(\theta _4\). For this reason, the identification problem has no unique solution. Additionally, the added noise is identified by a standard deviation mean of 0.001 (0.00099 as 5 % and 0.00102 as 95 % percentile) fitting the synthetic noise added in the data generation very well.
It is important to emphasize the ability of the PGD surrogate to speed-up the inference runs: for example, one identification run with the PGD reduced models \({\mathcal {M}}_{PGD}^{4,8}\) is more than 4000 times faster than the corresponding run with the full order finite element model. A complete inference with the PGD model is performed in a fraction of seconds (0.03 seconds).
5.3 Two span concrete test bridge
For the second example, the proposed inference approach is applied to the identification of the stiffness distribution of the real, pre-damaged concrete bridge with two spans shown in Fig. 12. This bridge was built as a demonstrator for investigating the assessment, service life forecast and repair of bridges. The two white blocks in the picture are load boxes of 2 tons, which can be moved along the bridge. Various measurement systems were involved, e.g., digital image correlation, stereophotogrammetry, fiber optic sensors, dynamic strain sensors, wavelength scanning as well as ultrasonic sensors [56,57,58]. In this paper, the displacement data, measured by the 49 stereophotogrammetry sensor points (black and white circles) distributed over the length of the bridge after some destructive tests, is used. As shown in Fig. 12, several cracks have occured.
The geometry and boundary conditions of the numerical model of the bridge are sketched in Fig. 13. A full 3D model of half of the cross-section, with symmetric boundary conditions, is used, where the moving load box is represented by a surface load (\(Q=10\)kN) over a length of 0.4m and the cross-section’s width (0.45m), at the current position \(X_p\). The supports are modeled by fixing the corresponding degrees of freedom (\(u_z\) and/or \(u_x\)) at \(x=0.2\)m, \(x=12.2\)m and \(x=24.2\)m. The spatial mesh is discretized with 118,224 quadratic elements, with an average mesh size of 0.05m. Separate PGD models are computed for each load position and the unknown model parameters (the random field parameters) are discretized in the interval \(\theta _i\in [-2.5:2.5]\) with linear elements and an element length of \(h_{\theta }=0.01\). Similar to the previous example, a log-normal distributed Young’s modulus \(E({\varvec{x}},{\varvec{\theta }}) \) given by Eq. (22), with \(E_0=25\cdot 10^{6}\)kN/\(\hbox {m}^2\) and fixed parameters: \(\mu =0\), \(\sigma =0.5\) and \(\varrho =8\)m. In this way, the stiffness variation over the length, caused by the cracks (see Fig. 12), can be identified. Based on a tolerance of \(tol_{RF}=0.01\) and Eq. (24), the first four random field modes are used. Since an isotropic exponential kernel is used for the random field with a correlation length of 8 m, the variations in the random field in y and z-direction are very small. If stiffness variations over the height or width of the bridge’s cross-section are of importance, anisotropic kernel functions could be chosen. The random field is discretized on a mesh with an element length of 0.4m and approximated by a Taylor expansion with 8 terms.
Bridge example: Posterior predictive of the displacement field for the new load position \(X_p=9\)m based on the identified Young’s modulus fields with different number of modes in the PGD model and the posterior’s mean noise precision \(\phi =s \, c\). The contour plot over the full domain gives the mean displacement field for a model with \(n=25\)
The vertical deflections \(\Delta u_z\) measured by the steoreophotogrammetry sensor points \({\varvec{x}}_s\), for different load positions, is used in the inference (see Fig. 14). For the identification process, the prior for the model parameters described by the random field variables is chosen as \(P({\varvec{\theta }}) \sim \mathcal {MVN}({\varvec{\theta }};{\varvec{0}},{\varvec{I}})\) and for the noise precision \(P(\phi ) \sim Ga(\phi ;c_0=0.84,s_0=93331.7)\) [\(\hbox {m}^{-2}\)]. The latter prior’s shape and scale parameters are defined by prescribing the pdfs \(5\%\) and \(95\%\)-percentile precision values to \(1/(0.02\mathrm {m})^2\) and \(1/(0.002\mathrm {m})^2\), respectively.
The adaptive inference process based on algorithm 2 is performed, automatically identifying the required number of modes in the PGD forward model. Since the reference measurement already includes the load box at its starting position, the forward model in the identification run consists of the difference between two PGD models (current load position \(X_p\) minus start load position \(X_p=0.5\)m). Thereby, linear superposition of the response for different load configurations is assumed. The proposed criteria, KL and BF, to track the influence of the model’s accuracy are computed during the inference runs with increasing number of modes. The resulting values are illustrated in Fig. 15. Additionally, the identified stiffness distributions over the length of the bridge x, for PGD models with increasing accuracy, are given in Fig. 16.
The inferred stiffness distribution (Fig. 16) shows a lower stiffness in both spans as well as a higher stiffness around the support in the middle. This accords with the observed crack pattern, where cracks are concentrated in the midspan of both fields. Contrary to our expectations, the inferred stiffness around the supports at the beginning and end of the bridge are significantly smaller than in the middle support. This could be caused by the chosen correlation length (8m) which maybe is to small or due to the chosen priors and a possible low sensitivity in this area. Nevertheless, the identified stiffness in Fig. 16 is almost identical when using 20 modes or more, suggesting that an increase of the number of modes would no longer influence the inference results. This is also confirmed in the KL and BF plots in Fig. 15. Since the BF value is derived from the free energy, the free energy values are also presented in Fig. 15 showing a smoother convergence to a fixed, problem dependent maximum. Based on this study, a sufficiently accurate model is chosen as the PGD model with \(n=25\), corresponding to tolerance values of \(KL^{modes}<2\cdot 10^{-2}\) and \(BF^{modes} \in [0.5,2]\) (as in the previous examples). Due to the non-smooth convergence of the PGD model, the KL divergence must stay under the tolerances for some number of modes. Note, in Fig. 15 the KL divergence is also less than the chosen tolerance for comparing a model with 13 modes to one with 14 modes but not comparing 14 with 15 modes. The resulting posterior distribution for the random field variables \({\varvec{\theta }}\) is given in Fig. 18. As many inverse problems, this example is also ill-posed, since correlations in the posterior between \(\theta _1\) and \(\theta _3\) as well as between \(\theta _2\) and \(\theta _4\) exist. In contrast to a deterministic approach with only a single set of parameters as the result, this is automatically identified in a Bayesian approach. The mean of the model error’s standard deviation is identified as 0.00047m (0.0004669m as \(5\%\) and 0.0004705m as \(95\%\) percentile).
Since the true stiffness function for this real example is not known, a testing data set (i.e., not used in the identification) is used for validation purposes. In Fig. 17, the predicted displacement field for the new (test) load case \(X_p=9\)m is given based on the different inference runs with varying the number of modes. A very good fit with the new measurement data is observed.
6 Conclusion
In this work, the influence of the surrogate model’s numerical accuracy on the model identification process is studied. A PGD forward model is used in a variational Bayesian inference method for nonlinear models, for improved efficiency of the model identification process.
It is demonstrated that the numerical model accuracy influences the identification results. An adaptive inference method is proposed, where the model is iteratively improved by increasing the number of PGD modes or refining the mesh. During the iterations, the influence of the model refinement is measured by the BF as well as the KL divergence between the predictive posterior pdfs and the free energy. While the BF converges to one and the KL to zero, the free energy smoothly converges to a problem dependent maximum value, which is not known a priori. It is shown that these criteria can measure the influence of the numerical model accuracy on the identification results and can be computed very efficiently due to the chosen variational approach. The proposed approach is also applied for the identification of stiffness fields of two structures: a truss (with synthetic data) and a concrete bridge (with real measurements). To that end, a PGD model for linear elasticity with a Young’s modulus represented by a log-normal random field is derived. For that purpose a separation of the log-normal field is derived and included in the PGD approach. For all examples, a tolerance for the KL divergence of \(2\cdot 10^{-2}\) and a BF in the range of [1/2 : 2] could be used as a convergence criterion to select a sufficiently accurate model, meaning that a further improvement of the model will not change the identified stiffness distribution significantly. Furthermore, it is demonstrated in a simple example with synthetic data that the proposed criteria can also consider different measurement accuracy. With the same tolerance values for KL and BF different accurate models are selected, if the given measurement standard deviation was changed.
The importance and difficulty of considering the model’s accuracy when performing model identification is shown and a possible approach for that is proposed. As the importance of numerical models for monitoring and digital twins continue to rise, so does the attention on surrogate models. Therefore, the discussed topic is of general research interest for all types of surrogates and identification methods in the future.
References
Chinesta F, Ammar A, Cueto E (2010) Recent advances and new challenges in the use of the proper generalized decomposition for solving multidimensional models. Arch Computat Methods Eng 17(4):327–350. https://doi.org/10.1007/s11831-010-9049-y
Chinesta F, Cueto E, Abisset-Chavanne E, Duval JL, Khaldi FE (2018) Virtual, digital and hybrid twins: A new paradigm in data-based engineering and engineered data. Arch Computat Methods Eng 27(1):105–134. https://doi.org/10.1007/s11831-018-9301-4
Chappell MA, Groves AR, Whitcher B, Woolrich MW (2009) Variational Bayesian inference for a nonlinear forward model. IEEE Trans Signal Process 57(1):223–236. https://doi.org/10.1109/tsp.2008.2005752
Robens-Radermacher A, Held F, Coelho Lima I, Titscher T, Unger JF (2021) Efficient identification of random fields coupling Bayesian inference and PGD reduced order model for damage localization. Proc Appl Math Mech 20(1):e202000063. https://doi.org/10.1002/pamm.202000063
Mohammad-Djafari A (1998) From deterministic to probabilistic approaches to solve inverse problems. In: Mohammad-Djafari, A. (ed.) Bayesian Inference for Inverse Problems, vol. 3459, pp. 2–11. SPIE. https://doi.org/10.1117/12.323787. International Society for Optics and Photonics
Tarantola A (2005) Inverse Problem Theory and Methods for Model Parameter Estimation, pp. 1–358. Society for Industrial and Applied Mathematics. https://doi.org/10.1137/1.9780898717921
Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E (1953) Equation of state calculations by fast computing machines. J Chem Phys 21(6):1087–1092. https://doi.org/10.1063/1.1699114
Hastings WK (1970) Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57(1):97–109. https://doi.org/10.1093/biomet/57.1.97
Geman S, Geman D (1984) Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans Pattern Anal Mach Intell PAMI 6(6):721–741. https://doi.org/10.1109/tpami.1984.4767596
Duane S, Kennedy AD, Pendleton BJ, Roweth D (1987) Hybrid Monte Carlo. Phys Lett B 195(2):216–222. https://doi.org/10.1016/0370-2693(87)91197-x
Salimans T, Kingma DP, Welling M (2015) Markov chain Monte Carlo and variational inference: Bridging the gap. In: ICML, pp. 1218–1226. http://proceedings.mlr.press/v37/salimans15.html
Jordan MI, Ghahramani Z, Jaakkola TS, Saul LK (1999) Introduction to variational methods for graphical models. Mach Learn 37(2):183–233. https://doi.org/10.1023/a:1007665907178
Blei DM, Kucukelbir A, McAuliffe JD (2017) Variational inference: A review for statisticians. J Amer Statist Assoc 112(518), 859–877 arXiv:1601.00670. https://doi.org/10.1080/01621459.2017.1285773
Franck IM, Koutsourelakis PS (2017) Constitutive model error and uncertainty quantification. Proc Appl Math Mech 17(1), 865–868 https://onlinelibrary.wiley.com/doi/pdf/10.1002/pamm.201710400. https://doi.org/10.1002/pamm.201710400
Bruder L, Koutsourelakis P-S (2018) Beyond black-boxes in Bayesian inverse problems and model validation: Applications in solid mechanics of elastography. Int J Uncertain Quantif 8(5):447–482
Grasedyck L, Kressner D, Tobler C (2013) A literature survey of low-rank tensor approximation techniques. GAMM-Mitt 36(1):53–78. https://doi.org/10.1002/gamm.201310004
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500. https://doi.org/10.1137/07070111X
Niroomandi S, González D, Alfaro I, Bordeu F, Leygue A, Cueto E, Chinesta F (2013) Real-time simulation of biological soft tissues: A PGD approach. Int J Numer Meth Biomed Engng 29(5):586–600. https://doi.org/10.1002/cnm.2544
Leygue A, Verron E (2010) A first step towards the use of proper general decomposition method for structural optimization. Arch Computat Methods Eng 17(4):465–472. https://doi.org/10.1007/s11831-010-9052-3
Ammar A, Huerta A, Chinesta F, Cueto E, Leygue A (2014) Parametric solutions involving geometry: A step towards efficient shape optimization. Comput Method Appl M 268:178–193. https://doi.org/10.1016/j.cma.2013.09.003
González D, Masson F, Poulhaon F, Leygue A, Cueto E, Chinesta F (2012) Proper generalized decomposition based dynamic data driven inverse identification. Math Comput Simulat 82(9):1677–1695. https://doi.org/10.1016/j.matcom.2012.04.001
Zuchiatti S, Feulvarch E, Roux J-C, Bergheau J-M, Perrin G, Tissot S (2015) Application of the proper generalized decomposition to elasto-plastic finite element analysis. In: ed. Barcelona: CIMNE, C. (ed.) COMPLAS XIII : Proceedings of the XIII International Conference on Computational Plasticity: Fundamentals and Applications, pp. 834–842. http://hdl.handle.net/2117/80447
Claus S, Kerfriden P (2017) A stable and optimally convergent LaTIn-CutFEM algorithm for multiple unilateral contact problems. Int J Numer Methods Eng 113(6), 938–966 https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.5694. 10.1002/nme.5694
Nouy A (2007) A generalized spectral decomposition technique to solve a class of linear stochastic partial differential equations. Comput Method Appl M 196(45–48):4521–4537. https://doi.org/10.1016/j.cma.2007.05.016
Nouy A (2008) Generalized spectral decomposition method for solving stochastic finite element equations: Invariant subspace problem and dedicated algorithms. Comput Method Appl M 197(51–52):4718–4736. https://doi.org/10.1016/j.cma.2008.06.012
Chevreuil M, Nouy A (2011) Model order reduction based on proper generalized decomposition for the propagation of uncertainties in structural dynamics. Int J Numer Meth Engng 89(2):241–268. https://doi.org/10.1002/nme.3249
Gallimard L, Vidal P, Polit O (2013) Coupling finite element and reliability analysis through proper generalized decomposition model reduction. Int J Numer Meth Engng 95(13), 1079–1093 https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.4548. 10.1002/nme.4548
Robens-Radermacher A, Unger JF (2020) Efficient structural reliability analysis by using a PGD model in an adaptive importance sampling schema. Adv Model and Simul in Eng Sci 7(1):1–29. https://doi.org/10.1186/s40323-020-00168-z
Ghnatios C, Rai KE, Hascoet N, Pires P-A, Duval J-L, Lambarri J, Hascoet J-Y, Chinesta F (2021) Reduced order modeling of selective laser melting: From calibration to parametric part distortion. Int J Mater Form 14(5):973–986. https://doi.org/10.1007/s12289-021-01613-z
Rubio P-B, Louf F, Chamoin L (2018) Fast model updating coupling Bayesian inference and PGD model reduction. Comput Mech 62(6):1485–1509. https://doi.org/10.1007/s00466-018-1575-8
Rubio P, Louf F, Chamoin L (2019) Transport map sampling with PGD model reduction for fast dynamical Bayesian data assimilation. Int J Numer Methods Eng 120(4), 447–472. https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.6143. 10.1002/nme.6143
Djatouti Z, Waeytens J, Chamoin L, Chatellier P (2020) Coupling a goal-oriented inverse method and proper generalized decomposition for fast and robust prediction of quantities of interest in building thermal problems. Build Simul 13(3):709–727. https://doi.org/10.1007/s12273-020-0603-8
Garikapati H, Zlotnik S, Díez P, Verhoosel CV, van Brummelen EH (2019) A proper generalized decomposition (PGD) approach to crack propagation in brittle materials: With application to random field material properties. Comput Mech 65(2):451–473. https://doi.org/10.1007/s00466-019-01778-0
Kucukelbir A, Blei DM, Gelman A, Ranganath R, Tran D (2017) Automatic differentiation variational inference. J Mach Learn Res. 18, 1–45 arXiv:1603.00788
Hoffman MD, Blei DM, Wang C, Paisley J (2013) Stochastic variational inference. J Mach Learn Res 14:1303–1347 arXiv:1206.7051
Craig M (2021) git project: vaby_avb. GitHub. https://github.com/physimals/vaby_avb
Titscher T, Unger JF (2021) git project: bayem. GitHub. https://github.com/BAMresearch/bayem
Girolami M, Febrianto E, Yin G, Cirak F (2021) The statistical finite element method (statFEM) for coherent synthesis of observation data and model predictions. Comput Method Appl M 375:113533. https://doi.org/10.1016/j.cma.2020.113533
Evans NJ (2019) Assessing the practical differences between model selection methods in inferences about choice response time tasks. Psychon Bull Rev 26(4):1070–1098. https://doi.org/10.3758/s13423-018-01563-9
Ly A, Verhagen J, Wagenmakers E-J (2016) Harold jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology. J Math Psychol 72:19–32. https://doi.org/10.1016/j.jmp.2015.06.004
Kass RE, Raftery AE (1995) Bayes factors. J Amer Statist Assoc 90(430):773–795. https://doi.org/10.1080/01621459.1995.10476572
Soch J, Allefeld C (2016) Kullback-leibler divergence for the normal-gamma distribution arXiv:1611.01437 [math.ST]
Gu M-H, Cho C, Chu H-Y, Kang N-W, Lee J-G (2021) Uncertainty propagation on a nonlinear measurement model based on taylor expansion. Measurement and Control 54(3–4):209–215. https://doi.org/10.1177/0020294021989740
Tellinghuisen J (2001) Statistical error propagation. J Phys Chem A 105(15):3917–3921. https://doi.org/10.1021/jp003484u
Alnæs MS, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, Richardson C, Ring J, Rognes ME, Wells GN (2015) The FEniCS project version 1.5. Archive of Numerical Software 3(100):9–23. https://doi.org/10.11588/ans.2015.100.20553
EN 1990: Eurocode - Basis of Structural Design. The European Union Per Regulation 302/2011. https://eurocodes.jrc.ec.europa.eu/showpage.php?id=130
Uribe F, Papaioannou I, Betz W, Straub D (2020) Bayesian inference of random fields represented with the Karhunen-Loève expansion. Comput Method Appl M 358:112632. https://doi.org/10.1016/j.cma.2019.112632
Rasmussen CE, Williams CKI (2005) Gaussian Processes for Machine Learning. The MIT Press, Cambridge, MA. https://doi.org/10.7551/mitpress/3206.001.0001
de Larrard T, Colliat JB, Benboudjema F, Torrenti JM, Nahas G (2010) Effect of the young modulus variability on the mechanical behaviour of a nuclear containment vessel. Nucl Eng Des 240(12):4051–4060. https://doi.org/10.1016/j.nucengdes.2010.09.031
Uribe F, Papaioannou I, Betz W, Ullmann E, Straub D (2017) Random fields in Bayesian inference: Effects of the random field discretization. In: Bucher, C., Ellingwood, B.R., Frangopol, D.M. (eds.) Safety, Reliability, Ris, Resilience and Sustainability of Structures and Infrastructure, pp. 799–808. TU-Verlag Viennna
Zlotnik S, Díez P, Gonzalez D, Cueto E, Huerta A (2015) Effect of the separated approximation of input data in the accuracy of the resulting PGD solution. Adv Model and Simul in Eng Sci 2(1):28. https://doi.org/10.1186/s40323-015-0052-6
Nouy A (2010) A priori model reduction through proper generalized decomposition for solving time-dependent partial differential equations. Comput Method Appl M 199(23–24):1603–1626. https://doi.org/10.1016/j.cma.2010.01.009
Falcó A, Nouy A (2011) A proper generalized decomposition for the solution of elliptic problems in abstract form by using a functional Eckart-Young approach. J Math Anal Appl 376(2):469–480. https://doi.org/10.1016/j.jmaa.2010.12.003
Falcó A, Montés N, Chinesta F, Hilario L, Mora MC (2018) On the existence of a progressive variational vademecum based on the proper generalized decomposition for a class of elliptic parameterized problems. J Comput Appl Math 330:1093–1107. https://doi.org/10.1016/j.cam.2017.08.007
Suárez F (2018) On the localisation of damage under pure bending using a nonlocal approach. Int J Solids Struct 141–142:45–59. https://doi.org/10.1016/j.ijsolstr.2018.02.010
Hüsken G, Pirskawetz S, Hofmann D, Basedau F, Gründer K-P, Kadoke D (2021) The load-bearing behaviour of a reinforced concrete beam investigated by optical measuring techniques. Mater Struct 54(3):1–11. https://doi.org/10.1617/s11527-021-01699-6
Chakraborty J, Wang X, Stolinski M (2021) Damage detection in multiple RC structures based on embedded ultrasonic sensors and wavelet transform. Buildings 11(2):56. https://doi.org/10.3390/buildings11020056
Liehr S, Münzenberger S, Krebber K (2018) Wavelength-scanning coherent OTDR for dynamic high strain resolution sensing. Opt Express 26(8):10573. https://doi.org/10.1364/oe.26.010573
Zou X, Conti M, Díez P, Auricchio F (2017) A nonintrusive proper generalized decomposition scheme with application in biomechanics. Int J Numer Methods Eng 113(2), 230–251. https://onlinelibrary.wiley.com/doi/pdf/10.1002/nme.5610. 10.1002/nme.5610
Acknowledgements
The authors thanks the German Research Foundation (DFG) especially for the funded project 326557591. The real measurement data used here were undertaken by D. Kadoke and the crack measurements (Fig. 12 right) by Dr. G. Hüsken & S. Pirskawetz as part of the BLEIB project within the Federal Institute for Materials Research and Testing (BAM) and funded by the Federal Ministry for Economic Affairs and Climate Action (BMWK), Germany.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A. KL in tractable terms
As mentioned before, the variational Bayesian algorithm is optimization-based and aims at minimizing the KL divergence between the true and approximate posteriors. However, the KL definition written in Eq. (5) depends on the true posterior pdf and therefore it needs to be reformulated in more tractable terms. This derivation can be seen below:
Appendix B. Prior and posterior pdfs
Following the work of [3], the prior pdfs are defined as follows:
While the posteriors are given by:
Appendix C. Taylor series of log-normal field
For the separation of the log-normal Young’s modulus in Eq. (22) the field \(\varkappa _{LN}\) is approximated as a Taylor series expansion around the mean \({\varvec{\theta }}_0\) as:
The approximation can be reordered to obtain the required modes depending on the space \({\varvec{x}}\) and the random field variables \(\theta _i\)
by computing the derivatives and expanding all products.
In the following this is shown for the first order terms and two parameters \({\varvec{\theta }}=[\theta _1,\theta _2]\):
Appendix D. PGD fixed point problems
In case of the progressive PGD solver, the PGD modes \(F_j^i\) in Eq. (25) are solved iteratively.
In each enrichment step \(m\in [1,M]\) a new set on PGD modes \([R, T_1, T_2,... ]\) in Eq. (D7) are computed in a fixed-point iteration considering the \(K+1\) low-dimensional problems.
For the here investigated problem the PGD weak form of Eq. (26) including the definition of the varying Young’s modulus as Eq. (30) is used. The volume load \({\varvec{f}}^{n_f}\) vanishes and the load is given as \({\varvec{t}}^{n_t}({\varvec{x}},{\varvec{\theta }})={\varvec{P}}_x({\varvec{x}})\prod _{j=1}^{K} P_{\theta _j}(\theta _j)\) with \(P_{\theta _j}=1\). In total, \(K+1\) problems must be solved in the fixed-point iteration (with K the number of random variables \(\theta _j\)).
The weak form for the first problem to calculate the new spatial mode \({\varvec{R}}\) is then given as
The spatial problem is solved using standard finite element method.
The weak form for the remaining \(\theta _j\) problems reads exemplary for mode \(T_1(\theta _1)\)
Since there are no derivatives according \(\theta _1\), the problem can be solved in strong from. Afterwards, it is remapped on a standard one-dimensional finite element problem to evaluate e.g., the integrals \(\int T_1 X^i_{1} T_1 d\theta _1\) in the following fixed-point problems.
As stopping criterion for the fixed-point iteration in each fixed-point step f
with
is used.
As stop criterion for the enrichment steps, the amplitude
according to Zou et al. [59] is used. If the tolerance is reached, the enrichment loop stops and the final solution is given, with n summations. Therefore, the same PGD algorithm as in the authors publication [28] is used here.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coelho Lima, I., Robens-Radermacher, A., Titscher, T. et al. Bayesian inference for random field parameters with a goal-oriented quality control of the PGD forward model’s accuracy. Comput Mech 70, 1189–1210 (2022). https://doi.org/10.1007/s00466-022-02214-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-022-02214-6