1 Introduction

In recent years additive manufacturing (AM) has experienced a tremendous increase in popularity [1]. Originally developed for rapid prototyping, AM has evolved into a tool which nowadays is also used to manufacture whole components. Besides the fact that the quality and the performance of the produced samples increased rapidly, a further aspect leading to this development is that AM opens the opportunity to fabricate meta-materials with cellular micro-structures. Such meta-materials are characterised by tailored mechanical properties such as anisotropy, spatially varying stiffness and density as well as sophisticated mechanical functionalities [2, 3], e.g. auxetic properties [4]. In the case considered in this contribution the cellular meta-material is build from slender rods resulting in a rod lattice structure. By varying the arrangement, thickness and cross-sectional geometry of individual rods engineers are able to control the resultant mechanical properties of lattice structures.

Common manufacturing processes used to produce lattices include electron beam melting, selective laser melting as well as selective laser sintering. Rod lattices find their applications mostly in the area of lightweight structures in the aerospace industries as well as in the medical field [1, 5]. In theses applications the lattice is assumed to be stiff and a linear stress-strain relation is typically employed. However, applications in which the stress-strain relation may no longer be assumed linear are emerging more and more often. Possible nonlinearities may appear on the geometrical level as well as on the material level - for instance due to hyperelastic or inelastic material behaviour in the micro-structure. Examples of materials combining both geometric and material nonlinearities include cushioning shoe soles [6], synthetic meshes, used for example in hernia repair surgery [7] and impact absorbing materials used in defence applications such as body and object protection [8,9,10]. The latter is designed to absorb maximum energy at nearly constant stress. Geometric nonlinearities bring new challenges to the mechanical modelling of rod lattices due to finite deformations and the possibility of buckling rods in the lattice structure. Then, the use of linear rod theory is no longer possible. A rod model allowing for large deformations and rotations must be introduced.

A common procedure used to estimate the effective macro-scale mechanical response of a meta-material is two-scale computational homogenization. This approach estimates the effective mechanical response by homogenizing the mechanical behaviour of a micro-structure (micro-scale) based on a representative volume element (RVE) where the RVE consists of periodically repeating unit cells of the meta-material. A widespread convention is to define the RVE as the smallest repeating unit cells. In this contribution different sizes of an RVE will be analysed, i.e. RVEs with different numbers of unit cells.

Two-scale homogenization of rod lattices has been addressed in numerous work [2, 11,12,13,14]. The two-scale homogenization may be used to derive a material model able to replicate the mechanical response of the meta-material for the purely elastic case. This may be done by e.g. fitting an appropriate strain energy function to the homogenized properties of an RVE consisting of the smallest repeating unit cell or by setting up an artificial neuronal network. Alternatively two-scale homogenization may also be used to obtain the constitutive behaviour of the meta-material by on-the-fly homogenization. The aim of this paper is to investigate if the number of unit cells within the RVE, i.e., the size of the RVE affects the homogenized properties. Especially, this is done for load cases leading to buckling within the RVE, since it is known from [15,16,17] that local instabilities at the level of the micro-structure may be influenced by the size of the RVE. Further, it is explored if the mechanical response converges by increasing the RVE’s sizes. To this end, a computational homogenization framework that combines well known three-dimensional continuum mechanics on the macro-scale with an appropriate beam formulation on the micro-scale is developed. The mechanical response of a representative lattice structure shall be analysed under the consideration of large deformations and inelastic behaviour. This involves both the pre- and post-buckling state for both the purely elastic and inelastic case. For this purpose an RVE modelled by geometrically exact elastoplastic rods is considered. In contrast to the classical beam formulation, such as Euler-Bernoulli or Timoshenko beams, the theory of geometrically exact rods (also known as the Cosserat theory of rods [18, 19]) is not restricted to the geometrically linear case and is suitable for large displacements and rotations [18,19,20,21]. Hence, this theory is widely used to model long nano wires and tubes, cables, hair and other biological fibres [22,23,24,25]. An extension to the inelastic case is presented in Smriti et al. [26] and further elaborated in [27]. The bottleneck in modelling elastoplastic geometrically exact rods is the lack of knowledge of an appropriate yield-function in terms of the rod’s stress resultants (internal contact forces and internal contact moments). Yield-functions have been derived for different rod cross-sections in [28,29,30,31] by applying the upper and lower bound techniques of limit analysis in which the rod’s cross-section is assumed to be fully plastified at the yield-limit. An approach where yield is not defined in terms of plastification but in terms of dissipated work has recently been formulated in Herrnböck et al. [32]. The method presented there is generic in terms of the rod’s cross-sectional shape and underlying constitutive model.

Considering the aim of this work, the following structure is prescribed. In Sect. 2 a brief review of the theory of geometrically exact rods with rigid cross-sections is presented for both the purely elastic and inelastic case. The presentation of the inelastic case involves the derivation of the evolution equations for the plastic quantities. In Sect. 3 the constraints necessary to model networks of multiple rods are introduced, where it is assumed that the displacement and rotation of two distinct rods are equal at their intersection. Finally, in Sect. 4 a first-order homogenization framework combining classical three-dimensional continuum mechanics on the macro-scale with the geometrically exact rod theory on the micro-scale is proposed. Thus, this homogenization framework allows for large deformations and rotations of rods constituting the underlying rod lattice while allowing inelastic behaviour. The concepts introduced in Sects. 2–4 are finally used to obtain numerical results investigating the macroscopic mechanical response of an exemplary periodic rod lattice. These results are presented in Sect. 5. Investigations are performed for different uniaxial strain cases. On the one hand, the focus of the investigations is on the influence of the rods cross-sectional size and, therefore, the change of the mechanical properties of a single rod. On the other hand, an investigation into the stability of the RVE as a function of its size is also performed. The examples presented in this work serve to demonstrate the introduced framework. Imperfections emerging from the manufacturing process are not considered here.

Before setting the stage by recalling the theory of geometrically exact rods the nomenclature used throughout this contribution is introduced. As in Herrnböck et al. [32] strain measures and their energetic conjugates are denoted differently in the context of three-dimensional continuum mechanics and geometrically exact rods. The different terminology is summarized in Table 1.

Table 1 Strain measures and their energetic conjugates are denoted differently in the context of geometrically exact rods and three-dimensional continuum mechanics. This nomenclature is consistent with [32]
Full size table

All simulations carried out to generate the results shown in this contribution are based on the open source finite-element library deal.II [33].

2 Geometrically exact rods with rigid cross-sections

In this section the theory of geometrically exact rods with rigid cross-sections is presented. This presentation begins with the kinematics followed by the stress resultants and the balance equations for linear and angular momentum. The derivations presented in this sections are based on those in [27, 32] and the references therein.

2.1 Kinematics

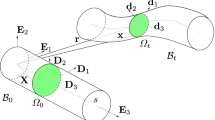
Figure 1 shows a typical rod deforming from its undeformed straight material configuration \(\mathcal {B}_0\) into its deformed spatial configuration \(\mathcal {B}_t\). In this contribution a rod is assumed to have a constant cross-section along its arc length s. Here \(\mathbf {X}\) denotes the position of a material point in the rod’s undeformed material configuration. Straight rods are considered with the orientation of the cross-sections in the material configuration, independent of the rod’s arc length s, described by the set of directors \(\mathbf {D}_{i}\). The orthogonal directors \(\mathbf {D}_{1}\) and \(\mathbf {D}_{2}\) span the plane of the undeformed planar cross-section \(\varOmega _0\) and are usually aligned with the cross-section ’s principal axis. \(\displaystyle {\mathbf {D}_{3}=\mathbf {D}_{1}\times \mathbf {D}_{2}}\) is perpendicular to the rod’s undeformed cross-section. The directors \(\mathbf {D}_{i}\) form an orthonormal basis and are related to the basis \(\mathbf {E}_{i}\) via

$$\begin{aligned} \mathbf {D}_{i}=\mathbf {R}_0\mathbf {E}_{i}, \end{aligned}$$
(1)

where \(\mathbf {R}_0\) denotes a three-dimensional rotation tensor, a member of the special orthogonal group SO(3). That is \(\mathbf {R}_0\) describes the orientation of the undeformed cross-sections with respect to the reference frame \(\mathbf {E}_i\). One may decompose \(\mathbf {X}\) as follows:

$$\begin{aligned} \mathbf {X}:= \mathbf {X}(s;\mathbf {X}_{CS})= \mathbf {s}(s)+\mathbf {X}_{CS}, \end{aligned}$$
(2)

where \(\mathbf {s}(s)=\mathbf {s}_0+s\mathbf {D}_{3}\) denotes the position along the rod’s arc length s by a starting point \(\mathbf {s}_0\) and the direction \(\mathbf {D}_3\). Additionally, \(\mathbf {X}_{CS}=X_{CS_{\alpha }}\mathbf {D}_{\alpha }\) describes the material points lying in the cross-section. Here, Latin indices run from 1 to 3, whereas Greek indices run from 1 to 2. The position of the deformed centerline is denoted by \(\mathbf {r}{(s)}\). The orthogonal directors \(\mathbf {d}_{1}{(s)}\), \(\mathbf {d}_{2}{(s)}\) span the plane of the deformed cross-section \(\varOmega _t\) which is assumed to be planar. An orthonormal basis is constructed with \(\mathbf {d}_{3}{(s)}=\mathbf {d}_{1}{(s)}\times \mathbf {d}_{2}{(s)}\). In this theory, it is not required that \(\mathbf {d}_{3}{(s)}\) is tangential to the deformed centerline \(\mathbf {r}\)(s) [20]. Together the directors \(\mathbf {d}_{i}{(s)}\) describe the orientation of the deformed cross-section. The directors in the spatial configuration are related to the directors in the material configuration via

$$\begin{aligned} \mathbf {d}_{i}{(s)}=\mathbf {R}{(s)}\mathbf {D}_{i}. \end{aligned}$$
(3)
Fig. 1
figure 1

Illustration of a geometrically exact rod undergoing a deformation from its straight material configuration \(\mathcal {B}_0\) into its deformed spatial configuration \(\mathcal {B}_t\). Any point in the material configuration is denoted by \(\mathbf {X}\). The position of the centerline of the deformed rod is defined by \(\mathbf {r}\). Material points in the spatial configuration are denoted by \(\mathbf {x}\)

Full size image

The quantities \(\mathbf {r}\)(s) and \(\mathbf {R}\)(s) are the kinematic unknowns of this theory. Note that the rotation described by the rotation matrix \(\mathbf {R}\)(s) can also be parametrised by a vector \(\varvec{\vartheta }(s)\), where \(\Vert \varvec{\vartheta }(s)\Vert \) gives the angle of the rotation, and \(\displaystyle {\frac{\varvec{\vartheta }(s)}{\Vert \varvec{\vartheta }(s)\Vert }}\) describes the direction of rotation [27].

Assuming a rigid cross-section the position \(\mathbf {x}(s)\) of any material point in the spatial configuration is described by

$$\begin{aligned} \mathbf {x}(s;\mathbf {X}_{CS})=\mathbf {r}{(s)}+\mathbf {R}{(s)}\mathbf {X}_{CS}. \end{aligned}$$
(4)

For the sake of readability, the dependencies on s and \(\mathbf {X}_{CS}\) are omitted from now on. In this contribution, the cross-section of the deformed rod remains rigid. A framework to model the cross-sectional deformation depending on strain measures only is outlined in [34, 35].

Strain-prescriptors are introduced as the translational strain \(\mathbf {v}_{}^{}{}\) and the rotational strain \(\mathbf {k}_{}^{}{}\) (also called curvature):

$$\begin{aligned} \begin{aligned}&\mathbf {v}_{}^{}{}=\mathbf {r}{}'=v _i\mathbf {d}_{i}{},\\&{\mathbf {K}}=\mathbf {R}{}'\mathbf {R}{}^{T},\quad \mathbf {k}_{}^{}{}=\text {ax}\left( \mathbf {K}\right) =k _i\mathbf {d}_{i}{}, \end{aligned} \end{aligned}$$
(5)

where \(\bullet '\) defines the derivative of an arbitrary quantity with respect to s as

$$\begin{aligned} \bullet ':=\frac{\partial \bullet }{\partial s}. \end{aligned}$$
(6)

The rotational pull backs \(\mathbf {v}_{0}^{}{}\) and \(\mathbf {k}_{0}^{}{}\) of \(\mathbf {v}_{}^{}{}\) and \(\mathbf {k}_{}^{}{}\) respectively are defined as:

$$\begin{aligned} \begin{aligned}&\mathbf {v}_{0}^{}{}=\mathbf {R}{}^{T}\mathbf {r}{}'=v _i\mathbf {D}_{i},\\&{\mathbf {K}}_0=\mathbf {R}{}^{T}{\mathbf {K}}\mathbf {R}{},\quad \mathbf {k}_{0}^{}{}=\text {ax}\left( \mathbf {K}_0\right) =\mathbf {R}{}^{T}\mathbf {k}_{}^{}{}=k _i\mathbf {D}_{i}{}. \end{aligned} \end{aligned}$$
(7)

Here \({\mathbf {K}}\) and \({\mathbf {K}}_0\) are skew-symmetric tensors whose axial vectors are \(\mathbf {k}_{}^{}{}\) and \(\mathbf {k}_{0}^{}{}\) respectively. The operator \(ax (\mathbf {A})\) transforms an arbitrary skew-symmetric tensor \(\mathbf {A}\) into its axial vector \(\mathbf {a}\) such that:

$$\begin{aligned} \mathbf {a}=\text {ax}(\mathbf {A})=\begin{bmatrix} A_{32} \\ A_{13} \\ A_{21} \end{bmatrix}= -\begin{bmatrix} A_{23} \\ A_{31} \\ A_{12} \end{bmatrix}. \end{aligned}$$
(8)

We now present the definition of the deformation gradient \(\mathbf {F}\) of the deformation map (4)

$$\begin{aligned} \mathbf {F}=\frac{\partial \mathbf {x}}{\partial \mathbf {X}} \end{aligned}$$
(9)

The origin of the undeformed rod is set to the origin of a global coordinate system defined by the reference frame \(\mathbf {E}_i\), i.e., \(\mathbf {s}_0=\mathbf {0}\). Inserting equation (4) into equation (9) yields

$$\begin{aligned} \begin{aligned} \mathbf {F}=&\frac{\partial \mathbf {r}}{\partial \mathbf {X}}+\frac{\mathbf {R}}{\partial \mathbf {X}} \mathbf {X}_{CS}+ \mathbf {R}\frac{\partial \mathbf {X}_{CS}}{\partial \mathbf {X}}. \end{aligned} \end{aligned}$$
(10)

Recalling the dependencies \(\mathbf {r}=\mathbf {r}(s)\), \(\mathbf {R}=\mathbf {R}(s)\) and \(\mathbf {X}=\mathbf {X}(s;\mathbf {X}_{CS})\) from equation (2) and (4) respectively the following relations hold:

$$\begin{aligned} \frac{\partial \mathbf {r}}{\partial X_1}=\frac{\partial \mathbf {r}}{\partial X_2}=\mathbf {0}\quad \text {and}\quad \frac{\partial \mathbf {R}}{\partial X_1}=\frac{\partial \mathbf {R}}{\partial X_2}=\mathbf {0}. \end{aligned}$$
(11)

Furthermore,

$$\begin{aligned} \frac{\partial \mathbf {r}}{\partial X_3}=\frac{\partial \mathbf {r}}{\partial s}=\mathbf {r}'\quad \text {and}\quad \frac{\partial \mathbf {R}}{\partial X_3}=\frac{\partial \mathbf {R}}{\partial s}=\mathbf {R}'. \end{aligned}$$
(12)

Finally, equation (10) is reformulated as

$$\begin{aligned} \begin{aligned} \mathbf {F}=&\mathbf {r}'\otimes \mathbf {D}_3+\left[ \mathbf {R}'\mathbf {X}_{CS}\right] \otimes \mathbf {D}_3+\mathbf {R}\left[ \mathbf {D}_{\alpha }\otimes \mathbf {D}_{\alpha }\right] . \end{aligned} \end{aligned}$$
(13)

By extracting \(\mathbf {R}\) in equation (13) the deformation gradient can be written in terms of strain prescriptors as follows:

$$\begin{aligned} \mathbf {F}=\mathbf {R}\bigg [\mathbf {v}_{0}^{}{}\otimes \mathbf {D}_{3}+\left[ \mathbf {k}_{0}^{}{}\times \mathbf {X}_{CS}\mathbf {D}_{\alpha }\right] \otimes \mathbf {D}_{3}+\mathbf {D}_{\alpha }\otimes \mathbf {D}_{\alpha }\bigg ]. \qquad \end{aligned}$$
(14)

2.2 Stress resultants and balance equations

The internal (contact) force and internal (contact) moment, collectively named stress resultants, are denoted by \(\mathbf {n}_{}{}\) and \(\mathbf {m}_{}{}\) respectively with:

$$\begin{aligned} \mathbf {n}_{}{}=n _i\mathbf {d}_{i}{},\quad \mathbf {m}_{}{}=m _i\mathbf {d}_{i}{}. \end{aligned}$$
(15)

Their rotational pull backs are

$$\begin{aligned} \begin{aligned} \mathbf {n}_{0}{}=n _i\mathbf {D}_{i},\quad \mathbf {m}_{0}{}=m _i\mathbf {D}_{i}. \end{aligned} \end{aligned}$$
(16)

For the elastic case and assuming the existence of a scalar valued strain energy density function \(\psi ^{rod}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{})\) the stress resultants follow as

$$\begin{aligned} \begin{aligned} \mathbf {n}_{0}{}=\frac{\partial \psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{}),\quad \mathbf {m}_{0}{}=\frac{\partial \psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{}). \end{aligned} \end{aligned}$$
(17)

The second derivative of \(\psi ^{rod}(\mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{})\) with respect to the strain prescriptors yields the \(6\times 6\) tangent stiffness matrix \(\mathbf {C}_0\)

$$\begin{aligned} \begin{aligned} \mathbf {C}_0&= \begin{bmatrix} \mathbf {C}_{0_{vv }} &{} \mathbf {C}_{0_{vk }}\\ \mathbf {C}_{0_{kv }} &{} \mathbf {C}_{0_{kk }} \end{bmatrix}\\&= \begin{bmatrix} \displaystyle { \frac{\partial ^2\psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}\partial \mathbf {v}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } &{} \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}\partial \mathbf {k}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } \\ \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}\partial \mathbf {v}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } &{} \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}\partial \mathbf {k}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } \end{bmatrix}, \end{aligned} \end{aligned}$$
(18)

which relates the change in the stress resultants to the change in the strain prescriptors as

$$\begin{aligned} \begin{bmatrix} d \mathbf{n }_0\\ d \mathbf{m }_0 \end{bmatrix} =\mathbf {C}_0 \begin{bmatrix} d \mathbf{v }_0 \\ d \mathbf{k }_0 \end{bmatrix}. \end{aligned}$$
(19)

Remark 1

A framework to obtain the tangent stiffness matrix of strained elastic rods was presented in Arora et al. [35]. In their work, the assumption is made that the rod’s cross-sections need not remain plane but can warp due to imposed strain prescriptors (\(\mathbf {v}_{0}^{}{}\) and \(\mathbf {k}_{0}^{}{}\)). The resulting stiffness is a function of the strain prescriptors. The framework allows for the use of arbitrary hyperelastic constitutive models on the cross-sectional level and is extended to the inelastic case in Herrnböck et al. [32]. In the contribution at hand the elastic tangent stiffness matrix is assumed to be constant. This yields a linear relation between stress resultants and strain prescriptors

$$\begin{aligned} \begin{bmatrix} \mathbf {n}_0\\ \mathbf {m}_0 \end{bmatrix} =\mathbf {C}_0 \begin{bmatrix} \mathbf {v}_0 \\ \mathbf {k}_0 \end{bmatrix}. \end{aligned}$$
(20)

Nevertheless, the constant tangent stiffness matrix must be evaluated by, for example, using the framework presented in [35].

In the elastoplastic case the above definition of the stress resultants is no longer valid (see equation (17)). The key components of modelling elastoplastic rods are briefly presented here. The strain prescriptors are assumed to decompose into an elastic and a plastic part as follows:

$$\begin{aligned} \mathbf {v}_{0}^{}{}=\mathbf {v}_{0}^{e}{}+\mathbf {v}_{0}^{p}{},\quad \mathbf {k}_{0}^{}{}=\mathbf {k}_{0}^{e}{}+\mathbf {k}_{0}^{p}{} \quad \text { [26,27]}. \end{aligned}$$
(21)

A free energy density function \({\varPsi }^{rod} \) is introduced as

$$\begin{aligned} {\varPsi }^{rod} (\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{},\varvec{\xi })=\psi ^{rod}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{})+\mathcal {H}(\varvec{\xi }), \end{aligned}$$
(22)

where \(\psi ^{rod}\) denotes the strain energy density and \(\mathcal {H}\) describes the hardening depending on the internal variables \(\varvec{\xi }\). The dissipation power \(\mathcal {D}\) is defined as the difference between the applied stress power and the material time derivative of the free energy density and is required to be greater than or equal to 0:

$$\begin{aligned} \mathcal {D} =\mathbf {n}_0\cdot \dot{\mathbf {v}}_0+\mathbf {m}_0\cdot \dot{\mathbf {k}}_0-\frac{d {\varPsi }^{rod}}{d t}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{},\varvec{\xi })\ge 0, \end{aligned}$$
(23)

where \(\displaystyle {\dot{\bullet }:=\left. \frac{d \bullet }{d t}\right| _{\mathbf {X}}}\). Performing the time derivative by applying chain rule and stating that the resulting equation has to hold for any admissible process one obtains the constitutive equations (similar to equation (17)):

$$\begin{aligned} \mathbf {n}_0=\frac{\partial \psi ^{rod}}{\partial \mathbf {v}_{0}^{e}{}}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{}),\quad \mathbf {m}_0=\frac{\partial \psi ^{rod}}{\partial \mathbf {k}_{0}^{e}{}}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{}). \end{aligned}$$
(24)

Furthermore, we define the hardening-stress \(\varvec{\beta }\) as

$$\begin{aligned} \varvec{\beta }=-\frac{\partial \mathcal {H}}{\partial \varvec{\xi }}(\varvec{\xi }). \end{aligned}$$
(25)

Inserting the equations (24) and (25) into the dissipation inequality yields the reduced form of the dissipation inequality

$$\begin{aligned} \mathcal {D}^{red}=\mathbf {n}_0\cdot \dot{\mathbf {v}}_0^p+\mathbf {m}_0\cdot \dot{\mathbf {k}}_0^p+\varvec{\beta }\cdot \dot{\varvec{\xi }}\ge 0. \end{aligned}$$
(26)

Equation (26) is maximised under the constraint \(\displaystyle {\varPhi }(\mathbf {n}_0,\mathbf {m}_0, \varvec{\beta })\le 0\). Here \(\varPhi \) describes a yield-function in terms of stress resultants. A framework to obtain such a function, is comprehensively presented in Herrnböck et al. [32]. Finally, the evolution equations for the plastic quantities are obtained:

$$\begin{aligned} \begin{aligned}&\dot{\mathbf {v}}_0^p=\dot{\gamma }\frac{\partial \varPhi }{\partial \mathbf {n}_0}(\mathbf {n}_0,\mathbf {m}_0,\varvec{\beta }), \quad \dot{\mathbf {k}}_0^p=\dot{\gamma }\frac{\partial \varPhi }{\partial \mathbf {m}_0}(\mathbf {n}_0,\mathbf {m}_0,\varvec{\beta }), \quad \\&\dot{\varvec{\xi }}=\dot{\gamma }\frac{\partial \varPhi }{\partial \varvec{\beta }}(\mathbf {n}_0,\mathbf {m}_0,\varvec{\beta }). \end{aligned} \end{aligned}$$
(27)

The Lagrange multiplier \(\dot{\gamma }\) ensures that the resulting stress resultants are admissible and satisfy the Karush-Kuhn-Tucker (KKT) conditions

$$\begin{aligned} \dot{\gamma }\ge 0,\quad \dot{\gamma }\varPhi (\mathbf {n}_0,\mathbf {m}_0,\varvec{\beta })=0,\quad \varPhi (\mathbf {n}_0,\mathbf {m}_0,\varvec{\beta })\le 0. \end{aligned}$$
(28)

The changes in stress resultants are related to the changes in strain prescriptors via the \(6\times 6\) elastoplastic tangent stiffness matrix \(\mathbf {C}_0^{ep}\)

$$\begin{aligned} \begin{bmatrix} d \mathbf{n }_0\\ d \mathbf{m }_0 \end{bmatrix} =\mathbf {C}_0^{ep} \begin{bmatrix} d \mathbf{v }_0 \\ d \mathbf{k }_0 \end{bmatrix}. \end{aligned}$$
(29)

Due to the additive nature of the strain prescriptors, well known methods from small-strain plasticity may be applied to derive an update algorithm and the algorithmic elastoplastic tangent (for three-dimensional small strain plasticity the reader is referred to [36], for the special case of inelastic rods [27] is recommended).

To conclude this section the balance equations of linear and angular momentum are presented and take the following localized forms

$$\begin{aligned} \begin{aligned}&\mathbf {n}'+\hat{\mathbf {n}}=\mathbf {0},\\&\mathbf {m}'+\hat{\mathbf {m}}+\mathbf {r}'\times \mathbf {n}=\mathbf {0}. \end{aligned} \end{aligned}$$
(30)

Here \(\hat{\mathbf {n}}\) and \(\hat{\mathbf {m}}\) represent the distributed external force and moment respectively. In this contribution they are assumed zero, thus:

$$\begin{aligned} \begin{aligned}&\mathbf {n}'=\mathbf {0},\\&\mathbf {m}'+\mathbf {r}'\times \mathbf {n}=\mathbf {0}. \end{aligned} \end{aligned}$$
(31)

The kinematic unknowns can be determined by solving (31) using the finite element method. The framework used in this work is presented in [21]. In this contribution the rods are discretized using two-noded finite elements with three translational degrees of freedom (DOF) and three rotational DOFs assigned to each node. The kinematic unknowns (\(\mathbf {r}\), \(\varvec{\vartheta }\)) within one element are approximated by linear shape functions. The discretized balance equations are evaluated using a one-point Gauss integration.

3 Network of rods

In this contribution not only one single rod but networks of multiple rods resulting in periodic lattices are considered. It is assumed that intersecting rods are fixed at their intersection, i.e., their kinematic unknowns \(\mathbf {r}\) and \(\mathbf {R}\) must coincide. Let the superscript A and B denote two distinct rods. Their material centerline is defined by

$$\begin{aligned} \mathbf {s}^A= \mathbf {s}_0^A+s^A\mathbf {D}_{3}^A,\quad \mathbf {s}^B= \mathbf {s}_0^B+s^B \mathbf {D}_{3}^B. \end{aligned}$$
(32)

Assuming that both rods intersect at \(s^A=l^A\) and \(s^B=l^B\) the spatial position and rotation are constrained via

$$\begin{aligned} \mathbf {r}^A(l^A)=\mathbf {r}^B(l^B),\quad \mathbf {R}^A(l^A)=\mathbf {R}^B(l^B). \end{aligned}$$
(33)

With (33) it is ensured that the connection is fixed througout the deformation and that the angle between two rods remains constant.

Perfectly rigid connections between the rods are assumed throughout this contribution. However, one could also think of pinned or semi-rigid joints. Pinned joints are easily realised by simply omitting the constraints on the rotation matrices \(\mathbf {R}\) in equation (33). To realise semi-rigid joints the following approach can be pursued. Instead of constraining the rotations of two intersecting rods the rods are connected by a rotational spring with stiffness K. Rigid joints are obtained for \(K\rightarrow \infty \), while pinned joints result from \(K\rightarrow 0\). For more details, the reader is referred to [37]. A rheological model that links the rotations and translations of two intersecting rods is also conceivable.

4 Homogenization

As described in the introduction of this paper the authors aim to investigate the mechanical response of periodic rod lattices. Assuming that the length-scale of a smallest repeating unit cell is sufficiently small compared to the length-scale of the overall lattice

$$\begin{aligned} l_m \ll l_M, \end{aligned}$$
(34)

the principle of scale-separation applies. Thus, the micro- and the macro-scale are introduced denoted by superscript m and M, respectively. A representative volume element (RVE) describing the smallest repeating unit of the overall lattice may be considered as a material point of the macro-scale. To transfer the mechanical properties of the RVE to the macro-scale methods from multiscale homogenization are useful tools. Such methods are well known and widely discussed for all kind of problems described by nonlinear three-dimensional continuum mechanics. Key references are [15, 16].

This section is devoted to a multiscale homogenization framework with the macro-scale described by classical nonlinear three-dimensional continuum mechanics and the micro-scale described by geometrically exact elastoplastic rods. First, the macro-to-micro transition is presented. A relation to transfer the kinematics between the scales is shown and appropriate boundary conditions are derived to successfully fulfil the Hill-Mandel condition. The starting point is the homogenization method from classical three-dimensional continuum theory. Here we strongly orient on Geers et al. [16]. It is then shown that the resulting boundary conditions can be transferred to the kinematic unknowns of the geometrically exact rod theory. Later, the micro-to-macro transition is presented. The rod’s stress resultants are transferred to three-dimensional stress measures. Similar approaches can be found in Glaesener et al. [11, 12], Weeger [13] and Gärtner et al. [14].

4.1 Macro-to-micro

In first-order homogenization a material point in the deformed configuration of the RVE is defined as:

$$\begin{aligned} \mathbf {x}=\mathbf {F}^M\mathbf {X}+\tilde{\mathbf {x}}. \end{aligned}$$
(35)

The first term in equation (35) denotes a homogeneous deformation defined by the macroscopic deformation gradient \(\mathbf {F}^M\) and the second term describes a field of fluctuations, which is a local contribution to the deformation superimposed to the homogenized deformation. The deformation gradient on the micro-scale is written as

$$\begin{aligned} \mathbf {F}^m=\nabla \mathbf {x}=\mathbf {F}^M+\nabla \tilde{\mathbf {x}}. \end{aligned}$$
(36)

A widely used relation to transfer the kinematics between the scales is given by

$$\begin{aligned} \mathbf {F}^M=\frac{1}{V_m}\int _{\mathcal {B}_{0}^m} \mathbf {F}^m d V, \end{aligned}$$
(37)

where \(V_m\) denotes the volume of the RVE’s undeformed configuration \(\mathcal {B}_0^m\).

The RVE has to be solved under appropriate boundary conditions, which have to be derived. This is done by fulfilling the Hill-Mandel condition. We begin by stating that the increment or variation of the work performed on the macro-scale equals the volume average of the variation of work on the micro-scale.

$$\begin{aligned} \begin{aligned} \mathbf {P}^{M}:\delta {\mathbf {F}}^{M}&=\frac{1}{V^m}\int _{\mathcal {B}_0^m}\mathbf {P}^{m}:\delta {\mathbf {F}}^{m}d V\\&=\frac{1}{V^m}\int _{\mathcal {B}_0^m}\mathbf {P}^{m}:\left[ \delta {\mathbf {F}}^M+\frac{\partial \delta {\tilde{\mathbf {x}}}}{\partial \mathbf {X}^m}\right] d V\\&=\frac{1}{V^m}\int _{\mathcal {B}_0^m}\mathbf {P}^md V:\delta {\mathbf {F}}^M\\&\quad + \frac{1}{V^m}\int _{\mathcal {B}_0^m}\mathbf {P}^m:\frac{\partial \delta {\tilde{\mathbf {x}}}}{\partial \mathbf {X}^m}d V, \end{aligned} \end{aligned}$$
(38)

where \(\mathbf {P}\) denotes the Piola stress, a non-symmetric twopoint tensor. The Hill-Mandel condition requires\(\displaystyle {\mathbf {P}^M=\frac{1}{V^m}\int _{\mathcal {B}_0^m}} {\mathbf {P}^md V}\). This means that the fluctuations in the second term of equation (38) have to vanish. Hereinafter, the index \(\bullet ^m\) is omitted for the sake of readability

$$\begin{aligned} \frac{1}{V}\int _{\mathcal {B}_0}\mathbf {P}:\frac{\partial \delta {\tilde{\mathbf {x}}}}{\partial \mathbf {X}}d V\doteq 0. \end{aligned}$$
(39)

Applying Einstein’s index notation equation (39) can be rewritten as

$$\begin{aligned} \frac{1}{V}\int _{\mathcal {B}_0} P_{iJ} \delta {\tilde{x}}_{i,J}d V\!=\!\frac{1}{V}\int _{\mathcal {B}_0}\left[ P_{iJ}\delta {\tilde{x}}_i\right] _{,J}-P_{iJ,J}\delta {\tilde{x}}_id V\!=\!0. \nonumber \\ \end{aligned}$$
(40)

The localized force balance in the RVE yields \(\displaystyle {P_{iJ,J}=0_i}\). Further, applying the Gauss divergence theorem equation (40) is reformulated as

$$\begin{aligned} \frac{1}{V}\int _{\partial {\mathcal {B}_0}}P_{iJ}\delta {\tilde{x}}_i N_Jd A=0, \end{aligned}$$
(41)

where \(N_J\) denotes the outwards pointing unit vector normal to \(\partial {\mathcal {B}_0}\). For the case of a porous RVE the boundary \(\partial \mathcal {B}_0\) of the body is split into the shell \(\partial \mathcal {B}_0^S\) and the faces \(\partial \mathcal {B}_0^F\) (shown in Fig. 2 for a cross-shaped RVE).

Fig. 2
figure 2

Visualisation of the shell \(\partial \mathcal {B}_0^F\) and the faces \(\partial \mathcal {B}_0^F\) of a porous RVE such that \(\partial \mathcal {B}_0=\partial \mathcal {B}_0^F\cup \partial \mathcal {B}_0^S\)

Full size image

By splitting the integral (41) one obtains:

$$\begin{aligned} \begin{aligned}&\frac{1}{V}\int _{\partial \mathcal {B}_0}P_{iJ}\delta {\tilde{x}}_i N_Jd A\\&=\frac{1}{V}\left[ \int _{\partial \mathcal {B}_0^S}P_{iJ}\delta {\tilde{x}}_i N_Jd A+\int _{\partial \mathcal {B}_0^F}P_{iJ}\delta {\tilde{x}}_i N_Jd A\right] =0. \end{aligned} \end{aligned}$$
(42)

Assuming traction free boundaries on the shell of the RVE the integral over the shell vanishes. This yields

$$\begin{aligned} \int _{\partial \mathcal {B}_0^F}P_{iJ}\delta {\tilde{x}}_i N_Jd A=0. \end{aligned}$$
(43)

Thus far the presented concepts are not distinguished from homogenization methods applied in three-dimensional continuum mechanics [16]. Now, however, the fluctuations \(\tilde{x}_i\) are described in terms of the rod’s kinematic unknowns. Therefore, recall that the deformed configuration of a geometrically exact rod is defined as

$$\begin{aligned} x_i=r_i+R_{iJ}{X}_{CS_J}, \end{aligned}$$
(44)

where \(X_{CS_J}\) denotes the coordinates in the cross-section. Finally, the fluctuations \(\tilde{x}_i\) are defined as

$$\begin{aligned} \tilde{x}_i=\tilde{r}_i+\tilde{R}_{iJ}{X}_{CS_J}, \end{aligned}$$
(45)

and their variations are

$$\begin{aligned} \delta {\tilde{x}}_i=\delta {\tilde{r}}_i+\delta {\tilde{R}}_{iJ}{X}_{CS_J}. \end{aligned}$$
(46)

Inserting equation (46) into equation (43) and splitting the boundary \(\partial \mathcal {B}_0^F\) into periodic pairs by \(\bullet ^+\) and \(\bullet ^-\) one obtains

$$\begin{aligned} \begin{aligned}&\frac{1}{V}\left[ \int _{\partial \mathcal {B}_0^{F^+}}P_{iJ}^+\delta {\tilde{r}}_i^+ N_J^+d A+ \int _{\partial \mathcal {B}_0^{F^-}}P_{iJ}^-\delta {\tilde{r}}_i^- N_J^-d A\right. \\&\qquad \left. +\int _{\partial \mathcal {B}_0^{F^+}}P_{iJ}^+ \delta {\tilde{R}}_{iK}^+{X}_{CS_K}^+ N_J^+d A\right. \\&\qquad \left. + \int _{\partial \mathcal {B}_0^{F^-}}P_{iJ}^-\delta {\tilde{R}}_{iK}^-{X}_{CS_K}^- N_J^-d A\right] =0. \end{aligned} \end{aligned}$$
(47)

Using the well known relation \(\displaystyle {T_i=P_{iJ}N_J}\), where \(\mathbf {T}\) denotes the traction vector, the above equation is reformulated as

$$\begin{aligned} \begin{aligned}&\frac{1}{V}\left[ \delta {\tilde{r}}_i^+\int _{\partial \mathcal {B}_0^{F^+}}T_{i}^+d A+ \delta {\tilde{r}}_i^-\int _{\partial \mathcal {B}_0^{F^-}}T_{i}^-d A\right. \\&\qquad +\left. \delta {\tilde{R}}_{iK}^+ \int _{\partial \mathcal {B}_0^{F^+}}T_{i}^+{X}_{CS_K}^+d A\right. \\&\qquad +\left. \delta {\tilde{R}}_{iK}^-\int _{\partial \mathcal {B}_0^{F^-}} T_{i}^-{X}_{CS_K}^-d A\right] =0. \end{aligned} \end{aligned}$$
(48)

To satisfy the above equation the following conditions have to be fulfilled

$$\begin{aligned} \begin{aligned}&\delta {\tilde{r}}_i^+=\delta {\tilde{r}}_i^-,\quad \delta {\tilde{R}}_{iJ}^+=\delta {\tilde{R}}_{iJ}^-\text { and}\quad {X}_{CS_I}^+={X}_{CS_I}^-,\quad \\&T_i^+=-T_i^-. \end{aligned} \end{aligned}$$
(49)

The first two conditions are ensured by applying periodic boundary conditions to the field of unknowns. The third and fourth ones are already satisfied since jumps on the boundary are not allowed and the normals are pointing counter-wise on the RVE’s periodic boundary.

4.2 Micro-to-macro

Having shown that periodic boundary conditions in term of the rod’s kinematic unknowns fulfil the Hill-Mandel condition it is now demonstrated how to obtain the averaged macro stress \(\mathbf {P}^M\). Again, one makes use of Einstein’s index notation. In index notation, the Hill-Mandel condition yields

$$\begin{aligned} \begin{aligned} P_{iJ}^M&=\frac{1}{V}\int _{\mathcal {B}_0} P_{iJ} d V=\frac{1}{V}\int _{\mathcal {B}_0}\left( X_J P_{iK}\right) _{,K}d V\\&=\frac{1}{V}\int _{\partial {\mathcal {B}_0}} X_J P_{iK} N_Kd A. \end{aligned} \end{aligned}$$
(50)

The rod’s material points \(\mathbf {X}\) are given by equation (2). Substituting equation (2) into equation (50) one obtains

$$\begin{aligned} P_{iJ}^M\!=\!\frac{1}{V}\left[ s_J\int _{\partial {\mathcal {B}_0}} P_{iK}^m N_Kd A+\int _{\partial {\mathcal {B}_0}}{X}_{CS_J}P_{iK} N_Kd A\right] .\nonumber \\ \end{aligned}$$
(51)

The integrals are again split into their periodic pairs as

$$\begin{aligned} \begin{aligned} P_{iJ}^M=&\frac{1}{V}\left[ s_J^+\int _{\partial {\mathcal {B}_0} ^{F^+}} P_{iK}^{+} N_K^+d A\right. \\&\left. +s_J^-\int _{\partial {\mathcal {B}_0} ^{F^-}} P_{iK}^{-} N_K^-d A\right. \\&\left. +\int _{\partial {\mathcal {B}_0} ^{F^+}}{X}_{CS_J}^+P_{iK}^{+} N_K^+d A\right. \\&\left. +\int _{\partial {\mathcal {B}_0} ^{F^-}}{X}_{CS_J}^-P_{iK}^{-} N_K^-d A\right] . \end{aligned} \end{aligned}$$
(52)

Rewriting equation (52) in terms of tractions yields

$$\begin{aligned} \begin{aligned} P_{iJ}^M=&\frac{1}{V}\left[ s_J^+\int _{\partial {\mathcal {B}_0} ^{F^+}} T_i^+d A+s_J^- \int _{\partial {\mathcal {B}_0} ^{F^-}}T_i^-d A\right. \\&\left. +\int _{\partial {\mathcal {B}_0} ^{F^+}}{X}_{CS_J}^+T_i^+d A\right. \\&+\left. \int _{\partial {\mathcal {B}_0} ^{F^-}}{X}_{CS_J}^-T_i^-d A\right] . \end{aligned} \end{aligned}$$
(53)

The integral over the periodic boundaries can be rewritten as

$$\begin{aligned} \int _{\partial \mathcal {B}_0^{\square }}\left( \bullet \right) d A=\sum _{I}^{n_{CS}}\int _{\partial \mathcal {B}_{0_I}^{\square }} \left( \bullet \right) _Id A, \end{aligned}$$
(54)

where \(\square \) is a place-holder for either \(+\) or −. The upper boundary \(n_{CS}\) of the sum indicates the number of cross-sections laying on the RVE’s boundary. Finally, this yields

$$\begin{aligned} P_{iJ}^M=\frac{1}{V}\sum _I^{n_{CS}} n_{0_{I_i}} s_{I_J}. \end{aligned}$$
(55)

The above statement implies

$$\begin{aligned} \mathbf {n}_0=\int _{\partial \mathcal {B}_0^\square } \mathbf {T}d A\quad \text {shown in [32,34,35]}, \end{aligned}$$
(56)

and

$$\begin{aligned} \int _{\partial \mathcal {B}_0^{F^+}}T_i^+{X}_{CS_J}^+d A=-\int _{\partial \mathcal {B}_0^{F^-}}T_i^-{X}_{CS_J}^-d A, \end{aligned}$$
(57)

since \({X}_{CS_J}^+={X}_{CS_J}^-\) and \(T_i^+=-T_i^-\). Equation (56) shows that by choosing the boundary of the RVE to coincide with the rod’s cross-section (i.e \(\mathbf {N}=\mathbf {D}_3\)) one can represent the averaged stress in terms of the rod’s stress resultants. Further, it is noted that only the resulting forces \(\mathbf {n}_0\) contribute to the stresses in the macro-scale. The moments do not contribute. In the above derivations the scale-separation is assumed to be given.

In the next section use will often be made of the Piola-Kirchhoff stress, the pull-back of the Piola stress:

$$\begin{aligned} \mathbf {S}=\mathbf {F}^{-1}\mathbf {P}. \end{aligned}$$
(58)

5 Numerical results

The mechanical properties discussed in this section result from multiscale homogenization of an exemplary rod lattice, which is not directly motivated by a real-life application. However, there are countless conceivable applications requiring geometrical and material nonlinearities. Consider, for example the presented lattice as an impact absorbing meta-material in which the consideration of geometrical and material nonlinearities is crucial. The rod lattice considered here is illustrated in Fig. 3. It consists of smallest repeating unit cells with edge length 1 constructed by 8 rods coinciding with the space-diagonals of the unit cell (returning rods with length \(\displaystyle {l=\frac{\sqrt{3}}{2}}\)). The rods intersect at the barycentre of the unit cell. The structure of the unit cell is called body-centred cubic (BCC). The cross-section of the rods is circular with diameter d.

Fig. 3
figure 3

Cutout of the considered rod lattice. The smallest repeating unit (the unit cell) is highlighted in solid black. The displayed lattice consists of \(1\times 2\times 2\) unit cells

Full size image

To neglect the fact that multiple rods intersect, and therefore the stiffness at the intersection may vary from the stiffness of a single rod, we assume that the rods are thin, i.e. \(\displaystyle {\frac{l}{d}}\gg 1\).

As stated in remark 1, the elastic tangent stiffness matrix \(\mathbf {C}_0\) is assumed to be constant. The material on the cross-sectional level is modelled by a St.-Venant-Kirchhoff model. In the examples that follow the compression modulus \(\kappa \) and the shear modulus \(\mu \) are set to

$$\begin{aligned} \kappa =164.21~GPa ,\quad \mu =80.1938~GPa . \end{aligned}$$
(59)

For circular cross-sections \(\mathbf {C}_0\) takes following diagonal form

$$\begin{aligned} \mathbf {C}_0= \begin{bmatrix} \mathcal {A} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \mathcal {A} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{}\mathcal {B} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \mathcal {C} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \mathcal {C} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \mathcal {D} \end{bmatrix}, \end{aligned}$$
(60)

where \(\mathcal {A}=\mu A\) denotes the shearing stiffness and \(\mathcal {B}=E A\) the tensile stiffness. The parameters \(\mathcal {C}=EI\) and \(\mathcal {D}=\mu J\) define the bending and torsional stiffness, respectively. Further, A defines the cross-sectional area, I the planar moment of inertia and J the polar moment of inertia. The Young’s modulus is denoted by E. It is special to circular cross-sections that they do not show any coupled stiffnesses on the off-diagonals in the strain free state.

In addition to the tangent stiffness matrix, one needs an appropriately defined yield-function in terms of stress resultants to properly model inelastic rods. Obtaining such a yield-function is not trivial. Herrnböck et al. [32] is fully devoted to the development of a framework to determine yield-functions depending on the cross-sectional shape and its underlying three-dimensional constitutive relation. Here let the inelastic behaviour of the continuous rod be described by the von-Mises yield criterion

$$\begin{aligned} \varPhi ^{vM }(\varvec{\tau },q) =\Vert dev (\varvec{\tau })\Vert - \sqrt{\frac{2}{3}}\left[ \sigma _y-q\right] \le 0, \end{aligned}$$
(61)

with the Kirchhoff stress \(\varvec{\tau }\) and q being the energetic conjugate to an internal hardening variable. The yield stress \(\sigma _y\) is set to \(\sigma _y=0.45~GPa \). The introduced material parameters are taken from Simo et al. [38] and describe standard steel. Together with the circular cross-section, the following yield-function in terms of stress resultants results:

$$\begin{aligned} \begin{aligned} \varPhi (\mathbf {n}_0,\mathbf {m}_0)=&\left| \frac{n _1}{n _{1_y} -\beta _1}\right| ^\alpha +\left| \frac{n _2}{n _{2_y} -\beta _2}\right| ^\alpha \\&+\left| \frac{n _3}{n _{3_y}-\beta _3}\right| ^\gamma + \left| \frac{m _1}{m _{1_y}-\beta _4}\right| ^\delta \\&+\left| \frac{m _2}{m _{2_y}-\beta _5}\right| ^\delta +\left| \frac{m _3}{m _{3_y}-\beta _6}\right| ^\eta -1, \end{aligned} \end{aligned}$$
(62)

where the values with subscript y represent the components of the stress resultants at yield. Note that for the sake of readability the subscript 0 is omitted. The hardening-stresses are denoted by \(\beta _i\) (see Eq. 25). They result from a quadratic hardening potential

$$\begin{aligned} \mathcal {H}=\frac{1}{2}\varvec{\xi }\cdot \left[ \mathbf {H}\varvec{\xi }\right] , \end{aligned}$$
(63)

where \(\mathbf {H}\) is a \(6\times 6\) diagonal matrix with

$$\begin{aligned} {H}_{ii}=\frac{1}{10}{C}_{0_{ii}}. \end{aligned}$$
(64)

Note that nonzero hardening is favourable to ensure a stable simulation. It is shown in [32] that the stress resultants at yield can be scaled by the size of the cross-section without noticeable loss in accuracy. In the following the dimensionless exponents in equation (62) take the values \(\alpha =2.04\), \(\gamma =1.76\), \(\delta =2.09\), \(\eta =1.73\). The yield limits are set to \(n_{1_y}=n_{2_y}=0.70\theta ^2~\text {kN}\), \(n_{3_y}=1.47\theta ^2~\text {kN}\),\(m_{1_y}=m_{2_y}=0.62\theta ^3~\text {kNmm}\), \(m_{3_y}=0.56\theta ^3~\text {kNmm}\). The dimensionless scaling ratio is given by \(\displaystyle {\theta :=\frac{d}{\left[ \text {mm}\right] }}\).

In the following examples, the mechanical response of the RVE undergoing small macroscopic strains (\(\varepsilon <5\%\)) will be investigated. The examples will demonstrate that, despite assuming moderate strains on the macro-scale, the deformation in the RVE can be large and geometric nonlinearities as well as structural instabilities may appear. The presented results follow from an RVE subjected to periodic boundary conditions.

The aim of this section is to find out if the mechanical response shows a dependency on the number of unit cells constituting the RVE and to find the smallest RVE whose mechanical response is no more sensitive to the RVE’s size. Therefore, the size of the RVE is varied. A parameter \(n_{RVE }\) is introduced that describes how many unit cells the RVE consists of. Choosing \(n_{RVE } =2\) results in a single repetition of the unit cell in every space direction. Thus, instead of one single unit cell, the RVE consists of \(\displaystyle {n_{RVE } ^3}\) unit cells (assuming three-dimensional space).

Remark 2

Prescribing a macroscopic deformation to an RVE consisting of thin rods may lead to structural instabilities on the microscopic level, i.e. buckling and bifurcation points may occur. To capture bifurcation points and to follow the energetically favourable post-bifurcation path methods as presented in [39,40,41] are used. The bifurcation point is searched by an eigenvalue-analysis of the RVE’s stiffness matrix. At the instability point the solution is perturbed by the eigenvector corresponding to the smallest eigenvalue. This method ensures that the exact buckling load is found and that the deformation chooses the energetically favourable secondary path. However, this approach is expensive, since an eigenvalue problem must be solved. When considering RVEs of large size (\(n_{RVE } >2\)) a different approach is used. To capture the favourable secondary path the undeformed configuration of the lattice is slightly perturbed by a linear combination of buckling modes [2, 14]. The perturbed lattice does no longer face any structural instabilities. The search of the exact instability point and the correct secondary path is no longer necessary and no longer possible. This approach may be motivated by imperfections in the lattice. If the perturbation is small enough the lattice approaches the behaviour of a perfect lattice without any imperfection.

5.1 Stiffness of RVE at zero strain

Before analysing the mechanical response of the RVE subjected to uniaxial strains, its stiffness at zero strain is briefly discussed with the help of the Young’s modulus surface [42]. To numerically evaluate the stiffness matrix perturbation techniques such as those presented in Miehe et al. [43] are applied. Figure 4 displays the normalised Young’s modulus surface of the introduced rod lattice with varying cross-section’s diameter d. The Young’s modulus surface visualises the direction dependency of the Young’s modulus.

Fig. 4
figure 4

Normalised Young’s modulus surface of the introduced lattice. Independent on d, orthotropic behaviour is discernible. For small d the Young’s modulus in \(\mathbf {E}_i\) direction is negligible. It, however, increases with d

Full size image

The Young’s modulus surfaces for BCC lattices are well known from literature [44, 45]. Their interpretation is recaptured as follows. Independent of d the behaviour of the homogenized lattice is orthotropic. Leaving magnitudes of the Young’s modulus E aside, one notices differences in the surfaces for increasing d. While E is almost negligible in all directions except the space diagonals for \(d=0.035\), higher values of d show less extreme distributions of E. The reason, therefore, lies in the loading of the rods in the micro-scale resulting from the macroscopic deformation. When the RVE is strained in the \(\mathbf {E}_i\) direction the rod á priori bends microscopically. Macroscopic loading in space diagonal direction leads to tensile loading of the rods in the micro-scale. For small d rods with circular cross-section show much smaller bending stiffness than tensile stiffness. This leads to the displayed extreme distribution of E. With increasing magnitude of d the magnitude of tensile and bending stiffness approach each other. The differences in E are less pronounced.

In the following examples, the maximum value for d is chosen to be \(d=0.08~mm \). Thus, the requirement \(\displaystyle {\frac{l}{d}}\gg 1\) is still satisfied.

5.2 Uniaxial tension

In this section the mechanical response of the RVE subjected to uniaxial tension is considered. Let the macroscopic deformation gradient be

$$\begin{aligned} \mathbf {F}^M\widehat{=}\begin{bmatrix} 1+\lambda &{} 0 &{} 0\\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$
(65)

with the load parameter \(\lambda \). In the following the tensile component of the Piola-Kirchhoff stress \(S_{11}\) is plotted as a function of \(\lambda \). The purely elastic case as well as the inelastic case is considered. Furthermore, the curves are shown for different diameters d of the rod’s cross-section resulting in different stiffnesses. Since the course of the curves is qualitatively identical for varying d the stress-strain relation is only represented for few values of d in Fig. 5.

Fig. 5
figure 5

Tensile stress \(S_{11}\) as a function of the load parameter \(\lambda \) for uniaxial tension. For the purely elastic case a linear relation of \(S_{11}\) and \(\lambda \) is visible. The inelastic cases show a sudden decrease in stiffness at the beginning of yield. No difference in the result is visible for different values of \(n_{RVE }\)

Full size image

All plots in figure 5 depict a linear relation of \(S_{11}\) and \(\lambda \) in the elastic region. For the inelastic cases (dotted lines) the start of yield is sudden and a considerable loss in stiffness is clearly visible. The results differ quantitatively but not qualitatively with respect to the rod’s cross-sectional dimension. The present load case does not result in any structural instabilities. Further, the size of the RVE (parametrized by \(n_{RVE } =1,~4,~6\)) does not affect the results. It is evident, but still mentioned for completeness, that the homogenized tensile stress \(S_{11}\) increases with increasing cross-sectional diameter d.

We now investigate the onset of yield in terms of the rod’s diameter d and the RVE’s size \(n_{RVE }\) (for sake of visibility we choose \(n_{RVE } =1,~4,~6\)). Therefore, the load parameter \(\lambda \) at yield is visualised as a function of d in Fig. 6.

Fig. 6
figure 6

Onset of yield as a function of the rod’s diameter d for uniaxial tension. The tensile load parameter \(\lambda \) leading to yield is independent of d and \(n_{RVE } \). The tensile stress \(S_{11}\) at yield increases with d

Full size image

Here, it occurs that onset of yield (subsequently marked by a cross) is not a function of the rod’s diameter d for the case of uniaxial tension. The structure begins yielding at very small values of \(\lambda \) (less than 0.01). In this state the structure has not yet largely deformed. Considering the tensile stress \(S_{11}\) at the onset of yield one observes a nonlinear increase (quadratic in d). Since the case of uniaxial tension does not show any instability in the structure the shown plots do not reveal any dependency on \(n_{RVE }\), which can be regarded as a validation of the homogenization framework. An RVE consisting of only one unit cell is sufficient to show the macroscopic material behaviour for the case of uniaxial tension.

5.3 RVE under compression

The case of uniaxial compression yields more noteworthy results. This is due to the appearance of buckling. It is possible to subdivide the deformation state into a pre- and post-buckling region. The macroscopic deformation gradient is set to

$$\begin{aligned} \mathbf {F}^M\widehat{=} \left[ \begin{array}{ccc} 1-\lambda &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right] , \end{aligned}$$
(66)

with \(\displaystyle {\lambda \in ] 0,1 ]}\). Figure 7 displays \(S_{11}\) as a function of \(\lambda \) for the purely elastic case. Further, the number of unit cells within the RVE is varied. In all curves, one can discern a kink in \(S_{11}\). At this point the RVE shows a structural instability. Further loading leads to buckling of the structure and tremendous loss in stiffness. The onset of buckling varies with the cross-sectional diameter d. With increasing d both the compressive stress, and the loading parameter \(\lambda \) at buckling increases. In contrast to tensile loading, the size of the RVE (parametrized by \(n_{RVE }\)) clearly impacts the simulation outcome. However, with increasing \(n_{RVE } \) the discrepancy between the curves reduces and reaches a converged state for \(n_{RVE } =6\). In the pre-buckled region \(n_{RVE }\) does not show any influence on the results.

Fig. 7
figure 7

Compressive stress \(S_{11}\) as a function of the load parameter \(\lambda \) for purely elastic uniaxial compression. First an increase in \(S_{11}\) is visible. Then, instantaneously \(S_{11}\) remains nearly constant. The structure is buckling and can not support more load. The strain at buckling differs for different cross-sectional diameters d. In general, for increasing \(n_{RVE } \), \(\lambda \) and the corresponding stress \(S_{11}\) at buckling decreases and finally converges to a constant value

Full size image

A more complex course of \(S_{11}\) with respect to \(\lambda \) stands out for the inelastic case in Fig. 8. Here the lattice not only undergoes buckling but also starts yielding. Both the onset of buckling as well as the onset of yield are dependent on the cross-sectional size. For thin rods \((\approx d<0.05)\) the structure first buckles and starts yielding afterwards. Thicker rods show the opposite tendency. There the material first yields and the structure buckles afterwards. However this observation is also strongly dependent on \(n_{RVE } \). Throughout all cases the stiffness strongly changes when passing the onset of yield and the onset of buckling. With increasing \(n_{RVE } \) a converged state is reached. For \(n_{RVE } =6\) a sensitivity towards the RVE’s size is no longer discernible. Thus, the smallest RVE able to return the homogenized properties for the case of uniaxial compression consists of \(6\times 6\times 6=216\) unit cells. This applies both for the elastic and inelastic case. Recall that for \(n_{RVE } \le 2\) the undeformed lattice has no imperfections, whereas for \(n_{RVE } >2\) the undeformed lattice is slightly perturbed enabling buckling (see remark 2). In perfect lattices the plastification propagates simultaneously throughout the lattice. In perturbed lattices, the plastification may begin locally in the lattice. One have to be aware that this may influence the mechanical response of the lattice, for instance by showing a smoother transition between the elastic and plastic region.

Fig. 8
figure 8

Compressive stress \(S_{11}\) as a function of the load parameter \(\lambda \) for inelastic uniaxial compression. First a linear relation between \(S_{11}\) and \(\lambda \) is visible. Then different courses depending on d and \(n_{RVE }\) get obvious. Depending on these two parameters, the structure may yield in the pre- or post-buckled state. Simultaneous buckling and yielding is also possible

Full size image

Figure 9 shows the load parameter \(\lambda \) at onset of buckling and yield and the corresponding compressive stress \(S_{11}\) as a function of the cross-sectional diameter d for different \(n_{RVE } \). For sake of visibility, here we choose \(n_{RVE } =1,~2,~4,~6\). The values of \(\lambda \) and \(S_{11}\) at buckling and yield reveals the following. The onset of buckling (marked by a circle) clearly shows a dependency on d and \(n_{RVE } \). The load parameter \(\lambda \) at buckling increases with d but decreases with \(n_{RVE } \). Besides this, \(S_{11}\) at onset of buckling and yield decrease with increasing \(n_{RVE }\).

Fig. 9
figure 9

Onset of buckling and yield and corresponding compressive stress as a function of the rod’s diameter d for uniaxial compression. The load parameter and its respective stress at onset of buckling are marked by a circle. The values at onset of yield are marked by a cross. Three distinct cases get obvious. In the first case the structure yields in the pre-buckled state. The second case is characterized by yield in the post-buckled state. Finally in the third case buckling and yield take place simultaneously. The onset of buckling and yield shows dependencies of d and \(n_{RVE } \)

Full size image

To further discuss the results, the following distinct cases are introduced. In the first case, the compressive load parameter at onset of yield is smaller than the load parameter at onset of buckling, that is, the structure yields in the pre-buckled state (e.g. \(d=0.07\text {mm}\), \(n_{RVE } =1\)). The second case is characterized by yielding in the post-buckled state (e.g. \(d=0.035\text {mm}\), \(n_{RVE } =1\)). A third case is introduced, where buckling and yield takes place simultaneously (e.g. \(d=0.07\text {mm}\), \(n_{RVE } =6\)). It strongly depends on d and \(n_{RVE }\) which case applies. The appearing case also impacts the resulting stresses at yield and buckling. Finally, let us state here that with increasing \(n_{RVE }\) the third case gains in relevance: buckling and yield take place simultaneously. These relations get visible in Fig. 8, too.

To give the reader an impression of how the lattice deforms we depict the deformed configuration of the compressed RVE (\(\lambda =0.05\)) in Fig. 10 for both \(n_{RVE } =1\) and \(n_{RVE } =2\). In particular, we choose \(d=0.035\) and an elastoplastic constitutive behaviour. For the sake of better visibility the deformation is shown in two orientations (in the planar view the periodic boundary of the RVE is approximated by dashed lines).

Fig. 10
figure 10

Buckled configuration of an RVE with \(n_{RVE } =1\) and\(n_{RVE } =2\), respectively, subjected to uniaxial compression. Despite moderate macroscopic deformation, the displacements and rotations on the constituting rods is remarkable large. Furthermore, the unit cells do not deform equally when \(n_{RVE } =1\) or \(n_{RVE } =2\)

Full size image

Even with moderate prescribed macroscopic deformation the deformation and rotation of the constituting rods are large. Additionally, it is visible that the deformation of the unit cells varies for \(n_{RVE } =1\) and \(n_{RVE } =2\) (the planar view clearly displays this phenomenon). The rods in the RVE buckle in a wave-like manner. The wavelength of the buckled rods in the RVE with \(n_{RVE } =1\) is half the wavelength of the rods in the RVE with \(n_{RVE } =2\), which results into a higher curvature of the rods for \(n_{RVE } =1\) than for \(n_{RVE } =2\). The observation is made that the prescribed load case results in a micro-buckling wavelength which is dependent on the RVE’s size.

In Fig. 11 it is shown that despite a significant difference in the mechanical response there are hardly any variations to be seen in the deformed configurations of the RVE when considering elastic or inelastic material: the only visible difference is the slightly smoother bending of the rods for the elastic case, compared to the inelastic case. To make the plastified regions of the rods visible the norm of the plastic curvature \(\displaystyle {\Vert \mathbf {k}_0^p\Vert }\) is coloured. It is obvious that no plastified regions appear when assuming purely elastic material. When considering inelastic material the plastified regions concentrate on the most bent regions of the rod. The location of these regions depends on the choice of \(n_{RVE } \). The highest plastic curvature lies in the middle of each rod for \(n_{RVE } =1\), while for \(n_{RVE } =2\) most plastification takes place at the joints.

Fig. 11
figure 11

Comparison of buckled configurations of uniaxially compressed RVEs with \(n_{RVE } =1\) and \(n_{RVE } =2\) under consideration of elastic and elastoplastic constitutive behaviour, respectively. The magnitude of plastic curvature \(\displaystyle {\Vert \mathbf {k}_0^p\Vert }\) is coloured. The elastoplastic deformation is slightly less smooth than it is the case for the elastic case. The plastified regions differ when \(n_{RVE } =1\) or \(n_{RVE } =2\)

Full size image

5.4 RVE under shear

Finally, the RVE undergoes uniaxial shear. The macroscopic deformation gradient is given by

$$\begin{aligned} \mathbf {F}^M\widehat{=}\begin{bmatrix} 1 &{} \lambda &{} 0\\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{bmatrix}. \end{aligned}$$
(67)

In analogy to the case of uniaxial compression, shear may lead to buckling in the micro structure. The shearing stress component \(S_{12}\) is presented as a function of \(\lambda \) for the purely elastic case in Fig. 12. In analogy to the case of uniaxial compression one detects a kink in \(S_{12}\). This point denotes the start of buckling. The change in stiffness is less pronounced than for the case of uniaxial compression. This results from the fact that under shear some rods in the RVE are loaded in the tensile direction. These rods do not buckle. Whereas for the case of uniaxial compression all rods are loaded compressively, which leads to buckling in all of them. The onset of buckling is both a function of the rod’s cross-sectional dimension d and of the RVE’s size (parametrized by \(n_{RVE }\)). However, here the curves already converge for \(n_{RVE } = 2\). This is in contrast to the case of uniaxial compression, where convergence is only reached for \(n_{RVE } =6\).

Fig. 12
figure 12

Shearing stress \(S_{12}\) as a function of the load parameter \(\lambda \) for purely elastic uniaxial shear. \(S_{12}\) increases with a kink. There, the lattice buckles. Besides a dependency on d the onset of buckling also shows a dependency on \(n_{RVE } \). However, in contrast to the case of elastic uniaxial compression, the results already converge for \(n_{RVE } =2\)

Full size image

Let us now consider the case of uniaxial elastoplastic shear in Fig. 13. Again, \(S_{12}\) is displayed as a function of the load parameter \(\lambda \) for different d and \(n_{RVE } \). The curves reveal two kinks that are more or less pronounced. One kink denotes the buckling at the structural instability. A second kink denotes the onset of yield within the underlying rods. In analogy to the case discussed in Sect. 5.3 yield may take place in the pre- or post-buckled region.

Fig. 13
figure 13

Shearing stress \(S_{12}\) as a function of the load parameter \(\lambda \) for inelastic uniaxial shear. Besides a dependency on d the onset of buckling and yield also shows a dependency on \(n_{RVE } \). In contrast to the purely elastic case, convergence is reached for \(n_{RVE } =6\)

Full size image

The plastified structure shows a considerably lower stiffness than the elastic structure. Compared to the purely elastic case (Fig. 12) convergence is only attained for \(n_{RVE } =6\). Thus, the smallest RVE able to show the homogenized properties resulting uniaxial shear consists of \(6\times 6\times 6=216\) unit cells.

Figure 14 depicts the load parameter \(\lambda \) and its corresponding shear stress \(S_{12}\) at onset of buckling (marked by a circle) and yield (marked by a cross) as a function of d. Again, for sake of visibility we restrict ourselves to four different values for \(n_{RVE }\). In analogy to the case of uniaxial compression, the load parameter \(\lambda \) at onset of buckling shows a strong dependency on both d and \(n_{RVE }\). The shearing load at buckling increases with d and decreases with \(n_{RVE }\). With increasing \(n_{RVE } \) the stress at both onset of yield and buckling decreases. Three distinct cases are introduced: pre-buckled yield, post-buckled yield and simultaneous yield and buckling. As for the case of uniaxial compression the first case is defined in that the load parameter \(\lambda \) at buckling is higher than the shear at yield (e.g. \(d=0.05\), \(n_{RVE } =1\)). In the second case this relation is opposite (e.g. \(d=0.035\), \(n_{RVE } =1\)). In the third case both values coincide (eg. \(d=0.07\), \(n_{RVE } =6\)). The choice of d and \(n_{RVE }\) impacts the appearing case.

Fig. 14
figure 14

Onset of buckling and yield and corresponding shear stress \(S_{12}\) as a function of the rod’s diameter d for uniaxial shear. The load parameter and its respective shear stress at onset of buckling are marked by a circle. The values at yield are denoted by a cross. Three distinct cases get obvious: pre-buckled yield, post-buckled yield and simultaneous yield and buckling. Onset of yield and buckling depends both on d and \(n_{RVE } \)

Full size image

5.5 The inluence of \(n_{RVE }\)

The results shown in previous sections revealed that the homogenized properties of the RVE are dependent on the number of unit cells within the RVE, i.e., the size of the RVE (parametrized by \(n_{RVE } \)). This dependency only appears if the RVE faces structural instabilities. The homogenized response in the pre-buckled state is independent of \(n_{RVE } \). The same occurs for load cases that do not lead to buckling, such as uniaxial tension. There the results do not depend on \(n_{RVE } \). These findings are consistent with those in [15, 17, 41, 46]. One can conclude from this that the choice of an appropriate number of unit cells within the RVE is of critical importance for the determination of macroscopic mechanical properties. Recalling Fig. 10 possible reasons for this phenomenon may be revealed. As already discussed for the case of uniaxial compression, micro-buckling wavelengths, which are dependent on the RVE’s size appear. The larger the RVE, the larger the wavelength. It can now be deduced that due to lower curvature the stored bending energy in high wavelength is less than in small wavelengths. Thus, buckling in high wavelengths takes place at lower stress and strain level. The reason for different wavelengths in different RVEs is that the prescribed periodic boundary conditions force the buckling wavelength to fit into the size of the RVE.

By increasing the RVE’s size, convergence in the homogenized properties may be reached. This brings up the following train of thoughts. The presented homogenization framework requires that the scale-separation (34) must be fulfilled. This means that the scale of the macro-problem must be larger than the scale of the micro-problem. It has been shown that here the homogenized properties of the micro-problem converge for \(n_{RVE } \ge 6\), which is now defined as the smallest possible size the RVE must take to show no more sensitivity towards \(n_{RVE } \). This RVE can be used to derive a material model for the meta-material in a sequential homogenization framework. Alternatively it may be used in a concurrent homogenization framework such as in the \(FE ^2\) method. Then one must make sure that the size of the macroscopic problem is significantly larger than the size of the RVE, which means that the macro-problem must consist of way more that \(6\times 6\times 6\) unit cells. Especially in applications emerging from additive manufacturing this may not be the case. In this case, the use of an RVE with \(n_{RVE } =6\) would lead to the violation of scale-separation. Resolving the whole macro-structure with fully nonlinear beam elements may be a convenient alternative.

6 Summary

This contribution introduces a multiscale homogenization framework combining well known three-dimensional continuum mechanics on the macro-scale with geometrically exact elastoplastic rods on the micro-scale. This framework allows the modelling of lattice micro-structures undergoing large deformations. Additionally, the theory of geometrically exact rods has been presented briefly for both the elastic and the inelastic case. A multiscale homogenization framework was deduced from its well established three-dimensional setting. Considering the example of a specific rod lattice homogenized mechanical response for the cases of uniaxial tension, compression and shear were analysed with respect to varying cross-sectional dimension d and RVE’s size. The results clearly demonstrated the appearance of particular properties resulting from the slender character of the rod structure: the appearance of structural instabilities (buckling) and yield. The influence of the rod’s dimension and the RVE’s size on its homogenized properties were discussed in a comprehensive way.

The results and findings of this work will be used to drive further research. In this work rods without imperfections were considered. However, this is by no means representative of practical applications. For example in the field of additive manufacturing imperfections are present in the lattice. Thus, the implementation of such shall be included in future work. These may be included for example by perturbing the geometry of the lattice (as done in Sect. 5.5 to obtain a buckled configuration), tapering the underlying rods, or by considering heterogeneous properties in the rod’s cross-section. A method which would also consider the imperfections appearing during the manufacturing process is to resolve the crystalline structure and therein spatially varying material properties of the cross-section. Imperfections in the crystalline structure would then manifest as changes of the rod’s stiffness and inelastic behaviour. This would, of course, require the modelling of crystal plasticity within the cross-sectional level.

The presented homogenization framework can be used to derive an effective constitutive model for different lattice structures by fitting the parameters of an appropriate material model to the data of uniaxial and biaxial strain states or by setting up an artificial neuronal network (as demonstrated in [14]). Additionally, the consideration of inelastic behaviour allows one to find an effective yield-surface. Strategies to do so are presented in [32]. If one is not interested in a sequential but concurrent homogenization the \(\text {FE}^2\) method is a promising but expensive tool. Regardless of the chosen method (sequentially or concurrent), first the right size of the RVE must be investigated to make sure that the homogenized mechanical response does not show dependencies on the RVE’s size. Further the assumption of scale-separation must be preserved. That means that the macro-scale must be a lot larger than the micro-scale. If this is not the case, the lattice shall better be fully resolved.