Introducing regularization into the virtual fields method (VFM) to identify nonhomogeneous elastic property distributions

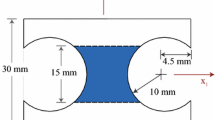
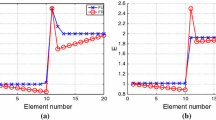
Abstract

The identification of nonhomogeneous elastic property distributions has been traditionally achieved with well acknowledged optimization based inverse approaches, but when full-field displacement measurements are available, the virtual fields method (VFM) can be computationally more efficient by converting the large-scale optimization problem into multiple small-scale optimization problems. A possible downside of the VFM so far was not to take into account prior knowledge, which is often available and needed when there is a very large number of unknowns and the inverse problem is ill-posed. In this work, different approaches are proposed for introducing regularization into the VFM, aiming to penalize the local variations of identified stiffness properties in order to reduce the effects of uncertainty in the inverse problem resolution. The feasibility and accuracy of the regularized VFM are tested through several numerical and experimental datasets. It is shown that the main advantage of the novel VFM approaches is the low computational cost, as large-scale inverse problems with 10,000 unknown parameters can be solved within several seconds using a standard personal computer. Although the regularized VFM can successfully detect a stiff inclusion in a soft solid with high accuracy, regularization also introduces unexpected spurious effects in the results, blurring the interface between soft and stiff regions. We also observed that the regularization did not improve the smoothness significantly due to local effects of the small-scale optimization problem introduced in the proposed VFM method. Therefore, traditional regularization, which penalizes local variations of identified stiffness properties, can be combined with the VFM to solve inverse problems with a high computational efficiency, but supplemental regularization conditions will need to be adapted in the future to better delineate soft-stiff interfaces with this methodology.

Appendix

Without loss of generality, a discretized two-dimensional domain is considered and two neighboring elements A and B are arbitrarily selected for analysis as shown in Fig. 21a. The corresponding values of Young’s modulus for element A and B are set to $E_{A}$ and $E_{B}$, respectively. A local coordinate system is introduced where the directions of the two coordinate axes s and t are along the interface between these two neighboring elements and perpendicular to it, respectively. The relationship between the s-t coordinates and Cartesian coordinates is shown in Fig. 21b. The local coordinates are defined as the axes obtained by rotating the Cartesian coordinates by an angle θ. As the material property distribution is discontinuous in the domain of interest, the material properties are assumed to be constant over every element to preserve the discontinuous transition well. In this case, Young’s modulus does not vary along the interface, i.e. $\partial E/\partial s = 0$. Therefore, the Young’s modulus depends only on the variable t. Recall the continuous form of the TVD regularization formulation can be expressed as:

$${\text{Reg}}_{AB} = \int\limits_{{\Omega_{A} \cup \Omega_{B} }} {\sqrt {\left| {\nabla E} \right|^{2} } } dxdy$$

(19)

Fig. 21

a Two arbitrary elements in the domain; b the coordinate transformation

According to the rules of coordinate transformation, Eq. (19) can be rewritten in terms of s and t, which is:

$${\text{Reg}}_{AB} = \int\limits_{{\Omega_{A} \cup \Omega_{B} }} {\left| {\frac{\partial E}{{\partial t}}} \right|} dsdt = l\left| {\frac{\partial E}{{\partial t}}} \right|$$

(20)

To satisfy Eq. (20), the condition, $\partial E/\partial s = 0$, is utilized. And based upon jump conditions, the TVD formulation can be further reduced to:

$${\text{Reg}}_{AB} = l_{AB} \left| {E_{A} - E_{B} } \right|$$

(21)

where l_AB is the length of the interface between the element A and B. It can be seen in Eq. (21) that the discrete TVD regularization is linearly proportional to the difference in the shear modulus between neighboring elements and the length of the interface. So the regularization term reduces to just Eq. (21) since element-wise constant distribution of the shear modulus is assumed.