Adaptive numerical integration of exponential finite elements for a phase field fracture model

Abstract

Phase field models for fracture are energy-based and employ a continuous field variable, the phase field, to indicate cracks. The width of the transition zone of this field variable between damaged and intact regions is controlled by a regularization parameter. Narrow transition zones are required for a good approximation of the fracture energy which involves steep gradients of the phase field. This demands a high mesh density in finite element simulations if 4-node elements with standard bilinear shape functions are used. In order to improve the quality of the results with coarser meshes, exponential shape functions derived from the analytic solution of the 1D model are introduced for the discretization of the phase field variable. Compared to the bilinear shape functions these special shape functions allow for a better approximation of the fracture field. Unfortunately, lower-order Gauss-Legendre quadrature schemes, which are sufficiently accurate for the integration of bilinear shape functions, are not sufficient for an accurate integration of the exponential shape functions. Therefore in this work, the numerical accuracy of higher-order Gauss-Legendre formulas and a double exponential formula for numerical integration is analyzed.

1 Introduction

From an engineering stand point, the prediction of structural failures is a challenging task, due to the complexity of the phenomena that influence the process on different scales. One promising approach is the phase field method, in which a continuous approximation of cracks simplifies the mathematical treatment of numerical fracture analysis, [1, 2]. The research topic of fracture phase field models has been expanded for dynamic [3,4,5] and ductile [6,7,8] fracture to name a few research directions. The present work is essentially based on [9]. The model in [9] describes the integrity of a continuum by an order parameter, which is implemented as an 1D degree of freedom. Two values of the parameter can be associated with a physical interpretation, 1 as intact and 0 as broken. The surface of cracks is represented by the volume integral of the transition zone between 0 and 1 with a continuous course and high gradients. Though cracks are sharp in reality, this approximation can be sufficient for relatively narrow transition zones. The width of cracks can be controlled by a regularization parameter $\epsilon$. The smaller the value of $\epsilon$, the higher the gradients of the phase field become. In a finite element model with standard linear shape functions, a high mesh density is required to approximate these high gradients. This increases the computing time.

There are many approaches for the implementation of fine spatial resolutions in the context of a phase field model for fractures such as mesh adaptivity [10] and hp-FEM [11]. The technique, discussed in this paper, is based on the work presented by Kuhn and Müller, [12]. They implemented exponential shape functions for the phase field with a behaviour similar to the analytical solution of a crack for the 1D problem. In test cases, finite elements with a linearly interpolated displacement field and an exponentially interpolated fracture field have proven to be very efficient and can approximate thin cracks with a coarse discretization rather accurately. Unfortunately, the lower effort in the discretization requires other expenses like e.g. a more extensive numerical integration. On the one hand the standard linear finite elements are relatively inexpensive with regard to numerical integration, because of the low number of quadrature points, which are required for an appropriate integration. On the other hand the exponential elements approximate fractures more accurate with far less elements, but need an adjusted integration scheme. This adjustment is analyzed in the present study.

While in general the majority of a fractured body remains undamaged, i.e. shows a constant phase field value of 1, the regions with high gradients are usually concentrated in a limited part of the specimen. Therefore adaptive refinement techniques are of special interest. Some example for adaptive refinement in fracture phase field simulations can be found in [11, 13], but unlike the h- or hp-refinement, which is presented in [11, 13], the proposed approach is of a different character. In this work, the adaptive routine will be used to reduce unnecessary integration effort for shape functions that are able to approximate extreme steep gradients. In order for the method to remain computationally efficient, the quadrature method will be chosen in dependence of the local gradient of the phase field.

2 Phase field modeling of brittle fracture

The regularized phase field model for brittle fracture includes two energy densities, the surface energy density $\psi ^{\text {s}}$ and the elastic energy density $\psi ^{\text {e}}$. Both depend quadratically on the fracture field s, introduced as an order parameter of the material integrity. The surface energy also depends on the gradient ($\nabla s$). The material behaviour is described by the linear elasticity tensor $\mathbb {C}$ and the cracking resistance $\mathscr {G}_c$ as well as parameters $\eta$ and $\epsilon$. The equation of the total energy density is

$$\begin{aligned} \psi (\pmb {\varepsilon } , s)= & {} \underbrace{\dfrac{1}{2} (s^2 + \eta ) \pmb {\varepsilon } : [ {\mathbb {C}} \pmb {\varepsilon }]}_{\psi ^{\text {e}}(\pmb {\varepsilon } , s)} + \underbrace{\mathscr {G}_c \left( \dfrac{(1-s)^2}{4\epsilon } + \epsilon |\nabla s|^2\right) }_{\psi ^{\text {s}}(s)}. \end{aligned}$$

(1)

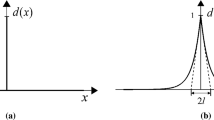
As primary fields in the domain $\varOmega$ we consider the displacements $\pmb {u}$, which affect the energy density via the linearized strain tensor $\pmb {\varepsilon }=\tfrac{1}{2}(\nabla \pmb {u}+\nabla ^{T}\pmb {u})$, and the phase field variable s. The boundary conditions on the boundary are $\partial \varOmega _t$ set for the loads ($\pmb {\sigma } \mathbf {n} = \mathbf {t}^{\,*}$) and an $\partial \varOmega _u$ for the displacements ($\mathbf {u} = \mathbf {u}^{\,*}$). The geometrically important parameter for a sufficient approximation of cracks is $\epsilon$. It controls the width of the continuous representation of cracks, see Fig. 1.

Fig. 1

Approximation of a crack by an phase field variable s

In essence, the energy density $\psi$ is based on Griffith’s theory of fracture, which states that the energy that is consumed by an increase of the crack surface must be balanced by the released elastic energy during crack growth. In addition, the elastic energy density contains the parameter $\eta$ for numerical stabilization to ensure a minimal stiffness in case of a total rupture. The first field equation that is included in the model is the balance of momentum

$$\begin{aligned} {\mathrm{div}}\, {\sigma }= {\mathsf {0}} . \end{aligned}$$

(2)

Due to the limitation to stationary problems and neglecting body forces, the divergence of the Cauchy stress tensor ${\sigma }$ is zero.

In order to describe the rate of the fracture field consistent with Griffiths theory of fracture, an evolution equation of Ginzburg and Landau type

$$\begin{aligned} \dot{s} = -M \dfrac{\delta \psi }{\delta s} = -M \left[ s \pmb {\varepsilon } [ {\mathbb {C}} \pmb {\varepsilon }] - \mathscr {G}_c \left( 2 \epsilon \, \nabla s + \dfrac{1-s}{2\epsilon }\right) \right] \end{aligned}$$

(3)

is used, see e.g. [14].

Hereby, the symbol “$\delta$” denotes the variational derivative in this equation. This means, that the rate $\dot{s}$ requires the variational derivative of the total energy density. Another quantity is the mobility parameter M, which controls the rate of the phase field and the dissipation in the process zone [14]. For the quasistatic analysis of Griffith-like fracture problems the value M has to be sufficiently large, see [12].

At last, an irreversibility condition needs be implemented. There are two major approaches to prevent crack healing in phase field models that are extensively used in the literature. On the one hand, a Dirichlet boundary condition can be imposed once s reaches 0, or on the other hand, a negative sign of the phase field time derivate $\dot{s}<0$ can be enforced. In the following work we apply a Dirichlet boundary condition, see e.g. [14] for details.

3 Exponential shape functions

The approximation of cracks with a phase field model requires narrow transition zones, in order to represent a fractured elastic body accurately. Due to the high gradients arising at crack surfaces, a fine discretization is necessary for a sufficient approximation of these gradients and the surface energy. This leads to a higher computational effort.

Fig. 2

Analytical 1D solution of a stationary crack

In order to approximate cracks without a very fine discretization, Kuhn and Müller [12] introduced exponential shape functions to approximate the phase field variable. The choice of the exponential functions as shape functions for the fracture phase field is motivated by the analytical solution for a fractured 1D bar, see Fig. 2.

The 1D linear and exponential shape functions are defined as functions of the natural coordinate $\xi \in [-1,1]$, see Fig. 3 . They are defined as

$$\begin{aligned}&N^{\text { lin}}_{1}(\xi ) = \frac{1}{2}(1-\xi ),\\&N^{\text { lin}}_2(\xi ) = \frac{1}{2}(1+\xi )\,{ \quad \quad \text {and}} \\&N^{\text { exp}}_1(\xi ,\delta ) = 1-\frac{\exp \left( -\delta (1+\xi )/4\right) -1}{\exp \left( -\delta /2\right) -1},\\&N^{\text {exp}}_2(\xi ,\delta ) = {0 +} \frac{\exp \left( -\delta (1+\xi )/4\right) -1}{\exp \left( -\delta /2\right) -1}.\\ \end{aligned}$$

Fig. 3

a Linear and b exponential shape functions ($\delta = 10$) for an 1D element with two nodes

The exponential shape functions are parametrized by $\delta \, = \, h/\epsilon$ in order to capture the typical 1D solution accurately. In the following, $\delta$ keeps the notation as the coefficient for the exponential shape function and shouldn’t be confused with the variational symbol. The applicability of 1D exponential shape functions is verified by an approximation of the analytical solution of a stationary crack displayed in Fig. 2. The analytical solution is derived from the $\psi ^S$ of Eq. (3) with the boundary conditions $s'(\pm 1) = 0$ and $s(0)=0$ in the domain $x \in [-1,1]$. Due to the stationary approximation of a crack the displacement field becomes irrelevant.

In comparison to the linear shape functions, the exponential functions can describe the diffuse 1D crack surface more efficiently, see Fig. 4. The graph displays the numerical solutions for a stationary one dimensional phase field with a crack at x $=$ 0, defined by the Dirichlet boundary condition $s(0)=0$ for different choices of shape functions. The displacement field is zero and can therefore be neglected.

Fig. 4

Fracture field s for an 1D body with a stationary crack at $x=0$

In order to obtain the exponential shape functions for the analysis of two- or three-dimensional problems, the 1D shape functions can simply be composed, by tensor products as described in [10] for Lagrange elements. Thereby, the linear combination of these 1D shape functions are combined for different spatial coordinates and the consideration of the allocation of the 1D nodal shape function to the 2D or 3D node in dependence of the adjoining edges. In this regard, the exponential shape functions need particular attention, because the element edge lengths in the shape functions need to be consistent, see e.g. [12]. The advantage of the exponential elements is the good approximation of steep gradients even for low mesh densities. Unfortunately there are some drawbacks. The major problem is that elements have to be “oriented” properly. Due to the unsymmetry of the exponential shape functions, the fracture field s would also be incorrectly unsymmetrical if the shape functions are not oriented properly. This deficiency can be resolved by an adaptive reorientation of the local coordinates according to the nodal values of s if necessary, see e.g. [12]. As an example this simple technique is indicated in Fig. 4. The orientation of the elements in the spatial domain x < 0 is illustrated by the orientation of the triangles (normal orientation: $\triangleright$, reversed orientation: $\triangleleft$).

3.1 Finite element discretization

In order to employ the finite element method to numerically solve a phase field fracture problem, we have to derive the weak forms of (2) and (3). The approximation of actual and virtual fields of the displacement and crack state is done via $C_0$ continuous shape functions, which were introduced before. Further details are given in [14]. The global system can be described in form of a residual $\underline{{\mathsf {R}}}$ by the equation

$$\begin{aligned} \underline{{\mathsf {R}}} = \underline{{\mathsf {F}}} - \underline{{\mathsf {P}}}(\underline{{\mathsf {d}}},\underline{\dot{{\mathsf {d}}}}) = \underline{{\mathsf {0}}} , \end{aligned}$$

with the external and internal forces $\underline{{\mathsf {F}}}$ and $\underline{{\mathsf {P}}}$. The variables are the degrees of freedom $\underline{{\mathsf {d}}}$ (nodal displacement $\underline{{\mathsf {u}}}$ and fracture field $\underline{{\mathsf {s}}}$) and their time derivatives $\underline{\dot{{\mathsf {d}}}}$. The spatial discretization is performed by standard quadrilateral elements with bilinear shape functions for the displacement field. However, the phase field is approximated with special shape functions of exponential characteristic. Time discretization by the backward Euler scheme yields a non-linear system for which an incremental solutions is used by a Newton-Raphson method. It uses the linearized system

$$\begin{aligned} {\underline{{\mathsf {0}}}} = {\underline{{\mathsf {R}}}} - \underbrace{ \left( {\underline{{\mathsf {K}}}} +\dfrac{1}{\varDelta t} {\underline{{\mathsf {D}}}} \right) }_{{\underline{{\mathsf {S}}}} } \varDelta {\underline{{\mathsf {d}}}}. \end{aligned}$$

(4)

The system matrix ${\underline{{\mathsf {S}}}}$ contains the stiffness matrix ${\underline{{\mathsf {K}}}}$ as well as the damping matrix ${\underline{{\mathsf {D}}}}$ multiplied by a time increment $\varDelta t$ and the inverted mobility constant M. On the element level the stiffness matrix

$$\begin{aligned} {\underline{{\mathsf {K}}}}_{IJ,e} =\int _{\varOmega _e} \left[ \begin{array}{rcc} [{\underline{{\mathsf {B}}}^{\delta {\mathsf {u}}}_{I}}]^{T} \, (s^2 + \eta ) {\underline{{\mathsf {\mathbb {C}}}}} \, {\underline{{\mathsf {B}}}^{ {\mathsf {u}}}_{J}} &{} [{\underline{{\mathsf {B}}}^{\delta {\mathsf {u}}}_{I}}]^{T} 2\, s \, {\underline{{\mathsf {\mathbb {C}}}}} \, {\underline{{\varepsilon }}_h} {N}_{J}^{s}\\ {N}_{I}^{\delta s} \, 2 \, s \, ({\underline{{\mathsf {\mathbb {C}}}}} \,\underline{{\varepsilon }}_h)^T \, {\underline{{\mathsf {B}}}^{ {\mathsf {u}}}_{J}} &{} 2\, \mathscr {G}_c \, \epsilon [{\underline{{\mathsf {B}}}^{\delta s}_{I}}]^{T} \, \, {\underline{{\mathsf {B}}}^{ s}_{J}} + {N}_{I}^{\delta s} \left( {{\underline{{\varepsilon }}}_{h}^{T}} \, {\underline{{\mathsf {\mathbb {C}}} }} \, {{\underline{{\varepsilon }}}} \, + \dfrac{ \mathscr {G}_c}{2 \epsilon } \right) {N}_{J}^{s} \end{array}\right] \text {d}V {\text {, }} \end{aligned}$$

(5)

the damping matrix

$$\begin{aligned} {\underline{{\mathsf {D}}}}_{IJ,e} =\int _{\varOmega _e} \left[ \begin{array}{cc} {\underline{{\mathsf {0}}}} &{} {\underline{{\mathsf {0}}}} \\ {\underline{{\mathsf {0}}}} &{} {N}_{I}^{\delta s} \dfrac{1}{M} {N}_{J}^{s} \end{array}\right] \text {d}V. \end{aligned}$$

(6)

and the nodal residual

$$\begin{aligned} {\underline{{\mathsf {R}}}}_{{I},e} =\int _{\varOmega _e} \left[ \begin{array}{cc} [{\underline{{\mathsf {B}}}^{\delta {\mathsf {u}}}_{I}}]^{T} \, \underline{\pmb {\sigma }} \\ {N}_{I}^{\delta s} \dfrac{\dot{s}}{M} - 2\, \mathscr {G}_c \, \epsilon [{\underline{{\mathsf {B}}}^{\delta s}_{I}}]^{\text {T}} \nabla s + {N}_{I}^{\delta s} \left( s\, {{\underline{{\varepsilon }}}_{h}^{T}} \, {\underline{{\mathsf {\mathbb {C}}} }} \, {{\underline{{\varepsilon }}}} \, + \dfrac{ \mathscr {G}_c}{2 \epsilon } (s-1) \right) \end{array}\right] \text {d}V \end{aligned}$$

(7)

are computed. Whereby the indices I, J stem from the contributions of the different element nodes. The following passage is concerned with the adaptive numerical integration of these terms. Whereby the focus lies on the accurate integration of the shape functions ${{{N}}}_I$ and their derivatives ${\underline{{\mathsf {B}}}}_I$ that are used for the approximation of the phase field s.

3.2 Numerical integration

As mentioned before, the model is discretised with four-node quadrilateral elements, see Fig. 5. For a calculation in the natural coordinate system $\xi -\eta$, it is necessary to compute the determinant of the Jacobian matrix

$$\begin{aligned} {\mathsf {\underline{J}}} = \left[ \begin{array}{cc} \dfrac{\text {d} x}{\text {d} \xi } &{} \dfrac{\text {d} x}{\text {d} \eta } \\ \dfrac{\text {d} y}{\text {d} \xi } &{} \dfrac{\text {d} y}{\text {d} \eta } \end{array}\right] , \end{aligned}$$

which converts the global $x-y$ coordinate system to the natural element $\xi -\eta$ coordinate system. Since linear shape functions are used for the approximation of the geometry $\underline{x}_h = \sum N_I^{\text {lin}} \underline{x}_I$, the Jacobi matrix does not depend on the choice of the approximation of the s-field.

Fig. 5

2D isoparametric element

The general equation for the numerical integration of a 2D integral in the parent space can be described by

$$\begin{aligned}&\int _{\varOmega _e} \textit{f} \, (x , y)\, \text {d}x \, \text {d}y = \int _{\square } \textit{f} \, (\xi , \eta ) \, \text {det}({{\mathsf {\underline{J}}}}^{-1}) \, \text {d}\xi \, \text {d}\eta \nonumber \\&\quad \approx \sum \limits _{p=1}^{n_{\text {GP}}} \textit{f} \, ({\xi _{p}, \eta _{p}}) \, \text {det}({{\mathsf {\underline{J}}}_p}^{-1}) \, w_{p}. \end{aligned}$$

(8)

The square ($\square$) represents unit square ($\xi \in [-1, 1]$ and $\eta \in [-1,1]$) for the natural configuration. The function f represents any arbitrary function of the coordinates $\xi ,\, \eta$. Thus, the integral is approximated by a sum, and f needs to be evaluated only in the quadrature points. The function values are multiplied by weights $w_{p}$ and then summed up for all $n_{\text {GP}}$ Gauss points. Like mentioned before, the transformation of the integration in different coordinate systems require the Jacobian matrix and in particular the inverse matrix ${{\mathsf {\underline{J}}}_p}^{-1}$. The quality of the numerical integration depends on the continuity of the function the spatial position and number of the quadrature points. Especially for higher order shape functions, the integration error by an inappropriate quadrature scheme can be crucial. This needs to be counteracted by a sufficient number of quadrature points or an adequate quadrature scheme.

3.3 Numerical integration with Gauss–Legendre formulas

In standard finite element methods, the numerical integration is performed by the Gauss–Legendre rule, because of its optimal accuracy for polynomial shape functions, see e.g. [10]. In the case of rectangular Lagrange elements with a 1 : 1 ratio of nodes to Gauss points the result of the numerical integration of Eqs. (5)–(7) becomes exact. By contrast, the result of the quadrature with an phase field approximated with exponential shape functions has always an analytical deviation. This can be explained by the consideration of an exponential functions as a power series

$$\begin{aligned} e^x \, = \, 1 \, + \, x \, + \, \dfrac{x^2}{2!} \, + \, \dfrac{x^3}{3!} \, + \, \dfrac{x^4}{4!} \, + \, \cdots \quad . \end{aligned}$$

Due to the infinite power series of exponential functions, the Gauss integration would only be exact in case of an infinite number of quadrature points.

Table 1 Parameter for the fracture mode I

An obvious approach to meet a sufficient accuracy for the quadrature of exponential elements is the increase of the number of Gauss points. Prior to that a marking strategy is useful to select the elements that require an modification of the quadrature. Those elements would possess e.g. a threshold gradient of the phase field. In unmarked elements the number of Gauss points solely depend on the sufficient approximation of the displacement field and is fixed to the standard quadrature scheme.

Fig. 6

Elastic energy for crack growth tests with different element sizes and number of Gauss points

In the next step, the number of Gauss points for the marked elements has to be determined. A key parameter of the approximation of the phase field gradient is $\delta$. It controls the possible phase field gradient within an element, due to the formulation of the exponential shape functions. The parameter $\delta$ is calculated by the ratio of the element edge length $h_i$ and the regularization width $\epsilon$. By relating the number of quadrature points to the value of $\delta$, the number of integration would decrease with increasing mesh size h and decreasing crack width $\epsilon$.

For the consideration, we analyze a simple fracture mode I setup. The 2D model is a square domain with an initial crack with the half length of the specimen and positioned in the centre. In order to reduce the computational time, the model will be bisected along its symmetry line, which also halves the initial crack. The model parameter are reported in Table 1. The monitored value for this test case is the elastic energy during crack propagation. In the simulation different discretization normal to the crack face with 8 or 16 elements are used. The number of elements along the crack path remains constant for both cases. The number of Gauss points will be increased from the standard $2\times 2$ up to $13 \times 13$. The results show that while the crack width is identical for both cases the element size normal to the crack surface differs by factor 2, see Fig. 6. Because of this difference, the required number of quadrature points for the same precision varies. This relation will be used to derive an adaptive scheme for the number of Gauss points.

3.4 Adaptive quadrature

Although exponential elements reduce the required mesh density for the approximation of sharp cracks, they require a more elaborate quadrature. In order to benefit from the applied advanced discretization technique, an adaptive quadrature shall be implemented. This necessitates a modification of the quadrature, which can be obtained in different ways like the use of a different scheme, an increase of quadrature points or a remeshing. The last approach would make the concept of the exponential shape functions obsolete . Therefore we will focus on an adaptive choice of Gauss points and a different quadrature scheme.

3.4.1 Localization for adaptivity

Before the discussion of an adaptive routine, a reasonable preparation is covered. As the whole body has a nearly constant intact phase field value, the regions of high gradients are rather small. Therefore the adaptivity of the number of Gauss points can be locally constrained in order to avoid a waste of computational time for a more precise integration, see Fig. 11. This is achieved by a straightforward condition

$$\begin{aligned} \prod _{I = 1}^{N_e} s_I < 0.5 \end{aligned}$$

(9)

which multiplies all $N_e$ nodal values of the fracture field within an element, whereby the value 0.5 has been proven satisfactory. This condition is checked in every iteration. So, while the default quadrature rule is a $2\times 2$ Gauss–Legendre scheme, a different number of Gauss points is choosen for elements fulfilling (9). The number of points is computed by a $n_{\text {GP}}$-function which depends on exponential element coefficient $\delta$ (Fig. 7).

Fig. 7

Local adaptation of quadrature

Fig. 8

Test case: stationary crack (fracture field left, mesh right)

3.4.2 Order adaptivity of the numerical integration

Elements which fulfill the requirement for an adapted quadrature should be checked for a higher order numerical integration. A scalable straightforward approach is the increase of quadrature points. An ad-hoc criterion for the determination of the value of $n_{\text {GP}}$ is the shape function parameter $\delta$. In general, this relation can be expressed by a function

$$\begin{aligned} n_{GP} = f(\delta _{\text {max}}). \end{aligned}$$

(10)

Fig. 9

Parameter analysis for a stationary crack over different element sizes and regularized length

Fig. 10

Formulation of the choice of the number of Gauss points

The parameter $\delta$ contains the element edge lengths. In an quadrilateral element, this leads to four different values. The following routine chooses the number of quadrature points for all dimensions to be equal. Thus, only one $\delta$ is used in the element. The largest $\delta$, $\delta _{\text {max}}$, is chosen as input variable for f, because it is related to the highest gradient in the element.

Like in [12], the 2D exponential shape functions are evaluated in two test cases for a straight stationary crack.

The setup for the first stationary test is depicted in Fig. 8. The body is discretized homogeneously with $n \times n$ elements and contains a horizontal crack of length L. No mechanical loading is considered.

In the second test case a mechanical loading is considered. In both cases, the symmetry of the problem is considered. The applied load is a constant displacement along an edge parallel to the initial crack, which increases linearly in time. In contrast to the stationary case, the mesh will only be refined in the direction perpendicular to the crack surface for the convergence study. In the direction of the crack, the edge length of the elements remains constant, like in [12].

The construction of a $n_{\text {GP}}$-function requires data points. For this purpose, the case with the stationary crack is utilized in a parameter study. The parameters nondimensionalized regularization length $\overline{\epsilon }$ ($=$ ${\epsilon }$/2L), element edge length $\overline{h}$ ($={h}/{2L}$) and the number of Gauss points $n_{\text {GP}}$ are varied to obtain the surface plots of Fig. 9. The plots show the relative error of the surface energy, which is calculated by

$$\begin{aligned} \underbrace{\int \psi ^{\text {s}} \text {d} \varOmega }_{\text {numerical approx.}} -\underbrace{{\int } 2 \,\epsilon \, L \, \mathscr {G}_c .}_{\text {analytical approx.}} \end{aligned}$$

(11)

From the different subfigures of Fig. 9, the dependency of the accuracy on the number of Gauss points $n_{\text {GP}}$ can be identified, thereby an ideal function $f(\delta )$ can be defined to limit the error for a certain $\delta$ range.

The values $\overline{h}$ and $\overline{\epsilon }$ are considered by the parameter $\delta = \frac{\overline{h}}{\overline{\epsilon }}$. The graphs are then approximated by a linear regression for an error range of 2–10%, see Fig. 10a. It is our goal to derive a function $f(\delta )$ that guarantees an error smaller than 5%.

The function is characterized by the intersection points of the error curves of the different Gauss point numbers with an error level, which is in our case 0.05. As shown in Fig. 10b, the jump points $\varvec{\times }$ are reported. In the next step, the points are used for the interpolated third order polynomial, see Fig. 10b. The functional value are then rounded to provide integer values for $n_{\text {GP}}$-function, see Fig. 10b.

Fig. 11

Local adaptation of the number of quadrature points

A distribution of the adaptive routine is depicted in Fig. 11. The figure shows the adaptive adjustment of the number of Gauss points $n_{\text {GP}}$ for an initial phase field s. Most of the elements have $2 \times 2$ quadrature points, because of the large intact area of the domain. Higher values for $n_{\text {GP}}$ can be seen at the crack surface as intended. Because of a decreasing mesh size towards the crack tip, the number of Gauss points show the same trend. The elements in the second row on the crack surface are coarser and therefore are integrated by $9\times 9$ Gauss points. In practical terms, if an element fulfills (9), the number of Gauss points is calculated by the integer value of the function f.

Fig. 12

DE formula: quadrature points and weights for an 1D-reference domain

Fig. 13

Parameter analysis for a stationary crack over different element sizes and regularization length

3.4.3 Double exponential formula

An improvement of the numerical integration can also be achieved by the use of a better quadrature scheme. The special shape function inherits characteristics of exponential functions like the infinite number of continuous derivatives. Functions with this property are integrated more accurately by the Double Exponential (DE) formula, see [15]. It consists of an infinite series of integration points and tends to distribute the major proportion of its quadrature points towards the integration limits, see Fig. 12. Due to the infinite series, a truncation is necessary. As a consequence a residual in the sum of the weights appears, see Fig. 12 (=1.998). This deviation leads to an error, because of the lower deployed domain size. Thereby, the sum should be two for an interval from − 1 to 1. This problem can be corrected by a normalization. Although the DE formulas is in general less precise than quadrature scheme based on Gauss rule, it is more accurate for certain types of functions. For instance, the accuracy of the quadrature of functions which possess singularities or infinite derivatives, like in our case, benefit from the DE formula, see [15]. The equations for the general formula, position and weights of the quadrature points are

$$\begin{aligned} I&= \int _{-1}^{1} f(x) \text {d}x = \sum _{-\infty }^{+\infty } w_k f(x_k), \\ x_k&= \text {tanh}\left( \dfrac{1}{2} \pi \, \text {sinh}(k c)\right) \quad \text {and}\\ w_k&= \dfrac{\dfrac{1}{2} c \pi \, \text {cosh}(k c)}{\text { cosh}^2 \left( \dfrac{1}{2} \pi \, \text {sinh}(kh)\right) }. \end{aligned}$$

The parameter h is a step size, which is described in [16]. Because of the necessary centre point and the symmetry of the GP positions, the amount of quadrature point is always odd.

Similar to the Gauss–Legendre method, the DE formula is also used in a parameter study to obtain the correlation of the surface energy with the elements size h and crack width $\epsilon$. The results are displayed in Fig. 13. Unfortunately, different non-monotonous behaviour of the error of the surface energy can be identified. This could be derived from the exponential quadrature rule, which is based on trigonometric functions. Therefore, it is necessary to apply at least $13\times 13$ quadrature points to minimize the maximal error and achieve a robust precision. The comparison in terms of accuracy shows an advantage of the DE formula, but is only beneficial for cases in which the Gauss integration with $12\times 12$ doesn’t meet the requirements.

Fig. 14

Elastic energy during a fracture mode I for different implementation

Table 2 Total number of quadrature points for the different discretizations of Fig. 14

4 Numerical results

The performance of the numerical integration is tested in a 2D simulation of a fracture mode I, which is introduced as the second test case in Sect. 3.4.2. Thereby, the behaviour of the elastic energy $E^e =\int \psi ^{\text {e}} \text {d}\varOmega$ during the crack propagation is observed. In order to study the convergence, the number of elements normal to the crack surface is varied from two to 100 elements. The important quantities are the load factor and maximal elastic energy at which crack propagation occurs. In Fig. 14 an overall comparison of the different quadrature concepts is shown. Also included are the results for standard linear elements. The different variants are categorized by quadrature method and adaptive(adap)/non-adaptive. Furthermore there are differences between the number of quadrature points of the numerical integration methods. The DE formula uses always 13 points per direction and in the adaptive form switches for elements with low phase field gradient to a Gauss–Legendre integration with $2 \times 2$ GP. Furthermore, the $n_{\text {GP}}$ for the adaptive Gauss quadrature is limited to 10 and starts with the standard 2 per direction like for standard Lagrange elements.

In this setting the solution of the elements integrated with the DE formula already converge for a extremely coarse mesh. While in case of a static $5\times 5$ Gauss points approach a sufficient approximation of the elastic energy is only obtained for at least 32 elements towards the fracture plane. The improvement by an adaptive number of Gauss points reduce the required mesh density by 50$\%$. The difference between the integration methods can partially be explained by the lower amount of quadrature points for the adaptive routines, but even with the same number the DE formula is more efficient, see Fig. 14.

The total number quadrature points of the models are reported in Table 2. For the adaptive cases the numbers of the last load step are considered, because they are the largest numbers during the simulation. While the adaptive integration with Gauss–Legendre method uses less points, it is also less accurate. When it is used for fine meshes or wide cracks it becomes more efficient due to the necessary high amount of quadrature points of the DE formula, which is visible in the Table 2 for $n = 100$.

5 Conclusion

This work presents a study of an adaptive numerical integration method for exponential finite elements in a phase field fracture model. The focus is on an accurate computation of the elastic and surface energy.

The accuracy increase of the numerical integration of Lagrange elements is capped by the 1 : 1 ratio of nodes to Gauss points and would not increase with a higher number of points. The exponential elements on the other hand can be characterized by an infinite Taylor series and would require infinite quadrature points to obtain an exact integration. In order to estimate the sufficient number of $\text {GP}$, the number of quadrature points is evaluated by the error of the surface energy, which is an essential value for a good approximation of the crack surface in a phase field model. Besides a simple adaptation of the amount of quadrature points, another numerical integration method is tested, which is more effective for the integration of exponential functions, the DE formula. Though it is less effective with smoothness, it has an accuracy advantage for functions with $C^{\infty }$-smoothness.

A higher order quadrature with Gauss–Legendre method or the DE formula is computationally expensive and also always unnecessary, because of the required node density for a certain crack path. The fracture field is mainly described by two conditions whereby cracks only make up a small percentage of the whole domain. This means that only a small area, more precisely, the crack surfaces require additional quadrature points. In order to make the integration more efficient an adaptive routine is reasonable. So only in elements with large enough phase field gradients the number of quadrature points should be increased. In the undamaged domain the quadrature method has to be only sufficient for the approximation of the displacement field, which is fulfilled by a $2\times 2$ Gauss quadrature. Based on a simulation of a stationary crack, the error of the surface energy is evaluated and compared in terms of accuracy between different numbers of Gauss points. Then the routine was tested for a growing crack and the effectiveness is observed.

In summary a function that adaptively determines the number of Gauss points, as a function of the element size and regularization length, is proposed. To further improve the accuracy the DE formula can be used, but would require a higher initial number of quadrature points and would only make a difference for a very low mesh density.

But even if it’s possible to solve problems with extreme coarse meshing, problems would arise in the sufficient possible sets of cracks. The phase field fracture simulation in FEM relies on nodes on the approximated crack path. So the limit of the lowest mesh density does not only depend on the approximation of the phase field transition zones but also on the shape of crack. Thus, the relevant range for element sizes and crack width is still properly covered by the adaptive control of $n_{\text {GP}}$.

In future, an expansion of the adaptivity is required to make use of the new shape functions in more general studies. In this context, the emphasis lies on the orientation of the elements to describe the symmetrical cracks with unsymmetrical shape functions for 2D and 3D.

The authors gratefully acknowledge support by the Deutsche Forschungsgemeinschaft in the Priority Program 1748: “Reliable Simulation Techniques in Solid Mechanics. Development of Non-Standard Discretization Methods, Mechanical and Mathematical Analysis” under the project “Advanced Finite Element Modeling of 3D Crack Propagation by a Phase Field Approach”.