A computational modeling approach based on random fields for short fiber-reinforced composites with experimental verification by nanoindentation and tensile tests

Abstract

In this study a modeling approach for short fiber-reinforced composites is presented which allows one to consider information from the microstructure of the compound while modeling on the component level. The proposed technique is based on the determination of correlation functions by the moving window method. Using these correlation functions random fields are generated by the Karhunen–Loève expansion. Linear elastic numerical simulations are conducted on the mesoscale and component level based on the probabilistic characteristics of the microstructure derived from a two-dimensional micrograph. The experimental validation by nanoindentation on the mesoscale shows good conformity with the numerical simulations. For the numerical modeling on the component level the comparison of experimentally obtained Young’s modulus by tensile tests with numerical simulations indicate that the presented approach requires three-dimensional information of the probabilistic characteristics of the microstructure. Using this information not only the overall material properties are approximated sufficiently, but also the local distribution of the material properties shows the same trend as the results of conducted tensile tests.

1 Introduction

The compatibility of thermoplastic material for automated serial production like mold injection allows high production rates with a reasonable price per piece. Adding short fibers or nanoparticles to the base material of pure plastics leads to a significant increase of the stiffness and strength of the material without losing the ability to process the material by automated serial production. Hence, this combination results into a high interest in short fiber-reinforced composite (SFRC) not only in the automotive industry.

The main disadvantage due to the reinforcing elements is the spatial fluctuation of the material properties. The representation of the non-equally distributed material properties is hence, challenging and connected with high computational costs due to the use of probabilistic methods. This consequently is worthwhile to represent the probabilistic characteristics of the microstructure on the component level by appropriate stochastic methods without extensive computational costs.

The spatial distribution of the material properties is mainly assigned to the finite fiber length as well as a production process induced variation of the fiber orientation due to different melt flow velocities and shear forces over the cross-section [35]. Since the fiber length is usually much smaller in comparison to the component the microstructural information must be transferred from the micro- and mesoscale to the component level. Therefore, a multi-scale approach appears advantageous for a sufficient modeling procedure for SFRC.

In the literature many different approaches are presented for the modeling of the probabilistic characteristics of reinforced materials. One approach is based on the orientation tensor introduced in [1]. In [3] the orientation tensor is implemented directly in the material description. An extended approach is used in [10], where the orientation tensor is combined with a material model based on a coupled micro-mechanical and phenomenological approach. The suitability is also discussed in [50]. A second approach is based on the extended finite element method (XFEM), which was developed for the numerical simulation of crack growth and interfaces [49]. In [32] the method is applied to reinforced concrete. It is also used in [58], where it is combined with a cohesive zone model. All these approaches have in common the lack of a scale transition. A first attempt for a scale transition is presented in [61] where XFEM is combined with a Monte Carlo simulation to estimate the size of a representative volume element (RVE) for random composites.

One technique for the representation of spatial varying parameters with a scale transition is the use of random fields [71] and hence, allow the modeling of inhomogeneous material properties [52]. For the discretization of random fields for the use in a numerical simulation the Karhunen–Loève expansion is a suitable tool. This allows a separation of the deterministic numerical modeling and the probabilistic representation of the material properties. In context of structural mechanics this approach is also referred to as the stochastic finite element method (SFEM) [47, 55]. In [39] SFEM is combined with cohesive zone models for the analysis of crack growth in fiber reinforced cementitious composites. The fluctuation of the volume fraction is represented by random fields in [24]. The influence of the fiber mass fraction, the window size, and the contrast between the phases on the correlation structure is discussed in [62]. Finally, a combination of the SFEM with the concept of RVE is presented in [23, 65].

The main objective of this research is to establish a robust computational modeling approach for components made of SFRC using homogeneous second-order random fields discretized by the Karhunen–Loève expansion. In this study a tensile test specimen is used exemplary. First the microstructural properties of the material are extracted from a two-dimensional micrograph as shown in [63]. Using the probabilistic characteristics of the fiber length, fiber orientation, fiber diameter, and the information about the layered structure of the tensile test specimen, cross-sections with different micromechanical representations of the specimen are analyzed and compared with each other. This is done by linear elastic numerical simulations that are validated by experimental investigations. For the numerical simulation artificial microstructures are generated on the basis of the derived microstructural characteristics. Using these artificial microstructures, a numerical model is established and the Young’s modulus is determined by simulating tensile tests. In addition, the Young’s modulus is also experimentally obtained by nanoindentation. This allows one to reduce the three-dimensional effects on the results and hence, to determine the near surface material properties [20]. Based on the results of the numerical and experimental investigations on the mesoscale the best approach is derived by taking also into account the aspect of computational costs. The selected approach is then used to expand the procedure to a representation of the material on the component level by taking into account the spatial distribution of the material properties induced by the microstructural characteristics. This is achieved by representing the components of the elasticity tensor by homogeneous second-order random fields. Therefore, the material properties are still modeled probabilistically and not deterministically. This also indicates that there is no scale transition to the macroscale. For the discretization of these fields the Karhunen–Loève expansion is used, which requires the determination of correlation functions first.

Finally, the influence of the probabilistic microstructure characteristics on material properties obtained on the component level is analyzed. This is done by simulating tensile tests on a numerical basis. Again the numerically obtained values for the Young’s modulus are compared with experimental results. Consequently, this study gives a comprehensive analysis of a computational modeling approach for components made of SFRC by numerical simulation, that is validated by experimental investigations.

The structure of the presented work is as follows. Sect. 2 gives a brief overview of the most important theoretical background including homogeneous second-order random fields, the Karhunen–Loève expansion for the discretization of random fields as well as the main aspects of the multi-scale modeling with respect to Hill’s condition. In Sect. 3 the different specimens used in this study are presented. This is followed by the extraction of the probabilistic characteristics from a micrograph in Sect. 4. The numerical simulations and experimental investigations on the mesoscale and the impact of the resulting microstructural characteristics on the component level are shown in Sects. 5 and 6, respectively. Finally, Sect. 7 gives a summary and a conclusion of the presented work.

2 Karhunen–Loève expansion

2.1 Second-order random fields

Among others probabilistic quantities are described by random variables $Z(\omega )$. A realized value, e.g. of a material parameter, is denoted by z. In context of random fields $Z(\omega , {\mathbf {x}})$ the random variables are also assigned to spatial coordinates ${\mathbf {x}}$. For the synthesis of random fields by using the Karhunen–Loève expansion, it is necessary that the variance of the random field as well as the random variable are finite. In this case the following definition for random fields holds

$$\begin{aligned} Z({\mathbf {x}}) = Z(\omega ,{\mathbf {x}}) \in L^2(\varOmega ; {\mathbb {R}}) \end{aligned}$$

(1)

and one speaks of second-order random fields [4]. Their main properties are briefly presented below.

Random fields are characterized by moments of their probability distribution [66, 71]. In general, the n-th moment of a single random variable Z is defined as

$$\begin{aligned} {\mathbb {E}} [ Z^n ] = \int _{-\infty }^{\infty } z^n f_Z(z) {\text {d}}z, \end{aligned}$$

(2)

where $f_Z(z)$ is the probability density function. Based on this definition the first moment of a random field, also called expected value, is given by

$$\begin{aligned} {\mathbb {E}} [Z({\mathbf {x}})] = \mu _Z({\mathbf {x}}) = \int _{-\infty }^{\infty } z({\mathbf {x}}) f_Z(z,{\mathbf {x}}) {\text {d}}z. \end{aligned}$$

(3)

The mean square of $Z({\mathbf {x}})$ is given by the second moment. Besides these two moments central moments with respect to the expected value are introduced. The deviation of a value to the expected value is given by the second central moment, also known as the variance. Reformulating Eq. (2) provides the definition for the variance of a random field $Z({\mathbf {x}})$

$$\begin{aligned} {\text {Var}}[Z({\mathbf {x}})] = \int _{-\infty }^{\infty } z({\mathbf {x}})^2 f_Z(z,{\mathbf {x}}) {\text {d}}z - \mu _z({\mathbf {x}})^2 . \end{aligned}$$

(4)

In addition, the standard deviation is often used, which is derived from the variance by

$$\begin{aligned} \sigma _Z({\mathbf {x}}) = \sqrt{{\text {Var}}[Z({\mathbf {x}})]}. \end{aligned}$$

(5)

Hence, the expected value as well as the variance are functions of the spatial coordinates ${\mathbf {x}}$. However, in case of a homogeneous random field both the expected value and the variance become constants [71].

The observation of a random field at different locations ${\mathbf {x}}_i$ is described by corresponding random variables ${\mathbf {Z}} = Z_i$. Besides the relation between an observation and the expected value of the random field the relation between observations at different points of a random field is of great interest. This relation is expressed by the covariance and reads for two random variables $Z_1$ and $Z_2$

$$\begin{aligned} {\text {Cov}}[Z_1,Z_2] = {\mathbb {E}}[Z_1Z_2] - \mu _1\mu _2. \end{aligned}$$

(6)

Usually this expression is reduced to a dimensionless correlation parameter $\rho _{12}$ by dividing Eq. (6) by $\sigma _1$ and $\sigma _2$

$$\begin{aligned} \rho _{12} = \rho _{Z_1,Z_2} = \frac{{\text {Cov}}[Z_1,Z_2]}{\sigma _1\sigma _2}. \end{aligned}$$

(7)

Equations (6) and (7) are referred to as the auto-covariance and auto-correlation, respectively, if $Z_1$ and $Z_2$ are part of the same random field $Z({\mathbf {x}})$. Otherwise, Eqs. (6) and (7) are the cross-covariance and cross-correlation, respectively.

Since the probability density function is unknown for most times the random field is represented by a discrete number of realizations $\omega _i$ [56]. In this case the mean of the discrete values

$$\begin{aligned} \overline{Z({\mathbf {x}})} = \frac{1}{N} \sum _{i=1}^N Z(\omega _i, {\mathbf {x}}) \end{aligned}$$

(8)

is used as expected value of the random field. In addition, the variance is rewritten as

$$\begin{aligned} s^2({\mathbf {x}}) = \overline{Z({\mathbf {x}})^2} - \overline{Z({\mathbf {x}})}^2. \end{aligned}$$

(9)

Finally, the dimensionless correlation coefficient for two random variables $Z_1$ and $Z_2$ is given by

$$\begin{aligned} \rho _{Z_1,Z_2} = \frac{[\overline{Z_1-\overline{Z_1}}][\overline{Z_2-\overline{Z_2}}]}{s_1s_2}. \end{aligned}$$

(10)

2.2 Auto-correlated random fields

The Karhunen–Loève expansion is a generalization of the Fourier transform to probabilistic processes. A commonly used formulation for the expansion of a stochastic process $X(\omega ,{\mathbf {x}})$ is given by [8]

$$\begin{aligned} X(\omega , {\mathbf {x}}) = \sum _{n=0}^{\infty } \sqrt{\lambda _n} \phi _n({\mathbf {x}})Z_n(\omega ), \end{aligned}$$

(11)

where $Z_n$ are a set of uncorrelated random variables and $\lambda _n$ and $\phi _n({\mathbf {x}})$ are an eigenpair of a Fredholm integral equation of the second kind. The derivation of the integral equation is briefly summarized below by using the analogy to the Fourier transform as done in [45]. Hence, stochastic processes $X({\mathbf {x}})$ are represented by a series expansion of orthonormal functions $\phi _n({\mathbf {x}})$ as

$$\begin{aligned} X(\omega , {\mathbf {x}}) = \sum _{n=1}^\infty Z_n \phi _n({\mathbf {x}}). \end{aligned}$$

(12)

With this series expansion the position-dependent part is separated from the probabilistic component of the stochastic process, where the functions $\phi _n({\mathbf {x}})$ are orthonormal. Furthermore, it is beneficial to split the random field additively into a deterministic and a stochastic field. This separation can be written as

$$\begin{aligned} Z(\omega , {\mathbf {x}})&= \mu ({\mathbf {x}}) + \alpha (\omega , {\mathbf {x}}), \nonumber \\&= \mu + X(\omega , {\mathbf {x}}) \end{aligned}$$

(13)

where the mean of the random field $\mu ({\mathbf {x}})$ represents the deterministic part and $\alpha (\omega , {\mathbf {x}})$ gives a random field with an expected value of zero. Due to this separation the expected value of the series expansion ${\mathbb {E}}[X({\mathbf {x}})]$ and the expected value of the random variables $Z_n$ equal zero. In addition to the expected value the variance of the random variable is given by

$$\begin{aligned} \sigma ^2_{Z_n} = {\mathbb {E}} [ Z_n^2 ] = \lambda _n > 0 \end{aligned}$$

(14)

In context of random variables orthogonality is equivalent to independent and uncorrelated random variables, respectively. In this case the covariance reads for values of the same homogeneous random field $X({\mathbf {x}})$ at the two locations ${\mathbf {x}}$ and ${\mathbf {x}}^\prime$

$$\begin{aligned} {\text {Cov}}[X({\mathbf {x}}),X({\mathbf {x}}^\prime )] = {\mathbb {E}}[ X({\mathbf {x}}) X({\mathbf {x}}^\prime ) ] - \mu \mu ^\prime \end{aligned}$$

(15)

Introducing $\mu =0$ and the independence of the random variables leads to

$$\begin{aligned} {\mathbb {E}}[ X_m({\mathbf {x}}) X_n({\mathbf {x}}^\prime ) ] = \lambda _n \delta _{mn}. \end{aligned}$$

(16)

In addition, combining the series expansion in Eq. (12) with the orthogonality provides

$$\begin{aligned} Z_n = \int _0^x X({\mathbf {x}}) \phi _n({\mathbf {x}}) {\text {d}} {\mathbf {x}} \end{aligned}$$

(17)

for the random variables, where $\phi _n({\mathbf {x}})$ are the eigenfunctions of the auto-correlation. The corresponding eigenvalues are given by $\lambda _n$. Therefore, before generating random fields by using the Karhunen–Loève expansion the auto-correlation must be determined. Expressing $X({\mathbf {x}})$ and $X({\mathbf {x}}^\prime )$ by using Eq. (12) and taking into account the independence of the random variables the auto-correlation is written as

$$\begin{aligned} {\mathbb {E}}[ X({\mathbf {x}}) X({\mathbf {x}}^\prime )] = \sum _{m=1}^\infty \phi _m({\mathbf {x}}) \phi _m({\mathbf {x}}^\prime ) \lambda _m \end{aligned}$$

(18)

which leads finally to the following eigenvalue problem

$$\begin{aligned} \int _0^X {\text {Cov}}[Z_1,Z_2] \phi _n({\mathbf {x}}) {\text {d}} {\mathbf {x}} = \sum _{n=1}^\infty \lambda _n \phi _n({\mathbf {x}}^\prime ). \end{aligned}$$

(19)

For a known correlation function the eigenvalues $\lambda _n$ and eigenfunctions $\phi _n({\mathbf {x}})$ can be calculated by solving the Fredholm integral equation of the second kind in Eq. (19). A closed solution is only possible for a few correlation functions. One example here is the exponential correlation function, which is given for homogeneous random fields by [17, 53, 66]

$$\begin{aligned} {\text {Cov}}[X({\mathbf {x}}),X({\mathbf {x}}^\prime )] = \sigma ({\mathbf {x}}) \sigma ({\mathbf {x}}^\prime ) \exp \left( - \frac{\vert x_i - x_i^\prime \vert }{b_i} \right) , \end{aligned}$$

(20)

with the correlation length $b_i$. An important property is the multiplicative decomposition of the different directions, which is used for the generation of two-dimensional random fields, as shown in Sect. 2.3.

Introducing the correlation function the eigenvalue problem in Eq. (19) is rewritten for a one-dimensional field $[-l,l]$ as

$$\begin{aligned} \int _{-l}^l \exp {\left( -\frac{x-x^\prime }{b}\right) } \phi _n(x^\prime ) {\text {d}} x^\prime = \sum _{n=1}^{\infty } \lambda _n \phi _n(x). \end{aligned}$$

(21)

The solution of this eigenvalue problem is given by [66]

$$\begin{aligned} \lambda _i&= \frac{2b}{1+\omega _i^2 b^2} \end{aligned}$$

(22)

$$\begin{aligned} \phi _i&= \alpha _i \cos \omega _i x \end{aligned}$$

(23)

with

$$\begin{aligned} \alpha _i&= \frac{1}{\sqrt{l+\frac{\sin 2 \omega _i l}{2 \omega _i}}} \end{aligned}$$

(24)

for odd i and

$$\begin{aligned} \lambda _i&= \frac{2b}{1+\omega _i^2 b^2} \end{aligned}$$

(25)

$$\begin{aligned} \phi _i&= \alpha _i \sin \omega _i x \end{aligned}$$

(26)

with

$$\begin{aligned} \alpha _i&= \frac{1}{\sqrt{l-\frac{\sin 2 \omega _i l}{2 \omega _i}}} \end{aligned}$$

(27)

for even i. The values of $\omega _i$ are obtained by solving

$$\begin{aligned} \frac{1}{l} - \omega _i \tan \omega _i l&= 0 \ \text {in} \ \left[ (i-1) \frac{\pi }{l}, \left( i - \frac{1}{2}\right) \frac{\pi }{l} \right] \end{aligned}$$

(28)

and

$$\begin{aligned} \frac{1}{l} \tan \omega _i l + \omega _i&= 0 \ \text {in} \ \left[ \left( i - \frac{1}{2}\right) \frac{\pi }{l}, i \frac{\pi }{l} \right] \end{aligned}$$

(29)

for odd and even values of i, respectively.

Fig. 1

Evaluation of the transcendental equation for $\omega _i$

The computational solution of Eqs. (28) and (29) is not trivial since the range boundaries are poles with a transition from a positive to a negative sign. Usually, algorithms for the determination of zeroing are based on a sign transition. However, precision limitations may lead to an inaccurate evaluation of the boundary values. Therefore, these algorithms require a manually defined offset to ensure a correct calculation of the zeroing, see Fig. 1. In [8] a different approximation for $\omega _i$ is given with

$$\begin{aligned} (\omega _i -c_i^2) \tan (\omega _i l) - 2 c_i \omega _i = 0. \end{aligned}$$

(30)

This approach does not require a case differentiation between odd and even values of i. However, the problem regarding the sign transition at poles is still not solved, resulting in a missing sign transition. Therefore, in this work a further approach for a robust determination of zeroing is achieved by multiplying Eqs. (28) and (29). In this case there is no sign transition at the poles but within the interval for the determination of $\omega$. Hence, a manually defined offset is no longer necessary. Figure 1 shows a comparison of the different approaches, for a correlation length of $b = 5\,\hbox {mm}$ and a field length of $l = 200\,\hbox {mm}$.

2.3 Two-dimensional random fields

Applying random fields to problems in the field of mechanical engineering mostly requires the representation of two-dimensional or even three-dimensional components. The Karhunen–Loève expansion is adapted to two-dimensional components by separating the correlation structure of the different directions following the multiplicative decomposition of the correlation functions. Hence, the two-dimensional eigenfunctions and eigenvalues are expressed by the product of the eigenfunctions and eigenvalues of each direction

$$\begin{aligned} \phi _n(x_1,x_2) = \phi ^1_i(x_1) \phi ^2_j(x_2) \end{aligned}$$

(31)

and

$$\begin{aligned} \lambda _n = \lambda _i^1 \lambda _j^2. \end{aligned}$$

(32)

For a rectangular component of the dimension $l_1 \times l_2$ and an exponential correlation function this leads to [18]

$$\begin{aligned}&\lambda _i^1 \lambda _j^2 \phi ^1_i(x_1) \phi ^2_j(x_2) = \int _{\frac{-l_1}{2}}^{\frac{l_1}{2}} \exp \left( - \frac{\vert x_1 - x_1^{\prime } \vert }{b_1} \right) \phi ^1_i(x_1^{\prime })\text {d}x_1^{\prime } \nonumber \\&\quad \int _{\frac{-l_2}{2}}^{\frac{l_2}{2}} \exp \left( - \frac{\vert x_2 - x_2^{\prime } \vert }{b_2} \right) \phi ^1_i(x_2^{\prime })\text {d}x_2^{\prime } \end{aligned}$$

(33)

with the individual solution of each direction

$$\begin{aligned} \lambda _i^1 \phi ^1_i(x_1) = \int _{\frac{-l_1}{2}}^{\frac{l_1}{2}} \exp \left( - \frac{\vert x_1 - x_1^{\prime } \vert }{b_1} \right) \phi ^1_i(x_1^{\prime })\text {d}x_1^{\prime } \end{aligned}$$

(34)

and

$$\begin{aligned} \lambda _j^2 \phi ^2_j(x_2) = \int _{\frac{-l_2}{2}}^{\frac{l_2}{2}} \exp \left( - \frac{\vert x_2 - x_2^{\prime } \vert }{b_2} \right) \phi ^1_i(x_2^{\prime })\text {d}x_2^{\prime }, \end{aligned}$$

(35)

respectively. The eigenvalues and eigenfunctions of these two individual equations are identical to the those presented in Sect. 2.2.

2.4 Apparent material properties

One technique to extract the relation between information of different locations ${\mathbf {x}}_i$ is the moving window method [2, 19]. Within this method a window of predefined size is used to extract segments of a larger microstructure. For these extractions the material properties are determined by numerical simulation. With the material properties available at different locations the correlation functions are obtained by a curve fit.

The numerical simulations for the determination of the material properties are conducted in accordance with Hill’s condition [33]

$$\begin{aligned} \langle \varvec{\sigma } : \varvec{\epsilon } \rangle = \langle \varvec{\sigma }\rangle : \langle \varvec{\epsilon } \rangle . \end{aligned}$$

(36)

This procedure ensures the correct calculation of the effective material properties.

For a RVE [34] the homogeneous material properties are written as

$$\begin{aligned} \langle \varvec{\sigma }\rangle = {\mathbb {C}}^{\text {eff}} : \langle \varvec{\epsilon } \rangle \end{aligned}$$

(37)

and

$$\begin{aligned} \langle \varvec{\epsilon }\rangle = {\mathbb {S}}^{\text {eff}} : \langle \varvec{\sigma } \rangle \end{aligned}$$

(38)

respectively. Here, ${\mathbb {C}}^{\text {eff}}$ and ${\mathbb {S}}^{\text {eff}}$ are the effective stiffness and compliance tensor. The strains $\varvec{\epsilon }$ and stresses $\varvec{\sigma }$ hold information about the microstructure. In contrast to this $\langle \cdot \rangle$ gives the volume average, defined by

$$\begin{aligned} \langle \cdot \rangle = \frac{1}{V} \int _V \cdot {\text {d}}V. \end{aligned}$$

(39)

For the determination of the effective material properties among others the following two kinds of boundary conditions can be derived from Hill’s condition. Based on the average strain theorem with linear elastic material properties as well as the average stress theorem [76] these boundary conditions read

$$\begin{aligned} {\mathbf {u}} = \varvec{\epsilon }_0 \cdot {\mathbf {x}} \end{aligned}$$

(40)

and

$$\begin{aligned} {\mathbf {t}} = {\mathbf {t}}_0 \cdot {\mathbf {x}}, \end{aligned}$$

(41)

respectively. Here Eq. (40) holds a boundary condition of Dirichlet type, because only pure displacement boundary conditions with the constant macroscopic strain $\varvec{\epsilon }_0$ are defined on the complete surface. In contrast to this Eq. (41) holds a boundary condition of Neumann type, since only pure traction boundary conditions, with a constant macroscopic stress ${\mathbf {t}}_0$ are defined on the complete surface. In case of a RVE the material properties obtained for these two boundary conditions are equal and hence, the material is assumed to be homogeneous. If the used volume is smaller than the RVE one speaks of apparent overall properties [30, 31, 37]. To determine these properties, the same procedure is used as for the effective material properties. However, in this case the results depend on the size of the extracted volume as well as the boundary conditions. Such kind of extraction on the mesoscale is referred to as a statistically volume element (SVE) [54].

Fig. 2

Specification of the experimental and numerical specimens

3 Specimen specification

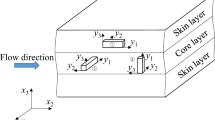
Figure 2 gives an overview of all specimens and their orientations used in this research. The raw material of the conducted analyses is a polybutylenterephthalat (PBT) filled with glass fibers. The fiber mass fraction is specified with $30\%$ (PBT GF 30). The initial component is a plate with the dimensions of $300\,\hbox {mm} \times 300\,\hbox {mm} \times 3\,\hbox {mm}$ fabricated by an injection mold process (1). With this plate a coordinate system is introduced that is used throughout the whole investigation. The main objective of this research is the implementation of a linear-elastic numerical modeling procedure for the numerical simulation of components made of SFRC that provides not only the global material behavior but also information about the spatial distribution of the material properties on the mesoscale. This is done exemplary for a tensile test specimen. Therefore, in a first step tensile test specimens are cut out of the plate, while the orientation of the tensile test specimen coincides with the main flow direction of the melt front (2). The tensile test specimens are used to obtain the global Young’s modulus on the component level in Sect. 6.2 of the material for a validation of the presented procedure. As the numerical model should also conclude information about the material microstructure a cross-section is defined (3), for which the microstructural properties are determined based on a micrograph (4). The selected cross-section of $3.37\,\hbox {mm} \times 3\,\hbox {mm}$ is parallel to the main flow direction and hence, coincide with the load direction of the tensile test in Sect. 6.2 (2). By doing so, the cross-section is used to analyze the Young’s modulus of the specimen’s microstructure on a numerical basis in Sect. 5.1 (5). Afterwards, the results are validated experimentally by nanoindentation in Sect. 5.2. Here, the specimens are small cuboids, where one side of the cuboid is perpendicular to the micrograph cross-section (6). The surface of the plate is the second side. This allows one to conduct indentation tests in the main flow direction as well as in thickness direction of the plate and specimens, respectively. The cuboids have an edge length of $20\,\hbox {mm} \times 5\,\hbox {mm} \times 3\,\hbox {mm}$.

The numerical simulation on the component level assuming linear elastic material behavior refers to the same cross-section as the microstructural analysis. Here, the dimensions coincide with the standard measurement length of a tensile test specimen defined in [38]. Therefore, the edge length is $50\,\hbox {mm} \times 3\,\hbox {mm}$.

The material properties of the two components used for the numerical simulations are provided in Table 1.

Table 1 Material properties of the fiber and matrix material

4 Extraction of the probabilistic characteristics

4.1 Theoretical description of the fiber orientation

The orientation of a single fiber is expressed by the unity vector ${\mathbf {p}}$, that points in the direction of the fiber axis as shown in Fig. 3. The components of this vector are expressed by the angles introduced in Fig. 3 as [43, 63]

$$\begin{aligned} {\mathbf {p}} = \begin{bmatrix} \sin \theta \cos \varphi \\ \sin \theta \sin \varphi \\ \cos \theta \end{bmatrix} \end{aligned}$$

(42)

To derive the orientation from the micrograph the components of the orientation vector are formulated in terms of the geometrical properties of the fiber cross-section. In this case the minor and major axis of the ellipse as well as its horizontal and vertical dimensions with respect to the coordinate system are used, which leads to the following expressions for the trigonometrical functions of $\varphi$

$$\begin{aligned} \sin \varphi = \frac{\varDelta _{\text {h}}}{l_{\text {ma}}} \qquad \cos \varphi = \frac{\varDelta _{\text {v}}}{l_{\text {ma}}} \end{aligned}$$

(43)

and $\theta$

$$\begin{aligned} \sin \theta = \sqrt{1-\frac{l_{\text {min}}^2}{l_{\text {ma}}^2}} \qquad \cos \theta = \frac{l_{\text {min}}}{l_{\text {ma}}}. \end{aligned}$$

(44)

Here $\varDelta _{\text {h}}$ and $\varDelta _{\text {v}}$ are the projection of the elliptic cross-section on the $x-$ and $y-$axis, respectively. The parameters $l_{\text {min}}$ and $l_{\text {ma}}$ are introduced in Fig. 3.

Fig. 3

Angle and cross-section definition for the description of the fiber orientation and fiber length, see also [26, 43, 63]

For a group of fibers, the orientation is given by the second order orientation tensor ${\mathbf {A}}$ introduced in [1] as

$$\begin{aligned} {\mathbf {A}} = \oint _S \varPsi ({\mathbf {p}}){\mathbf {p}}{\mathbf {p}} {\text {d}}S = \begin{bmatrix} A_{11} &{} A_{12} &{} A_{13} \\ A_{21} &{} A_{22} &{} A_{23} \\ A_{31} &{} A_{32} &{} A_{33} \end{bmatrix}. \end{aligned}$$

(45)

Here $\varPsi ({\mathbf {p}})$ is the probability density distribution function for the fiber orientation defined in [13] and S the surface of the unit square. In context of a component made by mold injection and with respect to the introduced coordinate system the elements on the diagonal represent a fiber orientation in the melt flow direction ($A_{11}$), perpendicular to the melt front ($A_{33}$), and in thickness direction ($A_{22}$). The sum of these three elements equals one [73]. With the fiber orientation vector defined in Eq. (42) the elements of the orientation tensor is written as

$$\begin{aligned} A_{ij}= & {} \langle p_i p_j \rangle \nonumber \\= & {} \begin{bmatrix} \langle \sin ^2 \theta \cos ^2 \varphi \rangle &{} \langle \sin ^2 \theta \sin \varphi \cos \varphi \rangle &{} \langle \sin \theta \cos \theta \cos \varphi \rangle \\ \langle \sin ^2 \theta \sin \varphi \cos \varphi \rangle &{} \langle \sin ^2 \theta \sin ^2 \varphi \rangle &{} \langle \sin \theta \cos \theta \sin \varphi \rangle \\ \langle \sin \theta \cos \theta \cos \varphi \rangle &{} \langle \sin \theta \cos \theta \sin \varphi \rangle &{} \langle \cos ^2 \theta \rangle \end{bmatrix}.\nonumber \\ \end{aligned}$$

(46)

In terms of the geometrical properties of the elliptic cross-section this leads to [63]

$$\begin{aligned} A_{ij}= & {} \langle p_i p_j \rangle \nonumber \\= & {} \begin{bmatrix} \left\langle \varDelta _{\text {v}}^2 \left( \frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}\right) \right\rangle &{} \left\langle \varDelta _{\text {v}}\varDelta _{\text {h}} \left( {\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right) \right\rangle &{} \left\langle \varDelta _{\text {v}}^2 \sqrt{\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right\rangle \\ \left\langle \varDelta _{\text {v}}\varDelta _{\text {h}} \left( {\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right) \right\rangle &{} \left\langle \varDelta _{\text {h}}^2 \left( \frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}\right) \right\rangle &{} \left\langle \varDelta _{\text {h}}^2 \sqrt{\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right\rangle \\ \left\langle \varDelta _{\text {v}}^2 \sqrt{\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right\rangle &{} \left\langle \varDelta _{\text {h}}^2 \sqrt{\frac{1}{l_{\text {ma}}^2} - \frac{l_{\text {min}}^2}{l_{\text {ma}}^4}} \right\rangle &{} \left\langle \frac{l_{\text {min}}^2}{l_{\text {ma}}^2} \right\rangle \end{bmatrix}.\nonumber \\ \end{aligned}$$

(47)

Fig. 4

Different stages of the image processing routine

4.2 Methodology

For the numerical simulation of SFRC the probabilistic characteristics of the microstructure are required. In [63] a procedure is presented, that allows one to derive the second-order orientation tensor of the fibers from a micrograph. This procedure is adapted to obtain the probabilistic characteristics and their spatial distribution of the fiber length, diameter, and orientation as well as the second-order orientation tensor from a micrograph in this study. All presented results are based on a micrograph with a size of $3370\,\upmu \hbox {m}$ x $3000\,\upmu \hbox {m}$ captured with a digital microscope KEYENCE VHX-5000. The panorama image is generated by stitching 323 individual images with a magnification of 1500. This leads to a resolution of 558 px per $100\,\upmu \hbox {m}$. Hence, the procedure implies ergodicity for the extracted microstructural properties with respect to the manufactured plate with an edge length of $300\,\upmu \hbox {m}$.

The main steps for the extraction of the probabilistic characteristics are depicted in Fig. 4. Based on the original micrograph first the fibers are detected before the image is transformed to a binary image. This binary image is then further processed with the image processing toolbox of Matlab^®. Using the function regionprops the orientation, centroid as well as major and minor axes of each ellipse are determined. With these values the elements of the orientation tensor $A_{ij}$ given in Eq. (47) are calculated.

4.3 Probabilistic characteristics

4.3.1 General results

For the determination of the probabilistic characteristics only fibers are taken into account that are within the boundaries of the micrograph. Fibers reaching over the micrograph edges are neglected since a correct determination of the major axis is not possible. In total 9721 fibers are detected within the micrograph cross-section. Below the results of the main fiber characteristics like fiber length (major axis), fiber diameter (minor axis), fiber orientation, and fiber volume fraction as well as their spatial distribution are discussed. Figure 5a shows the spatial distribution of the obtained fiber length. As the probability of detection for a single fiber depends strongly on the orientation of the fiber, in [63] a procedure is proposed that weights the fiber length with respect to its probability of detection. It is assumed, that fibers parallel to the micrograph cross-section are less likely to be detected in a micrograph than fibers perpendicular to it. In context of the presented framework this component of the fiber orientation is given by the angle $\theta$ as defined in Fig. 3 and Eq. (44). Using this angle the weighting factor is given by [63]

$$\begin{aligned} w_i = \frac{1}{\cos \theta } = \frac{l_{\text {ma}}}{l_{\text {min}}}. \end{aligned}$$

(48)

Fig. 5

Results of the fiber length, fiber orientation, as well as correlation between fiber length and fiber orientation based on the micrograph

The results given in Fig. 5a already include the weighting. Even then a profuse amount of short fibers with a length of less than $20\,\upmu \hbox {m}$ is indicated. This is also supported by a mean fiber length of $46.6\,\upmu \hbox {m}$. Besides this, the results lead to the conclusion of a layered structure due to the mold injection process as shown in [5, 12, 14, 16, 48, 60]. This is discussed more in detail in Sect. 4.3.2.

Next is the fiber orientation $\varphi$, that describes the angle between the major axis of the ellipse and the horizontal axis as shown in Fig. 3. The results are depicted in Fig. 5b. Again the distribution is plotted against the specimen thickness coordinate. The distribution clearly shows a preferred orientation of the fibers along the specimen and therefore, with the melt flow direction. In contrast to the fiber length, the orientation is independent of the location of the fiber. The preferred orientation of the fibers and therefore, an orientation dependence of the material properties of the compound with respect to the overall specimen orientation is further confirmed by the correlation analysis of the fiber length and the fiber orientation. With an increasing fiber length, the fiber orientation shows a decreasing spreading around an orientation angle of $0^{\circ }$, see Fig. 5c.

The overall results of the fiber diameter are given in Fig. 6. The probability density function of the fiber diameter meets the expectation of a normal distribution with a mean of $9.6\,\upmu \hbox {m}$. Compared to the results of other studies this value appears a little bit low. Usually, the diameter of glass fibers is approximated with $10\,\upmu \hbox {m}$ [25]. The fiber diameter corresponds with the minor axis of the pattern recognition results. If the fibers are cut perpendicular to the fiber length these two magnitudes coincide very well. Only if the fiber is almost parallel to the micrograph cross-section there might be a significant deviation. However, since the probability of detection of these fibers is small and there is no weighting considered for the fiber diameter the influence is neglectable. Another influence is more significant.

Fig. 6

PDF fiber diameter

As shown in Fig. 4 (left) there is a dark shadow between the fiber and the matrix material that cannot be clearly assigned to one of the two components. The difference between the inner and outer circle of the shadow is approximately $3-5$ px. This leads to a deviation of up to $1\,\upmu \hbox {m}$ by a resolution of $0.18\,\upmu \hbox {m}$ per px in vertical and horizontal direction. Hence, the deviation of the obtained fiber diameter and the values taken from the literature can be assigned to this phenomenon.

Finally, the overall fiber volume fraction is $16.7\%$, which equals a fiber mass fraction of $28\%$ based on the material properties provided in Table 1. For the raw material a fiber mass fraction of $30\%$ was specified. Therefore, the overall fiber mass fraction appears a little bit below the specification. The fiber mass and fiber volume fraction are connected by the density of the matrix and fiber material, respectively. The precise density of the two components is unknown and the data provided in Table 1 are taken from literature, which usually gives only approximated values since the specific values vary between different charges. Taking these variations into account a fiber volume fraction of $16.7\%$ leads to a fiber mass fraction in a range of $27\%$ up to $30\%$, which meets the specifications.

4.3.2 Analysis of the layered structure

During the injection mold process, the fiber orientation varies over the specimen thickness due to different flow velocities and shear forces [35]. With respect to the fiber orientation the cross-section of the component made by mold injection is divided into different layers. Figure 7 gives an overview of the two commonly used orientation schemes [5, 12, 14, 16, 48, 60].

Fig. 7

Fiber orientation schemes due to mold injection process, compare [60]

The results of the fiber length distribution over the thickness indicates that the used specimen shows this kind of layered structure as well. To analyze the layered structure more in detail the components $A_{11}$ and $A_{33}$ of the orientation tensor introduced in Eq. (47) are calculated and plotted over the cross-section thickness. As discussed in Sect. 4.1 the probability of detection of a fiber orientation parallel to the molt flow direction is given by $A_{11}$ ($\varphi = 0^\circ , \ \theta = 90^\circ$). Perpendicular to the melt flow direction the probability is expressed by $A_{33}$ ($\varphi = \theta = 0^\circ$). The results depicted in Fig. 8 confirm the assumption based on the fiber length distribution. Five individual layers are recognizable.

Fig. 8

Results for the elements $A_{11}$ and $A_{33}$ of the orientation tensor based on the micrograph

Furthermore, the values of $A_{11}$ and $A_{33}$ indicate also that the orientation component in thickness direction $A_{22}$ is small compared to the other two components. This supports the overall assumption of mainly horizontally aligned fibers, since high values of $A_{22}$ would indicate vertically orientated fibers.

In the following sections a numerical modeling procedure for SFRC is presented. Since the main objective is the representation of the microstructural effects on the component level the layered structure must also be taken into account. Therefore, the layer thicknesses are determined based on the obtained orientation tensor as well as the distribution of the fiber length. The fiber length is an indirect measurement of the fiber orientation as short fibers with an almost circular cross-section are orientated perpendicular to the micrograph cross-section ($\theta = 0^\circ \ \rightarrow \ A_{33}$), whereas long fibers are parallel to the micrograph cross-section ($\theta = 90^\circ \ \rightarrow \ A_{11}$). Based on the results shown in Fig. 8 for the orientation tensor elements $A_{11}$ and $A_{33}$ as well as the results for the fiber length distribution Fig. 5a the cross-section consists of five layers. The thickness of the skin layers at the top and bottom of the cross-section is approximated with $100\,\upmu \hbox {m}$, the core layer in the middle of the cross-section is $300\,\upmu \hbox {m}$ thick. Therefore, the shell layers between the skin and core layers have a thickness of $1250\,\upmu \hbox {m}$ each.

Fig. 9

Histogram of the fiber length for the shell and core layers

To determine the probabilistic characteristics of the numerical simulation in Sect. 5 the layers are analyzed individually and the results are compared with each other. However, due to the limited number of fibers within the skin layers these are not taken into account. In Fig. 9 the histogram of the fiber length is shown for the two shell layers (left) and the core layers (right). The results of the two shell layers (colored in red and blue) coincide very well. Therefore, these two layers can be modeled using the same probabilistic characteristics for the fiber length.

The fiber diameter distribution is independent of the layer scheme as the fiber diameter is only minimally affected by the mold injection process. The main influence is the initial fiber production [25]. Therefore, no further analysis is conducted regarding the fiber diameter.

For the fiber orientation both aspects the information about the layer as well as the correlation with the fiber length as depicted in Fig. 5b, c are taken into account. As already derived from Fig. 5b the fiber orientation distribution described by $\varphi$ does not vary significantly between the different layers. However, as indicated in Fig. 5c the correlation between $\varphi$ and the fiber length must be considered for the modeling of artificial SFRC microstructures.

The presented results seem to contradict the assumption of ergodicity of the micrograph at first, because the probabilistic characteristics of the fiber length depends on the spatial coordinates due to the layered structure of the cross-section. This means that the microstructural properties are no longer homogeneous or stationary, which implies that they cannot be ergodic. But as shown in Fig. 9 and discussed before the fiber length characteristics for the two analyzed shell layers show almost identical characteristics. The same holds for the orientation of the fibers as depicted in Fig. 8. Based on this and the fact that the fiber diameter characteristics are independent of the layered structure, each layer is assumed to be homogeneous and hence, layer-wise ergodic estimators appear appropriate.

5 Modeling on the mesoscale

In this section a procedure is introduced for the numerical modeling of SFRC on the mesoscale. The first approach is based on the micrograph used in Sect. 4 to extract the probabilistic characteristics of the microstructure. This is followed by the use of artificial microstructures. Here, the numerical model still represents the microstructure and hence, shows the same probabilistic properties on the microscale as the micrograph.

5.1 Numerical simulations

5.1.1 Model description

The numerical model on the mesoscale represents the micrograph used in Sect. 4 to extract the probabilistic properties of the microstructure. It has a rectangular shape with an edge length of $3370\,\upmu \hbox {m} \times 3000\,\upmu \hbox {m}$. The material definition and mesh generation follow the results presented in [59]. Therefore, the model is discretized by a mapped mash consisting of second order Lagrange elements with an edge length of $10\,\upmu \hbox {m} \times 10\,\upmu \hbox {m}$ and the material properties are passed to the integration points by arrays that represent the underlying microstructure. In contrast to the results presented in [59] a plain strain state is assumed as the micrograph is a cross-section of a larger tensile test specimen. An overview of the specimen’s geometry as well as the material properties of the two components are provided in Sect. 3, Fig. 2(3) and Table 1.

For the numerical simulation of the tensile test, the horizontal displacement is fixed at the left edge and the vertical displacement is fixed at the lower edge of the numerical model. Two load cases are analyzed with this model. First a load of $100\,\hbox {MPa}$ is applied at the right edge, second is a load of $100\,\hbox {MPa}$ at the upper edge. Using these two load cases the Young’s modulus in horizontal and vertical direction are obtained by extracting the horizontal (x) and vertical (y) displacement components at the right and upper edges, respectively. The Young’s modulus is then calculated by

$$\begin{aligned} E_\text {h} = \frac{\sigma _\text {r}}{\langle u_\text {h} \rangle } l_\text {h} \qquad \text {and} \qquad E_\text {v} = \frac{\sigma _\text {u}}{\langle u_\text {v} \rangle } l_\text {v}, \end{aligned}$$

(49)

where the indices h and v represent the horizontal and vertical component and the indices r and u the right and upper edge, respectively. All numerical simulations are based on linear theory. Finite deformations are not taken into account.

5.1.2 Numerical simulation based on the micrograph

In a first step the material properties of the micrograph cross-section itself are analyzed. This is done by generating three different arrays, one for each material parameter. The arrays represent the micrograph cross-section with a resolution of $1\,\upmu \hbox {m} \times 1\,\upmu \hbox {m}$. This is in accordance with the findings in [59]. With these arrays the material properties are passed to the integration points.

Table 2 contains the results of the mean strain as well as Young’s modulus in horizontal and vertical direction.

Table 2 Results of the numerical simulation based on the micrograph analyzed in Sect. 4

5.1.3 Numerical simulation based on the artificial microstructure

Below the analyzed configurations, the generation process of the microstructure as well as the numerical results are presented

Analyzed configurations

The analysis of the microstructure emanates from a layered structure of the cross-section. As presented in Sect. 4.3.2 the cross-section can be divided into five layers. Based on this finding three different configurations are investigated here. With this approach the influence of the layered structure on the material properties is analyzed. This is important for the representation of the microstructure by random fields in Sect. 6. The following, three different configurations are under investigation. (I) For the first configuration the probabilistic characteristics of the microstructural properties of the whole cross-section are used. This leads to some kind of homogenized material properties. (II) Next is the generation of an artificial microstructure based on the probabilistic characteristics of the microstructural properties of the shell layers only. Therefore, the influence of the skin layers as well as the core layer are neglected. (III) In a last step the core layer is taken into account as well. Therefore, in this case the numerical model consists of three different layers. As discussed in Sect. 4.1 the probabilistic properties of the skin layers are not sufficient to derive the probabilistic characteristics of these layers. Due to this an artificial five-layer microstructure is not investigated. Furthermore, the representation of all layers contradicts a compact and cost saving approach of modeling SFRC.

Generation of the microstructure

The microstructure of the SFRC is generated in accordance with the procedure presented in [59]. In addition, the correlation between the fiber length and fiber orientation is taken into account. Hence, the generation of the microstructure comprises the following steps. First the fiber centroid is generated by a Monte Carlo sampling. If necessary, the coordinates are then assigned to one of the layers and the fiber length is sampled based on the corresponding layer characteristics. The layer identification is only required for configuration III, though. The overall characteristics are used to set a fiber diameter due to the missing correlation as shown in Sect. 4.3. For the assignment of the fiber orientation however, the correlation with the fiber length is essential. Finally, the fiber is added to the preset area if there is no overlap with an already existing fiber. The procedure is repeated until a predefined fiber volume fraction is reached. Since the fiber volume fraction of the different layers are not equal, the threshold varies for each configuration and the different layers. Table 3 gives an overview of the fiber mass fraction for each configuration and layer. In Fig. 10 the shell layers of the microstructure and an artificial microstructure are mapped one above the other. There are no major differences between the images recognizable.

Table 3 Fiber mass fraction for each layer of the artificial microstructure

Fig. 10

Comparison of shell layers of the micrograph (upper two images) and an artificial microstructure (lower image). All measures in $\upmu \hbox {m}$

The generated microstructures are analyzed in the same way as the numerical model of the micrograph. Instead of the micrograph cross-section the arrays represent now the artificial microstructure. For statistical reasons the simulation is done for 500 different microstructures of each configuration.

Results of the numerical simulation

Table 4 Results of the numerical simulation based on the artificial microstructures

Table 4 gives an overview of the numerical results for the artificial microstructures. In addition to the mean value and standard deviation of the Young’s modulus for the horizontal and vertical direction the deviation to the results of the micrograph are calculated. The results of the artificial microstructures meet the results based on the micrograph within a maximal deviation of $5\%$ for the horizontal and $8\%$ for the vertical direction. In both directions the highest deviations are observed for configuration I, where the different layers and their probabilistic characteristics are not distinguished. The deviation to the micrograph decreases for configuration II and III. The impact of modeling three different layers instead of only one is marginal compared to the computational costs. Hence, it appears to be convenient to reduce the modeling of the microstructure to the shell layers for the determination of the correlation structure, that is required for the numerical simulation on the component level in Sect. 6. This assumption is verified experimentally first. Furthermore, the numerical results indicate only a minor anisotropy of the material. This can be assigned to the derived aspect ratio of 4.9 based on the mean values of the fiber length and fiber diameter.

5.2 Experimental validation

The results of the numerical simulation presented in Sect. 5.1 are verified by an experimental investigation of the Young’s modulus based on the material, that was characterized in Sect. 4. As the presented results and the probabilistic characteristics of the material are based on a two-dimensional analysis of the cross-section the Young’s modulus is experimentally determined by nanoindentation. Compared to standard tensile tests this procedure allows one to measure the near surface material properties [20] and hence, in combination with a projected indentation area of approximately $7000\,\upmu \hbox {m}^{2}$ characterize the material on the mesoscale.

Fig. 11

Scheme load cycle nanoindentation [44, 67] (left), micrograph of the indentation location after unloading (right)

5.2.1 Framework nanoindentation

For the experimental determination of the material properties by nanoindentation the slope of the force-displacement curve of the unloading process is calculated, see Fig. 11 (left). The indentation or reduced modulus is obtained by [51, 57]

$$\begin{aligned} E_r = \frac{{\text {d}} P}{{\text {d}} h} = \frac{1}{\beta } \frac{\sqrt{\pi }}{2}\frac{S}{\sqrt{A_p(h_c)}}, \end{aligned}$$

(50)

where S is the stiffness of the contact, $A_p$ the projected area of the indentation tip for a contact depth $h_c$, and $\beta$ an empirical correction factor of the indenter uniaxial symmetry when using pyramidal indenter [29, 69]. As done in [41] $\beta$ is set to one in this analysis. This is possible as the value of $\beta$ usually varies between 1.02 and 1.08, which leads to a deviation of the indentation modulus of up to 3% [51, 57]. The projected area of a perfectly sharp Berkovich tip, which is used in this study, is usually approximated by [11]

$$\begin{aligned} A_p = \pi h_c^2 \tan ^2 \varphi = 24.5 h_c^2, \end{aligned}$$

(51)

with an effective semi-angle of $\varphi = 70.32^{\circ }$ [6]. Due to imperfections, a calibration of the projected surface is mostly used. For this calibration the projected surface is approximated with the function [51]

$$\begin{aligned} A_p(h_c)= & {} 24.56 h_c^2 + C_1 h_c^1 + C_2 h_c^{1/2} +\nonumber \\&+ C_3 h_c^{1/4} + \dots + C_8 h_c^{1/128} \end{aligned}$$

(52)

In Fig. 11 (right) the indentation mark of a Berkovich tip is depicted. Finally, between the indentation modulus and the Young’s modulus of the specimen material the following relation holds

$$\begin{aligned} \frac{1}{E_r} = \frac{1-\nu ^2}{E} + \frac{1-\nu _i^2}{E_i}. \end{aligned}$$

(53)

Here, $E_i$ and $\nu _i$ are the Young’s modulus and Poisson’s ratio of the indentation material, respectively. In this study the indentation tip is made of diamond with a Young’s modulus of 1143 GPa and a Poisson’s ratio of 0.0691 [40].

Table 5 Results of the indentation tests

5.2.2 Setup and results

For the experimental verification of the numerical simulation on the mesoscale the indentation modulus is measured at the surfaces of the cuboid. First is the measurement in x-direction. The measurement points are arranged in a grid of 37 $\times$ 9 points, that cover an area of $9000\,\upmu \hbox {m} \times 1600\,\upmu \hbox {m}$. Consequently, the distance between the measurement points is $200\,\upmu \hbox {m}$ in z- and $250\,\upmu \hbox {m}$ in y-direction, respectively. For this configuration the indentation modulus is measured with a maximum indentation force of 500 mN and 1500 mN. The results are given in Table 5. The indentation modulus for both load cases match within the standard deviation. Hence, the indentation modulus is independent of the maximum indentation force in a range of 500 mN to 1500 mN. As in the numerical simulations, the indentation modulus is also determined experimentally in a second direction. Therefore, the indentation test is repeated in y-direction. Here only one load case is conducted with a maximum load of 1500 mN. The result is also provided in Table 5.

In Table 5 not only the results of the indentation tests are summarized, but also the calculated values of the Young’s modulus are given. This is done be evaluating Eq. (53). For this the Poisson’s ratio of the analyzed cross-section is obtained by using the analytical material model introduced by Halpin and Tsai [27, 28, 70] and the probabilistic characteristics provided in Sect. 4.1. Besides a Poisson’s ratio of 0.379 a Young’s modulus of 6.21 GPa is calculated. As this value meets the numerical results of the micrograph with a deviation of less than 1% for the Young’s modulus, this Poisson’s ratio is used to derive the material Young’s modulus from the reduced modulus obtained by indentation in x-direction. However, the obtained Poisson’s ratio for the correction in x-direction cannot be used for a correction in y-direction, because the assumption of transversally isotropic material behavior is not applicable for the analyzed cross-section. The main reason is the varying orientation of the fibers. This holds not only when considering the layered structure of the cross-section, but also when reducing the representation of the cross-section to the shell layers only. This conclusion is supported by the mismatch of the Young’s modulus in x- and y-direction, as shown in Table 4.

Table 6 Comparison of the experimental and numerical obtained results

5.2.3 Comparison with numerical results

Table 6 gives an overview of the experimentally and numerically obtained values of the Young’s modulus on the mesoscale. For both directions the results of the numerical simulations meet the results of the experimental investigation within the standard deviation. Consequently, the presented modeling approach on the mesoscale is verified by the conducted experiments. Furthermore, the reduction of the cross-section representation to the shell layers, as suggested in Sect. 5.1.3, appears to be valid.

6 Modeling on the component level

So far the modeling process is based on the microstructural properties of the analyzed cross-section (see Sect. 4) given by the mean and standard deviation of the fiber length, fiber diameter, and fiber orientation. The aim of this section is to provide a numerical modeling approach on the component level including the microstructural properties of short fiber-reinforced material.

This is done by representing the material properties by homogeneous random fields. Since random fields also involve information about local correlation between the realization at each point the correlation structure and correlation function are determined first. In this context the artificial microstructures, introduced in Sect. 5 are used to derive the correlation functions of the elasticity tensor coefficients.

The procedure for the generation of the artificial microstructures for SFRC introduced in Sect. 5.1 leads to almost identical mechanical properties as the microstructure of the micrograph of Sect. 4.1. This is not only found on a numerical basis, but also verified experimentally by nanoindentation in Sect. 5.2. Hence, in this section the procedure is used to expand the modeling approach to the component level.

A crucial issue for the representation of material properties is their positive nature. Since Gaussian random fields assume normal distributed underlying random variables, negative realizations are possible [17, 66]. Therefore, due to the elliptic property of the elasticity partial differentiation operator the use of Gaussian random fields for the representation of material properties is not suitable in context of multi-scale modeling of heterogeneous material [64]. Hence, the use of non-Gaussian random fields is required to ensure a stochastic solution of second-order and the positive nature of the elasticity coefficients, which is also state of the art [9, 21, 22, 42, 46, 68].

A non-Gaussian random field $M(\omega ,{\mathbf {x}})$ is given by

$$\begin{aligned} M(\omega ,{\mathbf {x}}) = {\mathcal {G}} \lbrace X(\omega ,{\mathbf {x}}) \rbrace , \end{aligned}$$

(54)

where ${\mathcal {G}}$ is a non-linear mapping operator and $X(\omega ,{\mathbf {x}})$ a centered, homogeneous Gaussian random field as introduced in Sect. 2 [22]. In this study discretized random fields are used. Although the stochastic solution obtained here (using a Gaussian field) is not of second-order, computational (sample-wise) results may not be strongly impacted given the choice of model parameters and are thus presented below.

Table 7 Results of the auto-correlation lengths of the elasticity tensor coefficients using different correlation functions and a window size of $250\,\upmu \hbox {m}$

Fig. 12

Auto- and cross-correlation of the elasticity tensor elements

6.1 Numerical simulation

6.1.1 Correlation structure

As shown in Sect. 2.1 to Sect. 2.3 random fields describe the spatial distribution of random variables. The main characteristic is the correlation function which gives an information about the dependence of values at different locations. Hence, the correlation functions of the elasticity tensor elements must be determined first.

The correlation analysis is done in accordance with the procedure presented in [59] and hence, is based on the assumption of a SVE. As homogeneous second-order random fields are used to represent the material properties of a tensile test specimen, the correlation analysis as well as all remaining numerical simulations are based on the plain strain assumption. Using pure displacement and pure traction boundary condition as introduced in [74] the auto- and cross-correlation lengths of the elasticity tensor coefficients are calculated, respectively. Taking into account that the elasticity tensor coefficients for a plain strain state depend not only on the in-plane material properties but also on $\nu _{23}$ it is not possible to derive the engineering constants from the elasticity tensor coefficients without any further assumption. Due to this the correlation structure is obtained for the elasticity tensor coefficients instead of the engineering constants. In a next step these parameters are used to describe the material properties of the composite on the component level.

Using the moving window method, the auto- and cross-correlation is analyzed for a window size of $250\,\upmu \hbox {m}$, ${500}\,\upmu \hbox {m}$, and ${750}\,\upmu \hbox {m}$. As there are closed solutions for the Fredholm integral equation given in Eq. (19) for an exponential, Gaussian and triangle correlation function the use of one of these kernels is preferable.

Table 7 gives the results of the correlation lengths for these three correlation functions and the corresponding root mean square error (RMSE). The results indicate, that all correlation functions approximate the numerically obtained correlation behavior of the elasticity tensor coefficients within a RMSE of less than $1\,\upmu \hbox {m}$. Due to the common use of the exponential correlation function in the literature [17, 53, 66, 72], this correlation function is selected for the following generation of random fields using the Karhunen–Loève expansion.

6.1.2 Generation of random fields

Independent of the correlation function the Karhunen–Loève expansion always assume a linear correlation between the parameters. For the numerical model of the elasticity tensor coefficients of SFRC this assumption is satisfied not only for the auto-correlation but also the cross-correlation, as shown in Fig. 12.

One main parameter for the accuracy and convergence of the expansion of random fields is the amount of considered eigenvalues and hence, the number of terms used in the Karhunen–Loève expansion. Moreover, the required amount of terms is strongly affected by the ratio of the correlation length and the dimension of the random field [36]. Low ratios coincide with highly correlated random fields, which allows one to reduce the terms of the Karhunen–Loève expansion to represent the random field. However, for large domains or small correlation lengths and hence, an increasing ratio, more terms should be considered. Since the ratio of the correlation length and observed area is considerably large in this study 3000 terms are used during the series expansion. This meets the magnitude of terms used in [75] for the numerical simulation of the wave propagation in thin-walled structures, which is also characterized by a weak correlated random field and hence, a large ratio of domain expansion to correlation length.

Fig. 13

A realization for the four independent elasticity coefficients for the modeling of the material properties of SFRC based on the correlation length derived from a window size of $250\,\upmu \hbox {m}$ and an exponential correlation functions. All values in GPa

Figure 13 shows examples of random fields for the elasticity tensor elements, that are not equal to zero, based on a window size of $250\,\upmu \hbox {m}$ and exponential correlation functions, when assuming a two-dimensional model and fiber reinforced material. As shown in [59] the symmetry property still holds.

Table 8 Results of the analysis of the exemplary random fields with respect to possible negative realizations due to the underlying Gaussian distribution

As mentioned before, for the representation of the elasticity coefficients Gaussian random fields are used. This may lead to negative realization. To show, that in this case the use of Gaussian random fields is the generated fields are analyzed in detail. For this Table 8 provides the mean values, the standard deviation, as well as the minimal and maximal values. For the generation of these exemplary random field the underlying distribution is not modified to avoid negative realizations. Due to the moderate standard deviation only positive results are calculated, even if a Gaussian distribution is used for the elasticity coefficients. Furthermore, the results of this analysis may be checked for plausibility. The minimal and maximal values can be explained by areas where almost no fiber is found and by areas with a relatively high fiber volume fraction, respectively. Cases where $C_{11}$ is smaller than $C_{22}$ the fiber can be assigned to a variation of the fiber orientation.

6.1.3 Numerical model

The numerical model for the analysis of the material properties of SFRC is based on a tensile test specimen. Since the standard observation length defined in [38] is 50 mm the specimen is represented by a rectangle with an edge length of 50 mm $\times$ 3 mm. Vertical and horizontal displacements are fixed on the left and lower edge of the rectangle, respectively. As done in Sect. 5.1 100 MPa are applied on the right edge. Again all simulations are carried out assuming a plain strain state as well as linear theory.

For the determination of an adequate element size a convergence study is performed. This is done by increasing the number of elements in the vertical and horizontal direction until the variation of the resulting Young’s modulus is less than $0.5\%$. The aspect ratio of the element is not affected by the convergence analysis and therefore, is fixed with a value of 1. Table 9 gives the results for the convergence analysis based on the Young’s modulus. The element size is varied between an edge length of 200 mm up to 1 mm. Therefore, the smallest element size and hence, the distance between the integration points is comparable to the smallest correlation length. Based on the obtained mean value the results indicate that an element size of 1 mm $\times$ 1 mm is sufficient for the numerical simulation on the component level.

Table 9 Results of the convergence study for the element size of the numerical model on the component level

Table 10 Results of the experimentally obtained Young’s modulus and deviation to the previous observations

Compared to the obtained correlation length in Table 7 the material information at the integration points are independent of each other. This means that a Karhunen–Loève expansion is not stringently necessary to derive the random fields representing the material properties. The information can also be generated by a Monte Carlo sampling at each integration point. This circumstance allows one to neglect the cross-correlation between the elasticity tensor elements, that is provided in [59]. However, the auto-correlation and hence, the random fields used in this section to represent the material properties of the SFRC are still derived by Karhunen–Loève expansion. The simulations are carried out for all window sizes and boundary condition types used in Sect. 6.1.1 to analyze the correlation structure.

6.1.4 Results

The results of the numerical analysis based on the microstructural characteristics derived from a two-dimensional micrograph are summarized in Table 10. As expected the values based on an analysis with pure displacement boundary conditions (KUBC) decrease with an increasing window size whereas values based on pure traction boundary conditions (SUBC) increase with an increasing window size. This meets the multi-scale modeling approach with the Voigt and Reuss bounds [34] for a SVE. The very small standard deviation can be assigned to the element size, which has the same magnitude as the obtained correlation length.

6.2 Experimental validation

6.2.1 Experimental setup

The numerical results are validated experimentally by a standard tensile test. The tensile test specimens have the dimensions of 140 mm $\times$ 20 mm $\times$ 3 mm as shown in Fig. 2(2). As depicted in Fig. 2 the specimens are taken from a plate made by mold injection. The main orientation of the specimens coincides with the melt flow direction. In total 13 specimens are analyzed. To compare the results of the numerical simulation with the experimentally obtained values, the Young’s modulus is determined for the linear elastic range. Therefore, the Young’s modulus is calculated for a strain range of 0.05% to 0.25%. Based on the specimen geometry this equals a load range of 150 N to 750 N and is characterized by purely linear-elastic material behavior. The measurement length for the overall Young’s modulus of a specimen is 45 mm.

Table 11 Material properties of the matrix and fiber material of PA 6 GF 30 dry as molded

Table 12 Results of the auto-correlation lengths of the elasticity tensor coefficients using an exponential correlation functions and a window size of ${250}\, \upmu \hbox {m}$ based on the microstructure characteristics provided in [25] and the material properties of PA 6 GF 30

Table 13 Results of the numerically obtained Young’s modulus based on the microstructural characteristics of PA 6 given in [25] and deviation to the experimentally obtained Young’s modulus

6.2.2 Results and comparison

The results for the experimentally obtained Young’s modulus is given in Table 10. For a comparison with the numerical analyses the results of the modeling on the component level and their deviation to the experimental results are included as well. The results of the numerical simulation based on the probabilistic characteristics of the microstructure determined in Sect. 4.1 show a significant deviation from the experimental results of 34.3% up to 58.4%. However, the numerical data matches the results of the simulation on the mesoscale very good. The Young’s modulus in fiber direction is approximated on the mesoscale with 6 GPa in Sect. 5. This meets the numerical simulation conducted here with a minimal deviation of 2.2% for the correlation structure derived from a window size of ${500}\,\upmu \hbox {m}$ and pure displacement boundary condition. Therefore, the main reason for the significant deviation to the numerical simulation on the component level is assumed in the use of probabilistic characteristics of the microstructure obtained by a two-dimensional micrograph. This data is sufficient for numerical simulation of the material response on the mesoscale. However, for the representation of the material properties on the component level, which is done by the generation of homogeneous second-order random fields with the Karhunen–Loève expansion, requires a different set of input variables.

6.3 Modeling based on three-dimensional microstructure characteristics

6.3.1 Application of the procedure on values taken from literature

As discussed in Sect. 6.2.2 the results obtained by numerical simulation in Sect. 6.1.3 and the results of tensile tests presented in Sect. 6.2 do not match. It is assumed that the main reason is the lack of information about the three-dimensional micromechanical properties. To confirm this conclusion, the presented procedure is applied to three-dimensional microstructural data provided in [25]. In contrast to the analyses presented so far, tensile test specimens made of PA 6 are used in [25]. However, in both cases the fiber mass fraction is specified with $30\%$.

Table 14 Results of the auto-correlation lengths of the elasticity tensor coefficients using an exponential correlation functions and a window size of ${250}\,\upmu \hbox {m}$ based on the microstructure characteristics provided in [25] and the material properties of PBT GF 30

In a first step the correlation functions as well as the three-dimensional microstructure information of the elasticity tensor components are identified by taking into account the slightly different material parameters of PA 6 compared to PBT. The material properties provided in Table 11 are assumed dry as molded.

To generate the microstructure for the correlation function analysis the probabilistic characteristics of the fiber length, fiber diameter, and fiber orientation are taken from [25]. The characteristics of the fiber length and fiber orientation are given for tensile test specimens directly produced by mold injection. The probability density function of the fiber length meets a two-parameter Weibull distribution [7, 15] given by

$$\begin{aligned} f(l|a,b) = \frac{b}{a} \left( \frac{l}{a}\right) ^{b-1} \exp \left( -\frac{l}{a}\right) ^b. \end{aligned}$$

(55)

The Weibull parameters a and b are determined as

$$\begin{aligned} a = 292 \quad b = 1.96. \end{aligned}$$

(56)

The corresponding mean of the fiber length is ${\bar{l}} = {260}\,\upmu \hbox {m}$. The fiber orientation is described by an elliptic probability density function [25]. Therefore,

$$\begin{aligned} f(\theta ) = \frac{h_2}{\sqrt{1-\frac{h_1^2-h_2^2}{h_1^2}\cos ^2(\theta )}} \end{aligned}$$

(57)

holds. Here, $h_1$ and $h_2$ are the semi-minor and semi-major axis, respectively. The semi axes ratio for this probability density function measured by $\mu \hbox {CT}$ is 22.1. The fiber diameter d is analyzed for tensile test specimens cut out of a pre-produced plate. Since the fiber diameter is not influenced significantly by the mold injection process these values can be combined. As expected the fiber diameter shows a normal distribution. The corresponding probability density function is written as

$$\begin{aligned} f(d) = \frac{1}{\sigma \sqrt{2 \pi }} \exp \left[ -\frac{1}{2} \left( \frac{d-\mu }{\sigma } \right) ^2 \right] \end{aligned}$$

(58)

with a mean value $\mu = {10.9}\,\upmu \hbox {m}$ and a standard deviation $\sigma = {0.9}\,\upmu \hbox {m}$. The derived information of the correlation structure is summarized in Table 12.

The results of the numerical simulation of a tensile test using the presented data for the representation of the microstructure are provided in Table 13. In addition, the numerically obtained Young’s modulus of the material is characterized experimentally in [25] as well. Therefore, Table 13 also holds the results of the conducted experiments and the deviation between the numerical simulations and experiments.

The results presented in Table 13 indicate that the introduced procedure for the numerical simulation of SFRC on the component level including information of the three-dimensional microstructure leads to plausible results. The numerical simulations based on random fields characterized by correlation functions obtained for a window size of ${250}\,\upmu \hbox {m}$ and the mean values for pure displacement boundary conditions show a minimal deviation of 1.54%. The deviation starts to increase with an increasing window size. This indicates that the use of larger window sizes leads to a loss of information about the microstructure, that is necessary to obtain the correct material response on the component level. Due to the larger aspect ratio of 23.9 the results also reveal a more distinct anisotropy in contrast to the simulation based on the microstructure.

A further validation step is the comparison of an experimentally obtained local Young’s modulus distribution with the spatial fluctuation of the Young’s modulus based on the modeling with random fields. Unfortunately, a local distribution of the Young’s modulus is not provided in [25]. Therefore, in a last step the presented characteristics are combined with the material properties of PBT GF 30.

Table 15 Results of the numerically obtained Young’s modulus based on the microstructural characteristics of PA 6 given in [25] in combination with the material properties of PBT GF 30 and deviation to the experimentally obtained Young’s modulus

Table 16 Local distribution of the material properties based on numerical simulations and experiments. All values in GPa

6.3.2 Transfer of the microstructural characteristics to PBT GF 30

First a correlation analysis based on the new combination of microstructural and material properties is conducted, Table 14. As the previous analysis indicates that the representation of the microstructure with random fields for a correlation structure based on a window size of $250\,\upmu \hbox {m}$ shows the best fit, the final analysis is limited to this configuration. The results of the numerical and experimental analysis, given in Table 15, confirm the presented procedure. The deviation between the numerically and experimentally obtained values is less than $1\%$. Furthermore, the obtained minimal and maximal values show he same trend for the numerical simulation as well as the experiments. These values indicate the Young’s modulus range for the analyzed specimens.

However, a further important property is the local distribution of the material property within one specimen. Therefore, the Young’s modulus distribution over the observation length is measured by dividing the original measurement length into sections with a length of 5 mm. For each section the Young’s modulus is obtained individually on a numerical and experimental basis. The results are given in Table 16. The mean values of the chosen data sets fit very well. In contrast to this, the standard deviation of the experimentally obtained data set is higher than the one obtained for the numerical results. This is also indicated by the range of the values. The corresponding minimal and maximal values are marked in Table 16. The reason for this is determination of the correlation length on the mesoscale in combination with the used element size for the numerical simulation.

7 Summary and conclusion

The presented work consists of three steps that build together the proposed modeling approach for a tensile test specimen made of SFRC. These are the analysis of the microstructure, the determination of the correlation structure of the elasticity tensor elements and the generation of random fields for the representation of the material properties by the Karhunen–Loève expansion on the component level.

The analysis of the microstructure is based on a two-dimensional micrograph which reveals a layered structure of the cross-section. Based on the data the cross-section can be divided into five layers, namely a core layer, that is surrounded by a shell and a skin layer at the top and bottom. This meets the well-known orientation scheme due to mold injection process. Numerical simulation based on the derived probabilistic characteristics of the fiber length, fiber diameter, fiber orientation as well as fiber volume fraction show that the information about the layered structure influences the Young’s modulus of the analyzed cross-section. A validation with experimentally obtained Young’s modulus by nanoindentation indicates, that a homogenization based on the overall probabilistic characteristics underestimates the material properties of the cross-section. In contrast to this the modeling based on a layered structure consisting of the core and shell layers shows only a marginal deviation to an approach limited to the shell layers. Therefore, the representation of the microstructure by the shell layers only appears sufficient and is used for the determination of the correlation structure for the numerical simulation on the component level.

For the numerical simulation on the component level first the probabilistic characteristics based on a two-dimensional micrograph of the shell layers is used to derive the correlation structure. However, a comparison with conducted tensile tests show large deviations between the numerically and experimentally obtained results for the Young’s modulus. In fact, the numerical results meet the Young’s modulus obtained by nanoindentation instead. This leads to the conclusion that the numerical modeling on the component level requires a full three-dimensional analysis of the microstructure as a tensile test is no longer reduced to near surface measurements. This conclusion is proven by applying the presented approach to probabilistic characteristics of a microstructure of SFRC obtained by $\mu \hbox {CT}$. The resulting minimal deviation of the numerical simulation and the conducted experiment is about 1.5%. Finally, the local distribution of the material properties is investigated both numerically and experimentally. The results show the same trend. However, the spatial fluctuation seems to be more prominent experimentally than for the numerical simulations. One reason might be the used correlation lengths, that are smaller than the element size. This issue could be solved by deriving the correlation length of each elasticity tensor component not by the moving window method in the mesoscale. Instead the correlation lengths give additional independent parameters like the engineering constants. The correlation lengths are then determined in the same way as the material properties by fitting the parameters to experimental data. This approach is already successfully used in [74, 75], where the correlation length of the Young’s modulus is determined in such a way that the phenomenon of the continuous wave mode conversion, detected by the experimental observation of guided ultrasonic waves in carbon fiber reinforced plastics, can be observed in numerical simulations as well. This approach will be combined with the use of non-Gaussian random fields.

It is concluded, that the presented procedure is suitable for the numerical simulation of components made of SFRC. For an adequate representation on the mesoscale the probabilistic characteristics of a two-dimensional cross-section is sufficient. The numerical simulation on the component level, however, require a knowledge of the three-dimensional probabilistic properties of the microstructure.