Geometrically exact elastoplastic rods: determination of yield surface in terms of stress resultants

Abstract

This work addresses the determination of yield surfaces for geometrically exact elastoplastic rods. Use is made of a formulation where the rod is subjected to an uniform strain field along its arc length, thereby reducing the elastoplastic problem of the full rod to just its cross-section. By integrating the plastic work and the stresses over the rod’s cross-section, one then obtains discrete points of the yield surface in terms of stress resultants. Eventually, Lamé curves in their most general form are fitted to the discrete points by an appropriate optimisation method. The resulting continuous yield surfaces are examined for their scalability with respect to cross-section dimensions and also compared with existing analytical forms of yield surfaces.

Introduction

The theory of geometrically exact rods and its implementation have been applied in a wide range of research fields to model slender structures whose dimension in one direction is dominant compared to the other two dimensions. In contrast to classical beam theories such as the Euler-Bernoulli and Timoshenko beam theories, the theory of geometrically exact rods is not restricted to the geometrically linear case, but is able to describe large deformation as well as large rotation of the rod’s cross-section. This is the reason that rods are often used to model long nano wires and tubes [1, 2], cables [3], hair and other biological fibres [4]. The concept of modelling large rotation in slender structures goes back to the Cosserat brothers [5]. They consider every material point of the rod to be connected to the centerline and a triad of orthonormal vectors characterizing the orientation of the rod’s cross-section [6].

Table 1 In the sequel, strain measures and their energetically conjugates will be denoted differently for geometrically exact rods and for three-dimensional continuum mechanics, respectively

The modelling of three-dimensional elastoplasticity, both for the geometrically linear and nonlinear case, has been widely explored in the literature. As a key reference, the groundbreaking work of Simo and Hughes [7] can be mentioned. Attempts to reduce these theories to slender structures such as beams and rods have been made. For the case of linear beam theory, elastoplastic deformations have been taken into account in [8]. For the case of geometrically nonlinear beams, we refer to [9,10,11,12]. Attempts towards a direct approach to model viscoplastic and thermoelastoplastic rods are, e.g., [13] and [14, 15], respectively. There, the assumption is made that the strain prescriptors (the rod’s translational strains and curvatures) split additively into elastic and plastic parts. All attempts to model elastoplastic rods require profound knowledge of an appropriate yield criterion defined by a yield surface. Obtaining the yield surface in terms of stress resultants (the rod’s internal (contact) forces and internal (contact) moments) for rods of arbitrary cross-sectional shape and with arbitrary constitutive response still remains a challenge. Yield surfaces have been derived for different cross-sections in [10, 16,17,18,19], applying the upper and lower bound techniques of limit analysis. There, the rod’s cross-section at yield is assumed to be fully plastified at the state of yield limit. These yield surfaces are often used to investigate inelastic properties and limit loads of steel frames [20, 21]. The objective of this work is to present a framework enabling to determine a yield surface in terms of stress resultants for an arbitrary cross-section and deformation state. Especially, the rod’s cross-section need not be fully plastified at yield: the yield limit is defined in terms of plastic work done. This distinguishes the yield surface obtained here from the above mentioned ones and ensures versatility in the definition of the yield limit. In practice, the determination of such yield surface is made a priori for a specific cross-section and can then be incorporated into an elastoplastic rod model.

The paper is structured as follows. In Sect. 2, a brief review of the theory of geometrically exact rods with rigid cross-sections is given and extended to the inelastic case. For uniformly deformed rods, the deformation of a cross-section can be evaluated, exclusively depending on strain prescriptors. An appropriate model is outlined in Sect. 3 for both the elastic and the inelastic case. Forces and moments as well as the rod’s stiffnesses are evaluated from the deformed (warped) cross-section and the elastoplastic response of geometrically exact rods is investigated. The model presented in this section is used to evaluate the yield surfaces later on.

In Sect. 4, a framework is presented aiming to obtain yield surfaces in terms of stress resultants. Therefore, discrete points on yield surfaces resulting from numerical simulations are computed. Generalised Lamé curves are fitted to the discrete points on the yield surfaces to obtain a continuous yield surface in terms of stress resultants. Finally, the resulting yield surfaces are comprehensively discussed, examined regarding scalability of the cross-section dimension and compared with existing ones from the literature.

Table 1 summarises the different designation of strain measures and their energetically conjugates for geometrically exact rods and for three-dimensional continuum mechanics, respectively. This nomenclature will be used in the sequel.

The origin of the terms strain prescriptors and stress resultants is explained in chapter 3. Throughout the paper, the arc length of the rod in its undeformed configuration $\mathcal {B}_0$ is denoted by s. The derivative of an arbitrary quantity $(\bullet )$ with respect to s is defined by $\displaystyle {\frac{\partial (\bullet )}{\partial s}=:(\bullet )'}$.

All numerical simulations carried out to achive the results shown in this contribution base on the open source finite-element library deal.II [22].

Geometrically exact rods with rigid cross-sections

In this section the theory of geometrically exact rods with rigid cross-sections is briefly reviewed [23, 24]. First we present the kinematics, then we introduce stress resultants both for the case of elastic rods and elastoplastic rods.

Kinematics

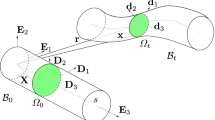
Figure 1 shows a typical rod deforming from its undeformed straight material configuration $\mathcal {B}_0$ into its deformed spatial configuration $\mathcal {B}_t$.

Fig. 1

Illustration of a geometrically exact rod deforming from its straight material configuration $\mathcal {B}_0$ into its deformed spatial configuration $\mathcal {B}_t$. Any point in the material configuration is denoted by $\mathbf {X}$. The position of the centerline of the deformed rod is denoted by $\mathbf {r}{}$. Material points in the spatial configuration are denoted by $\mathbf {x}$

Here, $\mathbf {X}=\hbox {X}_{i}\mathbf {E}_{i}$ with $\hbox {X}_{3}=s$ denotes the position of any material point in the undeformed material configuration. In the sequel, Latin indices run from 1 to 3, whereas Greek indices run from 1 to 2. The coordinates of the undeformed cross-section $\Omega _0$ are denoted by $X_{\alpha }$. The position of the deformed centerline is denoted by $\mathbf {r}{(s)}$. The orthogonal directors $\mathbf {d}_{1}{(s)}$, $\mathbf {d}_{2}{(s)}$ span the plane of the deformed cross-section $\Omega _t$, assumed planar. Together with $\mathbf {d}_{3}{(s)}=\mathbf {d}_{1}{(s)}\times \mathbf {d}_{2}{(s)}$, an orthogonal basis is constructed. It is not a requirement that $\mathbf {d}_{3}{(s)}$ is tangential to the deformed centerline $\mathbf {r}{(s)}$. Taken together, the directors $\mathbf {d}_{i}{\ }$describe the orientation of the deformed cross-section. In the material configuration the orientation of the cross-section is described by the directors $\mathbf {D}_{i}{(s)}$, where $\mathbf {D}_{i}{(s)}=\mathbf {E}_{i}$. Usually the directors $\mathbf {D}_{i}{(s)}$ are oriented along the principal directions of the undeformed cross-section $\Omega _0$. The directors in the spatial configuration are related to the directors in the material configuration via

$$\begin{aligned} \mathbf {d}_{i}{(s)}=\mathbf {R}{(s)}\mathbf {D}_{i}{(s)}. \end{aligned}$$

(1)

Here $\mathbf {R}{(s)}$ denotes a three-dimensional rotation tensor and is a member of the special orthogonal group SO(3). The quantities $\mathbf {r}{(s)}$ and $\mathbf {R}{(s)}$ are the kinematic variables of this theory. Assuming a rigid cross-section, the position $\mathbf {x}$ of any material point in the spatial configuration can be described as

$$\begin{aligned} \mathbf {x}(s,\hbox {X}_{\alpha })=\mathbf {r}{(s)}+\mathbf {R}{(s)}\hat{\mathbf {X}}(\hbox {X}_{\alpha }), \end{aligned}$$

(2)

with

$$\begin{aligned} \hat{\mathbf {X}}(\hbox {X}_{\alpha })=\hbox {X}_{\alpha }\mathbf {E}_{\alpha }. \end{aligned}$$

(3)

For the sake of readability, the dependencies on s and $\hbox {X}_{\alpha }$ are omitted from now on. In this restricted setting, the cross-section of the deformed rod remains rigid. A framework to model the cross-sectional deformation depending on strain measures only is outlined in Sect. 3, based on [25, 26].

Two strain measures for the rod are introduced: the translational strain $\mathbf {v}_{}^{}{}$, and the rotational strain $\mathbf {k}_{}^{}{}$ (also called curvature):

$$\begin{aligned}&\mathbf {v}_{}^{}{}=\mathbf {r}{}'=\hbox {v}_i\mathbf {d}_{i}{},\nonumber \\&{\mathbf {K}}=\mathbf {R}{}'\mathbf {R}{}^{T},\quad \mathbf {k}_{}^{}{}=\hbox {k}_i\mathbf {d}_{i}{}. \end{aligned}$$

(4)

Their rotational pull backs are defined as $\mathbf {v}_{0}^{}{}$ and $\mathbf {k}_{0}^{}{}$ in the following way:

$$\begin{aligned}&\mathbf {v}_{0}^{}{}=\mathbf {R}{}^{T}\mathbf {r}{}'=\hbox {v}_i\mathbf {E}_{i},\nonumber \\&{\mathbf {K}}_0=\mathbf {R}{}^{T}{\mathbf {K}}\mathbf {R}{},\quad \mathbf {k}_{0}^{}{}=\mathbf {R}{}^{T}\mathbf {k}_{}^{}{}=\hbox {k}_i\mathbf {E}_{i}{}. \end{aligned}$$

(5)

Here, ${\mathbf {K}}$ and ${\mathbf {K}}_0$ are skew-symmetric tensors whose axial vectors are $\mathbf {k}_{}^{}{}$ and $\mathbf {k}_{0}^{}{}$, respectively. We collectively denote $\mathbf {v}_{0}^{}{}$ and $\mathbf {k}_{0}^{}{}$ as strain prescriptors. Incorporating the strain prescriptors, the deformation gradient of map (2) can be written as

$$\begin{aligned} \mathbf {F}_{}^{{}^{}}{}=\mathbf {R}{}\bigg [\mathbf {v}_{0}^{}{}\otimes \mathbf {E}_{3}+\left[ \mathbf {k}_{0}^{}{}\times \hbox {X}_{\alpha }\mathbf {E}_{\alpha }\right] \otimes \mathbf {E}_{3}+\mathbf {E}_{\alpha }\otimes \mathbf {E}_{\alpha }\bigg ]. \end{aligned}$$

(6)

Elastic rods

Internal (contact) force and internal (contact) moment are denoted by $\mathbf {n}_{}{}$ and $\mathbf {m}_{}{}$, respectively:

$$\begin{aligned} \mathbf {n}_{}{}=\hbox {n}_i\mathbf {d}_{i}{},\quad \mathbf {m}_{}{}=\hbox {m}_i\mathbf {d}_{i}{}. \end{aligned}$$

(7)

Their rotational pull backs are

$$\begin{aligned} \mathbf {n}_{0}{}=\hbox {n}_i\mathbf {E}_{i},\quad \mathbf {m}_{0}{}=\hbox {m}_i\mathbf {E}_{i} \end{aligned}$$

(8)

which are also called stress resultants. For the elastic case, assuming the existence of a scalar valued stored energy density function $\psi ^{rod}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{})$, the stress resultants become

$$\begin{aligned} \mathbf {n}_{0}{}=\frac{\partial \psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{}),\quad \mathbf {m}_{0}{}=\frac{\partial \psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}}(\mathbf {v}_{0}^{}{}, \mathbf {k}_{0}^{}{}). \end{aligned}$$

(9)

The second derivative of $\psi ^{rod}(\mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{})$ with respect to the strain prescriptors returns the $6\times 6$ tangent stiffness matrix $\mathbf {C}_0$

$$\begin{aligned} \mathbf {C}_0:= \begin{bmatrix} \displaystyle { \frac{\partial ^2\psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}\partial \mathbf {v}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } &{} \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {v}_{0}^{}{}\partial \mathbf {k}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } \\ \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}\partial \mathbf {v}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } &{} \displaystyle {\frac{\partial ^2\psi ^{rod}}{\partial \mathbf {k}_{0}^{}{}\partial \mathbf {k}_{0}^{}{}}\left( \mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) } \end{bmatrix}, \end{aligned}$$

(10)

which relates the change in the stress resultants to the change in the strain prescriptors as

$$\begin{aligned} \begin{bmatrix} \hbox {d}{\mathbf{n}}_0\\ \hbox {d}{\mathbf{m}}_0 \end{bmatrix} =\mathbf {C}_0 \begin{bmatrix} \hbox {d}{\mathbf{v}}_0 \\ \hbox {d}{\mathbf{k}}_0 \end{bmatrix}. \end{aligned}$$

(11)

Elastoplastic rods

In the sequel, the key components to model geometrically exact elastoplastic rods are briefly outlined (see [14, 15] for details). The strain prescriptors are assumed to decompose into an elastic and a plastic part as follows:

$$\begin{aligned} \mathbf {v}_{0}^{}{}=\mathbf {v}_{0}^{e}{}+\mathbf {v}_{0}^{p}{}\quad \text {and}\quad \mathbf {k}_{0}^{}{}=\mathbf {k}_{0}^{e}{}+\mathbf {k}_{0}^{p}{}. \end{aligned}$$

(12)

Assuming that the stored energy density function $\psi ^{rod}$ is purely dependent on the elastic strain prescriptors, the free energy density $\Psi ^{rod}$ is introduced as

$$\begin{aligned} \Psi ^{rod}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{},\varvec{\xi }^{rod})=\psi ^{rod}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{})+\mathcal {H}^{rod}(\varvec{\xi }^{rod}), \end{aligned}$$

(13)

where $\mathcal {H}^{rod}(\varvec{\xi }^{rod})$ describes hardening depending on internal variables $\varvec{\xi }^{rod}$. For the special case of ideal elastoplasticity $\mathcal {H}^{rod}(\varvec{\xi }^{rod})=0$ and the dependency on $\varvec{\xi }^{rod}$ can be omitted. From now on, for elastoplastic rods, we restrict to the ideal elastoplastic case. The dissipation power $\mathcal {D}^{rod}$ is defined as the difference between the stress resultant power and the rate of the free energy density, i.e.,

$$\begin{aligned} \mathcal {D}^{rod}= \mathbf {n}_{0}{}\cdot \dot{\mathbf{v}}_0+\mathbf {m}_{0}{}\cdot \dot{\mathbf{k}}_0-\frac{\hbox {d}\Psi ^{rod}}{\hbox {d}t}(\mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{})\ge 0, \end{aligned}$$

(14)

where a superposed dot denotes the material time derivative $\displaystyle {\dot{\overline{\left( \bullet \right) }}:=\left. \frac{\partial \left( \bullet \right) }{\partial t}\right| _{\mathbf {X}}}$. Equation (14) holds for any admissible process, which renders the constitutive relation and the reduced form of the dissipation inequality, i.e.,

$$\begin{aligned}&\mathbf {n}_{0}{} =\frac{\partial \Psi ^{rod}}{\partial \mathbf {v}_{0}^{e}{}}\left( \mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{}\right) ,\quad \mathbf {m}_{0}{} =\frac{\partial \Psi ^{rod}}{\partial \mathbf {k}_{0}^{e}{}}\left( \mathbf {v}_{0}^{e}{},\mathbf {k}_{0}^{e}{}\right) , \end{aligned}$$

(15)

$$\begin{aligned}&\mathcal {D}_{red}^{rod}= \mathbf {n}_{0}{}\cdot \dot{\mathbf{v}}_0^p+ \mathbf {m}_{0}{}\cdot \dot{\mathbf{k}}_0^p\ge 0. \end{aligned}$$

(16)

Let us denote by $\Phi ^{rod}(\mathbf {n}_{0}{},\mathbf {m}_{0}{})$ the yield surface for rods. Maximising Eq. (16) under the constraint $\Phi ^{rod}\le 0$, one obtains the following evolution equations for the plastic strain prescriptors:

$$\begin{aligned} \dot{\mathbf{v}}_0^p=\dot{\gamma }\frac{\partial \Phi ^{rod}}{\partial \mathbf {n}_{0}{}}\left( \mathbf {n}_{0}{},\mathbf {m}_{0}{}\right) ,\quad \dot{\mathbf{k}}_0^p=\dot{\gamma }\frac{\partial \Phi ^{rod}}{\partial \mathbf {m}_{0}{}}\left( \mathbf {n}_{0}{},\mathbf {m}_{0}{}\right) . \end{aligned}$$

(17)

Here, $\dot{\gamma }$ represents the Lagrange multiplier, ensuring that the stress resultants are admissible and satisfy the following Karush-Kuhn-Tucker (KKT) conditions

$$\begin{aligned} \text {KKT:}\quad \dot{\gamma }\ge 0,\quad \Phi ^{rod}\left( \mathbf {n}_{0}{},\mathbf {m}_{0}{}\right) \le 0,\quad \dot{\gamma }\Phi ^{rod}\left( \mathbf {n}_{0}{},\mathbf {m}_{0}{}\right) =0. \end{aligned}$$

(18)

The $6\times 6$ elastoplastic tangent stiffness matrix $\mathbf {C}_0^{ep}$ relates the change in the stress resultants to the change in the total strain prescriptors as

$$\begin{aligned} \begin{bmatrix} \hbox {d}{\mathbf{n}}_0\\ \hbox {d}{\mathbf{m}}_0 \end{bmatrix} =\mathbf {C}_0^{ep} \begin{bmatrix} \hbox {d}{\mathbf{v}}_0 \\ \hbox {d}{\mathbf{k}}_0 \end{bmatrix}. \end{aligned}$$

(19)

We note that a detailled knowledge of a suitable yield surface in terms of stress resultants is crucial to successfully implement geometrically exact elastoplastic rods. This contribution is dedicated to the determination of such yield surfaces.

Incorporating cross-sectional warping

An approach to incorporate cross-sectional deformations and nonlinear elastic constitutive relations into the formulation of geometrically exact rods has been presented in [25] and further developed in [26]. It has, however, not yet been generalised to the case of inelasticity. Here, the approach is extended to elastoplasticity.

Outline of cross-sectional warping

The theory presented in [25] and [26] allows for the cross-section $\Omega _0$ of a rod to deform due to strain prescriptors, i.e., the cross-section may warp. In general, a rod deforms such that the strain prescriptors vary along the rod’s arc length s. Thus, the deformation of the cross-section at s depends not only on the strain prescriptors at s but also on the strain prescriptors in the neighborhood of s. If, however, the strain prescriptors vary slowly along s, the deformation can be assumed to depend only on the strain prescriptors at s. Eventually, a uniformly strained rod is constructed, i.e., $\mathbf {v}_{0}^{}{(s)}=\mathbf {v}_{0}^{}{}$ and $\mathbf {k}_{0}^{}{(s)}=\mathbf {k}_{0}^{}{}$: the strain prescriptors are no more dependent on the arc length. A uniformly strained rod takes the shape of a helix [25]. The deformation map of such a rod is

$$\begin{aligned} \mathbf {x}(s,\hbox {X}_{\alpha })=\mathbf {r}{(s)}+\mathbf {R}{(s)}\hat{\mathbf {X}}(\hbox {X}_{\alpha }), \end{aligned}$$

(20)

where the expressions of $\mathbf {r}{(s)}$ and $\mathbf {R}{(s)}$ for a uniformly strained rod are derived and presented in detail by Kumar et al. [25]. Here, $\hat{\mathbf {X}}(\hbox {X}_{\alpha })$ denotes the deformed material configuration of the cross-section. Due to the assumption of uniform deformation, $\hat{\mathbf {X}}$ is not dependent on s and can be rewritten as

$$\begin{aligned} \hat{\mathbf {X}}(\hbox {X}_{\alpha })=\hbox {X}_{\alpha }\mathbf {E}_{\alpha }+U_i(\hbox {X}_{\alpha })\mathbf {E}_{i}. \end{aligned}$$

(21)

Here, $U_i(\hbox {X}_{\alpha })$ denotes the cross-sectional displacement (warping) of the material configuration. According to the map (20), the deformed cross-section at s is obtained by rotating $\hat{\mathbf {X}}$ by $\mathbf {R}{(s)}$.

To evaluate $\hat{\mathbf {X}}$ for the purely elastic case, an energy approach is applied: the stored energy density $\psi \left( \mathbf {F}_{}^{{}^{}}\right)$ in the rod’s cross-section is minimised with respect to $\hat{\mathbf {X}}$, thus leading to

$$\begin{aligned} \underset{\hat{\mathbf {X}}}{\hbox {min}}\int _{\Omega _0}\psi \left( \mathbf {F}_{}^{{}^{}}\right) \hbox {dA}. \end{aligned}$$

(22)

The deformation gradient $\mathbf {F}$ of map (20) is

$$\begin{aligned} \mathbf {F}_{}^{{}^{}}{}=\mathbf {R}{}\left[ \mathbf {v}_{0}^{}{}\otimes \mathbf {E}_{3}+\left[ \mathbf {k}_{0}^{}{}\times \hat{\mathbf {X}}\right] \otimes \mathbf {E}_{3}+\frac{\partial \hat{\mathbf {X}}}{\partial \hbox {X}_{\alpha }}\otimes \mathbf {E}_{\alpha }\right] . \end{aligned}$$

(23)

If cross-sectional displacement (warping) is suppressed, i.e. $U_i=0$, one gets back to the deformation gradient introduced in Eq. (6).

Equation (23) highlights why $\mathbf {v}_{0}^{}{}$ and $\mathbf {k}_{0}^{}{}$ are collectively denoted as strain prescriptors: they prescribe the deformation and thus the local strains in the cross-section.

To assure uniqueness, the minimisation problem (22) has to be solved under two sets of constraints. Furthermore, the constraints ensure that the imposed strain prescriptors do not change during minimisation (for more details, the reader is referred to [25]). The first constraint fixes the mass center of the cross-section:

$$\begin{aligned} \int _{\Omega _0}\rho \hat{\mathbf {X}}\hbox {dA}=\mathbf {0}. \end{aligned}$$

(24)

The second constraint ensures that the average rotation about $\mathbf {E}_{3}$ vanishes and that the principal axes of the cross-section align with $\mathbf {E}_{1}$ and $\mathbf {E}_{2}$.

$$\begin{aligned} \int _{\Omega _0}\rho \varvec{\mathfrak {M}}\hbox {dA}=\mathbf {0}, \end{aligned}$$

(25)

where

$$\begin{aligned} \varvec{\mathfrak {M}}=\hat{\hbox {X}}_2\hat{\hbox {X}}_3\mathbf {E}_{1}+\hat{\hbox {X}}_1\hat{\hbox {X}}_3\mathbf {E}_{2}+\left[ \hbox {atan}\left( \frac{\hat{\hbox {X}}_1}{\hat{\hbox {X}}_2}\right) -\hbox {atan}\left( \frac{\hbox {X}_{1}}{\hbox {X}_{2}}\right) \right] \mathbf {E}_{3}. \end{aligned}$$

(26)

Here, $\rho$ denotes the mass density. Consequently, to solve the constrained minimisation problem, a constrained energy functional is defined:

$$\begin{aligned} \mathcal {F}\left( \hat{\mathbf {X}},\varvec{\lambda },\varvec{\mu },\mathbf {v}_{0}^{}{},\mathbf {k}_{0}^{}{}\right) = \int _{\Omega _0}\bigg [\psi \left( \mathbf {F}_{}^{{}^{}}\right) +\rho \left[ \varvec{\lambda }\cdot \hat{\mathbf {X}}+\varvec{\mu }\cdot \varvec{\mathfrak {M}}\right] \bigg ]\hbox {dA} \end{aligned}$$

(27)

with the Lagrange multipliers $\varvec{\lambda }$ and $\varvec{\mu }$ enforcing the constraints (24) and (25). The first variation of the functional (27) leads to an Euler Lagrange equation describing the cross-sectional balance of linear momentum with traction free boundary:

$$\begin{aligned} \text {Div}_{\alpha }\mathbf {P}-\mathbf {P}\mathbf {E}_{3}\times \mathbf {k}_{0}^{}{}-\rho \left[ \varvec{\lambda }+\varvec{\Xi }\varvec{\mu }\right] =&\mathbf {0}\quad \text {in}~ \Omega _0, \nonumber \\ \mathbf {P}\hat{\mathbf {N}}=&\mathbf {0} \quad \text {in}~\partial \Omega _0\text { (boundary of } \Omega _0). \end{aligned}$$

(28)

Here, $\mathbf {P}$ denotes the Piola stress and $\hat{\mathbf {N}}$ denotes the outwards pointing normal to $\partial \Omega _0$. $\hbox {Div}_{\alpha }$ denotes the divergence in the plane of the undeformed cross-section. Furthermore we introduce the following abbreviation

$$\begin{aligned} \varvec{\Xi }=&\rho \hat{\hbox {X}}_3\left[ \mathbf {E}_{1}\otimes \mathbf {E}_{2}+\mathbf {E}_{2}\otimes \mathbf {E}_{1}\right] -\frac{\hat{\hbox {X}}_2}{\hat{\hbox {X}}_1^2+\hat{\hbox {X}}_2^2}\left[ \mathbf {E}_{1}\otimes \mathbf {E}_{3}\right] \nonumber \\&+\frac{\hat{\hbox {X}}_1}{\hat{\hbox {X}}_1^2+\hat{\hbox {X}}_2^2}\left[ \mathbf {E}_{2}\otimes \mathbf {E}_{3}\right] + \rho \hat{\hbox {X}}_2\left[ \mathbf {E}_{3}\otimes \mathbf {E}_{1}\right] + \rho \hat{\hbox {X}}_1\left[ \mathbf {E}_{3}\otimes \mathbf {E}_{1}\right] . \end{aligned}$$

(29)

Restricting to the case of isotropy in this paper, the stored energy density $\psi$ depends on the left Cauchy-Green strain $\mathbf {b}_{}^{{}^{}}=\mathbf {F}\mathbf {F}^{\text {T}}$ only. The Piola stress then becomes $\displaystyle { \mathbf {P}=\varvec{\tau }\mathbf {F}^{-\text {T}}}$ with the Kirchhoff stress following from $\varvec{\tau }=\displaystyle {2\mathbf {b}\frac{\partial \psi }{\partial \mathbf {b}}\left( \mathbf {b}\right) }$.

For inelasticity, the energy approach (27) can not be applied. However, one can make use of the cross-sectional balance of linear momentum (28) which holds always. Together with the constraints (24) and (25) one can then solve for the elastoplastic cross-sectional deformation. The constitutive equation resulting from the dissipation inequality renders

$$\begin{aligned} \varvec{\tau }=2\mathbf {b}_{}^{{e}^{}}\frac{\partial \Psi }{\partial \mathbf {b}_{}^{{e}^{}}}\left( \mathbf {b}_{}^{{e}^{}},\xi \right) ,\quad \mathbf {P}=\varvec{\tau }\mathbf {F}_{}^{{-T}^{}}, \end{aligned}$$

(30)

where $\Psi$ denotes the free energy density. We note that for inelasticity, $\varvec{\tau }$ and thus $\mathbf {P}$ is no more a function of $\mathbf {b}_{}^{{}^{}}{}$ only, but a function of the elastic left Cauchy-Green strain $\mathbf {b}_{}^{{e}^{}}$ and an internal variable $\xi$. An associated plasticity model, incorporating the evolution equations for $\dot{\mathbf {b}}^e$ and $\dot{\xi }$ is comprehensively discussed in “Appendix A”.

In the sequel the problem to solve for the elastoplastic cross-sectional deformation is denoted as $\mathbb {Q}(\mathbf {v}_0,\mathbf {k}_0)$.

Stress resultants and stiffnesses

In three-dimensional continuum mechanics, the normal projection of the Piola stress $\mathbf {P}$ on to the undeformed boundary returns the traction $\mathbf {T}$. The cross-section in its material configuration has a normal aligned with the $\mathbf {E}_{3}$ direction, thus here $\mathbf {T}=\mathbf {P}\mathbf {E}_{3}$. Integrating $\mathbf {T}$ over the cross-section returns the (contact) force

$$\begin{aligned} \mathbf {n}_{0}{}=\int _{\Omega _0}\mathbf {T}\hbox {dA}. \end{aligned}$$

(31)

Integrating the cross product of $\mathbf {T}$ with the position vector $\hat{\mathbf {X}}$ over the cross-section results in the (contact) moment

$$\begin{aligned} \mathbf {m}_{0}{}=\int _{\Omega _0}\hat{\mathbf {X}}\times \mathbf {T}\hbox {dA}. \end{aligned}$$

(32)

Here, it is obvious why $\mathbf {n}_{0}{}$ and $\mathbf {m}_{0}{}$ are collectively denoted as stress resultants. They result from integration of stress measures over the undeformed cross-section and exclusively depend on the strain prescriptors.

As demonstrated in [26], the rod’s stiffness is obtained by taking the derivative of the stress resultants with respect to the total strain prescriptors. Here, the elastoplastic stiffness is obtained. Let $p\in \left\{ \hbox {v}_{0_1}, \hbox {v}_{0_2}, \hbox {v}_{0_3}, \hbox {k}_{0_1}, \hbox {k}_{0_2}, \hbox {k}_{0_3} \right\}$ denote any individual component of the total strain prescriptors. Elastoplastic stiffnesses are then obtained with

$$\begin{aligned} \frac{\partial \mathbf {n}_{0}{}}{\partial p}=\int _{\Omega _0}\frac{\partial \mathbf {P}}{\partial p}\mathbf {E}_{3}\hbox {dA}=\int _{\Omega _0}\left[ \frac{\partial \mathbf {P}}{\partial \mathbf {F}_{}^{{}^{}}}:\frac{\partial \mathbf {F}_{}^{{}^{}}}{\partial p}\right] \mathbf {E}_{3}\hbox {dA} \end{aligned}$$

(33)

and

$$\begin{aligned} \frac{\partial \mathbf {m}_{0}{}}{\partial p}=&\int _{\Omega _0}\left[ \hat{\mathbf {X}}\times \frac{\partial \mathbf {P}}{\partial p}\right] \mathbf {E}_{3}+\left[ \frac{\partial \hat{\mathbf {X}}}{\partial p}\times \mathbf {P}\right] \mathbf {E}_{3}\hbox {dA}\nonumber \\ =&\int _{\Omega _0}\left[ \hat{\mathbf {X}}\times \frac{\partial \mathbf {P}}{\partial \mathbf {F}_{}^{{}^{}}}:\frac{\partial \mathbf {F}_{}^{{}^{}}}{\partial p}\right] \mathbf {E}_{3}+\left[ \frac{\partial \hat{\mathbf {X}}}{\partial p}\times \mathbf {P}\right] \mathbf {E}_{3}\hbox {dA}. \end{aligned}$$

(34)

The elastoplastic tangent $\displaystyle {\mathbb {A}^{ep}=\frac{\partial \mathbf {P}}{\partial \mathbf {F}_{}^{{}^{}}}}$ in the above expression is not straightforward to obtain due to the dependence of $\mathbf {P}$ on internal variables (see “Appendix B.3” for details). Similarly, obtaining $\displaystyle {\frac{\partial \hat{\mathbf {X}}}{\partial p}}$ and $\displaystyle {\frac{\partial \mathbf {F}_{}^{{}^{}}}{\partial p}}$ is not trivial, the reader is referred to [26]. Eventually, the $6\times 6$ elastoplastic tangent stiffness tensor $\mathbf {C}_0^{ep}$ is arranged as

$$\begin{aligned} \mathbf {C}_0^{ep}=\begin{bmatrix} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_1}}{\partial {\hbox {k}_{0_3}}}} \\ \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_2}}{\partial {\hbox {k}_{0_3}}}} \\ \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {n}_{0_3}}{\partial {\hbox {k}_{0_3}}}} \\ \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_1}}{\partial {\hbox {k}_{0_3}}}} \\ \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_2}}{\partial {\hbox {k}_{0_3}}}} \\ \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {v}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {v}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {v}_{0_3}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {k}_{0_1}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {k}_{0_2}}}}&{} \displaystyle {\frac{\partial \hbox {m}_{0_3}}{\partial {\hbox {k}_{0_3}}}} \end{bmatrix}. \end{aligned}$$

(35)

Note that $\mathbf {C}_0^{ep}$ is symmetric for associated plasticity.

Elastoplastic response of rods

Now the elastoplastic response of rods is studied. Therefore, stress resultant versus strain prescriptor plots for cyclic loading are discussed and the progression of plastification in the cross-section is analysed. Later, the elastoplastic longitudinal and bending stiffnesses are examined.

The continuum inelastic constitutive response of the material is characterised by the J2-flow theory [27] which is summarised in “Appendix B.2”. The free energy density takes the form

$$\begin{aligned} \Psi (\mathbf {b}_{}^{{e}^{}},\xi )=\psi (\mathbf {b}_{}^{{e}^{}})+\mathcal {H}(\xi ), \end{aligned}$$

(36)

with the stored energy density $\psi (\mathbf {b}_{}^{{e}^{}})$ being a function of the elastic left Cauchy-Green strain $\displaystyle {\mathbf {b}_{}^{{e}^{}}=\mathbf {F}_{}^{{e}^{}}\mathbf {F}_{}^{{e}^{T}}}$. Here, the stored energy density $\psi (\mathbf {b}_{}^{{e}^{}})$ is defined in terms of the logarithmic principal stretches as shown in “Appendix B.2”, Eq. (B.11). $\mathcal {H}(\xi )$ denotes a hardening contribution, depending on the internal variable $\xi$ and a constant hardening parameter H. Here,

$$\begin{aligned} \mathcal {H}(\xi )=\frac{1}{2}H\xi ^2. \end{aligned}$$

(37)

The continuum yield criterion, describing the region of admissible stresses, is defined as the von-Mises yield criterion

$$\begin{aligned} \Phi (\varvec{\tau },q)=\Vert \hbox {dev}(\varvec{\tau })\Vert -\sqrt{\frac{2}{3}}\left[ \sigma _y-q\right] \le 0, \end{aligned}$$

(38)

where $\displaystyle {q=-\frac{\partial \mathcal {H}}{\partial \xi }(\xi )}$ is the thermodynamic force conjugate to the internal variable $\xi$. In the sequel, the compression modulus $\kappa$, the shear modulus $\mu$ and the yield stress $\sigma _y$ are set to

$$\begin{aligned} \kappa =164.21, \quad \mu =80.1938, \quad \sigma _y=0.45. \end{aligned}$$

(39)

The values for H are set in the subsequent sections. The material properties are taken from [27] and represent values of standard steel. Here, the system of units used is: length $[\text {mm}]$, stress $[\text {GPa}]$, force $[\text {kN}]$ and moment $[\text {Nm}]$. The rods discussed have a circular cross-section with radius $r=1$.

Cyclic loading is performed to obtain the well-known hystereses loop in terms of stress resultants and strain prescriptors. Simulations are firstly performed with $H=0$, i.e., for ideal plasticity, and subsequently with increasing $H> 0$. Figure 2 shows results for different values of the hardening parameter. For ideal plasticity, it is obvious that the curves for renewed loading coincide with the curves describing previous loading. The slope of the curves is horizontal in the plastic region. When incorporating hardening, however, the slope rises. This trend is clearly discernible in all four plots. The major difference in the four plots is between (a) and the remaining (b) to (d). In (a), the longitudinal straining yields uniform deformation in the cross-section, which leads to simultaneous plastification of the whole cross-section. In the other load cases (b) to (d), twist, bending and shearing do not lead to uniform deformation of the cross-section. Thus, different regions of the cross-section plastify earlier or later, leading to a gradual transition from purely elastic to plastic behaviour, when expressed in stress resultants.

Fig. 2

Hystereses loops resulting from cyclic loading. Strain prescriptors are prescribed and stress resultants are computed by solving $\mathbb {Q}(\mathbf {v}_0,\mathbf {k}_0)$. Different response curves are obtained for different hardening parameters. All plots have in common that for ideal plasticity the curve for reloading coincide with the curve of previous loading. Increasing hardening leads to increasing stiffness in the plastic region. In contrast to the remaining curves, the curves in (a) show a prompt transition between the elastic and the plastic deformation state. There, the whole cross-section plastifies simultaneously, whereas for shearing, bending and twisting, the plastification is not simultaneous throughout the whole cross-section. Thus the transition between elastic and plastic region is gradual

The plastification of the different regions in the cross-section can be visualised by the distribution of the plastic work density $\psi ^p$. The plastic work density is obtained with

$$\begin{aligned} \psi ^p(t):=\int _0^t\left[ \text {rate of plastic work density}\right] \text {dt}. \end{aligned}$$

(40)

The rate of plastic work density is defined in the appendix by Eq. (A.10). Figure 3 displays the distribution of $\psi ^p$ for a cross-section undergoing longitudinal strain, shear, twist and bending respectively. Here, $H=0.1\mu$. The discrete figures show the distribution for $t=0.2$, $t=0.8$ and $t=1$. The prescribed strain prescriptors are set to $\hbox {v}_{0_3}=0.01t$, $\hbox {v}_{0_1}=0.01t$, $\hbox {k}_{0_3}=0.01t$ and $\hbox {k}_{0_1}=0.01t$. The color plots nicely visualise that the distribution of $\psi ^p$ is not uniform in the whole cross-section, except for the case of longitudinal straining. The nonuniform distribution results in the effect displayed by the hystereses curves in Fig. 2: the transition from elastic to plastic deformation is gradual for the case of shearing, bending and twisting, but instantaneous for the case of longitudinal straining.

Fig. 3

Distribution of plastic work density $\psi ^p$ in the cross-section for longitudinal straining, shearing, twisting and bending. The distribution is shown for $t=0.2$, $t=0.8$ and $t=1$. The prescribed strain prescriptors are set to $\hbox {v}_{0_3}=0.01t$, $\hbox {v}_{0_1}=0.01t$, $\hbox {k}_{0_3}=0.01t$ and $\hbox {k}_{0_1}=0.01t$, respectively. Except for the case of longitudinal straining, $\psi ^p$ is not uniformly distributed in the cross-section

In the sequel, the stress resultants and the corresponding stiffnesses are analysed in detail as a function of strain prescriptors. First, the resulting axial force and the axial stiffness for longitudinal straining is displayed in Fig. 4. In (a) one can observe that the axial force increases linearly in the elastic region. Linear behaviour is also observed in the plastic region. In (b), the axial stiffness is displayed. It is equivalent to the slope of the curves shown in (a). It is obvious that the stiffness decreases drastically, when the material starts yielding. The decrease is less pronounced when the hardening parameter is high. It is notable that for the case of ideal plasticity, the stiffness gets slightly negative. Ideal plasticity would suggest that the stiffness reduces to zero. However, due to geometric nonlinearity, the cross-section of the strained rod shrinks. Thus, the cross-sectional area is reduced and geometrical softening is observed.

Fig. 4

Axial force and longitudinal stiffness as a function of longitudinal strain. A dramatic decrease in stiffness is observed when plastic deformation is attained. The higher the hardening parameter H, the lower the decrease in stiffness. It is remarkable that the stiffness gets not equal zero but negative for ideal plasticity. This phenomenon is explained with the presence of cross-sectional shrinking, a geometrical softening effect. Due to tension, the cross-section of the rod reduces in area

Figure 5 displays the bending moment as well as its corresponding stiffness as a function of bending. In the elastic region, a linear relation between moment and curvature gets visible (a). Then, the transition from purely elastic to plastic behaviour is gradual, due to nonuniform plastification of the cross-section. In contrast to the longitudinal stiffness (Fig. 4), the bending stiffness decreases gradually and remains positive, even for the case of ideal plasticity (b).

Fig. 5

Bending moment and bending stiffness as a function of bending. The transition from purely elastic to plastic behaviour is gradual. When reaching plastic deformation, a decrease in bending stiffness is visible. In the plastic region, the stiffness decreases gradually

This is not the case for the longitudinal stiffness, where it has been shown that the stiffness gets slightly negative. For completeness, stress resultants and their corresponding stiffnesses for the case of shear and twist are displayed in “Appendix C”.

Highly pronounced negative longitudinal stiffness can be obtained by increasing the longitudinal strain and raising the yield stress to $\sigma _y=45$. Even if this material does not represent a physical material, it visualises nicely, the effect that can occur. Figure 6a depicts the axial force as a function of longitudinal strain for different hardening parameters. The high strain results in a pronounced shrinking of the cross-section. Geometric softening is observed both for elastic as well as for plastic deformation. In (b) it is observed that the stiffness decreases from the beginning and reaches negative values when the rod is deforming plastically. In contrast to the results shown in Fig. 4, negative stiffness is present for all hardening parameters at hand. Negative stiffness can cause difficulties in load prescribed simulations, since the load can not be related uniquely to the deformation state.

Fig. 6

Axial force and longitudinal stiffness as a function of longitudinal strain, where $\sigma _y=45\text {~GPa}$. Here, the effect observed in Fig. 4 is intensified. Nonlinearities due to geometrical softening are observed in the elastic as well as in the plastic deformation state. Negative stiffnesses occur in the plastic region

Yield surfaces in terms of stress resultants

In Sect. 2, we showed that a suitable yield surface in terms of stress resultants $\Phi ^{rod}=\Phi ^{rod}(\mathbf {n}_{0}{},\mathbf {m}_{0}{})$ is required to properly model geometrically exact elastoplastic rods. The yield surface describes a five-dimensional surface in the six-dimensional stress resultants’ space. Eventually, the yield criterion describes the region of admissible stress resultants as $\Phi ^{rod}(\mathbf {n}_{0}{},\mathbf {m}_{0}{})\le 0$. In the following, a framework to determine yield surfaces in terms of stress resultants is outlined and the resulting yield surfaces are comprehensively discussed.

Determining yield surfaces in terms of stress resultants

Aiming to obtain a smooth yield surface in terms of stress resultants, an analytic function is fitted to discrete points on the yield surface, which are characterised by combinations of stress resultants $\mathbf {n}_{0}{}_y$ and $\mathbf {m}_{0}{}_y$ at the yield limit. Here, the stress resultants at yield result from discrete simulations of the cross-sectional warping problem $\mathbb {Q}(\mathbf {v}_0,\mathbf {k}_0)$. As the entire cross-section does not plastify simultaneously, the yield limit is defined to be the point when the plastic work $W^p$ in the cross-section reaches a prescribed limit $W^p_{limit}$. For a given direction $\displaystyle {\mathbf {d}=\frac{\left[ \mathbf {n}_{0}{}~\mathbf {m}_{0}{}\right] ^{\text {T}}}{\Vert \left[ \mathbf {n}_{0}{}~\mathbf {m}_{0}{}\right] ^{\text {T}}\Vert }}$ in the six-dimensional stress resultants’ space, the stress resultants at yield are evaluated via the below mentioned iterative approach:

Here, $W^p_{limit}$ is set to be the plastic work corresponding to $\hbox {v}_{0_3}^p=0.002$ for longitudinal loading, which corresponds to the yield strength. Other definitions of the yield limit are also conceivable. For example, instead of defining the limit in terms of the plastic work, one could define it in terms of the plastification ratio of the cross-section.

In the following, discrete points on a yield surface are obtained for rods with different cross-sections. Material parameters are chosen as summarised in Sect. 3.3 and the hardening parameter is set to $\displaystyle {H=0.1\mu }$. With non-zero hardening, geometric softening as shown in Figs. 4 and 6 is avoided. Furthermore, to determine the discrete points on the yield surface, the direction in the stress resultants’ space $\mathbf {d}$ is chosen such that $\mathbf {d}$ lies in the $x-y$ plane of the six-dimensional stress resultants’ space, with $x,y \in \lbrace \hbox {n}_{0_1}, \hbox {n}_{0_2}, \hbox {n}_{0_3}, \hbox {m}_{0_1}, \hbox {m}_{0_2}, \hbox {m}_{0_3} \rbrace$. In every plane 48 discrete points on the yield surface are evaluated. Together they define the discrete yield surface.

Eventually, the yield surface in terms of stress resultants is described by a smooth function. Here, a generalised five-dimensional Lamé curve

$$\begin{aligned} \Phi ^{rod}= & {} \left| \frac{\hbox {n}_{0_1}}{a}\right| ^{\alpha }+\left| \frac{\hbox {n}_{0_2}}{b}\right| ^{\beta }+\left| \frac{\hbox {n}_{0_3}}{c}\right| ^{\gamma }+\left| \frac{\hbox {m}_{0_1}}{d}\right| ^{\delta }+\left| \frac{\hbox {m}_{0_2}}{e}\right| ^{\epsilon }\nonumber \\&+\left| \frac{\hbox {m}_{0_3}}{f}\right| ^{\zeta }-1= 0, \end{aligned}$$

(41)

with twelve unknown parameters $\{a, b, c, d, e, f, \alpha , \beta , \gamma , \delta , \epsilon , \zeta \}$ is fitted to the discrete data. Later in this contribution, it will get visible that above function fits the discrete yield surface in a satisfactory way and stands out for its simple structure.

In the sequel, the index $\bullet _0$ is generally omitted for the sake of better readability.

Fitting a yield surface to the discrete data resulting from $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for a circular cross-section

Figure 7 shows the discrete yield surface data resulting from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for different combinations of stress resultants (blue dots). Here, the cross-section is circular with the radius $r=1$. Observe that the shapes of the discrete yield surfaces reflect the symmetry of the cross-section.

Fig. 7

Visualisation of discrete yield surfaces evaluated from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ (blue) and of the two-dimensional projections of the fitted continuous yield surface (red) for a circular cross-section with radius $r=1$. The continuous yield surface fits the discrete yield surface with good agreement. (Color figure online)

Here, symmetry reduces Eq. (41) to a Lamé curve with only eight parameters such as

$$\begin{aligned} \Phi ^{rod}= & {} \left| \frac{\hbox {n}_1}{a}\right| ^{\alpha }+\left| \frac{\hbox {n}_2}{a}\right| ^{\alpha }+\left| \frac{\hbox {n}_3}{c}\right| ^{\gamma }+\left| \frac{\hbox {m}_1}{d}\right| ^{\delta }+\left| \frac{\hbox {m}_2}{d}\right| ^{\delta }\nonumber \\&+\left| \frac{\hbox {m}_3}{f}\right| ^{\zeta }-1= 0. \end{aligned}$$

(42)

With a least-squares optimisation method, one can now fit Eq. (42) to the numerically obtained discrete yield surface. To ensure that the yield surface $\Phi ^{rod}$ is convex, the following condition has to be fulfilled

$$\begin{aligned} \theta \ge 1\quad \text {with}\quad \theta \in \lbrace \alpha , \gamma , \delta , \zeta \rbrace . \end{aligned}$$

(43)

For the example of a circular cross-section, the yield surface results in

$$\begin{aligned} \Phi ^{rod}= & {} \left| \frac{\hbox {n}_1}{0.70}\right| ^{2.04}+\left| \frac{\hbox {n}_2}{0.70}\right| ^{2.04}+\left| \frac{\hbox {n}_3}{1.47}\right| ^{1.76}+\left| \frac{\hbox {m}_1}{0.62}\right| ^{2.09}\nonumber \\&+\left| \frac{\hbox {m}_2}{0.62}\right| ^{2.09}+\left| \frac{\hbox {m}_3}{0.56}\right| ^{1.73}-1= 0 \end{aligned}$$

(44)

Two-dimensional projections of the continuous yield surface are shown in Fig. 7 in red lines. The projections are in good agreement with the discrete yield surface resulting from $\mathbb {Q}(\mathbf {v},\mathbf {k})$. Discrepancies can be observed in the projections which deviate from a smooth elliptic shape (shearing-bending and tension-bending). However, these deviations are considered as reasonably small.

In the following, Eq. (42) is interpreted from a geometrical and mechanical point of view. Geometrically, the values of the variables a, c, d and f represent the length of the half axes of the six-dimensional Lamé curve. From a mechanical point of view, they represent the magnitude of the stress resultants at yield for the load cases where all stress resultants except for one equal zero. The exponents define the shape of the Lamé curve and can not be interpreted in mechanical terms. The generalised form of the yield surface eventually becomes

$$\begin{aligned} \Phi ^{rod}= & {} \left| \frac{\hbox {n}_1}{\hbox {n}_{1_y}}\right| ^{\alpha }+\left| \frac{\hbox {n}_2}{\hbox {n}_{2_y}}\right| ^{\alpha }+\left| \frac{\hbox {n}_3}{\hbox {n}_{3_y}}\right| ^{\gamma }+\left| \frac{\hbox {m}_1}{\hbox {m}_{1_y}}\right| ^{\delta }+\left| \frac{\hbox {m}_2}{\hbox {m}_{2_y}}\right| ^{\delta }\nonumber \\&+\left| \frac{\hbox {m}_3}{\hbox {m}_{3_y}}\right| ^{\zeta }-1 = 0, \end{aligned}$$

(45)

where the stress resultants with subscript $\bullet _y$ denote the values at yield. This equation shows that it is sufficient to determine the yield limit for simple loading, where only one stress resultant is not-equal to zero, and fit the exponents to get the analytic yield surface.

Remark

We note that this contribution focusses on a yield criterion for geometrically exact ideal elastoplastic rods, i.e., without considering any hardening at the rod level. With hardening, the structure of the yield surface (45) would have to be extended by including the thermodynamic forces conjugated to internal hardening variables

$$\begin{aligned} \mathbf {q}^{rod}=-\frac{\partial \mathcal {H}^{rod}}{\partial \varvec{\xi }^{rod}}\left( \varvec{\xi }^{rod}\right) \end{aligned}$$

(46)

One such possibility is

Fig. 8

Visualisation of normalised discrete yield surfaces evaluated from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for different circular cross-sections with radius $r=\vartheta$. The normalised forces are obtained as $\displaystyle {\overline{\hbox {n}}_i}=\frac{\hbox {n}_i}{\vartheta ^2}$, whereas the normalised moments are obtained as $\displaystyle {\overline{\hbox {m}}_i}=\frac{\hbox {m}_i}{\vartheta ^3}$. One can observe that the normalised yield surfaces do not show a major dependency on $\vartheta$

$$\begin{aligned} \Phi ^{rod}&=\left| \frac{\hbox {n}_1+\text {q}_1}{\hbox {n}_{1_y}}\right| ^{\alpha }+\left| \frac{\hbox {n}_2+\text {q}_2}{\hbox {n}_{2_y}}\right| ^{\alpha }+\left| \frac{\hbox {n}_3+\text {q}_3}{\hbox {n}_{3_y}}\right| ^{\gamma }+ \left| \frac{\hbox {m}_1+\text {q}_4}{\hbox {m}_{1_y}}\right| ^{\delta } \nonumber \\&\quad +\left| \frac{\hbox {m}_2+\text {q}_5}{\hbox {m}_{2_y}}\right| ^{\delta }+\left| \frac{\hbox {m}_3+\text {q}_6}{\hbox {m}_{3_y}}\right| ^{\zeta }-f(\text {q}_0) = 0, \end{aligned}$$

(47)

where $f(\text {q}_0)$ describes isotropic hardening and the remaining force conjugates describe kinematic hardening. To extend the yield surface by the thermodynamic force conjugates, as shown in (47), $\displaystyle {\mathcal {H}^{rod}\left( \varvec{\xi }^{rod}\right) }$ has to be known. Such a function can be evaluated by comparing the yield surface resulting from different values of the limit plastic work $W^p_{limit}$. This will be a topic of subsequent publications.

Having derived a yield surface for a rod with circular cross-section with $r=1$, following question arises: how does the yield surface change, if the cross-section dimension is scaled by a scalar factor $\vartheta$? In general it is expected that the stress resultants at the yield limit increase for $\vartheta >1$ and decreases for $\vartheta <1$. To compare the resulting discrete yield surfaces, one has to normalise the stress resultants with respect to $\vartheta$. Therefore, Eqs. (31) and (32) are recalled, where it is obvious that the forces scale with the square of $\vartheta$ and the moments scale with its cube. The discrete yield surfaces resulting from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for different $\vartheta$ are plotted in Fig. 8, where the forces are normalised by the square, and the moments by the cubes of $\vartheta$ (for the sake of visibility, only the connections between the discrete points are plotted). It appears that the normalised curves fit one another almost perfectly. The reason for the good agreement of the curves is probably in the choice of the material parameters at hand. Here, yielding already appears at small deformations. Thus, the deformation state is almost geometrically linear and the relation between stresses and deformation scales linearly.

The fact that the normalised discrete yield surfaces are virtually identical leads to the conclusion that the scaling shall nearly not affect the values of the exponents in the yield surfaces. However, comparing in detail the exponents resulting from the fit of the general yield surface (Eq. 45) to the discrete yield surface, one can not fully confirm this assumption (see Table 2). While the half axes ($\hbox {n}_{1_y},\hbox {n}_{2_y}, \hbox {n}_{3_y}, \hbox {m}_{1_y},\hbox {m}_{2_y},$ and $\hbox {m}_{3_y}$) scale with $\vartheta ^2$ and $\vartheta ^3$, respectively, the exponents ($\alpha , \gamma , \delta$ and $\zeta$) show slight deviations. Nevertheless, the range of the exponents remains similar.

Table 2 Parameters of fitted yield surface $\Phi ^{rod}$ for different cross-sectional size scaled with $\vartheta$

This observation allows for the following statement: If the yield surface of a rod with given circular cross-section is known, one can easily obtain the yield surface for a circular cross-section of different size without big loss in accuracy by simply scaling the yield surface. Later, it can be seen that the scaling also applies for squared cross-sections (see Fig. 9).

Fitting a yield surface to the discrete data resulting from $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for a squared cross-section

Now, discrete points of the yield surface for a rod with squared cross-section are determined. The symmetry of the cross-section will be reflected in the discrete yield surface. Eventually, the parameters of the continuous yield surface (45) are fitted to the discrete data. Figure 9 shows the normalised discrete yield surfaces obtained from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for different cross-sectional sizes (again, for the sake of better visibility, only the connection lines between the discrete points are plotted). The edge length of the squared cross-section is $d=2\vartheta$. Again it appears that $\vartheta$ does not show any considerable impact on the normalised yield surfaces.

Fig. 9

Visualisation of normalised discrete yield surfaces evaluated from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ for different squared cross-sections with edge length $d=2\vartheta$. The normalised forces are obtained as $\displaystyle {\overline{\hbox {n}}_i}=\frac{\hbox {n}_i}{\vartheta ^2}$, whereas the normalised moments are obtained as $\displaystyle {\overline{\hbox {m}}_i}=\frac{\hbox {m}_i}{\vartheta ^3}$. Compared to Fig. 8, the shape of the curves differ slightly. In analogy, however, it can again be observed that the normalised yield surfaces do not show a considerable dependency on $\vartheta$

The parameters of the general yield surface (Eq. 45) are fitted to the data visualised in Fig. 9. The resulting parameters are summarised in table 3. In analogy to table 2, it is obvious that the forces and moments at yield scale with $\vartheta ^2$ and $\vartheta ^3$, respectively. The exponents do not remain equal but vary slightly with $\vartheta$.

Comparing the fitted yield surface for a squared cross-section to existing formulations of yield surfaces

Let us now compare the fitted yield surface of a rod with a squared cross-section to existing formulations of yield surfaces. Especially, we compare to a formulation used by Simo et al. [9] and another used by Duan et al. [16]. The cross-section has the edge length $d=2$.

Simo et al. [9] suggests a yield surface for a rod deforming in the $\mathbf {E}_1-\mathbf {E}_3$ plane. The yield surface is obtained by applying upper and lower bound techniques of limit analysis, which does not require to solve the cross-sectional problem. Thus, the yield surface there results from a different approach than the approach introduced in this contribution. The yield surface in Simo et al. reads:

$$\begin{aligned} \Phi ^{rod}= & {} \left| \frac{\hbox {m}_2}{\hbox {m}_{2_p}}\right| +\left[ \frac{\hbox {n}_3}{\hbox {n}_{3_p}}\right] ^2\left[ 1+\left[ \frac{\hbox {n}_1}{\hbox {n}_{1_p}}\right] ^2\right] +\left[ \frac{\hbox {n}_1}{\hbox {n}_{1_p}}\right] ^4-1\nonumber \\= & {} 0\quad \text {[9]}, \end{aligned}$$

(48)

where the stress resultants subscripted with $\bullet _p$ denote fully plastic stress resultants, i.e. the stress resultants leading to a fully plastified cross-section. However, in the present framework the definition of yield does not necessarily lead to a fully plastified cross-section (see Sect. 4.1). Thus, the following question arises: does the yield surface used by Simo et al. recover the discrete yield surface if we naively replace the fully plastic stress resultants in expression (48) with the stress resultants at yield evaluated from $\mathbb {Q}(\mathbf {v},\mathbf {k})$, i.e.,

$$\begin{aligned} \Phi ^{rod}=\left| \frac{\hbox {m}_2}{\hbox {m}_{2_y}}\right| +\left[ \frac{\hbox {n}_3}{\hbox {n}_{3_y}}\right] ^2\left[ 1+\left[ \frac{\hbox {n}_1}{\hbox {n}_{1_y}}\right] ^2\right] +\left[ \frac{\hbox {n}_1}{\hbox {n}_{1_y}}\right] ^4-1 = 0. \end{aligned}$$

(49)

One then can look for similarities between Eqs. (49) and (45). In both cases, the stress resultants are normalised with their corresponding yield limit and raised to the power of a variable exponent. The obvious difference in both expressions is in the mixed term $\displaystyle {\left[ \frac{\hbox {n}_3}{\hbox {n}_{3_y}}\right] ^2\left[ \frac{\hbox {n}_1}{\hbox {n}_{1_y}}\right] ^2}$. This term does not appear in Eq. (45). In Fig. 10, projections of the yield surface (49) are compared to projections of the yield surface obtained from the fitting of Eq. (45). The discrete yield surface resulting from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$ serves as the reference. In the $\hbox {n}_{1}-\hbox {n}_{3}$ and $\hbox {n}_{1}-\hbox {m}_{2}$ projections, both definitions of the yield surface fit the discrete yield surface equally well. We also note that the modified yield surface from Simo et al. matches the discrete yield surface slightly better in the $\hbox {n}_{3}-\hbox {m}_{2}$ projection. However, the difference is not large.

Table 3 Parameters of fitted yield surface $\Phi ^{rod}$ for squared cross-section in dependency on the cross-sectional size scaled with $\vartheta$

Fig. 10

Comparison between the yield surface used in Simo et al. [9] and the yield surface presented in this contribution with the discrete yield surfaces resulting from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$. The squared cross-section has edge length $d=2$. The plots show that Simo et al. approximates the yield surface slightly better than the above presented yield surface

Duan et al. [16] proposes a yield surface describing biaxial bending and stretching as follows

$$\begin{aligned} \left[ \frac{\left| \frac{\hbox {m}_1}{\hbox {m}_{1_p}}\right| }{1-\left| \frac{\hbox {n}_3}{\hbox {n}_{3_p}}\right| ^{\beta _1}}\right] ^{\alpha _1}+ \left[ \frac{\left| \frac{\hbox {m}_2}{\hbox {m}_{2_p}}\right| }{1-\left| \frac{\hbox {n}_3}{\hbox {n}_{3_p}}\right| ^{\beta _2}}\right] ^{\alpha _2}-1= 0\quad \text {[16]}. \end{aligned}$$

(50)

In analogy to Eq. (48), the yield surface is described in terms of fully plastic stress resultants The parameters $\alpha _1,\alpha _2,\beta _1$ and $\beta _2$ are introduced as $\displaystyle {\alpha _1=\alpha _2=1.7+1.3\left[ \frac{\text {n}_3}{\text {n}_{3_p}}\right] }$ and $\beta _1=\beta _2=2$ for squared cross-sections [16]. Again, we naively replace the fully plastic stress resultants in expression (50) with the stress resultants at yield evaluated from $\mathbb {Q}(\mathbf {v},\mathbf {k})$. The resulting yield surface is rewritten as

$$\begin{aligned}&\left| \frac{\text {m}_1}{\text {m}_{1_y}}\right| ^{1.7+1.3\left| \frac{\text {n}_3}{\text {n}_{3_y}}\right| }+\left| \frac{\text {m}_2}{\text {m}_{2_y}}\right| ^{1.7+1.3\left| \frac{\text {n}_3}{\text {n}_{3_y}}\right| }\nonumber \\&\quad -\left[ 1-\left| \frac{\text {n}_3}{\text {n}_{3_y}}\right| ^2\right] ^{1.7+1.3\left| \frac{\text {n}_3}{\text {n}_{3_y}}\right| }=0. \end{aligned}$$

(51)

Comparing Eq. (51) to the formulation presented in this framework (45), a significantly more complex structure stands out. In Fig. 11 projections of the yield surface (51) are compared to projections of the yield surface obtained from the fitting of Eq. (45). The discrete yield surface serves as a reference. It gets obvious that the yield surface proposed by Duan et al. fits the discrete points slightly better in the $\hbox {n}_{3}-\hbox {m}_{1}$ and $\hbox {n}_{3}-\hbox {m}_{2}$ projection than the yield surface introduced in this contribution. Again, the difference is not large.

Fig. 11

Comparison between the yield surface used in Duan et al. [16] and the yield surface presented in this contribution with the discrete yield surfaces resulting from the cross-sectional warping problem $\mathbb {Q}(\mathbf {v},\mathbf {k})$. The squared cross-section has edge length $d=2$. The plots show that Duan et al. approximates the yield surface slightly better in the $\hbox {n}_{3}-\hbox {m}_{1}$ and $\hbox {n}_{3}-\hbox {m}_{2}$ than the yield surface presented in this contribution

When comparing different formulation of yield surfaces one has to keep in mind that they possibly emerge from different approaches. In Simo et al. [9] and Duan et al. [16], the yield surface is described in terms of fully plastic stress resultants. In the present framework the yield surface is described in terms of stress resultants at yield defined by the plastic work. It is all the more astonishing that the yield surfaces used in Simo et al. and in Duan et al. fit the discrete yield surface, when naively replacing the fully plastic stress resultants with the stress resultants at yield. The yield surfaces described by Simo et al. and by Duan et al. just define a two-dimensional surface in three-dimensional stress resultants’ space. In contrast, the yield surface derived in this contribution shows a five-dimensional surface in six-dimensional stress resultants’ space. Thus, it is more general in the stress state of the rod. Furthermore, the yield surface presented here is smooth and of very simple structure. From the point of view of implementing geometrically exact elastoplastic rods, this is convenient, since derivatives with respect to the stress resultants are required. With the presented Lamé curve, the remaining projections also match the numerical data. This can not be investigated with the yield surface used in Simo et al. or in Duan et al.. Finally, here, the cross-sectional problem is solved. This ensures that the deformation of the cross-section is taken into account, when deriving yield surfaces.

As a final note, let us remark that the shape of the discrete yield surface may change depending on the chosen yield limit. In fact, its shape depends on the geometry of the cross-section, too. At the same time, it is also not guaranteed that the discrete yield function can be fitted by a six dimesional convex Lamé curve for all possible cross-sections. In that case, one has to use a different function that replicates the discrete yield surface best. The process to obtain the discrete yield surface, however, would remain unchanged.

Summary

A framework to obtain a yield surface in terms of stress resultants has been presented with the objective to model geometrically exact elastoplastic rods. Based on the cross-sectional deformation of a strained rod, stress resultants are computed. Here, the cross-section obeys a J2-elastoplastic constitutive model. The discrete yield surface results from performing sets of load controlled simulations of the cross-section. Eventually, smooth analytic functions are fitted to the discrete yield surface. The agreement between the fitted functions and the discrete yield surface obtained from simulations is remarkable. The fitted yield surfaces have been obtained both for circular and squared cross-sections. We have shown that in both cases, the yield surfaces are scalable with the size of the cross-section. For an exemplary squared cross-section, the resulting yield surface has been compared with the existing description used by Simo et al. and Duan et al., showing excellent agreement. The yield surface obtained from this contribution can now be used in a finite element formulation for geometrically exact elastoplastic rods such as the one presented in [15] for a more accurate simulation. The extension of the proposed scheme to yield surfaces with hardening will be investigated in a forthcoming contribution.

Appendices

Appendix A. Three-dimensional finite deformation elastoplasticity theory

This appendix reviews elastoplasticity at finite strains. The elastic domain is specified by means of a yield criterion, which is expressed in stresses defined in the deformed spatial configuration. For the case of small strains, the strain tensor $\varvec{\varepsilon }^{{}^{}}_{{}_{}}$ can be additively decomposed as $\varvec{\varepsilon }^{{}^{}}_{{}_{}}=\varvec{\varepsilon }^{{e}^{}}_{{}_{}}+\varvec{\varepsilon }^{{p}^{}}_{{}_{}}$. The resulting stress is then only dependent on the elastic strains $\varvec{\varepsilon }^{{e}^{}}_{{}_{}}$ and internal variables $\xi$. For the case of large deformations, an additive split of the strain measures is no more permitted. Instead, a multiplicative decomposition of the deformation gradient is used as introduced in [28] and well-rooted in the modelling of crystal-plasticity e.g. [29].

Appendix A.1. Kinematical background of multiplicative plasticity

To characterise the kinematics of finite deformations, the deformation map $\varvec{\varphi }({\mathbf {X}},{t})$ is introduced. It maps any point $\mathbf {X}$ from the undeformed material configuration $\mathcal {B}_0$ to its new position $\displaystyle {\mathbf {x}=\varvec{\varphi }({\mathbf {X}},{t})}$ in the deformed spatial configuration $\mathcal {B}_t$. The deformation gradient $\displaystyle {\mathbf {F}_{}^{{}^{}}=\frac{\partial \mathbf {\varvec{\varphi }}}{\partial \mathbf {X}}\left( \mathbf {X},t\right) }$ can be multiplicatively decomposed into an elastic and a plastic part $\mathbf {F}_{}^{{e}^{}}$ and $\mathbf {F}_{}^{{p}^{}}$, respectively:

$$\begin{aligned} \mathbf {F}_{}^{{}^{}}=\mathbf {F}_{}^{{e}^{}}\mathbf {F}_{}^{{p}^{}}. \end{aligned}$$

(A.1)

Figure 12 visualises the kinematics of elastoplasticity. The elastic left Cauchy-Green strain $\mathbf {b}_{}^{{e}^{}}$ and the plastic right Cauchy-Green strain $\mathbf {C}_{}^{{p}^{}}$ are introduced as

$$\begin{aligned} \mathbf {b}_{}^{{e}^{}}:=\mathbf {F}_{}^{{e}^{}}\mathbf {F}_{}^{{e}^{T}} \quad \text {and}\quad \mathbf {C}_{}^{{p}^{}}:=\mathbf {F}_{}^{{p}^{T}}\mathbf {F}_{}^{{p}^{}}. \end{aligned}$$

(A.2)

Both strain measures are related by $\displaystyle {\mathbf {b}_{}^{{e}^{}}=\mathbf {F}_{}^{{}^{}}\mathbf {C}_{}^{{p}^{-1}}\mathbf {F}_{}^{{T}^{}}}$. The spatial velocity gradient $\varvec{\ell }^{}_{}$ is defined as

$$\begin{aligned} \varvec{\ell }^{}_{}:=\dot{\mathbf {F}}_{}^{{}^{}}\mathbf {F}_{}^{{-1}^{}} \end{aligned}$$

(A.3)

and can be additively decomposed into a symmetric part d $\pmb {\mathscr {d}}$ and a skew-symmetric part w. Here, a superposed dot denotes the material time derivative $\displaystyle {\dot{\overline{\left( \bullet \right) }}=\left. \frac{\partial \left( \bullet \right) }{\partial t}\right| _{\mathbf {X}}}$.

Fig. 12

Multiplicative Decomposition of the deformation gradient $\mathbf {F}_{}^{{}^{}}$ into its elastic $\mathbf {F}_{}^{{e}^{}}$ and plastic part $\mathbf {F}_{}^{{p}^{}}$

Appendix A.2. Constitutive equations

It is assumed that the stored energy density $\psi$ depends on the elastic deformation. Restricting to isotropy, $\psi$ is a function of the elastic left Cauchy-Green strain $\mathbf {b}_{}^{{e}^{}}$ only, i.e.

$$\begin{aligned} \psi =\psi (\mathbf {b}_{}^{{e}^{}}). \end{aligned}$$

(A.4)

A possible hardening contribution $\mathcal {H}$ depends only on the internal variable $\xi$. Then, the free energy density is introduced as follows:

$$\begin{aligned} \Psi (\mathbf {b}_{}^{{e}^{}},\xi )=\psi (\mathbf {b}_{}^{{e}^{}})+\mathcal {H}(\xi ). \end{aligned}$$

(A.5)

The dissipation power $\mathcal {D}$ is defined as the difference between the stress power and the rate of the free energy density and is greater or equal zero

$$\begin{aligned} \mathcal {D}=\varvec{\tau }:\varvec{d}-\frac{\hbox {d}\Psi }{\hbox {d}t}(\mathbf {b}_{}^{{e}^{}},\xi )\ge 0. \end{aligned}$$

(A.6)

Here, $\varvec{\tau }$ denotes the (symmetric) Kirchhoff stress. Equation (A.6) denotes the Clausius-Duhem inequality. For a purely elastic response $\mathcal {D}=0$. For the inelastic case however, $\mathcal {D}>0$. Due to the isotropy assumption, Eq. (A.6) transforms to

$$\begin{aligned} \mathcal {D}=&\left[ \varvec{\tau }-2\frac{\partial \Psi }{\partial \mathbf {b}_{}^{{e}^{}}}(\mathbf {b}_{}^{{e}^{}},\xi )\mathbf {b}_{}^{{e}^{}}\right] :\varvec{d}\nonumber \\&+\left[ 2\frac{\partial \Psi }{\partial \mathbf {b}_{}^{{e}^{}}}(\mathbf {b}_{}^{{e}^{}},\xi )\mathbf {b}_{}^{{e}^{}}\right] :\left[ -\frac{1}{2}\mathcal {L}_{\upsilon }\left( \mathbf {b}^e\right) \mathbf {b}_{}^{{e}^{-1}}\right] \nonumber \\&+\left[ -\frac{\partial \Psi }{\partial \xi }(\mathbf {b}_{}^{{e}^{}},\xi )\dot{\xi }\right] \ge 0 \end{aligned}$$

(A.7)

with $\displaystyle {\mathcal {L}_{\upsilon }\left( \mathbf {b}^e\right) :=\mathbf {F}_{}^{{}^{}}\dot{\mathbf {C}}_{}^{{p}^{-1}}\mathbf {F}_{}^{{T}^{}}}$ denoting the Lie derivative of $\mathbf {b}_{}^{{e}^{}}$. Equation (A.7) has to hold for any admissible process. This standard argument renders the constitutive relation and the reduced form of the dissipation inequality as summarised below:

$$\begin{aligned}&\varvec{\tau }=2\frac{\partial \Psi }{\partial \mathbf {b}_{}^{{e}^{}}}(\mathbf {b}_{}^{{e}^{}},\xi )\mathbf {b}_{}^{{e}^{}}, \end{aligned}$$

(A.8)

$$\begin{aligned}&\mathcal {D}_{red}=\varvec{\tau }:\left[ -\frac{1}{2}\mathcal {L}_{\upsilon }\left( \mathbf {b}^e\right) \mathbf {b}_{}^{{e}^{-1}}\right] +q\dot{\xi }\ge 0. \end{aligned}$$

(A.9)

The thermodynamic force conjugate to the internal variable is: $\displaystyle {q=-\frac{\partial \Psi }{\partial \xi }}(\mathbf {b}_{}^{{e}^{}},\xi )$. Here, the first summand of Eq. (A.9) is defined to be the rate of the plastic work density $\psi ^p$. Thus,

$$\begin{aligned} \dot{\psi }^p=\varvec{\tau }:\left[ -\frac{1}{2}\mathcal {L}_{\upsilon }\left( \mathbf {b}^e\right) \mathbf {b}_{}^{{e}^{-1}}\right] . \end{aligned}$$

(A.10)

Appendix A.3. Evolution equation

According to the postulate of maximum dissipation, the actual state ($\varvec{\tau }$, q) of a plastically deformed body renders the maximum of the dissipation function $\mathcal {D}_{red}$ for the actual evolution quantities. To obtain the evolution equations for $\mathbf {b}_{}^{{e}^{}}$ and $\xi$, the dissipation has to be maximised under constraints. The constrained maximisation problem is then solved by means of the Lagrange multiplier method. Therefore, a Lagrange functional $\mathcal {L}$ is defined. The Lagrange functional is the sum of the negative reduced dissipation and a constraint multiplied with the Lagrange multiplier $\dot{\gamma }\ge 0$:

$$\begin{aligned} \mathcal {L}=-\mathcal {D}_{red}+\dot{\gamma }\Phi . \end{aligned}$$

(A.11)

The constraint $\Phi \le 0$ describes the region of admissible stresses, i.e. the yield surface. The Lagrange functional must be stationary. Necessary conditions are obtained with

$$\begin{aligned}&\frac{\partial \mathcal {L}}{\partial \varvec{\tau }}(\mathbf {b}_{}^{{e}^{}},\xi )=0\rightarrow -\frac{1}{2}\mathcal {L}_{\upsilon }\left( \mathbf {b}^e\right) =\dot{\gamma }\frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau },q)\mathbf {b}_{}^{{e}^{}}, \end{aligned}$$

(A.12)

$$\begin{aligned}&\frac{\partial \mathcal {L}}{\partial q}(\mathbf {b}_{}^{{e}^{}},\xi )=0\rightarrow \dot{\xi }=\dot{\gamma }\frac{\partial \Phi }{\partial q}(\varvec{\tau },q). \end{aligned}$$

(A.13)

Together with the Karush-Kuhn-Tucker (KKT) conditions, a first order system of equations is obtained:

$$\begin{aligned}&\dot{\xi }=\dot{\gamma }\frac{\partial \Phi }{\partial q}(\varvec{\tau },q) \end{aligned}$$

(A.14)

$$\begin{aligned}&\dot{\mathbf {b}}_{}^{{e}^{}}=\varvec{\ell }^{}_{}\mathbf {b}_{}^{{e}^{}}+\mathbf {b}_{}^{{e}^{}}\varvec{\ell }^{T}_{}-2\dot{\gamma }\frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau },q)\mathbf {b}_{}^{{e}^{}} \end{aligned}$$

(A.15)

$$\begin{aligned}&\hbox {KKT:}\quad \dot{\gamma }\ge 0,\quad \Phi (\varvec{\tau },q)\le 0,\quad \dot{\gamma }\Phi (\varvec{\tau },q)=0 \end{aligned}$$

(A.16)

In terms of material quantities, Eq. (A.15) is rewritten as

$$\begin{aligned} \dot{\mathbf {C}}_{}^{{p}^{-1}}=\left[ -2\dot{\gamma }\mathbf {C}_{}^{{-1}^{}}\mathbf {D}\right] \mathbf {C}_{}^{{p}^{-1}}, \end{aligned}$$

(A.17)

with the co-variant pull back of the flow direction

$$\begin{aligned} \mathbf {D}=\mathbf {F}_{}^{{T}^{}}\frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau }_,q)\mathbf {F}_{}^{{}^{}}. \end{aligned}$$

(A.18)

The description of the evolution equation in terms of material quantities returns a first order differential equation which can be easily solved with appropriate initial conditions. To evaluate the temporal evolution, a typical time step $\left[ t_n,t_{n+1}\right]$ is assumed. The variables $\mathbf {F}_{n}^{{}^{}}$, $\mathbf {C}_{n}^{{p}^{-1}}$ and $\xi _n$ at $t_n$ are known. The evolution equations are rewritten for general $t \in \left[ t_n,t_{n+1}\right]$

$$\begin{aligned} \dot{\xi }_t=\dot{\gamma }_t\frac{\partial \Phi }{\partial q}(\varvec{\tau }_t,q_t) \quad \text {and}\quad \dot{\mathbf {C}}_{t}^{{p}^{-1}}=\left[ -2\dot{\gamma }_t \mathbf {C}_{t}^{{-1}^{}}\mathbf {D}_t\right] \mathbf {C}_{t}^{{p}^{-1}} \end{aligned}$$

(A.19)

with

$$\begin{aligned}&\mathbf {D}_t=\mathbf {F}_{t}^{{T}^{}}\frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau }_t,q_t)\mathbf {F}_{t}^{{}^{}}, \end{aligned}$$

(A.20)

$$\begin{aligned}&\hbox {KKT:}\quad \dot{\gamma }_t\ge 0, \quad \Phi (\varvec{\tau }_t,q_t)\le 0,\quad \dot{\gamma }_t\Phi (\varvec{\tau }_t,q_t)=0.\nonumber \\ \end{aligned}$$

(A.21)

The following steps are motivated by the solution of general first order linear problems. The solution for $\displaystyle {\dot{y}(t)=my(t)}$ with $\displaystyle {y(t)\vert _{t=t_n}=y(t_n)}$ is given by $\displaystyle {y(t)=e^{m \Delta t}y(t_n)}$, where $\Delta t=t_{}-t_{n}$. The algorithmic approximation of the inverse plastic right Cauchy-Green strain thus reads

$$\begin{aligned} \tilde{\mathbf {C}}_{t}^{{p}^{-1}}=e^{\left( -2\Delta \gamma _{t}\mathbf {C}_{t}^{{-1}^{}}{\mathbf {D}}_{t}\right) }\mathbf {C}_{n}^{{p}^{-1}}. \end{aligned}$$

(A.22)

In the sequel, variables superposed by a $\tilde{\bullet }$ denote the algorithmic approximation. Freezing the plastic flow, and taking an elastic step, while ignoring constraints on the stress field by the yield criterion, returns an elastic trial step, identified by the superscript $^{tr}$. The trial elastic left Cauchy-Green strain $\mathbf {b}_{t}^{{e}^{tr}}$ is obtained as $\displaystyle {\mathbf {b}_{t}^{{e}^{tr}}=\mathbf {F}_{t}^{{}^{}}\mathbf {C}_{n}^{{p}^{-1}}\mathbf {F}_{t}^{{T}^{}}}$. Pre- and postmultiplying Eq. (A.22) with $\mathbf {F}_{t}^{{}^{}}$ and $\mathbf {F}_{t}^{{T}^{}}$, and making use of the property $\displaystyle {\mathbf {F}_{}^{{}^{}} e^{\mathbf {A}}\mathbf {F}_{}^{{-1}^{}}}=e^{\left( \mathbf {F}_{}^{{}^{}}\mathbf {A}\mathbf {F}_{}^{{-1}^{}}\right) }$ finally yields the discretised flow rule in terms of spatial quantities:

$$\begin{aligned} \tilde{\xi }_{t}=\xi _{n}+\Delta \gamma _{t}\frac{\partial \Phi }{\partial q}(\varvec{\tau }_t,q_t) \quad \text {and}\quad \tilde{\mathbf {b}}_{t}^{{e}^{}}=e^{\left( -2\Delta \gamma _{t}\frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau }_t,q_t)\right) }\mathbf {b}_{t}^{{e}^{tr}} \end{aligned}$$

(A.23)

with the KKT conditions in Eq. (A.21).

Appendix B. Implementation of isotropic plasticity

This appendix reiterates the implementation of multiplicative elastoplasticity. First, the discretised flow rule, introduced in “Appendix A.3” is reformulated in terms of logarithmic strains. Then, a return algorithm to map the stresses to the admissible region is introduced for the example of J2-plasticity.

To solve nonlinear elastoplastic problems, use is made of an iterative Newton-Raphson solver that requires the algorithmic elastoplastic tangent. Its derivation is outlined at the end of this appendix.

Appendix B.1. Reduction to principal strains and stresses

The assumption of isotropy renders the principal directions of the Kirchhoff stress $\varvec{\tau }$ to coincide with the principal directions of the elastic left Cauchy-Green strain $\mathbf {b}_{}^{{e}^{}}$ [27, 30]. Their spectral decompositions are, respectively

$$\begin{aligned} \mathbf {b}_{}^{{e}^{}}=\sum _{A=1}^3\left[ \lambda _{{A}_{}}^{{e}^{{}^{}}}\right] ^2\mathbf {n}^{}_{A_{}}\otimes \mathbf {n}^{}_{A_{}}\quad \hbox {and}\quad \varvec{\tau }=\sum _{A=1}^3\beta _A\mathbf {n}^{}_{A_{}}\otimes \mathbf {n}^{}_{A_{}}. \end{aligned}$$

(B.1)

The spectral decomposition of $\mathbf {b}_{t}^{{e}^{tr}}$ yields

$$\begin{aligned} \mathbf {b}_{t}^{{e}^{tr}}=\sum _{A=1}^3\left[ \lambda _{{A}_{t}}^{{e}^{{tr}^{}}}\right] ^2\mathbf {n}^{tr}_{A_{t}}\otimes \mathbf {n}^{tr}_{A_{t}}. \end{aligned}$$

(B.2)

The restriction to isotropy implies the existence of a function $\hat{\Phi }$ such that $\hat{\Phi }(\beta _1,\beta _2,\beta _3,q)=\Phi (\varvec{\tau },q)$ [27]. This leads to

$$\begin{aligned} \frac{\partial \Phi }{\partial \varvec{\tau }}(\varvec{\tau },q)=\sum _{A=1}^3\frac{\partial \hat{\Phi }}{\partial \beta _A}(\beta _A,q)\mathbf {n}^{}_{A_{}}\otimes \mathbf {n}^{}_{A_{}}. \end{aligned}$$

(B.3)

Applying relation (B.3) to Eq. (A.23), one obtains the spectral decomposition of $\mathbf {b}_{t}^{{e}^{tr}}$ as

$$\begin{aligned} \mathbf {b}_{t}^{{e}^{tr}}=\sum _{A=1}^3e^{\left( 2\Delta \gamma _{t}\frac{\partial \hat{\Phi }}{\partial \beta _A}(\beta _A,q)\right) }\left[ \tilde{\lambda }_{{A}_{}}^{{e}^{{}^{}}}\right] ^2\tilde{\mathbf {n}}^{}_{A_{t}}\otimes \tilde{\mathbf {n}}^{}_{A_{t}}. \end{aligned}$$

(B.4)

Comparing Eq. (B.2) and (B.4), the uniqueness of $\mathbf {b}_{t}^{{e}^{tr}}$ yields:

$$\begin{aligned} \tilde{\mathbf {n}}^{}_{A_{t}}=\mathbf {n}^{tr}_{A_{t}}, \quad \text {and}\quad \left[ \tilde{\lambda }_{{A}_{t}}^{{e}^{{}^{}}}\right] ^2=e^{\left( -2\Delta \gamma _{t}\frac{\partial \hat{\Phi }}{\partial \beta _A}(\beta _A,q)\right) }\left[ \lambda _{{A}_{t}}^{{e}^{{}^{tr}}}\right] ^2. \end{aligned}$$

(B.5)

Now, principal logarithmic stretches are defined as

$$\begin{aligned} \varepsilon ^{{e}^{tr}}_{{A}_{t}}:=\log \left( \lambda _{{A}_{t}}^{{e}^{{tr}^{}}}\right) , \quad \text {and}\quad \tilde{\varepsilon }^{{e}^{}}_{{A}_{t}}:=\log \left( \tilde{\lambda }_{{A}_{t}}^{{e}^{{}^{}}}\right) . \end{aligned}$$

(B.6)

Taking the logarithm on both sides of Eq. (B.5), the multiplicative update transforms into an additive update. Initializing $\tilde{\varvec{\varepsilon }}^{{e}^{}}_{{t}_{}}=\left[ \tilde{\varepsilon }^{{e}^{}}_{{1}_{t}}, \tilde{\varepsilon }^{{e}^{}}_{{2}_{t}}, \tilde{\varepsilon }^{{e}^{}}_{{3}_{t}}\right] ^{T}$ and $\varvec{\varepsilon }^{{e}^{tr}}_{{t}_{}}=\left[ \varepsilon ^{{e}^{tr}}_{{1}_{t}}, \varepsilon ^{{e}^{tr}}_{{2}_{t}}, \varepsilon ^{{e}^{tr}}_{{3}_{t}}\right] ^{T}$ one obtains

$$\begin{aligned}&\tilde{\xi }_{t}=\xi _{n}+\Delta \gamma _{t}\frac{\partial \hat{\Phi }}{\partial q}(\beta _A,q) \end{aligned}$$

(B.7)

$$\begin{aligned}&\tilde{\varepsilon }^{{e}^{}}_{{t}_{A}}=-\Delta \gamma _{t}\frac{\partial \hat{\Phi }}{\partial \beta _A}(\beta _A,q)+\varepsilon ^{{e}^{tr}}_{{t}_{A}} \end{aligned}$$

(B.8)

$$\begin{aligned}&\hbox {KKT:}\quad \Delta \gamma _{t}\ge 0,\quad \hat{\Phi }(\beta _A,q)\le 0,\quad \Delta \gamma _{t}\hat{\Phi }(\beta _A,q)=0 \nonumber \\ \end{aligned}$$

(B.9)

Appendix B.2. J2-Plasticity

J2-plasticity is formulated in terms of the second invariant of the deviatoric stress tensor. Here, the free energy density is assumed quadratic in the principal logarithmic stretches and takes the form:

$$\begin{aligned} \hat{\Psi }(\varepsilon _A^e,\xi )= & {} \frac{1}{2}\lambda \left[ \varepsilon _1^e+\varepsilon _2^e+\varepsilon ^e_3\right] ^2+\mu \left[ \left[ \varepsilon _1^{e}\right] ^2+\left[ \varepsilon _2^{e}\right] ^2+\left[ \varepsilon ^{e}_3\right] ^2\right] \nonumber \\&+\mathcal {H}(\xi ), \end{aligned}$$

(B.10)

where $\lambda$ and $\mu$ denote the Lamé Parameters. Thus, the stored energy density takes the form

$$\begin{aligned} \hat{\psi }(\varepsilon _A^e)=\frac{1}{2}\lambda \left[ \varepsilon _1^e+\varepsilon _2^e+\varepsilon ^e_3\right] ^2+\mu \left[ \left[ \varepsilon _1^{e}\right] ^2+\left[ \varepsilon _2^{e}\right] ^2+\left[ \varepsilon ^{e}_3\right] ^2\right] . \end{aligned}$$

(B.11)

Here, the hardening contribution is a quadratic function $\displaystyle {\mathcal {H}(\xi )=\frac{1}{2}H\xi ^2}$, with the hardening parameter H. The yield criterion is defined in terms of principal stresses:

$$\begin{aligned} \hat{\Phi }(\varvec{\beta },q)=\left\| \overline{\varvec{\beta }} \right\| - \sqrt{\frac{2}{3}}\left[ \sigma _y-q\right] \le 0, \end{aligned}$$

(B.12)

where $\varvec{\beta }=\left[ \beta _1,\beta _2,\beta _3\right]$ and $\displaystyle { \overline{\varvec{\beta }}=\varvec{\beta }-\frac{1}{3}\left[ \varvec{\beta }\cdot \mathbf {1}\right] \mathbf {1}}$ denotes the deviatoric principal stress. Here, $\mathbf {1}=\left[ 1, 1, 1\right] ^T$. The yield stress is denoted by $\sigma _y$, where $\sigma _y>0$. Further, the stress-strain relation in principal axes associated with the above constitutive model (see Eq. (B.10)) takes the form [27]:

$$\begin{aligned} \varvec{\beta }=\mathbf {a}\varvec{\varepsilon }^{{e}^{}}_{{}_{}}, \end{aligned}$$

(B.13)

where the constant elastic modulus $\mathbf {a}$ in principal stretches is

$$\begin{aligned} \mathbf {a}=\kappa \mathbf {1}\otimes \mathbf {1}+2\mu \left[ \mathbf {I}-\frac{1}{3}\mathbf {1}\otimes \mathbf {1}\right] . \end{aligned}$$

(B.14)

Here, $\mathbf {I}$ denotes the unit tensor and $\displaystyle {\kappa =\lambda +\frac{2}{3}\mu }$.

In the typical interval $t\in \left[ t_n, t_{n+1}\right]$ the state variables $\xi _n$ and $\mathbf {b}_{n}^{{e}^{}}$ are known. Here, let $t=t_{n+1}$. The size of the step is denoted by $\Delta t_{n+1}=t_{n+1}-t_n$. The return mapping algorithm in principal stresses is obtained by multiplying the principal stretches in Eq. (B.8) with the stiffness $\mathbf {a}$ and is summarised as follows

$$\begin{aligned}&\xi _{n+1}=\xi _{n}+\sqrt{\frac{2}{3}}\Delta \gamma _{n+1} \end{aligned}$$

(B.15)

$$\begin{aligned}&\varvec{\beta }_{n+1}=\varvec{\beta }_{n+1}^{tr}-2\mu \overline{\varvec{\nu }}^{}{}_{n+1}\Delta \gamma _{n+1} \end{aligned}$$

(B.16)

$$\begin{aligned}&\varvec{\varepsilon }^{{e}^{}}_{{n+1}_{}}=\varvec{\varepsilon }^{{e}^{tr}}_{{n+1}_{}}-\overline{\varvec{\nu }}^{}{}_{n+1}\Delta \gamma _{n+1} \end{aligned}$$

(B.17)

$$\begin{aligned}&\hbox {KKT:}\quad \Delta \gamma _{n+1}\ge 0,\quad \hat{\Phi }(\varvec{\beta }_{n+1},q_{n+1})\le 0,\nonumber \\&\Delta \gamma _{n+1}\hat{\Phi }(\varvec{\beta }_{n+1},q_{n+1})=0, \end{aligned}$$

(B.18)

where

$$\begin{aligned} \varvec{\beta }_{n+1}^{tr}=\mathbf {a}\varvec{\varepsilon }^{{e}^{tr}}_{{n+1}_{}} \end{aligned}$$

(B.19)

Implicit to above equations are the relations ${\frac{\partial \hat{\Phi }}{\partial q}(\varvec{\beta },q)=\sqrt{\frac{2}{3}}}$ and ${\frac{\partial \hat{\Phi }}{\partial \varvec{\beta }}(\varvec{\beta },q)=\overline{\varvec{\nu }}^{}=\frac{\overline{\varvec{\beta }}}{\Vert \overline{\varvec{\beta }}\Vert }}$. It remains to evaluate $\Delta \gamma _{n+1}$. For plastic loading, $\Delta \gamma _{n+1}\ne 0$, thus $\hat{\Phi }(\varvec{\beta }_{n+1},q_{n+1})\doteq 0$. This condition results in the following equation

$$\begin{aligned}&\Phi _{n+1}=\Phi ^{tr}-2\mu \Delta \gamma _{n+1}\nonumber \\&\quad -\sqrt{\frac{2}{3}}\left[ \frac{\partial \mathcal {H}}{\partial \xi }\left( \xi _n+\sqrt{\frac{2}{3}}\Delta \gamma _{n+1}\right) -\frac{\partial \mathcal {H}}{\partial \xi }\left( \xi _n\right) \right] \doteq 0. \nonumber \\ \end{aligned}$$

(B.20)

Equation (B.20) is solved for $\Delta \gamma _{n+1}$ via an iterative Newton-Raphson solver. However, for the special case of linear hardening as introduced above, one can solve for $\Delta \gamma _{n+1}$ in closed form.

Appendix B.3. Algorithmic elastoplastic tangent moduli

The algorithmic elastoplastic tangent modulus relates changes in the stress to changes in the total strain and is needed in finite-element simulations to set up the tangent stiffness matrix. Furthermore, it is indispensable for the calculation of the rod’s stiffness. Here, the algorithmic elastoplastic tangent modulus is defined as:

$$\begin{aligned} \mathbb {A}^{ep}=\frac{\partial \mathbf {P}_{}}{\partial \mathbf {F}_{}^{{}^{}}}=\frac{\partial \left( \mathbf {F}_{}^{{}^{}}\mathbf {S}_{}\right) }{\partial \mathbf {F}_{}^{{}^{}}}=\frac{\partial \mathbf {F}_{}^{{}^{}}}{\partial \mathbf {F}_{}^{{}^{}}}\mathbf {S}_{}+\mathbf {F}_{}^{{}^{}}\left[ \frac{\partial \mathbf {S}_{}}{\partial \mathbf {C}_{}^{{}^{}}}:\frac{\partial \mathbf {C}_{}^{{}^{}}}{\partial \mathbf {F}_{}^{{}^{}}}\right] . \end{aligned}$$

(B.21)

The computation of $\displaystyle {\frac{\partial \mathbf {F}_{}^{{}^{}}}{\partial \mathbf {F}_{}^{{}^{}}}}$ and $\displaystyle {\frac{\partial \mathbf {C}_{}^{{}^{}}}{\partial \mathbf {F}_{}^{{}^{}}}}$ is straightforward. Thus, the focus is on the computation of $\displaystyle {\frac{\partial \mathbf {S}_{}}{\partial \mathbf {C}_{}^{{}^{}}}}$, which is denoted as the fourth order material tangent moduli $\mathbb {C}_{}$. First, the Piola-Kirchoff stress is defined as the contra-variant pull back of the Kirchhoff stress $\varvec{\tau }$

$$\begin{aligned} \mathbf {S}_{}=\mathbf {F}_{}^{{-1}^{}}\varvec{\tau }_{}\mathbf {F}_{}^{{-T}^{}}=\sum _{A=1}^3\beta _{A_{}}\mathbf {F}_{}^{{-1}^{}}\left[ \mathbf {n}_{A_{}}\otimes \mathbf {n}_{A_{}}\right] \mathbf {F}_{}^{{-T}^{}}. \end{aligned}$$

(B.22)

Using the fact that $\mathbf {n}^{tr}_{A_{}}=\mathbf {n}_{A_{}}$, the above equation is rewritten as

$$\begin{aligned} \mathbf {S}_{}=\sum _{A=1}^3\beta _{A_{}}\mathbf {M}_{A_{}}^{tr} \end{aligned}$$

(B.23)

with $\mathbf {M}^{tr}_{A_{}}=\mathbf {F}_{}^{{-1}^{}}\left[ \mathbf {n}^{tr}_{A_{}}\otimes \mathbf {n}^{tr}_{A_{}}\right] \mathbf {F}_{}^{{-T}^{}}$. The derivative of Eq. (B.23) with respect to $\mathbf {C}_{}^{{}^{}}$ yields

$$\begin{aligned} \frac{\partial \mathbf {S}_{}}{\partial \mathbf {C}_{}^{{}^{}}}=\sum _{A=1}^3\sum _{B=1}^3\frac{\partial \beta _{A_{}}}{\partial \varepsilon _{B_{}}}\mathbf {M}^{tr}_{A_{}}\otimes \frac{\partial \varepsilon _{B_{}}}{\partial \mathbf {C}_{}^{{}^{}}}+\sum _{A=1}^3 \beta _{A_{}}\frac{\partial \mathbf {M}^{tr}_{A_{}}}{\partial \mathbf {C}_{}^{{}^{}}}. \end{aligned}$$

(B.24)

Here, $\displaystyle {\frac{\partial \beta _{A_{}}}{\partial \varepsilon _{B_{}}}}$ is the scalar component of a $3\times 3$ matrix, the algorithmic elastoplastic moduli $\mathbf {a}_{}^{ep}$. The result for $\displaystyle {\frac{\partial \varepsilon _{B}}{\partial \mathbf {C}_{}^{{}^{}}}}$ is derived in [27] and reads as

$$\begin{aligned} \frac{\partial \varepsilon _{B_{}}}{\partial \mathbf {C}_{}^{{}^{}}}=\frac{1}{2}\mathbf {M}^{tr}_{B_{}}. \end{aligned}$$

(B.25)

The derivative in the second sum is the pull back of its spatial counter part $\mathbb {c}$ derived in [27]

$$\begin{aligned} \frac{\partial M^{tr}_{A_{IJ}}}{\partial C_{KL}}=c_{ijkl}F^{-1}_{iI}F^{-1}_{jJ}F^{-1}_{kK}F^{-1}_{lL}. \end{aligned}$$

(B.26)

Inserting the terms, Eq. (B.24) is rewritten as

$$\begin{aligned} \frac{\partial \mathbf {S}_{}}{\partial \mathbf {C}_{}^{{}^{}}}=\sum _{A=1}^3\sum _{B=1}^3 \frac{1}{2}\text {a}^{ep}_{AB}\mathbf {M}^{tr}_{A_{}}\otimes \mathbf {M}^{tr}_{B_{}}+\sum _{A=1}^3 \beta _{A_{}}\frac{\partial \mathbf {M}^{tr}_{A_{}}}{\partial \mathbf {C}_{}^{{}^{}}}. \end{aligned}$$

(B.27)

The derivation of $\mathbf {a}^{ep}$ is given in [27] and is summarised as

$$\begin{aligned} \mathbf {a}_{}^{ep}= & {} \mathbf {a}-2\mu \left[ \frac{2\mu \Delta \gamma }{\Vert \overline{\varvec{\beta }}^{}\Vert }\left[ \mathbf {I}-\frac{1}{3}\mathbf {1}\otimes \mathbf {1}\right] \right. \nonumber \\&\qquad \qquad \left. +\left[ \frac{2\mu }{2\mu +\frac{2}{3}H}-\frac{2\mu \Delta \gamma }{\Vert \overline{\varvec{\beta }}^{}\Vert }\right] \overline{\varvec{\nu }}^{}{}\otimes \overline{\varvec{\nu }}^{}{}\right] . \end{aligned}$$

(B.28)

Implicit to the above equation is:

$$\begin{aligned} \mathbf {a}_{}^{ep}=\frac{\partial }{\partial \varvec{\varepsilon }^{{}^{}}_{{}_{}}}\left( \mathbf {a}\varvec{\varepsilon }^{{e}^{tr}}_{{}_{}}-2\mu \overline{\varvec{\nu }}^{}{}\Delta \gamma \right) . \end{aligned}$$

(B.29)

Obviously, for the case of elasticity $\Delta \gamma =0$ and $\mathbf {a}_{}^{ep}=\mathbf {a}$.

Appendix C. Stress resultants and stiffnesses for shearing and twisting

Figures 13 and 14 display transversal force and twisting moment as well as their corresponding stiffnesses as a function of shear and twist, respectively. Their course is similar to the case of bending discussed in Sect. 3.3.

Fig. 13

Transversal force and transversal stiffness as a function of shear. The transition from purely elastic to plastic behaviour and thus the decrease in stiffness is gradual

Fig. 14

Twisting moment and twisting stiffness as a function of twist. The transition from purely elastic to plastic behaviour is gradual. For ideal plasticity as well as for plasticity with hardening, the decrease in stiffness is smooth