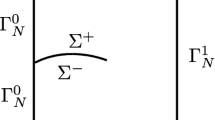A modelling framework for coupled hydrogen diffusion and mechanical behaviour of engineering components

Abstract

In this paper, we propose a finite element formulation for solving coupled mechanical/diffusion problems. In particular, we study hydrogen diffusion in metals and its impact on their mechanical behaviour (i.e. hydrogen embrittlement). The formulation can be used to model hydrogen diffusion through a material and its accumulation within different microstructural features of the material (dislocations, precipitates, interfaces, etc.). Further, the effect of hydrogen on the plastic response and cohesive strength of different interfaces can be incorporated. The formulation adopts a standard Galerkin method in the discretisation of both the diffusion and mechanical equilibrium equations. Thus, a displacement-based finite element formulation with chemical potential as an additional degree of freedom, rather than the concentration, is employed. Consequently, the diffusion equation can be expressed fundamentally in terms of the gradient in chemical potential, which reduces the continuity requirements on the shape functions to zero degree, ${\mathcal {C}}_{0}$, i.e. linear functions, compared to the ${\mathcal {C}}_{1}$ continuity condition required when concentration is adopted. Additionally, a consistent interface element formulation can be achieved due to the continuity of the chemical potential across the interface—concentration can be discontinuous at an interface which can lead to numerical problems. As a result, the coding of the FE equations is more straightforward. The details of the physical problem, the finite element formulation and constitutive models are initially discussed. Numerical results for various example problems are then presented, in which the efficiency and accuracy of the proposed formulation are explored and a comparison with the concentration-based formulations is presented.

1 Introduction

In the presence of hydrogen, many materials experience significant degradation of their mechanical properties, which is commonly known as hydrogen embrittlement (HE) [1, 2, 3]. These detrimental effects are reported in the literature in terms of reductions in ductility, strength and toughness. As a result, HE may result in premature catastrophic failure at load levels much lower than in the hydrogen free case. A number of mechanisms of embrittlement have been proposed in the literature [2, 3]. The two mechanisms that have received the most attention are hydrogen induced (or enhanced) decohesion (HID or HEDE) [4, 5] and hydrogen enhanced local plasticity (HELP) [6, 7]. In the HEDE mechanism [8, 9, 10], hydrogen accumulates at an interface and reduces the cohesive strength and hence the energy required to fracture the material. In the HELP mechanism [11, 12], hydrogen is assumed to enhance the dislocation mobility, change the core energy and also reduce the elastic interaction between dislocations, generally termed elastic shielding, each of which can result in material softening and localisation of plastic flow. In recent years, there has been significant interest in developing computational models for hydrogen embrittlement. Although there is still significant controversy and debate in the scientific literature concerning the detailed mechanisms responsible for embrittlement, it is generally agreed that any model should contain the following ingredients:

• Diffusion of hydrogen through the material and hydrogen accumulation within different microstructural features.

• The effect of hydrogen on the plastic response of the material.

• The effect of hydrogen on the cohesive properties of any interfaces in the material.

Most published finite element models of the embrittlement process follow the approach originally proposed by Sofronis and McMeeking [13] in which the governing equation for diffusion is expressed in terms of the gradient in concentration and gradient in the mean (or hydrostatic) stress, and the nodal degrees of freedom for the coupled mechanical/diffusion problem are taken as the displacements and concentration. As noted by Barrera et al. [14], the dependence of the diffusion equation on the stress gradient requires the use of finite elements with shape functions that are at least quadratic in terms of displacement. Also, for situations where interfaces are modelled, either between similar or dissimilar materials, there can be a discontinuity in concentration at an interface. This can lead to numerical problems.

In this work, we return to fundamentals and express the diffusion equation in terms of the gradient in chemical potential and we take the chemical potential as a degree of freedom, rather than the concentration. A consequence of this is that the finite element formalism no longer requires stress gradients to be determined, allowing the use of elements with linear shape functions and simplifying the finite element implementation (particularly when implemented in finite element packages such as Abaqus [15]). Also, the chemical potential is a continuous function within the body, and we do not need to confront problems arising from discontinuities in our solution dependent variables, particularly at interfaces.

In the following section, we provide a more detailed background to the class of physical problems considered here and a general statement of the combined mechanical–diffusion analysis of multi-component and/or multi-grained boundary value problems. This is followed by a statement of the fundamental diffusion and mechanical equations for the bulk material and interfaces. The governing finite element equations are developed in Sect. 3, using a Galerkin approach based on statements of conservation of mass and mechanical equilibrium. Implementation of the finite element approach further requires constitutive models for the mechanical response of the matrix and interfaces. Suitable models are presented in Sect. 4 and these are used in Sect. 5 to analyse some simple representative problems, where we compare the efficiency and accuracy of the approach with that described by Barrera et al. [14].

2 Background

In this study, we investigate a class of problems in which a material or multiple materials are subjected to mechanical loading in the presence of hydrogen, i.e. combined chemical-mechanical loading. In particular, we are interested in the response of polycrystalline metallic engineering alloys. Generally, hydrogen diffuses in metals through interstitial lattice sites (NILS). Dislocations and interfaces can provide additional paths for diffusion, but these sites tend to trap hydrogen (as discussed further below) and diffusion along them can be much more sluggish than through the matrix [16, 17]. We therefore ignore these minor contribution here. Hydrogen resides in NILS and the trapping sites, i.e. dislocations, grain boundaries, carbide/matrix interfaces, microvoids and other defects. The NILS are considered to be the dominant sites. However, the effect of shallow traps on diffusivity is very significant and deep traps can play an important role acting as a gutter for hydrogen and therefore cannot be ignored. Under mechanical loading, the hydrostatic stress gradient also plays an important role in determining the flux of hydrogen within a body. Moreover, in elastic–plastic materials, the number of trapping sites increases as the dislocation density increases with increasing plastic deformation. Hence, the chemical and mechanical fields are strongly coupled and the material behaviour is controlled by the characteristic time of the diffusion and deformation processes. Further, depending on the length scale and density of traps, they can either be treated as a continuous distribution in the material, such that their presence modifies the effective diffusivity in the matrix, or as discrete features, such as grain boundaries, carbide/matrix interfaces, precipitate, etc., wherein a direct interaction between the trap and mobile hydrogen is considered. We consider each of these here. In the following sub-section, we introduce a model problem that can be used to represent different material systems such as grains and their boundaries, precipitates in a matrix or any other situation where failure can occur at an interface.

2.1 The model problem

We consider a body which is comprised of two different materials $\mathrm {A}$ and $\mathrm {B}$ that can have different mechanical and diffusional (and thermodynamic) properties, which are separated by an interface, see Fig. 1. A common Cartesian coordinate system for the reference and deformed configurations $X_{i}$ and $x_{i}$, $i=1,2,3$, respectively, is assumed. The body occupies a volume $\varOmega$ with boundary $\varGamma$- materials $\mathrm {A}$ and $\mathrm {B}$ occupy $\varOmega _{\mathrm {A}}$ and $\varOmega _{\mathrm {B}}$ respectively, i.e. $\varOmega = \varOmega _{\mathrm {A}} \cup \varOmega _{\mathrm {B}}$, in the current configuration. The interface is defined by $\varGamma _{\mathrm {int}}$. Failure can occur along the interface as the material deforms, leading to complete separation of the interfacial planes either side of the interface. To allow for this, a material point along the interface is defined by the two normal vectors $n_{i}^{-}$ and $n_{i}^{+}$ either side of the interface, as shown in Fig. 1ii, where $n_{i}^{-} = -n_{i}^{+}$, i.e. the initially intact material point splits into two points with unit normals acting opposite to each other and into the material on either side of the interface (on the upper and lower interface surfaces $\varGamma _{\mathrm {int}}^{\pm }$ of Fig. 1ii, respectively).

Fig. 1

The schematic of the model problem. The figures illustrate: i a continuum body that is subjected to macroscopic deformation $\left( E_{ij},\varSigma _{ij} \right)$ in the presence of hydrogen that is defined by the chemical potential and concentration at the lattice and discrete traps $\left( \mu ,C_{\mathrm {L}},C_{\mathrm {Tr}} \right)$; and ii the microstructure is comprised of a bi-material system of materials $\mathrm {A}$ and $\mathrm {B}$ that are separated by an interface where the microscopic deformation is $\left( \varepsilon _{ij},\sigma _{ij} \right)$ and the hydrogen chemical potential and concentration in the lattice, distributed and discrete traps $\left( \mu _{i},C_{\mathrm {L}}^{i},C_{\mathrm {Tr}}^{i},\mu _{\mathrm {int}},C_{\mathrm {int}} \right)$, where $i \in \mathrm {A}, \mathrm {B}$

The body is assumed to be subjected to mechanical loading and contains hydrogen that may diffuse through the body and across interfaces and boundaries. The total concentration of hydrogen in the bulk, i.e. materials $\mathrm {A}$ and $\mathrm {B}$, at a material point is defined by the total number of H atoms in NILS and traps per unit volume (H $\mathrm {atoms}/\mathrm {m}^{3}$). The traps in the bulk are assumed to be continuous and locally in equilibrium with mobile hydrogen following Oriani’s theory [18]. Hence, the total concentration in materials $\mathrm {A}$ and $\mathrm {B}$, $C^{\mathrm {A}}_{\mathrm {T}}$ and $C^{\mathrm {B}}_{\mathrm {T}}$, respectively, can be written as

$$\begin{aligned} C^{\mathrm {A}}_{\mathrm {T}} = C^{\mathrm {A}}_{\mathrm {L}}+C^{\mathrm {A}}_{\mathrm {Tr}} \quad \text {and} \quad C^{\mathrm {B}}_{\mathrm {T}} = C^{\mathrm {B}}_{\mathrm {L}}+C^{\mathrm {B}}_{\mathrm {Tr}}, \end{aligned}$$

(1)

where $C_{\mathrm {L}}$ is the hydrogen concentration in the lattice, $C_{\mathrm {Tr}}$ is the concentration associated with the traps and the superscript indicates the material. The molar concentration ($\mathrm {mol}/\mathrm {m}^{3}$) are defined by ${\bar{C}}_{\mathrm {T}} = C_{\mathrm {T}}/N_{\mathrm {A}}$, ${\bar{C}}_{\mathrm {L}} = C_{\mathrm {L}}/N_{\mathrm {A}}$ and ${\bar{C}}_{\mathrm {Tr}} = C_{\mathrm {Tr}}/N_{\mathrm {A}}$, where $N_{\mathrm {A}} = 6.0232 \times 10^{23}$ $\mathrm {atoms}/\mathrm {mol}$ is Avogadro’s number and a bar over the symbol indicates a molar quantity. The interface is considered as a discrete trap with a concentration—now defined as the total number of H atoms per unit area of the interface (similarly, the molar concentration in the trap is ${\bar{C}}_{\mathrm {int}} = C_{\mathrm {int}}/N_{\mathrm {A}}$). It should be noted that the hydrogen concentration is not continuous across the interface, i.e. the concentration in the bulk materials is different to the concentration at an adjacent point in the interface. Furthermore, the hydrogen concentration in the interface is assumed to be in equilibrium with the mobile hydrogen in the bulk adjacent to the interface. We limit our consideration to the situation where hydrogen can cross the interface, i.e. in the normal direction, n, but not along the interface direction, t. This is consistent with the recent Monte Carlo simulations of Du et al. [17]. The chemical potential $\mu$ ($\mathrm {J}/\mathrm {mol}$) is assumed to be continuous at the interface, i.e. it has the same value in the matrix and the interface. Diffusion across the interface is allowed and this is assumed to be driven by a small difference in chemical potential of hydrogen in materials $\mathrm {A}$ and $\mathrm {B}$ either side of the interface. Hence, we effectively consider the interface to have a small thickness h, such that the chemical potential $\mu _{\mathrm {int}}$ is assumed to be given by a continuous function

$$\begin{aligned} \mu _{\mathrm {int}} = \mu _{\mathrm {int}} \left( \mu ^{+}, \mu ^{-}\right) , \end{aligned}$$

(2)

where $\mu ^{\pm }$ are the chemical potentials at the upper and lower interface surfaces $\varGamma _{\mathrm {int}}^{\pm }$ in the bulk materials, respectively, see Fig. 1ii. In practice, when we assign a chemical potential to the interface, this is taken as the mean of the values either side of the interface. Further, the diffusion distance for transport across the interface is small (of the order of atomic dimensions) and we assign a large kinetic constant for the diffusion constant, so that in the simulations $\mu ^{+} \approx \mu ^{-}$. This is discussed further below.

Materials $\mathrm {A}$ and $\mathrm {B}$ are assumed to exhibit elastic or elastic–plastic behaviour. Thus, under mechanical loading, the chemical potential may change due to the change of hydrostatic stress, allowing the hydrogen to diffuse. Also, the density of traps can increase as dislocation density increases during plastic flow, which results in an increase in concentration associated with the traps, $C_{\mathrm {Tr}}$, and a concomitant reduction of the concentration in the lattice. Further, swelling of the bulk material (i.e. volumetric deformation) may result from the hydrogen in the NILS and/or traps. The interface is assumed to be defined by a traction-separation law that undergoes full separation after reaching a critical value. The chemical potential at the interface changes under deformation allowing the concentration to increase or decrease. Moreover, the presence of hydrogen may reduce the cohesive strength of the interface and induce a separation (jacking) that may influence the deformation in the bulk adjacent to the interface and lead to a faster separation. Our representation of this process is guided by the recent atomistic simulations of Katzarov and Paxton [20] and is consistent with the thermodynamic framework described by Mishin et al. [20].

2.2 The governing equations

2.2.1 Hydrogen diffusion

The mass conservation of hydrogen states that the rate of change of the total hydrogen concentration ${\bar{C}}_{\mathrm {T}}$ in a volume $\varOmega$ is equal to the flux ${\bar{J}}_{i}$ through its boundaries $\varGamma$. The swelling and elastic deformations are assumed to be small and only plastic deformation is taken to be large which is essentially isochoric and therefore the total rate of change of the hydrogen concentration is equal to its local rate of change (for further details see “Appendix A”). Thus, it can be written as

$$\begin{aligned} \dfrac{\partial }{\partial t} \int \limits _{\varOmega } {\bar{C}}_{\mathrm {T}} \, \mathrm {d}V + \int \limits _{\varGamma } {\bar{J}}_{i} \, n_{i} \, \mathrm {d}S = 0, \end{aligned}$$

(3)

where $\mathrm {d}V$ and $\mathrm {d}S$ are the infinitesimal volume and surface elements in the current configuration, respectively, and $n_{i}$ is the unit outward normal on $\varGamma$. Applying the divergence theorem, we obtain

$$\begin{aligned} \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial t} + \dfrac{\partial {\bar{J}}_{i}}{\partial x_{i}} = 0, \end{aligned}$$

(4)

The molar hydrogen flux ${\bar{J}}_{i}$ ($\mathrm {mol}/(\mathrm {m}^{2} \cdot \mathrm {s} )$) in the bulk is related to the gradient of the chemical potential $\mu$ ($\mathrm {J}/\mathrm {mol}$) as

$$\begin{aligned} {\bar{J}}_{i} = -\dfrac{D_{\mathrm {L}} \, {\bar{C}}_{\mathrm {L}}}{R \, T} \, \dfrac{ \partial \mu }{\partial x_{i}}, \end{aligned}$$

(5)

where $D_{\mathrm {L}}$ is the lattice diffusivity ($\mathrm {m}^{2}/\mathrm {s}$). Hydrogen is allowed to diffuse across the interface and not along the interface, i.e. hydrogen diffusion within the interface is only in the n-direction. The hydrogen flux across the interface is written as

$$\begin{aligned} {\bar{J}}_{\mathrm {int}} = -h_{\mathrm {int}} \, \varDelta \mu _{\mathrm {int}}, \end{aligned}$$

(6)

where ${\bar{J}}_{\mathrm {int}}$ ($\mathrm {mol}/(\mathrm {m}^{2} \cdot \mathrm {s} )$) is the flux in the direction normal to the interface, $h_{\mathrm {int}}$ is the hydrogen transfer coefficient across the interface (a kinetic constant for the interface) ($\mathrm {mol}^{2}/(\mathrm {m}^{2} \cdot \mathrm {s} \cdot \mathrm {J})$) and $\varDelta \mu _{\mathrm {int}} = \mu ^{+}-\mu ^{-}$ is the chemical potential jump across the interface.

The boundary conditions of the diffusion equation for the model problem are defined by

$$\begin{aligned} \begin{array}{ll} {\hat{\mu }} = \mu &{} \text {on} \quad \varGamma _{\mu }, \\ \hat{{\bar{J}}} = {\bar{J}}_{i} \, n_{i} &{} \text {on} \quad \varGamma _{J}, \end{array} \end{aligned}$$

(7)

where ${\hat{\mu }}$ and $\hat{{\bar{J}}}$ are the applied chemical potential and hydrogen flux on the boundaries $\varGamma _{\mu }$ and $\varGamma _{J}$, respectively, and $n_{i}$ is the outward normal to $\varGamma$. The boundaries $\varGamma _{\mu }$ and $\varGamma _{J}$ should satisfy

$$\begin{aligned} \varGamma _{\mu } \cup \varGamma _{J} = \varGamma \quad \text {and} \quad \varGamma _{\mu } \cap \varGamma _{J} = \varnothing . \end{aligned}$$

(8)

The conditions on the interface $\varGamma _{\mathrm {int}}$ are defined as:

$$\begin{aligned} \mu _{\mathrm {int}} = \frac{1}{2} \, \left( \mu ^{+} + \mu ^{-}\right) \quad \text {on} \quad \varGamma _{\mathrm {int}}, \end{aligned}$$

(9)

where $\mu _{\mathrm {int}}$ is the chemical potential in the interface $\varGamma _{\mathrm {int}}$ and the hydrogen flux is given by ${\bar{J}}_{\mathrm {int}} = {\bar{J}}_{i} \, n^{\mathrm {int}}_{i}$ where $n^{\mathrm {int}}_{i}$ is the outward normal vector to $\varGamma _{\mathrm {int}}$. It should be mentioned that the interface is assumed to undergo complete separation when it fails such that the newly created free surfaces have flux boundary conditions specified. Hence, we introduce a scalar damage variable d that is assumed to evolve monotonically from 0 to 1, i.e. from an undamaged to a fully damaged state. It follows that the no flux boundary condition is defined as

$$\begin{aligned} {\bar{J}}_{\mathrm {int}} = 0 \quad \text {if} \quad d = 1 \quad \text {on} \quad \varGamma _{\mathrm {int}} \end{aligned}$$

(10)

2.2.2 Mechanical equilibrium

The balance of linear momentum, i.e. the mechanical equilibrium equations, in a quasi-static state and the absence of body forces can be written as

$$\begin{aligned} \dfrac{\partial \sigma _{ij}}{\partial x_{j}} = 0 \quad \text {in} \quad \varOmega , \end{aligned}$$

(11)

where $\sigma _{ij}$ is the Cauchy stress. The boundary conditions for the model problem is defined by

$$\begin{aligned} \begin{array}{ll} \hat{u}_{i} = u_{i} &{} \text {on} \quad \varGamma _{u}, \\ \hat{t}_{i} = \sigma _{ij} \, n_{j} &{} \text {on} \quad \varGamma _{t}, \end{array} \end{aligned}$$

(12)

where $\hat{u}_{i}$ and $\hat{t}_{i}$ are the applied displacement and traction values acting on $\varGamma _{u}$ and $\varGamma _{t}$, respectively, that should satisfy

$$\begin{aligned} \varGamma _{u} \cup \varGamma _{t} = \varGamma \quad \text {and} \quad \varGamma _{u} \cap \varGamma _{t} = \varnothing . \end{aligned}$$

(13)

The conditions on the interface $\varGamma _{\mathrm {int}}$ are defined as:

$$\begin{aligned} \varDelta u_{i}^{\mathrm {int}} = u_{i}^{+} - u_{i}^{-} \quad \text {on} \quad \varGamma _{\mathrm {int}}, \end{aligned}$$

(14)

where $\varDelta u_{i}^{\mathrm {int}}$ is the displacement jump across the interface $\varGamma _{\mathrm {int}}$, $u_{i}^{\pm }$ are the displacement vectors in the upper and lower interface surfaces $\varGamma _{\mathrm {int}}^{\pm }$, respectively, and the traction acting on the interface is given by $t_{i}^{\mathrm {int}} = \sigma _{ij} \, n_{j}^{\mathrm {int}}$. In the case of complete separation, the initially intact interface becomes two traction free surfaces that are defined by

$$\begin{aligned} t_{i}^{\mathrm {int}} = 0 \quad \text {if} \quad d =1 \quad \text {on} \quad \varGamma _{\mathrm {int}}. \end{aligned}$$

(15)

3 Finite Element implementation

In this section, we present the implementation of the model problem in Sect. 2. We consider the coupled diffusion–mechanical system given by the mass and linear momentum balance equations in Eqs. (4) and (11), respectively. These equations are usually expressed in terms of two primary variables that are the displacement field $u_{i}$ and the total hydrogen concentration ${\bar{C}}_{\mathrm {T}}$. Alternatively, we propose the use of the chemical potential $\mu$ as the diffusion degree of freedom instead of the total hydrogen concentration ${\bar{C}}_{\mathrm {T}}$. In most coupled diffusion–mechanical analysis, researchers use the concentration as a degree of freedom, e.g. Sofronis and McMeeking [13], Barrera et al. [14] and Oh and Kim [21]. Di Leo and Anand [22] have proposed a theory for coupled diffusion and large elastic–plastic deformations using chemical potential as a degree of freedom which they later used to study fracture of ferritic steels in the presence of hydrogen using a continuum damage approach (Anand et al. [23]). Further, the chemical potential has been used in similar problems such as coupled diffusion and mechanical deformation in elastomeric gels (Chester and Anand [24]) and in Li-ion batteries (Miehe et al. [25]). In comparison with these formulations, a broader description of material systems is consider here by including the behaviour of interfaces. We propose a thermodynamically consistent framework based on the work of Mishin et al. [20], see Sect. 4. The proposed formulation has many advantages in comparison with the standard formulation and a detailed comparison between these formulations will be discussed later in this section. In the following, we present the details of the proposed Finite Element formulation of the coupled diffusion–mechanical analysis in the presence of interfaces.

3.1 The variational formulation

The variational forms of the governing equations are required for the development of the Finite Element equations. Consider the mass balance equation in Eq. (4), and a virtual variation of the chemical potential $\delta \mu$, which is continuous and is assumed to vanish where the chemical potential is defined on a boundary, i.e.

$$\begin{aligned} \delta \mu = 0 \quad \text {on} \quad \varGamma _{\mu }. \end{aligned}$$

(16)

Multiplying Eq. (4) by $\delta \mu$ and integrating over the volume gives the variational form of the mass balance equation

$$\begin{aligned} \int \limits _{\varOmega } \delta \mu \, \left( \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial t} + \dfrac{\partial {\bar{J}}_{i}}{\partial x_{i}} \right) \, \mathrm {d}V = 0. \end{aligned}$$

(17)

Thus, integrating by parts and applying the divergence theorem yields

$$\begin{aligned} \int \limits _{\varOmega } \delta \mu \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial t} \, \mathrm {d}V - \int \limits _{\varGamma _{J}} \delta \mu \, \hat{{\bar{J}}}_{i} \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} \delta \mu \, {\bar{J}}_{\mathrm {int}} \, \mathrm {d}S = 0. \end{aligned}$$

(18)

Similarly, an admissible virtual displacement field, $\delta u_{i}$, is considered which vanishes on boundaries where the displacement is prescribed, i.e.

$$\begin{aligned} \delta u_{i} = 0 \quad \text {on} \quad \varGamma _{u}. \end{aligned}$$

(19)

Now, the variational form of the equilibrium equation of (11) takes the form

$$\begin{aligned} \int \limits _{\varOmega } \delta u_{i} \, \dfrac{\partial \sigma _{ij}}{\partial x_{j}} \, \mathrm {d}V = 0, \end{aligned}$$

(20)

and integration by parts and application of the divergence theorem gives

$$\begin{aligned} \int \limits _{\varOmega } \dfrac{\partial \delta u_{i}}{\partial x_{j}} \, \sigma _{ij} \, \mathrm {d}V - \int \limits _{\varGamma _{t}} \delta u_{i} \, {\hat{t}}_{i} \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} \delta \varDelta u_{i}^{\mathrm {int}} \, t_{i}^{\mathrm {int}} \, \mathrm {d}S = 0, \end{aligned}$$

(21)

3.2 Time integration

A fully implicit backward Euler scheme is employed here for time integration of the diffusion equations. Thus, the total concentration ${\bar{C}}_{\mathrm {T}}$ at time $t_{p+1}$ is approximated by

$$\begin{aligned} {\bar{C}}_{\mathrm {T}}^{p+1} = {\bar{C}}_{\mathrm {T}}^{p}+ \varDelta t \, \dot{{\bar{C}}}_{\mathrm {T}}^{p+1}, \end{aligned}$$

(22)

where indices $p+1$ and p denote variable values at instants $t_{p}$ and $t_{p+1}$, respectively, and $\varDelta t = t_{p+1} - t_{p}$ is the time increment.

3.3 The spatial discretisation

In the discretisation of the body in Fig. 1, two regions are considered: the bulk (materials $\mathrm {A}$ and $\mathrm {B}$); and the interface regions. We use continuum and cohesive elements to discretise the bulk and interface, respectively. We adopt the standard Galerkin method where the primary variable and their variations are discretised using the same shape functions, see for example Belytschko et al. [26] and Wriggers [27]. It should be noted that different interpolation may be used for the continuum and cohesive elements. Therefore, fields for the chemical potential and its variation are discretised in the bulk and interface regions as

$$\begin{aligned} \begin{aligned} \mu \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}} N_{I}\left( x_{i} \right) \mu _{I}\left( t\right) , \\ \mu _{\mathrm {int}} \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}^{\mathrm {int}}} N_{I}\left( x_{i} \right) \mu _{I}^{\mathrm {int}}\left( t\right) , \end{aligned} \end{aligned}$$

(23)

and

$$\begin{aligned} \begin{aligned} \delta \mu \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}} N_{I}\left( x_{i} \right) \delta \mu _{I}\left( t\right) , \\ \delta \mu _{\mathrm {int}} \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}^{\mathrm {int}}} N_{I}\left( x_{i} \right) \delta \mu _{I}^{\mathrm {int}}\left( t\right) , \end{aligned} \end{aligned}$$

(24)

respectively, where the superscript $\left( \bullet \right) ^{\mathrm {int}}$ is used to distinguished the variables associated with the interface from those in the bulk (no superscript is used for the bulk), $N_{I}$ are the standard finite element shape functions, $N_{\mathrm {node}}$ are the total number of nodes in the mesh, $\mu _{I}$ and $\delta \mu _{I}$ are the values of the chemical potential and its variation at node I, respectively, and a node is considered to be in the bulk if $I \in \varOmega$ and at the interface if $I \in \varGamma _{\mathrm {int}}$. The displacement field and its variation are interpolated in the same manner as

$$\begin{aligned} \begin{aligned} u_{i} \left( x_{j},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}} N_{I}\left( x_{j} \right) u_{iI}\left( t\right) , \\ u_{i}^{\mathrm {int}} \left( x_{j},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}^{\mathrm {int}}} N_{I}\left( x_{j} \right) u_{iI}^{\mathrm {int}}\left( t\right) , \end{aligned} \end{aligned}$$

(25)

and

$$\begin{aligned} \begin{aligned} \delta u_{i} \left( x_{j},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}} N_{I}\left( x_{j} \right) \delta u_{iI}\left( t\right) , \\ \delta u_{i}^{\mathrm {int}} \left( x_{j},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}^{\mathrm {int}}} N_{I}\left( x_{j} \right) \delta u_{iI}^{\mathrm {int}}\left( t\right) , \end{aligned} \end{aligned}$$

(26)

where $u_{iI}$ and $\delta u_{iI}$ are the values of the displacement fields and its variation at node I, respectively.

3.4 The Finite Element equations

In order to derive the Finite Element equations, we need to determine the discrete forms of the diffusion and mechanical equilibrium equations. This can be done by substituting the interpolations of the chemical potential, displacement and their variations, and the time integration into the variational forms of the diffusion and mechanical equilibrium equations. Thus, substitution of the time derivatives of the total concentration in Eq. (22) and chemical potential and its variation in Eqs. (23) and (24), respectively, into Eq. (18) gives the discrete form of the diffusion equation as the variation of a functional $\varPi _{\mu }$:

$$\begin{aligned} \delta \varPi _{\mu } =&\sum \limits _{I \in \varOmega } \delta \mu _{I} \Bigg [ \dfrac{1}{\varDelta t} \, \int \limits _{\varOmega } N_{I} \left( {\bar{C}}_{\mathrm {T}}^{p+1} -{\bar{C}}_{\mathrm {T}}^{p} \right) \, \mathrm {d}V\Bigg ] \nonumber \\&- \sum \limits _{I \in \varGamma _{J}} \delta \mu _{I} \, \int \limits _{\varGamma _{J}} N_{I} \, \hat{{\bar{J}}} \, \mathrm {d}S \nonumber \\&+ \sum \limits _{I \in \varGamma _{\mathrm {int}}} \delta \mu _{I}^{\mathrm {int}} \Bigg [ \dfrac{1}{\varDelta t} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \left( {\bar{C}}_{\mathrm {int}}^{p+1} -{\bar{C}}_{\mathrm {int}}^{p} \right) \, \mathrm {d}S\Bigg ] \nonumber \\&- \sum \limits _{I \in \varGamma _{\mathrm {int}}} \delta \mu _{I}^{\mathrm {int}} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I} \, {\bar{J}}_{\mathrm {int}} \, \mathrm {d}S, \end{aligned}$$

(27)

where the first sum is over the nodes of $\varOmega$, the second sum is over the nodes on $\varGamma _{\mathrm {J}}$ and the third and fourth sums are over the nodes on $\varGamma _{\mathrm {int}}$. This variation can be written in terms of the nodal chemical potential variation and diffusion forces as

$$\begin{aligned} \delta \varPi _{\mu } = \sum \limits _{I \in \varOmega } \delta \mu _{I} \, f_{I}^{\mu , \mathrm {in}}+ \sum \limits _{I \in \varGamma _{J}} \delta \mu _{I} \, f_{I}^{\mu , \mathrm {ext}} + \sum \limits _{I \in \varGamma _{\mathrm {int}}} \delta \mu _{I} \, f_{I}^{\mu , \mathrm {int}}, \end{aligned}$$

(28)

where the nodal chemical force in the continuum elements is $f_{I}^{\mu }=f_{I}^{\mu , \mathrm {in}}+f_{I}^{\mu , \mathrm {ext}}$, i.e. $f_{I}^{\mu , \mathrm {in}}$ and $f_{I}^{\mu , \mathrm {ext}}$ are the internal and external forces, respectively, and in the cohesive elements is $f_{I}^{\mu , \mathrm {int}}$, which are given by

$$\begin{aligned} \begin{aligned} f_{I}^{\mu , \mathrm {in}}&= \dfrac{1}{\varDelta t} \, \int \limits _{\varOmega } N_{I} \left( {\bar{C}}_{\mathrm {T}}^{p+1} -{\bar{C}}_{\mathrm {T}}^{p} \right) \, \mathrm {d}V, \\ f_{I}^{\mu , \mathrm {ext}}&= - \int \limits _{\varGamma _{J}} N_{I} \, \hat{{\bar{J}}} \, \mathrm {d}S, \\ f_{I}^{\mu , \mathrm {int}}&= \dfrac{1}{\varDelta t} \, \int \limits _{\varGamma _{\mathrm {int}}} A_{I}^{\mathrm {int}} \left( {\bar{C}}_{\mathrm {int}}^{p+1} -{\bar{C}}_{\mathrm {int}}^{p} \right) \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} A_{I}^{\mathrm {int}} \, {\bar{J}}_{\mathrm {int}} \, \mathrm {d}S, \end{aligned} \end{aligned}$$

(29)

where $A_{I}^{\mathrm {int}}= H_{I} \, N_{I}^{\mathrm {int}}$ and $H_{I}$ is a multiplier that relates the interface chemical potential to the bulk nodal chemical potential as in Eq. (2), i.e. $\mu _{I}^{\mathrm {int}} = H_{I} \, \mu _{I}$. Since the chemical potential variation $\delta \mu _{I}$ can be chosen arbitrarily, the residual of the diffusion equation at node I is then determined as

$$\begin{aligned} R_{I}^{\mu } = \sum \limits _{I \in \varOmega } f_{I}^{\mu , \mathrm {in}}+ \sum \limits _{I \in \varGamma _{J}} f_{I}^{\mu , \mathrm {ext}} + \sum \limits _{I \in \varGamma _{\mathrm {int}}} f_{I}^{\mu , \mathrm {int}}. \end{aligned}$$

(30)

Similarly, substitution of the test and displacement fields in Eqs. (25) and (26) into Eq. (21) gives the discrete form of the mechanical equilibrium equation as the variation of a functional $\varPi _{\mathbf{u}}$:

$$\begin{aligned} \delta \varPi _{\mathbf{u}} =&\sum \limits _{I \in \varOmega } \delta u_{iI} \int \limits _{\varOmega } \sigma _{ij} \, B_{jI} \, \mathrm {d}V - \sum \limits _{I \in \varGamma _{t}} \delta u_{iI} \, \int \limits _{\varGamma _{t}} N_{I} \, {\hat{t}}_{i} \, \mathrm {d}S \nonumber \\&- \sum \limits _{I \in \varGamma _{\mathrm {int}}} \delta u_{iI}^{\mathrm {int}} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, t_{i}^{\mathrm {int}} \, \mathrm {d}S, \end{aligned}$$

(31)

where $B_{jI}=\partial N_{I}/\partial x_{j}$. This variation can be written in terms of the nodal displacement variation and mechanical forces as

$$\begin{aligned} \begin{aligned} \delta \varPi _{\mathbf{u}} =&\sum \limits _{I \in \varOmega } \delta u_{iI} \, f_{iI}^{\mathbf{u}, \mathrm {in}}+ \sum \limits _{I \in \varGamma _{t}} \delta u_{iI} \, f_{iI}^{\mathbf{u}, \mathrm {ext}} \\&+ \sum \limits _{I \in \varGamma _{\mathrm {int}}} \delta u_{iI} \, f_{iI}^{\mathbf{u}, \mathrm {int}}, \end{aligned} \end{aligned}$$

(32)

where the nodal mechanical force in the continuum elements is $f_{iI}^{\mathbf{u}} = f_{iI}^{\mathbf{u}, \mathrm {in}}+f_{iI}^{\mathbf{u}, \mathrm {ext}}$, i.e. $f_{iI}^{\mathbf{u}, \mathrm {in}}$ and $f_{iI}^{\mathbf{u}, \mathrm {ext}}$ are the internal and external forces, respectively, and in the cohesive elements is $f_{iI}^{\mathbf{u}, \mathrm {int}}$, are given by

$$\begin{aligned} \begin{aligned} f_{iI}^{\mathbf{u}, \mathrm {in}}&= \int \limits _{\varOmega } \sigma _{ij} \, B_{jI} \, \mathrm {d}V, \\ f_{iI}^{\mathbf{u}, \mathrm {ext}}&= - \int \limits _{\varGamma _{t}} N_{I} \, {\hat{t}}_{i} \, \mathrm {d}S, \\ f_{iI}^{\mathbf{u}, \mathrm {int}}&= - \int \limits _{\varGamma _{\mathrm {int}}} B_{I}^{\mathrm {int}} \, t_{i}^{\mathrm {int}} \, \mathrm {d}S, \end{aligned} \end{aligned}$$

(33)

$B_{I}^{\mathrm {int}} = M_{I} \, N_{I}^{\mathrm {int}}$ and $M_{I}$ is a linear multiplier that relates the displacement jumps to the nodal displacements, i.e. $\varDelta u_{i}^{\mathrm {int}} = M_{I} \, u_{iI}$. Since $\delta u_{iI}$ can be chosen arbitrarily, the components of the residual of the mechanical equilibrium equation at node I are determined as

$$\begin{aligned} R_{iI}^{\mathbf{u}} = \sum \limits _{I \in \varOmega } f_{iI}^{\mathbf{u}, \mathrm {in}}+ \sum \limits _{I \in \varGamma _{t}} f_{iI}^{\mathbf{u}, \mathrm {ext}} + \sum \limits _{I \in \varGamma _{\mathrm {int}}} f_{iI}^{\mathbf{u}, \mathrm {int}}. \end{aligned}$$

(34)

To this end, we need to solve the coupled nonlinear diffusion–mechanical discrete equations, i.e. Eqs. (30) and (34), for the nodal chemical potential $\mu _{I}$ and displacements $u_{iI}$. In the next sub-section, the solution procedure is discussed.

3.5 Solution procedure

In order to solve the nonlinear set of discrete equations represented by (30) and (34) with a Newton–Raphson algorithm, a suitable linearisation is required. Thus, an iterative scheme can be determined using a first-order Taylor expansion of the residuals, i.e. the chemical and mechanical nodal residuals at node I are $R_{I}^{\mu }$ and $R_{I}^{\mathbf{u}}$, respectively. Assume that the nodal chemical potential and displacement components at node J at the start and end of an iteration r are $\left( \mu _{J},u_{jJ}\right)$ and $\left( \mu _{J}+\varDelta \mu _{J},u_{jJ}+\varDelta u_{jJ}\right)$, respectively. Hence, the residuals and unknown values can be written in vector form as $\text{ R }_{I} = \left[ R_{I}^{\mu } \quad R_{iI}^{\mathbf{u}} \right] ^{\mathrm {T}}$ and $\mathbf{d}_{J} = \left[ \mu _{J} \quad u_{jJ} \right] ^{\mathrm {T}}$, $i,j=1,2,3$, respectively. Therefore, the linearised form of the residuals becomes

$$\begin{aligned} \mathbf{R}_{I}^{r+1} = \mathbf{R}_{I}^{r}+ \dfrac{\partial \mathbf{R}_{I}}{\partial \mathbf{d}_{J}} \Bigg |_{r+1} \, \varDelta \mathbf{d}_{J} + \mathbf{O}\big ( \varDelta \mu _{J}^{2}, \varDelta u_{jJ}^{2}, \cdots \big ), \end{aligned}$$

(35)

where $\varDelta \mathbf{d}_{J}$ is the nodal increment vector of the unknown quantities, $\mathbf{O}\big ( \varDelta \mu _{J}^{2}, \varDelta u_{jJ}^{2}, \ldots \big )$ represents the higher order terms in vector form and the superscript denotes the iteration. Hence, by neglecting the higher order terms, the incremental form of these equations can be written as

$$\begin{aligned} \varDelta \mathbf{d}_{J} = -\mathbf{K}_{IJ}^{-1} \, \mathbf{R}_{I}^{r}, \end{aligned}$$

(36)

where $\mathbf{K}_{IJ}$ is the tangent stiffness matrix that is given by

$$\begin{aligned} \mathbf{K}_{IJ} = \left[ \begin{array}{ll} K_{IJ}^{\mu \, \mu } &{} \quad K_{jIJ}^{\mu \, \mathbf{u}} \\ K_{iIJ}^{\mathbf{u}\, \mu } &{} \quad K_{ijIJ}^{\mathbf{u}\, \mathbf{u}} \end{array} \right] , \end{aligned}$$

(37)

and the elements of the tangent stiffness matrix, i.e. the tangent operators, are

$$\begin{aligned} \begin{aligned} K_{IJ}^{\mu \, \mu }&= \dfrac{\partial R_{I}^{\mu }}{\partial \mu _{J}}, \ K_{jIJ}^{\mu \, \mathbf{u}} = \dfrac{\partial R_{I}^{\mu }}{\partial u_{jJ}}, \ K_{iIJ}^{\mathbf{u}\, \mu } = \dfrac{\partial R_{iI}^{\mathbf{u}}}{\partial \mu _{J}}, \ \text {and} \\ K_{ijIJ}^{\mathbf{u}\, \mathbf{u}}&= \dfrac{\partial R_{iI}^{\mathbf{u}}}{\partial u_{jJ}}. \end{aligned} \end{aligned}$$

(38)

The details of these operators are provided in “Appendix A”. It is worth mentioning that the residual and tangent matrix can be split into the bulk and interface contributions. In this study we use continuum and cohesive elements to implement the diffusion and mechanical models in the commercial FE code Abaqus. In particular, we use the user-defined subroutines $\mathrm {UMAT}$ or $\mathrm {UHARD}$ and $\mathrm {UMATH}$ for the bulk and $\mathrm {UEL}$ for the interface element. The implementations are provided in “Appendix B”.

3.6 The concentration versus chemical potential based formulations

To compare the two formulations, we recall the discrete form of the diffusion equation in Eq. (27). In the concentration based formulation, the total concentration in the bulk, ${\bar{C}}_{\mathrm {T}}$, and the trap concentration in the interface, ${\bar{C}}_{\mathrm {int}}$, are given as

$$\begin{aligned} \begin{aligned} {\bar{C}}_{\mathrm {T}} \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}} N_{I}\left( x_{i} \right) {\bar{C}}_{I}^{\mathrm {T}}\left( t\right) , \\ {\bar{C}}_{\mathrm {int}} \left( x_{i},t\right)&= \sum \limits _{I=1}^{N_{\mathrm {node}}^{\mathrm {int}}} N_{I}\left( x_{i} \right) {\bar{C}}_{I}^{\mathrm {int}}\left( t\right) , \end{aligned} \end{aligned}$$

(39)

where ${\bar{C}}_{I}^{\mathrm {T}}$ and ${\bar{C}}_{I}^{\mathrm {int}}$ are the values of the total concentration and trap concentration at node I, respectively. Hence, the linearisation of the discrete diffusion equation yields a system of equations similar to Eq. (35) where the chemical potential increment $\varDelta \mu _{I}$ is replaced by the total concentration and interface concentration increments $\varDelta {\bar{C}}_{I}^{\mathrm {T}}$ and $\varDelta {\bar{C}}_{I}^{\mathrm {int}}$, respectively. As a result, the derivative $\partial {\bar{J}} / \partial \mu$ in the tangent operator $K_{IJ}^{\mu \, \mu }$ is replaced by $\partial {\bar{J}} / \partial {\bar{C}}_{\mathrm {T}}$, see “Appendix A”. These derivatives are determined from the definition in Eq. (5) as

$$\begin{aligned} \dfrac{\partial {\bar{J}}_{i}}{\partial \mu } = -\dfrac{D_{\mathrm {L}}}{R \, T} \, \dfrac{ \partial {\bar{C}}_{\mathrm {L}}}{\partial \mu } \, \dfrac{ \partial \mu }{\partial x_{i}}, \end{aligned}$$

(40)

and

$$\begin{aligned} \dfrac{\partial {\bar{J}}_{i}}{\partial {\bar{C}}_{\mathrm {T}}} = -\dfrac{D_{\mathrm {L}}}{R \, T} \, \dfrac{ \partial \mu }{\partial x_{i}}. \end{aligned}$$

(41)

Examining the continuity requirements on the shape function, in the chemical potential based formulation, Eq. (40) implies that the shape functions in Eq. (23) should exist and be continuous, i.e. they satisfy ${\mathcal {C}}_{0}$ continuity. On the other hand, in the concentration based formulation, the gradient of the chemical potential contains the gradient of hydrostatic stress $\partial \sigma _{\mathrm {h}} / \partial x_{i}$, see Sect. 4. Hence, the strain gradient should now exist and be continuous. Consequently, the shape functions in Eq. (25) should be continuously differentiable, i.e. satisfy ${\mathcal {C}}_{1}$ continuity, which means that shape functions that are at least quadratic should be used. Therefore, the chemical potential based formulation has less restrictive continuity requirements which allow linear approximations to be used. This may result in a lower computational cost. The spatial discretisation of the model problem requires that the top and bottom faces of the cohesive elements to be attached to the continuum elements, see Fig. 2. Hence, in the case of a concentration based formulation, the concentration is defined at the nodes of these faces. Thus, the concentration will be discontinuous at each node bearing two different values from the bulk and interface. This inconsistency can be overcome using the chemical potential based formulation. The chemical potential is essentially continuous across the interface which leads to a consistent definition of its values at these surfaces. Further, the concentration at the interface is defined in the mid-surface of the cohesive element (the constitutive surface) which allows the concentration to differ from that in the bulk.

Fig. 2

The schematic of a dummy mesh of a region close to the interface of the model problem. The figure illustrates the mid-surface of the interface and the shared nodes between the bulk and the interface

4 Constitutive descriptions

In this section, we present the hydrogen transport and mechanical constitutive models for the bulk and interface.

4.1 The Bulk model

Consider a material in which the hydrogen concentration in the lattice is $C_{\mathrm {L}}$ and that from the distributed traps is $C_{\mathrm {Tr}}$. Thus, the total hydrogen concentration is $C_{\mathrm {T}} = C_{\mathrm {L}} + C_{\mathrm {Tr}}$. The hydrogen concentration in the lattice is given by Sofronis and McMeeking [13]

$$\begin{aligned} C_{\mathrm {L}} = \beta _{\mathrm {L}} \, \theta _{\mathrm {L}} \, N_{\mathrm {L}}, \end{aligned}$$

(42)

where $\beta _{\mathrm {L}}$ is the number of interstitial sites per solvent atom, $\theta _{\mathrm {L}} \in \left[ 0,1 \right]$ is the fraction of lattice sites occupied by hydrogen atoms and $N_{\mathrm {L}}=N_{\mathrm {A}}/V_{\mathrm {M}}$ is the number of atoms of solvent per unit volume ($\mathrm {atoms}/\mathrm {m}^{3}$). The molar volume of the solvent lattice is $V_{\mathrm {M}}=M/\rho$, where $\rho$ and M are the density and relative atomic mass of the lattice element, respectively.

We consider $n_{\mathrm {Tr}}$ types of traps such that the total concentration in the traps is given by

$$\begin{aligned} C_{\mathrm {Tr}} = \sum \limits _{i=1}^{n_{\mathrm {Tr}}} C_{i}, \end{aligned}$$

(43)

where $C_{i}$ is the concentration in the ith trap that is defined by

$$\begin{aligned} C_{i} = \alpha _{i} \, \theta _{i} \, N_{i}, \end{aligned}$$

(44)

where $\alpha _{i}=1$ denotes the number of trapping sites, $N_{i}$ ($\mathrm {atoms}/\mathrm {m}^{3}$) denotes the number of atomic trapping sites per unit volume and $\theta _{i} \in \left[ 0,1\right]$ is the fraction of trapping sites occupied by H atoms. We consider two types of traps—those in which the number of trap sites are fixed (fixed traps $i \equiv \mathrm {F}$) and those that increase with increasing plastic deformation (dislocation traps, $i \equiv \mathrm {D}$). The molar concentration of the ith trap is denoted as ${\bar{C}}_{i} = C_{i}/N_{\mathrm {A}}$. Hence, $N_{\mathrm {F}}$ is taken to be constant and $N_{\mathrm {D}}$ is assumed to be proportional to the dislocation density $\rho _{\mathrm {D}}$, which is assumed to be a function of the accumulated equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$:

$$\begin{aligned} N_{\mathrm {D}} = \dfrac{\sqrt{2}}{a} \, \rho _{\mathrm {D}} \left( \varepsilon _{\mathrm {e}}^{\mathrm {pl}} \right) , \end{aligned}$$

(45)

where a is the lattice constant and the prefactor is 1/b, where b is the magnitude of the a/2 <1 1 0> Burgers vector in $\mathrm {FCC}$ materials, which is a reasonable approximation for the atomic spacing along a dislocation line.

The traps are modelled using Oriani’s theory, in which the hydrogen concentration in the lattice is assumed to be in equilibrium with the concentration in the traps. This means that the concentration in the traps can directly be estimated from the concentration in the lattice. Hence, for finite populations of H in the lattice and trap sites, the equilibrium condition for the ith trap is given by

$$\begin{aligned} \dfrac{\theta _{i}}{1-\theta _{i}} = \dfrac{\theta _{\mathrm {L}}}{1-\theta _{\mathrm {L}}} \, K_{i}, \end{aligned}$$

(46)

where $K_{i} = \exp \left( -W_{i}/RT\right) = \mathrm {const}.$, represents equilibrium between the lattice and the ith type of trap site and $W_{i}<0$ is the binding energy for the ith trap, R is the universal gas constant and T is the absolute temperature. It should be noted that Eq. (46) reduces to $\theta _{i}/\left( 1-\theta _{i}\right) = K_{i} \, \theta _{\mathrm {L}}$ in the case of small lattice concentration, i.e. $\theta _{\mathrm {L}} \ll 1$, which is generally the situation in practice (note, however that the corresponding occupancy in the traps can approach 1, particularly for high trap binding energies [28]). The Gibbs free energy per unit volume of the bulk material, G, can be written as

$$\begin{aligned} G = \psi -\sigma _{ij} \, \varepsilon _{ij} + \mu _{0} \, {\bar{C}}_{\mathrm {L}} - T \, s, \end{aligned}$$

(47)

where $\psi$ is the free energy density per unit volume of the bulk material, $\sigma _{ij}$ is the applied macroscopic stress, $\varepsilon _{ij}$ is the corresponding strain, $\mu _{0}$ represents the chemical potential at a suitably defined standard condition, T is the absolute temperature and s is the entropy per volume in the bulk material, which we assume is dominated by the configurational entropy (i.e. entropy of mixing):

$$\begin{aligned} s&= -R \, {\bar{C}}_{\mathrm {L}}^{\mathrm {max}} \left( \dfrac{{\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}} \, \ln \dfrac{{\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}} + \dfrac{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}} - {\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}} \right. \nonumber \\&\quad \left. \ln \dfrac{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}-{\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}} \right) , \end{aligned}$$

(48)

where ${\bar{C}}_{\mathrm {L}}^{\mathrm {max}}$ is the hydrogen concentration corresponding to the saturated state in the lattice. The free energy density for elastic and elastic–plastic materials can be expressed as

$$\begin{aligned} \psi = \frac{1}{2} \big (\varepsilon _{ij} - \varepsilon _{ij}^{\mathrm {pl}} - \varepsilon _{ij}^{\mathrm {s}} \big ) {\mathbb {C}}_{ijkl} \big (\varepsilon _{kl} - \varepsilon _{kl}^{\mathrm {pl}} - \varepsilon _{kl}^{\mathrm {s}} \big ), \end{aligned}$$

(49)

where $\varepsilon _{ij}^{\mathrm {pl}}$ is the plastic strain, $\varepsilon _{ij}^{\mathrm {s}} = \varepsilon _{\mathrm {s}} \, \delta _{ij} = \frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {L}} \, \delta _{ij}$ is the swelling strain (here we have assumed that swelling is only associated with hydrogen in the lattice and that trapped hydrogen does not contribute to swelling observed macroscopically—this assumption can be readily relaxed if necessary, i.e. see “Appendix A)” and ${\mathbb {C}}_{ijkl}$ is the 4th order elasticity tensor. It is worth noting that both the swelling and elastic deformation are assumed to be small.

The chemical potential in the bulk is determined from the Gibbs free energy in Eq. (47) as

$$\begin{aligned} \mu&= \dfrac{\partial G}{\partial {\bar{C}}_{\mathrm {L}}} \nonumber \\&= \mu _{0} + R \, T \, \ln \dfrac{{\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}-{\bar{C}}_{\mathrm {L}}}+\mu _{\sigma }, \end{aligned}$$

(50)

where $\mu _{\sigma } = \partial \psi / \partial {\bar{C}}_{\mathrm {L}} = - \sigma _{\mathrm {h}} \, V_{\mathrm {M}}$ and $\sigma _{\mathrm {h}} = \sigma _{kk}/3$ is the hydrostatic stress. It should be noted that at low concentrations (${\bar{C}}_{\mathrm {L}} \ll {\bar{C}}_{\mathrm {L}}^{\mathrm {max}}$), the chemical potential becomes

$$\begin{aligned} \mu = \mu _{0} + R \, T \, \ln \dfrac{{\bar{C}}_{\mathrm {L}}}{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}} + \mu _{\sigma }. \end{aligned}$$

(51)

The mechanical response is determined by assuming that the bulk is in mechanical equilibrium, i.e. by solving $\partial G / \partial \varepsilon _{ij} = 0$ to give $\sigma _{ij}$. Note, when considering two different materials, e.g. $\mathrm {A}$ and $\mathrm {B}$ of Fig. 1b, $\mu _{0}$ can be different for each material. This needs to be taken into account when solving any boundary value problem – particularly when invoking continuity of chemical potential across an interface. In the following, for consistency of notation, we take H in one of the materials, say $\mathrm {A}$, as the reference, for which we designate $\mu _{0}^{\mathrm {A}} = \mu _{0}$ and write $\mu _{0}^{\mathrm {B}} = \mu _{0} + W_{\mathrm {B}}$. Oriani’s relationship, Eq. (46), can then be used to determine the occupancy in $\mathrm {B}$ in terms of that in $\mathrm {A}$ at interfaces where the chemical potential is required to be continuous.

4.2 The interface model

The interface is treated as a discrete trap. The description here parallels that for the bulk described above in Sect. 4.1 and is consistent with the thermodynamic description of Mishin et al. [20]. We assume that the hydrogen concentration, $C_{\mathrm {int}}$ ($\mathrm {atoms}/\mathrm {m}^{2}$), in the interface can differ from that in the bulk (i.e. the interface binding energy can be different from the bulk) and is defined by

$$\begin{aligned} C_{\mathrm {int}} = \alpha _{\mathrm {int}} \, \theta _{\mathrm {int}} \, N_{\mathrm {int}}, \end{aligned}$$

(52)

where $\alpha _{\mathrm {int}} = 1$ denotes the number of H trapping sites per interface site, $N_{\mathrm {int}}$ ($\mathrm {atoms}/\mathrm {m}^{2}$) denotes the number of atomic trapping sites per unit area of interface and $\theta _{\mathrm {int}} \in \left[ 0,1\right]$ is the fraction of trapping sites occupied by H atoms.

In this study, we limit our consideration to situations where failure at an interface is driven by the component of the traction normal to the interface, allowing the tangential response to be given by a stiff linear mechanical model. We can then simply concentrate on the response under the action of a normal traction to derive the necessary thermodynamic equations. The Gibbs free energy per unit area of the interface, $G_{\mathrm {int}}$, can then be written as

$$\begin{aligned} G_{\mathrm {int}} = \phi - T_{n} \, \delta _{n} + \mu _{0} \, {\bar{C}}_{\mathrm {int}} + W_{\mathrm {int}} \, {\bar{C}}_{\mathrm {int}} - T \, s_{\mathrm {int}}, \end{aligned}$$

(53)

where $\phi$ is a free energy density per unit area, $T_{n}$ is the traction in the normal direction, $\delta _{n}$ is the separation in the normal direction. $W_{\mathrm {int}}$ is the excess cohesive/interface zone binding energy compared to that in the reference matrix material (e.g. material $\mathrm {A}$ of Fig. 1ii) and $s_{\mathrm {int}}$ is the configurational entropy per unit area of interface, and is given by

$$\begin{aligned} s_{\mathrm {int}} =&-R \, {\bar{C}}_{\mathrm {int}}^{\mathrm {max}} \left( \dfrac{{\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}} \, \ln \dfrac{{\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}} + \dfrac{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}} - {\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}} \, \right. \nonumber \\&\left. \ln \dfrac{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}-{\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}} \right) , \end{aligned}$$

(54)

where ${\bar{C}}_{\mathrm {int}}^{\mathrm {max}}$ is the hydrogen concentration corresponding to the saturated state in the cohesive zone. The constitutive response for the cohesive interface is modelled in terms of the relationship between the traction and the displacement jump across the interface. The presence of hydrogen in the cohesive zone may introduce a volumetric change that can be expressed in terms of a jacking or swelling separation $\delta _{n}^{\mathrm {s}}$ [29] that can be defined as

$$\begin{aligned} \delta _{n}^{\mathrm {s}} = {\bar{C}}_{\mathrm {int}} \, V_{\mathrm {M}}^{\mathrm {int}}, \end{aligned}$$

(55)

where $V_{\mathrm {M}}^{\mathrm {int}}$ is the molar volume of hydrogen in the interface zone ($\mathrm {m}^{3}/\mathrm {mol}$) which can have a different value to $V_{\mathrm {M}}$ in the bulk. Hence, the total separation in the normal direction $\delta _{n}$ can be decomposed into mechanical and jacking components:

$$\begin{aligned} \delta _{n} = \delta _{n}^{\mathrm {m}} + \delta _{n}^{\mathrm {s}}, \end{aligned}$$

(56)

where $\delta _{n}^{\mathrm {m}}$ is the separation in the normal direction due to mechanical loading. Note that $\phi$ in Eq. (53) is a function of $\delta _{n}^{\mathrm {m}}$, i.e.

$$\begin{aligned} \phi = \phi \left( \delta _{n}^{\mathrm {m}}\right) = \phi \left( \delta _{n} - \delta _{n}^{\mathrm {s}}\right) . \end{aligned}$$

(57)

The chemical potential in the cohesive zone is determined from the Gibbs free energy in Eq. (53) as

$$\begin{aligned} \mu _{\mathrm {int}}&= \dfrac{\partial G_{\mathrm {int}}}{\partial {\bar{C}}_{\mathrm {int}}} \nonumber \\&= \dfrac{\partial \phi }{\partial {\bar{C}}_{\mathrm {int}}} + \mu _{0} + W_{\mathrm {int}} + R \, T \, \ln \dfrac{{\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}-{\bar{C}}_{\mathrm {int}}}, \end{aligned}$$

(58)

The traction-separation law ($\mathrm {TSL}$) is determined from the Gibbs free energy assuming that the interface is in mechanical equilibrium, i.e.

$$\begin{aligned} \dfrac{\partial G_{\mathrm {int}}}{\partial \delta _{n}^{\mathrm {m}}} = \dfrac{\partial \phi }{\partial \delta _{n}^{\mathrm {m}}} - T_{n} =0 \quad \Rightarrow \quad T_{n} = \dfrac{\partial \phi }{\partial \delta _{n}^{\mathrm {m}}}. \end{aligned}$$

(59)

Making use of Eqs. (56), (57) and (59), Eq. (58) becomes

$$\begin{aligned} \mu _{\mathrm {int}} = \mu _{0} + W_{\mathrm {int}} + R \, T \, \ln \dfrac{{\bar{C}}_{\mathrm {int}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}}-{\bar{C}}_{\mathrm {int}}} + \mu _{T}, \end{aligned}$$

(60)

where $\mu _{T} = {\partial \phi }/{\partial {\bar{C}}_{\mathrm {int}}} = - T_{n} \, V_{\mathrm {M}}^{\mathrm {int}}$.

The free energy density $\phi$ can be physically based or a phenomenological model that describes the relation between the traction and the displacement jump across the cohesive zone. The initial behaviour is assumed to be linear elastic until the onset of damage. When damage is initiated, the material stiffness decreases and the degradation is defined by the scalar damage variable d that evolves monotonically from 0 to 1, i.e. from an undamaged to a fully damaged state, and can take different forms, i.e. linear, exponential, trapezoidal etc. The irreversible traction-separation law is then written as

$$\begin{aligned} T_{n} = \left\{ \begin{array}{ll} K_{n} \delta _{n}^{\mathrm {m}} &{} \quad \text {if} \,\, \delta _{n}^{\mathrm {m}} \le \delta _{n}^{\mathrm {c}} \\ \left( 1-d\right) K_{n} \, \delta _{n}^{\mathrm {m}} &{} \quad \text {if} \,\, \delta _{n}^{\mathrm {m}} \ge \delta _{n}^{\mathrm {c}} \end{array} \right. \end{aligned}$$

(61)

where $K_{n}$ is the initial elastic or penalty stiffness and $\delta _{n}^{\mathrm {c}}$ is the critical separation in the normal direction. The linear elastic unloading behaviour is determined by the degraded stiffness $K_{n}'=\left( 1 - d\right) K_{n}$. A bilinear traction-separation law is used in this study. Hence, the damage variable, d, for linear softening is determined as

$$\begin{aligned} d = \dfrac{\delta _{n}^{\mathrm {f}} \left( \delta _{n}^{\mathrm {max}} - \delta _{n}^{\mathrm {c}}\right) }{\delta _{n}^{\mathrm {max}} \left( \delta _{n}^{\mathrm {f}} - \delta _{n}^{\mathrm {c}}\right) }, \end{aligned}$$

(62)

where $\delta _{n}^{\mathrm {max}}$ is the maximum value of the displacement attained during the loading history and $\delta _{n}^{\mathrm {f}}$ is the separation at failure.

The initial cohesive strength in the normal direction is defined by $\sigma _{\mathrm {c}0} = K_{n} \, \delta _{n}^{\mathrm {c}0}$ where $\delta _{n}^{\mathrm {c}0}$ is the hydrogen free critical separation. The cohesive strength is assumed to decrease with increasing hydrogen concentration. Hence, we assume that the softening takes the general form

$$\begin{aligned} \sigma _{\mathrm {c}} = \sigma _{\mathrm {c}0} \, \varPhi \left( {\bar{C}}_{\mathrm {int}}\right) , \end{aligned}$$

(63)

where $\varPhi$ is a softening function. For example, a linear form is given by Barrera and Cocks [29] as

$$\begin{aligned} \varPhi \left( {\bar{C}}_{\mathrm {int}}\right) = 1- \xi _{\mathrm {int}} \left( \dfrac{{\bar{C}}_{\mathrm {int}} - {\bar{C}}_{\mathrm {int}}^{\mathrm {min}}}{{\bar{C}}_{\mathrm {int}}^{\mathrm {max}} - {\bar{C}}_{\mathrm {int}}^{\mathrm {min}}}\right) , \end{aligned}$$

(64)

where $\xi _{\mathrm {int}} \in \left[ 0,1\right]$ is a hydrogen softening parameter, ${\bar{C}}_{\mathrm {int}}^{\mathrm {min}}$ is the concentration at the onset of softening and ${\bar{C}}_{\mathrm {int}}^{\mathrm {max}}$ is the maximum concentrations associated with softening. (The form of the softening function can be determined by fitting of experimental results (e.g. Raykar et al. [30] and Martínez-Pañeda et al. [31]) or using atomistic simulations (e.g. [32] and Katzarov and Paxton [33].) It is worth mentioning that this study is limited to pure mode-I loading; the damage evolution is only considered in the normal direction and the response of the tangential direction is taken to be purely elastic as

$$\begin{aligned} T_{t} = \left\{ \begin{array}{ll} K_{t} \delta _{t} &{} \quad \text {if} \,\, \delta _{n}^{\mathrm {m}} \le \delta _{n}^{\mathrm {c}} \\ \left( 1-d\right) K_{t} \, \delta _{t} &{} \quad \text {if} \,\, \delta _{n}^{\mathrm {m}} \ge \delta _{n}^{\mathrm {c}} \end{array} \right. \end{aligned}$$

(65)

where $T_{t}$ and $\delta _{t}$ are the traction and total separation in the tangential direction.

5 Numerical examples

In this section, we validate and demonstrate the effectiveness of the proposed formulation through studying two problems. Firstly, we consider a 2D fully coupled elastoplastic diffusion problem of a deep notched specimen in the absence of damage. This problem is analysed using both concentration and chemical potential based formulations and a detailed comparison showing the similarities in the solutions is provided. Additionally, we investigate the failure of the notched specimen using the interface model described in Sect. 4.2. The second problem is a micromechanical investigation of hydrogen-enhanced decohesion (HEDE) in a dissimilar metal weld. More specifically, we consider the failure in the presence of hydrogen of the carbide-matrix interfaces around fine $\mathrm {M}_{7} \, \mathrm {C}_{3}$ precipitates generated adjacent to the interface of an 8630 steel/IN625 nickel alloy dissimilar weld, which has been analysed extensively by Barrera et al. [33].

Fig. 3

The geometry of the plate with a deep V-notch. The computational domain is illustrated with the mechanical boundary conditions

Table 1 The material parameters used for nickel

5.1 Analysis of deformation, diffusion and failure in a deeply notched specimen

A plane strain plate with deep double-edged notches is considered as shown in Fig. 3. The width, height and thickness of the specimen are denoted by W, $2 \, H$ and B, respectively, and the notch radius, depth and angle are denoted by r, d and $\varphi$, respectively. The plate is made of a material that is assumed to exhibit elastic–plastic behaviour. The presence of hydrogen in the lattice and dislocation traps are considered. An interface model is used to simulate failure such that damage may accumulate at the interface leading to loss of load carrying capacity. Further, hydrogen can be trapped at the interface which is treated as a discrete trap. We assume a full coupling between the mechanical and diffusion responses and the constitutive descriptions are taken to be suitable for a high strength steel. The purpose of this analysis is to: (1) compare the concentration and chemical potential formulations; and (2) investigate the failure of the specimen using the chemical potential formulation. The deep double-edged notch geometry provides a high degree of plastic constraint and high level of hydrostatic stress across the minimum section which allows us to compare the two formulations for the fully coupled diffusion and elastic–plastic deformation processes. Furthermore, notched specimens are commonly used to study hydrogen embrittlement in steel [34, 35, 36]. The constitutive behaviour of the bulk material is assumed to be described by an isotropic von Mises plasticity model and the flow stress is assumed to be independent of the hydrogen content. Following Sofronis et al. [37], the hardening function is taken to be a power law, i.e. $\sigma _{\mathrm {y}} = \sigma _{0} \left( 1+ \varepsilon _{\mathrm {e}}^{\mathrm {pl}}/\varepsilon _{0}\right) ^{1/n}$, where $\sigma _{0}$ is the initial yield strength, $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ is the equivalent plastic strain, $\varepsilon _{0}=\sigma _{0}/E$, E is Young’s modulus and n is the hardening exponent. Further, the dislocation density $\rho _{\mathrm {D}}$ is assumed to be linearly related to the equivalent plastic strain according to $\rho _{\mathrm {D}} = \rho _{\mathrm {D}0}+\gamma \, \varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ for $\varepsilon _{\mathrm {e}}^{\mathrm {pl}} \le 0.5$ and $\rho _{\mathrm {D}} = \rho _{\mathrm {D}}^{\mathrm {max}}$ for $\varepsilon _{\mathrm {e}}^{\mathrm {pl}} > 0.5$, where $\rho _{\mathrm {D}0}$ is the initial dislocation density and $\gamma$ is a material parameter [21, 29]. The cohesive model in Sect. 4.2 is used to model failure. The hydrogen in the bulk material is assumed to reside in the lattice and dislocation sites, i.e. ${\bar{C}}_{\mathrm {T}} = {\bar{C}}_{\mathrm {L}} + {\bar{C}}_{\mathrm {D}}$, and it is also trapped in the interface. The hydrogen concentration in the dislocation traps ${\bar{C}}_{\mathrm {D}}$ increases with increasing plastic strain, i.e. due to the increase of the number of trap sites associated with the dislocation density Eq. (45). Further, the hydrogen trapped in the dislocations and the discrete trap represented by the interface are in equilibrium with the concentration in the lattice following Oriani’s theory, according to Eqs. (46) and (9), respectively. Hence, the displacement and concentration or chemical potential can be determined by solving a coupled mechanical–diffusion problem using the Finite Element Method based on the concentration or chemical potential formulation. The concentration formulation is adopted from Barrera et al. [14] and the chemical potential formulation described above is implemented in the FE code Abaqus [15]. The isotropic von Mises plasticity model is implemented using a UMAT subroutine and the diffusion equations are implemented using the UMATHT subroutine (the details of the implementations are provided in Appendices A and B). The material parameters used in the analysis are summarised in Table 1.

The computational domain of the deep double-edged notched specimen shown in Fig. 3 is analysed under plane strain conditions. (Only a quarter the specimen is analysed due to symmetry.) The dimensions are taken as $W = 10$ $\mathrm {mm}$, $H=12.5$ $\mathrm {mm}$, $B=1$ $\mathrm {mm}$, $r=5$ $\mathrm {mm}$, $D=5$ $\mathrm {mm}$ and $\varphi =30^{\circ }$. The 4-node bilinear and 8-node quadratic coupled temperature-displacement plane strain elements (CPE4RT and CPE8RT, respectively) are used in the different discretisations. In particular, the CPE4RT element is used in the failure simulations and the CPE8RT element is used to compare the two formulations. It should be mentioned that quadratic elements are necessary to compute the stress gradient in the concentration formulation (a detailed discussion is presented in Barrera et al. [14]). A 4-node two-dimensional linear interface element was implemented in Abaqus using the user-defined subroutine UEL. In the comparison between the formulations, no damage is considered and the Finite Element model comprised of the bulk elements only.

In the failure analysis, the Finite Element model is divided into two regions, in which the bulk and interface elements are defined. The interface elements are inserted along the predefined failure path, g $W \ge x \ge D+r$ and $y=0$, and bulk elements are defined elsewhere. The interface elements are modelled with zero initial thickness (i.e. the top and bottom face nodes coincide) and their top faces are attached to the bulk elements. In failure simulations, the mesh has 5682 elements, of which 5469 are bulk elements and 213 are interface elements. The total number of elements is reduced to 5469 elements in the simulation that are used to compare the formulations. This number of elements is found to be necessary to obtain converged solutions in both cases.

Fig. 4

Comparison between the chemical potential and concentration based formulations in i and ii, respectively. The different distributions are: a the hydrogen concentration at the lattice ${\bar{C}}_{\mathrm {L}}$; and b the chemical potential $\mu$

5.1.1 Comparison between the concentration and chemical potential formulations

Firstly, the concentration and chemical potential based formulations are compared. We assume that the hydrogen concentration in the lattice is initially uniform throughout the plate, i.e. the initial lattice concentration is ${\bar{C}}_{\mathrm {L}0} = 4.3$ $\mathrm {mol}/\mathrm {m}^{3}$ which corresponds to an occupancy of $\theta _{\mathrm {L}0} = 5 \times 10^{-6}$. All boundaries are insulated. The mechanical loading is applied in the form of a prescribed displacement in the y-direction, $u_{y}$, at the upper surface (i.e. $y=H$) as shown in Fig. 3. The displacement is ramped up monotonically from 0 to 0.025 $\mathrm {mm}$ which corresponds to an overall engineering strain of $\varepsilon _{yy} \in \left[ 0-0.002 \right]$. Under these loading conditions only elastic deformation is expected. The process time $t_{\mathrm {p}}$ is taken to be equal to the characteristic diffusion time, $\tau = l_{\mathrm {c}}^{2}/D_{\mathrm {L}}$ where $l_{\mathrm {c}}$ is the characteristic length scale, taken to be equal to the notch radius (1 $\mathrm {mm}$). Hence, transient diffusion is considered.

Figure 4a, b illustrate the distribution of the hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}}$ normalised by the initial concentration ${\bar{C}}_{\mathrm {L}0}$ and the chemical potential $\mu$ normalised by the initial chemical potential $\mu _{\mathrm {ini}}= 30.26$ $\mathrm {J}/\mathrm {mol}$ at strain level $\varepsilon _{yy} = 0.002$. The Fig. 4i, ii show that the two formulations agree. In the elastic regime, the concentration of hydrogen in the lattice is controlled by the hydrostatic stress distribution. Thus, the maximum concentration is at the notch root where the hydrostatic stress is a maximum. Far from the notch, the hydrostatic stress is much lower, which leads to a decrease in the hydrogen concentration locally to satisfy conservation of volume of hydrogen within the specimen.

Fig. 5

The macroscopic stress–strain behaviour in y-direction. Points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ are associated with the onset of the plastic deformation, damage initiation, damaged progression and complete failure, respectively

Fig. 6

The lattice hydrogen concentration distribution at: i the onset of the plastic deformation, ii damage initiation, iii damage progression and iv complete failure. These instants are associated with points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in Fig. 5, respectively

5.1.2 Failure of the double-edged notched specimen

In this section, we investigate the use of the interface model and the chemical potential formulation to simulate failure of the deep double-edged notched specimen. Similarly, we assume initially uniform hydrogen concentration in the lattice throughout the plate and the mechanical loading is applied in the form of a prescribed displacement in the y-direction at the upper surface. The initial hydrogen concentration in the lattice is taken to be ${\bar{C}}_{\mathrm {L}0} = 4.3$ $\mathrm {mol}/\mathrm {m}^{3}$ and zero flux at the boundaries is prescribed. The displacement at the upper surface is ramped up monotonically from zero to complete failure. The process time is taken to be $t_{\mathrm {p}} = \tau$ which yields a loading rate of 0.25 $\mathrm {mm}/\mathrm {s}$. The ratio between the interface cohesive strength and yield strength is chosen to be $\sigma _{\mathrm {c}}/\sigma _{0} = 3.0$ (i.e. $\xi _{\mathrm {int}} = 0$) and the separation at failure is taken to be $\delta _{n}^{\mathrm {f}} = 0.01$ $\mathrm {mm}$. It should be mentioned that these parameters are suitable to describe steel at the given concentration level [21]. Further, the softening of the interface (i.e. the reduction of cohesive strength) due to hydrogen is not investigated in this example. The interface stiffness is taken to be $K_{n} = 10^{6}$ $\mathrm {MPa}/\mathrm {mm}$ which is found to be necessary to prevent artificial compliance [38, 39]. The interface binding energy is $W_{\mathrm {int}} = -10$ $\mathrm {kJ}/\mathrm {mol}$, the molar volume is $V_{\mathrm {M}}^{\mathrm {int}} = V_{\mathrm {M}} = 2 \times 10^{-6}$ $\mathrm {m}^{3}/\mathrm {mol}$ and the kinetic constant for diffusion across the interface is $h_{\mathrm {int}} = 8 \times 10^{-6}$ $\mathrm {mol}^{2}/(\mathrm {m}^{2} \cdot \mathrm {s} \cdot \mathrm {J})$.

Figure 5 shows the macroscopic stress–strain responses in the y-direction for damaged and undamaged cases, i.e. the relationship between $\varepsilon _{yy}$ and $\sigma _{yy}$ as indicated in Fig. 3. The behaviour illustrates a typical elastic–plastic response for a notched specimen in which the onset of macroscopic yielding usually occurs at a lower stress level than the yield strength of the material due to the stress concentration, i.e. $\sigma _{yy}/\sigma _{0} \approx 0.6$. Damage initiation takes place at $\varepsilon _{yy} \approx 0.012$ and final failure occurs at $\varepsilon _{yy} \approx 0.0135$. In what follows, we investigate four points in the loading history, these points are associated with: $\mathrm {A}$, elastic deformation; $\mathrm {B}$, damage initiation; $\mathrm {C}$, damage progression and $\mathrm {D}$, complete failure of the interface, see Fig. 5.

Figure 6i–iv illustrate the distribution of the hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}}$ normalised by the initial concentration ${\bar{C}}_{\mathrm {L}0}$ at points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ of Fig. 5, respectively. At point $\mathrm {A}$, prior to any plastic deformation, hydrogen is concentrated at the notch root in the region of maximum hydrostatic stress. After the onset of plastic deformation and before damage initiation, the maximum hydrostatic stress moves to a position below the notch root. Consequently, the maximum concentration shifts to this location, i.e. the maximum value of ${\bar{C}}_{\mathrm {L}}$ is at $x/W \approx 0.65$ at point $\mathrm {B}$. After damage initiation, the stress relaxes along the interface which results in diffusion of hydrogen from the interface. At complete failure, the specimen is only loaded by the residual stresses that are caused by the plastic deformation. Hence, the hydrogen is redistributed according to this residual stress field.

Fig. 7

The distribution of: i the hydrogen concentration ${\bar{C}}_{\mathrm {Tr}}$; and ii the damage variable d along the interface at different instants, i.e. points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in Fig. 5

In order to investigate the interface, we consider the interface and the bulk material adjacent to the interface, i.e. along $W \ge x \ge D+r$ and $y=0$. Figure 7i, ii show the distribution of the hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {Tr}}$ normalised by the initial concentration ${\bar{C}}_{\mathrm {Tr}0}$ and the damage variable d, respectively, along the interface at different instants indicated by points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ as shown in Fig. 5. At point $\mathrm {A}$, prior to damage initiation, the damage variable is zero along the interface. The increase of deformation causes damage initiation at a distance from the notch root, i.e. $x/W \approx 0.65$, where the stress normal to the interface is maximum. Consequently, the damage spreads towards the notch root and the middle of the specimen, as indicated by the damage distribution at points $\mathrm {B}$ and $\mathrm {C}$. At failure, the interface is completely damaged such that the damage parameter is 1.0 along the entire interface. Initially, hydrogen is trapped at the interface and its concentration is ${\bar{C}}_{\mathrm {Tr}}/{\bar{C}}_{\mathrm {Tr}0}$ which is solely determined by the interface’s binding energy as the material is initially stress free. Since $V_{\mathrm {M}}^{\mathrm {int}}$ has been taken to be zero and there is no jacking due to the hydrogen that diffuses to the interface, the concentration remains uniform along the interface as the stress is increased. It’s magnitude gradually decreases, however, to supply some of the hydrogen that flows into the regions of high hydrostatic stress as the applied load is increased. Thus the concentration at $\mathrm {A}$ is less than that under zero stress. As damage develops the stress in the matrix decreases, hydrogen diffuses away from regions where the hydrostatic stress was high and some of this flows into the interface, leading to an increase in ${\bar{C}}_{\mathrm {Tr}}$. After more significant damage development, the traction decreases, which causes additional trapping of hydrogen in the interface, i.e. points $\mathrm {C}$ and $\mathrm {D}$. Figure 8i–iv show the distribution of the hydrostatic stress $\sigma _{\mathrm {h}}$ normalised by the yield strength $\sigma _{0}$, equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$, hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}}$ and hydrogen trapped in the dislocation sites ${\bar{C}}_{\mathrm {D}}$ normalised by the initial concentration in the lattice ${\bar{C}}_{\mathrm {L}0}$ in the bulk material adjacent to the interface at different instants that are indicated by points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ as shown in Fig. 5. The distributions of hydrostatic and equivalent stress imply that prior to the onset of plastic deformation, at point $\mathrm {A}$, the equivalent plastic strain is zero and the hydrostatic stress is maximum at the notch root. The plastic deformation develops at the notch root and spreads toward the centre of the specimen. Consequently, the maximum hydrostatic stress changes location from the notch root. As damage develops, the stresses relax which halts the development of plastic deformation and causes the maximum hydrostatic stress location to move to the partially damaged ligament at the centre of the specimen. After final failure, the hydrostatic stress is determined by the distribution of the residual stresses. The distribution of the hydrogen concentration in the lattice reflects the hydrostatic stress distribution. Further, the hydrogen trapped in dislocations is in equilibrium with the hydrogen in the lattice which is demonstrated by the similarities of the distributions. The number of dislocation sites in the vicinity of the notch increases as suggested by the plastic deformation distribution. However, a small change in the trapped hydrogen concentration is observed.

Fig. 8

The distribution of: i the hydrostatic stress $\sigma _{\mathrm {h}}$; ii the equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$; iii the hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}}$; and iv the hydrogen concentration in the dislocation trap ${\bar{C}}_{\mathrm {D}}$ at the bulk material adjacent to the interface at different instants, i.e. points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in Fig. 5

5.2 Analysis of hydrogen enhanced decohesion (HEDE) in a dissimilar metal weld system

In this example, we investigate hydrogen enhanced decohesion (HEDE) in an AISI8630/IN625 dissimilar weld system. (A comprehensive investigations of this system is provided in Barrera et al. [33].) In particular, we are interested in studying the decohesion process that takes place around fine $\mathrm {M}_{7} \, \mathrm {C}_{3}$ carbide particles in a ’featureless’ zone located on the Nickel side of the interface in the presence of hydrogen. Barrera et al. [33] report analyses of this system using TEM imagery and used a mesh generation scheme that converted these images into a finite element mesh [40]. Their simulations have shown that during deformation microcracks are initially formed at the carbide-matrix interface which then propagate along the interface. Thereafter, several microcracks connect together and form macrocracks through the localisation of plastic flow in a region adjacent to the region where (1) hydrogen content is high and (2) the carbide/matrix interface has debonded.

Fig. 9

The representative volume of the ’featureless’ region: i cluster of $\mathrm {M}_{7} \, \mathrm {C}_{3}$ carbides in a 623 Nickel alloy; and ii single precipitate RVE. The single precipitate vertices are numbered from 1 to 10 and a local coordinate $\xi$ along the interface with origin at vertex 1 is introduced

The featureless zone is located next to the fusion line on the Nickel side of the weld and is typically about 20 $\mu \mathrm {m}$ wide. It is rich in $\mathrm {M}_{7} \, \mathrm {C}_{3}$ carbides that occupy a volume fraction of about $15\%$ and the average length of their major axis is of the order of 40 $\mathrm {nm}$. In this analysis, we adopt the representative microstructure of the featureless zone from Barrera et al. [33] (see Fig. 9i) in which several precipitates are distributed in the Nickel matrix. Further, we focus on analysing a single precipitate and consider the volume element in Fig. 9ii assuming plane strain conditions. The objective of this analysis is to initially reproduce the results obtained by Barrera et al. [33] and then explore some of the features of this problem. Barrera et al. [33] did not undertake a fully coupled mechanical diffusion analysis. They assumed a simple steady state distribution of hydrogen, and expressed the material parameters in terms of this distribution. The current analysis consists of a fuller physical description of the problem, and captures the detailed evolution of the hydrogen concentration in the material as plastic deformation and damage develop. In particular, we are interested in investigating: (1) hydrogen enhanced decohesion at the interface and how this influences the hydrogen distribution; (2) the effect of swelling of the matrix and precipitate on the decohesion process and (3) the effect of hydrogen charging on deformation in the matrix. To analyse this problem, as noted above, we assume a full coupling between the mechanical and diffusion responses. The matrix material (i.e. 625 Nickel) is assumed to be described by an isotropic von Mises plasticity model with power law hardening as in Sect. 5.1. The flow stress in the bulk material is assumed to be independent of the hydrogen content. The relevant matrix material parameters are: Young’s modulus $E_{\mathrm {m}}$, Poisson’s ratio $\nu _{\mathrm {m}}$, initial yield strength $\sigma _{0}$, hardening exponent n, initial dislocation density $\rho _{\mathrm {D}0}$ and dislocation density parameter $\gamma$. The precipitate ( $\mathrm {M}_{7} \, \mathrm {C}_{3}$-carbide) is taken to be elastic with Young’s modulus $E_{\mathrm {p}}$ and Poisson’s ratio $\nu _{\mathrm {p}}$. The bilinear interface/cohesive model described in Sect. 4.2 is used to model the interface. The hydrogen in the bulk and precipitate materials is assume to reside in the lattice, dislocations and fixed traps, i.e. ${\bar{C}}_{\mathrm {T}} = {\bar{C}}_{\mathrm {L}} + {\bar{C}}_{\mathrm {D}} + {\bar{C}}_{\mathrm {F}}$. Hydrogen is also trapped in the interface, with concentration ${\bar{C}}_{\mathrm {Tr}}$. The Nickel alloy parameters are given in Table 1 and the precipitate parameters are taken to be $E_{\mathrm {p}} = 2 \, E_{\mathrm {m}}$ and $\nu _{\mathrm {p}} = \nu _{\mathrm {m}}$. The reference chemical potential for the matrix and the precipitate are taken to be $\mu _{0}^{\mathrm {m}} = 0$ and $\mu _{0}^{\mathrm {p}} = \mu _{0}^{\mathrm {m}} + W_{\mathrm {p}} = W_{\mathrm {p}}$, respectively, where $W_{\mathrm {p}}$ is the binding energy of the precipitate. The molar volume of the matrix and precipitate are taken to be $V_{\mathrm {M}}^{\mathrm {p}} = V_{\mathrm {M}} = 2 \times 10^{-6}$ $\mathrm {m}^{3}/\mathrm {mol}$. The effects of the trapping energies will be discussed later. The interface parameters are $W_{\mathrm {int}}$, $V_{\mathrm {M}}^{\mathrm {int}} = 2 \times 10^{-6}$ $\mathrm {m}^{3}/\mathrm {mol}$ and $h_{\mathrm {int}} = 8 \times 10^{-6}$ $\mathrm {mol}^{2}/(\mathrm {m}^{2} \cdot \mathrm {s} \cdot \mathrm {J} )$. The chemical potential formulation and its implementations in the FE code Abaqus [15], described in Sect. 3 and Appendices A and B, is used.

Fig. 10

The Finite Element model of the single precipitate RVE: i the mesh of the whole geometry and the mechanical boundary conditions; and ii mesh details along the interface

The Finite Element model of the single precipitate problem is shown in Fig. 10i, ii. The model is divided into three regions, namely; the matrix, precipitate and interface. Interface elements are inserted along the interface and the bulk elements are defined in the precipitate and the matrix regions. The interface elements are modelled with zero initial thickness (i.e. the top and bottom face nodes coincide) and their top and bottom faces are attached to the bulk elements in the matrix and precipitate regions, respectively, as shown in Fig. 10i. Further, a uniform refined element region is created adjacent to the interface for controlling the interface element length. The 4-node bilinear coupled temperature–displacement plane strain elements (CPE4R) are used in the discretisation for plane strain conditions, respectively. The 4-node two-dimensional linear cohesive user element in Appendices A and B is used to discretise the interface. The mesh has 19408 elements, of which 10662 and 8095 are bulk elements in the matrix and precipitate, respectively, and 651 are interface elements. The number of elements is found to be necessary to obtain converged solutions.

The hydrogen concentration in the lattice is initially assumed to be uniform throughout the body, i.e. the initial lattice concentration is ${\bar{C}}_{\mathrm {L}0} = 4.3$ $\mathrm {mol}/\mathrm {m}^{3}$ which corresponds to an occupancy $\theta _{0} = 5.0 \times 10^{-6}$. All boundaries are insulated. The mechanical loading is applied in the form of a prescribed displacement in the y-direction, $u_{y}$, at the upper surface as shown in Fig. 10i. The displacement is ramped up monotonically from zero to complete failure. The loading time $t_{\mathrm {p}}$ is taken to be equal to the characteristic time for diffusion $\tau = l_{\mathrm {c}}^{2} /D_{\mathrm {L}} = 31.1$ $\mathrm {ns}$ where the characteristic length scale is taken to be equal to the precipitate spacing $l_{\mathrm {c}} \approx 50$ $\mathrm {nm}$. In the following sections we will present the results of the different investigations.

5.2.1 Analysis of hydrogen enhanced decohesion at the interface

In order to study the hydrogen enhanced decohesion (HEDE) process along the interface, the interface strength is explicitly reduced. Thus, the ratio between the interface strength and yield strength is chosen to be in the range $\sigma _{\mathrm {c}}/\sigma _{0} \in \left[ 1.0-3.0\right]$, i.e. $\xi _{\mathrm {int}} = 0$. It should be mentioned that, in the absence of hydrogen, this ratio is typically greater than 1 which allows plastic deformation to spread in the matrix material prior to the failure of the interface. The separation at failure and interface stiffness are taken to be $\delta _{n}^{\mathrm {f}} = 0.5$ $\mu \mathrm {m}$ and $K_{n} = 10^{6}$ $\mathrm {MPa}/\mathrm {mm}$, respectively. The reference chemical potentials for the matrix and precipitates are taken to be $\mu _{0}^{\mathrm {m}} = \mu _{0}^{\mathrm {p}} = 0$, i.e . $W_{\mathrm {p}} = 0$.

Figure 11 shows the macroscopic stress–strain responses in the y-direction for different values of $\sigma _{\mathrm {c}}/\sigma _{0}$, i.e. the relation between $\varSigma _{yy}$ and $E_{yy}$ as indicated in Fig. 10i. The macroscopic stress–strain response shows that the material is initially elastic and yields at a stress level that is approximately equal to the macroscopic yield strength. After yielding, the material shows strain hardening behaviour which is followed by a significant drop in the stress due to damage development at the interface. Further, reducing the cohesive strength causes a significant decrease in the ductility. More specifically, at higher values of $\sigma _{\mathrm {c}}/\sigma _{0}$, the strain to failure drops by $50\%$ as the result of reducing the cohesive strength by $17\%$. Further, the reduction in ductility is smaller at lower values of $\sigma _{\mathrm {c}}/\sigma _{0}$, i.e. $\approx 20\%$. Additionally, stress softening is observed which is attributed to damage development along the interface.

Fig. 11

The macroscopic stress–strain behaviour in y-direction for different values of the ratio $\sigma _{\mathrm {c}}/\sigma _{0}$. Points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ are associated with the onset of the plastic deformation, damage initiation, damage progression and complete failure, respectively

To investigate the details of the deformation and diffusion processes, the distribution of lattice occupancy ${\bar{C}}_{\mathrm {L}}$ normalised by the initial concentration ${\bar{C}}_{\mathrm {L}0}$ and equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ for the case of $\sigma _{\mathrm {c}}/\sigma _{0} = 2.0$ at different instants are plotted in Fig. 12a, b, respectively. In particular, the results are explored at four points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in the loading history as illustrated in Fig. 11, representing: (1) the onset of the plastic deformation ($\mathrm {A}$); (2) damage initiation ($\mathrm {B}$); (3) beginning of softening ($\mathrm {C}$); and (4) complete failure ($\mathrm {D}$). At point $\mathrm {A}$, prior to any plastic deformation, hydrogen is concentrated at some of the vertices of the precipitate, i.e. 1, 5, 6, 7, 9 and 10, where the hydrostatic stress attains its maximum values. As deformation proceeds, plastic deformation develops at precipitate vertices and radiates toward the upper and lower surfaces. Further, the maximum hydrogen concentration remains at the vertices, where the hydrostatic stress is greatest. The damage at the interface initiates at the uppermost facet of the precipitate, i.e. facet $6-7$. This facet makes the largest angle with the loading direction, i.e. y-direction, which results in a maximum normal traction distribution along this segment. After damage initiation, the traction decreases along this part of the interface which causes stress relaxation in the matrix and in the precipitate adjacent to the interface. As a result, hydrogen diffuses away from the interface to regions where the hydrostatic stress is larger. Further, the damage continues to increase along this segment leading to a complete separation. The newly created crack propagates along interface segments $5-6$ and $7-8$. The intensive plastic deformation at the crack tips stops further growth of the crack. Further, hydrogen diffuses to the crack tips where now the hydrostatic stress is greatest. Simultaneously, the traction at the lowermost facet of the interface, i.e. facet $10-1$, increases and approaches the cohesive strength causing damage to initiate. It should be mentioned that this segment makes the second largest angle with the loading direction after the uppermost facet. Eventually, plastic deformation spreads widely in the element forming several bands wherein the equivalent plastic strain reaches a maximum value of $50\%$. At this strain level, plastic localisation is expected to take place between adjacent precipitates leading to complete failure.

Fig. 12

The distribution of: a the hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}}$; and b the equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$. The different distributions are at: i the onset of the plastic deformation; ii damage initiation; iii damage progression and iv complete failure. These instants are associated with points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in Fig. 11, respectively

To analyse the interface, the distribution of the damage variable d along the interface at the instants $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ are plotted in Fig. 13. The result shows that at point $\mathrm {A}$, prior to damage initiation, the damage variable is zero along the interface. The damage initiates at segment $6-7$ and propagate to segments $5-6$ and $7-8$. Further, damage initiates along segments $1-2$ and $10-1$ at a later stage of deformation. It should be mentioned that the hydrogen trapped in the interface remains constant during the deformation. After complete failure of the interface, i.e. point $\mathrm {D}$, a small increase is observed along segments $5-6$ and $6-7$.

Fig. 13

The distribution of the damage variable d along the interface at different instants, i.e. points $\mathrm {A}$, $\mathrm {B}$, $\mathrm {C}$ and $\mathrm {D}$ in Fig. 11

The result of this simulation is consistent with the findings reported in Barrera et al. [33], although the current study provides more details of the way in which the diffusional, deformation and interfacial failure processes are coupled, which provides more insight into the sequence of events leading to failure.

5.2.2 The effect of the swelling in the precipitate and matrix

To analyse the effect of the differential swelling of the matrix and precipitate on the failure of this material, the ratio between the precipitate and matrix reference chemical potentials, $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$, is varied over the range $0.5-2.0$. In particular, the reference energy of the matrix is taken to be $\mu _{0}^{\mathrm {m}} = -10$ $\mathrm {kJ}/\mathrm {mol}$ and the reference energy of the precipitate, $\mu _{0}^{\mathrm {p}}$, is then selected to give the required ratio. Hence, the simulations cover the cases where the matrix swells more than the precipitate and the vice versa. The ratio between the interface and yield strength is chosen to be $\sigma _{\mathrm {c}}/\sigma _{0} = 2.0$ and the separation at failure and interface stiffness are kept as $\delta _{n}^{\mathrm {f}} = 0.5$ $\mu \mathrm {m}$ and $K_{n} = 10^{6}$ $\mathrm {MPa}/\mathrm {mm}$, respectively.

Fig. 14

The macroscopic stress–strain behaviour in y-direction for different values of the ratio $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. The points indicate the damage initiation onset

Figure 14 shows the macroscopic stress–strain responses in the y-direction for different values of $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. The result implies that both critical stress (i.e. the stress at which damage is initiated) and ductility depend significantly on the swelling. More specifically, at lower values ($\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}} \le 1.0$), smaller changes are observed. At larger values ($\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}} > 1.0$), the swelling causes an increase in both the critical stress and the ductility. To better understand this increase in the critical stress and ductility, the initial distribution of the normal traction $T_{n}$ normalised by the cohesive strength $\sigma _{\mathrm {c}}$ along the interface is plotted in Fig. 15 for the different values of the ratio $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. It should be mentioned that, in Fig. 15, the local coordinate $\xi$ is normalized by the total length of the interface, i.e. $L_{\mathrm {int}} = 128.3$ $\mathrm {nm}$. The initial distribution of the normal traction is very small at lower values $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. Further, the interface is under tension, i.e. $T_{n}/\sigma _{\mathrm {c}} > 0$. At larger values of $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$, the interface is initially under compression ($T_{n}/\sigma _{\mathrm {c}} < 0$) such that the magnitude of the traction increases with the ratio $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. Hence, when the element is loaded, the traction along the interface increases from the initially negative values which results in an increase in both the critical stress and ductility. This behaviour can be explained by investigating the relative volumetric expansion between the matrix and precipitate. Thus, at the lower values of $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$, the hydrogen concentration in the matrix is larger than the precipitate which leads to a larger volumetric expansion in the matrix and a positive relative volumetric expansion, see Fig. 15. On the other hand, at the higher values $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$, the hydrogen concentration in the precipitate is larger than the matrix which leads to a larger volumetric expansion in the precipitate and negative relative volumetric expansion, see Fig. 16. Hence, the interface is subjected to a tensile loading at lower values of $\mu _{0}^{\mathrm {p}}/\mu _{0} ^{\mathrm {m}}$ due to the positive relative volumetric expansion and compressive loading at higher values due to the negative relative volumetric expansion.

5.2.3 The effect of hydrogen charging on deformation

Another aspect of the problem is to investigate the nature of the deformation induced by hydrogen charging. The deformation in the RVE is mainly induced by volumetric expansion of the matrix and the precipitate. Hence, the reference chemical potentials of the matrix and the precipitate $\mu _{0}^{\mathrm {m}}$ and $\mu _{0}^{\mathrm {p}}$, and the initial concentration of hydrogen ${\bar{C}}_{\mathrm {L}0}$ controls the deformation. Therefore, we consider the reference chemical potential of the matrix to be $\mu _{0}^{\mathrm {m}} = 0$ and the precipitate to be $\mu _{0}^{\mathrm {p}} = -20$ $\mathrm {kJ}/\mathrm {mol}$, i.e. $W_{\mathrm {p}} = -20$ $\mathrm {kJ}/\mathrm {mol}$. The initial concentration at the lattice in the range ${\bar{C}}_{\mathrm {L}0} \in \left[ 2.15-4.30\right]$ $\mathrm {mol}/\mathrm {m}^{3}$ which corresponds to an occupancy $\theta _{\mathrm {L}0} \in \left[ 2.5-7.5\right] \times 10^{-6}$. It should be mentioned that, the mechanical loading is omitted in this analysis. The interface and other matrix and precipitate material parameters are kept as in Sect. 5.2.2.

Figure 17 shows the distribution of the equivalent plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ for different values of the initial lattice concentration ${\bar{C}}_{\mathrm {L}0}$. The result shows that the plastic deformation initiates at the precipitate vertices where the stress is a maximum and at a concentration of ${\bar{C}}_{\mathrm {L}0} = 4.30$ $\mathrm {mol}/\mathrm {m}^{3}$. Further, increasing the initial concentration increases the plastic deformation. Thus, for the given values of $\mu _{0}^{\mathrm {m}}$, $\mu _{0}^{\mathrm {p}}$, $\sigma _{0}$ and E, there is a hydrogen concentration level at which plastic deformation may initiate. Moreover, the size of the plastic zone and the extent of plastic deformation additionally depends on the hardening exponent n.

Fig. 15

The initial distribution of the normal traction $T_{n}$ normalised by the cohesive strength $\sigma _{\mathrm {c}}$ along the interface for different values of the ratio $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$. The local coordinate $\xi$ is normalised by the total length of the interface $L_{\mathrm {int}}$

Fig. 16

The initial distribution of the total hydrogen concentration ${\bar{C}}_{\mathrm {T}}$ at different values of the ratio $\mu _{0}^{\mathrm {p}}/\mu _{0}^{\mathrm {m}}$: i 0.5; ii 1.0; iii 1.5 and iv 2.0

Fig. 17

The distribution of the equivalent plastic deformation at different initial hydrogen concentration in the lattice ${\bar{C}}_{\mathrm {L}0}$: i 2.15 $\mathrm {mol}/\mathrm {m}^{3}$; ii 3.23 $\mathrm {mol}/\mathrm {m}^{3}$; and iii 4.30 $\mathrm {mol}/\mathrm {m}^{3}$

6 Concluding remarks

In this paper, a finite element formulation for solving coupled mechanical/diffusion problems is proposed. The purpose is to investigate hydrogen diffusion in metals and its impact on their mechanical behaviour (i.e. hydrogen embrittlement). In particular, the hydrogen enhanced decohesion and hydrogen enhanced local plasticity mechanisms are incorporated. The hydrogen atoms are assumed to reside either at NILS or at trapping sites such as dislocations and/or fixed traps (e.g. precipitates, interfaces, etc.) that are taken to be in equilibrium following Oriani’s theory. The HELP mechanism is modelled using a continuum plasticity framework, e.g. isotropic von Mises model, in terms of a decrease in the flow stress as a result of increase of hydrogen content in the material as reported by Sofronis and McMeeking [13] and Barrera et al. [14]. The HEDE mechanism is modelled using a cohesive zone modelling approach such that an interface is treated as a discrete trap and its cohesive strength decreases with the increase of hydrogen concentration at the interface.

The proposed formulation adopts a standard Galerkin method in the discretisation of both the diffusion mass conservation and mechanical equilibrium equations. In particular, a displacement based finite element formulation with chemical potential as an additional degree of freedom is employed. Hence, in comparison with the commonly used concentration based formulation, we have substituted the concentration by the chemical potential in the discretisation of the diffusion equation. It follows that the diffusion equation can be expressed fundamentally in terms of the gradient in chemical potential, which reduces the continuity requirements on the shape functions to zero degree (i.e. ${\mathcal {C}}_{0}$). Therefore, a linear shape function can be used to interpolate the chemical potential. In the concentration based formulation, the continuity requirements is of the first degree ${\mathcal {C}}_{1}$, i.e. at least quadratic polynomial. Thus, using the chemical potential offers a lower continuity requirements in comparison with the concentration based formulation. We introduced a consistent interface element formulation that can be achieved due to the continuity of the chemical potential across the interface - concentration can be discontinuous at an interface and this can lead to numerical problems in formulations where concentration is employed as a state variable. Moreover, the coding of the FE equations is more straightforward in the proposed model.

In order to investigate the efficiency and accuracy of the proposed formulation, various example problems are studied. Initially, we have investigated a 2D fully coupled elastoplastic diffusion problem of a deep notched specimen in the absence of damage. The solutions using both concentration and chemical potential based formulations are compared and found to be identical. We have then studied the failure of the specimen using the chemical potential formulation. We have explored the effect of deformation and damage initiation and propagation on the hydrogen of the bulk and the cohesive zone. The results show that the concentration of hydrogen in the lattice is controlled by the hydrostatic stress distribution which takes its maximum value at the notch root in the elastic deformation regime and at a distance from the notch root in the elastic–plastic deformation regime. After the onset of damage, the stress relaxes along the interface which results in diffusion of hydrogen away from the interface and the maximum concentration of hydrogen in the lattice takes place at the tip of the region of extensive damage. The second problem is a micromechanical investigation of hydrogen enhanced decohesion (HEDE) in a dissimilar metal weld. More specifically, we consider the failure in the presence of hydrogen of carbide-matrix interfaces around fine precipitates generated adjacent to the interface of an 8630 steel/IN625 nickel alloy dissimilar weld, which has been analysed extensively by Barrera et al [26]. We have investigated the hydrogen induced decohesion at the interface and have shown that the reduction in cohesive strength significantly reduces the ductility and influences the hydrogen distribution. Further, we have studied the effect of differential swelling of the precipitate (arising from differences in the solubility of hydrogen in the matrix and precipitate) on the decohesion process and have illustrated that this differential may delay the onset of damage and consequently increase the ductility. Finally, we have shown that hydrogen charging may introduce localised plastic deformation in the matrix in the absence of any applied mechanical loading, which results in the generation of a residual state of stress in the vicinity of a particle.

Appendices

Finite element implementations of the coupled elastic–plastic mechanical, diffusion and interface models.

The Finite Element implementations of the continuum plasticity, diffusion and interface models in Sect. 3 are discussed in this Appendix. The purpose is to provide explicit expressions for the residual force vectors and consistent tangents for the Newton–Raphson solution procedure. Hence, we consider the system of equations that are given by the residual vectors and the solution procedure in Sects. 3.4 and 3.5, respectively. The model problem domain is divided into bulk and interface regions. The bulk material is assumed to exhibit elastic–plastic behaviour and the interface behaviour is determined by the cohesive zone model in Sect. 4.2. The hydrogen transport model for the bulk and interface are described in Sects. 4.1 and 4.2, respectively.

1.1 The bulk material

The contributions of the bulk material to the global residual vectors in Eqs. (30) and (34) are defined as

$$\begin{aligned} \begin{aligned} R_{I}^{\mu }&= \dfrac{1}{\varDelta t} \, \int \limits _{\varOmega } N_{I} \left( {\bar{C}}_{\mathrm {T}}^{p+1} -{\bar{C}}_{\mathrm {T}}^{p} \right) \, \mathrm {d}V - \int \limits _{\varGamma _{J}} N_{I} \, \hat{{\bar{J}}} \, \mathrm {d}S, \\ R_{iI}^{\mathbf{u}}&= \int \limits _{\varOmega } \sigma _{ij} \, B_{jI} \, \mathrm {d}V - \int \limits _{\varGamma _{t}} N_{I} \, {\hat{t}}_{i} \, \mathrm {d}S, \end{aligned} \end{aligned}$$

(A.1)

where node I belongs to $\varOmega$ and $\varGamma$ (i.e. $I \in \varOmega , \varGamma$) and the volume $\varOmega$ and the boundary $\varGamma$ define the bulk region. The lattice concentration ${\bar{C}}_{\mathrm {L}}$ is determined as described in Sect. 4.1 and the Cauchy stress $\sigma _{ij}$ is obtained using an elastic–plastic constitutive model that will be discussed later in this section. In the solution procedure in Sect. 3.5, the linearisation of the residuals yields the tangent stiffness matrix in Eqs. (37) and (38). Hence, the tangent operators for the residuals in Eqs. (A.1) are obtained as

$$\begin{aligned} K_{IJ}^{\mu \mu }&= \dfrac{1}{\varDelta t} \, \int \limits _{\varOmega } N_{I} \, D^{\mu \mu } \, N_{J} \, \mathrm {d}V - \int \limits _{\varGamma _{J}} N_{I} \, \dfrac{\partial \hat{{\bar{J}}}}{\partial \mu } \, N_{J} \, \mathrm {d}S, \nonumber \\ K_{jIJ}^{\mu \mathbf{u}}&= \dfrac{1}{\varDelta t} \, \int \limits _{\varOmega } N_{I} \, D^{\mu \mathbf{u}} \, B_{jJ} \, \mathrm {d}V - \int \limits _{\varGamma _{J}} N_{I} \, \dfrac{\partial \hat{{\bar{J}}}}{\partial u_{j}} \, N_{J} \, \mathrm {d}S, \nonumber \\ K_{iIJ}^{\mathbf{u}\mu }&= \int \limits _{\varOmega } B_{jI} \, D_{ij}^{\mathbf{u}\mu } \, N_{J} \, \mathrm {d}V - \int \limits _{\varGamma _{t}} N_{I} \, \dfrac{\partial {\hat{t}}_{i}}{\partial \mu } \, \mathrm {d}S, \nonumber \\ K_{ijIJ}^{\mathbf{u}\mathbf{u}}&= \int \limits _{\varOmega } B_{kI} \, {\mathbb {D}}_{ikjl}^{\mathbf{u}\mathbf{u}} \, B_{lJ} \, \mathrm {d}V - \int \limits _{\varGamma _{t}} N_{I} \, \dfrac{\partial {\hat{t}}_{i}}{\partial u_{j}} \, N_{J} \, \mathrm {d}S, \end{aligned}$$

(A.2)

where nodes I and J belongs to $\varOmega$ and $\varGamma$, and $D^{\mu \mu }$, $D_{j}^{\mu \mathbf{u}}$, $D_{ij}^{\mathbf{u}\mu }$, and ${\mathbb {D}}_{ikjl}^{\mathbf{u}\mathbf{u}}$ are the tangent moduli that can be determined from the variation of the total hydrogen concentration and the Cauchy stress. Therefore, the derivatives and tangent moduli in Eqs. (A.2) will be determined in the subsequent subsections.

1.1.1 The elastic–plastic model

The elastic–plastic constitutive relation is written in terms of the rate of deformation tensor $D_{ij}$ and Zaremba–Jaumann stress rate of Cauchy stress ${\mathop {\sigma }\limits ^{\triangledown }}_{ij}$. The Zaremba–Jaumann stress rate is used to meet the objectivity requirements, i.e. material invariance for rigid body rotation, and it is given by

$$\begin{aligned} {\mathop {\sigma }\limits ^{\triangledown }}_{ij} = {\dot{\sigma }}_{ij} + \sigma _{ik} \, W_{kj} - W_{ik} \, \sigma _{kj}, \end{aligned}$$

(A.3)

where ${\dot{\sigma }}_{ij}$ is the material time derivative of the Cauchy stress, and $D_{ij} = \mathrm {sym}\left( L_{ij} \right)$ and $W_{ij} = \mathrm {asym}\left( L_{ij} \right)$ are the rate of deformation and spin tensors that are equal to symmetric and antisymmetric parts of the velocity gradient $L_{ij} = {\dot{F}}_{ik} \, F_{kj}^{-1}$, respectively, and $F_{ij} = \partial x_{i} / \partial X_{j}$ is the deformation gradient. Following Sofronis et al. [37], the total rate of deformation is taken to be the sum of the elastic $D_{ij}^{\mathrm {el}}$, plastic $D_{ij}^{\mathrm {pl}}$ and swelling $D_{ij}^{\mathrm {s}}$ parts:

$$\begin{aligned} D_{ij} = D_{ij}^{\mathrm {el}} + D_{ij}^{\mathrm {pl}} + D_{ij}^{\mathrm {s}}. \end{aligned}$$

(A.4)

The elastic strains are assumed to be small and given by

$$\begin{aligned} D_{ij}^{\mathrm {el}} = {\mathbb {S}}_{ijkl} \, {\mathop {\sigma }\limits ^{\triangledown }}_{kl} = \dfrac{1+\nu }{E} \, {\mathop {\sigma }\limits ^{\triangledown }}_{kl} - \dfrac{\nu }{E} \, \, {\mathop {\sigma }\limits ^{\triangledown }}_{mm} \, \delta _{ij}. \end{aligned}$$

(A.5)

where ${\mathbb {S}}_{ijkl} = {\mathbb {C}}_{ijkl}^{-1}$ is the elastic compliance tensor. The presence of hydrogen may cause volumetric change that is given by the swelling rate of deformation

$$\begin{aligned} D_{ij}^{\mathrm {s}} = \dfrac{{\dot{\varepsilon }}_{\mathrm {s}}}{1+\varepsilon _{\mathrm {s}}} \, \delta _{ij}. \end{aligned}$$

(A.6)

and the material time derivative of $\varepsilon _{\mathrm {s}}$ is ${\dot{\varepsilon }}_{\mathrm {s}} = \frac{1}{3} \, V_{\mathrm {M}} \, \dot{{\bar{C}}}_{\mathrm {T}}$. It should be mentioned that, for the sake of generality, the swelling is taken to be associated with hydrogen in the lattice and traps, i.e. the total concentration, which is different from the definition used in Sect. 4.1. Consequently, the stress contribution to the chemical potential in Eq. (51) becomes $\mu _{\sigma } = - \sigma _{\mathrm {h}} \, V_{\mathrm {M}} \, \partial {\bar{C}}_{\mathrm {T}} / \partial {\bar{C}}_{\mathrm {L}}$. Further, the swelling deformation is assumed to be small. The plastic part of the rate of deformation tensor is given by the von Mises flow rule as

$$\begin{aligned} D_{ij}^{\mathrm {pl}} = {\dot{\lambda }} \, \dfrac{\partial f}{\partial \sigma _{ij}}. \end{aligned}$$

(A.7)

where $\lambda$ is the a positive scalar function and f is the yield function, i.e. $f < 0$ implies elastic unloading and $f=0$ represents the yielding, that is given by

$$\begin{aligned} f = \sigma _{\mathrm {e}} - \sigma _{\mathrm {y}} \big ( \varepsilon _{\mathrm {e}}^{\mathrm {pl}}, {\bar{C}}_{\mathrm {T}} \big ), \end{aligned}$$

(A.8)

for the case of von Mises materials, where $\sigma _{\mathrm {e}} = \sqrt{\frac{3}{2} \, s_{ij} \, s_{ij}}$ is von Mises equivalent stress, $s_{ij} = \sigma _{ij} - \frac{1}{3} \, \sigma _{kk} \, \delta _{ij}$ is the stress deviator, $\sigma _{\mathrm {y}}$ is the flow stress and $\varepsilon _{\mathrm {e}}^{pl} = \int \sqrt{\frac{2}{3} \, D_{ij}^{\mathrm {pl}} \, D_{ij}^{\mathrm {pl}}} \, \mathrm {d}t$ is the equivalent plastic strain, i.e. $D_{ij}^{\mathrm {pl}} = \frac{3}{2} \, \frac{{\dot{\varepsilon }}_{\mathrm {e}}^{\mathrm {pl}}}{\sigma _{\mathrm {e}}} \, s_{ij}$. Hence, the consistency condition of the yield function in Eq. (A.8) gives

$$\begin{aligned} {\dot{f}} = \dfrac{\partial f}{\partial \sigma _{ij}} \, {\dot{\sigma }}_{ij} + \dfrac{\partial f}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \, {\dot{\varepsilon }}_{\mathrm {e}}^{\mathrm {pl}} + \dfrac{\partial f}{\partial {\bar{C}}_{\mathrm {T}}} \, \dot{{\bar{C}}}_{\mathrm {T}}, \end{aligned}$$

(A.9)

where the yield function f is a function of $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ and ${\bar{C}}_{\mathrm {T}}$. Therefore, using Eqs. (A.6-A.9), the plastic part of the rate of deformation tensor becomes

$$\begin{aligned} D_{ij}^{\mathrm {pl}} = \dfrac{\left( \dfrac{\partial f}{\partial \sigma _{kl}} - \dfrac{\partial f}{\partial {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{mm}} \, \delta _{kl}\right) {\mathop {\sigma }\limits ^{\triangledown }}_{kl}}{\dfrac{\partial f}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} + \dfrac{\partial f}{\partial {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}} \, \dfrac{\partial f}{\partial \sigma _{ij}}, \end{aligned}$$

(A.10)

and the rate tangent expression for the Zaremba–Jaumann derivative of Cauchy stress is

$$\begin{aligned} {\mathbb {C}}_{ijkl}^{\mathrm {ep}}&= {\mathbb {C}}_{ijkl} - \dfrac{{\mathbb {C}}_{ijab} \Bigg ( \dfrac{\partial f}{\partial \sigma _{ab}} + \dfrac{\frac{1}{3} \, V_{\mathrm {M}}}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \, \delta _{ab}\Bigg ) \Bigg ( {\mathbb {C}}_{klcd} \, \dfrac{\partial f}{\partial \sigma _{cd}} - \dfrac{\frac{1}{3} \, V_{\mathrm {M}} \, K}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{ee}} \, \dfrac{\partial f}{\partial \sigma _{mn}} \, {\mathbb {C}}_{mncd} \, \delta _{cd} \, \delta _{kl} \Bigg )}{\dfrac{\partial f}{\partial \sigma _{mn}} \, {\mathbb {C}}_{mnop} \, \dfrac{\partial f}{\partial \sigma _{op}} - \dfrac{\partial f}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} + \dfrac{\frac{1}{3} \, V_{\mathrm {M}}}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \, \dfrac{\partial f}{\partial \sigma _{qr}} \, {\mathbb {C}}_{qrst} \, \delta _{st} } \nonumber \\&\quad - \dfrac{\frac{1}{3} \, V_{\mathrm {M}} \, K}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{vv}} \, {\mathbb {C}}_{ijuw} \, \delta _{uw} \, \delta _{kl}, \end{aligned}$$

(A.11)

where K is the bulk modulus, $\partial f/ \partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}} = \partial \sigma _{\mathrm {y}}/ \partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}} = H$ and $\partial f/ \partial {\bar{C}}_{\mathrm {T}} = \partial \sigma _{\mathrm {y}}/ \partial {\bar{C}}_{\mathrm {T}}$ can be determined from a hardening law and the associated hydrogen softening function (see Sect. B.2.1), respectively. The different derivatives in Eq. (A.11) determined from Eqs. (42-46) and (51) are

$$\begin{aligned} \begin{aligned} \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}&= \dfrac{\partial {\bar{C}}_{\mathrm {D}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} = \dfrac{\partial {\bar{C}}_{\mathrm {D}}}{\partial {\bar{N}}_{\mathrm {D}}} \, \dfrac{\partial {\bar{N}}_{\mathrm {D}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} = \left( \dfrac{K_{\mathrm {D}} \, {\bar{C}}_{\mathrm {L}}}{\beta _{\mathrm {L}} \, {\bar{N}}_{\mathrm {L}}+K_{\mathrm {D}} \, {\bar{C}}_{\mathrm {L}}} \right) \dfrac{\partial {\bar{N}}_{\mathrm {D}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}, \\ \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{kk}}&= \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial {\bar{C}}_{\mathrm {L}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {L}}}{\partial \sigma _{kk}} = \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial {\bar{C}}_{\mathrm {L}}} \, \dfrac{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}} \, V_{\mathrm {M}}}{3 \, R \, T} \, \exp \left( \dfrac{\mu -\mu _{0}-\mu _{\sigma }}{R \, T} \right) , \\ \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial {\bar{C}}_{\mathrm {L}}}&= 1+ \dfrac{\partial {\bar{C}}_{\mathrm {F}}}{\partial {\bar{C}}_{\mathrm {L}}} + \dfrac{\partial {\bar{C}}_{\mathrm {D}}}{\partial {\bar{C}}_{\mathrm {L}}} \\&= 1+ \dfrac{\beta _{\mathrm {L}} \, K_{\mathrm {F}} \, {\bar{N}}_{\mathrm {L}} \, {\bar{N}}_{\mathrm {F}}}{\left( \beta _{\mathrm {L}} \, {\bar{N}}_{\mathrm {L}}+K_{\mathrm {F}} \, {\bar{C}}_{\mathrm {L}} \right) ^{2}} + \dfrac{\beta _{\mathrm {L}} \, K_{\mathrm {D}} \, {\bar{N}}_{\mathrm {L}} \, {\bar{N}}_{\mathrm {D}}}{\left( \beta _{\mathrm {L}} \, {\bar{N}}_{\mathrm {L}}+K_{\mathrm {D}} \, {\bar{C}}_{\mathrm {L}} \right) ^{2}} \end{aligned} \end{aligned}$$

(A.12)

The change of Cauchy’s stress with respect to the chemical potential is determined as

$$\begin{aligned} \dfrac{\partial \sigma _{ij}}{\partial \mu } = \dfrac{\partial \sigma _{ij}}{\partial \sigma _{kk}} \, \dfrac{\partial \sigma _{kk}}{\partial {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \mu } = \dfrac{\partial \sigma _{kk}}{\partial {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \mu } \, \delta _{ij}, \end{aligned}$$

(A.13)

where

$$\begin{aligned} \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \mu } = \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial {\bar{C}}_{\mathrm {L}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {L}}}{\partial \mu } = \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial {\bar{C}}_{\mathrm {L}}} \, \dfrac{{\bar{C}}_{\mathrm {L}}^{\mathrm {max}}}{R \, T} \, \exp \left( \dfrac{\mu -\mu _{0}-\mu _{\sigma }}{R \, T} \right) . \end{aligned}$$

(A.14)

It follows that the tangent moduli in Eq. (A.2) can be determined as

$$\begin{aligned} {\mathbb {D}}_{ijkl}^{\mathbf{u}\mathbf{u}}&= {\mathbb {C}}_{ijkl}^{\mathrm {ep}} - \frac{1}{2} \left( \sigma _{ik} \, \delta _{jl} + \sigma _{jk} \, \delta _{il} + \sigma _{il} \, \delta _{jk} + \sigma _{jl} \, \delta _{ik} - \sigma _{ij} \, \delta _{kl} \right) , \nonumber \\ D_{ij}^{\mathbf{u}\mu }&= \dfrac{\partial \sigma _{ij}}{\partial \mu }. \end{aligned}$$

(A.15)

1.1.2 The diffusion model

The variation of the chemical potential is expressed as:

$$\begin{aligned} \dot{{\bar{C}}}_{\mathrm {T}} = D^{\mu \mu } \, {\dot{\mu }} + D_{ij}^{\mu \mathbf{u}} \, D_{ij}, \end{aligned}$$

(A.16)

where the diffusion moduli are defined by

$$\begin{aligned} \begin{aligned} D^{\mu \mu }&= \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \mu }, \\ D_{ij}^{\mu \mathbf{u}}&= \left[ \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{aa}} \, \delta _{kl} \, {\mathbb {C}}_{klmn} - \dfrac{\dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \left( \dfrac{\partial f}{\partial \sigma _{cd}} {\mathbb {C}}_{cdmn} + \dfrac{\frac{1}{3} \, V_{\mathrm {M}} \, K}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \sigma _{bb}} \, \dfrac{\partial f}{\partial \sigma }_{cd} \, {\mathbb {C}}_{cdeg} \, \delta _{eg} \, \delta _{mn} \right) }{\dfrac{\partial f}{\partial \sigma _{op}} \, {\mathbb {C}}_{opqr} \, \dfrac{\partial f}{\partial \sigma _{qr}} - \dfrac{\partial f}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} + \dfrac{\frac{1}{3} \, V_{\mathrm {M}}}{1+\frac{1}{3} \, V_{\mathrm {M}} \, {\bar{C}}_{\mathrm {T}}} \, \dfrac{\partial {\bar{C}}_{\mathrm {T}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \, \dfrac{\partial f}{\partial \sigma _{st}} \, {\mathbb {C}}_{stvw} \, \delta _{vw} } \right] \frac{1}{2} \left( \delta _{im} \,\delta _{jn} + \delta _{in} \,\delta _{jm} \right) . \end{aligned} \end{aligned}$$

(A.17)

1.2 The interface/cohesive model

The contributions of the interface material to the global residual vectors in Eqs. (30) and (34) are

$$\begin{aligned} R_{I}^{\mu }&= \dfrac{1}{\varDelta t} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \left( {\bar{C}}_{\mathrm {int}}^{p+1} -{\bar{C}}_{\mathrm {int}}^{p} \right) \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, {\bar{J}}_{\mathrm {int}} \, \mathrm {d}S, \nonumber \\ R_{iI}^{\mathbf{u}}&= \int \limits _{\varGamma _{\mathrm {int}}} B_{I}^{\mathrm {int}} \, T_{i}^{\mathrm {int}} \, \mathrm {d}S, \end{aligned}$$

(A.18)

where node I belongs to $\varGamma _{\mathrm {int}}$ (i.e. $I \in \varGamma _{\mathrm {int}}$), the surface $\varGamma _{\mathrm {int}}$ defines the interface region and $T_{i}^{\mathrm {int}} = t_{i}^{\mathrm {int}}$. The total concentration ${\bar{C}}_{\mathrm {int}}$ and the traction $T_{i}^{\mathrm {int}}$ are obtained using the cohesive model in Sect. 4.2 and the details of the processes will be discussed later in the subsequent subsections. Similarly, the linearisation of the residuals in Eqs. (A.18) yields

$$\begin{aligned} K_{IJ}^{\mu \mu }&= \dfrac{1}{\varDelta t} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, {\tilde{D}}^{\mu \mu } \, N_{J}^{\mathrm {int}} \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, \dfrac{\partial {\bar{J}}_{\mathrm {int}}}{\partial \mu } \, N_{J}^{\mathrm {int}} \, \mathrm {d}S, \nonumber \\ K_{jIJ}^{\mu \mathbf{u}}&= \dfrac{1}{\varDelta t} \, \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, {\tilde{D}}^{\mu \mathbf{u}}_{j} \, B_{J}^{\mathrm {int}} \, \mathrm {d}S - \int \limits _{\varGamma _{\mathrm {int}}} N_{I}^{\mathrm {int}} \, \dfrac{\partial {\bar{J}}_{\mathrm {int}}}{\partial u_{j}} \, N_{J}^{\mathrm {int}} \, \mathrm {d}S, \nonumber \\ K_{iIJ}^{\mathbf{u}\mu }&= \int \limits _{\varGamma _{\mathrm {int}}} B_{I}^{\mathrm {int}} \, {\tilde{D}}_{i}^{\mathbf{u}\mu } \, N_{J}^{\mathrm {int}} \, \mathrm {d}S, \nonumber \\ K_{ijIJ}^{\mathbf{u}\mathbf{u}}&= \int \limits _{\varGamma _{\mathrm {int}}} B_{I}^{\mathrm {int}} \, {\tilde{D}}_{ij}^{\mathbf{u}\mathbf{u}} \, B_{J}^{\mathrm {int}} \, \mathrm {d}S, \end{aligned}$$

(A.19)

where ${\tilde{D}}^{\mu \mu }$, ${\tilde{D}}_{j}^{\mu \mathbf{u}}$, ${\tilde{D}}_{i}^{\mathbf{u}\mu }$, and ${\tilde{D}}_{ij}^{\mathbf{u}\mathbf{u}}$ are the tangent moduli of the interface that can be determined from the variation of the total hydrogen concentration and the traction.

1.2.1 The interface concentration and traction

The chemical potential and the tractions at the interface are defined in Eqs. (60), (61) and (65). Using these equations, a set of equations in the incremental forms of the concentration and tractions, at a given values of $\varDelta \delta _{n}$, $\varDelta \delta _{t}$ and $\mu$, can be written as

$$\begin{aligned} \begin{aligned} F_{\mu }&= \mu _{\mathrm {int}} - \mu _{0} - W_{\mathrm {int}} - \mu _{T} - R \, T \, \ln \dfrac{{\bar{C}}_{\mathrm {int}}^{p+1} }{ {\bar{C}}_{\mathrm {int}}^{\mathrm {max}} - {\bar{C}}_{\mathrm {int}}^{p+1}}, \\ F_{t}&= \varDelta T_{t}^{\mathrm {int}} - \left( 1-d\right) \, K_{t} \, \varDelta \delta _{t}, \\ F_{n}&= \varDelta T_{n}^{\mathrm {int}} - \left( 1-d\right) \, K_{n} \, \varDelta \delta _{n}^{\mathrm {m}}, \end{aligned} \end{aligned}$$

(A.20)

where ${\bar{C}}_{\mathrm {int}}^{p+1}$ is the concentration at the end of the increment, i.e. ${\bar{C}}_{\mathrm {int}}^{p+1} = {\bar{C}}_{\mathrm {int}}^{p} + \varDelta {\bar{C}}_{\mathrm {int}}$. The increment of the normal separation $\varDelta \delta _{n}$ is decomposed into mechanical and jacking components as

$$\begin{aligned} \varDelta \delta _{n} = \varDelta \delta _{n}^{\mathrm {s}} + \varDelta \delta _{n}^{\mathrm {m}}, \end{aligned}$$

(A.21)

where the increment of the jacking separation is $\varDelta \delta _{n}^{\mathrm {s}}$. In order to solve these equations, we encapsulate the equations in a vector $\mathbf{F}=\left[ F_{\mu } \quad F_{t} \quad F_{n} \right] ^{\mathrm {T}}$ and define the unknown vector $\varDelta \mathbf{T}=\left[ \varDelta {\bar{C}}_{\mathrm {int}} \quad \varDelta T_{t}^{\mathrm {int}} \quad \varDelta T_{n}^{\mathrm {int}} \right] ^{\mathrm {T}}$. Using Newton–Raphson algorithm, the following linearised form of these equations is iteratively solved for the traction increment $\delta \varDelta \mathbf{T}$ until a convergence condition is achieved

$$\begin{aligned} \mathbf{F}\left( \varDelta \mathbf{T}+ \delta \varDelta \mathbf{T}\right) = \mathbf{F}\left( \varDelta \mathbf{T}\right) + \underbrace{\dfrac{\partial \mathbf{F}}{\partial \varDelta \mathbf{T}}}_{\mathbf{J}} \, \delta \varDelta \mathbf{T}+ \mathbf{O}\left( \delta \varDelta \mathbf{T}\cdot \delta \varDelta \mathbf{T}\right) \end{aligned}$$

(A.22)

where ${\mathbf {0}}$ is a zeros vector ($3 \times 1$) and the Jacobian $\mathbf{J}$ is defined as

$$\begin{aligned} \mathbf{J}= \left[ \begin{array}{lll} \dfrac{\partial F_{\mu }}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta T_{n}^{\mathrm {int}}} \\ \dfrac{\partial F_{t}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{t}}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{t}}{\partial \varDelta T_{n}^{\mathrm {int}}} \\ \dfrac{\partial F_{n}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{n}}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{n}}{\partial \varDelta T_{n}^{\mathrm {int}}} \end{array} \right] \end{aligned}$$

(A.23)

where the derivatives are determined from Eq. (A.20) as

$$\begin{aligned} \begin{aligned} \dfrac{\partial F_{\mu }}{\partial \varDelta \bar{C}_{\mathrm {int}}}&= - \dfrac{\bar{C}_{\mathrm {int}} ^{\mathrm {max}}}{\bar{C}_{\mathrm {int}}^{p+1}} \, \dfrac{R \, T}{ \bar{C}_{\mathrm {int}} ^{\mathrm {max}} - \bar{C}_{\mathrm {int}}^{p+1}}, \\ \dfrac{\partial F_{\mu }}{\partial \varDelta T_{t} ^{\mathrm {int}}}&= 0, \quad \dfrac{\partial F_{\mu }}{\partial \varDelta T_{n}^{\mathrm {int}}} = V_{\mathrm {M}}^{\mathrm {int}},\\ \dfrac{\partial F_{t}}{\partial \varDelta \bar{C}_{\mathrm {int}}}&= K_{t} \, \dfrac{\partial d}{\partial \varDelta \bar{C} _{\mathrm {int}}} \, \varDelta \delta _{t} , \quad \dfrac{\partial F_{t}}{\partial \varDelta T_{t} ^{\mathrm {int}}} = 1, \\ \dfrac{\partial F_{t}}{\partial \varDelta T_{n}^{\mathrm {int}}}&= 0,\\ \dfrac{\partial F_{n}}{\partial \varDelta \bar{C} _{\mathrm {int}}}&= K_{n} \, \dfrac{\partial d}{\partial \varDelta \bar{C}_{\mathrm {int}}} \, \varDelta \delta _{n}^{\mathrm {m}} + K_{n} \, \left( 1-d \right) \, V_{\mathrm {M}}^{\mathrm {int}}, \quad \dfrac{\partial F_{n}}{\partial \varDelta T_{t} ^{\mathrm {int}}} = 0, \\ \dfrac{\partial F_{n}}{\partial \varDelta T_{n}^{\mathrm {int}}}&= 1. \end{aligned} \end{aligned}$$

(A.24)

Using the definitions of the cohesive model in Eqs. (55) and (57), the different derivatives in Eq. (A.24) are

$$\begin{aligned} \dfrac{\partial d}{\partial \varDelta {\bar{C}}_{\mathrm {int}}}&= - V_{\mathrm {M}}^{\mathrm {int}} \, \dfrac{\partial d}{\partial \varDelta \delta _{n}^{\mathrm {m}}}, \quad \dfrac{\partial \varDelta \delta _{n}^{\mathrm {s}}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} = V_{\mathrm {M}}^{\mathrm {int}}, \nonumber \\ \dfrac{\partial \varDelta \delta _{n}^{\mathrm {s}}}{\partial \varDelta \delta _{n}^{\mathrm {m}}}&= -1. \end{aligned}$$

(A.25)

1.2.2 The cohesive zone Jacobian

The variation of the hydrogen concentration at the interface is defined by

$$\begin{aligned} \dot{{\bar{C}}}_{\mathrm {int}} = \dfrac{\partial {\bar{C}}_{\mathrm {int}}}{\partial \mu _{\mathrm {int}}} \, {\dot{\mu }} + \dfrac{\partial {\bar{C}}_{\mathrm {int}}}{\partial \delta _{i}} \, {\dot{\delta }}_{i}, \end{aligned}$$

(A.26)

where the diffusion moduli in Eqs. (A.2) are defined by

$$\begin{aligned} {\tilde{D}}^{\mu \mu } = \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \text {and} \quad {\tilde{D}}_{i}^{\mu \mathbf{u}} = \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \delta _{i}}. \end{aligned}$$

(A.27)

The variation of the traction at the interface is defined by

$$\begin{aligned} {\dot{T}}_{i}^{\mathrm {int}} = \dfrac{\partial T_{i}^{\mathrm {int}}}{\partial \mu _{\mathrm {int}}} \, {\dot{\mu }} + \dfrac{\partial T_{i}^{\mathrm {int}}}{\partial \delta _{j}} \, {\dot{\delta }}_{j}, \end{aligned}$$

(A.28)

where the deformation moduli in Eqs. (A.2) are defined by

$$\begin{aligned} \tilde{D}^{\mathbf{u}\mu } = \dfrac{\partial \varDelta T_{i}^{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \text {and} \quad \tilde{D}_{ij}^{\mathbf{u}\mathbf{u}} = \dfrac{\partial \varDelta T_{i}^{\mathrm {int}}}{\partial \varDelta \delta _{j}}. \end{aligned}$$

(A.29)

The elements of the tangent moduli can be determined from the variations of the incremental forms in Eqs. (A.20). The variation of $F_{i}$ is given by

$$\begin{aligned} \delta F_{i} = \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \mu _{\mathrm {int}}} \, \delta \varDelta \mu _{\mathrm {int}} + \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \delta _{t}} \, \delta \varDelta \delta _{t} + \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \delta _{n}} \, \delta \varDelta \delta _{n}, \end{aligned}$$

(A.30)

where $\mathrm {d} F_{i}/ \mathrm {d} \varDelta \delta _{j}$ denotes the total derivative of the function $F_{i}$ with respect to $\varDelta \delta _{j}$ in the unknown vector $\varDelta {\varvec{\delta }}=\left[ \varDelta \mu _{\mathrm {int}} \quad \varDelta \delta _{t} \quad \varDelta \delta _{n} \right] ^{\mathrm {T}}$, the variations of the separation increments $\delta \varDelta \mu _{\mathrm {int}}$, $\delta \varDelta \delta _{t}$ and $\delta \varDelta \delta _{n}$ can be chosen arbitrarily yielding ${\mathrm {d} F_{i}}/{\mathrm {d} \varDelta \mu _{\mathrm {int}}} = {\mathrm {d} F_{i}}/{\mathrm {d} \varDelta \delta _{t}} = {\mathrm {d} F_{i}}/{\mathrm {d} \varDelta \delta _{n}} = 0$. Hence, the variations of Eqs. (A.20) give 9 set of equations. Therefore, the variations of $F_{i}$ in Eqs. (A.30) yield

$$\begin{aligned} \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \mu _{\mathrm {int}}}&= \dfrac{\partial F_{i}}{\partial \varDelta \mu _{\mathrm {int}}} + \dfrac{\partial F_{i}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} \, \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} + \dfrac{\partial F_{i}}{\partial \varDelta T_{t}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \nonumber \\&\quad + \dfrac{\partial F_{i}}{\partial \varDelta T_{n}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} = 0,\nonumber \\ \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \delta _{t}}&= \dfrac{\partial F_{i}}{\partial \varDelta \delta _{t}} + \dfrac{\partial F_{i}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} \, \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \delta _{t}} + \dfrac{\partial F_{i}}{\partial \varDelta T_{t}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \delta _{t}} \nonumber \\&\quad +\dfrac{\partial F_{i}}{\partial \varDelta T_{n}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \delta _{t}} = 0,\nonumber \\ \dfrac{\mathrm {d} F_{i}}{\mathrm {d} \varDelta \delta _{n}}&= \dfrac{\partial F_{i}}{\partial \varDelta \delta _{n}} + \dfrac{\partial F_{i}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} \, \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \delta _{n}} + \dfrac{\partial F_{i}}{\partial \varDelta T_{t}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \delta _{n}} \nonumber \\&\quad +\dfrac{\partial F_{i}}{\partial \varDelta T_{n}^{\mathrm {int}}} \, \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \delta _{n}} = 0. \end{aligned}$$

(A.31)

Thus, the unknown derivatives in Eqs. (A.31) can be written in vector form as

$$\begin{aligned} \begin{aligned} \mathbf{X}=&\left[ \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \delta _{t}} \quad \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \delta _{t}} \right. \\&\left. \ \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \delta _{t}} \quad \dfrac{\partial \varDelta {\bar{C}}_{\mathrm {int}}}{\partial \varDelta \delta _{n}} \quad \dfrac{\partial \varDelta T_{t}^{\mathrm {int}}}{\partial \varDelta \delta _{n}} \quad \dfrac{\partial \varDelta T_{n}^{\mathrm {int}}}{\partial \varDelta \delta _{n}} \right] ^{\mathrm {T}} \end{aligned} \end{aligned}$$

(A.32)

Table 2 Analogy of variables between heat transfer and diffusion analysis in Abaqus

Hence, the unknown derivatives can be determined by solving the following set of equations

$$\begin{aligned} {\varvec{\varLambda }} \, \mathbf{X}= \mathbf{b}, \end{aligned}$$

(A.33)

where

$$\begin{aligned} {\varvec{\varLambda }}&= \left[ \begin{array}{lll} \mathbf{A}&{} \quad \mathbf{O}&{} \quad \mathbf{O}\\ \mathbf{O}&{} \quad \mathbf{A}&{} \quad \mathbf{O}\\ \mathbf{O}&{} \quad \mathbf{O}&{} \quad \mathbf{A}\\ \end{array} \right] , \quad \mathbf{A}= \left[ \begin{array}{lll} \dfrac{\partial F_{\mu }}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta T_{n}^{\mathrm {int}}} \\ \dfrac{\partial F_{t}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{t}}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{t}}{\partial \varDelta T_{n}^{\mathrm {int}}} \\ \dfrac{\partial F_{n}}{\partial \varDelta {\bar{C}}_{\mathrm {int}}} &{} \quad \dfrac{\partial F_{n}}{\partial \varDelta T_{t}^{\mathrm {int}}} &{} \quad \dfrac{\partial F_{n}}{\partial \varDelta T_{n}^{\mathrm {int}}} \\ \end{array} \right] , \nonumber \\ \mathbf{b}&= \left[ \dfrac{\partial F_{\mu }}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial F_{t}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial F_{n}}{\partial \varDelta \mu _{\mathrm {int}}} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta \delta _{t}} \quad \dfrac{\partial F_{t}}{\partial \varDelta \delta _{t}} \right. \nonumber \\&\left. \quad \ \dfrac{\partial F_{n}}{\partial \varDelta \delta _{t}} \quad \dfrac{\partial F_{\mu }}{\partial \varDelta \delta _{n}} \quad \dfrac{\partial F_{t}}{\partial \varDelta \delta _{n}} \quad \dfrac{\partial F_{n}}{\partial \varDelta \delta _{n}}\right] ^{\mathrm {T}}, \end{aligned}$$

(A.34)

$\mathbf{O}$ is a zeros matrix ($3 \times 3$), the derivatives in $\mathbf{A}$ are given in Eqs. (A.24) and $\mathbf{b}$ are determined from Eqs. (A.20) as

$$\begin{aligned} \begin{aligned} \dfrac{\partial F_{\mu }}{\partial \varDelta \mu _{\mathrm {int}}}&= 1, \quad \dfrac{\partial F_{\mu }}{\partial \varDelta \delta _{t}} = 0, \quad \dfrac{\partial F_{\mu }}{\partial \varDelta \delta _{n}} = 0,\\ \dfrac{\partial F_{t}}{\partial \varDelta \mu _{\mathrm {int}}}&= 0, \quad \dfrac{\partial F_{t}}{\partial \varDelta \delta _{t}} = -\left( 1-d \right) K_{t}, \\ \dfrac{\partial F_{t}}{\partial \varDelta \delta _{n}}&= \dfrac{\partial d}{\partial \varDelta \delta _{n}^{\mathrm {m}}} \, K_{t} \, \varDelta \delta _{t},\\ \dfrac{\partial F_{n}}{\partial \varDelta \mu _{\mathrm {int}}}&= 0, \quad \dfrac{\partial F_{n}}{\partial \varDelta \delta _{t}} = 0, \\ \dfrac{\partial F_{n}}{\partial \varDelta \delta _{n}}&= -\left( 1-d \right) K_{n} + \dfrac{\partial d}{\partial \varDelta \delta _{n}^{\mathrm {m}}} \, K_{n} \, \varDelta \delta _{n}. \end{aligned} \end{aligned}$$

(A.35)

The Finite Element implementation of coupled mechanical/diffusion framework in Abaqus

In this appendix, we present the implementations of the hydrogen transport, elastic–plastic and interface/cohesive models in Sect. 4 and “Appendix A”.

1.1 The hydrogen diffusion Model

The hydrogen transport equations are implemented using Finite Element Method using Abaqus [15]. We use the similarities with the heat equation as discussed in Oh and Kim [21] and Barrera et al. [14]. In these studies, taking advantage of the similar forms of heat and diffusion equations, the temperature T in the heat equation is replaced by the total concentration ${\bar{C}}_{\mathrm {T}}$ which yields the diffusion equation. This formulation requires the evaluation of the gradient of the stress tensor, i.e. substitution of Eqs. (50) or (51) into Eq. (5) yields a term that contains $\nabla \sigma _{\mathrm {h}}$. Hence, the Finite Element interpolation functions and its first derivative should exist and be continuous, i.e. ${\mathcal {C}}_{1}$. In other words, at least quadratic shape functions are needed in order for the gradient of the stress tensor to exist. Moreover, the determination of this gradient is not straight forward. In this study, we propose an alternative formulation in which we consider the chemical potential to be the degree of freedom in the diffusion equation. We summarize the analogy of variables between the heat transfer analysis and hydrogen diffusion analysis within Abaqus in Table B.1. The user subroutine UMATHT is used to implement the hydrogen diffusion model. In coupled thermo-mechanics analysis, the deformation related variables, i.e. $\sigma _{\mathrm {h}}$ and $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$, are passed to UMATHT using other user subroutines. The details of passing these variables are explained later in subsequent subsections. In UMATHT, the terms result from the weak form of the heat equation and its variation should be provided. In particular, the internal energy $U_{\mathrm {q}}$, flux $\mathbf{J}_{\mathrm {q}}$ and their derivatives with respect to the temperature and temperature gradient, i.e. $\partial U_{\mathrm {q}}/\partial T$, $\partial U_{\mathrm {q}}/\partial \nabla T$, $\partial \mathbf{J}_{\mathrm {q}}/\partial T$, $\partial \mathbf{J}_{\mathrm {q}}/\partial \nabla T$, have to be defined. Table B.2 shows the analogy between these quantities for the heat and diffusion problems. The total hydrogen concentration can be expressed in terms of the chemical potential $\mu$ and the trap density ${\bar{N}}_{\mathrm {D}}\big ( \varepsilon _{\mathrm {e}}^{\mathrm {pl}} \big )$. Further, the variation of the hydrogen flux with respect to the chemical potential $\mu$ and its gradient $\nabla \mu$ is required. Thus, the variation of the hydrogen concentration is given in Eqs. (A.16) and (A.17), and the variation of the hydrogen flux is

$$\begin{aligned} \dfrac{\partial {\bar{J}}_{i}^{\mathrm {m}}}{\partial \mu } = -\dfrac{D_{\mathrm {L}}}{R \, T} \, \dfrac{\partial {\bar{C}}_{\mathrm {L}}}{\partial \mu } \, \dfrac{\partial \mu }{\partial X_{i}} \quad \text {and} \quad \dfrac{\partial {\bar{J}}_{i}^{\mathrm {m}}}{\partial \left( \partial \mu / \partial X_{j} \right) } = -\dfrac{D_{\mathrm {L}} \, {\bar{C}}_{\mathrm {L}}}{R \, T} \, \delta _{ij}, \end{aligned}$$

(B.1)

It should be noted that the hydrostatic stress $\sigma _{\mathrm {h}}$ and effective plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ are passed into the UMATHT using other user subroutines. In the next section, the details of this procedure is presented

Table 3 Quantities that need to defined in the UMATHT in Abaqus

1.2 The elastic–plastic Model

The elastic–plastic model in “Appendix A” can be implemented in Abaqus code using two different user subroutines that are - UHARD and UMAT. In UHARD, the stress integration and the consistent tangent modulus are determined by Abaqus. Derivatives of the yield stress should be provided. In UMAT, the stress integration and the consistent tangent modulus should be provided. It should be mentioned that UHARD is limited to the case of no swelling.

1.2.1 Implementation of the model as an Abaqus UHARD subroutine

In UHARD, the derivatives of the hardening function that are required to evaluate the stress and its variation should be provided. Thus, the variation of the flow stress in Eq. (A.8) can be written as follows

$$\begin{aligned} {\dot{\sigma }}_{\mathrm {y}} = \dfrac{\partial \sigma _{\mathrm {y}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}} \, {\dot{\varepsilon }}_{\mathrm {e}}^{\mathrm {pl}} + \dfrac{\partial \sigma _{\mathrm {y}}}{\partial \mu } \, {\dot{\mu }}. \end{aligned}$$

(B.2)

Consider the power law hardening function in Sect. 5 with the form

$$\begin{aligned} \sigma _{\mathrm {y}} = \sigma _{0}^{\mathrm {H}} \left( 1+\dfrac{\varepsilon _{\mathrm {e}}^{\mathrm {pl}}}{\varepsilon _{0}}\right) ^{\frac{1}{n}}, \end{aligned}$$

(B.3)

where the initial yield $\sigma _{0}^{\mathrm {H}}$ is taken to be a function of the hydrogen concentraion by $\sigma _{0}^{\mathrm {H}} = \varPsi \left( {\bar{C}}_{\mathrm {L}}\right) \, \sigma _{0}$ and $\varPsi$ is a monotonically decreasing function of hydrogen concentration in the lattice. Therefore, the derivatives for the power law are

$$\begin{aligned} \begin{aligned} \dfrac{\partial \sigma _{\mathrm {y}}}{\partial \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}&= \dfrac{\sigma _{0}^{\mathrm {H}}}{n \, \varepsilon _{0}} \left( 1+\dfrac{ \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}{ \varepsilon _{0}}\right) ^{\frac{1-n}{n}}, \\ \dfrac{\partial \sigma _{\mathrm {y}}}{\partial \mu }&= \dfrac{\partial \sigma _{0}^{\mathrm {H}}}{\partial \mu } \left( 1+\dfrac{ \varepsilon _{\mathrm {e}}^{\mathrm {pl}}}{ \varepsilon _{0}}\right) ^{n}, \\ \dfrac{\partial \sigma _{0}^{\mathrm {H}}}{\partial \mu }&= \sigma _{0} \, \varPsi ' \, \dfrac{\partial {\bar{C}}_{\mathrm {L}}}{\partial \mu }. \end{aligned} \end{aligned}$$

(B.4)

The hydrostatic stress $\sigma _{\mathrm {h}}$ and effective plastic strain $\varepsilon _{\mathrm {e}}^{\mathrm {pl}}$ are passed to UMATHT as solution dependent variables at the start of the increment. We use USDFLD subroutine, which allows different field variables to be defined at a material point as a function of time, to obtain the hydrostatic stress and effective plastic strain, and store solution dependent variables (Barrera et al. [14]). More specifically, in USDFLD, the stress field and effective plastic strain are determined at a material point at the start of the increment using utility subroutine GETVRM. The hydrostatic stress is then evaluated using the normal stress components, i.e. $\sigma _{\mathrm {h}} = \sigma _{kk}/3$, and together with effective plastic strain are stored into solution dependent variables.

Fig. 18

The two-dimensional linear cohesive element i the physical domain and the definition of the local and global coordinates and ii the parent domain

1.2.2 Implementation of the model as an Abaqus UMAT subroutine

The implementation of the elastic–plastic model using UMAT subroutine requires the determination of stress and the consistent tangent modulus at the end of increment. In particular, the rate tangent required by UMAT takes the form

$$\begin{aligned} {\mathbb {C}}_{ijkl}^{\mathrm {UMAT}} = {\mathbb {C}}_{ijkl}^{\mathrm {pl}} + \sigma _{ij} \, \delta _{kl}, \end{aligned}$$

(B.5)

which is the rate tangent for the Jaumann derivative of Kirchhoff stress that is scaled by the Jacobian of the deformation. Hence, the stress and the mechanical and chemical tangent moduli ${\mathbb {C}}_{ijkl}^{\mathrm {UMAT}}$ and $D_{i}^{\mu \mathbf{u}}$, respectively, should be provided in the UMAT subroutine.

1.3 The cohesive/interface zone Model

The interface model in Sect. 4.2 and “Appendix A”, is implemented into the Finite Element method using a cohesive element approach and UEL subroutine. The surface-like cohesive formulation is adopted in this work (e.g. see [41, 42, 43, 44]). In this formulation, a cohesive element consists of two surface elements which coincide in the reference configuration. A 4-node two-dimensional linear element is used in this study following the formulation by Elmukashfi and Cocks [45]. The element upper and lower surface elements are denoted $S^{+}$ and $S^{-}$, respectively, see Fig. B.1. The constitutive behaviour of the cohesive element is defined in the middle surface, ${\bar{S}}$. The middle surface is defined by the two points 1 and 2 which are the mid-points between nodes $1^{-}-1^{+}$ and $2^{-}-2^{+}$, respectively. Hence, the middle surface is then defined by the interpolation

$$\begin{aligned} \bar{x}_{i}^{\mathrm {int}} = \sum \limits _{I=1}^{2} N_{I}^{\mathrm {int}} \, \bar{x}_{iI}^{\mathrm {int}}, \end{aligned}$$

(B.6)

where $\bar{x}_{iI}^{\mathrm {int}}$ is the current coordinates vector of the middle surface which is related to the current nodal coordinates of the upper and lower surface elements $x_{iI}^{+}$ and $x_{iI}^{-}$, respectively, by

$$\begin{aligned} \bar{x}_{iI}^{\mathrm {int}} = \frac{1}{2} \left( x_{iI}^{+} + x_{iI}^{-} \right) , \end{aligned}$$

(B.7)

The standard shape functions, $N_{I}^{\mathrm {int}}$, are defined in the local coordinates, $\xi \in \left[ -1, 1\right]$, as

$$\begin{aligned} N_{1}^{\mathrm {int}} = \frac{1}{2} \left( 1 - \xi \right) \quad \text {and} \quad N_{2}^{\mathrm {int}} = \frac{1}{2} \left( 1 + \xi \right) . \end{aligned}$$

(B.8)

Similarly, the global displacement, $\bar{u}_{i} ^{\mathrm {int}}$, and chemical potential, $\bar{\mu } _{\mathrm {int}}$, chemical potential jumps across the cohesive element, are defined as

$$\begin{aligned} \bar{u}_{i}^{\mathrm {int}} = \sum \limits _{I=1}^{2} N_{I}^{\mathrm {int}} \bar{u}_{iI}^{\mathrm {int}} \quad \text {and} \quad \bar{\mu }_{\mathrm {int}} = \sum \limits _{I=1}^{2} N_{I}^{\mathrm {int}} \bar{\mu }_{I} ^{\mathrm {int}}, \end{aligned}$$

(B.9)

where $\bar{u}_{iI}^{\mathrm {int}}$ and $\bar{\mu }_{I}^{\mathrm {int}}$ are the displacement jumps and chemical potential of the middle surface which are respectively related to the nodal displacement and chemical potential by

$$\begin{aligned} \begin{aligned} {\bar{u}}_{iI}^{\mathrm {int}}&= M_{I} \, u_{iI} = u_{iI}^{+} - u_{iI}^{-}, \quad \text {and} \\ {\bar{\mu }}_{I}^{\mathrm {int}}&= H_{I} \, \mu _{I} = \frac{1}{2} \left( \mu _{I}^{+} +\mu _{I}^{-} \right) , \end{aligned} \end{aligned}$$

(B.10)

where the multipliers $M_{I}$ and $H_{I}$ are introduced in Sect. 3.4. It should be mentioned that $H_{I}$ is chosen such that the chemical potential is continuous across the interface, i.e. Eq. (9) , and ${u}_{i}^{\mathrm {int}} = \varDelta u_{i} ^{\mathrm {int}}$ in Eq. (14).

The internal nodal forces and the consistent tangent stiffness matrices across the cohesive surface are determined from the tractions and chemical potential are detailed in the previous sections. In particular, the finite element formulation is detailed in Sect. 3, the interface model is given in Sect. 4.2 and the determination of the nodal forces and the stiffness matrix are illustrated in “Appendix” A.