Fracture simulation of viscoelastic polymers by the phase-field method

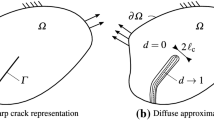
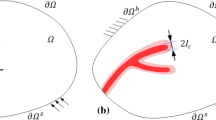
Abstract

The phase-field model has been employed for fracture analysis over the last decade. One of the main advantages is that the fracture evolution does not depend on any explicit criterion. Good agreement is obtained by comparing the results of simulations and experiments. Most elastomers exhibit both elastic and viscous behavior simultaneously, which yields rate-dependent properties for both the mechanical and fracture responses. In this contribution, a viscoelastic rheological model based on Reese and Govindjee (Int J Solids Struct 35:3455–3482, 1998) is coupled to phase-field modeling to investigate rate-dependent fracture within elastomers. The elastic strain energy potential supposed to evolve fracture is provided by both the equilibrium and non-equilibrium branches. The fracture mechanism is characterized by a volumetric–isochoric split, which specifies a varying driving force in the case of tensile or compressive deformation. Representative numerical examples are studied and related findings and potential perspectives are summarized to close the paper.

Appendices

Appendix A: Derivation of the tangent ${\mathscr {K}}_{ab}$ for the local Newton iteration

By linearization of Eq. (19), the local tangent ${\mathscr {K}}_{ab}$ is derived as

$$\begin{aligned} {\mathscr {K}}_{ab}= & {} -\delta _{\varepsilon _{b}^{e}}\,{\mathscr {R}}_{a}\nonumber \\= & {} -\left( \delta _{ab} + \eta _{0}\,\varDelta t\cdot \,\delta _{{\bar{\tau }}_{c}^{ne}}\,\text {dev} \left( {\bar{\tau }}_{a}^{ne}\right) \cdot \delta _{\varepsilon _{b}^{e}}{\bar{\tau }}_{c}^{ne} \right) , \end{aligned}$$

(37)

where ${\bar{\tau }}_{a}^{ne}$ is obtained by ${\bar{\tau }}_{a}^{ne}=2\,\delta _{{\bar{I}}_{1}^{e}} {\bar{\varPhi }}^{ne}\cdot {\bar{\lambda }}_{a}^{e^{2}}$. In order to achieve further simplifications, defining ${\mathscr {T}}_{ab}$ as

$$\begin{aligned} {\mathscr {T}}_{ab}=\delta _{\varepsilon _{b}^{e}}{\bar{\tau }}_{a}^{ne} =4\,\delta _{{\bar{I}}_{1}^{e}}{\bar{\varPhi }}^{ne} \cdot {\bar{\lambda }}_{a}^{e}\,{\bar{\lambda }}_{b}^{e}\,\delta _{ab} +4\delta ^{2}_{{\bar{I}}_{1}^{e}}{\bar{\varPhi }}^{ne}\cdot \, {\bar{\lambda }}_{a}^{e^{2}}{\bar{\lambda }}_{b}^{e^{2}}\nonumber \\ \end{aligned}$$

(38)

and employing the operator $\bar{{\mathscr {T}}}_{ab}={\mathscr {T}}_{ab}-\frac{1}{3}\sum ^{3}_{c=1} {\mathscr {T}}_{cb}$, the local stiffness ${\mathscr {K}}_{ab}$ in Eq. (37) consequently yields

$$\begin{aligned} {\mathscr {K}}_{ab}=-\left( \delta _{ab} + \eta _{0}\,\varDelta t\, \bar{{\mathscr {T}}}_{ab}\right) . \end{aligned}$$

(39)

Thus, the framework in Table. 1 can be conducted.

Appendix B: Derivation of the consistent Eulerian tangent

Knowing the Kirchhoff stresses in Sect. 2.1, the consistent Eulerian tangent moduli are derived. The volumetric tangent is obtained straightforwardly as

$$\begin{aligned} {\mathbb {C}}_{vol}=\left( J\,p+J^{2}\,s\right) {\mathbf {1}}\otimes {\mathbf {1}}-2Jp\,{\mathbb {I}}, \end{aligned}$$

(40)

where $s=U''\left( J \right)$. The fourth order identity tensor is defined by ${\mathbb {I}}_{abcd}=\frac{1}{2}\left( \delta _{ac}\delta _{bd}+\delta _{ad}\delta _{bc}\right)$. The isochoric tangents are

$$\begin{aligned} {\mathbb {C}}_{iso}^{eq}= & {} {\mathbb {P}}:\bar{{\mathbb {C}}}_{iso}^{eq}: {\mathbb {P}}\nonumber \\&+\frac{2}{3} \Big ( \left( \bar{\varvec{\tau }}^{eq} :{\mathbf {1}}\right) {\mathbb {P}}- \varvec{\tau }^{eq}_{iso} \otimes {\mathbf {1}} - {\mathbf {1}}\otimes \varvec{\tau }^{eq}_{iso} \Big ) \end{aligned}$$

(41)

and

$$\begin{aligned} {\mathbb {C}}_{iso}^{ne}= & {} {\mathbb {P}}:\bar{{\mathbb {C}}}_{iso}^{ne}: {\mathbb {P}}\nonumber \\&+\frac{2}{3} \Big ( \left( \bar{\varvec{\tau }}^{ne} :{\mathbf {1}}\right) {\mathbb {P}}- \varvec{\tau }^{ne}_{iso} \otimes {\mathbf {1}} - {\mathbf {1}}\otimes \varvec{\tau }^{ne}_{iso} \Big ), \end{aligned}$$

(42)

respectively. The terms $\varvec{\tau }^{eq}_{iso}$, $\bar{\varvec{\tau }}^{eq}$, $\varvec{\tau }^{ne}_{iso}$ and $\bar{\varvec{\tau }}^{ne}$ are already outlined in Eqs. (6) and (7). The isochoric tangent for the equilibrium branch in Eq. (41) is

$$\begin{aligned} \bar{{\mathbb {C}}}_{iso}^{eq}=4\, \bar{{\mathbf {b}}}\cdot \delta ^{2}_{\bar{{\mathbf {b}}}} {\bar{\varPhi }}_{iso}^{eq}\cdot \bar{{\mathbf {b}}} \end{aligned}$$

(43)

according to [68]. Nevertheless, a closed form of $\bar{{\mathbb {C}}}_{iso}^{ne}$ in Eq. (42) cannot be derived straightforwardly, see [11] and [14]. Regarding the inelastic response, a fictitious intermediate configuration is assumed between the initial and current configuration, where the eigenvectors are denoted by $\tilde{{\mathbf {N}}}^{a}$ with $a=1,2,3$. The trial deformation tensor $\bar{{\mathbf {F}}}_{e}^{tr}$ describes the kinetic relations from the fictitious intermediate configuration to the current configuration, which reads

$$\begin{aligned} \bar{{\mathbf {F}}}_{e}^{tr}=\sum _{a=1}^{3}{\bar{\lambda }}_{a}^{e,tr} {\varvec{n}}^{a}\otimes \tilde{{\mathbf {N}}}^{a}. \end{aligned}$$

(44)

Hence, the second Piola-Kirchhoff stress tensor $\bar{{\mathbf {S}}}_{iso}^{ne}$ is obtained by a pull back operation as

$$\begin{aligned} \bar{{\mathbf {S}}}_{iso}^{ne}=\bar{{\mathbf {F}}}_{e}^{tr^{-1}}\, \bar{\varvec{\tau }}^{ne} \,\bar{{\mathbf {F}}}_{e}^{tr^{-T}}=\sum _{a=1}^{3}\frac{{\bar{\tau }}_{a}^ {ne}}{{\bar{\lambda }}_{a}^{e,tr^{2}}}\,\tilde{{\mathbf {N}}}_{a} \otimes \tilde{{\mathbf {N}}}_{a}. \end{aligned}$$

(45)

The consistent tangent modulus $\tilde{{\mathbb {C}}}_{iso}^{ne}$ in the intermediate configuration is

$$\begin{aligned} \tilde{{\mathbb {C}}}_{iso}^{ne}= & {} 2\,\delta _{\bar{{\mathbf {C}}}_{e}^{tr}} \bar{{\mathbf {S}}}_{iso}^{ne} =\sum _{a=1}^{3}\sum _{b=1}^{3}\frac{\zeta _{ab}-2\, {\bar{\tau }}_{a}^{ne}\,\delta _{ab}}{{\bar{\lambda }}_{a}^{e,tr^{2}}\, {\bar{\lambda }}_{b}^{e,tr^{2}}}\tilde{{\mathbb {M}}}^{ab}\nonumber \\&+ \sum _{a=1}^{3}\sum _{b\ne a}^{3} \frac{{\bar{\tau }}_{a}^{ne}/{\bar{\lambda }}_{a}^{e,tr^{2}} -{\bar{\tau }}_{b}^{ne}/{\bar{\lambda }}_{b}^{e,tr^{2}}}{{\bar{\lambda }}_{a}^{e,tr^{2}}-{\bar{\lambda }}_{b}^{e,tr^{2}}} \tilde{{\mathbb {G}}}^{ab}, \end{aligned}$$

(46)

with the definitions

$$\begin{aligned}&\tilde{{\mathbb {M}}}^{ab} = \tilde{{\mathbf {N}}}^{a}\otimes \tilde{{\mathbf {N}}}^{a}\otimes \tilde{{\mathbf {N}}}^{b}\otimes \tilde{{\mathbf {N}}}^{b}\,\,\,\,\,\,\text {and}\nonumber \\&\tilde{{\mathbb {G}}}^{ab} = \tilde{{\mathbf {N}}}^{a}\otimes \tilde{{\mathbf {N}}}^{b}\otimes \left( \tilde{{\mathbf {N}}}^{a}\otimes \tilde{{\mathbf {N}}}^{b}+\tilde{{\mathbf {N}}}^{b}\otimes \tilde{{\mathbf {N}}}^{a} \right) . \end{aligned}$$

(47)

In Eq. (46), the quantity ${\bar{\tau }}_{a}^{ne}$ is illustrated in “Appendix A” and $\zeta _{ab}$ is defined as

$$\begin{aligned} \zeta _{ab}=\delta _{\varepsilon _{b}^{e,tr}} {\bar{\tau }}_{a}^{ne}=\delta _{\varepsilon _{c}^{e}}{\bar{\tau }}_{a}^{ne} \cdot \delta _{\varepsilon _{b}^{e,tr}}\varepsilon _{c}^{e} ={\mathscr {T}}_{ac}\cdot \delta _{\varepsilon _{b}^{e,tr}}\varepsilon _{c}^{e}, \end{aligned}$$

(48)

where the term $\delta _{\varepsilon _{b}^{e,tr}}\varepsilon _{c}^{e}$ is not directly computed. Due to the condition $\delta _{\varepsilon _{b}^{e,tr}}r_{a}=0$, it holds

$$\begin{aligned} -\delta _{ab}-{\mathscr {K}}_{ac}\cdot \delta _{\varepsilon _{b}^{e,tr}} \varepsilon _{c}^{e}=0, \end{aligned}$$

(49)

which leads to $\delta _{\varepsilon _{b}^{e,tr}}\varepsilon _{c}^{e}=-{\mathscr {K}}_{cb}^{-1}$. Thus, according to Eq. (48), the coefficient $\zeta _{ab}=-{\mathscr {T}}_{ac}\,{\mathscr {K}}_{cb}^{-1}$ is obtained.

In case of singularity problems of Eq. (46), e.g. equal eigenvalues ${\bar{\lambda }}_{a} = {\bar{\lambda }}_{b}$, L’ Hospital’s rule is applied, which yields

$$\begin{aligned} \lim _{{\bar{\lambda }}_{b} \rightarrow {\bar{\lambda }}_{a}} \frac{{\bar{\tau }}_{a}^{ne}/{\bar{\lambda }}_{a}^{e,tr^{2}} -{\bar{\tau }}_{b}^{ne}/{\bar{\lambda }}_{b}^{e,tr^{2}}}{{\bar{\lambda }}_{a}^{e,tr^{2}}-{\bar{\lambda }}_{b}^{e,tr^{2}}} =\frac{1}{2}\frac{\zeta _{aa}-2\,{\bar{\tau }}_{a}^{ne}}{{\bar{\lambda }}_{a}^{e,tr^{4}}}. \end{aligned}$$

(50)

Consequently, the consistent tangent in current configuration is obtained by push-forward operation of $\tilde{{\mathbb {C}}}_{iso}^{ne}$, reading

$$\begin{aligned} \bar{{\mathbb {C}}}_{iso_{ijkl}}^{ne}= \bar{{\mathbf {F}}}_{e_{iI}}^{tr}\,\bar{{\mathbf {F}}}_{e_{jJ}}^{tr} \,\bar{{\mathbf {F}}}_{e_{kK}}^{tr}\,\bar{{\mathbf {F}}}_{e_{lL}}^{tr} \,\tilde{{\mathbb {C}}}_{iso_{IJKL}}^{ne}. \end{aligned}$$

(51)

Appendix C: Numerical implementation at the element level

Based on the strong forms of Eqs. (34) and (35), the weak forms for both the mechanical response and the phase-field evolution are obtained by multiplying virtual field quantities, e.g. $\delta {\varvec{u}}$ and $\delta d$, which are simplified as

$$\begin{aligned} \int _{\varOmega _{0}} \bigg \{ -\rho _{0}\,\ddot{{\varvec{u}}}\,\delta {\varvec{u}} - \Big ( g\left( d\right) \varvec{\tau }^{+} + \varvec{\tau }^{-} \Big ):\nabla _{{\varvec{x}}} \delta {\varvec{u}} \bigg \}dV=0 \end{aligned}$$

(52)

and

$$\begin{aligned}&\int _{\varOmega _{0}} \bigg \{ -g'\left( d\right) \varPhi _{0}^{+}\,\delta d - \frac{{\mathcal {G}}_{c}}{l} d\, \delta d - \chi \frac{d-d^{n}}{\varDelta t} \, \delta d \nonumber \\&\qquad \qquad -\, {\mathcal {G}}_{c}l\,\nabla _{{\varvec{X}}} d\cdot \nabla _{{\varvec{X}}} \delta d \bigg \}dV=0, \end{aligned}$$

(53)

respectively. Within the FE framework, the unknowns are interpolated by the shape functions $N^{I}$ as well as the nodal values ${\varvec{u}}^{I}$ and $d^{I}$. The residuals and the tangents are obtained by

$$\begin{aligned} \begin{aligned} {\varvec{R}}_{{\varvec{u}}_{a}}^{I}&=-\int _{\varOmega } \bigg \{ \rho _{0}\,\ddot{{\varvec{u}}}_{a}\,N^{I} + \Big ( g\left( d \right) \,\varvec{\tau }_{ac}^{+} + \varvec{\tau }_{ac}^{-}\Big ) \nabla _{{\varvec{x}}_{c}} N^{I} \bigg \}dV, \\ {\varvec{R}}^{I}_{d}&=-\int _{\varOmega } \bigg \{ \left( g'(d)\,\varPhi _{0}^{+}\left( {\mathbf {F}}\right) +\frac{{\mathcal {G}}_{c}}{l}\, d + \chi \frac{d-d^{n}}{\varDelta t} \right) N^{I} \\&\qquad \qquad \quad + {\mathcal {G}}_{c}\,l\,\nabla _{{\varvec{X}}_{a}} N^{I}\,\nabla _{{\varvec{X}}_{a}} d \bigg \}dV,\\ {\varvec{K}}^{IJ}_{{\varvec{u}}_{a} {\varvec{u}}_{b}}&=\int _{\varOmega } \bigg \{ \bigg ( g\left( d \right) \, \mathbf {{\mathbb {C}}}_{acbd}^{+} +\mathbf {{\mathbb {C}}}_{acbd}^{-}+ \Big ( g\left( d \right) \,\varvec{\tau }_{cd}^{+}\\&\qquad \qquad \quad + \varvec{\tau }_{cd}^{-}\Big )\delta _{ab} \bigg ) \nabla _{{\varvec{x}}_{c}} N^{I}\,\nabla _{{\varvec{x}}_{d}} N^{J} \bigg \}dV, \\ {\varvec{K}}^{IJ}_{d d}&=\int _{\varOmega } \bigg \{ \bigg ( g''(d)\,\varPhi _{0}^{+}\left( {\mathbf {F}}\right) + \frac{{\mathcal {G}}_{c}}{l} + \frac{\chi }{\varDelta t} \bigg ) \, N^{I}\, N^{J} \\&\qquad \qquad \quad + {\mathcal {G}}_{c}\, l\, \nabla _{{\varvec{X}}_{a}} N^{I} \,\nabla _{{\varvec{X}}_{a}} N^{J} \bigg \} dV, \\ {\varvec{K}}^{IJ}_{{\varvec{u}}_{a} d}&=\int _{\varOmega } \bigg \{ g'\left( d \right) \varvec{\tau }_{ac}^{+}\,\,N^{J}\, \nabla _{{\varvec{x}}_{c}} N^{I} \bigg \}dV, \\ {\varvec{K}}^{IJ}_{d {\varvec{u}}_{a}}&=\int _{\varOmega } \bigg \{ g'\left( d \right) \varvec{\tau }_{ac}^{+}\,\,N^{I}\, \nabla _{{\varvec{x}}_{c}} N^{J} \bigg \}dV, \end{aligned} \end{aligned}$$

(54)

and the mass matrix yields

$$\begin{aligned} {\varvec{M}}^{IJ}_{{\varvec{u}}_{a} {\varvec{u}}_{b}}=\int _{\varOmega } \bigg \{ \rho _{0}\, N^{I}N^{J}\,\delta _{ab} \bigg \} dV. \end{aligned}$$

(55)

Regarding a staggered solution strategy, the coupling terms ${\mathbf {K}}^{IJ}_{{\varvec{u}}_{a} d}$ and ${\mathbf {K}}^{IJ}_{d {\varvec{u}}_{a}}$ are not taken into account, since they are solved by freezing the other evolution. In the sequel, assembling these matrices over all elements yields the global equilibrium.