Conditional deep surrogate models for stochastic, high-dimensional, and multi-fidelity systems

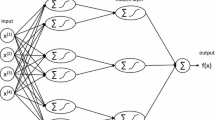
Abstract

We present a probabilistic deep learning methodology that enables the construction of predictive data-driven surrogates for stochastic systems. Leveraging recent advances in variational inference with implicit distributions, we put forth a statistical inference framework that enables the end-to-end training of surrogate models on paired input–output observations that may be stochastic in nature, originate from different information sources of variable fidelity, or be corrupted by complex noise processes. The resulting surrogates can accommodate high-dimensional inputs and outputs and are able to return predictions with quantified uncertainty. The effectiveness our approach is demonstrated through a series of canonical studies, including the regression of noisy data, multi-fidelity modeling of stochastic processes, and uncertainty propagation in high-dimensional dynamical systems.

Appendix: Sensitivity studies

Here we provide results on a series of comprehensive systematic studies that aim to quantify the sensitivity of the resulting predictions on:

• (i) the entropic regularization penalty parameter $\lambda$.

• (ii) the generator, discriminator and encoder neural network architectures.

• (iii) the adversarial training procedure.

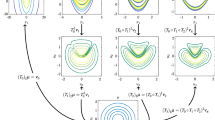
To this end, we consider a simple benchmark corresponding to the approximation of a Gaussian process $g(x)\sim \mathcal {GP}(\mu _H(x), k(x,x';\theta _H))$, where $\mu _H(x)$ corresponds to the high-fidelity mean function defined in Eq. 20 and $k(x,x';\theta _H)$ is a squared exponential kernel with hyper-parameters $\sigma _{f_H}^2 = 0.5, l_H^2=0.5$, as defined in Eq. 24. Figure 10a shows representative samples generated by this reference stochastic process. In all cases we have employed simple feed-forward neural network architectures as described below. The comparison metric used in all sensitivity studies is the average discrepancy between the predicted and the exact one-dimensional marginal densities, as measured by the reverse Kullback–Leibler divergence

$$\begin{aligned} \mathbb {E}_{p(x)}\{\mathbb {KL}[p_1(y|x)||p_2(y|x)]\} \end{aligned}$$

(28)

where $p_1(y|x)$ is the conditional distribution predicted by the generative model, $p_2(y|x)$ is the conditional distribution of the exact solution, and p(x) is the distribution of uniformly sampled test locations in the interval $x\in [0,1]$. For a given $x\sim p(x)$, we facilitate a tractable computation of the reverse KL-divergence using Eq. 25, by performing a Gaussian approximation of $p_2(y|x)$, while, by definition, $p_1(y|x)$ is a known uni-variate Gaussian density.

Fig. 10

Sensitivity studies on approximating a one-dimensional stochastic process. a Representative samples generated by this reference stochastic process, along with the observed data used for model training. b Representative samples generated by a conditional generative model with $\lambda =1.5$. Blue lines are the exact reference samples, red markers show the training data, and red lines are the generated samples. (Color figure online)

Table 1 Sensitivity with respect to the entropic regularization penalty parameter $\lambda$

Fig. 11

Sensitivity with respect to the entropic regularization penalty parameter $\lambda$. a Manifestation of mode collapse for $\lambda =1.0$. Blue lines are exact samples from the reference stochastic process, red lines are samples produced by the conditional generative model. b Generator and discriminator loss values as a function of the number of training iterations. (Color figure online)

1.1 A.1. Sensitivity with respect to the entropic regularization penalty parameter $\lambda$

In this study we aim to quantify the sensitivity of our predictions with respect to the penalty parameter $\lambda$ in Eq. 10. To this end, we have fixed the architecture for generator and encoder neural networks to include 3 hidden layers with 100 neurons each, and the discriminator neural network to include 2 hidden layers with 100 neurons each. In all cases, we have used a hyperbolic tangent non-linearity and a normal Xavier initialization [64]. For each iteration, we train the discriminator for 3 times and the generator for 1 time. We use a batch size of 500 data-points per stochastic gradient update, and the total number of training points is 10,000.

In Table 1 we report the reverse KL-divergence between the predicted data and the ground truth for different values of $\lambda$, 1.0, 1.2, 1.5, 1.8, 2.0, and 5.0. Recall that for $\lambda =1.0$ our model has a direct correspondence with generative adversarial networks [53, 54], while for $\lambda >1.0$ we obtain a regularized adversarial model that introduces flexibility in mitigating the issue of mode collapse. A manifestation of this pathology is evident in Fig. 11a in which the model with $\lambda =1.0$ collapses to a degenerate solution that severely underestimates the diversity observed in the true stochastic process samples, despite the fact that the model training dynamics seem to converge to a stable solution (see Fig. 11b). This is also confirmed by the computed average discrepancy in KL-divergence which is roughly an order of magnitude larger compared to the regularized models with $\lambda >1.0$. We also observe that model predictions remain robust for all values $\lambda >1.0$, while our best results are typically obtained for $\lambda =1.5$ which is the value used throughout this paper (see Fig. 10b for representative samples generated by the conditional generative model with $\lambda =1.5$).

1.2 A.2. Sensitivity with respect to the neural network architecture

In this study we aim to quantify the sensitivity of our predictions with respect to the architecture of the neural networks that parametrize the generator, the discriminator, and the encoder. Here, we choose the number of layers for the discriminator to always be one less than the number of layers for the generator and the encoder (e.g., if the number of layers for the generator is two then the number of layers for the discriminator is one, etc.). In all cases, we fix $\lambda = 1.5$ and we use a hyperbolic tangent non-linearity, and a normal Xavier initialization [64]. In Table 2 we report the computed average reverse KL-divergence between the predicted data and the ground truth for different feed-forward architectures for the generator, discriminator, and encoder (i.e., different number of layers and number of nodes in each layer). We denote the number of neurons in each layer as $N_{n}$ and the number of layers for the generator and the encoder as $N_g$.

The results of this sensitivity study are summarized in Table 2. Overall, we observe that model predictions remain robust for all neural network architectures considered.

Table 2 Sensitivity with respect to the neural network architecture

1.3 A.3. Sensitivity with respect to the adversarial training procedure

As discussed in [78], the adversarial training procedure plays a key role in the effectiveness of adversarial generative models, and it often requires a careful tuning of the training dynamics to ensure robustness in the model predictions. To this end, here we test the sensitivity of the proposed conditional generative model with respect to the relative frequency in which the generator and discriminator networks are updated during model training. To this end, we fix we the entropic regularization penalty to $\lambda = 1.5$, use the neural network architecture to be the same as the one described in “Appendix A.1” section, and vary the total number of training steps for the generator $K_g$ and the discriminator $K_d$ within each stochastic gradient descent iteration.

The results of this study are presented in Table 3 where we report the average reverse KL-divergence between the predicted data and the ground truth. These results reveal the high sensitivity of the training dynamics on the interplay between the generator and discriminator networks, and pinpoint the well known peculiarity of adversarial inference procedures which require a careful tuning of $K_g$ and $K_d$ for achieving stable performance in practice. Overall we observe that a one-to-three or one-to-five ratio of relative updates for the generator and discriminator, respectively, is the setting that typically works best in practice, although we must underline that this also depends on the capacity of the underlying neural network architectures as discussed in [78].

Finally, Fig. 12 depicts the convergence of the training algorithm for the case $K_g=1$ and $K_d=5$. According to [53], the theoretical optimal value of the discriminator loss is $\ln (4) = - 2 \times \ln (0.5) = 1.384$. As is shown in Fig. 12, the losses oscillate at the very beginning of the training and quickly converge to the optimal value after approximately 2000 iterations.

Table 3 Sensitivity with respect to the adversarial training procedure

Fig. 12

Optimal convergence of the discriminator loss. Convergence of the training algorithm for the case $K_g=1$ and $K_d=5$. The red line depicts the generator loss, the blue line is the discriminator loss, and the black dash line is the theoretical optimal loss of the discriminator. (Color figure online)