A numerical method for finite-strain mechanochemistry with localised chemical reactions treated using a Nitsche approach

Abstract

In this paper, a novel finite-element based method for finite-strain mechanochemistry with moving reaction fronts, which separate the chemically transformed and the untransformed phases, is proposed. The reaction front cuts through the finite elements and moves independently of the finite-element mesh, thereby removing the necessity for remeshing. The proposed method solves the coupled mechanics-diffusion–reaction problem. In the mechanical part of the problem, the force equilibrium and the displacement continuity conditions at the reaction front are enforced weakly using a Nitsche-like method. The formulation is applicable to the case of large deformations and arbitrary constitutive behaviour, and is also consistent with the minimisation of the total potential energy.

1 Introduction

Chemical reactions, such as oxidation or lithiation, in solid bodies lead to large volumetric expansions of materials and thereby lead to the emergence of mechanical stresses, which, in turn, affect the rates of the chemical reactions. This, for example, has been experimentally observed for the chemical reaction of silicon lithiation [40]. Chemical reactions in solids can be either volumetric or localised at a surface (a chemical reaction front) inside a solid body. In recent years, there has been an emergence of models that describe mechanochemistry of volumetric reactions, e.g. [16, 18], and localised reactions, e.g. [4, 6,7,8, 14, 43]. In this paper, the focus is on the latter.

From the physical point of view, in the case of localised reactions, the reaction front moves due to the consumption of the diffusive reactant, which is supplied to the reaction front by a diffusion process. The velocity of the front is also affected by the stresses, which, in turn, emerge due to transformation of the material as the front moves. This problem is similar to the classical stress-induced phase transformations in solids, where the phase boundaries move due to the configurational (driving) force (e.g. [1, 10, 21, 33] and references therein) equal to the jump of the normal component of the Eshelby stress tensor at the phase boundary. A few years ago it was shown that, in the case of a localised chemical reaction, the configurational force is the normal component of a chemical affinity tensor, which is equal to the combination of the chemical potential tensors of the reaction constituents, which, in turn, are equal to the Eshelby stress tensors divided by reference mass densities [6,7,8]. Both cases, phase transformations and chemical reactions, can be handled computationally in a similar way.

There are two major approaches to formulating the problem with the localised reactions. The first approach is the phase-field method, e.g. [37] in application to mechanochemistry and [31, 32] in application to the classical phase transformations. In this approach, an auxiliary field quantity is introduced, which takes distinct values inside the phases and smoothly changes between the phases. An additional partial differential equation (PDE) governs the evolution of this field. Thus, the interface¹ between the phases is of a finite thickness.

In the second approach, the reaction front is prescribed to be infinitely thin (“sharp”), i.e. curve in 2D or surface in 3D. The boundary conditions for the mechanical and/or diffusion equations are enforced at the moving reaction front, the velocity of which depends on the solutions of the equations. This paper focuses on “sharp” interface approach.

It is noteworthy to mention that there are also “hybrid” approaches, such as [44], where the mechanodiffusion with damage was considered, and where both mechanics and diffusion were solved in the entire computational domain; however, an infinitely thin interface was introduced and different material properties were used on the opposite sides of the interface. The kinetics of the interface was governed by the diffusion flux and by the stresses.

One established way of solving mechanochemical and phase transformation problems with sharp interfaces is the boundary integral method, e.g. [15, 35, 36] in application to modelling the formation of precipitates. Although term “mechanochemistry” was not used there, the problem in question was tracking the movement of phase boundaries influenced by both mechanics and diffusion, while the diffusion took place in the “untransformed” material. This approach, however, has only been formulated for linear elasticity and quasi-steady state diffusion. Moreover, it is difficult to handle topological changes during phase transformations within this approach.

Another popular computational approach to solving mechanochemical problems is the finite-element method (FEM). The major problem with the standard FEM is the requirement for the reaction front to coincide with the element edges/faces in 2D/3D. Therefore, the geometry should be remeshed each time the reaction front moves, e.g. [9]. This leads to accumulation of the numerical error and excessive computations. To avoid this, there has been a significant effort to create computational approaches that avoid remeshing.

An established way of modelling mechanochemistry and phase transformations using FEM without remeshing is the combination of the extended finite-element method (XFEM) to solve the mechanical problem and the level-set method to move the interface, e.g. [45, 46] in application to phase transformations and [5, 47] in application to mechanochemistry. In this case, FEM is modified such that the interface cuts through the elements and moves independently of the mesh. However, at the moment, to the best knowledge of the authors, XFEM and level-set combination has only been formulated for and applied to linear elastic problems in the context of phase transformation problems.

In [22], the application of isogeometric FEM was proposed for linear elastic mechanochemistry. In this approach, the reaction front still coincides with the element edges/faces; however, when the front moves, the elements are simply distorted, i.e. stretched or compressed, without changing topology or connectivity of the mesh. Distortion of the elements is utilised due to the nature of the isogeometric method, where higher aspect ratios of the elements compared to the standard FEM can be handled. The main advantage of this method is the well-defined normal to the reaction front at any point, due to the description of the front by B-splines. This property is important for calculation of the velocity of the front and moving the interface.

A computational approach for finite-strain mechanochemistry with the reaction fronts that are non-conforming to the finite-element mesh was first proposed in [27, 28], where the interface motion was handled using the level-set method, while the non-conforming interface was handled by the enhanced gradient FEM in the mechanical and the diffusion problems. The enhanced gradient method avoids remeshing; however, treatment of the elements that are intersected by the interface is relatively complicated. As in XFEM, special finite-element basis functions are constructed for these elements. These basis functions are piecewise polynomial and can be discontinuous; additional degrees of freedom are found from the interface conditions.

The aim of this paper is to develop a numerical method for finite-strain mechanochemistry that considers interfaces that are non-conforming to the finite-element mesh, avoids remeshing and is relatively simple to implement, i.e. which does not rely on special finite-element basis functions. The major difficulty for such approach is the correct enforcement of the interface conditions (displacement and traction continuity). One possible approach is the Nitsche method, which is a way of weakly imposing boundary/interface conditions for linear PDEs, e.g. [11, 12, 30] in application to mechanics with linear elastic constitutive laws. However, an extension of the Nitsche method to non-linear PDEs is non-trivial and has been less studied. One such extension, which, as explained below, has key differences to previous formulations, is proposed in this paper.

The first attempt of extension of the Nitsche method along with the discontinuous Galerkin method to large-deformation mechanics has been reported in [29]. As the Nitsche penalty terms in the weak form contain arbitrary multipliers, in [29], the first Piola-Kirchhoff tensor was used. This, however, is not consistent with the minimisation of the total potential energy, as will be shown in this paper. In [38], it was shown that when the weak form is obtained by finding the saddle point of the total potential energy, the fourth-order acoustic tensor (derivative of the first Piola-Kirchhoff tensor by the deformation gradient tensor) appears in the penalty term multiplier.

In this paper, the weak form of the finite-strain mechanical problem is obtained by minimising the total potential energy, which includes the Nitsche-like penalty terms. As the interface can cut a small volume fraction of an element in mechanochemical problems, in this paper, additional inter-element stabilisation term, similar to one presented in [2, 12, 34], is also introduced. The weak form of the coupled problem is then derived and discretised using finite-element formulation. Furthermore, in this paper, an algorithm for moving the points of the reaction front in the mechanochemical problem is presented. The method is illustrated with 2D numerical examples to show its numerical robustness in application to finite-strain mechanochemical problems with moving reaction fronts.

2 Notation

Vectors are denoted with an arrow, e.g. $\vec {a}$. The scalar and the vector products between vectors $\vec {a}$ and $\vec {b}$ are denoted as $\vec {a} \cdot \vec {b}$ and $\vec {a} \times \vec {b}$, respectively. Second-order tensors are denoted as bold capital letters, e.g. $\varvec{A}$. The tensor product between vectors $\vec {a}$ and $\vec {b}$ is denoted as $\vec {a} \vec {b}$. The coordinate representation of the tensor product is given by $A_{ij} = a_i b_j$, where $a_k$ and $b_k$ are components of vectors $\vec {a}$ and $\vec {b}$, respectively, and $A_{ij}$ are components of tensor $\varvec{A}$. The transpose of a tensor is denoted as $\varvec{B} = \varvec{A} ^\mathrm {T}$, which is $B_{ij} = A_{ji}$ in the coordinate representation. Standard second-order identity tensor is denoted as $\varvec{I}$. Einstein summation notation is used. The coordinate representations of the scalar and the vector products of a tensor by a vector from the right, $\vec {d} = \varvec{A} \cdot \vec {c}$ and $\varvec{C} = \varvec{A} \times \vec {c}$, respectively, are given by

$$\begin{aligned} d_i = A_{ij} c_j, \quad C_{in} = \xi _{njk} A_{ij} c_k, \end{aligned}$$

where $\xi _{njk}$ is the Levi-Civita symbol. The double inner product of two tensors is denoted as $f = \varvec{A} {:}\varvec{D}$ and in the coordinate representation is given by

$$\begin{aligned} f=A_{ij} D_{ji}. \end{aligned}$$

Higher-order tensors, which are formed by the tensor product of more than two vectors, are denoted with preceding superscript showing the order, e.g. ${}^3\!\varvec{E}$ is a third-order tensor. Standard fourth order identity tensor and its right transpose are denoted as

$$\begin{aligned} {}^4\!\varvec{I} = \vec {e} _s\vec {e} _k\vec {e} _k\vec {e} _s , \quad {}^4\!\varvec{I} ^\mathrm {RT} = \vec {e} _s\vec {e} _k\vec {e} _s\vec {e} _k , \end{aligned}$$

respectively, where $\vec {e} _i$, $i\in \left\{ 1, 2, 3 \right\}$ are basis vectors. It is useful to note that ${}^4\!\varvec{I} {:}\varvec{Q} = \varvec{Q} {:} {}^4\!\varvec{I} = \varvec{Q}$ and ${}^4\!\varvec{I} ^\mathrm {RT} {:} \varvec{Q} = \varvec{Q} {:} {}^4\!\varvec{I} ^\mathrm {RT} = \varvec{Q} ^\mathrm {T}$.

The derivative of the function $\varphi =\varphi \left( \varvec{Q} \right)$ with respect to the second-order tensor $\varvec{Q} = Q_{sk}\vec {e} _s\vec {e} _k$ and the variation of the function $\varphi$ are defined the following way [19, 20]:

$$\begin{aligned} \frac{\partial \,\varphi }{\partial \varvec{Q} } = \frac{\partial \,\varphi }{\partial Q_{sk}}\vec {e} _s\vec {e} _k , \quad \delta \,\varphi = \frac{\partial \,\varphi }{\partial \varvec{Q} } : \delta \varvec{Q} ^\mathrm {T} . \end{aligned}$$

The derivative of the second-order tensor $\varvec{P} =\varvec{P} \left( \varvec{Q} \right)$ by the second-order tensor $\varvec{Q}$ and its variation are defined in the following way [19, 20]:

$$\begin{aligned} \frac{\partial \varvec{P} }{\partial \varvec{Q} } = \frac{\partial P_{mn}}{\partial Q_{st}}\vec {e} _m\vec {e} _n\vec {e} _s\vec {e} _t , \quad \delta \varvec{P} = \frac{\partial \varvec{P} }{\partial \varvec{Q} } : \delta \varvec{Q} ^\mathrm {T} . \end{aligned}$$

It is useful to note that [19, 20]:

$$\begin{aligned} \begin{aligned}&\frac{\partial \varvec{Q} }{\partial \varvec{Q} } = {}^4\!\varvec{I} ^\mathrm {RT} , \\&\frac{\partial \,\varphi }{\partial \varvec{Q} } = \left( \frac{\partial \,\varphi }{\partial \varvec{S} }\right) ^\mathrm {T} : \frac{\partial \varvec{S} }{\partial \varvec{Q} } , \quad \frac{\partial \varvec{P} }{\partial \varvec{Q} } = \frac{\partial \varvec{P} }{\partial \varvec{S} } : {}^4\!\varvec{I} ^\mathrm {RT} : \frac{\partial \varvec{S} }{\partial \varvec{Q} } , \\&\frac{\partial \left( {\text {tr}} \left( \varvec{Q} \right) \right) }{\partial \varvec{Q} } = \varvec{I} , \quad \frac{\partial \left( {\text {det}} \left( \varvec{Q} \right) \right) }{\partial \varvec{Q} } = {\text {det}} \left( \varvec{Q} \right) \varvec{Q} ^\mathrm {-T} , \\&\frac{\partial \left( \varvec{Q} ^{-1}\right) }{\partial \varvec{Q} } = -\varvec{Q} ^{-1} \cdot {}^4\!\varvec{I} ^\mathrm {RT} \cdot \varvec{Q} ^\mathrm {-T} . \end{aligned} \end{aligned}$$

3 Mechanochemical problem formulation

In this section, a general mechanochemical problem formulation is presented, in which movement of a chemical reaction front takes place. No specific assumptions about constitutive relations are made below. However, for numerical examples, specific functional dependencies were chosen and are presented in Sect. 5.1.

From the physical point of view, mechanochemical problems are described by three coupled processes: mechanical deformation, diffusion and chemical reaction at the reaction front, as illustrated in Fig. 1a. In general, the deformation can be dependent on the concentration and the diffusion rate can be affected by the mechanical stresses. Moreover, the concentration and the stresses affect the velocity of the reaction front.

Fig. 1

The schematic representation of a mechanochemical problem with the chemical reaction front (a) and configurations that are used in the problem formulation (b) (similarly to [8]). The diffusive reactant diffuses from the outer surface of the body and through the transformed phase and participates in the chemical reaction at the reaction front

The solution of the mechanochemical problem consists in finding two time-dependent field quantities and one time-dependent curve (in a 2D setting) or surface (in a 3D setting). The first unknown field quantity is the displacement of all material points of a body. The second unknown field quantity is the concentration of the reactant. The last unknown is the configuration/position of reaction front. All these quantities are time-dependent, since the reaction front moves due to a chemical reaction.

3.1 Configurations and kinematics

The solid body is split into two domains: the chemically transformed and the untransformed phases, which are denoted as $B_+$ and $B_-$, respectively. Both phases undergo mechanical deformation. Therefore, there are three configurations: the current configuration, the reference configuration of the chemically untransformed material and the reference configuration of the chemically transformed material. The kinematics description used in this paper follows [6,7,8].

To perform numerical calculations, it is convenient to work only with one reference configuration. In this paper, the reference configuration of the untransformed material ($B_-$) is chosen and, in the rest of the text, is denoted as “the reference configuration”. The reference configuration of $B_+$ is referred to as “the chemically transformed configuration”.

In the current configuration, domains of $B_+$ and $B_-$ are denoted as $\omega _+$ and $\omega _-$, respectively. These domains are separated by the reaction front $\gamma _*$. The position vector in the current configuration is denoted as $\vec {x}$. Mappings of $\omega _+$ and $\omega _-$ onto the reference configuration are denoted as $\varOmega _+$ and $\varOmega _-$, respectively. These domains are separated by the reaction front $\varGamma _*$. The normal to the reaction front is defined as the outer normal to $\varOmega _+$ and is denoted as $\vec {N} _*$. The position vector in the reference configuration is denoted as $\vec {X}$. Mappings of $\omega _+$ and $\omega _-$ onto the chemically transformed configuration are denoted as $\varOmega _+'$ and $\varOmega _-'$, respectively.

Current position vector $\vec {x}$ of a material point is a function of the position position vector $\vec {X}$ of the point in the reference configuration, $\vec {x} = \vec {x} \left( \vec {X} \right)$, $\vec {X} \in \varOmega$. Thus, the displacement can be defined as

$$\begin{aligned} \vec {u} = \vec {u} \left( \vec {X} \right) = \vec {x} \left( \vec {X} \right) - \vec {X} , \quad \vec {X} \in \varOmega . \end{aligned}$$

(1)

Operators $\nabla$ and $\nabla _0$ are defined with respect to the current and the reference configurations, respectively. Moreover

$$\begin{aligned} \nabla = \varvec{F} ^\mathrm {-T} \cdot \nabla _0 , \quad \varvec{F} = \left( \nabla _0 \vec {x} \right) ^\mathrm {T} , \end{aligned}$$

(2)

where $\varvec{F}$ is the deformation gradient, which maps the reference configuration to the current configuration:

$$\begin{aligned} {\text {d}}\vec {x} = \varvec{F} \cdot {\text {d}}\vec {X} . \end{aligned}$$

(3)

For the transformed material, the multiplicative decomposition of the deformation gradient is used:

$$\begin{aligned} \varvec{F} _+ = \varvec{F} _+' \cdot \varvec{G} , \quad \vec {X} \in \varOmega _+ , \end{aligned}$$

(4)

where $\varvec{G}$ maps the reference configuration to the chemically transformed configuration and $\varvec{F} _+'$ maps the chemically transformed configuration to the current configuration, as illustrated in Fig. 1b. For the purpose of this paper, $\varvec{G}$ is assumed to be constant. However, additional concentration-dependent, therefore inhomogeneous, deformation can also be introduced in the constitutive law of the material.

Quantities (deformation gradient, stress, displacement, etc.) corresponding to phases $B_+$ and $B_-$ are denoted with subscripts “$+$” and “−”, respectively. To shorten the description in the rest of the text, subscript “±” is used on some occasions to combine equations corresponding to $B_+$ and $B_-$ into one equation.

3.2 Mechanics

The problem is assumed to be quasistatic. The balance of linear momentum equation is

$$\begin{aligned} \nabla \cdot \varvec{\sigma } _{\pm } = \vec {0} , \quad \vec {x} \in \omega _{\pm } , \end{aligned}$$

(5)

where $\varvec{\sigma }$ is the Cauchy stress tensor. The relation between the Cauchy stress tensor and other variables is defined by constitutive relations,

$$\begin{aligned}&\varvec{\sigma } _+ = \varvec{\sigma } _+ \left\{ \varvec{F} _+, \theta , c \right\} , \quad \varvec{\sigma } _- = \varvec{\sigma } _- \left\{ \varvec{F} _-, \theta \right\} ,\nonumber \\&\varvec{F} _\pm = \varvec{I} + \left( \nabla _0 \vec {u} _\pm \right) ^\mathrm {T} , \end{aligned}$$

(6)

where $\theta$ is the temperature and curly brackets denote arbitrary functional dependency on the variables, including dependencies on the derivatives.

The outer boundary of the body is split into $\gamma _\mathrm {D}$ and $\gamma _\mathrm {T}$, on which displacements and tractions are enforced, respectively. The normal to $\gamma _\mathrm {T}$ is denoted as $\vec {n} _\mathrm {T}$ and is defined as the outer normal to the body. The boundary conditions at the outer surface of the body are

$$\begin{aligned}&\vec {u} _\pm = \vec {d} , \quad \vec {x} \in \gamma _{\mathrm {D}\pm } , \quad \gamma _{\mathrm {D}\pm } = \gamma _\mathrm {D} \cap \partial \omega _\pm , \end{aligned}$$

(7)

$$\begin{aligned}&\varvec{\sigma } _\pm \cdot \vec {n} _\mathrm {T} = \vec {t} , \quad \vec {x} \in \gamma _{\mathrm {T}\pm } , \quad \gamma _{\mathrm {T}\pm } = \gamma _\mathrm {T} \cap \partial \omega _\pm , \end{aligned}$$

(8)

where $\vec {d}$ is the displacement vector and $\vec {t}$ is the traction vector. At the reaction front, the displacement and the traction continuity conditions are enforced

$$\begin{aligned}&\vec {u} _- = \vec {u} _+ , \quad \vec {x} \in \gamma _* , \end{aligned}$$

(9)

$$\begin{aligned}&\varvec{\sigma } _- \cdot \vec {n} _* = \varvec{\sigma } _+ \cdot \vec {n} _* , \quad \vec {x} \in \gamma _* , \end{aligned}$$

(10)

where $\vec {n} _*$ is the normal to $\gamma _*$, which is defined as the outer normal to $\omega _+$.

3.2.1 Boundary/interface conditions in the reference configuration

For convenience, it is also useful to rewrite the boundary and the interface conditions with respect to the reference configuration. Here, $\varGamma _\mathrm {D}$ and $\varGamma _\mathrm {T}$ are the images of $\gamma _\mathrm {D}$ and $\gamma _\mathrm {T}$, respectively, in the reference configuration. The normal to $\varGamma _\mathrm {T}$ is denoted as $\vec {N} _\mathrm {T}$ and is defined as the outer normal to the body. The boundary conditions at the outer surface of the body are

$$\begin{aligned}&\vec {u} _\pm = \vec {d} , \quad \vec {X} \in \varGamma _{\mathrm {D}\pm } , \quad \varGamma _{\mathrm {D}\pm } = \varGamma _\mathrm {D} \cap \partial \varOmega _\pm , \end{aligned}$$

(11)

$$\begin{aligned}&\varvec{P} _\pm \cdot \vec {N} _\mathrm {T} = \vec {T} , \quad \vec {X} \in \varGamma _{\mathrm {T}\pm } , \quad \varGamma _{\mathrm {T}\pm } = \varGamma _\mathrm {T} \cap \partial \varOmega _\pm , \end{aligned}$$

(12)

where $\varvec{P}$ is the first Piola-Kirchhoff stress tensor and $\vec {T}$ is the traction defined per unit surface in the reference configuration. As usual, for the purpose of presenting a numerical method, $\vec {T}$ is assumed to be independent of displacement $\vec {u}$; however, it is easy to construct the generalisation. At the reaction front, the displacement and the traction continuity conditions are enforced

$$\begin{aligned}&\vec {u} _- = \vec {u} _+ , \quad \vec {X} \in \varGamma _* , \end{aligned}$$

(13)

$$\begin{aligned}&\varvec{P} _- \cdot \vec {N} _* = \varvec{P} _+ \cdot \vec {N} _* , \quad \vec {X} \in \varGamma _* . \end{aligned}$$

(14)

3.3 Diffusion

For the purpose of this paper, the diffusion is assumed to be quasi-stationary. This assumption is motivated by the fact that in most cases, the rate of the diffusion is much higher than the rate of the chemical reaction [17, 42] and the diffusion process can be assumed to take place at the thermodynamic equilibrium.

The mass balance and the dissipation inequality are derived with respect to the reference configuration of a body, e.g. [16]. The diffusion process, which is considered here, takes place in phase $B_+$. Hence, the mass balance and the dissipation inequality should be written with respect to the chemically transformed configuration. However, since $\varvec{G}$, which maps the reference configuration to the chemically transformed configuration, is constant, integrals over volume $\varOmega _+'$ in the derivation can be transformed to integrals over volume $\varOmega _+$ using

$$\begin{aligned} {\text {d}}\varOmega _+' = \det \left( \varvec{G} \right) {\text {d}}\varOmega _+ . \end{aligned}$$

Thus, the mass balance and the dissipation inequality can be written with respect to the reference configuration.

The mass balance equation is

$$\begin{aligned} \nabla _0 \cdot \vec {j} = 0 , \quad \vec {X} \in \varOmega _+ , \end{aligned}$$

(15)

where $\vec {j}$ is the diffusion flux, which is given by the constitutive equation

$$\begin{aligned} \vec {j} = \vec {j} \left\{ c, \varvec{\sigma } _+, \varvec{F} _+, \theta \right\} , \end{aligned}$$

(16)

where, as above, curly brackets denote arbitrary functional dependency on the variables, including dependencies on the gradients.

The mixed boundary conditions for Eq. (15) are used at the reaction front,

$$\begin{aligned}&\vec {N} _* \cdot \vec {j} + f_* = 0 , \quad \vec {X} \in \varGamma _* , \end{aligned}$$

(17)

$$\begin{aligned}&f_* = f_* \left( c, V \right) , \end{aligned}$$

(18)

where V is the normal velocity of the reaction front and $f_*$ is some function. The specific expression for $f_*$ can be derived from the mass conservation [6,7,8]. Elsewhere on the boundary,

$$\begin{aligned} \vec {N} _\mathrm {M} \cdot \vec {j} + \alpha \left( c - s \right) = 0 , \quad \vec {X} \in \varGamma _\mathrm {M}, \quad \varGamma _\mathrm {M} = \partial \varOmega _+ \setminus \varGamma _* , \end{aligned}$$

(19)

are enforced, where $\vec {N} _\mathrm {M}$ is the outer normal to surface of the body, $\alpha$ is a constant, which is proportional to the surface mass transfer coefficient, and s is a constant, which is proportional to the solubility of the reactant in material $B_+$.

3.4 Chemical reaction

The chemical reaction takes place at the reaction front. The diffusive component reacts with the untransformed material, which leads to the formation of a new transformed material. Thereby, the position of the reaction front changes. The kinetics of the reaction front is stress- and concentration-dependent and varies for different mechanochemical models. There are models where an expression for the velocity of the reaction front is simply postulated. Recently, an expression for the thermodynamic driving force in the case of a localised chemical reaction has been derived [6,7,8]. This allows choosing an expression for the velocity as a function of this force.

The total velocity of the reaction front is defined in the reference configuration as the time derivative of the position of the front in the reference configuration. In mechanochemical models, only the normal component of the velocity is considered, since it can be shown that, in the case of coherent reaction fronts, without loss of genereality, it is sufficient to consider fronts moving along the normal in the reference configuration [7]. Thus, the normal velocity is defined as the scalar product of the total velocity and outer normal $\vec {N} _*$ to the reaction front:

$$\begin{aligned} V= & {} V \left( c, \varvec{\sigma } _\pm , \varvec{F} _\pm , W_\pm , \theta \right) \nonumber \\= & {} \frac{{\text {d}}\vec {X} _*}{{\text {d}}t} \cdot \vec {N} _* , \quad \vec {X} _* = \left\{ \vec {X} \left| \, \vec {X} \in \varGamma _* \right. \right\} , \end{aligned}$$

(20)

where $\vec {X} _*$ is the position of the reaction front in the reference configuration, $W_+$ and $W_-$ are the elastic strain energy densities of the transformed and the untransformed materials, respectively, per unit volume in the reference configuration.

It can be seen that the balance of momentum equation, Eq. (5), the mass balance equation, Eq. (15), and the velocity equation, Eq. (20), form a coupled system of PDEs with respect to unknown variables $\vec {u}$, c and $\vec {X} _*$. In general, there are two independent coupling mechanisms: via the constitutive equations and via the moving boundary. The first one results from the concentration entering the constitutive equation for the stresses, Eq. (6), and from the stresses entering the constitutive equation for the diffusion flux, Eq. (16). The second coupling mechanism is the dependence of solutions of (5) and (15), $\vec {u}$ and c, respectively, on the position of the reaction front, which, in turn, depends on both fields. Thus, even if the first mechanism is not present, the system of PDEs is still coupled. Further discussion of the mechanochemical coupling can be found in [26].

4 Numerical method

There are two general ways of dealing with the time stepping for the reaction front movement—explicit and implicit methods. The explicit scheme suggests that the position of the reaction front is known at a given time step. This allows solving the mechanical and the diffusion problems for displacement and concentration fields, calculating the reaction front velocity using these fields and, subsequently, finding the new position of the front using the velocity. In contrast, within the implicit scheme, the position of the front is unknown at a given time step. Therefore, all equations (mechanical, diffusion and front velocity/position) must be solved simultaneously with respect to the unknown displacement, concentration and position of the front. In this work, the explicit time stepping scheme for the interface movement is used to avoid an increase in complexity of numerical implementation (coding) associated with the implicit scheme and, in particular, evaluation of Jacobian components that correspond to degrees of freedom representing the front.

The description of the numerical method is split into three major parts: the mechanics, the diffusion and the movement of the reaction front. As presented in the problem formulation, the mechanical problem and the diffusion problem are fully coupled. Therefore, in the general case, the finite-element formulation for the fully coupled problem must be formulated. However, for clarity of the presentation of the method, the decoupled case is presented first: the mechanical problem (for the case when stresses do not depend on concentration), followed by the diffusion problem (for the case when the deformation and the stresses are already known). Afterwards, the finite-element formulation for the fully coupled problem is presented.

From an implementational point of view, when the concentration does not enter the constitutive law for stresses, the mechanical and the diffusion problems can be solved sequentially within a particular time step. This means that the mechanical problem is solved first, followed by the solution of the diffusion problem using known stresses, followed by the calculation of a new position of the reaction front. However, when the concentration enters the constitutive law for stresses, the mechanical and the diffusion problems must be solved as one system of coupled non-linear equations within a particular time step. After the solution is found, the reaction front is moved.

4.1 Mechanics

At first, the weak form of the mechanical problem is formulated. The idea follows [30], where the potential energy with an interface penalty term is formulated and the variation of the potential energy is performed; however, in this paper, the finite-strain case is considered.

The following potential energy of the mechanical system is considered:

(21)

where

(22)

(23)

and $W_\pm$ are the elastic strain energy densities of the transformed and the untransformed materials per unit volume in the reference configuration. Here $\beta$ is the numerical parameter, which is introduced in Nitsche-like methods, and I is the stabilisation term, which is explained further in the text. Brackets denote the jump of the quantity across the interface, brackets $\left\langle \cdot \right\rangle$ denote the average of the quantity across the interface. The fifth term in Eq. (21) is the penalty term, which leads to the enforcement of the interface conditions weakly.

4.1.1 Variation of the potential energy and the weak form

The weak form of the problem is found by the variation of the potential energy:

$$\begin{aligned} \delta \varPi = 0 . \end{aligned}$$

(24)

The variation is the following:

(25)

Since

$$\begin{aligned}&\delta W_\pm = \frac{\partial W_\pm }{\partial \varvec{F} _\pm } : \delta {\varvec{F} _\pm }^\mathrm {T} = \varvec{P} _\pm : \delta {\varvec{F} _\pm }^\mathrm {T} , \end{aligned}$$

(26)

$$\begin{aligned}&\delta \varvec{P} _\pm = \frac{\partial \varvec{P} _\pm }{\partial \varvec{F} _\pm } : \delta {\varvec{F} _\pm }^\mathrm {T} , \end{aligned}$$

(27)

the resulting variation of $\varPi$ becomes

(28)

The test function is introduced as the variation of displacement $\vec {u}$,

$$\begin{aligned} \vec {\varphi } _\pm = \delta \vec {u} _\pm , \end{aligned}$$

(29)

therefore,

$$\begin{aligned} \delta \varvec{F} _\pm = \left( \nabla _0 \vec {\varphi } _\pm \right) ^\mathrm {T} . \end{aligned}$$

(30)

Due to the boundary conditions on $\varGamma _\mathrm {D}$,

$$\begin{aligned} \vec {\varphi } _\pm = \vec {0} \text { on } \varGamma _{\mathrm {D}\pm } . \end{aligned}$$

To ensure that the functions under integrals are integrable, additional functional spaces are introduced:

$$\begin{aligned} \mathcal {R}_\pm&= \left\{ \vec {u} \left| \, u_i \in H^1\left( \varOmega _\pm \right) , \, \vec {u} = \vec {d} \text { on } \varGamma _{\mathrm {D}\pm } \right. \right\} ,\nonumber \\ u_i&= \vec {u} \cdot \vec {e} _i, \quad i \in \left\{ 1,2,3 \right\} , \end{aligned}$$

(31)

$$\begin{aligned} \mathcal {Q}_\pm&= \left\{ \vec {\varphi } \left| \, \varphi _i \in H^1\left( \varOmega _\pm \right) , \, \vec {\varphi } = \vec {0} \text { on } \varGamma _{\mathrm {D}\pm } \right. \right\} , \nonumber \\ \varphi _i&= \vec {\varphi } \cdot \vec {e} _i, \quad i \in \left\{ 1,2,3 \right\} . \end{aligned}$$

(32)

Here $u_i$ are components of vector function $\vec {u}$ and $H^1\left( \varOmega _\pm \right)$ is the Sobolev space with $L^2$-norm.

The resulting weak problem formulation is the following:

$$\begin{aligned}&\text {find } \vec {u} _+ \in \mathcal {R}_+,\text { } \vec {u} _- \in \mathcal {R}_- \text { such that}\\&a\left( \vec {u} _+, \vec {u} _-, \vec {\varphi } _+, \vec {\varphi } _- \right) = 0, \quad \forall \vec {\varphi } _+ \in \mathcal {Q}_+,\text { } \forall \vec {\varphi } _- \in \mathcal {Q}_- , \end{aligned}$$

where

(33)

Term $\delta I$ is given in Sect. 4.1.6. Here the following transformation was used:

since it is more convenient to work with the derivative of the transposed first Piola-Kirchhoff stress tensor when the transformation between the configurations is performed.

Weak form (33) is similar to the weak form of [38, 39], however, with different interface stabilisation terms. In [38, 39], the stabilised discontinuous Galerkin (DG) method was proposed for large deformations, while in [3], this approach was extended to include models of damage and debonding.

4.1.2 Transformation between configurations for some quantities

The first term in Eq. (21) can be also written with respect to the chemically transformed configuration:

$$\begin{aligned}&\int _{\varOmega _+} W_+ {\text {d}}\varOmega _+ = \int _{\varOmega _+'} W_+' {\text {d}}\varOmega _+' , \end{aligned}$$

(34)

$$\begin{aligned}&W_+ = W_+' \det \left( \varvec{G} \right) , \end{aligned}$$

(35)

$$\begin{aligned}&{\text {d}}\varOmega _+' = \det \left( \varvec{G} \right) {\text {d}}\varOmega _+, \end{aligned}$$

(36)

where $W_+'$ is the elastic strain energy density of the transformed material per unit volume in the chemically transformed configuration and $\varOmega _+'$ is the domain of $B_+$ in the chemically transformed configuration.

More importantly, since the chemically transformed configuration is the stress-free configuration of phase $B_+$, the constitutive laws for $B_+$ are expected to be prescribed in the chemically transformed configuration. Thus, $W_+'$ is expected to be prescribed instead of $W_+$. Moreover, since $\varvec{F} _+'$ maps the chemically transformed configuration to the current configuration, it is expected that $W_+'$ is given as a function of $\varvec{F} _+'$. Therefore, the first Piola-Kirchhoff stress tensor in the chemically transformed configuration

$$\begin{aligned} \varvec{P} _+' = \frac{\partial W_+'}{\partial \varvec{F} _+'} \end{aligned}$$

can be introduced. Since in (33), the first Piola-Kirchhoff stress tensor in the reference configuration is used, their relation must be derived. Using

$$\begin{aligned} \frac{\partial \varvec{F} _+'}{\partial \varvec{F} _+} = {}^4\!\varvec{I} ^\mathrm {RT} : \left( \varvec{G} ^\mathrm {-T} \cdot {}^4\!\varvec{I} \right) , \end{aligned}$$

the following is obtained:

$$\begin{aligned} \varvec{P} _+&= \frac{\partial W_+}{\partial \varvec{F} _+} = \det \left( \varvec{G} \right) \left( \frac{\partial W_+'}{\partial \varvec{F} _+'} \right) ^\mathrm {T} : \frac{\partial \varvec{F} _+'}{\partial \varvec{F} _+} \nonumber \\&= \det \left( \varvec{G} \right) \varvec{P} _+' \cdot \varvec{G} ^\mathrm {-T} . \end{aligned}$$

(37)

Similar transformation can be performed for the derivative of the first Piola-Kirchhoff stress tensor:

$$\begin{aligned} \frac{\partial {\varvec{P} _+}^\mathrm {T} }{\partial \varvec{F} _+}= & {} \det \left( \varvec{G} \right) \varvec{G} ^{-1} \cdot \frac{\partial {\varvec{P} _+'}^\mathrm {T} }{\partial \varvec{F} _+}\nonumber \\= & {} \det \left( \varvec{G} \right) \varvec{G} ^{-1} \cdot \frac{\partial {\varvec{P} _+'}^\mathrm {T} }{\partial \varvec{F} _+'} \cdot \varvec{G} ^\mathrm {-T} . \end{aligned}$$

(38)

Fig. 2

The schematic representation of a finite-element mesh of the body with an interface that cuts through the elements (a). For the nodes that belong to the intersected elements, the number of degrees of freedom (DOFs) is doubled. Here the 2D mechanical case is illustrated with 2 DOFs/node in standard elements. Alternative interpretation of the finite-element problem as two distinct “classical” finite-element meshes that overlap over the set of intersected elements (b). The areas marked with the grey hatching do not participate in the volumetric integration of the elements. The schematic representation of a case when the interface cuts a small volume faction of an element (c), which is marked with the dark brown hatching

4.1.3 Consistency with the strong form

The weak form of the problem, Eq. (33), without the stabilisation term, $\delta I$, is consistent with the strong form of the problem, Eq. (5) and boundary conditions (11), (12), (13), (14). Indeed, the first and the second terms of (33) are derived using the standard approach, i.e. by multiplying (5) by $\vec {\varphi } _\pm$ and integrating over the volume:

$$\begin{aligned} \int _{\omega _\pm } \vec {\varphi } _\pm \cdot \left( \nabla \cdot \varvec{\sigma } _\pm \right) {\text {d}}\omega _\pm = 0 . \end{aligned}$$

(39)

By applying the divergence theorem the following form is obtained

$$\begin{aligned} \int _{\omega _\pm } \left( \nabla \vec {\varphi } _\pm \right) ^\mathrm {T} : \varvec{\sigma } _\pm {\text {d}}\omega _\pm= & {} \int _{\gamma _{\mathrm {T}\pm }} \vec {\varphi } _\pm \cdot \varvec{\sigma } _\pm \cdot \vec {n} _\mathrm {T} {\text {d}}\gamma _{\mathrm {T}\pm } \nonumber \\&+ \int _{\gamma _*} \vec {\varphi } _\pm \cdot \varvec{\sigma } _\pm \cdot \left( \pm \vec {n} _* \right) {\text {d}}\gamma _* , \end{aligned}$$

(40)

where there is “$+$” sign in front of $\vec {n} _*$ when equation for $B_+$ is considered, as $\vec {n} _*$ is the outer normal to $\omega _+$, and there is “−” sign in front of $\vec {n} _*$ when equation for $B_-$ is considered. Since

$$\begin{aligned} \left( \nabla \vec {\varphi } _\pm \right) ^\mathrm {T} : \varvec{\sigma } _\pm = \left( \nabla _0 \vec {\varphi } _\pm \right) ^\mathrm {T} : \left( {\varvec{F} _\pm }^{-1} \cdot {\varvec{\sigma } _\pm } \right) , \end{aligned}$$

(41)

the following is obtained:

$$\begin{aligned} \begin{aligned}&\int _{\varOmega _\pm } \left( \nabla _0 \vec {\varphi } _\pm \right) ^\mathrm {T} : \left( {\varvec{F} _\pm }^{-1} \cdot \varvec{\sigma _\pm } \right) J_\pm {\text {d}}\varOmega _\pm \\&\quad = \int _{\varGamma _{\mathrm {T}\pm }} \vec {\varphi } _\pm \cdot \varvec{P} _\pm \cdot \vec {N} _\mathrm {T} {\text {d}}\varGamma _{\mathrm {T}\pm } \pm \int _{\varGamma _*} \vec {\varphi } _\pm \cdot \varvec{P} _\pm \cdot \vec {N} _* {\text {d}}\varGamma _* . \end{aligned} \end{aligned}$$

(42)

In the expression above, the domain of integration was changed and the standard definitions were used (subscripts omitted):

$$\begin{aligned}&J = {\text {det}} \left( \varvec{F} \right) , \quad \varvec{P} = J \varvec{\sigma } \cdot \varvec{F} ^\mathrm {-T} , \\&\vec {n} {\text {d}}\gamma = J \varvec{F} ^\mathrm {-T} \cdot \vec {N} {\text {d}}\varGamma \text {(Nanson's formula)}, {\text {d}}\omega = J {\text {d}}\varOmega . \end{aligned}$$

By using boundary condition (14),

(43)

When Eq. (42) for $B_+$ and Eq. (42) for $B_-$ are summed, the first, the second, the third, the fourth and the sixth terms of (33) are obtained. Furthermore, boundary condition (13) is scalar multiplied by

integrated over $\varGamma _*$ and added to the sum of equations above. This gives the fifth and the seventh terms of (33), respectively. The eighth term is not consistent with the strong form and is added for numerical stabilisation. This term is considered in Sect. 4.1.6.

4.1.4 Finite-element formulation

The finite-element mesh covers the entire volume of the body $\varOmega = \varOmega _+ \cup \varOmega _-$ and is arbitrary with respect to interface $\varGamma _*$, i.e. the interface cuts through elements, as illustrated in Fig. 2a. Without loss of generality, the mesh is considered to be conforming to the external boundary of the body, $\partial \varOmega$. Obviously, it is also possible to formulate the method in the case when the external boundary is also non-conforming to the mesh. However, since the reference configuration is considered and the external boundary does not move in this configuration, in most cases, there will be no practical purpose of creating a mesh that is non-conforming to the external boundary.

The mesh contains N nodes. The standard nodal basis function associated with node i is denoted as $\psi _i$. These functions are continuous piecewise-polynomial functions and are equal to 1 at node i and equal to 0 at all other nodes. The space of the standard nodal basis functions is denoted as

$$\begin{aligned} \mathcal {S}^h = {\text {span}}\left\{ \psi _i \right\} _{i=1}^N , \quad \psi _i = \psi _i\left( \vec {X} \right) . \end{aligned}$$

To shorten the notation, additional space is introduced,

$$\begin{aligned} \mathcal {Q}^h = \left\{ \vec {\varphi } \left| \, \varphi _j \in \mathcal {S}^h \right. \right\} , \quad \varphi _j = \vec {\varphi } \cdot \vec {e} _j , \quad j \in \left\{ 1,2,3 \right\} . \end{aligned}$$

Furthermore, globally defined functions $\vec {u} _+^h, \vec {u} _-^h \in \mathcal {Q}^h$ are introduced.² Restrictions of functions $\vec {u} _+^h$ and $\vec {u} _-^h$ to domains $\varOmega _+$ and $\varOmega _-$, respectively, approximate solutions $\vec {u} _+$ and $\vec {u} _-$, respectively, of (5).

The set of all elements is denoted as $\mathcal {T}$. Furthermore, the following sets can be defined:

$$\begin{aligned} \mathcal {T}_\pm = \left\{ E \left| \, E \in \mathcal {T}, \, E \cap \varOmega _\pm ^h \ne \emptyset \right. \right\} , \end{aligned}$$

where E denotes an element. Sets $\mathcal {T}_+$ and $\mathcal {T}_-$ overlap, i.e. they share the set of elements, which are crossed by $\varGamma _*^h$. The set of all elements intersected by the interface is denoted as

$$\begin{aligned} \mathcal {T}_* = \mathcal {T}_+ \cap \mathcal {T}_- . \end{aligned}$$

Here superscript h is added to $\varOmega _\pm$ to indicate the discretisation of the boundaries of the domains, as also explained below, while $\varGamma _*^h$ is the discretised interface $\varGamma _*$.

Thus, the finite-element formulation of the mechanical problem is the following:

$$\begin{aligned}&\text {find } \vec {u} _+^h , \vec {u} _-^h \in \mathcal {Q}^h \text { such that} \quad a\left( \vec {u} _+^h, \vec {u} _-^h, \vec {\varphi } _+^h, \vec {\varphi } _-^h \right) = 0 ,\\&\quad \forall \vec {\varphi } _+^h , \vec {\varphi } _-^h \in \mathcal {Q}^h , \\&\vec {u} _\pm ^h = \vec {0} \text { at nodes that do not belong to elements } \mathcal {T}_\pm , \\&\vec {u} _\pm ^h = \vec {g} \text { at nodes on } \varGamma _\mathrm {D}\cap \mathcal {T}_\pm , \end{aligned}$$

where functional a was defined in (33). Numerical parameter $\beta$ in (33), which is introduced in the Nitsche-like methods, is usually taken to be inversely proportional to spatial step h,

$$\begin{aligned} \beta = \frac{\lambda }{h} , \end{aligned}$$

where $\lambda$ is a constant. The above finite-element problem represents a system of non-linear algebraic equations with respect to nodal values of $\vec {u} _+^h$ and $\vec {u} _-^h$, which can be solved using the standard Newton-Raphson method. This problem formulation is valid for the case when $\varvec{\sigma } _+$ does not depend on c in (6). The coupled problem is formulated in 4.3.

Although the above finite-element formulation follows relatively standard notation accepted in numerical analysis, it should be emphasised that when integrals in (33) are calculated for $a\left( \vec {u} _+^h, \vec {u} _-^h, \vec {\varphi } _+^h, \vec {\varphi } _-^h \right)$, the domains, over which the integration is performed, have discretised piece-wise linear boundaries. Thus, for the finite-element formulation, domains of integration $\varOmega _\pm$, $\varGamma _*$ and $\varGamma _\mathrm {T}$ are replaced by $\varOmega _\pm ^h$, $\varGamma _*^h$ and $\varGamma _\mathrm {T}^h$, respectively. Interiors of $\varOmega _+^h$ and $\varOmega _-^h$ do not overlap and $\varGamma _*^h = \varOmega _+^h \cap \varOmega _-^h$. This is usually taken as obvious; however, in this paper, the distinction is made to separate $\varGamma _*$ and $\varGamma _*^h$. The rules, according to which $\varGamma _*^h$ is constructed, are discussed in Sect. 4.4.1.

4.1.5 Assembling finite-element equations

Nodal values of $\vec {u} _+^h$ and $\vec {u} _-^h$ are denoted as $\vec {U} ^+_i$ and $\vec {U} ^-_i$, respectively,

$$\begin{aligned} \vec {u} _\pm ^h = \sum _{i=1}^N \psi _i \vec {U} ^\pm _i , \quad \psi _i = \psi _i\left( \vec {X} \right) . \end{aligned}$$

Without loss of generality, it can be assumed that

$$\begin{aligned}&\text {nodes } 1,\ldots ,N_\mathrm {a} \text { do not belong to elements } \mathcal {T}_- \\&\quad \text { and do not belong to } \varGamma _\mathrm {D} , \\&\text {nodes } N_\mathrm {a}+1,\ldots ,N_\mathrm {b} \text { belong to elements } \mathcal {T}_* \\&\quad \text { and do not belong to } \varGamma _\mathrm {D} , \\&\text {nodes } N_\mathrm {b}+1,\ldots ,N_\mathrm {c} \text { do not belong to elements } \mathcal {T}_+\\&\quad \text { and do not belong to } \varGamma _\mathrm {D} , \\&\text {nodes } N_\mathrm {c}+1,\ldots ,N_\mathrm {d} \text { do not belong to elements } \mathcal {T}_- \\&\quad \text { and belong to } \varGamma _\mathrm {D} , \\&\text {nodes } N_\mathrm {d}+1,\ldots ,N_\mathrm {e} \text { belong to elements } \mathcal {T}_* \\&\quad \text { and belong to } \varGamma _\mathrm {D} , \\&\text {nodes } N_\mathrm {e}+1,\ldots ,N \text { do not belong to elements } \mathcal {T}_+ \\&\quad \text { and belong to } \varGamma _\mathrm {D} . \end{aligned}$$

Following the finite-element formulation, the system of non-linear algebraic equations with respect to $\vec {U} ^+_i$ and $\vec {U} ^-_i$, where $i \in \left\{ 1,\ldots ,N\right\}$, is assembled:

$$\begin{aligned} {\left\{ \begin{array}{ll} a\left( \vec {u} _+^h, \vec {u} _-^h, \psi _i \vec {e} _j, \vec {0} \right) = 0 , \quad i \in \left\{ 1,\ldots ,N_\mathrm {b}\right\} , \quad j \in \left\{ 1,2,3 \right\} , \\ a\left( \vec {u} _+^h, \vec {u} _-^h, \vec {0} , \psi _i \vec {e} _j \right) = 0 , \quad i \in \left\{ N_\mathrm {a}+1,\ldots ,N_\mathrm {c}\right\} , \quad j \in \left\{ 1,2,3 \right\} . \\ \vec {U} ^+_i = \vec {0} , \quad i \in \left\{ N_\mathrm {b}+1,\ldots ,N_\mathrm {c},N_\mathrm {e}+1,\ldots ,N\right\} , \\ \vec {U} ^-_i = \vec {0} , \quad i \in \left\{ 1,\ldots ,N_\mathrm {a},N_\mathrm {c}+1,\ldots ,N_\mathrm {d}\right\} , \\ \vec {U} ^+_i = \vec {g} , \quad i \in \left\{ N_\mathrm {c}+1,\ldots ,N_\mathrm {e}\right\} , \\ \vec {U} ^-_i = \vec {g} , \quad i \in \left\{ N_\mathrm {d}+1,\ldots ,N\right\} . \end{array}\right. } \end{aligned}$$

(44)

Since functions $\vec {u} _+^h$ and $\vec {u} _-^h$ are defined globally, each node contains degrees of freedom (DOFs) both corresponding to “$+$” solution and to “−” solution. Therefore, formally, there are 4N and 6N DOFs in 2D and 3D, respectively (further in this section only 3D case is discussed). However, as seen from system (44), $\vec {U} ^+_i$ and $\vec {U} ^-_i$ are restricted to zero outside of elements $\mathcal {T}_+$ and $\mathcal {T}_-$, respectively, hence, calculation of these DOFs is trivial and does not increase the computational complexity. The advantage of keeping these DOFs is the convenience of coding, as the sizes of arrays does not depend on the position of the interface. Such technique has been used previously in application to the Nitsche-like methods [41].

As seen from system (44), the actual number of non-linear equations is $3\left( N_\mathrm {b}+N_\mathrm {c}-N_\mathrm {a}\right)$. Thus, the number of non-linear equations is increased by $3\left( N_\mathrm {b}-N_\mathrm {a}\right)$, compared to the standard FEM problem (where an interface might be present, but is conforming to the mesh). Thus, compared to the standard FEM, in this approach, number of DOFs, calculation of which is non-trivial, is doubled for all nodes that belong to the elements that are cut by the interface.

As seen from the first equation of system (44), when equations corresponding to $\vec {U} ^+_i$ are assembled, $\vec {\varphi } _-^h = \vec {0}$ everywhere. Analogously, the second equation of system (44) indicates that when equations corresponding to $\vec {U} ^-_i$ are assembled, $\vec {\varphi } _+^h = \vec {0}$ everywhere.

There is another possible interpretation of the above finite-element formulation, which is as follows. There are two different meshes, which consist of sets of elements $\mathcal {T}_+$ and $\mathcal {T}_-$. These meshes overlap over a set of elements $\mathcal {T}_+ \cap \mathcal {T}_-$. There are two different solutions, $\vec {U} ^+_i$ and $\vec {U} ^-_i$, each defined on the corresponding mesh. Thus, there are 3 DOFs per node of each mesh. To assemble the system of equations for the mechanical problem, at first, the test function defined on the first mesh, $\vec {\varphi } _+^h$, takes all possible values, while $\vec {\varphi } _-^h = \vec {0}$; afterwards, the test function defined on the second mesh, $\vec {\varphi } _-^h$, takes all possible values, while $\vec {\varphi } _+^h = \vec {0}$. Such interpretation is illustrated schematically in Fig. 2b.

4.1.6 Stabilisation term

When interface $\varGamma _*$ cuts through elements $\mathcal {T}$, it is possible that some elements are partitioned into highly unequal area fractions, as illustrated in Fig. 2c. This can create a numerical problem—the system of equations can become ill-conditioned. Therefore, in Nitsche-like methods, additional stabilisation terms are introduced in such cases, e.g. [2, 12, 34].

The set of all element boundaries is denoted as $\mathcal {F}$. The following set can be defined:

$$\begin{aligned} \mathcal {F}_* = \left\{ F \left| \, F \in \mathcal {F}, \, F \cap \varGamma _*^h \ne \emptyset \right. \right\} , \end{aligned}$$

where F denotes a boundary of an element.

The stabilisation term is added as an additional term I to the potential energy:

(45)

where $\vec {N} _f$ is the normal to boundary $\varGamma _f$, $\kappa$ is the numerical parameter and denotes the jump of the quantity across the element boundary. The orientation of normal $\vec {N} _f$ is not important, as the jump is squared.

Variation of the stabilisation term in the potential energy leads to

(46)

In [34], the set of boundaries used for the stabilisation term also included adjacent boundaries to $\mathcal {F}_*$. It is also possible to include these boundaries here and thereby generalise term (46). The inclusion of adjacent boundaries to $\mathcal {F}_*$ becomes important when the interface cuts comparably small fractions from a large set of neighbouring elements, which should be a relatively unlikely scenario in applied problems. In the numerical examples of this paper, adjacent boundaries were not included and no numerical difficulties related to conditionality of the problem were encountered.

In Eq. (45), $\varvec{F} _\pm$ is stabilised across the inter-element boundary. This choice is rather arbitrary and follows analogous stabilisation term from [2]. For the mechanical problem it is possible to use $\varvec{P} _\pm$ instead of $\varvec{F} _\pm$ in Eq. (45), i.e. stabilise stresses instead of deformation gradients; however, this choice of stabilisation term is not investigated in this paper.

4.2 Diffusion

Since mixed boundary conditions are imposed for the diffusion problem, it does not require any special treatment and the standard transformation of the strong form to the weak form is applicable. Hence, Eq. (15) is multiplied by a test function and integrated over the volume, which leads to

$$\begin{aligned} 0= & {} -\int _{\varOmega _+} \varphi \nabla _0 \cdot \vec {j} {\text {d}}\varOmega _+ = \int _{\varOmega _+} \left( \nabla _0 \varphi \right) \cdot \vec {j} {\text {d}}\varOmega _+\nonumber \\&- \int _{\partial \varOmega _+} \varphi \vec {N} _{\partial \varOmega _+} \cdot \vec {j} {\text {d}}\left( \partial \varOmega _+\right) , \end{aligned}$$

(47)

where $\vec {N} _{\partial \varOmega _+}$ is the outer normal to the surface of the body $B_+$ in the reference configuration. Using boundary conditions (17) and (19), the weak form is obtained:

$$\begin{aligned} \text {find } c \in H^1\left( \varOmega _+\right) \text { such that} b\left( c, \varphi \right) = 0 , \forall \varphi \in H^1\left( \varOmega _+\right) , \end{aligned}$$

where

$$\begin{aligned} b\left( c, \varphi \right)= & {} \int _{\varOmega _+} \left( \nabla _0 \varphi \right) \cdot \vec {j} {\text {d}}\varOmega _+\nonumber \\&+ \int _{\varGamma _*} \varphi f_* {\text {d}}\varGamma _* + \int _{\varGamma _\mathrm {M}} \varphi f_\mathrm {M} {\text {d}}\varGamma _\mathrm {M} . \end{aligned}$$

(48)

4.2.1 Finite-element formulation

The same finite-element mesh as for the mechanical problem, Sect. 4.1.4, is used for the diffusion problem. Therefore, the same notation for the standard nodal basis functions, $\psi _i$, and for the space of the standard nodal basis functions, $\mathcal {S}^h$, is used. Furthermore, globally defined function $c^h \in \mathcal {S}^h$ is introduced. Restriction of function $c^h$ to domain $\varOmega _+$ approximate solution c of (15).

Fig. 3

The steps of the general scheme of the movement of the reaction front—discretisation of the interface (a), movement of the intersection points to construct a temporary interface (b) and construction of a new interface from the intersection points of the temporary interface and the mesh (c). The normals at the intersection points are determined by averaging the normals of the segments located in the neighbouring elements (d)

Thus, the finite-element formulation of the diffusion problem is the following:

$$\begin{aligned}&\text {find } c^h \in \mathcal {S}^h \text { such that} \quad b\left( c^h, \varphi ^h \right) = 0 , \quad \forall \varphi ^h \in \mathcal {S}^h , \\&c^h = 0 \text { at nodes that do not belong to elements } \mathcal {T}_+ , \end{aligned}$$

where functional b was defined in (48). The above finite-element problem represents a system of either linear or non-linear algebraic equations with respect to nodal values of $c^h$, depending on the choice of the constitutive laws. In the case when the system is non-linear, the standard Newton-Raphson method can be used for the solution.

The calculation of integrals in b requires $f_*$, which is a function of V, which, in turn, depends on $\varvec{\sigma } _+$, $\varvec{F} _+$ and $W_+$. These quantities result from the solution of the mechanical problem. Moreover, in general case, $\vec {j}$ depends on $\varvec{\sigma } _+$ and $\varvec{F} _+$. Therefore, the above problem formulation is valid for the case when $\varvec{\sigma } _+$, $\varvec{F} _+$ and $W_+$ are already known, i.e. the mechanical problem can be solved first within a particular time step, otherwise, the coupled problem should be solved, as presented in Sect. 4.3. Evaluation of V in the finite-element representation is discussed in Sect. 4.4.2.

Since in the case of diffusion problem, integrals in (48) are also evaluated in cut elements, similar inter-element stabilisation term as in the mechanical problem, Sect. 4.1.6, can be introduced. However, such term was not used in the numerical examples of this paper, as no issues related to the conditionality of the problem were observed.

4.2.2 Assembling finite-element equations

Nodal values of $c^h$ are denoted as $C_i$,

$$\begin{aligned} c^h = \sum _{i=1}^N \psi _i C_i , \quad \psi _i = \psi _i\left( \vec {X} \right) . \end{aligned}$$

The same notation for the node numbers as in Sect. 4.1.5 is used. Following the finite-element formulation, the system of algebraic equations with respect to $C_i$, where $i \in \left\{ 1,\ldots ,N\right\}$, is assembled:

$$\begin{aligned} {\left\{ \begin{array}{ll} b\left( c^h, \psi _i \right) = 0 , \quad i \in \left\{ 1,\ldots ,N_\mathrm {b},N_\mathrm {c}+1,\ldots ,N_\mathrm {e}\right\} , \\ C_i = 0 , \quad i \in \left\{ N_\mathrm {b}+1,\ldots ,N_\mathrm {c},N_\mathrm {e}+1,\ldots ,N\right\} . \end{array}\right. } \end{aligned}$$

(49)

Since function $c^h$ is defined globally, formally, there are N DOFs. However, as $C_i$ are restricted to zero outside of elements $\mathcal {T}_+$, calculation of extra DOFs is trivial and does not increase the computational complexity. As in Sect. 4.1.5, the advantage of keeping these DOFs is the convenience of coding, as the sizes of arrays does not depend on the position of the interface.

4.3 Coupled system

In the case when the stresses in the transformed material depend on the concentration of the reactant, the mechanical problem must be solved together with the diffusion problem. Thus, the finite-element formulation of the coupled problem is the following:

$$\begin{aligned}&\text {find } \vec {u} _+^h , \vec {u} _-^h \in \mathcal {Q}^h \text { and } c^h \in \mathcal {S}^h \\&\quad \text { such that } {\left\{ \begin{array}{ll} a\left( \vec {u} _+^h, \vec {u} _-^h, \vec {\varphi } _+^h, \vec {\varphi } _-^h \right) = 0 , \quad \forall \vec {\varphi } _+^h , \vec {\varphi } _-^h \in \mathcal {Q}^h , \\ b\left( c^h, \varphi ^h \right) = 0 , \quad \forall \varphi ^h \in \mathcal {S}^h , \end{array}\right. } \\&\vec {u} _\pm ^h = \vec {0} \text { at nodes that do not belong to elements } \mathcal {T}_\pm , \\&\vec {u} _\pm ^h = \vec {g} \text { at nodes on } \varGamma _\mathrm {D} \cap \mathcal {T}_\pm , \\&c^h = 0 \text { at nodes that do not belong to elements } \mathcal {T}_+ . \end{aligned}$$

Here the dependency of a on $c^h$ is via $\varvec{\sigma } _+$ and the dependency of b on $\vec {u} _+^h$ and $\vec {u} _-^h$ is via $\vec {j}$. The assembling of the finite-element equations for the coupled system leads to systems (44) and (49), which are now coupled and must be solved together.

4.4 Movement of the reaction front

Reaction front $\varGamma _*$ is a curve in a 2D setting or a surface in a 3D setting. In the finite-element formulation, reaction front $\varGamma _*$ is represented by a piece-wise linear continuous curve/surface $\varGamma _*^h$, which crosses the edges of finite elements. Within each element $\varGamma _*^h$ is strictly linear. There are two additional requirements imposed on $\varGamma _*^h$, as presented below. It should be noted that the method can be generalised to the case when $\varGamma _*^h$ is piece-wise polynomial; however, for clarity of the presentation, the piece-wise linear case is selected here.

The reaction front is moved using an explicit time stepping, i.e. for a certain position of $\varGamma _*^h$, the mechanical and the diffusion problems are solved, the current velocities are obtained and the points of the reaction front are moved using these velocities. The general scheme, which starts from the discretisation of a continuous interface, is illustrated in Fig. 3 and further details are provided in subsections below.

After the interface is moved, a new initial estimate for the Newton-Raphson scheme is required, which can be taken to be the solution at the previous time step. In this case, the major point of attention is the possible change of the set of intersected elements, which means that some nodes that belonged to $\varOmega _-^h$ at the previous time step, may belong to $\varOmega _+^h$ at the current time step. Therefore, all DOFs for these nodes must be initialised using solution $\vec {u} _-^h$ at the previous time step.

Fig. 4

The schematic representation of the discretisation of the interface. Continuous interface $\varGamma _*$ is illustrated in blue colour, discretised interface $\varGamma _*^h$ is illustrated in red colour. Hypothetical discretisation of $\varGamma _*$, which is forbidden by the imposed constraints, is illustrated in black colour. In subfigure (d), the formation of a closed loop is shown, as also discussed in Sect. 4.4.3

4.4.1 Intersection points and surface normals

The set of all element edges is denoted as $\mathcal {E}$. The set of intersection points of $\varGamma _*^h$ and the element edges is denoted as $\mathcal {I}$,

$$\begin{aligned} \mathcal {I} = \left\{ \vec {P} \left| \, \exists A \in \mathcal {E}, \, \vec {P} \in A \cap \varGamma _*^h \right. \right\} , \end{aligned}$$

where $\vec {P}$ denotes an intersection point and A denotes an element edge. Reaction front $\varGamma _*^h$ is constructed such that

• set $\mathcal {I}$ is finite;

• each element $E \in \mathcal {T}_*$ contains only a single linear segment of $\varGamma _*^h$.

The second requirement is introduced to avoid an ill-posed problem, while the first requirement is introduced for practical purposes as explained below.

The schematic illustration of the effect of these two requirements is demonstrated in Fig. 4, where $\varGamma _*^h$ does not cover all intersection points of $\varGamma _*$ and the mesh. In Fig. 4c, the effect of the first constraint is shown—the configuration of the interface shown in black colour is not allowed, as number of coinciding points of the interface and the element edges must be finite. The resulting discretised interface, after forbidden points are excluded, is shown in red colour. In Fig. 4b, the effect of the second constraint is shown—there cannot be two segments of the interface within one element. In Fig. 4a, the typical case when both constraints forbid a certain configuration of the interface is shown. Finally, in Fig. 4d, an interesting effect emerging from these constraints is shown—in some cases, a single interface curve can be separated into several curves, some of which can form closed loops.

It should be mentioned that the rules for discretising the interface are somewhat restrictive in this paper. From the mathematical point of view, it is perfectly allowable that a part of the interface coincides with a side of an element. The only reason for introducing the restriction, which forbids this, as shown in Fig. 4c, is the simplicity and the efficiency of the coding. In practice, occurrence of such case should be extremely rare, as in almost all cases the interface will fall inside the elements. However, from the programming point of view, accounting for such case requires creation of additional structure types for interface segments and coding additional conditional checks. Therefore, from the practical point of view, it is reasonable to exclude the case of Fig. 4c. Moreover, it should also be noted that, since in real applications the interface is expected to be “smooth” (on this occasion, this term is not used in strict mathematical sense, but implies small differences in orientation of line segments), occurrence of a case similar to the ones illustrated in Fig. 4 would mean that the background mesh is too coarse and thus the solution is imprecise.

If an intersection point of $\varGamma _*^h$ and the mesh is closer than $\zeta$ to a node, then this intersection point is moved to the location of the node. Here, $\zeta$ is a very small numerical parameter, which is introduced to avoid a very short segment of the interface influencing the calculation of normals. In the numerical examples of this paper $\zeta = 10^{-6}$ was taken.

For each element $E \in \mathcal {T}_*$, the normal to $\varGamma _*^h$ is defined as $\vec {N} _*^h$ and is the outer normal to $\varOmega _+^h$. Thus, $\vec {N} _*^h$ corresponds to $\vec {N} _*$. Since $\varGamma _*^h$ is linear within each element, $\vec {N} _*^h$ is constant within each element.

For each point $\vec {P} \in \mathcal {I}$, there is a number of neighbouring elements $E_j \in \mathcal {T}_*$, such that, $\vec {P} \in E_j$, $\forall j$. If point $\vec {P}$ is at $\partial \varOmega ^h$, then it might have only one neighbouring element, while if point $\vec {P}$ is inside $\varOmega ^h$, then it has at least two neighbouring elements. Formally, normal to $\varGamma _*^h$ is not defined at point $\vec {P}$; however, an approximation of normal to $\varGamma _*$ at point $\vec {P} \in \mathcal {I}$ can be defined. In this paper, this approximation is defined as the normalised average of the normals of all neighbouring elements,

$$\begin{aligned} \vec {N} _*^h\left( \vec {P} \right) = \left| \sum _j \vec {N} _*^h\left( E_j\right) \right| ^{-1} \sum _j \vec {N} _*^h\left( E_j\right) , \quad \vec {P} \in \mathcal {I}, \quad E_j \in \mathcal {T}_* , \end{aligned}$$

where $\vec {N} _*^h\left( \vec {P} \right)$ is an approximation of normal to $\varGamma _*$ at point $\vec {P}$ and $\vec {N} _*^h\left( E_j\right)$ is normal to $\varGamma _*^h$ within element $E_j$. The summation is performed over all neighbouring to $\vec {P}$ elements $E_j$.

Fig. 5

The schematic representation of the movement of an end point of the reaction front—movement of the intersection points to construct a temporary interface (a), linear fit for the points of the interface that are close to the edge (b), construction of a additional external intersection point (c) and construction of a new interface (d)

4.4.2 Points’ velocities

The velocities of the reaction front are calculated at each point $\vec {P} \in \mathcal {I}$ according to Eq. (20). This requires the calculation of c, $\varvec{\sigma } _\pm$, $\varvec{F} _\pm$ and $W_\pm$ at point $\vec {P}$. Obviously, some kind of inter-element averaging and interpolation can be used to obtain the values of these quantities at point $\vec {P}$.

In the case of linear finite-elements, concentration c at point $\vec {P}$ can easily be obtained by linearly interpolating nodal values of $c^h$ at the element edge, to which point $\vec {P}$ belongs. Quantities $\varvec{\sigma } _\pm$, $\varvec{F} _\pm$ and $W_\pm$ are defined inside the elements. In this case of linear finite elements, $\varvec{\sigma } _\pm$, $\varvec{F} _\pm$ and $W_\pm$ are constant within an element; therefore, the values at point $\vec {P}$ can be obtained by simple averaging of the values at neighbouring to $\vec {P}$ elements $E_j \in \mathcal {T}_*$. Such averaging scheme is the simplest; a more elaborate inter-element stress/energies averaging procedure might improve the overall accuracy of the method.

It should be noted that in this paper, velocity depending on is taken, as presented in Sect. 5.1. Therefore, in the numerical examples of this paper, inter-element averaging is applied directly to term .

In the case when the interface crosses the boundary of the body, the intersection points of the interface and the edges of the elements that belong to the boundary of the body, $\vec {P} \in \mathcal {I} \cap \partial \varOmega ^h$, may have fewer neighbouring elements than the rest of the intersection points. In the 2D case, these intersection points may have only one neighbouring element, while other intersection points have at least two. Therefore, due to a reduced number of available neighbouring elements to perform inter-element averaging/interpolation of quantities such as $\varvec{\sigma } _\pm$ and $\varvec{F} _\pm$, the accuracy of the calculated velocities at these intersection points may be reduced.

To mitigate the issue of the influence of non-averaged/non-interpolated quantities on the velocity of the interface, velocities at points $\vec {P} \in \mathcal {I} \cap \partial \varOmega ^h$ are obtained by extrapolation from velocities at neighbouring intersection points that do not belong to $\partial \varOmega ^h$. For the extrapolation, V is represented as a function on curve/surface $\varGamma _*^h$. It should be noted that in the numerical examples of this paper, such extrapolation (using 4 neighbouring points) is applied to quantity q, which is introduced in Sect. 5.1, and not to the velocity.

4.4.3 Moving points and finding new configuration of the interface

After point velocities $V\left( \vec {P} \right)$ and normals $\vec {N} _*^h\left( \vec {P} \right)$ are obtained, $\vec {P} \in \mathcal {I}$, new points $\vec {P} ^\Delta$ are calculated,

$$\begin{aligned} \vec {P} ^\Delta \left( \vec {P} \right) = \vec {P} + V\left( \vec {P} \right) \vec {N} _*^h\left( \vec {P} \right) \Delta t, \quad \vec {P} \in \mathcal {I} , \end{aligned}$$

where $\Delta t$ is the user-defined time step. Temporary interface $\hat{\varGamma }_*^h$ is obtained by linearly connecting points $\vec {P} ^\Delta \in \varOmega ^h$ in the same order as corresponding points $\vec {P}$ are connected to form $\varGamma _*^h$. Points $\vec {P} ^\Delta \notin \varOmega ^h$ do not participate in formation of $\hat{\varGamma }_*^h$, as shown in Fig. 5b.

Depending on the orientation of the interface and the velocities of the points, it may happen that neither of points $\vec {P} ^\Delta \in \varOmega ^h$ belongs to the boundary of the body, $\partial \varOmega ^h$, while $\varGamma _*^h \cap \partial \varOmega ^h \ne \emptyset$. In this case, extrapolation is used to extend curve/surface $\hat{\varGamma }_*^h$ upto $\partial \varOmega ^h$. The 2D case of such extrapolation is shown in Fig. 5c, d. For each end point of $\hat{\varGamma }_*^h$, a set of N points $\vec {P} ^\Delta$, which are closest to the end point of $\hat{\varGamma }_*^h$, are taken and a linear fit for these points is performed. The intersection point of the obtained line and a line parallel to $\partial \varOmega ^h$ and distanced from it by h is found. Curve $\hat{\varGamma }_*^h$ is extended to include this intersection point using a linear segment. In the numerical examples of this paper, $N=4$ was taken.

The set of intersection points of $\hat{\varGamma }_*^h$ and the element edges is denoted as $\hat{\mathcal {I}}$,

$$\begin{aligned} \hat{\mathcal {I}} = \left\{ \vec {R} \left| \, \exists A \in \mathcal {E}, \, \vec {R} \in A \cap \hat{\varGamma }_*^h \right. \right\} , \end{aligned}$$

where $\vec {R}$ denotes an intersection point and A denotes an element edge. The new position of the interface, which is denoted as $\tilde{\varGamma }_*^h$, is obtained by connecting points from set $\hat{\mathcal {I}}$ almost in the same order (with few possible exceptions) as corresponding linear segments of $\hat{\varGamma }_*^h$ are connected. The deviations from the connecting order are introduced when it is necessary to satisfy similar requirements as imposed on $\varGamma _*^h$:

• the set of intersection points of $\tilde{\varGamma }_*^h$ and element edges is finite;

• each element, which is crossed by $\tilde{\varGamma }_*^h$, contains only a single linear segment of $\tilde{\varGamma }_*^h$.

The connection is also made such that the formation of the closed curves/surfaces is tracked, as illustrated in Fig. 4d. In this case, $\tilde{\varGamma }_*^h$ may split into multiple curves/surfaces in proximity of points in $\hat{\mathcal {I}}$ that do not belong to $\tilde{\varGamma }_*^h$. As the interface moves, two separate segments of the interface might enter a single element, e.g. black segments in Fig. 4d, which is forbidden by the above constraints, and the interface splits into a closed loop and the rest of the interface. Splitting of the interface does not mean the loss of generality of the finite-element methods described in Sects. 4.1.4, 4.2.1 and 4.3.

5 Numerical examples

Since the purpose of this paper is the presentation of a numerical method, units are omitted for all the quantities, which is common in numerical analysis.

The unit square geometry is selected. The geometry is meshed using linear finite elements composing a structured mesh. All elements of the mesh are isosceles right triangles with side lengths of h. The example of finite-element mesh will be shown later.

In the mechanical part of the problem, the plane strain case is considered. Therefore, matrix notation of the total deformation gradient tensor with respect to an Euclidean basis is given by

$$\begin{aligned} \underline{F} = \begin{pmatrix} \frac{\partial x_1}{\partial X_1} &{} \frac{\partial x_1}{\partial X_2} &{} 0 \\ \frac{\partial x_2}{\partial X_1} &{} \frac{\partial x_2}{\partial X_2} &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{pmatrix} . \end{aligned}$$

Thus, unknown displacements $\vec {u}$ are in the 12-plane.

Fig. 6

The reference (a) and the current (b) configurations of the two-phase body with the interface non-conforming to the finite-element mesh. The phases below and above the interface are the transformed and the untransformed materials, respectively. The calculation was performed for $h = 1/32$, $\lambda = 10^4$, $\kappa = 0$

Fig. 7

The pressure (a) and the von Mises stress (b) field plots illustrated on the geometry in the reference configuration. The calculation was performed for $h = 1/128$, $\lambda = 10^4$, $\kappa = 0$

5.1 Constitutive relations for numerical examples

The hyperelastic mechanical constitutive relation is taken for both phases [13, 23]:

$$\begin{aligned}&W_+' = K_+ \left( J_+' - 1 - \ln J_+' \right) + \frac{G_+}{2}\left( {\text {tr}} \left( \bar{\varvec{B} }_+'\right) - 3 \right) , \end{aligned}$$

(50)

$$\begin{aligned}&W_- = K_- \left( J_- - 1 - \ln J_- \right) + \frac{G_-}{2}\left( {\text {tr}} \left( \bar{\varvec{B} }_-\right) - 3 \right) , \end{aligned}$$

(51)

where

$$\begin{aligned}&\bar{\varvec{B} }_+' = \left( J_+'\right) ^{-\frac{2}{3}} \varvec{F} _+' \cdot {\varvec{F} _+'}^\mathrm {T} , \quad J_+' = {\text {det}} \left( \varvec{F} _+' \right) , \nonumber \\&\varvec{F} _+' = \varvec{F} _+ \cdot \varvec{G} ^{-1} , \end{aligned}$$

(52)

$$\begin{aligned}&\bar{\varvec{B} }_- = \left( J_-\right) ^{-\frac{2}{3}} \varvec{F} _- \cdot \varvec{F} _-^\mathrm {T} , \quad J_- = {\text {det}} \left( \varvec{F} _- \right) . \end{aligned}$$

(53)

It should be emphasised that the elastic strain energy density for the transformed material is defined with respect to the chemically transformed configuration. The derivatives of $W_\pm$ required for the implementation are summarised in appendix 1.

The following chemical expansion is chosen:

$$\begin{aligned} \varvec{G} = g \left( \vec {e} _1 \vec {e} _1 + \vec {e} _2 \vec {e} _2 \right) + \vec {e} _3 \vec {e} _3 , \quad \text {for } \vec {X} \in \varOmega _+ . \end{aligned}$$

(54)

The diffusion flux according to the Fick’s law is taken:

$$\begin{aligned} \vec {j} = -D \nabla _0 c , \end{aligned}$$

(55)

where D is the diffusion coefficient.

The reaction kinetics, which is governed by the chemical affinity tensor [6,7,8], is considered. This tensor acts as a configurational driving force for the reaction front and was derived from the balance laws and the dissipation inequality. In this approach, the expression for the velocity has the following structure:

(56)

while function $f_*$ used in the boundary condition (17) for the diffusion problem at the reaction front now becomes

$$\begin{aligned} f_* = p_4 V , \end{aligned}$$

(57)

where s, $p_1$, $p_2$, $p_3$ and $p_4$ are physical parameters, which depend on temperature, reaction rate constant, solubility of the reactant in the transformed material, molar masses of the constituents, stoichiometric coefficients of the constituents, densities of the constituents in the corresponding reference configurations and temperature-dependent chemical energies.

In the numerical examples of this paper, the body is considered to be at a constant temperature. Thus, the temperature only influences the values of physical parameters and does not enter equations explicitly.

In the numerical examples, bulk moduli $K_+ = K_- = 10$ and shear moduli $G_+ = G_- = 2$ were taken. Diffusion parameters $D = s = 1$ and reaction parameters $p_1 = p_2 = p_3 = p_4 = 1$ were taken. Parameter $\alpha$ was taken to be different on different edges to take into account different boundary conditions, as described in Sect. 5.4. Chemical expansion ratio was taken as $g = 1.1$. In the Newton-Raphson method, absolute tolerances for the $\ell ^\infty$-norms of the function and of the change of the solution were taken to be $10^{-11}$. Numerical parameters $\lambda$ and $\kappa$ were varied and are provided below.

5.2 Example of a mechanical problem with stationary non-conforming interface

The purpose of this section is to demonstrate that the mechanical part of the problem for the case of stationary (fixed) interface provides a reliable solution. This is shown by demonstrating the expected convergence with respect to the mesh size and by comparing the non-conforming interface problem with conforming interface problem resolved via standard FEM.

For the examples in this section, the traction-free boundary conditions with removed rigid body motion were used:

$$\begin{aligned}&u_1 = 0, \quad u_2 = 0 \quad \text {at node } \left( 0,0\right) , \\&u_2 = 0 \quad \text {at node } \left( 1,0\right) . \end{aligned}$$

5.2.1 Case 1: flat interface

The case when the interface between two phases is flat can be easily compared with the standard FEM approach. In this example, the interface was taken to be line $X_2 = 7/12$, while the materials below and above the interface were taken to be the transformed and the untransformed materials, respectively. In the case of the standard FEM, the interface was lying exactly along the element edges, such that elements were entirely assigned to either the transformed or the untransformed material. It is useful to define the mesh size as $h = 1/N$. For the standard FEM, $N \in \left\{ 12, 24, 48, 96, 192, 840 \right\}$ was used, while for the non-conforming interface case, $N \in \left\{ 4, 8, 16, 32, 64, 128, 256 \right\}$ was used.

Fig. 8

The dependence of the error on the mesh size for the standard FEM and the non-conforming interface FEM problems. The error was calculated as the $\ell ^2$-norm of the difference between the current solution and the reference standard FEM solution with the mesh size of $h = 1/840$. For the non-conforming interface problem, $\lambda = 10^4$ and $\kappa = 0$ were taken

The examples of the reference and the current configurations of the problem with the non-conforming interface are illustrated in Fig. 6. The contour plots of the pressure and the von Mises stress,

$$\begin{aligned} p = -\frac{1}{3} {\text {tr}} \left( \varvec{\sigma } \right) , \quad \sigma _\mathrm {VM} = \sqrt{\frac{3}{2} \varvec{\sigma } ^\mathrm {d} :\varvec{\sigma } ^\mathrm {d} } , \end{aligned}$$

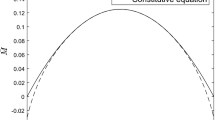
are shown in Fig. 7. As it can be expected, the positive pressure emerges in the area below the interface, which indicates the compression of the transformed material, while the negative pressure emerges above the interface, indicating tension of the untransformed material. The von Mises stress is obviously large around the interface indicating significant deviatoric stresses in this region.

Fig. 9

The dependence of the error on numerical parameters $\lambda$ (a) and $\kappa$ (b) for the non-conforming interface FEM problem. The calculation in subfigure a was performed for $h = 1/32$ and $\kappa = 0$, the calculation in subfigure b was performed for $\lambda = 10^4$

Since the number of DOFs is doubled for the nodes that belong to the elements, which are intersected by the interface (i.e. the intersected elements are doubled), the full Cauchy stress tensor in the intersected elements was averaged first and the pressure and the von Mises stress were calculated afterwards. This explains the non-physical stress values in the intersected elements in Fig. 7. Thus, when the non-conforming mesh is used, a somewhat more elaborate stress visualisation technique might be beneficial, where parts of the intersected elements are coloured according to the stresses in the corresponding phases.

To compare the standard FEM and the non-conforming interface FEM, the standard FEM solution with the mesh size of $h = 1/840$ was taken as the reference solution. The solutions with different mesh sizes were compared at the nodes of the mesh with $h_\mathrm {c}=1/4$, i.e. $M = 25$ comparison points were selected. The error was calculated as the $\ell ^2$-norm of the difference between the solutions taken at the comparison points:

$$\begin{aligned} e \left( h_1, h_2 \right) = \frac{1}{M} \left\| U^{h_1} - U^{h_2} \right\| _{\ell ^2} , \end{aligned}$$

(58)

where $U^{h_1}$ and $U^{h_2}$ are solutions with mesh sizes $h_1$ and $h_2$, respectively, taken at the comparison points.³

The main result of this section, the convergence of the non-conforming interface FEM problem, is shown in Fig. 8. The error was calculated according to (58), where the reference solution was compared to solutions with various mesh sizes. It can be seen that the non-conforming interface FEM problem has the same convergence rate with respect to the mesh size as the standard FEM problem. The calculated convergence rate for the non-conforming interface FEM (i.e. the slope of the linear fit in Fig. 8) is $r = 1.994$, which is close to the theoretical convergence rate of the linear FEM that is equal to 2.

Fig. 10

The reference (a) and the current (b) configurations of the two-phase body with the interface non-conforming to the finite-element mesh. The phases below and above the interface are the transformed and the untransformed materials, respectively. The calculation was performed for $h = 1/32$, $\lambda = 10^4$, $\kappa = 10^{-3}$

Fig. 11

The pressure (a) and the von Mises stress (b) field plots illustrated on the geometry in the reference configuration. The calculation was performed for $h = 1/128$, $\lambda = 10^4$, $\kappa = 10^{-3}$

Furthermore, the influence of numerical parameters $\lambda$ and $\kappa$ on the numerical error was investigated for the the non-conforming interface FEM problem. In Fig. 9a, the influence of $\lambda$ on the error is shown. For $\lambda < 10^{1.5}$, the solution sometimes did not converge, hence there are some gaps in the plot. Moreover, for small $\lambda$, the error somewhat oscillates and levels off for large $\lambda$. In Fig. 9b, the influence of $\kappa$ on the error is shown. Obviously, the introduction of the stabilisation term somewhat increases the error; however, it can be seen that for small $\kappa$ this increase is negligible, while such stabilisation term can be important for cases when the interface cuts a small area fraction in some elements.

5.2.2 Case 2: curved interface

In this example, the interface was taken to be parabolic curve $X_2 = 11/17 - \left( X_1-1/2\right) ^2$, while the materials below and above the interface were taken to be the transformed and the untransformed materials, respectively. This example is less trivial than the previous example and shows the main advantage of the method—an ability to handle curved interfaces non-conforming to the mesh. Mesh sizes $h = 1/N$, $N \in \left\{ 32, 64, 128 \right\}$ were used.

The examples of the reference and the current configurations are illustrated in Fig. 10. The pressure and the von Mises stress field plots are illustrated in Fig. 11. As in the case of flat interface, the positive and the negative pressure emerge in the areas below and above the interface, respectively. Moreover, similar von Mises stress distribution is observed.

Fig. 12

The pointwise convergence rate on lines $X_2 = 1/4$ (a, d), $X_2 = 1/2$ (b, e) and $X_2 = 3/4$ (c, f) as a function of $X_1$. Parameters $\lambda$ (a–c) and $\kappa$ (d–f) are varied

For the problem with the curved interface, the convergence rate was evaluated pointwise:

$$\begin{aligned} r \left( \vec {X} _j, h \right) = \log _2 \frac{ \left| \vec {u} ^h\left( \vec {X} _j\right) - \vec {u} ^{h/2}\left( \vec {X} _j\right) \right| }{ \left| \vec {u} ^{h/2}\left( \vec {X} _j\right) - \vec {u} ^{h/4}\left( \vec {X} _j\right) \right| } , \end{aligned}$$

(59)

where $r \left( \vec {X} _j, h \right)$ is the convergence rate at point $\vec {X} _j$. The pointwise convergence rate on three lines across the computational domain, $X_2 = 1/4$, $X_2 = 1/2$, $X_2 = 3/4$, is illustrated in Fig. 12 as a function of $X_1$. For small values of parameter $\kappa$, the convergence rate is around 2, which is the expected theoretical convergence rate of linear FEM. However, there are some oscillations in pointwise convergence rate, especially at $X_2 = 3/4$ and $\kappa = 10^{-3}$, which means that the solution with the used mesh sizes and parameter values was not entirely in the asymptotic region.

In Fig. 12a–c, parameter $\lambda$ was varied and it can be observed that for large $\lambda$, its influence on the convergence rate is negligible. Parameter $\lambda$ should only be large enough for the solution to converge, as was discussed in Sect. 5.2.1. Parameter $\kappa$ influences convergence rate in a non-linear way. As seen in Fig. 12d–f, up to $\kappa = 10^{-1}$ the convergence rate is still around the theoretical convergence value, which is 2; however, for $\kappa = 1$, the convergence rate drops to 1. This obviously happens due to overconstrained inter-element jump of the deformation gradient in the intersected elements, as prescribed in Eq. (45). The main advantage of the inter-element stabilisation term is the regularisation of the solution for certain values of $\kappa$, which can be seen in Fig. 12d–f, where for $\kappa = 10^{-2}$ and $10^{-1}$ the convergence rate becomes more spatially homogeneous than for $\kappa = 0$ (absence of the inter-element stabilisation term).

It can be concluded that there are optimal values of numerical parameters $\lambda$ and $\kappa$. Parameter $\lambda$ is the coefficient in front of the interface stabilisation term, which is usually introduced in Nitsche-like methods, and should be relatively large, although extremely large values of $\lambda$ lead to the large norm of the function in the Newton-Raphson method, which makes it difficult to determine when the convergence is reached. Parameter $\kappa$ controls the inter-element stabilisation and should be relatively small, however, very small values lead to insufficient stabilisation and hence ill-conditionality of the problem.

5.3 Testing the interface movement scheme

The full mechanochemical problem relies on the scheme of the interface movement. Therefore, it is important to test this scheme as a separate component of the full method.

To test the interface movement separately, initially circular interface $\left( X_1 - 13/23 \right) ^2 + \left( X_2 - 13/23 \right) ^2 = \left( 5/23 \right) ^2$ was created. Furthermore, the influence of stresses on the velocity was removed and the uniform concentration field was imposed, i.e. $q = 0$ and $c = 1$ in Eq. (56) were taken. Under these conditions, the interface is an expanding in time circle, thus, the analytical solution for the interface position is known. To obtain the numerical solution, 10 time steps of the interface movement on different meshes were performed with $\Delta t = 0.02$. Mesh sizes $h = 1/N$, $N \in \left\{ 8, 16, 32, 64, 128, 256 \right\}$ were used.

Fig. 13

The reference configuration of the two-phase body with the interface configuration at different times (a) for $h =1/32$ and $\Delta t = 1/32$. The dependence of the velocities of 4 interface points on time (b) for $h = 1/64$ and $\Delta t = 1/128$

The expected second-order convergence of the error of the radius of the circular interface was obtained (the plot is not shown here for brevity). This error was calculated as the $\ell ^1$-norm of the vector-column containing all intersection points, divided by the number of points. This illustrates the expected performance of the interface discretisation and movement method.

5.4 Example of a coupled problem with moving non-conforming interface in a constrained 2D body

In this section, an example of a constrained body, in which the chemical reaction takes place, is considered. Due to chemically-induced expansion of the transformed material, there is a build up of mechanical stresses which affect the chemical reaction rate.

Fig. 14

The pressure (a) and the von Mises stress (b) field plots at $t=2.5$ illustrated on the geometry in the reference configuration. The calculation was performed for $h = 1/64$ and $\Delta t = 1/128$

Fig. 15

The current configurations of the two-phase body at $t=0$ (a) and $t=2.5$ (b). The phases below and above the interface are the transformed and the untransformed materials, respectively. The calculation was performed for $h = 1/32$ and $\Delta t = 1/32$

Fig. 16

The concentration field plot (a) at $t=2.5$ illustrated on the geometry in the reference configuration. The concentration profile at the reaction front for different times (b) illustrated as the function of $X_1$. The calculation was performed for $h = 1/64$ and $\Delta t = 1/128$

For the example in this section, in the mechanical part of the problem, the bottom boundary was clamped and the top boundary was indented as follows:

$$\begin{aligned}&u_1 = 0, \quad u_2 = 0 \quad \text {at nodes on } X_2 = 0 , \\&u_1 = 0, \quad u_2 = -0.1 X_1 \quad \text {at nodes on } X_2 = 1 . \end{aligned}$$

The left and the right boundaries were traction-free. Such boundary conditions create inhomogeneous non-symmetric stress field within the body and the effect of stress concentrations on the local kinetics of the reaction front can be observed.

In the diffusion part of the problem, mixed boundary conditions were enforced on the bottom boundary and zero-flux boundary conditions were enforced on the left and the right boundaries:

$$\begin{aligned}&\alpha = 1 \quad \text {on } X_2 = 0 , \\&\alpha = 0 \quad \text {on } X_1 = 0 \text { and } X_1 = 1 . \end{aligned}$$

This corresponds to the inflow of the reactant from the bottom boundary.

The initial position of the interface was taken to be line $X_2 = 2/17$. The materials below and above the interface were taken to be the transformed and the untransformed materials, respectively. The movement of the interface was simulated from $t_0 = 0$ to $t_\mathrm {e} = 2.5$.

Mesh sizes $h = 1/N$, $N \in \left\{ 4, 8, 16, 32, 64 \right\}$ were used. Time steps $\Delta t = 1/N_\mathrm {t}$, $N_\mathrm {t} \in \lbrace 8,16,32,64,128,256,512 \rbrace$ were used. Numerical parameters $\lambda = 10^4$ and $\kappa = 10^{-3}$ were used based on the examples from the previous section.

5.4.1 Interface movement and stresses

The configuration of the interface at different times is illustrated in Fig. 13a. It can be seen that the initially flat interface acquires certain curvature, as the central part of the interface has lower velocity than the edges. Moreover, as the interface approaches the top boundary, the right edge of the interface slows down in comparison to the left edge. In Fig. 13b, the velocities of 4 interface points are shown as functions of time. It can be seen that there is a general decrease in the velocity of the interface as it moves. Initially, point $X_1 = 7/8$ has higher velocity than points $X_1 = 3/8$ and $X_1 = 5/8$; however, its velocity drops below the velocities of central points as the interface approaches the top boundary. The oscillations of the velocity in Fig. 13b are discussed further.

The reason for the progressive curvature of the interface is the stress-affected kinetics of the reaction front. As it can be seen in Fig. 14, there is a build-up of the hydrostatic as well as the deviatoric stresses in the centre-right part of the computational region. Higher stresses lead to the decrease of the normal velocity according to the chosen kinetic law (56). The stresses, in turn, develop due to propagation of the reaction front, i.e. creation of the transformed material, which has intrinsic volumetric expansion in comparison to the untransformed material. Moreover, the inclination of the top boundary (fixed displacements) creates non-symmetric stress distribution which slows down the right-hand side of the reaction front more than the left-hand side. The current configurations at the initial and the final positions of the reaction front are shown in Fig. 15.

In Fig. 13b, there are small, although visible, oscillations of the velocities of interface points related to the points moving from one inter-element boundary to another. Since the interface normal velocity depends on the stress (as well as the deformation gradients and the strain energy densities), the reason for these oscillations is the discontinuous stress field (as well as $\varvec{F}$ and W) as given by the finite-element solution with piece-wise linear test functions. As the point jumps from one inter-element boundary to another, different elements become involved in calculation/averaging of the velocity at the intersection point, hence, there is a jump in the velocity. These oscillations can be significantly reduced by using a more elaborate inter-element stress averaging, higher-order test functions or stress calculation procedures with an improved accuracy, for example [24, 25], but this is outside of the scope of this paper.

5.4.2 Concentration of the reactant

As seen from Eq. (56), the reaction front is driven by the concentration of the reactant at the reaction front. The example of the concentration distribution resulting from the solution of the diffusion equation is shown in Fig. 16a. The concentration field plot occupies only $\varOmega _+^h$, as the reactant is present only within the transformed material. As the supply of the reactant is provided at the bottom boundary (according to the imposed boundary conditions), the highest concentration is at $X_2 = 0$. There is a non-linear decay of the concentration with the increase of $X_2$ due to the mixed boundary conditions at the reaction front. The concentration at the reaction front is illustrated in Fig. 16b, where it can be seen that even at $t=0$, when the reaction front is flat, as illustrated in Fig. 13a, the concentration profile at the reaction front is non-linear. This is due to the stress-dependent velocity entering the mixed boundary conditions at the reaction front according to Eqs. (17), (56) and (57), while the stress profile being non-linear and non-symmetric due to the mechanical boundary conditions. As the reaction front moves, the concentration at the reaction front becomes even more spatially non-linear with higher concentration close to the centre of the reaction front.

Fig. 17

The convergence rates with respect to the time step (a) and with respect to the mesh size (c) for the interface position along $X_2$ as a function of $X_1$. The dependencies of the $\ell ^2$-norms of the difference between the reference interface position and the current interface position on the time step (b) and the mesh size (d)

5.4.3 Convergence

As discussed in previous subsections, the non-conforming interface FEM has the same convergence rate as the standard FEM with respect to the mesh size for the case of fixed interface. In the mechanochemical problems, the interface moves in time, therefore, it is also necessary to demonstrate that the coupled problem converges with respect to the mesh size and the time step. Obviously, since solution $\vec {u} _\pm ^h$ depends on the configuration of the interface, the error in the configuration of the interface affects the solution. Hence, the convergence rate for the solution cannot be higher than the convergence rate for the configuration of the interface with respect to the mesh size and the time step.

Since the points of the interface are moved using the explicit scheme similar to the forward Euler method, as described in Sect. 4.4.3, the convergence rate of the interface position and consequently of solution $\vec {u} _\pm ^h$ with respect to the time step should be 1. Moreover, as this problem involves the explicit time integration, while the interface is spatially discretised, the existence of a stability condition, similar to the Courant–Friedrichs–Lewy (CFL) condition, can be expected, i.e. the time step must be decreased with the decrease of the spatial step, otherwise the interface configuration becomes numerically unstable. Loss of stability was observed in the numerical simulations when relatively large time steps were used; however, the non-linear nature of the problem makes it difficult to derive an analytical expression for the stability condition and this has to be a subject of a separate study.

There is also another limitation that arises in the full mechanochemical problem with stress-dependent velocity of the reaction front. In this case, the interface velocity and consequently its configuration are affected by the numerical error in the stresses (as well as in the deformation gradients and in the strain energy densities). It is well-known that in FEM, the convergence rate for the stresses with respect to the mesh size is lower by 1 than the convergence rate for the displacements. Therefore, in the full mechanochemical problem with stress-dependent velocity, the convergence rate for the displacements with respect to the mesh size drops by 1, following the convergence rate for the stresses. This issue is not specific to the considered method and is expected in any method dealing with the stress-dependent velocity. The major potential improvement of the numerical framework is an addition of a stress calculation procedure with superior convergence rates, e.g. [24, 25]. This will affect the calculated velocities, hence the interface configuration and consequently the solution (the nodal displacements).

In previous subsections, it has been shown that the non-conforming interface FEM provides a reliable solution for a fixed interface. Therefore, in the case of moving interface, it is sufficient to consider the interface configuration/position as the quantity, convergence of which is verified. Due to the orientation of the interface, it is convenient to consider pointwise convergence rate for the intersection points of the interface with the vertical element edges. Thus, the convergence rate with respect to the time step can be introduced:

$$\begin{aligned} r_{\Delta t} \left( X_1 \right)= & {} \log _2 \frac{ \left| X_2^{\Delta t}\left( X_1\right) - X_2^{\Delta t/2}\left( X_1\right) \right| }{ \left| X_2^{\Delta t/2}\left( X_1\right) - X_2^{\Delta t/4}\left( X_1\right) \right| } , \nonumber \\&\left( X_1,X_2^{\Delta t}\right) \in \varGamma _*^h \text { at } t = t_\mathrm {e} , \end{aligned}$$

(60)

where $r_{\Delta t} \left( X_1 \right)$ is the convergence rate for $X_2^{\Delta t}$ with respect to $\Delta t$, given that $\left( X_1,X_2^{\Delta t}\right)$ belongs to interface $\varGamma _*^h$ at $t = t_\mathrm {e}$, the position of which was obtained by solving the mechanochemical problem on the mesh with size h and with time step $\Delta t$. Similarly, the convergence rate with respect to the mesh size can be introduced:

$$\begin{aligned} r_h \left( X_1 \right)= & {} \log _2 \frac{ \left| X_2^h\left( X_1\right) - X_2^{h/2}\left( X_1\right) \right| }{ \left| X_2^{h/2}\left( X_1\right) - X_2^{h/4}\left( X_1\right) \right| } ,\nonumber \\&\left( X_1,X_2^h\right) \in \varGamma _*^h \text { at } t = t_\mathrm {e} , \end{aligned}$$

(61)

where $r_h \left( X_1 \right)$ is the convergence rate for $X_2^h$ with respect to h, given that $\left( X_1,X_2^h\right)$ belongs to the interface. Rates $r_{\Delta t}$ and $r_h$ as functions of $X_1$ are illustrated in Fig. 17a, c, where it can be seen that although there are significant oscillations in the rates, the average rate is around 1, both with respect to $\Delta t$ and h.

The oscillations in pointwise convergence rates do not prevent the $\ell ^2$-norms of the errors of $X_2^{\Delta t}$ and $X_2^h$ to converge. These norms are defined as

$$\begin{aligned}&e_\varGamma ^{\Delta t} \left( {\Delta t}_1, {\Delta t}_2 \right) = \left\| U^{{\Delta t}_1} - U^{{\Delta t}_2} \right\| _{\ell ^2} ,\nonumber \\&\quad U^{\Delta t}_i = X_2^{\Delta t} \left( h_\mathrm {c} i\right) , \quad i \in \left\{ 0, 1, \ldots , N_\mathrm {c} \right\} , \end{aligned}$$

(62)

$$\begin{aligned}&e_\varGamma ^h \left( h_1, h_2 \right) = \left\| U^{h_1} - U^{h_2} \right\| _{\ell ^2} , \nonumber \\&\quad U^h_i = X_2^h \left( h_\mathrm {c} i\right) , \quad i \in \left\{ 0, 1, \ldots , N_\mathrm {c} \right\} , \end{aligned}$$

(63)

where $X_2^{\Delta t}$ and $X_2^h$ are taken as in Eqs. (60) and (61), respectively, and $h_\mathrm {c} = 1/N_\mathrm {c}$ is the size of the coarse mesh, nodes of which are taken as the comparison points. In the computational examples, reference time step $\Delta t = 1/512$ was taken for the calculation of $e_\varGamma ^{\Delta t}$ as a function of current time step, using $h = 1/32$ and $h_\mathrm {c} = 1/32$. For the calculation of $e_\varGamma ^h$ as a function of current mesh size, reference mesh size $h = 1/64$ was used, with $h_\mathrm {c} = 1/4$ and $\Delta t = 1/128$. The dependencies of $e_\varGamma ^{\Delta t}$ and $e_\varGamma ^h$ on $\Delta t$ and h are illustrated in Fig. 17b, d, respectively. Although the reference time step and the reference mesh size cannot be considered to be small enough for the reference solutions to be used as approximations of the exact solution (hence the convergence rate estimation from $e_\varGamma ^{\Delta t}$ and $e_\varGamma ^h$ will not be precise), it can be seen that with the decrease of $\Delta t$ and h, the difference between the current and the reference solutions decreases.

6 Conclusions

In this paper, a numerical method for solving finite-strain mechanochemical problems with moving sharp chemical reaction fronts separating chemically transformed and untransformed phases has been presented. The main advantage of the method is the ability to track the propagation of the front without remeshing the geometry each time step. The method is general in a sense that it does not rely on any constitutive laws, including functional dependency of the velocity on stresses/energies. Furthermore, it is applicable not only to mechanochemical problems, but to all problems where sharp interfaces move in deformable bodies due to configurational forces, such as classical phase transformations (in this case there is no reactant and the velocity does not depend on the concentration), and modelling surfaces of growth in biomechanics.

The proposed method accounts for three interdependent problems: the mechanical problem, the diffusion problem and the movement of the interface (the chemical reaction front). The method relies on using fixed finite-element mesh and the interface that cuts through the elements. In the mechanical part of the problem, the interface conditions are enforced weakly using a Nitsche-like method. One of the novelties of this work consists in derivation of the weak form of the problem from the total potential energy for the case of large deformations, thereby ensuring that the Nitsche-like interface penalty terms are consistent with the energy minimisation. Furthermore, the algorithm that moves the points of the interface has been proposed.

The method was illustrated with several case studies assuming hyperelastic constitutive behaviour. The mechanical part of the problem was tested separately for the case of a stationary interface. The interface, which is non-conforming to the mesh and is handled using the Nitsche-like method, was compared to the standard FEM. The expected second-order convergence in the case of linear elements was observed.

The fully coupled mechanochemical problem capturing the propagation of a chemical reaction front in a clamped 2D body was solved to illustrate the applicability of the method. The kinetics of the chemical reaction front was chosen to be governed by the chemical affinity tensor [6,7,8], where the velocity of the chemical reaction front depends on stresses and elastic strain energy densities. In the computational example, the stress-affected deceleration of the reaction front was observed, with inhomogeneous stress distribution leading to the change of the curvature of the front.

Although 2D numerical examples were presented in this paper, the method is directly applicable to 3D. The main challenge for 3D applications is developing the code that builds the new position of the interface, i.e. the code that tracks correctly the intersection points of 3D element edges and the surface of the interface.

Finally, as the spatially discretised interface is moved explicitly, the existence of a CFL-like stability condition can be expected. In the numerical simulations, the loss of numerical stability for large time steps was observed (results are not included in the paper), however, the analytical derivation of this stability condition is yet to be performed and must be a subject of a separate study.

Appendix: A tensor derivatives for hyperelasticity

When the method is implemented, closed-form expressions for

$$\begin{aligned} \varvec{P} _\pm = \frac{\partial W_\pm }{\partial \varvec{F} _\pm } \quad \text {and} \quad \frac{\partial {\varvec{P} _\pm }^\mathrm {T} }{\partial \varvec{F} _\pm } \end{aligned}$$

are required. Moreover, as the Newton-Raphson method is used to solve the system of non-linear equations, closed-form expression for

$$\begin{aligned} \frac{\partial }{\partial \varvec{F} _\pm } \left( \varvec{Q} : \frac{\partial {\varvec{P} _\pm }^\mathrm {T} }{\partial \varvec{F} _\pm } : \varvec{S} \right) \end{aligned}$$

is also required for constructing the Jacobian, where $\varvec{Q}$ and $\varvec{S}$ are independent of $\varvec{F} _\pm$ tensors. This term is required when parts of the Jacobian corresponding to the fifth term of (33) are assembled.

In this paper, hyperelastic mechanical constitutive relations were used for both phases, as given by (50) and (51). Below tensor derivatives of $W_-$ by $\varvec{F} _-$ are presented, while subscript “−” is omitted for simplicity of the notation. Tensor derivatives of $W_+$ by $\varvec{F} _+$ can be obtained using transformation formulas between the configurations, as presented in Sect. 4.1.2.

The expression for the first derivative of W by $\varvec{F}$ is the following:

$$\begin{aligned} \varvec{P}= & {} \frac{\partial W}{\partial \varvec{F} } = K \left( J - 1 \right) \varvec{F} ^\mathrm {-T} \\&+ G J^{-\frac{2}{3}} \left( \varvec{F} \cdot \varvec{F} ^\mathrm {T} - \frac{1}{3} \varvec{F} : \varvec{F} ^\mathrm {T} \varvec{I} \right) \cdot \varvec{F} ^\mathrm {-T} . \end{aligned}$$

The derivative of $\varvec{P} ^\mathrm {T}$ by $\varvec{F}$ (i.e. left-transposed second derivative of W by $\varvec{F}$) is the following:

$$\begin{aligned} \frac{\partial \varvec{P} ^\mathrm {T} }{\partial \varvec{F} }= & {} K J \varvec{F} ^{-1}\varvec{F} ^\mathrm {-T} + G J^{-\frac{2}{3}} \left( {}^4\!\varvec{I} - \frac{2}{3} \varvec{F} ^\mathrm {T} \varvec{F} ^\mathrm {-T} \right. \\&\left. + \varvec{F} ^{-1} \cdot {}^4\!\varvec{I} ^\mathrm {RT} \cdot \varvec{F} + \frac{2}{9} \varvec{F} : \varvec{F} ^\mathrm {T} \varvec{F} ^{-1}\varvec{F} ^\mathrm {-T} - \frac{2}{3} \varvec{F} ^{-1}\varvec{F} \right) \\&- \varvec{F} ^{-1} \cdot {}^4\!\varvec{I} ^\mathrm {RT} \cdot \varvec{P} . \end{aligned}$$

Finally, the tangent required for constructing the Jacobian is the following:

$$\begin{aligned}&\frac{\partial }{\partial \varvec{F} } \left( \varvec{Q} : \frac{\partial \varvec{P} ^\mathrm {T} }{\partial \varvec{F} } : \varvec{S} \right) \\&\quad = K J \varvec{Q} : \varvec{F} ^{-1}\varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} ^\mathrm {-T} - K J \varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} ^\mathrm {-T} \cdot \varvec{Q} ^\mathrm {T} \cdot \varvec{F} ^\mathrm {-T} \\&\qquad -\, K J \varvec{Q} : \varvec{F} ^{-1} \varvec{F} ^\mathrm {-T} \cdot \varvec{S} \cdot \varvec{F} ^\mathrm {-T} - \frac{2}{3} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{S} \varvec{F} ^\mathrm {-T} \\&\qquad +\, \frac{4}{9} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{F} ^\mathrm {T} \varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} ^\mathrm {-T} \\&\qquad -\, \frac{2}{3} G J^{-\frac{2}{3}} \varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{Q} + \frac{2}{3} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{F} ^\mathrm {T} \varvec{F} ^\mathrm {-T} \cdot \varvec{S} \cdot \varvec{F} ^\mathrm {-T} \\&\qquad -\, \frac{2}{3} G J^{-\frac{2}{3}} \left( \varvec{Q} \cdot \varvec{F} ^{-1} \cdot \varvec{S} ^\mathrm {T} \right) : \varvec{F} ^\mathrm {T} \varvec{F} ^\mathrm {-T} \\&\qquad -\, G J^{-\frac{2}{3}} \varvec{F} ^\mathrm {-T} \cdot \varvec{Q} ^\mathrm {T} \cdot \varvec{F} \cdot \varvec{S} \cdot \varvec{F} ^\mathrm {-T} + G J^{-\frac{2}{3}} \varvec{Q} \cdot \varvec{F} ^{-1} \cdot \varvec{S} ^\mathrm {T} \\&\qquad -\, \frac{4}{27} G J^{-\frac{2}{3}} \varvec{F} : \varvec{F} ^\mathrm {T} \varvec{Q} : \varvec{F} ^{-1}\varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} ^\mathrm {-T} \\&\qquad +\, \frac{4}{9} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{F} ^{-1}\varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} \\&\qquad -\, \frac{2}{9} G J^{-\frac{2}{3}} \varvec{F} : \varvec{F} ^\mathrm {T} \varvec{F} ^\mathrm {-T} : \varvec{S} \varvec{F} ^\mathrm {-T} \cdot \varvec{Q} ^\mathrm {T} \cdot \varvec{F} ^\mathrm {-T} \\&\qquad -\, \frac{2}{9} G J^{-\frac{2}{3}} \varvec{F} : \varvec{F} ^\mathrm {T} \varvec{Q} : \varvec{F} ^{-1} \varvec{F} ^\mathrm {-T} \cdot \varvec{S} \cdot \varvec{F} ^\mathrm {-T} \\&\qquad +\, \frac{4}{9} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{F} ^{-1}\varvec{F} : \varvec{S} \varvec{F} ^\mathrm {-T} \\&\qquad +\, \frac{2}{3} G J^{-\frac{2}{3}} \varvec{F} : \varvec{S} \varvec{F} ^\mathrm {-T} \cdot \varvec{Q} ^\mathrm {T} \cdot \varvec{F} ^\mathrm {-T} - \frac{2}{3} G J^{-\frac{2}{3}} \varvec{Q} : \varvec{F} ^{-1}\varvec{S} ^\mathrm {T} \\&\qquad + \,\varvec{F} ^\mathrm {-T} \cdot \varvec{Q} ^\mathrm {T} \cdot \varvec{P} \cdot \varvec{S} \cdot \varvec{F} ^\mathrm {-T} - \left( \varvec{Q} \cdot \varvec{F} ^{-1} \cdot \varvec{S} ^\mathrm {T} \right) : \frac{\partial \varvec{P} ^\mathrm {T} }{\partial \varvec{F} } . \end{aligned}$$