Skip to main content
SpringerLink
Log in

A finite element formulation preserving symmetric and banded diffusion stiffness matrix characteristics for fractional differential equations

  • Original Paper
  • Published:
Computational Mechanics Aims and scope Submit manuscript

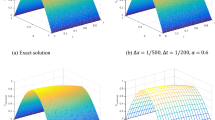
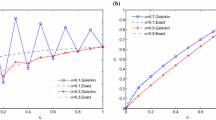
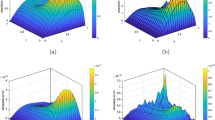
Abstract

Due to the nonlocal property of the fractional derivative, the finite element analysis of fractional diffusion equation often leads to a dense and non-symmetric stiffness matrix, in contrast to the conventional finite element formulation with a particularly desirable symmetric and banded stiffness matrix structure for the typical diffusion equation. This work first proposes a finite element formulation that preserves the symmetry and banded stiffness matrix characteristics for the fractional diffusion equation. The key point of the proposed formulation is the symmetric weak form construction through introducing a fractional weight function. It turns out that the stiffness part of the present formulation is identical to its counterpart of the finite element method for the conventional diffusion equation and thus the stiffness matrix formulation becomes trivial. Meanwhile, the fractional derivative effect in the discrete formulation is completely transferred to the force vector, which is obviously much easier and efficient to compute than the dense fractional derivative stiffness matrix. Subsequently, it is further shown that for the general fractional advection–diffusion–reaction equation, the symmetric and banded structure can also be maintained for the diffusion stiffness matrix, although the total stiffness matrix is not symmetric in this case. More importantly, it is demonstrated that under certain conditions this symmetric diffusion stiffness matrix formulation is capable of producing very favorable numerical solutions in comparison with the conventional non-symmetric diffusion stiffness matrix finite element formulation. The effectiveness of the proposed methodology is illustrated through a series of numerical examples.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. Hughes TJR, Franca LP, Hulbert GM (1989) A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective–diffusive equations. Comput Methods Appl Mech Eng 73:173–189

    Article  MathSciNet  MATH  Google Scholar 

  2. Codina R (1998) Comparison of some finite element methods for solving the diffusion–convection–reaction equation. Comput Methods Appl Mech Eng 156:185–210

    Article  MathSciNet  MATH  Google Scholar 

  3. Hsieh PW, Yang SY (2016) A new stabilized linear finite element method for solving reaction–convection–diffusion equations. Comput Methods Appl Mech Eng 307:362–382

    Article  MathSciNet  Google Scholar 

  4. Borker R, Farhat C, Tezaur R (2016) A high-order discontinuous Galerkin method for unsteady advection–diffusion problems. J Comput Phys 332:520–537

    Article  MathSciNet  MATH  Google Scholar 

  5. Ciambella J, Paolone A, Vidoli S (2014) Identification of the viscoelastic properties of soft materials at low frequency: performance, ill-conditioning and extrapolation capabilities of fractional and exponential models. J Mech Behav Biomed Mater 37:286–298

    Article  Google Scholar 

  6. Nadzharyan TA, Sorokin VV, Stepanov GV, Bogolyubov AN, Kramarenko EY (2016) A fractional calculus approach to modeling rheological behavior of soft magnetic elastomers. Polymer 92:179–188

    Article  Google Scholar 

  7. Zbiciak A, Kozyra Z (2015) Dynamic analysis of a soft-contact problem using viscoelastic and fractional-elastic rheological models. Arch Civ Mech Eng 15:286–291

    Article  Google Scholar 

  8. Metzler R, Klafter J (2004) The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J Phys A Math Gen 37:R161

    Article  MathSciNet  MATH  Google Scholar 

  9. Shi L, Yu ZG, Mao Z, Xiao AG, Huang HL (2013) Space-time fractional diffusion equations and asymptotic behaviors of a coupled continuous time random walk model. Physica A 392:5801–5807

    Article  MathSciNet  Google Scholar 

  10. Jurlewicz A, Kern P, Meerschaert MM, Scheffler HP (2012) Fractional governing equations for coupled random walks. Comput Math Appl 64:3021–3036

    Article  MathSciNet  MATH  Google Scholar 

  11. Churbanov AG, Vabishchevich PN (2016) Numerical investigation of a space-fractional model of turbulent fluid flow in rectangular ducts. J Comput Phys 321:846–859

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhang X, Liu L, Wu Y (2014) The uniqueness of positive solution for a fractional order model of turbulent flow in a porous medium. Appl Math Lett 37:26–33

    Article  MathSciNet  MATH  Google Scholar 

  13. Suzuki A, Fomin SA, Chugunov VA, Niibori Y, Hashida T (2016) Fractional diffusion modeling of heat transfer in porous and fractured media. Int J Heat Mass Transf 103:611–618

    Article  Google Scholar 

  14. Choudhary A, Kumar D, Singh J (2015) A fractional model of fluid flow through porous media with mean capillary pressure. J Assoc Arab Univ Basic Appl Sci 21:59–63

    Google Scholar 

  15. Chen W, Sun HG, Zhang XD, Korosak D (2010) Anomalous diffusion modeling by fractal and fractional derivatives. Comput Math Appl 59:1754–1758

    Article  MathSciNet  MATH  Google Scholar 

  16. Craiem D, Magin RL (2010) Fractional order models of viscoelasticity as an alternative in the analysis of red blood cell (RBC) membrane mechanics. Phys Biol 7:013001

    Article  Google Scholar 

  17. Miller KS, Ross B (1993) An introduction to the fractional calculus and differential equations. Wiley, New York

    MATH  Google Scholar 

  18. Podlubny I (1999) Fractional differential equations. Academic Press, London

    MATH  Google Scholar 

  19. Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam

    MATH  Google Scholar 

  20. Baleanu D, Machado JAT, Luo ACJ (2011) Fractional dynamics and control. Springer, New York

    Google Scholar 

  21. Tadjeran C, Meerschaert MM, Scheffler HP (2006) A second-order accurate numerical approximation for the fractional diffusion equation. J Comput Phys 213:205–213

    Article  MathSciNet  MATH  Google Scholar 

  22. Çelik C, Duman M (2012) Crank–Nicolson method for the fractional diffusion equation with the Riesz fractional derivative. J Comput Phys 231:1743–1750

    Article  MathSciNet  MATH  Google Scholar 

  23. Li D, Zhang C, Ran M (2016) A linear finite difference scheme for generalized time fractional Burgers equation. Appl Math Model 40:6069–6081

    Article  MathSciNet  Google Scholar 

  24. Pang G, Chen W, Sze KY (2016) A comparative study of finite element and finite difference methods for two-dimensional space-fractional advection–dispersion equation. Adv Appl Math Mech 8:166–186

    Article  MathSciNet  Google Scholar 

  25. Ying YP, Lian YP, Tang SQ, Liu WK (2017) High-order central difference scheme for Caputo fractional derivative. Comput Methods Appl Mech Eng 317:42–54

    Article  MathSciNet  Google Scholar 

  26. Fix GJ, Roof JP (2004) Least squares finite-element solution of a fractional order two-point boundary value problem. Comput Math Appl 48:1017–1033

    Article  MathSciNet  MATH  Google Scholar 

  27. Zheng Y, Li C, Zhao Z (2010) A note on the finite element method for the space-fractional advection diffusion equation. Comput Math Appl 59:1718–1726

    Article  MathSciNet  MATH  Google Scholar 

  28. Wang H, Yang D, Zhu S (2015) A Petrov–Galerkin finite element method for variable-coefficient fractional diffusion equations. Comput Methods Appl Mech Eng 290:45–56

    Article  MathSciNet  Google Scholar 

  29. Qiu L, Deng W, Hesthaven JS (2015) Nodal discontinuous Galerkin methods for fractional diffusion equations on 2D domain with triangular meshes. J Comput Phys 298:678–694

    Article  MathSciNet  MATH  Google Scholar 

  30. Zhao Y, Zhang Y, Shi D, Liu F, Turner I (2016) Superconvergence analysis of nonconforming finite element method for two-dimensional time fractional diffusion equations. Appl Math Lett 59:38–47

    Article  MathSciNet  MATH  Google Scholar 

  31. Luan SZ, Lian YP, Ying YP, Tang SQ, Wagner GJ, Liu WK (2017) An enriched finite element method to fractional advection–diffusion equation. Comput Mech 60:181–201

    Article  MathSciNet  MATH  Google Scholar 

  32. Lin YM, Xu CJ (2007) Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys 225:1533–1552

    Article  MathSciNet  MATH  Google Scholar 

  33. Wang H, Zhang X (2015) A high-accuracy preserving spectral Galerkin method for the Dirichlet boundary-value problem of variable-coefficient conservative fractional diffusion equations. J Comput Phys 281:67–81

    Article  MathSciNet  MATH  Google Scholar 

  34. Chen H, Lü SJ, Chen WP (2016) Finite difference/spectral approximations for the distributed order time fractional reaction–diffusion equation on an unbounded domain. J Comput Phys 315:84–97

    Article  MathSciNet  MATH  Google Scholar 

  35. Shirzadi A, Ling L, Abbasbandy S (2012) Meshless simulations of the two-dimensional fractional-time convection–diffusion–reaction equations. Eng Anal Bound Elem 36:1522–1527

    Article  MathSciNet  MATH  Google Scholar 

  36. Liu Q, Liu F, Gu YT, Zhuang P, Chen J, Turner I (2015) A meshless method based on point interpolation method (PIM) for the space fractional diffusion equation. Appl Math Comput 256:930–938

    MathSciNet  MATH  Google Scholar 

  37. Lian YP, Wagner GJ, Liu WK (2017) A meshfree method for the fractional advection–diffusion equation. In: Meshfree methods for partial differential equations VIII. Lecture notes in computational science and engineering, vol 115, pp 53–66

  38. Lian YP, Ying YP, Tang SQ, Lin S, Wagner GJ, Liu WK (2016) A Petrov–Galerkin finite element method for the fractional advection–diffusion equation. Comput Methods Appl Mech Eng 309:388–410

    Article  MathSciNet  Google Scholar 

  39. Samko SG, Kilbas AA, Marichev OI (1993) Fractional integrals and derivatives: theory and applications. Gordon and Breach Science Publishers, Philadelphia

    MATH  Google Scholar 

  40. Lions JL, Magenes E (1972) Non-homogeneous boundary value problems and applications. Springer, New York

    Book  MATH  Google Scholar 

  41. Li XJ, Xu CJ (2009) A space–time spectral method for the time fractional diffusion equation. SIAM J Numer Anal 47:2108–2131

    Article  MathSciNet  MATH  Google Scholar 

  42. Tang SQ, Ying YP, Lian YP, Lin S, Yang YB, Wagner GJ, Liu WK (2016) Differential operator multiplication method for fractional differential equations. Comput Mech 58:879–888

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The support of this work by the National Natural Science Foundation of China (11472233, 11772280) and the Natural Science Foundation of Fujian Province of China (2014J06001, 2014J01208) is gratefully acknowledged.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Xiamen University, Xiamen, 361005, Fujian, China

    Zeng Lin & Dongdong Wang

  2. School of Mathematical Sciences, Xiamen University, Xiamen, 361005, Fujian, China

    Zeng Lin

Authors
  1. Zeng Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dongdong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dongdong Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lin, Z., Wang, D. A finite element formulation preserving symmetric and banded diffusion stiffness matrix characteristics for fractional differential equations. Comput Mech 62, 185–211 (2018). https://doi.org/10.1007/s00466-017-1492-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00466-017-1492-2

Keywords

Search

Navigation