Appendix 1
In this appendix, the following formula is demonstrated.
$$\begin{aligned}&\sum _{J=1}^{k,k\le I-2}\check{K}_{IJ}\left( \alpha ,M\right) \phi _{J}^{\text {ex}} =\frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{k^{\alpha }\left( k+1\right) ^{\alpha }}{\left( k+1\right) ^{\alpha }-k^{\alpha }}\nonumber \\&\quad \times \frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}\left( M_{G}^{\alpha }\mid _{\frac{k}{I-1}}^{\frac{k}{I}}-M_{G}^{\alpha }\mid _{\frac{k+1}{I-1}}^{\frac{k+1}{I}}\right) \nonumber \\&\qquad - \frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{k^{\alpha }\left( k+1\right) ^{\alpha }}{\left( k+1\right) ^{\alpha }-k^{\alpha }}\nonumber \\&\quad \times \frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}\left( M_{G}^{\alpha }\mid _{\frac{k}{I}}^{\frac{k}{I+1}}-M_{G}^{\alpha }\mid _{\frac{k+1}{I}}^{\frac{k+1}{I+1}}\right) , \end{aligned}$$
(72)
where \(\check{K}_{IJ}\left( \alpha ,M\right) \) is part of stiffness matrix following the formula in Eq. (17), and \(\phi _{J}^{\text {ex}}\left( x\right) =\left( J\triangle x\right) ^{\alpha }\) is the nodal exact solution. Hence, Eq. (72)can be rewritten as
$$\begin{aligned} \sum _{J=1}^{k,k\le I-2}\check{K}_{IJ}\left( \alpha ,M\right) \phi _{J}^{\text {ex}}=\frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\sum _{J=1}^{k,k\le I-2}A_{J}B_{J}. \end{aligned}$$
(73)
The mathematical expression of \(A_{J}\) and \(B_{J}\) in Eq. (73) are defined as
$$\begin{aligned} A_{J}= & {} \frac{J^{\alpha }}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] \left[ J^{\alpha }-\left( J-1\right) ^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J}{I-1}}^{\frac{J}{I}}\nonumber \\&-\,\frac{\left( J-1\right) ^{\alpha }}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] \left[ J^{\alpha }-\left( J-1\right) ^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J-1}{I-1}}^{\frac{J-1}{I}}\nonumber \\&+\,\frac{J^{\alpha }}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] \left[ \left( J+1\right) ^{\alpha }-J^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J}{I-1}}^{\frac{J}{I}}\nonumber \\&-\,\frac{\left( J+1\right) ^{\alpha }}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] \left[ \left( J+1\right) ^{\alpha }-J^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J+1}{I-1}}^{\frac{J+1}{I}}\nonumber \\&-\,\frac{J^{\alpha }}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] \left[ J^{\alpha }-\left( J-1\right) ^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J}{I}}^{\frac{J}{I+1}}\nonumber \\&+\,\frac{\left( J-1\right) ^{\alpha }}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] \left[ J^{\alpha }-\left( J-1\right) ^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J-1}{I}}^{\frac{J-1}{I+1}}\nonumber \\&-\,\frac{J^{\alpha }}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] \left[ \left( J+1\right) ^{\alpha }-J^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J}{I}}^{\frac{J}{I+1}}\nonumber \\&+\,\frac{\left( J+1\right) ^{\alpha }}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] \left[ \left( J+1\right) ^{\alpha }-J^{\alpha }\right] }M_{G}^{\alpha }\mid _{\frac{J+1}{I}}^{\frac{J+1}{I+1}}. \end{aligned}$$
(74)
$$\begin{aligned} B_{J}= & {} J^{\alpha }. \end{aligned}$$
(75)
By mathematical induction, Eq. (72) can be demonstrated as following steps.
$$\begin{aligned} S_{1}= & {} A_{1}B_{1}=\frac{1^{\alpha }2^{\alpha }}{2^{\alpha }-1^{\alpha }}\left[ \frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{1}{I-1}}^{\frac{1}{I}}\right. \nonumber \\&-\,\frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{1}{I}}^{\frac{1}{I+1}}+\frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{2}{I}}^{\frac{2}{I+1}}\nonumber \\&\left. -\,\frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{2}{I-1}}^{\frac{2}{I}}\right] . \end{aligned}$$
(76)
Assuming
$$\begin{aligned} S_{n}=&\sum _{J=1}^{n}A_{J}B_{J}=\frac{n^{\alpha }\left( n+1\right) ^{\alpha }}{\left( n+1\right) ^{\alpha }-n^{\alpha }}\left[ \frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n}{I-1}}^{\frac{n}{I}}\right. \nonumber \\&\left. -\,\frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n}{I}}^{\frac{n}{I+1}}\right] \nonumber \\&+\, \frac{n^{\alpha }\left( n+1\right) ^{\alpha }}{\left( n+1\right) ^{\alpha }-n^{\alpha }}\left[ \frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+1}{I}}^{\frac{n+1}{I+1}}\right. \nonumber \\&\left. -\,\frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+1}{I-1}}^{\frac{n+1}{I}}\right] . \end{aligned}$$
(77)
Then, by some simple algerbaric calculations
$$\begin{aligned} S_{n+1}&=\sum _{J=1}^{n+1}A_{J}B_{J}=\frac{\left( n+1\right) ^{\alpha }\left( n+2\right) ^{\alpha }}{\left( n+2\right) ^{\alpha }-\left( n+1\right) ^{\alpha }}\nonumber \\&\times \left[ \frac{1}{I^{\alpha }{-}\left( I{-}1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+1}{I-1}}^{\frac{n+1}{I}}{-}\frac{1}{\left( I{+}1\right) ^{\alpha }{-}I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+1}{I}}^{\frac{n+1}{I+1}}\right] \nonumber \\&\quad +\, \frac{\left( n+1\right) ^{\alpha }\left( n+2\right) ^{\alpha }}{\left( n+2\right) ^{\alpha }-\left( n+1\right) ^{\alpha }}\left[ \frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+2}{I}}^{\frac{n+2}{I+1}}\right. \nonumber \\&\quad \left. -\,\frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}M_{G}^{\alpha }\mid _{\frac{n+2}{I-1}}^{\frac{n+2}{I}}\right] . \end{aligned}$$
(78)
Hence, Eq. (72) is proved.
$$\begin{aligned}&\sum _{J=1}^{k,k\le I-2}\check{K}_{IJ}\left( \alpha ,M\right) \phi _{J}^{\text {ex}} =\frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }S_{k}\nonumber \\&\quad = \frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{k^{\alpha }\left( k+1\right) ^{\alpha }}{\left( k+1\right) ^{\alpha }-k^{\alpha }}\nonumber \\&\qquad \times \frac{1}{I^{\alpha }-\left( I-1\right) ^{\alpha }}\left( M_{G}^{\alpha }\mid _{\frac{k}{I-1}}^{\frac{k}{I}}-M_{G}^{\alpha }\mid _{\frac{k+1}{I-1}}^{\frac{k+1}{I}}\right) \nonumber \\&\qquad - \frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{k^{\alpha }\left( k+1\right) ^{\alpha }}{\left( k+1\right) ^{\alpha }-k^{\alpha }}\nonumber \\&\qquad \times \frac{1}{\left( I+1\right) ^{\alpha }-I^{\alpha }}\left( M_{G}^{\alpha }\mid _{\frac{k}{I}}^{\frac{k}{I+1}}-M_{G}^{\alpha }\mid _{\frac{k+1}{I}}^{\frac{k+1}{I+1}}\right) . \end{aligned}$$
(79)
Appendix 2
In this appendix, the appropriate fractional element Peclet number \(\hat{P}e\) is formulated, and the matrix form of Galekrin discretization is rewritten with fractional element Peclet number.
Based on the formula of fractional diffusion stiffness matrix in Eq. (15), \(\varvec{K}\left( \alpha ,M\right) \) can be rewritten as
$$\begin{aligned}&\varvec{K}\left( \alpha ,M\right) =\left[ \begin{array}{ccccccc} \lambda _{1} &{} \lambda _{2} &{} \lambda _{3} &{} \cdots &{} \cdots &{} \cdots &{} \lambda _{M-1}\\ \lambda _{1} &{} \lambda _{2} &{} \lambda _{3} &{} \cdots &{} \cdots &{} \cdots &{} \lambda _{M-1}\\ \lambda _{1} &{} \lambda _{2} &{} \lambda _{3} &{} \cdots &{} \cdots &{} \cdots &{} \lambda _{M-1}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \lambda _{1} &{} \lambda _{2} &{} \lambda _{3} &{} \cdots &{} \cdots &{} \cdots &{} \lambda _{M-1} \end{array}\right] \nonumber \\&\quad \times \left[ \begin{array}{ccccccc} \omega _{11} &{} -1\\ \omega _{22} &{} \omega _{21} &{} -1 &{} &{} &{} 0\\ \omega _{33} &{} \omega _{32} &{} \omega _{31} &{} -1\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} &{} -1\\ \omega _{M-1,1} &{} \omega _{M-1,2} &{} \omega _{M-1,3} &{} \cdots &{} \cdots &{} \cdots &{} \omega _{M-1,M-1} \end{array}\right] .\nonumber \\ \end{aligned}$$
(80)
The stiffness matrix \(\varvec{K}\left( 0,M\right) \) is calculated as
$$\begin{aligned} K_{IJ}\left( 0,M\right) =\left\{ \begin{array}{lll} -0.5, &{} &{} J=I+1\\ 0, &{} &{} J=I\\ 0.5, &{} &{} J=I-1. \end{array}\right. \end{aligned}$$
(81)
Therefore, the matrix form of fractional advection–diffusion equation can be rewritten as
$$\begin{aligned} -\tilde{\varvec{K}}\left( 0,M\right) +\tilde{\varvec{K}}\left( \alpha ,M\right) =\tilde{\varvec{F}}, \end{aligned}$$
(82)
where,
$$\begin{aligned}&\tilde{\varvec{K}}\left( 0,M\right) =\left[ \begin{array}{lllllll} 0 &{} -1\\ 1 &{} 0 &{} -1\\ &{} 1 &{} 0 &{} -1\\ &{} &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} &{} &{} \ddots &{} \ddots &{} -1\\ &{} &{} &{} &{} &{} 1 &{} 0 \end{array}\right] ,\end{aligned}$$
(83)
$$\begin{aligned}&\tilde{\varvec{K}}\left( \alpha ,M\right) =\left[ \begin{array}{ccccccc} \bar{\lambda }_{1} &{} \bar{\lambda }_{2} &{} \bar{\lambda }_{3} &{} \cdots &{} \cdots &{} \cdots &{} \bar{\lambda }_{M-1}\\ \bar{\lambda }_{1} &{} \bar{\lambda }_{2} &{} \bar{\lambda }_{3} &{} \cdots &{} \cdots &{} \cdots &{} \bar{\lambda }_{M-1}\\ \bar{\lambda }_{1} &{} \bar{\lambda }_{2} &{} \bar{\lambda }_{3} &{} \cdots &{} \cdots &{} \cdots &{} \bar{\lambda }_{M-1}\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ \bar{\lambda }_{1} &{} \bar{\lambda }_{2} &{} \bar{\lambda }_{3} &{} \cdots &{} \cdots &{} \cdots &{} \bar{\lambda }_{M-1} \end{array}\right] \nonumber \\&\quad \times \left[ \begin{array}{ccccccc} \omega _{11} &{} -1\\ \omega _{22} &{} \omega _{21} &{} -1 &{} &{} &{} 0\\ \omega _{33} &{} \omega _{32} &{} \omega _{31} &{} -1\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} &{} -1\\ \omega _{M-1,1} &{} \omega _{M-1,2} &{} \omega _{M-1,3} &{} \cdots &{} \cdots &{} \cdots &{} \omega _{M-1,M-1} \end{array}\right] ,\nonumber \\ \end{aligned}$$
(84)
$$\begin{aligned}&\tilde{\varvec{F}}=\left[ \begin{array}{c} 0\\ 0\\ 0\\ \vdots \\ \vdots \\ 0\\ \bar{\lambda }_{M}-1 \end{array}\right] , \end{aligned}$$
(85)
where
$$\begin{aligned} \bar{\lambda }_{I}= & {} \frac{2v}{u\triangle x^{\alpha }}\left[ \frac{\varGamma \left( 1+\alpha \right) }{\left( I+1\right) ^{\alpha }-I^{\alpha }}-\frac{\alpha \varGamma \left( 1+\alpha \right) }{\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\right. \nonumber \\&\quad \times \left. \frac{I^{\alpha }}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] ^{2}}M_{G}^{\alpha }\mid _{1}^{\frac{I}{I+1}}\right] =\frac{2v}{u\triangle x^{\alpha }}\vartheta _{I}. \end{aligned}$$
(86)
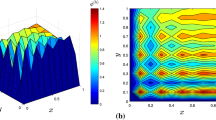
Here, \(\vartheta _{I}\) always has almost the same value of \(\frac{1}{\varGamma \left( 3-\alpha \right) }\), which can be numerically demonstrated as shown in Fig. 12.
Hence, we assume all the element value of \(\vartheta _{I}\) has the same value of \(\frac{1}{\varGamma \left( 3-\alpha \right) }\) and then all the element value of \(\bar{\lambda }_{I}\) becomes \(\frac{2v}{u\triangle x^{\alpha }\varGamma \left( 3-\alpha \right) }\).
Therefore, the matrix form in Eq. (82) can be rewritten as
$$\begin{aligned}&-\hat{P}e\left[ \begin{array}{lllllll} 0 &{} -1\\ 1 &{} 0 &{} -1\\ &{} 1 &{} 0 &{} -1\\ &{} &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} &{} \ddots &{} \ddots &{} \ddots \\ &{} &{} &{} &{} \ddots &{} \ddots &{} -1\\ &{} &{} &{} &{} &{} 1 &{} 0 \end{array}\right] \nonumber \\&\qquad +\left[ \begin{array}{ccccccc} \omega _{11} &{} -1\\ \omega _{22} &{} \omega _{21} &{} -1 &{} &{} &{} 0\\ \omega _{33} &{} \omega _{32} &{} \omega _{31} &{} -1\\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} \ddots \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} &{} &{} -1\\ \omega _{M-1,1} &{} \omega _{M-1,2} &{} \omega _{M-1,3} &{} \cdots &{} \cdots &{} \cdots &{} \omega _{M-1,M-1} \end{array}\right] \nonumber \\&\quad =\left[ \begin{array}{c} 0\\ 0\\ 0\\ \vdots \\ \vdots \\ 0\\ 1-\hat{P}e \end{array}\right] . \end{aligned}$$
(87)
The matrix form of Eq. (87) is denoted as
$$\begin{aligned} -\hat{P}e\bar{\varvec{K}}\left( 0,M\right) +\bar{\varvec{K}}\left( \alpha ,M\right) =\bar{F}. \end{aligned}$$
(88)
Appendix 3
In this appendix, the detailed formula of stiffness matrices \(\varvec{K}\left( 1,M\right) \) and \(\varvec{K}\left( 1+\alpha ,M\right) \) are derived as follows.
\(\varvec{K}\left( 1,M\right) \) is a tri-diagonal matrix, formulated as
$$\begin{aligned}&K_{IJ}\left( 1,M\right) =\frac{\alpha ^{2}}{2\alpha -1}\frac{1}{\triangle x}\nonumber \\&\quad \times \left\{ \begin{array}{lll} -\frac{J^{2\alpha -1}-I^{2\alpha -1}}{\left( J^{\alpha }-I^{\alpha }\right) ^{2}}, &{} &{} J=I+1\\ \frac{\left( I+1\right) ^{2\alpha -1}-I^{2\alpha -1}}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] ^{2}}+\frac{I^{2\alpha -1}-\left( I-1\right) ^{2\alpha -1}}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] ^{2}}, &{} &{} J=I\\ -\frac{I^{2\alpha -1}-J^{2\alpha -1}}{\left( I^{\alpha }-J^{\alpha }\right) ^{2}}, &{} &{} J=I-1. \end{array}\right. \end{aligned}$$
(89)
\(\varvec{K}\left( 1+\alpha ,M\right) \) is a lower triangular matrix, formulated as
$$\begin{aligned}&K_{IJ}\left( 1+\alpha ,M\right) =\frac{1}{\varGamma \left( 2-\alpha \right) }\frac{\alpha ^{2}}{\triangle x^{1+\alpha }}\nonumber \\&\quad \times \left\{ \begin{array}{lll} 0, &{} &{} J\ge I+2\\ -\frac{1}{\left( J^{\alpha }-I^{\alpha }\right) ^{2}}\frac{1}{\left( IJ\right) ^{1-\alpha }}, &{} &{} J=I+1\\ \frac{1}{\left[ \left( I+1\right) I\right] ^{1-\alpha }}\left\{ \frac{1}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] \left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] }+\frac{1}{\left[ \left( I+1\right) ^{\alpha }-I^{\alpha }\right] ^{2}}\right\} , &{} &{} J=I\\ \sum _{m=I-1}^{I}\sum _{n=J-1}^{J}\frac{1}{\left( m+1\right) ^{\alpha }-m^{\alpha }}\frac{1}{\left( n+1\right) ^{\alpha }-n^{\alpha }}\\ \left[ \sum _{p=m}^{m+1}\sum _{q=n}^{n+1}\left( -1\right) ^{p+q-I-J+1}\left( \frac{p-q}{pq}\right) ^{1-\alpha }\right] -\frac{1}{\left[ I^{\alpha }-\left( I-1\right) ^{\alpha }\right] ^{2}}\frac{1}{I^{1-\alpha }\left( I-1\right) ^{1-\alpha }}, &{} &{} J=I-1\\ \sum _{m=I-1}^{I}\sum _{n=J-1}^{J}\frac{1}{\left( m+1\right) ^{\alpha }-m^{\alpha }}\frac{1}{\left( n+1\right) ^{\alpha }-n^{\alpha }}\\ \left[ \sum _{p=m}^{m+1}\sum _{q=n}^{n+1}\left( -1\right) ^{p+q-I-J+1}\left( \frac{p-q}{pq}\right) ^{1-\alpha }\right] , &{} &{} J\le I-2. \end{array}\right. \end{aligned}$$
(90)
From the formula of stiffness \(\varvec{K}\left( 1,M\right) \) , one special case is that \(K_{11}\left( 1,M\right) \) may not exist when the fractional order \(\alpha <0.5\), which reads
$$\begin{aligned} K_{11}\left( 1,M\right) =\frac{\alpha ^{2}}{\triangle x}\left[ \int _{0}^{\triangle x}x^{2\alpha -2}\text {d}x+\int _{\triangle x}^{2\triangle x}x^{2\alpha -2}\text {d}x\right] . \end{aligned}$$
(91)
Therefore, we rewritte the formula of \(K_{11}\left( 1,M\right) \) as
$$\begin{aligned}&K_{11}\left( 1,M\right) \!=\!\frac{\alpha ^{2}}{\triangle x\left( 2\alpha -1\right) \left( 2^{\alpha }-1\right) ^{2}}\nonumber \\&\quad \times \left\{ \begin{array}{lll} \left( 2^{2\alpha -1}\!-\!1\right) +2^{1-2\alpha }\left( 2\alpha -1\right) \left( 2^{\alpha }\!-\!1\right) ^{2}\varepsilon , &{} &{} \alpha \le 0.5\\ \left( 2^{2\alpha -1}-1\right) +\left( 2^{\alpha }-1\right) ^{2}, &{} &{} \alpha >0.5, \end{array}\right. \nonumber \\ \end{aligned}$$
(92)
where \(\varepsilon \) represents the approximation of integration \(\left( \frac{2}{\triangle x}\right) ^{2\alpha -1}\int _{0}^{\triangle x}x^{2\alpha -2}\text {d}x\). In this article, it is recommended by the author to use Gaussian quadrature approximation to calculate \(\varepsilon \) in Eq. (92), and takes three Gaussian points as an example, \(\varepsilon \) is calculated as
$$\begin{aligned}&\varepsilon =\left( \frac{2}{\triangle x}\right) ^{2\alpha -1}\int _{0}^{\triangle x}x^{2\alpha -2}\text {d}x=\int _{-1}^{1}\left( 1+\xi \right) ^{2\alpha -2}\text {d}\xi \nonumber \\&\quad \thickapprox \frac{8}{9}+\frac{5}{9}\left[ \left( 1-\sqrt{0.6}\right) ^{2\alpha -2}+\left( 1+\sqrt{0.6}\right) ^{2\alpha -2}\right] . \end{aligned}$$
(93)
Additionally, the load vector \(\varvec{F}\) is formulated as
$$\begin{aligned} F_{I}=\left\{ \begin{array}{ll@{\quad }l} 0, &{} &{} I<M-1\\ -\frac{1}{2}u+v\left\{ \frac{\varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }}\frac{1}{M^{\alpha }-\left( M-1\right) ^{\alpha }}-\frac{\alpha \varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{\left( M-1\right) ^{\alpha }}{\left[ M^{\alpha }-\left( M-1\right) ^{\alpha }\right] ^{2}}M_{G}^{\alpha }\mid _{1}^{\frac{M-1}{M}}\right\} \\ +u\gamma \frac{\alpha ^{2}}{2\alpha -1}\frac{1}{\triangle x}\frac{M^{2\alpha -1}-\left( M-1\right) ^{2\alpha -1}}{\left[ M^{\alpha }-\left( M-1\right) ^{\alpha }\right] ^{2}}-v\gamma \frac{1}{\varGamma \left( 2-\alpha \right) }\frac{\alpha ^{2}}{\triangle x^{1+\alpha }}\frac{1}{\left[ M^{\alpha }-\left( M-1\right) ^{\alpha }\right] ^{2}}\frac{1}{\left[ M\left( M-1\right) \right] ^{1-\alpha }}, &{} &{} I=M-1. \end{array}\right. \end{aligned}$$
(94)
Appendix 4
In this appendix, the detailed derivations of the artificial viscosity coefficient of the enriched Petrov–Galerkin finite element method to fractional advection–diffusion equation is proposed.
The load vector residual is defined as
$$\begin{aligned} \varvec{R}=\left\| \varvec{F}^{*}-\varvec{F}\right\| , \end{aligned}$$
(95)
Considering the first term in Eq. (95), the load vector at first node reads
$$\begin{aligned} F_{1}= & {} 0,\end{aligned}$$
(96)
$$\begin{aligned} F_{1}^{*}= & {} \left[ -uK_{11}\left( 0,M\right) +vK_{11}\left( \alpha ,M\right) \right. \nonumber \\&\left. +u\gamma K_{11}\left( 1,M\right) -v\gamma K_{11}\left( 1+\alpha ,M\right) \right] \phi _{1}^{\text {ex}}\nonumber \\&+ \left[ -uK_{12}\left( 0,M\right) +vK_{12}\left( \alpha ,M\right) +u\gamma K_{12}\left( 1,M\right) \right. \nonumber \\&\left. -v\gamma K_{12}\left( 1+\alpha ,M\right) \right] \phi _{2}^{\text {ex}} \end{aligned}$$
(97)
Based on the formulas of stiffness matrix in Eq. (15), (81), (89), (90), and exact nodal solution in Eq. (37), the details in Eq. (97) are formulated as
$$\begin{aligned}&K_{11}\left( 0,M\right) =0,\end{aligned}$$
(98)
$$\begin{aligned}&K_{12}\left( 0,M\right) =-\frac{1}{2},\end{aligned}$$
(99)
$$\begin{aligned}&K_{11}\left( \alpha ,M\right) =\frac{\varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }}\frac{2^{\alpha }}{2^{\alpha }-1}\nonumber \\&\quad -\,\frac{\alpha \varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{2^{\alpha }}{\left( 2^{\alpha }-1\right) ^{2}}M_{G}^{\alpha }\mid _{1}^{0.5},\end{aligned}$$
(100)
$$\begin{aligned}&K_{12}\left( \alpha ,M\right) =-\frac{\varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }}\frac{1}{2^{\alpha }-1}\nonumber \\&\quad +\,\frac{\alpha \varGamma \left( 1+\alpha \right) }{\triangle x^{\alpha }\varGamma \left( 1-\alpha \right) \varGamma ^{2}\left( \alpha \right) }\frac{1}{\left( 2^{\alpha }-1\right) ^{2}}M_{G}^{\alpha }\mid _{1}^{0.5}, \end{aligned}$$
(101)
$$\begin{aligned}&K_{11}\left( 1,M\right) =\frac{\alpha ^{2}}{\triangle x\left( 2\alpha -1\right) \left( 2^{\alpha }-1\right) ^{2}}\nonumber \\&\quad \times \left\{ \begin{array}{lll} \left( 2^{2\alpha {-}1}{-}1\right) +2^{1-2\alpha }\left( 2\alpha -1\right) \left( 2^{\alpha }{-}1\right) ^{2}\varepsilon , &{} &{} \alpha \le 0.5\\ \left( 2^{2\alpha {-}1}{-}1\right) +\left( 2^{\alpha }{-}1\right) ^{2}, &{} &{} \alpha >0.5, \end{array}\right. \nonumber \\ \end{aligned}$$
(102)
$$\begin{aligned}&K_{12}\left( 1,M\right) =-\frac{2^{2\alpha -1}-1}{\left( 2^{\alpha }-1\right) ^{2}}\frac{\alpha ^{2}}{2\alpha -1}\frac{1}{\triangle x}, \end{aligned}$$
(103)
$$\begin{aligned}&K_{11}\left( 1+\alpha ,M\right) =\frac{1}{\varGamma \left( 2-\alpha \right) }\frac{2^{2\alpha -1}}{\left( 2^{\alpha }-1\right) ^{2}}\frac{\alpha ^{2}}{\triangle x^{1+\alpha }}, \end{aligned}$$
(104)
$$\begin{aligned}&K_{12}\left( 1+\alpha ,M\right) =-\frac{1}{\varGamma \left( 2-\alpha \right) }\frac{2^{\alpha -1}}{\left( 2^{\alpha }-1\right) ^{2}}\frac{\alpha ^{2}}{\triangle x^{1+\alpha }}, \end{aligned}$$
(105)
$$\begin{aligned}&\phi _{1}^{\text {ex}}=\frac{E_{\alpha ,1}\left( \frac{u}{v}\triangle x^{\alpha }\right) -1}{E_{\alpha ,1}\left( \frac{u}{v}\right) -1}, \end{aligned}$$
(106)
$$\begin{aligned}&\phi _{2}^{\text {ex}}=\frac{E_{\alpha ,1}\left( \frac{u}{v}\left( 2\triangle x\right) ^{\alpha }\right) -1}{E_{\alpha ,1}\left( \frac{u}{v}\right) -1}. \end{aligned}$$
(107)
Substituting all the formulas above into Eq. (97), by expanding and minimizing \(R_{1}=\left| F_{1}^{*}-F_{1}\right| =0\), the artificial viscosity coefficient is formulated as
$$\begin{aligned} \gamma =\frac{\triangle x}{2}\frac{\hat{P}e\left( 2^{\alpha }-1\right) ^{2}\varTheta +\alpha \varGamma \left( 3-\alpha \right) \left( 2^{\alpha }-\varTheta \right) \left[ \left( 2^{\alpha }-1\right) \varGamma \left( \alpha \right) -\frac{\alpha sin\left( \pi \alpha \right) }{\pi }M_{G}^{\alpha }\mid _{1}^{0.5}\right] }{\left[ 2^{\alpha -2}\left( 2^{\alpha }-\varTheta \right) \left( 2-\alpha \right) -\hat{P}e\chi \right] \alpha ^{2}}, \end{aligned}$$
(108)
where \(\varTheta \) is a function of fractional Peclet number defined as
$$\begin{aligned} \varTheta =\frac{E_{\alpha ,1}\left( 2^{1+\alpha }\hat{P}e/\varGamma \left( 3-\alpha \right) \right) -1}{E_{\alpha ,1}\left( 2\hat{P}e/\varGamma \left( 3-\alpha \right) \right) -1}. \end{aligned}$$
(109)
\(\chi \) is a function of parameter \(\varepsilon \) introduced by the special case of \(K_{11}\left( 1,M\right) \) as shown in “Appendix 3”, and defined as
$$\begin{aligned} \chi =\frac{1}{2\alpha -1}\left\{ \begin{array}{lll} \left( 2^{2\alpha -1}-1\right) \left( 1-\varTheta \right) \\ \quad +2^{1-2\alpha }\left( 2\alpha -1\right) \left( 2^{\alpha }-1\right) ^{2}\varepsilon , &{} &{} \alpha \le 0.5\\ \left( 2^{2\alpha -1}-1\right) \left( 1-\varTheta \right) \\ \quad +\left( 2^{\alpha }-1\right) ^{2}, &{} &{} \alpha >0.5. \end{array}\right. \end{aligned}$$
(110)