A semi-numerical algorithm for instability of compressible multilayered structures

Abstract

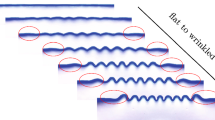
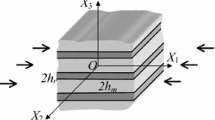
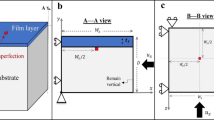
A computational method is proposed for the analysis and prediction of instability (wrinkling or necking) of multilayered compressible plates and sheets made by metals or polymers under plane strain conditions. In previous works, a basic assumption (or a physical argument) that has been frequently made is that materials are incompressible to simplify mathematical derivations. To account for the compressibility of metals and polymers (the lower Poisson’s ratio leads to the more compressible material), we propose a combined semi-numerical algorithm and finite element method for instability analysis. Our proposed algorithm is herein verified by comparing its predictions with published results in literature for thin films with polymer/metal substrates and for polymer/metal systems. The new combined method is then used to predict the effects of compressibility on instability behaviors. Results suggest potential utility for compressibility in the design of multilayered structures.

Appendix

1.1 Derivation for neo-Hookean model

For neo-Hookean model, we start with the right Cauchy–Green tensor:

$$\begin{aligned} \mathbf {C}=\mathbf {F}^{T}\mathbf {F} \end{aligned}$$

We have

$$\begin{aligned} J=\det (\mathbf {F})=\sqrt{\det \mathbf {C}}=\sqrt{I_{3}}\qquad I_{1}= \text {trace}\left( \mathbf {C}\right) \end{aligned}$$

where $I_{1}$ and $I_{3}$ is the first and third invariant of $\mathbf {C.}$ The elastic deformation energy in Eq. (1) can be rewritten as:

$$\begin{aligned} W=\frac{\mu }{2}\left( I_{3}^{-1/3}I_{1}-3\right) +K_{m}\left( I_{3}^{1/2}-1\right) ^{2}. \end{aligned}$$

If we define

$$\begin{aligned} W_{1}= & {} \frac{\partial W}{\partial I_{1}}=\frac{\mu }{2}I_{3}^{-1/3} \\ W_{3}= & {} \frac{\partial W}{\partial I_{3}}=-\frac{\mu }{6} I_{3}^{-4/3}I_{1}+K_{m}\left( 1-I_{3}^{-1/2}\right) \\ W_{11}= & {} \frac{\partial ^{2}W}{\partial I_{1}\partial I_{1}}=0 \\ W_{13}= & {} \frac{\partial ^{2}W}{\partial I_{1}\partial I_{3}}=-\frac{\mu }{6} I_{3}^{-4/3} \\ W_{33}= & {} \frac{\partial ^{2}W}{\partial I_{3}\partial I_{3}}=\frac{2\mu }{9} I_{3}^{-7/3}I_{1}+\frac{K_{m}}{2}I_{3}^{-3/2} \end{aligned}$$

and apply the following results,

$$\begin{aligned} \frac{\partial C_{AP}^{-1}}{\partial C_{MN}}= & {} -C_{AM}^{-1}C_{NP}^{-1}\qquad \frac{\partial I_{1}}{\partial F_{ij}} =2F_{ij}\\ \frac{\partial I_{3}}{ \partial F_{ij}}= & {} I_{3}\left( C_{nj}^{-1}F_{in}+C_{jm}^{-1}F_{im}\right) , \end{aligned}$$

then first PK stress may be obtained from Eq. (2) as,

$$\begin{aligned} P_{kl}= & {} \frac{\partial W}{\partial I_{1}}\frac{\partial I_{1}}{\partial F_{kl}}+\frac{\partial W}{\partial I_{3}}\frac{\partial I_{3}}{\partial F_{kl}} \nonumber \\= & {} 2W_{1}F_{kl}+W_{3}I_{3}\left( C_{ml}^{-1}F_{km}+C_{lm}^{-1}F_{km}\right) \end{aligned}$$

(20)

The tangent modulus tensor in the undeformed configuration is,

$$\begin{aligned} B_{ijkl}^{0}= & {} \frac{\partial ^{2}W}{\partial F_{ij}\partial F_{kl}} \\= & {} 2\left[ 2W_{11}F_{ij}+W_{13}I_{3}\left( C_{nj}^{-1}F_{in}+C_{jm}^{-1}F_{im}\right) \right] F_{kl}\\&+\,2W_{1}\delta _{ki}\delta _{lj} +\,\left[ 2W_{13}F_{ij}+W_{33}I_{3}\right. \\&\times \left. \left( C_{nj}^{-1}F_{in}+C_{jm}^{-1}F_{im}\right) \right] I_{3}\left( C_{ml}^{-1}F_{km}+C_{lm}^{-1}F_{km}\right) \\&+\, W_{3}I_{3}\left( C_{nj}^{-1}F_{in}+C_{jm}^{-1}F_{im}\right) \left( C_{ml}^{-1}F_{km}+C_{lm}^{-1}F_{km}\right) \\&+\,W_{3}I_{3}\left[ 2\left( -C_{lN}^{-1}F_{iN}C_{mj}^{-1}-C_{in}^{-1}F_{mn}C_{lj}^{-1}\right) F_{km}\right. \\&\left. +\,2C_{jl}^{-1}\delta _{ki}\right] \end{aligned}$$

After we obtain the tangent modulus tensor in the undeformed configuration, in the updated Lagrangian configuration it can be computed through Eq. (13). Substituting into Eqs. (12) and (14), then the coefficients in Eq. (15) can be obtained from,

$$\begin{aligned} a_{11}= & {} \frac{2W_{1}a^{2}}{J} \nonumber \\ a_{12}= & {} -\frac{K^{2}\lambda ^{2}\left( 4W_{11}\lambda ^{2}+8W_{13}I_{3}+4W_{33}I_{3}^{2}/\lambda ^{2}+2W_{1}+2W_{3}I_{3}/\lambda ^{2}\right) }{J} \nonumber \\ a_{13}= & {} -\frac{K\lambda a\left( 4W_{11}\lambda a+4W_{13}I_{3}a/\lambda +4W_{13}I_{3}\lambda /a+4W_{33}I_{3}^{2}/\!(\lambda a)+ 2W_{3}I_{3}/\!\left( \lambda a\!\right) \!\right) }{J} \nonumber \\ a_{22}= & {} \frac{a^{2}\left( 4W_{11}a^{2}+8W_{13}I_{3}+4W_{33}I_{3}^{2}/a^{2}+2W_{1}+2W_{3}I_{3}/a^{2} \right) }{J} \nonumber \\ a_{21}= & {} -\frac{2W_{1}K^{2}\lambda ^{2}}{J} \nonumber \\ a_{23}= & {} \frac{Ka\lambda \left[ 4W_{11}a\lambda +4W_{13}I_{3}\lambda /a+4W_{13}I_{3}a/\lambda +4W_{33}I_{3}^{2}/\left( a\lambda \right) +2W_{3}I_{3}/\left( a\lambda \right) \right] }{J}\nonumber \\ \end{aligned}$$

(21)

The coefficients for the stress increments can be computed in the same way, giving,

$$\begin{aligned} b_{11}= & {} \frac{2W_{1}a^{2}}{J} \nonumber \\ b_{12}= & {} \frac{2W_{3}I_{3}K}{J} \nonumber \\ b_{22}= & {} \frac{K\lambda a\left[ 4W_{11}a\lambda +4W_{13}I_{3}\lambda /a\!+\!4W_{13}I_{3}a/\lambda +4W_{33}I_{3}^{2}/\!\left( a\lambda \right) +4W_{3}I_{3}/\!\left( a\lambda \right) \right] }{J} \nonumber \\ b_{21}= & {} \frac{a^{2}\left( 4W_{11}a^{2}+8W_{13}I_{3}+4W_{33}I_{3}^{2}/a^{2}+2W_{1}+2W_{3}I_{3}/a^{2} \right) }{J} \end{aligned}$$

(22)

1.2 Derivation for J2 deformation plasticity model

Suppose $a_{i}$ is the ith eigenvalue, and $\mathbf {a}_{i}$ the corresponding eigenvector of $\bar{\mathbf {C}}$, then we have (see [43]),

$$\begin{aligned} \frac{da_{i}}{d{\bar{\mathbf {C}}}}=\mathbf {a}_{i}\otimes \mathbf {a}_{i}= \mathbf {A}_{i} \end{aligned}$$

and,

$$\begin{aligned} \frac{d\mathbf {A}_{i}}{d{\bar{\mathbf {C}}}}= & {} \frac{\mathbf {A}_{i}\boxtimes \mathbf {A}_{j}+\mathbf {A}_{j}\boxtimes \mathbf {A}_{i}}{a_{i}-a_{j}}+\frac{ \mathbf {A}_{i}\boxtimes \mathbf {A}_{k}+\mathbf {A}_{k}\boxtimes \mathbf {A}_{i} }{a_{i}-a_{k}}, \\&i\ne j,k,\quad i,j,k\in \left\{ 1,2,3\right\} \end{aligned}$$

where $\boxtimes$ is defined as follows,

$$\begin{aligned} \left( \mathbf {A}\boxtimes \mathbf {B}\right) \mathbf {C=ACB}^{T} \end{aligned}$$

and $\mathbf {A,B,C}$ are second order tensors. With these results at hand, the first PK stress (4) is given by,

$$\begin{aligned} P_{ij}= & {} \frac{\partial W^{M}}{\partial a_{I}}\left( a_{I}\right) _{m}\left( a_{I}\right) _{n}\left( \delta _{mg}F_{nh}+F_{mh}\delta _{ng}\right) \nonumber \\&\left[ \left( -\frac{1}{3}\right) \left( F_{ji}\right) ^{-1}F_{gh}+\delta _{gi}\delta _{hj}\right] J^{-2/3}\nonumber \\&+2K^{M}\left( J-1\right) JF_{ji}^{-1} \end{aligned}$$

(23)

and the tangent modulus tensor

$$\begin{aligned} B_{ijkl}^{0}= & {} \frac{\partial P_{ij}}{\partial F_{kl}}=\frac{\partial ^{2}W^{M}}{\partial a_{I}\partial a_{K}}\left( \mathbf {a}_{I}\right) _{m}\left( \mathbf {a}_{I}\right) _{n}\left( \mathbf {a}_{K}\right) _{m1}\left( \mathbf {a}_{K}\right) _{n1}\nonumber \\&\times \left( \delta _{mg}F_{nh}+F_{mh}\delta _{ng}\right) \left[ \left( -\frac{1}{3}\right) F_{ji}^{-1}F_{gh}+\delta _{gi}\delta _{hj}\right] \nonumber \\&\times \left( \delta _{m1g1}F_{n1h1}+F_{m1h1}\delta _{n1g1}\right) \nonumber \\&\times \left[ \left( - \frac{1}{3}\right) F_{lk}^{-1}F_{g1h1}+\delta _{g1k}\delta _{h1l}\right] J^{-4/3} \nonumber \\&+\,\frac{\partial W^{M}}{\partial a_{I}}\left[ \left( \mathbf {a}_{I}\right) _{m}\left( \mathbf {a}_{I}\right) _{c}\left( \mathbf {a}_{M}\right) _{n}\left( \mathbf {a}_{M}\right) _{d}\right. \nonumber \\&\left. +\left( \mathbf {a}_{M}\right) _{m}\left( \mathbf {a} _{M}\right) _{c}\left( \mathbf {a}_{I}\right) _{n}\left( \mathbf {a} _{I}\right) _{d}\right] \frac{1}{a_{I}-a_{M}} \nonumber \\&\times \left( \delta _{cg}F_{dh}+F_{ch}\delta _{dg}\right) \left[ \left( -\frac{1}{3}\right) F_{lk}^{-1}F_{gh}+\delta _{gk}\delta _{hl} \right] \nonumber \\&\times \left( \delta _{mg1}F_{nh1}+F_{mh1}\delta _{ng1}\right) \nonumber \\&\times \left[ \left( - \frac{1}{3}\right) F_{ji}^{-1}F_{g1h1}+\delta _{g1i}\delta _{h1j}\right] J^{-4/3} \nonumber \\&+\, \frac{\partial W^{M}}{\partial a_{I}}\left( a_{I}\right) _{m}\left( a_{I}\right) _{n}\left( \delta _{mg}\delta _{nk}\delta _{hl}+\delta _{mk}\delta _{hl}\delta _{ng}\right) \nonumber \\&\times \left[ \left( -\frac{1}{3}\right) F_{ji}^{-1}F_{gh}+\delta _{gi}\delta _{hj}\right] J^{-2/3} \nonumber \\&+\frac{1}{3}\frac{\partial W^{M}}{\partial a_{I}}\left( a_{I}\right) _{m}\left( a_{I}\right) _{n}\left( \delta _{mg}F_{nh}+F_{mh}\delta _{ng}\right) \nonumber \\&\times \left[ -F_{ji}^{-1}\delta _{gk}\delta _{hl}+F_{gh}F_{jk}^{-1}F_{li}^{-1} \right] J^{-2/3} \nonumber \\&+\,\frac{\partial W^{M}}{\partial a_{I}}\left( a_{I}\right) _{m}\left( a_{I}\right) _{n}\left( \delta _{mg}F_{nh}+F_{mh}\delta _{ng}\right) \nonumber \\&\times \left[ \left( -\frac{1}{3}\right) F_{ji}^{-1}F_{gh}+\delta _{gi}\delta _{hj}\right] \left( -\frac{2}{3}\right) J^{-2/3}F_{lk}^{-1} \nonumber \\&+\,2K^{M}\left[ \left( 2J-1\right) JF_{lk}^{-1}F_{ji}^{-1}\!-\!\left( J\!-\!1\right) JF_{jk}^{-1}F_{li}^{-1}\right] \nonumber \\ \end{aligned}$$

(24)

where subscripts $I$ and $M$ range from 1 to 3 ($I\ne M=1\ldots 3$). Through Eq. (13) we can obtain stress increments by Eq. (12). Substituting into Eq. (14), the coefficients in Eq. (15) $a_{11},a_{12},a_{13},a_{22},a_{21},a_{23}$ and $b_{11},b_{12},b_{21},b_{22}$ can be computed for hard metals. Unlike the hyperelastic materials, the resulting expressions turn out to be much more complicated. As such, they are not listed here. We instead compute them automatically.