A reverse updated Lagrangian finite element formulation for determining material properties from measured force and displacement data

Abstract

The mechanical response of solids exhibiting complex material behavior has traditionally been determined by fitting constitutive models of specified functional form to experimentally derived force-displacement (stress-strain) data. However, characterizing the nonlinear mechanical behavior of complex materials requires a method of quantifying material behavior that is not restricted by a specific constitutive relation. To this end, a new method, termed the reverse updated Lagrangian finite element method (RULFEM), which is based on the three-dimensional displacement field of the deformed solid and the finite element method, is developed for incrementally linear materials. Using the RULEFM, the body is discretized by finite elements and its material properties are determined element-wise, i.e., the properties are assumed to be uniform at the element level and may vary from one element to another. The validity of RULFEM is demonstrated by three noise-free numerical examples and three numerical examples with various input noise levels. Two methods to assess the global and local errors of the results due to error in the measured input data (noisy data) are also discussed.

Appendix: updated Lagrangian finite element formulation

Consider the solid body $\Omega$ in the coordinate system shown in Fig. 18. The equilibrium position at time $t +\Delta t$ (i.e., configuration $R_1$) can be obtained from the equation of motion:

$$\begin{aligned}&\hbox {div}\mathbf{P}+\rho _0 \mathbf{b}=\rho _0 \mathbf{a} \hbox { in }R_0 \end{aligned}$$

(31a)

$$\begin{aligned}&\mathbf{P}\cdot \mathbf{N}=\overline{{\mathbf{p}}}\hbox { on }\Gamma _{q0} \end{aligned}$$

(31b)

$$\begin{aligned}&\mathbf{u}=\overline{\mathbf{u}}\hbox { on }\Gamma _{u0} \end{aligned}$$

(31c)

where P is the first Piola–Kirchhoff stress, $\rho _0=\hat{{\rho }}_0 (\mathbf{X})$ is the density, b is the body force, a is the acceleration, N is the unit normal vector, $\overline{\mathbf{p}}$ is the traction acting on boundary $\Gamma _{q0}$, and $\overline{\mathbf{u}}$ is the displacement specified over boundary $\Gamma _{u0}$.

The position vector of any material point $X$ in the new configuration $R$ is defined as $\mathbf{x}=\mathbf{X}+\mathbf{u}(\mathbf{X},t)$, where the displacement field u is defined in the following set $\mathcal{S}_u$:

$$\begin{aligned} \mathcal{S}_u&= \left\{ \mathbf{u}:R_0 \times {\mathbb {R}}^{3}\mapsto \left. {{\mathbb {R}}^{3}} \right| \mathbf{u}=\overline{{\mathbf{u}}} \hbox { on } \Gamma _{u0}, \mathbf{u}\left( {\mathbf{X},t_0} \right) =\overline{{\mathbf{u}}},\right. \nonumber \\&\left. J_0=\hbox {det}\!\left( {\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{X}}} \right) >0,\quad \frac{d\mathbf{u}(\mathbf{X},t_0 )}{dt}=\mathbf{0}\hbox { in }R_0 \right\} \nonumber \\ \end{aligned}$$

(32)

where I is the second-order identity tensor.

Consequently, the deformation gradient tensor F is expressed as

$$\begin{aligned} \mathbf{F}=\mathbf{I}+\frac{\partial \mathbf{u}}{\partial \mathbf{X}}=\mathbf{I}+\mathbf{H} \end{aligned}$$

(33)

where H is the displacement gradient tensor.

To find the displacement function of the body $\mathbf{u}(\mathbf{X},t)$ under the given boundary conditions [Eqs. (31b) and (31c)], the weak-form of the problem is generated by applying a tangent vector field $\varvec{\zeta }$ (also known as the test function), which is typically expressed as the product of a test function of time $\theta ( t )$ and a test function of space $\hat{{\varvec{\upxi }}} (\mathbf{X})$, i.e.,

$$\begin{aligned} \zeta =\hat{{\zeta }} (\mathbf{X},t)=\theta ( t )\hat{{\varvec{\upxi }}} (\mathbf{X}) \end{aligned}$$

(34a)

for any admissible $\varvec{\upxi } =\hat{{\varvec{\upxi }}} (\mathbf{X})$ defined in a set $\mathcal{S}_\xi$ as

$$\begin{aligned} \mathcal{S}_\xi =\left\{ \varvec{\upxi } :R_0 \times \mathbb {R}^{3}\mapsto \left. {\mathbb {R}}^{3} \right| \varvec{\upxi } =\mathbf{0} \hbox { on } \Gamma _{u0} \right\} \end{aligned}$$

(34b)

Fig. 18

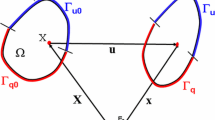
A solid body $\Omega$ shown in two configurations – the reference configuration $R_0$ with an outward normal vector N and displacement and traction boundary conditions prescribed on $\Gamma _{u0}$ and $\Gamma _{q0}$, respectively, and the deformed configuration $R_1$ with an outward normal vector n and displacement and traction boundary conditions prescribed on $\Gamma _u$ and $\Gamma _q$, respectively

Fig. 19

Schematic of updated Lagrangian configurations of a solid body $\Omega$ corresponding to $n$+1 infinitesimal movements from reference configuration $R_0$ to deformed configuration $R_n$

Figure 19 shows a body $\Omega$ in the reference configuration $R_0$ at time $t_0$, which, after $n$ infinitesimal deformations in time increments $\Delta t$, attains configuration $R_n$ at time $t_0 +n\Delta t$. A solution of the incremental displacement field $\left. \mathbf{u} \right| _{n+1}^n$, using configuration $R_n$ as a reference, can be obtained by considering the general updated Lagrangian weak-form [12] expressed as

$$\begin{aligned}&r_{n+1} \!=\!\int \nolimits _{R_n}\left( {\left. \varvec{\upxi } \right| _{n+1}^n \rho _n \left. { \mathbf{a}} \right| _{n+1}^n} \right) \textit{dV}_n \!+\!\int \nolimits _{R_n}\big ( {\left. \mathbf{P} \right| _{n+1}^n \frac{\left. {\partial \varvec{\upxi }} \right| _{n+1}^n}{\partial \mathbf{x}_{\varvec{n}}}} \big ) \textit{dV}_n \nonumber \\&\quad -\int \nolimits _{R_n} \left( {\left. \varvec{\upxi } \right| _{n+1}^n \rho _n \left. { \mathbf{b}} \right| _n^n} \right) \textit{dV}_n -\int \nolimits _{\Gamma _{qn}} \left( {\left. \varvec{\upxi } \right| _{n+1}^n \overline{{\mathbf{p}}}_n^n} \right) \textit{dA}_n =0\nonumber \\ \end{aligned}$$

(35)

where $r_{n+1}$ is the residual of the weak-form at time $t_0 +(n+1)\Delta t$ (i.e., body configuration $R_{n+1}$), $\left. \varvec{\upxi } \right| _{n+1}^n, \left. \mathbf{a} \right| _{n+1}^n =\frac{d^{2}\left. \! \mathbf{x} \right| _{n+1}^n}{dt^{2}}, \left. \mathbf{b} \right| _n^n, \left. {\overline{\mathbf{p}}} \right| _n^n$, and $\left. \mathbf{P} \right| _{n+1}^n =\left. \widehat{{\mathbf{P}}}( \mathbf{H} \right| _{n+1}^n, \left. {\dot{\mathbf{H}}} \right| _{n+1}^n )$ are the tangent vector field, acceleration, body force, Piola–Kirchhoff surface traction, and the first Piola–Kirchhoff stress, respectively, $\rho _n$ is the material density of body $\Omega$ at time $t_0 +n\Delta t$, and $\textit{dV}_n$ and $\textit{dA}_n$ are the elemental volume and area, respectively.

In addition to $\left. \mathbf{u} \right| _{n+1}^n \in \mathcal{S}_u$ [Eq. (32)] and $\left. \varvec{\upxi } \right| _{n+1}^n \in \mathcal{S}_\xi$ [Eq. (34b)], for the integrals in the updated Lagrangian weak-form [Eq. (35)] to be bounded, $\left. \mathbf{u} \right| _{n+1}^n$ and $\left. \varvec{\upxi } \right| _{n+1}^n$ must also belong to an appropriate Hilbert space ${\mathbb {H}}^{1}(R_n)$. Thus, the corresponding sets of $\left. \mathbf{u} \right| _{n+1}^n$ and $\left. \varvec{\upxi } \right| _{n+1}^n$ in the updated Lagrangian weak-form, $\mathcal{S}_u^{wf}$ and $\mathcal{S}_{\varvec{\upxi }}^{wf}$, respectively, are defined as

$$\begin{aligned} \mathcal{S}_{u_n}^{wf}&= \mathcal{S}_u \mathop \cap \left\{ \mathbf{u}\!\!\left. \big |_{n+1}^n \in {\mathbb {H}^{1}\left( {R_n} \right) } \right| \mathbf{u}\! \left| _{n+1}^n =\overline{{\mathbf{u}}}\right| _{n+1}^n \hbox { on } \Gamma _{u_n} \right\} \nonumber \\ \end{aligned}$$

(36a)

$$\begin{aligned} \mathcal{S}_\xi ^{wf}&= \mathcal{S}_{\varvec{\xi }} \mathop \cap \left\{ { \varvec{\upxi }\!\!\left. \big |_{n+1}^n \in {\mathbb {H}}^{1}\left( {R_n} \right) \right| \varvec{\upxi }\!\left| _{n+1}^n \right. =\mathbf{0} \hbox { on } \Gamma _{u_n}} \right\} \end{aligned}$$

(36b)

Assume that the domain represented by configuration $R_n$ is discretized by $N_e$ elements so that $R_n =\mathop {\cup }\nolimits _1^{N_e} \Omega ^{e}$, where $\Omega ^{e}$ represents the element domain, and that the corresponding total number of nodes is $N_n$. Then, Eq. (35) can be solved for all nodal points of the finite element mesh. The displacement field within each element is described by $N_p$ polynomials, known as the shape functions $\phi _1^e, \phi _2^e, \ldots$, and $\phi _{N_e}^e$. Thus, the displacement field in each element can be expressed as

$$\begin{aligned} \left. { \mathbf{u}^{e}} \right| _{n+1}^n&=\left. {\mathbf{x}_{{\varvec{h}}}^{{\varvec{e}}}} \right| _{n+1}^n \left. {-\mathbf{x}_{{\varvec{h}}}^{{\varvec{e}}}} \right| _n^n = \mathop \sum \limits _{i=1}^{N_p} \left[ {\phi _i^e\! \left( {\left. {\mathbf{x}_{{\varvec{h}}}^{{\varvec{e}}}} \right| _n^n} \right) \left. {\mathbf{u}_{{\varvec{h}},i}^{{\varvec{e}}}} \right| _{n+1}^n} \right] \nonumber \\&= \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\mathbf{u}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \end{aligned}$$

(37)

where superscript $e$ and subscript $h$ denote elemental quantities defined at nodal points, $\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right]$ is the elemental shape function matrix, and $\left\{ {\mathbf{u}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$ is the vector of finite element nodal displacements. For a 3D space, the size of the elemental vectors $\left\{ {\mathbf{u}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$ and $\left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$ is equal to $(3N_p \times 1).$ Consequently, the size of $\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right]$ is $(3\times 3N_p )$. However, these vectors must belong to weak-form admissible subsets $\mathcal{S}_{u_{n,h}}^{wf}$ and $\mathcal{S}_{\xi , h}^{wf}$, such that $\mathcal{S}_{u_{n,h}}^{wf} \in \mathcal{S}_{u_n}^{wf}$ and $\mathcal{S}_{\xi , h}^{wf} \in \mathcal{S}_\xi ^{wf}$ [12, 13].

The other vector and tensor quantities of each element [Eq. (35)] in the domain of configuration $R_n$ can also be expressed in terms of elemental shape functions as shown below.

• (i) The acceleration vector:

  $$\begin{aligned} \left. {\mathbf{a}^{{\varvec{e}}}} \right| _{n+1}^n&=\frac{d^{2}\!\left. \! {\mathbf{x}^{{\varvec{e}}}} \right| _{n+1}^n}{dt^{2}}= \mathop \sum \limits _{i=1}^{N_p} \left[ {\phi _i^e \left. { \mathbf{a}_{{\varvec{h}},i}^{{\varvec{e}}}} \right| _{n+1}^n} \right] \nonumber \\&=\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\mathbf{a}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \end{aligned}$$

  (38)

  where the size of $\left. {\mathbf{a}^{{\varvec{e}}}} \right| _{n+1}^n$ and nodal acceleration vector $\left\{ {\mathbf{a}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$ is equal to $(3\times 1)$ and $(3N_p \times 1)$, respectively.

• (ii) The displacement gradient tensor:

  $$\begin{aligned}&\left. {\mathbf{H}^{{\varvec{e}}}} \right| _{n+1}^n \left( {\left. {\mathbf{u}^{{\varvec{e}}}} \right| _{n+1}^n} \right) = \frac{\partial \!\!\left. {\mathbf{u}^{{\varvec{e}}}} \right| _{n+1}^n}{\partial \!\!\left. \mathbf{x} \right| _n^n}\nonumber \\&\quad =\mathop \sum \limits _{i=1}^{N_p} \left[ {\frac{\partial \phi _i^e}{\partial \!\! \left. \mathbf{x} \right| _n^n} \left. {\mathbf{u}_{{\varvec{h}},i}^{{\varvec{e}}}} \right| _{n+1}^n} \right] =\left[ {\mathbf{B}^{{\varvec{e}}}} \right] \left\{ {\mathbf{u}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \end{aligned}$$

  (39)

Although $\left. {\mathbf{H}^{{\varvec{e}}}} \right| _{n+1}^n$ is a second-order tensor and its components are typically represented by a $(3\times 3)$ matrix, in the present weak formulation it is represented by a $(9\times 1)$ vector, i.e., $\left\{ {\left. {\mathbf{H}^{{\varvec{e}}}} \right| _{n+1}^n} \right\}$; therefore, $\left[ {\mathbf{B}^{{\varvec{e}}}} \right]$ is formulated as a $(9\times 3N_p )$ matrix.

• (iii) The gradient of the tangent vector tensor:

  $$\begin{aligned} \left. {\varvec{\upxi }^{{\varvec{e}}}} \right| _{n+1}^n = \mathop \sum \limits _{i=1}^{N_p} \left[ {\phi _i^e \left. {\varvec{\upxi }_{{\varvec{h}},i}^{\varvec{e}}} \right| _{n+1}^n} \right] =\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \end{aligned}$$

  (40)

  Because $\left. {\varvec{\xi }^{{\varvec{e}}}} \right| _{n+1}^n$ is a $(3\times 1)$ vector, its gradient is defined by

  $$\begin{aligned}&\left. {\mathbf{H}^{{\varvec{e}}}} \right| _{n+1}^n\!\left( {\left. {\varvec{\upxi }^{{\varvec{e}}}} \right| _{n+1}^n} \right) = \frac{\partial \!\!\left. {\varvec{\upxi }^{{\varvec{e}}}} \right| _{n+1}^n}{\partial \!\!\left. \mathbf{x} \right| _n^n}\nonumber \\&\quad =\mathop \sum \limits _{i=1}^{N_p} \left[ {\frac{\partial \phi _i^e}{\partial \!\! \left. \mathbf{x} \right| _n^n}\!\left. {\varvec{\upxi }_{{\varvec{h}},i}^{\varvec{e}}} \right| _{n+1}^n} \right] =\left[ {\mathbf{B}^{{\varvec{e}}}} \right] \left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \end{aligned}$$

  (41)

• (iv) The body force vector:

  $$\begin{aligned} \left. {\mathbf{b}^{{\varvec{e}}}} \right| _n^n = \mathop \sum \limits _{i=1}^{N_p} \left[ {\phi _i^e \left. { \mathbf{b}_{{\varvec{h}},i}^{{\varvec{e}}}} \right| _n^n} \right] =\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\mathbf{b}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _n^n \end{aligned}$$

  (42)

  where the size of $\left. {\mathbf{b}^{{\varvec{e}}}} \right| _n^n$ and the nodal body force vector $\left\{ {\mathbf{b}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _n^n$ are equal to $(3\times 1)$ and $(3N_p \times 1)$, respectively.

• (v) The Piola–Kirchhoff traction vector:

  $$\begin{aligned} \left. {\overline{\mathbf{p}}^{{\varvec{e}}}} \right| _n^n = \mathop \sum \limits _{i=1}^{N_p} \left[ {\phi _i^e \left. { \mathbf{p}_{{\varvec{h}},i}^{{\varvec{e}}}} \right| _{n+1}^n} \right] =\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\overline{\mathbf{p}}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _n^n \end{aligned}$$

  (43)

  where the sizes of $\left. {\mathbf{p}^{{\varvec{e}}}} \right| _n^n$ and the nodal traction vector $\left\{ {\overline{\mathbf{p}}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _n^n$ are equal to $(3\times 1)$ and $(3N_p \times 1)$, respectively.

The numerical form of Eq. (35) is obtained by substituting Eqs. (38)–(43) into Eq. (35), factoring out the nodal tangent vector $\left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$, and assembling over the entire domain of the body. However, numerical approximation of Eq. (35) yields a nonzero residual $r_{n+1}$ at each increment step. Therefore, an assembly operator $\varvec{\mathcal{A}}_{e=1}^{N_e}$ that combines all the common nodal DOF of the finite elements is introduced in the re-formulated Eq. (35) as shown below:

$$\begin{aligned} r_{n+1} \!&= \!\varvec{\mathcal{A}}_{e=1}^{N_e} \left\{ \left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^{n^{\mathrm{T}}} \left\{ \int \nolimits _{R_n} \left[ {\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \rho _{n}^e \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] } \right) \textit{dV}_n^e} \right] \left\{ {\mathbf{a}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n \right. \right. \nonumber \\&+\int \nolimits _{R_n} \left( \left[ {\mathbf{B}^{{\varvec{e}}}} \right] ^{\mathrm{T}} \widehat{{\mathbf{P}}}^{{\varvec{e}}}\!\!\left( \mathbf{H}^{{\varvec{e}}}\left. \right| _{n+1}^n, \left. {\dot{\mathbf{H}}}^{{\varvec{e}}} \right| _{n+1}^n\right) \right) \textit{dV}_n^e \nonumber \\&-\int \nolimits _{R_n} \left[ {\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \rho _{n}^e \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] } \right) \textit{dV}_n^e} \right] \left\{ {\mathbf{b}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n}^n\nonumber \\&\left. \left. -\int \nolimits _{\Gamma _{qn}}\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\overline{{\mathbf{p}}}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n}^n} \right) \textit{dA}_n^e\right\} \right\} \end{aligned}$$

(44)

A numerical solution of Eq. (44) that yields $r_{n+1} =0$ is incrementally obtained at each step. Since the tangent vector $\left\{ {\varvec{\upxi }_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n+1}^n$ is an arbitrary vector that vanishes at the boundary [Eq. (34b)], the solution can be found by setting the terms inside the second bracket equal to zero, i.e.,

$$\begin{aligned}&{\varvec{\mathcal {A}}}_{{e = 1}}^{{N_{e} }} \left\{ \int \nolimits _{{R_{n} }}\left[ {\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{{\text {T}}} \rho _{n}^{e} \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] } \right) \,\textit{dV}_{n}^{e} } \right] \left\{ {{\mathbf {a}}_{{\varvec{h}}}^{{\varvec{e}}}}\right\} _{{n + 1 }}^{n}\right. \nonumber \\&\quad +\int \nolimits _{{R_{n} }} \left( \left[ {{\mathbf {B}}^{{\varvec{e}}}} \right] ^{{\text {T}}} {\widehat{\mathbf{P}}}^{{\varvec{e}}}\! (\left. \mathbf{H}^{{\varvec{e}}} \right| _{{n + 1}}^{n},\left. {{\dot{\mathbf{H}}}^{{\varvec{e}}}}\right| _{{n + 1}}^{n}) \right) \textit{dV}_{n}^{e}\nonumber \\&\quad -\int \nolimits _{{R_{n}}}\left[ \left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}}\right] ^{{\text {T}}}\rho _{n}^{e} \left[ {\varvec{\upphi }^{{\varvec{e}}}}\right] }\right) \,\textit{dV}_{n}^{e}\right] \left\{ {{\mathbf {b}}_{{\varvec{h}}}^{{\varvec{e}}} } \right\} _{{n }}^{n} \nonumber \\&\quad \left. -\int \nolimits _{{{\Gamma }_{{qn}} }} \left( {\left[ {\varvec{\upphi }^{{\varvec{e}}} } \right] ^{{\text {T}}} \left[ {\varvec{\upphi }^{{\varvec{e}}} } \right] \left\{ {{\mathbf {\overline{p}}}_{{\varvec{h}}}^{{\varvec{e}}} } \right\} _{{n }}^{n} } \right) \,\textit{dA}_{n}^{e}\right\} = 0 \end{aligned}$$

(45)

Equation (45) can be written in more concise form by introducing the mass matrix, the stiffness-displacement vector, and the force vector, defined below.

• (i) The mass matrix in configuration $R_n$:

  $$\begin{aligned} \left[ \mathbf{M} \right] _n^n =\varvec{\mathcal{A}}_{e=1}^{N_e} \left\{ {\int \nolimits _{R_n} \left[ {\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \rho _n^e \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] } \right) \textit{dV}_n^e} \right] } \right\} \end{aligned}$$

  (46a)

• (ii) The stiffness-displacement vector with respect to configuration $R_n$ and displacement vector, mapping configuration $R_n$ to configuration $R_{n+1}$:

  $$\begin{aligned} \left\{ \mathbf{R} \right\} _{n+1}^n&= \varvec{\mathcal{A}}_{e=1}^{N_e} \left\{ \int \nolimits _{R_n}\!\! \left( \left[ {\mathbf{B}^{{\varvec{e}}}} \right] ^{\mathrm{T}}\widehat{{\mathbf{P}}}^{{\varvec{e}}}\!\left( \mathbf{H}^{{\varvec{e}}}\! \left| _{n+1}^n, {\dot{\mathbf{H}}} \right| _{n+1}^n\right) \right) \textit{dV}_n^e\right\} \nonumber \\ \end{aligned}$$

  (46b)

• (iii) The force vector in configuration $R_n$:

  $$\begin{aligned} \left\{ \mathbf{f} \right\} _n^n&= \varvec{\mathcal{A}}_{e=1}^{N_e} \left\{ \int \nolimits _{R_n} \left[ {\left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \rho _n^e \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] } \right) \textit{dV}_n^e} \right] \left\{ {\mathbf{b}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n}^n\right. \nonumber \\&\left. +\int \nolimits _{\Gamma _{qn}} \left( {\left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] ^{\mathrm{T}} \left[ {\varvec{\upphi }^{{\varvec{e}}}} \right] \left\{ {\overline{{\mathbf{p}}}_{{\varvec{h}}}^{{\varvec{e}}}} \right\} _{n}^n} \right) \textit{dA}_n^e \right\} \end{aligned}$$

  (46c)

  Substitution of Eqs. (46a)–(46c) into Eq. (45) yields

  $$\begin{aligned} \left[ \mathbf{M} \right] _n^n \left\{ {\mathbf{a}_{{\varvec{h}}}} \right\} _{n+1}^n + \left\{ \mathbf{R} \right\} _{n+1}^n =\left\{ \mathbf{f} \right\} _n^n \end{aligned}$$

  (47)

Hence, the problem reduces to finding a discrete deformation vector $\left\{ {\mathbf{u}_{{\varvec{h}}}} \right\} _{n+1}^n$ that satisfies Eqs. (45) and (47). The integral terms can be computed by a common numerical integration method, such as Gaussian quadrature [13].