Bounds for the Regularity Radius of Delone Sets

Abstract

Delone sets are discrete point sets X in ${\mathbb {R}}^d$ characterized by parameters (r, R), where (usually) 2r is the smallest inter-point distance of X, and R is the radius of a largest “empty ball” that can be inserted into the interstices of X. The regularity radius ${\hat{\rho }}_d$ is defined as the smallest positive number $\rho$ such that each Delone set with congruent clusters of radius $\rho$ is a regular system, that is, a point orbit under a crystallographic group. We discuss two conjectures on the growth behavior of the regularity radius. Our “Weak Conjecture” states that ${\hat{\rho }}_{d}={\textrm{O}(d^2\log _2 d)}R$ as $d\rightarrow \infty$, independent of r. This is verified in the paper for two important subfamilies of Delone sets: those with full-dimensional clusters of radius 2r and those with full-dimensional sets of d-reachable points. We also offer support for the plausibility of a “Strong Conjecture”, stating that ${\hat{\rho }}_{d}={\textrm{O}(d\log _2 d)}R$ as $d\rightarrow \infty$, independent of r.

1 Introduction

In this paper we continue the mathematical study of crystal structure from a local viewpoint, to understand the conditions under which a discrete point set in ${\mathbb {R}}^d$ is an orbit (or the union of a finite number of orbits) of a crystallographic group.

Our main focus is on “self-assembly”¹ properties of point sets in ${{\mathbb {R}}}^d$ as the usual model for atomic structure of a solid structure. That is we study how local conditions for clusters of point sets imply periodicity of the global points sets. A good example of a similar self-assembly for tilings can be seen in the recently announced breakthrough solution to the “Ein Stein problem”² [3, 25, 26] where one polygonal tile can self-assemble itself into a tiling of ${\mathbb {R}}^2$ but only in an aperiodic way, this property is also refered to being an aperiodic monotile. The Socolar–Taylor tile [27] was the first example of a single tile that enforces aperiodicity of the associated tiling in ${{\mathbb {R}}}^2$, but this tile is not simply connected. We refer to [4] for more background and history of the study of aperiodic order.

One of the ways to model atomic structures is by using point sets that avoid small interpoint distances and large voids. This is usually done by assuming that the set $X \subset {\mathbb {R}}^d$ under investigation is a Delone set. Thus we assume that for the point set $X \subset {\mathbb {R}}^d$ there are positive real numbers r and R such that

• the open balls $B_{{{\textbf{x}}}}^o(r)$ and $B_{{{\textbf{x}}}'}^o(r)$ of radius r centered at distinct points ${{{\textbf{x}}}}, {{{\textbf{x}}}'} \in X$ do not intersect:

  $$\begin{aligned} B_{{{\textbf{x}}}}^o(r)\cap B_{{{\textbf{x}}}'}^o(r)=\emptyset \;\;\; \forall \,{{{\textbf{x}}}}, {{{\textbf{x}}}}'\in X,\, {{{\textbf{x}}}}\ne {{{\textbf{x}}}}; \end{aligned}$$

  (1)

• the family of closed balls $B_{{{\textbf{x}}}}(R)$ of radius R centered at ${{{\textbf{x}}}}\in X$ covers the entire space ${{\mathbb {R}}}^d$:

  $$\begin{aligned} \bigcup _{{{{\textbf{x}}}}\in X}B_{{{\textbf{x}}}}(R)={\mathbb {R}}^d. \end{aligned}$$

  (2)

From (1) and (2) follows that $r< R$. Moreover, these two defining conditions are satisfied for any positive numbers $r',R'$ with $r'<r$ and $R<R'$, respectively. We adopt the convention that in designating the parameters (r, R) of a Delone set X we choose the largest possible value of r and the smallest possible value of R that satisfy the two defining conditions; these values are given by the supremum of all r satisfying (1) and the infimum of all R satisfying (2), respectively. As a consequence, the smallest inter-point distance in X (if it exists) is 2r and the radius of the largest “empty ball” of X (if it exists) is R. Here, a closed ball in ${\mathbb {R}}^d$ is called an empty ball of X if no point of X lies in its interior. Thus, the values of r and R are the “exact” parameters of X. We later make assumptions on X which guarantee that the smallest inter-point distance is attained and that there are largest empty balls.

Delone sets are a modern version of the point sets B. N. Delone introduced in the early 1930s; he called them (r, R) systems; see, e.g., [11]. Here we discuss relations between the local and global (group-theoretic) viewpoints for the special case of regular (or multiregular) point sets.

A Delone set X is a regular system if its symmetry group S(X) is point-transitive, i.e.., if for any points ${{{\textbf{x}}}}$ and ${{{\textbf{x}}}'}$ of X there is an isometry g such that $g({{{\textbf{x}}}}) = {{{\textbf{x}}}'}$ and $g(X) = X$. For each radius $\rho > 0$, the isometry g also maps the $\rho$-cluster $C_{{{\textbf{x}}}}(\rho ):= X \cap B_{{{\textbf{x}}}}(\rho )$ of ${{{\textbf{x}}}}$ onto the $\rho$-cluster $C_{{{\textbf{x}}}'}(\rho )$ of ${{{\textbf{x}}}'}$.

The number $N(\rho )$ of non-congruent (non-equivalent) cluster classes is called the cluster-counting function of X; it is non-decreasing. If X is regular, then clearly $N(\rho )=1$ for all $\rho > 0$. We also study the group $S_{{{\textbf{x}}}}(\rho )$ of isometries that stabilize both ${{{\textbf{x}}}}$ and the cluster $C_{{{\textbf{x}}}}(\rho )$. These cluster groups $S_{{\textbf{x}}}(\rho )$ are non-increasing. Note that $N(\rho )$ and $S_{{\textbf{x}}}(\rho )$ are interrelated: for example, X is regular if $N(2R)=1$ and $C_{{{\textbf{x}}}}(2R)$ is centro-symmetric [17].

A criterion for regularity, due to Delone, Dolbilin, Shtogrin, and Galiulin [12], is fundamental for the local theory; we state and discuss it in the next section.

We define the regularity radius ${{{\hat{\rho }}}_d}={{\hat{\rho }}}_d(r,R)$ to be the smallest value of the radius $\rho$ of the clusters such that every Delone set with $N(\rho ) = 1$ is regular. The main problem of the local theory is to find an upper bound for ${{\hat{\rho }}}_d$. The order of the 2R-cluster group $S_{{{\textbf{x}}}}(2R)$ and the behavior of the groups $S_{{{\textbf{x}}}}(\rho )$ play key roles.

For $d = 2,3$ it is known that ${{\hat{\rho }}}_2=4R$ [14, 15] and $6R \le {{\hat{\rho }}}_3 \le 10R$ [6, 19]. Moreover, for $d = 3$, if $N(2R) = 1$, then the order of any axis in $S_{{{\textbf{x}}}}(2R)$ does not exceed 6 [24]. This is a “local version” of the so-called “crystallographic restriction,” which states that the orders of rotation in a lattice in ${\mathbb {R}}^2$ and ${\mathbb {R}}^3$ can only be 2, 3, 4 or 6.

In this paper we offer two conjectures about the growth rate of ${\hat{\rho }}_{d}$. Our Weak Conjecture claims that ${\hat{\rho }}_{d}={\textrm{O}(d^2\log _2 d)}R$ as $d\rightarrow \infty$, independent of r; and our Strong Conjecture proposes the even lower bound ${\hat{\rho }}_{d}={\textrm{O}(d\log _2 d)}R$ as $d\rightarrow \infty$, again independent of r. We verify the Weak Conjecture in important special cases that naturally originate from perceived atomic structure of crystals, and also provide some plausibility for the Strong Conjecture.

The paper is organized as follows. In Sect. 2 we introduce basic notions related to Delone sets and regularity radius and recall main results that describe how local structure of Delone sets implies global symmetry.

In Sect. 3 we consider the family of d-dimensional Delone sets with congruent 2R-clusters that satisfy the additional condition that the boundaries of the smaller 2r-clusters are full-dimensional. For this family, we prove that the regularity radius grows at most as fast as ${\textrm{O}(d^2)}R$ as $d\rightarrow \infty$, see Theorem 3.4. We all also formulate our main Conjectures 3.5 and 3.6 on the growth rate of the regularity radius for general 2R-regular Delone sets in this section.

In Sect. 4 we extend our study of the regularity radius to the family of t-reachable sets, see also [9, 13]. In Theorems 4.1 and 4.2 we prove an upper bound ${\textrm{O}(d^2\log _2 d)}R$ for the family of t-reachable Delone sets provided $t\le ar$ for some fixed constant a. These results confirm Conjecture 3.5 for the family of Delone sets under consideration.

We would like to point out that the family of Delone sets of Theorem 4.2 has a reasonable description as the family describing atomic structures of solid crystals, as the minimal distance between atoms in such crystals together with the types of atoms used may dictate the size of voids provided the structure is kept solid by particle interactions.

In the concluding Sect. 5 we formulate several open problems that provide further insight in how local structures and their symmetries give rise to global structures within Delone sets.

2 Basic Notions

Points, or vectors, in ${\mathbb {R}}^d$ are denoted by bold-faced letters. If ${{{\textbf{x}}}}\in {\mathbb {R}}^d$ and $\rho \ge 0$, we let $B_{{{\textbf{x}}}}(\rho )$ and $B_{{{\textbf{x}}}}^o(\rho )$ denote the closed respectively open d-ball in ${\mathbb {R}}^d$ of radius $\rho$ centered at ${{{\textbf{x}}}}$. For $M\subseteq {\mathbb {R}}^d$ we let $\textrm{aff}\,M$ denote the affine hull of a set M, i.e. the smallest affine subspace containing the set M. The dimension of $\textrm{aff}\,M$ is called the rank of M and is denoted $\textrm{rk}\,M$.

Delone sets were already defined in the Introduction. Let X be a Delone set and $\rho \ge 0$. For a point ${{{\textbf{x}}}}\in X$, we call

$$\begin{aligned} C_{{{\textbf{x}}}}(\rho ):=X\cap B_{{{\textbf{x}}}}(\rho ) \end{aligned}$$

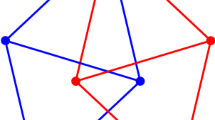
the cluster of radius $\rho$ of X with center ${{{\textbf{x}}}}$, or simply the $\rho$-cluster of X at ${{{\textbf{x}}}}$. Clusters of the same radius at different points x and y of X may coincide set-theoretically, and it is important to keep track on which point is the center. For example, in the Delone set of blue and red points shown in Fig. 1, the $\rho$-clusters $C_{{{\textbf{x}}}}(\rho )$ and $C_{{\textbf{y}}}(\rho )$ are the same as sets but surround the points ${{\textbf{x}}}$ and ${\textbf{y}}$ in different ways. It is this difference that motivates the notions of equivalence and non-equivalence of clusters described below. In our applications below, the centers of clusters are usually determined uniquely.

Fig. 1

Equivalent and non-equivalent $\rho$-clusters

For a Delone set X, the $\rho$-cluster group $S_{{\textbf{x}}}(\rho )$ at a point ${{{\textbf{x}}}}\in X$ is the stabilizer of ${{\textbf{x}}}$ in the full symmetry group of the $\rho$-cluster $C_{{{\textbf{x}}}}(\rho )$. Thus $S_{{{\textbf{x}}}}(\rho )$ consists of all isometries of ${\mathbb {R}}^d$ which fix ${{{\textbf{x}}}}$ and map $C_{{{\textbf{x}}}}(\rho )$ to itself. Note that $S_{{{\textbf{x}}}}(\rho )$ consists of d-dimensional isometries, even though the underlying cluster itself may lie in a subspace of dimension smaller than d (and then also have a symmetry group in that subspace).

For the Delone set of Fig. 1, the $\rho$-cluster groups at the points ${{\textbf{x}}}$ and ${\textbf{y}}$ are not isomorphic and are given by $S_{{{\textbf{x}}}}(\rho ) \simeq D_4$ and $S_{{\textbf{y}}}(\rho )\simeq D_1$, the dihedral groups of orders 8 and 2, respectively.

Clusters of Delone sets are finite point sets. If the rank of a cluster is at most $d-2$, the corresponding cluster group must necessarily be infinite. In particular, if $\rho <2r$, then $C_{{{\textbf{x}}}}(\rho )=\{{{\textbf{x}}}\}$ and $S_{{{\textbf{x}}}}(\rho )$ is isomorphic to the full orthogonal group of ${\mathbb {R}}^d$. On the other hand, if the rank of a cluster is at least $d-1$, then since clusters are finite, the corresponding cluster group is finite as well. For $\rho \ge 2R$, all $\rho$-clusters of X are d-dimensional, meaning that the affine hull is ${\mathbb {R}}^d$, and thus have finite cluster groups [12]. Note that the cluster groups of X at a point ${\textbf{x}}$ are non-increasing as a function of $\rho$, that is, $S_{{{\textbf{x}}}}(\rho )\supseteq S_{{{\textbf{x}}}}(\rho ')$ whenever $\rho \le \rho '$. In particular, $S_{{{\textbf{x}}}}(\rho )$ is a subgroup of the finite group $S_{{{\textbf{x}}}}(2R)$ whenever $\rho \ge 2R$. Hence there is a natural interest in bounding the size of $S_{{{\textbf{x}}}}(2R)$.

Two $\rho$-clusters $C_{{{\textbf{x}}}}(\rho )$ and $C_{{{{\textbf{x}}}}'}(\rho )$ at points ${{{\textbf{x}}}},{{{\textbf{x}}}}'$ of X are said to be equivalent if there exists an isometry of ${\mathbb {R}}^d$ that maps ${{{\textbf{x}}}}$ to ${{{\textbf{x}}}}'$ and $C_{{{\textbf{x}}}}(\rho )$ to $C_{{{{\textbf{x}}}}'}(\rho )$. As the isometry must map centers to centers, equivalence of clusters is stronger than mere congruence, i.e. Euclidean isometry, of point sets. The example of Fig. 1 illustrates the difference between congruence and equivalence. The two $\rho$-clusters $C_{{{\textbf{x}}}}(\rho )$ and $C_{{\textbf{y}}}(\rho )$ shown are the same point sets and thus are congruent. However, they are not equivalent, as no isometry can simultaneously map ${{{\textbf{x}}}}$ to ${\textbf{y}}$ and $C_{{{\textbf{x}}}}(\rho )$ to $C_{{\textbf{y}}}(\rho )$, or the other way around.

Note that the cluster groups of any two equivalent $\rho$-clusters in a Delone set are conjugate subgroups of $\textrm{Iso}(d)$, the group of all Euclidean isometries of ${\mathbb {R}}^d$. This is consistent with the example of Fig. 1: the two non-equivalent clusters $C_{{{\textbf{x}}}}(\rho )$ and $C_{{\textbf{y}}}(\rho )$ have non-isomorphic cluster groups.

A Delone set X in ${\mathbb {R}}^d$ is said to be $\rho$-regular (or alternatively, $\rho$-isometric) if any two $\rho$-clusters of X are equivalent. We are particularly interested in 2R-regular Delone sets.

A Delone set X in ${\mathbb {R}}^d$ is called regular, or a regular system, if its symmetry group S(X) acts transitively on X. Thus a regular system coincides with the orbit of any one of its points under the symmetry group. A regular system is $\rho$-regular for every $\rho \ge 0$. For the Delone set of Fig. 1, the subset of red points and the subset of blue points are two examples of regular Delone sets.

Note that while for a regular Delone set X any two points can be matched up under an isometry of the ambient space that maps the whole Delone set X to itself, in a $\rho$-regular Delone set any two points and their $\rho$-clusters can only be matched up under an isometry of the ambient space that may or may not map X to itself.

Cluster groups occur naturally in the following Local Theorem for Delone Sets, which provides a characterization of the regularity of a Delone set.

Theorem 2.1

(Local Regularity Criterion [12]) A Delone set X in ${\mathbb {R}}^d$ is a regular system if and only if X satisfies the following two conditions for some $\rho _0>0$ and some ${{{\textbf{x}}}}_0\in X$:

• X is $(\rho _0 + 2R)$-regular (that is, any two clusters of X of radius $\rho _0 + 2R$ are equivalent).

• $S_{{{{\textbf{x}}}}_{0}}(\rho _0) = S_{{{{\textbf{x}}}}_{0}}(\rho _0 + 2R)$, this meaning equality as sets of Euclidean isometries preserving ${{\textbf{x}}}_0$.

Moreover, in this situation, $S_{{{\textbf{x}}}}(\rho _0) = S_{{{\textbf{x}}}}(\rho _0 + 2R)$ for all ${{{\textbf{x}}}}\in X$; the cluster groups stabilize at radius $\rho _0$, that is, $S_{{{\textbf{x}}}}(\rho ) = S_{{{\textbf{x}}}}(\rho _0)$ for all ${{{\textbf{x}}}}\in X$ and all $\rho \ge \rho _0$; and the entire regular system X is uniquely determined (as a $(\rho _0 + 2R)$-regular point set) by the cluster $C_{{{{\textbf{x}}}}_{0}}(\rho _0 + 2R)$.

Theorem 2.1 provides an affirmative answer to the fundamental question asking whether or not the regularity of Delone sets in ${\mathbb {R}}^d$ can be recognized on clusters of bounded radius. The smallest such radius, over all Delone sets with parameters (r, R), is called the regularity radius and is denoted ${\hat{\rho }}_d$. Thus ${\hat{\rho }}_d$ is the smallest positive number $\rho$ with the property that each $\rho$-regular Delone set X is a regular system. From Dolbilin, Lagarias & Senechal [18, Thm. 1.3] it is known that

$$\begin{aligned} \hat{\rho _d} \le 2R(d^2+1) \log _2 (2R/r+2). \end{aligned}$$

(1)

Our Conjectures 3.5 and 3.6 below propose an upper bound for ${\hat{\rho }}_d$ which is independent of r.

The next theorem is a reformulation of [16, Prop. 2.1] (see also [19]) and provides an important tool for bounding the regularity radius ${\hat{\rho }}_d$ in terms of the dimension d and the radius R of the largest empty ball. It gives a necessary condition for the regularity of a Delone set X in terms of the total number of prime factors of the order of its 2R-cluster groups.

For a finite group G, let $\Omega (G)$ denote the number of prime factors of its group order |G| (counted with multiplicity). Then,

$$\begin{aligned} \Omega (G) +1\,\le \,\log _2 (2|G|). \end{aligned}$$

(2)

If X is a Delone set, ${\textbf{x}}\in X$, and $\rho >0$, we define $\Omega _{{{\textbf{x}}}}(\rho ):= \Omega (S_{{\textbf{x}}}(\rho ))$, which is the number of prime factors of the order of the $\rho$-cluster group $S_{{\textbf{x}}}(\rho )$. This number will not depend on ${\textbf{x}}$ if X is $\rho$-regular. In our applications, $\rho =2r$ or a constant multiple of 2r, or $\rho =2R$. In particular, if X is 2R-regular, then $\Omega _{{{\textbf{x}}}}(2R)$ is defined and does not depend on ${\textbf{x}}\in X$.

Theorem 2.2

(Tower Bound) Let X be a 2R-regular Delone set in ${\mathbb {R}}^d$, and let $\Omega :=\Omega _{{{\textbf{x}}}}(2R)$ where ${\textbf{x}}$ is any point in X. If X is also $2(\Omega +2)R$-regular, then X is a regular system.

As shown in [16, 19], the Tower Bound theorem is a direct corollary of the Local Regularity Criterion. Theorem 2.2 indicates that it is very desirable to establish good upper bounds for the size of the cluster groups in a Delone set, and thus for the total number of prime factors. In fact, the theorem shows that

$$\begin{aligned} {\hat{\rho }}_d\le 2(\Omega _{{\textbf{x}}}(2R) +2)R, \end{aligned}$$

(3)

for the family of 2R-regular Delone sets X that have a bounded number of prime factors in the order of the corresponding cluster group.

In this paper, we study how the regularity radius behaves on specific families ${\mathcal {X}}$ of Delone sets within the collection of all Delone set with parameters (r, R). This will allow us to motivate our conjecture on an upper bound for ${\hat{\rho }}_d$.

For a family ${\mathcal {X}}$ of Delone sets, all with the same parameters (r, R), the ${\mathcal {X}}$-regularity radius ${\hat{\rho }}_d({\mathcal {X}})$ is the smallest positive number $\rho$ with the property that each $\rho$-regular Delone set X from ${\mathcal {X}}$ is a regular system. When ${\mathcal {X}}$ is the set of all Delone sets with parameters (r, R), this is just the usual regularity radius ${\hat{\rho }}_d$. From the definition it is clear that ${\hat{\rho }}_d({\mathcal {X}})\le {\hat{\rho }}_d$ for each family ${\mathcal {X}}$.

3 Upper Bounds for Cluster Groups and a Conjecture for ${\hat{\rho }}_d$

The following property goes back to the original work of Delone, Dolbilin, Shtogrin, and Galiulin [12]. To make the paper self-contained, we give a short proof here.

Lemma 3.1

In a Delone set X, all 2R-clusters $C_\textbf{x}(2R)$, $\textbf{x}\in X$, are full-dimensional and therefore have finite cluster groups $S_\textbf{x}(2R)$.

Proof

Suppose to the contrary that $C_\textbf{x}(2R)$ lies in a hyperplane H. Choose a sufficiently small $\varepsilon >0$ such that $C_\textbf{x}(2R+\varepsilon )=C_\textbf{x}(2R)$. Then, since the largest empty balls of X have R, a closed ball of radius R centered at a point on the line perpendicular to H at ${{\textbf{x}}}$, and at distance $R+\varepsilon$ from ${{\textbf{x}}}$, must contain a point of X that then also lies in $C_\textbf{x}(2R+\varepsilon )=C_\textbf{x}(2R)$ outside of H. Thus $C_\textbf{x}(2R)$ must be full-dimensional. Finiteness of the cluster groups follows from the finiteness of the groups permuting points of the clusters.$\square$

If X is 2R-regular, then any two 2R-cluster groups are isomorphic (in fact, conjugate in $\textrm{Iso}(d)$, the group of Euclidean isometries of ${\mathbb {R}}^d$). We are interested in finding upper bounds for the order of these groups.

Our first results concern the 2r-clusters of 2R-regular Delone sets. Let X be a 2R-regular Delone set, and let ${{{\textbf{x}}}}\in X$. Then the 2r-cluster $C_{{{\textbf{x}}}}(2r)$ consists of the center ${{{\textbf{x}}}}$ and the points of X at minimal distance 2r from ${\textbf{x}}$. By definition, $C_{{{\textbf{x}}}}(2r)$ is invariant under the cluster group $S_{{{\textbf{x}}}}(2r)$. It follows that the affine hull of $C_{{{\textbf{x}}}}(2r)$ is also invariant under $S_{{{\textbf{x}}}}(2r)$. Note that in general this subspace may not have full dimension d.

Recall that the kissing number $\tau _d$ for balls (spheres) is the maximum number of mutually non-overlapping congruent d-balls in ${\mathbb {R}}^d$ that can touch a given d-ball of the same size.

The kissing number provides an easy upper bound for the cardinality of $C_{{{\textbf{x}}}}(2r)$, namely

$$\begin{aligned} |C_{{{\textbf{x}}}}(2r)|\le 1+ \tau _d. \end{aligned}$$

In fact, since any two points of X are at least 2r apart, the balls of radius r centered at points in $C_{{{\textbf{x}}}}(2r)\setminus \{{{\textbf{x}}}\}$ all touch the ball of radius r centered at ${{{\textbf{x}}}}$ and are mutually non-overlapping. Hence there can be at most $\tau _d$ such balls. The currently best known upper bound for $\tau _d$ is

$$\begin{aligned} \tau _d \le 2^{0.4011d(1+\,\textrm{o}(1))}\;(= 1.3205^{d(1+\,\textrm{o}(1))}) \, \text{ as } d\rightarrow \infty \end{aligned}$$

(see [8, 10, 22]).

Proposition 3.2

Let X be a Delone set in ${\mathbb {R}}^d$, let ${\textbf{x}}\in X$, and suppose $C_{{{\textbf{x}}}}(2r)$ is full-dimensional. Then,

$$\begin{aligned} |S_{{\textbf{x}}}(2R)|\le |S_{{\textbf{x}}}(2r)|\, \le \tau _{d}\cdot \tau _{d-1}\cdot \ldots \cdot \tau _{1} \,\le \,\tau _d^{\,d}, \end{aligned}$$

and

$$\begin{aligned} \Omega _{{{\textbf{x}}}}(2R)\le \Omega _{{{\textbf{x}}}}(2r)\le d\log _2 \tau _d. \end{aligned}$$

Proof

Without loss of generality we may assume that ${\textbf{x}}$ is the origin. Then $S_{\textbf{x}}(2r)$ is a finite subgroup of the full orthogonal group of ${\mathbb {R}}^d$ acting faithfully as a permutation group on the full-dimensional set $C_{{{\textbf{x}}}}(2r)$. Now choose a vector space basis of ${\mathbb {R}}^d$ from the elements of $C_{{{\textbf{x}}}}(2r)\setminus \{{{\textbf{x}}}\}$. This is possible since $C_{{{\textbf{x}}}}(2r)$ is full-dimensional. Clearly, each element of $S_{\textbf{x}}(2r)$ is uniquely determined by its effect on this basis. But $C_{{{\textbf{x}}}}(2r)\setminus \{{{\textbf{x}}}\}$ contains at most $\tau _d$ elements, so there are at most $\tau _d$ choices for the image point of the first basis vector.

The image of the second point is now restricted to a sphere of codimension 1 within the sphere of radius 2r centered at ${{\textbf{x}}}$ because the distance between the images of the first and second basis vectors is fixed. This gives at most $\tau _{d-1}$ choices for the image point of the second basis vector once the image of the first is chosen. Using similar arguments, we have at most $\tau _{d-2}$ choices for the image point of the third basis vector once the images of the first and second are chosen, and so on. Hence,

$$\begin{aligned} |S_{\textbf{x}}(2r)| \le \tau _{d}\cdot \tau _{d-1}\cdot \ldots \cdot \tau _{1}\le \tau _d^{\,d}. \end{aligned}$$

As $S_{{\textbf{x}}}(2R)$ is a subgroup of $S_{{\textbf{x}}}(2r)$, then this proves the first part. This subgroup relationship also establishes the first inequality of the second part, while the second inequality uses (2) and follows directly from

$$\begin{aligned} \Omega _{{{\textbf{x}}}}(2r) +1 \le \log _2 (2|S_{{{\textbf{x}}}}(2r)|) \le \log _2 {2\tau _d^d} =1 + d\log _2\tau _d. \end{aligned}$$

$\square$

Remark 3.3

Asymptotically, as $d\rightarrow \infty$, the smaller upper bound $\tau _{d}\cdot \tau _{d-1}\cdot \ldots \cdot \tau _{1}$ for $|S_{{\textbf{x}}}(2R)|$ in Proposition 3.2 is significantly better than the larger upper bound $\tau _d^{\,d}$. However, after taking the logarithm and using the general upper bound $\tau _d \le 2^{0.4011d(1+\,\textrm{o}(1))}$, the resulting terms differ only by a constant factor and thus we use the simpler bound of $\tau _d^d$ instead.

The kissing number argument underlying Proposition 3.2 allows us to analyze the behavior of the regularity radius on the important family of 2R-regular Delone sets for which the points at minimal distance from a given point form a full-dimensional set.

Theorem 3.4

Suppose ${\mathcal {X}}$ is the family of 2R-regular Delone sets X in ${\mathbb {R}}^d$ with the property that $C_{{{\textbf{x}}}}(2r)$ is full-dimensional for some (and thus all) ${\textbf{x}}\in X$. Then

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}})\,\le 2(d\log _2 \tau _d +2)R \le \, 4+0.8022{d^2 (1+\,\textrm{o}(1))}R \,= \, {\textrm{O}(d^2)}R \, \text{ as } d\rightarrow \infty . \end{aligned}$$

The $\textrm{O}(d^2)$-term and the $\textrm{o}(1)$-term only depend on the dimension d, not the parameters of X.

Proof

This follows from Theorem 2.2 and Proposition 3.2. So let $X\in {\mathcal {X}}$; in other words, X is a 2R-regular Delone set in ${\mathbb {R}}^d$ with the property that $C_{{{\textbf{x}}}}(2r)$ is full-dimensional for each ${\textbf{x}}\in X$. By Proposition 3.2,

$$\begin{aligned} \Omega _{{\textbf{x}}}(2R)\le d\log _2 \tau _d \end{aligned}$$

for each ${\textbf{x}}\in X$, and therefore, using the upper bound for $\tau _d$ and Theorem 2.2, we get

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}})\le 2(\Omega _{{\textbf{x}}}(2R) +2)R \le 2 (d\log _2 \tau _d +2)R \le 2(2+0.4011{d^2(1+\,\textrm{o}(1)))}R. \end{aligned}$$

This is the desired inequality. $\square$

Theorem 3.4 bounds the asymptotic growth of the regularity radius for 2R-regular Delone sets with full-dimensional 2r-clusters. For dimensions 2 and 3, the upper bound $2(d\log _2 \tau _d +2)R$ is poor compared with known values or upper bounds for ${{\hat{\rho }}}_d$. As noted in the Introduction, ${{\hat{\rho }}}_2=4R$ [14, 15] and ${{\hat{\rho }}}_3\le 10R$ [6, 19]. On the other hand, using $\tau _{2}=6$ and $\tau _{3}=12$ we see that Theorem 3.4 only gives ${\hat{\rho }}_2({\mathcal {X}})\le 14.34R$ and ${\hat{\rho }}_3({\mathcal {X}})\le 25.51R$, respectively. For $d=4$, Theorem 3.4 shows ${\hat{\rho }}_4({\mathcal {X}})\le 40.68R$.

Based on the results above (and the discussion in Sect. 5) we offer two conjectures for the growth behavior of the regularity radius. The following Weak Conjecture is supported by both Theorem 3.4 above and Theorem 4.1 below. It states that the usual regularity radius ${\hat{\rho }}_d$ grows at most linearly in the radius of the largest empty ball R, and like $d^2\log _2 d$ in the dimension d, independent of r. In other words, ${\hat{\rho }}_{d}/R$ grows at most like $d^2\log _2 d$ in the dimension d, independent of r.

Conjecture 3.5

(Weak Conjecture) There exists a constant c, not depending on d and R, such that ${\hat{\rho }}_d \le c (d^2\log _2 d)R$ for each $d\ge 1$.

Note that Theorem 3.4 actually gives a slightly better bound than Conjecture 3.5 for that specific family ${\mathcal {X}}$, namely ${\textrm{O}(d^2)}R$. Together with the lower bound of 2dR for ${\hat{\rho }}_d$ established in [6] (see also [20]), settling Conjecture 3.5 would narrow down the possible range for ${\hat{\rho }}_d$ to

$$\begin{aligned} 2dR\, \le \,{\hat{\rho }}_d\, \le \, c(d^2\log _2 d)R \end{aligned}$$

and therefore considerably close the gap between the best known lower and upper bounds for ${\hat{\rho }}_d$.

Motivated by the linear lower bound of [6] and further plausibility considerations in Sect. 5, we are also proposing the following Strong Conjecture for the growth rate of ${\hat{\rho }}_d$.

Conjecture 3.6

(Strong Conjecture) There exists a constant c, not depending on d and R, such that ${\hat{\rho }}_d \le c (d\log _2 d)R$ for each $d\ge 1$.

4 The Conjecture and 2r-Reachability

There is further evidence in support of the Conjecture 3.5, as we explain in this section. We begin by introducing the concept of t-reachability.

Let X be a Delone set, and let t with $2r\le t$ be fixed. For ${\textbf{x}}\in X$ and $k\ge 0$, let $M_{{\textbf{x}}}(k)$ denote the set of all points ${\textbf{y}}\in X$ for which there exists a finite chain of points

$$\begin{aligned} {\textbf{x}}=:{\textbf{x}}_0,{\textbf{x}}_1,\ldots ,{\textbf{x}}_{m-1},{\textbf{x}}_{m}:={\textbf{y}} \end{aligned}$$

in X such that $0\le m\le k$ and $||{\textbf{x}}_{i+1}-{\textbf{x}}_i||\le t$ for all $i=0,\ldots ,m-1$. (Our notation suppresses the dependence of $M_{{\textbf{x}}}(k)$ on t, as later the value of t will be clear from the context.) Hence $M_{{\textbf{x}}}(k)$ consists of all points ${\textbf{y}}$ of X that are t-reachable from ${\textbf{x}}$ in at most k steps of size at most t, and in particular contains ${\textbf{x}}$ itself. Then $M_{{\textbf{x}}}(0)=\{x\}$, $M_{{\textbf{x}}}(1)=C_{{{\textbf{x}}}}(t)$, and $M_{{\textbf{x}}}(k)\subseteq C_{{{\textbf{x}}}}(kt)$ for all $k\ge 0$. We also let

$$\begin{aligned} M_{{\textbf{x}}}:=\bigcup _{k\ge 0} M_{{\textbf{x}}}(k) \end{aligned}$$

and call $M_{{\textbf{x}}}$ the set of t-reachable points for ${\textbf{x}}$. Note that $M_{{\textbf{x}}}=M_{{\textbf{y}}}$ if and only if ${{\textbf{y}}}\in M_{{\textbf{x}}}$.

Our discussion of t-reachable points is inspired by the concept of t-bonded sets introduced in Dolbilin [13] and developed in Bouniaev & Dolbilin [9]. A Delone set X is called t-bonded for a parameter $t>0$ if every two points ${{\textbf{x}}},{\textbf{y}}\in X$ can be connected by a finite chain ${{\textbf{x}}}={{\textbf{x}}}_0,\ldots ,{{\textbf{x}}}_k={\textbf{y}}$ in X such that $||{{\textbf{x}}}_{i+1}-{{\textbf{x}}}_{i}||\le t$ for every i.

Notice that X is t-bonded if and only if X coincides with the set of t-reachable points $M_{{{\textbf{x}}}}$ for each ${{{\textbf{x}}}}\in X$. In this case $M_{{{\textbf{x}}}}=X$ and in particular, $M_{{{\textbf{x}}}}$ is full-dimensional. On the other hand, as the example of

$$\begin{aligned} X={\mathbb {Z}}^d\cup \bigg ( \textstyle {(\frac{1}{2},\ldots ,\frac{1}{2})} + {\mathbb {Z}}^d\bigg ) \end{aligned}$$

with $d>4$ and $t=2r$ shows, there exists a Delone set X with full-dimensional sets $M_{{{\textbf{x}}}}$ for every ${{\textbf{x}}}\in X$, which, nevertheless, is not 2r-bonded. Here the distance of $(\frac{1}{2},\ldots ,\frac{1}{2})$ from the origin is $\frac{1}{2}\sqrt{d}$, and thus the minimum inter-point distance in X is $\frac{1}{2}\sqrt{d}$ if $d\le 3$ and 1 if $d\ge 4$. Moreover, for $d>4$ the minimum inter-point distance in X can only occur between two points in ${\mathbb {Z}}^d$ or two points in $(\frac{1}{2},\ldots ,\frac{1}{2}) +{\mathbb {Z}}^d$, while for $d\le 3$ it can only occur between a point in ${\mathbb {Z}}^d$ and a point in $(\frac{1}{2},\ldots ,\frac{1}{2}) +{\mathbb {Z}}^d$; if $d=4$, there are no such restrictions on the two points (in this case X is the vertex-set of the regular tessellation of ${\mathbb {R}}^4$ by 4-crosspolytopes). Now, if $d>4$, then $t=2r=1$ and the sets of t-reachable points $M_{{{\textbf{x}}}}$ are either ${\mathbb {Z}}^d$ if ${{{\textbf{x}}}}\in {\mathbb {Z}}^d$, or $M_{{{\textbf{x}}}}= (\frac{1}{2},\ldots ,\frac{1}{2}) +{\mathbb {Z}}^d$ if ${{{\textbf{x}}}}\in (\frac{1}{2},\ldots ,\frac{1}{2}) +{\mathbb {Z}}^d$. In either case, $M_{{{\textbf{x}}}}$ is full-dimensional but $M_{{{\textbf{x}}}}\ne X$. Thus X is not t-bonded if $d>4$. On the other hand, if $d\le 4$, then $t=2r=\frac{1}{2}\sqrt{d}$ and $M_{{{\textbf{x}}}}=X$ for each ${{{\textbf{x}}}}\in X$. In this case X is t-bonded.

It follows from the definition of the parameters (r, R) that a Delone set X is t-bonded for every $t\ge 2R$, and thus $M_{{{\textbf{x}}}}=X$ in this case.

We are particularly interested in the case when X is 2R-regular and $t=2r$. In this case successive points in the chain connecting ${\textbf{x}}$ to ${\textbf{y}}$ are exactly at distance 2r.

Our next theorem confirms Conjecture 3.5 under the assumption that the set of 2r-reachable points $M_{{\textbf{x}}}$ is d-dimensional for each ${\textbf{x}}\in X$.

Theorem 4.1

Suppose ${\mathcal {X}}$ is the family of 2R-regular Delone sets X with the property that the set of 2r-reachable points $M_{{{\textbf{x}}}}$ is full-dimensional for each ${\textbf{x}}\in X$. Then

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}) \le {\textrm{O}(d^2\log _2 d)}R \, \text{ as } d\rightarrow \infty . \end{aligned}$$

The $\textrm{O}(d^2\log _2 d)$-term only depends on the dimension d, not the parameters (r, R) of X.

Proof

We split ${\mathcal {X}}$ into two subfamilies and deal with each subfamily separately. Let ${\mathcal {X}}'$ and ${\mathcal {X}}''$ denote the subfamilies of ${\mathcal {X}}$ consisting of all Delone sets X in ${\mathcal {X}}$ with $2dr\le 2R$ or $2dr>2R$, respectively.

First suppose that X lies in ${\mathcal {X}}'$. In this case we claim that already $M_{{{\textbf{x}}}}(d)$ is full-dimensional for each ${{{\textbf{x}}}}\in X$. Suppose that $\textrm{rk}\, M_{{{\textbf{x}}}}(d)\le d-1$ for some ${{\textbf{x}}}\in X$. Then there is $1<k\le d$ such that

$$\begin{aligned} \textrm{rk}\, M_{{{\textbf{x}}}}(k)= {\textrm{rk}\, M_{{{\textbf{x}}}}(k-1)}=:m\le d-1. \end{aligned}$$

We prove by induction that for every ${{\textbf{x}}}\in X$ and for every $l\ge k$,

$$\begin{aligned} \textrm{rk}\, M_{{\textbf{x}}}(l)=\textrm{rk}\, M_{{\textbf{x}}}(l-1)=m. \end{aligned}$$

The basis of induction $l=k$ has been established as $\textrm{rk}\, M_{{{\textbf{x}}}}(k)= {\textrm{rk}\, M_{{{\textbf{x}}}}(k-1)}=m$. Assume we proved that for every ${{\textbf{x}}}$ and for a given l, $\textrm{rk}\, M_{{\textbf{x}}}(l)=\textrm{rk}\, M_{{\textbf{x}}}(l-1)=m$ and we want to prove that $\textrm{rk}\, M_{{\textbf{x}}}(l+1)=m$.

Let ${\textbf{y}}_1,\ldots ,{\textbf{y}}_n$ be all the points of $M_{{\textbf{x}}}(1)$ except ${{\textbf{x}}}$ itself. From the definition of $M_{{\textbf{x}}}(l+1)$,

$$\begin{aligned} M_{{\textbf{x}}}(l+1)=\bigcup _{i=1}^nM_{{\textbf{y}}_i}(l). \end{aligned}$$

By the induction hypothesis, for every $i=1,\ldots ,n$, $\textrm{rk}\, M_{{\textbf{y}}_i}(l)= m$. On the other hand, $M_{{\textbf{x}}} (l-1) \subseteq M_{{\textbf{y}}_i}(l)$ and since $\textrm{rk}\, M_{{\textbf{x}}}(l-1)=m$, it follows that $\textrm{aff}\, M_{{\textbf{x}}}(l-1) = \textrm{aff}\, M_{{\textbf{y}}_i}(l)$ for all $i=1,\ldots ,n$ because these affine spaces have equal dimensions. Therefore $\textrm{aff}\, M_{{\textbf{x}}}(l+1) = \textrm{aff}\, M_{{\textbf{x}}}(l-1)$ and $\textrm{rk}\, M_{{\textbf{x}}}(l+1)=m$ as claimed.

Thus $M_{{{\textbf{x}}}}(l)$ has rank m for each $l\ge k$. Then it follows that $\textrm{rk}\, M_{{{\textbf{x}}}}=m<d$, which is a contradiction to our assumption on X. Thus $M_{{{\textbf{x}}}}(d)$ must be full-dimensional for each $x\in X$ if X lies in ${\mathcal {X}}'$.

Since X is 2R-regular and $M_{{{\textbf{x}}}}(d)\subseteq C_{{{\textbf{x}}}}(2dr)\subseteq C_{{{\textbf{x}}}}(2R)$ for each ${{{\textbf{x}}}}\in X$, any two sets $M_{{{\textbf{x}}}}(d), M_{{{\textbf{x}}}'}(d)$ with ${{{\textbf{x}}}},{{{\textbf{x}}}'}\in X$ are congruent and thus have the same cardinality denoted $\mu$. We claim that

$$\begin{aligned} \mu \le (2d+1)^d. \end{aligned}$$

In fact, since the smallest inter-point distance of X is 2r, it follows that for any ${{{\textbf{x}}}}\in X$, the family of d-balls $B_{{\textbf{y}}}(r)$, ${{\textbf{y}}}\in M_{{{\textbf{x}}}}(d)$, forms a packing of d-balls of radius r all contained in $B_{{{\textbf{x}}}}(2dr +r)$. If $\kappa _d$ denotes the volume of the d-ball of radius 1, then the packing property shows that $\mu \, r^d\kappa _{d} \le (2dr+r)^d\kappa _d$ and thus $\mu \le (2d+1)^d$.

A similar argument as at the beginning of the proof of Proposition 3.2 then shows that

$$\begin{aligned} |S_{\textbf{x}}(2R)|\le |S_{\textbf{x}}(2dr)|\le \mu ^{d}\le (2d+1)^{d^2}. \end{aligned}$$

(In this case there are at most $\mu$ choices for the image point of each basis vector.) Hence

$$\begin{aligned} \Omega _{{{\textbf{x}}}}(2R) +1 \le \log _2 (2|S_{{{\textbf{x}}}}(2R)|)\le 1+d^{2}\log _2 (2d+1) \end{aligned}$$

and in analogy to (3),

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}') \le 2(\Omega _{{\textbf{x}}}(2R) +2)R \le (4+2d^{2}\log _2 (2d+1))R ={\textrm{O}(d^2\log _2 d)}R. \end{aligned}$$

The case when X lies in ${\mathcal {X}}''$ can be settled by appealing to the upper bound for $\hat{\rho _d}$ established in Dolbilin, Lagarias & Senechal [18, Thm. 1.3],

$$\begin{aligned} \hat{\rho _d} \le 2R(d^2+1) \log _2 (2R/r+2). \end{aligned}$$

Since now $2dr>2R$, this gives

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}'')\le 2R(d^2+1) \log _2 (2d+2) ={\textrm{O}(d^2\log _2 d)}R. \end{aligned}$$

Finally, combining the bounds for the two families ${\mathcal {X}}'$ and ${\mathcal {X}}''$ we obtain the desired upper bound for ${\mathcal {X}}$ itself,

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}) = \textrm{max}\bigg ({\hat{\rho }}_d({\mathcal {X}}'),{\hat{\rho }}_d({\mathcal {X}}'')\bigg ) =\textrm{O}(d^2\log _2 d)R. \end{aligned}$$

$\square$

Our next theorem is a generalization of Theorem 4.1. It provides further evidence in support of Conjecture 3.5 and exploits t-reachability for other values of t.

Let $a\ge 1$ be a fixed real number, and set $t:=2ar$. Write $M_{{\textbf{x}}}^{a}(k)$ instead of $M_{{\textbf{x}}}(k)$ for the set of all points of X that can be reached from ${\textbf{x}}$ in at most k steps of size at most $2ar=t$, and write $M^a_{{\textbf{x}}}$ instead of $M_{{\textbf{x}}}$ for the set of 2ar-reachable points for ${\textbf{x}}$. When $a=1$ we are back in the case $t=2r$.

Theorem 4.1 above is the most appealing special case of the following more general theorem and corresponds to specifying $a=1$ in Theorem 4.2. We are keeping the two theorems separate, as the case $a=1$ deals with 2r-reachability and is by far the most intuitive case.

Theorem 4.2

Suppose ${\mathcal {X}}_a$, $a\ge 1$, is the family of 2R-regular Delone sets X with the property that $M^a_{{\textbf{x}}}$ is full-dimensional for each ${\textbf{x}}\in X$. Then

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}_a) = {\textrm{O}(d^2\log _2 d)}R \, \text{ as } d\rightarrow \infty , \end{aligned}$$

with an ${\textrm{O}(d^2\log _2 d)}$-term depending on both d and a.

Proof

Similarly to the proof of Theorem 4.1, we split ${\mathcal {X}}_a$ into two subfamilies and deal with each subfamily separately. Let ${\mathcal {X}}'_a$ and ${\mathcal {X}}''_a$ denote the subfamilies of ${\mathcal {X}}$ consisting of all Delone sets X in ${\mathcal {X}}$ with $2dar\le 2R$ or $2dar>2R$, respectively.

If $X\in {\mathcal {X}}'_a$, then we can use the same arguments as in the proof of Theorem 4.1 to show that already $M^a_{{{\textbf{x}}}}(d)$ is full-dimensional for every ${{\textbf{x}}}\in X$. Yet another appeal to the proof of Theorem 4.1 then shows that the cardinality $\mu$ of $M^a_{{{\textbf{x}}}}(d)$ satisfies the inequality $\mu \le (2da+1)^d$. Hence

$$\begin{aligned} |S_{\textbf{x}}(2R)|\le |S_{\textbf{x}}(2dar)|\le \mu ^{d}\le (2da+1)^{d^2} \end{aligned}$$

and

$$\begin{aligned} \Omega _x(2R) +1 \le \log _2 (2|S_{x}(2R)|)\le 1+d^{2}\log _2 (2da+1). \end{aligned}$$

Proceeding as in (3) then establishes

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}'_a) \le 2(\Omega _{{\textbf{x}}}(2R) +2)R \le (4+2d^{2}\log _2 (2da+1))R ={\textrm{O}(d^2\log _2 d)}R, \end{aligned}$$

but now the ${\textrm{O}(d^2\log _2 d)}$-term depends on a as well.

The case when X belongs to ${\mathcal {X}}''_a$ can be settled as in the previous theorem by using the bound from Dolbilin, Lagarias & Senechal [18, Thm. 1.3]. Combining the bound

$$\begin{aligned} \hat{\rho _d} \le 2R(d^2+1) \log _2 (2R/r+2) \end{aligned}$$

from [18, Thm. 1.3] with the inequality $2dar>2R$ we obtain

$$\begin{aligned} {\hat{\rho }}_d({\mathcal {X}}''_a)\le 2R(d^2+1) \log _2 (2da+2) ={\textrm{O}(d^2\log _2 d)}R, \end{aligned}$$

again with an ${\textrm{O}(d^2\log _2 d)}$-term that depends on a.

The statement of the theorem now follows from combining the two upper bounds for ${\hat{\rho }}_d({\mathcal {X}}'_a)$ and ${\hat{\rho }}_d({\mathcal {X}}''_a)$. $\square$

Note that the growth behavior of the two upper bounds for ${\hat{\rho }}_d({\mathcal {X}}'_a)$ and ${\hat{\rho }}_d({\mathcal {X}}''_a)$ in the proof of Theorem 4.2 is essentially controlled by

$$\begin{aligned} d^2 \log _2 (da) = d^2 \log _2 (d) + d^2 \log _2 (a) \end{aligned}$$

as the dominant term. This shows that a change in the reachability step size from 2r to 2ar, $a\ge 1$, results (essentially) in the addition of a term $d^2\log _2 (a)$ to the bound of Theorem 4.1 for $a=1$.

Remark 4.3

In Theorem 4.2, if $2ar\ge 2R$ then $M^a_{{\textbf{x}}}=X$ and ${\mathcal {X}}_a$ coincides with the family of all Delone sets with parameters (r, R). In particular this holds for $a=R/r$. In Theorem 4.2 it therefore suffices to assume that $1\le a \le R/r$. For any $a< R/r$ there exists a Delone set X where the sets of 2ar-reachable points $M^a_{{\textbf{x}}}$, $x\in X$, are proper subsets of X of rank less than d. On the other hand, the extreme case $a=R/r$ is covered by Theorem 4.2, and in this case the bound of Theorem 4.2 provides an explicit upper bound for the regularity radius for the whole family of Delone sets that depends on R and R/r.

Concluding this section, we note that while our asymptotic results describe the behavior of the regularity radius in high dimensions rather than in ordinary 3-space (where we have better results [19]), we are expecting that a vast majority of structured solid materials can be modelled using Delone sets with full-dimensional sets $M^a_{{{\textbf{x}}}}$ for some $a\ge 1$; the reason is that such short-range interactions between atoms should more likely enforce a solid structure than the lack of such interactions.

5 Open Problems

We conclude with several open problems.

5.1 The Group Order Problem

This problem concerns the size of the 2R-cluster groups $S_{{{\textbf{x}}}}(2R)$ in a 2R-regular Delone set in ${\mathbb {R}}^d$. We let $h_d$ denote an upper bound for the order $|S_{{{\textbf{x}}}}(2R)|$ of these groups, and note that our notation suppresses a possible dependence on the parameters of X. It is known that $h_2 = 12$ and $h_3 = 48$. For $d \ge 4$, there is a known upper bound depending on the parameters of X that comes from the cardinality of the 2R-clusters [18, Lem. 4.3].

Problem 5.1

For 2R-regular Delone sets X in ${\mathbb {R}}^d$ with $d\ge 4$, find an upper bound $h_d$ for $|S_{{{\textbf{x}}}}(2R)|$, ${{{\textbf{x}}}}\in X$, that does not depend on the ratio R/r.

Conjecture 5.2

For 2R-regular Delone sets X in ${\mathbb {R}}^d$ with $d\ge 4$, the group order $|S_{{{\textbf{x}}}}(2R)|$, ${{{\textbf{x}}}}\in X$, is bounded by $h_d = 2^d\cdot d!$ for all sufficiently large d, independent of the parameters of X.

This conjecture is related to the problem of bounding the order of finite subgroups in the general linear group ${\mathrm GL}_d(\mathbb Q)$ (see [21]). If true, Conjecture 5.2 implies a better bound on the regularity radius than the ${\textrm{O}(d^2\log _2 d)}R$ bound of our Weak Conjecture 3.5. In fact, if $h_d = 2^d\cdot d!$ for all sufficiently large d, then

$$\begin{aligned} \Omega _{{{\textbf{x}}}}(2R) +1 \le \log _2 (2|S_{{{\textbf{x}}}}(2R)|) \le \log _2 (2h_d) = 1+d+ \log _2 (d!) = \textrm{O}(d\log _2 d)R, \end{aligned}$$

independent of r, and therefore also ${\hat{\rho }}_{d}=\textrm{O}(d\log _2 d)R$. This lends plausibility to our Strong Conjecture 3.6.

The case $d=4$ deserves special attention.

Problem 5.3

Find a positive constant c, independent of the parameters (r, R), such that

$$\begin{aligned} {\hat{\rho }}_{4}\le 2cR. \end{aligned}$$

Here it would be helpful to establish a good upper bound for the order of the 2R-cluster groups in a 2R-regular 4-dimensional Delone set.

5.2 Drop of Symmetries

Our next question concerns the stabilization of the cluster group as the radius of the cluster grows.

Let X be a regular Delone set, and let ${{\textbf{x}}} \in X$. We define the drop of X, denoted D(X) as the number of proper inclusions in the sequence of the subgroups

$$\begin{aligned} S_{{{\textbf{x}}}}(2R)\supseteq S_{{{\textbf{x}}}}(4R) \supseteq S_{{{\textbf{x}}}}(6R) \supseteq \ldots \end{aligned}$$

Note that, since X is regular, the number of proper inclusions does not depend on the point ${{\textbf{x}}}$.

If X is locally asymmetric, that is, if $S_{{{\textbf{x}}}}(2R)$ is trivial, then clearly $D(X)=0$. However, if the symmetry group of the 2R-cluster of X is rich, then theoretically the drop could be as large as the number of prime factors in its order.

On the other hand, the treatment of Delone sets with octahedral and tetrahedral symmetries in ${\mathbb {R}}^3$ in [16] suggests that rich local symmetries may enforce regularity without requiring too many drops.

Let $D_d$ denote the maximal drop D(X) among all regular d-dimensional Delone sets X.

Problem 5.4

Determine, or bound, the maximal drop value $D_d$ as a function of d.

Note that certain regular Delone sets X among the Engel sets of [6] give examples in dimension d with $D(X)=d-2$, and therefore $D_d$ is at least linear in d. We expect that a detailed study of the maximal drop value $D_d$, and of constructions of regular sets with maximal drop, may lead to improved lower bounds for the regularity radius, much like the construction of Engel sets leads to the currently best known lower bound.

5.3 Non-regular yet orderly Delone sets

Delone sets have been extensively studied in the literature and include a wide variety of point sets ranging from regular sets, to multi-regular sets (finite unions of translates of a lattice), to Meyer sets, to amorphous discrete sets (see [4, 5, 18]). They are more than a descriptive tool for discrete point sets: as this paper shows, they are also a tool for characterizing the relation between global regularity and local structure. On the other hand, finding local criteria for orderly but non-regular sets (with “orderly” suitably defined) would benefit from further exploration. Delone sets on the line would be one good place to start (see, for example, [23] and [7]).

For multi-regular sets, the analogue of the regularity radius was introduced as the ‘stable radius’ in [1, 2], with some upper bounds in terms of the underlying unit cell in [2, Lem. 3.7]. Dolbilin, Lagarias & Senechal [18, Thm. 1.3] give an upper bound on the size of the cluster that implies multiregularity depending on the number of clusters of that size and parameters (r, R), but we are not aware about any bounds that are independent of r.