Skip to main content
SpringerLink
Log in

Numerical Semigroups via Projections and via Quotients

  • Published:
Discrete & Computational Geometry Aims and scope Submit manuscript

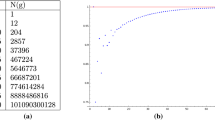
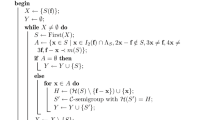Abstract

We examine two natural operations to create numerical semigroups. We say that a numerical semigroup \({\mathcal {S}}\) is k-normalescent if it is the projection of the set of integer points in a k-dimensional polyhedral cone, and we say that \({\mathcal {S}}\) is a k-quotient if it is the quotient of a numerical semigroup with k generators. We prove that all k-quotients are k-normalescent, and although the converse is false in general, we prove that the projection of the set of integer points in a cone with k extreme rays (possibly lying in a dimension smaller than k) is a k-quotient. The discrete geometric perspective of studying cones is useful for studying k-quotients: in particular, we use it to prove that the sum of a \(k_1\)-quotient and a \(k_2\)-quotient is a \((k_1+k_2)\)-quotient. In addition, we prove several results about when a numerical semigroup is not k-normalescent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. It is more standard to also require that \(\gcd ({\mathcal {S}})=1\), but we would like to prove our results in greater generality. In Proposition 2.1 and Remark 2.2, we will see that the two options are actually equivalent from our perspective.

  2. The word normalescent is meant to evoke that it is obtained from a normal semigroup via the process of projection; similar variants on the word “normal” tend to have some established meaning.

References

  1. Adeniran, A., Butler, S., Defant, C., Gao, Y., Harris, P., Hettle, C., Liang, Q., Nam, H., Volk, A.: On the genus of a quotient of a numerical semigroup. Semigroup Forum 98(3), 690–700 (2019)

    Article  MathSciNet  Google Scholar 

  2. Bogart, T., O’Neill, C., Woods, K.: When is a numerical semigroup a quotient?, Bull. Aust. Math. Soc., to appear (2023)

  3. Cox, D., Little, J., Schenck, H.: Toric Varieties, Graduate Texts in Mathematics, vol. 124. Springer, New York (2011)

    Google Scholar 

  4. Danzer, L., Grünbaum, B., Klee, V.: Helly’s theorem and its relatives. Monatsh. Math. 31, 60–97 (1921)

    Google Scholar 

  5. Elizalde, S., Woods, K.: The probability of choosing primitive sets. J. Number Theory 125, 39–49 (2007)

    Article  MathSciNet  Google Scholar 

  6. Lekkerkerker, C.A.: Geometry of Numbers, Series Biblioteca, Vol. 8, Elsevier (2014)

  7. Moscariello, A.: Generators of a fraction of a numerical semigroup. J. Commut. Algebra 11(3), 389–400 (2019)

    Article  MathSciNet  Google Scholar 

  8. Newman, M.: The Smith normal form. Linear Algebra Appl. 254, 367–381 (1997)

    Article  MathSciNet  Google Scholar 

  9. Rosales, J.C.: Numerical semigroups that differ from a symmetric numerical semigroup in one element. Algebra Colloq. 15(1), 23–32 (2008)

    Article  MathSciNet  Google Scholar 

  10. Rosales, J., García-Sánchez, P.: Pseudo-symmetric numerical semigroups with three generators. J. Algebra 291(1), 46–54 (2005)

    Article  MathSciNet  Google Scholar 

  11. Rosales, J., García-Sánchez, P.: Numerical Semigroups, Developments in Mathematics, vol. 20. Springer, New York (2009)

    Book  Google Scholar 

  12. Rosales, J., García-Sánchez, P., García-García, J., Jiménez Madrid, J.: Fundamental gaps in numerical semigroups. J. Pure Appl. Algebra 189(1–3), 301–313 (2004)

    Article  MathSciNet  Google Scholar 

  13. Rosales, J., García-Sánchez, P., García-García, J., Urbano-Blanco, J.: Proportionally modular Diophantine inequalities. J. Number Theory 103(2), 281–294 (2003)

    Article  MathSciNet  Google Scholar 

  14. Rosales, J., García-Sánchez, P., Urbano-Blanco, J.: The set of solutions of a proportionally modular Diophantine inequality. J. Number Theory 128(3), 453–467 (2008)

    Article  MathSciNet  Google Scholar 

  15. Rosales, J.C., Urbano-Blanco, J.M.: Proportionally modular Diophantine inequalities and full semigroups. Semigroup Forum 72, no. 3, 362–374 (2006)

  16. Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1998)

    Google Scholar 

  17. Smith, H.J.S.: On systems of linear indeterminate equations and congruences. Philos. Trans. R. Soc. Lond. 151, 293–326 (1861)

    Google Scholar 

  18. Stanley, R.: Smith normal form in combinatorics. J. Comb. Theory A 144, 476–495 (2016)

    Article  MathSciNet  Google Scholar 

  19. Wang, Y., Stanley, R.: The Smith normal form distribution of a random integer matrix. SIAM J. Discrete Math. 31, 2247–2268 (2017)

    Article  MathSciNet  Google Scholar 

  20. Wolfram, S.: The MATHEMATICA® book, version 4. Cambridge University Press, Cambridge (1999)

    Google Scholar 

  21. Woods, K.: GitHub repository (2023). github.com/kevwoods/Normalescense

Download references

Acknowledgements

Tristram Bogart was supported by internal research grant INV-2020-105-2076 from the Faculty of Sciences of the Universidad de los Andes.

Author information

Authors and Affiliations

  1. Departamento de Matemáticas, Universidad de los Andes, Bogotá, Colombia

    Tristram Bogart

  2. Mathematics Department, San Diego State University, San Diego, CA, 92182, USA

    Christopher O’Neill

  3. Department of Mathematics, Oberlin College, Oberlin, OH, 44074, USA

    Kevin Woods

Authors
  1. Tristram Bogart
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Christopher O’Neill
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kevin Woods
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Christopher O’Neill.

Additional information

Editor in Charge: Kenneth Clarkson

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bogart, T., O’Neill, C. & Woods, K. Numerical Semigroups via Projections and via Quotients. Discrete Comput Geom (2024). https://doi.org/10.1007/s00454-024-00643-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00454-024-00643-z

Keywords

Mathematics Subject Classification

Search

Navigation