Trilateration Using Unlabeled Path or Loop Lengths

Abstract

Let $\textbf{p}$ be a configuration of n points in $\mathbb R^d$ for some n and some $d \ge 2$. Each pair of points defines an edge, which has a Euclidean length in the configuration. A path is an ordered sequence of the points, and a loop is a path that begins and ends at the same point. A path or loop, as a sequence of edges, also has a Euclidean length, which is simply the sum of its Euclidean edge lengths. We are interested in reconstructing $\textbf{p}$ given a set of edge, path and loop lengths. In particular, we consider the unlabeled setting where the lengths are given simply as a set of real numbers, and are not labeled with the combinatorial data describing which paths or loops gave rise to these lengths. In this paper, we study the question of when $\textbf{p}$ will be uniquely determined (up to an unknowable Euclidean transform) from some given set of path or loop lengths through an exhaustive trilateration process. Such a process has already been used for the simpler problem of reconstruction using unlabeled edge lengths. This paper also provides a complete proof that this process must work in that edge-setting when given a sufficiently rich set of edge measurements and assuming that $\textbf{p}$ is generic.

1 Introduction

We are motivated by the following signal processing scenario. Suppose there is a “configuration” $\textbf{p}=(\textbf{p}_1, \dots , \textbf{p}_{n})$ of n points in, say, $\mathbb R^2$ or $\mathbb R^3$. Let a “path” be a finite sequence of these points, and a “loop” be a path that begins and ends at the same point. (We will use these terms to refer to the formal graph-theoretic notions of a “walk” and a “closed walk”.) Each such path or loop in $\textbf{p}$ has a Euclidean length.

Fig. 1

An emitter-receiver at point $\textbf{p}_1$ emits an omnidirectional pulse that bounces among points $\textbf{p}_i$. The same emitter-receiver records the arrival times of pulse fronts that eventually return. These arrival times measure the Euclidean lengths of loops that begin and end at $\textbf{p}_1$

Let $\textbf{p}_1$ be a distinguished point. In our scenario, it may represent the location of an omnidirectional emitter and receiver of sound or radiation. Let the other points in $\textbf{p}$ represent the positions of small objects that behave as omnidirectional scatterers.

An omnidirectional pulse is emitted from $\textbf{p}_1$ and travels outward at, say, unit speed. Whenever the pulse front encounters an object $\textbf{p}_i$, an additional omnidirectional pulse is created there through scattering. Pulses continue to bounce around in this manner, and the receiver at $\textbf{p}_1$ records the arrival times of the pulse fronts that return. We allow for the possibility that some pulse fronts might vanish or not be measurable back at $\textbf{p}_1$.

By recording the times of flight between emission and reception, we effectively measure the lengths of loops traveled. In the case of light, these are travel times of photons that leave $\textbf{p}_1$ and return after one or more bounces. In the case of sound, these are delays of direct or indirect echoes.

Each recorded length measurement is a single real number v. Importantly, we do not obtain any labeling information about which points were visited or how many bounces occurred during the loop. We also do not obtain any information about the direction from which energy arrives.

We wish to understand if we can recover the point configuration (up to Euclidean congruence) from a sufficiently rich sequence of unlabeled loop measurements. Once the loop measurements are labeled, the reconstruction problem is closely related to the well-studied graph realization (or “distance geometry”) problem [21]. Various techniques work well in practice for sufficiently rich inputs. The primary difficulty in our settings arises from the lack of labeling.

Having no combinatorial information appears, at first sight, to be a very daunting problem. Our first insight is to apply the notion of trilateration, which has been proposed as a method to recover a molecular shape from unlabeled inter-atomic distances [12]. As a side contribution of this paper, we provide a complete proof that “unlabeled trilateration” must work given a sufficiently rich set of such distances as well as a genericity assumption on $\textbf{p}$.

In our scenario, trilateration lets us decompose our labeling problem into a sequence of smaller ones, but in applying this technique to our problem we find a crucial distinction from the molecular one. In molecular applications, one relies on the assumption that each measurement arises due to some atomic pair in the configuration (represented as an edge between two points). The story changes if we additionally allow for the possibility of path-length measurements to be mixed in with edge-length measurements, because path-length measurements could perhaps be incorrectly interpreted as edge-lengths and thus confuse such a method. Our second insight is that we can characterize the effect of such additional path-length data by studying a novel algebraic variety that we call the “unsquared measurement variety”. Briefly, path-data that we could confuse for edge-data must arise from a linear automorphism of this variety. Since we have classified such linear automorphisms [14], we can understand the effect that extra path-length data has on our ability to recover a configuration.

Using these insights, we will prove in this paper that if $\textbf{p}$ is a “generic” point configuration in $\mathbb R^d$ for $d\ge 2$, and we measure the lengths of a sufficiently rich set of loops, namely one that “allows for trilateration” (formally defined later), then the configuration $\textbf{p}$ is uniquely determined from these measurements up to congruence. Moreover, this leads to an algorithm, under a real computation model [4], to calculate $\textbf{p}$ from such data. The assumption of genericity (defined later) roughly means that while there are some special $\textbf{p}$ where these conclusions do not hold, these special cases are very rare. In deriving our results, we will not concern ourselves with noise or numerical issues. We plan to address some of these issues in future work.

2 Idea Overview

2.1 Edge Measurements

To put this work in the context of previous mathematical results, let us begin with the simpler setting, where we are given an unlabeled set of edge-lengths.

2.1.1 First Case: Complete Graphs $K_n$

Boutin and Kemper [7] (Theorem 5.1 below) have shown that if $\textbf{p}$ is a generic n-point configuration in $\mathbb R^d$ with $n \ge d+2$, and we are given the complete set of all $N:=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ edge lengths as an unlabeled set, then $\textbf{p}$ is uniquely determined up to Euclidean congruence and point relabeling from this data. Since, in this case, we have all possible N edge measurements, we can associate these measurements with the edges of the complete graph $K_n$.

The main idea behind the Boutin–Kemper result is to study the linear automorphisms of the squared measurement variety $M_{d,n} \subseteq \mathbb {C}^N$, defined below, of n points in d dimensions. The variety $M_{d,n}$ represents all of the possible N-sets of squared edge-length measurements over all possible configurations of n points in d dimensions. (For technical reasons, such varieties are most easily studied in the complex setting.) Boutin and Kemper show (Theorem 5.7 below) that if an “edge permutation” (permutation of the coordinate axes of $\mathbb {C}^N$) gives rise to a linear automorphism of $M_{d,n}$ (maps the variety to itself), then this edge permutation must arise due to a relabeling of the n vertices.

Theorem 5.1 then follows from Theorem 5.7 and the following general principle (see Appendix A for a proof).

Theorem 2.1

Let $V \subseteq \mathbb {C}^N$ be an irreducible algebraic variety and $\textbf{l}$ a generic point of V. Let $\textbf{A}$ be a bijective linear map on $\mathbb {C}^N$ that maps $\textbf{l}$ to a point in V. Let all the above be defined over ${\mathbb Q}$. Then $\textbf{A}(V) = V$, that is, $\textbf{A}$ acts as a linear automorphism of V.

In the intended application, $\textbf{l}\in \mathbb {C}^N$ is the correctly ordered set of edge lengths. Since it represents a consistent set of edge lengths from $K_n$, it is a point in $V:=M_{d,n}$. The linear map $\textbf{A}$ represents some potential edge permutation. If the permuted squared lengths still fit together consistently as an n-point configuration, then $\textbf{A}(\textbf{l})$ is also in $M_{d,n}$ and from Theorem 2.1$\textbf{A}$ must act as a linear automorphism of $M_{d,n}$. Then from Theorem 5.7, we can conclude that this permutation can only arise from a vertex relabeling. Any other type of permutation must place $A(\textbf{l})$, with $\textbf{l}$ generic, outside of $M_{d,n}$.

We can turn Boutin–Kemper’s theorem into an algorithm for reconstructing a generic $\textbf{p}$ from its unordered edge length measurements. To check whether an ordering $\textbf{l}= (l_{ij})$ of the edge measurements is in the complex variety, $M_{d,n}$, we compute the rank of the $(n-1)\times (n-1)$ Gram matrix:

$$\begin{aligned} \begin{pmatrix} 2l^2_{1n} &{} \cdots &{} \cdots &{} l^2_{1n} + l^2_{(n-1)n} - l^2_{1(n-1)} \\ \vdots &{} \ddots &{} &{} \vdots \\ \vdots &{} &{} \ddots &{} \vdots \\ l^2_{1n} + l^2_{(n-1)n} - l^2_{1(n-1)} &{} \cdots &{} \cdots &{} 2l^2_{(n-1)n} \end{pmatrix} \end{aligned}$$

If this rank is at most d, then $\textbf{l}\in M_{d,n}$. Due to the genericity assumption, if $\textbf{l}$ is not correctly ordered, then $\textbf{l}$ will not be in $M_{d,n}$ and the matrix will have a larger rank. As such, no explicit positive semidefiniteness test is needed for this step; see Remark 5.9. Algorithmically, we can simply try different orderings for $\textbf{l}$ until we find one that is in $M_{d,n}$. Such an ordering will exist due to the assumption that this data arose from an actual configuration $\textbf{p}$. From the assumed genericity, this ordering will be unique (up to vertex relabeling). So this ordering must correspond to the ordered complete graph that was used to measure $\textbf{p}$. Next, since $\textbf{p}$ was real, the Gram matrix must be positive semidefinite (PSD). Thus, it can be factored to find the real-valued configuration [24, 28].

This algorithm is only applicable in practice for very small n, but a more efficient approach is based on applying it iteratively to smaller subsets of the data, as described below. The overall approach of generating candidate combinatorial types and testing them with polynomial predicates will appear throughout what follows.

2.1.2 Second Case: $K_{d+2}$ Subconfigurations

Next, suppose that $\textbf{p}$ is a generic n-point configuration in $\mathbb R^d$ with $n \ge d+2$, and we are given a set of $D:=\left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ edge lengths as an unlabeled sequence. Suppose that these D lengths are consistent with the measured edge set over one small complete graph, $K_{d+2}$. We can show (Proposition 5.16 below) that these lengths must actually have arisen through the edges of a $K_{d+2}$. To do this we will invoke the following general result (see Appendix A for a proof) which generalizes Theorem 2.1:

Theorem 2.2

Let V be an irreducible algebraic variety and $\textbf{l}$ a generic point of V. Let $\textbf{E}$ be a linear map that maps $\textbf{l}$ to a point in some variety W. Let all the above be defined over ${\mathbb Q}$. Then $\textbf{E}(V) \subseteq W$.

In our application, $\textbf{E}$ will be the linear map that projects $M_{d,n}$ onto a specific set of coordinates corresponding to D edges, and W will be $M_{d,d+2}$. A rigidity-theoretic argument tells us that if the D edges do not form a $K_{d+2}$ subgraph of $K_n$, the image $\textbf{E}(M_{d,n})$ will be D-dimensional. On the other hand, $M_{d,d+2}$ has dimension $D-1$. From Theorem 2.2, we then see that if $\textbf{l}$ is generic and $\textbf{E}(\textbf{l})$ is in $M_{d,d+2}$, then $\textbf{E}$ must correspond to a $K_{d+2}$, since this is the only way for $\textbf{E}(M_{d,n})$ to have dimension less than D.

As in the previous section, we can test whether D ordered measurements are in $M_{d,d+2}$ by a matrix rank computation. (No PSD test is needed here, as described in Remark 5.17.) If they are in $M_{d,d+2}$, we can then apply Boutin and Kemper’s result to this subset, and uniquely reconstruct the associated subconfiguration of these $d+2$ points, up to congruence.

2.1.3 Trilateration

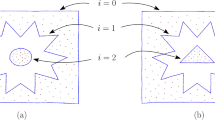
This idea can now be used (when $d\ge 2)$ to reconstruct all n of the points under the assumption that our unlabeled data includes the measurements of an edge subset that is rich enough to allow for trilateration [12]. Loosely speaking, this means that the measured edge set contains one complete graph $K_{d+2}$, and then includes more edges that allow us to inductively glue all of the vertices, one by one, onto the currently reconstructed point set. Each such inductive step involves one new vertex v with $d+1$ edge measurements connecting v to the already reconstructed set. This essentially allows us to find another $K_{d+2}$ graph that overlaps sufficiently with the already reconstructed point set so that they can be glued together in a unique manner. (See Fig. 2, top.) As argued above, the geometry of each such $K_{d+2}$ is completely determined by its unlabeled edge lengths.

Assuming our full data set allows for trilateration, then there is a unique n-point configuration consistent with the data, up to congruence. Finding these $K_{d+2}$ subgraphs requires a somewhat exhaustive search over the data set, giving us a running time that is exponential in d (which we think of as fixed) but only polynomial in n.

In this context, we prove two statements of slightly different flavors: Theorem 5.21 is a “global rigidity statement”. It says that if $\textbf{v}$ is the measurements of a generic configuration $\textbf{p}$ of n points by a set of edges G allowing for trilateration, then there is no other set of edges H (maybe not allowing for trilateration) and n-point configuration $\textbf{q}$ (maybe not generic) such that measuring $\textbf{q}$ by H produces $\textbf{v}$.

Of course, in an algorithmic setting, we may have no way to know in advance either the number of points n in the configuration that was measured or whether the graph G describing the combinatorics of the measurements allowed for trilateration. Our second “certificate” statement, Theorem 5.22, says the following: Let $\textbf{p}$ be an (unknown) generic configuration and G an (unknown) edge set producing the (known) measurements $\textbf{v}$. Let H be a (reconstructed) edge set that allows for trilateration and let $\textbf{q}$ be a (reconstructed) configuration. Suppose that the measurements $\textbf{v}^-$ resulting from $\textbf{q}$ through H agrees with a subset of $\textbf{v}$. Then, in fact, $\textbf{q}$ is congruent to a subconfiguration of $\textbf{p}$. We interpret Theorem 5.22 as saying that a trilateration-based algorithm can correctly reconstruct (part of) $\textbf{p}$, without any assumptions beyond $\textbf{p}$ being generic. The algorithm does not even need to figure out how to explain all of $\textbf{v}$, but rather only needs to find a trilaterizable subset. For edge measurements, our unlabeled trilateration algorithm coincides with the TRIBOND algorithm described in proposed in [12]. However, the analysis of its correctness is new, and the statements we formulate reveal some subtleties that have not appeared before.

These two theorems, while complementary, are incomparable, because of the different types of assumptions. Since each has a natural application, we will prove analogues of both for path and loop ensembles below.

2.2 Path Measurements Included

Suppose next that we want to look at data sets that may include path lengths in addition to edge lengths. In this case can trilateration still work? This is a much harder problem. In particular, suppose we find a subset of D measurements that are consistent with the edges of a $K_{d+2}$ subgraph. It is conceivable that there is some adversarial, oddball set of D paths among the n points that, for all configurations, can be misinterpreted as a consistent collection of D measurements from the edges of a $K_{d+2}$. Theorem 5.7 and Proposition 5.15 are no longer sufficient, as now we are not guaranteed that we are just looking at a subset of edge measurements.

To answer these questions, we need a better understanding of the behaviour of more general linear maps applied to edge lengths over $K_n$. (Recall, a path length is just some sum of edge lengths.) We do this by introducing a new variety, $L_{d,n}$, called the unsquared measurement variety. We study its group of linear automorphisms (so we can apply Theorem 2.1) and study which linear maps have images with deficient dimension images (so we can apply Theorem 2.2). We have relegated this technical study of these linear automorphism groups to its own dedicated paper [14]. With this in hand, we then argue in this paper that trilateration can still work!

2.3 Loops Instead of Paths

Finally, we now can move to the case where all of our measurements are loops, and there are no simple edge measurements at all. In reality, most of the hard work though has already been done by the reasoning of Sect. 2.2.

To reconstruct a configuration of $d+2$ points, we can no longer use the D edges of a $K_{d+2}$. We instead assume that we have a specific canonical collection of D loop measurements that we can use to reconstruct $d+2$ points. In fact, we will use two types of canonical loop sets: one to reconstruct an isolated $K_{d+2}$, and another to reconstruct a single new point during trilateration. When describing these, it helps to have dedicated terms for two particular types of loops. So we use ping for a loop that contains only two points (and so has length equal to twice an edge length) and triangle for a loop that contains three points (and so has length equal to the sum of three edge lengths).

To reconstruct an isolated $K_{d+2}$, our hope is to find the measurements of lengths comprising $d+1$ pings with one common point, and the $\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$ triangles that include the pinged $d+1$ points (see Fig. 2, bottom left). To add an additional point v during trilateration, our hope is to use all of the edge lengths amongst $d+1$ previously reconstructed points, and to find the measurements of lengths comprising one ping and d triangles that include v (see Fig. 2, bottom right). Thus, in the loop setting, we change our definition of allowing for trilateration to mean that our loop data includes sufficient canonical data of this type to inductively include all of the points. In the application described in the introduction, all of the pings and triangles will contain the common point $\textbf{p}_1$, but we will not require that assumption in what follows.

With these altered definitions, we can again apply the reasoning of Sect. 2.2 and argue that loop-based trilateration will work as well.

Fig. 2

Comparison between path measurements (top row) and loop measurements (bottom row). Top row: A $K_{4}$ contained within a path measurement ensemble consists of six edges (blue lines) (left). During trilateration using path measurement data, three points $\textbf{p}_1$, $\textbf{p}_2$, $\textbf{p}_3$ are known, and a fourth point $\textbf{p}_4$ is reconstructed from three edge length measurements (right). Bottom row: A $K_{4}$ contained within a loop measurement ensemble consists of three pings (double black lines) and three triangles (red lines) (left). During trilateration using loop measurement data, three points $\textbf{p}_1$, $\textbf{p}_2$, $\textbf{p}_3$ are known, and a fourth point $\textbf{p}_4$ is reconstructed from one ping and two triangle length measurements (right)

3 Definitions and Main Results

We start by establishing our basic terminology.

Definition 3.1

Fix positive integers d (dimension) and n (number of points). Throughout the paper, we will set $N:= \left( {\begin{array}{c}n\\ 2\end{array}}\right)$, $C:=\left( {\begin{array}{c}d+1\\ 2\end{array}}\right)$, and $D:= \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$. These constants appear often because they are, respectively, the number of pairwise distances between n points, the dimension of the group of congruences in $\mathbb R^d$, and the number of edges in a complete $K_{d+2}$ graph.

Definition 3.2

A configuration, $\textbf{p}=(\textbf{p}_1, \dots , \textbf{p}_{n})$ is a sequence of n points in $\mathbb R^d$. (If we want to talk about sequences of points in $\mathbb {C}^d$, we will explicitly call this a complex configuration.)

We think of each integer in $\{1,\dots ,n\}$ as a vertex of an abstract complete graph $K_n$. An edge, $\{i,j\}$, is an unordered distinct pair of vertices. The complete edge set of $K_n$ has cardinality N.

A path $\alpha :=(i_1, \dots , i_z)$ is a finite sequence of $z \ge 2$ vertices, with no vertex immediately repeated. (The simplest kind of path, (i, j), is comprised by a single edge.) A loop is a path with $z \ge 3$ vertices where $i_1=i_z$. (The simplest kind of loop (i, j, i) is called a ping. Another important kind of loop (i, j, k, i) is a triangle.)

Fixing a configuration $\textbf{p}$ in $\mathbb R^d$, we define the length of an edge $\{i,j\}$ to be the Euclidean distance between the points $\textbf{p}_i$ and $\textbf{p}_j$, a real number.

We define the length v of a path or loop $\alpha$ to be the sum of the lengths of its comprising edges.

Definition 3.3

An edge multiset is simply a multiset of edges. A path or loop naturally gives rise to the edge multiset which contains each of the edges traversed, with repetition. We will also denote an edge multiset as $\alpha$. The length v of an edge multiset $\alpha$ is the sum of the lengths of its comprising edges. We denote this measurement process as $v = \langle \alpha , \textbf{p}\rangle$.

The motivation for the notation $\langle \alpha , \textbf{p}\rangle$ will become evident in Definition 6.6, where we describe the measurement process in terms of a linear functional.

Definition 3.4

An edge measurement ensemble $\pmb {\alpha }:=(\alpha _1,\dots ,\alpha _k)$ is a finite sequence of edges. (This is the same as an “ordered graph” on the vertex set $\{1,\dots ,n\}$.) A path measurement ensemble $\pmb {\alpha }:=(\alpha _1,\dots ,\alpha _k)$ is a finite sequence of paths. We define a loop measurement ensemble similarly. We also define an edge multiset measurement ensemble in the same way.

A configuration $\textbf{p}$ and a measurement ensemble $\pmb {\alpha }$ give rise to a data set $\textbf{v}$ that is the finite sequence of real numbers made up of the lengths of its paths or loops or edge multisets. We denote this as $\textbf{v}= \langle \pmb {\alpha }, \textbf{p}\rangle$. We say that this data set arises from this measurement ensemble. Notably, a data set $\textbf{v}$ itself does not include any labeling information about the measurement ensemble it arose from.

We denote by $|\textbf{v}|$ the number of elements in $\textbf{v}$.

Definition 3.5

We say that a path or loop $\alpha$ is b-bounded, for some positive integer b, if no edge appears more than b times in $\alpha$. We say that a path or loop measurement ensemble $\pmb {\alpha }$ is b-bounded if it comprises only b-bounded loops or paths.

Remark 3.6

In a practical setting, we may not know the actual bound b of a b-bounded ensemble, but instead know that it must exist for other reasons. In particular, suppose we have some bound on the maximal distance between any pair of points in $\textbf{p}$. Then we can safely assume that any sufficiently huge length value v arises from a sufficiently complicated path or loop that we will not use in our trilateration, and discard it. Suppose then that we also have some bound on the minimal distance between any pair of points in $\textbf{p}$. Then we know that any non-discarded value must arise from a b-bounded loop or path with some appropriate b.

The process of trilateration will involve gluing together smaller pieces of the configuration. Thus we introduce the following notation.

Definition 3.7

We use $\textbf{p}_I$ to refer to a subconfiguration of a configuration $\textbf{p}$ indexed by an index sequence I, that is a (possibly reordered) subsequence of $\{1,\dots ,n\}$. In particular, we use $\textbf{p}_T$ to refer to a $(d+2)$-point subconfiguration in $\textbf{p}$, indexed by a sequence $T=(i_1,\dots ,i_{d+2})$ of $\{1,\dots ,n\}$. Similarly, we use $\textbf{p}_R$ to refer to a $(d+1)$-point subconfiguration of $\textbf{p}$.

We use $\textbf{v}_J$ to refer to a sub data set, a (possibly reordered) subsequence of the data set $\textbf{v}$ indexed by an index sequence J, and similarly for a subensemble $\pmb {\alpha }_J$.

We will be interested in measurement ensembles that are sufficient to uniquely determine the configuration in a greedy manner using trilateration. Trilateration starts by finding enough data to reconstruct the location of ${d+2}$ points. In the path setting, this is done by looking for the edges of a $K_{d+2}$ graph. In the loop setting, this is done by looking for a different canonical data set over $d+2$ points.

Definition 3.8

In the edge or path setting, we say that a $K_{d+2}$ subgraph of $K_n$ is contained within a path measurement ensemble $\pmb {\alpha }$ if the ensemble includes a subensemble of size D comprising the edges of this subgraph. For the 2-dimensional case, see Fig. 2 (upper left).

In the loop setting, we say that a $K_{d+2}$ subgraph of $K_n$ with vertices $\{i_1,\dots , i_{d+2}\}$ is contained within a loop measurement ensemble $\pmb {\alpha }$ if the ensemble includes a subensemble of size D comprising: the $d+1$ pings $(i_1, i_j, i_1)$ for j spanning $\{2,\dots ,d+2\}$; and also the triangles $(i_1, i_j, i_k, i_1)$ for $j < k$ spanning $\{2,\dots ,d+2\}$. That is, the ensemble includes all pings and triangles in this $K_{d+2}$ with endpoints at vertex $i_1$. For the 2-dimensional case, see Fig. 2 (bottom left).

Trilateration proceeds by iteratively adding one more vertex onto an already reconstructed subset of point locations. This is done by looking for a canonical, sufficient set of data. Such data sets differ between the path and the loop setting.

Definition 3.9

We say that an edge or a path measurement ensemble allows for trilateration¹ if, after reordering the vertices: (i) it contains an initial base $K_{d+2}$ over $\{1,\dots ,d+2\}$; and (ii) for all subsequent $(d+2) <j \le n$, it includes as a subsequence a trilateration sequence comprising the edges $\{i_1,j\},\dots ,\{i_{d+1},j\}$ where all $i_k < j$. For the 2-dimensional case, see Fig. 2 (top right).

We say that a loop measurement ensemble allows for trilateration if, after reordering the vertices: (i) it contains an initial base $K_{d+2}$ over $\{1,\dots , d+2\}$; and (ii) for all subsequent $(d+2) <j \le n$, it includes as a subsequence a trilateration sequence comprising the triangles $(i_1,i_2,j,i_1),\dots ,(i_1,i_{d+1},j,i_1)$, and also the ping $(i_1,j,i_1)$, where all $i_k < j$. That is, it includes one ping from j back to one previous $i_1$, and d triangles back to the previous vertices and including $i_1$. (See Fig. 2 (bottom right) for the 2-dimensional case.)

Definition 3.10

Trilateration refers to the greedy reconstruction process whereby one starts by reconstructing a base configuration and then inductively adds new vertices to the already reconstructed configuration. We call each such step trilaterizing a vertex.

As the process runs, it maintains a set of already reconstructed points, and, at each step, reconstructs a single new point. To find the new point, the algorithm searches for an ordered $d+1$-tuple of reconstructed points and $d+1$ ordered measurement values in the data set so that: the $d+1$ measurements, along with the $C = D - (d+1)$ imputed edge lengths among the reconstructed points satisfy a certain polynomial predicate. The predicate is based on a Cayley–Menger determinant and proves that these D values arose from $d+2$ points in dimensions d. The C imputed lengths may or may not be in the data set.

Since $d+1$ of the points are already reconstructed, it is then possible to solve uniquely for the last one.

Note that a path (resp. loop) measurement ensemble that allows for trilateration may include any other additional paths (resp. loops) beyond those specified in Definition 3.9. There may also be more than one trilateration sequence in the ensemble.

Unlabeled reconstruction from paths or loops can have difficulties distinguishing between two points with some length between them, and two points that are half as far from each other but where the edge between them is measured twice (as in a ping). Thus we introduce the following scaling notation.

Definition 3.11

For s a real number, the s-scaled configuration $s\cdot \textbf{p}$ is the configuration obtained by scaling each of the coordinates of each point in $\textbf{p}$ by s. The subconfiguration $s\cdot \textbf{p}_I$ is defined similarly. For s a positive integer and an edge multiset $\alpha$, the s-scaled edge multiset $s\cdot \alpha$ is the edge multiset obtained by scaling the multiplicity of each edge by s. For s a positive integer, the s-scaled edge multiset measurement ensemble $s\cdot \pmb {\alpha }$ is defined by scaling each element of the ensemble.

We can then define, for a positive integer s, the s-scaling of a path or loop measurement ensemble by considering the elements as edge multisets.

The main results in this paper do not hold unconditionally. There can be special inputs that will fool us or are even inherently ambiguous. We explicitly rule out such special inputs in what follows.

Definition 3.12

We say that a real point in $\mathbb R^{dn}$ is generic if its coordinates do not satisfy any non-trivial polynomial equation with coefficients in ${\mathbb Q}$. The set of generic real points have full measure and are standard-topology dense in $\mathbb R^{dn}$.

We say that a configuration $\textbf{p}$ of n points in $\mathbb R^d$ is generic if it is generic when thought of as a single point in $\mathbb R^{dn}$.

Various theorems in this paper will be shown to hold, for each n, for all generic configurations of the configuration space, $\mathbb R^{dn}$. For example, Boutin and Kemper [7, 8] study the question of when an n-point configuration in $\mathbb R^d$ with $n \ge d+2$ will be uniquely determined from the complete set of all $N:=\left( {\begin{array}{c}n\\ 2\end{array}}\right)$ edge lengths as an unlabeled set. Their results show that the configuration will be determined unless the coordinates of the configuration satisfy a polynomial equation with rational coefficients (see Remark 5.8). This means that such a non-determined configuration must be non-generic. Contrapositively, genericity rules out such non-determined configurations.

We note that the set of generic points is not open in $\mathbb R^{dn}$. However, if one imposes any notion of finiteness on the combinatorial objects in question, such as only considering measurement ensembles that are b-bounded, for some chosen b, then the same statements will, in fact, hold over some open and dense subset of $\mathbb R^{dn}$. (This set will be Zariski open; i.e., the complement of a proper algebraic set.)

Remark 3.13

Without some kind of genericity hypothesis, theorems like the ones presented in this paper are false: there do exist rare “bad” inputs for which uniqueness will fail. Whether it is safe to make a genericity assumption depends on the application. In settings where the inputs are unconstrained, such as the sensing ones described in the introduction, genericity is a reasonable assumption. Other applications may impose additional symmetries on the input; for example, all the distances might be drawn from a small set, or the structures in question may be invariant to some Euclidean group. For those applications, whether we typically observe the generic behaviour becomes an experimental question.

3.1 Results

The first central conclusion of this paper will be the following “global rigidity” statement:

When $\langle \pmb {\alpha },\textbf{p}\rangle$ agrees with $\langle \pmb {\beta },\textbf{q}\rangle$ after some permutation, then the theorem can be applied after appropriately permuting $\pmb {\beta }$.

Note that if one lets $\textbf{q}$ be non-generic and puts no restrictions on the number of points, then one can obtain any target $\textbf{v}$ by letting $\pmb {\beta }$ be a tree of edges and then placing $\textbf{q}$ appropriately.

For algorithmic purposes we are better served by the following variant of Theorem 3.14.

Definition 3.15

Given a finite sequence of k complex numbers $w_i$, we say that they are rationally linearly dependent if there is a sequence of rational coefficients $c^i$, not all zero, such that $0= \sum _i c^i w_i$. Otherwise we say that they are rationally linearly independent. We define the rational rank of $w_i$ to be the size of the maximal subset that is rationally linearly independent.

Definition 3.16

Suppose that $\textbf{q}$ is a configuration and $\pmb {\beta }$ an ensemble that allows for trilateration. We say that a vertex trilateration step is nice if the D trilaterating length values ($d+1$ of these are in the data and C are imputed from previously reconstructed vertices) used as inputs to the the polynomial predicate have rational rank D. We say that $\pmb {\beta }$ trilaterates $\textbf{q}$ nicely if it has a trilateration sequence such that each step is nice.

In this theorem, we make no prior assumptions on $\pmb {\alpha }$ and the number of vertices that are endpoints of edges in its support. The existence of $\textbf{q}$ and $\pmb {\beta }$ with the appropriate properties is itself a certificate of correctness (we still need to assume that $\textbf{p}$ is generic). Thus if we are able, in any way, to find a way to interpret a portion, which is called $\textbf{v}^-$ in the statement of the theorem, of $\textbf{v}$ using a nice trilaterating ensemble $\pmb {\beta }$ we know that we have correctly realized a corresponding part $\textbf{p}_S$ of $\textbf{p}$ (up to similarity).

Theorem 3.17 provides the basis for a computational attack on this reconstruction process. In particular, we will establish the following.

For fixed d, this algorithm (over a real computation model) will have worst case time complexity that is polynomial in $(|\textbf{v}|, b)$, though with a moderately large exponent.

Fig. 3

Counterexample in 1 dimension. The configuration $\textbf{p}$ with the shown (upper) three edge measurements gives rise to the same length values as the configuration $\textbf{q}$ with the shown (lower) three path measurements. This behavior is stable; as $\textbf{p}$ is perturbed, $\textbf{q}$ can be appropriately perturbed to maintain this ambiguity, and vice-versa for $\textbf{q}$ perturbations

Theorem 3.14 fails for $d=1$. A simple counterexample to the theorem for the path case is shown in Fig. 3: Let $\textbf{p}_1< \textbf{p}_2 < \textbf{p}_3$ be three generic points on the line. Let $\alpha _1$ measure the edge $\{1,2\}$, $\alpha _2$ measure the edge $\{2,3\}$ and $\alpha _3$ measure the edge $\{1,3\}$. This ensemble clearly allows for trilateration. In this case we will have $\textbf{v}= \langle \pmb {\alpha },\textbf{p}\rangle = [ \textbf{p}_2-\textbf{p}_1, \textbf{p}_3-\textbf{p}_2, \textbf{p}_3-\textbf{p}_1]$. Now let $\textbf{q}_1$ be arbitrary, and set $\textbf{q}_2:= \textbf{q}_1 + (\textbf{p}_2-\textbf{p}_1) - 1/2 (\textbf{p}_3-\textbf{p}_1)$ and $\textbf{q}_3:= \textbf{q}_1 + 1/2(\textbf{p}_3-\textbf{p}_1)$. This will give us $\textbf{q}_3-\textbf{q}_2= (\textbf{p}_3-\textbf{p}_1) - (\textbf{p}_2-\textbf{p}_1)= \textbf{p}_3-\textbf{p}_2$. Let us also assume that $\textbf{p}_3-\textbf{p}_2<\textbf{p}_2-\textbf{p}_1$, then this will give us the ordering: $\textbf{q}_1< \textbf{q}_2 < \textbf{q}_3$. Now, let $\beta _1$ measure the path (2, 1, 3), $\beta _2$ measure the edge $\{2,3\}$, and $\beta _3$ measure the path (1, 3, 1). Then in this case, we will also get $\textbf{v}=\langle \pmb {\beta },\textbf{q}\rangle$. But the two (edge multiset) measurement ensembles $\pmb {\alpha }$ and $\pmb {\beta }$ are not related by a scale.

Likewise, regarding Theorem 3.17, let $\textbf{q}$ be the underlying unknown generic configuration measured with the unknown $\beta _i$. Looking at these measurement values, we might incorrectly assume that it comes from the reconstructed triangular, and thus trilaterizable, measurements described by the $\alpha _i$ on the reconstructed configuration $\textbf{p}$. Since we cannot uniquely reconstruct a triangle on the line, this will kill off any attempts at using trilateration for reconstruction in 1 dimension.

In the language we develop later, the failure described in this example essentially happens because the variety $L_{1,3}$ is reducible, and thus Theorem 2.1 does not apply. The relationship between these $\pmb {\alpha }$ and $\pmb {\beta }$ is not described by a linear automorphism of $L_{1,3}$. Instead, the relationship is described by only a linear automorphism of one of its (planar) components.

Fig. 4

2-Flips ambiguity in 1 dimension

There is a second way in which our theorems fail in 1 dimension, as demonstrated in Fig. 4: Let $\textbf{p}$ consist of 4 points on a line and $\pmb {\alpha }$ consist of 5 of the 6 possible edges. In this case, there is a vertex, say $\textbf{p}_4$, with only two measured edges, say $\{2,4\}$ and $\{3,4\}$. If $\pmb {\beta }$ is obtained from $\pmb {\alpha }$ by simply swapping the order of these two edges, we can maintain $\textbf{v}$ by appropriately re-locating the fourth point. Essentially, in the unlabeled setting, there are two ways we can glue $\textbf{p}_4$ and its two edges on the triangle of the first three points. We return to this issue in Remark 5.24.

We close out this section by remarking that our proofs establish slightly stronger statements than Theorem 3.14 and Theorem 3.17. In particular, the edge multiset measurement ensembles $\pmb {\beta }$ in Theorem 3.14 and $\pmb {\alpha }$ in Theorem 3.17 can, in fact, be any length functional measurement ensembles (see Definintion 6.6 below), which are a generalization of edge multiset measurement ensembles.

4 Measurement Varieties

In this section, we will study the basic properties of two related families of varieties, the squared and unsquared measurement varieties. The structure of these varieties will be critical to understanding the problem of reconstruction from unlabeled measurements. The squared variety is very well studied in the literature, where it is often called the Cayley–Menger variety, but the unsquared variety is much less so. Since we are interested in integer sums of unsquared edge lengths, we will need to understand the structure of this unsquared variety. Although we are ultimately interested in measuring real lengths in Euclidean space, we will pass to the complex setting where we can utilize some tools from algebraic geometry.

Definition 4.1

Let us index the coordinates of $\mathbb {C}^N$ as ij, with $i < j$ and both between 1 and n. We also fix an ordering on the ij pairs to index the coordinates of $\mathbb {C}^N$ using a single coordinate index with values between 1 and N.²

Let us begin with a complex configuration $\textbf{p}$ of n points in $\mathbb {C}^d$ with $d \ge 1$. There are $N$ vertex pairs (edges), along which we can measure the complex squared length as

$$\begin{aligned} m_{ij}(\textbf{p}):= \sum _{k=1}^{d}(\textbf{p}^k_i-\textbf{p}^k_j)^2 \end{aligned}$$

where k indexes over the d dimension-coordinates. Here, we measure complex squared length using the complex squaring operation with no conjugation. We consider the vector $[m_{ij}(\textbf{p})]$ over all of the vertex pairs, with $i<j$, as a single point in $\mathbb {C}^{N}$, which we denote as $m(\textbf{p})$.

Definition 4.2

Let $M_{d,n}\subseteq \mathbb {C}^{N}$ be of $m(\cdot )$ over all n-point complex configurations in $\mathbb {C}^d$. This is called the Cayley–Menger variety of n points in d dimensions. We also call this the squared measurement variety of n points in d dimensions.

When $n \le (d+1)$, then $M_{d,n}= \mathbb {C}^{N}$. (See also Proposition 5.12 below.)

The next definition, though not needed in what follows, is given for context.

Definition 4.3

If we restrict the domain to real configurations, then we call under $m(\cdot )$ the Euclidean squared measurement set denoted as $M^{\mathbb E}_{d,n} \subseteq \mathbb R^{N}$. This set has real dimension $dn-C$.

The following theorem, save for the last statement, reviews some basic facts. For more details, see [6] or [14]. See Appendix A for our definitions of terms from algebraic geometry.

Theorem 4.4

Let $n \ge d+2$. The set $M_{d,n}$ is linearly isomorphic to ${{\mathcal {S}}}^{n-1}_d$, the variety of complex, symmetric $(n-1)\times (n-1)$ matrices of rank d or less. Thus, $M_{d,n}$ is a variety, and also defined over ${\mathbb Q}$. It is irreducible. Its dimension is $dn-C$. Its singular set ${{\,\textrm{Sing}\,}}(M_{d,n})$ consists of squared measurements of configurations with affine spans of dimension strictly less than d. If $\textbf{p}$ is a generic complex configuration in $\mathbb {C}^d$ or a generic configuration in $\mathbb R^d$, then $m(\textbf{p})$ is generic in $M_{d,n}$.

The last statement follows from Lemma A.5.

Remark 4.5

We note, but will not need, the following: For $d\ge 1$, the smallest complex variety containing $M^{\mathbb E}_{d,n}$ is $M_{d,n}$.

As an example, the smallest interesting instance, $M_{1,3} \subseteq \mathbb {C}^3$, is defined by the vanishing of the Cayley–Menger determinant, that is, the determinant of the following matrix:

$$\begin{aligned} \begin{pmatrix} 2m_{13}&{} (m_{13} + m_{23} - m_{12})\\ (m_{13} + m_{23} - m_{12})&{} 2m_{23}\\ \end{pmatrix} \end{aligned}$$

where we use $(m_{12}, m_{13}, m_{23})$ to represent the coordinates of $\mathbb {C}^3$ [14].

In the real setting, the square root of the Cayley–Menger determinant of $d+2$ points in $\mathbb R^N$ is $(d+1)!2^{d+1}$ times the unsigned $(d+1)$-volume of the simplex formed by the points. In this paper, we are interested in the case where $N=d$, so this volume must be zero. Hence, the vanishing of the Cayley–Menger determinant is a predicate showing that the input measurements arose from a configuration in dimension d.

Next we move on to unsquared lengths.

Definition 4.6

We define the squaring map $s(\cdot )$ as the map from $\mathbb {C}^{N}$ onto $\mathbb {C}^{N}$ that acts by squaring each of the $N$ coordinates of a point. Let $L_{d,n}$ be the preimage of $M_{d,n}$ under the squaring map. (Each point in $M_{d,n}$ has $2^{N}$ preimages in $L_{d,n}$, arising through coordinate negations.) We call this the unsquared measurement variety of n points in d dimensions.

Definition 4.7

We can define the Euclidean length map of a real configuration $\textbf{p}$ as

$$\begin{aligned} l_{ij}(\textbf{p}):= \sqrt{\sum _{k=1}^{d}(\textbf{p}^k_i-\textbf{p}^k_j)^2} \end{aligned}$$

where we use the positive square root. We denote by $l(\textbf{p})$ the vector $[l_{ij}(\textbf{p})]$ over all vertex pairs.

The next definition, though not needed in what follows, is given for context.

Definition 4.8

We call of $\textbf{p}$ under l the Euclidean unsquared measurement set denoted as $L^{\mathbb E}_{d,n} \subseteq \mathbb R^{N}$. Under the squaring map, we get $M^{\mathbb E}_{d,n}$. We may consider $l(\textbf{p})$ either as a point in the real valued $L^{\mathbb E}_{d,n}$ or as a point in the complex variety $L_{d,n}$.

Indeed, $L^{\mathbb E}_{d,n}$ is the set we are truly interested in, but it will be easier to work with the whole variety $L_{d,n}$. For example, Theorem 2.1 requires us to work with varieties, and not, say, with real “semi-algebraic sets”.

Remark 4.9

The locus of ${L_{2,4}}$ where the edge lengths of a triangle, $(l_{12}, l_{13}, l_{23})$, are held fixed is studied in beautiful detail in [9], where it is shown to be a Kummer surface.

The following theorem, save for the last statement, is a result from our companion paper [14].

Theorem 4.10

Let $n \ge d+2$. ${L_{d,n}}$ is a variety, defined over ${\mathbb Q}$. It is pure dimensional, with dimension $dn-C$. Now additionally assume that $d \ge 2$. ${L_{d,n}}$ is irreducible. If $\textbf{m}$ is generic in $M_{d,n}$, then each point in $s^{-1}(\textbf{m})$ is generic in ${L_{d,n}}$. If $\textbf{p}$ is a generic configuration in $\mathbb R^d$, then $l(\textbf{p})$ is generic in ${L_{d,n}}$.

The last statement of this theorem follows from Lemma A.6 and Theorem 4.4.

In 1 dimension, the variety $L_{1,3}$ is reducible and thus has no generic points. We elaborate on this below.

Remark 4.11

We note, but will not need the following: For $d\ge 2$, the smallest complex variety containing $L^{\mathbb E}_{d,n}$ is $L_{d,n}$.

Returning to our minimal example: The variety $L_{1,3} \subseteq \mathbb {C}^3$ is defined by the vanishing of the determinant of the following matrix

$$\begin{aligned} \begin{pmatrix} 2l^2_{13}&{} (l^2_{13} + l^2_{23} - l^2_{12}) \\ (l^2_{13} + l^2_{23} - l^2_{12})&{} 2l^2_{23} \end{pmatrix} \end{aligned}$$

where we use $(l_{12}, l_{13}, l_{23})$ to represent the coordinates of $\mathbb {C}^3$.

Fig. 5

A model of the real locus of $L_{1,3}$, a subset of $\mathbb R^3$. It comprises 4 planes. Coordinate axes are in white

Remark 4.12

It turns out that $L_{1,3}$ is reducible and consists of the four hyperspaces defined, respectively, by the vanishing of one of the following equations:

$$\begin{aligned} l_{12} + l_{23} - l_{13} \\ l_{12} - l_{23} + l_{13} \\ -l_{12} +l_{23} + l_{13} \\ l_{12} + l_{23} + l_{13} \end{aligned}$$

This reducibility can make the 1-dimensional case quite different from dimensions 2 and 3, as already discussed in Sect. 3.1. See also Fig. 5.

Notice that the first octant of the real locus of 3 of these hyperspaces arises as the Euclidean lengths of a triangle in $\mathbb R^1$ (that is, these make up $L^{\mathbb E}_{1,3}$). The specific hyperplane is determined by the order of the 3 points on the line.

5 The Case of Edge Measurement Ensembles

We will first look at the case when our measurement ensemble consists only of edge measurements. Within this, we will start with the case where the measurement ensemble consists of the complete edge set of cardinality $N$, which was studied carefully in [7]. The results from [7] have been cleverly applied in [11] to determine the shape of a room from acoustic echo data (this connection is made explicit in [10]). Then we will consider the case of a trilateration ensemble of edges, and prove the correctness of the TRIBOND algorithm described in [12].

5.1 First Case: Complete Graphs $K_n$

In this section, we will consider an edge measurement ensemble $G:=(E_1,\dots ,E_k)$, a finite sequence of distinct edges of $K_n$. This is the same thing as a graph on n vertices with some ordering on its edges. For an edge measurement ensemble G, we will write $\langle G, \textbf{p}\rangle ^2$ to denote the sequence of squared edge lengths.

We start with a central result of Boutin and Kemper [7], stated in our terminology.

Theorem 5.1

Let the dimension be d, and $n \ge d+2$. Let $\textbf{p}$ be a generic configuration of n points in d dimensions. Let $\textbf{v}= \langle G, \textbf{p}\rangle ^2$, where G is an edge measurement ensemble made up of exactly the $N$ edges of $K_n$ in some order.

Suppose there is a configuration $\textbf{q}$, also of n points, along with an edge measurement ensemble H, where H is an edge measurement ensemble made up of exactly the $N$ edges of $K_n$, in some other order such that $\textbf{v}=\langle H,\textbf{q}\rangle ^2$.

Then there is a vertex relabeling of $\textbf{q}$ such that, up to congruence, $\textbf{q}=\textbf{p}$. Moreover, under this vertex relabeling, $G=H$.

By way of comparison, the labeled setting is classical. Recall that configurations $\textbf{p}$ and $\textbf{q}$ of n points in dimension d are congruent if there is a Euclidean isometry T of $\mathbb R^d$ so that $\textbf{q}_i = T(\textbf{p}_i)$ for all $1\le i\le n$.

Lemma 5.2

([28]) Suppose that $\textbf{p}$ and $\textbf{q}$ are configurations of n points and that for all N edges ij of $K_n$, we have $|\textbf{p}_i - \textbf{p}_j| = |\textbf{q}_i - \textbf{q}_j|$. Then $\textbf{p}$ and $\textbf{q}$ are congruent.

Boutin and Kemper prove Theorem 5.1 using a characterization of permutation automorphisms of $M_{d,n}$.

Definition 5.3

A linear automorphism of a variety V in $\mathbb {C}^N$ is map that bijectively takes V to itself that arises as the restriction of a non-singular linear transformation acting on $\mathbb {C}^N$.

In our setting, V will always have a full linear span in $\mathbb {C}^N$. So a linear automorphism on V will uniquely correspond to a linear map acting on $\mathbb {C}^N$. Thus, we may identify a linear automorphism with a linear map on $\mathbb {C}^N$. In our setting, the embedding space $\mathbb {C}^N$ is equipped with a fixed set of coordinate axes that are associated with the edges of $K_n$. Thus, we may identify a linear transformation with the complex $N\times N$ matrix representing it in the standard basis of $\mathbb {C}^N$. We will freely use the symbol $\textbf{A}$ to represent a linear automorphism, a linear transformation acting on $\mathbb {C}^N$, or its representing matrix as needed.

Definition 5.4

An $N\times N$ matrix $\textbf{P}$ is a permutation matrix if each row and column has a single non-zero entry, and this entry is 1.

Definition 5.5

A permutation $\pi$ of the coordinate axes of $\mathbb {C}^N$ is induced by a vertex relabeling if, under the association between the edges of the complete graph $K_n$ and the coordinate axes of $\mathbb {C}^N$ from Definition 4.1, there is a permutation $\sigma$ of the vertices of $K_n$ so that, for all edges ij, $\pi (ij) = \sigma (i)\sigma (j)$.

Definition 5.6

An $N\times N$ permutation matrix $\textbf{P}$ is induced by a vertex relabeling if it corresponds to a permutation, $\pi$, of the edges of $K_n$, that is induced by a vertex relabeling.

The key result of [7] is the following:

Theorem 5.7

([7, Lem. 2.4]) Suppose that $\textbf{A}$ is a permutation matrix that gives rise to a linear automorphism of $M_{d,n}$. Then $\textbf{A}$ is induced by a vertex relabeling.

Indeed, Theorem 5.7 together with Theorem 2.1 directly provide a proof for Theorem 5.1.

Remark 5.8

Suppose for some specific $(G,\textbf{p})$, there is also an $(H,\textbf{q})$ with the same edge measurements $\textbf{v}$, where G and H are comprised of different orderings of the edges of $K_n$, but H is not related to G via a vertex relabeling. Then $\textbf{v}$ lies in both $M_{d,n}$ and in $\textbf{P}_{HG}(M_{d,n})$, where $\textbf{P}_{HG}$ is a permutation matrix that does not give rise to a linear automorphism of $M_{d,n}$. So this $\textbf{v}$, by virtue of it also being in $\textbf{P}_{HG}(M_{d,n})$, is not generic in $M_{d,n}$ and thus $\textbf{p}$ is not a generic configuration (Lemma A.5).

Remark 5.9

Theorems 5.7 and 2.1 tell us that, for a generic $\textbf{p}$, there will be only one ordering (up to vertex labeling) of the N squared lengths that will give us a point in $M_{d,n}$. Testing for membership in $M_{d,n}$ is just a rank test, and does not require any PSD testing. Since, by assumption, $\textbf{p}$ exists and is real, its correctly ordered squared lengths must then automatically satisfy any relevant PSD conditions.

5.2 Small Images

We next wish to show that if our point configuration is generic, and we have an ordered subsequence of D edge lengths that are consistent with $K_{d+2}$, then indeed, it must arise due to exactly this subgraph. Using Theorem 5.1, we can then uniquely reconstruct these $d+2$ points.

To this end, our first step is to establish that if the D edges do not form a $K_{d+2}$ graph, then as we vary over $\textbf{p}$, we should be able to vary each of these D numbers independently.

Definition 5.10

Let d be some fixed dimension. Let $E:= (E_1,\ldots , E_k)$ be an edge measurement ensemble over n vertices. The ordering on the edges of E fixes an association between each edge in E and a coordinate axis of $\mathbb {C}^{k}$. Let $m_E(\textbf{p}):= \langle E, \textbf{p}\rangle ^2$ be the map from d-dimensional configuration space to $\mathbb {C}^{k}$ measuring the squared lengths of the edges of E.

We denote by $\pi _{{E}}$ the linear map from $\mathbb {C}^N$ to $\mathbb {C}^{k}$ that forgets the edges not in E, and is consistent with the ordering of E. Specifically, we have an association between each edge of $K_n$ and an index in $\{1,\dots ,N\}$, and thus we can think of each $E_i$ as simply its index in $\{1,\dots ,N\}$. Then, $\pi _{{E}}$ is defined by the conditions: $\pi _{{E}}(e_j) = 0$ when $j\in \bar{E}$ and $\pi _{{E}}(e_j) = e'_i$ when $E_i=j$, where $\{e_1, \ldots , e_N\}$ denotes the coordinate basis for $\mathbb {C}^N$ and $\{e'_1, \ldots , e'_k\}$ denotes the coordinate basis for $\mathbb {C}^k$. We call $\pi _{{E}}$ an edge map.

The map $m_E(\cdot )$ is simply the composition of the complex measurement map $m(\cdot )$ and $\pi _{{E}}$.

Finally, we denote by $M_{d,E}$ the Zariski closure of of $m_E(\cdot )$ over all d-dimensional configurations.

Definition 5.11

We say an edge set E is infinitesimally independent in d dimensions if, starting from a generic complex configuration $\textbf{p}$ in $\mathbb {C}^d$, we can differentially vary each of the |E| squared lengths independently by appropriately differentially varying our configuration $\textbf{p}$. Formally, this means that the image of the differential of $m_E(\cdot )$ at a generic $\textbf{p}$ is |E|-dimensional. This exactly coincides with the notion of infinitesimal independence from graph rigidity theory [20].

An edge set that is not infinitesimally independent in d dimensions is called infinitesimally dependent in d dimensions. Note that in this case the rank of the differential, $dm_E$, can never rise to |E|.

The following is implicit in the rigidity theory literature.

Proposition 5.12

An edge measurement ensemble E is infinitesimally independent in d dimensions iff of $m_E(\cdot )$ over all complex configurations of n points has dimension |E|.

Proof

sketch The basic principle is that the generic rank of the differential tells us the dimension of. In particular we consider the map $m_E(\cdot )$. First remove the non-smooth points of, and then remove the preimages of these non-smooth points from the domain (all non-generic). Sard’s Theorem (e.g., [17, Thm. 14.4]) then tells us that the inverse image of every generic point in this image consists entirely of configurations $\textbf{p}$ where the differential has rank equal to the dimension of of $m_E(\cdot )$. $\square$

Remark 5.13

These notions are usually studied in the real setting, but the tools used in the proof sketch above work the same way in the complex setting. Complexification is used to study rigidity problems in, e.g., [6, 15, 23, 25].

The following is a standard result from rigidity theory.

Proposition 5.14

Let E be an edge measurement ensemble (with all its edges distinct). Suppose $|E| \le \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ and E is infinitesimally dependent in d dimensions. Then $|E| = \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ and E consists of the edges of a $K_{d+2}$ subgraph (in some order).

Proof

Sketch Assume, without loss of generality, that E is infinitesimally dependent and inclusion-wise minimal with this property. If E does not consist of the edges of a $K_{d+2}$ subgraph, then it has a vertex v of degree at most d. Suppose that $\textbf{p}$ is a configuration in affine general position. A geometric argument then shows that the coordinate subspaces spanned by the edges incident to v must be in of $dm_E$ at $\textbf{p}$. Since of $dm_E$ at $\textbf{p}$ is not |E|-dimensional, removing the edges incident to v yields a smaller set of edges $E'\subseteq E$ that is still infinitesimally dependent. This contradicts the assumed minimality of E. $\square$

Combining Propositions 5.12 and 5.14 we arrive at the following:

Proposition 5.15

Let E be an edge measurement ensemble (with all its edges distinct). Suppose $|E| \le \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ and of $m_E(\cdot )$ over all complex configurations of n points has dimension less than |E|. Then $|E| = \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$ and E consists of the edges of a $K_{d+2}$ subgraph (in some order).

5.3 Consistent with $K_{d+2}$

We can now complete the argument that when our data looks consistent with a single $K_{d+2}$, then we can be certain that this must be how this data arose. The key idea is that unless we were measuring a $K_{d+2}$, then for a generic $\textbf{p}$, and using Proposition 5.15, we should not expect to find a measurement that satisfies any extra algebraic condition defined using rational coefficients.

Proposition 5.16

Let the dimension be $d\ge 1$. Let $\textbf{p}$ be an n-point configuration in $\mathbb R^d$ such that $m(\textbf{p})$ is generic in $M_{d,n}$. Suppose there is a sequence of D, not-necessarily distinct, edges $E = (E_1, \ldots , E_D)$, such that $w_i:=\langle E_i,\textbf{p}\rangle ^2$ form a vector $\textbf{w}:=(w_1, \dots , w_D)$ that is in $M_{d,d+2}$.

Then there must be a subconfiguration $\textbf{p}_T$ of $\textbf{p}$ with $d+2$ points such that $\textbf{w}= m(\textbf{p}_T)$.

The condition that $m(\textbf{p})$ is generic in $M_{d,n}$ allows for the possibility that $\textbf{p}$ itself is non-generic. Here, we are essentially only requiring that $\textbf{p}$ is congruent to a generic configuration. Since the proof requires several lemmas, we defer it for now.

Remark 5.17

This proposition only requires that $\textbf{w}\in M_{d,d+2}$ which is a zero-determinant test; no PSD test is required. The conclusion tells us that these squared lengths come from a real configuration, and so must automatically satisfy the relevant PSD conditions.

In the statement, we do not assume, a priori, that the D edges in E are distinct. So we will prove first that under our genericity assumption on $\textbf{p}$, this will be automatically guaranteed.

Lemma 5.18

Let $d\ge 1$. Let $I = \{I_1, \ldots , I_{r}\}$, for $r < D$, be a partition of $\{1, \ldots , D\}$ into r subsets. Let $X_I\subseteq \mathbb {C}^D$ be the linear span of the vectors $\textbf{v}_j = \sum _{i\in I_j} \textbf{e}_i$, for $1\le j\le r$ and elementary vectors $\textbf{e}_i$; i.e., these are vectors with only r distinct values.

Then $M_{d,d+2}$ does not contain the space $X_I$.

Proof

Observe that, for any partition I of the coordinates, the all ones vector is a linear combination of the vectors $\textbf{v}_j$. Hence any $X_I$ contains the all ones vector.

On the other hand, it is well-known that the $(d+2)$-simplex with all edge lengths equal to one has non-zero $(d+1)$-volume. Hence the all ones vector is not in $M_{d,d+2}$. $\square$

Lemma 5.19

Let the dimension be $d\ge 1$. Let $\textbf{p}$ be a n-point configuration in $\mathbb R^d$ such that $m(\textbf{p})$ is generic in $M_{d,n}$. Suppose there is a sequence of D, not-necessarily distinct, edges $E = (E_1, \ldots , E_D)$, such that $w_i:=\langle E_i,\textbf{p}\rangle ^2$ form a vector $\textbf{w}:=(w_1, \dots , w_D)$ that is in $M_{d,d+2}$.

Then the D edges must be distinct.

Proof

Let $\textbf{E}$ be the D by N matrix with ij-th entry set to 1 if $E_i$ is the jth edge of $K_n$, and 0 otherwise. We identify $\textbf{E}$ with the linear map it induces from $\mathbb {C}^N$ to $\mathbb {C}^D$. Then $\textbf{E}(m(\textbf{p}))$ gives us the D measurements $w_i=\langle E_i,\textbf{p}\rangle ^2$.

From Theorem 2.2, since $m(\textbf{p})$ is generic in $M_{d,n}$, we see that $\textbf{E}(M_{d,n}) \subseteq M_{d,d+2}$.

Suppose that the D edges comprising E are not all distinct. Then $E'$, the collection of $r<D$ distinct edges, is infinitesimally independent (Proposition 5.14). From Proposition 5.12, $\textbf{E}(M_{d,n})$ must be an r-dimensional constructible subset S of one of the r-dimensional linear (and irreducible) spaces $X_I$ described in Lemma 5.18. Its Zariski closure, $\bar{S}$, would then be equal to this $X_I$. Since $M_{d,d+2}$ contains S and is Zariski closed, $M_{d,d+2}$ must contain $X_I$.

But from Lemma 5.18, $X_I$ is not contained in $M_{d,d+2}$. This contradiction establishes the lemma. $\square$

Proof of Proposition 5.16

From Lemma 5.19 we know that the edges in E are all distinct. Our measurement sequence $\textbf{w}$ arises from D distinct coordinates of $m(\textbf{p})$, giving us $\textbf{w}= \pi _{{E}}(m(\textbf{p}))$. Since $\textbf{p}$ is generic, $m(\textbf{p})$ is generic in $M_{d,n}$. Recall also that, from Theorem 4.4, $M_{d,n}$ is irreducible.

From Theorem 2.2, we see that $\pi _{{E}}(M_{d,n}) \subseteq M_{d,{d+2}}$, since $\pi _{{E}}(m(\textbf{p}))\in M_{d,{d+2}}$.

Since dimension of $\pi _{{E}}(M_{d,n})$ is less than D, from Proposition 5.15 (which required us to know that the edges were distinct), we see that E must consist of the edges of a $K_{d+2}$.

Let $\pi _{{K}}$ be the edge map where K comprises the edges of this $K_{d+2}$, and where K is ordered such that $\pi _{{K}}(M_{d,n}) = M_{d,d+2}$. Let $\textbf{K}$ be the matrix representing $\pi _{K}$, and let $\textbf{E}$ be the matrix representing $\pi _{E}$.

Then we must have $\textbf{E}= \textbf{P}\textbf{K}$ where $\textbf{P}$ is some $D\times D$ permutation matrix. We identify $\textbf{P}$ with the linear map that it induces on $\mathbb {C}^D$. And we have $\textbf{P}(M_{d,d+2}) = \textbf{P}(\pi _{{K}}(M_{d,n})) = \pi _{{E}}(M_{d,n}) \subseteq M_{d,d+2}$.

Thus, from Theorem 2.1, $\textbf{P}$ must induce a linear automorphism on $M_{d,d+2}$. Then from Theorem 5.7, $\textbf{P}$ must be induced from a vertex relabeling. As $\textbf{E}=\textbf{P}\textbf{K}$ for such a $\textbf{P}$, there must be an ordered $(d+2)$-point subconfiguration $\textbf{p}_T$ of $\textbf{p}$ such that $\textbf{w}= m(\textbf{p}_T)$. $\square$

Remark 5.20

Because of the way Proposition 5.15 is used in the above proof, $K_{d+2}$ cannot simply be replaced by some other generically globally rigid graph to obtain a similar result.

5.4 Trilateration

Now we wish to extend this result to the case where our edge measurement ensemble is not complete, but does allow for trilateration in the sense of Definition 3.9. Due to the gluing ambiguity we saw in Fig. 4, we will restrict our discussion here to $d\ge 2$. The key idea is to use Proposition 5.16 iteratively, applied to $K_{d+2}$ subsets of $K_n$. This will lead to the following global rigidity theorem.

We note that this result has recently been greatly strengthened to apply to a much larger class of graphs than just the complete graphs or trilateration graphs [16]. The proof we give here, for trilateration graphs, is much more direct, as it is based on greedily constructing the relabeling of $\textbf{q}$, one point at a time.

The following variant describes a certificate for correct reconstruction.

The assumption that no two points in $\textbf{q}$ are coincident is required. Otherwise one could create a $\textbf{q}$ that is identical to $\textbf{p}$ except that one high valence vertex in $(G,\textbf{p})$ is split in $(H,\textbf{q})$ into two distinct vertices with coincident locations, each with enough edges to the rest of $\textbf{q}$ so that both new vertices can be trilaterated.

In this theorem, we make no prior assumptions on G and its number of vertices. Nor do we assume, a priori, that $\textbf{q}$ is generic. The existence of $\textbf{q}$ and H with the appropriate properties is itself a certificate of correctness, though we still need to assume that $\textbf{p}$ is generic. Thus if we are able to interpret some portion of $\textbf{v}$, corresponding to $\textbf{v}^-$ in the statement of the theorem, using a trilateration H, then we know that we have correctly realized a corresponding part $\textbf{p}_S$ of $\textbf{p}$.

Finally, suppose we assume that $\textbf{p}$ is a generic configuration of n points and that G allows for trilateration with $\textbf{v}= \langle G, \textbf{p}\rangle ^2$. Thus we must be able to take the data $\textbf{v}$, and find (using brute force) some H and $\textbf{q}$ of n points such that H trilaterates $\textbf{q}$, and such that $\textbf{v}=\langle H,\textbf{q}\rangle ^2$. From Theorem 5.22, we then know that $\textbf{q}=\textbf{p}$. This gives us a formal justification for TRIBOND, the brute force unlabeled trilateration algorithm of [12].

Theorems 5.21and 5.22, sketch Informally, Theorems 5.21 and 5.22 say that, generically, we do not need to know the edge labels for the trilateration reconstruction to succeed.

The intuitive reasoning is as follows. The trilateration process starts from a known $K_{d+2}$ and then locates each additional point by “gluing” a new $K_{d+2}$ (with one new point) onto a $K_{d+1}$ inside the already visited $K_{v}$ over the v previously reconstructed vertices. The idea, then, is to find the labels as we locate points by using Proposition 5.16 iteratively: initially to find a “base” $K_{d+2}$ to start the trilateration process, and then, after measuring all the edges between the visited points, to find subsequent $K_{d+2}$ subconfigurations that, each, add one more point. When $d\ge 2$, there is only one way to do the gluing, because generic $(d+1)$-simplices do not have any “self-congruences”.

Even though the steps above are conceptually very simple, the details require some care. We now fill in the sketch above.

Lemma 5.23

Suppose that $\textbf{p}$ is a configuration of n points in dimension d so that either $l(\textbf{p})$ is generic in $L_{d,n}$ or $m(\textbf{p})$ is generic in $M_{d,n}$. Then no two subconfigurations of at least three points in $\textbf{p}$ are similar to each other, unless the two subconfigurations consist of the same points, in the same order.

Only the case of congruence is needed now, but similarities will be needed later in Sect. 6.5.

Proof

Two ordered configurations $\textbf{q}$ and $\textbf{r}$ of k points are related by a similarity if and only if their vectors of $\left( {\begin{array}{c}k\\ 2\end{array}}\right)$ (un)squared edges lengths are proportional (in the squared case, if the scaling in the similarity is $\lambda$, the effect on $m(\textbf{q})$ is to multiply it by $\lambda ^2$). That is, if and only if both of the $\left( {\begin{array}{c}k\\ 2\end{array}}\right) \times 2$ matrices

$$\begin{aligned} \begin{pmatrix} m(\textbf{q})&m(\textbf{r}) \end{pmatrix} \qquad \text {and}\qquad \begin{pmatrix} l(\textbf{q})&l(\textbf{r}) \end{pmatrix} \end{aligned}$$

have rank at most one, which is a polynomial condition defined over ${\mathbb Q}$ that is non-trivial when $k \ge 3$ (so that $\left( {\begin{array}{c}k\\ 2\end{array}}\right) > 1$).

If $\textbf{q}$ and $\textbf{r}$ are similar subconfigurations of $\textbf{p}$ with $k\ge 3$ points, then, by the argument above $l(\textbf{p})$ and $m(\textbf{p})$ satisify a non-trivial polynomial condition that does not hold over all of $L_{d,n}$ and $M_{d,n}$ respectively (there are configurations where $\textbf{q}$ and $\textbf{r}$ are not similar). Hence, $l(\textbf{p})$ and $m(\textbf{p})$ are non-generic when $\textbf{p}$ contains similar subconfigurations. $\square$

Remark 5.24

The statement of Lemma 5.23 is not true with only two points because any pair of two-point configurations are similar. Even worse for our intended application, any subconfiguration $(\textbf{p}_i, \textbf{p}_j)$ is congruent to the subconfiguration $(\textbf{p}_j, \textbf{p}_i)$. Because of this, unlabeled trilateration over an edge measurement ensemble will not directly work for $d=1$. (See Fig. 4.) In order to use trilateration over an unlabeled edge measurement ensemble in 1 dimension, we would need to have an edge ensemble that not only allows for trilateration in 1 dimension but also has enough edges to allow for trilateration in 2 dimensions.

The next lemma describes our main inductive step.

Lemma 5.25

Let $d\ge 2$ and let $\textbf{p}$ and $\textbf{q}$ be configurations of n and $n'$ points respectively, with $m(\textbf{p})$ generic in $M_{d,n}$. We also suppose that no two points in $\textbf{q}$ are coincident. Let G and H be two edge measurement ensembles such that $\langle G, \textbf{p}\rangle ^2 = \langle H, \textbf{q}\rangle ^2$.

Suppose that we have two “already visited” subconfigurations $\textbf{q}_{V'}$ and $\textbf{p}_{V}$ with $\textbf{q}_{V'} =\textbf{p}_{V}$.

Suppose we can find a set F of $d+1$ edges in H connecting some unvisited vertex $\textbf{q}_{i'}\in \textbf{q}_{\bar{V'}}$ to some visited subconfiguration $\textbf{q}_{R'}$ of $\textbf{q}_{V'}$ with $d+1$ vertices.

Then we can find an unvisited $\textbf{p}_{i}\in \textbf{p}_{\bar{V}}$ such that the two subconfigurations $\textbf{q}_{V'\cup \{i'\}}$ and $\textbf{p}_{V\cup \{i\}}$ are equal.

Proof

Let $\textbf{q}_{T'}$ be a subconfiguration consisting of, in some order, all the points of $\textbf{q}_{R'}$ along with $\textbf{q}_{i'}$. Let $\textbf{w}:=m(\textbf{q}_{T'})$.

The $d+1$ points of $\textbf{q}_{R'}$ give rise to C edge length measurements in $\textbf{w}$. Because $\textbf{p}_{V} = \textbf{q}_{V'}$ the corresponding $d+1$ points $\textbf{p}_R$ induce the same measurements. By assumption, there must be $D - C = d+1$ edges $E_0\subseteq G$, corresponding to the the $d+1$ edges $F\subseteq H$ connecting the points of $\textbf{q}_{R'}$ to $\textbf{q}_{i'}$, so that $\langle E_0,\textbf{p}\rangle ^2 = \langle F,\textbf{q}\rangle ^2$. Adding the C imputed edges from $\textbf{p}_V$ to $E_0$ we get a set of D edges $E\subseteq G$ (not necessarily distinct), so that $\textbf{w}= \langle E,\textbf{p}\rangle ^2$.

Since $m(\textbf{p})$ is generic, we can now apply Proposition 5.16 using the existence of E to conclude that there must be a subconfiguration $\textbf{p}_{T}$ of $\textbf{p}$ with $\textbf{w}= m(\textbf{p}_{T})$. Now, we use Lemma 5.2 to conclude that $\textbf{q}_{T'}$ and $\textbf{p}_{T}$ are related by a congruence. (Now that we have $\textbf{p}_{T}$, we don’t need E any more.)

Since $\textbf{q}_{R'}$ is a subconfiguration of $\textbf{q}_{T'}$, $\textbf{q}_{R'}$ must be congruent to its associated subconfiguration of $\textbf{p}_{T}$, which we may call $\textbf{p}_{R_0}$. Thus from Lemma 5.23, we know that $\textbf{q}_{R'}$ is congruent to no other subconfiguration of $\textbf{p}$. Meanwhile, $\textbf{q}_{R'}$ is a subconfiguration of $\textbf{q}_{V'}$ and thus also equal to some subconfiguration $\textbf{p}_{R}$ of $\textbf{p}_{V}$. Thus $\textbf{q}_{R'}$, $\textbf{p}_{R_0}$ and $\textbf{p}_{R}$ must all be equal. Since the congruence $\sigma$ that maps $\textbf{q}_{T'}$ to $\textbf{p}_{T}$ fixes the $d+1$ points of $\textbf{q}_{R'}$, $\sigma$ must be the identity and we must have $\textbf{q}_{T'}=\textbf{p}_{T}$.

Let $\textbf{p}_{i}$ be the “new” point in $\textbf{p}_{T}\setminus \textbf{p}_{R}$, which also must equal $\textbf{q}_{i'}$. If $\textbf{p}_{i}$ was already visited in $\textbf{p}_{V}$, then the same position would have already been visited by some point in $\textbf{q}_{V'}$. This together with the fact that no points are coincident in $\textbf{q}$ would contradict the assumption that $\textbf{q}_{i'}\in \textbf{q}_{\bar{V'}}$. Thus $\textbf{q}_{V'\cup \{i'\}}=\textbf{p}_{V\cup \{i\}}$. $\square$

We can now apply the above lemma iteratively.

Lemma 5.26

Let the dimension $d \ge 2$. Let $\textbf{p}$ be a configuration of n points such that $m(\textbf{p})$ is generic in $M_{d,n}$. Let G be a measurement ensemble. Let $\textbf{v}:=\langle G,\textbf{p}\rangle ^2$.

Suppose that $\textbf{q}$ is a configuration of $n'$ points with no two points in $\textbf{q}$ being coincident. And suppose that H is an edge measurement ensemble that allows for trilateration and such that $\langle H, \textbf{q}\rangle ^2$ also equals $\textbf{v}$.

Then, there is a sequence of indices $S=(s_1,\ldots , s_{n'})$ so that, up to congruence, $\textbf{p}_{S} = \textbf{q}$. Moreover, the vertices appearing in S are exactly those that are endpoints of edges in the support of G. After renaming each edge $\{i,j\}$ in H as $\{s_i,s_j\}$, we have $H = G$.

Proof

For the base case, the trilateration assumed in H guarantees a $K_{d+2}$ contained in H, over a $(d+2)$-point subconfiguration $\textbf{q}_{T'}$ of $\textbf{q}$. Define $\textbf{w}:=m(\textbf{q}_{T'})$. We have $\textbf{q}\in M_{d,d+2}$.

Using the fact that $\langle G, \textbf{p}\rangle ^2 = \langle H, \textbf{q}\rangle ^2$ we can apply Proposition 5.16 to this $\textbf{w}$, $\textbf{p}$ and appropriate sequence of edges E taken from G. From this, we conclude that there is a ${d+2}$ point subconfiguration $\textbf{p}_{T}$ of $\textbf{p}$ such that $\textbf{w}=m(\textbf{p}_{T})$. From Lemma 5.2, up to congruence, we have $\textbf{q}_{T'} = \textbf{p}_{T}$.

Going forward, assume that this congruence has been factored into $\textbf{p}$. Then, to proceed inductively, assume that we have two “visited” subconfigurations such that $\textbf{q}_{V'}=\textbf{p}_{V}$. Initially $V = T$ and $V' = T'$. With this setup, we may now follow the trilateration of $\textbf{q}$, iteratively applying Lemma 5.25 until we have visited all of $\textbf{q}$. At the end of the process, $\textbf{q}_{V'} = \textbf{p}_{V}$ with $\textbf{q}_{V'}$ a reordering of $\textbf{q}$. Inverting this ordering, we have $\textbf{q}=\textbf{p}_{S}$, where S is an ordering of the visited points in $\textbf{p}$.

Since $\textbf{p}$ is generic, then no two distinct edges can have the same squared length. Since $\textbf{q}$ is a subconfiguration of our generic $\textbf{p}$ then no two distinct edges among points in $\textbf{q}$ can have the same squared length. This means there is a unique way for $\textbf{v}$ to arise from $\textbf{q}$ and a unique way for $\textbf{v}$ to arise from $\textbf{p}$. Hence, after vertex relabeling from S, we have $H = G$. Since the vertices that are endpoints of edges in the support of H correspond exactly to the points of $\textbf{q}$, then the vertices that are endpoints of edges in the support of G correspond to the points of $\textbf{p}_{S}$, as in the statement. $\square$

And we can now finish the proof of one of the main theorems of this section:

Proof of Theorem 5.22

First we remove from $\textbf{v}$ the measurements which do not appear in $\textbf{v}^-$. We also remove the associated edges from G, to obtain $G^-$. Since $\textbf{p}$ is generic, then $m(\textbf{p})$ is generic in $M_{d,n}$ from Theorem 4.4. Then we simply apply Lemma 5.26. $\square$

With some other added assumptions, we can use an assumption of genericity on $\textbf{p}$ to automatically obtain genericity for $m(\textbf{q})$ in $M_{d,n}$. To see this, we first use the following definition.

Definition 5.27

Let d be a fixed dimension. Let E be an edge measurement ensemble with $n\ge d+1$. We say E is infinitesimally rigid in d dimensions, if, starting at some generic (real or complex) configuration $\textbf{p}$, there are no differential motions of $\textbf{p}$ in d dimensions that preserve all of the squared lengths among the edges of E, except for differential congruences.

When an edge measurement ensemble is infinitesimally rigid, then the lack of differential motions holds over a Zariski open subset of configurations that includes all generic configurations.

Letting $m_E(\textbf{p})$ be the map from configuration space to $\mathbb {C}^{|E|}$ measuring the squared lengths of the edges of E, infinitesimal rigidity means that of the differential of $m_E(\cdot )$ at $\textbf{p}$ is $(dn-C)$-dimensional.

The following proposition follows exactly as Proposition 5.12.

Proposition 5.28

If E is infinitesimally rigid, then of $m_E(\cdot )$ acting on all configurations is $(dn-C)$-dimensional. Otherwise, the dimension of is smaller.

Lemma 5.29

In dimension $d \ge 1$, let $\textbf{p}$ and $\textbf{q}$ be two configurations with the same number of points $n \ge d+1$. Suppose that G and H are two edge measurement ensembles, each with the same number k of edges, and with G infinitesimally rigid in d dimensions. And suppose that $\textbf{v}:=\langle G,\textbf{p}\rangle ^2 = \langle H,\textbf{q}\rangle ^2$.

If $\textbf{p}$ is a generic configuration, then $m(\textbf{q})$ is generic in $M_{d,n}$.

Proof

Recall the notation introduced in Definition 5.10. The varieties $M_{d,G}$ and $M_{d,H}$, both subsets of $\mathbb {C}^k$, are defined over ${\mathbb Q}$. They are irreducible since they arise from closing images of $M_{d,n}$, which is irreducible, under polynomial (in fact linear) maps. Because G is infinitesimally rigid, $M_{d,G}$ is of dimension $dn-C$ from Proposition 5.28. Likewise, $M_{d,H}$ is of dimension at most $dn-C$.

Our assumptions give us $\textbf{v}\in M_{d,G}$ and $\textbf{v}\in M_{d,H}$.

We claim $M_{d,G} = M_{d,H}$. If not, then $M_{d,G} \cap M_{d,H}$ is an algebraic variety, defined over ${\mathbb Q}$, of dimension strictly less than $dn-C$ (due to irreducibility), and thus could contain no generic points of $M_{d,G}$. But we have assumed that $\textbf{v}$ is in both, and thus also in this intersection set. But since $\textbf{p}$ is generic, then $\textbf{v}$ is generic in $M_{d,G}$ (Lemma A.5). This contradiction thus establishes our claim.

Since $M_{d,G} = M_{d,H}$, then $\textbf{v}$ is also a generic point of of $M_{d,H}$.

Finally, since $M_{d,H}$ is the Zariski closure of the image of $M_{d,n}$ under the linear map $\pi _{{H}}(\cdot )$, and since they have the same dimension, then from Lemma A.6 the preimage of $\textbf{v}$ under $\pi _{{H}}(\cdot )$, which is $m(\textbf{q})$, must be a generic point in $M_{d,n}$. $\square$

And we can now finish the proof of the other main theorem of this section:

Proof of Theorem 5.21

An edge measurement ensemble that allows for trilateration is always infinitesimally rigid. We apply Lemma 5.29 to conclude that $m(\textbf{q})$ is generic in $M_{d,n}$. By assumption G allows for trilateration. Thus we can now apply Lemma 5.26, but with the roles of $\textbf{p}$ and $\textbf{q}$ reversed, as well as the roles of G and H. $\square$

6 Paths and Loops

Now we are ready to tackle the setting of paths and loops. Our reasoning will parallel that of Sect. 5, but we will need to upgrade most of the ingredients.

6.1 First Case: Complete Graphs $K_n$

Our first step is to upgrade Theorem 5.7. Dealing with the possibility of paths will make us look at $L_{d,n}$ instead of $M_{d,n}$. Moreover this will require us to understand the full group of linear automorphisms, instead of the simpler setting of coordinate permutations. This is a non-trivial algebraic geometry study, which we have relegated to a companion paper [14]. Here we summarize those results.

Any coordinate permutation that is induced by a vertex relabeling must give rise to a linear automorphism of $L_{d,n}$. Also due to the squaring construction, the negation of any coordinate will give rise to a linear automorphism. We call the linear automorphisms arising from vertex relabelings and coordinate negations the signed vertex relabelings. Any uniform scale on $\mathbb {C}^N$ will also give rise to a linear automorphism of $L_{d,n}$ because uniformly scaling a configuration $\textbf{p}$ in $\mathbb R^d$ by a positive factor produces another configuration with edge lengths scaled by the same amount. Let us refer to the linear automorphism set generated by the above as the expected linear automorphisms of $L_{d,n}$.

In our application, we are concerned that the measurement data of some complicated set of paths could yield a generic point in $L_{d,n}$. If this were to happen, there would necessarily be a linear automorphism of $L_{d,n}$ that is not one of the expected ones. The following theorem rules this out, except when $\{d,n\} = \{2,4\}$.

Theorem 6.1

([14]) Let $d \ge 1$ and let $n \ge d+2$. Assume that $\{d,n\}\ne \{2,4\}$. Then any linear automorphism $\textbf{A}$ of $L_{d,n}$ is a scalar multiple of a signed vertex relabeling.

Interestingly, for $L_{2,4}$, there is, up to scale, a discrete set of unexpected linear automorphisms, which we can fully characterize. Luckily for us, when an unexpected linear automorphism is representable by a matrix with real elements, this matrix must include some negative coefficients. Such negative numbers cannot occur in any measurement ensemble based on paths or loops.

A linear automorphism $\textbf{A}$ of $L_{d,n}$ is real if its matrix has only real entries and non-negative if its matrix contains only real and non-negative entries.

Theorem 6.2

([14]) The group of real linear automorphisms of $L_{2,4}$, up to positive scale, is of order 23040 and is isomorphic to the Weyl group $D_6$. The subset of this group that are represented by matrices consisting of non-negative elements is a subgroup of order 24 and acts by relabeling the vertices of $K_4$.

6.2 Small Images

Proposition 5.15 above is a theorem about edge measurement ensembles where over all configurations is low dimensional. Here we need a similar proposition that applies to linear maps acting on $L_{d,n}$. This will also require some non-trivial analysis of linear maps acting on $L_{d,n}$ which we relegate to the companion paper [14].

Let $d \ge 1$. Recall that $D:= \left( {\begin{array}{c}d+2\\ 2\end{array}}\right)$. In this section, $\textbf{E}$ will be a $D\times N$ matrix of rank r where r is some number at most D. We will also identify the symbol $\textbf{E}$ with the linear map from $\mathbb {C}^N$ to $\mathbb {C}^D$ that it induces. We will restrict this map to its action on ${L_{d,n}}$. Our goal is to study these restricted linear maps where the dimension of is strictly less than r. In particular, this will occur when $\textbf{E}({L_{d,n}}) = L_{d,d+2}$.

Definition 6.3

We say that $\textbf{E}$ has $K_{d+2}$ support if it depends only on measurements supported over the D edges corresponding to a $K_{d+2}$ subgraph of $K_n$. Specifically, all the columns of the matrix $\textbf{E}$ are zero, except for at most D of them, and these non-zero columns index edges contained within a single $K_{d+2}$.

The following is proven in [14].

Theorem 6.4

Let $d\ge 1$ and $n\ge d+2$. Let $\textbf{E}$ be a $D\times N$ matrix with rank r. Suppose that $\textbf{E}(L_{d,n})$, a constructible set, is not of dimension r. Then $r=D$ and $\textbf{E}$ has $K_{d+2}$ support.

Remark 6.5

Theorem 6.4 does not hold when ${L_{d,n}}$ is replaced by $M_{d,n}$. The linear automorphism group of ${{\mathcal {S}}}^{n-1}_d$ arises from all the maps of the form

$$\begin{aligned} \textbf{S}\mapsto \textbf{A}^t\textbf{S}\textbf{A}\end{aligned}$$

with $\textbf{A}$ an invertible $(n-1)\times (n-1)$ matrix.

Correspondingly, there are linear automorphisms of $M_{d,n}$ arising from matrices $\textbf{A}$ that have dense support. Thus, even if some $\textbf{E}$ has $K_{d+2}$ support the matrix $\textbf{E}\textbf{A}$ would not, and it could still have a small-dimensional image.

If, in our motivating application, we observed sums of squared edge lengths, we would have no hope to recover $\textbf{p}$ without some combinatorial information.

6.3 Consistent $K_{d+2}$

Now we can use these ingredients to upgrade Proposition 5.16. We want to show that: If we take D values from our data set of path measurements, and they are consistent with the D edge lengths of a $K_{d+2}$ in $\mathbb R^d$, then in fact they do arise, up to scale, in this way. Likewise, in the loop setting, if they “look like” an appropriate canonical set of D loops, then in fact they do arise, up to scale, in this way.

First we generalize our notion of measurement ensembles from Definition 3.4.

Definition 6.6

A length functional $\alpha$ is a linear mapping from ${L_{d,n}}$ to $\mathbb {C}$. We write its application to $\textbf{l}\in {L_{d,n}}$ as $\langle \alpha ,\textbf{l}\rangle$. In coordinates, it has the form $\sum _{ij} \alpha ^{ij} l_{ij}$, with $\alpha ^{ij} \in \mathbb {C}$. When $\textbf{p}$ is a real configuration, and thus $l(\textbf{p})$ is well defined, then we also define $\langle \alpha , \textbf{p}\rangle := \langle \alpha , l(\textbf{p})\rangle$. Similarly, we can define a functional measurement ensemble $\pmb {\gamma }$. Then we define $\langle \pmb {\gamma }, \textbf{l}\rangle$ and $\langle \pmb {\gamma }, \textbf{p}\rangle$ to be the sequence that arises from the application of the measurement ensemble $\pmb {\gamma }$ to $\textbf{l}$ and $l(\textbf{p})$ respectively.

We can apply to a length functional the adjectives: rational, non-negative, integer or whole (non-negative integer) if all of its coordinates have these properties. We say that an integer or whole length functional is b-bounded if all of its coordinates have magnitudes no greater than b.

An edge multiset naturally gives rise to a unique whole length functional. Analogously, an edge multiset measurement ensemble gives rise to a unique whole length ensemble matrix.

Theorem 6.7

Let $d \ge 2$. Let $\textbf{p}$ be a n-point configuration in $\mathbb R^d$ such that $l(\textbf{p})$ is generic in ${L_{d,n}}$. Suppose there is a sequence of D non-negative rational functionals $\gamma _i$ such that $w_i=\langle \gamma _i,\textbf{p}\rangle$ form a (necessarily non-negative) vector $\textbf{w}:=(w_1,\dots ,w_D)$ that has rational rank D and is in $L_{d,d+2}$.

Then there must be a $(d+2)$-point subconfiguration $\textbf{p}_T$ of $\textbf{p}$ such that $\langle \pmb {\gamma }, \textbf{p}\rangle = \textbf{w}= s\cdot l(\textbf{p}_T)$, where s is a positive scale factor.

Proof

We can use the D functionals, $\gamma _i$, as the rows of a matrix $\textbf{E}$. We identify this matrix with the linear map from $\mathbb {C}^N$ to $\mathbb {C}^D$ that it induces. This matrix $\textbf{E}$ maps $l(\textbf{p})$ to $\textbf{w}$, which we have assumed to be in $L_{d,d+2}$. Since $d\ge 2$, then from Theorem 4.10, $L_{d,n}$ is irreducible.

From Theorem 2.2 we see that $\textbf{E}({L_{d,n}}) \subseteq L_{d,d+2}$.

From Lemma B.3 and the assumed rational rank of $\textbf{w}$, the rank of $\textbf{E}$ must be D. Since of $\textbf{E}({L_{d,n}})$ is not D-dimensional, then from Theorem 6.4, $\textbf{E}$ is $K_{d+2}$ supported.

Let $\pi _{{K}}$ be the edge map where K comprises the edges of this $K_{d+2}$, and where K is ordered such that $\pi _{{K}}(L_{d,n}) = L_{d,d+2}$. Let $\textbf{K}$ be the matrix representing $\pi _{K}$. Then $\textbf{E}$ can be written in the form $\textbf{A}\textbf{K}$ where $\textbf{A}$ is a $D \times D$ non-singular and non-negative rational matrix.

We have $\textbf{A}(L_{d,d+2}) = \textbf{A}(\pi _{{K}}(L_{d,n})) = \textbf{E}(L_{d,n}) \subseteq L_{d,d+2}$. Thus, from Theorem 2.1, $\textbf{A}$ must be the matrix of a real non-negative linear automorphism of $L_{d,d+2}$. From Theorems 6.1 (for $d \ge 3$) and 6.2 (for $d=2$) $\textbf{A}$ arises from a permutation on $d+2$ vertices and a positive global scale. As $\textbf{E}=\textbf{A}\textbf{K}$ for such an $\textbf{A}$, there must exist an (ordered) $(d+2)$-point subconfiguration $\textbf{p}_T$ of $\textbf{p}$, such that $\langle \pmb {\gamma }, \textbf{p}\rangle = \textbf{w}= s\cdot l(\textbf{p}_T)$. $\square$

Theorem 6.7$'$, in Sect. 6.4 below, is the generalization to the case of loop ensembles.

Remark 6.8

If the $\gamma _i$ are whole valued, then s must be an integer, greater than or equal to 1 for any such $\textbf{p}_T$. This is because, in the proof above, the matrices $\textbf{E}$ and $\textbf{A}$ will be integer valued.

Remark 6.9

The rational rank D hypothesis is essential as the following example in dimension 2 shows. Let $\gamma _i$ be any functional, and measure using the ensemble $(3\gamma _i, 4\gamma _i, 5\gamma _i, 5\gamma _i, 4\gamma _i, 3\gamma _i)$. These measurement values (with rational rank 1) correspond to a $K_4$ made by gluing “345 triangles” together, no matter what $\textbf{p}$ is. In fact, using an arithmetic construction from [1], we can even make infinitely many non-congruent rational rank 1 measurement sets that have no repeated measurement values or 3 collinear points.

When we are proving “global rigidity” results in Sect. 6.5, the assumed trilateration sequence automatically gives rational rank D. On the other hand, a reconstruction algorithm (see Sect. 7) based on Theorem 6.7 will have to find the trilateration sequence as it goes. The examples here show that such an algorithm has to test rational rank.

6.4 Loop Setting

We also wish to alter Theorem 6.7 so that it can be applied to the loop setting. In particular, instead of looking for measurements of D edges of a $K_{d+2}$ we will look for D canonical measurements over a $K_{d+2}$. Indeed, we consider two such canonical measurements: one to identify a $K_{d+2}$ ex-nihilo, and one to identify a $K_{d+2}$ using a known $(d+1)$-point subconfiguration along with $d+1$ additional measurements.

Definition 6.10

Given a single $K_{d+2}$, with ordered vertices and edges, we can describe the D measurements described in Definition 3.8 using a fixed canonical $D\times D$ matrix $\textbf{N}^d_1$. Each row represents the edge multiplicities of one measurement loop. For notational convenience, we order the rows of this matrix so that each of the first C rows is supported only over the C edges of the first $d+1$ points.

In 2 dimensions, we associate the columns of this matrix with the following edge ordering: $\{1,2\}, \{1,3\}, \{2,3\}, \{1,4\}, \{2,4\}, \{3,4\}$. This then gives us the following tetrahedral measurement matrix that measures three pings and three triangles

$$\begin{aligned} \textbf{N}^2_1:= \begin{pmatrix} 2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 1&{}\quad 1&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 2&{}\quad 0&{}\quad 0 \\ 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

See Fig. 2 (bottom left) for the 2-dimensional case.

Given an initial $K_{d+1}$, with ordered vertices and edges, we can describe an ordered D measurements describing the trilateration of an additional vertex off of the first $d+1$ vertices, as defined in Definition 3.9, using fixed a $D\times D$ matrix $\textbf{N}^d_2$. The first C rows measure the edges of the initial $K_{d+1}$ subconfiguration, and the remaining $d+1$ rows measure the appropriate pings and triangles.

In 2 dimensions, this gives us the following trilateration measurement matrix that measures three edges, one ping, and two triangles

$$\begin{aligned} \textbf{N}^2_2:= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 2&{}\quad 0&{}\quad 0 \\ 1&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

See Fig. 2 (bottom right) for the 2-dimensional case.

Theorem 6.7$'$ With these definitions in place, we can alter the condition in Theorem 6.7that $\textbf{w}$ describes a point of $L_{d,d+2}$, to the condition that $\textbf{w}$ describes a of point of $\textbf{N}^d_i(L_{d,d+2})$. And we can generalize the conclusion to read: $\langle \pmb {\gamma }, \textbf{p}\rangle = \textbf{w}= s\cdot \textbf{N}^d_i(l(\textbf{p}_T))$.

Proof

We follow the structure of the proof of Theorem 6.7. From Lemma A.7, $\textbf{N}^d_i(L_{d,d+2})$ is an irreducible variety. Our loop assumptions give us $\textbf{w}= \textbf{E}(\textbf{l}) \in \textbf{N}^d_i(L_{d,d+2})$ and thus from genericity of $\textbf{l}$, $\textbf{E}(L_{d,n})\subseteq \textbf{N}^d_i(L_{d,d+2})$.

As above, $\textbf{E}$ has $K_{d+2}$ support. Let $\pi _{{K}}$ be the edge map where K comprises the edges of this $K_{d+2}$, and where K is ordered such that $\pi _{{K}}(L_{d,n}) = L_{d,d+2}$. Let $\textbf{K}$ be the matrix representing $\pi _{K}$. The matrix $\textbf{E}$ can be written in the form $\textbf{B}\textbf{K}$ where $\textbf{B}$ is a $D \times D$ non-singular and non-negative rational matrix.

We have $\textbf{B}(L_{d,d+2}) = \textbf{B}(\pi _{{K}}(L_{d,n})) = \textbf{E}(L_{d,n}) \subseteq \textbf{N}^d_i(L_{d,d+2})$. It follows from Theorem 2.1 that $\textbf{A}:=(\textbf{N}^d_i)^{-1}\textbf{B}$ is the matrix of a linear automorphism of $L_{d,d+2}$. Thus we are left with determining the linear automorphisms with matrices $\textbf{A}$ such that $\textbf{N}^d_i\textbf{A}=\textbf{B}$ is non-negative.

For $d\ge 3$, from Theorem 6.1, we see that this only occurs when $\textbf{A}$ is a positive scale of a vertex relabeling. For $d=2$, we need to explicitly do a non-negativity check on our $\textbf{N}^2_i\textbf{A}$ over all linear automorphism matrices $\textbf{A}$ of $L_{2,4}$, as characterized in Theorem 6.2 and described in detail in [14]. This only requires checking 23040 matrices, for both $\textbf{N}^2_1$ and $\textbf{N}^2_2$ and has been done in the Magma computer algebra system [14]. In both cases, non-negativity only arises for $\textbf{A}$ that are positive scales of a vertex relabeling.

Thus $\textbf{E}$ is of the form $\textbf{N}^d_i\textbf{A}\textbf{K}$ for such an $\textbf{A}$, and the result follows. $\square$

6.5 Trilateration

Now we can upgrade our results in Sect. 5.4 to prove our main theorems.

Lemma 6.11

Let $d\ge 2$ and let $\textbf{p}$ and $\textbf{q}$ be configurations of n and $n'$ points respectively, so that $l(\textbf{p})$ is generic in $L_{d,n}$. We also suppose that no two points in $\textbf{q}$ are coincident. Let $\pmb {\alpha }$ be an edge multiset measurement ensemble and $\pmb {\beta }$ be a path or loop ensemble such that $\langle \pmb {\alpha }, \textbf{p}\rangle = \langle \pmb {\beta }, \textbf{q}\rangle$.

Suppose that we have two “already visited” subconfigurations $\textbf{p}_V$ and $\textbf{q}_{V'}$ with $\textbf{p}_V =\textbf{q}_{V'}$.

Suppose we can find $\pmb {\delta }$, a subset of $d+1$ paths or loops in $\pmb {\beta }$, that can used to nicely trilaterate some unvisited vertex $\textbf{q}_{i'}\in \textbf{q}_{\bar{V'}}$ over some visited ${d+1}$ point subconfiguration $\textbf{q}_{R'}$ of $\textbf{q}_{V'}$.

Then we can find an unvisited $\textbf{p}_{i}\in \textbf{p}_{\bar{V}}$ such that the two subconfigurations $\textbf{p}_{V\cup \{i\}}$ and $\textbf{q}_{V'\cup \{i'\}}$ are equal.

Proof

Let $\textbf{q}_{T'}$ be a subconfiguration consisting of, in some order, all the points of $\textbf{q}_{R'}$ along with $\textbf{q}_{i'}$. Let $\textbf{w}:= \textbf{N}(l(\textbf{q}_{T'}))$, with $\textbf{N}=\textbf{I}$ in the path setting and $\textbf{N}=\textbf{N}^d_2$ in the loop setting. We have $\textbf{w}\in L_{d,d+2}$. By assumption, $\textbf{w}$ has rational rank D.

We have $\langle \pmb {\alpha }, \textbf{p}\rangle = \langle \pmb {\beta }, \textbf{q}\rangle$ and $\textbf{p}_V = \textbf{q}_{V'}$. Thus, the assumption that $\pmb {\delta } \subseteq \pmb {\beta }$ nicely trilaterates an unvisited vertex in $\textbf{q}$ implies that we can use $\pmb {\alpha }$ to find a measurement ensemble $\pmb {\gamma }$ of D measurements so that $\langle \pmb {\gamma }, \textbf{p}\rangle = \textbf{w}$. The ensemble $\pmb {\gamma }$ plays the role of E in the proof of Lemma 5.25, and it is constructed in a similar way: from $d+1$ measurements in $\pmb {\alpha }$ and C distances imputed from a set of $d+1$ points in $\textbf{p}_V$.

Theorem 6.7 in the path setting (or Theorem 6.7$'$ in the loop setting) can be applied using $\textbf{p}$ together with this $\pmb {\gamma }$ and $\textbf{w}$. This guarantees a $(d+2)$-point subconfiguration $\textbf{p}_{T}$ of $\textbf{p}$ such that $\textbf{w}= t \cdot \textbf{N}(l(\textbf{p}_{T}))$, with $\textbf{N}=\textbf{I}$ in the path setting and $\textbf{N}=\textbf{N}^d_2$ in the loop setting. From Lemma 5.2, we conclude that $\textbf{p}_T$ and $\textbf{q}_{T'}$ are related by a similarity.

Since $\textbf{q}_{R'}$ is a subconfiguration of $\textbf{q}_{T'}$, $\textbf{q}_{R'}$ must be similar to the associated subconfiguration of $\textbf{p}_{T}$, which we may call $\textbf{p}_{R_0}$. From genericity of $l(\textbf{p})$ in $L_{d,n}$ and Lemma 5.23, $\textbf{q}_{R'}$ is similar to no other subconfiguration of $\textbf{p}$. Meanwhile, $\textbf{q}_{R'}$ is a subconfiguration of $\textbf{q}_{V'}$ and thus also equal to some subconfiguration $\textbf{p}_{R}$ of $\textbf{p}_{V}$. Thus $\textbf{p}_R$, $\textbf{p}_{R_0}$ and $\textbf{q}_{R'}$ must all be equal. Since the similarity $\sigma$ that maps $\textbf{q}_{T'}$ to $\textbf{p}_{T}$ fixes the $d+1$ points of $\textbf{q}_{R'}$, $\sigma$ must be the identity and $\textbf{p}_T=\textbf{q}_{T'}$.

Let $\textbf{p}_{i}$ be the “new” point in $\textbf{p}_{T}\setminus \textbf{p}_{R}$, which must be equal to $\textbf{q}_{i'}$. If $\textbf{p}_{i}$ was already visited in $\textbf{p}_{V}$, then the same position would have already been visited by some point in $\textbf{q}_{V'}$. This together with the fact that no points are coincident in $\textbf{q}$ would contradict the assumption that $\textbf{q}_{i'}\in \textbf{q}_{\bar{V'}}$. Thus $\textbf{p}_{V\cup \{i\}}=\textbf{q}_{V'\cup \{i'\}}$. $\square$

Applying the above iteratively yields the following:

Lemma 6.12

Let $d \ge 2$. Let $\textbf{p}$ be a configuration of n points such that $l(\textbf{p})$ is generic in $L_{d,n}$. Let $\pmb {\alpha }$ be an edge multiset measurement ensemble. Let $\textbf{v}:=\langle \pmb {\alpha },\textbf{p}\rangle$.

Suppose that there is a configuration $\textbf{q}$ of $n'\ge d+2$ points with no two points in $\textbf{q}$ coincident. And suppose that $\pmb {\beta }$ is a path (resp. loop) measurement ensemble that allows for trilateration, and such that $\pmb {\beta }$ trilaterates $\textbf{q}$ nicely, and such that $\langle \pmb {\beta }, \textbf{q}\rangle$ also equals $\textbf{v}$.

Then, there is a sequence of indices S so that, up to congruence, $s\cdot \textbf{p}_{S} = \textbf{q}$, with s an integer $\ge 1$. Moreover, the vertices appearing in S are exactly those that are endpoints of edges in the support of $\pmb {\alpha }$. Under the vertex relabeling implicit in S, we have $\pmb {\alpha } = s\cdot \pmb {\beta }$.

Proof

For the base case, the nice trilateration assumed in $\pmb {\beta }$ guarantees a $K_{d+2}$ contained in $\pmb {\beta }$ over a $(d+2)$-point subconfiguration $\textbf{q}_{T'}$ of $\textbf{q}$. Define $\textbf{w}:= \textbf{N}(l(\textbf{q}_{T'}))$ with $\textbf{N}=\textbf{I}$ in the path setting and $\textbf{N}=\textbf{N}^d_1$ in the loop setting. From the niceness assumption, we can find such a $K_{d+1}$ so that these $w_i$ have rational rank D. We have $\textbf{w}\in \textbf{N}(L_{d,d+2})$.

Using the fact that $\langle \pmb {\alpha }, \textbf{p}\rangle = \langle \pmb {\beta }, \textbf{q}\rangle$ we can apply Theorem 6.7 in the path setting, or Theorem 6.7$'$ in the loop setting, to this $\textbf{w}$ and $\textbf{p}$ and an appropriate subensemble $\pmb {\gamma }$ of $\pmb {\alpha }$. We conclude that there is a $(d+2)$-point subconfiguration $\textbf{p}_{T}$ of $\textbf{p}$ such that $\textbf{w}= s \cdot \textbf{N}(l(\textbf{p}_{T}))$, with $\textbf{N}=\textbf{I}$ in the path setting and $\textbf{N}=\textbf{N}^d_1$ in the loop setting. Here $s \ge 1$ is an integer scale factor (see Remark 6.8). Also, from Lemma 5.2, up to a similarity, we have $\textbf{p}_T = \textbf{q}_{T'}$.

In order to use the simpler terminology of equality instead of similarity going forward, we will apply the similarity to $\textbf{p}$ and replace each functional $\alpha$ in $\pmb {\alpha }$ by $(1/s)\alpha$. Then, to proceed inductively, assume that we have two “visited” subconfigurations such that $\textbf{p}_{V}=\textbf{q}_{V'}$. Initially $V = T$ and $V' = T'$. With this setup, we may now follow the trilateration of $\textbf{q}$, iteratively applying Lemma 6.11 until we have visited all of $\textbf{q}$. At the end of the process, $\textbf{p}_V = \textbf{q}_{V'}$ with $\textbf{q}_{V'}$ a reordering of $\textbf{q}$. Inverting this ordering, we have $\textbf{q}=\textbf{p}_{S}$, where S is an ordering of the visited points in $\textbf{p}$.

Since $l(\textbf{p})$ is generic in $L_{d,n}$, from Theorem B.1, no two distinct functionals can give the same measurement. Since $\textbf{q}$ is a subconfiguration of our generic $\textbf{p}$, then no two distinct functionals can give the same measurement. This means there is a unique way for $\textbf{v}$ to arise from $\textbf{p}$ and a unique way for $\textbf{v}$ to arise from $\textbf{q}$. Hence, after vertex relabeling from S, we have $\pmb {\alpha }= \pmb {\beta }$. Since the vertices with endpoints in the support of $\pmb {\beta }$ correspond exactly to the points of $\textbf{q}$, then the vertices that are endpoints of the edges in the support of $\pmb {\alpha }$ are exactly S, as in the statement. $\square$

Now we can prove one of our main theorems.

Proof of Theorem 3.17

First we remove from $\textbf{v}$ the measurements which do not appear in $\textbf{v}^-$. We also remove the associated edge multisets from $\pmb {\alpha }$. Since $\textbf{p}$ is generic, then $l(\textbf{p})$ is generic in $L_{d,n}$ from Theorem 4.10. Then we simply apply Lemma 6.12. $\square$

Next we want to use a genericity assumption on $\textbf{p}$ to automatically obtain genericity for $l(\textbf{q})$ in $L_{d,n}$ under the assumption that $n'=n$.

Definition 6.13

Let $n \ge d+1$. A path or loop measurement ensemble is infinitesimally rigid in d dimensions if, starting at some (equiv. any) generic real configuration $\textbf{p}$, there are no differential motions of $\textbf{p}$ that preserve all of the measurement values, except for differential congruences.

Remark 6.14

We defined infinitesimal rigidity of an edge measurement ensemble in terms of a generic real of complex configuration $\textbf{p}$. For paths and loops, since we are using unsquared measurements, we restrict our attention to real configurations, so that the measurement map can be defined.

Lemma 6.15

In dimension $d\ge 2$, let $\textbf{p}$ and $\textbf{q}$ be two configurations with the same number of points $n \ge d+1$. Suppose that $\pmb {\alpha }$ is a path or loop measurement ensemble that is infinitesimally rigid in d dimensions. Suppose that $\pmb {\beta }$ is an edge multiset measurement ensemble. And suppose that $\textbf{v}:=\langle \pmb {\alpha },\textbf{p}\rangle = \langle \pmb {\beta },\textbf{q}\rangle$.

If $\textbf{p}$ is a generic configuration, then $l(\textbf{q})$ is generic in $L_{d,n}$.

Proof

Since $d\ge 2$, we know that $L_{d,n}$ is irreducible (Theorem 4.10), and so too is any linear image of it (see Definition A.3). We define $L_{d,\pmb {\alpha }}$ and $L_{d,\pmb {\beta }}$ to be the Zariski closures of s of $L_{d,n}$ under the linear maps corresponding to $\pmb {\alpha }$ and $\pmb {\beta }$, respectively. They are both defined over ${\mathbb Q}$. We define the measurement map $l_{\pmb {\alpha }}(\textbf{p})$ acting on (real) configuration space to be the map that takes $\textbf{p}$ to $\langle {\pmb {\alpha }}, l(\textbf{p})\rangle$.

If $\pmb {\alpha }$ is infinitesimally rigid then, as in the proof of Proposition 5.12, we see that the real dimension of the image s of $l_{\pmb {\alpha }}(\textbf{p})$ over all real configurations is $dn-C$ (constant rank theorem). The set s is semi-algebraic (using quantifier elimination). Let V be the (complex) Zariski closure of s. From Lemma A.12, the complex dimension of V equals the real dimension of s. Since we have $s\subseteq L_{d,\pmb {\alpha }}$ and $L_{d,\pmb {\alpha }}$ is Zariski closed, we have $V \subseteq L_{d,\pmb {\alpha }}$. Using this containment and the fact that $L_{d,\pmb {\alpha }}$ a linear image of $L_{d,n}$ we obtain

$$\begin{aligned} dn - C \le \dim L_{d,\pmb {\alpha }} \le \dim L_{d,n} = dn - C, \end{aligned}$$

which shows that equality holds throughout. Using the fact that $L_{d,\pmb {\beta }}$ a linear image of $L_{d,n}$ we obtain $\dim L_{d,\pmb {\beta }} \le dn - C$.

The proof then follows like that of Lemma 5.29. $\square$

And now we can prove our other main theorem.

Proof of Theorem 3.14

By assumption, $\pmb {\alpha }$ allows for trilateration. A path or loop measurement ensemble that allows for trilateration is always infinitesimally rigid. (The ability to trilaterate makes a generic real $\textbf{p}$ uniquely determined (globally rigid) from its labelled measurements. Thus, one cannot continuously change $\textbf{p}$ while keeping the measurements fixed (local rigidity). If the ensemble was not infinitesimally rigid at a generic $\textbf{p}$, then using the proof from [2], it could not be locally rigid.) So from Lemma 6.15 we know that $l(\textbf{q})$ is generic in $L_{d,n}$. We next argue that this trilateration must be nice: During a trilateration step, the D functionals are linearly independent. So from Lemma B.4 and the genericity of $\textbf{p}$, the D measurement values must have rational rank D.

So we can now apply Lemma 6.12 with the roles of $\textbf{p}$ and $\textbf{q}$ reversed as well as the roles of $\pmb {\alpha }$ and $\pmb {\beta }$. $\square$

7 Reconstruction Algorithm

A straightforward iterative application of Theorem 3.17 leads to a real-computation algorithm for reconstructing an unknown generic configuration $\textbf{p}$ from an unlabeled path or loop measurement ensemble that allows for trilateration. The algorithm performs a brute force combinatorial search for a trilateration sequence, testing validity along the way using rational rank tests and Cayley–Menger determinants. This generalizes the TRIBOND algorithm from [12]. The TRIBOND algorithm only works on edge-length ensembles, while ours works in the path and loop setting.

Theorem 3.17 tells us that, assuming genericity of $\textbf{p}$, we can apply trilateration greedily without backtracking. At each step, if we can interpret some of our measurement data as being consistent with a nicely trilaterated point set $\textbf{q}$, then this is a certificate of correctness for that step, up to scale. Meanwhile, if we also assume that our data arose from an ensemble that allows for trilateration (which must be nice by Lemma B.4), then this means that by searching, we will be able to find such a certifiably nicely trilaterated configuration $\textbf{q}$, and with the same number of points as $\textbf{p}$. Moreover (see below), we can also determine the correct scale.

For the path (resp. loop) algorithm we have the following specification.

Input: dimension, bounce bound, and real-valued data set, $(d, b, \textbf{v})$.

Assumption: Data set $\textbf{v}$ arises from some generic configuration $\textbf{p}$ of n points (for some n) in $\mathbb R^d$, under some b-bounded path (resp. loop) ensemble that allows for trilateration.

Output: A configuration $\textbf{q}$, where $\textbf{q}$ is related to $\textbf{p}$ through a vertex relabeling and a Euclidean congruence.

Theorem 7.1

There is an algorithm in a real computational model that solves the generic path or loop reconstruction problem. Its running time is polynomial in $|\textbf{v}|$ and b, and exponential in d.

The algorithm first exhaustively searches for all ordered D-tuples of $\textbf{v}$ that describe $K_{d+2}$ subconfigurations of $\textbf{p}$. Each of these is treated as a “candidate base”: We do not know at first which of these candidates will ultimately form the base of a complete trilateration sequence. Each candidate base is then grown into an expanding sequence of “candidate subconfigurations" by finding new points that connect to an existing candidate subconfiguration through a trilaterating set of $d+1$ edges or loops.

To expand a candidate subconfiguration by one point, we search exhaustively over all subsets of $d+1$ points in the configuration and subsets of $d+1$-tuples of values in $\textbf{v}$ to find a valid trilateration step. Besides the Cayley–Menger determinant test, a valid step is also required to have the appropriate rational rank. If the values of $\textbf{w}$ are not rationally independent, Lemma B.4 implies that there is a rational relation on its underlying functionals. In the b-bounded setting, Lemma B.3 then implies that the coefficients describing this relation are bounded integers. This bound is polynomial in b. Thus, we can simply do an exhaustive search for possible integer relations satisfying this bound.

If a new point is found, we extend the candidate subconfiguration and we continue searching exhaustively over the extended configuration. If an already-localized point is found, we ignore it and continue to search for a trilateration step that produces a new point. If, after trying all the possibilities, we do not find a new point, the candidate subconfiguration is maximal, and we stop searching for this subconfiguration. The whole algorithm stops when no candidate subconfiguration can be expanded any further.

Theorem 6.7 only gives us a $K_{d+2}$ configuration up to a scale. Fortunately, as we grow a candidate base, as in the proof of Lemma 6.12, we will only be able to do so using the same shared scale. Still, since our algorithm uses a number of candidate bases, it may be the case that we reconstruct various subsets of $\textbf{p}$ at various scales. In more detail, there may be a subensemble of $\pmb {\alpha }$ that is actually of the form of a trilateration sequence, but with each path (resp. loop) measured s times per measurement. During the trilateration, we treat these as if they were unscaled, which is effectively equivalent to scaling the length of each underlying edge by s. This results in the reconstruction of a candidate configuration $s\cdot \textbf{p}$ that is a scaled up version of the true configuration.

The existence of at least one correctly scaled reconstruction is guaranteed by the trilateration assumption on the underlying $\pmb {\alpha }$. Thus, at the end of the trilateration process, we identify the true configuration as the reconstructed subset with the smallest scale among all configurations with the same maximal number of points. This configuration, $\textbf{q}$, will be equal (up to vertex relabeling and congruence) to the one true configuration $\textbf{p}$.

7.1 Ideas for Efficiency

There are a few interesting ideas for reducing the cost of the the rational rank test.

First of all, testing for rational rank can be done much more efficiently using the basis reduction algorithm for integer relation testing [13, 18]. This algorithm works under a real computational model that includes a constant-time floor operation. Roughly speaking, given a vector $\textbf{w}$ of D real numbers and an integer bound B, the integer relation testing algorithm will either report that there is no “small” integer linear relation on $\textbf{w}$ having integer coefficients with vector norm less than B, or it will provide a “medium-sized” integer relation with vector norm smaller than $2^{D/2} B$. If the algorithm reports that no small relation exists, then we can conclude that our $\textbf{w}$ has the necessary rational rank. If the algorithm returns a medium sized relation we know that we do not have the necessary rational rank. (In fact, we know from Lemma B.3, that there must also be a small integer relation.) For fixed d, this algorithm has running time $O(\log (B))$, which for us is $O(\log (b))$.

Secondly, in the two dimensional setting, we have shown in [14] that the only linear subspaces of dimension 3 or higher that are contained in $L_{2,4}$ are those making up its singular locus. When a linear map has rank less than 6, then, from Theorem 6.4, of $L_{2,n}$ will be a Zariski open subset of a linear subspace of $\mathbb {C}^6$. Under the genericity assumption on $\textbf{p}$, that space will be contained in $L_{2,4}$. Thus, if we know or can verify that a non-singular point $\textbf{w}$ of $L_{2,4}$ has rational rank at least 3, then it must have rational rank 6. This condition can be verified on any three values of $\textbf{w}$.

Finally, the rational rank test can be completely omitted under certain assumptions about the measurement process of the generic configuration $\textbf{p}$. For example, in the loop setting with dimension 3, suppose we assume that $\pmb {\alpha }$ consists only of pings and triangles, with each passing through $\textbf{p}_1$. This is not an unreasonable assumption for our signal processing scenario described in Sect. 1. Under this assumption, it can be shown that if $\textbf{w}$ consists of 10 distinct values, then it has rational rank 10, and thus no explicit test is needed.

7.2 Practical Application

As is often the case in computational geometry, if we implement an algorithm that relies on exact real computation with a digital computer, we obtain an approximation that does not come with the same guarantees. We are currently experimenting with such methods in ongoing research, and there are recent experiments by others [22] in the loop setting with dimension 3 and with $\pmb {\alpha }$ comprising pings and triangles through $\textbf{p}_1$. But to date, it remains unclear to us what conditions are required for a numerical implementation to succeed with approximate loop lengths.

In the unlabelled edge-only setting, the greedy TRIBOND algorithm has been extended to the more robust (but expensive) LIGA algorithm [12, 19]. LIGA ranks its reconstruction candidates to minimize error. Moreover, LIGA allows for backtracking during the reconstruction process. For non-generic or approximate input, incorrect early decisions can often be detected as erroneous using subsequent data; they can then be undone. Such ideas could prove useful in the path or loop setting as well.

Appendices

Appendix A: Algebraic Geometry Preliminaries

We summarize the needed definitions and facts about complex algebraic varieties. For more see [17].

In this section, N and D will represent arbitrary numbers.

Definition A.1

A (complex embedded affine) variety (or algebraic set), V, is a (not necessarily strict) subset of $\mathbb {C}^N$, for some N, that is defined by the simultaneous vanishing of a finite set of polynomial equations with coefficients in $\mathbb {C}$ in the variables $x_1, x_2, \ldots , x_N$ which are associated with the coordinate axes of $\mathbb {C}^N$. We say that V is defined over ${\mathbb Q}$ if it can be defined by polynomials with coefficients in ${\mathbb Q}$.

A finite union of varieties is a variety. An arbitrary intersection of varieties is a variety.

A variety V is reducible if it is the proper union of two varieties $V_1$ and $V_2$. (Proper means that $V_1$ is not contained in $V_2$ and vice-versa.) Otherwise (assuming it is non-empty) it is called irreducible. A non-empty variety has a unique decomposition as a finite proper union of its maximal irreducible subvarieties called components. (Maximal means that a component cannot be contained in a larger irreducible subvariety of V).

A variety V has a well-defined (maximal) dimension ${{\,\textrm{Dim}\,}}(V)$, which will agree with the largest D for which there is an open subset of V, in the standard topology, that is a D-dimensional complex submanifold of $\mathbb {C}^N$.

Any strict subvariety W of an irreducible variety V must be of strictly lower dimension.

The local dimension ${{\,\textrm{Dim}\,}}_\textbf{l}(V)$ at a point $\textbf{l}$ in a variety V is the dimension of the highest-dimensional irreducible component of V that contains $\textbf{l}$. A point $\textbf{l}$ is called smooth in a variety V if the dimension of the Zariski tangent space (see [17]) equals ${{\,\textrm{Dim}\,}}_\textbf{l}(V)$. Otherwise $\textbf{l}$ is called singular in V. The locus of singular points of V is denoted ${{\,\textrm{Sing}\,}}(V)$. A smooth point has an open neighborhood in  V, in the standard topology, that is a ${{\,\textrm{Dim}\,}}_\textbf{l}(V)$-dimensional complex submanifold of $\mathbb {C}^N$.

Remark A.2

We will say that an ideal in $L[X_1,\ldots ,X_N]$ is defined over a field $K \subset L$ if it can be generated by polynomials with coefficients in K.

In the present setting, there is no difference between set-theoretic and ideal-theoretic notions of the field of definition of a variety. Suppose that V is cut out as $V(J')$ for some ideal $J'$ of $\mathbb {C}[X_1,\ldots ,X_N]$ that is defined over ${\mathbb Q}$. Since $\mathbb {C}$ is algebraically closed, we know that $J:=I(V)=\sqrt{J'}$ (Nullstellensatz). Meanwhile, since ${\mathbb Q}$ is a perfect field, the radical ideal $\sqrt{J'}$ is also defined over ${\mathbb Q}$ (see [26, tag 030V]).

Definition A.3

A constructible set S is a set that can be defined using a finite number of Boolean set operations over a finite number of varieties. We say that S is defined over ${\mathbb Q}$ if the varieties can be defined by polynomials with coefficients in ${\mathbb Q}$.

The Zariski closure of S is the smallest variety V containing it. The set S has the same dimension as its Zariski closure V. If S is defined over ${\mathbb Q}$, then so too is V (see Theorem A.8 below).

of a variety V of dimension D under a polynomial map m is a constructible set S of dimension at most D. If V is irreducible, then so too is the Zariski closure of S. (We say that S is irreducible.) If V and m are defined over ${\mathbb Q}$, then so too is S [3, Theorem 1.22].

Next we define the notion of generic points in a variety. The motivation is that nothing algebraically special (and which is expressible with rational coefficients) is allowed to happen at such points. Thus, any such algebraic property holding at one generic point must hold at all generic points.

Definition A.4

A point in an irreducible variety or constructible set V defined over ${\mathbb Q}$ is called generic if its coordinates do not satisfy any algebraic equation with coefficients in ${\mathbb Q}$ besides those that are satisfied by every point in V.

A generic real point in $\mathbb R^N$ as in Definition 3.12 is also a generic point in $\mathbb {C}^N$, considered as a variety, as in the current definition.

Lemma A.5

Let C and M be irreducible affine varieties, and m be a polynomial map, all defined over ${\mathbb Q}$, such that the Zariski closure of m(C) is equal to M. If there exists a polynomial $\phi$, defined over ${\mathbb Q}$, that does not vanish identically over M but does vanish at $m(\textbf{p})$ for some $\textbf{p}\in C$, then there is a polynomial $\psi$, defined over ${\mathbb Q}$, that does not vanish identically over C but does vanish at $\textbf{p}$.

Thus, if $\textbf{p}\in C$ is generic in C, then $m(\textbf{p})$ is generic in M.

Proof

The polynomial is simply $\psi (\textbf{x}) = \phi (m(\textbf{x}))$. This $\psi$ is clearly defined over ${\mathbb Q}$. The subset of $X \subseteq M$ for which $\phi$ vanishes is proper, by assumption, and a subvariety, by construction. Thus, m(C), cannot be contained in X: Indeed, if it were, then the Zariski closure of m(C) would be a subset of X, and then not all of M. Hence, there is an $\textbf{x}\in C$ so that $\phi (m(\textbf{x}))\ne 0$. Thus $\psi$ is not identically zero over C. $\square$

Lemma A.6

Let L and M be irreducible affine varieties of the same dimension, and s be a polynomial map, all defined over ${\mathbb Q}$, such that the Zariski closure of s(L) equals M. If there exists a polynomial $\psi$, defined over ${\mathbb Q}$, that does not vanish identically over L but does vanish at some $\textbf{l}\in L$, then there is a polynomial $\phi$, defined over ${\mathbb Q}$, that does not vanish identically over M but does vanish at $s(\textbf{l})$.

Thus, if $\textbf{l}\in L$ is not generic in L, then $s(\textbf{l})$ is not generic in M.

Proof

Sketch Since L is irreducible, the vanishing locus of $\psi$ must be of lower dimension. This subvariety must map under s into to a lower-dimensional subvariety of M (defined over ${\mathbb Q}$). This guarantees the existence of an appropriate $\phi$. $\square$

With our notion of generic fixed, we can prove the two principles of Sect. 1.

Lemma A.7

If $\textbf{A}$ is a bijective linear map on $\mathbb {C}^N$, then under $\textbf{A}$ of a variety V is a variety of the same dimension. If V is irreducible, then so too is this image.

Proof

Let $S:= \textbf{A}(V)$. Since $\textbf{A}$ is bijective, then there is also a map $\textbf{A}^{-1}$ acting on $\mathbb {C}^N$, and S must be the inverse image of V under this map. Thus, by pulling back the defining equations of V through this map, we see that S must be a variety.

The dimension follows from the fact that maps cannot raise dimension, and our map is invertible. $\square$

Proof of Theorem 2.2

Suppose $\textbf{E}(V)$ does not lie in W. Then the preimage $\textbf{E}^{-1}(W)$, which is a variety defined over ${\mathbb Q}$, does not contain V, and the inclusion of $\textbf{l}$ in this preimage would render $\textbf{l}$ a non-generic point of V. $\square$

Proof of Theorem 2.1

From Theorem 2.2, $\textbf{A}(V) \subseteq V$. From Lemma A.7, A(V) is an algebraic subvariety of V of the same dimension, which from the assumed irreducibility must be V itself. $\square$

For completeness, we next prove the following theorem. Its proof was suggested by Brian Osserman.

Theorem A.8

Let S be a constructible set defined over ${\mathbb Q}$. Then its Zariski closure is also defined over ${\mathbb Q}$.

The following material is a bit more technical.

Lemma A.9

Let S be a constructible set in $\mathbb {C}^N$ which is defined over ${\overline{\mathbb Q}}$. Let V be the Zariski closure of S. Let J be the ideal of V. Let s be the ${\overline{\mathbb Q}}$ points of S. Let v be the Zariski closure of s in ${\overline{\mathbb Q}}^N$. Let j be the ideal of v. Then $J=j^*$, the complex extension of j.

Proof

As a constructible set, $S = \bigcup _i (U_i \cap Z_i)$ where $U_i$ is Zariski open and $Z_i$ is Zariski closed. After splitting into irreducible components, each $Z_i$ can be assumed to be irreducible. From [26, Tag 038I], each $Z_i$ is still defined over ${\overline{\mathbb Q}}$. We can also assume that $Z_i \subsetneq U_i$ (otherwise, we can just remove this term from the union). Thus we can write $S=\bigcup _i (Z_i-X_i)$ where $Z_i$ and $X_i$ are both Zariski closed, $Z_i$ is irreducible and $Z_i \nsubseteq X_i$. A finite union operation will commute with complex extensions and so henceforth, we can just look at the single component case where $S=Z-X$.

Let I(Z) and I(X) be the associated ideals in $\mathbb {C}[X_1,\ldots ,X_N]$, both defined over ${\overline{\mathbb Q}}$. I(Z) is prime and I(X) is radical. Moreover, by assumption, $I(X) \nsubseteq I(Z)$. Under these assumptions, S is a non-empty, Zariski open subset of an irreducible Z, so it is dense in Z; the Zariski closure V of S will just be Z, with ideal $J=I(Z)$.

Now we restrict S, Z, and X to ${\overline{\mathbb Q}}^N$, where we switch to lower case and write $s=z-x$. Associated with z and x, we have the ideals I(z) and I(x) in ${\overline{\mathbb Q}}[X_1,\ldots ,X_N]$.

Next we show that I(Z) is the complex extension of I(z) (and likewise for I(X)): Since I(Z) is defined over ${\overline{\mathbb Q}}$, we can pick a set of polynomials with coefficients in ${\overline{\mathbb Q}}$ that generate the complex ideal I(Z). These same polynomials define an ideal, m in ${\overline{\mathbb Q}}[X_1,\ldots ,X_N]$. The ideal m is still prime (as we are making the field smaller). Since they share the same generating polynomials, the complex extension of m is I(Z). We now have $z=V(m)$, and since ${\overline{\mathbb Q}}$ is closed, from the Nullstellensatz we have $I(z)=m$, which proves our claim. Moreover z must be irreducible. A similar argument shows that under complex extension, I(x) (which is likewise radical) becomes I(X).

Meanwhile, since for the extensions we have $I(X) \nsubseteq I(Z)$, we must also have $I(x) \nsubseteq I(z)$. This gives us $z \nsubseteq x$. Thus s is a non-empty, open subset of an irreducible z, and so it is dense in z; as above, the Zariski closure v of s will just be z, with ideal $j=I(z)$. Since I(Z) is the complex extension of I(z), we see that J is the complex extension of j. $\square$

Lemma A.10

Let s be a set of points in ${\overline{\mathbb Q}}^N$ which is invariant under the Galois group ${\text {Aut}}({\overline{\mathbb Q}}/{\mathbb Q})$. Then the Zariski closure v of s in ${\overline{\mathbb Q}}^N$ is defined over ${\mathbb Q}$.

Proof

Suppose that $f_1,\ldots ,f_n$ cut out v. For each i, consider all the Galois conjugates of $f_i$. Each $f_i$ has finitely many coefficients, and each of them lies in a finite-degree extension of ${\mathbb Q}$. Hence each of the $f_i$ has a finite Galois orbit. The union of these conjugates is a finite collection of polynomials $g_1,\ldots ,g_m$.

Each $g_i$ vanishes on s, by the assumed Galois invariance of s. Thus each $g_i$ is in I(s). By the definition of Zariski closure, we have $I(s)=I(v)$. And so we have each $g_i$ vanishing on v.

Now, for each $1\le i\le m$, we define $h_i = e_i(g_1,\ldots ,g_m)$, where $e_i$ is the ith elementary symmetric polynomial. Each $h_i$ is Galois invariant, since applying a Galois automorphism to $h_i$ will permute the $g_j$, and $e_i$ is symmetric. As Galois invariant polynomials, the $h_i$ are defined over ${\mathbb Q}$.

Since all $g_i$ vanish over v, we know that $v \subseteq V(\{h_i\})$. For the other direction, let $p \notin v$. Then one of our $f_i$ does not vanish at p. So there is some specific $i_0$ so that $g_{i_0}(p)\ne 0$.

Recall that Vieta’s formula says that, for a univariate polynomial P(x), if

$$\begin{aligned} P(x)= (x - r_1)\cdots (x - r_m) = x^m + a_{m-1}x^{m-1} + \cdots + a_0 \end{aligned}$$

then

$$\begin{aligned} e_i(r_1, \ldots , r_m) = (-1)^{i}a_{m-i} \end{aligned}$$

Getting back to our setting, for each $1\le k\le m$, let us fix the numbers $r_k:= g_k(p)$. Suppose that for all i, we had $e_i(r_1, \ldots , r_n) = 0$, then in Vieta’s formula, we would have $P(x)=x^m$, which would mean that all of the roots $(r_1, \ldots , r_n)$ of P(x) were 0. But we have at least one $r_{i_0}\ne 0$, a contradiction. So there must be some ${i_1}$ so that $e_{i_1}(r_1,\ldots ,r_m) \ne 0$. But this means that $h_{i_1}(p) = e_{i_1}(g_1(p),\ldots ,g_m(p)) \ne 0$. Thus $v\supseteq V(\{h_i\})$ and so $v = V(\{h_i\})$. Since the $h_i$ are defined over ${\mathbb Q}$, this establishes the lemma. $\square$

Remark A.11

The lemma can also be proven in a related but more abstract fashion by first establishing that the Zariski closure, v, is Galois invariant and then directly appealing to [26, Tag 038B].

Proof of Theorem A.8

Let us consider s, the ${\overline{\mathbb Q}}^N$ restriction of S, along with its Zariski closure v. Since s is defined using the vanishing and non-vanishing of polynomials defined over ${\mathbb Q}$, the set s must be invariant to ${\text {Aut}}({\overline{\mathbb Q}}/{\mathbb Q})$. From Lemma A.10, its Zariski closure v in ${\overline{\mathbb Q}}^N$ must be cut out (set theoretically) as $V(j')$ for some ideal $j'$ of ${\overline{\mathbb Q}}[X_1,\ldots ,X_N]$ that is defined over ${\mathbb Q}$. As in Remark A.2, since ${\overline{\mathbb Q}}$ is closed, $j:=I(v)$ is equal to $\sqrt{j'}$, its radical ideal in ${\overline{\mathbb Q}}[X_1,\ldots ,X_N]$, which is also defined over ${\mathbb Q}$. Meanwhile from Lemma A.9, the ideal J of the (complex) Zariski closure of S is just the complex extension of j. Thus J too must be defined over ${\mathbb Q}$. $\square$

Lemma A.12

Let s be a real semi-algebraic set. Let $V:=V(s)$ be its complex Zariski closure. Then the complex dimension of V equals the real dimension of s.

Proof

We say that s is irreducible if its real Zariski closure is irreducible. If s is not irreducible, we can write it is as a finite proper union of irreducible semi-algebraic sets $s_k$. We have ${{\,\textrm{Dim}\,}}(s) = \max _k({{\,\textrm{Dim}\,}}(s_k))$, and so we can work over each component separately. Thus, in what follows, we will assume that s is irreducible.

Let $i:= i(s)$ be the ideal of real polynomials vanishing on s, and $v:= v(i(s))$ be the real Zariski closure. (We use lower case v and i to make it clear that this is all done in the real setting.) Let $I:= I(s)$ be the ideal of complex polynomials vanishing on s, and $V:= V(I(s))$ be the complex Zariski closure. As described in [5, Section 2.8], the real dimension of s equals the real dimension of v. Meanwhile, from [27, Proof of Lemma 6], the ideal I equals $i^*$, the complex extension of i. From [27, Proof of Lemma 9], for any radical real ideal j, the maximal Jacobian rank of $V(j^*)$ must equal the maximal Jacobian rank of of v(j). Since v is irreducible, then from [27, Lemma 7], so too is V. Since v and V are both irreducible, this maximal Jacobian rank gives us the real (resp. complex) codimensions of v and V. $\square$

Appendix B: Rational Functionals and Relations

In this section, we prove some generally useful facts about rational functionals and relations acting on generic point configurations $\textbf{p}$.

Theorem B.1

Let $\textbf{l}$ be a generic point in ${L_{d,n}}$ with $d \ge 2$, and let $\alpha$ be a rational length functional. Suppose $\langle \alpha , \textbf{l}\rangle =0$, then $\alpha =0$. Likewise (due to linearity), if $\langle \alpha ,\textbf{l}\rangle =\langle \alpha ',\textbf{l}\rangle$, then $\alpha =\alpha '$.

Similarly, let $\textbf{p}$ be a generic configuration in $\mathbb R^d$ with $d\ge 2$. Suppose $\langle \alpha , \textbf{p}\rangle =0$, then $\alpha =0$. Likewise, if $\langle \alpha , \textbf{p}\rangle =\langle \alpha ',\textbf{p}\rangle$, then $\alpha =\alpha '$.

Recall from Theorem 4.10 that, assuming $d\ge 2$, ${L_{d,n}}$ is irreducible, hence it has generic points. Additionally, when $\textbf{p}$ is a generic configuration, then $l(\textbf{p})$ is generic in ${L_{d,n}}$.

Proof

The equation $\langle \alpha , \textbf{l}\rangle =0$ describes an algebraic equation over ${L_{d,n}}$ with coefficients in ${\mathbb Q}$ and that vanishes at $\textbf{l}$. Genericity of $\textbf{l}$ implies that $\alpha$ vanishes over all of ${L_{d,n}}$.

Suppose, for a contradiction, that $\alpha \ne 0$. First observe that there are points $\textbf{x}$ in ${L_{d,n}}$ that have all real and non-zero coordinates. Because ${L_{d,n}}$ is symmetric under sign-negation, given $\alpha$, we can construct from $\textbf{x}$ a point $\textbf{x}'$ in $L_{d,n}$ so that the coefficient $\alpha ^{ij}$ and $\textbf{x}'_{ij}$ have the same sign for all ij with $\alpha ^{ij}\ne 0$. But then $\langle \alpha ,\textbf{x}'\rangle > 0$, which is a contradiction. Hence $\alpha = 0$. $\square$

Remark B.2

When $d=1$, there can be generic configurations $\textbf{p}$ such that $\langle \alpha , \textbf{p}\rangle =0$ with $\alpha \ne 0$. For example, suppose $n=3$, and let $\alpha _{12}=1, \alpha _{23}=1, \alpha _{13}=-1$. Then, $\langle \alpha , \textbf{p}\rangle =0$, whenever we have the order $\textbf{p}_1 \le \textbf{p}_2 \le \textbf{p}_3$, or the reverse order $\textbf{p}_1 \ge \textbf{p}_2 \ge \textbf{p}_3$, and $\langle \alpha , \textbf{p}\rangle \ne 0$ otherwise. In this case, $L_{1,3}$ is reducible, and we have an equation that vanishes identically on one component of the variety but not on the others.

The following is useful to tell when a set of rational functionals is linearly dependent.

Lemma B.3

Let $\textbf{p}$ be a configuration, $\alpha _i$ a sequence of k rational functionals, and $v_i:= \langle \alpha _i,\textbf{p}\rangle$. Suppose that the functionals $\alpha _i$ are linearly dependent. Then, there is a linear dependence that can be expressed as $\sum _i c^i \alpha _i=0$, where the coefficients $c^i$ are rational, not all vanishing. Moreover, this gives us the relation $\sum _i c^i v_i =0$ with the same coefficients. If the functionals $\alpha _i$ are integer and b-bounded, then we can find such coefficients $c^i$ that are integers, bounded in magnitude by $(k')^{k'/2}b^{k'}$.

Proof

Let $k'<k$ be the dimension of the span of the $\alpha _i$.

i) Let us look at the case $k' < N$.

Pick a subset of the $\alpha _i$ that is minimally linearly dependent with size $k'+1$. Let us use these as the $k'+1$ rows of a matrix $\textbf{M}$ with $N$ columns. Each of its minors of size $k'+1$ must vanish.

Pick $k'$ columns that are linearly independent. Append to these, one column made up of $k'+1$ variables. The condition that the determinant of this $(k'+1)\times (k'+1)$ matrix vanishes gives us a non-trivial linear homogeneous equation in the variables. In the b-bounded setting, Hadamard’s bound implies that the coefficients of this equation have magnitude at most $(k')^{k'/2}b^{k'}$. As every column of $\textbf{M}$ is in the span of our chosen $k'$ columns, the entries in each column of $\textbf{M}$ must satisfy this equation. Thus we have found a rational relation on the $k'+1$ rows of $\textbf{M}$, giving us a rational relation on the $\alpha _i$.

ii) Let us look at the case $k' = N$.

Pick a subset of the $\alpha _i$ of size $N$ that is linearly independent. Let us use these as the rows of a square non-singular matrix $\textbf{M}$. Pick one more functional $\beta$ from the $\alpha _i$. Let us think of $\beta$ as a row vector of length $N$. Since $\beta$ is in the span of our selected rows, we have $[\beta \, \textrm{adj}(\textbf{M})] \textbf{M}= \beta [\det (\textbf{M})]$. Here “adj” denotes the adjugate matrix. This gives us a rational relation between the rows of $\textbf{M}$ and $\beta$, with the coefficients in brackets above. Again in the b-bounded setting, the coefficients are bounded in magnitude by $(k')^{k'/2}b^{k'}$.

In both cases i) and ii), the relation on the $v_i$ follows immediately. $\square$

Lemma B.4

Let $\textbf{p}$ be a generic configuration in two or more dimensions. Let $\alpha _i$ be a sequence of k rational functionals. Let $v_i:= \langle \alpha _i,\textbf{p}\rangle$. Suppose there is a sequence of k rational coefficients $c^i$, not all zero, such that $\sum _i c^i v_i=0$. Then, there is a linear dependence in the functionals $\alpha _i$.

Proof

$$\begin{aligned} 0= & {} \sum _i c^i v_i \\= & {} \sum _i c^i \langle \alpha _i, \textbf{p}\rangle \\= & {} \langle \sum _i c^i \alpha _i, \textbf{p}\rangle \end{aligned}$$

Then, from Theorem B.1, $\sum _i c^i \alpha _i$ must be the zero functional. $\square$