Abstract
A grounded L-graph is the intersection graph of a collection of “L” shapes whose topmost points belong to a common horizontal line. We prove that every grounded L-graph with clique number \(\omega \) has chromatic number at most \(17\omega ^4\). This improves the doubly-exponential bound of McGuinness and generalizes the recent result that the class of circle graphs is polynomially \(\chi \)-bounded. We also survey \(\chi \)-boundedness problems for grounded geometric intersection graphs and give a high-level overview of recent techniques to obtain polynomial bounds.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Following Gyárfás [17], we say that a class of graphs \(\mathcal {G}\) is \(\chi \)-bounded if there is a function \(f:\mathbb {N}\rightarrow \mathbb {N}\) such that the chromatic number \(\chi \) of any graph in \(\mathcal {G}\) is at most \(f(\omega )\), where \(\omega \) is the clique number of the graph. Additionally, \(\mathcal {G}\) is polynomially \(\chi \)-bounded if f can be taken to be a polynomial function. A flurry of research has been devoted to distinguishing which classes of graphs are \(\chi \)-bounded and which are polynomially \(\chi \)-bounded. In particular, Esperet [12] conjectured that every \(\chi \)-bounded class of graphs that is closed under taking induced subgraphs is polynomially \(\chi \)-bounded. This has been recently disproved by Briański et al. [2]. We refer the reader to the recent survey [31] for more information on \(\chi \)-boundedness.
An important branch of this research is focused on geometric intersection graphs. The intersection graph of a family of geometric objects has these objects as vertices and the pairs of objects with non-empty intersection as edges. We restrict our attention to intersection graphs of objects in the plane, where by an object we mean a compact arc-connected set in \(\mathbb {R}^2\). By considering objects of some particular kind, for example, having a specific geometric shape, we obtain various classes of graphs.
In this paper we focus on grounded L-graphs, which are geometric intersection graphs of grounded L-shapes. An L-shape consists of a vertical segment and a horizontal segment that meet at their uppermost and leftmost endpoints respectively, i.e., form an upside-down “L”. An L-shape is grounded if its lowermost point is on the x-axis. Grounded L-graphs were introduced by McGuinness [26], who showed that they satisfy \(\chi =2^{O(4^\omega )}\). Our main result is that this class is in fact polynomially \(\chi \)-bounded.
Theorem 1.1
Every grounded L-graph with clique number \(\omega \) has chromatic number at most \(17\omega ^4\).
Theorem 1.1 implies the recent result of Davies and McCarty [10] that the class of circle graphs is polynomially \(\chi \)-bounded (albeit with a worse bound). Our proof appropriately adapts and extends their techniques. It is tempting to see how far this method can be pushed. With this in mind, we will now survey \(\chi \)-boundedness problems for geometric intersection graphs. We refer the reader in advance to Fig. 4, which depicts the graph classes that will be discussed as well as all possible inclusions between them and all of the best known bounds on \(\chi \) in terms of \(\omega \). We will give a high-level overview of the proof technique in Sect. 2 in order to make this area more accessible.
1.1 Coloring Geometric Intersection Graphs
Due to practical and theoretical applications, the following graph classes have been particularly intensively studied:
-
rectangle graphs – intersection graphs of axis-parallel rectangles,
-
segment graphs – intersection graphs of straight-line segments,
-
L-graphs – intersection graphs of L-shapes,
-
string graphs – intersection graphs of strings, where a string is a bounded continuous curve in the plane.
The class of string graphs is the most general class of intersection graphs of objects in the plane, as every such graph can be easily represented as an intersection graph of strings “filling” these objects.
The study of chromatic properties of geometric intersection graphs was initiated by Asplund and Grünbaum [1], who proved that rectangle graphs satisfy \(\chi \leqslant 4\omega ^2-4\omega \) (when \(\omega \geqslant 2\)). This was later improved to \(\chi \leqslant 3\omega ^2-2\omega -1\) by Hendler [18]. Chalermsook [7] showed the bound \(\chi =O(\omega \log \omega )\) for the special case that none of the rectangles is contained in another. Recently, Chalermsook and Walczak [8] showed that rectangle graphs satisfy \(\chi =O(\omega \log \omega )\), improving the quadratic bound that lasted for 60 years. From below, Kostochka [21] constructed rectangle intersection graphs satisfying \(\chi =3\omega \), and this remains the best known lower bound.
In general, \(\chi \)-boundedness is a rather rare feature among intersection graphs of geometric objects in the plane. Pawlik et al. [29] proved that intersection graphs of objects obtained by independent horizontal and vertical scaling and translation of some fixed template that is not an axis-parallel rectangle, are not \(\chi \)-bounded. In particular, L-graphs, segment graphs, and string graphs are not \(\chi \)-bounded. Fox and Pach [13] showed that every n-vertex string graph satisfies \(\chi =(\log n)^{O(\log \omega )}\). From below, Krawczyk and Walczak [24] constructed string graphs satisfying \(\chi =\Theta _\omega ((\log \log n)^{\omega -1})\). It is possible that all string graphs have chromatic number of order at most \((\log \log n)^{f(\omega )}\) for some function \(f:\mathbb {N}\rightarrow \mathbb {N}\). So far, such a bound is proved for some particular, still not \(\chi \)-bounded, subclasses of string graphs [23, 24, 33].
A quite different picture emerges when we consider intersection graphs of so-called “grounded objects”. Following terminology introduced by Cardinal et al. [5] (used in a similar form by Jelínek and Töpfer [19]), we say that a family of objects in the plane is grounded if all these objects are contained in a closed half-plane and intersect the boundary of this half-plane, called a grounding line.Footnote 1 Jelínek and Töpfer [19], who were the first to systematically study relations (containments and separations) between most known classes of this kind, considered the following classes of graphs:
-
outerstring graphs – intersection graphs of grounded strings, that is, strings whose one end intersects the horizontal grounding line and the remaining points are contained above the line.
-
outer-1-string graphs – intersection graphs of simple families of grounded strings, where a family of strings is simple if any two of them intersect in at most one point.
-
grounded segment graphs – intersection graphs of grounded segments, that is, segments such that one end intersects the grounding line.
-
grounded
 -graphs – intersection graphs of grounded L-shapes and their mirror images, grounded
-graphs – intersection graphs of grounded L-shapes and their mirror images, grounded  -shapes, where a grounded L-shape is an L-shape with the bottommost point on the grounding line. An argument of Middendorf and Pfeiffer [28] shows that grounded
-shapes, where a grounded L-shape is an L-shape with the bottommost point on the grounding line. An argument of Middendorf and Pfeiffer [28] shows that grounded  -graphs form a subclass of grounded segment graphs.
-graphs form a subclass of grounded segment graphs. -
grounded L-graphs – intersection graphs of grounded L-shapes.
-
circle graphs – intersection graphs of chords in a circle. Circle graphs can be equivalently defined as intersection graphs of grounded semicircles, that is, semicircles with both ends touching the grounding line. The class of circle graphs is contained in the class of grounded L-graphs – see Fig. 1.
-
permutation graphs – intersection graphs of segments spanned between two horizontal lines. Permutation graphs can be equivalently defined as intersection graphs of semicircles which are pairwise grounded on intersecting intervals; as such, they are contained in the class of circle graphs – see Fig. 2.
-
monotone L-graphs, also known as max point-tolerance graphs – intersection graphs of L-shapes all of whose bends belong to a common downward-sloping line.
-
interval graphs – intersection graphs of intervals contained in the grounding line. The class of interval graphs is contained in the class of grounded L-graphs and in the class of monotone L-graphs – see Fig. 2.
In the context of the coloring problem, the following two classes of intersection graphs of grounded objects were considered:
-
interval filament graphs – intersection graphs of interval filaments, which are continuous non-negative functions defined on closed intervals attaining zero values at their endpoints. Interval filament graphs are contained in the class of outerstring graphs (two interval filaments may intersect in many points).
-
polygon-circle graphs – intersection graphs of polygons inscribed into a circle. Polygon-circle graphs can be equivalently defined as intersection graphs of circle filaments, which are interval filaments consisting of some number of externally touching grounded semicircles. In particular, polygon-circle graphs form a subclass of interval filament graphs and extend the classes of circle graphs and interval graphs – see Fig. 3.
Figure 4 presents a diagram showing all possible inclusions between the graph classes defined above (so any inclusions which are not depicted are known to not exist). It also depicts the best known upper and lower bounds for \(\chi \) in terms of \(\omega \). In the rest of the introduction, we describe where the depicted inclusions/non-inclusions and upper/lower bounds come from.
Interval graphs and permutation graphs are well known to be perfectFootnote 2 (see [15], for instance), so they satisfy \(\chi =\omega \). Circle graphs and monotone L-graphs are no longer perfect, and hence no other class shown in the diagram is perfect.
Catanzaro et al. [6] observed that monotone L-graphs can be alternatively defined as intersection graph of rectangles whose top-left vertices lie in a common upward-sloping line. In such a representation no rectangle is contained in another, which proves that monotone L-graphs satisfy \(\chi =O(\omega \log \omega )\) by the result of Chalermsook [7]. To our knowledge, no non-trivial lower bound on the chromatic number in this class of graphs is known.
The study of chromatic properties of circle graphs was initiated by Gyárfás [16], who proved \(\chi =O(\omega ^24^\omega )\) for this class of graphs. This bound was later improved to \(\chi =O(\omega ^22^\omega )\) by Kostochka [20], and to \(\chi =O(2^\omega )\) by Kostochka and Kratochvíl [22]. The latter bound was actually obtained for polygon-circle graphs. McGuinness [26] introduced L-graphs and showed that they satisfy \(\chi =2^{O(4^\omega )}\). McGuinness [27] also proved that the chromatic number of triangle-free intersection graphs of simpleFootnote 3 families of grounded objects is bounded by a constant. Suk [32] showed that intersection graphs of grounded simple y-monotoneFootnote 4 curves satisfy \(\chi =2^{O(5^\omega )}\). In particular, Suk’s result proves \(\chi =2^{O(5^\omega )}\) for grounded segment graphs. The last two results were extended by Lasoń et al. [25], who showed that intersection graphs of simple families of grounded objects satisfy \(\chi =2^{O(2^\omega )}\). In particular, this proves \(\chi =2^{O(2^\omega )}\) for outer-1-string graphs. Finally, Rok and Walczak [30] showed that outerstring graphs satisfy \(\chi =2^{O(2^{\omega (\omega -1)/2})}\).
The above-mentioned upper bounds on the chromatic number of graph classes extending circle graphs are at least exponential. Introducing an entirely new technique, Davies and McCarty [10] showed that circle graphs satisfy \(\chi =(1+o(1))\omega ^2\), thus obtaining the first polynomial upper bound on \(\chi \) in terms of \(\omega \) for a non-trivial class of intersection graphs of grounded objects. Very recently, Davies [9] extended these techniques to further improve this bound to \((2+o(1))\omega \log _2\omega \). Krawczyk and Walczak [24] showed that every interval filament graph satisfies \(\chi \leqslant \left( {\begin{array}{c}\omega +1\\ 2\end{array}}\right) \cdot \chi _{\textrm{circ},\omega }\), where \(\chi _{\textrm{circ},\omega }\) is the maximum chromatic number of circle graph with clique number \(\omega \). The last two bounds imply that interval filament graphs (and hence polygon-circle graphs) satisfy \(\chi =O(\omega ^3\log \omega )\). Our main result, Theorem 1.1, adds the class of grounded L-graphs to the list of known polynomially \(\chi \)-bounded classes of graphs, showing that they satisfy \(\chi =O(\omega ^4)\).
Clearly, the same asymptotic upper bound holds for grounded  -graphs (we color grounded L-shapes and grounded
-graphs (we color grounded L-shapes and grounded  -shapes with different sets of colors). Furthermore, we also note that a simple twist in the proof of Davies and McCarty allows to show the bound \(\chi =(1+o(1))\omega ^2\) also for polygon-circle graphs. Interestingly this appears to fail for the proof of the \((2+o(1))\omega \log _2\omega \) bound. We will discuss this matter further, including the modifications required for proving the \((1+o(1))\omega ^2\) bound for polygon-circle graphs in Sect. 2. Questions about polynomial \(\chi \)-boundedness for other graph classes shown in Fig. 4 remain open. In particular, it is tempting to ask whether the existing techniques can be extended to prove the following conjecture.
-shapes with different sets of colors). Furthermore, we also note that a simple twist in the proof of Davies and McCarty allows to show the bound \(\chi =(1+o(1))\omega ^2\) also for polygon-circle graphs. Interestingly this appears to fail for the proof of the \((2+o(1))\omega \log _2\omega \) bound. We will discuss this matter further, including the modifications required for proving the \((1+o(1))\omega ^2\) bound for polygon-circle graphs in Sect. 2. Questions about polynomial \(\chi \)-boundedness for other graph classes shown in Fig. 4 remain open. In particular, it is tempting to ask whether the existing techniques can be extended to prove the following conjecture.
Conjecture 1.2
The class of grounded segment graphs is polynomially \(\chi \)-bounded.
Davies’s aforementioned linear-logarithmic upper bound for circle graphs is tight up to a multiplicative constant – Kostochka [20, 21] constructed circle graphs that satisfy \(\chi \geqslant \frac{1}{2}\omega (\ln \omega -2)\), and Davies [9] improved this to \(\chi \geqslant \omega (\ln \omega -2)\). This lower bound is also best known in the classes of polygon-circle graphs, L-graphs, and outer-1-string graphs. For interval filament graphs, Krawczyk and Walczak [24] provided a construction that achieves \(\chi =\left( {\begin{array}{c}\omega +1\\ 2\end{array}}\right) \), and this is also the best lower bound known for outerstring graphs. It would be desirable to tighten the gaps between the lower and upper bounds on \(\chi \) in terms of \(\omega \) for the above-mentioned polynomially \(\chi \)-bounded classes: polygon-circle graphs, interval filament graphs, and L-graphs.
1.2 Containments and Separations
An important direction in the study of geometric intersection graphs concerns containment and separation relations between such classes of graphs; see e.g. Cabello and Jejčič [3] as well as Cardinal et al. [5]. Such a study for intersection graphs of grounded objects was conducted by Jelínek and Töpfer [19]. In particular, they indicated all inclusions for graph classes mentioned above except for polygon-circle graphs and interval filament graphs. We extend their work by putting these two graph classes in the right place. To this end, we prove the following separation results.
Theorem 1.3
-
(1)
There is a grounded L-graph which is not an interval filament graph.
-
(2)
There is an L-monotone graph which is not an interval filament graph.
-
(3)
There is a polygon-circle graph which is not an outer-1-string graph.
Gavril [14] noticed that there is an interval filament graph which is not a polygon-circle graph. Catanzaro et al. [6] showed a permutation graph which is not a monotone L-graph (this shows that no superclass of permutation graphs is a subclass of monotone L-graphs). Cardinal et al. [5] constructed an outer-1-string graph which is not a grounded segment graph. Jelínek and Töpfer [19] proved that:
-
there is a grounded segment graph which is not a grounded
 -graph,
-graph, -
there is a grounded
 -graph which is not a grounded L-graph,
-graph which is not a grounded L-graph, -
there is a monotone L-graph which is not an outer-1-string graph.
All these results, together with Theorem 1.3 and the folklore results concerning separations between interval, permutation, and circle graphs, show that there are no other inclusions between graph classes shown in Fig. 4 apart from those implied by the depicted arrows.
2 Preliminaries
At a broad level, our proof follows the strategy used by two of the authors to color circle graphs with clique number \(\omega \) using \((1+o(1))\omega ^2\) colors [10]. To explain the connection, and because it will be needed in our proof, we shall introduce circle and permutation graphs again from different perspectives. We then sketch the proof strategy used for circle graphs in order to give an idea of how our proof for grounded L-graphs will go. Afterwards we take a slight detour to sketch the modification required for extending the \((1+o(1))\omega ^2\) bound to polygon-circle graphs and discuss the difficulty in extending the improved \(O(\omega \log \omega )\) bound to polygon-circle graphs. Then we discuss the strategy for grounded L-graphs, in particular highlighting some differences between the two proofs. Lastly we introduce a few more definitions and prove a simple reduction lemma for coloring grounded L-graphs.
2.1 Circle Graphs
Two open intervals overlap if they intersect and neither is contained in the other. The overlap graph of a set of open intervals \(\mathcal {J}\) has vertex set \(\mathcal {J}\), and two intervals are adjacent if they overlap. Note that the class of circle graphs is exactly the class of overlap graphs of intervals (up to graph isomorphism).
Another equivalent definition of permutation graphs is that a graph is a permutation graph if there exist total orders \(\prec _1\) and \(\prec _2\) of its vertex set such that two distinct vertices are adjacent if and only if their relative order is different in \(\prec _1\) and \(\prec _2\). Permutation graphs are precisely the intersection graphs of collections of grounded L-shapes such that there exists a vertical line which intersects each L-shape exactly once. We will utilize this connection, giving proofs as needed.
The strategy for coloring overlap graphs of intervals \(\mathcal {J}\) with clique number \(\omega \) is to find a suitable finite collection of points \(B\subseteq \mathbb {R}\) and to equip them with a total ordering \(\prec \) and a coloring c. From such a triple \((B,\prec ,c)\), we can then obtain a partial improper coloring of the overlap graph of \(\mathcal {J}\) by assigning each vertex v to the first point in the total order \(\prec \) on B that is contained in the interval corresponding to v and coloring v with the color of that point in c. If we ensure that no pair of adjacent vertices are assigned to distinct points of the same color, then each monochromatic component consists of vertices assigned to a single point, so it induces a permutation graph and thus can be further colored with \(\omega \) colors. In this case we call the triple \((B,\prec ,c)\) a pillar assignment. (We shall use a different definition of pillar assignment for grounded L-graphs.)
With this idea of pillar assignments in mind, at a basic level the proof strategy is to prove that a pillar assignment (which provides a partial improper coloring of our graph) that uses few colors can be extended to one that colors every vertex, still without using too many colors. The vertices assigned to each point of B form well-structured cuts of the graph, in the sense that the intervals corresponding to each connected component of the overlap graph induced by the uncolored vertices must be contained within some component of \(\mathbb {R}\setminus B\), which we call a segment. This motivates the idea of the degree of a segment, which roughly speaking is the number of points in B to which intervals from \(\mathcal {J}\) with one endpoint in the segment are assigned. So the strategy is to prove that a pillar assignment using a bounded number of colors and with segments of bounded degree (with the latter bound being less than the former) can be extended to a pillar assignment that colors every vertex, still without using too many colors.
Very roughly this is done as follows. Given a segment \(S=(b^-,b^+)\) of bounded degree that we wish to extend the pillar assignment within, we begin by partitioning S into a collection of smaller segments \(\mathcal {S}=\{(b^-,b_1),(b_1,b_2),\ldots ,(b_n,b^+)\}\), each with a much smaller (but still suitably large) degree. From here we aim to use a divide-and-conquer argument to extend the pillar assignment \((B,\prec ,c)\) to a new one \((B^*,\prec ^*,c^*)\) so that \(B^*=B\cup \{b_1,\ldots ,b_n\}\) and more vertices of the overlap graph are colored. The divide-and-conquer argument shall use colors distinct from those given to vertices with corresponding intervals having an endpoint in the segment S (the number of which is measured by the degree of S). The number of colors required to carry out the divide-and-conquer argument depends on \(|\mathcal {S}|\), and so if \(|\mathcal {S}|\) is small enough, then we succeed in extending the pillar assignment \((B,\prec ,c)\).
The trickier case is when \(|\mathcal {S}|\) is too large to carry out the divide-and-conquer argument. In this case we aim to derive a contradiction by finding a clique of size \(\omega +1\). This is done as follows. First, we create a collection of intervals \(\mathcal {I}\): for every point \(b\in B\) and every interval \(S'\) in \(\mathcal {S}\), if b contributes to the degree of \(S'\), we add the interval I whose endpoints are b and the middle of \(S'\) to the set \(\mathcal {I}\). Moreover, for any such interval I in \(\mathcal {I}\), we choose an interval from \(\mathcal {J}\) witnessing this contribution; that is, an interval from \(\mathcal {J}\) assigned to b with an endpoint in \(S'\). Now, we complete the proof as follows. Since the degree of each segment contained in \(\mathcal {S}\) is suitably large, and since \(\mathcal {S}\) is large, we can find in the set \(\mathcal {I}\) a set of \(\omega +1\) pairwise overlapping intervals (see Lemma 4.1). Eventually, an extremal lemma asserts that the witnesses associated to those intervals form a set of \(\omega +1\) pairwise overlapping intervals in \(\mathcal {J}\). Such a set corresponds to a clique of size \(\omega +1\) in the overlap graph of \(\mathcal {J}\).
This completes the proof for circle graphs, because every pillar assignment that does not color all vertices can be extended to one that colors more vertices.
2.2 Polygon-Circle Graphs
Before returning to grounded L-graphs, we briefly discuss extending bounds for circle graphs to polygon-circle graphs. We begin with a sketch of how to tweak the proof of Davies and McCarty [10] that circle graphs have chromatic number at most \((1+o(1))\omega ^2\) so that it further applies to polygon-circle graphs.
By viewing polygon-circle graphs as intersection graphs of circle filaments, the pillars can be defined in essentially the same way as for circle graphs; filaments are assigned to the first point b of the ordered pillars that is contained in the domain of the filament. Then the induced subgraph corresponding to a pillar is again a perfect graph. With this notion of pillar, the divide-and-conquer argument is exactly the same as for circle graphs. The corresponding notion of degree of a segment for polygon-circle graphs is similar: it counts the number of pillars with at least one circle filament intersecting the segment assigned.
The main difference is in the extremal lemma required to show that the set \(\mathcal {S}\) is not too large. We create a set of intervals \(\mathcal {I}\) analogously; that is, for every \(b\in B\) and every \(S'\in \mathcal {S}\), we add the interval whose endpoints are b and the middle of \(S'\) to \(\mathcal {I}\) if b contributes to the degree of \(S'\). Clearly, this contribution is witnessed by a circle filament assigned to b intersecting the segment \(S'\). Here it is worth noting the main difference that distinguishes the proofs for polygon-circle graphs and circle graphs: a single circle filament might be a witness for many intervals from \(\mathcal {I}\), but if this is the case, all of them share the same endpoint b to which this circle filament is assigned. Again, if \(\mathcal {S}\) and the degree of every segment in \(\mathcal {S}\) are large enough, then we can find a set of \(\omega +1\) pairwise overlapping intervals in \(\mathcal {I}\). The previous observation asserts that circle filaments witnessing those intervals are pairwise distinct. Moreover, it is proved in the same way that their domains are pairwise overlapping. In particular, these circle filaments must be pairwise intersecting.
An old problem of Kostochka and Kratochvíl [22] asks whether the optimal \(\chi \)-bounding function for polygon-circle graphs is within a constant fraction of the optimal \(\chi \)-bounding function for circle graphs. Since circle graphs are now known to have an optimal \(\chi \)-bounding function of \(\Theta (\omega \log \omega )\) [9], two reasonable approaches to this problem would be either to improve the lower bound construction or to extend the \(O(\omega \log \omega )\) proof for circle graphs to polygon-circle graphs. However, the latter does not appear to extend as easily as the proof of the \((1+o(1))\omega ^2\) bound.
The \(O(\omega \log \omega )\) proof for circle graphs uses a notion of pillar assignment that directly stores a proper coloring of the vertices rather than an improper coloring which is later refined. The induced permutation graphs assigned to each pillar are colored as we go in a particularly well-structured way so that certain configurations of intervals with corresponding vertices colored by the pillar assignment yield pairwise overlapping intervals elsewhere. This part is critical in allowing for the improved bound. However, for polygon-circle graphs, the vertices assigned to each pillar would instead induce trapezoid graphs, a more complex class that contains permutation graphs. Although trapezoid graphs are again perfect, they appear to be more difficult to color in a well-structured way that would facilitate the rest of the proof.
2.3 Grounded L-Graphs
Next we sketch some of the main differences in the strategy that we use for grounded L-graphs. The reader may wish to refer to Figs. 6 and 7 for an idea of the algorithm we use to draw pillars as well as the definition of pillar assignments for grounded L-graphs.
Now let \(\mathcal {L}\) be a collection of grounded L-shapes whose intersection graph, which we denote by \(G(\mathcal {L})\), has clique number \(\omega \). The basic strategy is the same – we shall use a triple \((B,\prec ,c)\) to color our grounded L-graph, where this time B consists of points of the x-axis, which we will call “pillar bases”. As before, we shall color vertices with the same color of the pillar base that their corresponding L-shape is assigned to.
What is not so obvious however is how one should decide which pillar base of B a vertex corresponding to a given L-shape should be assigned to. Given the first pillar base b in the totally ordered set \((B,\prec )\), we use an algorithm to define a curve \(P_b\), called a “pillar”, beginning at b and going up and to the left. This algorithm is dependent on the collection of grounded L-shapes \(\mathcal {L}\), and this curve ends up being a staircase which ends at a one-way infinite vertical segment (see Fig. 6). We then continue with the next pillar base \(b'\) in the total order, defining its pillar \(P_{b'}\) again with an algorithm that depends on \(\mathcal {L}\). Again the pillar \(P_{b'}\) begins at \(b'\) and is a staircase that goes up and to the left; we only stop \(P_{b'}\) if it runs into an earlier pillar. This process is carried out for every pillar base of B in order (see Fig. 7).
The total order \(\prec \) of B also naturally orders the pillars \(\mathcal {P}=\{P_b:b\in B\}\), and we can also consider c as a coloring of \(\mathcal {P}\). Then we assign each vertex of \(G(\mathcal {L})\) to the earliest pillar P in the totally ordered set \((\mathcal {P},\prec )\) that intersects its corresponding L-shape. Then for grounded L-graphs, we call such a triple \((\mathcal {P},\prec ,c)\) a pillar assignment.
This definition of pillars and pillar assignment may seem somewhat convoluted compared to that for circle graphs, but the algorithm defining the pillars is carefully designed so that certain configurations of L-shapes with corresponding vertices of certain colors given by the pillar assignment yield pairwise intersecting L-shapes elsewhere in \(\mathcal {L}\). Crucially, this gives us another way to find cliques in the intersection graph rather than just finding them directly. This extra way of finding cliques is needed for one of our required extremal results.
For grounded L-graphs, there are more ways that a grounded L-shape L with corresponding vertex v colored by our pillar assignment could intersect an L-shape \(L'\) whose corresponding vertex \(v'\) is uncolored. So instead of one notion for the degree of a segment, we require a few that depend on the position of the L-shape contributing to the degree. This mainly consists of definitions for the “left degree” and the “right degree” of a segment. Then, with extremal results that are tailored to our notion of pillar assignment and these individual notions of degree, the inductive argument on extending pillar assignments can be carried out in a way similar to that for circle graphs with another divide-and-conquer argument.
This pillar assignment approach could potentially be used to prove polynomial \(\chi \)-bounds for other classes of graphs, but it seems difficult to define a workable notion of a “pillar”. We need to be able to color the induced subgraph corresponding to a “pillar”, we need some kind of divide-and-conquer argument, and we need a suitable extremal lemma. All three of these steps are entirely dependent on the chosen notion of “pillar”. So defining pillars seems like a major roadblock in using this approach to prove polynomial \(\chi \)-bounds. Nevertheless, we are hopeful that the approach can be further developed and applied to other classes of graphs, particularly (but not necessarily exclusively) to other geometrically defined classes of graphs.
2.4 Flat L-Collections
We finish this section with some further definitions on grounded L-shapes, as well as a reduction that allows us to instead color simpler collections of L-shapes which we call “flat L-collections”.
Let L be an L-shape. We let h(L) denote the y-coordinate of the topmost endpoint of the vertical segment of L, and we let \(\ell (L)\) and r(L) denote the x-coordinates of the leftmost and rightmost endpoints of the horizontal segment of L, respectively. So L is totally determined by its height h(L), left endpoint \(\ell (L)\), and right endpoint r(L). We call the point \((\ell (L),h(L))\), where the vertical and horizontal segments meet, the corner of L. Finally, we let p(L) denote the closed interval \([\ell (L),r(L)]\); we call p(L) the projection of L as it is the projection onto the x-axis.
We will consider collections \(\mathcal {L}\) of grounded L-shapes such that for each distinct pair \(L_1,L_2\in \mathcal {L}\), the intervals \(p(L_1)\) and \(p(L_2)\) do not share an endpoint and \(h(L_1)\ne h(L_2)\). We call such a collection an L-collection and write \(G(\mathcal {L})\) for its intersection graph. Notice that every grounded L-graph is isomorphic to \(G(\mathcal {L})\) for some L-collection \(\mathcal {L}\). We say that \(\mathcal {L}\) is flat if there are no \(L_1,L_2\in \mathcal {L}\) such that \(p(L_1)\subseteq p(L_2)\) and \(h(L_1)>h(L_2)\). A flat grounded L-graph is an intersection graph of a flat L-collection. We now give a simple reduction to flat L-collections.
Lemma 2.1
If \(\mathcal {L}\) is an L-collection such that \(G(\mathcal {L})\) has clique number \(\omega \), then there is an improper coloring of \(\mathcal {L}\) with \(\omega \) colors so that each color class is flat.
Proof
We construct a partial order \((\mathcal {L},\preceq )\). For two L-shapes \(L_1\) and \(L_2\), we have \(L_1\preceq L_2\) if and only if \(p(L_1)\subseteq p(L_2)\) and \(h(L_1)>h(L_2)\), as in Fig. 5. It is straightforward to verify that \((\mathcal {L},\preceq )\) is a partial order. The maximum size of a chain in \((\mathcal {L},\preceq )\) is at most \(\omega \), because such a chain yields a clique in \(G(\mathcal {L})\). By the dual Dilworth Theorem, there is a partition of \(\mathcal {L}\) into at most \(\omega \) antichains, and this gives the desired improper coloring. \(\square \)
We remark that there are flat L-collections whose intersection graphs are not interval filament graphs. The example of a grounded L-graph that is not an interval filament graph given in the proof Theorem 1.3 is actually a flat grounded L-graph (see Fig. 12). We mention this because, due to other work by the authors [10, 24], interval filament graphs are polynomially \(\chi \)-bounded.
3 Pillar Assignments
In this section we will define a “pillar assignment”, which consists of points placed on the x-axis, the order in which they are placed, and their “pillars”.
Let \(\mathcal {L}\) be a flat L-collection. A base of \(\mathcal {L}\) is a point in \(\mathbb {R}\) which is not an endpoint of p(L) for any \(L\in \mathcal {L}\). This is mainly to avoid any ambiguity. Given a set of bases B and a total ordering \(\prec \) of B, we will generate a collection of (simple) curves \(\mathcal {P}=\{P_b:b\in B\}\). Each curve \(P_b\) will be a “staircase” which starts at the point (b, 0) on the x-axis and goes up and to the left. Refer to Figs. 6 and 7 for the definitions that follow.
Inductively suppose that \(b\in B\) is the smallest base according to \(\prec \) for which \(P_b\) is not yet defined. Now starting at the point (b, 0) on the x-axis we draw the curve \(P_b\) as follows.
-
(1)
If the end of the curve we are drawing is contained in some previous curve \(P_{b'}\) with \(b'\prec b\), then we immediately stop drawing, thus completing \(P_b\).
-
(2)
If the end of the curve we are drawing is contained in the horizontal segment of an L-shape \(L\in \mathcal {L}\) such that \(b\in p(L)\), and the end of the curve is not the corner of L, then we continue going horizontally to the left until either (1) occurs or we reach the corner of L.
-
(3)
Otherwise, we continue drawing the curve vertically upwards until either (1) or (2) occurs, or if neither occurs again, then we complete \(P_b\) with a one-way infinite segment.
We call the curves in \(\mathcal {P}\) constructed in this way pillars. For each \(b\in B\), we call b the base of \(P_b\). We give \(\mathcal {P}\) the same total ordering as B; thus we use \((\mathcal {P},\prec )\) and \((B,\prec )\) interchangeably. We call such a tuple \((\mathcal {P},\prec )\) ordered pillars (and \((B,\prec )\) ordered bases). We will usually not name the ordered bases; instead we will just talk about the ordered pillars \((\mathcal {P},\prec )\) and their bases.
Notice that a pillar P is formed from horizontal and vertical segments (from steps (2) and (3) respectively). We say that an L-shape \(L\in \mathcal {L}\) is a support of a pillar P if L intersects P in more than one point (equivalently, if L caused P to have a horizontal segment in some step (2)).
Next we have a key observation.
Lemma 3.1
Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\), and let \(\omega \) be the clique number of \(G(\mathcal {L})\). Then for any pillar P, the subgraph of \(G(\mathcal {L})\) induced on the L-shapes which intersect P is \(2\omega \)-colorable.
Proof
Let P be a pillar in \(\mathcal {P}\). Let \(\mathcal {L}_1\) be the set of L-shapes that intersect a horizontal segment of P, and let \(\mathcal {L}_2\) be the set of all other L-shapes that intersect P. It is enough to verify that for \(i\in \{1,2\}\), \(G(\mathcal {L}_i)\) is a permutation graph.
First we claim that each \(L\in \mathcal {L}_1\) satisfies \(b\in p(L)\), where b is the base of P. This is true if L is a support of P, so we can assume that L is not a support. Then, as L intersects a horizontal segment of P, there is a support \(L'\) of P such that \(\ell (L')<\ell (L)\) and \(h(L')<h(L)\). Since \(\mathcal {L}\) is flat, \(r(L)>r(L')>b\), and so \(b\in p(L)\) as required.
Now we give \(\mathcal {L}_1\) two total orderings \(\prec ^1\) and \(\prec ^2\). Let \(\prec ^1\) be the total ordering such that \(L\prec ^1L'\) whenever \(\ell (L)<\ell (L')\), and let \(\prec ^2\) be the total ordering such that \(L\prec ^2L'\) whenever \(h(L)>h(L')\). Thus \(\prec ^1\) orders \(\mathcal {L}_1\) from left to right by where the L-shapes intersect the x-axis and \(\prec ^2\) orders \(\mathcal {L}_1\) from top to bottom by where the L-shapes intersect the vertical line with x-coordinate b. It follows that two L-shapes in \(\mathcal {L}_1\) intersect if and only if their relative orders are different in \(\prec ^1\) and \(\prec ^2\). So \(G(\mathcal {L}_1)\) is a permutation graph.
The same idea works to show that \(G(\mathcal {L}_2)\) is a permutation graph; note that the horizontal segments of the L-shapes \(L\in \mathcal {L}_2\) can be extended to the right until \(b\in p(L)\) without changing the graph \(G(\mathcal {L}_2)\). \(\square \)
We aim to use ordered pillars to color our intersection graph. Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\). We say that an L-shape \(L\in \mathcal {L}\) is assigned to a pillar \(P\in \mathcal {P}\) if L intersects P and all other pillars in \(\mathcal {P}\) that intersect L occur later than P in the total ordering \(\prec \) on \(\mathcal {P}\). Thus each L-shape is assigned to at most one pillar in \(\mathcal {P}\). Let \(c:\mathcal {P}\rightarrow \mathbb {Z}^+\) be a coloring of \(\mathcal {P}\) and let \(\phi _{(\mathcal {P},\prec ,c)}\) be the partial, improper coloring of \(\mathcal {L}\) where an L-shape that is assigned to a pillar P is given the color c(P).
A pillar assignment of a flat L-collection \(\mathcal {L}\) is a tuple \((\mathcal {P},\prec ,c)\) such that \((\mathcal {P},\prec )\) are ordered pillars and \(c:\mathcal {P}\rightarrow \mathbb {Z}^+\) is a coloring such that if \(L_1\) and \(L_2\) are intersecting L-shapes assigned to distinct pillars \(P_1\) and \(P_2\), then \(c(P_1)\ne c(P_2)\). A pillar assignment \((\mathcal {P},\prec ,c)\) is complete if every L-shape in \(\mathcal {L}\) intersects (and so is assigned to) some pillar. Figure 7 depicts a pillar assignment and the corresponding improper coloring of the L-shapes.
We have the following lemma as a corollary to Lemma 3.1.
Lemma 3.2
Let \(\mathcal {L}\) be a flat L-collection such that \(G(\mathcal {L})\) has clique number at most \(\omega \), and let \((\mathcal {P},\prec ,c)\) be a complete pillar assignment of \(\mathcal {L}\) using at most k colors. Then the graph \(G(\mathcal {L})\) is \(2\omega k\)-colorable.
Proof
Let i be a color used by \(\phi \) and let \(\mathcal {L}_i=\{L\in \mathcal {L}:\phi _{(\mathcal {P},\prec ,c)}(L)=i\}\). It is enough to show that \(G(\mathcal {L}_i)\) is \(2\omega \)-colorable.
By the definition of pillar assignment, if two L-shapes in \(\mathcal {L}\) intersect and are assigned to different pillars, then those pillars are colored differently. Hence the L-shapes of each connected component of \(G(\mathcal {L}_i)\) all intersect a single pillar. So by Lemma 3.1, each connected component of \(G(\mathcal {L}_i)\) is \(2\omega \)-colorable and thus \(G(\mathcal {L}_i)\) itself is \(2\omega \)-colorable. \(\square \)
At this point we have reduced the coloring problem to the problem of finding a complete pillar assignment of a flat L-collection. To be more precise, by Lemmas 2.1 and 3.2, if each flat L-collection whose intersection graph has clique number \(\omega \) has a complete pillar assignment using at most k colors, then each grounded L-graph with clique number at most \(\omega \) is \(2\omega ^2 k\)-colorable.
Now we prove another important feature. The next lemma implies that if an L-shape L is uncolored, then we can color it by placing a base anywhere in p(L). Note that we write \(p(L)\times [0,h(L)]\) for the rectangle “underneath” L.
Lemma 3.3
If \(\mathcal {L}\) is a flat L-collection with ordered pillars \((\mathcal {P},\prec )\) and \(L\in \mathcal {L}\) is such that \(p(L)\times [0,h(L)]\) contains a point of a pillar P, then L is assigned to a pillar which is at most P according to \(\prec \).
Proof
It is enough to observe that if P is the smallest pillar according to \(\prec \) such that \(p(L)\times [0,h(L)]\) contains a point in P, then L must be assigned to P. \(\square \)
We will apply the following divide-and-conquer lemma to a set of bases so that we can order and color them.
Lemma 3.4
For any positive integer k and set \(B\subset \mathbb {R}\) of size at most \(2^k-1\), there exist a total ordering \(\prec \) and a k-coloring c of B such that for any \(b_1,b_2\in B\) with \(c(b_1)=c(b_2)\) and \(b_1<b_2\), there exists \(b\in (b_1,b_2)\cap B\) such that \(b\prec b_1\) and \(b\prec b_2\).
Proof
It is trivial to find such \(\prec \) and c for \(k=1\). Now we proceed by induction on k assuming that the lemma holds for \(k-1\). Choose \(b\in B\) so that \(|B_-|,|B_+|\leqslant 2^{k-1}-1\), where \(B_-=(-\infty ,b)\cap B\) and \(B_+=(b,\infty )\cap B\). Let \(\prec _-\), \(\prec _+\) and \(c_-,c_+\) be total orderings and \((k-1)\)-colorings for \(B_-\) and \(B_+\) respectively (using the same set of colors, say \(\{1,\ldots ,k-1\}\)) claimed by the lemma. Let \(\prec \) be the total ordering obtained from \(\prec _-\cup \prec _+\) by having b precede all other elements (and each element in \(B^-\) precede each element in \(B^+\)). Let c be the k-coloring obtained from \(c_-\cup c_+\) by setting \(c(b)=k\). Now \(\prec \) and c provide the desired total ordering and coloring. \(\square \)
4 Extremal Lemmas and Degree
Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\) with bases \(B\subset \mathbb {R}\). A segment of B is an open interval with ends in \(B\cup \{-\infty ,\infty \}\) that contains no point in B. So there is a unique partition of \(\mathbb {R}\setminus B\) into \(|\mathcal {P}|+1\) segments.
Recall from Sect. 2 that we wish to prove an extremal lemma regarding the “degrees” of disjoint intervals which are contained within a single segment. The “degree” of a segment \(S=(b^-,b^+)\) is the number of pillars assigned to L-shapes \(L\in \mathcal {L}\) which satisfy either condition (a) or (b), where:
-
(a)
L intersects the x-axis to the left of \(b^-\) and intersects an uncolored L-shape grounded in S,
-
(b)
L intersects the x-axis at a point between \(b^-\) and \(b^+\).
So it is helpful to break up the “degree” into two parts: the “left-degree” corresponding to condition (a) and the “right-degree” corresponding to condition (b). Unfortunately, we also need a third type of degree, called the “buffer-degree”, for technical reasons. The issue is that when we break S up into parts, the left-degree of a part can jump up suddenly. So we use the buffer-degree to provide a buffer for the left-degree. We refer the reader to Fig. 8 for an example that illustrates the following definitions of the left and right degree.
For a segment \(S=(b^-,b^+)\) and an open interval \(J\subseteq S\), the left-degree of J is the number of pillars P with base b such that \(b\leqslant b^-\) and there exist intersecting L-shapes \(L,L'\in \mathcal {L}\) such that L is assigned to pillar P and \(p(L')\subseteq J\). We denote the left-degree of J by \(d_{(\mathcal {P},\prec )}^\ell (J)\). The left \((\mathcal {P},\prec )\)-neighborhood \(N_{(\mathcal {P},\prec )}^\ell (J)\) is the set of all such pillars P. We will omit subscripts \((\mathcal {P},\prec )\) when the ordered pillars are clear from context.
In a similar manner, the buffer-degree of J is the number of pillars P with base b such that \(b\leqslant b^-\) and there exist intersecting L-shapes \(L,L'\in \mathcal {L}\) such that L is assigned to pillar P, and \(\ell (L')\in J\), and \(r(L')\in S\), and \(p(L')\setminus J\) does not contain the left endpoint of any L-shape in \(\mathcal {L}\). We denote the buffer-degree by \(d^b(J)\), and the buffer-neighborhood \(N^b(J)\) is the set of all such pillars P. Notice that \(N^\ell (J)\subseteq N^b(J)\subseteq N^\ell (S)\). It is the elements of \(N^b(J)\setminus N^\ell (J)\) that will act as the aforementioned buffer for the left-degree.
The right-degree of J is the number of pillars P with base b such that \(b\geqslant b^+\) and there exists an L-shape \(L\in \mathcal {L}\) such that L is assigned to pillar P and \(\ell (L)\in J\). Similarly, we denote the right-degree of J by \(d^r(J)\), and the right-neighborhood \(N^r(J)\) is the set of all such pillars P. Finally, the degree of J, denoted by d(J), is the sum of the left-degree and the right-degree of J.
We assume \(b_1\prec b_2\prec \cdots \prec b_6\). The pillar \(P_{b_3}\) belongs to the left neighborhood of \((b_5,b_6)\), which is witnessed by \(L_3\) and \(L_6\). The pillar \(P_{b_4}\) belongs to the right neighborhood of \((b_5,b_6)\), which is witnessed by \(L_9\). The left neighborhood of \((b_5,b_6)\) consists of \(P_{b_1},P_{b_3},P_{b_5}\), the right neighborhood of \((b_5,b_6)\) consists of \(P_{b_2},P_{b_4},P_{b_6}\). The gray area shows a region where unassigned L-shapes from \((b_5,b_6)\) must be contained
We require a lemma which was used to prove the quadratic \(\chi \)-bounding function for overlap graphs [10]. The lemma is stated somewhat differently in this paper, so we include a proof for completeness. As hinted at earlier, the lemma can be seen as a permutation graph analogue of a theorem of Capoyleas and Pach [4]. A somewhat more abstract version of this lemma with tight bounds was also proven in [9].
Lemma 4.1
(Davies and McCarty [10]) Let \(\mathcal {I}\) be a finite set of open intervals with non-empty intersection. If A is the set of endpoints of intervals in \(\mathcal {I}\) and \(\omega \) is the clique number of the overlap graph of \(\mathcal {I}\), then \(|\mathcal {I}|\leqslant \omega (|A|-1)\).
Proof
Let \(c\in \mathbb {R}\) be a point which is contained in every interval in \(\mathcal {I}\). The overlap graph of \(\mathcal {I}\) is a permutation graph where the two permutations are given by (1) the order of the leftmost endpoints of intervals in \(\mathcal {I}\) (which are all less than c) and (2) the order of the rightmost endpoints of intervals in \(\mathcal {I}\) (which are all greater than c). Since permutation graphs are perfect, there is a partition of \(\mathcal {I}\) into \(\omega \) sets, each containing no pair of overlapping intervals. Hence it is enough to prove the lemma in the case that \(\omega =1\).
This is trivial if \(|\mathcal {I}|=1\), so we can proceed inductively. It is enough to show that there exists a point in A which is an endpoint of just one interval in \(\mathcal {I}\). Let \(a^-=\max \{a\in A:a<c\}\) and \(a^+=\min \{a\in A:a>c\}\). Suppose that each of \(a^-\) and \(a^+\) are endpoints of at least two intervals in \(\mathcal {I}\). Then there exist points \(b^+,b^-\in A\) with \(b^+>a^+\) and \(b^-<a^-\) such that \((a^-,b^+)\) and \((b^-,a^+)\) are intervals in \(\mathcal {I}\). But then \((a^-,b^+)\) and \((b^-,a^+)\) overlap, a contradiction. So we conclude that either \(a^-\) or \(a^+\) is an endpoint of just one interval in \(\mathcal {I}\), as we require. \(\square \)
We now prove an extremal lemma for the buffer- and left-degrees, and then we conclude this section by proving an extremal lemma for the right-degree.
Lemma 4.2
Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\) such that \(G(\mathcal {L})\) has clique number \(\omega \). Let \(\mathcal {J}\) be a finite, non-empty collection of disjoint open intervals contained in some segment S. Then \(\sum _{J\in \mathcal {J}}d^b(J)\leqslant \omega (|\mathcal {J}|+d^\ell (S)-1)\).
Proof
We construct an auxiliary collection of open intervals \(\mathcal {I}\) where, for each \(J\in \mathcal {J}\) and \(P\in N^b(J)\), we add the interval whose endpoints are the base of P and the right endpoint of J. We can assume that \(\mathcal {I}\) is non-empty, otherwise the lemma is trivially true. Thus \(\mathcal {I}\) has non-empty intersection (as every interval in \(\mathcal {I}\) contains the leftmost interval in \(\mathcal {J}\)). Furthermore, \(|\mathcal {I}|=\sum _{J\in \mathcal {J}}d^b(J)\) and the intervals in \(\mathcal {I}\) have at most \(|\mathcal {J}|+|\bigcup _{J\in \mathcal {J}}N^b(J)|\) different endpoints. By the definition of the buffer- and left-degrees, \(|\bigcup _{J\in \mathcal {J}}N^b(J)|\leqslant d^\ell (S)\). Therefore, by Lemma 4.1, if the overlap graph of \(\mathcal {I}\) has clique number at most \(\omega \), then \(\sum _{J\in \mathcal {J}}d^b(J)\leqslant \omega (|\mathcal {J}|+d^\ell (S)-1)\) as required.
So suppose the overlap graph of \(\mathcal {I}\) has clique number greater than \(\omega \). It follows that there are intervals \(J_1,\ldots ,J_{\omega +1}\in \mathcal {J}\) and pillars \(P_1\in N^b(J_1),\ldots ,P_{\omega +1}\in N^b(J_{\omega +1})\) with \(b_1<\cdots<b_{\omega +1}<j_1<\cdots <j_{\omega +1}\), where \(b_1,\ldots ,b_{\omega +1}\) are the bases of \(P_1,\ldots ,P_{\omega +1}\) and \(j_1,\ldots ,j_{\omega +1}\) are the rightmost endpoints of \(J_1,\ldots ,J_{\omega +1}\), respectively. Therefore, there exist L-shapes \(L_1,\ldots ,L_{\omega +1},L_1',\ldots L_{\omega +1}'\in \mathcal {L}\) such that for each \(i\in \{1,\ldots ,\omega +1\}\), \(L_i\) is assigned to \(P_i\) and intersects \(L_i'\), and \(\ell (L_i')\in J_i\), and \(p(L_i'){\setminus } J_i\) does not contain the left endpoint of any L-shape in \(\mathcal {L}\).
Notice that \(P_1\prec \cdots \prec P_{\omega +1}\); this follows from Lemma 3.3 since \(b_i,\ldots ,b_{\omega +1}\in p(L_i)\) for each \(i\in \{1,\ldots ,\omega +1\}\). Hence, again by Lemma 3.3, \(\ell (L_1)\in (-\infty ,b_1)\) and \(\ell (L_i)\in (b_{i-1},b_i)\) for \(i>1\). So in particular \(\ell (L_1)<\cdots <\ell (L_{\omega +1})\). Since the clique number of the intersection graph of \(\mathcal {L}\) is at most \(\omega \), there exist some \(i<j\) such that \(L_i\) does not intersect \(L_j\). So \(h(L_i)>h(L_j)\). But then, as \(L_j\) intersects \(L_j'\), and \(L_i\) intersects \(L_i'\), and \(\mathcal {L}\) is flat, it follows that \(\ell (L_j')\in p(L_i')\setminus J_i\), a contradiction. \(\square \)
We now wish to obtain a similar lemma for the right-degree. This one requires an extra factor of \(\omega \). In order to prove the lemma for the right degree, it is helpful to introduce another configuration that yields a clique elsewhere. Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\). We say that L-shapes \(L_1,\ldots ,L_t\) are cascading if there exist pillars \(P_1,\ldots ,P_t\) with bases \(b_1,\ldots ,b_t\) respectively such that
-
(1)
\(\ell (L_1)<\cdots<\ell (L_t)<b_1<\cdots <b_t\),
-
(2)
\(h(L_1)>\cdots >h(L_t)\) and \(P_1\succ \cdots \succ P_t\), and
-
(3)
\(L_t\) is a support of \(P_t\) and for each \(i<t\), \(L_i\) is assigned to \(P_i\).
We purposefully do not require that \(L_t\) is assigned to \(P_t\). See Fig. 9 for an example of cascading L-shapes, as well as one way that they may yield a clique.
Next we prove that cascading L-shapes \(L_1,\ldots ,L_t\) yield a clique of size t. It is convenient for the sake of induction to prove the following stronger statement.
Lemma 4.3
Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((\mathcal {P},\prec )\) and cascading L-shapes \(L_1,\ldots ,L_t\). Then there is a clique \(\{L_1^*,\ldots ,L_t^*\}\) in the intersection graph \(G(\mathcal {L})\) such that \(\ell (L_1^*)<\cdots <\ell (L_t^*)\), \(L^*_i\) supports \(P_i\) for each \(i\leqslant t\), and \(L_t^*=L_t\).
Cascading L-shapes \(L_1,L_2,L_3,L_4\), and one possible configuration of pairwise intersecting L-shapes \(L_1^*,L_2^*,L_3^*,L_4^*=L_4\) as in the conclusion of Lemma 4.3
Proof
We prove the claim by induction on t. The base case of \(t=1\) holds trivially. For the induction step, let \(P_1,\ldots ,P_t\) be the pillars corresponding to \(L_1,\ldots ,L_t\), with bases \(b_1,\ldots ,b_t\) respectively.
By condition (3), \(b_t\in p(L_t)\); so \(b_1,\ldots ,b_t\in p(L_t)\) as well. By condition (2), the pillar \(P_{t-1}\) must intersect \(L_t\). In fact, since \(L_t\) supports \(P_t\) and \(P_t\prec P_{t-1}\), the pillar \(P_{t-1}\) first intersects \(L_t\) at a point on the vertical segment of \(L_t\) (otherwise it would end on the horizontal segment of \(L_t\) without ever reaching \(L_{t-1}\)). So there is a support \(L_{t-1}^*\) of \(P_{t-1}\) with \(\ell (L_{t-1}^*)<\ell (L_t)\) such that \(L_{t-1}^*\) and \(L_t\) intersect. If \(t=2\), then we are done, so assume \(t\geqslant 3\). If \(\ell (L_{t-1}^*)<\ell (L_{t-2})\), then \(L_{t-1}^*\) and \(L_{t-2}\) intersect, as \(h(L_{t-1}^*)<h(L_t)<h(L_{t-2})\). But then, by Lemma 3.3, \(L_{t-2}\) cannot be assigned to pillar \(P_{t-2}\), as \(L_{t-1}^*\) supports \(P_{t-1}\) and \(P_{t-1}\prec P_{t-2}\), a contradiction. Thus \(\ell (L_{t-2})<\ell (L_{t-1}^*)\), so \(L_1,\ldots ,L_{t-2},L_{t-1}^*\) are cascading. The induction hypothesis yields a clique \(\{L_1^*,\ldots ,L_{t-1}^*\}\) such that \(\ell (L_1^*)<\cdots <\ell (L_{t-1}^*)\) and \(L_i^*\) supports \(P_i\) for each \(i\leqslant t-1\). Adding \(L_t\) to extends this clique to a requested clique for t. \(\square \)
We complete this section by proving the extremal lemma for the right-degree.
Lemma 4.4
Let \(\mathcal {L}\) be a flat L-collection with ordered pillars \((P,\prec )\) such that \(G(\mathcal {L})\) has clique number \(\omega \). Let \(\mathcal {J}\) be a finite, non-empty collection of disjoint open intervals contained in some segment S. Then \(\sum _{J\in \mathcal {J}}d^r(J)\leqslant 2\omega (2\omega -1)(|\mathcal {J}|+d^r(S)-1)\).
Proof
Like in the proof of Lemma 4.2, we construct a collection of open intervals \(\mathcal {I}\) where, for each \(J\in \mathcal {J}\) and \(P\in N^r(J)\), we add an interval between the left endpoint of J and the base of P. We can assume that \(\mathcal {I}\) is non-empty, otherwise the lemma is trivially true. Thus \(\mathcal {I}\) has non-empty intersection (as every interval in \(\mathcal {J}\) contains the rightmost interval in \(\mathcal {J}\)). Furthermore, \(|\mathcal {I}|=\sum _{J\in \mathcal {J}}d^r(J)\) and the intervals in \(\mathcal {I}\) have at most \(|\mathcal {J}|+|\bigcup _{J\in \mathcal {J}}N^r(J)|\leqslant |\mathcal {J}|+d^r(S)\) different endpoints. Therefore, by Lemma 4.1, if the overlap graph of \(\mathcal {I}\) has clique number at most \(2\omega (2\omega -1)\), then \(\sum _{J\in \mathcal {J}}d^r(J)\leqslant 2\omega (2\omega -1)(|\mathcal {J}|+d^r(S)-1)\) as required.
So suppose the overlap graph of \(\mathcal {I}\) has clique number greater than \(2\omega (2\omega -1)\). It follows that there are L-shapes \(L_1,\ldots ,L_{2\omega (2\omega -1)+1}\) which are assigned to pillars \(P_1,\ldots ,P_{2\omega (2\omega -1)+1}\) with bases \(b_1,\ldots ,b_{2\omega (2\omega -1)+1}\) respectively, such that
We claim that \(P_1\succ \cdots \succ P_{2\omega (2\omega -1)+1}\) as well. Otherwise, if \(P_i\prec P_j\) for some \(i<j\), then \(L_j\) intersects \(L_i\), as \(L_j\) must intersect \(P_j\) and not \(P_i\). Furthermore, since \(\mathcal {L}\) is flat, we have \(r(L_j)>r(L_i)\). But then \([\ell (L_j),r(L_i)]\times [0,h(L_i)]\subset p(L_j)\times [0,h(L_j)]\) must contain a point of \(P_i\), contradicting Lemma 3.3.
Now, by the Erdős–Szekeres Theorem [11], the sequence \(h(L_1),\ldots ,h(L_{2\omega (2\omega -1)+1})\) contains either a decreasing subsequence of size \(2\omega +1\) or an increasing subsequence of size \(2\omega \). We take care of the two cases separately.
Case 1. There are indices \(i_1<\cdots <i_{2\omega +1}\) such that \(h(L_{i_1})>\cdots >h(L_{i_{2\omega +1}})\).
We already have conditions (1) and (2) for the L-shapes \(L_{i_1},\ldots ,L_{i_{2\omega +1}}\) to be cascading. So, roughly, it remains to find a special L-shape \(L'\) which supports its pillar. First, if \(b_{i_{\omega +1}}\notin p(L_{i_{2\omega +1}})\), then (since \(\mathcal {L}\) is flat) there must exist an L-shape \(L'\) supporting \(P_{i_{2\omega +1}}\) with \(\ell (L_{i_{2\omega +1}})<\ell (L')<b_{i_{\omega +1}}\) and \(h(L')<h(L_{i_{2\omega +1}})\). But then the L-shapes \(L_{i_{\omega +1}},\ldots ,L_{i_{2\omega }},L'\) are cascading, and by Lemma 4.3 there is a clique of size \(\omega +1\), a contradiction.
Hence \(b_{i_{\omega +1}}\in p(L_{i_{2\omega +1}})\). Now there exists an L-shape \(L'\) supporting \(P_{i_{\omega +1}}\) with \(\ell (L')\leqslant \ell (L_{i_{2\omega +1}})\) and \(h(L')\leqslant h(L_{i_{2\omega +1}})\) (possibly with \(L'=L_{i_{2\omega +1}}\)). We also have \(\ell (L_\omega )<\ell (L')\), otherwise \(L_\omega \) and \(L'\) intersect and, since \(\mathcal {L}\) is flat, \(b_{i_{\omega +1}}\in p(L_{\omega })\), which contradicts the fact that \(L_\omega \) is assigned to \(P_\omega \). But now the L-shapes \(L_{i_1},\ldots ,L_{i_{\omega }},L'\) are cascading, again contradicting Lemma 4.3.
Case 2. There are indices \(j_1<\cdots <j_{2\omega }\) such that \(h(L_{j_1})<\cdots <h(L_{j_{2\omega }})\).
Now there exists \(t\in \{1,\ldots ,\omega \}\) such that \(\ell (L_{j_{\omega +1}})\notin p(L_{j_t})\), otherwise \(L_{j_1},\ldots ,L_{j_{\omega +1}}\) would form a clique of size \(\omega +1\). Since \(L_{j_t}\) intersects the pillar \(P_{j_t}\), there exists an L-shape \(L'\) with \(\ell (L')<\ell (L_{j_{\omega +1}})\) and \(h(L')<h(L_{j_t})<h(L_{j_{\omega +1}})\) that supports \(P_{j_t}\). But now, since \(\mathcal {L}\) is flat, the L-shapes \(L',L_{j_{\omega +1}},\ldots ,L_{j_{2\omega }}\) form a clique of size \(\omega +1\), a contradiction. This completes the proof of Lemma 4.4. \(\square \)
5 Main Result
Theorem 1.1 will follow quickly from the main proposition below on finding complete pillar assignments. Recall that the degree is the sum of the left- and right-degrees.
Proposition 5.1
Every flat L-collection whose intersection graph has clique number \(\omega \) has a complete pillar assignment using at most \(4\omega ^2-\omega +2\lceil 4\log _2\omega \rceil +11\) colors.
Proof
This is certainly true when \(\omega =1\) because, by Lemma 3.3, we can continue placing bases until every L-shape is assigned (we give every pillar the same color). So we can assume that \(\omega \geqslant 2\).
Throughout the proof we will only use colors in \(\{1,\ldots ,4\omega ^2-\omega +2\lceil 4\log _2\omega \rceil +11\}\). Now, choose a pillar assignment \((\mathcal {P},\prec ,c)\) so that
-
(1)
each segment has degree at most \(4\omega ^2-\omega +\lceil 4\log _2\omega \rceil +6\), and
-
(2)
subject to the above, \(\phi _{(\mathcal {P},\prec ,c)}\) colors as many L-shapes in \(\mathcal {L}\) as possible.
Suppose for the sake of contraction that \((\mathcal {P},\prec ,c)\) is not complete. Then there is an L-shape \(L^*\in \mathcal {L}\) which is not assigned to any pillar. Let \(S=(b^-,b^+)\) be the segment containing \(\ell (L^*)\). Also, let B be the set of the bases of the pillars in \(\mathcal {P}\).
We have the following key claim. Note that in both the statement of the claim and its proof, all degrees are with respect to the ordered pillars \((\mathcal {P},\prec )\).
Claim 5.1.1
There exists a set \(B^*\subset S\) of at most \(32\omega ^4-1\) bases such that the set \(B^*\cap p(L^*)\) is non-empty and each segment of \(B\cup B^*\) which is contained in S has degree at most \(4\omega ^2-\omega +1\).
Proof
Choose bases \(b^-=b_0<\cdots<b_t<b^+\) so that for each \(i\in \{1,\ldots ,t\}\), the degree of \((b_{i-1},b_i)\) is at most \(4\omega ^2-\omega +1\), and either \(d^b(b_{i-1},b_i)\geqslant \omega +1\) or \(d^r(b_{i-1},b_i)\geqslant 4\omega ^2-2\omega +1\), and subject to this, \(t\geqslant 0\) is maximized. A maximum t exists because the second condition ensures that there is an L-shape with left endpoint in \((b_{i-1},b_i)\), and \(\mathcal {L}\) is finite.
We claim that the degree of \((b_t,b^+)\) is at most \(4\omega ^2-\omega +1\). Otherwise we will place another base \(b_{t+1}\) between \(b_t\) and \(b^+\); consider starting with \(b_{t+1}\) just slightly past \(b_t\) and moving \(b_{t+1}\) past a single point in \(\{\ell (L):L\in \mathcal {L}\}\cup \{r(L):L\in \mathcal {L}\}\) at a time. If \(b_{t+1}\) is moved past a left endpoint, then the left-degree does not change and the right-degree goes up by at most 1. Otherwise, \(b_{t+1}\) is moved past some right endpoint to a new location \(b_{t+1}'\). Then the right-degree does not change and the left-degree goes up by at most \(d^b(b_t,b_{t+1})-d^\ell (b_t,b_{t+1})\) because \(N^\ell (b_t,b_{t+1}')\subseteq N^b(b_t,b_{t+1})\). It follows that if \(b_{t+1}'\) is the first location where the degree is greater than \(4\omega ^2-\omega +1\), then the previous location \(b_{t+1}\) gives a contradiction to the choice of t.
Now, let \(\mathcal {J}_a\) be the set of segments of \(B\cup \{b_1,\ldots ,b_t\}\) which are contained in S and have buffer-degree at least \(\omega +1\), and let \(\mathcal {J}_r\) be the set of segments of \(B\cup \{b_1,\ldots ,b_t\}\) which are contained in S and have right-degree at least \(4\omega ^2-2\omega +1\). By definition, we have \(|\mathcal {J}_a|+|\mathcal {J}_r|\geqslant t\). By Lemmas 4.2 and 4.4, we have
As a consequence, we have
As both sides of the inequalities are integers and \(t\leqslant |\mathcal {J}_a|+|\mathcal {J}_r|\), summing the right sides and then using the fact that \(\omega \geqslant 2\), we obtain
Finally, let \(b\in p(L^*)\); then \(B^*=\{b,b_1,\ldots ,b_t\}\) provides the desired subset of S. \(\square \)
Now fix \(B^*\subset S\) as in the claim, with \(|B^*|\leqslant 32\omega ^4-1\). Observe that, by the choice of \((\mathcal {P},\prec ,c)\), there are \(\lceil 4\log _2\omega \rceil +5=\lceil \log _2(32\omega ^4)\rceil \) colors available which are not used to color any pillar in \(N^\ell (S)\cup N^r(S)\) (where neighborhoods are with respect to \((\mathcal {P},\prec )\)). So by Lemma 3.4 (the divide-and-conquer lemma), there exist a total ordering \(\prec ^*\) and a coloring \(c^*\) of \(B^*\) such that \(c^*\) uses only these available colors and, for all \(b,b'\in B^*\) with \(b<b'\) and \(c^*(b)=c^*(b')\), there exists \(b^*\in (b,b')\cap B^*\) such that \(b^*\prec ^*b\) and \(b^*\prec ^*b'\).
Now, beginning with \((\mathcal {P},\prec ,c)\), we place additional pillars \(\mathcal {P}^*\) at the bases in \(B^*\) according to the ordering \(\prec ^*\) and color them according to \(c^*\) in order to obtain a new pillar assignment \(\mathcal {A}^*=(\mathcal {P}\cup \mathcal {P}^*,\prec \cup \prec ^*,c\cup c^*)\) (note that we also view \(c^*\) as a coloring of \(\mathcal {P}^*\) and that each pillar in \(\mathcal {P}\) precedes each pillar in \(\mathcal {P}^*\)). We will show that \(\mathcal {A}^*\) is a pillar assignment which contradicts the choice of \((\mathcal {P},\prec ,c)\).
Claim 5.1.2
If \(L\in \mathcal {L}\) is colored by \(\phi _{\mathcal {A}^*}\) but not \(\phi _{(\mathcal {P},\prec ,c)}\), then \(p(L)\subset S\).
Proof
By Lemma 3.3 we know that p(L) is contained in a segment of B. So if p(L) is not contained in \(S=(b^-,b^+)\), then \(\ell (L)<b^-\) and L would have been colored by either the pillar with base \(b^-\) or an earlier pillar, a contradiction. \(\square \)
The next two claims will complete the proof.
Claim 5.1.3
The tuple \(\mathcal {A}^*\) is a pillar assignment such that \(\phi _{\mathcal {A}^*}\) colors more L-shapes than \(\phi _{(\mathcal {P},\prec ,c)}\) does.
Proof
The latter statement will be easy, as \(L^*\) is not colored by \(\phi _{(\mathcal {P},\prec ,c)}\) but is colored by \(\phi _{\mathcal {A}^*}\) (since \(B^*\cap p(L^*)\) is non-empty). So it just remains to show that \(\mathcal {A}^*\) is a pillar assignment. Going for a contradiction, suppose that \(L_1\) and \(L_2\) are intersecting L-shapes assigned respectively to pillars \(P_1\) and \(P_2\) of the same color. Then one of the L-shapes, say \(L_1\), is not colored by \(\phi _{(\mathcal {P},\prec ,c)}\). So \(p(L_1)\subset S\) by Claim 5.1.2. Then, by the choice of \(c^*\), the other L-shape \(L_2\) is not colored by \(\phi _{(\mathcal {P},\prec ,c)}\) either. Thus, there is a base \(b^*\in B^*\) which lies between the bases of \(P_1\) and \(P_2\) and earlier than both according to \(\prec ^*\). But then either \(L_1\) or \(L_2\) would have been colored by the pillar with base \(b^*\) or an earlier pillar, a contradiction. \(\square \)
Claim 5.1.4
The degree of each segment of \(\mathcal {A}^*\) with respect to \((\mathcal {P}\cup \mathcal {P}^*,\prec \cup \prec ^*)\) is at most \(4\omega ^2-\omega +\lceil 4\log _2\omega \rceil +6\).
Proof
Let \(S^*\) be a segment of \(\mathcal {A}^*\). If \(S^*\) is disjoint from S, then its degree does not change, so we can assume that \(S^*\subset S\). Now consider a pillar P with base b which contributes to the degree of \(S^*\) in \((\mathcal {P}\cup \mathcal {P}^*,\prec \cup \prec ^*)\). If \(b\in B\), then P contributes to the degree of \(S^*\) in \((\mathcal {P},\prec )\) as well; by Claim 5.1.1 there are at most \(4\omega ^2-\omega +1\) such pillars P. If \(b\in B^*\), then there cannot be any earlier base in \(\prec ^*\) which is between b and the endpoint of \(S^*\) closer to b; so there is at most one such pillar P for each color of \(c^*\). In total the new degree is at most
which completes the proof of the claim. \(\square \)
By the above two claims, \(\mathcal {A}^*\) is a pillar assignment which contradicts the choice of \((\mathcal {P},\prec ,c)\). This therefore completes the proof of Proposition 5.1. \(\square \)
Theorem 1.1 now quickly follows.
Proof of Theorem 1.1
We can assume that \(\omega \geqslant 2\), otherwise the theorem is trivially true. Combining Proposition 5.1 with Lemmas 2.1 and 3.2, we infer that the grounded L-graph has chromatic number at most \((2\omega ^2)(4\omega ^2-\omega +2\lceil 4\log _2\omega \rceil +11)\). So the theorem holds if \(\omega =2\). If \(\omega \geqslant 3\), then
and still the theorem holds. \(\square \)
6 Separation Results
The goal of this section is to prove the separation results of Theorem 1.3. For all of our constructions, we would like to force that some objects are attached to the grounding line in some specific order. Such an approach was already used by Cardinal et al. [5], who observed that a simple family of grounded strings representing a cycle has a fairly rigid structure, which yields a specific order of the base points of strings from this family and the base points of strings representing vertices “appropriately” adjacent to the cycle. This is formalized in the so-called Cycle Lemma [5, Lem. 6], which was proved for various subclasses of outer-1-string graphs. The separation results obtained by Jelínek and Töpfer [19] are based on similar ideas. In our work, we use a weaker version of Cycle Lemma for outer-1-string graphs, sufficient for our applications. Moreover, it turns out that in the class of interval filament graphs, a cycle also has a fairly rigid representation, which allows us to control the ranges of the domains representing the vertices from the cycle as well as vertices “appropriately” adjacent to the cycle. This idea is brought to life in what we call the Cycle Lemma for Interval Filament Graphs.
Before we prove the Cycle Lemma for Interval Filament Graphs, we need some preparation. Suppose G is an intersection graph of a family of interval filaments \(\mathcal {F}\). Given a vertex v in G, we let \(r_\mathcal {F}(v)\) denote the interval filament in \(\mathcal {F}\) representing v and \({{\,\textrm{dom}\,}}_\mathcal {F}(v)\) denote the domain of \(r_\mathcal {F}(v)\). Usually we omit the subscript if the family \(\mathcal {F}\) is clear from the context. Given a path P in G, we say that P is represented in \(\mathcal {F}\) by a chain of overlapping interval filaments if the consecutive vertices on P can be labeled by \(v_1,\ldots ,v_k\) so that the following holds:
-
for every \(i\in [k-2]\), we have \({{\,\textrm{dom}\,}}(v_i)<{{\,\textrm{dom}\,}}(v_{i+2})\),
-
for every \(i\in [k-1]\), the intervals \({{\,\textrm{dom}\,}}(v_i)\) and \({{\,\textrm{dom}\,}}(v_{i+1})\) overlap.
See Fig. 10 for an illustration.
A path \(P=v_1\ldots v_7\) in C (depicted in red) is represented by a chain of overlapping interval filaments. A curve J (defined in the proof of Lemma 6.1) is drawn with a dashed blue line
Lemma 6.1
(Cycle Lemma for Interval Filament Graphs) Let G be the intersection graph of a family of interval filaments \(\mathcal {F}\). Suppose a set \(C\subset V(G)\) induces a cycle of size n in G for some \(n\geqslant 7\). Then there is a path P of size \(n-4\) in C such that P is represented in \(\mathcal {F}\) by a chain of overlapping interval filaments (see Fig. 10).
Suppose \(k=n-4\) and \(v_1\ldots v_k\) are the consecutive vertices of P enumerated so that \({{\,\textrm{dom}\,}}(v_i)\) is to the left of \({{\,\textrm{dom}\,}}(v_j)\) for \(i<j\). If v is a vertex in \(V\setminus C\) adjacent to the vertices \(v_i\) and \(v_j\) for some \(i,j\in [2,k-1]\) with \(i<j\) and all the neighbors of v from C are contained in the set \(\{v_i,\ldots ,v_j\}\), then the left endpoint of \({{\,\textrm{dom}\,}}(v)\) is contained in \({{\,\textrm{dom}\,}}(v_i)\) and the right endpoint of \({{\,\textrm{dom}\,}}(v)\) is contained in \({{\,\textrm{dom}\,}}(v_j)\).
Proof
Suppose a, b, and c are three pairwise non-adjacent vertices in C. Consider the intervals \({{\,\textrm{dom}\,}}(a)\), \({{\,\textrm{dom}\,}}(b)\), and \({{\,\textrm{dom}\,}}(c)\). We claim that they are pairwise disjoint or one of them contains the remaining two, which are disjoint. Suppose otherwise. Assume without loss of generality that \({{\,\textrm{dom}\,}}(a)\) is contained in \({{\,\textrm{dom}\,}}(b)\) and that either \({{\,\textrm{dom}\,}}(b)\) is contained in \({{\,\textrm{dom}\,}}(c)\) or \({{\,\textrm{dom}\,}}(b)\) and \({{\,\textrm{dom}\,}}(c)\) are disjoint. In either case, some vertex on the path in C that joins a and c and avoids b is represented by an interval filament that intersects r(b), which cannot happen.
Next, we claim that there are two non-adjacent vertices \(u,w\in C\) such that \({{\,\textrm{dom}\,}}(u)\) is contained in \({{\,\textrm{dom}\,}}(w)\). Suppose otherwise. Since \(n\geqslant 7\), it follows from the above that any two non-adjacent vertices in C have disjoint domains, which implies that the domains of any two adjacent vertices in C overlap. Consequently, the two neighbors of the vertex in C with left-most (or right-most) domain must overlap, which is a contradiction.
Let \(u,w\in C\) be such that \({{\,\textrm{dom}\,}}(u)\) is contained in \({{\,\textrm{dom}\,}}(w)\). Let \(P'\) be the set that consists of all the vertices from C except for w and its two neighbors, \(w'\) and \(w''\). Thus \(P'\) induces a path \(w_1\ldots w_{n-3}\) in G where \(w'w_1\) and \(w_{n-3}w''\) are edges of C. Since \(P'\) contains u and no vertex of \(P'\) is adjacent to w, the domains of the interval filaments representing the vertices in \(P'\) are contained in \({{\,\textrm{dom}\,}}(w)\). In view of our first claim, this implies that any two non-adjacent vertices in P have disjoint domains. It follows that the domains of any two inner vertices in \(P'\) that are adjacent must overlap. It could happen that \({{\,\textrm{dom}\,}}(w_1)\subset {{\,\textrm{dom}\,}}(w_2)\) or \({{\,\textrm{dom}\,}}(w_{n-3})\subset {{\,\textrm{dom}\,}}(w_{n-4})\) – see Fig. 11. Still, we cannot have \({{\,\textrm{dom}\,}}(w_1)\subset {{\,\textrm{dom}\,}}(w_2)\) and \({{\,\textrm{dom}\,}}(w_{n-3})\subset {{\,\textrm{dom}\,}}(w_{n-4})\) at the same time. Indeed, supposing otherwise, the domains of \(w'\) and \(w''\) would contain the interval \(\bigcup _{i\in [n-3]}{{\,\textrm{dom}\,}}(w_i)\), which would imply that the intervals \({{\,\textrm{dom}\,}}(w'')\) and \({{\,\textrm{dom}\,}}(w')\) are nested. If \({{\,\textrm{dom}\,}}(w'')\subset {{\,\textrm{dom}\,}}(w')\), then \(r(w_1)\) intersects \(r(w'')\), as \(r(w_1)\) intersects \(r(w')\) and \(r(w'')\) and \(r(w')\) are disjoint, which cannot happen. See Fig. 11 for an illustration. We obtain an analogous contradiction if \({{\,\textrm{dom}\,}}(w')\subset {{\,\textrm{dom}\,}}(w'')\). We conclude that \(P'-\{w_1\}\) or \(P'-\{w_{n-3}\}\) is a path of size \(n-4\) represented by a chain of overlapping interval filaments.
Illustration for the proof of Lemma 6.1
For the proof of the second part of the lemma, let L and R denote the right endpoint of \({{\,\textrm{dom}\,}}(v_1)\) and the left endpoint of \({{\,\textrm{dom}\,}}(v_k)\), respectively. We have \(L<R\) as \(k\geqslant 3\). Let J be any curve from L to R that is contained in the interval filaments representing the path \(P''\) of C from \(v_1\) to \(v_k\) avoiding \(v_2,\ldots ,v_{k-1}\). See Fig. 10 for an illustration. Since v is not adjacent to the vertices of \(P''\), the curve J does not intersect r(v). It follows that \({{\,\textrm{dom}\,}}(v)\) is contained in the interval (L, R). Now the assertion follows directly from the fact that the vertices \(v_1,\ldots ,v_k\) are represented by a chain of overlapping intervals. \(\square \)
Suppose that G is the intersection graph of a simple family of grounded curves \(\mathcal {F}\). Given a vertex \(v\in G\), we let \(s_\mathcal {F}(v)\) denote the string representing the vertex v and \(b_\mathcal {F}(v)\) denote the base of \(s_\mathcal {F}(v)\). Again, we omit the subscript if \(\mathcal {F}\) is clear from the context. The next lemma is a weaker version of the Cycle Lemma proved in [5]. For the sake of completeness, we include its proof, which follows the same reasoning as the proof in [5].
Lemma 6.2
(Cycle Lemma for Outer-1-string Graphs) Suppose G is the intersection graph of a simple family of grounded curves \(\mathcal {F}\). Let \(I\subset C\subset V(G)\) be such that G[C] induces a cycle in G and I is an independent set in C. Then the cyclic order of the vertices from I given by their occurrence on C coincides, up to reversal, with the cyclic order of their base points on the grounding line obtained by making the leftmost base point follow the rightmost one.
Proof
For every \(c\in C\), the string s(c) intersects two strings \(s(c')\) and \(s(c'')\), where \(c'\) and \(c''\) are the neighbors of c in C: the part of s(c) between b(c) and the first intersection point is called the initial part of s(c) and denoted by i(c), and the part between the two intersection points is called the central part of s(c). The union of all the central parts of the vertices of C forms a Jordan curve, denoted by J(C). Note that the interiors of the initial parts i(c) for \(c\in C\) as well as J(C) are pairwise disjoint.
Let \(v_0,\ldots ,v_{n-1}\) be the vertices in I ordered so that \(b(v_i)<b(v_j)\) whenever \(i<j\). The endpoints of \(i(v_0)\) and \(i(v_{n-1})\) on J(C) partition J(C) into two parts, exactly one of which, say \(J'(C)\), contains the central parts of all the vertices \(v_1,\ldots ,v_{n-2}\), otherwise some vertex from \(v_1,\ldots ,v_{n-2}\) would have its base outside the interval \([b(v_0),b(v_{n-1})]\). Now, we easily observe that when we traverse \(J'(C)\) from the endpoint of \(i(v_0)\) to the endpoint of \(i(v_{n-1})\), we encounter the central parts of the vertices \(v_1,\ldots ,v_{n-2}\) in that exact order. The lemma follows, as the central parts of the vertices from C occur in J(C) in the order corresponding to their occurrence on C. \(\square \)
Now, we are ready to prove the separation theorem.
Proof of Theorem 1.3
Recall that we need to prove the following:
-
(1)
There is a (flat) grounded L-graph which is not an interval filament graph.
-
(2)
There is a monotone L-graph which is not an interval filament graph.
-
(3)
There is a polygon-circle graph which is not an outer-1-string graph.
First we prove statement (1). For an integer \(n\geqslant 3\), consider the graph \(G_n\) that consists of:
-
a cycle C of size 2n, whose consecutive vertices are denoted by \(v_0\), \(v_{\{0,1\}}\), \(v_1\), \(v_{\{1,2\}}\), \(\ldots \), \(v_{n-1}\), \(v_{\{n-1,0\}}\),
-
a vertex \(v_{\{i,i+1,i+2\}}\) for every \(i\in [n-1]\), adjacent to the vertices \(v_i,v_{i+1},v_{i+2}\) (where we take indices modulo n). Note that there is no vertex \(v_{\{0,1,2\}}\).
Observe that \(G_n\) is the intersection graph of a flat L-collection – see Fig. 12 for an illustration of \(G_5\).
For large enough n, the graph \(G_n\) is not an interval filament graph. Suppose for the sake of contradiction that \(G_n\) has an intersection model in the set of interval filaments for some \(n\geqslant 9\). First, consider the cycle C in \(G_n\). By the Cycle Lemma for Interval Filament Graphs, in any representation of C as an interval filament graph, there is a subpath P of size \(2n-4>13\) such that the vertices of P are represented by a chain of overlapping interval filaments. Note that P is long enough so that there exists \(i\in [n-1]\) such that \(v_i,v_{i+1},v_{i+2},v_{i+3}\) are the inner vertices of P and \(v_{\{i,i+1,i+2\}}\) and \(v_{\{i+1,i+2,i+3\}}\) are vertices of \(G_n\). Then, by the Cycle Lemma for Interval Filament Graphs, the left endpoint of \({{\,\textrm{dom}\,}}(v_{\{i,i+1,i+2\}})\) needs to be contained in \({{\,\textrm{dom}\,}}(v_i)\) and its right endpoint in \({{\,\textrm{dom}\,}}(v_{i+2})\), and similarly the left endpoint of \({{\,\textrm{dom}\,}}(v_{\{i+1,i+2,i+3\}})\) needs to be contained in \({{\,\textrm{dom}\,}}(v_{i+1})\) and its right endpoint in \({{\,\textrm{dom}\,}}(v_{i+3})\). However, then the interval filaments of \(v_{\{i,i+1,i+2\}}\) and \(v_{\{i+1,i+2,i+3\}}\) intersect, which is a contradiction.
To prove statement (2), consider the graph G that consists of:
-
a cycle C whose consecutive vertices are denoted by \(v^1_0,\ldots ,v^1_{10}\), \(v^2_0,\ldots ,v^2_{10}\),
-
four vertices \(a^1,b^1,a^2,b^2\) such that for every \(i\in [2]\) the vertex \(a^i\) is adjacent to \(b^i,v^i_1,v^i_2\) and the vertex \(b^i\) is adjacent to \(a^i,v^i_4,v^i_5\).
See Fig. 13 that illustrates G as the intersection graph of monotone L-shapes.
We will show that G is not an interval filament graph. Suppose otherwise, that G has an intersection model in the set of interval filaments. By the Cycle Lemma for Interval Filament Graphs, there is \(i\in [2]\) such that the path \(v^i_0,\ldots ,v^i_6\) is represented by a chain of overlapping interval filaments – see Fig. 13 to the right. Again by the same lemma, \({{\,\textrm{dom}\,}}(a^i)\) is contained in \({{\,\textrm{dom}\,}}(v^i_1)\cup {{\,\textrm{dom}\,}}(v^i_2)\) and \({{\,\textrm{dom}\,}}(b^i)\) is contained in \({{\,\textrm{dom}\,}}(v^i_4)\cup {{\,\textrm{dom}\,}}(v^i_5)\). However, since these sets are disjoint, the interval filaments representing \(a^i\) and \(b^i\) are disjoint as well, which is a contradiction.
To prove statement (3), consider the graph G that consists of
-
a cycle C, whose consecutive vertices are denoted by \(v^0_0,\ldots ,v^0_5\), \(v^1_0,\ldots ,v^1_5\), \(\ldots \), \(v^4_0,\ldots ,v^4_5\),
-
two adjacent vertices a and b such that a is adjacent to \(v^i_0,v^i_4\) for every \(i\in [0,4]\) and b is adjacent to \(v^i_2\) for every \(i\in [0,4]\).
Note that G is a polygon-circle graph – see Fig. 14 for an illustration of G.
We will show that G is not an outer-1-string graph. Suppose G is the intersection graph of a simple family of grounded curves \(\mathcal {F}\). Let I be the independent set in G consisting of the vertices \(\{v^i_0,v^i_2,v^i_4:i\in [4]\}\). The Cycle Lemma for Outer-1-string Graphs asserts that the order of the bases of the strings representing the vertices of I coincides with its order on the cycle C. It follows that there is \(i\in [0,4]\) such that either
-
\(b(v^j_0)<b(v^j_2)<b(v^j_4)\) for \(j\in [i,i+3]\) and \([b(v^j_0),b(v^j_4)]<[b(v^{j+1}_0),b(v^{j+1}_4)]\) for \(j\in [i,i+2]\), or
-
\(b(v^j_4)<b(v^j_2)<b(v^j_0)\) for \(j\in [i,i+3]\) and \([b(v^{j+1}_4),b(v^{j+1}_0)]<[b(v^j_4),b(v^j_0)]\) for \(j\in [i,i+2]\).
Again, the superscripts are taken modulo 4. Suppose the first case holds. Clearly, there are two indices \(j<k\) in \([i,i+3]\) such that both the bases of s(a) and of s(b) are outside of the intervals \([b(v^j_0),b(v^j_4)]\) and \([b(v^k_0),b(v^k_4)]\). Consider a Jordan curve J(j) that consists of
-
a substring of \(s(v^j_0)\) between \(b(v^j_0)\) and the intersection point of \(s(v^j_0)\) and s(a),
-
a substring of s(a) between the intersection points of s(a) with the strings \(s(v^j_0)\) and \(s(v^j_4)\),
-
a substring of \(s(v^j_4)\) between \(b(v^j_4)\) and the intersection point of \(s(v^j_4)\) and s(a),
-
the segment of the grounding line between \(b(v^j_0)\) and \(b(v^j_4)\).
Note that the interior of \(s(v^j_2)\) is contained in the interior of J(j) – see Fig. 14 for an illustration. We define a Jordan curve J(k) similarly, and we note that the interior of \(s(v^k_2)\) is contained in the interior of J(k). Since the strings \(s(v^j_0),s(v^j_4),s(v^k_0),s(v^k_4)\) are pairwise disjoint and \([b(v^j_0),b(v^j_4)]<[b(v^k_0),b(v^k_4)]\), the interiors of J(j) and J(k) are also disjoint (despite the fact that J(j) and J(k) may touch each other). Now, consider the string s(b). Note that the base of s(b) is contained in the exteriors of J(i) and J(k). Now, since s(b) intersects \(s(v^j_2)\) and \(s(v^k_2)\), we infer that s(b) must enter the interiors of J(j) and of J(k). Since s(b) is disjoint with \(s(v^j_0),s(v^j_4),s(v^k_0),s(v^k_4)\), we conclude that s(b) intersects s(a) at least two times, once when entering the interior of J(j) and the second time when entering the interior of J(k). This is a contradiction with the fact that \(\mathcal {F}\) is a simple family of grounded strings. \(\square \)
Notes
Note that for the class of grounded L-graphs, we can always take the grounding line to be the x-axis, and the half-plane to lie above the x-axis.
A graph is perfect if \(\chi =\omega \) holds for all of its induced subgraphs.
A family of grounded objects is simple if the intersection of any subset of them is arc-connected.
A curve is y-monotone if it intersects every horizontal line in at most one point.
References
Asplund, E., Grünbaum, B.: On a coloring problem. Math. Scand. 8, 181–188 (1960)
Briański, M., Davies, J., Walczak, B.: Separating polynomial \(\chi \)-boundedness from \(\chi \)-boundedness. Combinatorica, in press. https://doi.org/10.1007/s00493-023-00054-3
Cabello, S., Jejčič, M.: Refining the hierarchies of classes of geometric intersection graphs. Electron. J. Comb. 24(1):P1.33 (2017)
Capoyleas, V., Pach, J.: A Turán-type theorem on chords of a convex polygon. J. Comb. Theory Ser. B 56(1), 9–15 (1992)
Cardinal, J., Felsner, S., Miltzow, T., Tompkins, C., Vogtenhuber, B.: Intersection graphs of rays and grounded segments. J. Graph Algorithms Appl. 22(2), 273–295 (2018)
Catanzaro, D., Chaplick, S., Felsner, S., Halldórsson, B.V., Halldórsson, M.M., Hixon, T., Stacho, J.: Max point-tolerance graphs. Discrete Appl. Math. 216(1), 84–97 (2017)
Chalermsook, P.: Coloring and maximum independent set of rectangles. In Leslie Ann Goldberg, Klaus Jansen, R. Ravi, and José D. P. Rolim, editors, 14th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems and 15th International Workshop on Randomization and Computation (APPROX/RANDOM 2011), volume 6845 of Lect. Notes Comput. Sci., pages 123–134. Springer, Heidelberg, (2011)
Chalermsook, P., Walczak, B.: Coloring and maximum weight independent set of rectangles. In Dániel Marx, editor, 32nd ACM-SIAM Symposium on Discrete Algorithms (SODA 2021), pages 860–868. SIAM, Philadelphia, (2021)
Davies, J.: Improved bounds for colouring circle graphs. Proc. Am. Math. Soc. 150(12), 5121–5135 (2022)
Davies, J., McCarty, R.: Circle graphs are quadratically \(\chi \)-bounded. Bull. Lond. Math. Soc. 53(3), 673–679 (2021)
Erdős, P., Szekeres, G.: A combinatorial problem in geometry. Compos. Math. 2, 463–470 (1935)
Esperet, L.: Graph Colorings, Flows and Perfect Matchings. Habilitation thesis, Université Grenoble Alpes, (2017)
Fox, J., Pach, J.: Applications of a new separator theorem for string graphs. Comb. Probab. Comput. 23(1), 66–74 (2014)
Gavril, F.: Maximum weight independent sets and cliques in intersection graphs of filaments. Inf. Process. Lett. 73(5–6), 181–188 (2000)
Golumbic, M. C.: Algorithmic Graph Theory and Perfect Graphs, volume 57 of Annals of Discrete Mathematics, 2nd edition. North Holland, Amsterdam (2004)
Gyárfás, A.: On the chromatic number of multiple interval graphs and overlap graphs. Discrete Math. 55(2), 161–166 (1985)
Gyárfás, A.: Problems from the world surrounding perfect graphs. Appl. Math. 19(3–4), 413–441 (1987)
Hendler, C.: Schranken für Färbungs- und Cliquenüberdeckungszahl geometrisch repräsentierbarer Graphen (Bounds for chromatic and clique cover number of geometrically representable graphs). Master’s thesis, Freie Universität Berlin, (1998)
Jelínek, V., Töpfer, M.: On grounded L-graphs and their relatives. Electron. J. Comb. 26(3):P3.17 (2019)
Kostochka, A.: O verkhnikh otsenkakh khromaticheskogo chisla grafov (On upper bounds for the chromatic number of graphs). In Vladimir T. Dementyev, editor, Modeli i metody optimizacii, volume 10 of Trudy Institute of Mathematics, pp. 204–226. Akad. Nauk SSSR SO, Novosibirsk (1988)
Kostochka, A.: Coloring intersection graphs of geometric figures with a given clique number. In J. Pach, editor, Towards a theory of geometric graphs, volume 342 of Contemporary Mathematics, pp. 127–138. AMS, Providence (2004)
Kostochka, A., Kratochvíl, J.: Covering and coloring polygon-circle graphs. Discrete Math. 163(1–3), 299–305 (1997)
Krawczyk, T., Pawlik, A., Walczak, B.: Coloring triangle-free rectangle overlap graphs with \(O(\log \log n)\) colors. Discrete Comput. Geom. 53(1), 199–220 (2015)
Krawczyk, T., Walczak, B.: On-line approach to off-line coloring problems on graphs with geometric representations. Combinatorica 37(6), 1139–1179 (2017)
Lasoń, M., Micek, P., Pawlik, A., Walczak, B.: Coloring intersection graphs of arc-connected sets in the plane. Discrete Comput. Geom. 52(2), 399–415 (2014)
McGuinness, S.: On bounding the chromatic number of L-graphs. Discrete Math. 154(1–3), 179–187 (1996)
McGuinness, S.: Colouring arcwise connected sets in the plane I. Graphs Comb. 16(4), 429–439 (2000)
Middendorf, M., Pfeiffer, F.: The max clique problem in classes of string-graphs. Discrete Math. 108(1), 365–372 (1992)
Pawlik, A., Kozik, J., Krawczyk, T., Lasoń, M., Micek, P., Trotter, W.T., Walczak, B.: Triangle-free geometric intersection graphs with large chromatic number. Discrete Comput. Geom. 50(3), 714–726 (2013)
Rok, A., Walczak, B.: Outerstring graphs are \(\chi \)-bounded. SIAM J. Discrete Math. 33(4), 2181–2199 (2019)
Scott, A., Seymour, P.: A survey of \(\chi \)-boundedness. J. Graph Theory 95(3), 473–504 (2020)
Suk, A.: Coloring intersection graphs of \(x\)-monotone curves in the plane. Combinatorica 34(4), 487–505 (2014)
Walczak, B.: Coloring triangle-free L-graphs with \(O(\log \log n)\) colors. Eur. J. Comb. (2023). https://doi.org/10.1016/j.ejc.2023.103831
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Csaba D. Tóth
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Tomasz Krawczyk and Bartosz Walczak were partially supported by National Science Center of Poland Grant 2015/17/D/ST1/00585.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Davies, J., Krawczyk, T., McCarty, R. et al. Grounded L-Graphs Are Polynomially \(\chi \)-Bounded. Discrete Comput Geom 70, 1523–1550 (2023). https://doi.org/10.1007/s00454-023-00592-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-023-00592-z


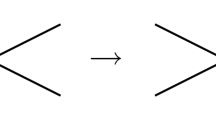

 -graphs – intersection graphs of grounded L-shapes and their mirror images, grounded
-graphs – intersection graphs of grounded L-shapes and their mirror images, grounded  -shapes, where a grounded L-shape is an L-shape with the bottommost point on the grounding line. An argument of Middendorf and Pfeiffer [
-shapes, where a grounded L-shape is an L-shape with the bottommost point on the grounding line. An argument of Middendorf and Pfeiffer [ -graphs form a subclass of grounded segment graphs.
-graphs form a subclass of grounded segment graphs.



 -graph,
-graph, -graph which is not a grounded L-graph,
-graph which is not a grounded L-graph,








