1 Introduction

Let \(M=(V,E)\) be a multigraph on \(V=[n]\). A tournament on M is an orientation of its multiset of edges E. Informally, for each edge \(\{i,j\}\in E\), teams i and j play a match, and then this edge is directed towards the winner. The score sequence \(s=(s_1,\ldots ,s_n)\) lists the number of wins by each team.

For a sequence \(z\in \mathbb {R}^n\), let \(z_\uparrow \) be its non-decreasing rearrangement. For \(x,y\in \mathbb {R}^n\) we say that x is majorized by y, and write \(x\preceq y\), if, for all \(1\leqslant k\leqslant n\), we have that \(\sum _{i=1}^k (x_\uparrow )_i\geqslant \sum _{i=1}^k (y_\uparrow )_i\), with equality when \(k=n\). Informally, \(x\preceq y\) means that x is at most as “spread out” as y. See, e.g., Marshall et al. [28] for more information. Note that \(v_n=(0,1,\ldots ,n-1)\) is the score sequence of the tournament in which each team i wins against all teams \(j<i\), and loses against all teams \(j>i\). Landau [25] classified the set of possible score sequences, when M is the complete graph \(K_n\), as those for which \(s\preceq v_n\). Since \(v_n=(v_n)_\uparrow \) and \(\sum _{i=1}^k (v_n)_i=\sum _{i=1}^k (i-1)={k\atopwithdelims ()2}\), a vector \(s\preceq v_n\) if and only if \(\sum _i s_i={n\atopwithdelims ()2}\) and \(\sum _{i\in A} s_i\geqslant {\#\,A\atopwithdelims ()2}\) for all \(A\subset [n]\). Clearly, any score sequence s of a tournament on \(K_n\) must satisfy these conditions, since the total number of games won by any set A of teams must be at least the number \({\#\,A\atopwithdelims ()2}\) of games played between them. It is less clear, but true, that any such \(s\preceq v_n\) is a score sequence.

Theorem 1.1

(Landau’s Theorem) A sequence \(s\in \mathbb {Z}^n\) is the score sequence of a tournament on \(K_n\) if and only if \(s\preceq v_n\).

Ten years later, Moon [29] studied the random setting. A random tournament on M is a collection of real numbers \(p_{ij}^{(k)}\in [0,1]\), \(i<j\), one for each edge \(\{i,j\}^{(k)}\!\in E\). Here, \(\{i,j\}^{(k)}\!\in E\) denotes the kth copy of the edge \(\{i,j\}\) in the multiset of edges E. The mean score sequence \(x=(x_1,\ldots ,x_n)\) lists the expected number of wins by each team, that is,

$$\begin{aligned} x_i\,=\!\! \sum _{\begin{array}{c} j>i \\ \{i,j\}^{(k)} \in E \end{array}}\!\!\! p_{ij}^{(k)} \, +\!\! \sum _{\begin{array}{c} j<i \\ \{i,j\}^{(k)} \in E \end{array}}\!\!\!\bigl (1 - p_{ji}^{(k)}\bigr ). \end{aligned}$$
(1)

In other words, for edge \(\{i,j\}^{(k)}\!\in E\), a match is held between teams i and j. If \(i<j\) then team i wins this match with probability \(p_{ij}^{(k)}\), and loses (i.e., team j wins) with the remaining probability \({1-p_{ij}^{(k)}}\). Since team i wins a point for each game it wins against a team \(j>i\), and a point for each game a team \(j<i\) loses against it, \(x_i\) as in (1) is indeed the expected number of points won by team i. Note that, if we define \(p_{ji}^{(k)}=1-p_{ij}^{(k)}\) for \(\{i,j\}^{(k)}\!\in E\), \(i<j\), then we can write (1) more succinctly as

$$\begin{aligned} x_i\,=\!\!\sum _{\{i,j\}^{(k)}\in E}\!\!\! p_{ij}^{(k)}. \end{aligned}$$

Theorem 1.2

(Moon’s Theorem) A sequence \(x\in \mathbb {R}^n\) is the mean score sequence of a random tournament on \(K_n\) if and only if \(x\preceq v_n\).

We note here that a random tournament with all \(p_{ij}^{(k)}\in \{0,1\}\) is a usual (deterministic) tournament (where each edge \(\{i,j\}^{(k)}\) is directed towards i if \({p_{ij}=1}\), and towards j if \({p_{ij}=0}\)), as discussed above. Moreover, in this special case, the mean score sequence becomes the score sequence. Therefore, Theorem 1.2 generalizes Theorem 1.1. Many proofs of Theorems 1.1 and 1.2 have appeared (e.g., [1,2,3, 5,6,7,8, 10,11,16, 18, 19, 21,22,23, 25,26,27, 29, 30, 33, 34, 37, 38]). For instance, Thomassen’s [37] short proof by contradiction of Theorem 1.1 has been cited widely for its elegance. The proofs of Theorem 1.2 in [3] are (to the best of our knowledge) the only ones in the literature that are probabilistic, and one of these can be made fully constructive.

The purpose of this note is to highlight the connection between combinatorics, probability, and geometry that lies behind these results. Taking a zonotopal point of view, we find very short and natural proofs that work not only in the traditional case of the complete graph \(K_n\), but indeed for any multigraph M. Although some related observations exist in the literature (see, e.g., [20, 35]) it does not appear that this connection is widely-known, given the large number of proofs (some fairly complicated) of Theorems 1.1 and 1.2 that have appeared, even very recently. In any case, this connection has not been fully exploited. For example, in an upcoming article [24], we use the perspective of the current article as a starting point to define and study the Coxeter generalization of tournaments, and to explore their connections with the Coxeter permutahedra developed recently by Ardila et al. [4].

1.1 Outline

In Sect. 2, we begin with a short, geometric proof of Theorem 1.2. Then, in Sect. 3 we show how this reasoning extends naturally to give a generalized Moon’s Theorem (see Theorem 3.1) for tournaments on any multigraph M. In Sect. 4, we prove our main result (see Theorem 4.1). This result is a refinement of Moon’s Theorem that yields Landau’s Theorem as a special case. Informally, we show that any possible mean score sequence x can be realized by a tournament with at most a “forest’s worth of randomness.” More precisely, we show that, for any given x, there is a (simple) forest \(F\subset M\) and a random tournament on M, with mean score sequence x, such that all games are deterministic, except possibly for games corresponding to edges in F. If x is integer-valued, then it turns out that all games are deterministic in this tournament, establishing a generalized Landau’s Theorem (see Corollary 4.2).

1.2 Notation

Throughout this work, we fix a multigraph \(M=(V,E)\) on vertex set \(V=[n]\) that has \(\#\,E=m\) many edges. As noted above, we let \(\{i,j\}^{(k)}\in E\) denote the kth copy of the edge \(\{i,j\}\) in the multiset of edges E.

2 A Short, Geometric Proof of Moon’s Theorem

Recall that the permutahedron \(\Pi _{n-1}\) is the convex hull of all permutations of \(v_n\). Prior to the work of Landau (1953) and Moon (1963) on tournaments, Rado [32] showed in 1952 that the conditions in Theorems 1.1 and 1.2 coincide with the hyperplane description of the permutahedron.

Theorem 2.1

(Rado’s Theorem) \(\Pi _{n-1}=\{x\in \mathbb {R}^n:x\preceq v_n\}\).

The permutahedron is a zonotope, that is, the affine image of a higher dimensional cube (see, e.g., Ziegler [39] and Braun and Vindas-Meléndez [9]). Indeed (see, e.g., [39, Ex. 7.15]),

$$\begin{aligned} \Pi _{n-1}=\{v_n+a E_n:a\in U_n\}, \end{aligned}$$
(2)

where \(U_n=[0,1]^{{n\atopwithdelims ()2}}\) is the \({n\atopwithdelims ()2}\)-dimensional unit cube and \(E_n\) is the matrix whose rows are the unit vector differences \(e_{ij}=e_i-e_j\), \(i<j\), listed lexicographically. Recall (see, e.g., [39]) that the Minkowski sum of two sets \(X,Y\subset \mathbb {R}^n\) is the sum \(X+Y=\{x+y:x\in X,y\in Y\}\). Moreover, \(\Pi _{n-1}\) is in fact the graphical zonotope of \(K_n\), given by (the translation of) the Minkowski sum of line segments

$$\begin{aligned} \Pi _{n-1} = v_n + \sum _{i<j}\, [0, e_{ij}]. \end{aligned}$$
(3)

Note that each line segment \([0, e_{ij}]\) corresponds with an edge \(\{i,j\}\) in \(K_n\). This, of course, strongly suggests what to do when the tournament is on a general multigraph M instead of \(K_n\). See Sect. 3 below.

Viewed in this light, Theorem 1.2 becomes quite apparent. Indeed, Moon’s Theorem follows simply by viewing points \(\{a_{ij}:i<j\}\in U_n\) in the cube as probability distributions on tournaments (i.e., a probability \(a_{ij}\in [0,1]\) for each edge in \(K_n\)), and then identifying the projection map from \(U_n\) to \(\Pi _{n-1}\) as the expectation operator, which sends any given random tournament to its mean score sequence. We conclude this section with a short, geometric proof of this classical result, for the record. See Fig. 1.

Proof of Theorem 1.2

If \(x\preceq v_n\) then by Theorem 2.1 and (2) we have \(x=v_n+a E_n\) for some \(a=\{a_{ij}:i<j\}\in U_n\). Hence, by the definition of \(E_n\),

$$\begin{aligned} (a E_n)_i=-\sum _{j<i}a_{ji}+\sum _{j>i}a_{ij}={}-(i-1)+\sum _{j>i}a_{ij}+\sum _{j<i}\,(1-a_{ji}). \end{aligned}$$

Therefore, by (1) and since \(x=v_n+a E_n\), if we set \(p_{ij}=a_{ij}\) then we obtain a random tournament in which team i wins \(x_i\) games on average. \(\square \)

Fig. 1
figure 1

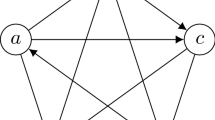
In this figure, the unit cube \(U_3=[0,1]^3\) is projected onto the permutahedron \(\Pi _2\) (a hexagon). Each point \((p_{12},p_{13},p_{23})\in U_3\) in the cube corresponds to a random tournament on the complete graph \(K_3\) (where team i wins against team \(j>i\) with probability \(p_{ij}\)), with corresponding mean score sequence \((p_{12}+p_{13},1-p_{12}+p_{23},2-p_{13}-p_{23})\). Note that, for each of the six vertices of \(\Pi _2\), there is a unique (deterministic) tournament with this score sequence. The lattice point \(111\in \Pi _2\), however, is realized by two (deterministic) tournaments \(101,010\in U_3\), and also by all random tournaments inside the line \(\{(p,1-p,p):p\in [0,1]\}\) connecting these two antipodal points of \(U_3\)

Full size image

3 Extending Moon’s Theorem

In this section, we show how the zonotopal perspective used in Sect. 2 yields a generalized version of Moon’s Theorem. Replacing \(\Pi _{n-1}\) (the graphical zonotope of \(K_n\)) with a natural analogue \(Z_M\), we find that essentially the same proof works for any multigraph M.

The graphical zonotope \(Z_M\) of the multigraph \(M=(V,E)\) is the polytope given by the Minkowski sum

$$\begin{aligned} Z_M\, = \!\!\sum _{\begin{array}{c} \{i,j\}^{(k)} \in E \\ i<j \end{array}}\!\! [e_i, e_j]. \end{aligned}$$
(4)

In this case, \(Z_M\) is the image of the cube \([0,1]^{m}\) (recalling that \(\#\,E=m\) throughout this work). To understand the projection map, let \(e_{ij}^{(k)}\), for \(i<j\) and \(\{i,j\}^{(k)} \!\in E\), denote a basis vector of \(\mathbb {R}^{m}\), and let \(e_i\) denote a basis vector of \(\mathbb {R}^n\). Then the projection map \(\pi :\mathbb {R}^{m} \!\rightarrow \mathbb {R}^n\) satisfies

$$\begin{aligned} \pi \bigl (a_{ij}^{(k)} e_{ij}^{(k)}\bigr ) = a_{ij}^{(k)}e_i + \bigl (1- a_{ij}^{(k)}\bigr )\hspace{1.111pt}e_j. \end{aligned}$$
(5)

Hence, for any \(\{a_{ij}^{(k)}\hspace{-0.88882pt}:i<j\}\in [0,1]^{m}\), the image under \(\pi \) of any

$$\begin{aligned} \sum _{\begin{array}{c} i<j \\ \{i,j\}^{(k)} \in E \end{array}}\!\!\! a_{ij}^{(k)} e_{ij}^{(k)} \end{aligned}$$

is the vector x with ith coordinate (cf. (1))

$$\begin{aligned} x_i\hspace{1.111pt}=\!\hspace{-0.83328pt}\sum _{\begin{array}{c} j>i \\ \{i,j\} \in E \end{array}}\!\!\! a_{ij}^{(k)}\,+\!\!\sum _{\begin{array}{c} j<i \\ \{i,j\} \in E \end{array}}\!\!\bigl (1-a_{ji}^{(k)}\bigr ). \end{aligned}$$

Theorem 3.1

(Generalized Moon’s Theorem) For any \( A \subset [n]\), let \(\phi (A)\) be the number of edges in the submultigraph M[A] of M induced by A. Then a sequence \(x\in \mathbb {R}^n\) is the mean score sequence of a random tournament on M if and only if \(\sum _{i} x_i =m\) and \(\sum _{i\in A}x_i\geqslant \phi (A)\) for all \(A\subset [n]\).

Proof

Identify the cube \([0,1]^{m}\) with the set of random tournaments on M by mapping each point \(\{a_{ij}^{(k)}\hspace{-0.88882pt}:i < j\}\) in the cube to the random tournament X on M where \(p_{ij}^{(k)} = a_{ij}^{(k)}\). Then by (5) the image of X under \(\pi \) is its mean score sequence x. Therefore, \(x \in \mathbb {R}^n\) is a mean score sequence if and only if \(x \in {\text {image}}\hspace{0.33325pt}(\pi )\). Finally, since \({\text {image}}\hspace{0.33325pt}(\pi )=Z_M\), we conclude using the following hyperplane description of \(Z_M\):

$$\begin{aligned} Z_M = \left\{ x \in \mathbb {R}^n: \sum _{i}\hspace{0.55542pt}x_i = m, \,\sum _{i \in A}\hspace{0.55542pt}x_i \geqslant \phi (A), \, \forall \hspace{1.111pt}A \subset [n] \right\} . \end{aligned}$$
(6)

This description is obtained from the one in [31] by realizing that \(\phi (A) = \mu ([n]) - \mu (A)\), where \(\mu \) is the submodular function that defines \(Z_M\). \(\square \)

Remark 3.2

In the classical case, when \(M=K_n\), the conditions above coincide with those in Theorem 1.2 (i.e., \(x\preceq v_n\)) and (6) reduces to Theorem 2.1.

4 Refining Moon’s Theorem

Finally, in this last section, by combining the theories of zonotopal tilings and mixed subdivisions, we obtain a refinement of Theorem 3.1 that implies a generalization of Landau’s theorem. Informally, we find that any mean score sequence x can be realized by a tournament with at most a “forest’s worth of randomness.” The work of Stanley [36] plays a key role.

Theorem 4.1

For any \(x \in Z_M\) there exists a (simple) forest \(F \subset M\) and a random tournament X on M with mean score sequence x such that for every edge \(\{i,j\}^{(k)} \!\notin E(F)\), we have \(p_{ij}^{(k)}\in \{0,1\}\) in the tournament X. Furthermore, if \(x\in \mathbb {Z}^n\), then the same is true for \(\{i,j\}^{(k)}\! \in E(F)\). Hence, in this case, x is the score sequence of a (deterministic) tournament on M.

We obtain the following immediately.

Corollary 4.2

(Generalized Landau’s Theorem) A sequence \(s\in \mathbb {Z}^n\) is the score sequence of a tournament on M if and only if \(\sum _{i} s_i = m\) and \(\sum _{i\in A}s_i\geqslant \phi (A)\) for all \(A\subset [n]\).

To prove these results, we will need to recall two different types of subdivisions of polytopes. The first such notion is as follows.

Definition 4.3

A zonotopal subdivision of a zonotope P is a collection of zonotopes \(\{P_i\}\) such that \(\bigcup _i P_i = P\) and any two zonotopes \(P_i\) and \(P_j\) intersect properly (i.e., \(P_i\) and \(P_j\) intersect at a face of both, or else not at all) and their intersection is also in the collection \(\{P_i\}\). We call the zonotopes \(P_i\) the tiles of the subdivision.

The following lemma is implicit in the proof of [36, Thm. 2.2].

Lemma 4.4

There are vectors \(v_F \in \mathbb {R}^n\) for each forest \(F \subset M\) such that \(\{v_F + Z_F\}\) is a zonotopal subdivision of \(Z_M\). The full-dimensional tiles are those corresponding to spanning forests. Furthermore, every lattice point in \(Z_M\) appears as a vertex of a zonotope \(v_F + Z_M\) for some spanning forest F.

The last statement of this lemma is true since the number of lattice points contained in the half-open parallelepiped generated by a linearly independent set of vectors is given by the determinant of the matrix whose columns are vectors in the set. In the case of graphical zonotopes, each half-open paralleopiped is generated by vectors corresponding to an edge in a forest and the corresponding matrix has determinant \(\pm 1\). See [36] for more details.

The second type of subdivison is from the theory of mixed subdivisions.

Definition 4.5

Let \(P = P_1 + \cdots + P_k\) be the Minkowski sum of polytopes. A mixed cell (or Minkowski cell) \(\sum _{i} B_i\) is a Minkowski sum of polytopes, where the vertices of \(B_i\) are contained in the vertices of \(P_i\). A mixed subdivision of P is a collection of mixed cells which cover P and intersect properly (i.e., for any two mixed cells \(\sum B_i\) and \(\sum B_i'\) the polytopes \(B_i\) and \(B_j'\) intersect at a face of both, or else not at all).

In the case of graphical zonotopes, the subdivision given by Lemma 4.4 is a mixed subdivision, see De Loera et al. [17], Lem. 9.2.10]. This means that every tile \(v_F + Z_F\) can be written as \(\sum _{\{i,j\}^{(k)} \in E}\) \(B_{i,j}\), where \(B_{i,j}\) is a face of the line segment \([e_i, e_j]\). The only faces of these segments are the vectors \(e_i\) and \(e_j\) and the entire segment \([e_i,e_j]\). Since \(Z_F = \sum _{\{i,j\}^{(k)} \in E(F)} [e_i, e_j]\), this means that E can be partitioned as \(A\cup B\cup E(F)=E\) in such a way that

$$\begin{aligned} v_F + Z_F\,= \!\sum _{\begin{array}{c} \{i,j\}^{(k)} \in A \\ i< j \end{array}}\!\!\! e_i \, +\! \sum _{\begin{array}{c} \{i,j\}^{(k)} \in B \\ i< j \end{array}}\!\!\! e_j\, + \!\!\sum _{\begin{array}{c} \{i,j\}^{(k)} \in E(F)\\ i<j \end{array}}\!\!\! [e_i, e_j]. \end{aligned}$$
(7)

With this at hand, we prove our main result.

Proof of Theorem 4.1

If \(x \in Z_M\), then it is contained in one of the full-dimensional tiles of the subdivision of \(Z_M\) given by Lemma . Let F be a forest corresponding to one of the tiles \(v_F + Z_F\) that contains x. Then (7) tells us that x is of the form

$$\begin{aligned} x\,=\!\sum _{\begin{array}{c} \{i,j\}^{(k)} \in A \\ i< j \end{array}}\!\!\! e_i \, +\! \sum _{\begin{array}{c} \{i,j\}^{(k)} \in B \\ i< j \end{array}}\!\!\! e_j\, + \!\sum _{\begin{array}{c} \{i,j\}^{(k)} \in E(F)\\ i<j \end{array}}\!\!\bigl [a_{ij}^{(k)}e_i + \bigl (1- a_{ij}^{(k)}\bigr )\hspace{1.111pt}e_j\bigr ], \end{aligned}$$

for some \(0 \leqslant a_{ij}^{(k)} \leqslant 1\). Let X be the random tournament where, for \(i<j\),

$$\begin{aligned} p_{ij}^{(k)} = {\left\{ \begin{array}{ll}0 &{} \text {if}\ \{i,j\}^{(k)}\! \in A, \\ 1 &{} \text {if}\ \{i,j\}^{(k)} \!\in B, \\ a_{ij}^{(k)} &{} \text {otherwise.}\end{array}\right. } \end{aligned}$$

Then the mean score sequence of X is x. If \(x\in \mathbb {Z}^n\) is integer-valued, then in fact (also by Lemma 4.4) all \(a_{ij}\in \{0,1\}\), in which case X is a (deterministic) tournament. \(\square \)

Remark 4.6

Geometrically, this theorem states that every lattice point of \(Z_G\) is the image of some vertex of the cube \([0,1]^{m}\) under the map \(\pi \).