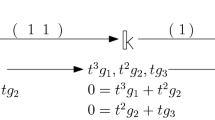Abstract
We set up the theory for a distributed algorithm for computing persistent homology. For this purpose we develop linear algebra of persistence modules. We present bases of persistence modules, together with an operation \(\boxplus \) that leads to a method for obtaining images, kernels and cokernels of tame persistence morphisms. Our focus is on developing efficient methods for the computation of homology of chains of persistence modules. Later we give a brief, self-contained presentation of the Mayer–Vietoris spectral sequence. Then we study the Persistent Mayer–Vietoris spectral sequence and present a solution to the extension problem. This solution is given by finding coefficients that indicate gluings between bars on the same dimension. Finally, we review PerMaViss, an algorithm that computes all pages in the spectral sequence and solves the extension problem. This procedure distributes computations on subcomplexes, while focusing on merging homological information. Additionally, some computational bounds are found which confirm the distribution of the method.
Similar content being viewed by others
1 Introduction
1.1 Motivation
Persistent homology has existed for about two decades [15]. This tool introduced the field of Topological Data Analysis which, very soon, was applied to a multitude of problems, see [5, 16]. Among others, persistent homology has been applied to study the geometric structure of sets of points lying in \(\mathbb {R}^n\) [12, 15], coverage in sensor networks [25], pattern detection [23], classification and recovery of signals [24] and it has also had an impact on shape recognition using machine learning techniques, see [1, 13]. All these applications motivate the need for fast algorithms for computing persistent homology. The usual algorithm used for these computations was introduced in [15], with some later additions to speed up such as those of [7, 8, 26]. In [21] persistent homology is proven to be computable in matrix multiplication time. However, since these matrices become large very quickly, the computations are generally very expensive, both in terms of computational time and in memory required.
In practice, computing the persistent homology of a given filtered complex is equivalent to computing its matrices of differentials and perform successive Gaussian eliminations; see [14, 15]. In recent years, some methods have been developed for the parallelization of persistent homology. The first approach was introduced in [14] as the spectral sequence algorithm, and was successfully implemented in [2]. This consists in dividing the original matrix M into groups of rows, and sending these to different processors. These processors will, in turn, perform a local Gaussian Elimination and share the necessary information between them, see [2]. On the other hand, a more topological approach is presented in [18]. It uses the blow-up complex introduced in [33]. This approach first takes a cover \({\mathcal {C}}\) of a filtered simplicial complex K, and uses the result that the persistent homology of K is isomorphic to that of the blow-up complex \(K^{\mathcal {C}}\). This proceeds by computing the sparsified persistent homology for each cover, and then using this information to reduce the differential of \(K^{\mathcal {C}}\) efficiently. Both of these parallelization methods have provided substantial speedups compared to the standard method presented in [15].
The relation between homology classes and a cover is known as Localized Homology, which was introduced in [33]. It would be useful to have a method that leads to the speedups from [2, 18], while keeping Localized Homology information. Further, such covers should have no restrictions, such as those used in the mapper algorithm, see [27]. This last point limits substantially the use of the blowup-complex, since the number of simplices increases very quickly when we allow the intersections to grow. In fact, in the extreme case where a complex K is covered by n copies of K, the blowup complex \(K^{\mathcal {C}}\) has size \(2^n\vert K\vert \).
1.2 Literature Review
Since distribution is an important issue in persistent homology, it is worth exploring which classical tools of algebraic topology could be used in this context. A well-known tool for distributing homology computations is the Mayer–Vietoris spectral sequence [3, Sect. 8], see [9] for a quick introduction to spectral sequences and [20] as a general reference. Since the category of persistence modules and persistence morphisms is an abelian category, the process of computing a spectral sequence should be more or less straightforward. However, implementing this in practice is a difficult task. Furthermore, this approach has been proposed in [19], although without a solution to the extension problem. Later, spectral sequences were used for distributing computations of cohomology groups in [11], and recently in [31] and [32] spectral sequences are used for distributing persistent homology computations. However, all of [11, 31, 32] assume that the nerve of the cover is one-dimensional.
The first problem when dealing with spectral sequences is that we need to be able to compute images, kernels and quotients as well as their representatives. This question has already been studied in [10], where the authors give a very efficient algorithm. However, there are couple of problems that come up when using [10] in spectral sequences. First, in [10] the authors consider a persistence morphism induced by a simplicial morphism \(f:X\rightarrow Y\). However, when working with the Mayer–Vietoris spectral sequence we consider maps in the second, third and higher pages which are not induced by a simplicial morphism at all. Furthermore, even when working with the first page differentials, we cannot adapt the work from [10]; as a simplex from an intersection is sent to several copies along lower degree intersections. Second, a key assumption in [10] is that the filtrations in X and Y are both general in the sense that a simplex in either X or Y is born at a time. However, in spectral sequences generality hardly ever holds. Indeed, this follows from the fact that a simplex might be contained in various overlapping covers.
Thus, if we want to compute images, kernels and cokernels, we will need to be able to overcome these two difficulties first. Also, notice that a good solution should lead to the representatives, as these are needed for the spectral sequence. It is worth to mention that in [28] such images, kernels and cokernels where studied in terms of Smith Normal Forms of presentations associated to persistence modules. Further, as mentioned in [28], such work was developed with the aim of computing persistence spectral sequences [19] in mind. However, adapting [28] to an algorithm which computes spectral sequences is still a challenge.
The other difficulty with spectral sequences is the extension problem, which we explain in Sect. 5.1. Within the context of persistent homology, the extension problem first appeared in [17, Sect. 6]. There the authors give an approximate result that holds in the case of acyclic coverings. This allows them to compare the persistent homology to the lower row of the infinity page in the spectral sequence. This leads to an \(\varepsilon \)-interleaving between the global persistent homology and that of the filtered nerve. Later, the extension problem appeared in the PhD thesis of Yoon [31], and also in the recent joint work with Ghrist [32]. In Sect. 4.2.3 from Yoon’s Thesis, there is a detailed solution for the extension problem in the case when the nerve of the cover is one-dimensional.
1.3 Original Contribution
In this paper, we set the theoretical foundations for a distributed method on the input data. In order to do this, we use the algebraic power of the Mayer–Vietoris spectral sequence. Since the aim is to build up an explicit algorithm, we need to develop linear algebra of persistence modules, as done through Sect. 3. There, we define barcode bases and also we develop an operation \(\boxplus \) that allows to determine whether a set of barcode vectors is linearly independent or not. Using this machinery, we are able to encapsulate all the information related to a persistence morphism in a matrix that depends on the choice of two barcode bases. This allows defining a Gaussian elimination outlined in the box_gauss_reduce algorithm—see Algorithm 1—which addresses the two issues raised above with regards to [10].
Next in Sect. 4, we give a detailed review of the Mayer–Vietoris spectral sequence in the homology case. This is followed by Sect. 5.1, where we give a solution to the extension problem. The solution is given by a careful consideration of the total complex homology, together with the use of barcode basis machinery developed in Sect. 3. In Sect. 5.2 we introduce PerMaViss, an algorithm for computing the persistence Mayer–Vietoris spectral sequence and solving the extension problem. The advantage of this procedure is that all the simplicial information is enclosed within local matrices. This has one powerful consequence; this method consists in computing local Gaussian eliminations plus computing image_kernel on matrices whose order is that of homology classes. In particular, given enough processors and a ‘good’ cover of our data, one has that the complexity is about
where X is the order of the maximal local complex and H is the overall number of nontrivial persistence bars on the whole dataset.Footnote 1 For more details on this, we refer the reader to Sect. 5.4.
By using the ideas in this text we developed PerMaViss, a Python library that computes the Persistence Mayer–Vietoris spectral sequence. In the results from [29], one can see that nontrivial higher differentials come up and also the extension problem cannot be solved in a trivial way in general. This supports the idea that the spectral sequence adds more information on top of persistent homology. Finally, we outline future directions, both for the study of the Persistence Mayer–Vietoris spectral sequence and future versions of PerMaViss.
2 Preliminaries
2.1 Simplicial Complexes
Definition 1.1
Given a set X, a simplicial complex K is a subset of the power set \(K\subseteq P(X)\) such that if \(\sigma \in K\), then for all subsets \(\tau \subseteq \sigma \) we have that \(\tau \in K\). An element \(\sigma \in K\) will be called an n-simplex whenever \(\vert \sigma \vert =n+1\), whereas a subset \(\tau \subseteq \sigma \) will be called a face. Thus, if a simplex is contained in K all its faces must also be contained in K. Given a simplicial complex K, we denote by \(K_n\) the set containing all the n-simplices from K. Given a pair of simplicial complexes K and L, if \(L \subseteq K\), then we say that L is a subcomplex of K. Also, given a mapping \(f:K \rightarrow L\) between two simplicial complexes K and L, we call f a simplicial morphism whenever \(f(K_n) \subseteq \bigcup _{l=0}^n L_l\) for all \(n \geqslant 0\). The category composed of simplicial complexes and simplicial morphisms will be denoted by \(\mathrm{\textbf{SpCpx}}\).
We represent the simplices from K as equivalence classes of tuples from X which are equal up to even permutations, see [22, Sect. 5]. Let \(\mathbb {F}\) be a field. For each \(n \geqslant 0\) we define the free vector space \(S_n(K)\, {:}{=}\, \mathbb {F}[K_n]\). We also consider linear maps \(d_n :S_n(K) \rightarrow S_{n-1}(K)\) usually called differentials, defined by
Setting \(S_n(K) = 0\) for all \(n < 0\), we put all of these in a sequence
It follows from formula (1) that the composition of two consecutive differentials vanishes: \(d_n\circ d_{n-1}=0\) for all \(n \geqslant 0\). In this case we say that (2) is a chain complex. As a consequence, we have that \(\textrm{Im}\hspace{0.55542pt}(d_{n+1}) \subseteq \textrm{Ker}\hspace{0.55542pt}(d_n)\), and we can define the homology with coefficients in \(\mathbb {F}\) to be \(\textrm{H}_n(K;\mathbb {F}) = \textrm{Ker}\hspace{0.55542pt}(d_n)/\textrm{Im}\hspace{0.55542pt}(d_{n+1})\) for all \(n \geqslant 0\). In general, \(\mathbb {F}\) will be understood by the context and the notation \(\textrm{H}_n(K)\) might be used instead. On the other hand, we consider the augmentation map \(\varepsilon :S_0(K) \rightarrow \mathbb {F}\) defined by the assignment \(s \mapsto 1_\mathbb {F}\), for any simplex \(s \in S_0(K)\). Then, we define the reduced homology by \(\widetilde{\textrm{H}}_0(K;\mathbb {F}) = \textrm{Ker}\hspace{0.55542pt}(\varepsilon )/\textrm{Im}\hspace{0.55542pt}(d_{1})\) and \(\widetilde{\textrm{H}}_n(K;\mathbb {F}) =\textrm{H}_n(K;\mathbb {F})\) for all \(n>0\). Consider \(\widetilde{S}_*(K)\), obtained by augmenting (2) by \(\varepsilon \) and a copy of \(\mathbb {F}\) in degree \(-1\):
Then, computing homology on \(\widetilde{S}_*(K)\) we obtain the reduced homology groups.
Definition 1.2
(standard m-simplex) Given \(m > 0\), we define \(\varDelta ^m = P\hspace{0.33325pt}(\{0, 1, \ldots , m \})\), which will be called the standard m-simplex. This leads to a chain complex \(\widetilde{S}_*(\varDelta ^m)\)
By [22, Thm. 8.3], \(\widetilde{S}_*(\varDelta ^m)\) is exact, that is, \(\widetilde{\textrm{H}}_n(\varDelta ^m) = 0\) for all \(n \geqslant 0\).
Definition 1.3
Let K be a simplicial complex. A finite set \({\mathcal {U}}= \{ U_i \}_{i = 0}^m\) of subcomplexes from K, is a cover of K whenever \(K = \bigcup _{i = 0}^m U_i\). Let \(\sigma \in \varDelta ^m\) and denote \(U_\sigma = \bigcap _{i \in \sigma } U_i\). The nerve of \({\mathcal {U}}\) is defined by
In particular, given a simplex \(\sigma \in N^{\mathcal {U}}\), there is an injection \(f^\sigma :\varDelta ^{\vert \sigma \vert } \hookrightarrow N^{\mathcal {U}}\) which induces an injection of chain complexes \(f^\sigma _*:\widetilde{S}_*(\varDelta ^{\vert \sigma \vert }) \hookrightarrow \widetilde{S}_*(N^{\mathcal {U}})\) whose image \(f^\sigma _*(\widetilde{S}_*(\varDelta ^{\vert \sigma \vert }))\) is exact.
Definition 1.4
(Čech chain complex) Let K be a simplicial complex and let \({\mathcal {U}}= \{ U_i \}_{i=0}^{m}\) be a cover of K. Given \(s \in K\), there exists \(\sigma (s) \in N^{\mathcal {U}}\) with maximal cardinality \(\vert \sigma (s)\vert \), so that \(s \in U_{\sigma (s)}\). Then, we define the \((n, {\mathcal {U}})\)-Čech chain complex by
For \(k \geqslant -1\), we use the notation \((\tau )_s\) with \(s \in K_n\) and \(\tau \in \widetilde{S}_k(\varDelta ^{\vert \sigma (s)\vert })\), to denote an element in \(\check{C}_k(n, {\mathcal {U}};\mathbb {F})\) that is zero everywhere except for \(\tau \) in the component indexed by s. Then the image of the k-Čech differential is defined by the assignment \(\check{\delta }_k^{\mathcal {U}}((\tau )_s) = (d_k^{N^{\mathcal {U}}} \tau )_s\), where \(d^{N^{\mathcal {U}}}_k\) denotes the kth differential of \(\widetilde{S}_*(N^{\mathcal {U}})\). By definition, the Čech complex is a chain complex and is exact. Also, \(\check{C}_{-1}(n, {\mathcal {U}};\mathbb {F}) \simeq S_n(K)\) follows easily. On the other hand, for each \(k \geqslant 0\) we define an isomorphism
by sending \((\tau )_s\) to \((s)_\tau \) for any pair of simplices \(s \in K_n\) and \(\tau \in f^{\sigma (s)}_k\varDelta ^{\vert \sigma (s)\vert }\). In particular, we can rewrite the \((n, {\mathcal {U}})\)-Čech chain complex as a sequence
where, for any pair \(\sigma \in N^{\mathcal {U}}_k\) and \(s \in (U_\sigma )_n\), the differentials \(\delta _i\) are defined as follows:
and where \(\{d^{N^{\mathcal {U}}}_k\!(\sigma )\}_\tau \in \mathbb {F}\) is the coefficient of \(d^{N^{\mathcal {U}}}_k\!(\sigma )\) in the simplex \(\tau \in N^{\mathcal {U}}_{k-1}\).
Remark 2.5
Alternatively, the Čech chain complex can be defined straight away as the sequence (3), and prove exactness by using cosheaf theory. Namely, given a simplicial complex K, we consider the topology where the open sets are subcomplexes. Then, for each integer \(n \geqslant 0\), consider the simplicial precosheaf as an assignment \({\mathcal {S}}_n :V \mapsto S_n(V)\) for each subcomplex \(V \subseteq K\). This precosheaf is in fact a flabby cosheaf. Then, using 2.5, 4.3, and 4.4 from [4, Sect. VI], one has exactness of the Čech chain complex.
2.2 Persistence Modules
Let \(\textbf{R}\) be the category of real numbers as a poset, where \(\hom _\mathbb {R}(s,t)\) contains a single morphism whenever \(s \leqslant t\), and is empty otherwise. Let \(\mathbb {F}\) be a field and let \(\textbf{Vect}\) denote the category of \(\mathbb {F}\)-vector spaces.
Definition 1.6
A filtered simplicial complex is a functor \(K :\textbf{R}\rightarrow \mathrm{\textbf{SpCpx}}\), with \(K_s \subseteq K_t\) for all \(s \leqslant t\). Define \(\textrm{PH}_n(K)\), the n-persistent homology of K as the composition \(\textrm{H}_n(K) :\textbf{R}\rightarrow \textbf{Vect}\).
Definition 1.7
A persistence module \(\mathbb {V}\) is a functor \(\mathbb {V}:\textbf{R}\rightarrow \textbf{Vect}\). That is, to any \(r \in \textbf{R}\), \(\mathbb {V}\) assigns a vector space in \(\textbf{Vect}\) which is denoted either by \(\mathbb {V}(r)\) or \(\mathbb {V}^r\). Additionally, to any pair \(s \leqslant t\), there is a linear morphism \(\mathbb {V}\hspace{0.33325pt}(s \,{\leqslant }\, t) :\mathbb {V}^s \rightarrow \mathbb {V}^t\). These morphisms satisfy \(\mathbb {V}\hspace{0.33325pt}(s \,{\leqslant }\, s) = \textrm{Id}_{\mathbb {V}^s}\) for any \(s \in \textbf{R}\) and the relation \(\mathbb {V}\hspace{0.33325pt}(r \,{\leqslant }\, t) = \mathbb {V}\hspace{0.33325pt}(s \,{\leqslant }\, t) \circ \mathbb {V}\hspace{0.33325pt}(r \,{\leqslant }\, s)\) for all \(r \leqslant s \leqslant t\) in \(\textbf{R}\). Given two persistence modules \(\mathbb {V}\) and \(\mathbb {W}\), a persistence morphism is a natural transformation \(f:\mathbb {V}\rightarrow \mathbb {W}\). Thus, for any pair \(s \leqslant t\), there is a commutative square
We denote by PMod the category of persistence modules and persistence morphisms.
By naturality of f we refer to the commutative square above. A persistence morphism \(f:\mathbb {V}\rightarrow \mathbb {W}\) is an isomorphism whenever \(f_t\) is an isomorphism for all \(t \in \textbf{R}\), which we denote by \(\mathbb {V}\simeq \mathbb {W}\).
Example 2.8
Let \(s \leqslant t\) from \(\textbf{R}\). We define the interval module \(\mathbb {F}_{[s, t)}\) by \(\mathbb {F}_{[s, t)}(r) = \mathbb {F}\) for all \(r \in [s, t)\) and \(\mathbb {F}_{[s, t)}(r) = 0\) otherwise. The morphisms \(\mathbb {F}_{[s, t)}(a \,{\leqslant }\, b)\) are the identity for any two \(a,b \in [s,t)\) and 0 otherwise.
Given \(\mathbb {F}_{[s, t)}\), s and t are the birth and death values respectively. If \(\mathbb {V}(r)\) is finite dimensional for all \(r \in \textbf{R}\), then there is an isomorphism \(\mathbb {V}\simeq \bigoplus _{i \in J}\mathbb {F}_{[s_i, t_i)}\), as shown in [6]. This is the barcode decomposition of \(\mathbb {V}\).
Definition 1.9
\(\mathbb {V}\in \textbf{PMod}\) is tame iff it has a finite barcode decomposition: \(\mathbb {V}\simeq \bigoplus _{i = 1}^N\mathbb {F}_{[a_i, b_i)}\).
Throughout this work all persistence modules are assumed to be tame.
Definition 1.10
A chain of persistence modules is a sequence of persistence modules \(\mathbb {V}_k\) and differentials \(\delta _k:\mathbb {V}_k\rightarrow \mathbb {V}_{k-1}\) such that \(\delta _{k-1} \hspace{0.55542pt}{\circ }\hspace{1.111pt}\delta _k = 0\) for all \(k \in \mathbb {Z}\). Elements from \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V}_k)\), for all \(k \in \mathbb {Z}\), are sometimes called chains.
3 Homology of Persistence Modules
3.1 Barcode Bases
In this section, we introduce barcode bases and the operation \(\boxplus \). This framework allows to introduce the matrix associated to a persistence morphism \(f :\mathbb {V}\rightarrow \mathbb {W}\) and a choice of bases. This theory is applied to develop algorithms for computing images and kernels of persistence morphisms as well as quotients of persistence modules. In addition, we evaluate the respective computational complexities. Additionally, we illustrate how to compute homology in the category of persistence modules.
Definition 1.11
(barcode basis) A barcode basis \({\mathcal {A}}\) of a tame persistence module \(\mathbb {V}\) is a choice of an isomorphism, \(\alpha :\bigoplus _{i=1}^N \mathbb {F}_{[a_i, b_i)}\rightarrow \mathbb {V}\). A direct summand of \(\alpha \) is a restricted morphism \(\alpha _i:\mathbb {F}_{[a_i, b_i)}\rightarrow \mathbb {V}\) which we call a barcode generator. Often, we denote a barcode basis \({\mathcal {A}}\) by the set of barcode generators \({\mathcal {A}}= \{\alpha _i\}_{i=1}^N\).
Within the context of Definition 3.1, we make some notational remarks.
-
Given a barcode generator \(\alpha _i \in {\mathcal {A}}\), we write \(\alpha _i\hspace{-0.55542pt}\sim [a_i, b_i)\) to indicate that the domain of \(\alpha _i\) is \(\mathbb {F}_{[a_i, b_i)}\) and say that \(\alpha _i\) is associated to the interval \([a_i, b_i)\).
-
Given \(\alpha _i \in {\mathcal {A}}\) with \(\alpha _i\hspace{-0.55542pt}\sim [a_i, b_i)\), we have linear transformations \(\alpha _i(r) :\mathbb {F}_{[a_i, b_i)}(r)\rightarrow \mathbb {V}(r)\) for all \(r \in \textbf{R}\). In particular, since \(\mathbb {F}_{[a_i, b_i)}(r)\) is either 0 or \(\mathbb {F}\), \(\alpha _i(r)\) is uniquely determined by \(\alpha _i(r)(1_\mathbb {F}) \in \mathbb {V}(r)\) for \(r \in [a_i,b_i)\). In addition, notice that \(\alpha _i(r)\ne 0\) for all \(r \in [a_i,b_i)\) since otherwise \(\alpha \) would not be injective.
-
For any given \(r \in \textbf{R}\), we define a subset of \({\mathcal {A}}\),
$$\begin{aligned} {\mathcal {A}}^r = \{ \alpha _i: 1 \leqslant i \leqslant N,\, \alpha _i(r) \ne 0 \}. \end{aligned}$$In this case, if \(\alpha _i \in {\mathcal {A}}^{r}\) and \(\alpha _i\hspace{-0.55542pt}\sim [a_i,b_i)\), then \(a_i \leqslant r<b_i\) by naturality of \(\alpha _i\). Also, evaluating all the elements from \({\mathcal {A}}^r\) on \(1_\mathbb {F}\) leads to a basis \({\mathcal {A}}^r(1_\mathbb {F})\) for \(\mathbb {V}(r)\), where
$$\begin{aligned} {\mathcal {A}}^r(1_\mathbb {F}) = \{ \alpha _i(r)(1_\mathbb {F}): \alpha _i \in {\mathcal {A}}^r \}. \end{aligned}$$
Proposition 1.12
Given a persistence morphism \(\alpha :\bigoplus _{i=1}^N \mathbb {F}_{[a_i, b_i)}\rightarrow \mathbb {V}\), consider \({\mathcal {A}}= \{\alpha _i\}_{i=1}^N\). Then, \({\mathcal {A}}\) is a barcode basis for \(\mathbb {V}\) if and only if \({\mathcal {A}}^r(1_\mathbb {F})\) is a basis for \(\mathbb {V}(r)\) for all \(r \in \textbf{R}\).
Proof
Since \(\textbf{Vect}_{\hspace{0.55542pt}\mathbb {F}}\) is an abelian category and \(\textbf{R}\) is a small category, \(\alpha \) is an isomorphism if and only if \(\alpha (r)\) is an isomorphism for all \(r \in \textbf{R}\). That is, the kernel \(\textrm{Ker}\hspace{0.55542pt}(\alpha ) \hookrightarrow \bigoplus _{i=1}^N \mathbb {F}_{[a_i, b_i)}\) vanishes iff \(\textrm{Ker}\hspace{0.55542pt}(\alpha )(r) = 0\) for all \(r \in \textbf{R}\). A similar argument is done for surjectivity. Then, \(\alpha (r)\) is an isomorphism iff \({\mathcal {A}}^r(1_\mathbb {F})\) is a base for \(\mathbb {V}(r)\) and the result follows. \(\square \)
Next, we use barcode bases to understand persistence morphisms \(f:\mathbb {V}\rightarrow \mathbb {W}\). In particular, fixing a pair of barcode bases \({\mathcal {A}}\) and \({\mathcal {B}}\) for \(\mathbb {V}\) and \(\mathbb {W}\) respectively, we show that there is a unique matrix F associated to f, see Corollary 3.12. However, this makes no sense unless we are able to perform additions on barcode generators, which, as shown in the following example, cannot be done in a straight-away manner.
Example 3.3
Consider \(\mathbb {V}\simeq \mathbb {F}_{[0, 2)}\hspace{1.111pt}{\oplus }\hspace{1.111pt}\mathbb {F}_{[1, 3)}\) together with the canonical basis \({\mathcal {A}}\) given by generators \(\alpha _1\hspace{-0.55542pt}\sim [0, 2)\) and \(\alpha _2\hspace{-0.55542pt}\sim [1,3)\). Then, it is not possible to add \(\alpha _1\) and \(\alpha _2\) since at some points the domains differ; for example at filtration value 0 we have that \(\alpha _1(0)\) has \(\mathbb {F}\) as domain but \(\alpha _2(0)\) has 0 as domain.
To fix this, consider the following set of pairs:
Given \((\gamma , (a_\gamma ,b_\gamma )) \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), we call the first component, \(\gamma \), a persistence vector and say that \(\gamma \) is associated to the pair \((a_\gamma ,b_\gamma )\), which we denote as \(\gamma \sim [a_\gamma ,b_\gamma )\). Notice that in our definition of \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) we include \((Z_r, (r,r))\) where \(Z_r :0\rightarrow \mathbb {V}\) is the zero morphism; here we can distinguish \(Z_r\) and \(Z_s\) since they are associated to different pairs for \(r \ne s\). We define \({\mathcal {Z}}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) to be the subset of zero element pairs \((Z_r, (r,r))\) for all \(r \in \textbf{R}\). We show that \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) has many properties analogous to those of vector spaces.
Definition 1.14
(barcode sum) We define the barcode sum as the assignment
which sends \(( (\gamma , (a_\gamma ,b_\gamma )), (\tau , (a_\tau , b_\tau )))\) to the pair \((\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau ,(\max \hspace{0.94437pt}(a_\gamma ,a_\tau ),B_{\gamma \tau }))\) where we set
and
We define \(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau \) for each \(r \in [\max \hspace{0.94437pt}(a_\gamma , a_\tau ), B_{\gamma \tau })\) by
One can check that \(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau :\mathbb {F}_{[\max (a_\gamma , a_\tau ), B_{\gamma \tau })} \rightarrow \mathbb {V}\) is a well-defined persistence morphism.
By definition, \(\boxplus \) is commutative and \(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau (r)\ne 0\) iff \(r \in [\max \hspace{0.55542pt}(a_\gamma , a_\tau ), B_{\gamma \tau })\). For brevity, given \((\gamma , (a_\gamma ,b_\gamma )) \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), we refer only to the first component \(\gamma \). By abuse of notation, we say “given a persistence vector \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\)” or “given a subset of persistence vectors \({\mathcal {S}}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\)”. Also, elements \(Z_r \in {\mathcal {Z}}\) behave nontrivially with respect to \(\boxplus \); for example, given a persistence vector \(\gamma \sim [a_\gamma , b_\gamma )\) and considering \(c > b_\gamma \) we have that \(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}Z_c = Z_c\).
Proposition 1.15
\(\boxplus \) is associative in \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\).
Proof
Consider three persistence vectors \(\gamma \sim [a_\gamma , b_\gamma )\), \(\tau \sim [a_\tau , b_\tau )\), and \(\rho \sim [a_\rho , b_\rho )\) from \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\). We show \(L=R\) for \(L{:}{=}(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau ) \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\rho \) and \(R{:}{=}\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}(\tau \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\rho )\). Notice that both L and R will share the same startpoint \(A=\max \hspace{0.99991pt}(a_\gamma , a_\tau , a_\rho )\); thus L and R are associated to a pair of intervals \([A, B_L)\) and \([A, B_R)\) respectively. Additionally, we have that \(L(A) = \gamma (A)+\tau (A)+\rho (A)=R(A)\). Thus, by naturality, it follows that
for all \(r \in \textbf{R}\) with \(A \leqslant r\). Since \(L(r)\ne 0\) iff \(r \in [A, B_L)\) and \(R(r) \ne 0\) iff \(r \in [A, B_R)\) we must have \(B_L = B_R\) and the equality \(L=R\) holds. \(\square \)
Definition 1.16
(scalar multiplication) Define \(\lambda :\mathbb {F}\times {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\rightarrow {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) to send \((c, \gamma )\), with \(\gamma \sim [a_\gamma , b_\gamma )\), to either \(c\gamma \), if \(c \ne 0\) (where \(c\gamma (r)=c\cdot \gamma (r)\) for all \(r \in \textbf{R}\)), or to \(Z_{a_\gamma }\), if \(c=0\).
Now we are ready to introduce the key for characterizing barcode bases.
Definition 1.17
Let \({\mathcal {T}}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\setminus {\mathcal {Z}}\). We say that \({\mathcal {T}}\) is linearly independent or the elements from \({\mathcal {T}}\) are linearly independent iff for any nonempty subset \({\mathcal {S}}\subseteq {\mathcal {T}}\) and any coefficients \(k_\gamma \in \mathbb {F}\setminus \{0\}\) with \(\gamma \in {\mathcal {S}}\), the sum 
is associated to \([\max _{\gamma \in {\mathcal {S}}}(a_\gamma ), \max _{\gamma \in {\mathcal {S}}}(b_\gamma ))\), where \(\gamma \sim [a_\gamma ,b_\gamma )\) for all \(\gamma \in {\mathcal {S}}\).
Example 3.8
Suppose that \(\{\alpha _1\hspace{0.77774pt}{\sim }\,[0,2), \alpha _2\hspace{0.94437pt}{\sim }\,[0,1)\}\) is a barcode basis of \(\mathbb {V}\simeq \mathbb {F}_{[0, 2)}\hspace{0.55542pt}{\oplus }\hspace{1.66656pt}\mathbb {F}_{[0, 1)}\). Then, \(\{\alpha _1,\alpha _2\}\) is linearly independent as will follow from Proposition 3.11. On the contrary, \(\alpha _1\) and \(\alpha _1\hspace{0.55542pt}{\boxplus }\hspace{1.111pt}\alpha _2\) are not linearly independent since \((-\alpha _1) \hspace{1.111pt}{\boxplus }\hspace{1.111pt}(\alpha _1\hspace{0.55542pt}{\boxplus }\hspace{1.111pt}\alpha _2)=\alpha _2\) is associated to [0, 1) but \(-\alpha _1\hspace{-0.55542pt}\sim [0,2)\) and \(\alpha _1 \hspace{0.55542pt}{\boxplus }\hspace{1.111pt}\alpha _2\sim [0,2)\).
In Proposition 3.11 we show that a barcode base is linearly independent. However, we would like that a barcode base also generates the set \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\). For this, we need to introduce a further ingredient.
Definition 1.19
(barcode cuts) Let \(s \in \textbf{R}\). We define \(\textbf{1}_{s}:{{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\rightarrow {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) as \(\textbf{1}_{s}(\alpha ) = \alpha \hspace{1.111pt}{\boxplus }\hspace{1.111pt}Z_s\), for all \(\alpha \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\).
Notice that \(\lambda \) and \(\{\textbf{1}_{s}\}_{s\in \textbf{R}}\) are compatible, in the sense that \(\textbf{1}_{r}(c\gamma )=c\textbf{1}_{r}(\gamma )\) for all \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), all \(r \in \textbf{R}\) and all \(c \in \mathbb {F}\). Also, given \(\gamma , \tau \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) and \(s,r \in \textbf{R}\), it follows that \(\textbf{1}_{s}(\gamma )\hspace{1.111pt}{\boxplus }\hspace{1.111pt}\textbf{1}_{r}(\tau )=\textbf{1}_{\max \hspace{0.55542pt}(s,r)}(\gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}\tau )\). Thus, persistence vectors on \(\mathbb {V}\) correspond to a tuple \(\bigl ({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V}), \hspace{1.111pt}{\boxplus }\hspace{1.111pt}, \lambda , \{\textbf{1}_{s}\}_{s\in \textbf{R}}\bigr )\).
Definition 1.20
Given \({\mathcal {T}}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), we say that \({\mathcal {T}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) iff for any \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V}){\setminus }{\mathcal {Z}}\), there exists \({\mathcal {S}}\subseteq {\mathcal {T}}\) together with coefficients \(k_\gamma \in \mathbb {F}{\setminus }\{0\}\) for all \(\gamma \in {\mathcal {S}}\), and some \(s \in \textbf{R}\) such that
Proposition 1.21
\({\mathcal {A}}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) is a barcode basis for \(\mathbb {V}\) iff it generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) and is linearly independent.
Proof
Assume first that \({\mathcal {A}}\) is a barcode basis. By Proposition 3.2, \({\mathcal {A}}^{r}(1_\mathbb {F})\) is a basis for \(\mathbb {V}(r)\) for all \(r \in \mathbb {F}\). Then, for any \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) with \(\gamma \sim [a_\gamma ,b_\gamma )\), we must have \(\gamma (a_\gamma )(1_\mathbb {F}) = \sum _{\alpha \in {\mathcal {A}}^{a_\gamma }}k_\alpha \alpha (a_\gamma )(1_\mathbb {F})\) for some coefficients \(k_\alpha \in \mathbb {F}\) and all \(\alpha \in {\mathcal {A}}^{a_\gamma }\). By naturality of \(\gamma \), this implies 
, which proves that \({\mathcal {A}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\). On the other hand, assume that \({\mathcal {A}}\) is not linearly independent. Then there exist some nonempty subset \({\mathcal {S}}\subseteq {\mathcal {A}}\) together with coefficients \(k_\alpha \in \mathbb {F}{\setminus }\{0\}\) such that 
is associated to an interval \([\max _{\alpha \in {\mathcal {S}}}(a_\alpha ), B)\) with \(B < \max _{\alpha \in {\mathcal {S}}}(b_\alpha )\). However, this implies that \({\mathcal {A}}^B(1_\mathbb {F})\) is not linearly independent in \(\mathbb {V}(B)\), since \(\sum _{\alpha \in {\mathcal {S}}\cap {\mathcal {A}}^B}k_\alpha \alpha (B)(1_\mathbb {F}) = 0\), but \(k_\alpha \in \mathbb {F}{\setminus }\{0\}\) for all \(\alpha \in {\mathcal {S}}\cap {\mathcal {A}}^B \ne \emptyset \), reaching a contradiction. Thus, \({\mathcal {A}}\) must be linearly independent.
Now, suppose that \({\mathcal {A}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) and is linearly independent. We prove that \({\mathcal {A}}\) is a barcode base by using Proposition 3.2. That is, we only need to show that \({\mathcal {A}}^{r}(1_\mathbb {F})\) is a basis for \(\mathbb {V}(r)\) for all \(r \in \textbf{R}\). Thus, let us show that \({\mathcal {A}}^{r}(1_\mathbb {F})\) generates \(\mathbb {V}(r)\) for all \(r \in \textbf{R}\). Let \(g \in \mathbb {V}(r)\) with \(g\ne 0\) and define the persistence vector \(\gamma :\mathbb {F}_{[r, s)}\rightarrow \mathbb {V}\) by setting \(\gamma (r)(1_\mathbb {F})=g\), where \(s=\sup {\{a:\mathbb {V}\hspace{0.33325pt}(r \,{\leqslant }\, a)(g)\ne 0\}}\). Thus, by generation of \({\mathcal {A}}\), there exists some subset \({\mathcal {S}}\subseteq {\mathcal {A}}\) together with some coefficients \(k_\alpha \in \mathbb {F}\) such that 
. In particular, \(g = \gamma (r)(1_\mathbb {F}) = \sum _{\alpha \in {\mathcal {S}}} k_\alpha \alpha (r)(1_\mathbb {F})\) and the claim follows. To show that \({\mathcal {A}}^{r}(1_\mathbb {F})\) is linearly independent, we consider any non-empty subset \({\mathcal {S}}\subseteq {\mathcal {A}}^r\) together with coefficients \(k_\alpha \in \mathbb {F}{\setminus }\{0\}\) for all \(\alpha \in {\mathcal {S}}\). Then 
is associated to \([\max _{\alpha \in {\mathcal {S}}}(a_\alpha ), \max _{\alpha \in {\mathcal {S}}}(b_\alpha ))\) which must contain r, and so \(\varGamma (r)(1_\mathbb {F})= \sum _{\alpha \in {\mathcal {S}}} k_\alpha \alpha (r)(1_\mathbb {F}) \ne 0\). Altogether \({\mathcal {A}}^r(1_\mathbb {F})\) is a basis for \(\mathbb {V}(r)\). \(\square \)
Let \(f:\mathbb {V}\rightarrow \mathbb {W}\) be a persistence morphism and consider two bases \({\mathcal {A}}\) and \({\mathcal {B}}\) for \(\mathbb {V}\) and \(\mathbb {W}\) respectively. Given \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) such that \(\gamma \sim [a_\gamma , b_\gamma )\), we define \(f(\gamma )\) as the persistence vector \(f(\gamma ):\mathbb {F}_{[a_\gamma , b_{f(\gamma )})}\!\rightarrow \mathbb {W}\) where \(b_{f(\gamma )}=\sup {\{ r \in [a_\gamma , b_\gamma ): f(r) \circ \gamma (r) \ne 0 \}}\) and \(f(\gamma )(r)\, {:}{=}\,f(r)\circ \gamma (r)\) for all \(r\! \in \! [a_\gamma , b_{f(\gamma )})\). Now, for each \(\alpha \in {\mathcal {A}}\) with \(\alpha \sim [a_\alpha , b_\alpha )\), as \({\mathcal {B}}\) is a barcode base, there exist some subset \({\mathcal {S}}\subseteq {\mathcal {B}}\) together with coefficients \(k_{\beta , \alpha } \in \mathbb {F}\setminus \{0\}\) for all \(\beta \in {\mathcal {S}}\) such that
It follows that \({\mathcal {S}}\subset {\mathcal {B}}^{a_\alpha }\) since adding elements from \({\mathcal {B}}\setminus {\mathcal {B}}^{a_\alpha }\) would have no effect or would cut the startpoint to a value greater than \(a_\alpha \). Also, notice that if \(\beta (b_\alpha )\ne 0\) then \(\beta \notin {\mathcal {S}}\), since otherwise f would not be natural as a persistence morphism. Thus, \({\mathcal {S}}\) must be a subset of
By pointwise-linearity and naturality of f, for any \({\mathcal {S}}\subseteq {\mathcal {A}}\) the equality
holds, where \(k_\alpha \in \mathbb {F}\) for all \(\alpha \in {\mathcal {S}}\).
Corollary 1.22
Let \(\mathbb {V}\) and \(\mathbb {W}\) be a pair of persistence modules together with their respective barcode bases \({\mathcal {A}}\) and \({\mathcal {B}}\). Given a persistence morphism \({f:\mathbb {V}\rightarrow \mathbb {W}}\), there is a unique associated matrix \(F=( k_{\beta , \alpha })_{\beta \in {\mathcal {B}}, \alpha \in {\mathcal {A}}}\) which is well defined in the sense that whenever \(k_{\beta \alpha }\ne 0\) then \(\beta \in {\mathcal {B}}(\alpha )\). Conversely, assume that F is well defined, then there exists a unique persistence morphism \(f:\mathbb {V}\rightarrow \mathbb {W}\) whose associated matrix is F.
Proof
By the reasoning above, we only need to prove the converse statement. First, for each \(\alpha \in {\mathcal {A}}\) such that \(\alpha \sim [a_\alpha , b_\alpha )\), we define 
. By linear independence of \({\mathcal {B}}\), \(f(\alpha )\) is associated to the interval \([a_\alpha , B)\) for \(B=\max _{\beta \in {\mathcal {S}}}(b_\beta )\) with \({\mathcal {S}}\) being the set \(\{ \beta \in {\mathcal {B}}(\alpha ): k_{\beta , \alpha }\ne 0\}\). We can extend the definition of f by the linear formula 
for any coefficients \(c_\alpha \in \mathbb {F}\) for all \(\alpha \in {\mathcal {A}}\). This implies the claim as f is then natural and pointwise linear. \(\square \)
We end this section by introducing different orders of barcode bases. These orders are important to introduce Gaussian eliminations in the barcode basis context.
Definition 1.23
Let \(\mathbb {V}\) be a persistence module with barcode base \({\mathcal {A}}\). Also, let \(\alpha _i, \alpha _j \in {\mathcal {A}}\) with \(\alpha _i\hspace{-0.55542pt}\sim [a_i, b_i)\) and \(\alpha _j \hspace{-0.55542pt}\sim [a_j, b_j)\). We consider two orders in \({\mathcal {A}}\):
- The standard order::
-
\(\alpha _i < \alpha _j\) if either \(a_i < a_j\) or \(a_i = a_j\) and \(b_i > b_j\).
- The endpoint order::
-
\(\alpha _i < \alpha _j\) if either \(b_i < b_j\) or \(b_i = b_j\) and \(a_i < a_j\).
If \(\mathbb {V}\) is tame, it is straightforward to extend these orders to total orders for \({\mathcal {A}}\).
3.2 Computing Kernels and Images
Consider two finite barcode bases \({\mathcal {A}}= \{\alpha _i\}_{i=1}^n\) and \({\mathcal {B}}= \{\beta _j\}_{j=1}^m\) for \(\mathbb {V}\) and \(\mathbb {W}\), respectively. Additionally, suppose that \({\mathcal {A}}\) is ordered according to the standard order while \({\mathcal {B}}\) is ordered using the endpoint order. We assume such orders are total; e.g., even if \(\alpha _r,\alpha _s \hspace{-0.55542pt}\sim [a, b)\) for \(r\ne s\), either \(\alpha _r < \alpha _s\) or \(\alpha _s < \alpha _r\) holds. Then, we consider \(f({\mathcal {A}})_{\mathcal {B}}= ( f(\alpha _1), \ldots , f(\alpha _n) )\), the matrix of f in the bases \({\mathcal {A}}\) and \({\mathcal {B}}\). In Sect. 3.3, we transform \(f({\mathcal {A}})_{\mathcal {B}}\) performing left to right column additions until obtaining a reduced matrix, i.e., with unique column pivots,
for suitable \(k_{i,j} \in \mathbb {F}\) and \(1 \leqslant j < i \leqslant n\). This \({\mathcal {I}}_{\mathcal {B}}\) has the property that its non-zero columns form a basis \(\widetilde{{\mathcal {I}}}\) for \(\textrm{Im}\hspace{0.55542pt}(f)\).
Definition 1.24
Given \({\mathcal {S}}\subseteq {\mathcal {B}}\), consider a vector \(V = (k_{\beta })_{\beta \in {\mathcal {B}}}\) such that \(k_\beta \ne 0\) iff \(\beta \in {\mathcal {S}}\). The pivot of V is the greatest element from \({\mathcal {S}}\) in the endpoint order. We also refer to the pivot of \({\mathcal {S}}\) or the pivot of 
.
Consider again the matrix \({\mathcal {I}}_{\mathcal {B}}\) from (4). By linearity, the jth column from \({\mathcal {I}}\) is
; thus, its preimage is
and we define the set of preimages of
\({\mathcal {I}}\) by
\({\mathcal {P}}{\mathcal {I}}= \{ p_j\}_{j=1}^n\). Given
\(p_j\in {\mathcal {P}}{\mathcal {I}}\), notice that
\(p_j \hspace{-0.55542pt}\sim [a_j, b_j)\) while
\(f(p_j)\sim [a_j, c_j)\) for filtration values
\(c_j \leqslant b_j\). Thus, we must have that
\(\textbf{1}_{c_j}(p_j) \in \ker \hspace{0.55542pt}(f)\) for all
\(1 \leqslant j \leqslant n\). We consider
\({\mathcal {G}}{\mathcal {K}}= \{ \textbf{1}_{c_j}(p_j)\}_{1 \leqslant j \leqslant n}\) which generates
\(\ker \hspace{0.55542pt}(f)\), as it is shown later in Proposition 3.17. Then, we order
\({\mathcal {G}}{\mathcal {K}}\) by choosing a permutation
\(\sigma :\{1, 2, \ldots , n\}\rightarrow \{1, 2, \ldots , n\}\) such that it is consistent with the standard order. Using the order from \({\mathcal {G}}{\mathcal {K}}\) we consider the matrix \({\mathcal {G}}{\mathcal {K}}_{\mathcal {A}}= \bigl (\textbf{1}_{c_{\sigma (1)}}(p_{\sigma (1)}), \ldots , \textbf{1}_{c_{\sigma (n)}}(p_{\sigma (n)})\bigr )\) where the rows correspond to generators from \({\mathcal {A}}\) with the endpoint order. Reducing columns we find some coefficients \(q_{i,j} \in \mathbb {F}\) so that the resulting matrix has unique pivots:
Taking the non-zero columns from \({\mathcal {K}}_{\mathcal {A}}\) leads to a basis \(\widetilde{{\mathcal {K}}}\) for \(\textrm{Ker}\hspace{0.55542pt}(f)\). In the following we present an algorithm obtaining such bases for \(\textrm{Im}\hspace{0.55542pt}(f)\) and \(\ker \hspace{0.55542pt}(f)\). First we go through an illustrative example:
Example 3.15
Consider two persistence modules (see Fig. 1)
with canonical barcode bases \((\alpha _1,\alpha _2,\alpha _3)\) and \((\beta _1,\beta _2,\beta _3)\) ordered respectively using the standard and endpoint orders. Let \(f:\mathbb {V}\rightarrow \mathbb {W}\) be given by the \(\vert {\mathcal {B}}\vert \hspace{1.111pt}{\times }\hspace{1.111pt}\vert {\mathcal {A}}\vert \) matrix \(f({\mathcal {A}})_{\mathcal {B}}\):
Decomposition of barcodes in image, kernel, domain and codomain of \(f:\mathbb {V}\rightarrow \mathbb {W}\). The colors correspond to the different generators associated to \(\widetilde{{\mathcal {I}}}\) and \(\widetilde{{\mathcal {K}}}\)
Then notice that the first two columns from \(f({\mathcal {A}})_{\mathcal {B}}\) share the same pivot \(\beta _2\), while the third’s column pivot is \(\beta _3\). We subtract the first column to the second, leading to the matrix \({\mathcal {I}}_{\mathcal {B}}\) above which has unique pivots for each column. From \({\mathcal {I}}_{\mathcal {B}}\) we obtain
In particular, we obtain a basis for the image
which leads to the barcode decomposition \(\textrm{Im}\hspace{0.55542pt}(f)\simeq \mathbb {F}_{[1, 4)}\hspace{0.55542pt}{\oplus }\hspace{1.111pt}\mathbb {F}_{[1, 3)} \hspace{0.55542pt}{\oplus }\hspace{1.111pt}\mathbb {F}_{[2, 5)}\). At the same time, we obtain a corresponding set of preimages \({\mathcal {P}}{\mathcal {I}}=\{\alpha _1,\alpha _2\hspace{0.55542pt}{\boxplus }\hspace{1.111pt}(-\alpha _1),\alpha _3\}\) From this we deduce the set of kernel generators \({\mathcal {G}}{\mathcal {K}}\) and order it by the standard barcode order \({\mathcal {G}}{\mathcal {K}}= \{\textbf{1}_{3}(\alpha _2\hspace{0.55542pt}{\boxplus }\hspace{1.111pt}(-\alpha _1)), \, \textbf{1}_{4}(\alpha _1), \, \textbf{1}_{5}(\alpha _3)\}\). Thus, we consider the matrix \({\mathcal {G}}{\mathcal {K}}_{\mathcal {A}}\) for the kernels,where the rows correspond to the endpoint order on \({\mathcal {A}}\), and reduce it:
Notice that the second and third columns from \({\mathcal {K}}\) are trivial since \(\textbf{1}_{4}(\alpha _2) = Z_4\) and \(\textbf{1}_{5}(\alpha _3)=Z_5\). Since \({\mathcal {K}}\) contains a single nontrivial element we have obtained a basis for the kernel \(\widetilde{{\mathcal {K}}} = \{ \textbf{1}_{3}(\alpha _2 \hspace{0.55542pt}{\boxplus }\hspace{1.111pt}(-\alpha _1)) \}\). Thus, \(\ker \hspace{0.55542pt}(f)\simeq \mathbb {F}_{[3, 5)}\).
Finally, we explain why uniqueness of pivots leads to linear independence.
Proposition 1.26
Let \(\mathbb {V}\) be a persistence module with a barcode basis \({\mathcal {A}}\) ordered using the endpoint order. Consider a subset of persistence vectors \({\mathcal {M}}\subset {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) and suppose that their pivots on \({\mathcal {A}}\) are all different. Then \({\mathcal {M}}\) is linearly independent.
Proof
Let \(m \in {\mathcal {M}}\), \(m\sim [a_m, b_m)\), and write it in terms of \({\mathcal {A}}\) as 
, where \({\mathcal {S}}_m \subseteq {\mathcal {A}}\) and \(k_\alpha \in \mathbb {F}{\setminus }\{0\}\) for all \(\alpha \in {\mathcal {S}}_m\). Let \(\alpha _m \in {\mathcal {S}}_m\) be the pivot of m. In particular, by the definition of pivot we must have \(\alpha _m \hspace{-0.55542pt}\sim [c_m, b_m)\) for some filtration value \(c_m \leqslant a_m\). Now, consider a nonempty subset \({\mathcal {R}}\subseteq {\mathcal {M}}\) together with coefficients \(q_m \in \mathbb {F}{\setminus }\{0\}\) for all \(m \in {\mathcal {R}}\) and take the sum 
. We claim that \(V \sim [\max _{m \in {\mathcal {R}}}(a_m), \max _{m \in {\mathcal {R}}}(b_m))\). Consider the element \(P \in {\mathcal {R}}\) whose pivot \(\alpha _P\) is the highest according to the endpoint order. Consequently, we have that \(b_P = \max _{m \in {\mathcal {R}}}(b_m)\). Notice that P is unique, since otherwise there would be two elements from \({\mathcal {M}}\) with the same pivots, contradicting our assumption. This implies that V is written in terms of \({\mathcal {A}}\) with a nonzero coefficient for \(\alpha _P\). By linear independence of \({\mathcal {A}}\) the claim follows. \(\square \)
3.3 The box_gauss_reduce Algorithm
Suppose that \(f:\mathbb {V}\rightarrow \mathbb {W}\) is a morphism between two tame persistence modules. Let \({\mathcal {A}}\), with the standard order, and \({\mathcal {B}}\), with the endpoint order, be barcode bases for \(\mathbb {V}\) and \(\mathbb {W}\) respectively. Suppose also that we know \(f({\mathcal {A}})_{{\mathcal {B}}}\), the matrix associated to f with respect to \({\mathcal {A}}\) and \({\mathcal {B}}\). Sending this information to Algorithm 1, called box_gauss_reduceFootnote 2, we obtain a set of persistence vectors \({\mathcal {I}}\subseteq {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(f(\mathbb {V}))\) together with the coordinates, in \({\mathcal {A}}\), of their respective preimages stored in \({\mathcal {P}}{\mathcal {I}}_{\mathcal {A}}\). Then, using \({\mathcal {P}}{\mathcal {I}}_{\mathcal {A}}\), we obtain a set of generators \({\mathcal {G}}{\mathcal {K}}\) for \(\ker \hspace{0.55542pt}(f)\), order it according to the standard order and define a matrix \({\mathcal {G}}{\mathcal {K}}_{\mathcal {A}}\) which expresses the elements from \({\mathcal {G}}{\mathcal {K}}\) in terms of \({\mathcal {A}}\). Reducing \({\mathcal {G}}{\mathcal {K}}_{\mathcal {A}}\) by using Algorithm 1 again, we end up with \({\mathcal {K}}\). Taking the nonzero elements from \({\mathcal {I}}\) and \({\mathcal {K}}\) leads to the barcode bases \(\widetilde{{\mathcal {I}}}\) and \(\widetilde{{\mathcal {K}}}\). An outline of this procedure is shown in Algorithm 2, which we call image_kernel.
box_gauss_reduce
image_kernel
Proposition 1.27
Algorithm 2 computes \(\widetilde{{\mathcal {K}}}\) and \(\widetilde{{\mathcal {I}}}\) bases for the kernel and image of f.
Proof
First of all, by Proposition 3.16, we know that \(\widetilde{{\mathcal {I}}}\) and \(\widetilde{{\mathcal {K}}}\) are linearly independent, as these are both sets of persistence vectors with different pivots. Thus, all we need to show is that both sets generate \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\textrm{Im}\hspace{0.55542pt}(f))\) and \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\textrm{Ker}\hspace{0.55542pt}(f))\), respectively.
Let us prove that \(\widetilde{{\mathcal {I}}}\) generates \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\textrm{Im}\hspace{0.55542pt}(f))\). First, we will show that \({\mathcal {P}}{\mathcal {I}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\). Consider \(\gamma \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\) and write 
for coefficients \(k_i \in \mathbb {F}{\setminus }\{0\}\) with \(i \in I\) for some subset \(I\subseteq \{1,2,\ldots , \vert {\mathcal {A}}\vert \}\). Then, consider the maximum index m from I and compute \(\widetilde{\gamma } = \gamma \hspace{1.111pt}{\boxplus }\hspace{1.111pt}(- k_m p_m)\). Here it is key to recall that the preimage \(p_m\in {\mathcal {P}}{\mathcal {I}}\) is written as 
for coefficients \(k_{m, i} \in \mathbb {F}\) for \(1 \leqslant i < m\). Now, 
for coefficients \(\widetilde{k_i} \in \mathbb {F}{\setminus }\{0\}\) with \(i \in J\) for some subset \(J\subseteq \{1,2,\ldots , m-1\}\). Repeating this argument, eventually, we write \(\gamma \) in terms of \({\mathcal {G}}{\mathcal {I}}\). This implies that \(f(\gamma )\) can be expressed in terms of \(\widetilde{{\mathcal {I}}}\). Thus, \(\widetilde{{\mathcal {I}}}\) generates \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\textrm{Im}\hspace{0.55542pt}(f))\).
Now, let us show that \(\widetilde{{\mathcal {K}}}\) generates \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\textrm{Ker}\hspace{0.55542pt}(f))\). In fact, it will be enough to show that \({\mathcal {G}}{\mathcal {K}}\) generates \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\ker \hspace{0.55542pt}(f))\). This is because \(\widetilde{{\mathcal {K}}}\) is obtained from reducing \({\mathcal {G}}{\mathcal {K}}_{\mathcal {A}}\) in a similar manner as \(\widetilde{{\mathcal {I}}}\) was obtained by reducing \(f({\mathcal {A}})_{\mathcal {B}}\). Consequently, by replicating the argument which proved that \({\mathcal {P}}{\mathcal {I}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), it follows that \(\widetilde{{\mathcal {K}}}\) generates \({{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(\ker \hspace{0.55542pt}(f))\). So let us prove our claim. Suppose that \(\gamma :\mathbb {F}_{[a, b)}{\rightarrow } \mathbb {V}\) lies in the kernel; i.e., \(f(\gamma )=Z_a\). As \({\mathcal {P}}{\mathcal {I}}\) generates \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {V})\), we have that 
for coefficients \(k_i \in \mathbb {F}{\setminus }\{0\}\) with \(i \in I\) for some subset \(I \subseteq \{1,2,\ldots , \vert {\mathcal {A}}\vert \}\). Applying f, we obtain the equality 
and notice that \(f(p_i)(a)=0\) for all \(i \in I\); otherwise linear independence of \(\widetilde{{\mathcal {I}}}\), and in particular that of \(\widetilde{{\mathcal {I}}}^a(1_\mathbb {F})\), would be contradicted. However, if \(f(p_i)(a)=0\) for all \(i \in I\), then \(\textbf{1}_{c_i}(p_i)\in {\mathcal {G}}{\mathcal {K}}\) for some \(c_i \leqslant a\) and all \(i \in I\). Altogether we obtain that \(\gamma \) must be generated by \({\mathcal {G}}{\mathcal {K}}\). \(\square \)
Notice that Algorithm 1 for the cases from Proposition 3.17 is simply a Gaussian elimination where the procedure differs from the standard method. In the former case, the input \({\mathcal {A}}\) in Algorithm 1 is given ordered in the startpoint order. However, this hypotheses is not assumed in Sect. 3.4. Next, we give a computational bound.
Proposition 1.28
Algorithm 2 takes at most \({\mathcal {O}}(N^2 \vert {\mathcal {A}}\vert )\) time, where \(N = \textrm{max}(\vert {\mathcal {A}}\vert , \vert {\mathcal {B}}\vert )\).
Proof
Let us start by measuring the computational complexity of Algorithm 1, box_gauss_reduce. First, the for loop from line 4 iterates \(\vert {\mathcal {B}}\vert \) times. Next, for each iteration of line 4 the pop() function from line 9 cannot be executed more than L times, where \(L \leqslant \vert {\mathcal {A}}\vert \). Then, lines 9 to 15 have a computational cost of about \(\vert {\mathcal {B}}\vert \). Altogether, the computational complexity of box_gauss_reduce is about \({\mathcal {O}}(\vert {\mathcal {A}}\vert \vert {\mathcal {B}}\vert ^2)\). Now, let us compute the complexity of Algorithm 2. Executing line 1 should take \({\mathcal {O}}(\vert {\mathcal {A}}\vert \vert {\mathcal {B}}\vert ^2)\) time, while executing line 7 should take about \({\mathcal {O}}(\vert {\mathcal {A}}\vert ^3)\) time. This leads to the expected result. \(\square \)
3.4 Computing Quotients
Suppose that we have inclusions \(\mathbb {H}\subseteq \mathbb {G}\subseteq \mathbb {V}\) of finite dimensional persistence modules, together with barcode bases \({\mathcal {H}}\), \({\mathcal {G}}\), and \({\mathcal {A}}\) respectively. Suppose that \({\mathcal {H}}\) and \({\mathcal {G}}\) are ordered using the standard order, while \({\mathcal {A}}\) is ordered using the endpoint order. Consider the inclusions \(\iota ^\mathbb {H}:\mathbb {H}\hookrightarrow \mathbb {V}\) and \(\iota ^\mathbb {G}:\mathbb {G}\hookrightarrow \mathbb {V}\) together with their respective associated matrices \(\iota ^\mathbb {H}({\mathcal {H}})_{\mathcal {A}}\in {\mathcal {M}}_{\vert {\mathcal {A}}\vert \times \vert {\mathcal {H}}\vert }(\mathbb {F})\) and \(\iota ^\mathbb {G}({\mathcal {G}})_{\mathcal {A}}\in {\mathcal {M}}_{\vert {\mathcal {A}}\vert \times \vert {\mathcal {G}}\vert }(\mathbb {F})\). Without loss of generality, we assume that \(\iota ^\mathbb {H}({\mathcal {H}})_{\mathcal {A}}\) is already reduced and \(\iota ^\mathbb {H}({\mathcal {H}})\) is a barcode base for \(\iota ^\mathbb {H}(\mathbb {H})\). Given all this data, the aim is to find a barcode base for \(\mathbb {G}/ \mathbb {H}\).
Let \(\mathbb {H}\oplus \mathbb {G}\) together with a barcode base given by the pair \(({\mathcal {H}}\,{\vert }\, {\mathcal {G}})\); here we extend the orders from \({\mathcal {H}}\) and \({\mathcal {G}}\) with the rule \(h<g\) for any pair of generators \(h \in {\mathcal {H}}\) and \(g \in {\mathcal {G}}\); of course, this might break the standard persistence vector order. Then, we consider \(\iota = \iota ^\mathbb {H}+ \iota ^\mathbb {G}:\mathbb {H}\hspace{1.111pt}{\oplus }\hspace{1.111pt}\mathbb {G}\rightarrow \mathbb {V}\) which will have the associated block matrix \((\iota ^\mathbb {H}({\mathcal {H}})_{\mathcal {A}}\,{\vert }\, \iota ^\mathbb {G}({\mathcal {G}})_{\mathcal {A}})\). We send the triple \((({\mathcal {H}}\vert {\mathcal {G}}), {\mathcal {A}}, (\iota ^\mathbb {H}({\mathcal {H}})_{\mathcal {A}}\,{\vert }\, \iota ^\mathbb {G}({\mathcal {G}})_{\mathcal {A}}))\) to the box_gauss_reduce algorithm and obtain the output \({\mathcal {I}},{\mathcal {P}}{\mathcal {I}}_{\mathcal {A}}\). We focus on the subset \({\mathcal {I}}[{\mathcal {G}}]\) containing the last \(\vert {\mathcal {G}}\vert \) elements from \({\mathcal {I}}\).
Recall that the box_gauss_reduce algorithm adds columns from \(\iota ^\mathbb {H}({\mathcal {H}})_{\mathcal {A}}\) and \(\iota ^\mathbb {G}({\mathcal {G}})_{\mathcal {A}}\) to eventually obtain a matrix \({\mathcal {I}}[{\mathcal {G}}]_{\mathcal {A}}\) from which we deduce the elements in \({\mathcal {I}}[{\mathcal {G}}]\). Further, using \({\mathcal {P}}{\mathcal {I}}_{\mathcal {A}}\), we are able to know exactly which combinations of columns were performed in the reduction procedure. Thus, each \(\varGamma \in {\mathcal {I}}[{\mathcal {G}}]\) can be written as \(\varGamma = \varGamma ^\mathbb {H}\hspace{0.55542pt}{\boxplus }\hspace{1.111pt}\varGamma ^\mathbb {G}\) where \(\varGamma ^\mathbb {H}\) and \(\varGamma ^\mathbb {G}\) denote the respective linear combinations of elements from \(\iota ^\mathbb {H}({\mathcal {H}})\) and \(\iota ^\mathbb {G}({\mathcal {G}})\). Given \(\varGamma \in {\mathcal {I}}[{\mathcal {G}}]\), we use the notation \(\varGamma ^\mathbb {G}\sim [a_\varGamma , d_\varGamma )\) and \(\varGamma \sim [b_\varGamma , c_\varGamma )\) for the corresponding associated intervals; in particular, notice that \(a_\varGamma \leqslant b_\varGamma \). Then, we define the persistence vector
which is defined by \(\overline{\varGamma ^\mathbb {G}}(r) = p_\mathbb {H}(r) \hspace{1.111pt}{\circ }\hspace{1.111pt}\varGamma ^\mathbb {G}(r)\) for all \(r \in [a_\varGamma , c_\varGamma )\), where we use the projection \(p_\mathbb {H}:\mathbb {V}\twoheadrightarrow \mathbb {V}/\mathbb {H}\). We claim that \(\overline{\varGamma ^\mathbb {G}}\) is well defined, i.e., \(\overline{\varGamma ^\mathbb {G}}(r)\ne \overline{0}\) iff \(r \in [a_\varGamma , c_\varGamma )\). First, notice that \(\overline{\varGamma ^\mathbb {G}}(c_\varGamma )= \overline{0}\) since by definition \(\varGamma (c_\varGamma )=0\), which implies \(\varGamma ^\mathbb {G}(c_\varGamma ) = -\varGamma ^\mathbb {H}(c_\varGamma )\). Next, we need to show that \(\overline{\varGamma ^\mathbb {G}}(r)\ne 0\) for all \(r \in [a_\varGamma , c_\varGamma )\). In fact, we prove the stronger statement that
is linearly independent. Take a subset \({\mathcal {S}}\subseteq {\mathcal {I}}[{\mathcal {G}}]\) such that \(\{\overline{\varGamma ^\mathbb {G}}\}_{\varGamma \in {\mathcal {S}}}\) is a nonempty subset of \(\widetilde{{\mathcal {Q}}}\). Also, take some coefficients \(k_\varGamma \in \mathbb {F}{\setminus } \{0\}\) for all \(\varGamma \in {\mathcal {S}}\). We want to show that 
is associated to the interval [A, C), where we use the notation \(A = \max _{\varGamma \in {\mathcal {S}}}(a_\varGamma )\) and \(C = \max _{\varGamma \in {\mathcal {S}}}(c_\varGamma )\). By contradiction, suppose that \(\overline{V^\mathbb {G}}\) is associated to [A, r) for some value \(r \in [A,C)\). This implies that \(\textbf{1}_{r}(V^\mathbb {G})\) is in \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {H})\), where we define 
.
Next, take the greatest \(\varGamma \in {\mathcal {S}}\) whose endpoint is C. Thus, there must exist \(R\in \mathbb {R}\) such that \(r \leqslant R < C\) and \(\textbf{1}_{R}(\varUpsilon )=Z_R\) for all \(\varUpsilon \in {\mathcal {S}}\) such that \(\varUpsilon >\varGamma \). Equivalently, \(\textbf{1}_{R}(\varUpsilon ^\mathbb {G}) \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {H})\) for all \(\varUpsilon \in {\mathcal {S}}\) such that \(\varUpsilon >\varGamma \). Since \(\textbf{1}_{R}(V^\mathbb {G})\) is in \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {H})\), we conclude that \(\textbf{1}_{R}(\varGamma ^\mathbb {G})\) can be written in terms of generators from \(\iota ^\mathbb {H}({\mathcal {H}})^R\) and elements \(\widetilde{\varGamma }^\mathbb {G}\) with \({\widetilde{\varGamma }<\varGamma }\); where, from the third bullet point after Definition 3.1, \(\iota ^\mathbb {H}({\mathcal {H}})^R\) denotes the set of generators \(\gamma \in \iota ^\mathbb {H}({\mathcal {H}})\) such that \(\gamma (R)\ne 0\). Now, consider the matrix \({\mathcal {I}}[{\mathcal {G}}]^\mathbb {G}_{\mathcal {A}}\) whose columns correspond to the coordinates of \(\varUpsilon ^\mathbb {G}\) in terms of \({\mathcal {A}}\) for all \(\varUpsilon \in {\mathcal {I}}[{\mathcal {G}}]\). Then, consider the block matrix \(M=(\iota ^\mathbb {H}({\mathcal {H}})^R_{\mathcal {A}}\,{\vert }\,{\mathcal {I}}[{\mathcal {G}}]^\mathbb {G}_{\mathcal {A}})\). In matrix terms, our hypotheses on \(\textbf{1}_{R}(\varGamma ^\mathbb {G})\) means that its corresponding column from M can be reduced by left to right column additions on M up to a pivot whose associated interval endpoint is smaller or equal to R.
Now, denote \(N = (\iota ^\mathbb {H}({\mathcal {H}})^R_{\mathcal {A}}\,{\vert }\,\iota ^\mathbb {G}({\mathcal {G}})_{\mathcal {A}})\). It is not difficult to notice that M is the result of applying left-to-right column additions to N. Consequently, denoting by \(C_\varGamma \) the column from N that corresponds to \(\varGamma ^\mathbb {G}\), the column \(C_\varGamma \) can be reduced by left columns in N up to a pivot whose associated interval endpoint is smaller or equal to R. There are two options:
-
Assume \(\varGamma \sim [b_\varGamma , C)\), with \(b_\varGamma < C\). By hypotheses, \(C_\varGamma \) is a combination of previous columns up to a pivot with death value \(\leqslant R\). Thus, following the instructions from Algorithm 1, we should reduce \(C_\varGamma \) (at least) to a pivot with death value \(\leqslant R\). However, in such a case, \(\varGamma \) would be associated to an interval with endpoint \(\leqslant R\). But \(R<C\), reaching a contradiction.
-
Assume \(\varGamma =Z_C\). There exists a pivot of index p in the reduction process where we first add to \(C_\varGamma \) a column \(\widetilde{C}\) with start value strictly bigger than R; as \(\varGamma =Z_C\) and \(a_\varGamma \leqslant r \leqslant R<C\). By step 7 in Algorithm 1 and by our hypotheses on \(C_\varGamma \), such a pivot must have an endpoint smaller or equal to R. However, the column \(\widetilde{C}\) has a startpoint strictly bigger than R. This contradicts Corollary 3.12 as well as step 13 in Algorithm 1.
It can be shown that \(\widetilde{{\mathcal {Q}}}\) generates \(\mathbb {G}/\mathbb {H}\) by a similar reasoning as used in Proposition 3.17. Consequently, \(\widetilde{{\mathcal {Q}}}\) is a barcode base for the quotient.
3.5 Homology of Persistence Modules
Consider a chain of tame persistence modules:
where each term has basis \({\mathcal {B}}_j\) for \(0 \leqslant j \leqslant n\). Then applying image_kernel we obtain bases \({\mathcal {I}}_{j-1}\) and \({\mathcal {K}}_j\) for the image and kernel of \(d_j\) for all \(0 \leqslant j \leqslant n\). Proceeding as on the previous section, we send triples \(\bigl (({\mathcal {I}}_j \,{\vert }\, {\mathcal {K}}_j), {\mathcal {B}}_j, (({\mathcal {I}}_j)_{{\mathcal {B}}_j} \,{\vert }\, ({\mathcal {K}}_j)_{{\mathcal {B}}_j})\bigr )\) to box_gauss_reduce for all \(0 \leqslant j \leqslant n\). This leads to bases \({\mathcal {Q}}_j\) for the quotients \(\textrm{Ker}\hspace{0.55542pt}(d_j)/ \textrm{Im}\hspace{0.55542pt}(d_{j+1})\) for all \(0 \leqslant j \leqslant n\).
4 A Review on the Mayer–Vietoris Spectral Sequence
In this section, we give an introduction to the Mayer–Vietoris spectral sequence. These ideas come mainly from [3, 20]. Here, we outline a minimal, self-contained explanation of the procedure. Also, this is used in Sect. 5. For simplicity we focus on ordinary homology over a field \(\mathbb {F}\). Later, in Sect. 5, we go back to the case of persistent homology over a field.
4.1 The Mayer–Vietoris Long Exact Sequence
Consider a torus \(\mathbb {T}^2\) covered by two cylinders U and V, as illustrated in Fig. 2. Naively, one could think that \(\textrm{H}_n(\mathbb {T}^2)\cong \textrm{H}_n(U)\hspace{1.111pt}{\oplus }\hspace{1.111pt}\textrm{H}_n(V)\) for all \(n \geqslant 0\). However, this does not hold in dimensions 0 and 2:
To amend this, one has to look at the information given by the intersection \(U\cap V\). This information comes as identifications and new loops. For example, U and V are connected through \(U\cap V\). Also, the loop going around each cylinder U and V is identified in \(U\cap V\). These identifications are performed by taking the quotient
for all \(n \geqslant 0\). Where the previous morphism is the Čech differential \(\delta _1^n :S_n(U\cap V) \rightarrow S_n(U)\hspace{1.111pt}{\oplus }\hspace{1.111pt}S_n(V)\). Additionally, the 1-loops in the intersection merge to the same loop when included in each cylinder U or V. This situation creates a 2-loop or “void”, see Fig. 2. Thus we have the n-loops detected by the kernel
for all \(n \geqslant 0\). Notice that n-loops are found by \(n-1\) information on the intersection. Putting all together, we have that
Torus covered by a pair of cylinders U and V
On a more theoretical level, what we have presented here is commonly known as the Mayer–Vietoris Theorem. That is, \(\textrm{H}_n(U\,{\cup }\, V)\) is a filtered object,
and there are expressions for the different ratios between consecutive filtrations,
In particular, as we are working with vector spaces, \(\textrm{H}_n(U \cup V) \cong I_n \hspace{0.55542pt}{\oplus }\hspace{1.111pt}L_n\) for all \(n \geqslant 0\).
The above discussion gives rise to the total chain complex,
with morphism \(d^Tot _n = (d, d, d - \delta _1) \) for all \(n \geqslant 0\). Notice that the first two morphisms do not change components, whereas the third encodes the “merging” of information. This last morphism is represented by red arrows on the diagram:
where the rectangle of red arrows is commutative. In particular, this implies that \(d_n^Tot \hspace{1.111pt}{\circ }\hspace{1.111pt}d_{n+1}^Tot =0\) for all \(n\geqslant 0\). Computing the homology with respect to the total differentials and using the previous characterization of \(I_n\) and \(L_n\), one obtains
This result is generalized in Proposition 4.1.
4.2 The Mayer–Vietoris Spectral Sequence
Consider a simplicial complex K with a covering \({\mathcal {U}}=\{ U_i\}_{i=0}^m\) by subcomplexes. We can extend the intuition from the previous subsection, by recalling the definition of the \((n, {\mathcal {U}})\)-Čech chain complex given on the preliminaries. Stacking all these sequences on top of each other, and also multiplying differentials in odd rows by \(-1\), we obtain a diagram:
This leads to a double complex \(({\mathcal {S}}_{*,*}, \bar{\delta }, d)\) defined as
for all \(p,q \geqslant 0\), and also \({\mathcal {S}}_{p,q}\, {:}{=}\, 0\) otherwise. We denote \(\bar{\delta } = (-1)^q \delta \), the Čech differential multiplied by a \(-1\) on odd rows. The reason for this change of sign is because we want \({\mathcal {S}}_{*,*}\) to be a double complex, in the sense that the following equalities hold:
Since \({\mathcal {S}}_{*,*}\) is a double complex, we can study the associated chain complex \({\mathcal {S}}_*^Tot \), commonly known as the total complex. This is formed by taking the sums of anti-diagonals
for \(n\geqslant 0\). The differentials on the total complex are defined by \(d^Tot \,{=}\, d \!+\! \bar{\delta }\), which satisfy \(d^Tot \hspace{0.55542pt}{\circ }\hspace{1.111pt}d^Tot =0\) from (5), see Fig. 3 for a depiction of this. Later, in Proposition 4.1, we prove that \(\textrm{H}_n(K) \cong \textrm{H}_n({\mathcal {S}}^Tot _*)\) for all \(n \geqslant 0\). The problem still remains difficult, since computing \(\textrm{H}_n({\mathcal {S}}^Tot _*)\) directly might be even harder than computing \(\textrm{H}_n(K)\). The key is that the Mayer–Vietoris spectral sequence allows us to break apart the calculation of \(\textrm{H}_n({\mathcal {S}}^Tot _*)\) into small, computable steps.
\({\mathcal {S}}_{*,*}\) represented as a lattice for convenience. On the left, the total complex \({\mathcal {S}}^Tot \) associated to \({\mathcal {S}}_{*,*}\). Here \((\beta _0, \ldots , \beta _4) \in {\mathcal {S}}^Tot _4\) maps to \((\alpha _0, \ldots , \alpha _3) \in {\mathcal {S}}^Tot _3\), where \(d(\beta _i) + \bar{\delta }(\beta _{i+1}) = \alpha _i\) for all \(0 \leqslant i \leqslant 3\). On the right, the kernel \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )_4\), where \(d(\beta _i)+\overline{\delta }(\beta _{i+1}) = 0\) for all \(0 \leqslant i \leqslant 3\)
Let us start by computing the kernel \(\textrm{Ker}\hspace{0.55542pt}(d^Tot _n)\), which is depicted in Fig. 3. Recall that in this section we are working with vector spaces and linear maps. Let \(s = (s_{k,n-k})_{0 \leqslant k \leqslant n} \in {\mathcal {S}}^Tot _n\) be in \(\textrm{Ker}\hspace{0.55542pt}(d^Tot _n)\). Then, the equations \(d(s_{k,n-k}) = -\bar{\delta }(s_{k+1,n-k-1})\) hold for all \(0 \leqslant k < n\). This leads to subspaces \(\textrm{GK}_{p,q} \subseteq {\mathcal {S}}_{p,q}\) composed of elements \(s_{p,q} \in {\mathcal {S}}_{p,q}\) such that \(d(s_{p,q})=0\) and such that there exists a sequence \(s_{p-r,q+r} \in {\mathcal {S}}_{p-r,q+r}\) with \(d(s_{p-r,q+r}) = -\bar{\delta }(s_{p-r+1,q+r-1})\) for all \(0 < r \leqslant p\). Notice that \(\textrm{GK}_{p,q}\) is a subspace of \({\mathcal {S}}_{p,q}\) since both d and \(\bar{\delta }\) are linear. This is depicted in Fig. 4. There are (non-canonical) isomorphisms,
It turns out that (6) only holds when we are working with vector spaces. Later, we work with a more general case where we have to solve nontrivial extension problems.
On the left, in cyan the four direct summands of \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )_4\). The corresponding \(\textrm{GK}_{r,3-r}\) are framed to indicate that these are subspaces of \({\mathcal {S}}_{r,3-r}\) for all \(0 \leqslant r \leqslant 3\). On the right, in orange the subspaces \(\textrm{GZ}^r_{2,1}\), eventually shrinking to \(\textrm{GK}_{2,1}\). For convenience, we denote \( \alpha _2 = d(\beta _2)\), \(\alpha _1 = \bar{\delta }(\beta _2)\) and \(\alpha _0 = \bar{\delta }(\beta _1) \)
By (6), recovering all \(\textrm{GK}_{p,q}\) leads to the kernel of \(d^Tot _*\). However, computing \(\textrm{GK}_{p,q}\) still requires a large set of equations to be checked. A step-by-step way of computing these is by adding one equation at a time. For this, we define the subspaces \(\textrm{GZ}^r_{p,q} \subseteq {\mathcal {S}}_{p,q}\) where we add the first r equations progressively. That is, we start setting \(\textrm{GZ}^0_{p,q} = {\mathcal {S}}_{p,q}\). Then we define \(\textrm{GZ}^1_{p,q}\) to be elements \(s_{p,q} \in {\mathcal {S}}_{p,q}\) such that \(d(s_{p,q})=0\), or equivalently \(\textrm{GZ}^1_{p,q} = \textrm{Ker}\hspace{0.55542pt}(d)_{p,q}\). For \(r \geqslant 2\), we define \(\textrm{GZ}^r_{p,q}\) to be formed by elements \(s_{p,q} \in \textrm{Ker}\hspace{0.55542pt}(d)_{p,q}\) such that there exists a sequence \(s_{p-k,q+k} \in {\mathcal {S}}_{p-k,q+k}\) with \(d(s_{p-k, q+k}) = -\bar{\delta }(s_{p-k+1, q+k-1})\) for all \(1 \leqslant k < r\). Altogether,
for all \(p,q \geqslant 0\). For intuition see Fig. 4, and also Fig. 6 for a depiction of \(\textrm{GZ}^2_{3,1}\) on a lattice. We also write \(\textrm{GZ}^r_{p,q} = \textrm{Ker}\hspace{0.55542pt}(d) \cap (\bar{\delta }^{-1}\circ d)^{r-1} ({\mathcal {S}}_{p-r+1,q+r-1})\) for all \(r \geqslant 1\), where by \((\bar{\delta }^{-1} \hspace{1.111pt}{\circ }\hspace{1.111pt}d)^r\) we denote composing r times \(\bar{\delta }^{-1} \hspace{1.111pt}{\circ }\hspace{1.111pt}d\). In particular, since \(\textrm{GZ}^r_{p,q} = \textrm{GZ}^{p+1}_{p,q}\) for all \(r \geqslant p+1\), we use the convention \(\textrm{GZ}^\infty _{p,q}\, {:}{=}\, \textrm{GZ}^{p+1}_{p,q} = \textrm{GK}_{p,q}\).
Now, we explain the notation \(\textrm{GK}_{p,q}\) and the isomorphism (6). We start defining a vertical filtration \(F^*\) on \({\mathcal {S}}_{*,*}\) by the following subcomplexes for all \(r \geqslant 0\):
This is an increasing filtration, i.e., \(F^r({\mathcal {S}}_{*,*}) \subseteq F^{r+1}({\mathcal {S}}_{*,*})\) for all \(r \geqslant 0\). Additionally, there are isomorphisms \(F^r({\mathcal {S}}_{*,*})/ F^{r-1}({\mathcal {S}}_{*,*}) \cong {\mathcal {S}}_{r,*}\) for all \(r \geqslant 0\). See Fig. 5 for a depiction of \(F^*\). Also, \(F^*\) respects the differentials from \({\mathcal {S}}_{*,*}\) in the sense that \(d(F^r({\mathcal {S}}_{*,*})) \subseteq F^r({\mathcal {S}}_{*,*})\) and \(\bar{\delta }(F^r({\mathcal {S}}_{*,*})) \subseteq F^r({\mathcal {S}}_{*,*})\) for all \(r \geqslant 0\). Consequently, \(F^*\) filters the total complex \({\mathcal {S}}_*^Tot \), respecting its differential \(d^Tot \). That is, \({\mathcal {S}}^Tot _n\) is filtered by subcomplexes, \(F^r {\mathcal {S}}^Tot _n\, {:}{=}\, \bigoplus _{p + q = n}^{p \leqslant r} {\mathcal {S}}_{p,q}\), for all \(r \geqslant 0\).
Note that \(F^3({\mathcal {S}}_{*,*})/ F^2({\mathcal {S}}_{*,*}) \cong {\mathcal {S}}_{3,*}\). Also notice that \(\bar{\delta }\) and d respect the vertical filtration \(F^*\)
In particular, \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )\) also inherits the filtration \(F^*\), where \(F^r \textrm{Ker}\hspace{0.55542pt}(d^Tot )_n=F^r {\mathcal {S}}^Tot _n \cap \textrm{Ker}\hspace{0.55542pt}(d^Tot )_n\) for all \(r\geqslant 0\). We define the associated modules of \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )_n\) to be the quotients \(G^p \textrm{Ker}\hspace{0.55542pt}(d^Tot )_n = F^p \textrm{Ker}\hspace{0.55542pt}(d^Tot )_n / F^{p-1}\textrm{Ker}\hspace{0.55542pt}(d^Tot )_n\), which can be checked to be isomorphic with \(\textrm{GK}_{p,q}\) for all \(p+q = n\). This follows by considering morphisms
which are well defined since \(s_{p,q}\) does not change for representatives of the same class. In fact, this morphism is injective since two classes with the same image will be equal by definition of \(G^p \textrm{Ker}\hspace{0.55542pt}(d^Tot )_n\). On the other hand, the definition of \(\textrm{GK}_{p,q}\) ensures surjectivity. In particular, as we are working with vector spaces, we have that
which justifies isomorphism (6).
Next, we explain the notation \(\textrm{GZ}^r_{p,q}\). We introduce the objects
for all \(r \geqslant 0\). We can think of these as kernels of \(d^Tot \) up to some previous filtration. Then, by definition, we have that \(Z^0_{p,q} = F^p{\mathcal {S}}^Tot _{p+q}\) and \(Z^{p+1}_{p,q} = Z^\infty _{p,q}= F^p \textrm{Ker}\hspace{0.55542pt}(d^Tot _{p+q})\). Using a morphism analogous to (7), one can check that the quotients \(Z^{r+1}_{p,q}/Z^r_{p-1, q+1}\) are isomorphic to \(\textrm{GZ}^{r+1}_{p,q}\) for all \(p + q = n\). This is depicted in Fig. 6. Thus, computing these quotients increasing \(r\geqslant 0\) leads to \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )\). With a little more work, we can do the same for computing the homology.
On the left the sets \(Z^2_{3,1}\) and \(Z^1_{2,2}\). On the right their respective quotient \(\textrm{GZ}^2_{3,1}\)
The Mayer–Vietoris spectral sequence leads to \(\textrm{H}_n({\mathcal {S}}^Tot _*)\) after a series of small, computable steps. This is done similarly as we did before for computing \(\textrm{Ker}\hspace{0.55542pt}(d^Tot )\). However, in this case we need to take quotients by the images of \(d^Tot \). First, notice that the vertical filtration \(F^*\) transfers to homology \(\textrm{H}_n({\mathcal {S}}^Tot _*)\) by the inclusions \(F^p{\mathcal {S}}^Tot _* \subseteq {\mathcal {S}}^Tot _*\) for all \(p \geqslant 0\). That is, we have filtered sets
which induce a filtration on \(\textrm{H}_n({\mathcal {S}}^Tot _*)\). For this filtration, the associated modules are defined by the quotients \(G^r \textrm{H}_n({\mathcal {S}}^Tot _*) = F^r \textrm{H}_n({\mathcal {S}}^Tot _*) / F^{r-1} \textrm{H}_n({\mathcal {S}}^Tot _*)\) for all \(r \geqslant 0\). As we are working over a field, we recover the homology by taking direct sums:
Previously, we defined the sets \(Z^r_{p,q}\) which are kernels “up to filtration”. In an analogous way, we define boundaries “up to filtration” by settingFootnote 3
for all \(r \geqslant 0\) and \(p,q \geqslant 0\). These are images of \(d^Tot \) coming from a previous filtration. In particular, the equalities \(d^Tot (Z^r_{p,q}) = B^r_{p-r,q+r-1}\) and \(d^Tot (B^r_{p,q}) = 0\) hold. Additionally, for all \(p,q \geqslant 0\), there is a sequence of inclusions,
Hence, we define the first page of the spectral sequence as the quotient
for all \(p, q \geqslant 0\). Recall that \(\textrm{Ker}\hspace{0.55542pt}(d)_{p,q} = \textrm{GZ}^1_{p,q} = Z^1_{p,q} / Z^0_{p-1, q+1}\) and also one can see that \(\textrm{Im}\hspace{0.55542pt}\hspace{0.99991pt}(B^0_{p,q}\,{\rightarrow }\,\textrm{GZ}^1_{p,q})\) is isomorphic to \(\textrm{Im}\hspace{0.55542pt}(d)_{p,q}\). Then we deduce that \(E^1_{p,q} \cong \textrm{H}_q({\mathcal {S}}_{p,*}, d)\). On this page \(d^Tot \) induces differentials \(d^1:E^1_{p,q}~ \rightarrow \,\,\, E^1_{p-1,q}\).
I.e., noticing that \(d^Tot (Z_{p,q}^1) = B_{p-1,q}^1 \subset Z_{p-1,q}^1\) and also \(d^Tot ( Z^0_{p-1, q+1} + B^0_{p,q}) = d^Tot ( Z^0_{p-1, q+1}) + 0 = B^0_{p-1,q}\) we have that \(d^1:E^1_{p,q}\rightarrow E^1_{p-1,q}\) is well defined.
Next, we compute the second page. First, notice that
Since \(d^Tot \circ d^Tot = 0\) we also have \(d^1\circ d^1 = 0\) and, in particular, \(\textrm{Im}\hspace{0.55542pt}(d^1) \subseteq \textrm{Ker}\hspace{0.55542pt}(d^1)\). Then, the second page terms are given by
The second page has differential \(d^2\) induced by the total complex differential \(d^Tot \). Figure 7 illustrates this principle. Doing the same for all pages we obtain the definition of the r-page terms
On the left, the different subspaces on \({\mathcal {S}}_{2,1}\). Here \(\textrm{IB}_{2,1}^r = \textrm{Im}\hspace{0.55542pt}\hspace{0.7222pt}(B^{r}_{2,1}\,{\rightarrow }\, \textrm{GZ}^{r+1}_{2,1} )\), for all \(0 \leqslant r \leqslant 2\). The framed region represents \({\mathcal {S}}_{2,1}\). Brighter colours represent bigger regions than darker colours. Note that blue and orange colours have been assigned to \(\textrm{GZ}^*_{2,1}\) and \(\textrm{IB}^*_{2,1}\) respectively. On the right, the morphism \(d^2:E_{3,1}^2 \rightarrow E_{1,2}^2\) on the second page. The two framed regions represent the codomain and domain of \(d^2\), these have been assigned brighter and darker colours, respectively
for all \(r \geqslant 2\). Of course, we can express alternatively the r-page terms as
Thus, the \(\infty \)-page is
Then, for \(n=p+q\), one has that \(G^p \textrm{H}_n({\mathcal {S}}^Tot _*)\) is isomorphic to
since \(B_{p-1, q+1}^\infty \subseteq B_{p,q}^\infty \). Therefore, computing the spectral sequence is a way of approximating the associated module \(G^p\textrm{H}_n({\mathcal {S}}^Tot _*)\). By (8), adding up these leads to \(\textrm{H}_n({\mathcal {S}}^Tot _*)\). Also, since \(E^\infty _{p,q} \cong G^p\textrm{H}_n({\mathcal {S}}^Tot _*)\), we say that \(E^*_{p,q}\) converges to \(\textrm{H}_n({\mathcal {S}}^Tot )\) and we denote this as \(E^*_{p,q} \Rightarrow \textrm{H}_n({\mathcal {S}}^Tot )\). As the rows from \({\mathcal {S}}_{p,q}\) are exact, the following result is standard; see for example [3, Prop. 8.8] for a similar proof.
Proposition 1.29
\(\textrm{H}_n({\mathcal {S}}^Tot _*) \cong \textrm{H}_n(K)\).
Proof
Consider the horizontal filtration \(F_H\) by \(F_H^r {\mathcal {S}}^Tot _n \,{:}{=}\, \bigoplus _{p+q=n}^{q \leqslant r}{\mathcal {S}}_{p,q}\). This whole section can be adapted to this filtration and one obtains a corresponding spectral sequence \(_H E^*_{p,q}\Rightarrow \textrm{H}_n({\mathcal {S}}^Tot )\). As the Čech sequence (3) is exact, \(_H E^*_{p,q}\) collapses on the first page, where the only nontrivial terms are \(_H E^1_{0,n}\simeq \textrm{H}_n(K)\) for all \(n \geqslant 0\). This implies the claim. See [20, Thm. 2.15] for a general result on the spectral sequence of a double complex. \(\square \)
Therefore, using Proposition 4.1, we have that \(E^*_{p,q} \Rightarrow \textrm{H}_n(K)\). In particular, since we are working with vector spaces, \(\textrm{H}_n(K) \cong \bigoplus _{p+q = n} E^\infty _{p,q}\) for all \(n\geqslant 0\). Throughout the following section, we adapt these results to the category of persistence modules.
5 Persistent Mayer–Vietoris
One can translate the method from Sect. 4 to PMod. The reason for this is that PMod is an abelian category, since Vect is an abelian category and \(\textbf{R}\) is a small category. The theory of spectral sequences can be developed for arbitrary abelian categories. For an introduction to this, see [30, Chap. 5].
Consider a filtered simplicial complex, K, together with a cover of K by filtered subcomplexes, \({\mathcal {U}}= \{ U_i\}_{i \in I}\), so that \(K =\bigcup _{i \in I} U_i\). Then, the persistence Mayer–Vietoris spectral sequence is given by
where \(p + q = n\). However, unlike the case of vector spaces, we might have that \(\bigoplus _{p+q=n} E^\infty _{p,q} \ncong \textrm{PH}_n(K)\). All that we know is that \(E^\infty _{p,q} \cong G^p \textrm{PH}_{p+q}(K)\) for all \(p,q \geqslant 0\). In the literature, recovering \(\textrm{PH}_n(K)\) from the terms \(G^p \textrm{PH}_{p+q}(K)\) is known as the extension problem, which we solve in Sect. 5.1. Furthermore, we even obtain more information; as pointed out in [31], the knowledge of which subset \(J \subset I\) detects a feature from \(\textrm{PH}_n(K)\) can potentially add insight into the information given by ordinary persistent homology. The following example illustrates this.
As the radius increases, more edges are added. At radius \(r=0.5\) a circle will be across the two covers U and V. Later on, at radius \(r=0.6\) this circle will be split into two
Example 5.1
Consider the case of a point cloud X covered by two open sets as in Fig. 8. From Sects. 3 and 4, we know how to compute the \(\infty \)-page \((E_{*,*}^\infty )^r\) associated to any value \(r \in \textbf{R}\). In particular, when we take \(r=0.5\), then the combination of U and V detects a 1-cycle. On the other hand, when \(r=0.6\) this cycle splits into two smaller cycles which are detected by U and V individually. Notice that if we want to come up with a persistent Mayer–Vietoris method then we need to be able to track this behaviour. That is, we need to know how cycles develop as r increases. In particular, the barcode from \(\textrm{PH}_1(X)\) is broken down into \(E^\infty _{1,0}\cong \mathbb {F}_{[0.5, 0.6)}\) and also \(E_{0,1}^\infty \cong \mathbb {F}_{[0.6, 1.0)} \hspace{0.55542pt}{\oplus }\hspace{1.111pt}\mathbb {F}_{[0.6, 1.0)}\), see Fig. 9.
Figure 10 illustrates a filtered complex covered by three regions where, as in Example 5.1, there is a nontrivial extension problem.
Barcode on associated module
5.1 The Extension Problem
Recall the definition of the total complex, vertical filtrations and associated modules from Sect. 4. Through this section we study the extension problem, that is, we recover \(\textrm{H}_n({\mathcal {S}}_*^Tot )\) from the associated modules \(G^p ( \textrm{H}_{n}( {\mathcal {S}}_*^Tot ) )\). Also, we assume that the spectral sequence collapses after a finite number of pages. Consider the persistence module
together with the corresponding filtration
We define the associated modules of \((\mathbb {V}, F^*)\) as the quotients \(\mathbb {G}^k = F^k \mathbb {V}/ F^{k-1} \mathbb {V}\) for all \(0 \leqslant k \leqslant n\). This gives rise to short exact sequences,
for all \(0\leqslant k\leqslant n\). On the sequences (9) we consider successive extension problems where we know the first and last term and want to know the middle term for \(0 \leqslant k \leqslant n\). This leads to \(\mathbb {V}\); however, in this work we obtain directly a persistence module isomorphic to \(\mathbb {V}\) (see Proposition 5.2). Adding up all associated modules we obtain a persistence module \(\mathbb {G}\,{:}{=}\, \bigoplus _{i = 0}^n \mathbb {G}^i\) with an additional filtration given by \(F^k\mathbb {G}=\bigoplus _{i=0}^k\mathbb {G}^i\) for all \(0\leqslant k\leqslant n\). Since \(\mathbb {G}^k \cong E^\infty _{k,n-k}\) for all \(0 \leqslant k\leqslant n\), a spectral sequence algorithm leads to a barcode basis for \(\mathbb {G}\). We formulate the extension problem as computing a basis for \(\mathbb {V}\) from the obtained basis \({\mathcal {G}}\) of \(\mathbb {G}\).
A one loop is detected at value \(r\sim 0.208\) which goes through three covers. Later, at radius \(r=0.5\), this loop splits into three loops, each included in one of the three covers
To start, notice that for each \(r \in \textbf{R}\) the sequence (9) splits, leading to morphisms
such that \(p^k(r)\circ {\mathcal {F}}^k(r) = \textrm{Id}_{\mathbb {G}^k(r)}\) for all \(0\leqslant k \leqslant n\). In particular, \({\mathcal {F}}^k(r)\) is injective for all \(0 \leqslant k \leqslant n\). On the other hand, for any class \([\beta _k]^\infty _{k,n-k}\) of \(E^\infty _{k,n-k}(r)\) with representative \(\beta _k \in E^0_{k,n-k}(r)\), since \(\beta _k \in \textrm{GK}_{k,n-k}(r)\), we have that \(d(\beta _k) = 0\) and there exists a sequence of \(\beta _i \in {\mathcal {S}}_{i,n-i}(r)\) such that \(d(\beta _{i}) = -\bar{\delta }(\beta _{i+1})\) for all \(0 \leqslant i < k\). The choice of this sequence determines \({\mathcal {F}}^k(r)\), so that
where \([\,{\cdot }\,]^Tot _{n}\) denotes the n-homology class of the total complex. Notice that if we already computed \({\mathcal {G}}\) from the Mayer–Vietoris spectral sequence, then there is no need to do any extra computations to obtain these morphisms \({\mathcal {F}}^k(r)\). All we need to do is to store our previous results. Adding over all \(0 \leqslant k \leqslant n\) we obtain the isomorphism \({\mathcal {F}}(r) = \bigoplus _{k=0}^n {\mathcal {F}}^k(r) :\bigoplus _{k=0}^n \mathbb {G}^k(r) \rightarrow \mathbb {V}(r)\). This last morphism is an isomorphism since all its summands are injective, their images have mutual trivial intersection, and the dimensions of the domain and codomain coincide.
Recall that \(\mathbb {G}\) has induced morphisms \(\mathbb {G}\hspace{0.33325pt}(r \,{\leqslant }\, s)\) from \(\mathbb {V}\hspace{0.33325pt}(r \,{\leqslant }\, s)\) for all values \(r \leqslant s\) in \(\textbf{R}\). Given a basis \({\mathcal {G}}\) for \(\mathbb {G}\), we would like to compute a basis \({\mathcal {B}}\) for \(\mathbb {V}\) from this information. Notice that this is not a straightforward problem since (10) does not imply that one has an isomorphism \({\mathcal {F}}:\mathbb {G}\rightarrow \mathbb {V}\). A point to start is to define the image along each generator in \({\mathcal {G}}\). That is, for each barcode generator \(g_i \hspace{-0.55542pt}\sim [a_i, b_i)\) in \({\mathcal {G}}\), we choose an image at the start \({\mathcal {F}}(a_i)(g_i(a_i))\). Then, we set \({\mathcal {F}}(r)(g_i(r))\,{:}{=}\,\mathbb {V}\hspace{0.33325pt}(a_i\,{<}\,r)\circ {\mathcal {F}}(a_i)(g_i(a_i))\) for all \(a_i<r<b_i\). This leads to commutativity of \({\mathcal {F}}\) along each generator \(g_i\). Nevertheless this is still far from even defining a morphism \({\mathcal {F}}:\mathbb {G}\rightarrow \mathbb {V}\).
The solution to the problem above is to define a new persistence module \(\widetilde{\mathbb {G}}\). We define \(\widetilde{\mathbb {G}}(s) \,{:}{=}\, \mathbb {G}(s)\) for all \(s \in \textbf{R}\). Then, if \({\mathcal {G}}= \{g_i\}_{i=1}^{\vert {\mathcal {G}}\vert }\) is a barcode basis for \(\mathbb {G}\), by Proposition 3.2, \({\mathcal {G}}^s(1_\mathbb {F})\) will be a basis of \(\widetilde{\mathbb {G}}(s)\) for all \(s \in \textbf{R}\). Now, given \(g_i\hspace{-0.55542pt}\sim [a_i, b_i)\) a generator in \({\mathcal {G}}\), we define the morphism \(\widetilde{\mathbb {G}}\hspace{0.33325pt}(r \,{\leqslant }\, s)\) by the recursive formula
where \(c_{i,j} \in \mathbb {F}\) for all \(1 \leqslant i,j \leqslant \vert {\mathcal {G}}\vert \). We want to define \(c_{i,j}\) in such a way that \(\widetilde{\mathbb {G}}\) is isomorphic to \(\mathbb {V}\). For this we impose the commutativity condition
which leads to the equation
This determines uniquely the coefficients \(c_{i,j}\) for all \(1 \leqslant i,j \leqslant \vert {\mathcal {G}}\vert \). Notice that \(\widetilde{\mathbb {G}}\) respects the filtration on \(\mathbb {V}\), since the right hand side in (11) is a composition of filtration preserving morphisms. In particular, if \(g_i\in {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(F^k\widetilde{\mathbb {G}})\), then \(c_{i,j} = 0\) for all \(1 \leqslant j \leqslant \vert {\mathcal {G}}\vert \) such that \(g_j \notin {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(F^k\mathbb {G})\).
Fix a generator \(g_i \in {\mathcal {G}}\) such that \(g_i \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {G}^k)\) and such that \(g_i\hspace{-0.55542pt}\sim [a_i, b_i)\). Let us calculate the coefficients \(c_{i,j}\). Suppose that we have a representative \(\widetilde{g}_j = (\beta _0^j, \beta _1^j, \ldots , \beta _k^j, 0, \ldots , 0) \in {\mathcal {S}}^Tot _n\) for each generator \(g_j\in {\mathcal {G}}\), with \(g_j = [ \beta ^j_k ]^\infty _{k, n-k}\). Also, for all \(0 \leqslant q \leqslant n\) we define the subset \(I^q\subseteq \{1,\ldots , \vert {\mathcal {G}}\vert \}\) of indices \(1 \leqslant j \leqslant \vert {\mathcal {G}}\vert \) such that \(g_j \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {G}^q)\). Then, the coefficients \(c_{i,j}\) for \(j\in I^k \setminus \{i\}\) are determined by the following equality in \(\mathbb {G}^k(b_i)\) (where we use \(p^k\) from the sequence (9))
Thus, we have
Hence, by (9), there must exist some chain \(\varGamma \in {\mathcal {S}}_{n+1}^Tot (b_i)\) such that
is contained in \(F^{k-1} {\mathcal {S}}_n^Tot (b_i)\). How do we compute \(\varGamma \)? We start by searching for the first page \(r \geqslant 2\) such that
where \([\,{\cdot }\,]^r_{k,n-k}\) denotes the class in the r-page in position \((k, n-k)\). Notice that this r must exist since we assumed that (13) vanishes at the \(\infty \)-page. Consequently, there exists \(\varGamma _{k + r-1} \in E_{k+r-1,n-k-r+2}^{r-1}(b_i)\) such that
on \(E^{r-1}_{k,n-k}(b_i)\). Repeating for all pages leads to \(\varGamma _{k + t} \in E_{k+t, n - k - t + 1}^t(b_i)\) for all \( 0 \leqslant t \leqslant r-1\), such that
where \(\widetilde{d^{t}(\varGamma _{k + t})} \in {\mathcal {S}}_{k, n-k}(b_i)\) is a representative for the class \(d^{t}(\varGamma _{k+t})\in E^t_{k,n-k}(b_i)\). Notice that (14) holds independently of the representatives, since if we changed some term, then the other representatives would adjust to the change. In particular, we have that the k component of (12) vanishes, whereas the \(k-1\) component will be equal to
Next we proceed to find coefficients \(c_{i,j} \in \mathbb {F}\) so that in \(\mathbb {G}^{k-1}(b_i)\) we get the equality
Then we proceed as we did on \(\mathbb {G}^k\). Doing this for all parameters \(0 \leqslant r \leqslant k\), there are coefficients \(c_{i,j} \in \mathbb {F}\), and an element \(\widetilde{\varGamma } \in {\mathcal {S}}_{n+1}^Tot (b_i)\) so that
Thus, recalling that \(c_{i,j}=0\) for all \(g_j \notin {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(F^k\mathbb {G})\), we have
Proposition 1.31
\(\widetilde{\mathbb {G}} \cong \mathbb {V}\).
Proof
Since each \({\mathcal {F}}(s)\) is an isomorphism, and also we have commutative squares:
for all \(r \leqslant s\), then \({\mathcal {F}}\) must be an isomorphism of persistence modules. \(\square \)
This gives \(\widetilde{\mathbb {G}} \cong \mathbb {V}\), but we still need to compute a barcode basis. In fact, this can be done by considering a quotient. Define \(\mathbb {A}\simeq \bigoplus _{g_i \in {\mathcal {G}}} \mathbb {F}_{[a_i, \infty )}\) where \(g_i\hspace{-0.55542pt}\sim [a_i,b_i)\) for all \(g_i \in {\mathcal {G}}\); here the \({\mathcal {A}}=\{\alpha _i\}_{1\leqslant i\leqslant \vert {\mathcal {G}}\vert }\) denotes the canonical base for \(\mathbb {A}\). Consider the coefficients \(c_{i,j}\) for \(1 \leqslant i, j \leqslant \vert {\mathcal {G}}\vert \) from the construction of \(\widetilde{\mathbb {G}}\) and define the sets of indices \({\mathcal {S}}_i = \{1 \leqslant j \leqslant \vert {\mathcal {G}}\vert : c_{i,j} \ne 0\}\) for all \(1\leqslant i \leqslant \vert {\mathcal {G}}\vert \). We consider a submodule \(\mathbb {B}\subseteq \mathbb {A}\) such that \({{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(\mathbb {B})\) is generated by
Also, notice that \(\mathbb {B}\simeq \bigoplus _{1\leqslant i\leqslant \vert {\mathcal {G}}\vert } \mathbb {F}_{[b_i, \infty )}\) and that, by construction, \(\widetilde{\mathbb {G}} \simeq \mathbb {A}/ \mathbb {B}\). Now, we pick up the canonical base for \(\mathbb {B}\) and consider the inclusion \(\iota {:}\mathbb {B}{\hookrightarrow } \mathbb {A}\); this will lead to an associated matrix \((\iota ({\mathcal {B}}))_{\mathcal {A}}\). Thus, we send \((({\mathcal {B}}\,{\vert }\,{\mathcal {A}}), {\mathcal {A}}, ((\iota ({\mathcal {B}}))_{\mathcal {A}}\,{\vert }\, \textrm{Id}_{\vert {\mathcal {A}}\vert }))\) to box_gauss_reduce and obtain a basis for the quotient \(\mathbb {A}/\mathbb {B}\); i.e., a basis for \(\widetilde{\mathbb {G}}\).
5.2 PerMaViss
Here we outline a procedure for implementing the persistence Mayer–Vietoris spectral sequence. In Sect. 5.1 we worked with \(\textrm{GZ}^r_{p,q}\) and \(\textrm{IB}^r_{p,q}\), which is very intuitive from a mathematical perspective. However, it is more efficient to work directly with the sets \(Z^r_{p,q}\) and \(B^r_{p,q}\). By storing representatives in \(Z^r_{p,q}\), we avoid repeating computations on each page and in the extension problem. Furthermore, this approach allows to easily track the complexity of the algorithm. For compactness, we work with barcode bases through this section. Before we study the algorithm, we make some notational remarks. Given a spectral sequence term \(E^r_{p,q}\), we denote by \({\mathcal {E}}^r_{p,q}\) its barcode basis. Additionally, for a generator \(\alpha \in {\mathcal {E}}^r_{p,q}\), we denote by \(\widetilde{\alpha }\) its representative in \({\mathcal {S}}^Tot _{p+q}\) and, if \(r>0\), by \(\overline{\alpha }\) its representative in \(E^{r-1}_{p,q}\). Also, we denote by \([\,{ \cdot }\,]^r_{p,q}\) a class in \(E^r_{p,q}\). Thus, given \(\alpha \in {\mathcal {E}}^r_{p,q}\) we have that \(\alpha = [\overline{\alpha }]^r_{p,q} = [\widetilde{\alpha }]^r_{p,q}\).
0-Page We start by defining the 0-page as the quotient
for all pairs of integers \(p,q \geqslant 0\). The 0 differential, \(d^0\), is isomorphic to the standard chain differential
In particular, for each simplex \(\sigma \in N^{\mathcal {U}}_q\), the morphism \(d^0_{p,q}\) restricts to a local differential
Thus, we can compute a basis, \({\mathcal {E}}^1_{\sigma , q}\), for the persistent homology \(\textrm{PH}_q(U_\sigma )\) as well as a basis for the image \(\textrm{Im}\hspace{0.55542pt}(d^\sigma _{q+1})\). Putting all of these together, we get a basis for \(E^1_{p,q}\) as the union \({\mathcal {E}}^1_{p,q} = \bigcup _{\sigma \in N_p^{\mathcal {U}}} {\mathcal {E}}^1_{\sigma , q}\). Further, for each generator \(\alpha \in {\mathcal {E}}^1_{p,q}\subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^1_{p,q})\), we store a chain \(\alpha _p \in {\mathcal {S}}_{p,q}\) so that \(\alpha = [(0, \ldots , 0, \alpha _p, 0, \ldots , 0)]^1_{p, q}\). We define \(\widetilde{{\mathcal {E}}}^1_{p,q}\) to be the set of representatives in \({\mathcal {S}}^Tot _{p+q}\) given by \((0, \ldots , 0, \alpha _0, 0, \ldots , 0)\).
1-Page Recall that the first page elements are given as classes in the quotient
Therefore, for each generator \(\alpha \in {\mathcal {E}}^1_{p,q}\), with \(\alpha \sim [a_\alpha , b_\alpha )\), there is a chain \(\alpha _p \in {\mathcal {S}}_{p,q}\), so that \(\alpha = [(0,\ldots , 0,\alpha _p, 0, \ldots ,0)]^0_{p,q}\). Then we compute
Now, for each simplex \(\tau \in N^{\mathcal {U}}_{p-1}\), we consider the local chain \((\bar{\delta }_p(\alpha _p) )_\tau \in S_q(U_\tau )\) and proceed to compute a subset \({\mathcal {J}}_{\tau ,q}^1\subseteq ({\mathcal {E}}^1_{\tau ,q})^{a_\alpha }\) together with \(c^1_{\beta } \in \mathbb {F}\) for all \(\beta \in {\mathcal {J}}_{\tau ,q}^1\) and an element \(\varGamma _{\tau } \in {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(S_{q+1}(U_\tau ))\) such that
where recall that \(\overline{\beta }\) denotes a representative in \(S_q(U_\tau )\subseteq E^0_{p-1,q}\). This computation can be performed by using Algorithm 1. That is, we consider \(({\mathcal {E}}^1_{\tau ,q})^{a_\alpha }\) and a basis for \(\textrm{Im}\hspace{0.55542pt}((d_{q+1})_\tau )\) and write \((\bar{\delta }_p(\alpha _p))_\tau \) in terms of these; the preimages lead to \(\varGamma _\tau \). Repeating this for all \(\tau \in N^{\mathcal {U}}_{p-1}\), we get a subset \({\mathcal {J}}_{p-1,q}^1\subseteq ({\mathcal {E}}^1_{p-1,q})^{a_\alpha }\) together with coefficients \(c^1_{\beta } \in \mathbb {F}{\setminus }\{0\}\) for all \(\beta \in {\mathcal {J}}_{p-1,q}^1\) and an element \(\varGamma _{p-1}\in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^0_{p-1, q+1})\) so that
This leads to
. Repeating this procedure for all generators
\(\alpha \in {\mathcal {E}}^1_{p,q}\) leads to an associated matrix
\(D^1_{p,q}\) for
\(d^1_{p,q}\). Using image_kernel, we compute bases for the kernel and image, together with the corresponding preimages. Next, we compute a base
\({\mathcal {E}}^2_{p,q}\) for the second page term
\(E^2_{p,q}\) by applying box_gauss_reduce to compute the quotient
\(\textrm{Ker}\hspace{0.55542pt}(d^1_{p, q})/ \textrm{Im}\hspace{0.55542pt}(d^1_{p+1, q})\). This also leads to first page representatives
\(\overline{\alpha } \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^1_{p,q})\) for all \(\alpha \in {\mathcal {E}}^2_{p,q}\). Finally, for each generator \(\alpha \in {\mathcal {E}}^2_{p,q}\), we proceed to find a good representative by using \(\widetilde{{\mathcal {E}}}^1_{p,q}\) together with the computed coordinates of \(\alpha \) in terms of \({\mathcal {E}}^1_{p,q}\). This leads to \(\widetilde{\alpha } = (0, \ldots , 0, \alpha _p, 0, \ldots , 0) \in {\mathcal {S}}^Tot _{p+q}\), so that \(\alpha = [\widetilde{\alpha }]^2_{p,q}\). Since by hypotheses \([\widetilde{\alpha }]^1_{p,q} \in \textrm{Ker}\hspace{0.55542pt}(d^1_{p,q})\), we might find \(\alpha _{p-1} \in E^0_{p-1, q+1}\) such that \(d^0_{p-1, q} (\alpha _{p-1}) = -\overline{\delta }(\alpha _p)\). Altogether, we set \(\widetilde{\alpha } \leftarrow (0, \ldots , 0, \alpha _{p-1}, \alpha _p, 0, \ldots , 0)\) and store it in \(\widetilde{{\mathcal {E}}}^2_{p,q}\); notice that \(d^Tot (\widetilde{\alpha }) \in F^{p-2}{\mathcal {S}}^Tot \).
k-Page Suppose that we have computed generators \({\mathcal {E}}^k_{p,q} \subseteq {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^{k-1}_{p,q})\), together with total complex representatives \(\widetilde{{\mathcal {E}}}^{k}_{p,q}\) for some \(k \geqslant 3\). Assume also that \(d^Tot (\widetilde{\alpha })\in F^{p-k}({\mathcal {S}}^Tot )\) for all \(\widetilde{\alpha } \in \widetilde{{\mathcal {E}}}^{k}_{p,q}\). Notice that if \(k\geqslant p+1\), then \(d^k_{p,q} = 0\). Thus, we focus on the case that \(k < p+1\). Let \(\alpha \in {\mathcal {E}}^k_{p,q}\) with \(\alpha \sim [a_\alpha , b_\alpha )\) together with a representative \(\widetilde{\alpha } \in \widetilde{{\mathcal {E}}}^{k}_{p,q}\) with \(\widetilde{\alpha }=(0,\ldots , 0, \alpha _{p-k+1}, \ldots , \alpha _p, 0, \ldots , 0)\) so that
We proceed by ‘lifting’ \(d^Tot (\widetilde{\alpha })\) to the k-page. As before, using Algorithm 1 in parallel, we obtain a subset \({\mathcal {J}}^1_{p-k,q+k-1} \subseteq {\mathcal {E}}^1_{p-k,q+k-1}\) together with coefficients \(c^1_\beta \in \mathbb {F}{\setminus } \{ 0 \}\) for all \(\beta \in {\mathcal {T}}^1_{p-k,q+k-1} \subseteq {\mathcal {S}}^Tot _{p+q-1}\) giving us an expression in terms of the first page basis
. Next, using Algorithm 1, we compute a subset
\({\mathcal {J}}^{r}_{p-k,q+k-1}\subseteq ({\mathcal {E}}^{r}_{p-k,q+k-1})^{a_\alpha }\) together with coefficients
\(c_\beta ^{r}\in \mathbb {F}{\setminus } \{0\}\) for all
\(\beta \in {\mathcal {J}}^{r}_{p-k, q+k-1}\), and
\(\varGamma _{p-k+r-1} \in {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(E^{r-1}_{p-k+r-1, q+k-r+1})\) such that
Thus, we deduce an expression of
\([ d^Tot \widetilde{\alpha }]^r_{p-k, q+k-1}\) in terms of
\({\mathcal {E}}^r_{p-k,q+k-1}\). In particular, this holds for
\(r=k\), which leads to the associated matrix of
\(d^k_{p,q}\), and then we can compute image_kernel to obtain bases for images and kernels of
\(d^k_{p,q}\). Also, using box_gauss_reduce we obtain basis,
\({\mathcal {E}}^{k+1}_{p,q}\), for the terms \(E^{k+1}_{p,q}\). As a byproduct of this computation, for each \(\alpha \in {\mathcal {E}}^{k+1}_{p,q}\) we obtain a previous page representative \(\overline{\alpha } \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^k_{p,q})\), so that \([\overline{\alpha }]^{k+1}_{p,q} = \alpha \). Now, consider \(\alpha \in {\mathcal {E}}^{k+1}_{p,q}\) with \(\alpha \sim [a_\kappa , b_\kappa )\) and proceed to obtain a ‘good’ total complex representative. There exists \({\mathcal {T}}(\alpha ) \subseteq {\mathcal {E}}^{k}_{p,q}\) together with coefficients \(c_\beta ^\alpha \) for all \(\beta \in {\mathcal {T}}(\alpha )\) such that 
. Then we define 
, and notice that \(\alpha = [\widetilde{\alpha }]^{k+1}_{p,q}\) as well as \(d^Tot (\widetilde{\alpha })\in F^{p-k}({\mathcal {S}}^Tot )\). We denote \(\widetilde{\alpha }=(0, \ldots , 0,\alpha _{p-k+1}, \ldots , \alpha _p, 0, \ldots , 0)\). Now, by hypotheses
Then, there exist \(\gamma _{p-1} \in {{\,\mathrm{PVect\hspace{0.33325pt}}\,}}(E^{k-1}_{p-1,q+1})\) with
By writing \(\gamma _{p-1}\) in terms of \({\mathcal {E}}^{k-1}_{p-1,q+1}\) and using their stored representatives, we may get \(\widetilde{\gamma }_{p-1}\in {\mathcal {S}}^Tot _{p+q}\) such that \(\gamma _{p-1} = [\widetilde{\gamma }_{p-1}]^{k-1}\) and also \(d^Tot (\widetilde{\gamma }_{p-1})\in F^{p-k}{\mathcal {S}}^Tot _{p+q-1}\). In particular,
and we set \(\widetilde{\alpha } \leftarrow \widetilde{\alpha } \hspace{1.33331pt}{\boxplus }\hspace{1.33331pt}( - \widetilde{\gamma }_{k-1})\). Hence, by induction, we can repeat this procedure for all \(1\leqslant r \leqslant k\). Eventually, we should obtain a representative \(\widetilde{\alpha }= (0,\ldots , 0, \alpha _{p-k}, \ldots , \alpha _p, 0, \ldots , 0)\) such that \(d^Tot (\widetilde{\alpha }) \in F^{p-k-1}{\mathcal {S}}^Tot _{p+q-1}\). We denote the new set of representatives as \(\widetilde{{\mathcal {E}}}^{k+1}_{p,q}\).
5.3 Extension Problem
After computing all pages of the spectral sequence, we still have to solve the extension problem. Recall that a solution was given in Sect. 5.1; here we only give some algorithmic guidelines. We start from a basis \({\mathcal {E}}^\infty _{p,q}\), with total complex representatives \(\widetilde{{\mathcal {E}}}^\infty _{p,q}\). Since we assume that the spectral sequence is bounded, it collapses at an \(L>0\) page. Then, for each generator \(\alpha \in {\mathcal {E}}^L_{p,q}\), with \(\alpha \sim [a_\alpha , b_\alpha )\), we have a corresponding representative \(\widetilde{\alpha } \in \widetilde{{\mathcal {E}}}^L_{p,q}\). Consider \(\widetilde{\gamma } \leftarrow \textbf{1}_{b_\alpha }(\widetilde{\alpha })\); we perform changes to \(\widetilde{\gamma }\) similarly as in Sect. 5.1. We start by computing the classes \([\widetilde{\gamma }]^r_{p,q}\) for all \(1 \leqslant r \leqslant L\). We do this by using Algorithm 1 in parallel, as done on the 1-page. This leads to a subset \({\mathcal {J}}^1_{p,q} \subseteq ({\mathcal {E}}^1_{p,q})^{b_\alpha }\) together with coefficients \(c^1_\beta \in \mathbb {F}{\setminus }\{0\}\) for all \(\beta \in {\mathcal {J}}^1_{p,q}\) and \(\varGamma _p \in {\mathcal {S}}_{p, q+1}\), so that
. The same happens for all pages
\(2 \leqslant r \leqslant L\); we find
\({\mathcal {J}}^r_{p,q} \subseteq ({\mathcal {E}}^r_{p,q})^{b_\alpha }\) together with coefficients
\(c^r_\beta \in \mathbb {F}{\setminus }\{0\}\) for all
\(\beta \in {\mathcal {J}}^r_{p,q}\) and
\(\varGamma _{p+r -1} \in {{\,\mathrm{PVect\hspace{0.83328pt}}\,}}(E^{r-1}_{p+r-1, q-r+2})\), so that
Now, we change the total complex representative by an assignment
In particular, notice that \([\widetilde{\gamma }]^L_{p, q} = 0\). We might repeat this procedure for all integers \(L-1 \geqslant r \geqslant 0\) so that one has that \([\widetilde{\gamma }]^r_{p, q} =0\). As a consequence the p-component of \(\widetilde{\gamma }\) vanishes, so \(\widetilde{\gamma } \in F^{p-1}{\mathcal {S}}^Tot _{p+q}\). Then, as in Sect. 5.1, one can repeat this process for all \(p-1 \geqslant r \geqslant 0\). This leads to all coefficients \((c^L_\beta )_{\beta \in {\mathcal {E}}^L_{p - r, q + r}}\) for all \(0 \leqslant r \leqslant p\). These can be used to define a basis for the submodule \(\mathbb {B}\) from end of Sect. 5.1; this solves the extension problem by computing the corresponding quotient.
5.4 Complexity Analysis
Let \(D_s\) be the maximum simplex dimension in K, and let L be the number of pages. Denote by \(\textrm{dim}\hspace{0.33325pt}(N^{\mathcal {U}})\) the dimension of the nerve. Let
On the other hand, we define
Assume P is the number of processors.
0-Page When computing the first page, all we need to do is calculate persistent homology in parallel. Then, the complexity is
This leads to generators for the first page.
1-Page For the first page, recall that we start from a generator \(\alpha \in {\mathcal {E}}^1_{p,q}\) with \(\alpha \sim [a_\alpha , b_\alpha )\) and proceed to solve \(\vert N^{\mathcal {U}}_{p-1}\vert \) linear equations. Notice that this can be done for all generators from \({\mathcal {E}}^1_{p,q}\) simultaneously. This is because as the value \(a_\alpha \) changes, we might select the columns associated to \(({\mathcal {E}}^1_{p,q})^{a_\alpha }\) from the columns of \({\mathcal {E}}^1_{p,q}\) which does not affect the complexity of Algorithm 1. On the other hand, we need to execute image_kernel on at most \(\textrm{dim}\hspace{0.33325pt}(N^{\mathcal {U}})\cdot D_s\) elements on the first page. Notice that for each of these, we first compute a basis for the images and kernels. Afterwards, we perform the quotients using box_gauss_reduce which takes a complexity of at most \({\mathcal {O}}(H^3)\). Also, we need to add the complexity of the Čech differential. An option for computing this, is to compare simplices in different covers by their vertices; two simplices are the same iff they share the same vertex set. This would take less than \({\mathcal {O}}\hspace{0.33325pt}(\vert N^{\mathcal {U}}\vert \hspace{0.55542pt}D_sX^2H)\) operations. Thus the overall complexity becomes
k-Page Now, we proceed for the complexity of the page \(k \geqslant 2\). This is the same as for the 1 page, with the addition of Gaussian eliminations of higher pages. These take at most \({\mathcal {O}}(H^3)\) time. Denoting by L the infinity page, we have the new term
which added to the complexity of the 1-page gives
Extension problem If the spectral sequence collapses at \(L>0\), then the complexity of extending all generators in \({\mathcal {E}}^L_{p,q}\) is bounded by that of computing the L page about \(D_s\) times.
Overall complexity Altogether, we have a complexity bounded by that of computing the first page plus that of computing the L page \(L+D_s\) times. Here the L comes from computing the L page L times and \(D_s\) from the extension problem. Thus, the overall complexity is bounded by
Notice that in general \(D_s,L\) and \(\textrm{dim}\hspace{0.33325pt}(N^{\mathcal {U}})\) are much smaller than H and X. Thus, for covers such that \(\vert N^{\mathcal {U}}\vert \ll X\), and assuming we have enough processors, the complexity can be simplified to the two dominating terms \({\mathcal {O}}(X^3) + {\mathcal {O}}(H^3)\). Notice that this last case is satisfied for those covers whose mutual intersections are generally smaller than each cover. Also, in this case H is approximately of the order of nontrivial barcodes over all the input complex. This shows that PerMaViss isolates simplicial data, while only merging homological information. It is worth to notice that in general H, being the number of nontrivial bars, is much smaller than the size of the whole simplicial complex.
6 Conclusion
We started by developing linear algebra for persistence modules. In doing so, we introduced bases of persistence modules, as well as associated matrices to morphisms. Also, we presented Algorithm 2, which computes bases for the image and the kernel of a persistence morphism between any pair of tame persistence modules. Then a generalization of traditional persistent homology was introduced in Sect. 3.5. This theory has helped us to define and understand the Persistent Mayer–Vietoris spectral sequence. Furthermore, we have provided specific guidelines for a distributed algorithm, with a solution to the extension problem presented in Sect. 5.1. The PerMaViss method presented in Sect. 5.2 isolates simplicial information to local matrices, while merging only homological information between different covers. Thus, the complexity of this method is dominated by the size of a local complex plus the order of barcodes over all the data. A first implementation of these results can be found in [29]. Coding an efficient implementation from the pseudo-code given in this paper, and benchmarking its performance compared to other methods, will be a matter of future research. Another interesting direction of research is how to merge this method with existing algorithms, such as those from [7, 8, 21, 26]. Especially it would be interesting to explore the possible interactions of discrete Morse theory and this approach, see [11]. Additionally, it will be worth exploring, both theoretically and practically, which are the most suitable covers for different applications. Finally, we would also like to study the additional information given by the covering. This will add locality information from persistent homology.
Data availability
There is no data associated to this article.
Notes
Notice that in a filtration indexed by integers where we introduce a simplex at a time there are no trivial bars and the number of these is about \((\#\,\text {simplices})/2\). Here we are referring to the case where the filtration is over the real numbers; where many simplices are introduced at the same time. In this case the number of nontrivial persistent homology bars should be much smaller than the number of simplices.
Here we use the Numpy notation for matrices, where for a matrix M, the (i, j)-entry is denoted by \(\texttt {M[i,j]}\) and the jth column is denoted by \(\texttt {M[:,j]}\). Also, we use indexing starting at 1 instead of 0 to be consistent with the rest of the article. In addition, we make use of the pop() function, which simultaneously returns and deletes the last element from a list.
References
Adams, H., Emerson, T., Kirby, M., Neville, R., Peterson, C., Shipman, P., Chepushtanova, S., Han-son, E., Motta, F., Ziegelmeier, L.: Persistence images: a stable vector representation of persistent homology. J. Mach. Learn. Res. 18, # 8 (2017)
Bauer, U., Kerber, M., Reininghaus, J.: Clear and compress: computing persistent homology in chunks. In: Topological Methods in Data Analysis and Visualization III (Davis 2013), pp. 103–117. Springer, Berlin (2014)
Bott, R., Tu, L.W.: Differential Forms in Algebraic Topology. Graduate Texts in Mathematics, vol. 82. Springer, New York (1982)
Bredon, G.E.: Sheaf Theory. Graduate Texts in Mathematics, vol. 170. Springer, New York (1997)
Carlsson, G.: Topology and data. Bull. Am. Math. Soc. 46(2), 255–308 (2009)
Chazal, F., de Silva, V., Glisse, M., Oudot, S.: The Structure and Stability of Persistence Modules. SpringerBriefs in Mathematics. Springer, Cham (2016)
Chen, C., Kerber, M.: Persistent homology computation with a twist. In: 27th European Workshop on Computational Geometry (Morschach 2011), pp. 197–200 (2011). https://eurocg11.inf.ethz.ch/docs/Booklet.pdf
Chen, C., Kerber, M.: An output-sensitive algorithm for persistent homology. Comput. Geom. 46(4), 435–447 (2013)
Chow, T.Y.: You could have invented spectral sequences. Not. Am. Math. Soc. 53(1), 15–19 (2006)
Cohen-Steiner, D., Edelsbrunner, H., Harer, J., Morozov, D.: Persistent homology for kernels, images, and cokernels. In: 20th Annual ACM-SIAM Symposium on Discrete Algorithms (New York 2009), pp. 1011–1020. SIAM, Philadelphia (2009)
Curry, J., Ghrist, R., Nanda, V.: Discrete Morse theory for computing cellular sheaf cohomology. Found. Comput. Math. 16(4), 875–897 (2016)
Delfinado, C.J.A., Edelsbrunner, H.: An incremental algorithm for Betti numbers of simplicial complexes on the \(3\)-sphere. Comput. Aided Geom. Des. 12(7), 771–784 (1995)
Di Fabio, B., Landi, C.: Persistent homology and partial similarity of shapes. Pattern Recognit. Lett. 33(11), 1445–1450 (2012)
Edelsbrunner, H., Harer, J.L.: Computational Topology: An Introduction. American Mathematical Society, Providence (2010)
Edelsbrunner, H., Letscher, D., Zomorodian, A.: Topological persistence and simplification. Discrete Comput. Geom. 28(4), 511–533 (2002)
Ghrist, R.: Elementary Applied Topology. Createspace (2014)
Govc, D., Skraba, P.: An approximate nerve theorem. Found. Comput. Math. 18(5), 1245–1297 (2018)
Lewis, R., Morozov, D.: Parallel computation of persistent homology using the blowup complex. In: 27th ACM Symposium on Parallelism in Algorithms and Architectures (Portland 2015), pp. 323–331. ACM, New York (2015)
Lipsky, D., Skraba, P., Vejdemo-Johansson, M.: A spectral sequence for parallelized persistence (2011). arXiv:1112.1245
McCleary, J.: A User’s Guide to Spectral Sequences. Cambridge Studies in Advanced Mathematics, vol. 58. Cambridge University Press, Cambridge (2001)
Milosavljević, N., Morozov, D., Škraba, P.: Zigzag persistent homology in matrix multiplication time. In: 27th Annual Symposium on Computational Geometry (Paris 2011), pp. 216–225. ACM, New York (2011)
Munkres, J.R.: Elements of Algebraic Topology. Addison-Wesley, San Francisco (2018)
Robins, V., Turner, K.: Principal component analysis of persistent homology rank functions with case studies of spatial point patterns, sphere packing and colloids. Physica D 334, 99–117 (2016)
Robinson, M.: Topological Signal Processing. Mathematical Engineering. Springer, Heidelberg (2014)
de Silva, V., Ghrist, R.: Coverage in sensor networks via persistent homology. Algebr. Geom. Topol. 7(1), 339–358 (2007)
de Silva, V., Morozov, D., Vejdemo-Johansson, M.: Dualities in persistent (co)homology. Inverse Probl. 27(12), # 124003 (2011)
Singh, G., Mémoli, F., Carlsson, G.: Topological methods for the analysis of high dimensional data sets and 3D object recognition. In: Eurographics Symposium on Point-Based Graphics (Prague 2007), pp. 91–100. Eurographics Association (2007)
Skraba, P., Vejdemo-Johansson, M.: Persistence modules: algebra and algorithms (2013). arXiv:1302.2015
Torras Casas, Á.: PerMaViss: persistence Mayer Vietoris spectral sequence (2020). https://doi.org/10.5281/zenodo.3613870
Weibel, C.A.: An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics, vol. 38. Cambridge University Press, Cambridge (1994)
Yoon, H.R.: Cellular Sheaves and Cosheaves for Distributed Topological Data Analysis. PhD thesis, University of Pennsylvania (2018). https://repository.upenn.edu/edissertations/2936
Yoon, H.R., Ghrist, R.: Persistence by parts: multiscale feature detection via distributed persistent homology (2020). arXiv:2001.01623
Zomorodian, A., Carlsson, G.: Localized homology. Comput. Geom. 41(3), 126–148 (2008)
Acknowledgements
The author would like to thank his supervisor Dr. Ulrich Pennig who suggested this topic and has been very helpful and supportive in the development of these ideas. Also, the author would like to express his gratitude to EPSRC for the Grant EP/N509449/1 support with Project Number 1941653, without which the author would not have been able to write this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor in Charge: Kenneth Clarkson
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Torras-Casas, Á. Distributing Persistent Homology via Spectral Sequences. Discrete Comput Geom 70, 580–619 (2023). https://doi.org/10.1007/s00454-023-00549-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00454-023-00549-2